Geochemical Assessment of Long-Term CO2 Storage from Core- to Field-Scale Models
Abstract
1. Introduction
2. Materials and Methods
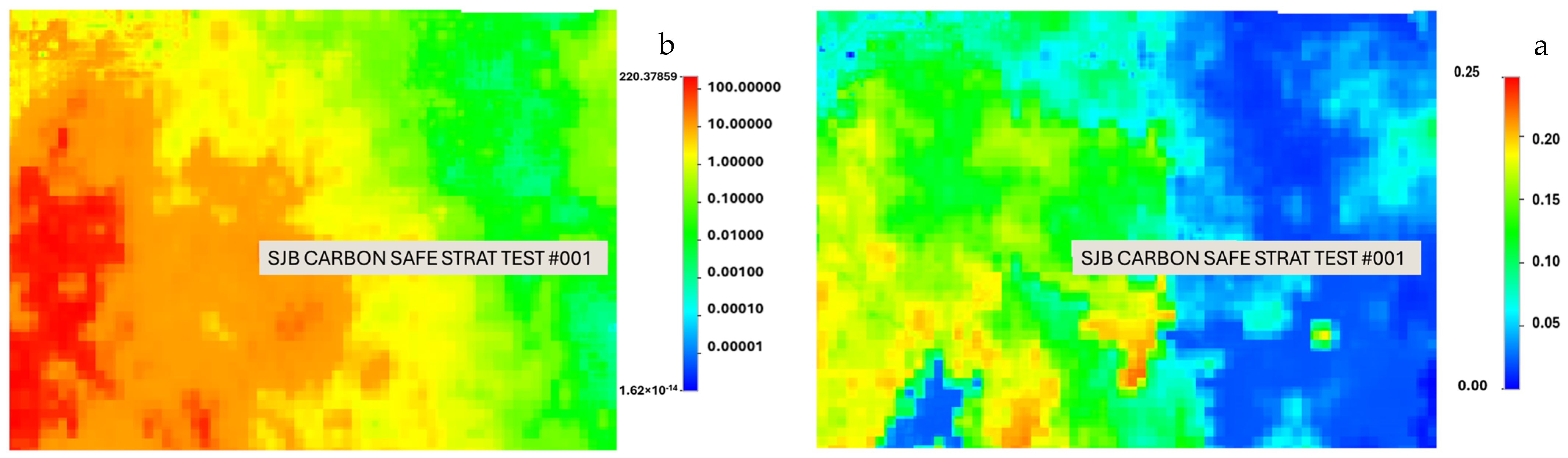
2.1. Study Area and Geological Model
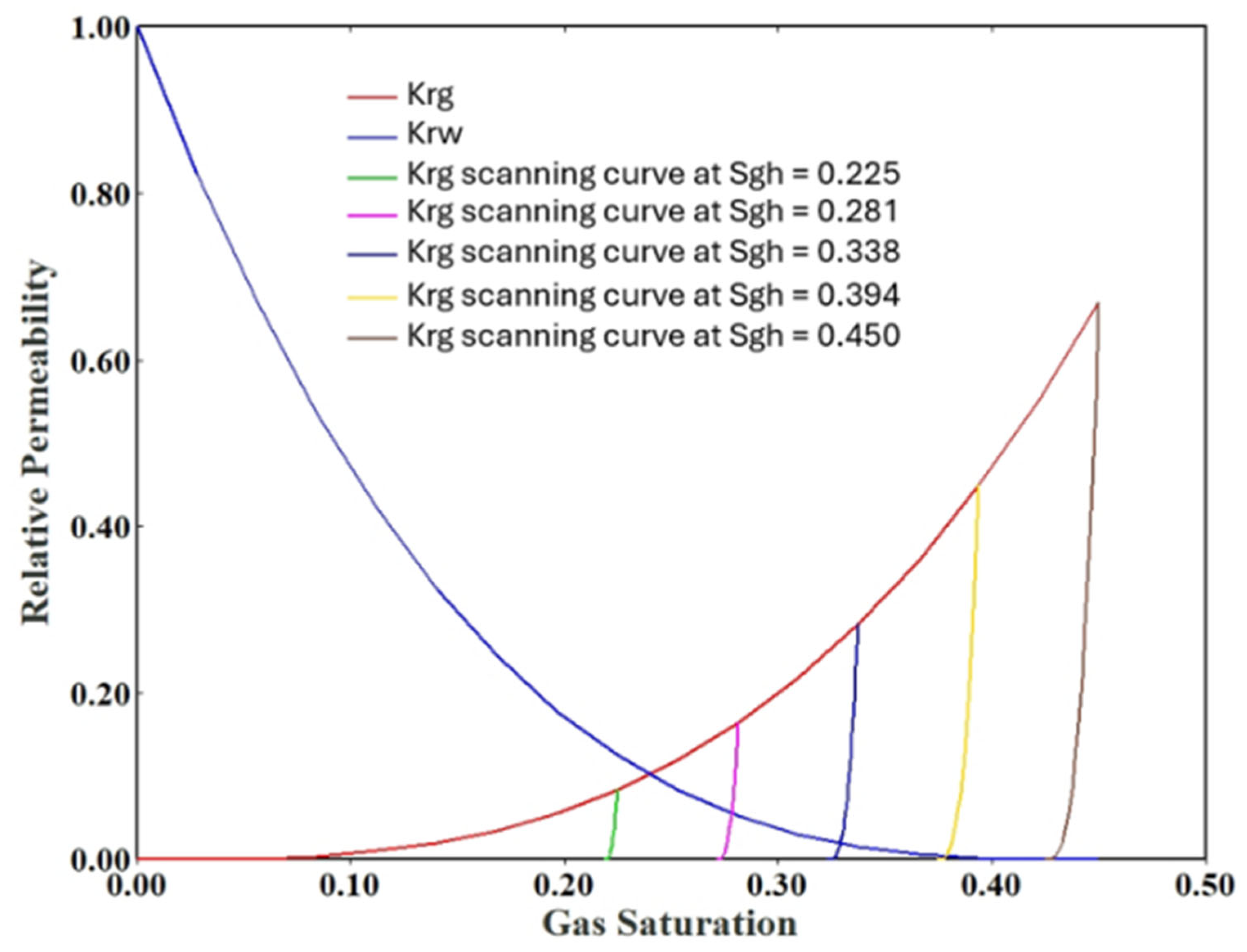
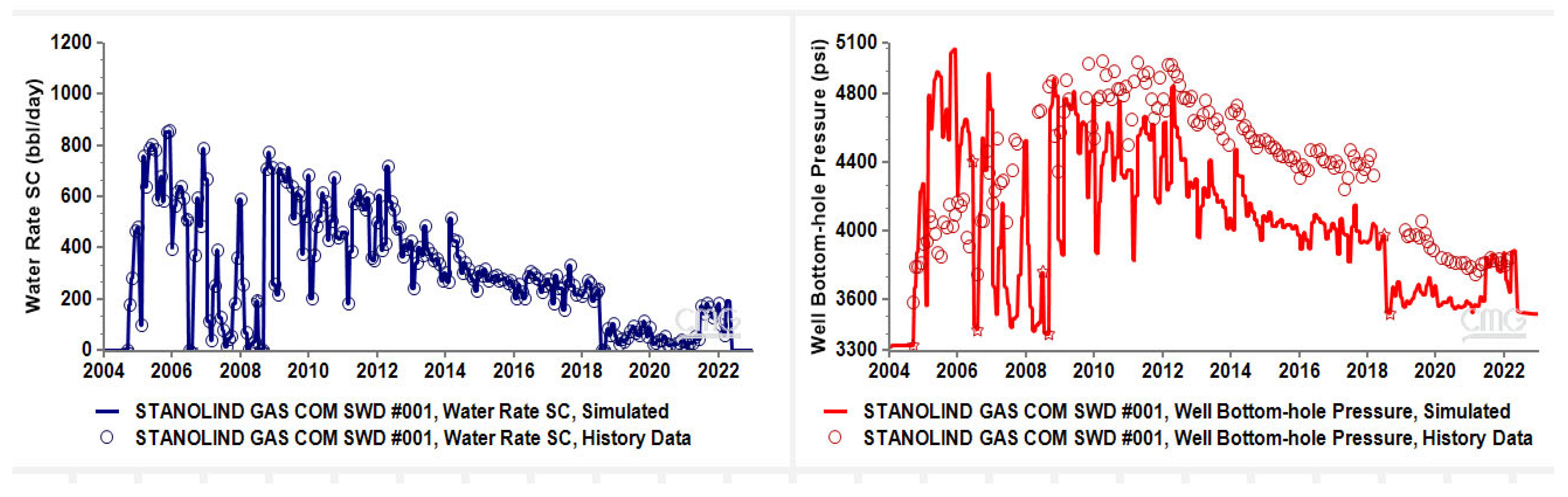
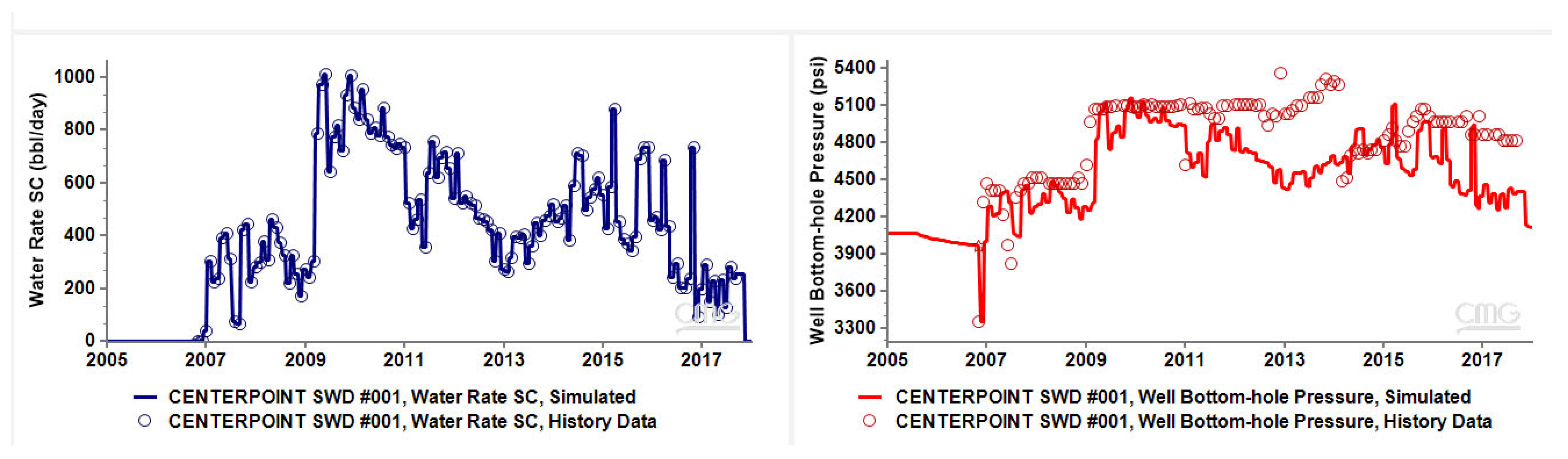
2.2. Hydrodynamic Model History-Matching
History Match Error
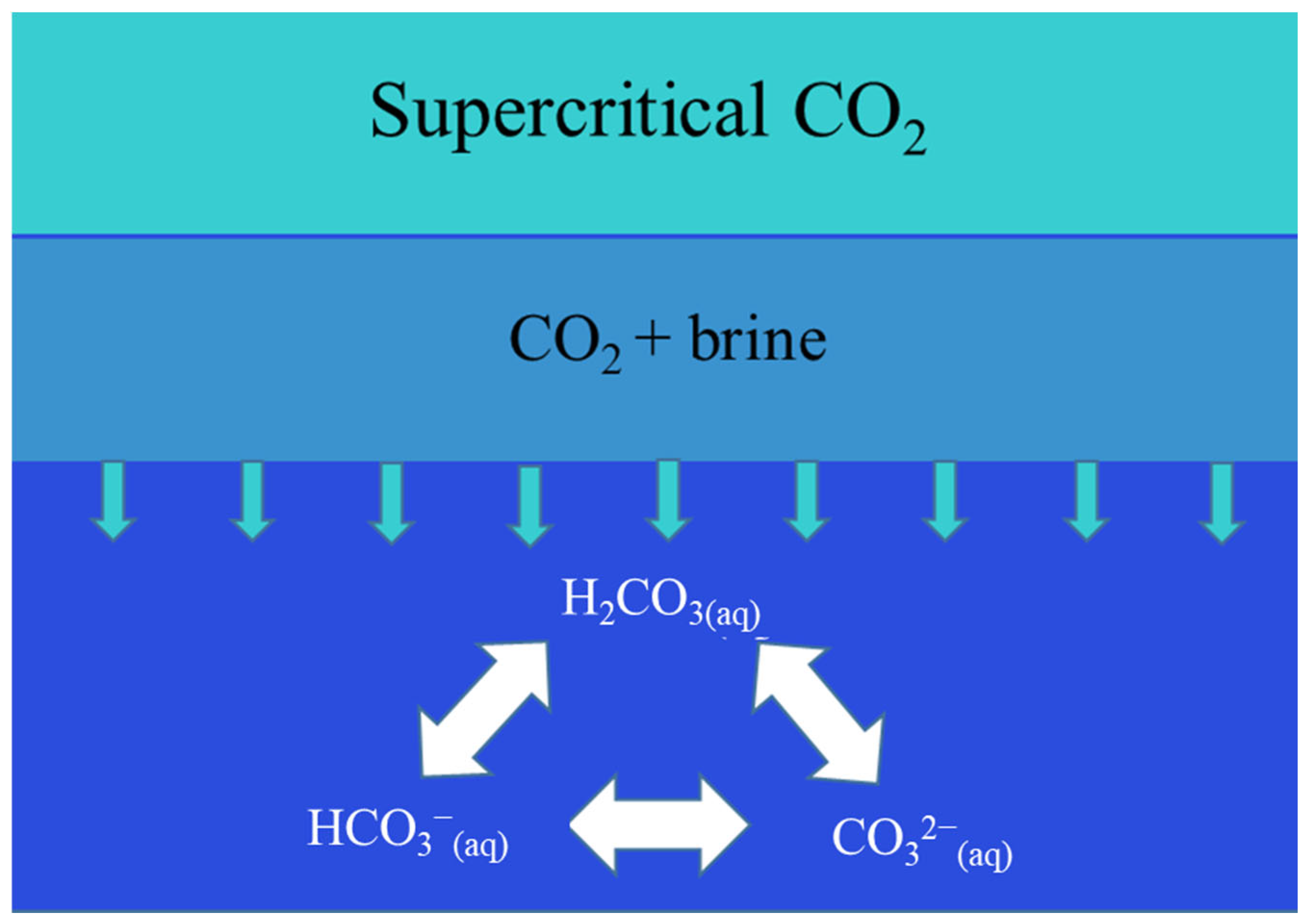
2.3. Geochemical Modeling
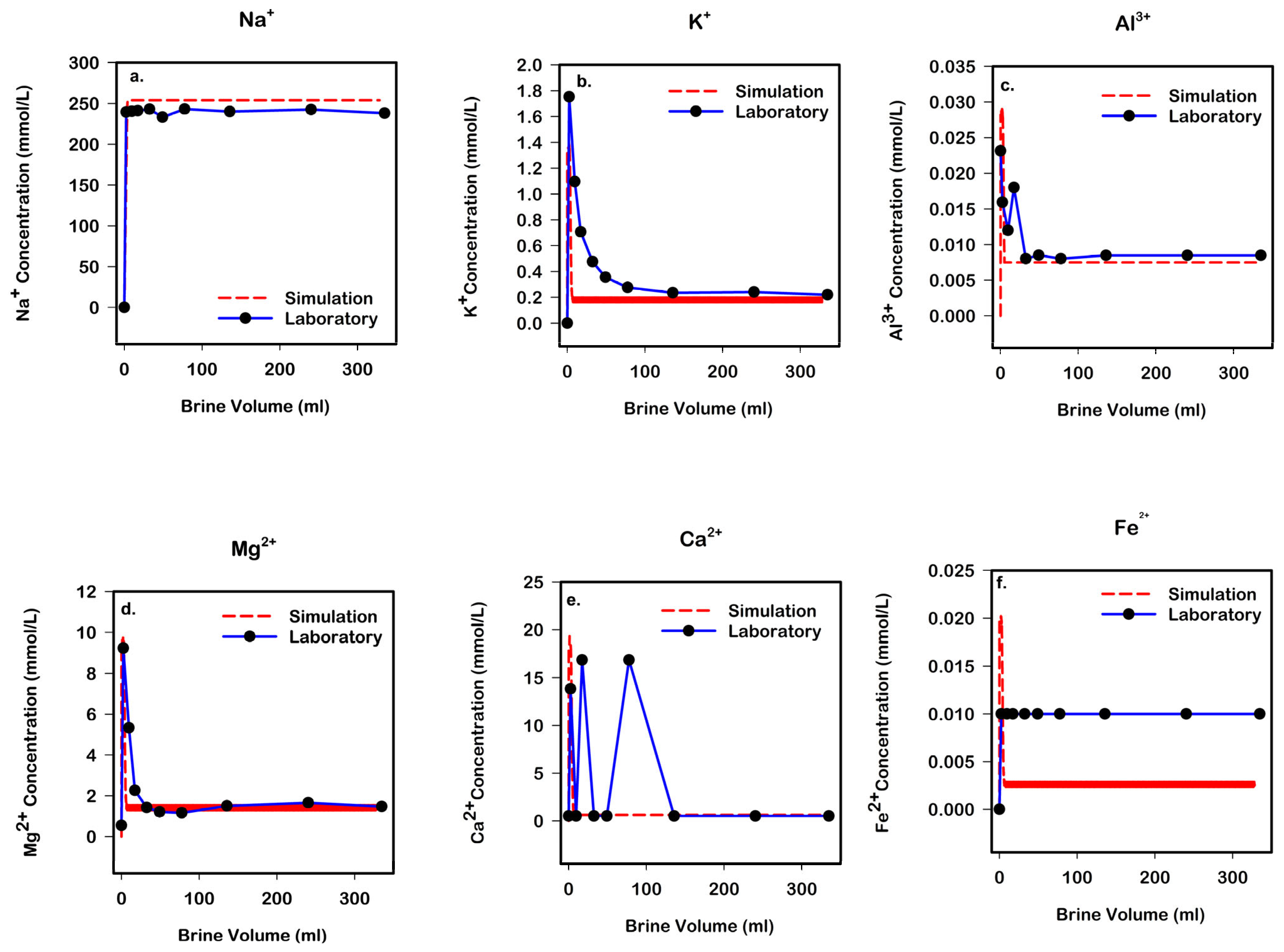
Geochemical History-Matching
2.4. Field-Scale Modeling
3. Results
3.1. History Match
3.2. Laboratory and Core-Scale Simulation Analysis
3.3. CO2 Plume Containment
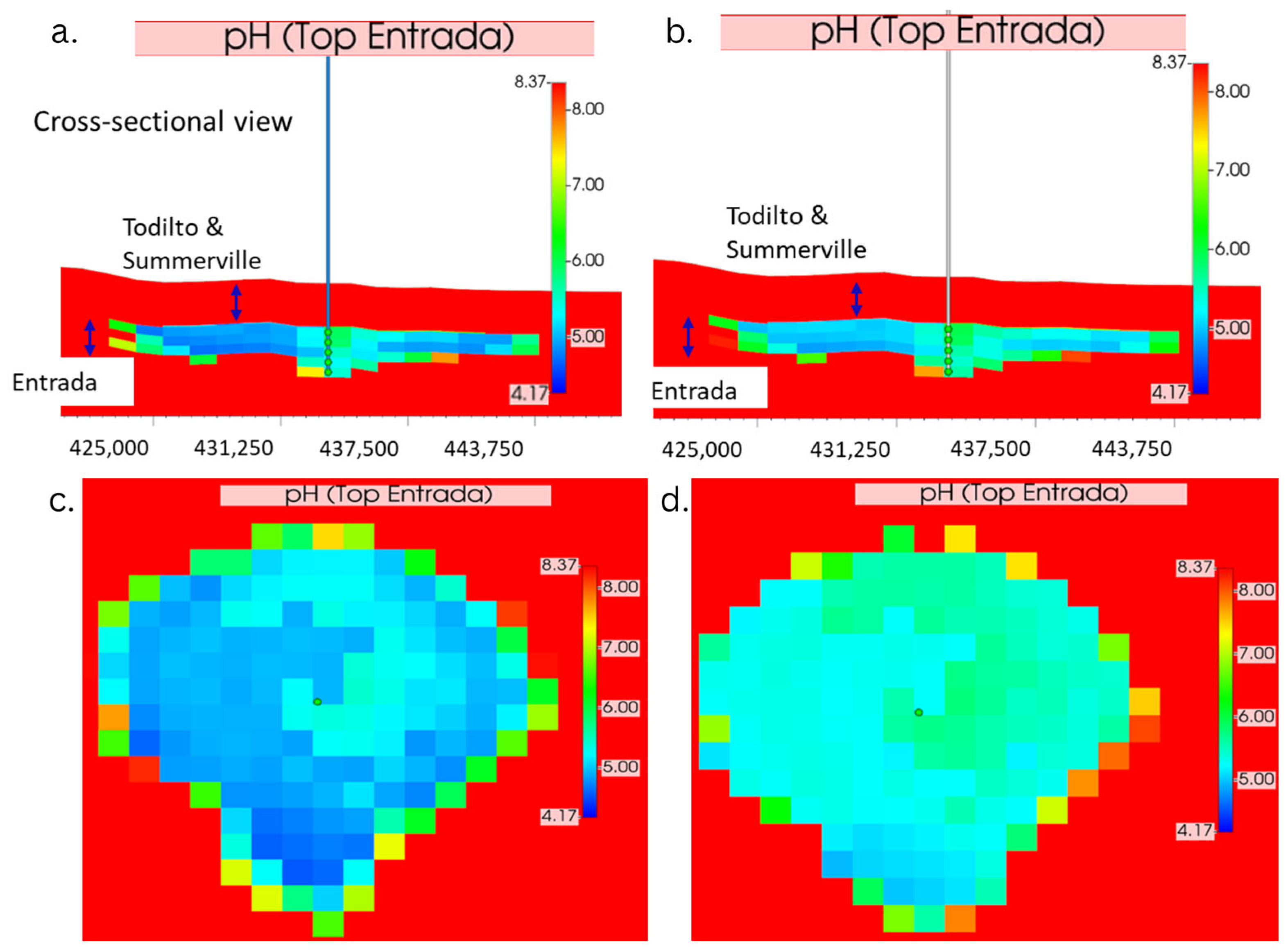
3.4. Changes in pH Due to CO2 Injection Across Different Distances and Depths
3.5. Temporal Dynamics of CO2 Trapping Mechanisms
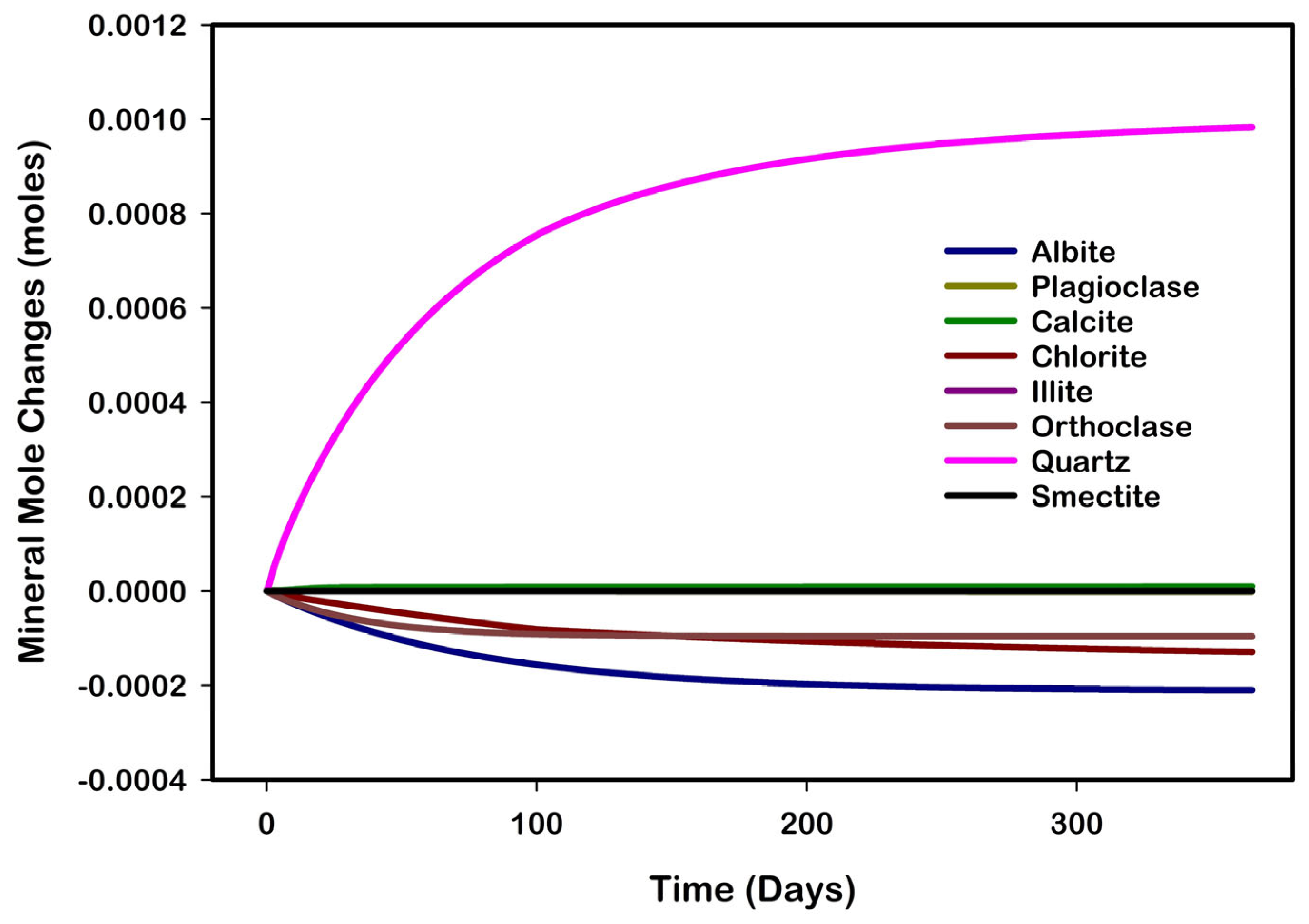
3.6. Characteristics of Mineralization and Its Influence on Flow Properties
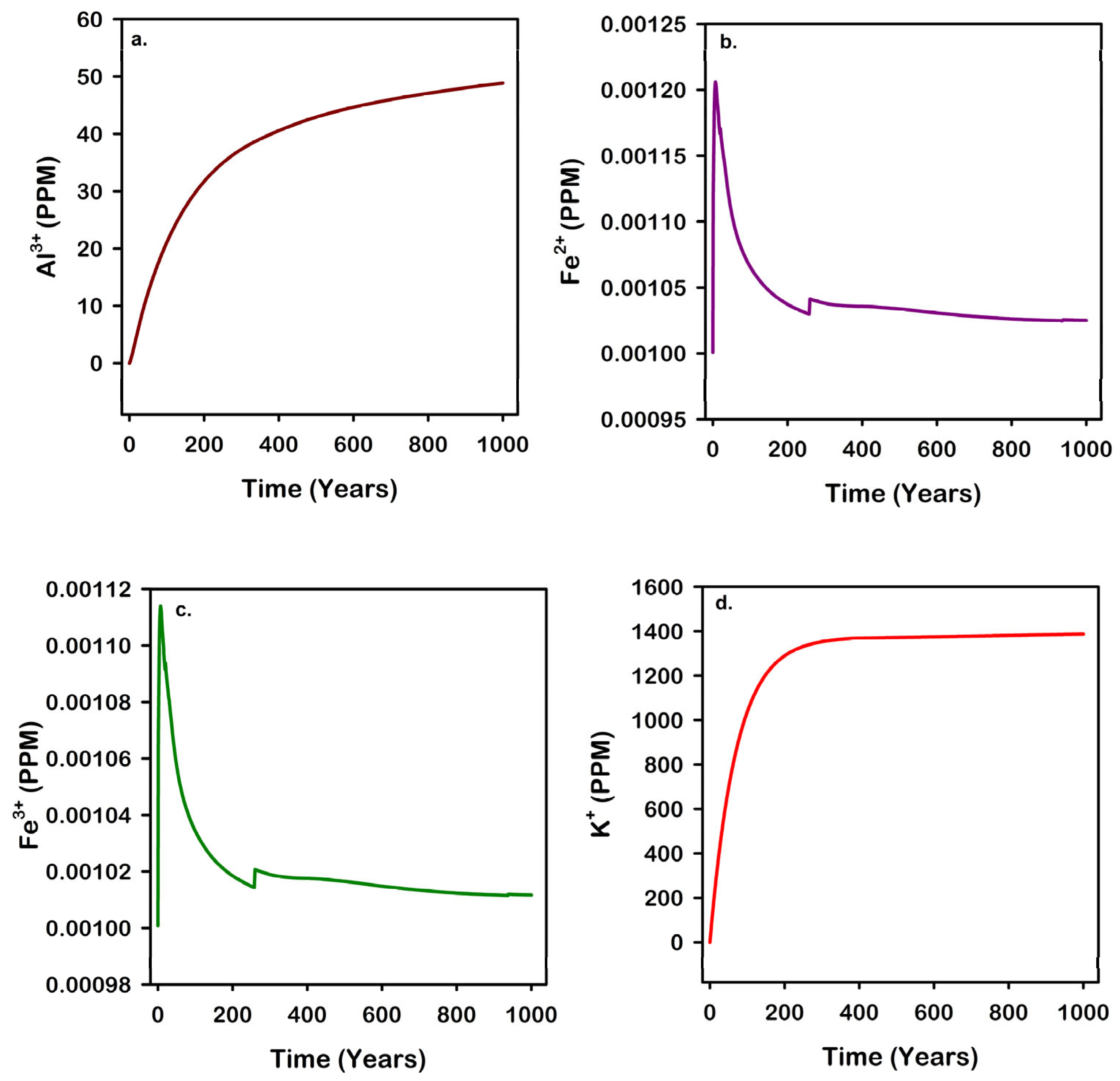
3.7. Impact of Geochemical Reactions on Ions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SJB | San Juan Basin |
| CO2 | Carbon dioxide |
| GCS | Geological Carbon Storage |
Appendix A
Appendix A.1. Multiphase Multicomponent Transport in Porous Media
Appendix A.2. Stoichiometry of Geochemical Reactions and Chemical Equilibrium
Appendix A.3. Kinetics of Mineral Dissolution and Precipitation
Appendix A.4. Changes in Porosity–Permeability Due to Reactions
References
- IEA. CO2 Emissions in 2023; IEA: Paris, France, 2024; Available online: https://www.iea.org/reports/co2-emissions-in-2023 (accessed on 14 May 2024).
- NASA’s Scientific Visualization Studio. Available online: https://svs.gsfc.nasa.gov/5207/#section_credits (accessed on 14 May 2024).
- Bachu, S. CO2 Storage in Geological Media: Role, Means, Status and Barriers to Deployment. Prog. Energy Combust. Sci. 2008, 34, 254–273. [Google Scholar] [CrossRef]
- Jiang, X. A Review of Physical Modelling and Numerical Simulation of Long-Term Geological Storage of CO2. Appl. Energy 2011, 88, 3557–3566. [Google Scholar] [CrossRef]
- Al Hameli, F.; Belhaj, H.; Al Dhuhoori, M. CO2 Sequestration Overview in Geological Formations: Trapping Mechanisms Matrix Assessment. Energies 2022, 15, 7805. [Google Scholar] [CrossRef]
- Nath, F.; Mahmood, M.N.; Ofosu, E.; Khanal, A. Enhanced Geothermal Systems: A Critical Review of Recent Advancements and Future Potential for Clean Energy Production. Geoenergy Sci. Eng. 2024, 243, 213370. [Google Scholar] [CrossRef]
- Gyimah, E.; Tomomewo, O.; Nkok, L.Y.; Bade, S.O.; Ofosu, E.A.; Bawuah, M.C. A Probabilistic Study of CO2 Plume Geothermal and Hydrothermal Systems: A Sensitivity Study of Different Reservoir Conditions in Williston Basin, North Dakota. Eng 2024, 5, 1407–1421. [Google Scholar] [CrossRef]
- Ike, I.A.; Adjimah, M.; Ike, G.U.; Ezugwu, C. Activated Carbon, a Possible Carbon Solution in Nigeria. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5–7 August 2013; SPE: Singapore, 2013. [Google Scholar]
- Ajayi, T.; Gomes, J.S.; Bera, A. A Review of CO2 Storage in Geological Formations Emphasizing Modeling, Monitoring and Capacity Estimation Approaches. Pet. Sci. 2019, 16, 1028–1063. [Google Scholar] [CrossRef]
- Kumar, S.; Foroozesh, J.; Edlmann, K.; Rezk, M.G.; Lim, C.Y. A Comprehensive Review of Value-Added CO2 Sequestration in Subsurface Saline Aquifers. J. Nat. Gas Sci. Eng. 2020, 81, 103437. [Google Scholar] [CrossRef]
- Esposito, R.A.; Kuuskraa, V.A.; Rossman, C.G.; Corser, M.M. Reconsidering CCS in the US Fossil-Fuel Fired Electricity Industry under Section 45Q Tax Credits. Greenh. Gases Sci. Technol. 2019, 9, 1288–1301. [Google Scholar] [CrossRef]
- Adu-Gyamfi, B.; Ampomah, W.; Tu, J.; Sun, Q.; Erzuah, S.; Acheampong, S. Assessment of Chemo-Mechanical Impacts of CO2 Sequestration on the Caprock Formation in Farnsworth Oil Field, Texas. Sci. Rep. 2022, 12, 13023. [Google Scholar] [CrossRef]
- Ringrose, P.S.; Furre, A.-K.; Gilfillan, S.M.V.; Krevor, S.; Landrø, M.; Leslie, R.; Meckel, T.; Nazarian, B.; Zahid, A. Storage of Carbon Dioxide in Saline Aquifers: Physicochemical Processes, Key Constraints, and Scale-Up Potential. Annu. Rev. Chem. Biomol. Eng. 2021, 12, 471–494. [Google Scholar] [CrossRef]
- Dai, Z.; Xu, L.; Xiao, T.; McPherson, B.; Zhang, X.; Zheng, L.; Dong, S.; Yang, Z.; Soltanian, M.R.; Yang, C.; et al. Reactive Chemical Transport Simulations of Geologic Carbon Sequestration: Methods and Applications. Earth Sci. Rev. 2020, 208, 103265. [Google Scholar] [CrossRef]
- Ampomah, W.; Balch, R.; Cather, M.; Rose-Coss, D.; Dai, Z.; Heath, J.; Dewers, T.; Mozley, P. Evaluation of CO2 Storage Mechanisms in CO2 Enhanced Oil Recovery Sites: Application to Morrow Sandstone Reservoir. Energy Fuels 2016, 30, 8545–8555. [Google Scholar] [CrossRef]
- Adu-Gyamfi, B.; Ampomah, W.; Tu, J.; Sun, Q.; Erzuah, S.; Sarkodie-Kyeremeh, J. Simulation Study of Chemo-mechanical Impacts of CO2 Injection in Morrow b Sandstone Reservoir. Greenh. Gases Sci. Technol. 2022, 12, 764–783. [Google Scholar] [CrossRef]
- Pearce, J.; Raza, S.; Baublys, K.; Hayes, P.; Firouzi, M.; Rudolph, V. Unconventional CO2 Storage: CO2 Mineral Trapping Predicted in Characterized Shales, Sandstones, and Coal Seam Interburden. SPE J. 2022, 27, 3218–3239. [Google Scholar] [CrossRef]
- Kashim, M.Z.; Tsegab, H.; Rahmani, O.; Abu Bakar, Z.A.; Aminpour, S.M. Reaction Mechanism of Wollastonite In Situ Mineral Carbonation for CO2 Sequestration: Effects of Saline Conditions, Temperature, and Pressure. ACS Omega 2020, 5, 28942–28954. [Google Scholar] [CrossRef]
- Abousif, A.; Wronkiewicz, D.; Masoud, A. Geochemical Assessment of Mineral Sequestration of Carbon Dioxide in the Midcontinent Rift. Greenh. Gases Sci. Technol. 2024, 14, 295–318. [Google Scholar] [CrossRef]
- Raza, A.; Glatz, G.; Gholami, R.; Mahmoud, M.; Alafnan, S. Carbon Mineralization and Geological Storage of CO2 in Basalt: Mechanisms and Technical Challenges. Earth Sci. Rev. 2022, 229, 104036. [Google Scholar] [CrossRef]
- Fatah, A.; Ben Mahmud, H.; Bennour, Z.; Gholami, R.; Hossain, M. Geochemical Modelling of CO2 Interactions with Shale: Kinetics of Mineral Dissolution and Precipitation on Geological Time Scales. Chem. Geol. 2022, 592, 120742. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Liu, S.; Zhao, C.; Dong, S.; Song, Y. CO2 Transport and Carbonate Precipitation in the Coupled Diffusion-Reaction Process during CO2 Storage. Fuel 2023, 334, 126805. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Garcia, E.A.; Ballesteros, F.C.; Garcia-Segura, S.; Lu, M.-C. A Review on Chemical Precipitation in Carbon Capture, Utilization and Storage. Sustain. Environ. Res. 2022, 32, 45. [Google Scholar] [CrossRef]
- Akono, A.-T.; Dávila, G.; Druhan, J.; Shi, Z.; Jessen, K.; Tsotsis, T. Influence of Geochemical Reactions on the Creep Behavior of Mt. Simon Sandstone. Int. J. Greenh. Gas Control 2020, 103, 103183. [Google Scholar] [CrossRef]
- Fuchs, S.J.; Espinoza, D.N.; Lopano, C.L.; Akono, A.-T.; Werth, C.J. Geochemical and Geomechanical Alteration of Siliciclastic Reservoir Rock by Supercritical CO2-Saturated Brine Formed during Geological Carbon Sequestration. Int. J. Greenh. Gas Control 2019, 88, 251–260. [Google Scholar] [CrossRef]
- Shi, Z.; Sun, L.; Haljasmaa, I.; Harbert, W.; Sanguinito, S.; Tkach, M.; Goodman, A.; Tsotsis, T.T.; Jessen, K. Impact of Brine/CO2 Exposure on the Transport and Mechanical Properties of the Mt Simon Sandstone. J. Pet. Sci. Eng. 2019, 177, 295–305. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Zou, Y.; Ma, X.; Ding, Y.; Li, N.; Zhang, X.; Kasperczyk, D. Pore Structure Alteration Induced by CO2–Brine–Rock Interaction during CO2 Energetic Fracturing in Tight Oil Reservoirs. J. Pet. Sci. Eng. 2020, 191, 107147. [Google Scholar] [CrossRef]
- Harbert, W.; Goodman, A.; Spaulding, R.; Haljasmaa, I.; Crandall, D.; Sanguinito, S.; Kutchko, B.; Tkach, M.; Fuchs, S.; Werth, C.J.; et al. CO2 Induced Changes in Mount Simon Sandstone: Understanding Links to Post CO2 Injection Monitoring, Seismicity, and Reservoir Integrity. Int. J. Greenh. Gas Control 2020, 100, 103109. [Google Scholar] [CrossRef]
- Tarokh, A.; Makhnenko, R.Y.; Kim, K.; Zhu, X.; Popovics, J.S.; Segvic, B.; Sweet, D.E. Influence of CO2 Injection on the Poromechanical Response of Berea Sandstone. Int. J. Greenh. Gas Control 2020, 95, 102959. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, S.; Liu, K.; Zhuo, Q.; Yang, L. An Experimental and Numerical Study of CO2–Brine-Synthetic Sandstone Interactions under High-Pressure (P)–Temperature (T) Reservoir Conditions. Appl. Sci. 2019, 9, 3354. [Google Scholar] [CrossRef]
- Kim, K.; Makhnenko, R.Y. Changes in Rock Matrix Compressibility during Deep CO2 Storage. Greenh. Gases Sci. Technol. 2021, 11, 954–973. [Google Scholar] [CrossRef]
- Foroutan, M.; Ghazanfari, E.; Amirlatifi, A. Variation of Failure Properties, Creep Response and Ultrasonic Velocities of Sandstone upon Injecting CO2-Enriched Brine. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 27. [Google Scholar] [CrossRef]
- Koukouzas, N.; Kypritidou, Z.; Purser, G.; Rochelle, C.A.; Vasilatos, C.; Tsoukalas, N. Assessment of the Impact of CO2 Storage in Sandstone Formations by Experimental Studies and Geochemical Modeling: The Case of the Mesohellenic Trough, NW Greece. Int. J. Greenh. Gas Control 2018, 71, 116–132. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Li, Y.; Sun, S.; Gao, X. A Self-Adaptive Deep Learning Algorithm for Accelerating Multi-Component Flash Calculation. Comput. Methods Appl. Mech. Eng. 2020, 369, 113207. [Google Scholar] [CrossRef]
- Zhang, T.; Li, Y.; Sun, S.; Bai, H. Accelerating Flash Calculations in Unconventional Reservoirs Considering Capillary Pressure Using an Optimized Deep Learning Algorithm. J. Pet. Sci. Eng. 2020, 195, 107886. [Google Scholar] [CrossRef]
- Xiao, T.; Xu, H.; Moodie, N.; Esser, R.; Jia, W.; Zheng, L.; Rutqvist, J.; McPherson, B. Chemical-Mechanical Impacts of CO2 Intrusion Into Heterogeneous Caprock. Water Resour. Res. 2020, 56, e2020WR027193. [Google Scholar] [CrossRef]
- Sun, E.W.-H.; Bourg, I.C. Molecular Dynamics Simulations of Mineral Surface Wettability by Water Versus CO2: Thin Films, Contact Angles, and Capillary Pressure in a Silica Nanopore. J. Phys. Chem. C 2020, 124, 25382–25395. [Google Scholar] [CrossRef]
- Elgendy, A.M.S.; Ricci, S.; Cojocariu, E.I.; Geloni, C.; Castellani, S.; Massara, E.P.; Ortenzi, A.; Consonni, A.; Casali, P.; Idiomi, M. Geochemical Modelling of CO2 Injection: Role of Capillary-Driven Transport of Dissolved Salt on CO2 Injectivity. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–5 October 2022. [Google Scholar]
- Ma, B.; Cao, Y.; Zhang, Y.; Eriksson, K.A. Role of CO2-Water-Rock Interactions and Implications for CO2 Sequestration in Eocene Deeply Buried Sandstones in the Bonan Sag, Eastern Bohai Bay Basin, China. Chem. Geol. 2020, 541, 119585. [Google Scholar] [CrossRef]
- Soltanian, M.R.; Hajirezaie, S.; Hosseini, S.A.; Dashtian, H.; Amooie, M.A.; Meyal, A.; Ershadnia, R.; Ampomah, W.; Islam, A.; Zhang, X. Multicomponent Reactive Transport of Carbon Dioxide in Fluvial Heterogeneous Aquifers. J. Nat. Gas Sci. Eng. 2019, 65, 212–223. [Google Scholar] [CrossRef]
- Akai, T.; Kuriyama, T.; Kato, S.; Okabe, H. Numerical Modelling of Long-Term CO2 Storage Mechanisms in Saline Aquifers Using the Sleipner Benchmark Dataset. Int. J. Greenh. Gas Control 2021, 110, 103405. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Tian, H.; Feng, G.; Yang, Z.; Zhou, B. Understanding of Long-Term CO2-Brine-Rock Geochemical Reactions Using Numerical Modeling and Natural Analogue Study. Geofluids 2019, 2019, 1426061. [Google Scholar] [CrossRef]
- Suchodolska, K.; Labus, K. Simplified Models for Reactive Transport and Chemical Reactions During CO2 Storage in Saline Aquifers. Energy Procedia 2016, 97, 509–514. [Google Scholar] [CrossRef]
- Boison, P.K.N.; Ampomah, W.; Simmons, J.; Bui, D. Integrated Geochemical Modeling for CO2 Sequestration in the San Juan Basin, New Mexico. In Proceedings of the SPE Eastern Regional Meeting, Wheeling, WV, USA, 8–10 October 2024. [Google Scholar]
- Boison, P.K.; Ampomah, W.; Sibaweihi, N. Impact of Vaporization on Mineral Changes and Salt Precipitation During CO2 Storage. In Proceedings of the SPE/AAPG/SEG Carbon, Capture, Utilization, and Storage Conference and Exhibition, Houston, TX, USA, 3–5 March 2025. [Google Scholar] [CrossRef]
- Computer Modelling Group Ltd. GEM User Guide; Computer Modelling Group Ltd.: Calgary, AB, Canada, 2021; Volume 2021, p. 10. [Google Scholar]
- Kharaka, Y.K.; Gunter, W.D.; Aggarwal, P.K.; Perkins, E.H.; Dedraal, J.D. SOLMINEQ. 88–A Computer Program for Geochemical Modeling of Water—Rock Interactions; U.S. Geological Survey: Menlo Park, CA, USA, 1988.
- Xu, P.; Zhang, Q.; Qian, H.; Yang, F.; Zheng, L. Investigating the Mechanism of PH Effect on Saturated Permeability of Remolded Loess. Eng. Geol. 2021, 284, 105978. [Google Scholar] [CrossRef]
- Soetaert, K.; Hofmann, A.F.; Middelburg, J.J.; Meysman, F.J.R.; Greenwood, J. The Effect of Biogeochemical Processes on PH. Mar. Chem. 2007, 105, 30–51. [Google Scholar] [CrossRef]
- Parkhurst, D.L. and A.C. and others Description of Input and Examples for PHREEQC Version 3—A Computer Program for Speciation, Batch-Reaction, One-Dimensional Transport, and Inverse Geochemical Calculations. US Geol. Surv. Tech. Methods 2013, 6, 497. [Google Scholar]
- Dullien, F.A. Porous Media: Fluid Transport and Pore Structure; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Simmons, J.; Rinehart, A.; Luhmann, A.; Mozley, P.; Heath, J.; Majumdar, B. Using Petrographically Observable Microstructure to Predict Hydromechanical Changes in a Complex Siliciclastic Storage Site during CO2 Injection. Int. J. Greenh. Gas Control 2022, 119, 103724. [Google Scholar] [CrossRef]
- Simmons, J.D.; Wang, S.; Luhmann, A.J.; Rinehart, A.J.; Heath, J.E.; Majumdar, B.S. Paragenetic Controls on CO2-Fluid-Rock Interaction and Weakening in a Macroporous-Dominated Sandstone. Appl. Geochem. 2023, 156, 105744. [Google Scholar] [CrossRef]
- Khanal, A.; Irfan Khan, M.; Fahim Shahriar, M. Comprehensive Parametric Study of CO2 Sequestration in Deep Saline Aquifers. Chem. Eng. Sci. 2024, 287, 119734. [Google Scholar] [CrossRef]
- Hoteit, H.; Firoozabadi, A. Numerical Modeling of Diffusion in Fractured Media for Gas-Injection and -Recycling Schemes. SPE J. 2009, 14, 323–337. [Google Scholar] [CrossRef]
- Xu, T.; Sonnenthal, E.; Spycher, N.; Pruess, K.; Brimhall, G.; Apps, J. Modeling Multiphase Non-Isothermal Fluid Flow and Reactive Geochemical Transport in Variably Saturated Fractured Rocks: 2. Applications to Supergene Copper Enrichment and Hydrothermal Flows. Am. J. Sci. 2001, 301, 34–59. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Phys. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Bethke, C.M. Geochemical Reaction Modeling: Concepts and Applications; Oxford University Press: Oxford, UK, 1996; ISBN 0195094751. [Google Scholar]
- Delany, J.M.; Lundeen, S.R. The LLNL Thermochemical Data Base—Revised Data and File Format for the EQ3/6 Package (No. UCID-21658); Lawrence Livermore National Lab.(LLNL): Livermore, CA, USA, 1991.
- Nghiem, L.; Sammon, P.; Grabenstetter, J.; Ohkuma, H. Modeling CO2 Storage in Aquifers with a Fully-Coupled Geochemical EOS Compositional Simulator. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Society of Petroleum Engineers, Tulsa, OK, USA, 17–21 April 2004. [Google Scholar]
- Carman, P.C. Permeability of Saturated Sands, Soils and Clays. J. Agric. Sci. 1939, 29, 262–273. [Google Scholar] [CrossRef]





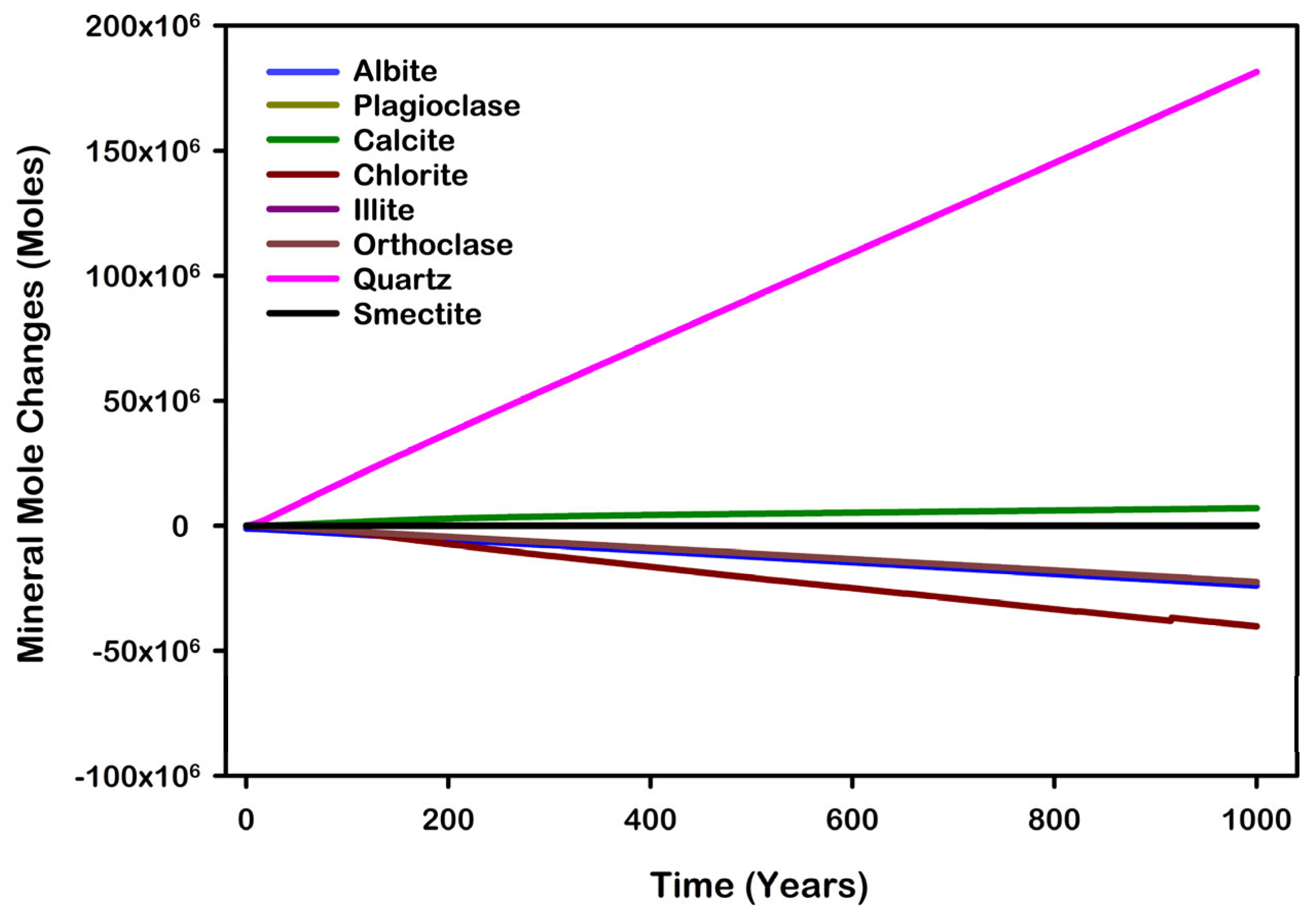
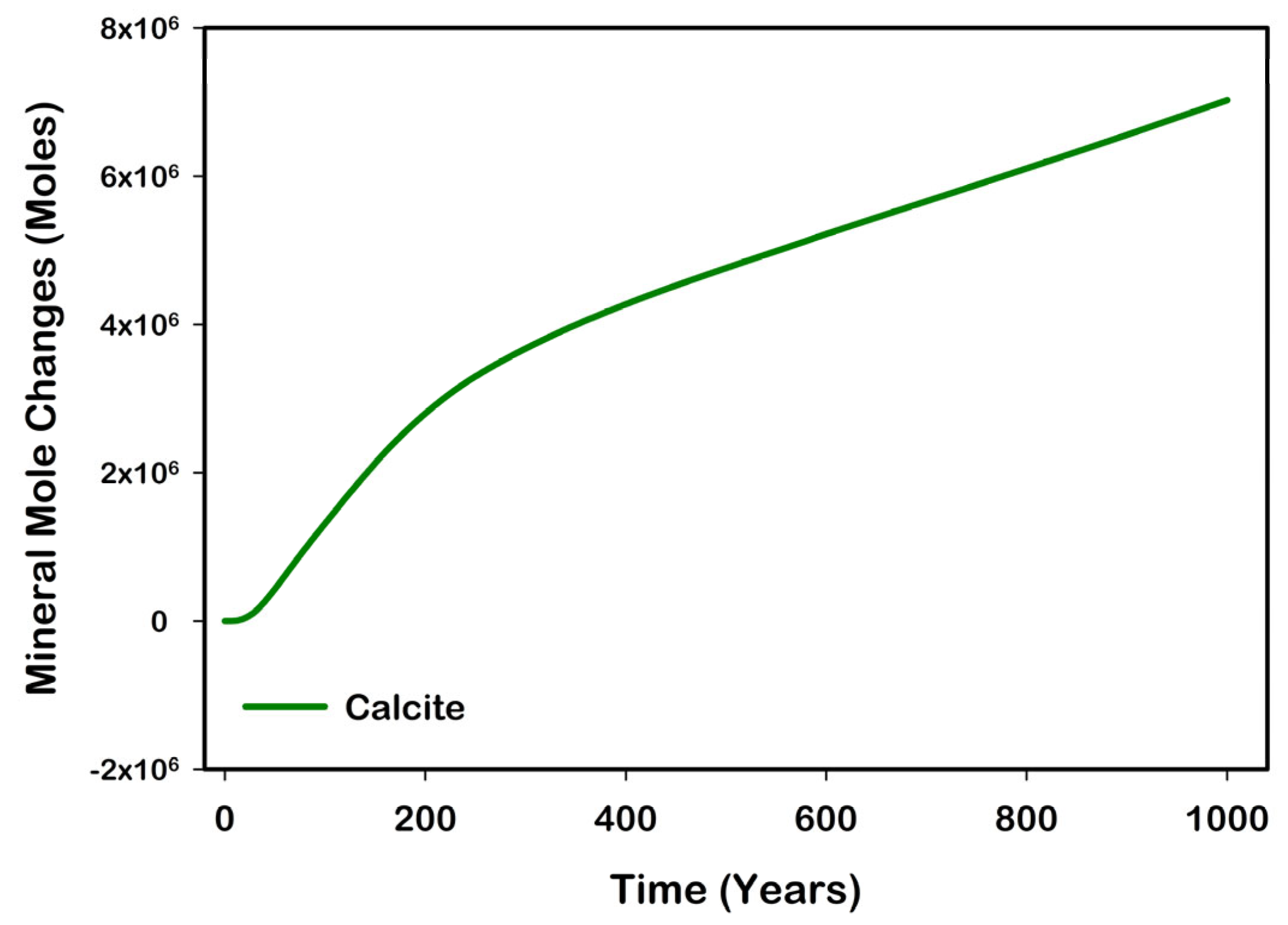
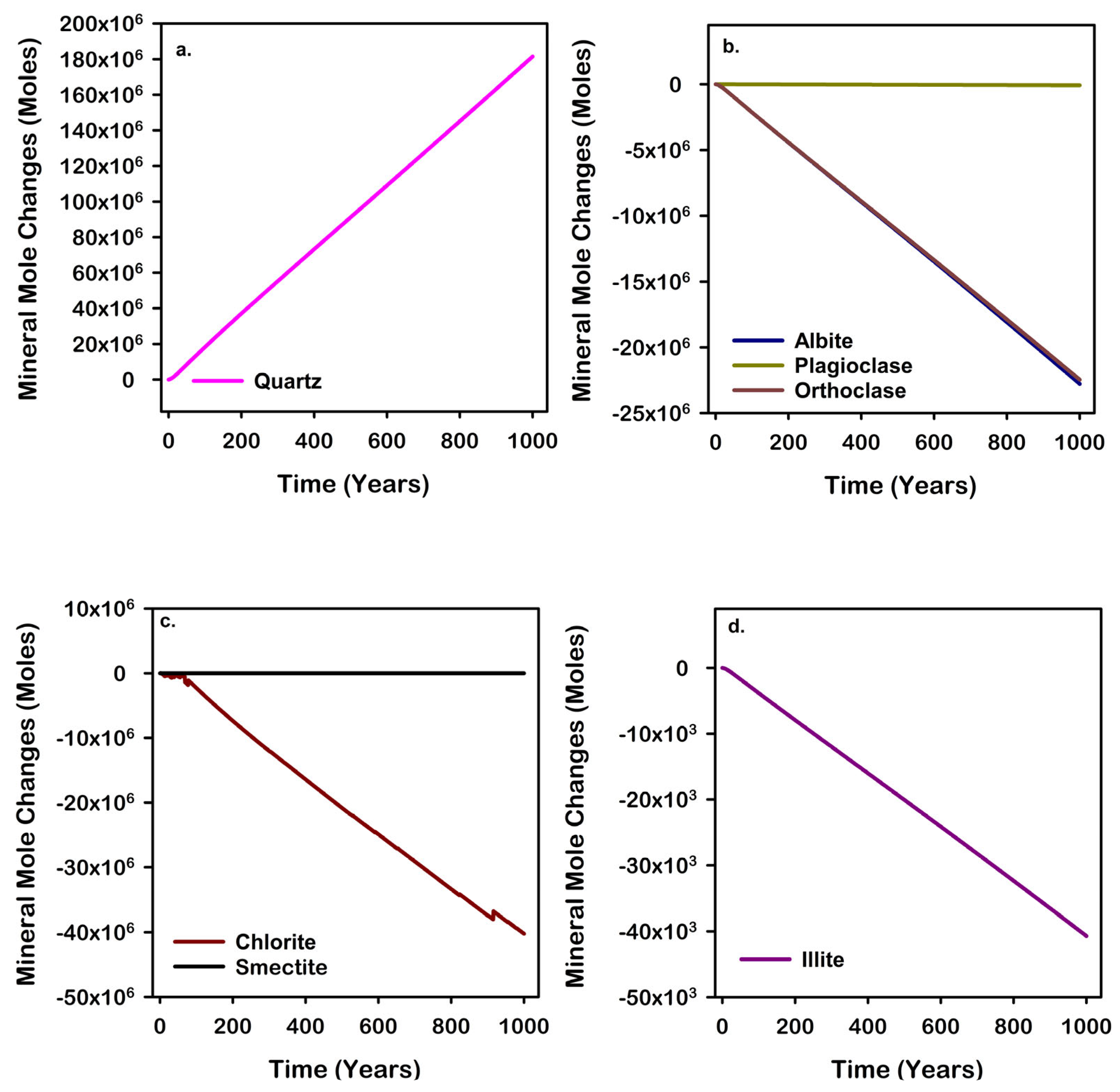


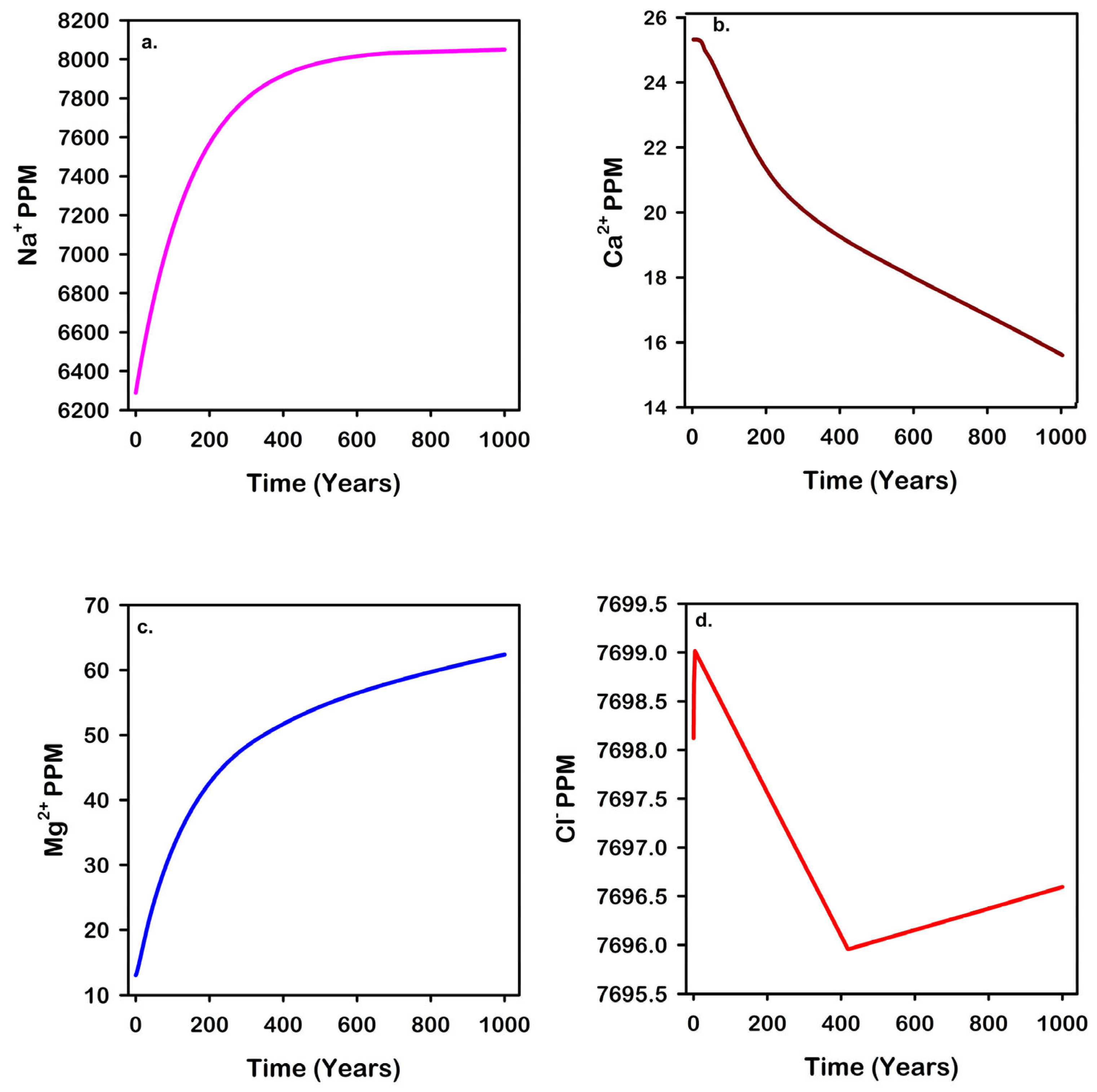

| Mineral | Chemical Formula | Initial Volume Fraction |
|---|---|---|
| Quartz | SiO2 | 0.734 |
| Illite | K0.6Mg0.25Al2.3Si3.5O10(OH)2 | 0.048 |
| Calcite | CaCO3 | 0.043 |
| Albite | Na(AlSi3O6) | 0.037 |
| Plagioclase | CaAl2Si2O8 | 0.018 |
| Orthoclase | K(AlSi3O6) | 0.014 |
| Chlorite | (14A)(Mg5Al2Si3O10(OH)8 | 0.013 |
| Smectite | (Na,Ca)0.33(Al,Mg)2Si4O10(OH)2·(H2O)n | 0.0001 |
| Ions | Concentration (ppm) |
|---|---|
| Na+ | 5245 |
| Ca2+ | 24 |
| Mg2+ | 13 |
| Cl− | 7633 |
| HCO3− | 336 |
| CO32− | 450 |
| SO42− | 1900 |
| Intra-Aqueous Chemical Equilibrium Reactions | Equilibrium Constant (log K at 25 °C) |
|---|---|
| CO2 (aq.) + H2O = (CO32−) + 2 (H+) | −16.88 |
| (CO32−) + (H+) = (HCO3−) | 10.33 |
| H2O = (OH−) + (H+) | −14.00 |
| Mineral Dissolution/Precipitation Reactions | Activation Energy J/mol | Reactive Surface Area (m2/m3) | Log 10 of Reaction Rate at 25 °C (1/s) |
|---|---|---|---|
| Quartz + 2 H2O = H4SiO4 | 90,900 | 2650.00 | −13.4 |
| Illite + 11.2 H2O = (K+) + (Mg2+) + (Al(OH)4−) + H4SiO4 + (H+) | 23,600 | 2763.07 | −10.98 |
| Calcite = (CO3−) + (Ca2+) | 14,400 | 2709.95 | −0.3 |
| Albite + 8 H2O = (Na+) + (Al(OH)4−) + H4SiO4 | 69,800 | 2620.00 | −12.04 |
| Plagioclase + 8 H2O = (Ca2+) + (Al(OH)4−) + H4SiO4 | 16,600 | 2760.29 | −3.50 |
| Orthoclase + 8 H2O = (K+) + (Al(OH)4−) + H4SiO4 | 51,700 | 2560.00 | −10.06 |
| Chlorite + 16 (H+) = (Mg2+) + (Al3+) + H4SiO4+ H2O | 88,000 | 2600.00 | −11.11 |
| Smectite + 7 (H+) = (Al3+) + (Ca2+) + (Fe2+) + (Fe3+) + H2O + (K+) + (Mg2+) + (Na+) + SiO2 | 35,000 | 2350.00 | −12.78 |
| Parameter | Value |
|---|---|
| Core diameter | 0.0248 m |
| Core length | 0.0513 m |
| Flow rate | 1.44 × 10−4 m3/day |
| Injection duration | 23 days |
| Initial porosity | 10.29 |
| Initial permeability | 10.34 mD |
| Parameter | Value |
|---|---|
| Grid dimension | 164 × 116 × 25 |
| Total number of grid blocks | 475,600 |
| Initial water saturation | 100% |
| Initial reservoir pressure gradient | 0.42 psi/ft (9.5 kpa/m) |
| Reference depth for initial pressure | 8300 ft (2529.84 m) |
| Injection rate | 20 MMscf/day (566,336.94 m3/day) |
| Fracture pressure gradient | 0.62 psi/ft (14 kpa/m) |
| Porosity range | Up to 25% |
| Permeability range | Up to 220 mD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boison, P.K.N.; Ampomah, W.; Simmons, J.D.; Bui, D.; Sibaweihi, N.; Amosu, A.; Opoku Duartey, K. Geochemical Assessment of Long-Term CO2 Storage from Core- to Field-Scale Models. Energies 2025, 18, 4089. https://doi.org/10.3390/en18154089
Boison PKN, Ampomah W, Simmons JD, Bui D, Sibaweihi N, Amosu A, Opoku Duartey K. Geochemical Assessment of Long-Term CO2 Storage from Core- to Field-Scale Models. Energies. 2025; 18(15):4089. https://doi.org/10.3390/en18154089
Chicago/Turabian StyleBoison, Paa Kwesi Ntaako, William Ampomah, Jason D. Simmons, Dung Bui, Najmudeen Sibaweihi, Adewale Amosu, and Kwamena Opoku Duartey. 2025. "Geochemical Assessment of Long-Term CO2 Storage from Core- to Field-Scale Models" Energies 18, no. 15: 4089. https://doi.org/10.3390/en18154089
APA StyleBoison, P. K. N., Ampomah, W., Simmons, J. D., Bui, D., Sibaweihi, N., Amosu, A., & Opoku Duartey, K. (2025). Geochemical Assessment of Long-Term CO2 Storage from Core- to Field-Scale Models. Energies, 18(15), 4089. https://doi.org/10.3390/en18154089





