Abstract
This article presents a comprehensive review of methods used for forecasting electricity consumption. The studies analyzed by the authors encompass both classical statistical models and modern approaches based on artificial intelligence, including machine-learning and deep-learning techniques. Electricity load forecasting is categorized into four time horizons: very short term, short term, medium term, and long term. The authors conducted a comparative analysis of various models, such as autoregressive models, neural networks, fuzzy logic systems, hybrid models, and evolutionary algorithms. Particular attention was paid to the effectiveness of these methods in the context of variable input data, such as weather conditions, seasonal fluctuations, and changes in energy consumption patterns. The article emphasizes the growing importance of accurate forecasts in the context of the energy transition, integration of renewable energy sources, and the management of the evolving electricity system, shaped by decentralization, renewable integration, and data-intensive forecasting demands. In conclusion, the authors highlight the lack of a universal forecasting approach and the need for further research on hybrid models that combine interpretability with high predictive accuracy. This review can serve as a valuable resource for decision-makers, grid operators, and researchers involved in energy system planning.
1. Introduction
Electricity is a fundamental pillar of modern society, powering everything from household appliances to industrial machinery and digital infrastructure. The efficient production, distribution, and consumption of electricity are crucial for economic growth, technological innovation, and improving quality of life. However, the increasing demand for electricity, coupled with the need to reduce carbon emissions, presents significant challenges. Balancing supply and demand, integrating renewable energy, and modernizing aging grids are key issues that require innovative solutions and accurate forecasting to ensure a sustainable and reliable energy future [1]. Advanced machine-learning algorithms and data-driven predictive models play a crucial role in optimizing energy consumption, enhancing grid efficiency, and facilitating the seamless integration of renewable energy sources [2,3]. Figure 1 shows the consumption of primary energy (in TWh) in selected countries from 1998 to 2023. The largest growth was recorded in China, where consumption more than tripled, exceeding 45,000 TWh in 2023, well ahead of the United States, which remains stable at around 25,000 TWh. Poland, like other European countries (e.g., France, Sweden), has a much lower and relatively stable level of consumption [4]. One of the most pressing issues in energy management is the imbalance between production and consumption. Additionally, the reliance on coal for electricity generation has posed environmental and regulatory challenges, pushing the countries toward cleaner but more variable energy sources like wind and solar. This variability introduces new complexities in forecasting, as renewable energy generation is inherently less predictable than traditional fossil fuel-based systems.
Another critical problem is the aging infrastructure, which can lead to inefficiency and vulnerabilities in the energy grid. Modernizing the grid to accommodate decentralized energy sources and smart technologies is essential but requires significant investment and planning. Furthermore, the growing emphasis on sustainability and carbon neutrality adds another layer of complexity, as policymakers and energy providers must balance immediate energy needs with long-term environmental goals.
Accurate forecasting of electricity consumption is therefore more important than ever. It enables better planning, reduces the risk of shortages, and supports the integration of renewable energy sources. Load forecasting plays a critical role in various operational decisions, including management, planning, scheduling, and load dispatching. As a result, achieving precise forecasting is essential for ensuring the reliable, secure, and stable functioning of electric power systems. Inaccurate forecasts can lead to significant economic losses for power companies, driving up operating costs. Research indicates that even a 1% increase in forecasting error can result in an additional USD 10 million in operating expenses annually [5].
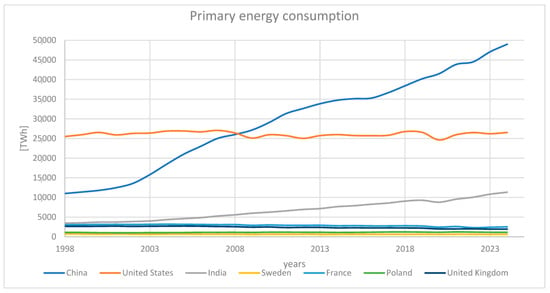
Figure 1.
Primary energy consumption in selected countries (1998–2023). Own study based on [6].
In this article, we will explore the methodologies and models used for forecasting electricity consumption. By examining various approaches from traditional statistical methods to advanced machine-learning techniques we aim to provide a clear understanding of their strength, limitations, and applicability in different context [7]. This review will highlight the challenges inherent in forecasting, such as dealing with variable renewable energy inputs, changing consumption patterns, and the need for real-time data processing. By exploring these methods, we aim to offer insights into how robust forecasting models can be developed to navigate the complexities of the evolving energy landscape [8].
2. Methods and Materials
In this paper, we have conducted a comprehensive review of existing studies on forecasting electricity consumption. Our review encompasses research and review articles from 2024 and earlier, with a particular focus on recent works published over the past 5 years. Additionally, we have included classical studies that highlight the key developmental trends in the field of electricity consumption forecasting.
Following this approach, we performed a comparative analysis of studies that explore various methods used for forecasting electricity consumption, evaluating them based on several criteria. The findings of this analysis are thoroughly detailed in Section 3, which is divided into four subsections. Each subsection provides a comparative evaluation of methods corresponding to different forecasting horizons. Section 4 summarizes the main outcomes of our review and identifies potential directions for future research. Various statistical metrics were employed in the article. However, it should be emphasized that this review aims to synthesize and analyze findings presented in the scientific literature. The reported values of these statistical indicators are derived from the cited studies and do not result from the authors’ own experiments.
Electricity load forecasting is divided into four categories based on the time domain: (i) long-term load forecasting (LTLF), (ii) medium-term load forecasting (MTLF), (iii) short-term load forecasting (STLF), and (iv) very short-term load forecasting (VSTLF), as illustrated in Figure 2 with their respective time distributions [9]. Various forecasting methods have been applied to these time domains, including knowledge-based expert systems, statistical techniques, artificial intelligence (AI) approaches such as machine-learning models, hybrid techniques, and deep-learning models [10,11,12].
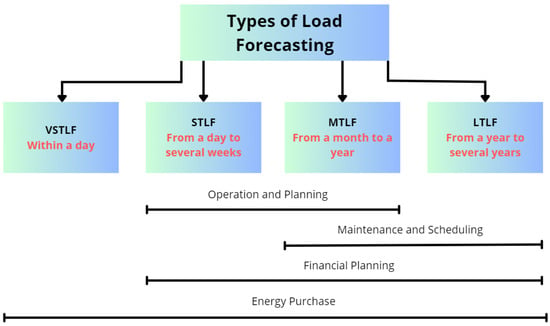
Figure 2.
Categories of electrical load forecasting based on various time horizons and their corresponding operational domains [9,13].
Traditional Statistical Methods in Electricity Forecasting
While machine-learning and deep-learning approaches have gained significant traction in electricity load forecasting, conventional statistical methods continue to play a vital role in both theoretical studies and real-world implementations. These established techniques prove especially useful when dealing with data-scarce environments, restricted processing capabilities, or situations requiring transparent and explainable forecasting models. Among classical approaches, ARIMA/SARIMA (AutoRegressive Integrated Moving Average/Seasonal ARIMA) models remain particularly valuable, as demonstrated by the authors’ analysis is this study [13]. They are classical statistical models widely used in time-series forecasting. The ARIMA model was formally introduced in the early 1970s by Box and Jenkins as part of their influential methodology for time-series forecasting. ARIMA is designed for non-stationary data and incorporates differencing to remove trends, allowing for more accurate modeling of the underlying structure. SARIMA extends ARIMA by also addressing seasonal patterns through seasonal differencing. These models are particularly effective when the time series exhibits autocorrelation and consistent seasonal cycles. Despite the rise of machine-learning methods, ARIMA and SARIMA remain popular due to their interpretability, simplicity, and solid performance in many real-world applications [14].
Exponential smoothing is a time-series forecasting method that applies decreasing weights to past observations, placing more emphasis on recent data. The Holt-Winters method is an extension of this technique that accounts for both trend and seasonality, making it suitable for series with systematic patterns. Holt-Winters is widely used in operational settings due to its simplicity, low computational cost, and reasonable performance with limited data. Although it may not capture complex nonlinearities, it remains a robust baseline model in many practical applications [15].
Linear regression is a foundational statistical technique used to model the relationship between a dependent variable and one or more explanatory variables. In the context of electricity consumption forecasting, it can capture linear trends over time and incorporate external factors such as temperature, economic indicators, or calendar effects. The model is valued for its interpretability and ease of implementation, especially in settings with small datasets or where model transparency is required. However, its predictive accuracy may be limited in highly nonlinear or complex systems. Linear regression is often used as a benchmark model or a component of hybrid forecasting frameworks [16].
In summary, traditional statistical methods such as ARIMA, Holt-Winters exponential smoothing, and linear regression continue to serve as essential tools in electricity load forecasting. Over the past 2 decades, however, the field has witnessed a rapid evolution with the emergence of machine-learning and deep-learning techniques. These modern approaches offer greater flexibility in handling complex, high-dimensional, and nonlinear data structures, paving the way for more accurate and adaptive forecasting systems in dynamic energy environments.
3. Types of Load Forecasting—Comparative Analysis of Methods
Forecasting electricity consumption is a crucial tool for informed management decisions and effective planning of electricity expenditures. An analysis of scientific research highlights two key points: first, there is no universal method for predicting electricity consumption, and second, the increasing demand for higher forecasting accuracy drives the development of new approaches. As a result, we have conducted a review of the methodological foundations of electricity consumption. While similar reviews have been out in previous studies [6,7,8], this work stands out by providing review of the newest articles with an evaluation of their potential advantages and risks. Next, we will examine the specific objectives associated with each type of forecasting.
Very short-term and short-term objectives play a crucial role in effectively managing electricity demand and assessing opportunities for energy storage. Accurate forecasts for a day or several days ahead help mitigate peak loads. Research indicates that very short- and short-term forecasting is particularly relevant for planning electricity demand in regional energy systems, as well as in microgrids, which include individual large consumers such as buildings (offices, schools, hotels, etc.), infrastructure facilities, and industrial enterprises [17].
Medium-term forecasting is essential for planning electricity production and maintaining the power grid. Monthly forecasting, in particular, is critical for the operation of thermal power plants, which play a central role in coal dispatch and electricity trade [18].
Long-term forecasting is used for strategic planning of energy system development at the national level, within specific sectors, and for planning capital investment or major infrastructure and production facility maintenance. To generate long-term forecasts, multiple development scenarios are typically considered, such as GDP growth or production rate. Moreover, precise long-term forecasts are fundamental for designing effective environmental strategies, such as industrial decarbonization [13,19].
The choice of forecasting methods depends on the time horizon. Currently, the most commonly used methods include classical and deep machine-learning algorithms, genetic algorithms, wavelet analysis, and singular spectral analysis. However, the selection of methods varies depending on the specific problem being addressed and the structure of the available data. Interestingly, numerous studies have shown that traditional forecasting methods can achieve accuracy levels comparable to those of more advanced and computationally demanding intelligent techniques [20,21].
In the subsequent sections, we will examine the most widely adopted and recommended forecasting approaches discussed in the literature, organized based on their respective forecasting time horizons [17].
3.1. Very Short-Term Load Forecasting
Very short-term electricity load forecasting is a critical process used to predict electricity demand in intervals as brief as 30 min, usually performed 1 day ahead. This forecasting plays a crucial role in the effective management and operation of power systems, ensuring that electricity supply aligns with demand while balancing economic efficiency and operational requirements [22].
Reference [22], discusses the methodology for very short-term electric load forecasting using the Interval Type-1 Fuzzy Inference System (IT-1 FIS). The forecasting is conducted 1 day in advance at 30 min intervals, which is crucial for operational planning, maintenance, and cost optimization in energy management. The study focuses on the impact of different time difference settings on forecast accuracy. Traditionally, forecasting is performed by analyzing historical data from the same day of the week in previous years. The authors propose an alternative approach, where instead of analyzing past Fridays, data from previous weekdays (Thursday, Wednesday, and Tuesday) are used. The results indicate that the classical method (using past Fridays) produced a lower forecast error (0.4695%) compared to the alternative approach (0.6123%).
In Ref. [23], the focus is on residential load forecasting using a Long Short-Term Memory (LSTM) recurrent neural network (RNN) [24]. The study addresses the challenges of predicting electricity consumption at the individual household level, where high volatility and unpredictability make accurate forecasting difficult. The forecasting model employs a time step of 30 min, meaning it generates real smart meter readings from residential households, providing a detailed view of energy usage patterns. The LSTM-based model is trained and tested against benchmark forecasting methods, including Backpropagation Neural Networks (BPNN), K-Nearest Neighbors (KNN), Extreme Learning Machines (ELM), and empirical methods such as mean and a mean absolute percentage error (MAPE) minimization predictors. The results indicate that the LSTM model outperforms all other methods in predicting very short-term residential electricity consumption. The study evaluates forecasting accuracy using Root Mean Square Error (RMSE) and Root Mean Square Percentage Error (RMSPE), showing that the LSTM model achieves lower error rates than traditional approaches. The RMSE results indicate a significant improvement in forecasting precision, while the lower RMSPE values confirm the model’s ability to capture variations in consumption patterns effectively. Additionally, the study examines the effect of aggregating individual household forecasts, finding that this approach results in lower errors compared to directly forecasting total load. The LSTM model achieves an RMSE improvement of approximately 10–15 over traditional machine-learning models in aggregated forecasting scenarios. The study concludes that LSTM networks effectively learn complex temporal dependencies in residential energy consumption and can significantly improve forecasting accuracy. Future research should focus on optimizing LSTM hyperparameters and incorporating external factors such as weather data and appliance usage to further enhance predictions. The study also suggests that hybrid forecasting models, combining LSTM with statistical techniques, may further improve load forecasting reliability.
The article [25] introduces a hybrid approach that combines convolutional neural networks and long short-term memory networks to forecast residential energy usage. The CNN component extracts spatial features and reduces noises from multivariate time-series data, while the LSTM component captures long-term temporal dependencies and irregular trends. The model employs a sliding window algorithm to segment continuous data into fixed intervals, typically 60 min windows, allowing it to capture both local and global patterns effectively. Quantitatively, the CNN- LSTM model achieves a mean square error (MSE) of 0.3738, a mean absolute error (MAE) of 0.3493, and a mean absolute percentage error (MAPE) of 34.84, outperforming traditional methods such as linear regression and standalone LSTM models. Overall, the study demonstrates that the hybrid CNN-LSTM model is a robust and effective tool for forecasting residential energy consumption across various time resolutions, offering valuable insights for energy management and optimization.
The article [26] presents a model for forecasting electricity consumption in Spain using a deep LSTM network. The model predicts electricity consumption with a 4 h forecast horizon based on historical data recorded at 10 min intervals over a period of 9.5 years. The optimization of the network’s hyperparameters was conducted using two methods: random search and a heuristic algorithm inspired by the propagation of the SARS-CoV-2 virus, known as the Coronavirus Optimization Algorithm (CVOA). The time step used in the forecasting model is based on a historical window of 168 past values, covering a full day and 4 additional hours, to predict the next 24 values, equivalent to 4 hours ahead. The model’s performance was evaluated using typical error metrics. The MAPE indicates the relative accuracy of the model, with the best-performing LSTM model, optimized using random search, achieving a MAPE of 1.4472%, outperforming other forecasting techniques such as Temporal Fusion Transformers (TFT), Deep Feed-Forward Neural Networks (DFFNN), linear regression, decision trees, random forests, and gradient boosting. The most significant challenges in accuracy were observed during spring months and in August, while the worst predictions occurred on holiday periods such as Christmas Eve.
The article [27] shows a methodology for peak load forecasting in an open-pit mine using advanced machine-learning techniques. A key aspect of the analysis is the application of the Fast Forest Quantile Regression (FFQR) model, which enables precise predictions of energy consumption under various operational conditions [28]. The forecasting process begins with collecting historical data on energy consumption, machine-operating hours, and production indicators. These data are then processed and validated using k-fold cross-validation, ensuring their high quality and accuracy. FFQR was chosen as the primary algorithm due to its ability to model different energy consumption scenarios and its robustness against unforeseen changes in the data. Two experiments were conducted, varying the number of decision trees and leaves in the model to optimize forecasting accuracy. The results demonstrated that the FFQR model achieves high effectiveness in predicting energy consumption, allowing better management of the power grid and minimizing operational costs. Peak load forecasting is a crucial component of smart energy management in open-pit mining, supporting the transition to Energy 4.0 strategies and ensuring more efficient utilization of energy resources [29].
The paper [30] presents a model based on the Transformer architecture, designed for 1-day forecasting of electricity consumption (short-term) based on data from Baghdad, Iraq, collected every 15 min since 2015. The model uses a self-attention mechanism that, according to the authors and the literature they cited, handles long time dependencies better than traditional RNNs or LSTMs. Before using the model, the data were thoroughly processed (cleaning, gap filling, scaling, dimension reduction) to ensure high-quality inputs. The model achieved a low prediction error—RMSE ≈ 2.0 and a high correlation coefficient (CC) between actual and predicted values. The results prove that the transformer approach is competitive with existing methods and is suitable for practical use in forecasting energy demand in real systems.
The reference [31] presents a new approach to electrical load forecasting based on Transformer architecture with sparse attention. The motivation was to overcome the limitations of traditional deep-learning methods, such as RNN and CNN, in time-series forecasting, especially parallelization problems and long dependencies. The proposed model uses sparse attention, including a Big Bird implementation, to effectively address the quadratic memory costs associated with long data sequences in Transformers. The model architecture is based on an encoder and decoder, also handling multidimensional input data such as weather information to improve accuracy. Experiments were conducted on public datasets (from the United Kingdom, the United States, and Spain) for short-term (1 day) and longer-term (1 week) forecasts. The results showed that the model achieves comparable accuracy to the best RNN methods while being up to five times faster in the inference process, confirming its scalability and efficiency. Table 1 provides a summary of the forecasting methods for very short-term electricity consumption, as discussed in this section.

Table 1.
Summary of very short-term load forecasting consumption methods.
3.2. Short-Term Load Forecasting
This part of the article will focus on short-term load forecasting (STFL), a critical component in energy management and power system operations. STFL aims to predict electricity consumption over short time horizons, typically ranging from a day to several weeks [32]. Accurate short-term load forecasting is essential for balancing supply and demand, optimizing energy dispatch, and reducing operational costs in modern smart grids. Several approaches have a time-series forecasting method that models linear dependencies in electricity consumption data. ARIMA is effective for stationary time series but struggles with complex, nonlinear relationships [7]. Seasonal ARIMA or SARIMA is a special form of ARIMA model that is used mainly to model a wide range of seasonal data. This is attained by incorporating an additional seasonal parameter to handle a period of seasonality. Linear regression is one of the simplest and most widely used statistical methods for forecasting electricity consumption. It establishes a relationship between electricity consumption (dependent variable) and one or more independent variables, such as temperature, time of day, day of the week, and economic factors. The model assumes that electricity consumption changes linearly with these influencing factors, allowing for easy interpretation of results. In its basic form, simple linear regression uses a single predictor (e.g., temperature) to estimate future consumption, while multiple linear regression (MLR) incorporates several variables to improve accuracy. Despite its ease of implementation and interpretability, linear regression has limitations; it struggles to capture nonlinear dependencies and sudden fluctuations in energy demand. As a result, it is often used as a baseline model or in combination with machine-learning techniques for more accurate short-term electricity load forecasting [33,34].
The study aimed [35] to apply univariate Box-Jenkins time-series analysis (ARIMA) to model and forecast monthly electricity consumption in the Eastern Province of Saudi Arabia. Additionally, the study compared the effectiveness of this approach with regression models and machine-learning techniques. The selected model, the ARIMA model, achieved an average percentage error of 3.8%, which was better than regression models (8.1%) and artificial neural networks (5.6%). The ARIMA model had a 70% lower absolute error and 58% lower mean square error than the moving average (MA) model. All actual consumption values fell within the 95% confidence interval of the forecasts, indicating high model accuracy. Seasonality was a key factor in achieving accurate predictions, as peak electricity consumption occurred in summer due to increased demand for air conditioning. The ARIMA model outperformed both regression and machine-learning models in forecasting monthly electricity consumption. It did not require additional variables (e.g., temperature, population), making it a more universal forecasting tool. The strong fit to test data suggests that this model can be effectively used for energy consumption planning in regions with distinct seasonality. In conclusion, ARIMA is an effective method for short-term forecasting of monthly electricity consumption, surpassing regression and machine-learning approaches in prediction accuracy. This model can be successfully applied to energy management and planning in areas with clear seasonal consumption patterns.
The study [29] aimed to use the Box-Jenkins ARIMA model to forecast monthly household electricity consumption in the Eastern Province of Saudi Arabia. The study utilizes 5 years of historical data for model training and evaluates its forecasting accuracy using the 6th year’s data Although the article dates back to the previous century, it may still provide valuable insights into the conclusions drawn by researchers at that time.. Scientists used the ARIMA approach, which demonstrates superior forecasting performance. The optimal model is a multiplicative combination of seasonal and non-seasonal autoregressive components, both of the first order, with first differencing applied at both seasonal and non-seasonal levels. The ARIMA model achieves an average percentage error of 3.8%, outperforming regression models (8.1%) and abductive network models (5.6%). The mean square forecasting error is also significantly lower, reduced by factors of 3.2 and 1.6, respectively. The study highlights the advantages of ARIMA models, including lower data requirements, fewer parameters, and higher accuracy compared to regression-based and machine-learning-based models. While machine-learning techniques allow for automated model discovery, ARIMA remains a robust choice due to its interpretability and reduced dependency on external variables. The findings suggest that time-series analysis can effectively capture seasonal and long-term electricity consumption trends, making it a valuable tool for energy planning and management.
The article [36] shows developing a real-time energy monitoring system and using Artificial Neural Networks (ANNs) to forecast peak electrical consumption 60 min ahead in a large government building. The study compared the ANN model’s performance with three other forecasting methods, which are Simple Moving Average (SMA), Linear Regression, and Multivariate Adaptive Regression Splines (MARSplines). The Linear Regression model was developed using a 90-day dataset and included the following independent variables: Ltime of day, type of day, HVAC energy consumption, outdoor temperature, and humidity. The regression equation was applied to a 24 h test period, and its performance was evaluated. However, the Linear Regression model was the least accurate among the tested methods, with a MAPE of 17.3% and Absolute Maximum Error (AME) of 45.1%, making it the weakest model in terms of forecasting peak electrical demand. In contrast, the ANN model significantly outperformed all other models, achieving a MAPE of 3.9% and AME of 8.2%. The ANN model was designed using key building parameters such as HVAC energy consumption, time of day, type of day, outdoor temperature, and humidity as inputs. It was able to dynamically adjust to complex patterns in energy consumption, making it the most effective forecasting approach. The Simple Moving Average model was also tested, using a 60 min window of past data to predict the next 60 min. It had a MAPE of 7.7% and an AME of 26.2%, performing better than Linear Regression but still far less accurate than ANN. The MARSplines model, which is a nonparametric regression technique, was included as another benchmark method. It offered improved flexibility over traditional regression but still underperformed compared to ANN. The MAPE for MARSplines was 7.0%, and the AME was 22.5%, making it the second-best method after ANN. Overall, the study concluded that ANNs provide the best forecasting accuracy for short-term peak electrical demand in large buildings, outperforming statistical models such as Linear Regression, SMA, and MARSplines. The ANN-based forecasting approach demonstrated its ability to effectively reduce peak demand charges by providing real-time predictive insights, enabling building management to take proactive steps to reduce energy consumption.
The study [33] explores the use of ANN for short-term load forecasting in microgrids. The study analyzes various prediction models and examines the impact of different input variables, including solar radiation, on forecast accuracy.
The research is motivated by the increasing complexity of modern power systems, particularly with the integration of renewable energy sources and distributed generation, which makes demand forecasting more challenging. The study is based on the CEDER-CIEMAT microgrid in SPAIN, using two datasets: one covering 4.5 years of electricity consumption data, and another covering 4 months that includes solar radiation data. The forecasting models use a multi-layer perceptron (MLP) neural network and test different learning algorithms, such as Levenberg-Marquardt, gradient descent, and resilient propagation. Several input configurations are tested, including previous data consumption, workday classification, and day of the week and month. The study evaluates model performance using MAPE as the key metric. The best-performing model includes previous-day consumption, workday classification, and month as input. This model achieves a MAPE of 15.34% when trained on the larger dataset and 16.69% when trained on the smaller dataset. Surprisingly, adding solar radiation as an input variable does not improve forecast accuracy. The study also finds that a model trained on only 3 months of data can achieve similar accuracy to one trained on 3 years of data. The results highlight the challenges of load forecasting in microgrids due to high variability in demand profiles. The findings suggest that while ANN models are effective for STFL, careful selection of input variables is crucial. Future research will explore additional factors influencing demand patterns and validate new models in microgrid environments.
The study [37] uses an ensemble deep-learning method combining three models: Long Short-Term Memory, Gated Recurrent Unit (GRU), and Temporal Convolutional Networks (TCN). The dataset includes 14 years of monthly electricity consumption data from nearly 2000 clients in Bejaia, Algeria. The proposed models are evaluated using statistical metrics such as MAE, MAPE, and RMSE. The results show that the ensemble models significantly outperform individual models and traditional forecasting methods, providing more accurate electricity consumption predictions. The research concludes that ensemble deep-learning approaches offer substantial improvements in forecasting performance and can be effectively used by energy suppliers like Sonelgaz to enhance electricity planning and management.
The article [38] presents a novel hybrid approach that integrates classical statistical techniques and machine learning for national electricity demand forecasting. The study addresses the need for long-term forecasts with high-resolution data, essential for energy system planning and investment. Using hourly electricity consumption data from Ukraine between 2013 and 2020, the model decomposes demand into long-term, medium-term, and short-term components. The long-term trend is modeled using macroeconomic regression analysis, the medium-term model incorporates temperature and calendar regressors while combining ARIMA and LSTM approaches to capture residual patterns, and the short-term model accounts for hourly seasonality using calendar-based regression and ARMA models for residuals. The results show that the best-performing model is a hybrid approach combining multiple regression models with LSTM for residual forecasting, achieving an accuracy of 96.83% over a 2-year test period with 17,520 time steps. The short-term forecasting analysis confirmed that daily electricity consumption patterns remained stable over the years, and ARMA models effectively captured hourly variations, making the use of LSTM unnecessary for short-term residual prediction. The study demonstrates that integrating statistical and machine-learning methods enhances forecasting accuracy by addressing different time scales while allowing for interpretability in energy demand drivers. However, the model’s reliance on accurate macroeconomic and weather forecasts poses a challenge for long-term predictions. The authors suggest that the methodology can be applied to other countries and emphasize the importance of automation for future implementations [39].
The study [40] focuses on short-term (daily) and middle-term (yearly) electricity load forecasting at a local level within the French distribution grid. The authors propose a semi-parametric approach based on Generalized Additive Models (GAMs) to estimate the relationship between electricity demand and various explanatory variables, such as temperature (current and lagged), calendar effects (days of the week, holidays, and special tariffs), and seasonal patterns (daily, weekly, and yearly cycles). GAMs offer flexibility by modeling nonlinear relationships, making them well-suited for analyzing large datasets. The dataset used in this study consists of electricity consumption recorded every 10 minutes from 2260 substations across France between 2006 and 2011, combined with temperature data from 63 weather stations. Each substation was assigned to the nearest relevant weather station. The results show that the middle-term forecasts achieved a median Mean Absolute Percentage Error of 8%, which was reduced to 6% after applying an additional detrending step. For short-term forecasting, incorporating lagged electricity consumption significantly improved accuracy, lowering MAPE to 5%. Compared to naïve benchmarks, such as using the previous year’s load, the proposed models performed significantly better. The study highlights the effectiveness, interpretability, and scalability of GAM-based models for electricity load forecasting. However, the authors suggest potential improvements, such as automatic variable selection using techniques like LASSO, integrating additional weather and demographic variables, and developing multivariate models to capture dependencies between substations. The findings demonstrate that semi-parametric additive models provide a promising balance between accuracy, interpretability, and computational efficiency for electricity demand forecasting.
The article [41] explores short-term forecasting of renewable energy consumption and generation in a Peer-to-Peer (P2P) energy trading system in Western Australia. The research is based on real-time energy data collected from smart meters installed in residential households between August 2018 and April 2019, with a time resolution of 5 s. The dataset includes energy imported from and exported to the grid, rooftop photovoltaic (PV) generation, household energy consumption, and outdoor temperature. A variety of forecasting methods were tested, including statistical models, traditional machine-learning techniques, and deep learning models. The results demonstrate that the LSTM model significantly outperforms all other approaches, achieving the lowest RMSE and MAE for both energy consumption and generation forecasting. The optimized LSTM model successfully captured the periodicity and temporal dependencies of energy patterns, making it more accurate than classical methods like ARIMA, VAR, and linear regression, as well as AutoML-based models, such as those implemented in RapidMiner. Classical models failed to capture the complex nonlinear relationships in energy generation and consumption, leading to higher errors. Machine-learning models implemented in RapidMiner (including Gradient Boosted Trees, Random Forest, and SVM) also underperformed compared to the deep-learning-based LSTM model. The study highlights that deep-learning approaches, particularly LSTM networks, provide significant accuracy improvements in short-term energy forecasting due to their ability to retain long-term dependencies and adapt to dynamic energy consumption patterns. The authors suggest further improvements by integrating Convolutional Neural Networks (CNNs) with LSTM to enhance feature extraction and employing advanced hyperparameter tuning techniques.
The study [32] investigates short-term forecasting of photovoltaic power production in a self-consumption system using hybrid deep-learning models. The authors propose two hybrid models, CNN-LSTM and ConvLSTM, which combine CNN and LSTM networks. These models aim to capture both spatial and temporal dependencies in PV power generation data. Their performance is compared against a standard LSTM model, which serves as the baseline. The study employs two datasets, an univariate dataset, which only includes historical PV power output, and a multivariate dataset, which incorporates additional weather features such as temperature, wind speed, humidity, cloud cover, and solar irradiation. The forecasts cover time horizons ranging from 1 day to 1 week ahead. The models are evaluated by using RMSE, MAE, and MAPE. Shorter forecast horizons yielded more accurate predictions across all models. The 1-day-ahead forecast performed the best, with CNN-LSTM and ConvLSTM achieving the lowest error rates. Hybrid models (CNN-LSTM and ConvLSTM) outperformed the standalone LSTM model across all forecast horizons. This confirms that integrating CNN with LSTM enhances feature extraction and learning capabilities. Multivariate datasets improved forecast accuracy for longer horizons, highlighting the importance of incorporating weather-related variables in PV power prediction. The accuracy of all models declined as the forecast horizon increased, but the hybrid models retained a significant edge over the baseline LSTM.
The article [42] proposes adapting the Transformer architecture for electrical load forecasting. The proposed Transformer-based model addresses these limitations by leveraging its inherent parallel processing capabilities and is designed to handle diverse data streams to ensure portability and reproducibility. The authors modified the standard NLP Transformer workflow by introducing an N-space transformation module and a novel technique for incorporating contextual features directly within the Transformer architecture. This approach aims to improve forecasting accuracy while overcoming the performance challenges of deep-learning models in load forecasting. Evaluation across 20 distinct data streams and various forecasting horizons demonstrated that the adapted Transformer successfully handles time series with contextual data and outperforms state-of-the-art Seq2Seq models.
The reference [43] applies a Transformer-based model to forecast electric vehicle (EV) charging demand. The aim of the study was to accurately predict hourly energy demand at EV charging stations, which is crucial for infrastructure management and network stability. The model was tested on actual data from a German charging station operator, including charging time, session length, energy volume, and location ID. The model architecture used a Transformer Encoder with a self-attention mechanism to capture temporal and seasonal dependencies without the need to process the data sequentially, as in RNN or LSTM. The input data included a time window of 24 h, and the model forecasted demand for the next 24 h—which means forecasting with a time step of 1 h, 24 h ahead. The model achieved better results (lower MAE and RMSE) than the classic LSTM and GRU, demonstrating its effectiveness in environments with high data variability. The authors emphasize that this approach can be an important tool for network operators, especially in the context of increasing EV and dynamic loads.
This scientific paper [44] introduces a new and improved method for forecasting the output of renewable energy sources like solar and wind power. Accurate predictions are vital because the variability of these energy sources can make managing the electrical grid challenging. The authors propose a novel system called H-Transformer, which is a hybrid model designed to tackle this uncertainty. It uniquely combines a more traditional, straightforward forecasting method called SARIMA (which handles clear, linear patterns) with a cutting-edge Transformer neural network. The Transformer component is specifically used to predict the “leftover” complex, non-linear patterns that SARIMA might miss, and the system also integrates external information like weather data for better accuracy. The H-Transformer works in three stages: first, SARIMA makes an initial prediction; then, the Transformer analyzes and forecasts the errors from that first prediction; finally, these two forecasts are combined. This intelligent design aims to capitalize on the strengths of both linear and advanced non-linear modeling. The model’s settings are fine-tuned using a smart optimization technique called Bayesian Optimization. Through extensive tests on five different datasets of wind speed and solar energy, the H-Transformer consistently showed better prediction accuracy than various standalone machine-learning models. It also frequently outperformed other hybrid forecasting approaches, proving to be a highly effective and reliable tool for short-term renewable energy forecasting. Table 2 provides a summary of the forecasting methods for short-term electricity consumption, as discussed in this section.

Table 2.
Summary of short-term load forecasting consumption methods.
3.3. Medium-Term Load Forecasting
This part of the article will focus on Medium-Term Load Forecasting, which plays a big role in energy planning and grid management by predicting electricity demand over a period of several months to a few years.
The study [45] compared the performance of ARIMA and ANN models to predict Taiwan’s energy consumption over different time horizons, including a medium-term period of 1 year, but also 3 years, 5 years, and 10 years. The single-variable ARIMA model demonstrated high accuracy for the 1-year prediction, with a MAPE of 3.14%, which is classified as “highly accurate” according to Lewis [46]. The ARIMA model is a linear statistical approach that relies on historical data to forecast future trends, making it particularly effective for stationary time-series data. In this study, the ARIMA model was applied to a single variable—energy consumption—and outperformed the single-variable ANNs1 model in most timeframes, except for the medium term (3 years), where the 2008 financial crisis likely impacted its accuracy. The ARIMA model’s strength lies in its ability to handle linear relationships and its simplicity, as it does not require additional explanatory variables like GDP or population. However, its performance can be limited in cases of extreme nonlinearity or when external shocks (e.g., economic crises) disrupt historical trends. Despite these limitations, the ARIMA model proved to be a reliable and practical tool for energy consumption forecasting, especially for medium-term and long-term predictions, where it consistently delivered highly accurate results. This makes it a valuable benchmark model for comparison with more complex approaches like ANNs. In the study, the ANN models were designed to predict Taiwan’s energy consumption using different combinations of input variables, such as energy consumption (ENG), GDP, population (POP), and exports (EXP). In this article, export refers to the value of goods and services exported from Taiwan to other countries. It is a key economic factor used in energy consumption forecasting models, as higher export levels often correlate with increased industrial production and energy demand [47]. The models ranged from simple single-variable setups (e.g., ANNs1, which only used energy consumption) to more complex multivariable configurations (e.g., ANNs10, which included energy consumption, exports, population, and GDP). The goal was to determine which variables had the most significant impact on prediction accuracy across different time horizons (short term, medium term, medium–long term, and long term). For the 1-year prediction horizon, the ANNs8 model, which included energy consumption and exports, achieved the highest accuracy with a MAPE of 0.32%, indicating that exports play a crucial role in short-term energy consumption forecasting. In contrast, the ANNs5 model, which used energy consumption and population, performed best for long-term predictions (10 years), suggesting that population growth is a key driver of energy demand over extended periods. The study also found that while adding more variables (e.g., GDP, population, exports) generally improved prediction accuracy, simpler models with fewer variables (e.g., ANNs8 or ANNs5) often performed just as well or even better in certain timeframes. This highlights the importance of selecting the right variables for specific prediction horizons, as overly complex models may not always yield better results. Overall, the ANN models demonstrated flexibility and effectiveness in capturing both linear and nonlinear relationships in energy consumption data, making them valuable tools for policymakers and energy planners in Taiwan.
The article [48] focuses on predicting the maximum hourly electricity consumption per day in Slovakia using Grey Models (GM) and Artificial Neural Networks, aiming to develop more accurate forecasting models than the official predictions provided by SEPS (Slovak Transmission System Operator). The study utilized Grey Models for trend analysis and a multi-layer feed-forward back-propagation neural network for capturing complex consumption patterns, with a hybrid model combining both approaches to improve accuracy. The models were trained on data from 2010–2018 and tested on data from 2019 and 2020, with the ANN model achieving the best results, particularly in 1-year horizon forecasts, while the GM model performed well in medium-term 2-year horizon predictions. The hybrid model, combining ANN and GM in an 85/15 ratio, showed slight but measurable improvements in accuracy. All proposed models outperformed the official SEPS predictions, even during the COVID-19 pandemic in 2020, which disrupted energy consumption patterns. The study concludes that the hybrid model, along with Grey Models and ANN, offers a reliable approach for forecasting electricity consumption in Slovakia, providing valuable tools for energy industry planning and management.
The study [49] explores predicting electricity consumption in industrial enterprises with continuous production processes, using the ARIMA model. The study aimed to develop accurate forecasting models that address the challenges of predicting energy consumption in industrial settings, where traditional methods may struggle due to the complexity of the data. The article outlines a detailed algorithm for forecasting energy consumption using ARIMA, including steps for differencing, determining autoregression and moving average orders, and utilizing the Dickey-Fuller test to check stationarity, along with autocorrelation (ACF) and partial autocorrelation (PACF) functions to determine model parameters. The ARIMA model was applied to predict energy consumption in a metallurgical enterprise, and the comparison between actual and forecasted values showed high accuracy, with a forecasting error of 6%. The results demonstrate that the ARIMA model is suitable for predicting energy consumption in industrial enterprises with continuous production processes. The study concludes that the ARIMA model is an effective tool for energy consumption forecasting, providing high accuracy and reliability, and it can be used for planning and optimizing energy use in industrial enterprises, thereby improving energy efficiency.
The article [50] analyzes different forecasting models for Turkish electricity consumption, comparing single time-series models like SARIMA with hybrid machine-learning models such as SARIMA-ANNs and SARIMA-MLPs. The main objective of the study was to determine the most accurate forecasting model for electricity consumption in Türkiye by evaluating both traditional statistical models and advanced hybrid models. The researchers tested various hybrid models, including the Zhang additive hybrid model, the multiplicative Wang et al. model, and the combined model by Khashei & Bijari [51,52,53]. The study examined how these models handle linear and nonlinear components of the time series, which are often difficult to separate in electricity consumption data. The results confirm that hybrid models are more effective than single models when forecasting electricity consumption in Türkiye. The Khashei & Bijari (SARIMA-ANNs) hybrid model is the most suitable approach when linear and nonlinear structures cannot be easily separated and had the lowest RMSE (0.0792) and MAE (0.04463), making it the most accurate model. The traditional SARIMA model performed worse, with an RMSE of 0.0823 and an MAE of 0.0523. Machine-learning techniques, particularly ANNs with the GRprop algorithm, can significantly enhance forecasting accuracy. In cases where electricity consumption patterns are highly complex and nonlinear, traditional statistical models like SARIMA may not be sufficient. The study suggests that future forecasting approaches should integrate hybrid techniques to achieve more reliable predictions for electricity demand planning.
The study [54] presents an optimized deep-learning-based LSTM model for electric load forecasting. The research focuses on enhancing forecasting accuracy through feature selection and the use of a genetic algorithm (GA) to optimize time lags and the LSTM network architecture. The dataset used for validation consists of electricity consumption data from metropolitan France. The LSTM model was compared against conventional machine-learning models, including linear regression, k-nearest neighbors, random forests, gradient boosting, and artificial neural networks. Among these, the Extra Trees Regressor model performed best and was used as a benchmark. Feature importance analysis revealed that time lags played a crucial role in forecasting accuracy, whereas weather-related variables, such as temperature, had a limited influence. The GA was applied to determine the optimal number of time lags and hidden layers in the LSTM model, ensuring improved predictive performance while avoiding overfitting. The results showed that the optimized LSTM model significantly outperformed conventional machine-learning models. The LSTM model achieved a root mean square error (RMSE) of 378 compared to 513.8 for the Extra Trees model, representing an improvement of approximately 26.4%. Similarly, the MAE for the LSTM model was 270.4, compared to 344 for the Extra Trees model, yielding a 21.4% improvement. The coefficient of variation for RMSE (CV RMSE) was also reduced from 1.95% in the Extra Trees model to 1.31% in the LSTM model. The study evaluated both short-term (2 weeks) and medium-term (up to 4 months) forecasting horizons. For short-term predictions, the RMSE was 339, while for medium-term predictions, it ranged between 258 and 294, depending on the forecasting window. The CV RMSE for short-term forecasts was 0.61%, while for medium-term forecasts, it averaged 0.56%, indicating stable and reliable performance over varying forecasting periods. The proposed approach demonstrated the effectiveness of deep learning in capturing complex time-series patterns and optimizing forecasting performance. By leveraging feature selection and genetic algorithms, the LSTM model provides a robust solution for electric load forecasting, outperforming traditional machine-learning models in both accuracy and stability.
The study [55] explores the application of time-series models for forecasting energy consumption in India, with a particular focus on electricity consumption. Three models were used: the Grey-Markov model, the Grey model with a rolling mechanism, and Singular Spectrum Analysis (SSA). The Grey model with a rolling mechanism was specifically employed to predict electricity consumption trends. The research analyzed historical electricity consumption data from 1970 to 2007, revealing a significant increase from 43.7 TWh to 443.1 TWh. Due to the rapid growth in energy demand, accurate forecasting is crucial for energy policy planning and sustainability. For electricity consumption forecasting, the Grey model with a rolling mechanism was chosen due to its suitability for capturing exponential growth trends in time-series data. The model was trained using 5 years of historical data to predict the next year’s consumption. Two out-of-sample forecasts were performed to validate the model, and the results showed a MAPE of 3.4%. The prediction accuracy for the last 2 years of validation data was 96.9% and 95.1%, demonstrating the model’s effectiveness. The study concluded that this time-series approach provides a viable and accurate alternative for electricity consumption forecasting. Compared to the projections from the Planning Commission of India, the model demonstrated comparable or even better forecasting accuracy, making it a useful tool for energy planning and decision-making. Table 3 provides a summary of the forecasting methods for medium-term electricity consumption, as discussed in this section.

Table 3.
Summary of medium-term load forecasting consumption methods.
3.4. Long-Term Load Forecasting
Long-term load forecasting (LTLF) has a pivotal role in energy planning and management, enabling utilities, policymakers, and grid operators to anticipate future electricity demand over extended periods, typically ranging from several years to decades. Accurate long-term forecasts support investment decisions in power generation, transmission, and distribution infrastructure, ensuring a stable and efficient energy supply. Various methods, including statistical models like ARIMA and machine-learning approaches, are employed to predict consumption patterns based on historical data, economic growth, population expansion, and technological advancements. As electricity demand continues to evolve due to urbanization, industrialization, and the integration of renewable energy sources, reliable long-term forecasting becomes increasingly vital for sustainable energy planning and policy development [56].
The article [57] presents a methodology that integrates the bottom-up approach with hierarchical linear models and Bayesian inference to forecast long-term electricity consumption. This approach allows for a more detailed and structured analysis by breaking down electricity consumption at the process level and aggregating results for an entire industrial sector. Bayesian inference, combined with Markov Chain Monte Carlo (MCMC) methods, enables uncertainty quantification, making the forecasts more reliable. The study applies this methodology to the Brazilian pulp and paper industry, analyzing historical electricity consumption from 2008 to 2014 and projecting it up to 2050. The model successfully captures past consumption patterns with high accuracy (MAPE = 2%) and generates probabilistic forecasts rather than single-point estimates. The results indicate a steady increase in electricity consumption, reaching 170 PJ by 2050 in a scenario where no energy efficiency measures (EEMs) are applied. However, implementing cost-effective EEMs could reduce consumption by 25%, leading to a total of 128 PJ in 2050. Compared to deterministic models, the Bayesian stochastic model provides probability distributions for each forecasted year, offering credible intervals that aid in decision-making. The study highlights the importance of incorporating energy efficiency measures and presents different technological diffusion scenarios, showing that proactive policies can significantly reduce energy demand. The findings contribute to long-term energy planning, offering a novel probabilistic approach that enhances the robustness of electricity consumption forecasts.
The article [58] presents a regression-based approach to forecasting monthly electricity demand in South Korea. The proposed model integrates key external variables, including weather conditions (temperature, solar radiation), calendar data (working days, holidays), and industrial activity (number of registered factories), which significantly influence electricity consumption. The study aims to identify the most impactful factors and construct a regression model that provides accurate mid-term forecasts. The dataset covers historical electricity consumption from 2012 to 2021, and the model is used to predict monthly demand for 2022 and 2023. The data sources include the International Energy Agency (IEA) for electricity consumption, the Korean Meteorological Administration for weather data, the Korean Statistical Information Service (KOSIS) for industrial activity, and the WHO COVID-19 Dashboard for pandemic-related impacts. The regression model captures seasonal trends, temperature effects, industrial production levels, and calendar influences, improving forecasting accuracy. The regression equation includes key predictors such as electricity consumption from the same month in the previous year (seasonality), month as a categorical variable (seasonal fluctuations), average temperature (non-linear effects on energy demand), number of working days (calendar influence), number of holidays (reduced industrial activity), number of registered factories (industrial electricity consumption), and an interaction term between industrial activity and seasonality. Additionally, the study incorporates log-transformed COVID-19 cases to examine the pandemic’s impact on electricity demand. Correlation analysis confirms that temperature, industrial production, and seasonal factors play a significant role in predicting electricity consumption. To evaluate the performance of the proposed model, the study compares it with various forecasting techniques, including traditional time-series models (Holt–Winters, SARIMA, Prophet), machine-learning methods (Random Forest, XGBoost, LightGBM, RNN, LSTM), and ensemble approaches (combinations of multiple models). The results demonstrate that the regression model outperforms all tested methods, achieving a MAPE of 2.01%, the lowest among all models. Benchmark models such as SARIMA and LSTM performed worse, with MAPE values exceeding 4%, highlighting the efficiency of the regression approach in handling mid-term load forecasting. One key finding is that machine-learning models did not consistently outperform the regression model, particularly due to limited available monthly data. While ML models generally perform well with large datasets, the study suggests that a well-structured regression model with carefully selected variables can achieve superior performance with smaller datasets. Furthermore, ensemble methods improved the accuracy of individual models but failed to surpass the performance of the proposed regression model. The study concludes that considering external factors such as industrial activity, calendar effects, and weather conditions significantly enhances forecasting accuracy. The findings are particularly relevant for energy policymakers, grid operators, and industry planners, providing a reliable and interpretable tool for mid-term electricity demand forecasting. The research also suggests that future work should explore additional economic indicators, hybrid models combining statistical and machine-learning approaches, and adaptive learning techniques to further enhance predictive accuracy.
This study [59] examines long-term electricity consumption forecasting in Algeria by comparing two forecasting models: ARIMA and GM. The research highlights the critical role of electricity consumption in economic development and energy security, emphasizing the need for accurate forecasting methods to support strategic planning and policy-making. The study utilizes annual electricity consumption data from 1982 to 2020, dividing the dataset into a training period (1980–2015) and a testing period (2016–2021). Both ARIMA and GM models are applied to forecast consumption trends, with performance evaluated using the MAPE metric. The results indicate that the ARIMA model significantly outperforms the GM model, with a much lower MAPE value of 4.47% for ARIMA vs. 67.95 for GM, demonstrating superior predictive accuracy. The ARIMA model is then used to generate forecasts from 2022–2030, predicting a steady increase in electricity consumption, with values rising from 65,333 GWh in 2022 to 76,976 GWh in 2030. The study underscores the importance of robust forecasting techniques in guiding Algeria’s energy policies, infrastructure development, and sustainable energy strategies. The findings suggest that ARIMA is a more reliable model for electricity consumption forecasting, while the GM model, despite its lower data requirements, is less accurate in long-term predictions.
The study [60] forecasts renewable energy consumption and gross final energy consumption (GFEC) in six European countries (France, Germany, Italy, Spain, Turkey, and the UK) for the period 2020–2030, based on historical data from 2004–2018. The forecasting method applies an optimized fractional nonlinear grey Bernoulli model (OFANGBM), enhanced with genetic algorithm (GA) optimization, which improves predictive accuracy over the traditional FANGBM model. Key findings indicate that total energy consumption (GFEC) and renewable energy consumption (RES) will increase across all countries, with the highest share of renewables in 2030 expected in the UK (29.7%) and Spain (27.5%), while Turkey is projected to have the lowest share (15.1%). Germany will have the highest absolute renewable energy consumption (53.8 Mtoe), while Italy and Turkey will experience slower growth. The study highlights that some countries may struggle to meet their renewable energy targets, emphasizing the need for strategic policy planning. The results demonstrate that the OFANGBM model outperforms previous grey forecasting approaches, providing more reliable predictions for energy policymakers.
The study [61] focuses on long-term electricity consumption forecasting in Italy using linear regression models based on historical data from 1970 to 2007. The forecasting models incorporate key economic and demographic variables, particularly GDP, GDP per capita, and population growth, to estimate future electricity demand. The results indicate that GDP is the most significant driver of electricity consumption, with a strong positive correlation between economic growth and energy demand. Forecasts suggest that electricity consumption in Italy will continue to grow at an average annual rate of approximately 2% until 2030. Models that include GDP and population provide the most accurate predictions, while those relying solely on GDP per capita are less effective. The study compares its forecasts with official projections from Terna (Italy’s transmission system operator) and CESI (a research institute), finding that the developed models align closely with official estimates, with deviations ranging from ±1% (best-case) to ±11% (worst-case). This validation highlights the reliability of simple regression-based forecasting methods for long-term energy planning. One of the key policy implications is that electricity prices have a limited impact on consumption, making them an ineffective tool for demand regulation. Instead, forecasting energy consumption should be closely linked to GDP growth projections, as economic expansion remains the primary factor influencing energy demand. The article about Italy is from 2009, and the model proposed had little in common with the actual conditions and challenges faced by the Italian energy sector in the following years.
The study [62] examines electricity consumption forecasting in Brazil’s industrial sector using statistical time-series models and artificial neural networks (ANNs). The research compares the effectiveness of traditional forecasting approaches, including Holt-Winters, SARIMA, Dynamic Linear Model (DLM), and TBATS, against AI-based models such as Neural Network Autoregression (NNAR) and MLP. Monthly electricity consumption data from January 1979 to December 2020 were used, with models trained on data from 1979 to 2018 and tested on the 2019–2020 period. The results indicate that the MLP model achieved the highest accuracy, outperforming all statistical models, with a MAPE of 3.41%. In comparison, SARIMA had the highest error at 6.17%, while TBATS and Holt-Winters performed moderately well with MAPE values of 3.77% and 4.09%, respectively. The study highlights that economic crises, particularly in 2001, 2009, and 2020, significantly impacted electricity consumption patterns. AI-based models, particularly MLP, demonstrated superior capability in capturing nonlinear trends and seasonal variations. The findings suggest that while traditional models remain useful for short-term forecasting, neural networks provide more robust long-term predictions.
The article [63] focuses on long-term electricity consumption forecasting in Indonesia using ANNs. The study aims to compare the accuracy of ANN-based predictions with official government forecasts from RUPTL (Electricity Supply Business Plan), developed by Indonesia’s Ministry of Energy and Mineral Resources. The ANN-based forecasting model was compared with traditional forecasting methods, including exponential smoothing, ARIMA, and linear regression. The study utilized historical electricity consumption data from 2000 to 2018, incorporating key variables such as GDP, population, and the number of PLN electricity customers. The results showed that ANNs achieved high accuracy in training, with a minimal MSE = 0.019560 compared to exponential smoothing MSE = 24.04682. However, forecasts for 2019–2025 showed significant deviations from official RUPTL projections. The ANN model predicted electricity consumption of 249.34 TWh in 2025, while RUPTL estimated 360.93 TWh. This discrepancy is primarily due to the limited number of input variables in the ANN model, as RUPTL incorporates additional economic factors such as inflation, electrification rates, and energy prices. In conclusion, Artificial Neural Networks proved highly effective in modeling historical electricity consumption, but their application for long-term forecasting requires incorporating additional economic variables.
The article [56] explores long-term electricity consumption forecasting for both developing and developed economies, focusing on Iran and the United States. The study applies ANN optimized using Improved Particle Swarm Optimization (IPSO) to enhance forecasting accuracy. The model uses historical data from 1967 to 2009 and predicts energy consumption trends from 2010 to 2030, incorporating economic and demographic indicators such as GDP, energy imports and exports, and population. The results indicate that ANN models optimized with IPSO outperform traditional regression models, achieving MAPE values of 1.94% for Iran and 1.51% for the United States, significantly improving predictive accuracy. The study finds that economic indicators provide better forecasting accuracy than relying solely on historical energy consumption data. The forecasts show that Iran’s energy consumption will increase 2.73 times by 2030, whereas the US will experience a much slower growth rate of approximately 1.09% annually due to effective demand-side management (DSM) policies. The IPSO algorithm enhances classical PSO by introducing mutation operators that prevent premature convergence and improve global search capabilities. The findings suggest that AI-based forecasting models, particularly IPSO-ANN, provide a reliable tool for long-term energy planning, particularly when incorporating macroeconomic variables.
The article [64] explores a deep-learning approach for electricity consumption forecasting, focusing on capturing both short-term and long-term temporal dependencies in time-series data. Traditional methods like ARIMA and Gaussian Processes often struggle with modeling multi-scale patterns, leading to suboptimal forecasting accuracy. To address this issue, the authors propose Long- and Short-term Time-series Network (LSTNet), a deep neural network architecture designed to handle complex temporal dependencies in energy consumption data. LSTNet integrates CNNs to extract short-term local patterns, RNNs to model long-term dependencies, and anmAR components to enhance prediction stability. The model is evaluated on real-world datasets of electricity consumption, demonstrating its superiority over classical statistical models and standard deep-learning approaches like LSTM and GRU. The results show that LSTNet significantly improves long-term forecasting accuracy by effectively capturing periodic trends and external influences on energy demand. The article presents a novel approach to probabilistic individual load forecasting using an LSTM network guided by the Pinball Loss function. Unlike traditional load forecasting methods that focus on aggregated demand, the increasing availability of smart meter data enables more accurate modeling of individual energy consumption patterns. One of the main challenges in individual load forecasting is the stochastic and non-stationary nature of energy consumption, which limits the effectiveness of classical methods such as ARIMA, linear regression, and SVR. To address this, the study proposes an LSTM-based model capable of capturing both short-term fluctuations and long-term dependencies in time-series data. Instead of providing point estimates, the model generates quantile forecasts, allowing a more comprehensive representation of uncertainty in energy demand predictions. The main contributions of this research include the integration of LSTM with Pinball Loss, which estimates an entire distribution of future demand rather than a single predicted value, and the development of a multi-output quantile model, which enables the simultaneous forecasting of multiple quantiles with lower computational cost. The study compares the proposed model against other probabilistic forecasting techniques, including QRNN, Quantile Gradient Boosting Regression Tree (QGBRT), and standard LSTM with error estimation. Experiments were conducted using the Smart Metering Electricity Customer Behavior Trials (CBTs) dataset from Ireland, covering both individual consumers and small and medium enterprises (SMEs). The results indicate that Pinball Loss Guided LSTM achieved the lowest forecast error among all tested models, improving accuracy by 2.19% to 7.52% for individual consumers and 3.79% to 25.80% for SMEs. The study also highlights that forecasting errors are highest during morning and evening peak hours, particularly between 7:00–8:00 and 17:30–22:00 for residential consumers, and 9:30–20:00 for SMEs, confirming that energy usage is most volatile during these periods. The findings suggest that quantile-based forecasting is essential for managing demand uncertainty and optimizing energy distribution strategies, making this method particularly valuable for demand response programs, smart tariffs, and energy storage optimization in residential and commercial sectors. Table 4 provides a summary of the forecasting methods for long-term electricity consumption, as discussed in this section.

Table 4.
Summary of long-term load forecasting consumption methods.
3.5. Problems of Selecting Forecasting Methods in the Context of Data Variation: Review and Recommendations
The literature on electricity forecasting analyzes data of varying aggregation levels, ranging from national aggregates to individual smart meter readings. Method selection must account for both the temporal forecast horizon and the specific characteristics of the dataset, including its structure, resolution, and availability. Consequently, key data categories necessitate the application of distinct approaches, which we can see in Table 5.

Table 5.
Mapping of forecasting methods to data types and applications.
It is crucial to recognize that these recommendations are not definitive and should be considered in conjunction with the unique attributes of the forecasting task, such as data availability, forecast granularity, and real-time demands. However, a clear comprehension of the link between data typology and modeling approach provides invaluable guidance for selecting optimal forecasting methodologies across both academic research and practical operational settings.
4. Conclusions
Forecasting electricity consumption is a critical issue for the effective management of energy systems and infrastructure development planning. This article reviews a wide range of methods—from classical statistical models, such as ARIMA, to advanced artificial intelligence techniques, including deep-learning models. Different forecast time horizons and diverse sources of input data were taken into account. Based on the studies analyzed, a number of conclusions can be drawn about the effectiveness of the various approaches, their applications, and limitations. These conclusions provide a basis for further discussion of the directions of development of forecasting methods in the context of the energy transition and the growing share of renewable energy sources.
The reviewed studies on very short-term electricity load forecasting indicate that LSTM models are particularly effective in forecasting household-level electricity consumption, especially in the presence of high data volatility. Hybrid models, such as CNN-LSTM, allow for the simultaneous capture of both local and global patterns in time-series data, leading to improved forecasting accuracy. The fuzzy logic-based approach (IT-1 FIS) can also be effective for very short-term forecasts, provided that input data is appropriately selected. The use of advanced hyperparameter optimization techniques, such as the CVOA, further enhances predictive performance. In industrial applications, such as open-pit mining FFQR, has proven to be highly effective in forecasting peak loads, supporting smarter energy management in the context of Industry 4.0 strategies.
The reviewed studies on short-term load forecasting highlight the diversity and evolution of modeling approaches, ranging from traditional statistical methods like ARIMA and linear regression to more advanced machine-learning and deep-learning models, such as ANNs, LSTM, and hybrid architectures. While ARIMA proves effective in capturing seasonality in structured time-series data, its limitations in handling nonlinear patterns are evident. Artificial Neural Networks consistently outperform classical models in complex environments, especially in buildings, microgrids, and peer-to-peer systems, due to their ability to model dynamic and nonlinear relationships. Hybrid and ensemble models, particularly those combining CNNs and LSTMs or integrating statistical and machine-learning techniques, demonstrate superior forecasting accuracy and robustness, especially in the presence of multiple input variables like weather data. Overall, the results confirm that while simpler models remain useful for baseline comparisons and interpretable applications, deep-learning-based solutions offer the highest accuracy and adaptability for modern short-term electricity consumption forecasting challenges.
Conclusions arising from medium-term load forecasting, covering periods from several months to a few years, emphasize the relevance of both traditional and modern forecasting techniques for strategic energy planning. ARIMA models, due to their simplicity and effectiveness for stationary time series, performed well in forecasting energy consumption, particularly in scenarios with stable historical trends and limited external shocks. However, in more dynamic environments or when external factors like economic crises affect consumption patterns, machine-learning models—especially ANNs—demonstrated superior flexibility and accuracy, particularly when enhanced with relevant input variables such as exports, population, or GDP. Hybrid approaches, combining statistical methods with ANNs or Grey Models, showed measurable improvements in predictive performance, as observed in Slovakia and Türkiye. In industrial settings, ARIMA continued to prove effective, especially in enterprises with continuous production processes. Studies employing ensemble deep-learning architectures (e.g., LSTM + GRU + TCN) or optimization algorithms like genetic algorithms demonstrated that model tuning and feature selection significantly impact forecast accuracy and stability over multi-month periods. Additionally, methods such as Grey-Markov models and Singular Spectrum Analysis offered reliable results for long-range forecasting in rapidly developing economies like India, particularly when data volume or quality was limited. Overall, the results indicate that while classical models remain useful as baselines or for specific applications, hybrid and deep-learning models offer superior performance for medium-term electricity forecasting, provided they are carefully calibrated and contextualized to the application environment.
A review of research on long-term load forecasting shows that there is no one-size-fits-all model, but the best results are achieved by methods tailored to the specific data context and forecast goal. ARIMA models remain effective with stable, linear time series, especially with limited availability of external variables. Regression models perform well when reliable data on economic factors (e.g., GDP, population, industrial activity) are available, offering high accuracy and interpretability. Neural networks, on the other hand, especially ANNs and LSTMs, provide better representation of nonlinear trends and responses to disturbing factors (e.g., crises, pandemic), especially after optimizing hyperparameters. Hybrid models (e.g., SARIMA-ANN, CNN-LSTM, regression + LSTM), which combine the simplicity of statistical models with the flexibility of machine learning, and probabilistic models, which offer a distribution of possible values instead of a single forecast, perform best, supporting risk management. In practice, it is worthwhile to use a mixed approach, in which classical models act as a reference, and strategic forecasts are based on AI models supported by analysis of economic variables and development scenarios.
When choosing forecasting models, a significant limitation is their dependence on external variables like temperature, economic indicators, or calendar effects. While these variables often boost retrospective (ex post) accuracy, their use in real-time (ex ante) forecasting is challenging due to uncertainty or unavailability. Predicting variables such as average monthly temperature or GDP accurately enough for short-term operational models can be particularly difficult. Therefore, many practical forecasting systems employ hybrid designs that blend autoregressive elements with restricted exogenous data, or they use lagged proxies for uncertain inputs. Recognizing this inherent trade-off is crucial for developing reliable, deployable forecasting systems.
This article provides a comprehensive and structured review of electricity load forecasting methods across different time horizons, ranging from very short term to long term. By systematically comparing traditional statistical techniques with modern machine-learning and deep-learning approaches, the article highlights their respective strengths, limitations, and suitability in various forecasting contexts. A key contribution of this work is the synthesis of findings across multiple application domains—residential, industrial, and national energy systems—showing how the choice of forecasting model should align with data availability, volatility, and strategic planning needs. Moreover, the article emphasizes the growing importance of hybrid and probabilistic models, offering practical insights into model selection and optimization strategies. This review supports researchers, energy planners, and decision-makers in identifying effective forecasting solutions, especially in the context of increasing energy system complexity and the integration of renewable energy sources.
Author Contributions
Conceptualization, K.M., T.O., and J.Z.; methodology, K.M., T.O., and J.Z.; software, K.M., T.O., and J.Z.; validation, K.M., T.O., and J.Z.; formal analysis, K.M., T.O., and J.Z.; investigation, K.M., T.O., and J.Z.; resources, K.M., T.O., and J.Z.; data curation, K.M., T.O., and J.Z.; writing—original draft preparation, K.M., T.O., and J.Z.; writing—review and editing, K.M., T.O., and J.Z.; visualization, K.M., T.O., and J.Z.; supervision, K.M., T.O., and J.Z.; project administration, K.M., T.O., and J.Z.; funding acquisition, K.M., T.O., and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work received financial support from the funding of AGH University of Krakow, Faculty of Energy and Fuels (grant number 16.16.210.476).
Data Availability Statement
No datasets were generated or analyzed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ministerstwo Klimatu i Środowiska. Polityka Energetyczna Polski do 2040 r. 2021. Available online: https://www.gov.pl/web/klimat/polityka-energetyczna-polski (accessed on 25 April 2025).
- Waheed, W.; Xu, Q. The COVID-19 pandemic’s impact on user consumption: A shift towards very efficient load forecasting. Sustain. Energy Grids Netw. 2024, 39, 101426. [Google Scholar] [CrossRef]
- Khan, N.; Haq, I.U.; Khan, S.U.; Rho, S.; Lee, M.Y.; Baik, S.W. DB-Net: A novel dilated CNN based multi-step forecasting model for power consumption in integrated local energy systems. Int. J. Electr. Power Energy Syst. 2021, 133, 107023. [Google Scholar] [CrossRef]
- PSE. Raport 2022 KSE Zestawienie Danych Ilościowych Dotyczących Funkcjonowania kse w 2022 Roku; PSE: Warszawa, Poland, 2022; Available online: https://www.pse.pl/dane-systemowe/funkcjonowanie-kse/raporty-roczne-z-funkcjonowania-kse-za-rok/raporty-za-rok-2022 (accessed on 14 February 2025).
- Singh, P.; Dwivedi, P.; Kant, V. A hybrid method based on neural network and improved environmental adaptation method using Controlled Gaussian Mutation with real parameter for short-term load forecasting. Energy 2019, 174, 460–477. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. Energy Production and Consumption. Our World in Data. Available online: https://ourworldindata.org/energy-production-consumption (accessed on 17 July 2025).
- Leite Coelho Da Silva, F.; Da Costa, K.; Canas Rodrigues, P.; Salas, R.; López-Gonzales, J.L. Statistical and Artificial Neural Networks Models for Electricity Consumption Forecasting in the Brazilian Industrial Sector. Energies 2022, 15, 588. [Google Scholar] [CrossRef]
- Krstev, S.; Forcan, J.; Krneta, D. An Overview of Forecasting Methods for Monthly Electricity Consumption. Teh. Vjesn. Tech. Gaz. 2023, 30, 993–1001. [Google Scholar] [CrossRef]
- Azeem, A.; Ismail, I.; Jameel, S.M.; Harindran, V.R. Electrical Load Forecasting Models for Different Generation Modalities: A Review. IEEE Access 2021, 9, 142239–142263. [Google Scholar] [CrossRef]
- Kaytez, F.; Taplamacioglu, M.C.; Cam, E.; Hardalac, F. Forecasting electricity consumption: A comparison of regression analysis, neural networks and least squares support vector machines. Int. J. Electr. Power Energy Syst. 2015, 67, 431–438. [Google Scholar] [CrossRef]
- Zang, H.; Xu, R.; Cheng, L.; Ding, T.; Liu, L.; Wei, Z.; Sun, G. Residential load forecasting based on LSTM fusing self-attention mechanism with pooling. Energy 2021, 229, 120682. [Google Scholar] [CrossRef]
- Galicia, A.; Talavera-Llames, R.; Troncoso, A.; Koprinska, I.; Martínez-Álvarez, F. Multi-step forecasting for big data time series based on ensemble learning. Knowl. Based Syst. 2019, 163, 830–841. [Google Scholar] [CrossRef]
- Klyuev, R.V.; Morgoev, I.D.; Morgoeva, A.D.; Gavrina, O.A.; Martyushev, N.V.; Efremenkov, E.A.; Mengxu, Q. Methods of Forecasting Electric Energy Consumption: A Literature Review. Energies 2022, 15, 8919. [Google Scholar] [CrossRef]
- Ediger, V.Ş.; Akar, S. ARIMA forecasting of primary energy demand by fuel in Turkey. Energy Policy 2007, 35, 1701–1708. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples; Springer Texts in Statistics; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-3-319-52451-1. [Google Scholar]
- Holt, C.C. Forecasting seasonals and trends by exponentially weighted moving averages. Int. J. Forecast. 2004, 20, 5–10. [Google Scholar] [CrossRef]
- Hawkins, D.M. On the Investigation of Alternative Regressions by Principal Component Analysis. Appl. Stat. 1973, 22, 275. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, R.; Liu, J.; Liu, X.; Petrosian, O.; Krinkin, K. Comparison and Explanation of Forecasting Algorithms for Energy Time Series. Mathematics 2021, 9, 2794. [Google Scholar] [CrossRef]
- Ahmad, T.; Zhang, H.; Yan, B. A review on renewable energy and electricity requirement forecasting models for smart grid and buildings. Sustain. Cities Soc. 2020, 55, 102052. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, L.; Ren, Y.; Suganthan, P.; Amaratunga, G. Ensemble deep learning for regression and time series forecasting. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Ensemble Learning (CIEL), Orlando, FL, USA, 9–12 December 2014; IEEE: Orlando, FL, USA, 2014; pp. 1–6. [Google Scholar]
- Bedi, J.; Toshniwal, D. Deep learning framework to forecast electricity demand. Appl. Energy 2019, 238, 1312–1326. [Google Scholar] [CrossRef]
- Jamaaluddin; Robandi, I.; Anshory, I. Time Difference Calculation Settings for Very Short Term Electric Load Forecasting Using Interval Type-1 Fuzzy Inference System (IT-1 FIS). IOP Conf. Ser. Mater. Sci. Eng. 2020, 874, 012011. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A data-driven strategy using long short term memory models and reinforcement learning to predict building electricity consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Torres, J.F.; Martínez-Álvarez, F.; Troncoso, A. A deep LSTM network for the Spanish electricity consumption forecasting. Neural Comput. Appl. 2022, 34, 10533–10545. [Google Scholar] [CrossRef] [PubMed]
- Laayati, O.; Bouzi, M.; Chebak, A. Smart Energy Management System: Design of a Monitoring and Peak Load Forecasting System for an Experimental Open-Pit Mine. Appl. Syst. Innov. 2022, 5, 18. [Google Scholar] [CrossRef]
- Zahid, M.; Chen, Y.; Jamal, A.; Mamadou, C.Z. Freeway Short-Term Travel Speed Prediction Based on Data Collection Time-Horizons: A Fast Forest Quantile Regression Approach. Sustainability 2020, 12, 646. [Google Scholar] [CrossRef]
- Carvalho, A.; Chouchene, A.; Lima, T.; Charrua-Santos, F. Cognitive Manufacturing in Industry 4.0 toward Cognitive Load Reduction: A Conceptual Framework. Appl. Syst. Innov. 2020, 3, 55. [Google Scholar] [CrossRef]
- Mahmood, A.M.; Abdul Zahra, M.M.; Hamed, W.; Bashar, B.S.; Abdulaal, A.H.; Alawsi, T.; Adhab, A.H. Electricity Demand Prediction by a Transformer-Based Model. Majlesi J. Electr. Eng. 2022, 16, 97. [Google Scholar]
- Chan, J.W.; Yeo, C.K. A Transformer based approach to electricity load forecasting. Electr. J. 2024, 37, 107370. [Google Scholar] [CrossRef]
- Agga, A.; Abbou, A.; Labbadi, M.; El Houm, Y. Short-term self consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models. Renew. Energy 2021, 177, 101–112. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2018. [Google Scholar]
- Hernández, L.; Baladrón, C.; Aguiar, J.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Pérez, F.; Fernández, Á.; Lloret, J. Artificial Neural Network for Short-Term Load Forecasting in Distribution Systems. Energies 2014, 7, 1576–1598. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.Y.; Baik, S.W. A Novel CNN-GRU-Based Hybrid Approach for Short-Term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Lee, Y.W.; Tay, K.G.; Choy, Y.Y. Forecasting Electricity Consumption Using Time Series Model. Int. J. Eng. Technol. 2018, 7, 218–223. [Google Scholar] [CrossRef]
- Grant, J.; Eltoukhy, M.; Asfour, S. Short-Term Electrical Peak Demand Forecasting in a Large Government Building Using Artificial Neural Networks. Energies 2014, 7, 1935–1953. [Google Scholar] [CrossRef]
- Hadjout, D.; Torres, J.F.; Troncoso, A.; Sebaa, A.; Martínez-Álvarez, F. Electricity consumption forecasting based on ensemble deep learning with application to the Algerian market. Energy 2022, 243, 123060. [Google Scholar] [CrossRef]
- González Grandón, T.; Schwenzer, J.; Steens, T.; Breuing, J. Electricity demand forecasting with hybrid classical statistical and machine learning algorithms: Case study of Ukraine. Appl. Energy 2024, 355, 122249. [Google Scholar] [CrossRef]
- Mustaqeem; Ishaq, M.; Kwon, S. Short-Term Energy Forecasting Framework Using an Ensemble Deep Learning Approach. IEEE Access 2021, 9, 94262–94271. [Google Scholar] [CrossRef]
- Goude, Y.; Nedellec, R.; Kong, N. Local Short and Middle Term Electricity Load Forecasting With Semi-Parametric Additive Models. IEEE Trans. Smart Grid 2014, 5, 440–446. [Google Scholar] [CrossRef]
- Abu-Salih, B.; Wongthongtham, P.; Morrison, G.; Coutinho, K.; Al-Okaily, M.; Huneiti, A. Short-term renewable energy consumption and generation forecasting: A case study of Western Australia. Heliyon 2022, 8, e09152. [Google Scholar] [CrossRef]
- L’Heureux, A.; Grolinger, K.; Capretz, M.A.M. Transformer-Based Model for Electrical Load Forecasting. Energies 2022, 15, 4993. [Google Scholar] [CrossRef]
- Koohfar, S.; Woldemariam, W.; Kumar, A. Prediction of Electric Vehicles Charging Demand: A Transformer-Based Deep Learning Approach. Sustainability 2023, 15, 2105. [Google Scholar] [CrossRef]
- Galindo Padilha, G.A.; Ko, J.; Jung, J.J.; De Mattos Neto, P.S.G. Transformer-Based Hybrid Forecasting Model for Multivariate Renewable Energy. Appl. Sci. 2022, 12, 10985. [Google Scholar] [CrossRef]
- Chuang, F.-K.; Hung, C.-Y.; Chang, C.-Y.; Kuo, K.-C. Deploying Arima and Artificial Neural Networks Models to Predict Energy Consumption in Taiwan. Sens. Lett. 2013, 11, 2333–2340. [Google Scholar] [CrossRef]
- Meade, N. Industrial and business forecasting methods, Lewis, C.D., Borough Green, Sevenoaks, Kent: Butterworth, 1982. Price: £9.25. Pages: 144. J. Forecast. 1983, 2, 194–196. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, S.; Lee, C.-C.; Zhou, D. Effects of trade openness on renewable energy consumption in OECD countries: New insights from panel smooth transition regression modelling. Energy Econ. 2021, 104, 105649. [Google Scholar] [CrossRef]
- Pavlicko, M.; Vojteková, M.; Blažeková, O. Forecasting of Electrical Energy Consumption in Slovakia. Mathematics 2022, 10, 577. [Google Scholar] [CrossRef]
- Rakhmonov, I.U.; Niyozov, N.N.; Kurbonov, N.N.; Umarov, B.S. Forecasting of electricity consumption by industrial enterprises with a continuous nature of production. E3S Web Conf. 2023, 384, 01030. [Google Scholar] [CrossRef]
- Çağlayan-Akay, E.; Topal, K.H. Forecasting Turkish electricity consumption: A critical analysis of single and hybrid models. Energy 2024, 305, 132115. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Khashei, M.; Bijari, M. A novel hybridization of artificial neural networks and ARIMA models for time series forecasting. Appl. Soft Comput. 2011, 11, 2664–2675. [Google Scholar] [CrossRef]
- Wang, L.; Zou, H.; Su, J.; Li, L.; Chaudhry, S. An ARIMA-ANN Hybrid Model for Time Series Forecasting. Syst. Res. Behav. Sci. 2013, 30, 244–259. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Kumar, U.; Jain, V.K. Time series models (Grey-Markov, Grey Model with rolling mechanism and singular spectrum analysis) to forecast energy consumption in India. Energy 2010, 35, 1709–1716. [Google Scholar] [CrossRef]
- Ardakani, F.J.; Ardehali, M.M. Long-term electrical energy consumption forecasting for developing and developed economies based on different optimized models and historical data types. Energy 2014, 65, 452–461. [Google Scholar] [CrossRef]
- Da Silva, F.L.C.; Cyrino Oliveira, F.L.; Souza, R.C. A bottom-up bayesian extension for long term electricity consumption forecasting. Energy 2019, 167, 198–210. [Google Scholar] [CrossRef]
- Lee, G.-C. A Regression-Based Method for Monthly Electric Load Forecasting in South Korea. Energies 2024, 17, 5860. [Google Scholar] [CrossRef]
- Kadri, R.; Kahoui, H.; Sahed, A. Electricity Consumption Forecasting in Algeria: A Comparison of ARIMA and GM (1,1) Models. Glob. Bus. 2023, 8, 15–24. [Google Scholar] [CrossRef]
- Şahin, U. Future of renewable energy consumption in France, Germany, Italy, Spain, Turkey and UK by 2030 using optimized fractional nonlinear grey Bernoulli model. Sustain. Prod. Consum. 2021, 25, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Bianco, V.; Manca, O.; Nardini, S. Electricity consumption forecasting in Italy using linear regression models. Energy 2009, 34, 1413–1421. [Google Scholar] [CrossRef]
- Adhiswara, R.; Abdullah, A.G.; Mulyadi, Y. Long-term electrical consumption forecasting using Artificial Neural Network (ANN). J. Phys. Conf. Ser. 2019, 1402, 033081. [Google Scholar] [CrossRef]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic individual load forecasting using pinball loss guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).