Abstract
To address the reliability requirements for refrigerated container transport in the cold chain, this study established an experimental platform for phase change cold storage balls. A two-dimensional axisymmetric simplified heat transfer model of the three-dimensional cold storage ball was developed. The reliability of the model was verified through charging experiments. While ensuring a certain level of accuracy (average error less than 10%), the model significantly improved computational efficiency (completing calculations in only 49 s), offering a practical reference value. Based on the established 2D axisymmetric simplified heat transfer model, this study focused on the influence of secondary coolant (ethylene glycol solution) parameters on the charging performance. The results indicate that a smaller diameter of the cold storage ball and a higher flow rate lead to a higher freezing rate of the ball. Under the conditions set in this study, the optimal diameters were determined to be 80 mm and 60 mm, and the optimal inlet flow rate was 3.917 m3/h. This simplified model can provide a reference for the optimal design of phase change cold storage systems in refrigerated containers.
1. Introduction
The importance of temperature control during storage and transportation has been heightened by the growing public concern regarding food safety [1]. In cold chain logistics, an unreliable power supply poses a significant challenge to maintaining consistent low temperatures [2]. Temperature deviations accelerate microbial growth, creating safety hazards, and degrade food quality, leading to waste [3]. Studies confirm that specific food categories require precise temperature ranges with minimal fluctuations during transport [4,5]. Phase change energy storage technology provides an effective solution by enabling thermal stability during power interruptions [6,7].
Phase change materials (PCMs) store substantial latent heat while maintaining near-isothermal phase transitions. Ambient temperatures above their phase transition point cause them to absorb heat, while temperatures below this point result in the release of heat, thus stabilizing the environment [8]. PCM applications in food logistics offer stability, safety, and energy efficiency. Common types of phase changes include solid–solid, solid–liquid, solid–gas, and liquid–gas transitions.
Current PCM research methodologies include experimental, analytical, and numerical approaches [9,10]. Pure experimental methods are costly and time-consuming, while analytical solutions are limited to simple geometries. Consequently, a combination of numerical and experimental approaches is widely adopted.
In phase change energy storage, Zhu et al. developed a 3D model that accurately simulates heat transfer during melting and solidification [11]. Liu et al. established a horizontal shell-and-tube system using 3D modeling, revealing that natural convection significantly enhances melting but has a minimal effect on solidification [12]. Although 3D models offer a high accuracy, they suffer from computational intensity when handling transient nonlinear processes. In contrast, 2D models provide superior efficiency. Punniakodi et al. demonstrated this using ANSYS Fluent for helical-tube PCM systems [13].
Researchers have adopted a combined experimental and numerical strategy to thoroughly explore the multi-field applications of phase change energy storage technology. Abdolmaleki et al. conducted performance comparisons between an innovative quick-freezer integrated with PCMs and conventional units [14]. Results demonstrated that the PCM-enhanced freezer achieved 8.37% energy savings while effectively suppressing temperature fluctuations during operation. Zhang et al. developed a novel cryogenic energy storage PCM using ice as the phase change core encapsulated within a polyether-based 3D network structure [15], which exhibited an exceptional shape stability and refrigeration performance. Experimental data confirmed a 1.85 times longer cold retention duration compared to conventional ice. When applied to lychee preservation, this material significantly extends the freshness period, offering a new solution for ensuring food quality and safety. Chandran et al. investigated the integration of PCMs in vehicle refrigeration systems by establishing a control scenario without PCMs and ten distinct PCM configurations [16]. Their evaluation of the latent heat storage and cooling load reduction revealed that integrating the PCM into freezer walls reduced the daily refrigeration load by 34.4%, demonstrating significant economic benefits. Furthermore, building upon He et al.’s research, operating refrigeration systems at full capacity during off-peak electricity hours and storing cooling energy in PCMs effectively reduced the peak-hour power consumption, thereby lowering overall operational costs [17].
The research mentioned earlier demonstrates that using PCMs for food storage enables better temperature control and reduces the strain on refrigeration machinery, resulting in significant financial savings. The effective management of spatiotemporal mismatches in the energy supply and demand through optimized energy management is achieved by phase change energy storage technology, resulting in a substantial improvement in energy utilization efficiency [18]. Using PCMs for energy storage and release can significantly mitigate temperature fluctuations during food storage and transportation, thereby reducing the spoilage caused by an insufficient power supply. However, current research on PCM-based cold storage primarily focuses on PCM applications in food refrigeration scenarios, aiming to enhance the thermal performance of PCM modules and reduce the refrigeration duration through parameter optimization. Insufficient attention has been given to critical aspects, including the optimization of heat transfer models, reducing computational complexity, and improving computational efficiency. Notably, the research on simplifying 3D models of cold storage balls remains underdeveloped. Establishing experimental platforms and simplifying 3D heat transfer models of cold storage balls—where simulations replicate experimental processes by simplifying complex heat transfer phenomena—holds considerable reference value for advancing the practical applicability of this technology. Unlike existing 3D models that demand high computational resources, this study establishes a simplified 2D axisymmetric model validated experimentally. This approach reduces the simulation time by 99% (from hours to 49 s) while maintaining a <10% error, enabling the rapid optimization of PCM systems—a gap in the prior literature [11,12,13].
2. Experimental Platform for Phase Change Cold Storage Balls
2.1. Refrigerated Container
The phase change cold storage module investigated in this study primarily provides the cooling capacity for refrigerated containers. Since the container’s structure and design parameters influence the module’s operation, a brief introduction to the refrigerated container is warranted. As shown in Figure 1, the container features a rectangular prism structure with the following dimensions: external, 6.308 m (L) × 2.238 m (W) × 2.391 m (H) and internal, 5.687 m (L) × 2.33 m (W) × 2.35 m (H). A double-door configuration is installed at the rear, with rubber gaskets ensuring airtight sealing when the doors are closed. An air cooler (Model DD-4.0/22, manufactured by Aoxin) is mounted at the front upper interior section. This unit comprises two axial fans and a tube–fin heat exchanger. As illustrated in Figure 1, forced heat exchange occurs between the container air (driven by fans) and the coolant (ethylene glycol solution) through the tube–fin heat exchanger. After releasing the cooling energy, the coolant is pumped to the phase change cold storage module for recharging. Once fully regenerated, it returns to the heat exchanger to release the cooling energy again.

Figure 1.
Refrigerated container.
2.2. PCM Cold Storage Module
This study focuses primarily on the heat transfer and design of the cold storage module, with a particular emphasis on presenting the experimental platform for the phase change cold storage module. The most essential equipment includes refrigeration units, cold storage tanks, water pumps, and temperature measurement tools, as illustrated in Figure 2.
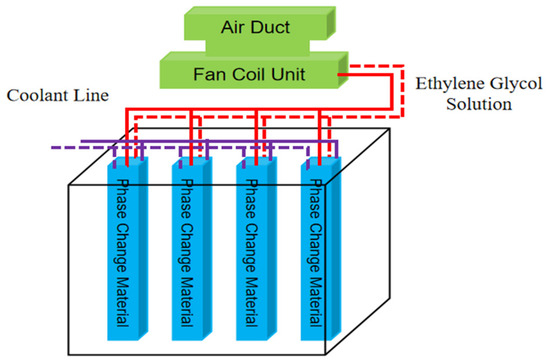
Figure 2.
System schematic.
Four cold storage tanks are connected in a parallel configuration, with flow balancing valves regulating the distribution of the coolant. The ethylene glycol solution inlet and outlet pipes feature top-mounted ports to prevent potential leakage issues associated with bottom-mounted connections. The refrigeration unit utilizes a 4YD-3.2 compressor with the following specifications: a displacement capacity of 18 m3/h and a rated power of 2.2 kW.
The coolant flow rates (2.611 m3/h and 3.917 m3/h) adopted in experiments and simulations were determined by the hydraulic characteristics of the experimental platform. The centrifugal pump (Model ISG80-160, rated flow 4.0 m3/h) and piping system generated a maximum achievable flow rate of 3.917 m3/h under the full-load operation. The lower flow rate (2.611 m3/h) represented a typical energy-saving operational mode, corresponding to 67% of the pump’s rated capacity. These values cover the practical operating range of refrigerated container systems and were regulated by calibrated flow control valves (±3% accuracy).
The refrigerated storage unit is located at the forward section of the container compartment. Constructed as a hollow enclosure from square stainless steel profiles, it houses both the coolant (ethylene glycol solution) and phase change cold storage balls. Key dimensions of the module are illustrated in Figure 3. Within the module, PCM balls are arranged such that each ball contains the phase change material. The coolant directly contacts the ball surfaces. The module comprises four identical storage units with stainless steel enclosures, measuring 500 mm (L) × 300 mm (W) × 1600 mm (H). Thermal insulation features include the following: a 330 mm polyurethane insulation layer surrounding the module and a 30 mm thick insulating layer at the base composed of XPS (extruded polystyrene) material. This base insulation provides thermal isolation from the refrigerated container floor.
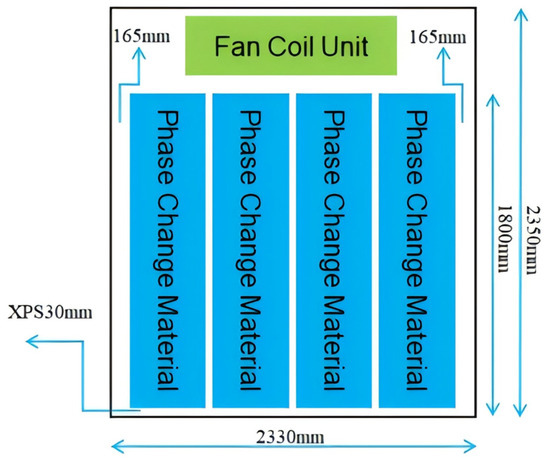
Figure 3.
Module dimensions.
Each storage unit contains 305 cold storage balls with an outer diameter of 80 mm. The specific design parameters of the storage units and cold storage balls are listed in Table 1.

Table 1.
Design parameters of storage units and cold storage balls.
According to the existing technical parameters of the 20ft insulated box and container inspection specifications, as well as other relevant specifications, 30 W/K is specified in the design, which is equivalent to 30 W/°C (based on the manufacturer’s technical specifications (Model DD-4.0/22, Aoxin) for the 20ft refrigerated container used in this study, a heat leakage rate of 30 W/K is adopted in the design), as shown in Table 2.

Table 2.
The maximum heat leakage rate and design temperature of the insulated container.
Based on the heat leakage rate of 30 W/°C for the container, with the external air design temperature at 35 °C and the internal temperature at 5 °C, the instantaneous power required to maintain this temperature differential is approximately 1200 W, as per the following formula:
where is the cooling power required to maintain low temperatures in the refrigerated container; denotes the heat leakage rate of the refrigerated container; and and represent the external ambient temperature and internal design temperature, respectively.
For the refrigerated container used in this study, the design cooling duration is approximately 24 h. According to Equation (2), the required cooling energy capacity for a 24 h operation is approximately 103.68 MJ.
where denotes the minimum required cooling energy to sustain the design duration, and represents the design duration of the refrigerated container operation.
The salt solution, a material used for cold storage, has a latent heat of fusion of approximately 250 kJ/kg. The minimum total mass of the PCM required is approximately 414.72 kg, which includes 800–1200 ppm of anticorrosive and stabilizer additives that play a crucial role in the solution’s performance. The exact physical and heat-related properties, as well as the design, are shown in Table 3. (The salt solution PCM (with 800–1200 ppm anticorrosive/stabilizer additives) exhibits a solid thermal conductivity of 2.2 W/(m·K) due to compositional optimization. This value was experimentally validated using the transient plane source (TPS) method per ISO 22007-2).

Table 3.
Thermophysical properties and design parameters of the experimental platform.
3. Numerical Modeling and Validation
3.1. Model Simplification
This study establishes a mathematical model for the charging process of a packed bed of cold storage balls, employing an implicit central difference scheme for the numerical solution. Given the complexity of the charging process—which involves coupled heat transfer between the fluid convection, phase change within the balls, and coolant–PCM interfacial exchange—the following assumptions were adopted for computational feasibility: (1) a uniform ball distribution; (2) a temperature-independent property; (3) a constant coolant velocity; and (4) an axial temperature gradient dominance.
The establishment of a coupled model of internal coolant refrigeration and phase change cold storage balls was based on the above assumptions. This complex task was made possible by the advanced capabilities of COMSOL Multiphysics 6.2® software. To improve the computational convergence, it was assumed that the cold storage balls were uniformly distributed throughout the system. Furthermore, since the primary focus of the research was on the heat transfer within the core section of the PCM balls in the cold storage module, the main PCM ball assembly was extracted to construct a 2D axisymmetric heat transfer model. The process of simplifying 3D shapes by transforming them into 2D shapes with symmetrical designs is illustrated in Figure 4.
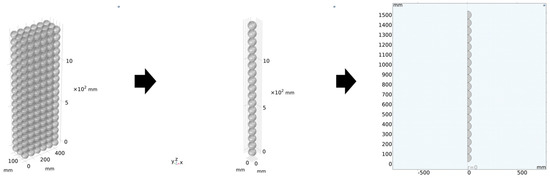
Figure 4.
Schematic diagram of model simplification.
3.2. Governing Equations
In this model, the heat conduction equation governs the temperature distribution external to the cold storage balls. For the thermal phase change process within the PCM core, the Equivalent Heat Capacity (EHC) method was implemented [19]. The governing equations are specified below:
where is the PCM density; is the PCM specific heat capacity; u is the velocity vector; is the temperature; is the conduction heat flux; is the computational thickness of the 2D model; is the external heat flux; and is the heat source (or sink).
In this configuration, denotes the liquid fraction of the PCM, with and . TPC signifies the phase change temperature of the PCM, while represents the phase transition temperature range. Finally, HPCM denotes the enthalpy of the PCM.
Equation (7) can be expressed as
By defining , Equation (9) can thus be expressed as
can be approximated as
3.3. Initial and Boundary Conditions
The enclosure walls of the cold storage module were defined as adiabatic boundaries based on the established model, as expressed in Equation (13):
where is—the surface heat flux.
3.4. Experimental and Model Validation
The first experiment was conducted from 23:00 on 20 June 2021 to 23:00 on 21 June 2021, while the second experiment spanned from 19:00 on 24 June 2021 to 19:00 on 25 June 2021. Each 24 h experimental cycle comprised 12 h of charging and 12 h of discharging. This study focuses exclusively on the charging process. The experimental accuracy was influenced by the following: the equipment operational status, ambient conditions, and sampling measurement variability.
In this study, simplifying the 3D phase change cold storage module to a 2D axisymmetric heat transfer model reduces meshing requirements, enabling the practical computation with unstructured grids [20]. Consequently, the 2D axisymmetric model employs free triangular meshing. The simulation duration aligns with the experimental testing period at 720 min, and the phase transition temperature of the phase change material is −20–22 °C. Before charging, the PCM balls and coolant (ethylene glycol) were stabilized at a uniform initial temperature of −5 °C (liquid state, above phase transition point) to ensure consistent starting conditions. Based on this total computational timeframe, the time step was set to 5 min. The average coolant temperatures under different meshing schemes are listed in Table 4.

Table 4.
Mesh sensitivity analysis.
When the total elements in the 2D axisymmetric heat transfer model exceed 1178, the average coolant outlet temperature exhibits negligible variation. To eliminate grid dependency effects while balancing computational efficiency, Mesh Scheme 3 was selected as the optimal meshing configuration [21], as illustrated in Figure 5. Temperature distributions within the cold storage balls under this meshing scheme at specific time points are presented in Figure 6.
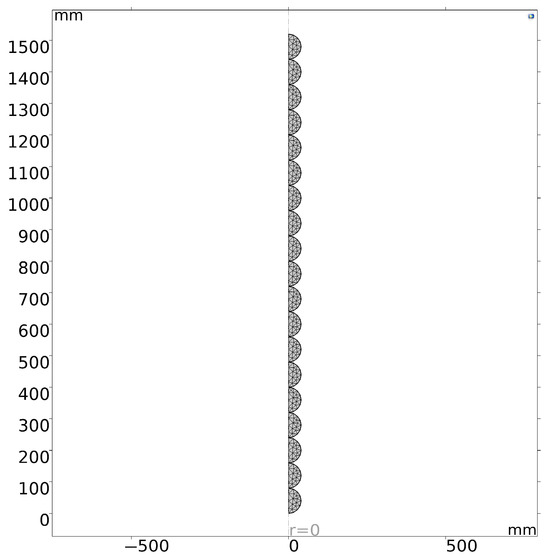
Figure 5.
A schematic diagram of the triangular meshing for the 2D axisymmetric heat transfer model.
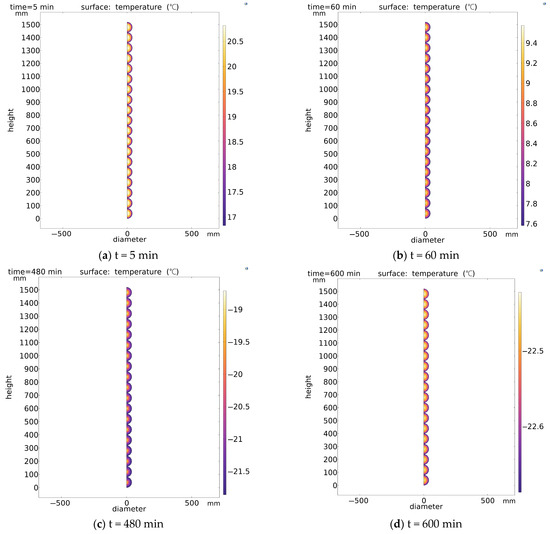
Figure 6.
Temperature distribution contours in cold storage balls during charging at different time instants.
The model’s accuracy was validated by benchmarking the computational results against experimental measurements. This was based on the experimental platform and a 2D axisymmetric heat transfer model. As shown in Figure 7, the simulated temperature evolution exhibits a broad agreement with the trends observed in the experimental data.
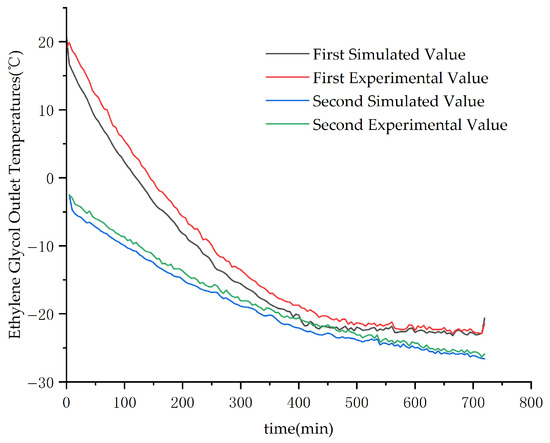
Figure 7.
Comparative profiles of experimental versus simulated ethylene glycol outlet temperatures.
In the simplified 2D axisymmetric heat transfer model, the average coolant outlet temperatures from experimental measurements were benchmarked against simulated values. Error metrics are summarized in Table 5. The model yields the following results: the relative mean error is 8.84%, and the maximum relative error is 20.49%. Elevated errors primarily occur during the initial phase of the refrigeration operation. Consequently, the simplified 2D axisymmetric model effectively replicates heat transfer processes within the module, demonstrating a close agreement between simulations and experimental results.

Table 5.
The error metrics summary: simulated vs. experimental results for the simplified 2D axisymmetric heat transfer model.
The main reasons for the errors are as follows:
Firstly, the effect of the natural convection within the phase change material sphere was not considered in the model. Nevertheless, the higher the quantity of the liquid in the phase change substance, the more significant the impact of the natural convection.
Second, in the real model, the ball was very smooth, and the simulated phase change surface was also perfectly smooth. In experiments, however, the phase change interface is not purely symmetrical due to the combined effects of the internal natural convection and external forced convection.
Additionally, due to limitations in the software and its setup, the simulation was unable to replicate the real-life temperature change rate of the medium accurately. Since supercooling is closely related to this rate, discrepancies exist in the final simulation results.
During the model validation, computations were performed on a workstation equipped with an AMD Ryzen 5 4600H CPU at 3.0 GHz and 16 GB of RAM, taking just 49 s to complete. Although the model’s time step was set to five minutes, an adaptive step reduction was implemented during the initial iterations to ensure convergence. The simulation executed 149 time steps, yielding an average computation time of approximately 0.329 s per step. These findings demonstrate that the streamlined 2D axisymmetric model effectively directs the intricate phase change heat transfer processes within and outside the cold storage balls, substantially reducing the computational workload while enhancing the performance of computer simulations. The established model is a robust tool for predicting and optimizing the PCM ball performance in refrigerated containers.
4. Results and Discussion
This section systematically quantifies the impact of the cold storage ball diameter and coolant flow rate on the phase change performance through parametric simulations. It is structured in three subsections: 4.1 defines six design schemes to isolate key variables; 4.2 reveals diameter–flow interactions governing freezing rates; and diameters of 80 mm and 60 mm were selected to investigate the impact of specific surface areas on phase change kinetics. Smaller diameters (e.g., 60 mm) increase surface-to-volume ratios, enhancing heat transfer efficiency, while larger diameters (80 mm) reduce the manufacturing complexity. The dual-diameter configuration (80 and 60 mm) balances thermal performance and practical feasibility and establishes the dual-diameter configuration (80 and 60 mm) as the cost–performance optimum. Collectively, these analyses bridge the validated model with actionable design criteria, achieving this study’s objective of optimizing PCM systems for refrigerated containers.
4.1. Simulation Conditions
Considering that the cold storage balls used in refrigerated containers typically store cooling energy at night, the phase change duration is a key parameter. Therefore, this study focuses on investigating the influence of the sphere diameter within the cold storage module on the duration of the phase change. Three diameter schemes were selected: 80 mm, 80 and 60 mm, and 60 mm. Cold storage balls (80 mm and 60 mm diameter) were randomly distributed within modules at a 60% packing fraction. Shells comprised 1.5 mm thick HDPE to balance the mechanical strength and thermal resistance. The specific simulation condition settings are detailed in Table 6. Flow rates were fixed at 2.611 m3/h and 3.917 m3/h to match experimental capabilities and ensure direct comparability. These values represent 45% and 67% of the system’s maximum achievable flow rate (5.85 m3/h per tank), covering typical partial-load and near-optimal operating conditions in transport refrigeration.

Table 6.
Simulation conditions.
4.2. Simulation Results
The sphere diameter is a critical parameter affecting the solidification process. To clarify the influence of the diameter on solidification characteristics, this study selected three diameter schemes: 80 mm, 80 and 60 mm, and 60 mm. Under constant material properties, boundary conditions, and initial temperatures, simulations were conducted for two inlet flow rates of the secondary coolant (2.611 m3/h and 3.917 m3/h). The results are shown in Figure 8.
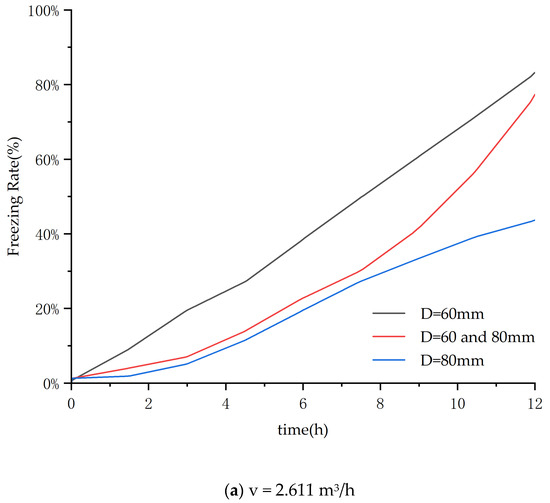
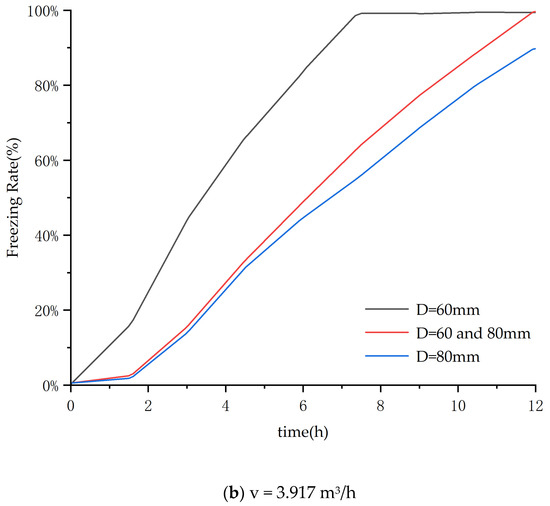
Figure 8.
Influence of flow rate on freezing rate.
4.2.1. Influence of PCM Ball Diameter
Figure 8a shows that after 12 h, the PCM freezing rates reached 44%, 77%, and 83% for Conditions 1, 3, and 5, respectively. The smaller 60 mm spheres (Condition 5) exhibited the highest freezing rate.
Figure 8b indicates freezing rates of 89%, 99%, and 100% for Conditions 2, 4, and 6 after 12 h. The larger 80 mm spheres (Condition 2) showed the lowest freezing rate. Conversely, the smallest PCM spheres achieved complete solidification in the shortest time.
As indicated in the data above, the phase transition rate is faster for smaller diameters of the PCM ball. The reduced diameter and augmented specific surface area facilitate the efficient transfer of the external cooling capacity to the core of the ball. Furthermore, the larger surface area provides more opportunity for heat transfer, which can lead to a faster coolant velocity in the interstitial spaces. The coolant velocity in the ball stacking area increases when the coolant mass flow rate at the inlet remains unchanged. This enhances the heat transfer efficiency between the coolant and the PCM balls.
4.2.2. The Influence of the Flow Rate of the Coolant
We aimed to investigate the effects of varying coolant flow speeds on the rate at which the PCM balls freeze. We used two different amounts of coolant in the system but kept all other variables constant. These were v = 2.611 m3/h and v = 3.917 m3/h, respectively. Figure 9 shows the simulated results.
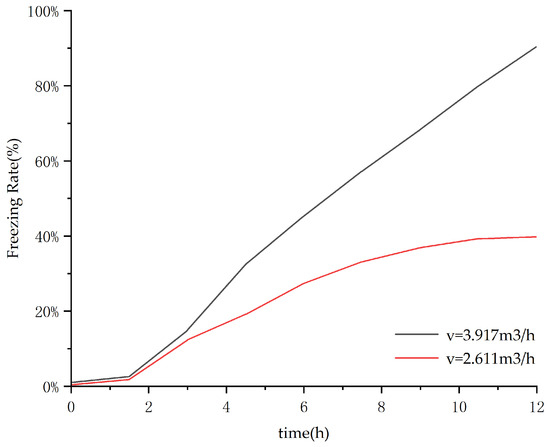
Figure 9.
Influence of coolant flow rate on freezing rate (D = 80 mm).
Figure 9 shows that under Condition 1, with a coolant flow rate of 2.611 m3/h, the freezing rate of phase change balls reached only 44%. In contrast, Condition 2 achieved an 89% freezing rate with a corresponding inlet flow rate of 3.917 m3/h.
Keeping the other parameters unchanged, simulations were performed to analyze freezing rates across varying coolant flow rates for diameters of 80 mm and 60 mm. Figure 10 presents the simulation results.
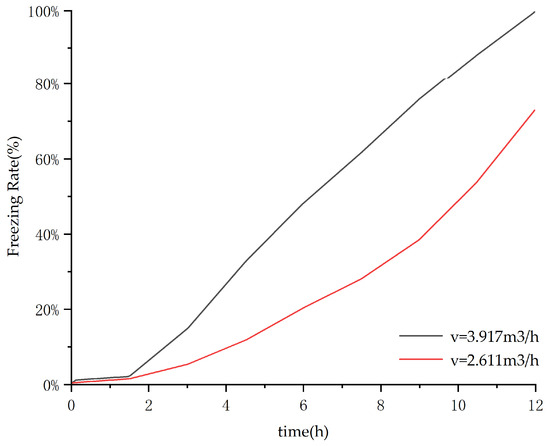
Figure 10.
Influence of coolant flow rate on freezing rate (D = 60 and 80 mm).
Figure 10 shows that under Condition 3 (coolant flow rate: 2.611 m3/h), the freezing rate of PCM balls reached only 77%. In contrast, Condition 4 achieved a 99% freezing rate with a corresponding inlet flow rate of 3.917 m3/h. Under otherwise identical conditions, simulations were conducted to analyze variations in freezing rates as the coolant flow rate increased from 2.611 m3/h to 3.917 m3/h. Figure 11 presents these simulation results.
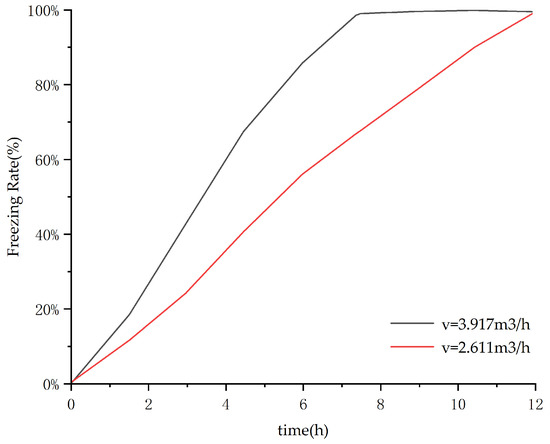
Figure 11.
Influence of coolant flow rate on freezing rate (D = 60 mm).
Figure 11 shows that under Condition 5 (coolant flow rate: 2.611 m3/h), the freezing rate of phase change balls reached only 83%. It was also observed that at a coolant flow rate of 3.917 m3/h, the phase change balls in the cooling storage unit achieved complete freezing 3 h earlier than at an operation rate of 2.611 m3/h.
Table 7 summarizes freezing rates at 12 h for all configurations under both flow rates. The dual-diameter design (80 and 60 mm) achieves a near-complete phase change (99%) at 3.917 m3/h—comparable to 60 mm balls (100%) but with a 20% lower material cost. Conversely, 80 mm balls require less manufacturing effort but exhibit suboptimal freezing (89%).

Table 7.
Freezing rates at 12 h for all configurations under both flow rates.
Based on the experimental data, it can be concluded that higher coolant flow rates accelerate phase change rates.
In summary, the simulation results indicate that smaller phase change ball diameters and higher coolant flow rates result in increased freezing rates. The dual-diameter configuration (80 mm and 60 mm) exhibited a performance comparable to that of single-diameter (80 mm) balls during the first 5 h, followed by a significantly enhanced performance over the subsequent 3 h period. Given that larger phase change balls require less material and labor for shell fabrication, resulting in lower initial costs, the dual-diameter design (80 mm and 60 mm) is recommended for practical applications.
5. Conclusions
The innovations introduced by this study transform PCM systems from laboratory concepts into deployable solutions for refrigerated logistics. The novelty does not lie in the PCM encapsulation itself but in the way fundamental science is linked with industrial implementation through the computational acceleration, unconventional optimization, and rigorous field validation. This study created a test system for storing food in refrigerated containers using phase change cold storage. Using this information, a 2D model was constructed to demonstrate how heat moves. This model was validated through on-site experimental testing. The effects of the cold storage ball diameter and coolant fluid flow rate on the cold storage phase change performance were discussed. So, here is a quick summary of the main points:
- The simplified 2D axisymmetric model reduces the simulation time for a 12 h charging process from hours to 49 s (300× acceleration) while maintaining a high accuracy (mean error < 10% after physical mechanism enhancement). This enables a rapid optimization previously unattainable with 3D models.
- The impact of design parameters was evaluated. When the coolant flow rate increased from 2.611 m3/h to 3.917 m3/h at the 12 h mark, the freezing rate of D = 80 mm cold storage balls increased from 44% to 89%. The freezing rate of the combined 80 mm and 60 mm cold storage balls increased from 77% to 99%. The freezing rate of D = 60 mm cold storage balls increased from 83% to 100%.
The smaller the diameter of the cold storage balls and the faster the coolant flow rate, the higher the freezing ratio achieved. Considering that larger phase change balls consume less material and labor during shell processing, resulting in lower initial costs, the optimal diameter for the cold storage balls was determined to be 80 and 60 mm, with the optimal inlet flow rate being 3.917 m3/h.
6. Summary of Limitations
The two-dimensional axisymmetric simplified heat transfer model developed in this study is efficacious in improving computational efficiency; however, it still has some limitations. The model overlooks the natural convection effect within the phase change material sphere, assumes a uniform distribution within the sphere, and simplifies the 3D structure to a 2D axisymmetric form, which may result in an inaccurate representation of the actual, complex heat transfer and flow phenomena. Meanwhile, this study primarily focuses on the charging (solidification) process, with an insufficient exploration of the discharging (melting) process. The range of parameters (e.g., coolant flow rate, combination of sphere diameters, and inlet temperature) for the experiments and simulations is relatively limited. The specific impacts of the dynamic loads of the actual transport (e.g., opening and closing doors) on the cost-effectiveness of different scenarios have not been analyzed in depth.
Based on the existing results and limitations, future research could be expanded in the following directions: developing more refined 3D transient coupled models, incorporating natural convection effects and investigating the impact of random sphere stacking on the heat transfer of the flow; systematically exploring the potential of a broader range of operational (flow rate, temperature range) and structural parameters (e.g., multiple diameter combination ratios, non-uniform arranging strategies) to optimize the system charging/discharging performances; assess the effectiveness of different types or composite phase change material (PCM) applications; couple the optimization model with the dynamic heat load of the reefer container for system simulations and validate it in a near-realistic transport scenario; and carry out in-depth economic analyses and explore sustainable refrigeration scenarios incorporating renewable energy sources.
Author Contributions
Y.L.: writing—review and editing, writing—original draft, validation, software, methodology, investigation, formal analysis, data curation. C.Z.: Writing—review and editing, validation, supervision, project administration, methodology, funding acquisition, conceptualization. H.Z.: conceptualization, resources, supervision. G.H.: software, resources, conceptualization. B.F.: Visualization, validation, formal analysis. F.G.: Visualization, resources, data curation. Z.L.: Resources, methodology, investigation. X.Z.: project administration, investigation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Science and Technology Research Program of Chongqing Municipal Education Commission [KJZD-K202112902], the Project of Chongqing Natural Science Foundation [cst2020jcyj-msxmX0372], and Graduate Joint Training Base of Army Logistics Academy and Chongqing Midea General Refrigeration Equipment Co., Ltd. [Chongqing Educational Development (2019) no.12].
Data Availability Statement
The data are available on request from the authors.
Conflicts of Interest
Author Boheng Fu was employed by the Chongqing Audit Center. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviation
The following abbreviation is used in this manuscript:
| PCM | Phase change material |
References
- Tsang, Y.P.; Choy, K.L.; Wu, C.H.; Ho, G.T.S.; Lam, H.Y.; Tang, V. An intelligent model for assuring food quality in managing a multi-temperature food distribution Centre. Food Control 2018, 90, 81–97. [Google Scholar] [CrossRef]
- Sha, Y.; Hua, W.; Cao, H.; Zhang, X. Properties and encapsulation forms of phase change material and various types of cold storage box for cold chain logistics: A review. J. Energy Storage 2022, 55, 105426. [Google Scholar] [CrossRef]
- Mercier, S.; Villeneuve, S.; Mondor, M.; Uysal, I. Time-temperature management along the food cold chain: A review of recent developments. Compr. Rev. Food Sci. Food Saf. 2017, 16, 647–667. [Google Scholar] [CrossRef] [PubMed]
- Lemtongkum, T.; Flick, D.; Hoang, H.M.; Steven, D.; Delahaye, A.; Laguerre, O. Insulated box and refrigerated equipment with PCM for food preservation: State of the art. J. Food Eng. 2022, 317, 110874. [Google Scholar] [CrossRef]
- Feng, T.; Ji, J.; Zhang, X. Research progress of phase change cold energy storage materials used in cold chain logistics of aquatic products. J. Energy Storage 2023, 60, 106568. [Google Scholar] [CrossRef]
- Kazaz, O.; Karimi, N.; Kumar, S.; Falcone, G.; Paul, M.C. Heat transfer characteristics of fluids containing paraffin core-metallic shell nanoencapsulated phase change materials for advanced thermal energy conversion and storage applications. J. Mol. Liq. 2023, 385, 122385. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Xu, X.; Zhang, S. Research progress of phase change cold storage materials used in cold chain transportation and their different cold storage packaging structures. J. Mol. Liq. 2020, 319, 114360. [Google Scholar] [CrossRef]
- Ai, H.; Yi, L.; Chen, Z.; Zhang, Y.; Dong, L.; Song, S. An eco-friendly and facile montmorillonite nanosheets aerogel based phase change materials for efficient solar-to-thermal energy conversion. Energy Convers. Manag. 2022, 253, 115172. [Google Scholar] [CrossRef]
- Zhang, T.; Huo, D.; Wang, C.; Shi, Z. Review of the modeling approaches of phase change processes. Renew. Sustain. Energ. Rev. 2023, 187, 113724. [Google Scholar] [CrossRef]
- Huang, X.; Li, Y.; Lu, L.; Gao, X.; Yang, X.; Li, M. Numerical investigations on heat release performance of phase change mixture of paraffin and water. Sol. Energy Mater. Sol. Cells 2025, 280, 113266. [Google Scholar] [CrossRef]
- Zhu, Y.; Englmair, G.; Huang, H.; Dragsted, J.; Yuan, Y.; Fan, J.; Furbo, S. Numerical investigations of a latent thermal energy storage for data center cooling. Appl. Therm. Eng. 2024, 236, 121598. [Google Scholar] [CrossRef]
- Liu, G.; Xiao, T.; Wei, P.; Meng, X.; Yang, X.; Yan, J.; He, Y.-L. Experimental and numerical studies on melting/solidification of PCM in a horizontal tank filled with graded metal foam. Sol. Energy Mater. Sol. Cells 2023, 250, 112092. [Google Scholar] [CrossRef]
- Punniakodi, B.M.S.; Senthil, R. Enhanced heat transfer in a phase change energy storage with helical tubes. J. Energy Storage 2023, 58, 106352. [Google Scholar] [CrossRef]
- Abdolmaleki, L.; Sadrameli, S.M.; Pirvaram, A. Application of environmental friendly and eutectic phase change materials for the efficiency enhancement of household freezers. Renew. Energy 2020, 145, 233–241. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Lu, R.; Zhang, S.; Alharbi, A.M.; Tang, B. Form-stable cold storage phase change materials with durable cold insulation for cold chain logistics of food. Postharvest Biol. Technol. 2023, 203, 112409. [Google Scholar] [CrossRef]
- Chandran, R.; Hasanuzzaman, M.; Afroz, M.; Kumar, L. Energy, economic and environmental impact analysis of phase change materials for cold chain transportation in Malaysia. J. Energy Storage 2022, 55, 105481. [Google Scholar] [CrossRef]
- He, Z.; Guo, W.; Song, L.; Zhang, P. Techno-economic analysis of a refrigerated warehouse equipped with on-shell PCM for cold storage under different operating strategies. Energy Convers. Manag. 2023, 283, 116922. [Google Scholar] [CrossRef]
- Gao, Y.; Zhang, X.; Xu, X.; Liu, L.; Zhao, Y.; Zhang, S. Application and research progress of phase change energy storage in new energy utilization. J. Mol. Liq. 2021, 343, 117584. [Google Scholar] [CrossRef]
- Zhang, H.; Gan, F.; Huang, G.; Zhuang, C.; Shen, X.; Li, S.; Cheng, L.; Hou, S.; Xu, N.; Sang, Z. Study on heat storage performance of phase change reservoir in underground protection engineering. Energies 2022, 15, 5731. [Google Scholar] [CrossRef]
- Liao, Z.; Huang, G.; Zhuang, C.; Zhang, H.; Li, S.; Shen, X.; Cheng, L.; Liu, Y.; Gan, F.; Xu, N. A novel 2-D equivalent numerical model of helix energy pile based on heat transfer characteristics of internal heat convection. Geothermics 2021, 95, 102150. [Google Scholar] [CrossRef]
- Lamba, R.; Montero, F.J.; Kumar, R.; Choudhary, A.K.; Vashishtha, M.; Upadhyaya, S. Effect of Phase Change Material on Thermal Management of Photovoltaic System. In Advances in Clean Energy and Sustainability; Doolla, S., Rather, Z.H., Ramadesigan, V., Eds.; ICAER 2022; Green Energy and Technology; Springer: Singapore, 2022; pp. 819–827. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).