An Analytical Method for Solar Heat Flux in Spacecraft Thermal Management Under Multidimensional Pointing Attitudes
Abstract
1. Introduction
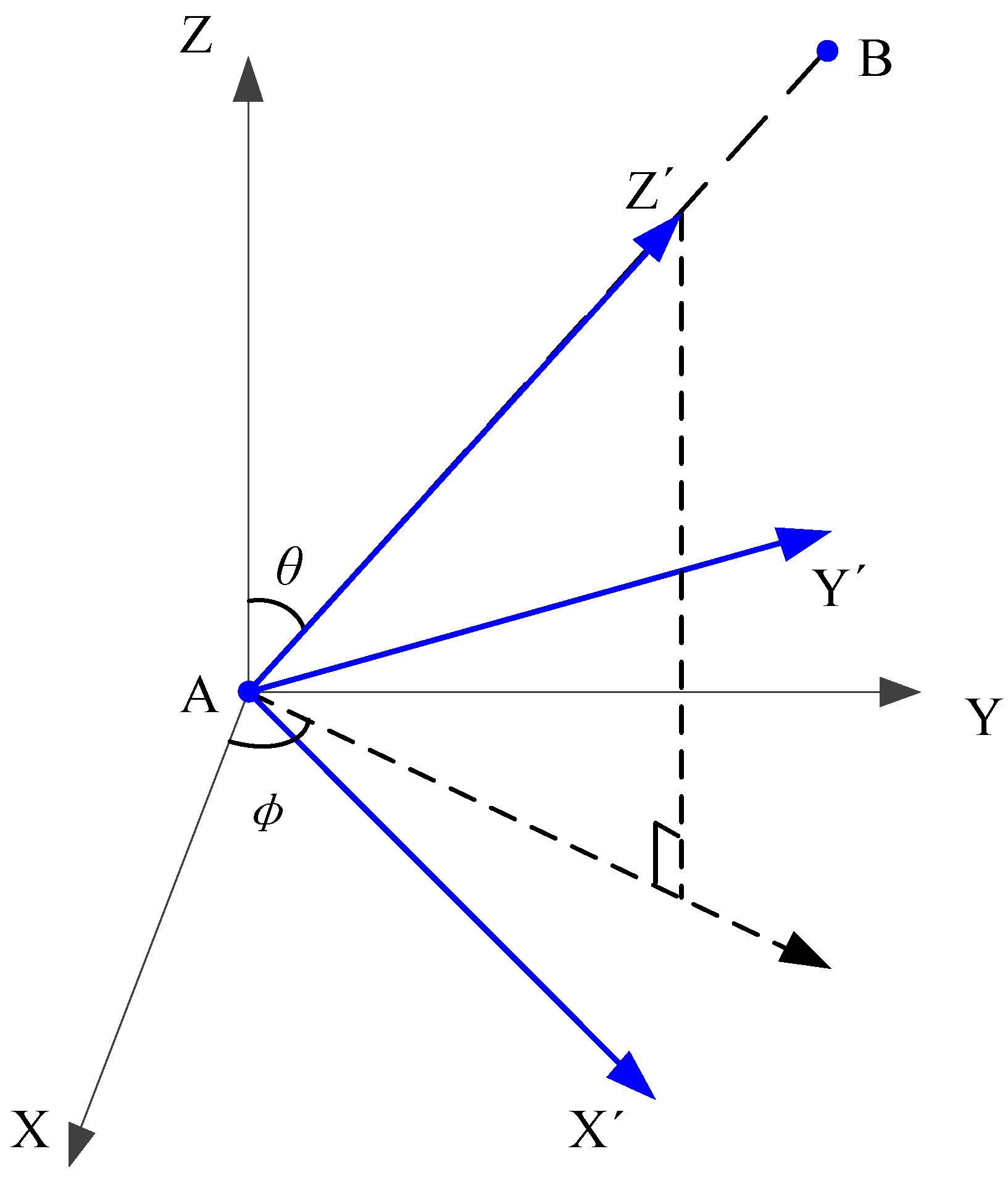
2. Analysis Method for Direct Solar Heat Flux of Pointing Attitude
- (1)
- The satellite body is assumed to be a hexahedron;
- (2)
- All edge lengths of the satellite are set to 1 m;
- (3)
- All surfaces of the satellite are flat;
- (4)
- To intuitively evaluate the external heat flux incident on each surface, various protrusions on the satellite surface are neglected, and the satellite surface is assumed to be unobstructed with each face being a convex surface.
- (1)
- The projection is in the first quadrant, namely η < 90° and α < 90°:
- (2)
- The projection is in the second quadrant, namely η < 90° and α > 90°:
- (3)
- The projection is in the third quadrant, namely η > 90° and α > 90°:
- (4)
- The projection is in the fourth quadrant, namely η > 90° and α < 90°:
- (1)
- While α = 90°, the pointing vector is in the YOZ plane. According to the geometric relation, the yaw angle φ = 90° (while η < 90°) or 270° (while η > 90°).
- (2)
- While η = 90°, the pointing vector is in the XOZ plane. According to the geometric relation, the yaw angle φ = 0° (while α ≤ 90°) or 180° (while α > 90°). In this case, the pointing vector is in the orbital plane. According to the position of the satellite relative to the object, the pointing attitude can be divided into forward pointing attitude and backward pointing attitude. For the forward pointing attitude, the object is in front of the satellite, namely in the +X direction of the satellite. In this case, there is no need for yaw to realize the pointing attitude, which matches the situation of α ≤ 90°. As for the backward pointing attitude, the object is at the back, which means α > 90°. To point to the object, the satellite should turn from the flight direction to the opposite flight direction, hence the yaw angle is 180°.
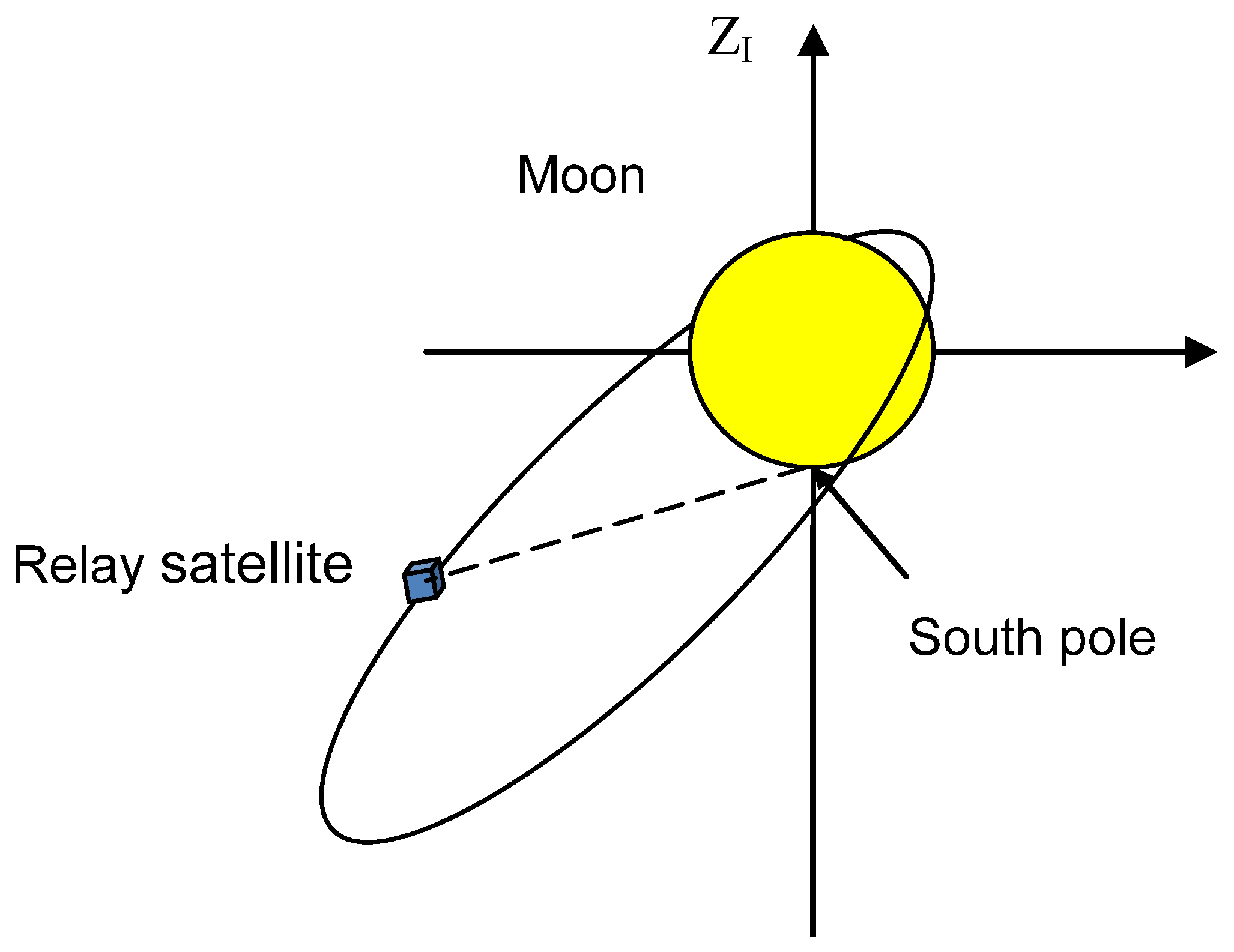
3. Analysis of Reaching Solar Heat Flux of Lunar Relay Satellite
3.1. Analysis of External Heat Flux for Relay Satellites in Halo Orbit
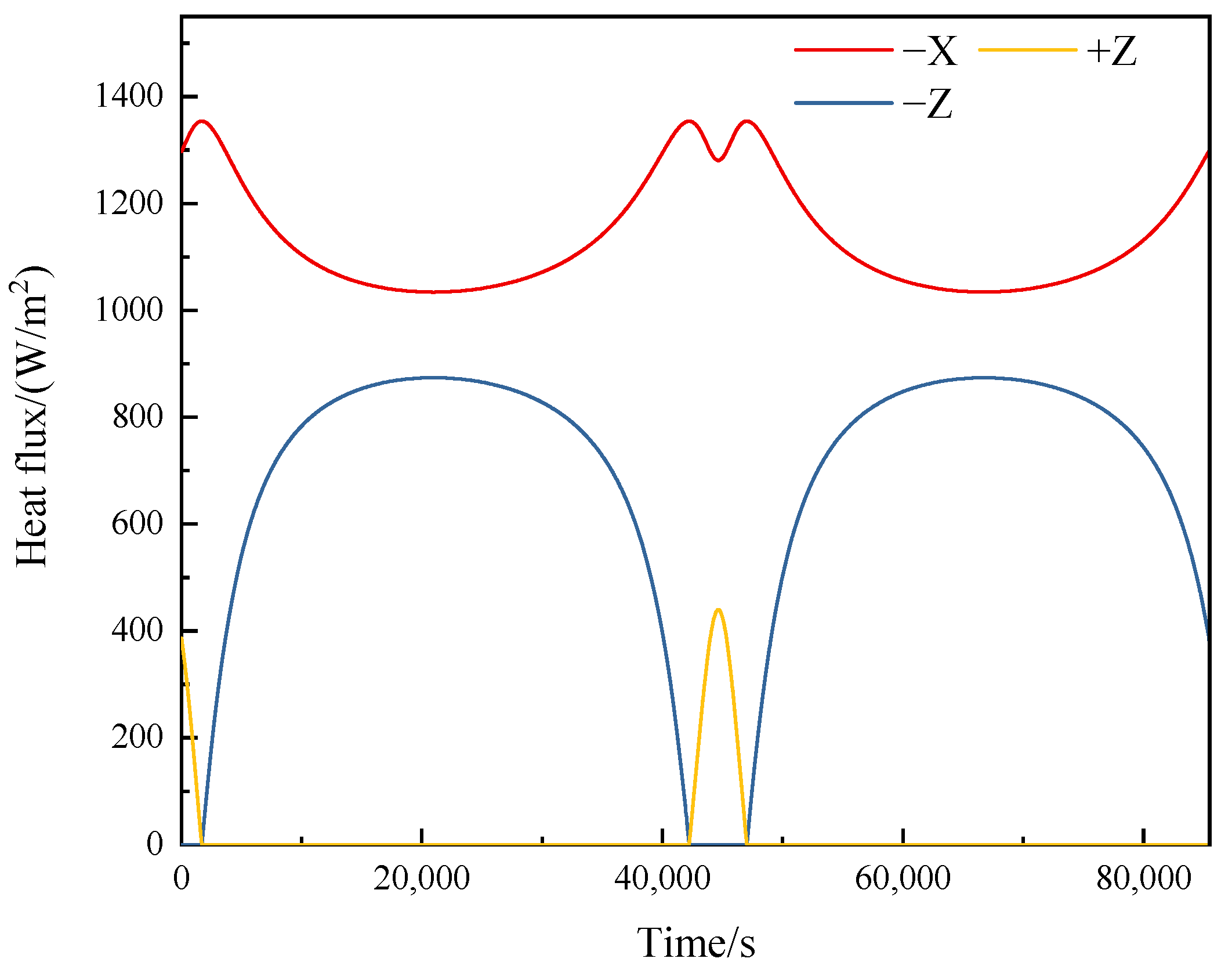
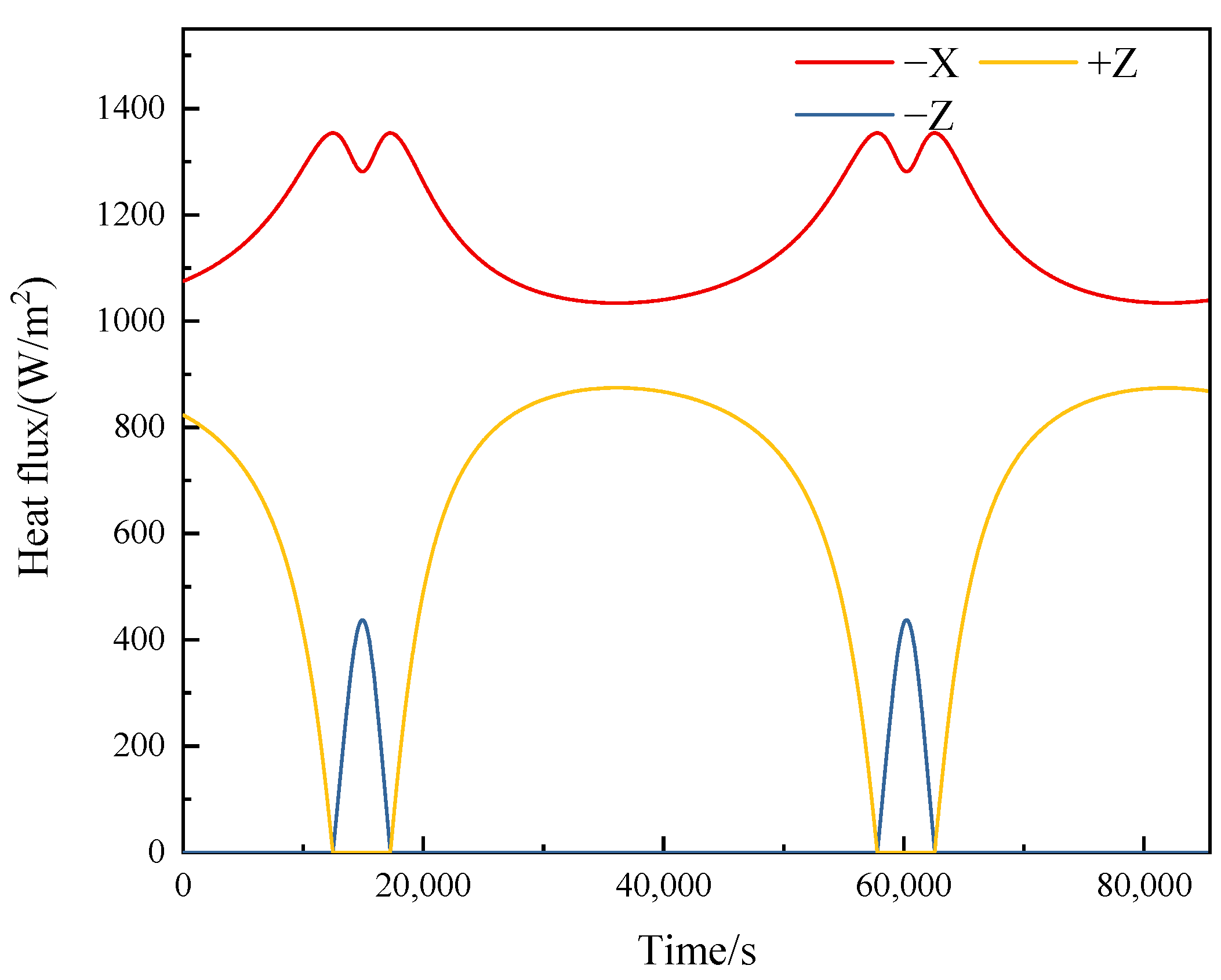
3.2. Analysis of External Heat Flux for Relay Satellites in Elliptic Orbit
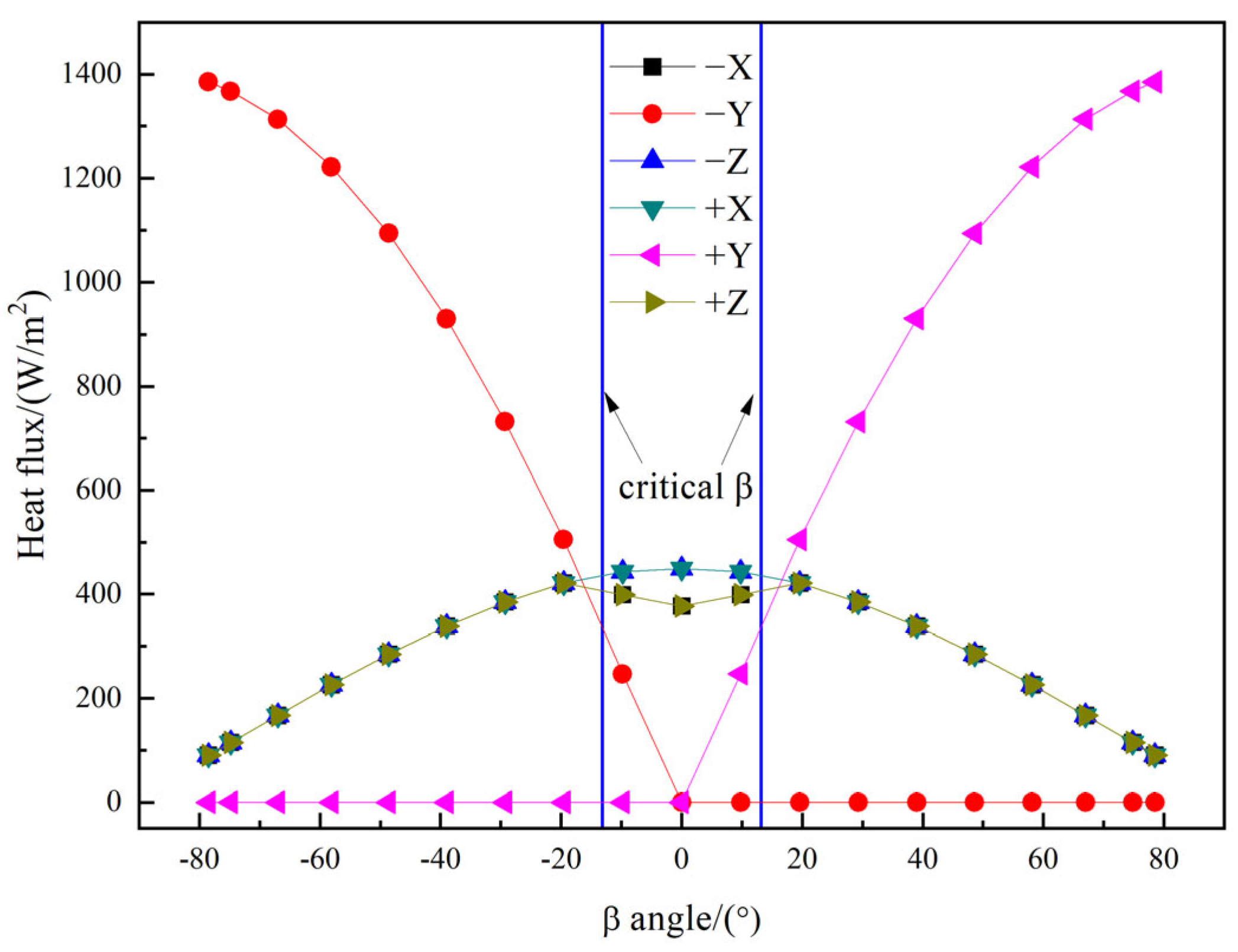
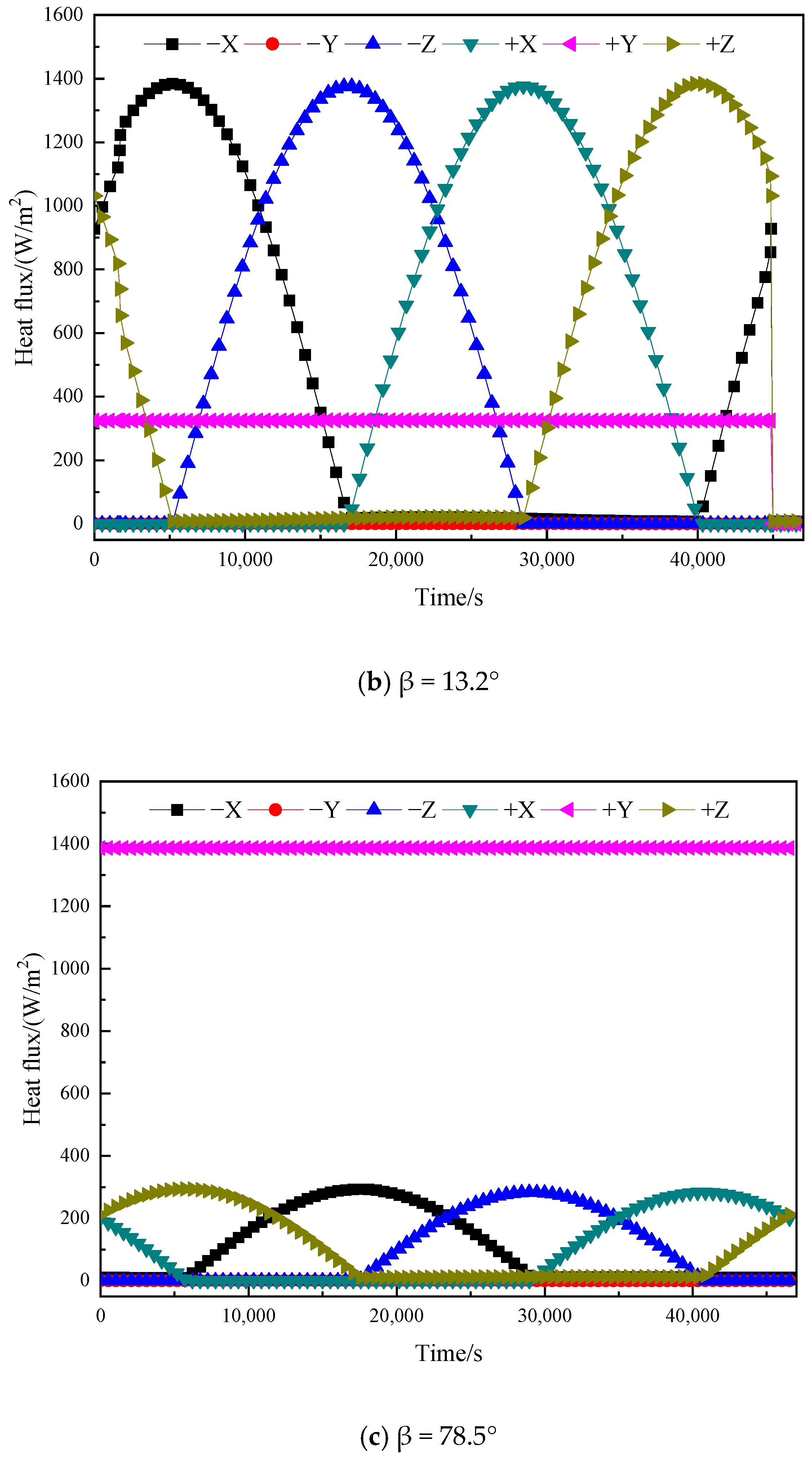
- (1)
- β = 0°
- (2)
- β = −56°
- (3)
- β = 56°
4. Thermal Analysis of Interstellar Laser Communication Payload
4.1. Analysis of External Heat Flux
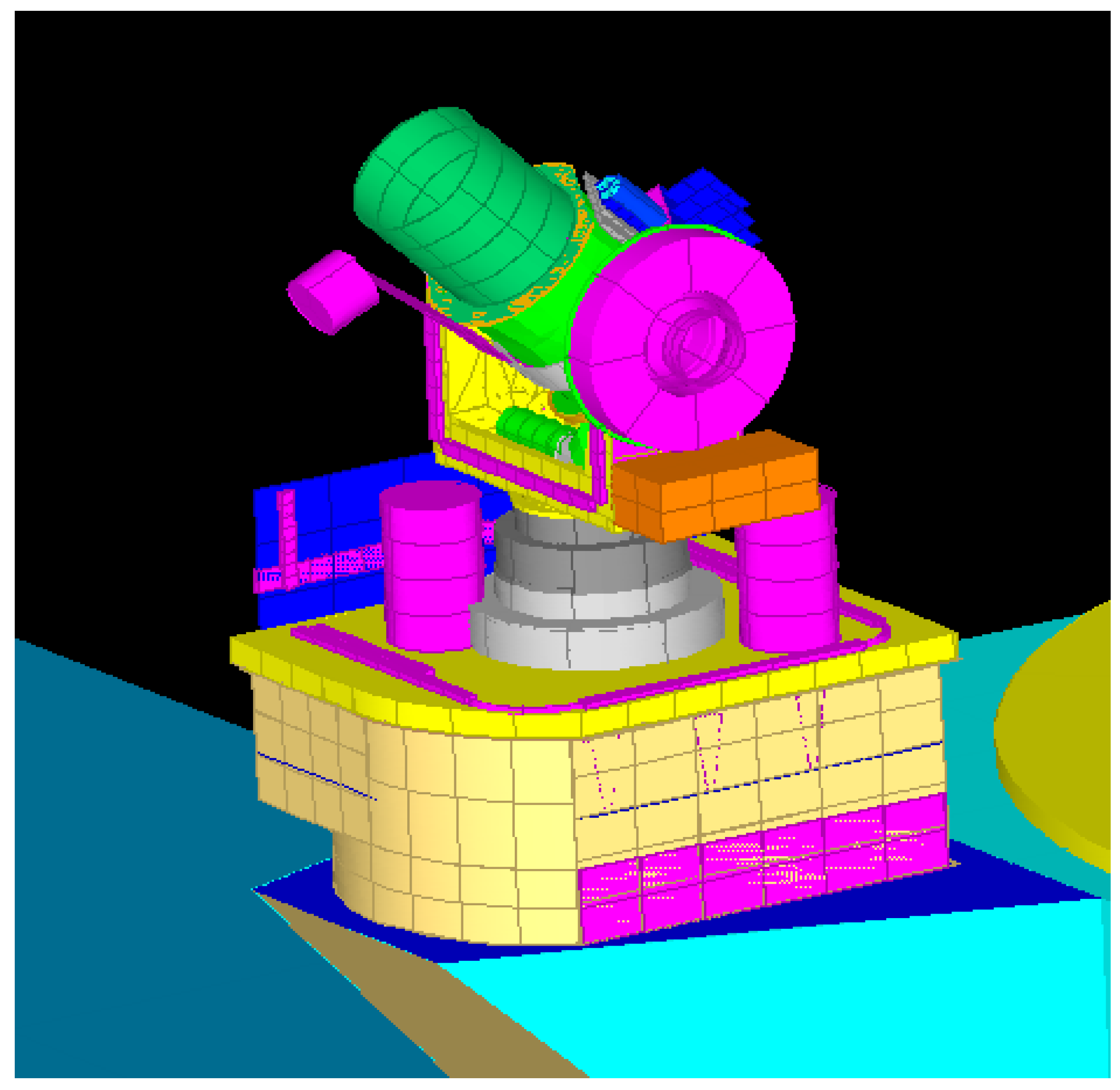
4.2. Modeling of Inter-Satellite Laser Communication Payload
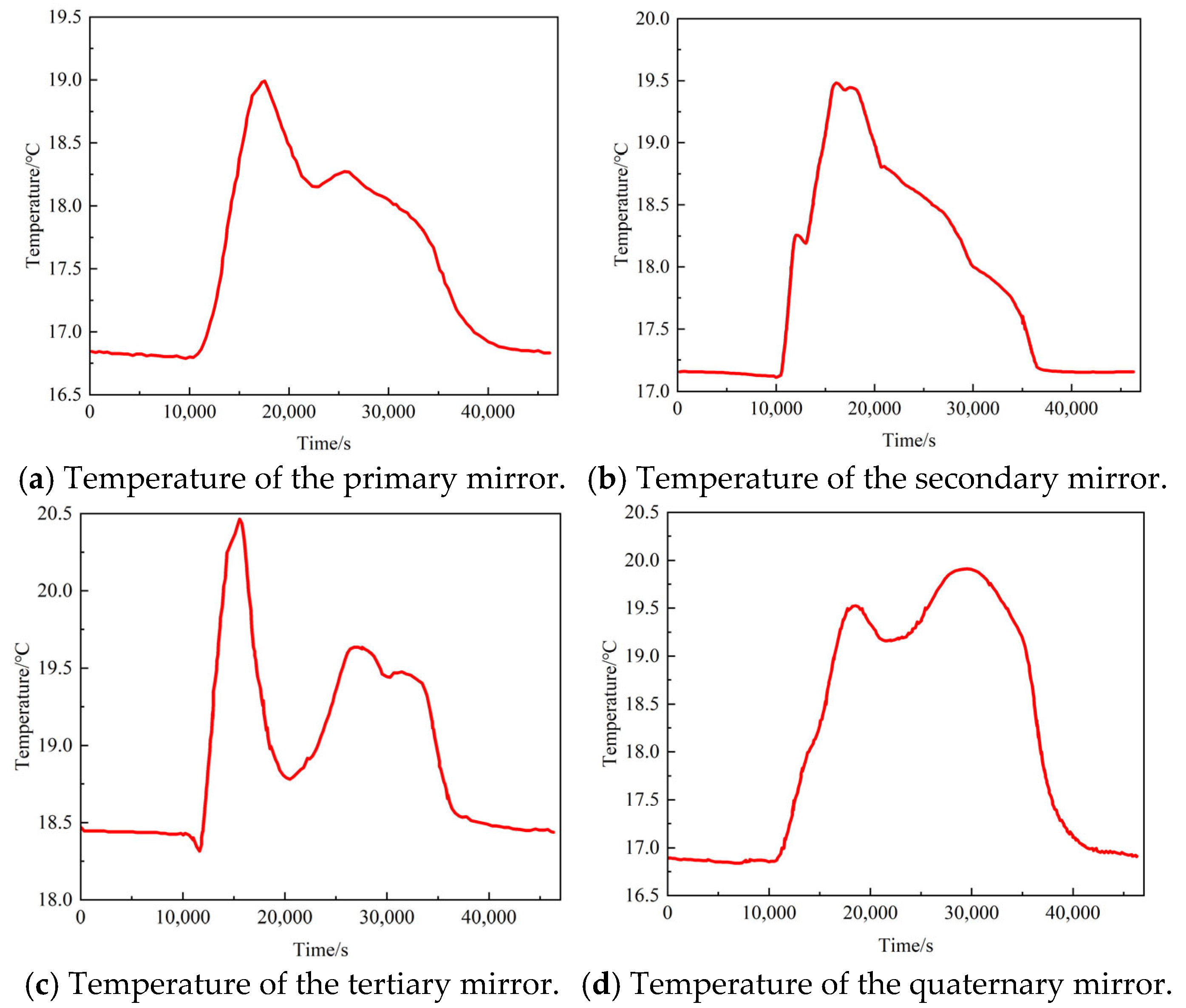
4.3. Payload Thermal Analysis of Typical Operating Conditions for Inter-Satellite Laser Communication Payload
5. Conclusions
- (1)
- A complex external heat flux analysis method for inter-satellite pointing attitudes has been proposed. A coordinate system for inter-satellite pointing attitudes was established, based on a three-axis Earth-pointing coordinate system. The +Z axis is rotated from Earth-pointing to the inter-satellite pointing vector direction through yaw and pitch. The calculation methods for yaw and pitch angles during coordinate system transformation were analyzed. Using the satellite orbit parameters and the calculated yaw and pitch angles, the external heat flux on each surface of the inter-satellite pointing attitude can be obtained using space thermal analysis software.
- (2)
- The solar heat flux for lunar relay satellites in Halo orbits and large elliptical frozen orbits was analyzed. For inclined elliptical orbits, the transient heat flux on each surface at different β angles was calculated, and the variations of solar heat flux were analyzed. This provides data references for thermal control design of relay satellites in inclined large elliptical orbits.
- (3)
- The temperature comparison results of key components of the laser communication payload show that the operational mode based on inter-satellite pointing attitudes aligns with its in-orbit operational conditions. The temperature calculation results obtained using the external heat flux analysis method for inter-satellite pointing attitudes matched the in-orbit temperatures. Therefore, the proposed analysis method is reasonable and feasible, and can provide references and bases for thermal control design of spacecraft/payloads in inter-satellite pointing attitudes.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, T.S.; Lin, P.; Dong, F.; Liu, X.Z.; Ma, W.Z.; Fu, Q. Progress and Prospect of Space Laser Communication Technology. Eng. Sci. 2020, 22, 92–99. [Google Scholar] [CrossRef]
- Liu, C.; Li, X.Y.; Zhang, K.H.; Lan, B.; Dai, T.J.; Xian, H. Research Progress and Future Directions in Deep Space Optical Communication. Laser Optoelectron. Prog. 2024, 61, 84–93. [Google Scholar]
- Liu, Z.; Jiang, Q.F.; Liu, S.T.; Tian, S.Q.; Zhu, L.Y.; Liu, X.Z.; Yu, J.X.; Zhao, J.T.; Yao, H.F.; Dong, K.Y. Research progress of space laser communication networking technology. Chin. Opt. 2025, 18, 429–451. [Google Scholar] [CrossRef]
- Yu, H.H.; Lu, S.W.; Hu, Q.; Fan, Y.B.; Zhu, F.N.; Xia, H.W.; Li, J.W.; Sun, J.F.; Hou, X.; Chen, W.B.; et al. In-orbit intersatellite laser communication experiment based on compound-axis tracking. Chin. Opt. Lett. 2025, 23, 42–48. [Google Scholar] [CrossRef]
- Carrizo, C.; Knapek, M.; Horwath, J.; Diaz Gonzalez, D.; Cornwell, P. Optical inter-satellite link terminals for next generation satellite constellations. In Proceedings of the Free-Space Laser Communications XXXII, San Francisco, CA, USA, 2 March 2020. [Google Scholar]
- Li, T.; Liu, B.G.; Tang, D.; Zhang, Q.Q. Space-Based TT&C and Communication Mode for Space Station. Aerosp. Shanghai 2023, 40, 134–139. [Google Scholar]
- Liu, B.G.; Wu, B. Application of TDRSS in Chinese Space TT&C. J. Spacecr. TT C Technol. 2012, 31, 1–5. [Google Scholar]
- Zhang, L.H.; Xiong, L.; Sun, J.; Gao, S.; Wang, X.L.; Zhang, A.B. Technical characteristics of the relay communication satellite “Queqiao” for Chang’e-4 lunar farside exploration mission. Sci. Sin. Technol. 2019, 49, 138–146. [Google Scholar] [CrossRef]
- Yang, M.F.; Zhang, G.; Zhang, W.; Ruan, J.H.; Huang, H.; Peng, J.; Deng, X.J.; Shi, W.; Wang, Y.; Zhang, H.H.; et al. Technical design and implementation of Chang’e-6 robotic sample return mission on the far side of the moon. Sci. Sin. Technol. 2025, 55, 1133–1146. [Google Scholar] [CrossRef]
- Zhao, X. Study on Change Rule of β Angle for Various Orbits in Satellite Thermal Design. Spacecr. Eng. 2008, 17, 57–61. [Google Scholar]
- Dou, Q.; Li, J.D.; Zhu, J.; Zhou, Y. Analysis on heat flux fluctuation and its inhibition strategies for agile satellite camera. Spacecr. Environ. Eng. 2014, 31, 62–67. [Google Scholar]
- Li, Z.S.; Ma, C.J.; Mao, Y.J.; Guo, T.; Wang, X.; Mou, X.N. Rapid analysis of temperature field for orbiting nanosatellites. Spacecr. Environ. Eng. 2021, 38, 122–129. [Google Scholar]
- Meng, H.H.; Geng, L.Y.; Li, G.Q. Thermal control design and experiment for laser communication equipment. Infrared Laser Eng. 2014, 43, 2295–2299. [Google Scholar]
- Mei, K.; Song, Y.W.; Liang, L.; Du, J.D.; Fu, S.; Jiang, Y.J. The effect of temperature characteristic variation due to thermal control design on the antenna of satellite laser communication terminals. In Proceedings of the 6th Global Conference on Materials Science and Engineering, Beijing, China, 24–27 October 2017. [Google Scholar]
- Liu, H.; Tan, J.; Tang, Z.B.; Ge, Z.J. Thermal control design and experimental verification of optical terminals for laser communication payloads of a satellite system. Spacecr. Environ. Eng. 2024, 41, 55–60. [Google Scholar]
- Liu, B.L.; Zhou, Z.X.; Li, J.; Tan, L.Y. Thermal control of optical antenna for spaceborne laser communication in geostationary orbit. Chin. J. Lasers. 2017, 44, 0306003. [Google Scholar]
- Han, Y.L.; Li, S.J.; Xie, T. Thermal control design and verification of co-orbital inter-satellite laser communication terminal. Spacecr. Environ. Eng. 2025, 42, 159–166. [Google Scholar]
- Liu, X.; Pan, Z.F. Simplified Calculating Method of the Sun Radiation Flux for On-orbit Satellite. Chin. Space Sci. Technol. 2012, 4, 15–21. [Google Scholar]
- Zhang, H.; Cao, J.G.; Wang, J.; Zeng, F.J. Analysis of Satellite’s Extreme Heat Flow in Inclined orbit. Aerosp. Shanghai. 2018, 35, 36–42. [Google Scholar]
- Yuan, M.; Li, Y.Z.; Sun, Y.H.; Ye, B.P. The space quadrant and intelligent occlusion calculation methods for the external heat flux of China space Station. Appl. Therm. Eng. 2022, 212, 1359–4311. [Google Scholar] [CrossRef]
- Zheng, H.R.; Ma, Y.; Zhang, S.; Wang, J.C.; Qu, Y.Y. Calculation of orbit external heat flow and radiation characteristics of space target. Chin. Opt. 2024, 17, 187–197. [Google Scholar] [CrossRef]
- Krainova, I.V.; Nenarokomov, A.V.; Nikolichev, I.A.; Titov, D.M.; Chumakov, V.A. Radiative Heat Fluxes in Orbital Space Flight. J. Eng. Thermophys 2022, 31, 441–457. [Google Scholar] [CrossRef]
- Yi, H.; Huang, X.; Zhou, Y.P. Study on general calculation method for external heat flux on convex surfaces on spacecraft in Keplerian orbit. Spacecr. Eng. 2024, 33, 59–64. [Google Scholar]
- Gao, S.; Zhou, W.Y.; Zhang, L.; Liang, W.G.; Liu, D.C.; Zhang, H. Trajectory design and flight results for Chang’e 4-relay satellite. Sci. Sin. Technol. 2019, 49, 156–165. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Gao, S.; Liu, D.C.; Zhang, X.Y.; Ma, J.N.; Yu, D.Y. Orbit design for lunar polar region exploration. J. Deep Space Explor. 2020, 7, 248–254. [Google Scholar]
- Lin, S.F.; Li, K.; Lin, B.J.; Jiang, G.Z.; Ma, E.R. Thermal Control Design and Validated for MEO Navigation Satellites. Chin. J. Space Sci. 2022, 42, 144–152. [Google Scholar] [CrossRef]





| Orbital Parameters | A Satellite | B Satellite |
|---|---|---|
| Altitude (km) | 21,586 | 21,586 |
| Eccentricity (°) | 0 | 0 |
| Inclination (°) | 55 | 55 |
| Argument of Periapsis (°) | 0 | 0 |
| Longitude of the Ascending Node (°) | 180 | 180 |
| True Anomaly (°) | 0 | −90 |
| Component | Minimum Temperature | Maximum Temperature |
|---|---|---|
| Primary Mirror | 16.6 | 19.3 |
| Secondary Mirror | 17.1 | 19.5 |
| Tertiary Mirror | 18.3 | 21.2 |
| Quaternary Mirror | 16.8 | 20.0 |
| Thermistor | Calculation Result | In-Orbit Data | ||
|---|---|---|---|---|
| Minimum Value | Maximum Value | Minimum Value | Maximum Value | |
| TZT102 | 18.5 | 20.5 | 18.7 | 19.2 |
| TZT103 | 18.5 | 20.6 | 18.5 | 19.1 |
| TZT104 | 18.4 | 20.9 | 18.5 | 23.2 |
| TZT105 | 18.8 | 19.5 | 18.6 | 22.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Li, T.; Yi, H.; Zhou, Y.; Xu, F.; Ren, Y. An Analytical Method for Solar Heat Flux in Spacecraft Thermal Management Under Multidimensional Pointing Attitudes. Energies 2025, 18, 3956. https://doi.org/10.3390/en18153956
Huang X, Li T, Yi H, Zhou Y, Xu F, Ren Y. An Analytical Method for Solar Heat Flux in Spacecraft Thermal Management Under Multidimensional Pointing Attitudes. Energies. 2025; 18(15):3956. https://doi.org/10.3390/en18153956
Chicago/Turabian StyleHuang, Xing, Tinghao Li, Hua Yi, Yupeng Zhou, Feng Xu, and Yatao Ren. 2025. "An Analytical Method for Solar Heat Flux in Spacecraft Thermal Management Under Multidimensional Pointing Attitudes" Energies 18, no. 15: 3956. https://doi.org/10.3390/en18153956
APA StyleHuang, X., Li, T., Yi, H., Zhou, Y., Xu, F., & Ren, Y. (2025). An Analytical Method for Solar Heat Flux in Spacecraft Thermal Management Under Multidimensional Pointing Attitudes. Energies, 18(15), 3956. https://doi.org/10.3390/en18153956







