The Influence of Variable Operating Conditions and Components on the Performance of Centrifugal Compressors in Natural Gas Storage Reservoirs
Abstract
1. Introduction
2. Methods
2.1. Introduction to Similar Conversion Methods
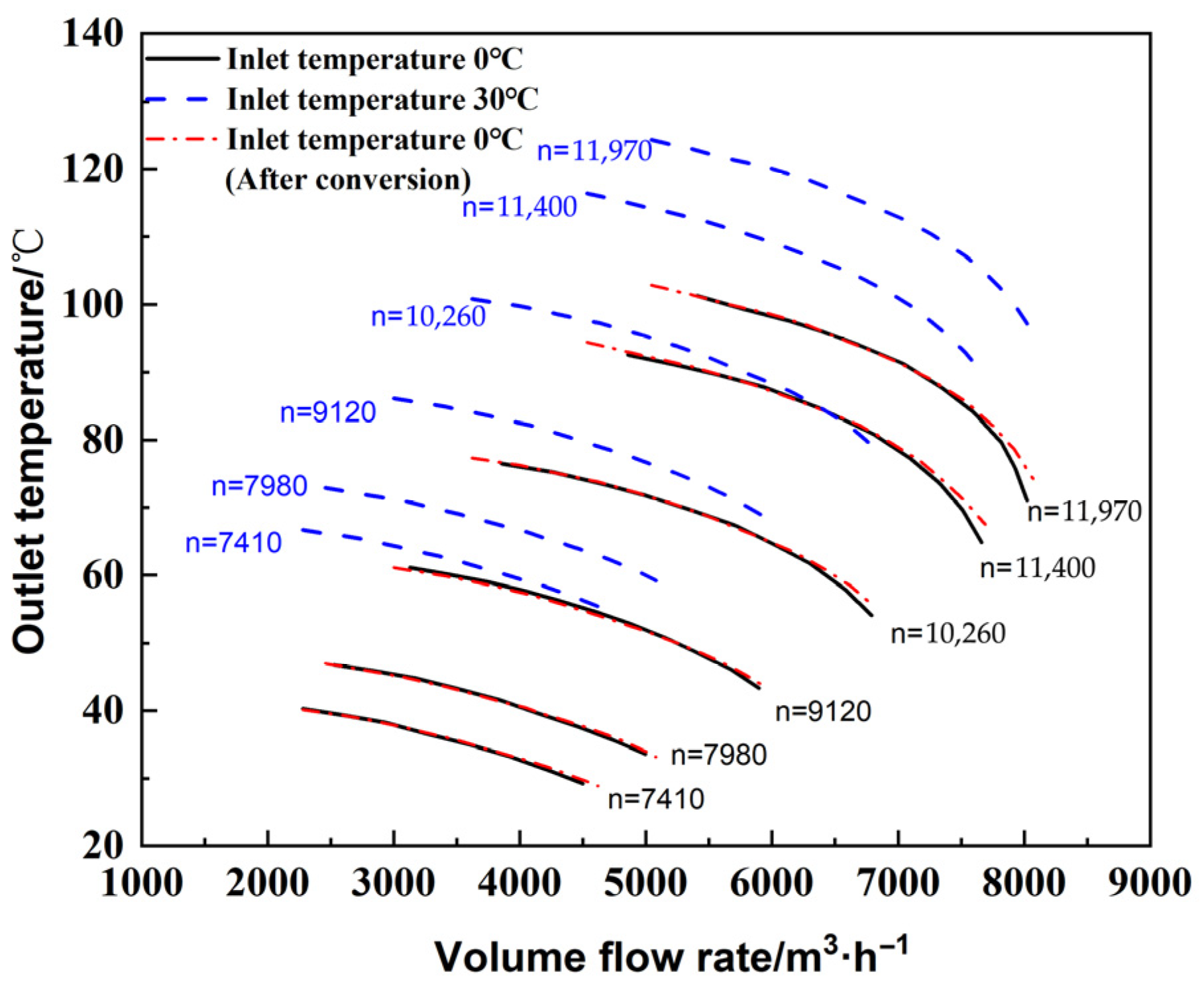
2.2. Conversion of Exhaust Temperature Curve
2.3. Calculation Methods for Compression Factor and Polytropic Exponent
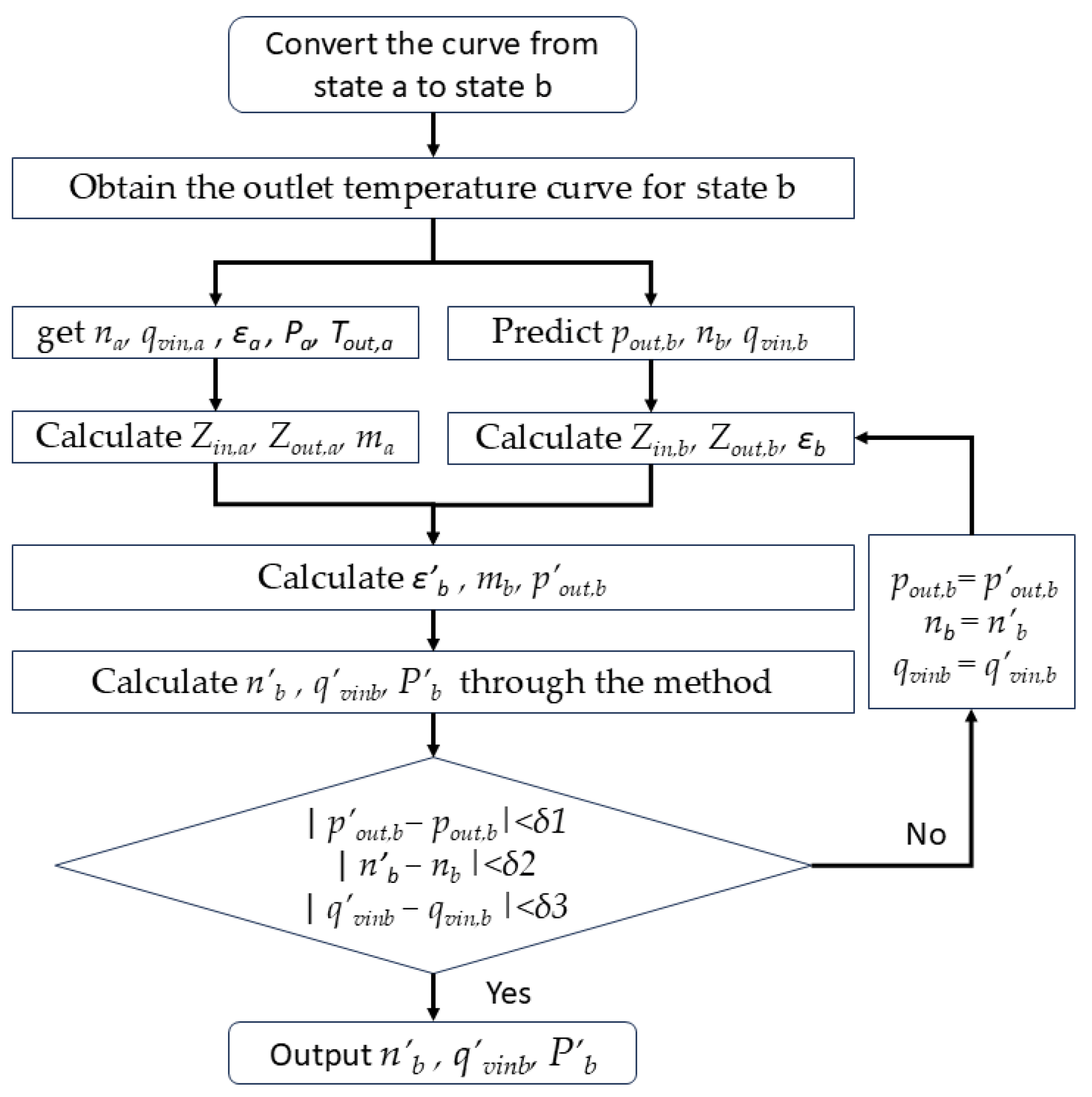
2.4. Calculation Methods for Off-Design Performance Conversion
- (1)
- Give the outlet pressure performance curve, power performance curve, and exhaust temperature curve of a known operating condition. At the same time, give the inlet temperature tin, inlet pressure pin, rotation speed n, and flow rate q of the operating condition to be determined.
- (2)
- Assume the outlet pressure pout, which satisfies pout > pin.
- (3)
- Convert the exhaust temperature curve of the known operating condition to the operating condition to be determined through the exhaust temperature conversion equation fitted with the existing data.
- (4)
- Look up the exhaust temperature tout of the operating condition to be determined on the exhaust temperature curve through the given flow rate and rotation speed of the operating condition to be determined.
- (5)
- Calculate the outlet pressure of the known operating condition through the pressure conversion equation and calculate the exhaust pressure of the known operating condition through the temperature conversion equation.
- (6)
- Look up the import and export compression factors Zin, Zout, Zin*, and Zout* of the known operating condition and the operating condition to be determined in refprop through temperature and pressure.
- (7)
- Calculate the outlet pressure of the known operating condition again through the pressure conversion equation and calculate the polytropic exponents m and m* of the operating condition to be determined and the known operating condition through the polytropic exponent calculation equation.
- (8)
- Calculate the rotation speed n* and flow rate qvin* of the known operating condition through the rotation speed and flow rate conversion equations in (4) and (5).
- (9)
- Look up the outlet pressure pout* through the flow rate and rotation speed in the outlet pressure curve of the known operating condition.
- (10)
- Calculate the outlet pressure pout1 of the operating condition to be determined through the pressure conversion equation.
- (11)
- If pout1 is much different from the initially assumed pout, then use pout1 as the assumed outlet pressure to recalculate until the difference between the calculated outlet pressure and the assumed outlet pressure is less than a certain value.
- (12)
- At this time the calculated outlet pressure is the outlet pressure of the operating condition to be determined, and the ratio of the outlet pressure to the inlet pressure is the pressure ratio of the operating condition to be determined.
- (13)
- Calculate the rotation speed n* and flow rate qvin* of the known operating condition through the rotation speed and flow rate conversion equations, obtain the power P* of the known operating condition through the power curve, and obtain the power P of the operating condition to be determined through the power conversion equation.
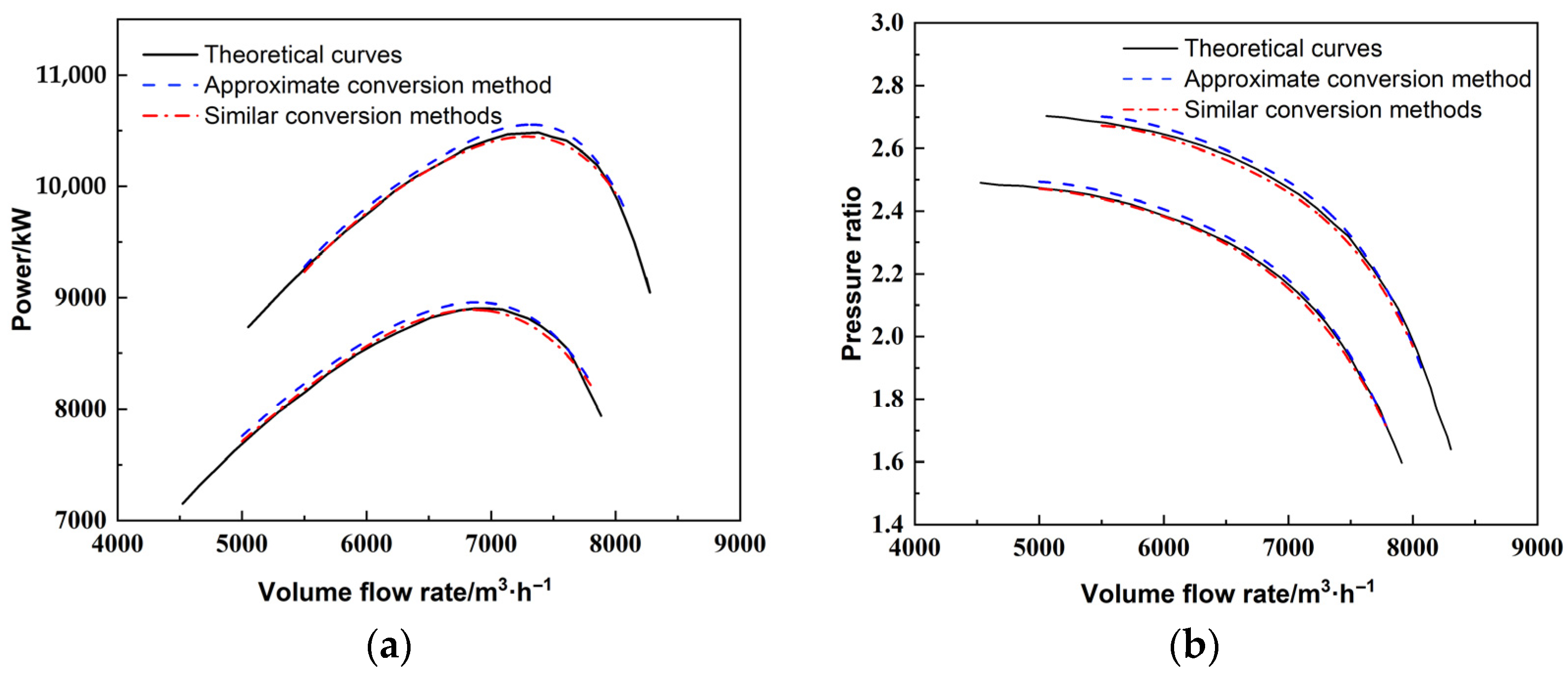
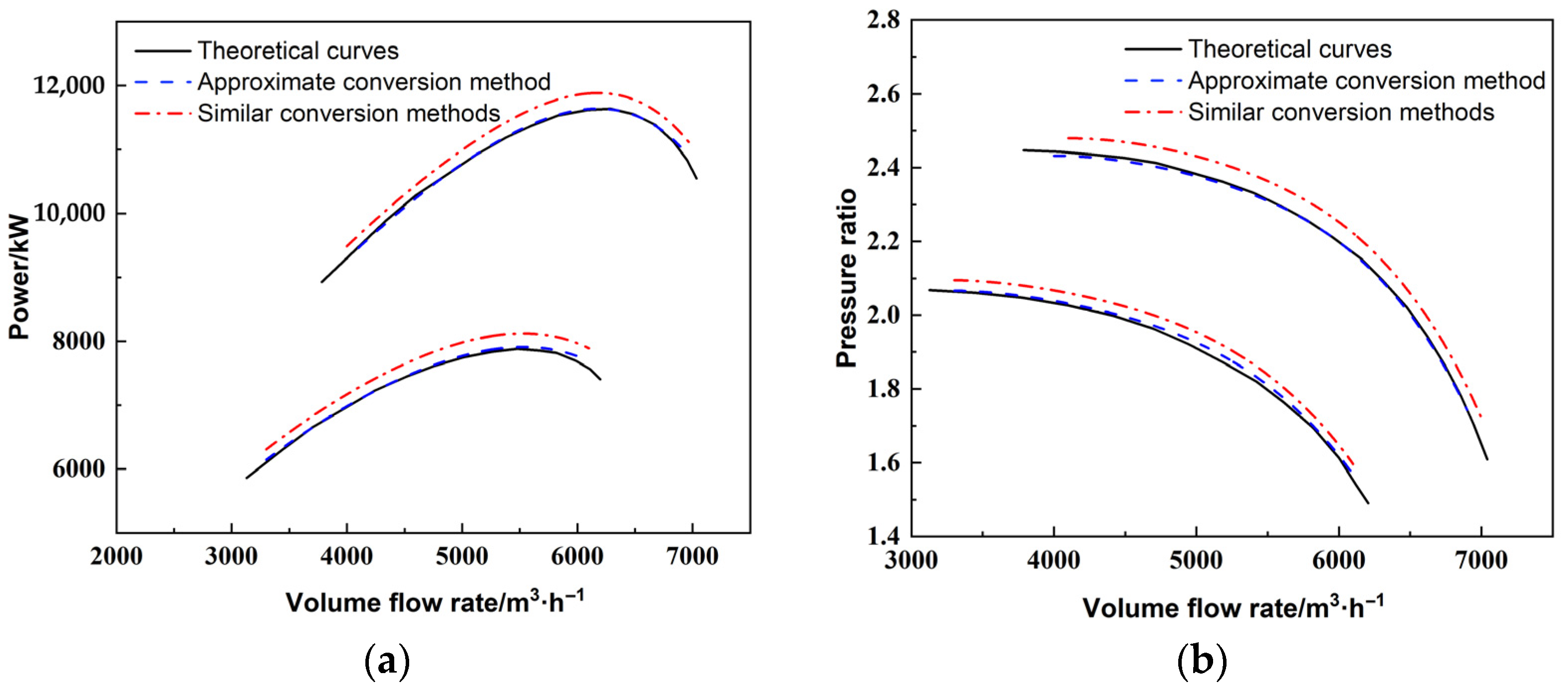
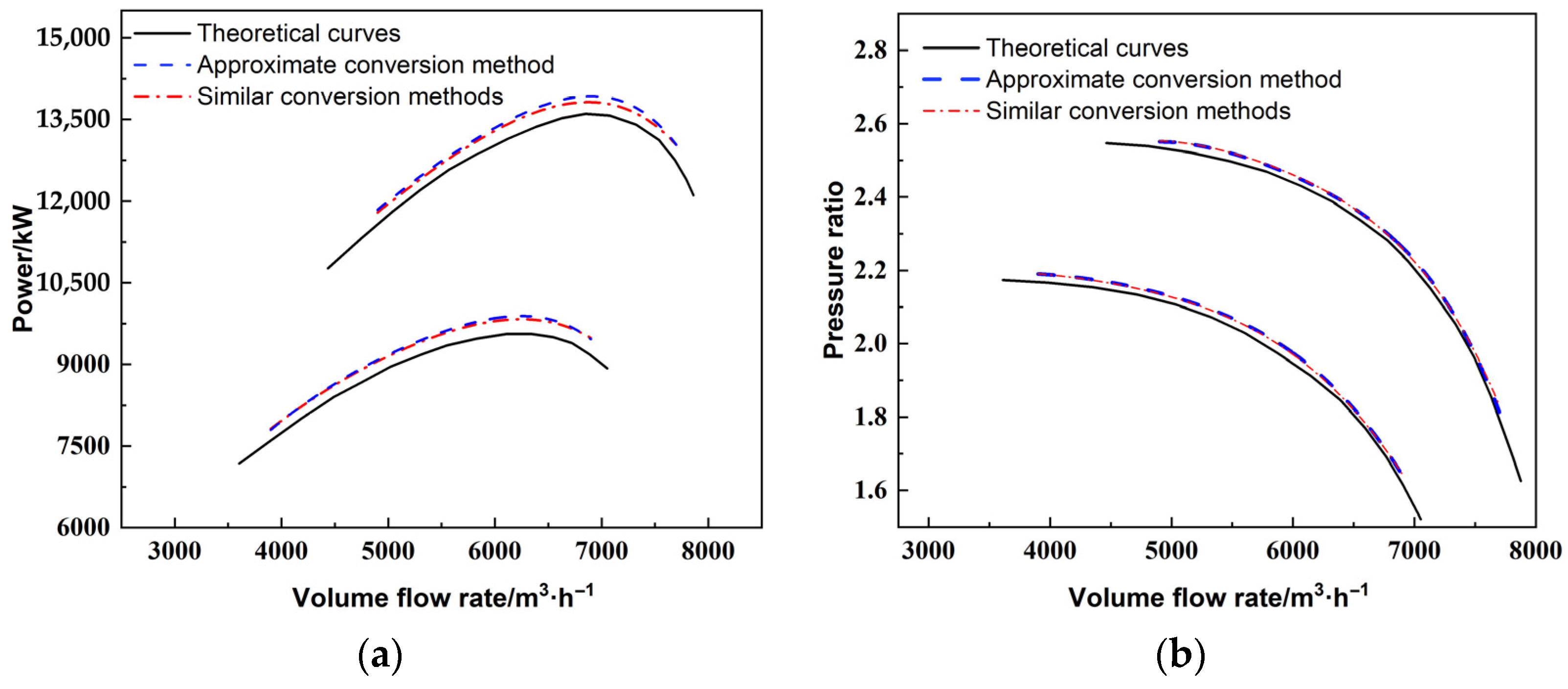
2.5. Verify the Calculation Results
3. Results and Discussion
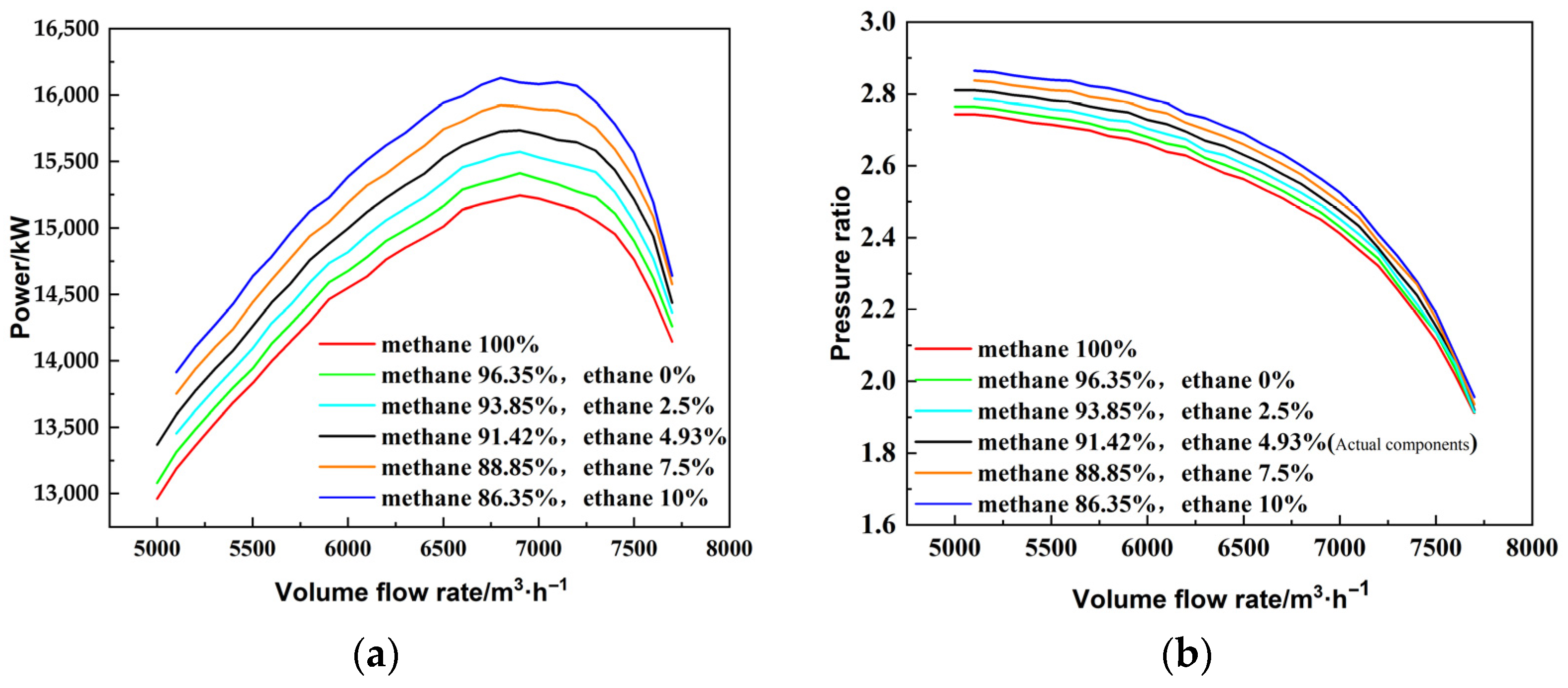
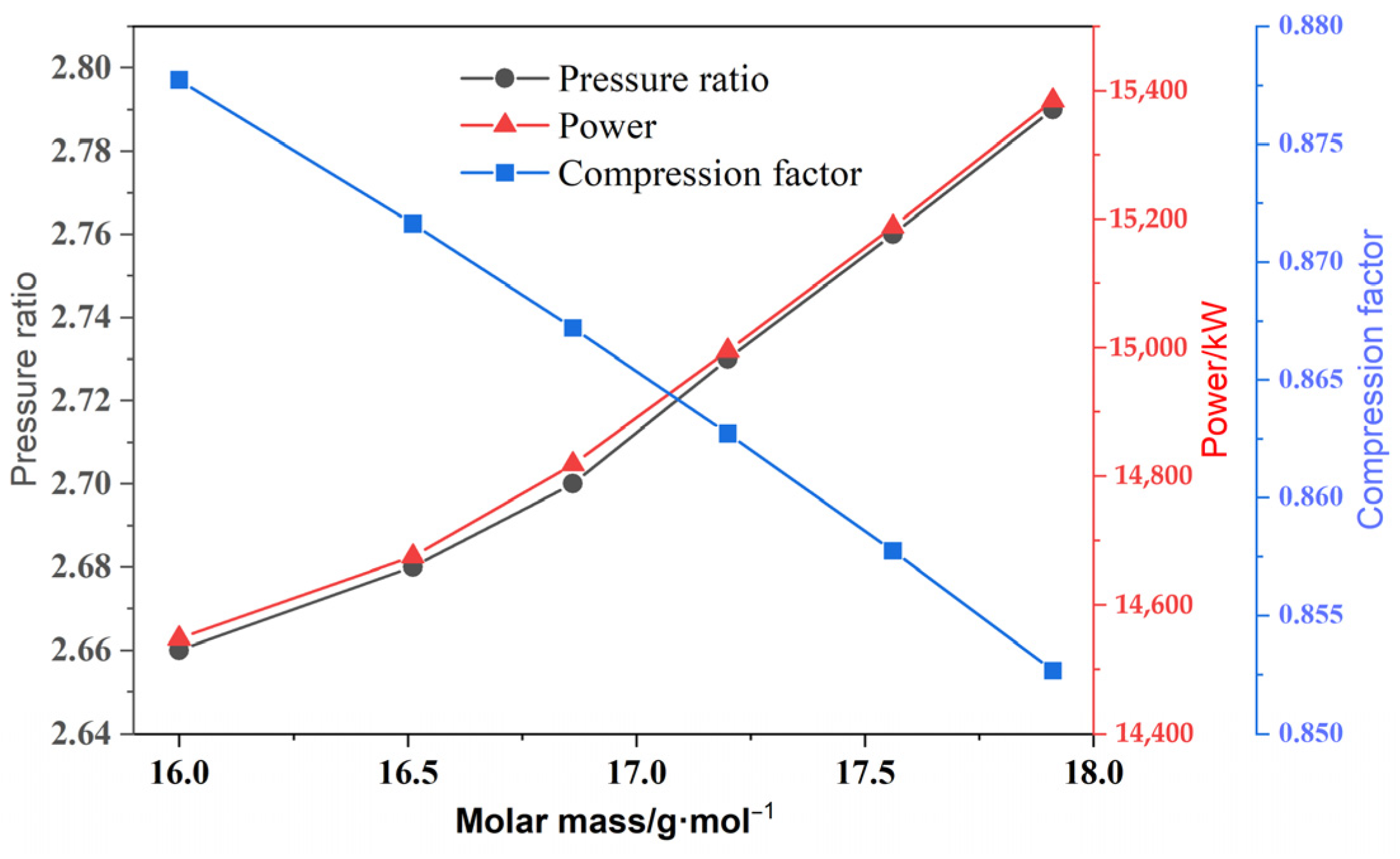
3.1. Research on Natural Gas Component Changes
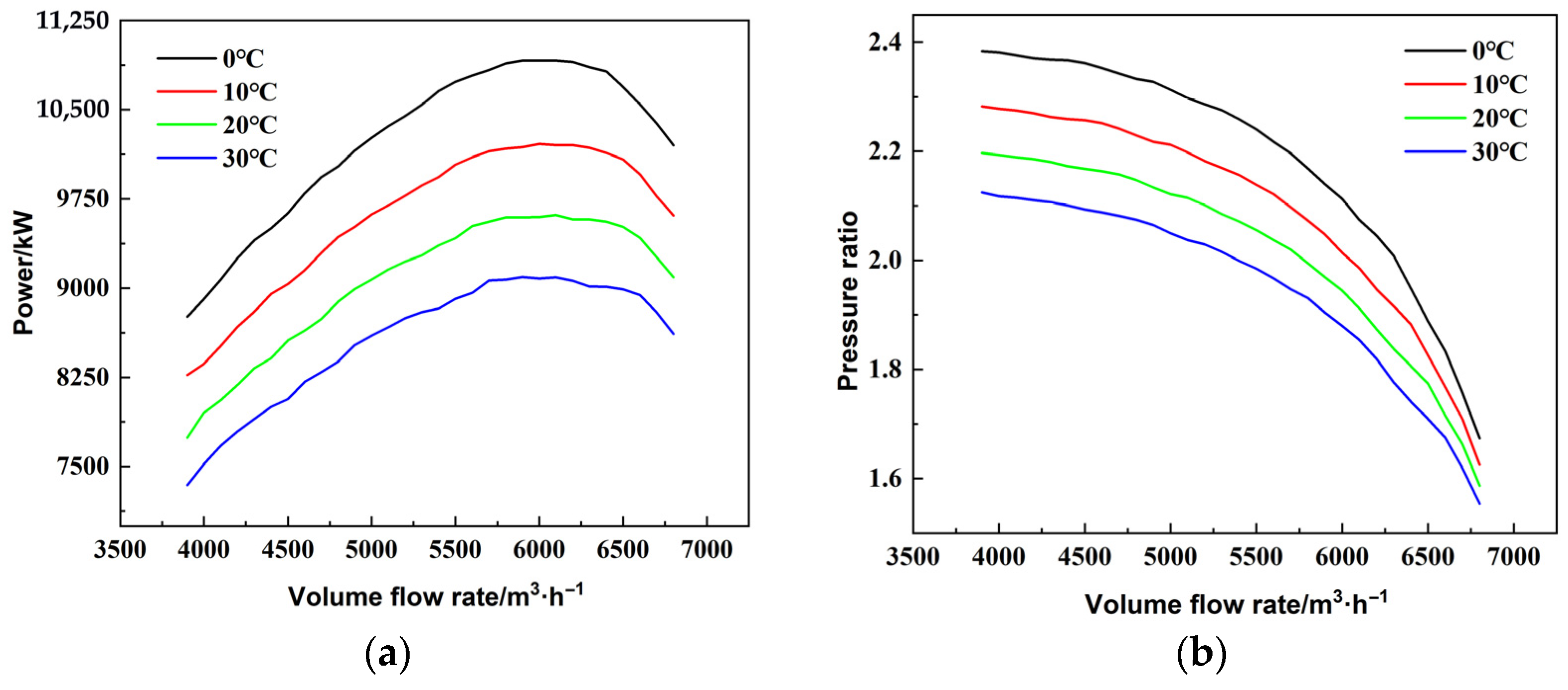
3.2. Research on the Change in Natural Gas Inlet Temperature
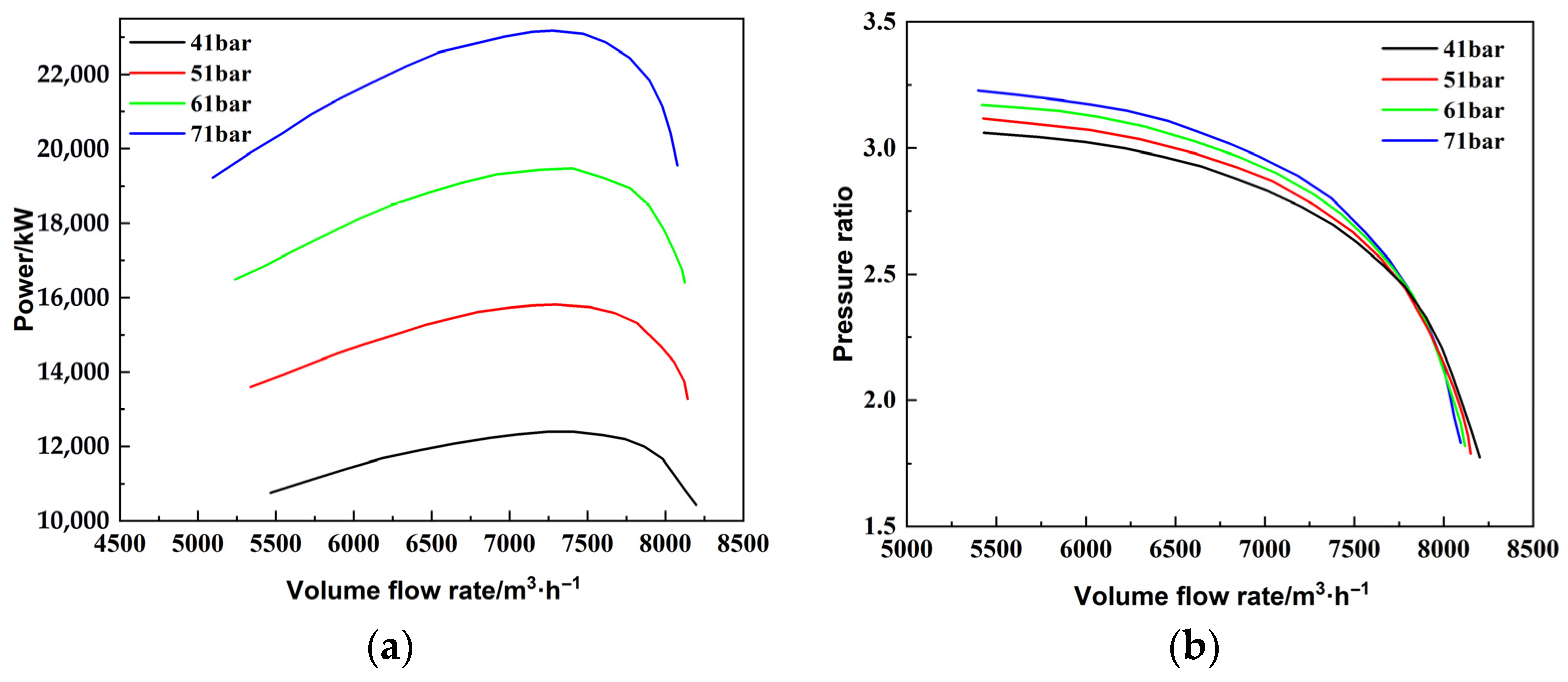
3.3. Research on the Change in Natural Gas Inlet Pressure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, X.; Wu, X.; Wu, Y.; Wang, Y. Energy system design of offshore natural gas hydrates mining platforms considering multi-period f loating wind farm optimization and production profile fluctuation. Energy 2023, 265, 126360. [Google Scholar] [CrossRef]
- Ma, T.B.; Chu, H.Y.; Li, J.W.; Zhang, J.X.; Gao, Y.B.; Zhu, W.Y.; Lee, W.J. Rate transient analysis for multilateral horizontal well in natural gas hydrate: Superposition principle and reciprocity. Int. J. Coal Sci. Technol 2024, 11, 70. [Google Scholar] [CrossRef]
- Weitemeyer, S.; Kleinhans, D.; Vogt, T.; Agert, C. Integration of renewable energy sources in future power systems: The role of storage. Renew. Energy 2015, 75, 14–20. [Google Scholar] [CrossRef]
- Ji, W.D.; Wan, J.F.; Li, J.C.; Chen, S.Z.; Ma, H.L.; Yu, H.B. Integration of large-scale underground energy storage technologies and renewable energy sources. Adv. Geo-Energy Res. 2024, 14, 81–85. [Google Scholar] [CrossRef]
- Lei, H. Opportunities and challenges to the construction of underground gas storages in China. Oil Gas Storage Transp. 2018, 37, 728–733. [Google Scholar]
- Marfatia, Z.; Li, X. Data-Driven Natural Gas Compressor Models for Gas Transport Network Optimization. Digit. Chem. Eng. 2022, 3, 100030. [Google Scholar] [CrossRef]
- Song, J.N.; Liu, G.B.; Gong, J.M.; Yang, Q.C.; Zhao, Y.Y.; Li, L.S. Simulation on performance and regulation strategy of centrifugal refrigeration compressor with gas bearings in water chiller. Appl. Therm. Eng. 2024, 236, 121650. [Google Scholar] [CrossRef]
- Navarro, E.; Redon, A.; Gonzalvez-Macia, J.; Martinez-Galvan, I.O.; Corberan, J.M. Characterization of a vapor injection scroll compressor as a function of low, intermediate and high pressures and temperature conditions. Int. J. Refrig. 2013, 36, 1821–1829. [Google Scholar] [CrossRef]
- Sun, D.K.; Shen, X.H.; Xu, D.K.; Ning, F.F.; Li, J.B.; Sun, X.F. Analysis of flow characteristics and flow stability on an axial compressor with inlet temperature ramp distortion. Aerosp. Sci. Technol. 2025, 164, 110457. [Google Scholar] [CrossRef]
- Chen, H.Y.; Shang, J.; Yi, L.; Zhao, B.H.; Liu, S.H.; Wang, J.Z.; Cui, L.; Wu, J.H. Investigations on control strategies for multi-stage cold compressors in superfluid helium system. Cryogenics 2025, 147, 104039. [Google Scholar] [CrossRef]
- Peng, Q.Q.; Bao, R.X.; Li, J.; Ren, J.; Tang, J.; Li, J.; Pan, Z.; Ma, G.; Gao, Y.; Kang, T.; et al. Centrifugal compressor performance prediction and dynamic simulation of natural gas hydrogen blended. Int. J. Hydrogen Energy 2024, 52, 872–893. [Google Scholar] [CrossRef]
- Wang, W.; Zhao, S.; Wang, X.F.; Xu, B.P.; Xu, R.D. Accurate and fast prediction of the viscosity of natural gascomponents based on the binary regression analysis method. J. Beijing Univ. Chem. Technol. 2017, 44, 13–19. [Google Scholar]
- Mahmood, F.G.; Amir, N.; Mahdi, D.D.; Hamid, R.R. Effects of natural gas compositions on CNG (compressed natural gas) reciprocating compressors performance. Energy 2015, 90, 1152–1162. [Google Scholar] [CrossRef]
- Wang, L.F.; Gu, B.; Wang, T. Fast Calculation Model of Fan Performance Based on Similarity Theory. Fluid Mach. 2012, 40, 24–28. [Google Scholar]
- Xie, J.X. Approximate Similarity Conversion of Performance Curves for Circulating Hydrogen Centrifugal Compressors in Hydrotreating Units. Compressor Technol. 2008, 30–32. [Google Scholar] [CrossRef]
- Qing, D.F. Performance Conversion and Application of Multistage Centrifugal Compressors under Partially Similar Conditions. Mod Mach. 2002, 2, 011. [Google Scholar]
- Wang, K.X.; Zuo, Z.T.; Liang, Q.; Guo, W.B.; Chen, H.S. Performance prediction methods for centrifugal compressors: A review. Energy Storage Sci. Technol. 2023, 12, 3435–3444. [Google Scholar]
- Wang, P.; Yang, F.; Sun, D.L.; Wang, L.Y.; Zuo, D. Performance conversion of centrifugal compressors based on predictor corrector method. Chin. Sci. Bull. 2018, 63, 571–578. [Google Scholar] [CrossRef][Green Version]
- Miao, X.G.; Liu, L.; Wang, Z.Y.; Chen, X.M. Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction. Energies 2024, 17, 2113. [Google Scholar] [CrossRef]
- Xu, P.C.; Zou, Z.P.; Yao, L.C. A unified performance conversion method for similar compressors working with different gases based on polytropic analysis and deep-learning improvement. Energy Convers. Manag. 2021, 247, 114747. [Google Scholar] [CrossRef]
- Jeong, H.; Ko, K.; Kim, J.; Kim, J.; Eom, S.; Na, S.; Choi, G. Evaluation of Prediction Model for Compressor Performance Using Artificial Neural Network Models and Reduced-Order Models. Energies 2024, 17, 3686. [Google Scholar] [CrossRef]
- Zhu, C.Y.; Qin, G.L.; Wu, R.L. Comparison of the Two Similar Con version of Centrifugal Compressor Based on Test. Chin. J. Turbomach. 2011, 53, 24–27. [Google Scholar]
- Xiong, Z.Y.; Liu, Y.H.; Cai, Y.J.; Zhang, W.C.; Wang, Z.Q.; Li, Z.L.; Peng, S.Y. Research on the effect of green hydrogen blending on natural gas centrifugal compressor performance. Renew. Energy 2025, 242, 122378. [Google Scholar] [CrossRef]
- Wu, F.; Jiang, J.B.; Peng, X.D.; Li, M.T.; Yu, M.F. Influence of natural gas composition and operating conditions on the phase change of dry gas seals for pipeline compressors. Int. J. Heat Fluid Flow 2025, 115, 109832. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Y.T. Study of Performance Changes in Centrifugal Compressors Working in Different Refrigerants. Energies 2024, 17, 2784. [Google Scholar] [CrossRef]
- Magee, J.W.; Haynes, W.M.; Hiza, M.J. Isochoric (p, ρ, T) measurements for five natural gas mixtures from T =(225 to 350) K at pressures to 35 MPa. J. Chem. Thermodyn. 1997, 29, 1439–1454. [Google Scholar] [CrossRef]
- Li, J.C.; Fan, Y.; Wu, T.; Wu, T.; Zhang, Y.; Zhou, K. Investigation on the Compressibility Factor of Hydrogen-Doped Natural Gas Using GERG-2008 Equation of State. Energies 2025, 18, 53. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Q. Analysis of energy consumption for multi-stage compression considering the compression ratio and inlet temperature. Comput. Appl. Chem. 2018, 35, 711–718. [Google Scholar]
- Huang, D.Y.; Zhou, B.W.; Jiang, D.J.; Pan, J.X. Numerical study on the effect of the inlet pressure on centrifugal compressor performance. Tsinghua Sci. Technol. 2024, 64, 1666–1676. [Google Scholar]
| Operating Conditions | Inlet Temperature/°C | Inlet Pressure/MPa |
|---|---|---|
| 1 | 0 | 4.1 |
| 2 | 30 | 4.1 |
| 3 | 0 | 6.1 |
| 4 | 30 | 6.1 |
| Operating Conditions | Inlet Pressure/MPa | Inlet Temperature/°C | Outlet Pressure/MPa | Rotate Speed/rpm | Volume Flow Rate/103·m3·h−1 |
|---|---|---|---|---|---|
| 1 | 5.94 | 8.4 | 9.16 | 7523 | 281.9 |
| 2 | 6.82 | 9.5 | 10.64 | 7410 | 316.6 |
| 3 | 6.82 | 12.2 | 10.82 | 7645 | 337.4 |
| 4 | 6.94 | 14.8 | 11.59 | 8007 | 348.5 |
| 5 | 6.9 | 14.9 | 11.97 | 8238 | 346.8 |
| Operating Conditions | Actual Power/kW | Converted Power/kW | δP/% | Actual Pressure Ratio | Converted Pressure Ratio | δε/% |
|---|---|---|---|---|---|---|
| 1 | 4667 | 4712 | 0.96 | 1.542 | 1.547 | 0.32 |
| 2 | 5167 | 5048 | 2.3 | 1.560 | 1.553 | 0.45 |
| 3 | 5625 | 5714 | 1.6 | 1.586 | 1.595 | 0.57 |
| 4 | 6417 | 6489 | 1.1 | 1.670 | 1.676 | 0.36 |
| 5 | 6917 | 6778 | 2.0 | 1.735 | 1.739 | 0.23 |
| Component | Molar Score/% |
|---|---|
| methane | 91.42 |
| ethane | 4.93 |
| propane | 0.96 |
| butane | 0.41 |
| C5+ | 0.24 |
| nitrogen | 1.63 |
| carbon dioxide | 0.12 |
| oxygen | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Li, G.; Wang, S.; Wang, N.; Zhou, L.; Zhou, H.; Sun, Y.; Liu, L. The Influence of Variable Operating Conditions and Components on the Performance of Centrifugal Compressors in Natural Gas Storage Reservoirs. Energies 2025, 18, 3930. https://doi.org/10.3390/en18153930
Chen H, Li G, Wang S, Wang N, Zhou L, Zhou H, Sun Y, Liu L. The Influence of Variable Operating Conditions and Components on the Performance of Centrifugal Compressors in Natural Gas Storage Reservoirs. Energies. 2025; 18(15):3930. https://doi.org/10.3390/en18153930
Chicago/Turabian StyleChen, Hua, Gang Li, Shengping Wang, Ning Wang, Lifeng Zhou, Hao Zhou, Yukang Sun, and Lijun Liu. 2025. "The Influence of Variable Operating Conditions and Components on the Performance of Centrifugal Compressors in Natural Gas Storage Reservoirs" Energies 18, no. 15: 3930. https://doi.org/10.3390/en18153930
APA StyleChen, H., Li, G., Wang, S., Wang, N., Zhou, L., Zhou, H., Sun, Y., & Liu, L. (2025). The Influence of Variable Operating Conditions and Components on the Performance of Centrifugal Compressors in Natural Gas Storage Reservoirs. Energies, 18(15), 3930. https://doi.org/10.3390/en18153930






