Impact Analysis of Price Cap on Bidding Strategies of VPP Considering Imbalance Penalty Structures
Abstract
1. Introduction
2. Literature Review
3. Imbalance Penalty and Optimization Model
3.1. Imbalance Penalty Structures
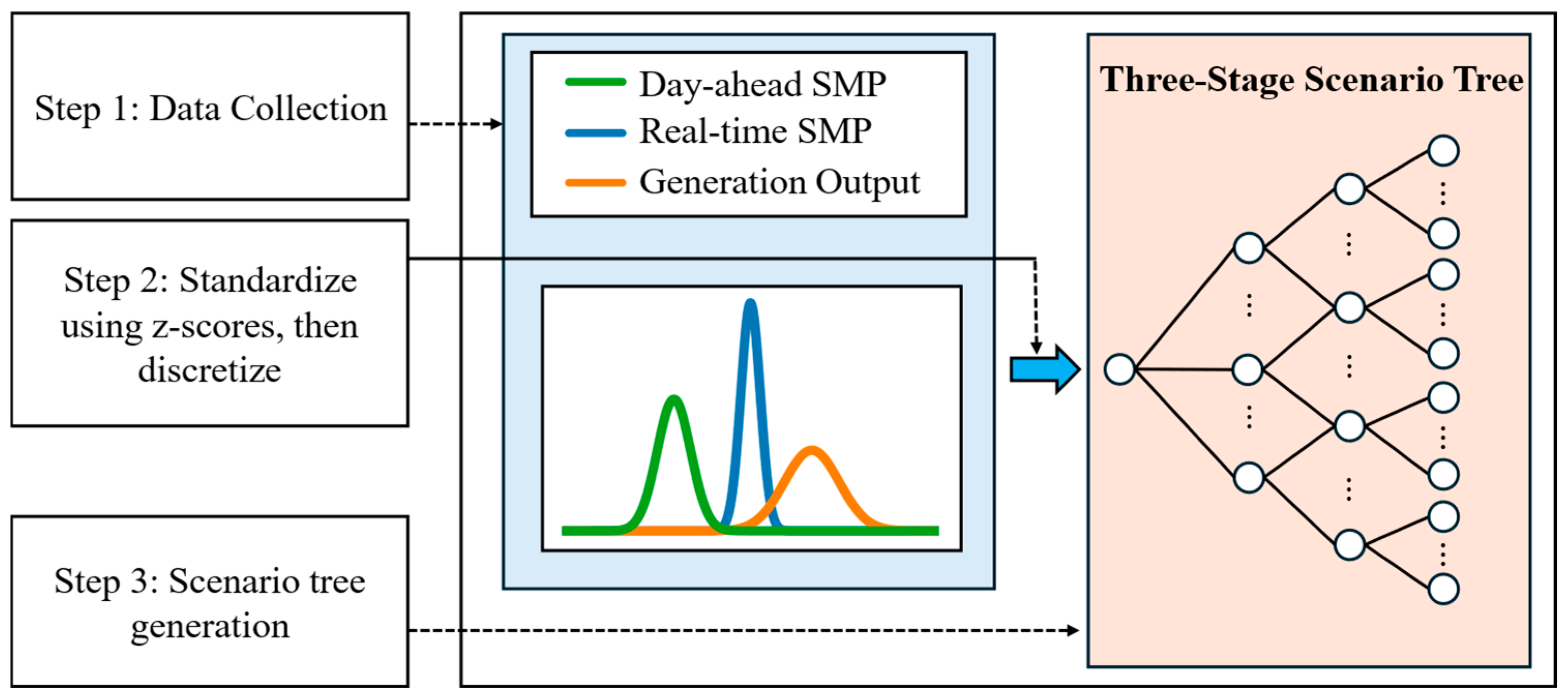
3.2. Optimization Model for Bidding Strategy
- Stage 1 represents the day-ahead market, where the VPP submits its bidding quantities based on forecasts of electricity prices and expected generation levels.
- Stage 2 captures the real-time market conditions, which may deviate from initial forecasts due to the fluctuation of prices and loads.
- Stage 3 accounts for the actual generation outcome, influenced by inherent variability in RESs.
4. Case Studies
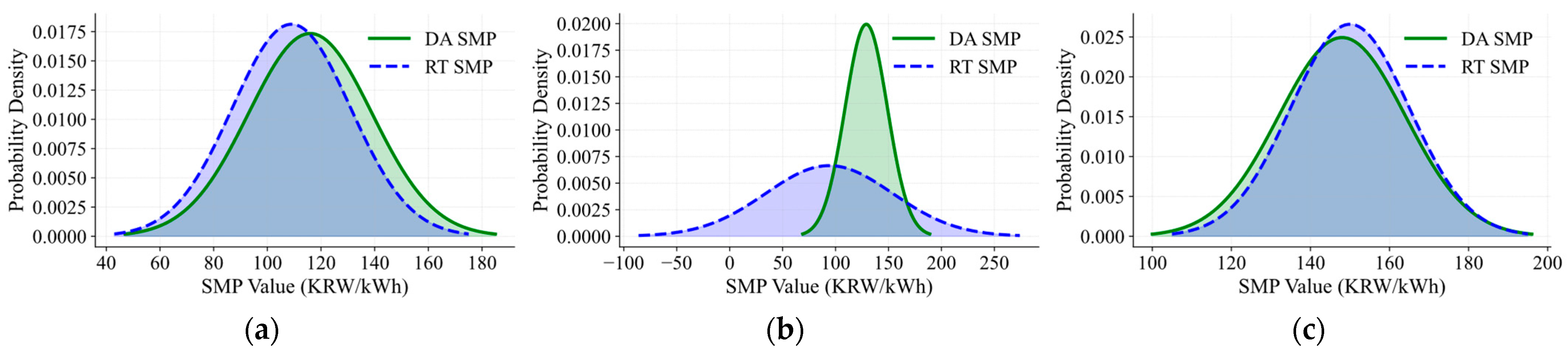
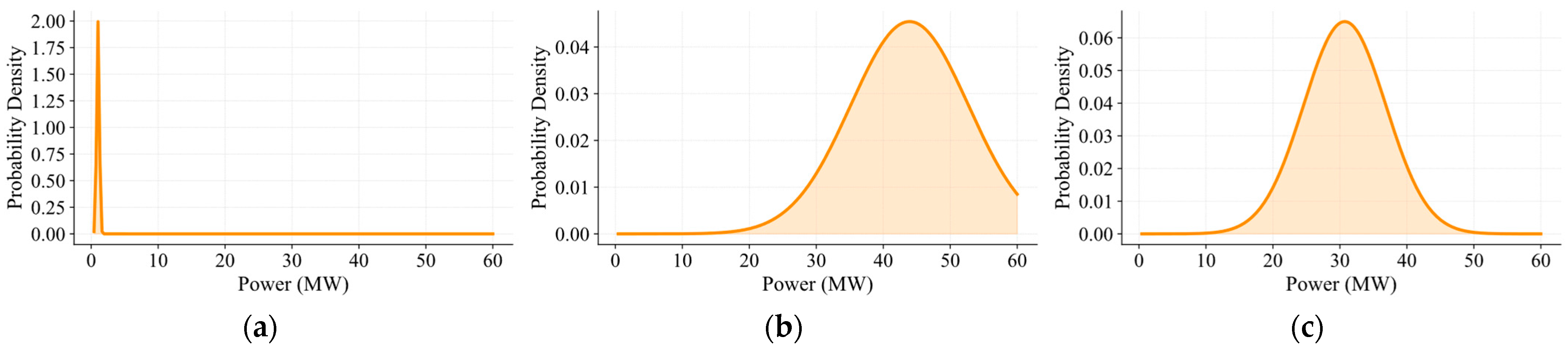
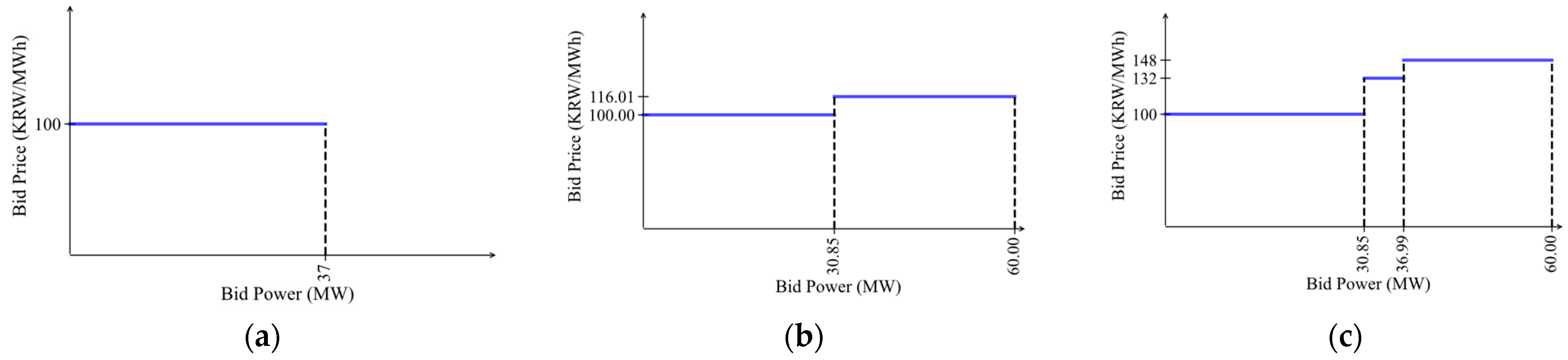
4.1. Simulation Environments
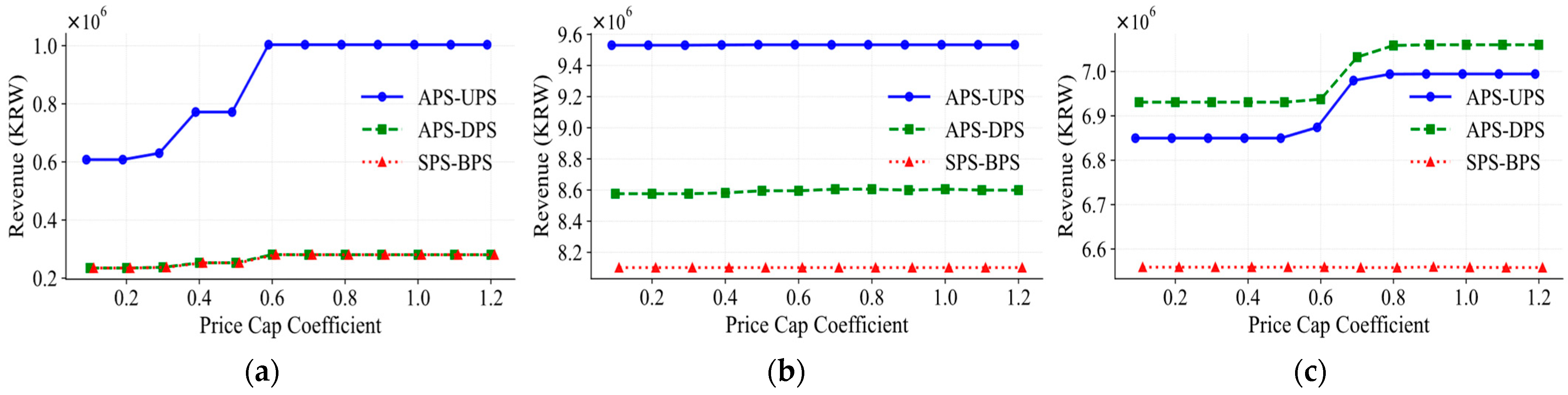
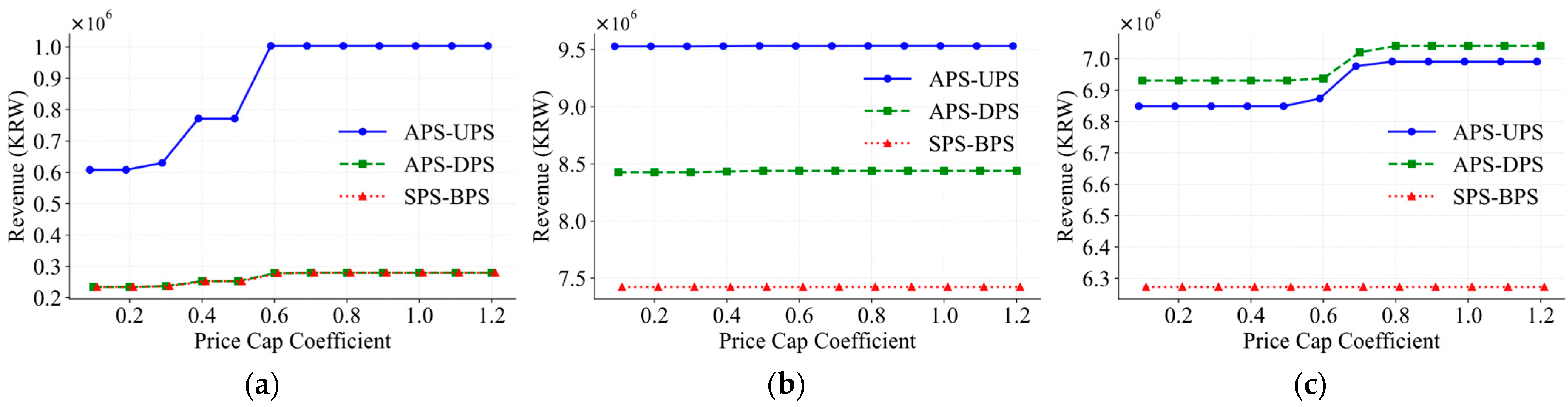
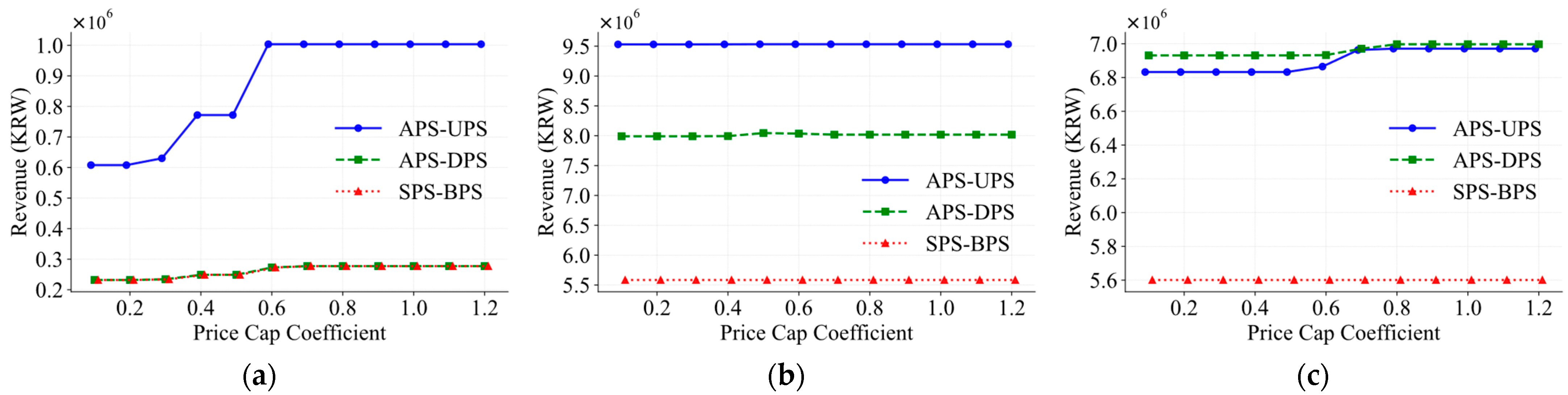
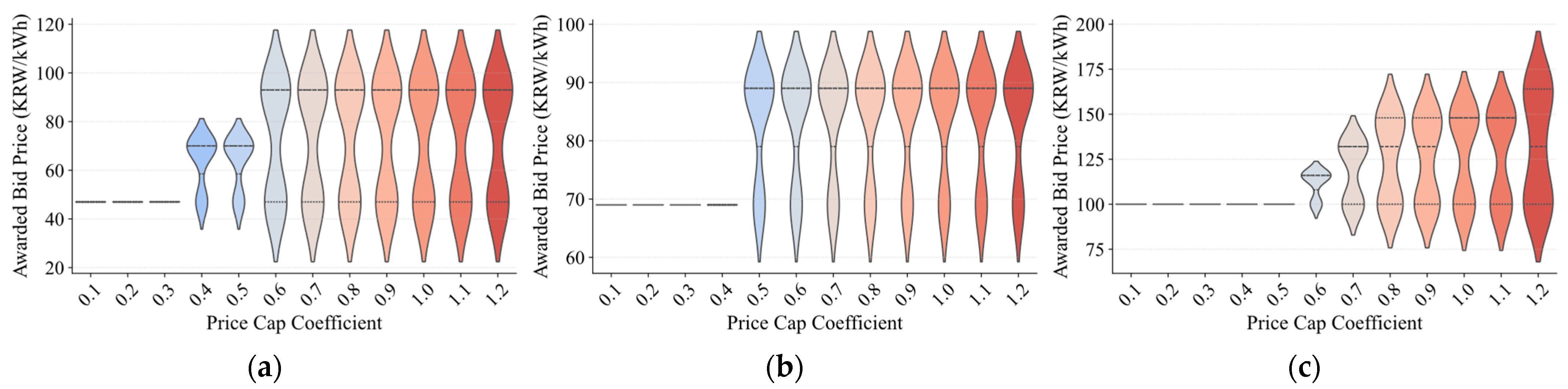
4.2. Simulation Results
5. Discussion
- Implement an adaptive price cap mechanism that adjusts dynamically in response to real-time indicators such as market volatility, generation uncertainty, and overall grid conditions. This can enhance market responsiveness while maintaining regulatory control.
- Recognize the existence of a saturation threshold in price cap levels. As shown in this study, beyond a certain coefficient, increases in the price cap yield diminishing returns in profitability while unnecessarily expanding the range of bidding prices—potentially complicating market operations.
- Acknowledge that factors such as generation uncertainty and penalty rates do influence participant revenue, but the effect of the price cap remains structurally robust across these conditions. This stability supports the use of price caps as a consistent regulatory tool.
- Consider adopting a hybrid penalty structure that incorporates both symmetric and asymmetric elements. Such a design can mitigate the risks of imbalances while preserving strategic flexibility and profit potential for VPPs and other market actors.
- Utilize bidding behavior diagnostics—such as segmentation density and bid price dispersion—as real-time indicators of market stress, participant flexibility, or potential regulatory inefficiencies. These metrics can provide early signals of how participants adapt their strategies in response to market constraints and policy changes.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, H.; Jin, T.; Feng, C.; Li, C.; Chen, Q.; Kang, C. Review of virtual power plant operations: Resource coordination and multidimensional interaction. Appl. Energy 2024, 357, 122284. [Google Scholar] [CrossRef]
- Shahinzadeh, H.; Moradi, J.; Pourmirza, Z.; Kabalci, E.; Benbouzid, M.; Muyeen, S.M. Optimal operation of distributed flexible generation sources incorporating VPP framework in market environment considering uncertainties. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022. [Google Scholar] [CrossRef]
- Fortune Business Insights. Virtual Power Plant Market Size, Share & COVID-19 Impact Analysis, by Technology (Demand Response, Distributed Generation, Mixed Asset), by End-User (Industrial, Commercial, Residential), Regional Forecasts 2024–2032. Available online: https://www.fortunebusinessinsights.com/industry-reports/virtual-power-plant-market-101669 (accessed on 1 June 2025).
- Algarvio, H.; Couto, A.; Estanqueiro, A. A Double Pricing and Penalties “Separated” Imbalance Settlement Mechanism to Incentive Self Balancing of Market Parties. In Proceedings of the 2024 20th International Conference on the European Energy Market (EEM), Istanbul, Türkiye, 3–7 June 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Song, Y.; Chae, M.; Chu, Y.; Yoon, Y.; Jin, Y. Impact of Penalty Structures on Virtual Power Plants in a Day-Ahead Electricity Market. Energies 2024, 17, 6042. [Google Scholar] [CrossRef]
- Yang, C.; Du, X.; Xu, D.; Tang, J.; Lin, X.; Xie, K.; Li, W. Optimal bidding strategy of renewable-based virtual power plant in the day-ahead market. Int. J. Electr. Power Energy Syst. 2023, 144, 108557. [Google Scholar] [CrossRef]
- Xiang, D.; He, K.; Zhang, G.; Zhang, S.; Chen, Y.; Zhao, L.; Zheng, H. Optimizing VPP Operations: A Novel Robust Demand-Side Management Approach with Energy Storage System. In Proceedings of the 2023 IEEE International Conference on Energy Internet (ICEI), Shenyang, China, 20–22 October 2023. [Google Scholar] [CrossRef]
- Zare, A.; Shafiyi, M.A. The Impact of Energy Storage System on the Flexible Operation of the Renewable-Based Virtual Power Plant. In Proceedings of the 2024 11th Iranian Conference on Renewable Energy and Distributed Generation (ICREDG), Yazd, Iran, 6–7 March 2024. [Google Scholar] [CrossRef]
- Li, W. The Virtual Power Plant Bidding Strategy Model based on Multi-stage Semi-anticipativity Distributionally Robust Optimization. Electr. Power Syst. Res. 2024, 237, 111015. [Google Scholar] [CrossRef]
- Song, C.; Jing, X. Bidding strategy for virtual power plants with the day-ahead and balancing markets using distributionally robust optimization approach. Energy Rep. 2023, 9, 637–644. [Google Scholar] [CrossRef]
- Jeitschko, T.D.; Kim, S.J.; Pal, P. Curbing price fluctuations in cap-and-trade auctions under changing demand expectations. Energy Econ. 2024, 139, 107804. [Google Scholar] [CrossRef]
- Kilinc-Ata, N.; Proskuryakova, L.N. The contribution of energy policies to green energy transition in the Asia-Pacific region. Renew. Energy 2024, 237, 121797. [Google Scholar] [CrossRef]
- Wilson, J.F. Scarcity, market power, and price caps in wholesale electric power markets. Electr. J. 2000, 13, 33–46. [Google Scholar] [CrossRef]
- Joskow, P.; Tirole, J. Reliability and Competitive Electricity Markets. RAND J. Econ. 2007, 38, 60–84. [Google Scholar] [CrossRef]
- Vossler, C.A.; Mount, T.D.; Thomas, R.J.; Zimmerman, R.D. An experimental investigation of soft price caps in uniform price auction markets for wholesale electricity. J. Regul. Econ. 2009, 36, 44–59. [Google Scholar] [CrossRef]
- Moshrefi, H.; Ebrahimnejad, A.; Mohaghegh, M. Strategic Bidding in Price-Capped Uniform Price Electricity Auctions. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4706221 (accessed on 1 June 2025).
- Rioux, B.; Galkin, P.; Murphy, F.; Pierru, A. How do price caps in China’s electricity sector impact the economics of coal, power and wind? Potential gains from reforms. Energy J. 2017, 38 (Suppl. S1), 63–76. [Google Scholar] [CrossRef]
- Berbey-Burgos, M.; Pardillos-Pobo, D.; Laporte-Azcué, M.; González-Gómez, P.Á.; Santana, D. Impact of Price Cap Policy on Concentrating Solar Power Plant Revenue in Electricity Markets. In Proceedings of the 2024 20th International Conference on the European Energy Market (EEM), Istanbul, Turkiye, 10–12 June 2024. [Google Scholar] [CrossRef]
- Briggs, R.J.; Kleit, A. Resource adequacy reliability and the impacts of capacity subsidies in competitive electricity markets. Energy Econ. 2013, 40, 297–305. [Google Scholar] [CrossRef]
- Sirin, S.M.; Erten, I. Price spikes, temporary price caps, and welfare effects of regulatory interventions on wholesale electricity markets. Energy Policy 2022, 163, 112816. [Google Scholar] [CrossRef]
- Song, Y.; Chu, Y.; Yoon, Y.; Jin, Y. Virtual Power Plant Bidding Strategies in Pay-as-Bid and Pay-as-Clear Markets: Analysis of Imbalance Penalties and Market Operations. Energies 2025, 18, 1383. [Google Scholar] [CrossRef]
- Shinde, P.; Kouveliotis-Lysikatos, I.; Amelin, M. Multistage stochastic programming for vpp trading in continuous intraday electricity markets. IEEE Trans. Sustain. Energy 2022, 13, 1037–1048. [Google Scholar] [CrossRef]
- Laitinen, L. Optimal Offering Strategy for a Base Station Virtual Power Plant via Stochastic Programming. Master’s Thesis, Aalto University, Espoo, Finland, November 2024. [Google Scholar]
- Chen, Y.; Niu, Y.; Qu, C.; Du, M.; Liu, P. A pricing strategy based on bi-level stochastic optimization for virtual power plant trading in multi-market: Energy, ancillary services and carbon trading market. Electr. Power Syst. Res. 2024, 231, 110371. [Google Scholar] [CrossRef]
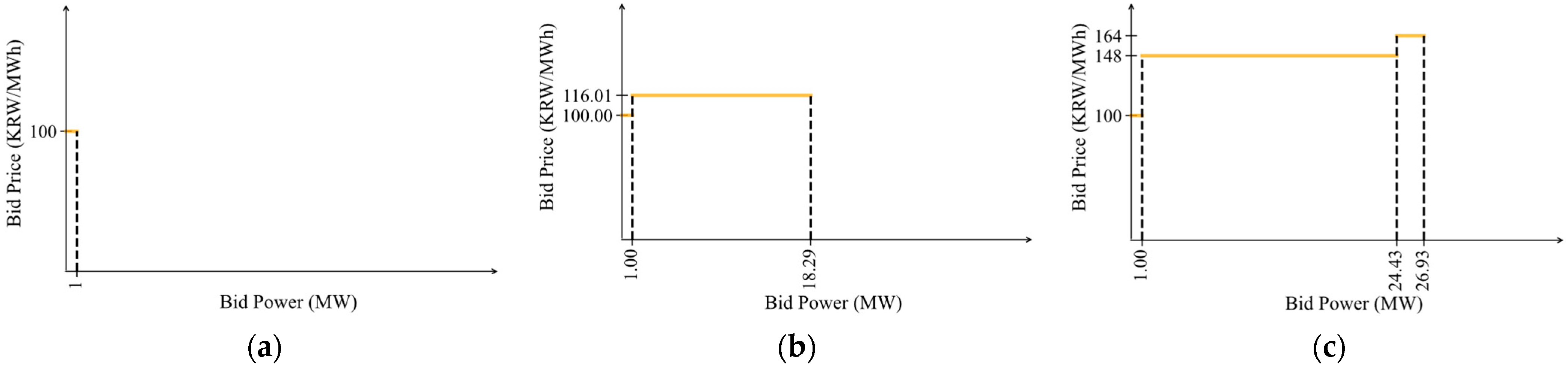
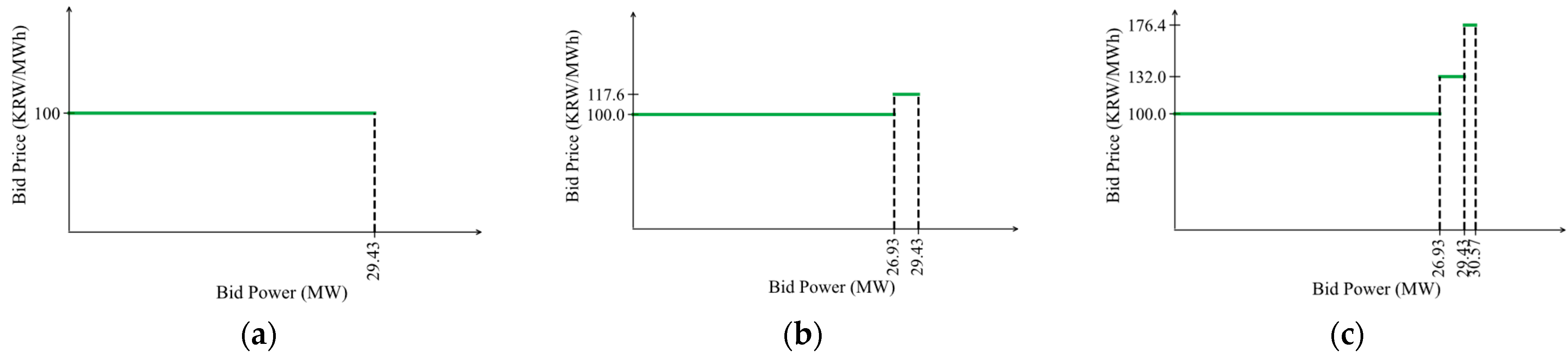
| Parameter | Value/Expression |
|---|---|
| 76 [KRW/kWh] | |
| 60 [MW] | |
| 0 [MW] | |
| [0.1–1.2] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Yoon, Y.; Jin, Y. Impact Analysis of Price Cap on Bidding Strategies of VPP Considering Imbalance Penalty Structures. Energies 2025, 18, 3927. https://doi.org/10.3390/en18153927
Song Y, Yoon Y, Jin Y. Impact Analysis of Price Cap on Bidding Strategies of VPP Considering Imbalance Penalty Structures. Energies. 2025; 18(15):3927. https://doi.org/10.3390/en18153927
Chicago/Turabian StyleSong, Youngkook, Yongtae Yoon, and Younggyu Jin. 2025. "Impact Analysis of Price Cap on Bidding Strategies of VPP Considering Imbalance Penalty Structures" Energies 18, no. 15: 3927. https://doi.org/10.3390/en18153927
APA StyleSong, Y., Yoon, Y., & Jin, Y. (2025). Impact Analysis of Price Cap on Bidding Strategies of VPP Considering Imbalance Penalty Structures. Energies, 18(15), 3927. https://doi.org/10.3390/en18153927







