Investigating the Influence of PWM-Driven Cascaded H-Bridges Multilevel Inverter on Interior Permanent Magnet Synchronous Motor Power Losses
Abstract
1. Introduction
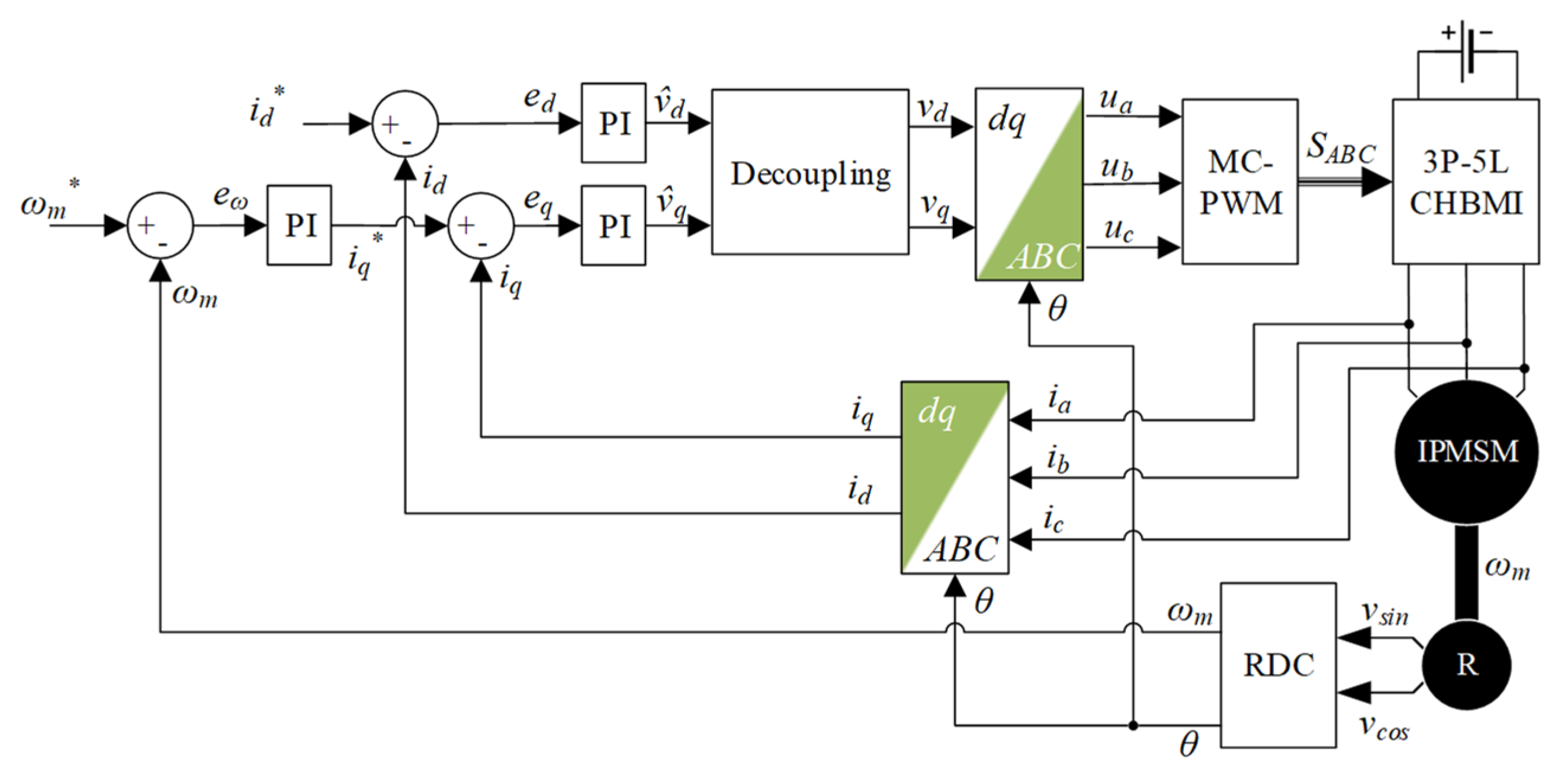
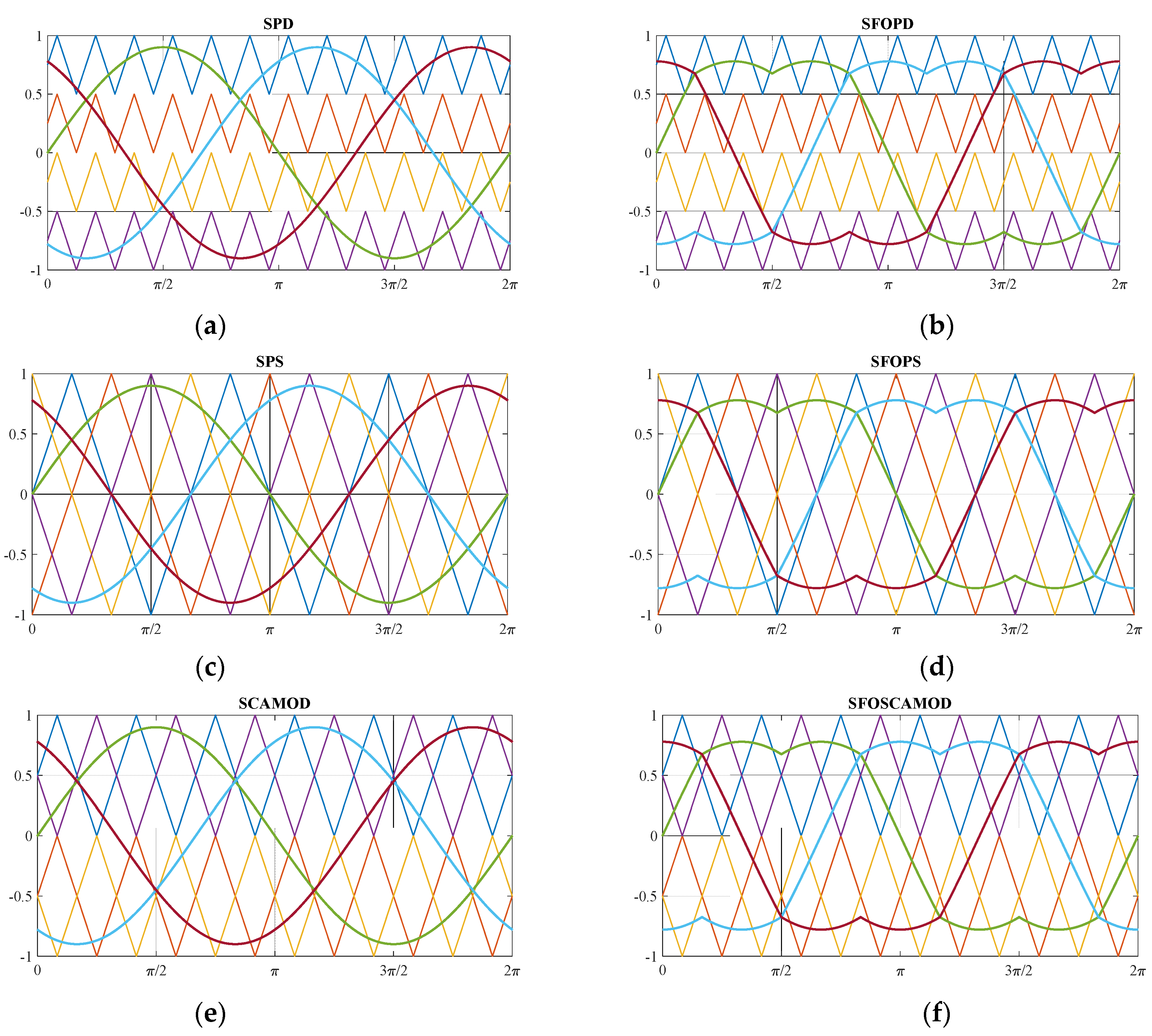
2. Field-Oriented Control and Multicarrier Pulse Width Modulation Strategies
- Phase Disposition (PD): all carriers are in phase;
- Phase Opposition Disposition (POD): carriers are in phase two-by-two;
- Alternative Phase Opposition Disposition (APOD): adjacent carriers are in phase opposition.
3. Harmonic Power Analysis
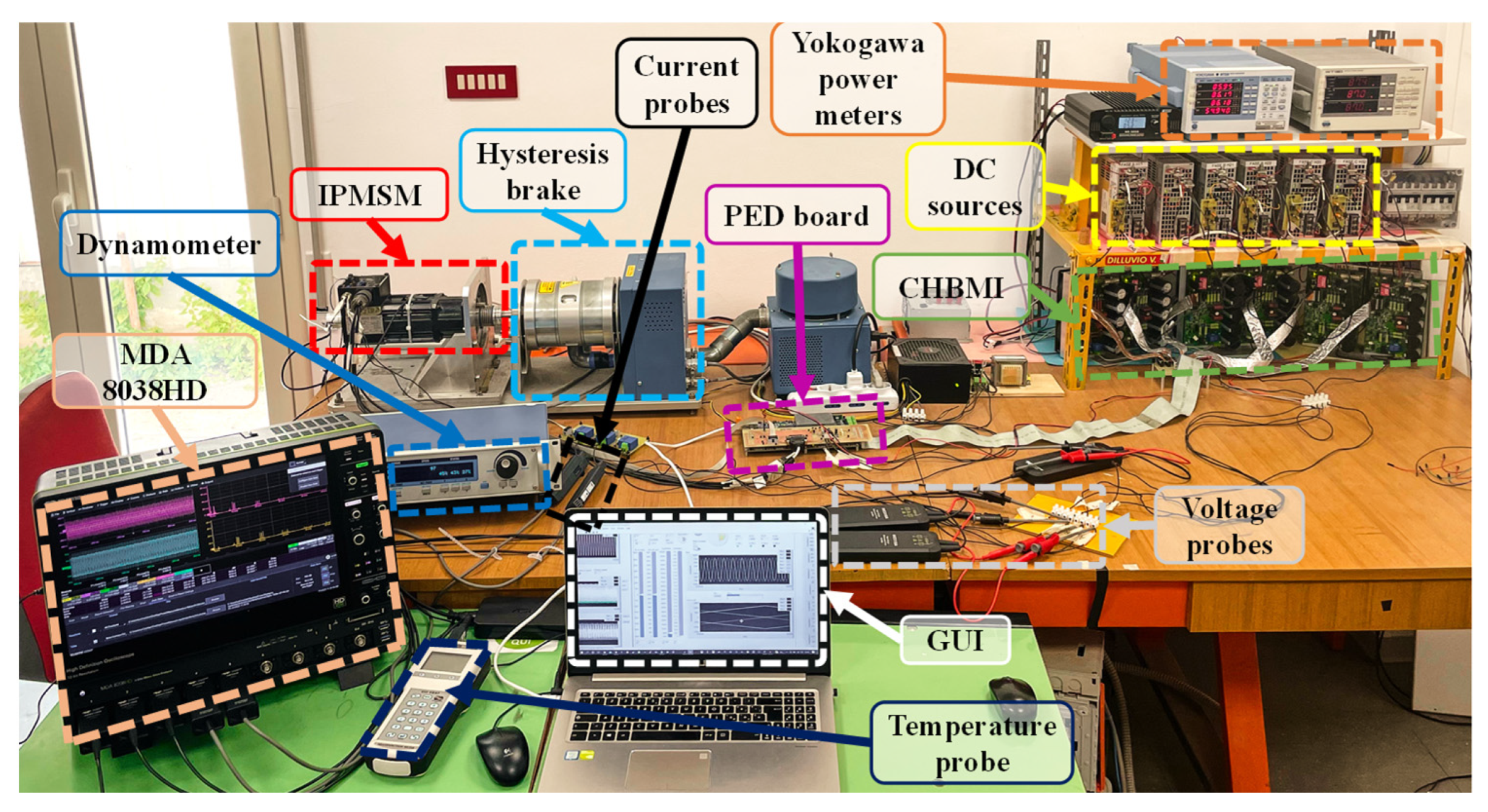
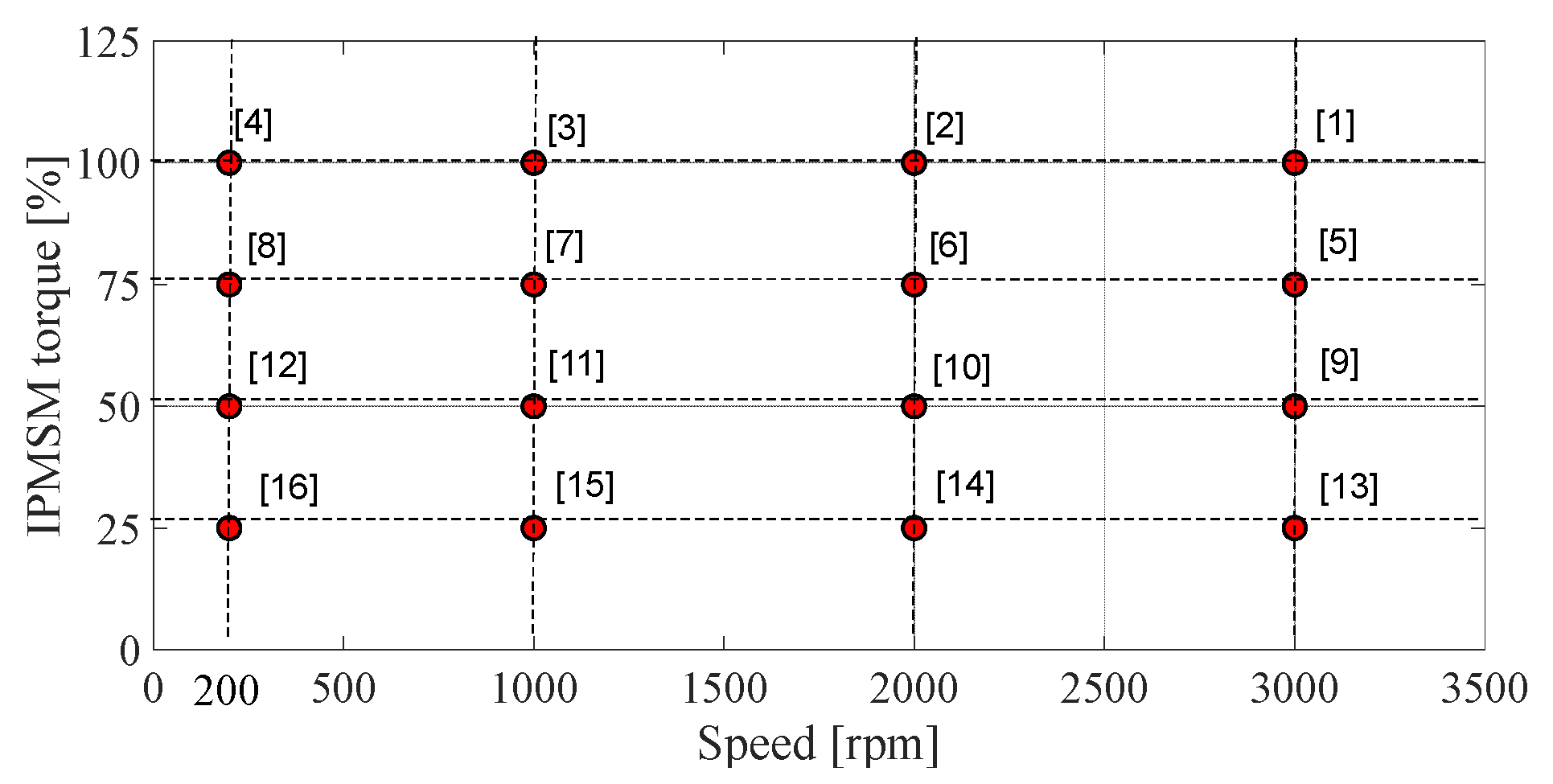
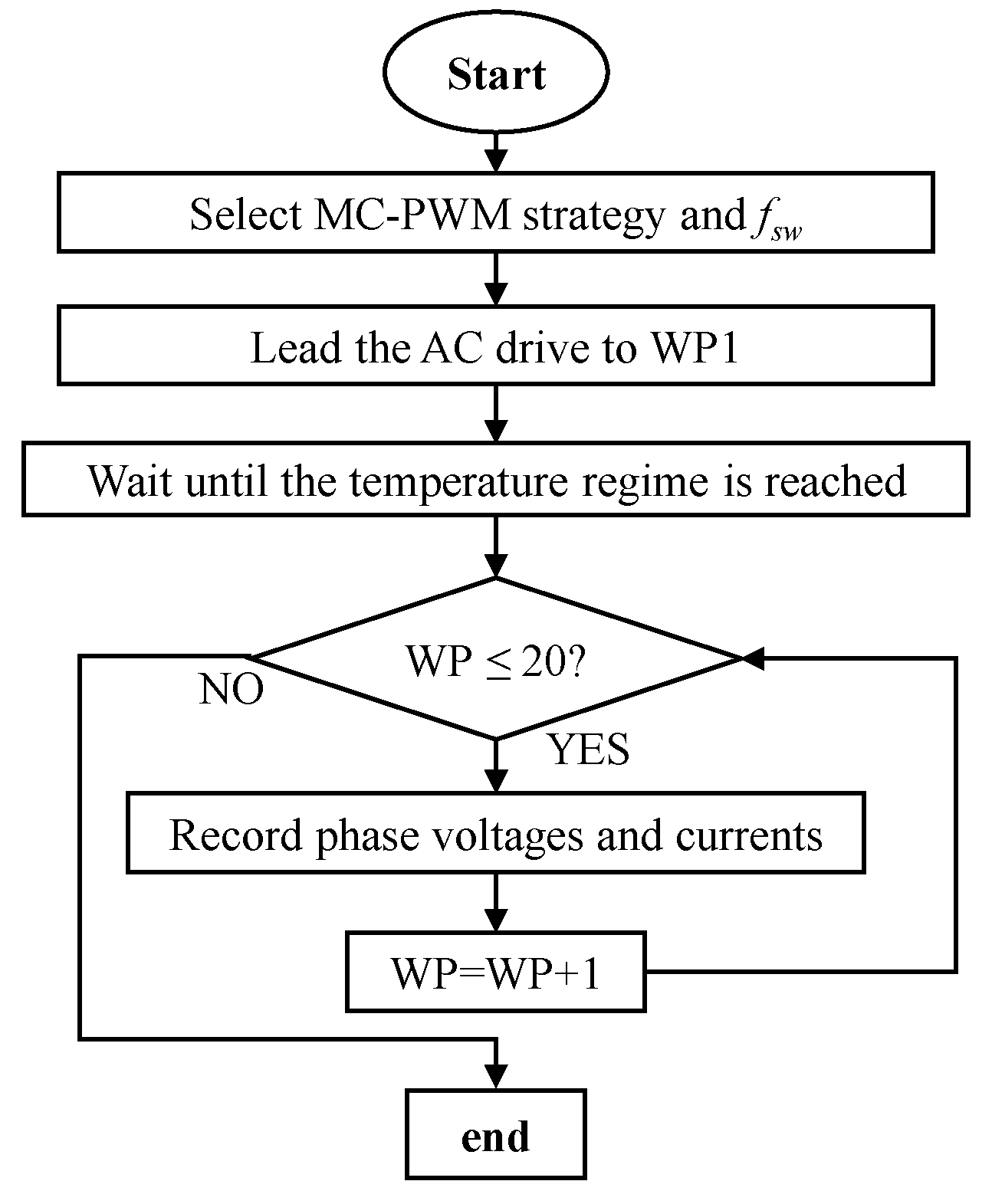
4. Test Setup
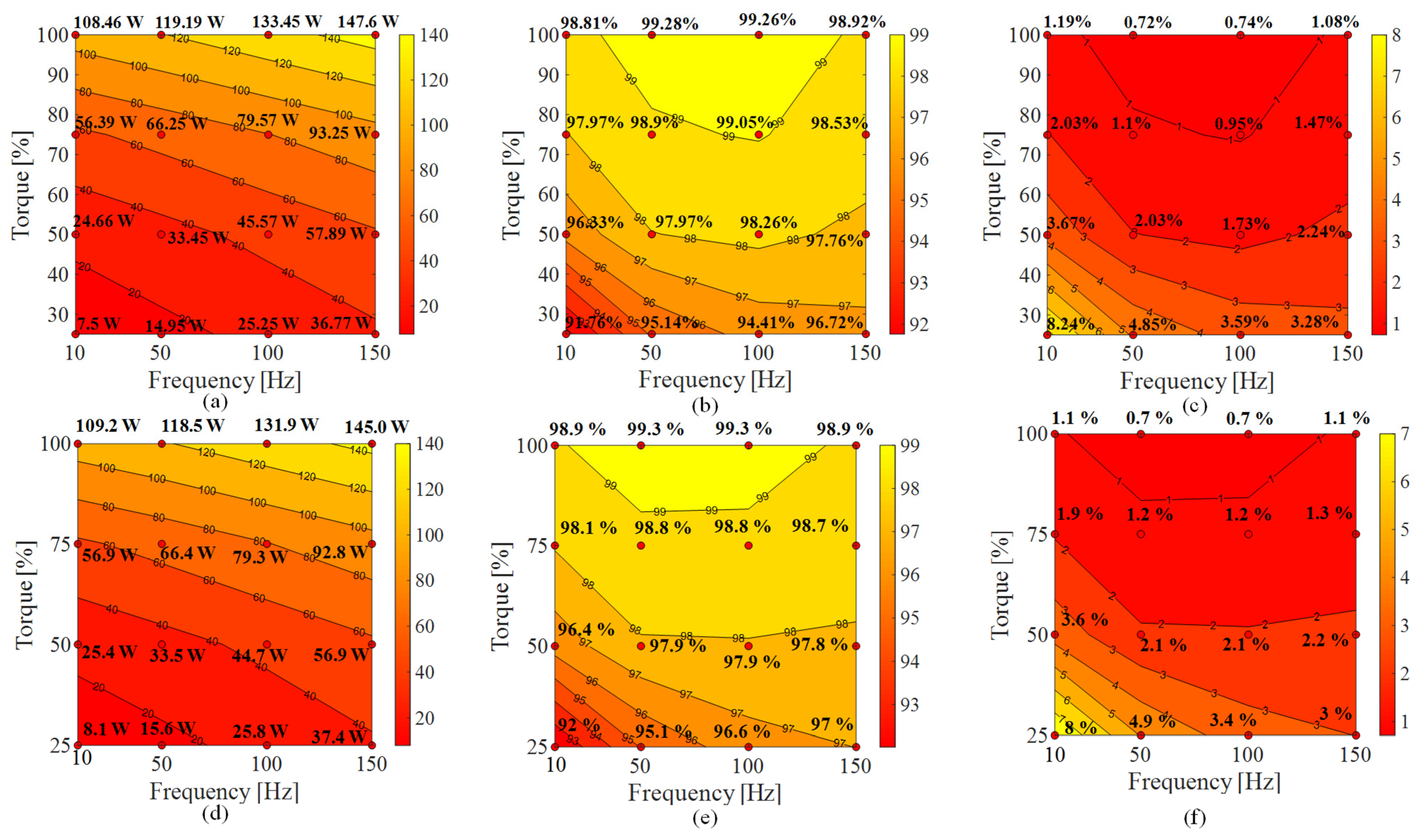
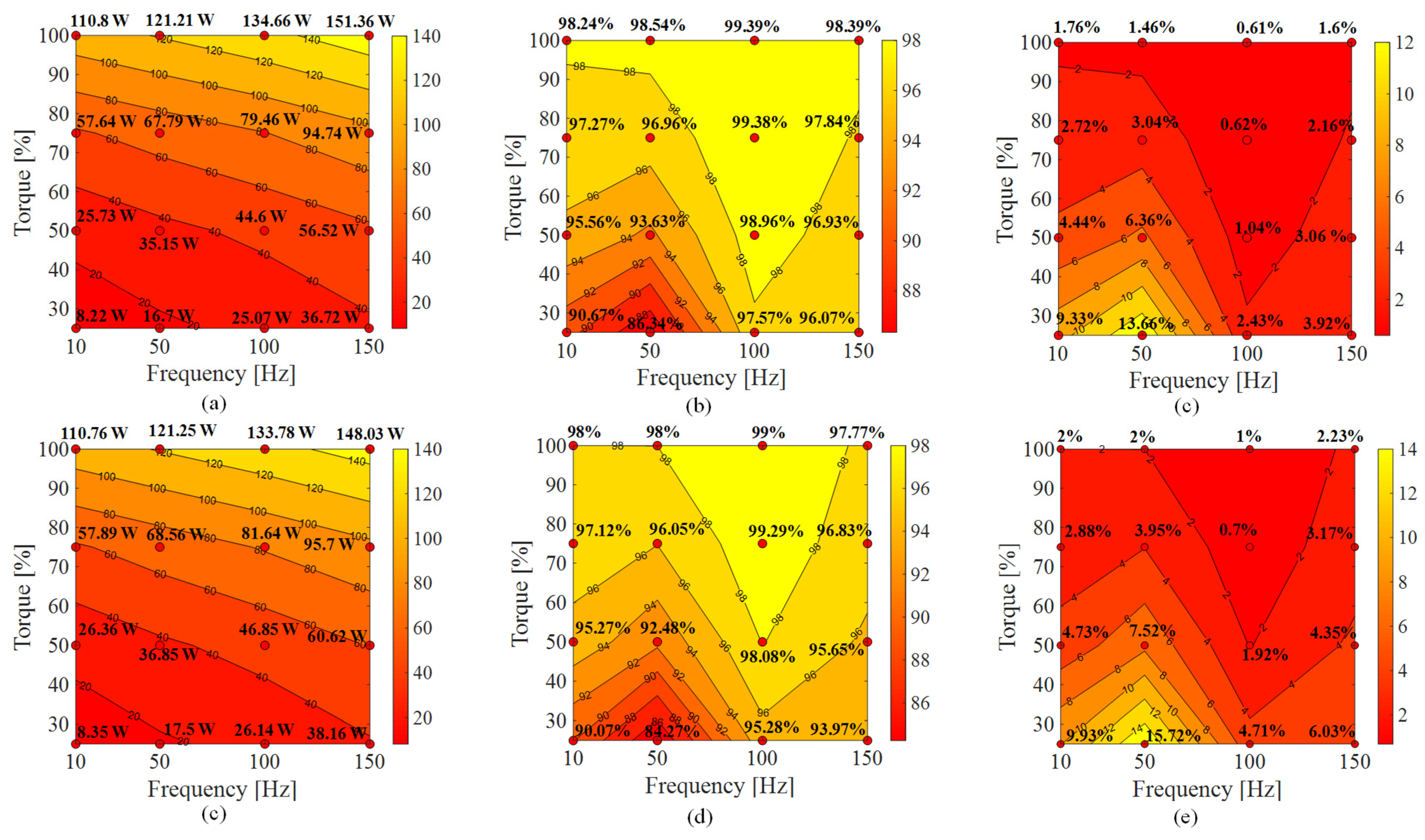
5. Experimental Results and Analysis
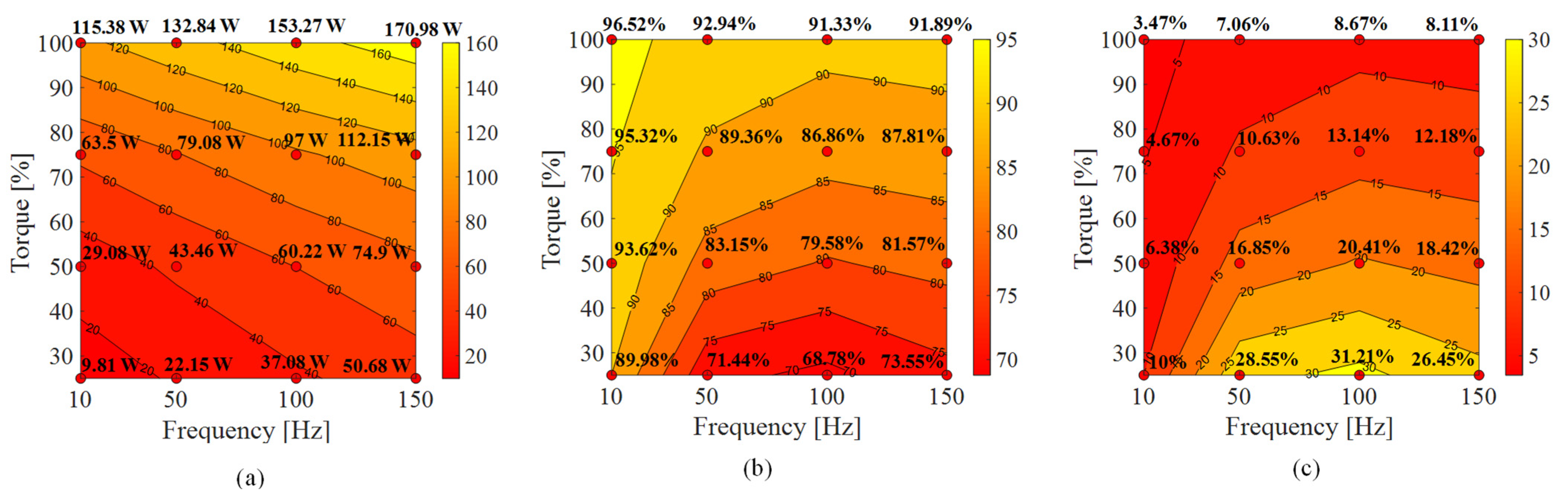
5.1. Power Losses Segregation Analysis at 4 kHz
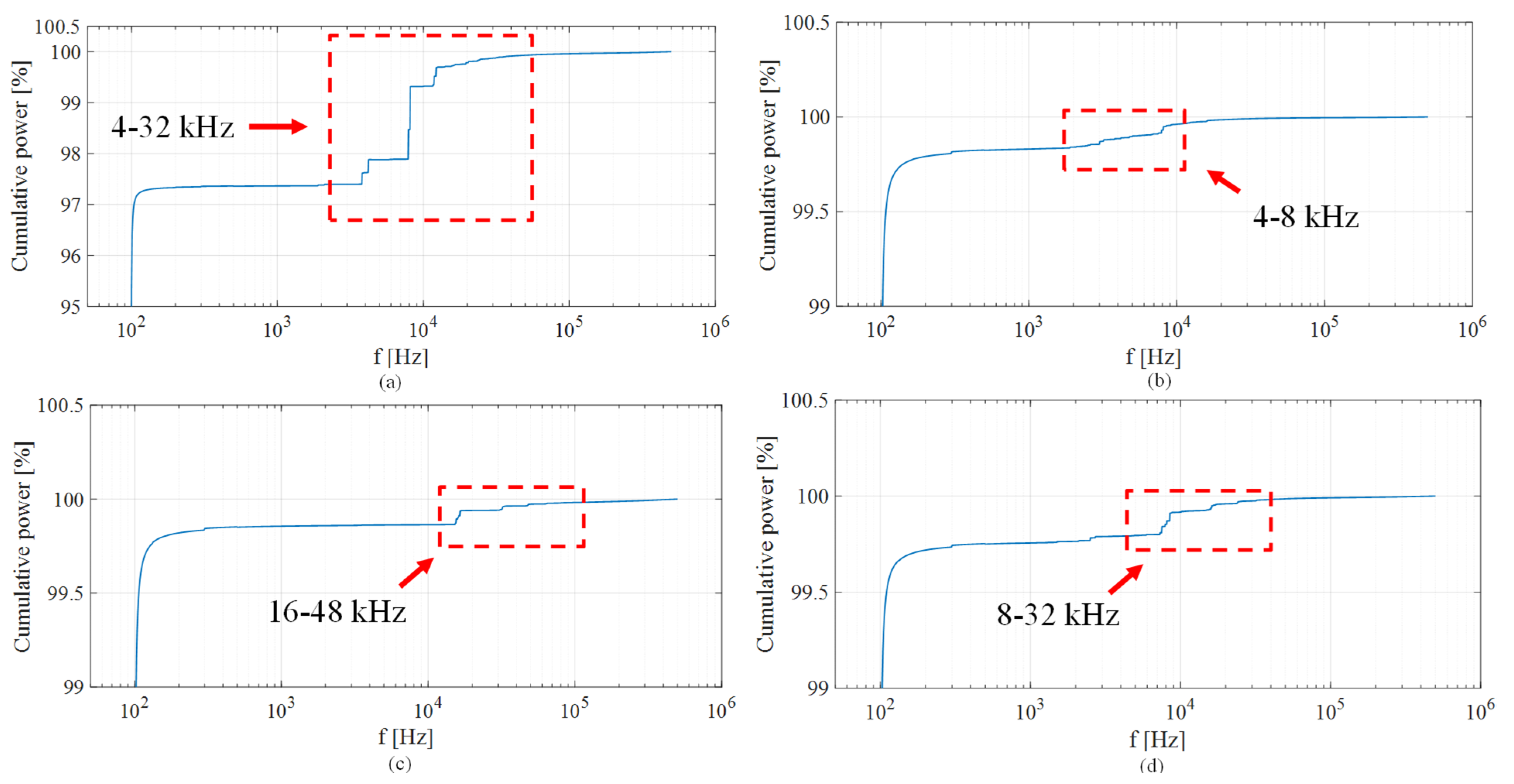
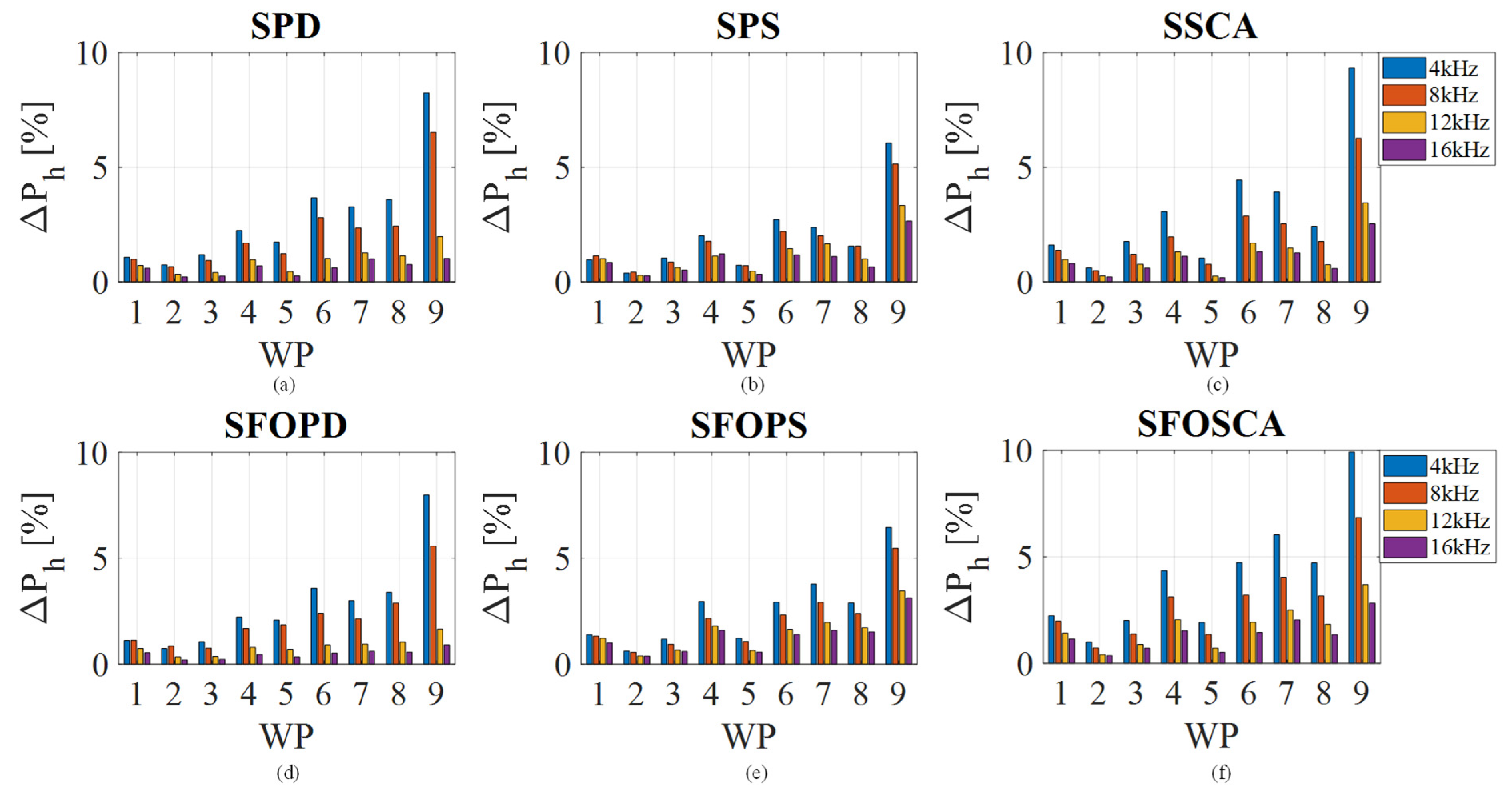
5.2. Switching Frequency Impact Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fong, J.; Ferreira, F.J.T.E.; Silva, A.M.; de Almeida, A.T. IEC61800-9 System Standards as a Tool to Boost the Efficiency of Electric Motor Driven Systems Worldwide. Inventions 2020, 5, 20. [Google Scholar] [CrossRef]
- Aarniovuori, L.; Karkkainen, H.; Anuchin, A.; Pyrhonen, J.J.; Lindh, P.; Cao, W. Voltage-Source Converter Energy Efficiency Classification in Accordance With IEC 61800-9-2. IEEE Trans. Ind. Electron. 2019, 67, 8242–8251. [Google Scholar] [CrossRef]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.C.; Machado, L.; Sousa, T.J.C.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- Rens, J.; Vandenbossche, L.; Dorez, O. Iron Loss Modelling of Electrical Traction Motors for Improved Prediction of Higher Harmonic Losses. World Electr. Veh. J. 2020, 11, 24. [Google Scholar] [CrossRef]
- Ibrahim, I.; Mohammadi, M.H.; Ghorbanian, V.; Lowther, D.A. Effect of Pulsewidth Modulation on Electromagnetic Noise of Interior Permanent Magnet Synchronous Motor Drives. IEEE Trans. Magn. 2019, 55, 7500805. [Google Scholar] [CrossRef]
- Guo, Y.; Yu, Y.; Lu, H.; Lei, G.; Zhu, J. Enhancing Performance of Permanent Magnet Motor Drives through Equivalent Circuit Models Considering Core Loss. Energies 2024, 17, 1837. [Google Scholar] [CrossRef]
- Rotating Electrical Machines—Part 30-2: Efficiency Classes of Variable Speed AC Motors (IE-Code); IEC TS 60034-30-2; IEC: Geneva, Switzerland, 2021.
- IEC 61800-9-1; Adjustable Speed Electrical Power Drive Systems—Part 9-1: Ecodesign for Power Drive Systems, Motor Starters, Power Electronics and Their Driven Applications—General Requirements for Setting Energy Efficiency Standards for Power Driven Equipment Using the Extended Product Approach (EPA) and Semi Analytic Model (SAM). IEC: Geneva, Switzerland, 2017.
- IEC 61800-9-2; Adjustable Speed Electrical Power Drive Systems—Part 9-2: Ecodesign for Power Drive Systems, Motor Starters, Power Electronics & Their Driven Applications—Energy Efficiency Indicators for Power Drive Systems and Motor Starters. IEC: Geneva, Switzerland, 2017.
- Barros, L.A.M.; Martins, A.P.; Pinto, J.G. A Comprehensive Review on Modular Multilevel Converters, Submodule Topologies, and Modulation Techniques. Energies 2022, 15, 1078. [Google Scholar] [CrossRef]
- Abu-Rub, H.; Holtz, J.; Rodriguez, J.; Baoming, G. Medium-Voltage Multilevel Converters—State of the Art, Challenges, and Requirements in Industrial Applications. IEEE Trans. Ind. Electron. 2010, 57, 2581–2596. [Google Scholar] [CrossRef]
- Scaglione, G.; Nevoloso, C.; Schettino, G.; Di Tommaso, A.O.; Miceli, R. A Novel Multiobjective Finite Control Set Model Predictive Control for IPMSM Drive Fed by a Five-Level Cascaded H-Bridge Inverter. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 1959–1973. [Google Scholar] [CrossRef]
- Choudhury, S.; Bajaj, M.; Dash, T.; Kamel, S.; Jurado, F. Multilevel Inverter: A Survey on Classical and Advanced Topologies, Control Schemes, Applications to Power System and Future Prospects. Energies 2021, 14, 5773. [Google Scholar] [CrossRef]
- Poorfakhraei, A.; Narimani, M.; Emadi, A. A Review of Modulation and Control Techniques for Multilevel Inverters in Traction Applications. IEEE Access 2021, 9, 24187–24204. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S.S. Modular Multilevel Converters for Transportation Electrification: Challenges and Opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 399–407. [Google Scholar] [CrossRef]
- Chang, F.; Ilina, O.; Lienkamp, M.; Voss, L. Improving the Overall Efficiency of Automotive Inverters Using a Multilevel Converter Composed of Low Voltage Si mosfets. IEEE Trans. Power Electron. 2019, 34, 3586–3602. [Google Scholar] [CrossRef]
- Karkkainen, H.; Aarniovuori, L.; Makkonen, S.; Niemela, M.; Pyrhonen, J. Determination of High-Frequency Harmonic Power in Converter-Fed Motors. In Proceedings of the 2022 International Conference on Electrical Machines (ICEM), Valencia, Spain, 5–8 September 2022; pp. 394–400. [Google Scholar]
- Miyama, Y.; Hazeyama, M.; Hanioka, S.; Watanabe, N.; Daikoku, A.; Inoue, M. PWM Carrier Harmonic Iron Loss Reduction Technique of Permanent-Magnet Motors for Electric Vehicles. IEEE Trans. Ind. Appl. 2016, 52, 2865–2871. [Google Scholar] [CrossRef]
- Balamurali, A.; Kundu, A.; Li, Z.; Kar, N.C. Improved Harmonic Iron Loss and Stator Current Vector Determination for Maximum Efficiency Control of PMSM in EV Applications. IEEE Trans. Ind. Appl. 2021, 57, 363–373. [Google Scholar] [CrossRef]
- Liu, L.; Ba, X.; Guo, Y.; Lei, G.; Sun, X.; Zhu, J. Improved Iron Loss Prediction Models for Interior PMSMs Considering Coupling Effects of Multiphysics Factors. IEEE Trans. Transp. Electrification 2023, 9, 416–427. [Google Scholar] [CrossRef]
- Agamloh, E.B.; Cavagnino, A.; Vaschetto, S. Standard Efficiency Determination of Induction Motors With a PWM Inverter Source. IEEE Trans. Ind. Appl. 2019, 55, 398–406. [Google Scholar] [CrossRef]
- Yogal, N.; Lehrmann, C.; Henke, M. Determination of the Measurement Uncertainty of Direct and Indirect Efficiency Measurement Methods in Permanent Magnet Synchronous Machines. In Proceedings of the 2018 XIII International Conference on Electrical Machines (ICEM), Alexandroupoli, Greece, 1–3 September 2018; pp. 1149–1156. [Google Scholar]
- Jiang, M.; Tian, J.; Goh, H.H.; Yi, J.; Li, S.; Zhang, D.; Wu, T. Experimental study on the influence of high frequency PWM harmonics on the losses of induction motor. Energy Rep. 2022, 8, 332–342. [Google Scholar] [CrossRef]
- Yamazaki, K.; Fukushima, Y.; Sato, M. Loss Analysis of Permanent-Magnet Motors With Concentrated Windings—Variation of Magnet Eddy-Current Loss Due to Stator and Rotor Shapes. IEEE Trans. Ind. Appl. 2009, 45, 1334–1342. [Google Scholar] [CrossRef]
- van der Geest, M.; Polinder, H.; Ferreira, J.A. Influence of PWM switching frequency on the losses in PM machines. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1243–1247. [Google Scholar]
- Chen, P.; Tang, R.; Tong, W.; Han, X.; Jia, J.; Zhu, X. Analysis of losses of permanent magnet synchronous motor with PWM supply. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 1119–1124. [Google Scholar]
- Stempfle, M.; Han, Y.; Woelfle, J.; Troester, N.; Roth-Stielow, J. Influence of Different Switching Frequencies and Modulation Techniques on IPMSM and Inverter Losses Optimizing the Overall Drive Train Efficiency. In Proceedings of the PCIM Europe 2017; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management, Nuremberg, Germany, 16–18 May 2017; pp. 1–5. [Google Scholar]
- Tong, W.; Wang, Y.; Sun, R.; Wu, S.; Jia, J. Simulation and Experimental Study on No-Load Loss Distributions of an IPM Motor Under the Conditions of Both Sinusoidal Supply and Converter Supply. IEEE Trans. Magn. 2018, 54, 8110306. [Google Scholar] [CrossRef]
- Hothongkham, P.; Kinnares, V. Investigation into Harmonic Losses in a PWM Multilevel cascaded H-Bridge Inverter Fed Induction Motor. In Proceedings of the 2007 7th International Conference on Power Electronics and Drive Systems, Bangkok, Thailand, 27–30 November 2007; pp. 1043–1048. [Google Scholar]
- Salem, A.; Abdallh, A.A.-E.; De Belie, F.; Dupré, L.; Melkebeek, J. A Comparative Study of the Effect of Different Converter Topologies on the Iron Loss of Nonoriented Electrical Steel. IEEE Trans. Magn. 2014, 50, 6000804. [Google Scholar] [CrossRef]
- Rasilo, P.; Salem, A.; Abouelyazied, A.; De Belie, F.; Dupré, L.; Melkebeek, J.A.; Abdallh, A. Effect of Multilevel Inverter Supply on Core Losses in Magnetic Materials and Electrical Machines. IEEE Trans. Energy Convers. 2015, 30, 736–744. [Google Scholar] [CrossRef]
- Rollbuhler, C.; Stefanski, L.; Gretzinger, S.; Kolb, J.; Hiller, M.; Doppelbauer, M. Measurement of inverter caused losses in permanent magnet synchronous machines using a modular multiphase multilevel converter. In Proceedings of the 2019 10th International Conference on Power Electronics and ECCE Asia (ICPE 2019)—ECCE Asia, Busan, Republic of Korea, 27–31 May 2019; pp. 1239–1245. [Google Scholar]
- Aarniovuori, L.; Kärkkäinen, H.; Niemelä, M.; Pyrhönen, J. PWM-Induced Harmonic Power in 75 kW IM Drive System. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. P.1–P.9. [Google Scholar]
- Busacca, A.; Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Schettino, G.; Scaglione, G.; Viola, F.; Colak, I. Switching Frequency Effects on the Efficiency and Harmonic Distortion in a Three-Phase Five-Level CHBMI Prototype with Multicarrier PWM Schemes: Experimental Analysis. Energies 2022, 15, 586. [Google Scholar] [CrossRef]
- Sarigiannidis, A.G.; Kladas, A.G. Switching Frequency Impact on Permanent Magnet Motors Drive System for Electric Actuation Applications. IEEE Trans. Magn. 2015, 51, 8202204. [Google Scholar] [CrossRef]
- Chang, L.; Alvi, M.; Lee, W.; Kim, J.; Jahns, T.M. Efficiency Optimization of PWM-Induced Power Losses in Traction Drive Systems With IPM Machines Using Wide Bandgap-Based Inverters. IEEE Trans. Ind. Appl. 2022, 58, 5635–5649. [Google Scholar] [CrossRef]
- Tornello, L.D.; Vaschetto, S.; Agamloh, E.B.; Scelba, G.; De Donato, G.; Cavagnino, A. Investigating PWM-Induced Iron Losses: Measurements and Estimation Models up to 350 kHz Switching Frequency. IEEE Open J. Ind. Appl. 2024, 5, 338–355. [Google Scholar] [CrossRef]
- Kremser, A. Calculation and measurement of motor and converter losses according to IEC 61800-9-2 ED2. Forsch. Ingenieurwesen 2024, 88, 45. [Google Scholar] [CrossRef]
- Gnaciński, P.; Hallmann, D.; Pepliński, M.; Jankowski, P. The effects of voltage subharmonics on cage induction machine. Int. J. Electr. Power Energy Syst. 2019, 111, 125–131. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Bhattacharya, T. Phase-Shifted Carrier-Based Synchronized Sinusoidal PWM Techniques for a Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Power Electron. 2018, 33, 513–524. [Google Scholar] [CrossRef]
- Yu, Y.; Zhao, W.; Chen, L.; Wang, Q.; Huang, S. Power measurement accuracy analysis in the presence of interharmonics. Measurement 2020, 154, 107484. [Google Scholar] [CrossRef]
- Arranz-Gimon, A.; Zorita-Lamadrid, A.; Morinigo-Sotelo, D.; Fernandez-Cavero, V.; Duque-Perez, O. Harmonic measurement and analysis system for characterization of adjustable speed drives. Int. J. Electr. Power Energy Syst. 2024, 162, 110217. [Google Scholar] [CrossRef]
- Available online: https://www.meanwell.com/Upload/PDF/RSP-2400/RSP-2400-SPEC.PDF (accessed on 18 July 2025).
- Caruso, M.; Di Tommaso, A.; Miceli, R.; Nevoloso, C.; Spataro, C.; Viola, F. Characterization of the parameters of interior permanent magnet synchronous motors for a loss model algorithm. Measurement 2017, 106, 196–202. [Google Scholar] [CrossRef]
- Aarniovuori, L.; Karkkainen, H.; Niemela, M.; Pyrhonen, J. Measurement Accuracy Requirements for the Efficiency Classification of Converters and Motors. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ‘19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.10. [Google Scholar]
- Caruso, M.; Di Tommaso, A.O.; Lisciandrello, G.; Mastromauro, R.A.; Miceli, R.; Nevoloso, C.; Spataro, C.; Trapanese, M. A General and Accurate Measurement Procedure for the Detection of Power Losses Variations in Permanent Magnet Synchronous Motor Drives. Energies 2020, 13, 5770. [Google Scholar] [CrossRef]
- Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Schettino, G.; Cecati, C.; Del Pizzo, A. Field Oriented Control of IPMSM Fed by Multilevel Cascaded H-Bridges Inverter with NI-SOM sbRIO-9651 FPGA controller. In Proceedings of the 2022 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 22–24 June 2022; pp. 88–93. [Google Scholar]
- Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Schettino, G.; Buccella, C.; Cecati, C. A Simple Software-based Resolver To Digital Conversion System. In Proceedings of the IECON 2022—48th Annual Conference of the IEEE Industrial Electronics Society, Brussels, Belgium, 17–20 October 2022; pp. 1–6. [Google Scholar]
- IEC 60034-2-3; Rotating Electrical Machines Part 2-3: Specific Test Methods for Determining the Losses and Efficiency of Converter-Fed AC Machines. IEC: Geneva, Switzerland, 2024.
- Gurpinar, E.; Castellazzi, A. Single-Phase T-Type Inverter Performance Benchmark Using Si IGBTs, SiC MOSFETs, and GaN HEMTs. IEEE Trans. Power Electron. 2016, 31, 7148–7160. [Google Scholar] [CrossRef]
- Mecke, R. Multilevel Inverter with New Wide-Bandgap SiC and GaN Power Switches. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14–16 July 2021; pp. 1–6. [Google Scholar]
- Zahwan, N.S.H.M.; Hasan, K.N.M.; Bin Zakaria, Z.A. Performance Analysis of SiC and GaN-Based Traction Inverter in Electric Vehicle Drive System. In Proceedings of the 2024 IEEE Sustainable Power and Energy Conference (iSPEC), Kuching, Sarawak, Malaysia, 24–27 November 2024; pp. 681–686. [Google Scholar]
- Geyer, T.; Spudic, V.; van der Merwe, W.; Guidi, E. Model Predictive Pulse Pattern Control of Medium-Voltage Neutral-Point-Clamped Inverter Drives. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 5047–5054. [Google Scholar]
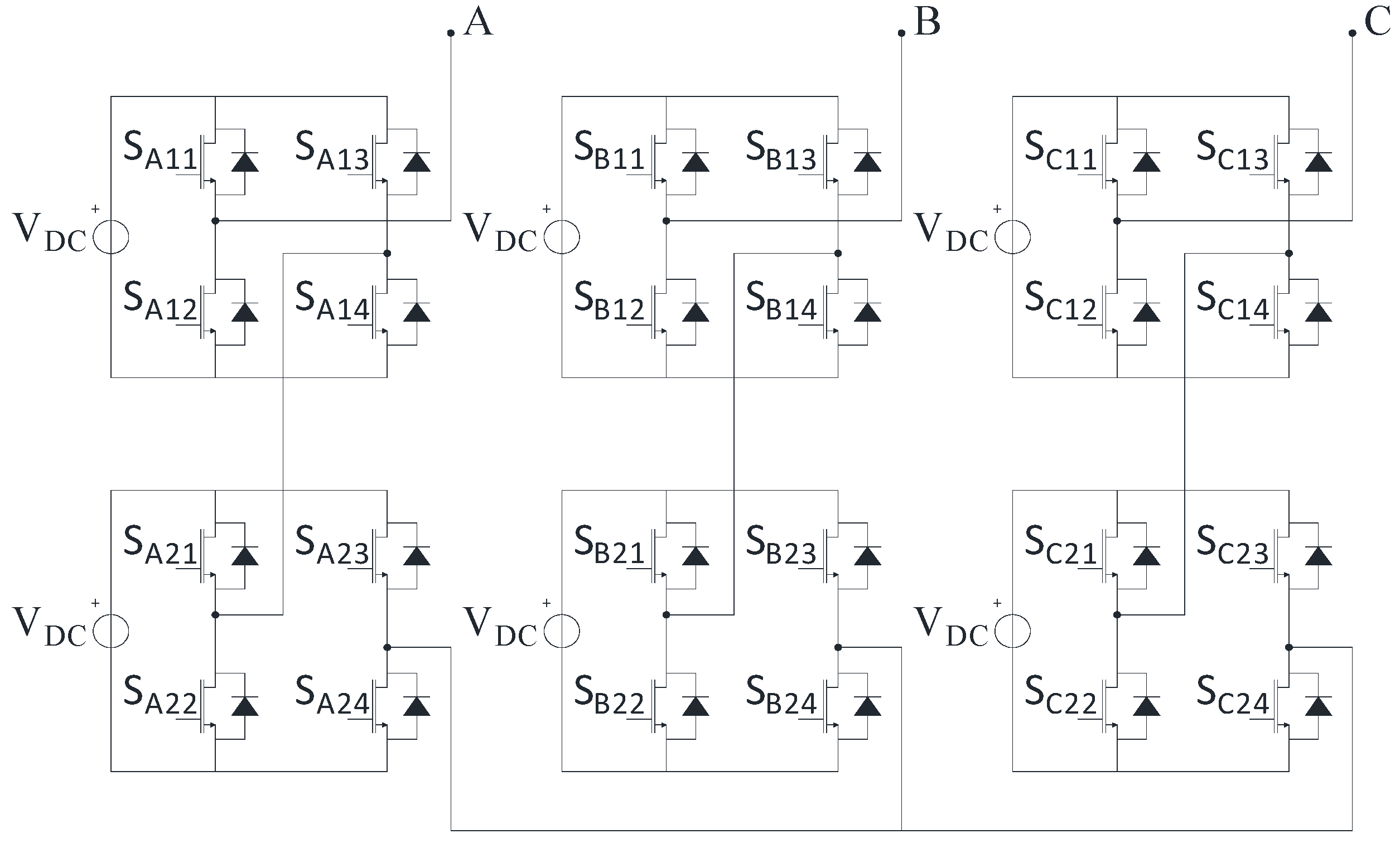






| Type | f with Maximum Harmonic Amplitude | Number of Voltage Levels | Instantaneous Maximum Value of Vn | Power-Balancing Capability | ||
|---|---|---|---|---|---|---|
| VN | VLL | S Modulating Signals | SFO Modulating Signals | |||
| PD | fsw | 5 | 9 | 7/3 Vdc | 7/3 Vdc | No |
| PS | 4 fsw | 5 | 9 | 2 Vdc | 8/3 Vdc | Yes |
| SCAMOD | 2 fsw | 5 | 9 | 2 Vdc | 8/3 Vdc | Yes |
| Quantity | Symbol | Value |
|---|---|---|
| Voltage | Vdss | 150 V |
| Resistance | RdSon | 9.3 mΩ |
| Current | ID | 104 A |
| Turn on delay | TDon | 18 ns |
| Rise time | TR | 73ns |
| Turn off delay | TDoff | 41 ns |
| Fall time | TF | 39ns |
| Reverse recovery | TRR | 86 ns |
| H-bridge DC-link voltage | VDC | 55 V |
| Switching frequency | fsw | 2–100 kHz |
| Quantity | Symbol | Value |
|---|---|---|
| Input voltage | Vin | 240 V |
| DC-link voltage | VDC | 320 V |
| Minimum input voltage | Vinmin | 70 V |
| Phase current peak | Ipeak | 30 A |
| Switching frequency | fsw | 2–20 kHz |
| Quantity | Symbol | Value |
|---|---|---|
| Nominal voltage | Vn | 132 V |
| Nominal current | In | 3.6 A |
| Nominal speed | n | 4000 rpm |
| Maximum speed | nmax | 6000 rpm |
| Pole pairs | P | 3 |
| Nr. of phases | M | 3 |
| Rated torque | Temn | 1.8 Nm |
| Peak torque | Temmax | 7.2 Nm |
| η[%] | |||||||
|---|---|---|---|---|---|---|---|
| 2L-VSO | 3P-5LCHBMI | ||||||
| WP | PWM | SPD | SFOPD | SPS | SFOPS | SSCA | SFOSCA |
| 1 | 76.8 | 79.1 | 79.6 | 79.4 | 79.2 | 78.9 | 79.2 |
| 2 | 71.1 | 73.7 | 74.1 | 74.1 | 73.9 | 73.7 | 73.8 |
| 3 | 58.7 | 61.1 | 61.4 | 61.3 | 61.1 | 60.9 | 60.9 |
| 4 | 24.6 | 25.6 | 25.7 | 25.7 | 25.6 | 25.4 | 25.4 |
| 5 | 79.1 | 81.8 | 82.1 | 81.9 | 81.6 | 81.7 | 81.6 |
| 6 | 74.5 | 77.9 | 78.1 | 78.1 | 77.6 | 78.1 | 77.6 |
| 7 | 64.1 | 67.8 | 68 | 67.9 | 67.4 | 67.6 | 67.3 |
| 8 | 30.1 | 32.9 | 33.2 | 33.2 | 32.7 | 32.9 | 32.9 |
| 9 | 79.1 | 82.7 | 83.2 | 83.1 | 83.1 | 83.3 | 82.3 |
| 10 | 75.8 | 80.3 | 80.8 | 80.7 | 80.8 | 80.9 | 80.1 |
| 11 | 68.4 | 73.4 | 73.8 | 73.4 | 73.2 | 72.8 | 71.9 |
| 12 | 39.3 | 42.4 | 42.6 | 42.8 | 42.6 | 42.3 | 41.7 |
| 13 | 73.6 | 78.8 | 79.1 | 78.9 | 79 | 79.4 | 78.7 |
| 14 | 71.8 | 78.2 | 78.5 | 78.4 | 78.4 | 79 | 78.3 |
| 15 | 68 | 75 | 75.1 | 74.2 | 74.2 | 73.8 | 72.9 |
| 16 | 49 | 53.6 | 53.9 | 54 | 54 | 53.4 | 53 |
| ΔPh [%] | 4 kHz | 8 kHz | 12 kHz | 16 kHz |
|---|---|---|---|---|
| SPD | <8% | <7% | <3% | <2% |
| SFOPD | <7% | <6% | <3% | <2% |
| SPS | <6% | <6% | <4% | <3% |
| SFOPS | <7% | <6% | <4% | <3% |
| SSCA | <10% | <7% | <4% | <3% |
| SFOSCA | <10% | <8% | <4% | <3% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nevoloso, C.; Scaglione, G.; Schettino, G.; Tommaso, A.O.D.; Viola, F.; Spataro, C.; Miceli, R. Investigating the Influence of PWM-Driven Cascaded H-Bridges Multilevel Inverter on Interior Permanent Magnet Synchronous Motor Power Losses. Energies 2025, 18, 3911. https://doi.org/10.3390/en18153911
Nevoloso C, Scaglione G, Schettino G, Tommaso AOD, Viola F, Spataro C, Miceli R. Investigating the Influence of PWM-Driven Cascaded H-Bridges Multilevel Inverter on Interior Permanent Magnet Synchronous Motor Power Losses. Energies. 2025; 18(15):3911. https://doi.org/10.3390/en18153911
Chicago/Turabian StyleNevoloso, Claudio, Gioacchino Scaglione, Giuseppe Schettino, Antonino Oscar Di Tommaso, Fabio Viola, Ciro Spataro, and Rosario Miceli. 2025. "Investigating the Influence of PWM-Driven Cascaded H-Bridges Multilevel Inverter on Interior Permanent Magnet Synchronous Motor Power Losses" Energies 18, no. 15: 3911. https://doi.org/10.3390/en18153911
APA StyleNevoloso, C., Scaglione, G., Schettino, G., Tommaso, A. O. D., Viola, F., Spataro, C., & Miceli, R. (2025). Investigating the Influence of PWM-Driven Cascaded H-Bridges Multilevel Inverter on Interior Permanent Magnet Synchronous Motor Power Losses. Energies, 18(15), 3911. https://doi.org/10.3390/en18153911









