Degradation-Aware Bi-Level Optimization of Second-Life Battery Energy Storage System Considering Demand Charge Reduction †
Abstract
1. Introduction
1.1. Literature Study
1.2. Contributions
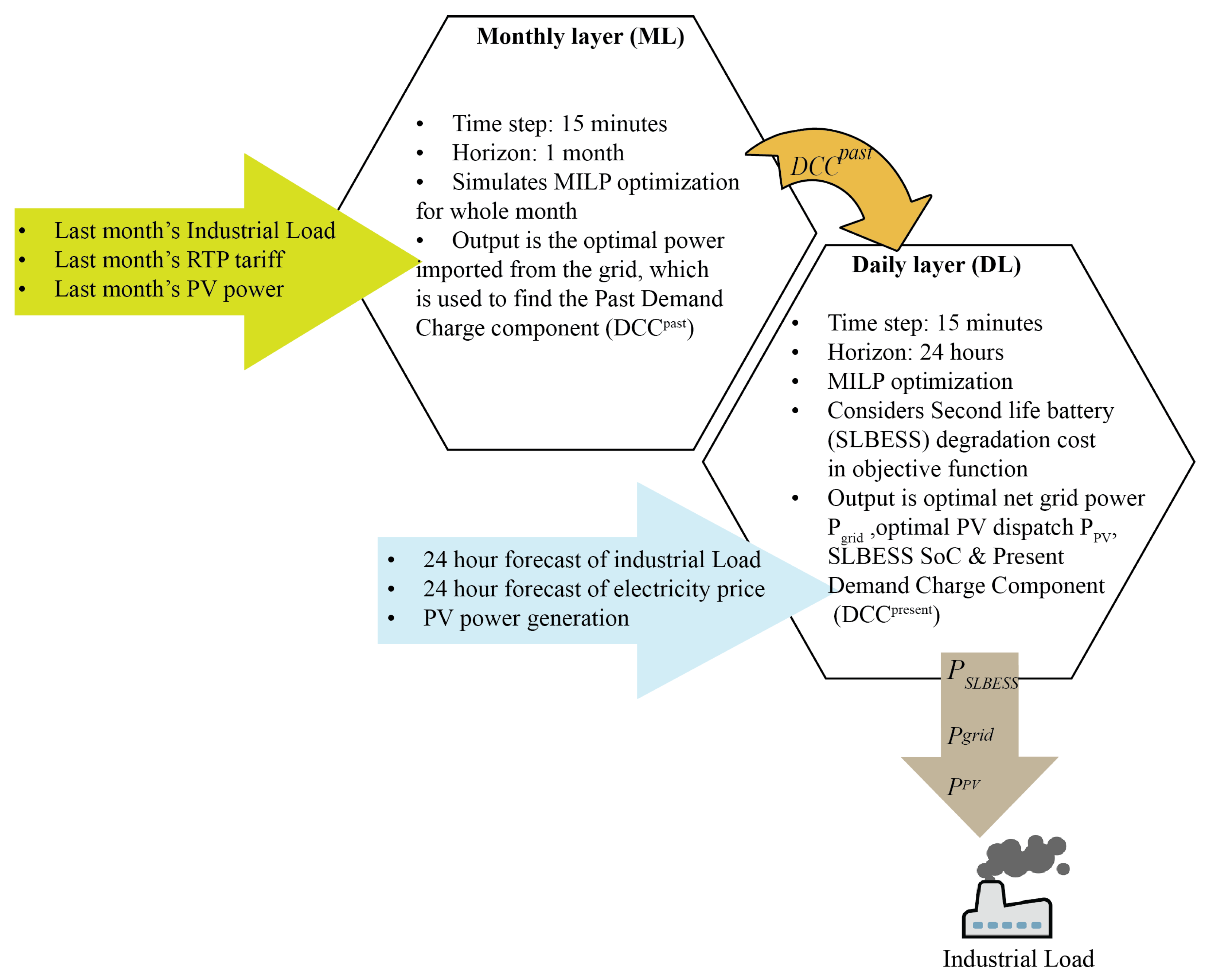
- A bi-level energy management (BL-EM) algorithm is proposed consisting of a monthly layer (ML) and daily layer (DL). The monthly dispatch and the previous month’s demand charge thresholds are calculated in the ML, which is fed into the DL calculating the optimal dispatch of second-life BESS, power imported from the grid, power exported to the grid, and photovoltaic (PV) power.
- In contrast with the literature, this article uses the real-world aging cycle data from [21] to generate a Wöhler curve (cycle vs. depth of discharge (DoD)) for a second-life Li-NMC (Lithium Nickel Manganese Cobalt oxides) battery pack. The equation obtained by applying piecewise fitting on the Wöhler curve is used to model the BESS degradation in the DL. Deep cycling and frequent use shorten the life of the BESS, causing it to reach the knee point. From the perspective of SLB, for the first time, an optimized trade-off is presented between BESS utilization and energy arbitrage (EA).
2. Bi-Layer Energy Management Framework
2.1. Monthly Layer (ML)
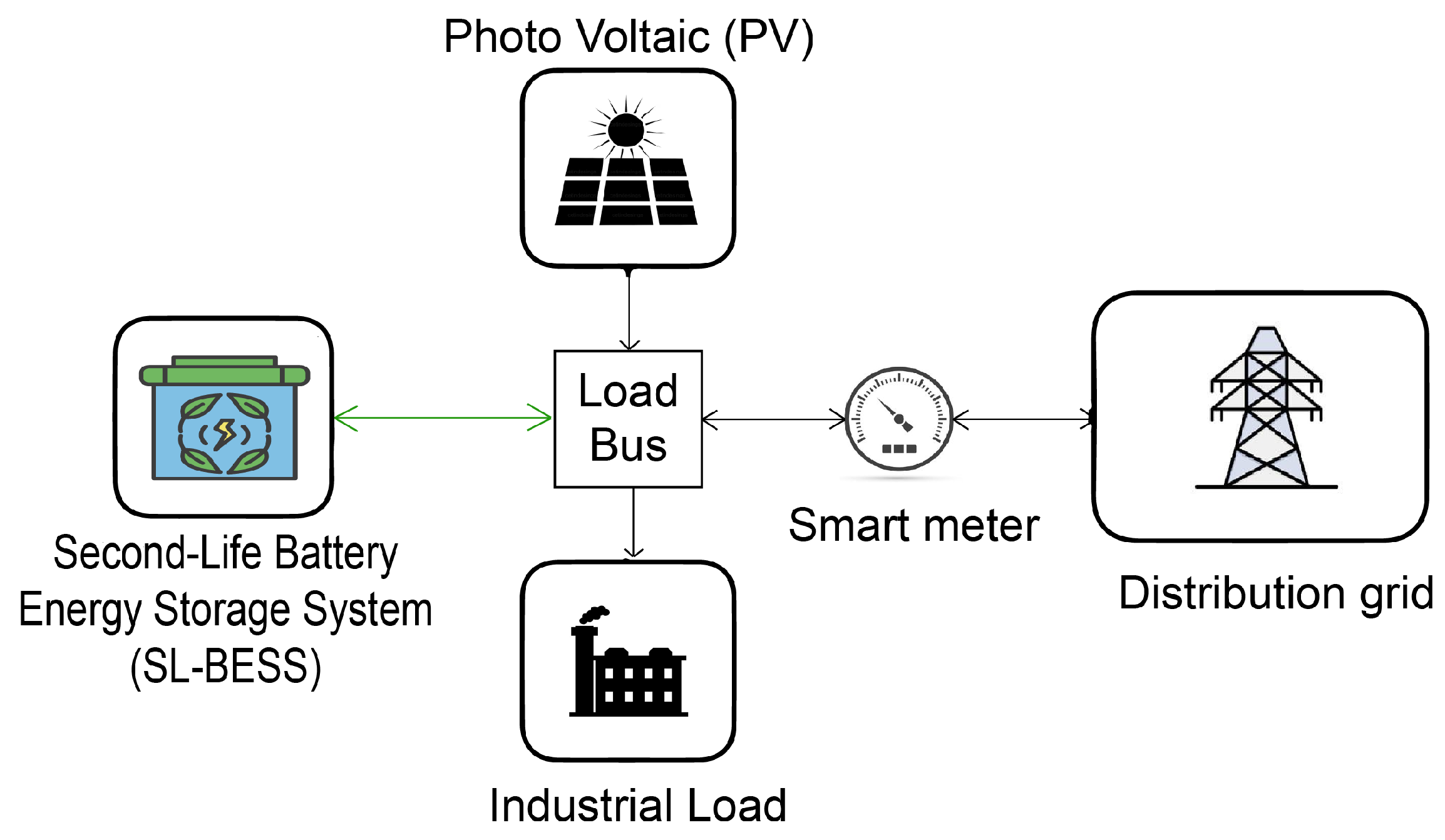
2.2. Second-Life Battery Energy Storage System Model
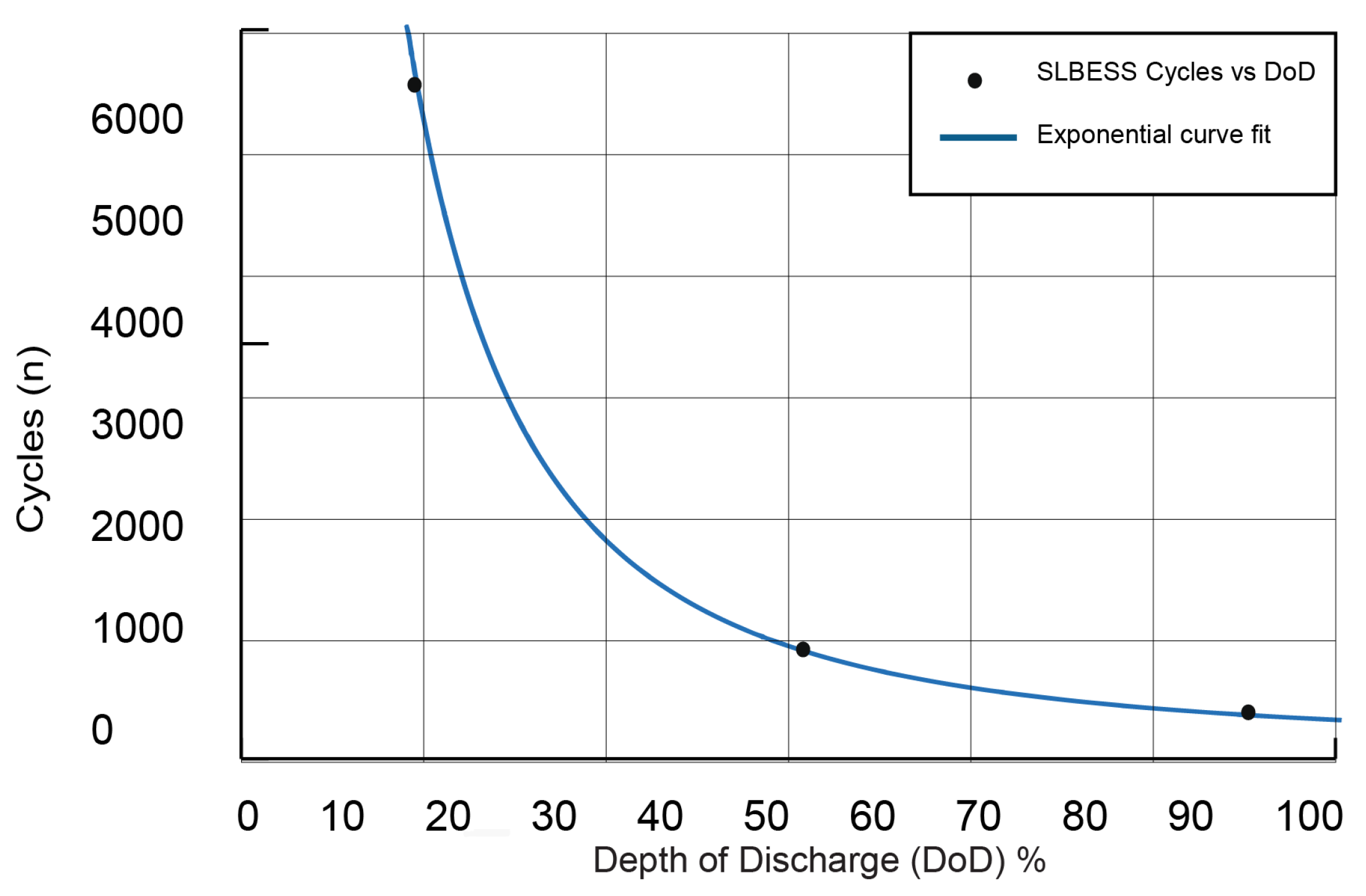
2.2.1. Wöhler Curve Derivation for Second-Life NMC+LMO Battery
2.2.2. Battery Degradation Model
2.3. Demand Charge Reduction Modeling
2.4. Daily Layer (DL)
2.4.1. Cost Function
2.4.2. Constraints
| Algorithm 1 BL-EM Algorithm |
|
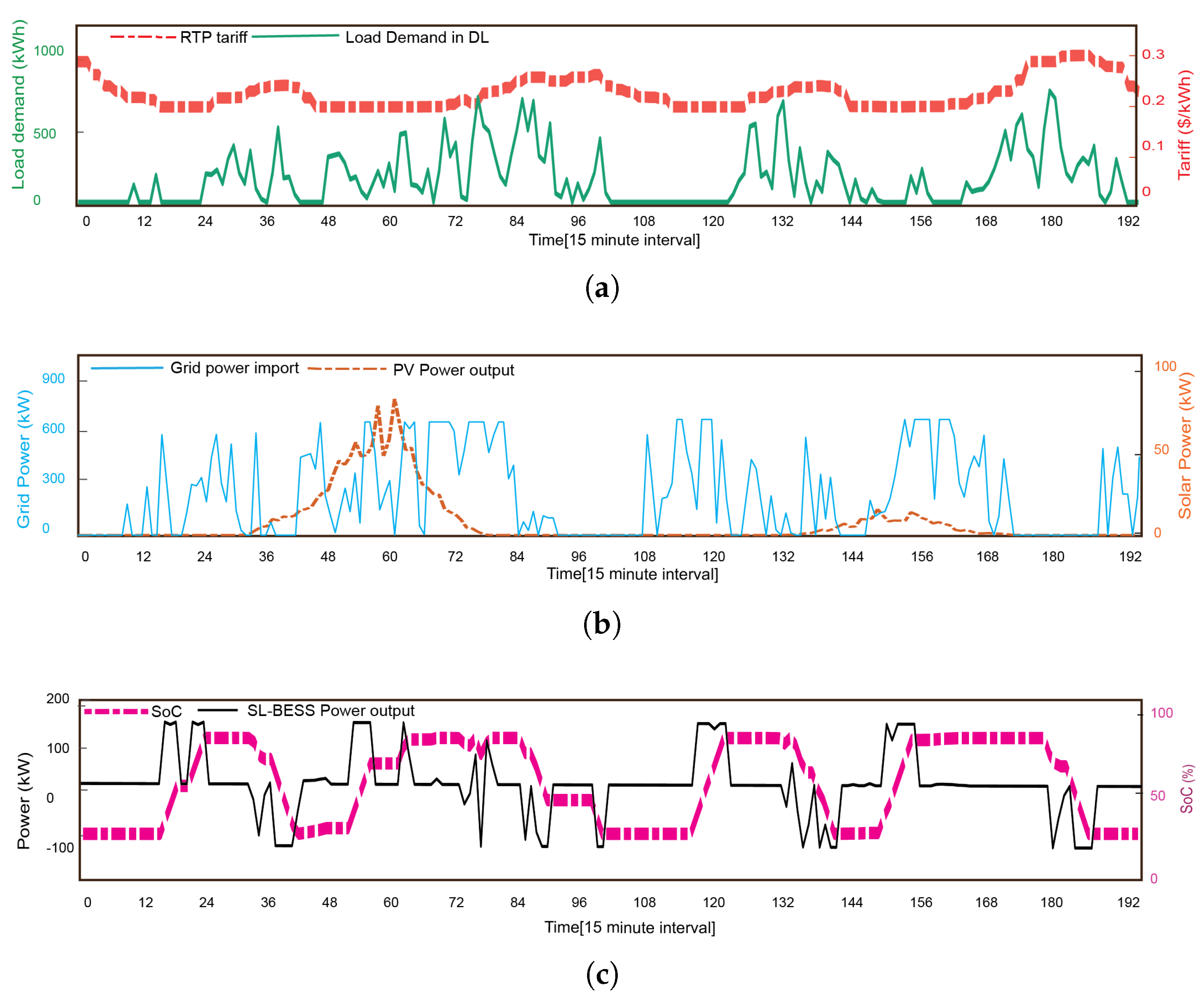
3. Results
- Since the original data used in the paper were from battery tests at the C/2 rate, we have assumed that SLBESS operates at the C/2 rate throughout its operation.
- The data used for SLB are for three cells. For a better Wöhler curve, more data can be used in the future.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BL-EM | bi-layered energy management |
| EA | energy arbitrage |
| SoH | state of health |
| UL | upper layer |
| ML | monthly layer |
| EoL | end of life |
| DoD | depth of discharge |
| RTP | Real-Time Pricing |
| indices | |
| segment index in BESS degradation model | |
| t | time index in ML/DL optimization |
| d | day index in DL optimization |
| parameters | |
| n | number of cycles |
| capacity throughput (Ah) | |
| rated capacity (kWh) | |
| capital cost of battery (USD) | |
| amortized variable for demand charge | |
| efficiency of power electronic converters | |
| discharge efficiency of BESS (%) |
| charge efficiency of BESS (%) | |
| upper SoC limit (%) | |
| lower SoC limit (%) | |
| selling cost of electricity (USD/kWh) | |
| buying cost of electricity (USD/kWh) | |
| M | large number used in the big-M method |
| ramp rate (maximum power that can be imported from the grid over one time step) | |
| (USD/15 min) | |
| capacity of BESS (kWh) | |
| solar irradiance | |
| variables | |
| discharge energy of the battery (kWh) | |
| energy imported from the grid (kWh) | |
| energy exported to the grid (kWh) | |
| degradation cost | |
| demand charge component of the present month (USD) | |
| demand charge component of the present month (USD) | |
| state of charge (%) | |
| dummy state of charge |
References
- International Energy Agency. Global EV Outlook 2024: Moving Towards Increased Affordability; Technical Report; International Energy Agency: Paris, France, 2024. [Google Scholar]
- Mc Kinsey & Company. Second-Life EV Batteries: The Newest Value Pool in Energy Storage. 2023. Available online: https://www.mckinsey.com/industries/automotive-and-assembly/our-insights/second-life-ev-batteries-the-newest-value-pool-in-energy-storage (accessed on 21 July 2024).
- Zhu, J.; Mathews, I.; Ren, D.; Li, W.; Cogswell, D.; Xing, B.; Sedlatschek, T.; Kantareddy, S.N.R.; Yi, M.; Gao, T.; et al. End-of-life or second-life options for retired electric vehicle batteries. Cell Rep. Phys. Sci. 2021, 2, 100537. [Google Scholar] [CrossRef]
- Hassan, A.; Khan, S.A.; Li, R.; Su, W.; Zhou, X.; Wang, M.; Wang, B. Second-Life Batteries: A Review on Power Grid Applications, Degradation Mechanisms, and Power Electronics Interface Architectures. Batteries 2023, 9, 571. [Google Scholar] [CrossRef]
- Ali, H.; Khan, H.A.; Pecht, M.G. Circular economy of Li Batteries: Technologies and trends. J. Energy Storage 2021, 40, 102690. [Google Scholar] [CrossRef]
- Data Center Frontier. Redwood and Crusoe Power AI with Circular Energy: Repurposed EV Batteries Drive Sustainable Infrastructure. 2025. Available online: https://www.datacenterfrontier.com/energy/article/55303589/redwood-and-crusoe-power-ai-with-circular-energy-repurposed-ev-batteries-drive-sustainable-infrastructure (accessed on 28 April 2025).
- Fitzgerald, G.; Mandel, J.; Morris, J.; Touati, H. The Economics of Battery Energy Storage: How Multi-Use, Customer-Sited Batteries Deliver the Most Services and Value to Customers and The Grid; Rocky Mountain Institute: Basalt, CO, USA, 2015; p. 6. [Google Scholar]
- Wang, Z.; Asghari, B.; Sharma, R. Stochastic demand charge management for commercial and industrial buildings. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Plug In America. Understanding Demand Charges. 2024. Available online: https://pluginamerica.org/understanding-demand-charges/ (accessed on 7 July 2024).
- Martinez-Laserna, E.; Sarasketa-Zabala, E.; Sarria, I.V.; Stroe, D.I.; Swierczynski, M.; Warnecke, A.; Timmermans, J.M.; Goutam, S.; Omar, N.; Rodriguez, P. Technical viability of battery second life: A study from the ageing perspective. IEEE Trans. Ind. Appl. 2018, 54, 2703–2713. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, Y.; Luo, F.; Mu, Y. Operational Planning of Centralized Charging Stations Utilizing Second-Life Battery Energy Storage Systems. IEEE Trans. Sustain. Energy 2021, 12, 387–399. [Google Scholar] [CrossRef]
- Leonori, S.; Rizzoni, G.; Frattale Mascioli, F.M.; Rizzi, A. Intelligent energy flow management of a nanogrid fast charging station equipped with second life batteries. Int. J. Electr. Power Energy Syst. 2021, 127, 106602. [Google Scholar] [CrossRef]
- Lin, J.; Qiu, J.; Yang, Y.; Lin, W. Planning of Electric Vehicle Charging Stations Considering Fuzzy Selection of Second Life Batteries. IEEE Trans. Power Syst. 2023, 99, 1–14. [Google Scholar] [CrossRef]
- Xu, L.; Lei, S.; Srinivasan, D.; Song, Z. Can retired lithium-ion batteries be a game changer in fast charging stations? eTransportation 2023, 18, 100297. [Google Scholar] [CrossRef]
- Haghighi, R.; Hassan, A.; Bui, V.H.; Hussain, A.; Su, W. Deep Reinforcement Learning-Based Optimization of Second-Life Battery Utilization in Electric Vehicles Charging Stations. arXiv 2025, arXiv:2502.03412. [Google Scholar]
- Terkes, M.; Öztürk, Z.; Demirci, A.; Tercan, S.M. Optimal sizing and feasibility analysis of second-life battery energy storage systems for community microgrids considering carbon reduction. J. Clean. Prod. 2023, 421, 138507. [Google Scholar] [CrossRef]
- Hu, S.; Sun, H.; Peng, F.; Zhou, W.; Cao, W.; Su, A.; Chen, X.; Sun, M. Optimization strategy for economic power dispatch utilizing retired EV batteries as flexible loads. Energies 2018, 11, 1657. [Google Scholar] [CrossRef]
- Huang, Z.; Xie, Z.; Zhang, C.; Chan, S.H.; Milewski, J.; Xie, Y.; Yang, Y.; Hu, X. Modeling and multi-objective optimization of a stand-alone PV-hydrogen-retired EV battery hybrid energy system. Energy Convers. Manag. 2019, 181, 80–92. [Google Scholar] [CrossRef]
- Cheng, M.; Zhang, X.; Ran, A.; Wei, G.; Sun, H. Optimal dispatch approach for second-life batteries considering degradation with online SoH estimation. Renew. Sustain. Energy Rev. 2023, 173, 113053. [Google Scholar] [CrossRef]
- Hassan, A.; Su, W. Degradation-Aware Optimization of Second-Life Battery Energy Storage System. In Proceedings of the IECON 2024—50th Annual Conference of the IEEE Industrial Electronics Society, Chicago, IL, USA, 3–6 November 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Seger, P.V.; Thivel, P.X.; Riu, D. A second life Li-ion battery ageing model with uncertainties: From cell to pack analysis. J. Power Sources 2022, 541, 231663. [Google Scholar] [CrossRef]
- DTE Energy. Primary Supply Agreement D11. 2023. Available online: https://www.dteenergy.com/content/dam/dteenergy/deg/website/business/service-and-price/pricing/rate-options/PrimarySupplyAgreementD11.pdf (accessed on 7 July 2024).
- Wang, H.; Rasheed, M.; Hassan, R.; Kamel, M.; Tong, S.; Zane, R. Life-extended active battery control for energy storage using electric vehicle retired batteries. IEEE Trans. Power Electron. 2023, 38, 6801–6805. [Google Scholar] [CrossRef]
- ur Rehman, W.; Bo, R.; Mehdipourpicha, H.; Kimball, J.W. Sizing battery energy storage and PV system in an extreme fast charging station considering uncertainties and battery degradation. Appl. Energy 2022, 313, 118745. [Google Scholar] [CrossRef]
- Braco, E.; San Martín, I.; Sanchis, P.; Ursúa, A.; Stroe, D.I. State of health estimation of second-life lithium-ion batteries under real profile operation. Appl. Energy 2022, 326, 119992. [Google Scholar] [CrossRef]
- Braco, E.; San Martín, I.; Berrueta, A.; Sanchis, P.; Ursúa, A. Experimental assessment of cycling ageing of lithium-ion second-life batteries from electric vehicles. J. Energy Storage 2020, 32, 101695. [Google Scholar] [CrossRef]
- Beatty, M.; Strickland, D.; Warren, J.; Chan, J.; Ferreira, P. Long-Term Sweat Testing Dataset for Second-Life Batteries. Sci. Data 2025, 12, 1068. [Google Scholar] [CrossRef] [PubMed]
- Ye, S.; An, D.; Wang, C.; Zhang, T.; Xi, H. Towards fast multi-scale state estimation for retired battery reusing via Pareto-efficient. Energy 2025, 319, 134848. [Google Scholar] [CrossRef]
- Gao, W.; Cao, Z.; Kurdkandi, N.V.; Fu, Y.; Mi, C. Evaluation of the second-life potential of the first-generation Nissan Leaf battery packs in energy storage systems. eTransportation 2024, 20, 100313. [Google Scholar] [CrossRef]
- Liu, K.; Ashwin, T.; Hu, X.; Lucu, M.; Widanage, W.D. An evaluation study of different modelling techniques for calendar ageing prediction of lithium-ion batteries. Renew. Sustain. Energy Rev. 2020, 131, 110017. [Google Scholar] [CrossRef]
- Xu, X.; Mi, J.; Fan, M.; Yang, K.; Wang, H.; Liu, J.; Yan, H. Study on the performance evaluation and echelon utilization of retired LiFePO4 power battery for smart grid. J. Clean. Prod. 2019, 213, 1080–1086. [Google Scholar] [CrossRef]
- Cui, X.; Khan, M.A.; Pozzato, G.; Singh, S.; Sharma, R.; Onori, S. Taking second-life batteries from exhausted to empowered using experiments, data analysis, and health estimation. Cell Rep. Phys. Sci. 2024, 5, 101941. [Google Scholar] [CrossRef]
- Sun, S.I.; Chipperfield, A.J.; Kiaee, M.; Wills, R.G. Effects of market dynamics on the time-evolving price of second-life electric vehicle batteries. J. Energy Storage 2018, 19, 41–51. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S. Novel battery degradation cost formulation for optimal scheduling of battery energy storage systems. Int. J. Electr. Power Energy Syst. 2022, 137, 107795. [Google Scholar] [CrossRef]
- ur Rehman, W.; Kimball, J.W.; Bo, R. Multilayered Energy Management Framework for Extreme Fast Charging Stations Considering Demand Charges, Battery Degradation, and Forecast Uncertainties. IEEE Trans. Transp. Electrif. 2023, 10, 760–776. [Google Scholar] [CrossRef]




| Reference | Focus Area | Approach/Limitation | Contribution |
|---|---|---|---|
| [11] | SLBs for EV fast charging | MILP-based planning for centralized charging with second-life batteries; no degradation modeling | Demonstrates cost-effective charging using SLBs |
| [12] | Nanogrid fast charging station with SLBs | Uses machine learning for fuzzy EMS, but lacks detailed SoH/degradation handling | Proposes EMS for urban nanogrids with SLB-PV setup |
| [14] | SLBs in fast charging | Simulation-based performance study; limited degradation modeling | Evaluates SLB viability for high-power charging needs |
| [16] | Microgrid planning with SLBs | Focuses on carbon reduction feasibility; excludes SLB degradation effects | Assesses shared SLB systems in renewable-powered microgrids |
| [17] | SLBs as flexible grid loads | Optimizes power dispatch; no online SoH modeling | Demonstrates SLBs as dispatchable DERs |
| [19] | SoH-aware SLB operation | Uses online SoH estimation for dispatch optimization | Introduces online degradation tracking into optimization |
| Cell number | 18,650 |
| Positive electrode material | NMC+LMO |
| Cell capacity | 2.15 Ah (fresh), 1.72Ah (@ 80% capacity) |
| Nominal Voltage | 3.65 V |
| Parameter | Value |
|---|---|
| PV panel rating [kW] | 100 kW |
| BESS rating [kWh] | 360 kWh |
| BESS no. of battery packs | 12 |
| Battery chemistry | Li-ion (NMC+LMO) |
| BESS pack ratings | 30 kWh capacity 24 modules 8 cells/module |
| BESS capital cost [$/kWh] | $50/kWh |
| AC/DC, DC/AC converter efficiency | 98% |
| BESS charge efficiency | 98% |
| BESS discharge efficiency | 98% |
| Demand charge tariff [$/kW] | 13.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hassan, A.; Hollweg, G.V.; Su, W.; Zhou, X.; Wang, M. Degradation-Aware Bi-Level Optimization of Second-Life Battery Energy Storage System Considering Demand Charge Reduction. Energies 2025, 18, 3894. https://doi.org/10.3390/en18153894
Hassan A, Hollweg GV, Su W, Zhou X, Wang M. Degradation-Aware Bi-Level Optimization of Second-Life Battery Energy Storage System Considering Demand Charge Reduction. Energies. 2025; 18(15):3894. https://doi.org/10.3390/en18153894
Chicago/Turabian StyleHassan, Ali, Guilherme Vieira Hollweg, Wencong Su, Xuan Zhou, and Mengqi Wang. 2025. "Degradation-Aware Bi-Level Optimization of Second-Life Battery Energy Storage System Considering Demand Charge Reduction" Energies 18, no. 15: 3894. https://doi.org/10.3390/en18153894
APA StyleHassan, A., Hollweg, G. V., Su, W., Zhou, X., & Wang, M. (2025). Degradation-Aware Bi-Level Optimization of Second-Life Battery Energy Storage System Considering Demand Charge Reduction. Energies, 18(15), 3894. https://doi.org/10.3390/en18153894











