State-Aware Energy Management Strategy for Marine Multi-Stack Hybrid Energy Storage Systems Considering Fuel Cell Health
Abstract
1. Introduction
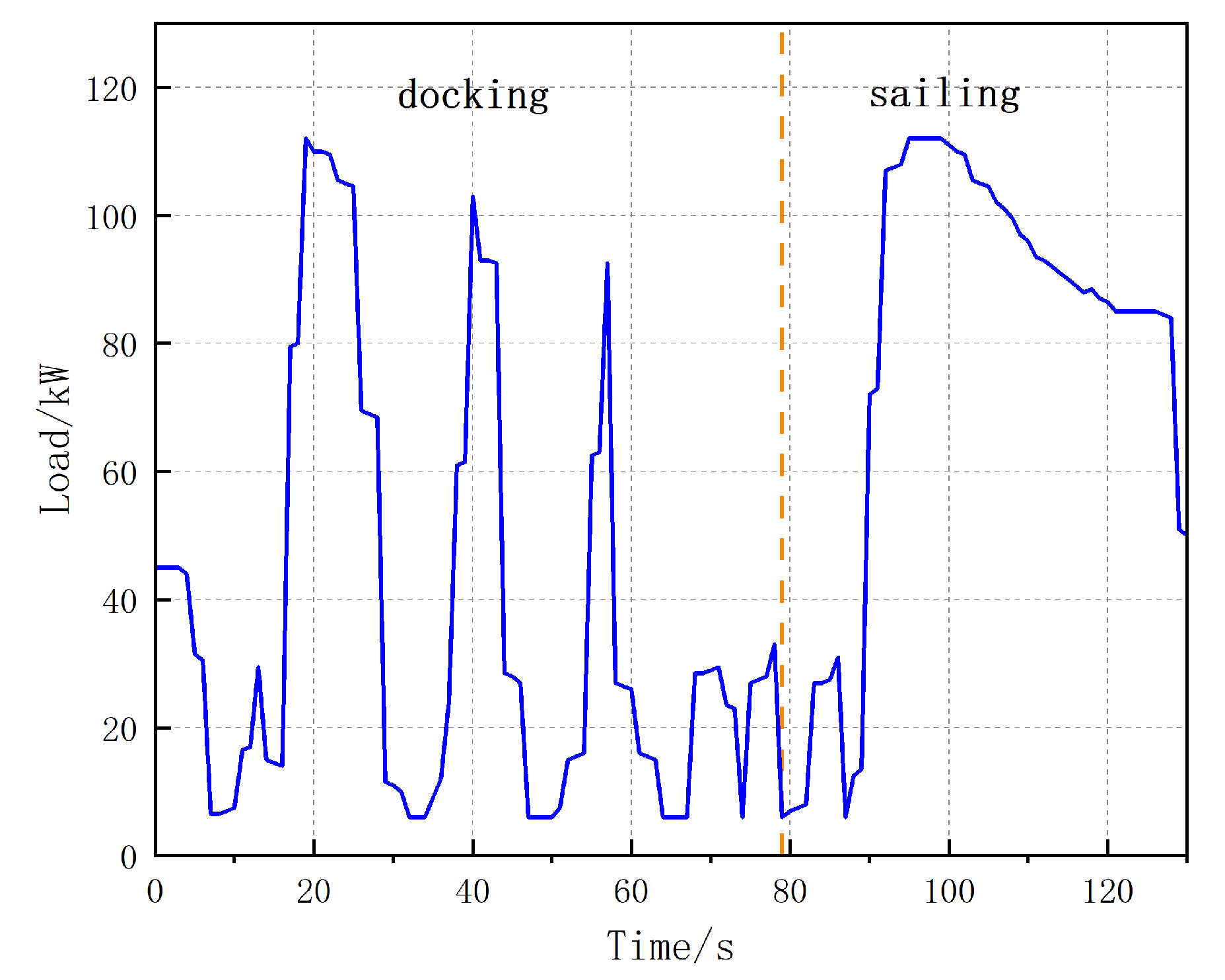
2. Ship Simulation Model
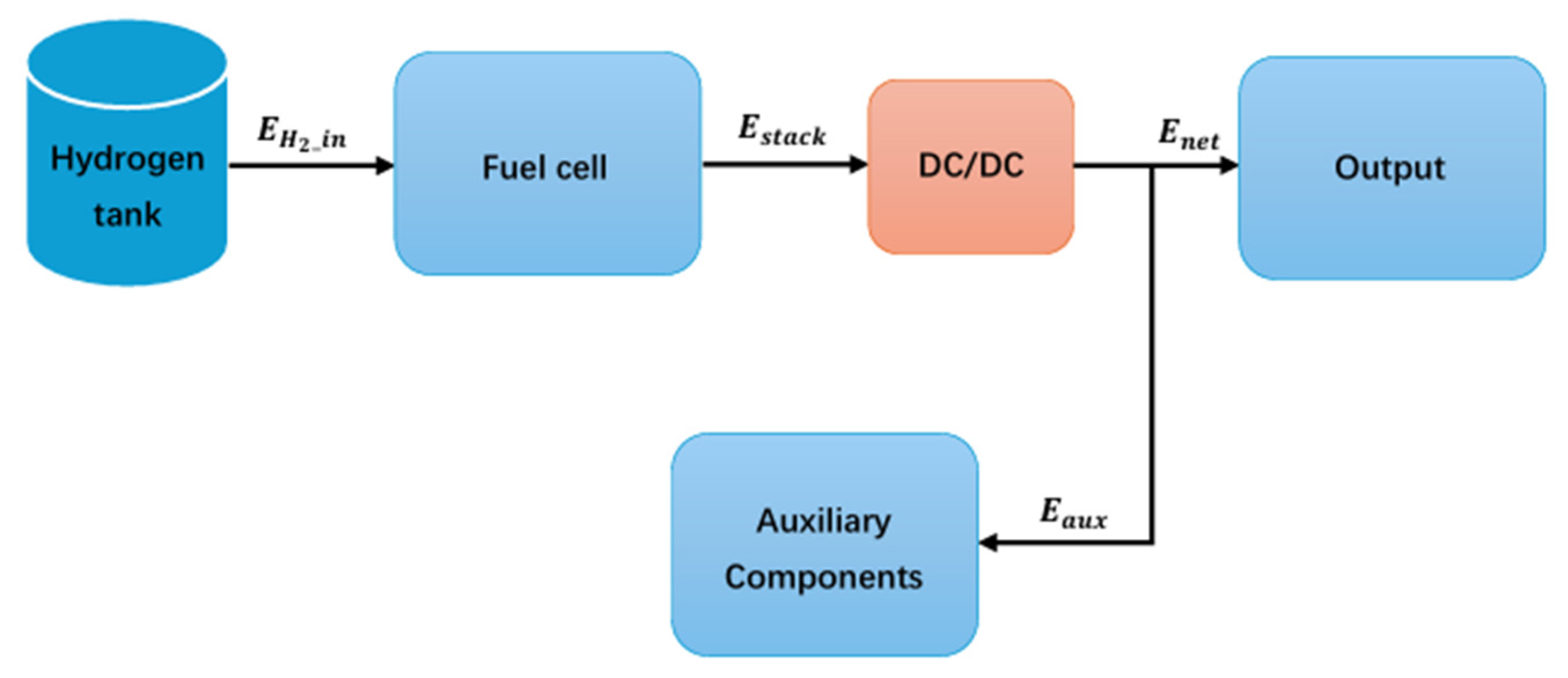
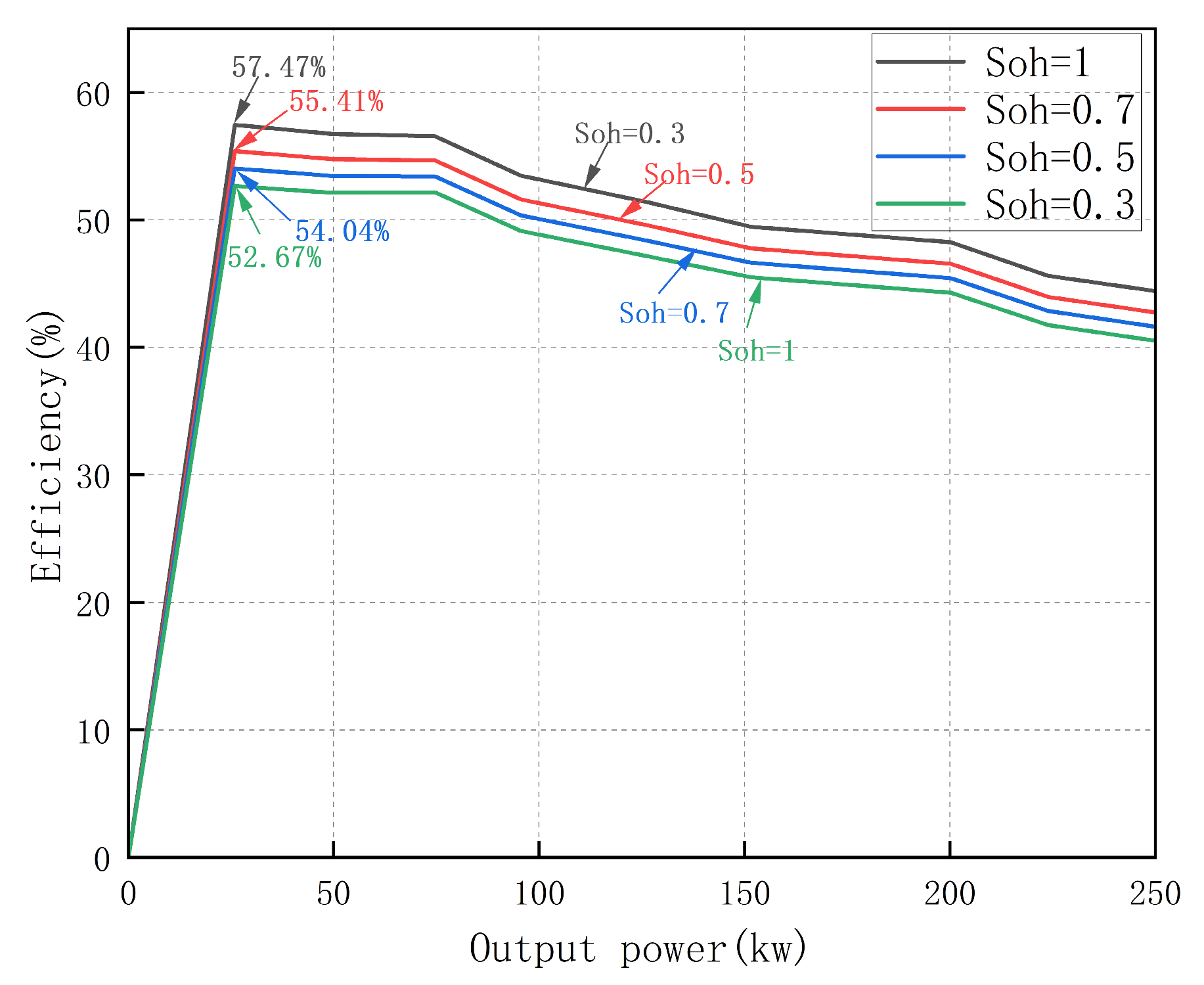
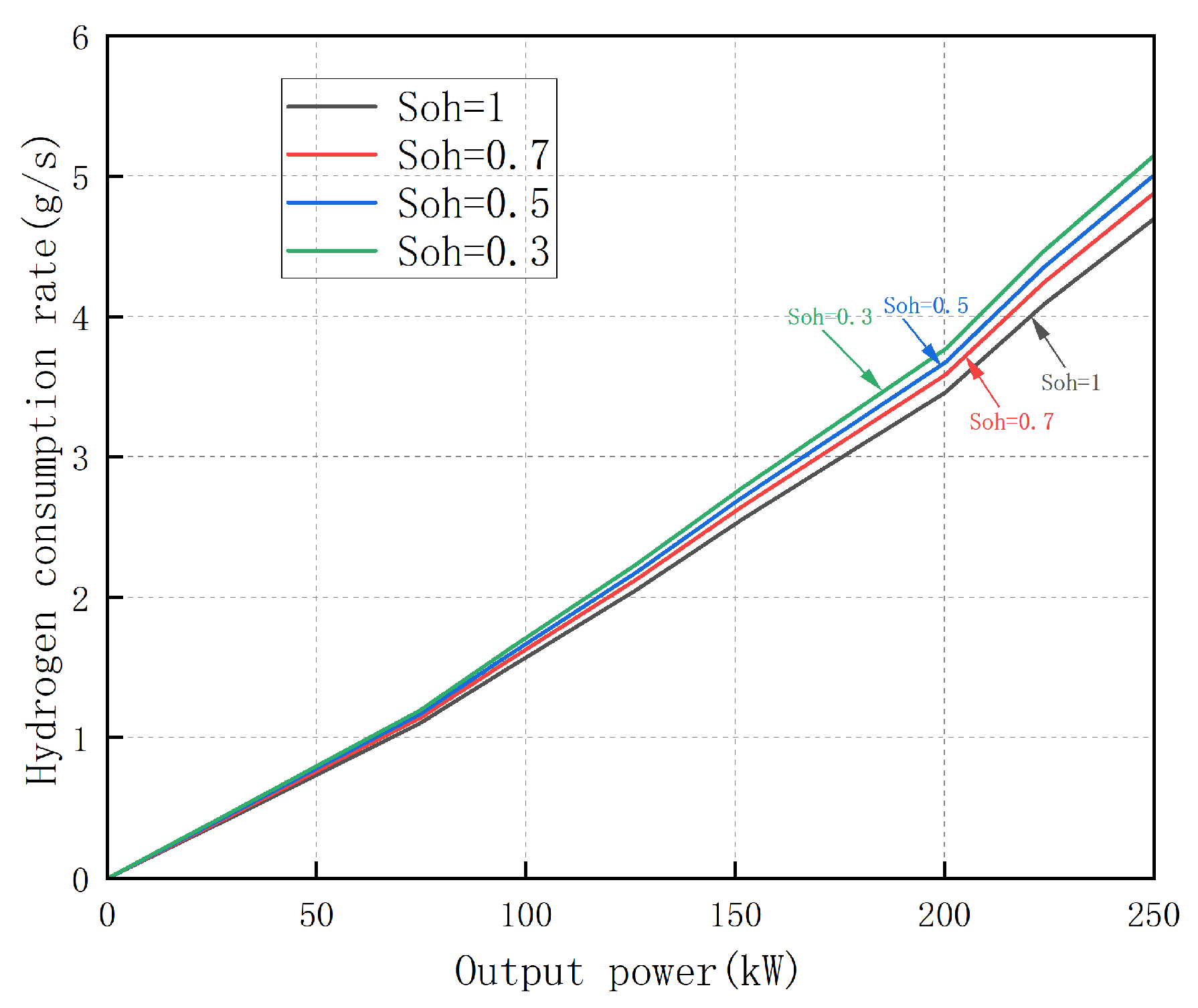
2.1. Fuel Cell Efficiency Modeling
2.2. Li-Ion Battery Model
3. Energy Management Strategy
- (1)
- A possible Li-ion battery and fuel cell output power.
- (2)
- Define the scope of the variables and .
- (3)
- Calculate the optimized equivalent hydrogen consumption using the PSO or GAPSO algorithms.
- (4)
- Repeat steps 1–3 until an optimal solution is found.
3.1. Comparison of Intelligent Optimization Algorithms
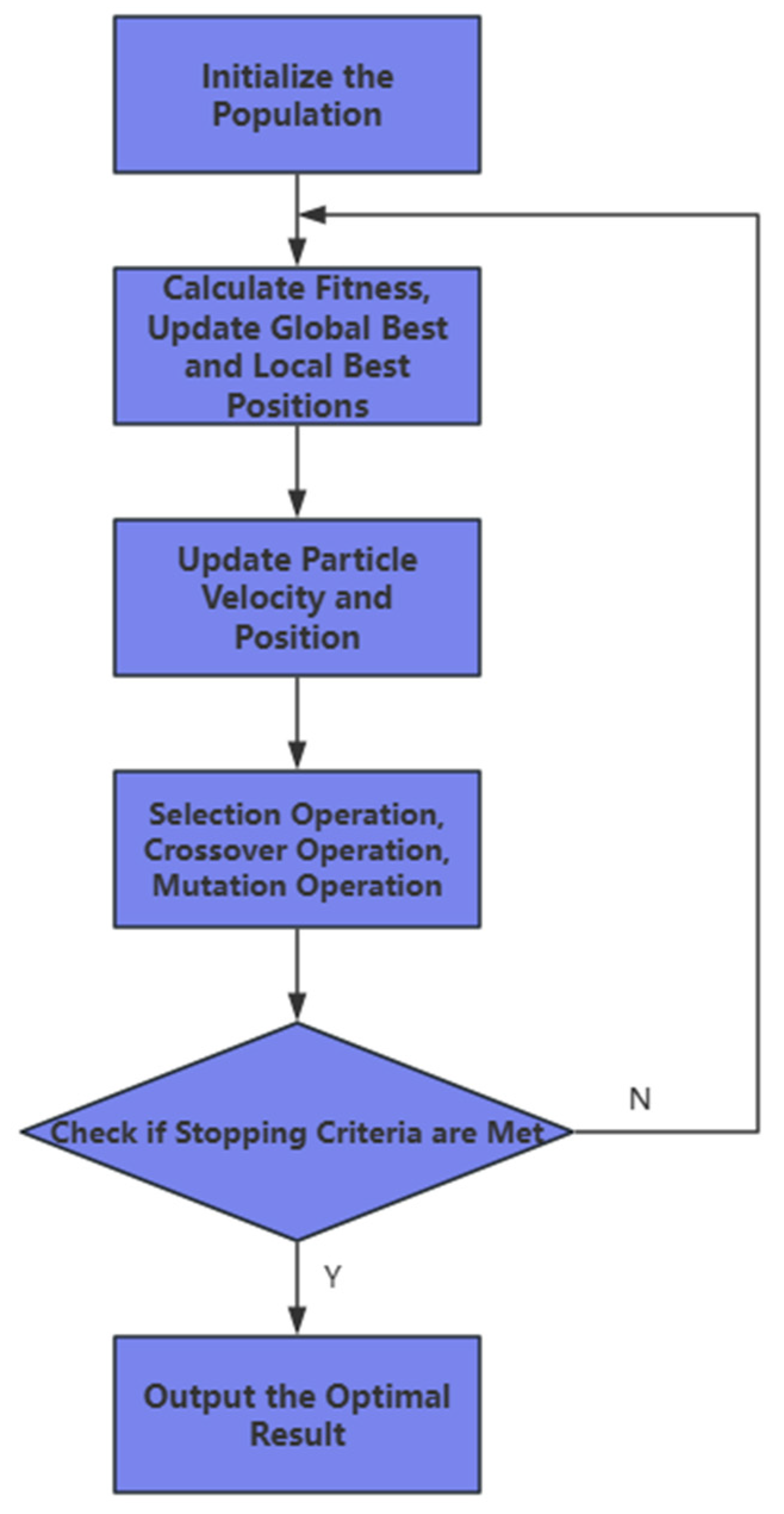
3.2. Hybrid GAPSO Algorithm
3.3. ECMS-Based Energy Management Strategies
3.3.1. Fuel Cell Equivalent Hydrogen Consumption
3.3.2. Li-Ion Battery Equivalent Hydrogen Consumption
3.3.3. Power Allocation Strategy
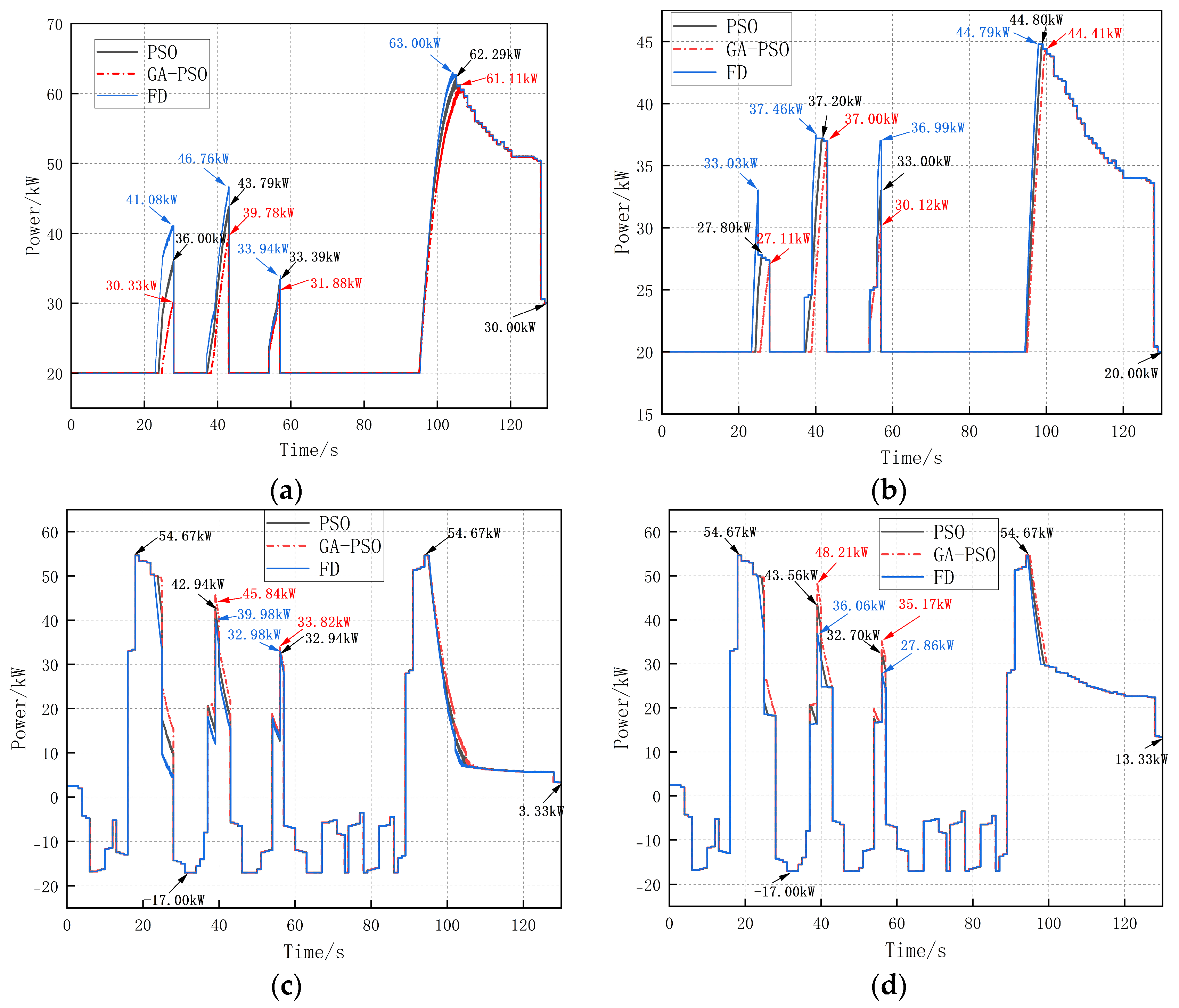
4. Results
4.1. Comparison of Power Under Different Algorithms
4.2. Comparison of Hydrogen Consumption
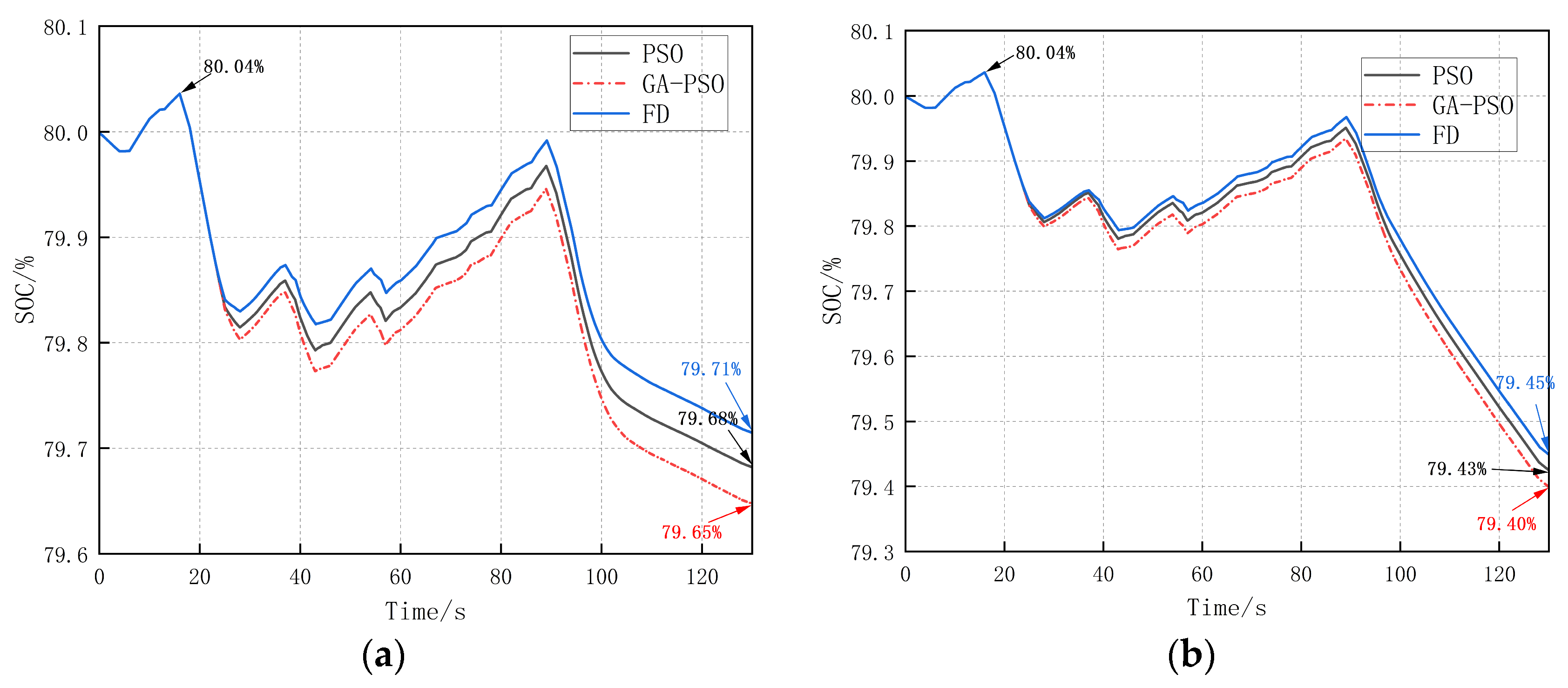
4.3. Battery SOC and Its Lifetime Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qazi, S.; Venugopal, P.; Rietveld, G.; Soeiro, T.B.; Shipurkar, U.; Grasman, A.; Watson, A.J.; Wheeler, P. Powering Maritime: Challenges and Prospects in Ship Electrification. IEEE Electrif. Mag. 2023, 11, 74–87. [Google Scholar] [CrossRef]
- Perčić, M.; Vladimir, N.; Jovanović, I.; Koričan, M. Application of Fuel Cells with Zero-Carbon Fuels in Short-Sea Shipping. Appl. Energy 2022, 309, 118463. [Google Scholar] [CrossRef]
- Li, X.; Ye, T.; Meng, X.; He, D.; Li, L.; Song, K.; Jiang, J.; Sun, C. Advances in the Application of Sulfonated Poly (Ether Ether Ketone) (Speek) and Its Organic Composite Membranes for Proton Exchange Membrane Fuel Cells (Pemfcs). Polymers 2024, 16, 2840. [Google Scholar] [CrossRef] [PubMed]
- Maaruf, M.; Khalid, M. Hybrid Solar/Pem Fuel Cell/and Water Electrolyzer Energy System for All-Electric Ship. In Proceedings of the 2022 IEEE Kansas Power and Energy Conference (KPEC), Manhattan, KS, USA, 25–26 April 2022. [Google Scholar]
- Bouisalmane, N.; Wang, T.; Breaz, E.; Doubabi, S.; Paire, D.; Oubraham, J.; Levy, M.; Gao, F. Hydrogen Consumption Minimization with Optimal Power Allocation of Multi-Stack Fuel Cell System Using Particle Swarm Optimization. In Proceedings of the 2021 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 21–25 June 2021. [Google Scholar]
- Moghadari, M.; Kandidayeni, M.; Boulon, L.; Chaoui, H. Hydrogen Minimization of a Hybrid Multi-Stack Fuel Cell Vehicle Using an Optimization-Based Strategy. In Proceedings of the 2021 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijon, Spain, 25–28 October 2021. [Google Scholar]
- Tang, X.; Shi, L.; Li, M.; Xu, S.; Sun, C. Health State Estimation and Long-Term Durability Prediction for Vehicular Pem Fuel Cell Stacks under Dynamic Operational Conditions. IEEE Trans. Power Electron. 2024, 40, 4498–4509. [Google Scholar] [CrossRef]
- Meng, X.; Sun, C.; Mei, J.; Tang, X.; Hasanien, H.M.; Jiang, J.; Fan, F.; Song, K. Fuel Cell Life Prediction Considering the Recovery Phenomenon of Reversible Voltage Loss. J. Power Sources 2025, 625, 235634. [Google Scholar] [CrossRef]
- Huang, W.; Liu, M.; Zhang, C.; Niu, T.; Fu, Z.; Ren, X.; Chin, C.S. Life Prediction for Proton Exchange Membrane Fuel Cell Based on Experimental Results and Combinatorial Optimization Algorithm. Int. J. Hydrogen Energy 2024, 79, 364–376. [Google Scholar] [CrossRef]
- Jiang, H.; Xu, L.; Li, J.; Hu, Z.; Ouyang, M. Energy Management and Component Sizing for a Fuel Cell/Battery/Supercapacitor Hybrid Powertrain Based on Two-Dimensional Optimization Algorithms. Energy 2019, 177, 386–396. [Google Scholar] [CrossRef]
- Fletcher, T.; Thring, R.; Watkinson, M. An Energy Management Strategy to Concurrently Optimise Fuel Consumption & Pem Fuel Cell Lifetime in a Hybrid Vehicle. Int. J. Hydrogen Energy 2016, 41, 21503–21515. [Google Scholar] [CrossRef]
- Hein, K.; Xu, Y.; Wilson, G.; Gupta, A.K. Coordinated Optimal Voyage Planning and Energy Management of All-Electric Ship with Hybrid Energy Storage System. IEEE Trans. Power Syst. 2020, 36, 2355–2365. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, H.; Han, J.; Chen, Y.; Kuang, J.; Charpentier, J.-F.; Aϊt-Ahmed, N.; Benbouzid, M. Optimal Soc Control and Rule-Based Energy Management Strategy for Fuel-Cell-Based Hybrid Vessel Including Batteries and Supercapacitors. J. Mar. Sci. Eng. 2023, 11, 398. [Google Scholar] [CrossRef]
- Meng, X.; Li, Q.; Zhang, G.; Wang, T.; Chen, W.; Cao, T. A Dual-Mode Energy Management Strategy Considering Fuel Cell Degradation for Energy Consumption and Fuel Cell Efficiency Comprehensive Optimization of Hybrid Vehicle. IEEE Access 2019, 7, 134475–134487. [Google Scholar] [CrossRef]
- Li, Z.; Xu, Y.; Fang, S.; Wang, Y.; Zheng, X. Multiobjective Coordinated Energy Dispatch and Voyage Scheduling for a Multienergy Ship Microgrid. IEEE Trans. Ind. Appl. 2019, 56, 989–999. [Google Scholar] [CrossRef]
- Sun, Y.; Xu, Q.; Yuan, Y.; Yang, B. Optimal Energy Management of Fuel Cell Hybrid Electric Ships Considering Fuel Cell Aging Cost. In Proceedings of the 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Weihai, China, 13–15 July 2020. [Google Scholar]
- Wang, N.; Song, B.; Gao, T.; Li, Y. Adaptive Equivalent Consumption Minimization Strategy for Fuel Cell Ships Suffering From Efficiency Degradation. In Proceedings of the 2024 36th Chinese Control and Decision Conference (CCDC), Xi’an, China, 25–27 May 2024. [Google Scholar]
- Zhu, L.; Liu, Y.; Zeng, Y.; Guo, H.; Ma, K.; Liu, S.; Zhang, Q. Energy Management Strategy for Fuel Cell Hybrid Ships Based on Deep Reinforcement Learning with Multi-Optimization Objectives. Int. J. Hydrogen Energy 2024, 93, 1258–1267. [Google Scholar] [CrossRef]
- Pang, B.; Liu, S.; Zhu, H.; Feng, Y.; Dong, Z. Real-Time Optimal Control of an Lng-Fueled Hybrid Electric Ship Considering Battery Degradations. Energy 2024, 296, 131170. [Google Scholar] [CrossRef]
- Song, K.; Ding, Y.; Hu, X.; Xu, H.; Wang, Y.; Cao, J. Degradation Adaptive Energy Management Strategy Using Fuel Cell State-of-Health for Fuel Economy Improvement of Hybrid Electric Vehicle. Appl. Energy 2021, 285, 116413. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Xu, L.; Ouyang, M. Optimization for a Fuel Cell/Battery/Capacity Tram with Equivalent Consumption Minimization Strategy. Energy Convers. Manag. 2017, 134, 59–69. [Google Scholar] [CrossRef]
- Cao, W.; Geng, P.; Xu, X. Optimization of Battery Energy Storage System Size and Power Allocation Strategy for Fuel Cell Ship. Energy Sci. Eng. 2023, 11, 2110–2121. [Google Scholar] [CrossRef]
- Ghorbani, N.; Kasaeian, A.; Toopshekan, A.; Bahrami, L.; Maghami, A. Optimizing a Hybrid Wind-Pv-Battery System Using Ga-Pso and Mopso for Reducing Cost and Increasing Reliability. Energy 2018, 154, 581–591. [Google Scholar] [CrossRef]
- Zhao, F.; Li, Y.; Zhou, M. Optimization of energy management strategy for marine multi-stack fuel cell hybrid power system. Ship Sci. Technol. 2024, 46, 134–140. [Google Scholar]
- Cao, W.; Geng, P.; Xu, X.; Tarasiuk, T. Energy Management Strategy Considering Energy Storage System Degradation for Hydrogen Fuel Cell Ship. Pol. Marit. Res. 2023, 30, 95–104. [Google Scholar] [CrossRef]
- Balsamo, F.; De Falco, P.; Mottola, F.; Pagano, M. Power Flow Approach for Modeling Shipboard Power System in Presence of Energy Storage and Energy Management Systems. IEEE Trans. Energy Convers. 2020, 35, 1944–1953. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, Z.; Guan, C.; Gao, H. Optimization of Sizing and Frequency Control in Battery/Supercapacitor Hybrid Energy Storage System for Fuel Cell Ship. Energy 2020, 197, 117285. [Google Scholar] [CrossRef]
- Li, Y.; Guo, Y.; Zhang, Y. Equivalent Consumption Minimization Energy Management Strategy Based on Frequency Decoupling for Unmanned Surface Vehicle. In Proceedings of the 2023 3rd International Conference on Energy, Power and Electrical Engineering (EPEE), Wuhan, China, 15–17 September 2023. [Google Scholar]



| DOD | Cycle Life (Day) |
|---|---|
| 0 | 10,610 |
| 0.2 | 8720 |
| 0.4 | 7200 |
| 0.6 | 5200 |
| 1 | 4700 |
| Algorithms | Advantage | Disadvantage |
|---|---|---|
| GA | Strong global search capability, robust performance, and broad applicability | Low local search precision, slow convergence, and complex parameter tuning |
| PSO | Simple implementation, fast convergence, and minimal parameters | Prone to local optima and ineffective for discrete optimization problems |
| ABC | Exhibits strong robustness and possesses powerful global search capability | Insufficient local search precision and low late-stage convergence efficiency |
| FA | Strong global exploration capability, particularly suitable for multimodal functions | Exhibits slow convergence speed and high sensitivity to parameters (e.g., light absorption coefficient |
| ACO | Strong global search capability, making it well-suited for discrete optimization problems | Suffers from slow convergence, is prone to local optima, and is parameter-intensive |
| Parameter | Value | |
|---|---|---|
| FCS | 20 kW | |
| 85 kW | ||
| 85 kW | ||
| Power ramp rate limit of FCS | ±4.24 kW/s | |
| ESS | Nominal voltage/capacity | 550 V/100 Ah |
| 110 kW | ||
| 90% | ||
| 30% | ||
| 80% |
| The Hydrogen Consumption (g) | Cost (USD) | |
|---|---|---|
| FD | 153.33 | 0.691 |
| PSO | 149.91 | 0.676 |
| GA-PSO | 146.30 | 0.658 |
| Algorithm | Batt1 SOC (%) | Batt2 SOC (%) | Batt1 Cycle Life (Day) | Batt2 Cycle Life (Day) |
|---|---|---|---|---|
| FD | 79.71 | 79.45 | 8704 | 8683 |
| PSO | 79.68 | 79.43 | 8702 | 8680 |
| GA-PSO | 79.65 | 79.40 | 8700 | 8678 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, P.; Xu, J. State-Aware Energy Management Strategy for Marine Multi-Stack Hybrid Energy Storage Systems Considering Fuel Cell Health. Energies 2025, 18, 3892. https://doi.org/10.3390/en18153892
Geng P, Xu J. State-Aware Energy Management Strategy for Marine Multi-Stack Hybrid Energy Storage Systems Considering Fuel Cell Health. Energies. 2025; 18(15):3892. https://doi.org/10.3390/en18153892
Chicago/Turabian StyleGeng, Pan, and Jingxuan Xu. 2025. "State-Aware Energy Management Strategy for Marine Multi-Stack Hybrid Energy Storage Systems Considering Fuel Cell Health" Energies 18, no. 15: 3892. https://doi.org/10.3390/en18153892
APA StyleGeng, P., & Xu, J. (2025). State-Aware Energy Management Strategy for Marine Multi-Stack Hybrid Energy Storage Systems Considering Fuel Cell Health. Energies, 18(15), 3892. https://doi.org/10.3390/en18153892






