Approaches to Proxy Modeling of Gas Reservoirs

Abstract

In the gas industry, accurate forecasting of gas production is critical for optimizing well operating conditions. Although traditional hydrodynamic models offer high accuracy, they are often computationally intensive and time-consuming, prompting a growing interest in proxy-based alternatives. This study proposes a hybrid methodology based on Spatio-Temporal Graph Neural Networks (ST-GNNs) for gas production forecasting. The methodology integrates graph neural networks to account for spatial interdependencies between wells with recurrent and convolutional neural networks for time-series analysis. The model was validated using an extensive set of hydrodynamic simulation calculations and real-world field data. On average, the ST-GNN method reduces computational time by a factor of 4.3 compared to traditional hydrodynamic models, with a median predictive error not exceeding 10% across diverse datasets, despite variability in specific scenarios. The ST-GNN framework demonstrates promising potential as a tool for operational and strategic planning.

1. Introduction

Predictive modeling allows subsurface resource companies to anticipate challenges, make more efficient use of resources, and cut both operational and capital costs, contributing to greater business sustainability and profitability [1].

The primary method for forecasting physical parameters of reservoir systems involves the use of hydrodynamic models, which rely on field and geological data derived from well tests, core analysis, and geophysical interpretations. However, this approach demands significant resources for model calibration and computational power, rendering it labor-intensive and costly [2]. Consequently, there is growing interest in proxy models, which provide rapid and efficient forecasting of reservoir behavior without the need for complex simulations [3]. Proxy models are simplified mathematical representations that approximate the behavior of reservoir systems based on available data. They offer an optimal alternative to classical approaches, combining sufficient accuracy with low computational costs, which is particularly critical for the operational identification of optimal development scenarios.

Various approaches exist for classifying proxy models used in forecasting oil and gas production. In the work by Bahrami P. et al. [4], the authors identify four categories of proxy models:

• Multifunctional Models (MFMs): Simplified models that employ coarse discretization to accelerate computations;
• Reduced-Order Models (ROMs): Models that reduce system dimensionality while preserving key physical characteristics;
• Traditional Proxy Models (TPMs): Data-driven models based on numerical simulations, requiring minimal understanding of the underlying physical processes;
• Smart Proxy Models (SPMs): Models leveraging machine learning to enhance accuracy by accounting for complex geological features.

In the study by Cao C. et al. [5], data-driven proxy models are explored, derived from historical field data and categorized into:

• Single Data-Driven Models: These encompass methods based on individual machine learning algorithms, such as multiple linear regression (MLR), support vector regression (SVR), ensemble learning techniques (e.g., random forest and gradient boosting), and neural networks. While these models can yield accurate results, they require meticulous preprocessing of input data to achieve stable performance;
• Combination of Proxy Models: These are developed by utilizing the maximum available data and integrating multiple models into a cohesive solution. Examples include combining neural networks with decision trees or incorporating physical constraints, such as fluid flow equations in porous media, into the model structure.

In the field of oil and gas reservoir development modeling, empirical methods hold a significant place. These approaches, characterized by their accessibility and minimal input data requirements, have long played a key role in evaluating production dynamics and forecasting reserves. In the works by [6,7], Decline Curve Analysis (DCA) is examined in detail. This method involves approximating historical well production rate data using various empirical mathematical models (e.g., modifications of the Arps equation, power-law, or other functional relationships) to extrapolate future productivity and estimate ultimate recoverable reserves. The primary advantages of DCA include its simplicity of implementation and low computational demands. However, the method has notable limitations: it is purely empirical, offering limited linkage to the physical processes occurring within the reservoir, and its application to unconventional reservoirs, characterized by complex filtration mechanisms, often results in significant predictive errors. Moreover, as noted in [7], estimating parameters for DCA models poses a mathematically ill-posed inverse problem, resulting in parameter ambiguity and significant uncertainty in long-term forecasts of recoverable reserves.

The next advancement in proxy modeling tools was the development of Capacitance–Resistance Models (CRMs). This method incorporates for inter-well interactions and reservoir pressure dynamics, overcoming some limitations of purely empirical methods. In the work by Holanda et al. [8], which provides a comprehensive review of this approach, CRM is described as a family of models based on the principle of material balance, analogous to electrical RC circuits. Within the CRM framework, the reservoir is conceptualized as a network of interconnected nodes (wells), where “capacitance” parameters reflect fluid compressibility and volume, and “resistance” parameters characterize filtration connections between wells. The model relies solely on historical injection and production data to determine inter-well influence coefficients and time constants, which represent the delayed response of production to injection. The forecasted production rates of producing wells are modeled as a function of the activity of surrounding injection wells and the operational history. Key advantages of CRMs include their computational efficiency and ability to function without detailed geological information. However, CRMs provide a simplified representation of complex filtration processes, do not directly account for the spatial distribution of reservoir properties, and the accuracy and reliability of their parameters heavily depend on the quality, duration, and informativeness of the available development history data. To address some of these limitations, advanced proxy models have been developed that utilize boundary element methods and automated parameter adaptation to generate accurate reservoir pressure maps and account for two-phase filtration, as demonstrated in a recent study by Yudin et al. [9].

As modeling tasks have grown more complex, the streamline method has emerged, offering a more detailed representation of fluid flow in porous media. In the works by Gross [10] and Thiele et al. [11], an approach based on tracing streamlines in three-dimensional space is presented, enabling efficient modeling of complex heterogeneous systems while accounting for well placement and reservoir filtration-capacity properties. This method decomposes a complex three-dimensional problem into multiple one-dimensional problems along designated fluid flow paths from injection to production wells. Its advantages include high computational efficiency and the ability to link well performance parameters (e.g., production rate, bottomhole pressure) with static reservoir properties (e.g., porosity, permeability) through the time-of-flight variable. However, limitations include the simplification of flow physics, which restricts the method’s applicability for modeling reservoir development under significant changes in operating conditions.

A distinct approach involves the integration of deterministic and probabilistic methods, particularly those based on Markov Chain Monte Carlo (MCMC) techniques. In the work by Goodwin et al. [12], a methodology is described that entails conducting multiple hydrodynamic simulations with varying pressure and filtration-capacity property parameters to generate production data. Based on these data, a set of proxy models (e.g., radial basis functions or Gaussian processes) is constructed for each well or time step. Each proxy model is trained to predict production based on specified parameters while providing a confidence estimate for its predictions. Subsequently, the Hamiltonian MCMC algorithm is employed to identify the parameter set that best matches historical production data. For each combination of proxy models, production values for past periods are calculated and compared with actual historical data using a likelihood function to select the most suitable parameter sets. The selected proxy model parameters are then used to forecast future production. The results are aggregated to form an S-curve, illustrating the probabilistic distribution of future production. To validate the models’ performance, several scenarios from this curve are selected, and full-scale hydrodynamic simulations are performed. If the simulation results align with the proxy model forecasts, the process is considered complete; otherwise, the proxy models are refined with additional data, and the MCMC algorithm is rerun until the forecasts achieve sufficient accuracy. This approach significantly reduces computational costs while maintaining statistical reliability of the forecasts, though it requires careful tuning of hyperparameters and rigorous validation.

The advancement of machine learning technologies and techniques, which partially integrate the principles of the approaches described earlier, has driven the emergence of proxy models based on these methods. A more detailed review of relevant studies is presented in

Table A1. Approaches to proxy modeling of oil and gas production processes based on machine learning algorithms.

Study Title	Research Objective	Methodology	Advantages	Disadvantages	Application Features
Data-driven approach for hydrocarbon production forecasting using machine learning techniques [22]	Compare various algorithms, including random forest, gradient boosting, and artificial neural networks, for the evaluation and prediction of daily oil production using data from the Norwegian Volve field as a case study.	Data analysis and preprocessing were performed, including data filtering to address missing values, correction of anomalies, and normalization. Based on Pearson correlation coefficients, key parameters were selected: well pressure, average choke size, volume of injected water, and daily production volume. The tuning of hyperparameters for each machine learning algorithm is described: for random forest, the depth and number of trees were adjusted; for gradient boosting, the learning rate and loss criterion were optimized; and for artificial neural networks (ANNs), activation functions and the number of neurons in hidden layers were selected. The final evaluation of model accuracy was conducted using the metrics MSE, MAE, and the coefficient of determination (R2).	The method does not require detailed physical-mathematical simulation of the reservoir; it effectively handles missing data, well shut-in periods, and complex nonlinear relationships.	The accuracy of the models depends on the quality and quantity of data; challenges arise in tuning hyperparameters; the need for individual algorithm selection for each well is evident, with ANN demonstrating the highest accuracy for one well, while random forest performed best for another.	With a large volume of historical data, machine learning models can complement classical methods of historical analysis and reservoir development modeling to enable rapid forecasting.
Machine Learning-Based Production Prediction Model and Its Application in Duvernay Formation [23]	This study examines proxy models based on machine learning for forecasting hydrocarbon production in the Duvernay shale basin, Canada. The research focuses on developing and evaluating the accuracy of three predictive models—MLR, SVR, and GPR—using a range of variables, including geological and technological well parameters.	Based on Grey Relational Analysis and Pearson correlation, key parameters were selected: volume of injected fluid, number of hydraulic fracturing stages, gas saturation, and total organic carbon, which significantly influence cumulative gas and condensate production. During model development, the authors split the dataset into training and testing subsets, employed four-fold cross-validation, and applied Bayesian optimization to tune the hyperparameters of SVR and GPR models,	The GPR model demonstrated the best performance, achieving an R2 of 0.8 for gas and 0.83 for condensate, with RMSE values of 280.54 × 104 m3 and 1884.3 t, respectively, indicating high predictive accuracy. The model is capable of operating with small datasets, making it suitable for fields with limited operational history.	All models require high-quality, preprocessed data to ensure accurate hyperparameter tuning.	The necessity of data preprocessing and the limited applicability to shale reservoirs with similar characteristics.
Smart Proxy Modeling of a Fractured Reservoir Model for Production Optimization: Implementation of Metaheuristic Algorithm and Probabilistic Application [24]	Development and demonstration of SPM based on ANN for optimizing hydrocarbon production from fractured reservoirs using metaheuristic algorithms and probabilistic analysis.	Construction of a synthetic model of a fractured reservoir using the dual-porosity dual-permeability (DPDP) method; training of ANN with backpropagation algorithms (SGD, Adam) and the metaheuristic PSO algorithm.	Significant reduction in computational time (50–120 s compared to 160–290 s for numerical modeling); high predictive accuracy (R2 > 0.99); ability to integrate metaheuristic algorithms and probabilistic analysis to enhance forecast reliability.	The model’s performance is limited in scenarios not covered by the training dataset; it is dependent on the quality of the spatio-temporal database.	Requires preliminary data normalization; applicable only to fractured reservoirs with similar characteristics.
Application of Machine Learning Method of Data-Driven Deep Learning Model to Predict Well Production Rate in the Shale Gas Reservoirs [25]	Development and validation of a proxy model based on machine learning methods (DNN) for forecasting cumulative gas production from shale reservoirs, using real data from the Montney Formation, Canada.	A deep neural network approach based on a multilayer perceptron was employed. Preliminary data analysis and variable importance analysis were conducted using Random Forest, Gradient Boosting Machine, and XGBoost. Dimensionality reduction was performed via Principal Component Analysis, and hyperparameter optimization (including one-hot encoding, ReLU activation, dropout, and others) was carried out based on data from 1150 wells.	Significant reduction in computational time compared to numerical modeling; high predictive accuracy (MAPE up to 22.14%); ability to integrate categorical and numerical data for the analysis of shale reservoirs.	Limited applicability in the absence of sufficient data volume or changes in geological conditions; dependence on the quality of input data and the accuracy of its preprocessing; lack of consideration for time-series data.	Requires thorough data preprocessing (normalization, outlier removal); applicable to horizontal wells with multistage hydraulic fracturing; recommended to perform sensitivity analysis of hyperparameters for model adaptation.
Forecasting oil production in unconventional reservoirs using long short term memory network coupled support vector regression method: A case study [26]	Development of a hybrid LSTM-SVR model for forecasting oil production in low-permeability reservoirs, incorporating time-series and operational parameters, and enhancing predictive accuracy through residual connections.	A hybrid LSTM-SVR model was employed: LSTM for initial production forecasting, SVR for predicting residuals, followed by correction of the LSTM forecast; data from the Ma-18 block of the Xinjiang field (two wells, 1182 and 1186 data points) were used; data preprocessing included Z-score normalization and imputation of missing values.	High predictive accuracy (RMSE up to 0.94); incorporation of time-series and operational parameters; effective residual correction via SVR improves forecasting with limited data.	Prediction error increases with longer forecasting horizons; high sensitivity to abrupt changes in operational parameters; complexity in hyperparameter tuning.	Requires thorough data preprocessing (normalization, imputation of missing values); applicable to low-permeability reservoirs with significant intra-reservoir heterogeneity.
Predicting field production rates for waterflooding using a machine learning-based proxy model [27]	Development and implementation of a proxy model based on a conditional deep convolutional generative adversarial network (cDC-GAN) for rapid calculation of dynamic fluid distribution and forecasting production volumes during water injection as a secondary oil recovery technique.	A cDC-GAN model was employed, comprising generative and discriminative components. Input data included reservoir properties (permeability distribution) and forecast time, with water saturation as the output; data were generated using geostatistical methods and the numerical simulator. Production rate calculations were based on the material balance principle.	Significant reduction in computational costs compared to numerical modeling; high predictive accuracy for water saturation and total fluid production (SSIM ≥ 0.96); ability to use raw input data without preliminary feature processing.	Limited extrapolation capability (error increases after three years); inability to separate production rates by individual wells; inability to adapt to abrupt changes, such as water breakthrough.	Applicable to 2D models for waterflooding; requires large datasets for training; recommended to incorporate additional geological and operational parameters to enhance accuracy.
Highly accurate oil production forecasting under adjustable policy by a physical approximation network [28]	Development of a neural network model for accurate forecasting of oil production, accounting for variable field development strategies, using a dynamic graph-based approach that incorporates physical processes occurring in the reservoir.	A Double-channel Heterogeneous Dynamical Graph network model was proposed; input data comprised historical production data, geological parameters, and control variables (injection and production fluid rates); the graph structure included wells as nodes and reservoir conditions between wells as edges; training was conducted on synthetic Egg and Brugge datasets (2400 days), validation on 10 days, and forecasting for 600 days, with comparisons against LSTM and the Eclipse simulator.	High forecasting accuracy incorporating physical processes (MSE ~ 1.15 × 10−5 for Egg, 2.35 × 10−5 for Brugge); significant reduction in computational time; automated training without manual tuning; ability to adapt to changing field development strategies.	Tested only on sandstone reservoirs, with applicability to carbonate reservoirs unconfirmed; reduced accuracy for forecasts beyond 600 days; sensitivity to insufficient reservoir energy.	Requires significant modifications to historical data for training; accounts for spatio-temporal dependencies.

(Appendix A).

The reviewed studies on machine learning-based proxy models demonstrate high computational speed and the ability to process large datasets. However, these models are not adapted to diverse development conditions and often fail to account for the physical aspects of processes. These limitations restrict their use as tools for long-term forecasting and reservoir development analysis. A potential solution to these challenges is a hybrid approach that combines various methods, providing a unified solution that integrates the advantages of machine learning with physically grounded models.

Table A2. Hybrid approaches to proxy modeling of oil and gas production processes.

Study Title	Research Objective	Methodology	Advantages	Disadvantages	Application Features
CO2 EOR Performance Evaluation in an Unconventional Reservoir through Mechanistic Constrained Proxy Modeling [29]	Evaluation of CO2 injection efficiency in unconventional reservoirs using a deep neural network to develop proxy models for forecasting oil production, incorporating reservoir characteristics and hydraulic fracturing parameters.	A 3D model with dual porosity and hydraulic fracturing was constructed; physical constraints were incorporated using data obtained from comprehensive numerical modeling; input data included reservoir pressure, matrix permeability, fracture permeability, and FCD; output data consisted of the oil recovery factor; the dataset comprised 396 simulations; the DNN model featured 10 hidden layers, over 1500 neurons, ReLU activation, Adam optimizer, and k-fold cross-validation; forecasts were made for 5 and 10 years.	High forecasting accuracy (R2 > 0.95); rapid generation of proxy models; reduced computational time compared to traditional simulations.	Limited accuracy at high fracture permeability and FCD values (underestimation); applicability restricted to unconventional reservoirs with low permeability; requires a large volume of data for training.	Applicable to unconventional reservoirs with low permeability; optimal for medium pressures; requires data normalization; sensitive to the quality of input data.
A Physics-Informed Neural Network Approach for Surrogating a Numerical Simulation of Fractured Horizontal Well Production Prediction [30]	Development of a PIED neural network to replace numerical simulations in forecasting production from horizontal wells with unequally spaced intersecting hydraulic fractures, incorporating physical constraints.	A PIED architecture based on Seq2Seq (LSTM-LSTM) was developed; input data included fracture length, permeability, and dip angle; the dataset comprised 500 simulations (10 fractures); the decoder’s intermediate input was production time; comparisons were made with MLP and LSTM-Attention-LSTM models.	High accuracy (MAE 168.81, error 2.7%); ability to operate with small datasets (500 samples over 3 days); incorporation of physical constraints; reduction in error accumulation; effective handling of high-dimensional data (30 variables).	Limited incorporation of physical information (only fracture geometry and production time); unverified applicability for a large number of fractures (>10); potential overfitting with increased data dimensionality.	Applicable to horizontal wells with intersecting fractures; requires data normalization; optimal for sequential data; sensitive to the order of fractures.
A physics-constrained long-term production prediction method for multiple fractured wells using deep learning [31]	Long-term forecasting of oil production from wells with multiple hydraulic fracturing operations under conditions of limited data and complex geological structures.	Development of a hybrid BiGRU-DHNN model combining bidirectional gated recurrent unit neural networks for time-series production analysis and a deep hybrid neural network to incorporate physical constraints; input data included well depth, horizontal section length, number of hydraulic fracturing stages, sand volume, fluid volume, gamma-ray logging, acoustic logging, reservoir resistivity, tubing pressure, choke sizes, and oil production.	Reduced forecasting errors: RMSE and MAE values of 5.4 and 4.2, respectively (compared to 10–15 for models without constraints), with R2 = 0.46 (compared to 0.2–0.3 for models without constraints); ability to capture complex relationships between production and system input parameters.	Error accumulation in iterative strategies: error increases with longer forecasting horizons (e.g., high accuracy in the first year, but deviations reach 20–30% by the third year); dependence on data volume (requires at least 11 wells for training).	Requires data normalization; applicable to wells with known hydraulic fracturing parameters.
A Physics-Informed Spatial-Temporal Neural Network for Reservoir Simulation and Uncertainty Quantification [32]	Modeling of reservoir development and quantitative assessment of uncertainties in oil production in heterogeneous reservoirs.	The PI-STNN model integrates a deep convolutional encoder–decoder for processing spatial data and a convolutional LSTM (ConvLSTM) to account for temporal dependencies; input data include permeability, porosity, pressure (initial reservoir, bottomhole, and average), oil viscosity, oil density, grid dimensions, time step, and production; physical constraints are incorporated by embedding partial differential equations describing fluid filtration in porous media into the loss function, with the Pisman formula used as the governing equation.	High accuracy: median R2 values range from ~0.95 (10 fractures) to ~0.9 (62 fractures), with a range of 0.85–1.0; accelerated computations, with 12,008.9 s compared to 237,504.2 s for traditional simulators.	Limited to single-phase flow; complexity in adapting to multiphase and multicomponent systems.	Applicable to heterogeneous reservoirs with fractures; effective for uncertainty analysis and NPV calculations.

(Appendix A) presents studies focused on the implementation of proxy models for oil and gas field development based on a hybrid approach.

2. Materials and Methods

Based on the analysis of the existing literature, this study adopts a hybrid approach to develop a proxy model for forecasting well production using operational parameters (bottomhole pressure and well operating time) and the spatial arrangement of wellbores.

A graph-based architecture is proposed to model the spatial relationships between wells and their mutual influence on production, while recurrent and convolutional neural networks are employed to model time-series data. These principles are characteristic of a class of neural networks known as Spatio-Temporal Graph Neural Networks. The essence of ST-GNNs lies in representing data as a graph, where nodes correspond to entities (wells) and edges represent spatial connections between them. Temporal dynamics are captured by analyzing changes in node characteristics over time. ST-GNNs combine graph convolutional operations to aggregate information from neighboring nodes with time-series processing techniques to capture temporal variations [13].

The model input consists of time-series data processed through three LSTM layers with ReLU activation functions between them to extract long-term temporal dependencies, and seven Conv1D layers with ReLU activation functions to capture short-term dependencies. The outputs are concatenated, normalized using BatchNorm, and regularized via Dropout. The processed information, along with the connectivity matrix, is fed into SpatialConv layers—graph convolutional layers that account for spatial dependencies between wells. Each convolution is followed by a ReLU activation function and Dropout regularization. Subsequently, fully connected (FC) layers with ReLU activation functions transform the input features and generate the model output–production values for each well at a given time step. Figure 1 illustrates the schematic workflow of the described ST-GNN model.

For the LSTM layers, an input sequence $X={\{X}_1,{ X}_2,\dots ,{ X}_T\}$, where $X_t\in {\mathbb{R}}^{N\times C}$ for each time step $t=1,2,\dots ,T$, is processed to compute the hidden state $h_t\in {\mathbb{R}}^{N\times H}$ and cell state $c_t\in {\mathbb{R}}^{N\times H}$ as follows [14]:

$$f_t =\sigma \left(W_f ·\left[h_{t-1} ,X_t\right]+b_t\right),$$

(1)

$$i_t=\sigma \left(W_i ·\left[h_{t-1} ,X_t\right]+b_i\right),$$

(2)

$$o_t=\sigma \left(W_o ·\left[h_{t-1} ,X_t\right]+b_o\right),$$

(3)

$$\widetilde{c_t}=\mathit{tanh}\left(W_c ·\left[h_{t-1} ,X_t\right]+b_c\right),$$

(4)

$$c_t=f_t \odot { c}_{t–1}+i_t \odot \widetilde{c_t} ,$$

(5)

$$h_t=o_t\odot \mathit{tanh}\left(c_t\right),$$

(6)

where N is the number of nodes in the graph, T is the number of time steps, C is the number of input channels, H is the hidden size $f_t$, $i_t$, $o_t$ are the forget, input, and output gates, $\widetilde{c_t}$, $c_t$ are the candidate and final cell states, $W_f$, $W_i$, $W_o$, $W_c$ are trainable weight matrices, $b_t$, $b_i$, $b_o$, $b_c$ are biases, $\sigma$ is the sigmoid activation function, $\mathit{tanh}$ is the hyperbolic tangent, and $\odot$ denotes element-wise multiplication. The output $h_t$ is then passed through a ReLU activation.

For the Conv1D layers, an input sequence $X={\{X}_1,X_2,\dots ,X_T\}$, where $X_t\in {\mathbb{R}}^{N\times C}$ for each time step $t=1,2,\dots ,T$ is processed with a kernel $K\in R^{C\times C_{\mathit{out}}\times K_s}$ to produce an output sequence $Y={\{Y}_1,{ Y}_2,\dots ,Y_{T^{\prime }}\}$, where $Y_t\in {\mathbb{R}}^{N\times C_{\mathit{out}}}$ as follows [15]:

$$Y_{i,j,t}=\sum _{c=1}^C\sum _{k=1}^{K_s}{ X}_{i,c,t+k–1} \cdot K_{c,j,k}+{ b}_j,$$

(7)

where $C_{\mathit{out}}$ is the number of output channels, $K_s$ is the kernel size, $T^{\prime }$ is the number of output time steps (dependent on padding and stride), ${ Y}_{i,j,t}$ is the output for the i-th node, j-th output channel, and time step t, ${ K}_{c,j,k}$ is the kernel weight for input channel c, output channel j, and kernel position k, and $b_j$ is the bias. Each convolution is followed by a ReLU activation.

For the SpatialConv layers, the input features $H^l\in {\mathbb{R}}^{N\times D}$, obtained by concatenating LSTM and Conv1D outputs and averaging over time steps, are processed via graph convolution as follows [16]:

$$H^{(l+1)}=\mathit{ReLU}\left({\tilde{D}}^{–\frac{1}{2}}\tilde{A}{\tilde{D}}^{–\frac{1}{2}}{H}^{\left(l\right)}{W}^{(l+1)}\right),$$

(8)

where D is the number of features, $\tilde{A}=A+I$ is the adjacency matrix with self-loops (I the identity matrix), ${\tilde{D}}_{\mathit{ii}}={\sum }_j{\tilde{A}}_{\mathit{ij}}$ is the degree matrix, $W^{(l+1)}$ is a trainable weight matrix, and ReLU is the activation function.

For the fully connected layers, an input tensor $X\in {\mathbb{R}}^{N\times D}$ is processed as follows [17]:

$$Y=\mathit{XW}+b,$$

(9)

where W is the trainable weight matrix, b is the bias, Y is the output. The first layer is followed by a ReLU activation, and the second maps to the predicted time steps.

Each model was trained and tested on various scenarios and variants of hydrodynamic models (HMs). Training utilized results from a hydrodynamic simulator, while field data were processed using wavelet transformation to eliminate noise introduced by sensors and instruments [18]. An example of the filter’s performance for one of the wells is shown in Figure 2.

The model receives input data in the form of time-series information, including:

1. Bottomhole pressure $P_{\mathit{bh}}$;

2. Bottomhole pressure change:

$$∆P_{\mathit{bh}}=P_{{\mathit{bh}}_t }– P_{{\mathit{bh}}_{t–1}},$$

(10)

where $t$—current time step; $t-1$—previous time step;

3. Change in well operating time:

$$∆O=O_t-O_{t–1},$$

(11)

where $O$—cumulative operating time of the well.

The model also receives an adjacency matrix as input, which characterizes the degree of interaction between wells based on their geometric arrangement relative to each other. In studies by Ngoc et al. [19] and Xu et al. [20], the influence coefficient of graph node i on node j is determined by the formula:

$${\alpha }_{\mathit{ij}}=\left\{\begin{array}{c}{e}^{-\frac{{{\mathit{dist}}_{\mathit{ij}}}^2}{\sigma }}, if { e}^{-\frac{{{\mathit{dist}}_{\mathit{ij}}}^2}{\sigma }} \ge K,\\ 0, otherwise\hfill \end{array}\right.$$

(12)

where ${\mathit{dist}}_{\mathit{ij}}$—distance between nodes i and j; $\sigma$—standard deviation of distances between all nodes; $K$—sparsity threshold value.

However, this approach relies on the statistical characteristics of distance distributions, where the key factor is not the absolute magnitude but their relative distribution, determined by the standard deviation parameter $\sigma$. Consequently, when distances between all nodes are small (e.g., less than 1000 m), the values of ${\alpha }_{\mathit{ij}}$ remain relatively low, which is interpreted as weak connectivity between nodes. However, in the general case, absent hydrodynamic barriers, closely located wells typically exhibit stronger interactions. Therefore, it is proposed to determine the influence coefficient of well i on well j using the formula:

$${\alpha }_{\mathit{ij}}=\left\{\begin{array}{c}{e}^{-\frac{d_{\mathit{ij}}}{d_0}}, if i \ne j\\ e^{-\frac{d_{\mathit{self}}}{d_0}}, if i=j\end{array}\right.,$$

(13)

where $d_{\mathit{ij}}$—distance between wells i and j; $d_0$—characteristic decay length of the connection; $d_{\mathit{self}}$—parameter defining the influence of a well on itself.

The parameters $d_0$ and $d_{\mathit{self}}$ are hyperparameters of the model and are selected empirically: various values are tested during experiments, and the optimal configuration is chosen.

Table 1. Datasets used for training and testing the models.

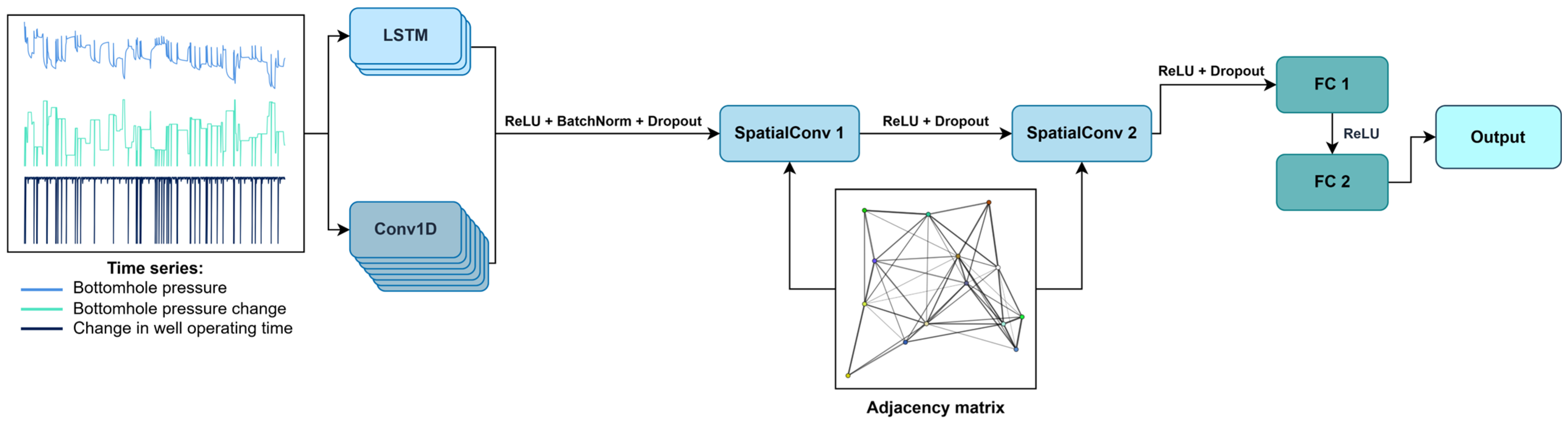
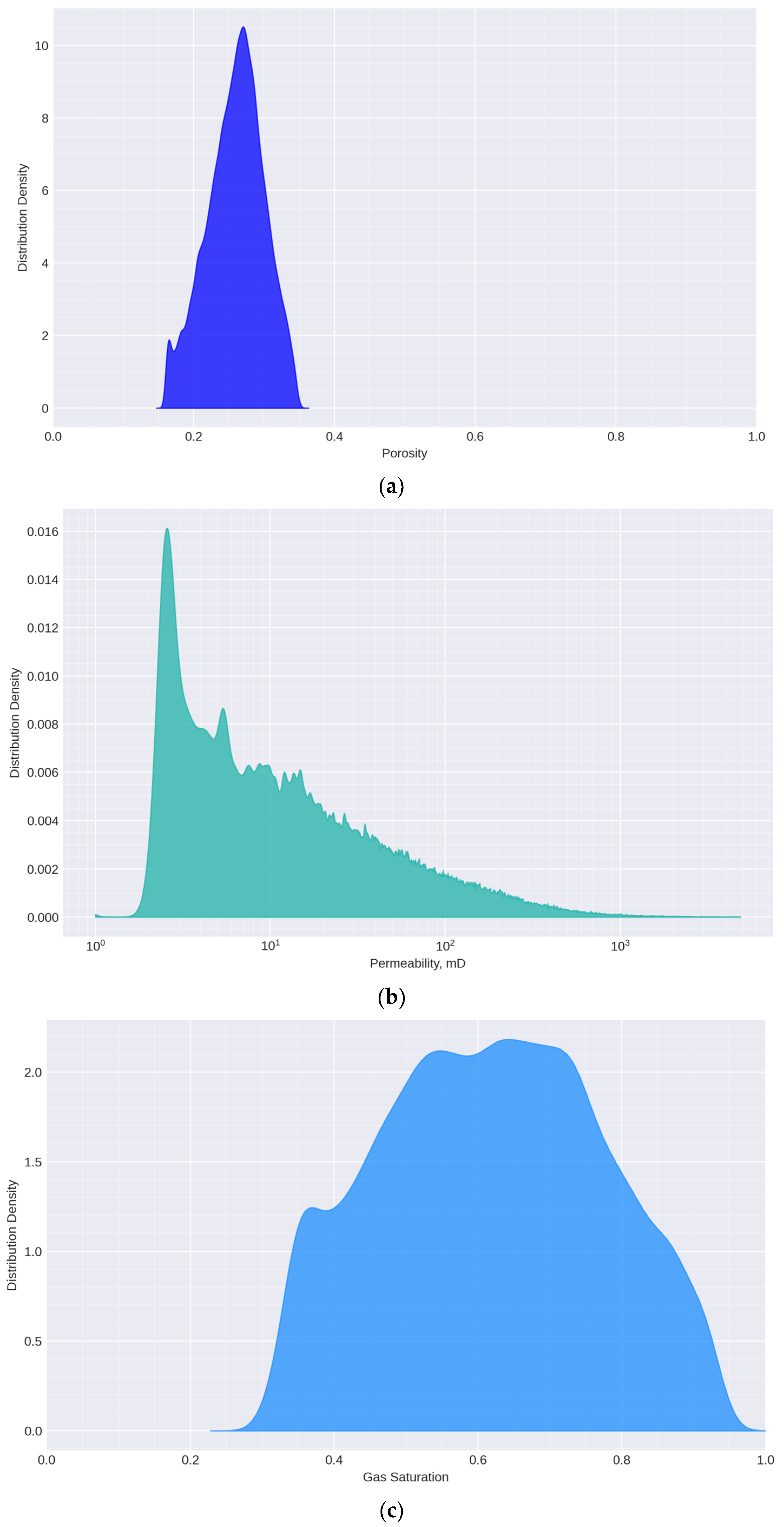
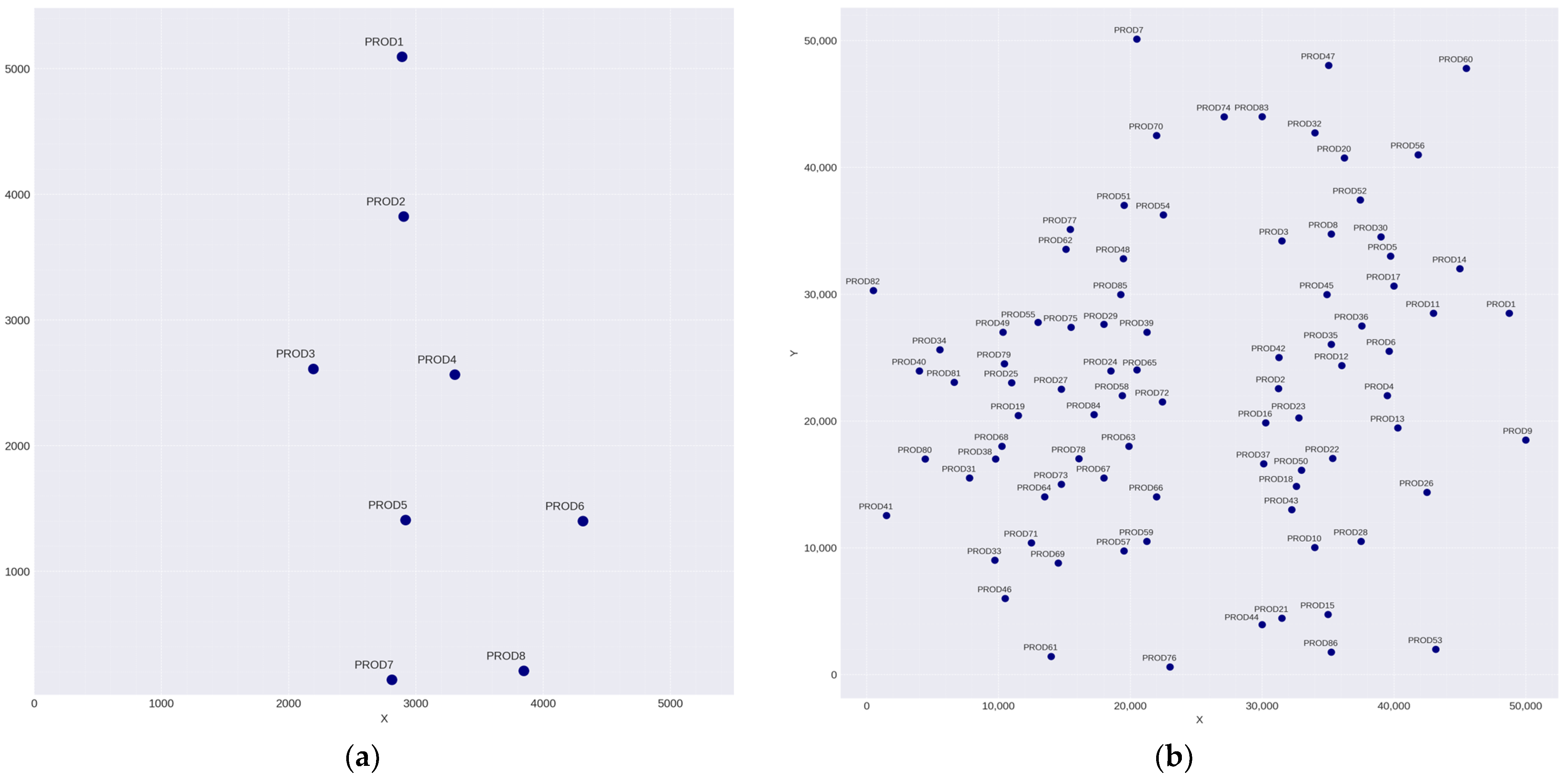
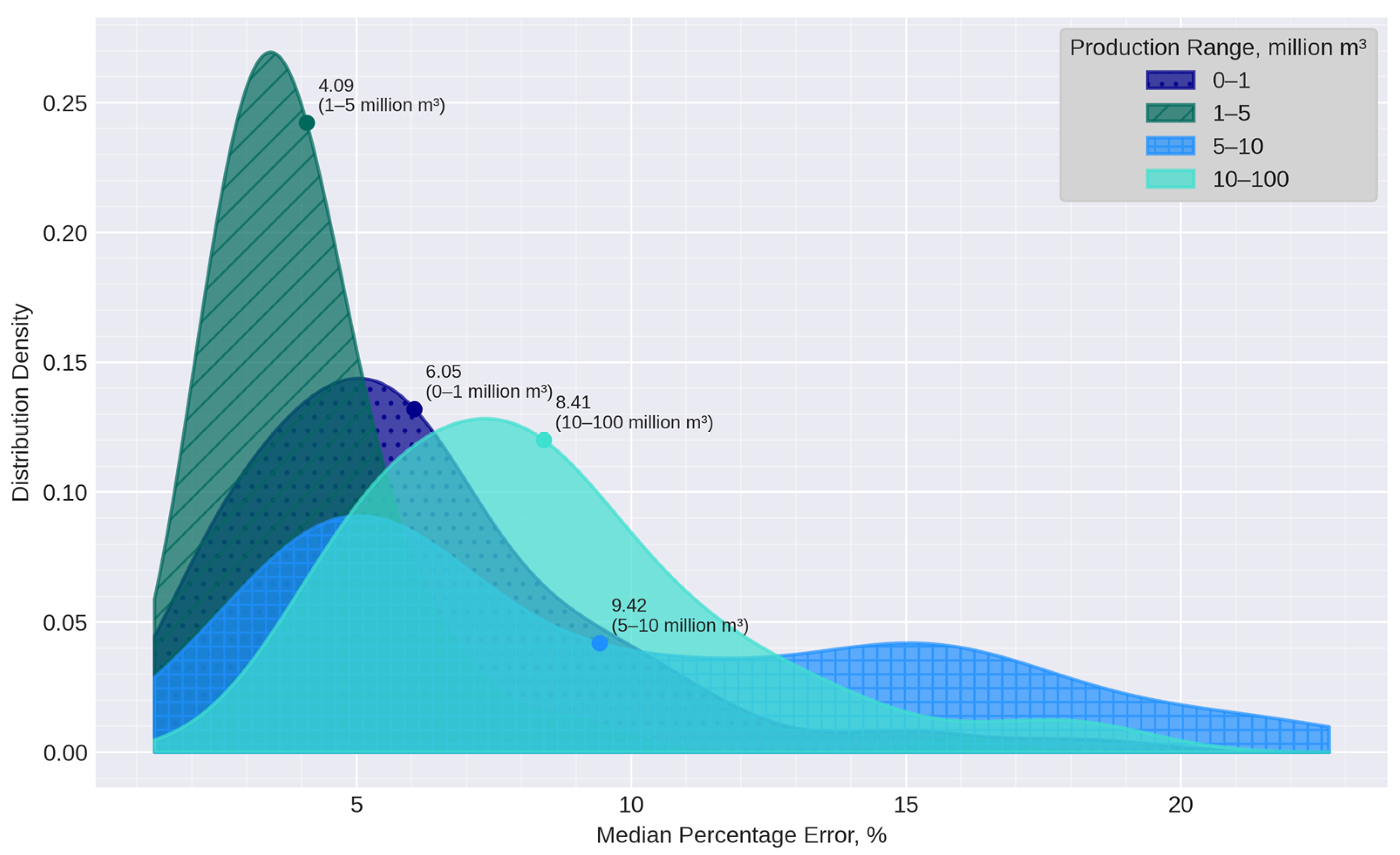
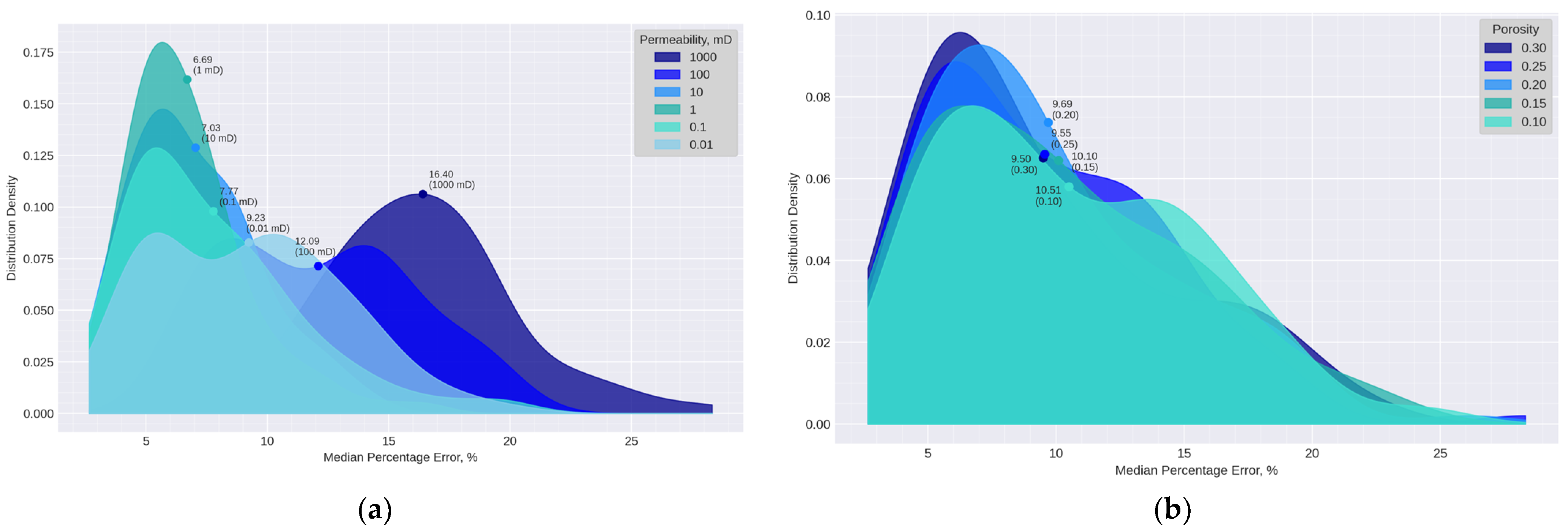
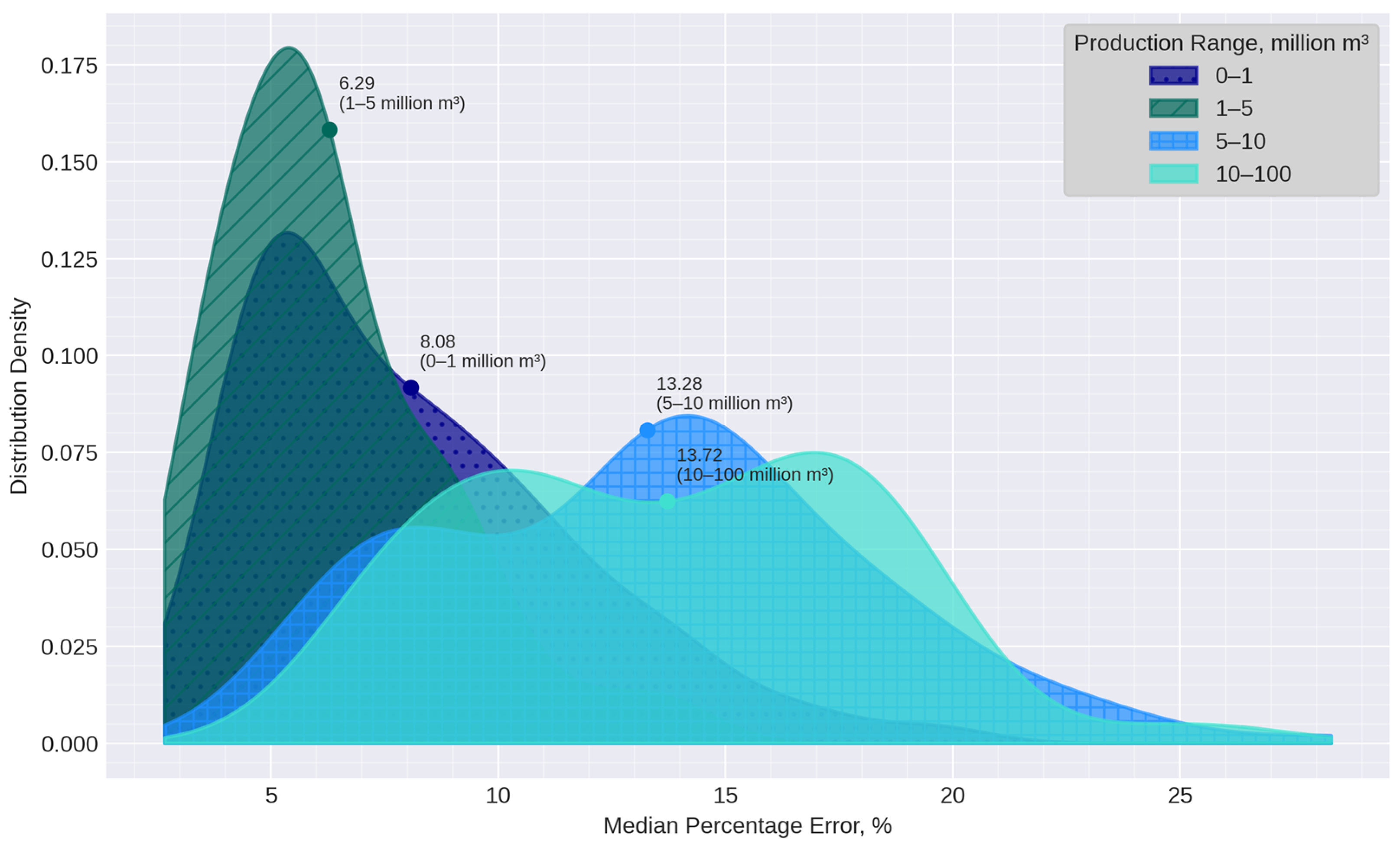
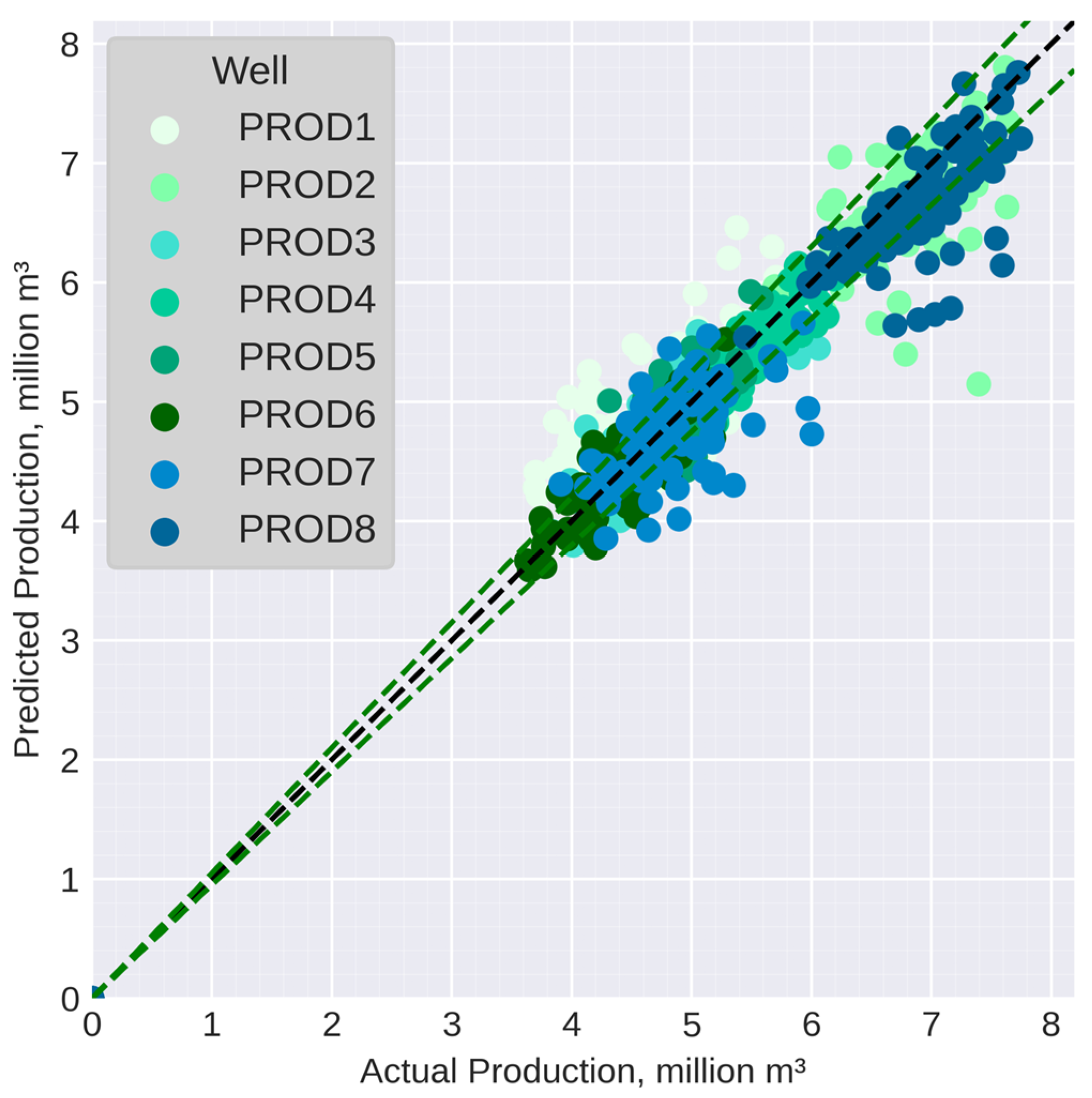
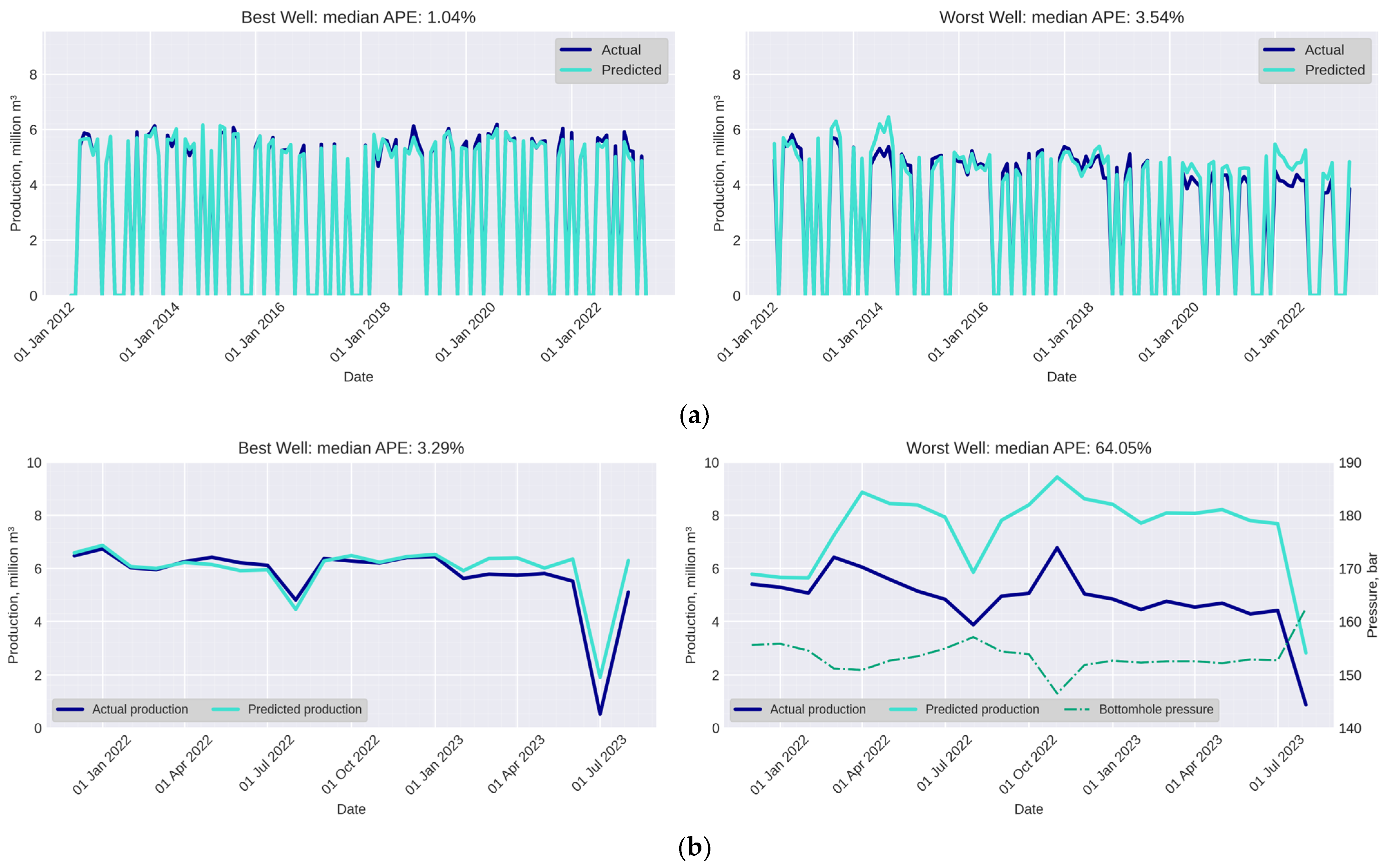
Dataset	Data Source	Entity	Distribution
Distantly located wells	Results of hydrodynamic simulator calculations on an artificial HM.	Two wells located 15 km apart (homogeneous geological properties).	• training set—15,120 simulations; • validation set—540 simulations; • test set—540 simulations.
Closely located wells	Results of hydrodynamic simulator calculations on an artificial HM.	Two wells located 1 km apart (homogeneous geological properties).	• training set—15,120 simulations; • validation set—540 simulations; • test set—540 simulations.
HM of the field	Results of hydrodynamic simulator calculations on the field’s HM.	Irregular grid of 8 wells (heterogeneous geological properties) penetrating a single hydrodynamically connected system.	• training set—23 simulations; • validation set—1 simulation; • test set—1 simulation.
Real data from sensors	Data from field sensors and devices.	Irregular grid of 86 wells (heterogeneous geological properties) penetrating a single hydrodynamically connected system.	• training set—89 measurements; • validation set—8 measurements; • test set—21 measurements.

provides information on the datasets used for training and testing the proposed ST-GNN model.

Hydrodynamic models for “Distantly located wells” and “Closely located wells” were developed with varying sets of parameters:

• permeability—0.01 mD; 0.1 mD; 1 mD; 10 mD; 100 mD; 1000 mD;
• porosity—0.10; 0.15; 0.20; 0.25; 0.30;
• initial gas saturation—0.8; 0.9;
• gas viscosity under reservoir conditions—0.01 mPa∙s; 0.03 mPa∙s; 0.05 mPa∙s;
• gas supercompressibility factor (z-factor) under reservoir conditions—0.7; 0.8; 0.9.

Thus, the total number of HMs for each of the two datasets amounted to 540. For each HM, simulations were performed for 30 different scenarios of well operating condition changes during development, resulting in a total of 16,200 simulations.

Figure 3 illustrates the distributions of key geological properties for the “HM of the field” dataset. The deposit type is layered, and the reservoir type is terrigenous porous.

The simulations covered a wide range of well operating regimes, including periods of operation at varying bottomhole pressures, shut-ins, and subsequent restarts. This data generation approach enabled the ST-GNN model to be trained to account for not only the internal dynamics of individual wells but also to effectively recognize the mutual influence of wells on each other.

For the “Real data from sensors” dataset, the deposit type is also layered, and the reservoir type is terrigenous porous. However, the distribution of geological properties is not provided, as a geological model for this case is absent.

For all datasets, the time-series data interval was set to one month. The forecasting horizon for the “HM of the field” dataset is 140 months, while for the “Real data from sensors” dataset, it is 21 months.

Figure 4 presents a map of the bottomhole locations of production wells for the datasets based on the field’s HM and real data from sensors.

Hydrodynamic simulations were performed using commercial reservoir simulation software, which employs a finite volume method to discretize the governing equations [21]. The software uses implicit numerical schemes for stability and applies a Cartesian grid for spatial discretization. The described ST-GNN model was implemented in Python (version 3.11.13) using the PyTorch library (version 2.6.0).

The model architecture for all datasets comprises LSTM, Conv1D, SpatialConv, and fully connected blocks. The LSTM block consists of three sequential LSTM layers with 128, 256, and 128 neurons, respectively. The Conv1D block includes seven sequential layers with neuron counts of 32, 64, 128, 256, 128, 64, and 32, each with a kernel size of 3 and padding of 1. The two SpatialConv layers have a hidden size of 300 neurons and an output size of 160 neurons. The fully connected layer has a hidden size of 320 neurons. The model was trained using the MSE loss function and the AdamW optimizer. Data preprocessing involved standardization and structuring the input as sequences. The sequence length, the learning rate, and the weight decay, specific to each dataset, are presented in

Table 2. Hyperparameters used in model training.

Dataset	Sequence Length	Learning Rate, 10−4	Weight Decay, 10−5
Distantly located wells	20	3	1
Closely located wells	20	3	1
HM of the field	7	5	10
Real data from sensors	7	5	1

.

3. Results and Discussion

Figure 5 and Figure 6 present the results of the ST-GNN model for the case of distantly located wells, showing the distribution of the median percentage error in production forecasting, grouped by permeability, porosity, and well production rates.

From Figure 5a, it is evident that forecasts for HM data with permeabilities of 0.01 mD and 1000 mD exhibit higher median percentage errors compared to other cases. The case with 1000 mD is likely associated with increased well interconnectivity, while the case with 0.01 mD is related to near-zero absolute gas production values. No similar patterns were observed for other parameters, such as porosity, initial gas saturation, gas viscosity, or gas supercompressibility factor under reservoir conditions (as exemplified by the grouping by porosity in Figure 5b).

Figure 6 illustrates the distribution of the median percentage error for the dataset with distantly located wells, grouped by gas production range.

From Figure 6, it is evident that for cases with high monthly well production rates (ranges of 5–10 million m³ and 10–100 million m³), the median percentage error increases. This is likely attributed to the high permeability values for these cases, the impact of which was discussed earlier.

Figure 7 and Figure 8 present the results of the ST-GNN model for the case of closely located wells, showing the distribution of the median percentage error in production forecasting, grouped by permeability, porosity, and well production rates.

The results shown in Figure 7 are similar to those presented in Figure 5: permeability is the primary factor influencing the model’s performance, with higher permeability values leading to increased forecasting errors. Figure 6 supports the earlier hypothesis: as well interconnectivity increases, the model’s predictive accuracy declines—median percentage errors are higher for closely spaced wells than for distant ones.

Figure 8 illustrates the distribution of the median percentage error for the dataset with closely located wells, grouped by gas production range.

The results in Figure 8 are identical to those in Figure 6—for cases with high monthly well production rates (ranges of 5–10 million m³ and 10–100 million m³), the median percentage error is higher than for other groups (0–1 million m³ and 1–5 million m³).

Figure 9 presents the distribution of cumulative percentage errors for both closely and distantly located wells.

Figure 9 further illustrates that as the mutual influence between wells increases, the error in production forecasting rises. With a 15-fold reduction in distance between wells (from 15 km to 1 km), the mean of the cumulative error distribution increases by 1.05% for well PROD1 and by 0.93% for well PROD2. This underscores the need to enhance time-series-based models with refining equations that account for well interactions. To validate the model’s performance on real field data, simulations were conducted and compared with forecasts based on HMs.

Table 3. Accuracy metrics of the ST-GNN model for datasets.

Dataset	Median AE, 103 m3	Max AE, 103 m3	RMSE, 103 m3	Median APE, %	Max APE, %
HM of the field	96	2246	272	1.8	30.3
Real data from sensors	819	15,942	1190	9.8	345

Median AE—median absolute error; max AE—maximum absolute error; RMSE—root mean square error; median APE—median absolute percentage error; max APE—maximum absolute percentage error.

presents the results of the ST-GNN model for the datasets based on the field’s HM and real data, including mean, median, and maximum values of key metrics. Mean and median values reflect the overall accuracy across all time steps, while maximum values indicate the largest deviations between forecasted and actual values, where actual values for the “HM of the field” dataset are derived from simulator calculations, and for the “Real data from sensors” dataset, they are obtained from sensors and instruments.

Figure 10 and Figure 11 present a cross-plot (actual vs. predicted) for each well in the dataset based on the field’s HM (Figure 10), as well as time-series plots of actual and forecasted production values for the wells with the worst and best prediction accuracy (Figure 11).

The changes in production depicted in Figure 11 are associated with variations in well operating conditions, specifically wellhead pressure. A value of 0 indicates a well shut-in.

Based on the data in Table 3, it can be concluded that the performance of the ST-GNN model on real data is inferior to that on synthetic data. However, the overall model performance remains satisfactory. As shown in Figure 11b, the proposed ST-GNN approach accurately captures the temporal dynamics of production changes, albeit with errors in the absolute forecast values. The performance on the field’s HM data is better—error metrics are lower (Table 3, Figure 10), and the model demonstrates a stronger ability to predict the dynamics of production changes (Figure 11a).

These results are primarily attributed to the greater volume and diversity of training data available for HM-based cases compared to real data. Meanwhile, the number of wells in the dataset with sensor data significantly exceeds that in other datasets, which is directly linked to the graph component of the ST-GNN model. As previously discussed, this component critically influences the quality of the results. Additionally, despite the application of wavelet transformation, the use of sensor and instrument data introduces noise and other deviations unrelated to the actual behavior of the hydrodynamic system. For example, Figure 11b shows that between March and April 2022, bottomhole pressure decreased by 0.3 bar, leading to an expected production increase in the ST-GNN model. However, sensor data indicate a production decline of 0.4 million m³. The forecasting error is likely due to inaccuracies in pressure sensor measurements, as the model correctly predicts production growth with decreasing bottomhole pressure, while sensor data suggest otherwise. Errors in production measurements are unlikely, indicating that pressure sensor inaccuracies are the primary cause. Consequently, the model requires accurate bottomhole pressure values for the forecast period, as errors in this parameter can lead to inaccurate production predictions.

Table 4. Computational time of hydrodynamic and ST-GNN models.

Dataset	ST-GNN Speedup Relative to HM Without Training	ST-GNN Speedup Relative to HM with Training
Distantly located wells	20,080	4.8
Closely located wells	20,830	1.7
HM of the field	23,900	6.6
Real data from sensors	–	–

presents the results of computational time measurements for training the ST-GNN model and performing forecasts, compared to simulations on a hydrodynamic simulator.

Based on the obtained results, the following conclusions can be drawn:

1. Across all four datasets, the model demonstrated satisfactory performance in forecasting both the dynamics of production changes and absolute production values. Error analysis indicates that the proposed ST-GNN approach accurately captures the temporal dynamics of production, though it may exhibit errors in absolute values. The largest discrepancies between forecasted and actual values occur during periods of abrupt changes in well operating conditions, likely due to the limited representation of such scenarios in the training data;

2. The graph component of the ST-GNN model plays a critical role in its performance. As the degree of well interconnectivity increases—due to their close proximity or reservoir rock properties—the quality of the results deteriorates;

3. The computational time required to obtain results using ST-GNN is, on average, 4.3 times less than that required by a hydrodynamic simulator.

4. Conclusions

This study proposes and investigates a spatio-temporal model based on graph neural networks for forecasting gas well production performance. The developed approach combines the advantages of deep learning methods with physical interpretation of fluid filtration processes in the reservoir, significantly enhancing forecasting speed compared to traditional hydrodynamic models.

The application of ST-GNN demonstrated notable advantages in adaptability and generalization across data derived from both synthetic models and real fields, particularly under conditions of limited and heterogeneous input data. The proposed method effectively captures dynamic changes in development parameters by constructing connectivity graphs and leveraging recurrent and convolutional neural network architectures. Experimental validation confirms the model’s ability to reproduce complex spatio-temporal dependencies of production influenced by input parameters, including absolute values and variations in bottomhole pressure, as well as changes in well operating time.

Despite these advantages, the proposed approach remains dependent on the quality of input data and requires careful hyperparameter tuning. Future improvements may involve incorporating automated hyperparameter tuning and increasing result interpretability. This would enhance model transparency and help experts understand the impact of geological and operational factors on production forecasts.

From a practical perspective, the developed model is valuable for operational and strategic planning horizons, enabling real-time optimization of well operating conditions for single-phase flow and fixed well grid configurations, followed by validation of the selected scenario using a hydrodynamic simulator to confirm the results. However, its industrial implementation requires regular updates as new data accumulate and adaptation to the specific characteristics of individual fields. Future enhancements to the model are planned, including the incorporation of capabilities to account for the commissioning of new wells.

Furthermore, addressing the incorporation of new wells and planned geological-technical interventions, which are currently absent from the model’s implementation, is critically important for future research. At present, the model is trained for a fixed number of wells and does not support the dynamic addition of interventions post-training.