Abstract
Double-Side-Cooled (DSC) power modules, widely utilized in various industrial and transportation applications, are favored for their remarkable high cooling efficiency and minimal packaging parasitics. To extend the life cycle, the design and optimization of metal or alloy spacers have garnered significant research attention due to their role in mitigating thermal-expansion-mismatch-induced stresses. Among the optimization approaches, topology optimization (TO) methods have the merit of generating innovative spacer shapes, thereby maximizing the buffering effects. However, without certain design considerations and constraints predetermined, the overall processes can become computationally costly. This paper proposes an efficient strategy for finding the optimized spacer topology for a double-sided 1700 V/400 A DSC SiC MOSFET power module. First, comparative thermal-stress investigations are carried out to predetermine the spacer height prior to TOs. Subsequently, to identify the appropriate optimization target, different objectives are employed in the TOs of a 2D simplified model. Following this, TO with the selected target function is performed on 3D simplified models featuring diverse spacer combination architectures, with the preferable one chosen based on the outcomes. Eventually, leveraging the predetermined spacer height, objective function, and preliminary structure, a 3D TO spacer design utilizing a full-domain model is conducted to validate the effectiveness of the proposed methodologies. The final spacer design reduces the maximum von-Mises stress in the attachment by 19.42% (from 111.78 MPa with brick spacers of the same height to 90.07 MPa). The proposed multi-step TO method can therefore be used to improve the thermo-mechanical lifetime of DSC power modules.
1. Introduction
Along with the fast development in modern electric and hybrid electric vehicles (EVs/HEVs), power modules based on wide bandgap (WBG) semiconductors, e.g., silicon carbide (SiC), are gaining increasing attention. In the existing packaging structures for WBG power modules, the double-sided cooled (DSC) structure has become a focus as it can cause significant reductions in thermal resistance and parasitic parameters [1,2,3]. However, since both sides of the power dies are restricted synchronously by direct bonded copper (DBC) or active metal bonding (AMB) substrates, the stresses introduced by thermal-expansion mismatches can concentrate severely in the soldered attachments, causing serious thermo-mechanical fatigues and even resulting in attachment fracture [4,5].
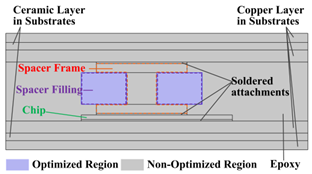
To overcome the aforementioned risks, conductive spacers (also known as bumps or interposers) are extensively used for interconnecting chip top electrodes with a substrate to buffer unbalanced thermal deformation and thereby reducing the thermo-mechanical stresses in the attachments, as illustrated in Figure 1. Silver or copper is most commonly utilized because of its high electrical and thermal conductivity [6,7,8,9]. For example, Ding et al. [9] chose sintered-Ag spacers for a double-sided half-bridge SiC MOSFET module to better reduce thermo-mechanical stresses. To better match the thermal expansion between spacers and chips, several other metallic or alloyed spacers have also been researched. In [10], Wang et al. used molybdenum spacers instead of copper ones. The feasibility was proved by both numerical simulations and experimental tests.
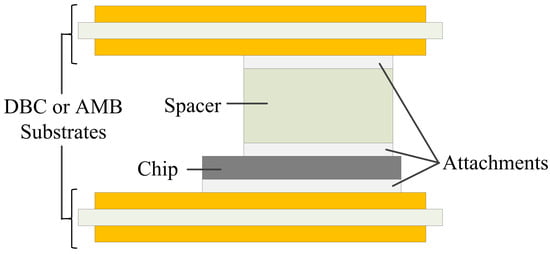
Figure 1.
Illustration on the DSC power module.
Besides the materials, the influences of the spacer structures on the buffering effectiveness have also been discussed [11,12,13]. For example, Cao et al. [11] presented a novel bridge-shaped spacer to improve heat dissipation performance as well as reduce thermo-mechanical stress in the attachments. Li et al. [12] claimed that a composite brick structure by sandwiching a thick molybdenum layer with two thin copper sheets can reduce thermo-mechanical stress greatly compared with the other four buffers. In [13], Jeon et al. proposed three novel spacer designs, i.e., 2 × 2 array trenched, X-shaped, and octagon-structured. These spacers led to significant reductions in residual stresses after a large number of thermal cycles.
In order to further optimize the thermo-mechanical performance of a DSC power module, it is critical to carry out the multi-disciplinary and multi-objective optimizations of power modules [14,15,16], but conventional optimization methods can only vary the sizes and numbers of the module components, while they are unable to vary the topology or shape. It is highly improbable to reach the best design only by engineering experience and using different materials [17,18]. It was noted that topology optimization (TO) methods can yield superior device performances by varying the material distributions in tessellated cells, and thus can realize the shape variations during the optimization processes [19,20]. Recently, TO has been utilized in designing heat sinks for power modules [21,22]. In [21], Santhanakrishnan et al. proposed a level-set TO approach for the heat sink shape design with copper-aluminum multi-material. In [22], Lee et al. reviewed and discussed the appropriateness and equivalence of various objective functions in the TOs of heat sinks.
However, as the spacers in the double-sided power modules should also act as the conducting bridges connecting the copper traces on the top and bottom substrates, to guarantee the basic electrical and thermal conduction, spacer combinations consist of unchanged spacer frames and shape-changed spacer fillings are preferable in the TO designs. In addition, to better balance the optimization efficacy and efficiency, in the objective function, the ratios between the stress in the soldered attachment and that in the whole region should also be discussed. Since hundreds or more times of thermal-mechanical coupled field simulations are often needed in finding a fine TO design, it could be very time-consuming to decide the aforementioned issues in 3D full-domain models.
To address the problems, in this article, an efficient TO strategy is proposed for the spacer shape design of a 1700 V/400 A DSC SiC power module, as the module is an automotive-grade one with pronounced thermo-mechanical loading. First, the spacer height is decided through comprehensive numerical simulations. Based on the suited spacer height, secondly, the various objective functions are used in the TOs of a 2D simplified model, and the preferable one is selected by balancing the effectiveness and efficiency of the TOs. The TO designs are then conducted on two 3D simplified models with different spacer combination architectures to choose the preferred one. Finally, the spacer shape with the 3D full-domain model is optimized.
Section 2 presents the methodologies and the optimization procedure of the proposed approach. Then, in Section 3, the thermo-mechanical stresses of DSC power modules using regular rectangular bulk buffers are simulated to predetermine the spacer height used in later TOs. In Section 4, the 2D TO designs of the spacers with different optimization objectives are determined for further 3D TO design. In Section 5, two preliminary spacer combination structures are proposed and utilized in the TO designs based on 3D simplified module models. The suitable preliminary structure is selected in this Section. In Section 6, a full-domain model is established and combined with the selected spacer height, objective function, and spacer combination structure to obtain the 3D TO design. The conclusions are presented in Section 7.
2. Methodologies
The module studied in this paper is a DSC 1700 V/400 A half-bridge multi-chip SiC MOSFET power module utilized in EVs and HEVs, the basic structure of the prototype is illustrated in Figure 2. As the module is an automotive-grade one with pronounced thermo-mechanical loading, the low thermo-mechanical stress TO design is essential.
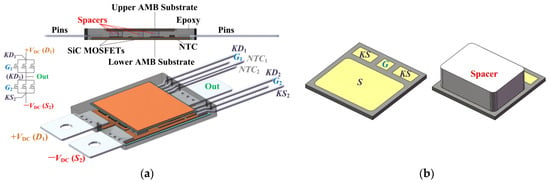
Figure 2.
Structure of the double-sided 1700 V/400 A half-bridge multi-chip SiC MOSFET power module prototype: (a) Module structure; (b) Chip and spacer structure.
During operation, the CTE mismatch between the substrates and the chips, combined with the presence of temperature gradients, results in differential thermal expansion. Since the chips and substrates are bonded through attachments, this differential expansion induces thermo-mechanical stress concentration within the attachments—particularly pronounced in DSC modules, where the chips are constrained by substrates on both sides. Under sustained thermo-mechanical stress, the attachments are prone to fatigue failure over long-term operations, thereby compromising modules’ reliabilities.
To mitigate this issue, spacers, as shown in Figure 1, have been introduced to alleviate the stresses arising from CTE mismatch, thereby enhancing the operational lifespan. However, conventional spacers adopt a simple brick-like geometry, as shown in Figure 2, which fails to fully exploit their stress-buffering potential. Addressing this limitation, this paper proposes a TO-based design methodology for spacer structures, aiming to maximize their stress-relief capacity. In this methodology, the solid isotropic material with the penalization (SIMP) method is combined with the method of moving asymptotes (MMAs) to realize the explicit of very complicated TOs [23,24,25], and the non-linear thermal-stress coupled simulations used in the TO designs are conducted using finite element analyses (FEAs) [26,27,28]. To improve the optimization efficiency and to reduce significantly the computational cost, several design considerations (the spacer height, the optimization objective, and the spacer combination structure) are predetermined before the TO of a full-domain model. The overall design scheme is illustrated in Figure 3, and the processes are as follows:
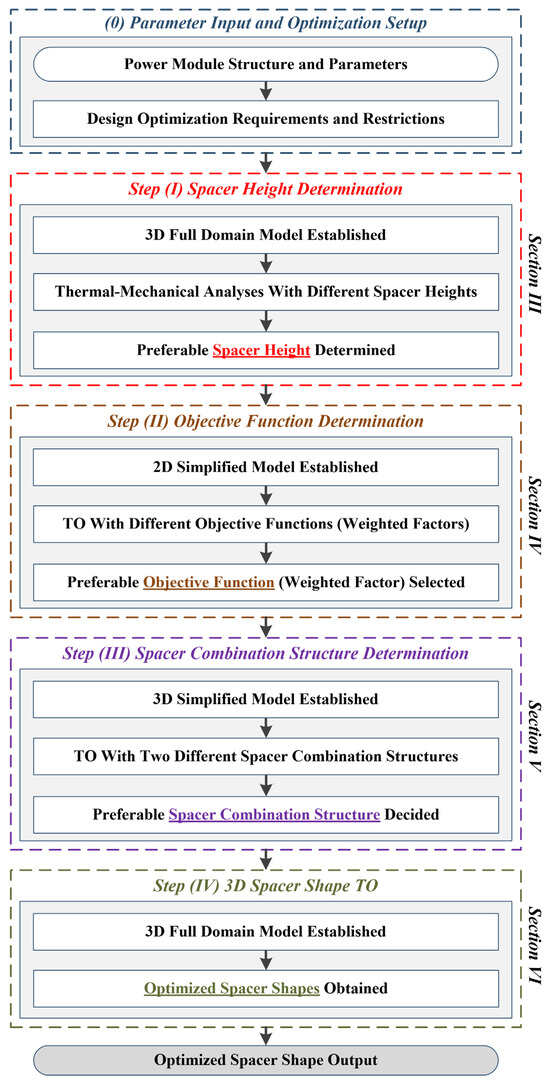
Figure 3.
Design optimization scheme and processes.
- (1)
- As the TOs are conducted with the governing variable θc varied in the tessellated and fixed grids [23,24,25], the influences of spacer height variations will have to be analyzed in multiple TOs with different spacer models and grids; therefore, increasing significantly the computational cost. To handle this problem, first, comparative numerical analyses are simulated based on conventional brick-shaped spacers with different heights, and the proper height is selected and predetermined in the first step.
- (2)
- Since the spacers are utilized to buffer the thermo-mechanical stresses, which may influence the working performances of the devices or even result in failures [29], the stress-related global variable, for example, the strain energy ws, should be considered in the optimization target function. However, whether to simply use the strain energy in the chip-substrate attachment ws_attachment or take the other components ws_others into consideration should also be analyzed. To better balance the optimization convergence and the optimization effectiveness [29], in the second step, the influence of the weight factors is investigated, and the weighted objective combinations are formulated as follows:where β is the weight factor. When β = 1, the objective function is the total strain energy, and when β = 0, only the strain energy in the attachment is considered.
- (3)
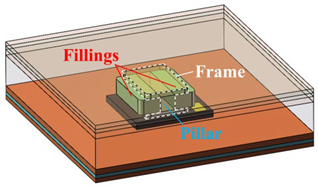
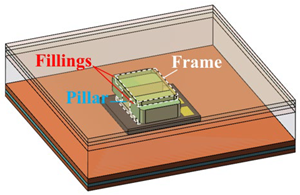
- In addition to the spacer height and the optimization objective function, the TO region of the spacers should be limited with a non-optimized spacer frame to guarantee basic electric and thermal conductivity. For 2D TOs, the non-optimized spacer frame and optimized spacer filling structure can be simple, but the 3D ones can be divided into two categories: (I) a spacer frame with two longitudinally placed fillers sandwiching the pillar of the frame, and (II) a frame with transversely located fillers. The spacer combination models are illustrated in Table 1. Based on the TO results, the preferable spacer combination structure is decided.
 Table 1. Simplified models with different spacer combination structures.
Table 1. Simplified models with different spacer combination structures. - (4)
- In step 4, the TO based on the power module’s full domain model with the spacer height determined in step 1, the optimization target function decided in step 2, and the preferable spacer combination structure settled in step 3, is conducted to output the final optimized spacer structure.
3. Step I: Thermo-Mechanical Coupled Analyses and Spacer Height Determination
The full domain model of the power module, as shown in Figure 2a, with conventional brick-shaped spacers, as shown in Figure 2b, is established. The thermal-stress coupled fields of the module with different spacer heights (varying from 1.2 mm to 2.2 mm, limited by the external mounting envelope of the power module) are numerically investigated. During simulations, the coolant temperature is set to 65 °C with a flow rate of 10 L/min, and a chip heating rate of 4.44 × 1010 W/m3 (200 W for each chip), to keep consistent with the actual working condition.
Figure 4a shows the maximum temperature in the module versus the spacer height and Figure 4b–g show the temperature distributions with the spacer height of 1.2 mm, 1.4 mm, 1.6 mm, 1.8 mm, 2.0 mm, and 2.2 mm, respectively.
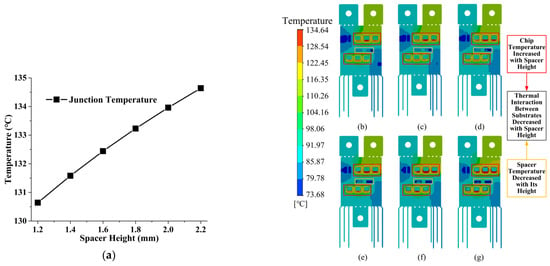
Figure 4.
Temperature field distributions of the module with different spacer heights: (a) Junction temperature change with spacer height; (b) Module temperature distribution with spacer height at 1.2 mm, (c) 1.4 mm, (d) 1.6 mm, (e) 1.8 mm, (f) 2.0 mm, (g) and 2.2 mm.
The only difference in the computed temperature distributions is the maximum value, and the highest temperature occurs at the unconnected area on the top surface of the chip, as the heat transfer efficiency at this location is weaker than that connected with spacers. The module could run at a greater temperature as the spacer rises because there is less thermal connection between the top and bottom substrates. However, because the temperature difference is so modest (under 3.99 K with the spacer height shift from 1.2 mm to 2.2 mm), it may not be as important to consider how the spacer heights affect thermal problems.
Figure 5a shows the maximum thermo-mechanical stress in the chip-substrate attachments versus spacer height. The stress distributions in the soldered attachments with the different spacer heights are shown in Figure 5b–g separately. The power dies’ edges, particularly its corners, are where the attachment stresses are concentrated. The solder portions covered by spacers often have low stresses because of the spacers’ efforts to act as buffers. Additionally, when the spacer height is below 1.8 mm, the stresses in the attachments decrease with increasing height, but they may increase when the spacer height is above 1.8 mm. Because they may offer the highest buffering performances, the 1.8 mm high spacers are preferred, and the spacers are set to 1.8 mm in later TOs.
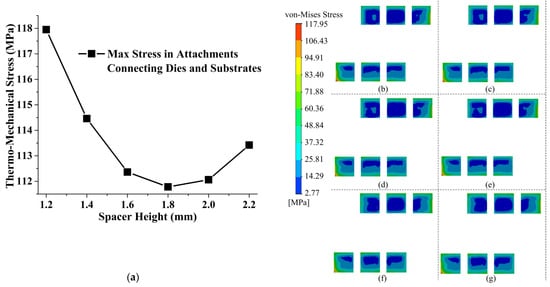
Figure 5.
Thermo-mechanical stress distributions of the die-substrate attachments: (a) Maximum stress change with spacer height; (b) Stress distribution with spacer height at 1.2 mm, (c) 1.4 mm, (d) 1.6 mm, (e) 1.8 mm, (f) 2.0 mm, and (g) 2.2 mm.
4. Step II: 2D Spacer TO Design and Objective Function Determination
Based on the 2D simplified model, as shown in Table 1, the TO designs are conducted by varying the governing variable θc to decide the material properties in different grids. During the TO processes, the overall areas considering both the spacer frame and the filling parts should be close enough to that of the original brick-shaped spacer (with an area difference ≤ 5%), as shown in Figure 6, and the design schemes that do not meet this regulation are automatically abandoned. To investigate the influences of the optimization target functions on the TO results and to determine the preferable weighted factor in (1), the TO designs with different factors are obtained as follows.
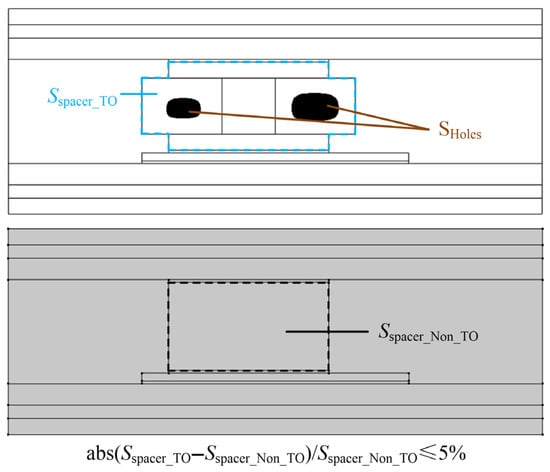
Figure 6.
Restrictions in TO designs.
4.1. Total Strain Energy in Whole Region (β = 1)
In this section, the 2D TO design of the spacers is conducted to minimize the total strain energy of the whole solution domain. The spacer shapes during the optimization iterations are shown in Figure 7a–h. As can be found from Figure 7a, the TO designs start with no holes in both sides of the fillings (initial design, step 0), but the design is abandoned since it cannot fit in with the rule of the constant spacer area in optimization. Then, two hollow holes with similar sizes appear synchronously in the forward and backward fillings (step 5), as shown in Figure 7b. The forward hollow hole is then growing larger with the backward hole getting smaller (step 10), as illustrated in Figure 7c, and the backward hole gradually flows into the forward hole to form a very large hole (step 20), as shown in Figure 7d. Later in step 40 of the TO iterations, the backward hole reappears while the forward hole gets “shoe-shaped”, as demonstrated in Figure 7e. For the designs obtained after 60 and 90 steps of iterations shown in Figure 7f,g, respectively, the backward hole is getting taller while the forward hole grows thinner. Finally, after 127 steps of iterations, the optimization converged with the TO design shown in Figure 7h, and the 2D TO design recommends a thin boot-shaped hole dug in the forward filling and an arc-shaped hole in the backward filling.
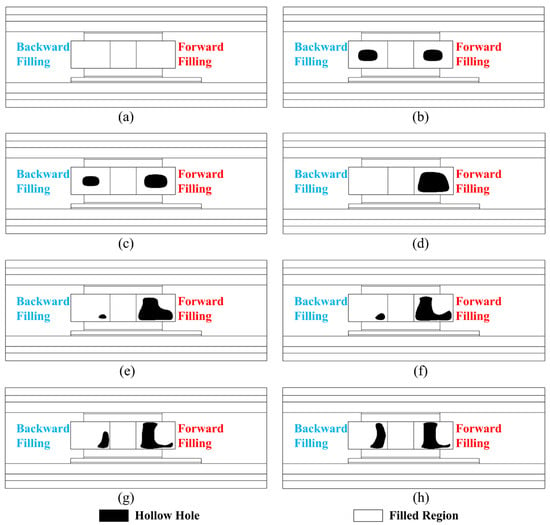
Figure 7.
TO design schemes during iteration processes with the optimization objective of least total strain energy: (a) step 1 (initial structure); (b) step 5; (c) step 10; (d) step 20; (e) step 40; (f) step 60; (g) step 90; (h) step 127 (optimization converged structure).
To validate the TO effect, the thermo-mechanical stress of the optimized model (case 1—Original brick spacer) is compared with that of two non-optimized ones (case 2—Spacer frame and case 3—TO-designed spacer frame). The structures and descriptions of the three cases are tabulated in Table 2. Figure 8a–c show the von-Mises stresses with cases 1, 2, and 3, respectively. By the TO of the spacer (case 3), the overall maximum thermo-mechanical stress, i.e., 110.60 MPa, is reduced by 13.69% when compared with that utilizing the original brick-shaped spacer (case 1), i.e., 128.14 MPa, and by 9.74% when compared with that using a spacer with non-optimized fillings (case 2), i.e., 122.53 MPa. By these means, the TO-designed module (case 3) can operate with lower stress than that even with more spacer material consumed (case 2). In addition, for the two non-optimized design schemes, the thermo-mechanical stress in the attachment is very close to the maximum one, i.e., 124.74 MPa, for that with the original brick-shaped spacer (case 1), as shown in Figure 8a, and 119.93 MPa for that with non-optimized spacer combination (case 2), as shown in Figure 8b. In addition, the TO one (case 3) can better release the high stress from the attachments to chips and substrates, the attachment maximum stress is reduced to 98.37 MPa, as shown in Figure 8c, 21.14% lower than that with the brick-shaped spacer (case 1) and 17.98% lower than that with the non-optimized spacer combination (case 2). Since the stress in the soldered attachment is highly decreased, the working reliability of modules employing TO spacers can thus be better guaranteed.

Table 2.
Structures and descriptions of the three 2D cases analyzed.
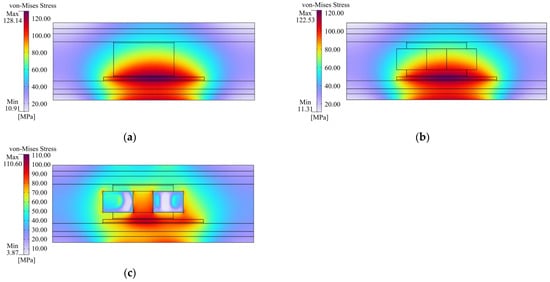
Figure 8.
Thermo-mechanical stress distributions of the 2D simplified model: (a) Case 1—Original brick spacer; (b) Case 2—Spacer frame; (c) Case 3—TO-designed spacer frame.
4.2. Strain Energy in Chip-Substrate Attachment (β = 0)
The least strain energy in the chip-substrate attachment is taken as the optimization aim in this section to better meet the attachment-stress-reduction criteria. After 319 iterations using the TO methods, the ideal spacer shape design is attained. The design with the least chip-substrate attachment strain energy, as shown in Figure 9a, suggests two hollow holes in the top area of the spacer fills in addition to the design with the lowest overall strain energy. Figure 9b displays the associated thermo-mechanical stress distribution with the ideal spacer design. The maximum stress, i.e., 146.43 MPa, obtained with the design is 32.40% larger than the total strain energy taken as the objective function, but the stress in the chip-substrate attachment is effectively reduced to 93.42 MPa, which is 5.03% smaller than that with minimum total strain energy. It was attributed to the stress that is more intensely concentrated in the spacer fillings.
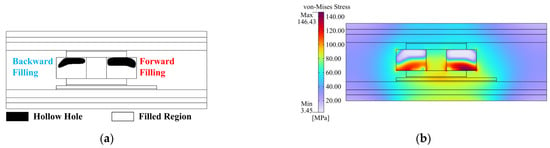
Figure 9.
TO design schemes and related thermo-mechanical stress distribution with optimization objective of least strain energy in chip-substrate attachment: (a) Converged TO design scheme; (b) Its von-Mises stress distribution.
4.3. Weighted Strain Energy Combinations (β = 0.2, 0.4, 0.6, 0.8)
The TO design with other factor combinations (β = 0.2, 0.4, 0.6, 0.8) is conducted and illustrated in Figure 10a–d. The interval of 0.2 is selected as the TO results can exhibit a clear trend; otherwise, the interval can be refined. The suggested spacer shapes were rapidly approaching those obtained with total strain energy as the target function, notwithstanding a little increase in the maximum stress in the soldered attachment as the weight factor increased. The overall total strain energy (β = 1) was chosen as the optimization objective in the TOs of the module in this paper because the iteration step for optimization convergence is also reduced with increasing β, e.g., 319 steps when β = 0, 241 steps when β = 0.2, 186 steps when β = 0.4, 150 steps when β = 0.6, 131 steps when β = 0.8, and 127 steps when β = 1.
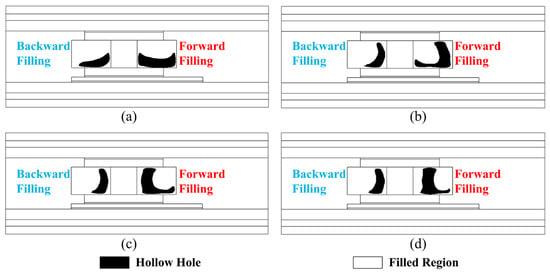
Figure 10.
TO designs with different weight factors: (a) Optimized structure with β = 0.2; (b) Optimized structure with β = 0.4; (c) Optimized structure with β = 0.6; (d) Optimized structure with β = 0.8.
5. Step III: 3D Spacer Combination Structure Determination
In this section, two 3D simplified models (marked by “3D model (I)” and “3D model (II)” in Table 1) with one SiC MOSFET and the areas extremely close to the single power die are constructed in order to find the preferable spacer combination structure. The first basic model, which is merely a 3D extension of the 2D model used in the previous section, uses a spacer frame with two longitudinally placed fillers sandwiching the pillar of the frame (marked by “3D model (I)” in Table 1). Contrarily, the second model (marked by “3D model (II)” in Table 1) positioned the filler transversely between the pillar of the spacer frame. In this phase, the TO designs are carried out using the two condensed 3D models, with the total strain energy as the optimization objective (β = 1). Due to the symmetry, 1/2 models divided by the intermediate profiles were used during optimization for the 3D TO design with longitudinally and transversely oriented fillers.
5.1. Spacer Frame with Longitudinally Arranged Fillings
After 171 MMA iterations, the TO processes for the model with longitudinally organized spacer fillings converged, and Figure 11a illustrates the optimal filler shape, which is separated by the intermediate profile. The forward filling is hollowed while the backward filling is kept solid to release tensions. The overall maximum stress is further decreased to 104.54 MPa, which is 5.48% lower than that with the 2D model, with the longitudinally placed fillers following 3D TO procedures. The maximum stress in soldered attachment is decreased to 93.64 MPa, which is 4.81% lower than that with the 2D model. Figure 11b depicts the distribution of thermo-mechanical stress.
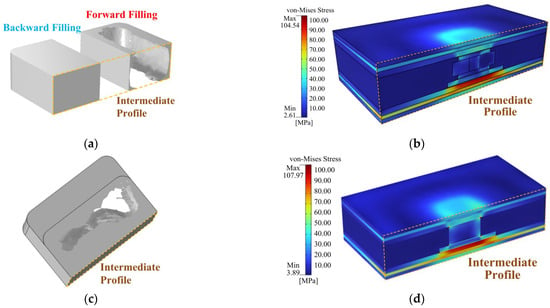
Figure 11.
Three-dimensional TO with the simplified model: (a) TO result with longitudinally arranged fillings; (b) Von-Mises stress distribution with longitudinally arranged fillings; (c) TO result with transversely arranged fillings; (d) Von-Mises stress distribution with transversely arranged fillings.
5.2. Spacer Frame with Transversely Arranged Fillings
The TO design of the filler is created after 187 iterations, as shown in Figure 11c. Figure 11d depicts the associated thermo-mechanical stress with the filling scheme. Based on the simulation results, the stress is still 3.28% higher than that with longitudinally organized fillings although the 3D TO-designed spacer can release stress more effectively than a 2D model. The total maximum stress can be lowered by 2.38%. Additionally, the maximum stress in the chip-substrate attachment rises to 94.77 MPa, which is 1.21% greater than that with the longitudinally oriented fillers and 3.66% lower than that produced by the 2D model. In order to reduce stress more effectively, the longitudinally organized fillers are integrated with spacer frames in the TO design using the 3D full-domain models.
6. Step IV: 3D Spacer TO Design Based on a Full Domain Model
6.1. Three-Dimensional Spacer TO Design and Discussion
To obtain the final spacer TO design with the full considerations of the module’s components, a 3D full-domain model is created, as illustrated in Figure 12, to consider the thermo-mechanical stress interactions among the power chips during TO operations. The pins were omitted in the model during optimization since the TO operations could generate hundreds or even thousands of numerical simulations. This reduced the computational strain.
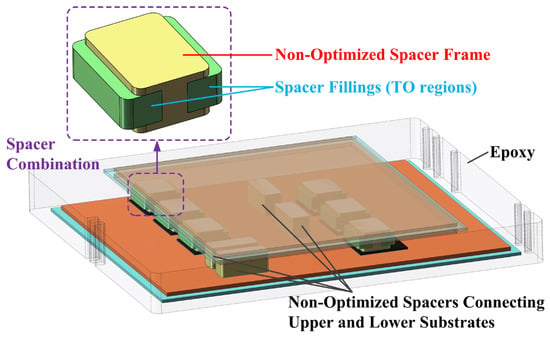
Figure 12.
Three-dimensional full domain model.
The TO converges in 462 steps based on the full-domain model, and Figure 13a shows the optimized spacer fillings. The spacer fillings of various chips vary greatly as a result of the mutual impacts among the internal chips and the imbalanced external cooling attempts on them. In general, the fillings attached to exterior chips have the wider hollow holes than those linked to inner chips. Figure 13b displays the thermo-mechanical stress distribution using the ideal spacer combinations. The operational reliability of the module under study in this paper was hence significantly improved after the TO, when the maximum stress in the whole model reduced to 105.48 MPa and the stress in the soldered attachment reduced to 90.07 MPa. Furthermore, as illustrated in Figure 13a, the spacer configuration generated by TO is highly intricate, featuring irregular perforations that pose formidable manufacturing challenges. Nevertheless, with the rapid advancements in additive manufacturing technologies [30], the precise fabrication of such small-scale, irregular metallic geometries has become increasingly feasible.
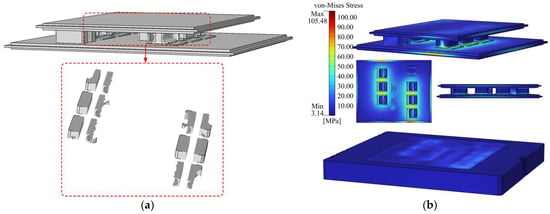
Figure 13.
Three-dimensional TO design based on the full domain model: (a) Spacer filling shape optimized; (b) Von-Mises stress distribution with the full-domain optimized spacer.
As summarized in Table 3, the maximum thermal stresses in the chip attachments of the module are compared across four spacer configurations: the conventional brick-typed one (output in Step I), that obtained through the 2D model (output in Step II), that obtained based on the 3D simplified model with longitudinally arranged spacer fillings (output in Step III), and that designed with the 3D full-domain model (output in Step IV). The results demonstrate that the spacers generated by the proposed method at Step IV—derived from the 3D full-domain model—achieve a pronounced reduction in thermo-mechanical stress within the chip attachments, thereby substantially enhancing the operational reliability of the module. The comparisons with the advanced designs in the literature are tabulated in Table 4. The results show the superiority of the proposed TO design.

Table 3.
Comparisons between the results of different steps.

Table 4.
Comparisons between the proposed design and that in literature [9,10,11,12,13].
6.2. Lifetime Predictions
To investigate the influence of the TO design of the spacer on the operational lifetime of the module, this chapter employs the Anand model [31] to calculate the equivalent plastic strain of the chip attachment through transient thermo-mechanical stress field analysis. The simulation settings are illustrated in Figure 14a, where each chip is subjected to a heat source of 200 W with an on-time of 1 s and an off-time of 1 s. By adjusting the heat transfer coefficient, the maximum junction temperature fluctuation of the chip is set to Tjmax = 100 °C (with Tjmin = 50 °C and Tjmax = 150 °C). Five power cycles are conducted, and the maximum equivalent plastic strain in the chip attachments is depicted in Figure 14b.
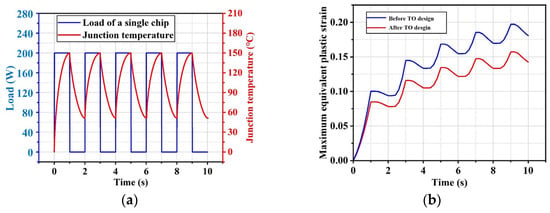
Figure 14.
Transient thermo-mechanical stress field analysis: (a) Simulation settings; (b) Maximum equivalent plastic strain in chip attachments.
Based on the calculated plastic strain values, the power cycling life is evaluated using the Coffin–Manson equation [32]:
Here, Nf denotes the number of failure cycles, and Δεplastic represents the plastic strain amplitude per cycle. The constants C and α are physical parameters of the attachment (C = 0.160 and α = 2.96 for this case studied). The computation results show that, using the spacers before the TO design, the lifetime of the module is limited to 80,120, while using the TO-designed spacers can prolong the lifetime to 131,131 (increased by 63.67%), thereby guaranteeing the effectiveness of the proposed methodology.
7. Conclusions
In this paper, a muti-step TO approach is proposed combining the SIMP method and thermal-stress coupled calculations for the spacer shape design optimization for a double-sided 1700 V/400 A SiC MOSFET power module. In the first step, the thermal and stress fields of the module with conventional brick-shaped spacers are numerically investigated to find out the spacer height effects on the thermo-mechanical stresses and to determine the basic spacer height used in later TO designs. In the second step, the preferable optimization objective is selected by comparing the stresses and the convergent steps of 2D TO designs based on a simplified single-chip module model with differently weighted objective functions. The total strain energy (the weighted factor β = 1) is resolved as the objective function in the 3D TOs for its superiority in both the optimization effectiveness and the convergent speed. To decide the basic spacer combination structure used in full-domain TO designs, in the third step, two simplified 3D single-chip models with different filling configurations are topologically optimized. The longitudinally arranged structure is selected based on the TO results. In the fourth step, a full-domain module model is established and combined with the chosen spacer height, objective function, and preliminary structure to obtain the spacer shape design, and the optimization effectiveness is proved by the reduced thermo-mechanical stress. Structural-optimized spacers for a 1700 V/400 A DSC module based on the proposed method can reduce the chip-attachment thermo-mechanical stress by 19.4% (from 111.78 MPa to 90.07 MPa), confirming that the proposed spacer-TO method reliably minimizes attachment stresses in DSC devices. The module’s lifetime simulation results indicate that the implementation of the TO-designed spacer can enhance the module’s lifespan by 63.67% (from 80,120 cycles to 131,131 cycles). This further substantiates the efficacy of the TO methodology. In addition, although the present study centers on a SiC MOSFET power module, the proposed methodology is applicable to the packaging design of a broad range of WBG semiconductors.
Owing to the pronounced geometric complexity and irregularity of the TO-designed spacer, together with the stringent precision requirements imposed by the power modules, future efforts will be directed toward the additive manufacturing of this component and its subsequent experimental validation.
Author Contributions
Conceptualization, K.C. and G.Z.; methodology, G.Z.; software, L.L., W.J. and G.Z.; validation, K.C., Y.G., L.L., W.J. and G.Z.; formal analysis, L.L., W.J. and G.Z.; investigation, K.C. and G.Z.; data curation, K.C. and G.Z.; writing—original draft preparation, Y.G., L.L. and G.Z.; writing—review and editing, W.J.; supervision, G.Z.; project administration, K.C., W.J. and G.Z.; funding acquisition, K.C. and G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the basic research project of Tianjin Fire Science and Technology Research Institute of MEM, grant number 2024SJ06, and in part by the China Postdoctoral Science Foundation, grant number 2024M761259.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request. The data are not publicly available due to the limitations of patent protection.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| TO | Topology optimization |
| WBG | Wide bandgap |
| SiC | Silicon carbide |
| GaN | Gallium nitride |
| DSC | Double-sided cooled |
| MOSFET | Metal-oxide-semiconductor field-effect transistor |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| SIMP | Solid isotropic material with penalization |
| MMAs | Method of moving asymptotes |
References
- Li, B.Y.; Yang, X.; Wang, K.P.; Zhu, H.K.; Wang, L.L.; Chen, W.J. A compact double-sided cooling 650V/30A GaN power module with low parasitic parameters. IEEE Trans. Power Electron. 2022, 37, 426–439. [Google Scholar] [CrossRef]
- Han, L.B.; Liang, L.; Zhang, Z.Y.; Kang, Y. Understanding inherent implication of thermal resistance in double-side cooling module. IEEE Trans. Power Electron. 2023, 38, 2435–2445. [Google Scholar] [CrossRef]
- Peng, C.; Zhu, W.H.; Ke, P.; Li, R.; Dai, X.P.; Wang, L.C. Investigation of vehicle-oriented double-sided cooling power module with BGA technology. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 6171–6179. [Google Scholar] [CrossRef]
- Peng, C.; Huang, Q.; Qi, F.; Ke, P.; Dai, X.P.; Zhu, W.H.; Wang, L.C. Investigation on the reliability of die-attach structures for double-sided cooling power module. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 793–801. [Google Scholar] [CrossRef]
- Liu, M.; Coppola, A.; Alvi, M.; Anwar, M. Comprehensive review and state of development of double-sided cooled package technology for automotive power modules. IEEE Open J. Power Electron. 2022, 3, 271–289. [Google Scholar] [CrossRef]
- Haque, S.; Xing, K.; Lin, R.L.; Suchicital, C.T.A.; Lu, G.Q.; Nelson, D.J.; Borojevic, D.; Lee, F.C. An innovative technique for packaging power electronic building blocks using metal posts interconnected parallel plate structures. IEEE Trans. Adv. Packag. 1999, 22, 136–144. [Google Scholar] [CrossRef]
- Catalano, A.P.; Scognamillo, C.; d’Alessandro, V.; Castellazzi, A. Numerical simulation and analytical modeling of the thermal behavior of single- and double-sided cooled power modules. IEEE Trans. Compon. Packag. Manuf. Technol. 2020, 10, 1446–1453. [Google Scholar] [CrossRef]
- Sun, P.; Niu, F.L.; Zeng, Z.; Li, H.Y.; Ou, H.H. FEA-dominant reliability and lifetime model of double-sided cooling SiC power module. IEEE Trans. Device Mater. Reliab. 2023, 23, 178–186. [Google Scholar] [CrossRef]
- Ding, C.; Liu, H.Z.Q.; Ngo, K.D.T.; Burgos, R.; Lu, G.Q. A double-side cooled SiC MOSFET power module with sintered-Silver interposers: I-design, simulation, fabrication, and performance characterization. IEEE Trans. Power Electron. 2021, 36, 11672–11680. [Google Scholar] [CrossRef]
- Wang, M.Y.; Mei, Y.H.; Liu, W.; Xie, Y.J.; Fu, S.C.; Li, X.; Lu, G.Q. Reliability improvement of a double-sided IGBT module by lowering stress gradient using molybdenum buffers. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 1637–1648. [Google Scholar] [CrossRef]
- Cao, J.L.; Li, J.; Mei, Y.H. A double-sided bidirectional power module with low heat concentration and low thermomechanical stress. IEEE Trans. Power Electron. 2021, 36, 9763–9766. [Google Scholar] [CrossRef]
- Li, J.F.; Castellazzi, A.; Dai, T.X.; Corfield, M.; Solomon, A.K.; Johnson, C.M. Built-in reliability design of highly integrated solid-state power switches with metal bump interconnects. IEEE Trans. Power Electron. 2015, 30, 2587–2600. [Google Scholar]
- Jeon, J.; Seong, J.; Lim, J.; Kim, M.K.; Kim, T.; Yoon, S.W. Finite element and experimental analysis of spacer designs for reducing the thermomechanical stress in double-sided cooling power modules. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3383–3391. [Google Scholar] [CrossRef]
- Zeng, Z.; Ou, K.H.; Wang, L.; Yu, Y. Reliability-oriented automated design of double-sided cooling power module: A thermo-mechanical-coordinated and multi-objective-oriented optimization methodology. IEEE Trans. Device Mater. Reliab. 2020, 20, 584–595. [Google Scholar] [CrossRef]
- Ji, B.; Song, X.G.; Sciberras, E.; Cao, W.P.; Hu, Y.H.; Pickert, V. Multiobjective design optimization of IGBT power modules considering power cycling and thermal cycling. IEEE Trans. Power Electron. 2015, 30, 2493–2504. [Google Scholar] [CrossRef]
- Qian, Y.C.; Hou, F.Z.; Fan, J.J.; Lv, Y.Q.; Fan, X.J.; Zhang, G.Q. Design of a fan-out panel-level SiC MOSFET power module using ant colony optimization-back propagation neural network. IEEE Trans. Electron. Devices 2021, 68, 3460–3467. [Google Scholar] [CrossRef]
- Wang, W.J.; Ho, S.L.; Fu, W.N. A multiscale topology optimization methodology based on sequential element rejection-admission and boundary element evolvement. IEEE Trans. Magn. 2019, 55, 7201304. [Google Scholar]
- Doi, S.; Sasaki, H.; Igarashi, H. Multi-Objective topology optimization of rotating machines using deep learning. IEEE Trans. Magn. 2019, 55, 7202605. [Google Scholar] [CrossRef]
- Jung, S.W.; Ro, J.S.; Jung, H.K. A hybrid algorithm using shape and topology optimization for the design of electric machines. IEEE Trans. Magn. 2018, 54, 8102604. [Google Scholar] [CrossRef]
- Xia, M.; Yang, S.Y.; Sykulski, J. A novel 3-D topology optimization methodology based on the min-cut theorem. IEEE Trans. Magn. 2021, 57, 7201005. [Google Scholar] [CrossRef]
- Santhanakrishnan, M.S.; Tilford, T.; Bailey, C. Multi-material heatsink design using level-set topology optimization. IEEE Trans. Compon. Packag. Manuf. Technol. 2019, 9, 1504–1513. [Google Scholar] [CrossRef]
- Lee, G.; Joo, Y.; Kim, S.J. On the objective function for topology optimization of heat sinks. IEEE Trans. Compon. Packag. Manuf. Technol. 2021, 11, 1776–1782. [Google Scholar] [CrossRef]
- Majdi, B.; Reza, A. Multi-Material topology optimization of compliant mechanisms via solid isotropic material with penalization approach and alternating active phase algorithm. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2020, 234, 2631–2642. [Google Scholar] [CrossRef]
- Li, L.N.; Zhu, G.J.; Wang, Z.; Liu, T.; Yang, S.Y. Topological design optimization approach for winding oil flow paths in oil-natural air-natural transformers based on a fluidic-thermal coupled model. IEEE Trans. Magn. 2023, 59, 8401405. [Google Scholar] [CrossRef]
- Ni, Q. A globally convergent method of moving asymptotes with trust region technique. Optim. Method Softw. 2003, 18, 283–297. [Google Scholar] [CrossRef]
- Wang, L.S.; Deng, J.Y.; Zeng, K.Q.; Cheng, H.G.; Wu, Q.; Lin, J.; Rietveld, G.; Hueting, R.J.E. Design and Fabrication of a Ceramic Substrate-Embedded SiC Power Module. IEEE Trans. Compon. Packag. Manuf. Technol. 2025, 15, 938–948. [Google Scholar] [CrossRef]
- Chang, Y.; Luo, H.Z.; Iannuzzo, F.; Bahman, A.S.; Li, W.H.; He, X.N.; Blaabjerg, F. Compact Sandwiched Press-Pack SiC Power Module With Low Stray Inductance and Balanced Thermal Stress. IEEE Trans. Power Electron. 2020, 35, 2237–2241. [Google Scholar] [CrossRef]
- Li, B.Y.; Yang, X.; Wang, K.P.; Wu, M.; Chen, W.J. Thermomechanical Stress Analysis, Characterization, and Optimization for Double-Side Cooled Power Modules With Ceramic Substrate. IEEE Trans. Compon. Packag. Manuf. Technol. 2024, 14, 561–572. [Google Scholar] [CrossRef]
- Xu, K.K. Silicon electro-optic micro-modulator fabricated in standard CMOS technology as components for all silicon monolithic integrated optoelectronic systems. J. Micromech. Microeng. 2021, 31, 054001. [Google Scholar] [CrossRef]
- Toenjes, A.; Zinn, C.; von Hehl, A.; Wang, H.C.; Hantzsche, K.; Hesselmann, M. Smart-Alloying for tailored microstructures in laser-based metal additive manufacturing. J. Laser Appl. 2025, 37, 054001. [Google Scholar] [CrossRef]
- Cheng, H.C.; Syu, J.Y.; Wang, H.H.; Liu, Y.C.; Kao, K.S.; Chang, T.C. Power Cycling Modeling and Lifetime Evaluation of SiC Power MOSFET Module Using a Modified Physical Lifetime Model. IEEE Trans. Device Mater. Reliab. 2024, 24, 142–153. [Google Scholar] [CrossRef]
- Ning, P.; Liu, J.; Wang, D.; Zhang, Y.; Li, Y. Assessing the Fatigue Life of SiC Power Modules in Different Package Structures. IEEE Access 2021, 9, 12074–12082. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).