Abstract
Power batteries and their management technology are crucial for the safe and efficient operation of electric vehicles (EVs). The life and safety issues of power batteries have always plagued the EV industry. To achieve an intelligent battery management system (BMS), it is crucial to accurately estimate the internal state of the power battery. The purpose of this review is to analyze the current status of research on multi-state estimation of power batteries, which mainly focuses on the estimation of state of charge (SOC), state of energy (SOE), state of health (SOH), state of power (SOP), state of temperature (SOT), and state of safety (SOS). Moreover, it also analyzes and prospects the research hotspots, development trends, and future challenges of battery state estimation. It is a significant guide for designing BMSs for EVs, as well as for achieving intelligent safety management and efficient power battery use.
1. Introduction
The development of electric vehicles (EVs) is the primary direction for future automobiles due to energy depletion and environmental pollution [1,2]. As the essential components of EVs, power batteries and battery management systems (BMS) are vital for the power, economy, and safety of EVs and have become a bottleneck that is preventing the development of EVs on a large scale. Among them, lithium-ion batteries (LIBs) have many advantages, such as high energy density, good cost performance, high cell voltage, etc. [3,4,5]. They are considered to be the most promising power batteries for EVs and have become a hot research focus.
The BMS functions as the central control unit of the battery system. It manages hundreds or thousands of battery cells in series and parallel configurations, continuously monitoring their health status. As a critical component, the BMS ensures the safe, reliable, and efficient operation of power batteries [6,7]. A high-performance BMS requires real-time measurement of voltage, temperature, current, and other data to master the complex internal and external states of all batteries in the battery system through battery models and control algorithms, diagnose various faults in the battery system in a timely and accurate manner, and accurately control the charging and discharging rate, working temperature, etc. of the batteries to ensure that all batteries operate within a reliable and efficient working range [8,9,10]. The safety, efficiency, and long-lasting operation of battery packs are greatly influenced by the use of BMS and intelligent control technology, which are essential components and research areas for EVs.
The internal state is an important measurement of the power battery’s performance and serves as the foundation for the BMS to manage the safe charge/discharge and balance of the battery. At present, the internal state of LIBs mainly includes state of charge (SOC), state of energy (SOE), state of health (SOH), state of peak power (SOP), state of function (SOF), state of temperature (SOT), state of safety (SOS), etc., but these states cannot be directly measured and can only be obtained through estimation algorithms based on the measured data such as battery voltage, current, and the temperature in real time [11,12]. The estimation accuracy is easily affected by battery temperature and aging [13,14]. The current methods are only suitable for occasions where the working conditions are relatively stable. To achieve accurate state estimation throughout the battery’s entire lifecycle, it is essential to develop more effective and reliable methods to mitigate or eliminate the various factors that compromise its accuracy. Therefore, it is extremely challenging to accurately estimate the internal state of the battery, and it has become an international research hotspot in the battery field.
This review provides a brief overview of battery state estimation, emphasizing its importance amid the rapid growth of EVs and advancements in intelligent technology. As these developments progress, the demands on BMS are becoming increasingly stringent. To enhance the quality of related research references, this paper offers a comprehensive review and outlook on various battery states, highlighting its novelty in the field. This paper distinguishes itself from other reviews on single-state estimation by focusing on current challenges and proposing solutions for both state estimation and multi-state joint estimation. This paper provides a comprehensive review of current methods for battery state estimation in EVs, highlighting their limitations. It covers essential parameters such as SOC, SOE, SOH, SOP, SOT, and SOS, which are crucial for monitoring LIBs.
The structure of this paper is as follows: The analysis of publications concerning battery state estimation is presented in Section 2. This section aims to present the latest research developments in this field, highlighting data-driven insights from recent publications to illustrate current trends and findings. In Section 3, the latest advancements in power battery state estimation technologies are examined, with particular emphasis on parameters such as SOC, SOE, SOH, SOP, SOF, SOT, and SOS. In Section 4, the characteristics of different state estimations across multiple time scales were analyzed. Additionally, a multi-state joint estimation scheme was proposed, which simultaneously estimates SOC, SOH, and SOP. Finally, discussion and conclusions are summarized in Section 5.
2. Analysis of Publications Published on Battery State Estimation
In this review, IEEE Xplore serves as a source database of references to analyze research status. The purpose is to showcase the research hotspots and directions in this field from the perspective of the number and trends of published papers and achievements. In this review, “battery state estimation” is used as the search keyword and “relevance” as the sorting. From the analysis of the search results, it can be seen that a total of more than 7000 publications for battery state estimation have been retrieved so far, including conferences (5143), journals (1809), magazines (29), books (15), standards (5), etc., and more than 5700 publications have been published since 2015, which showcases the rapid development of EVs in the past decade, and there is a significant growth trend in research publications on state estimation of power batteries in recent years, as shown in Figure 1.
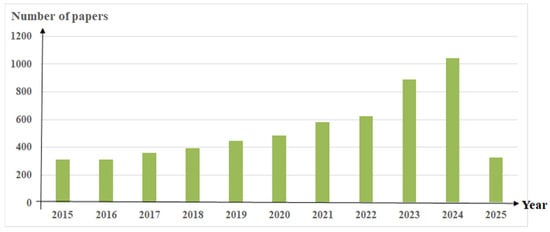
Figure 1.
The number of publications published on “battery state estimation” since 2015.
Figure 2 shows the research topics of more than 5700 publications about “battery state estimation” since 2015. The largest number of research topics is “state of charge” (3150), which this review focuses on. The second is the “battery management system” (2314), followed by “electric vehicles” (2193), and then there are various key technologies for battery modeling and state estimation, such as “battery model” (1522), “battery capacity” (1385), “equivalent circuit model” (1268), “Kalman filters” (1234), “open-circuit voltage” (1233), “root mean square error” (1140), and “extended Kalman filter” (1047). Of course, it also includes some intelligence technologies, such as “neural network” (928), “long short-term memory” (585), etc. From the statistics and analysis of the number of keywords in the research results, it can be seen that SOC estimation is still a hot research topic in the field of battery state estimation, especially the methods based on battery models using the Kalman filtering algorithm and various improved and optimized Kalman algorithms, such as the extended Kalman filter (EKF) and the unscented Kalman filter (UKF).
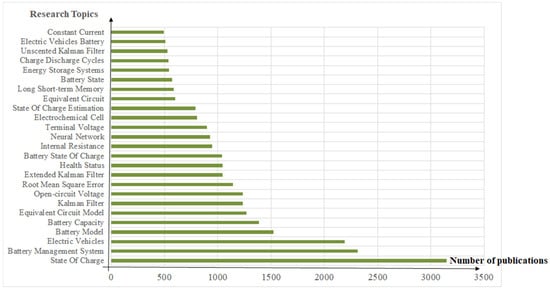
Figure 2.
The research topics and quantity of publications published since 2015.
3. State of the Art of Technologies in State Estimation of Power Batteries
In BMS, SOC, SOE, SOH, SOP, SOF, SOT, SOS, and other key parameters are used to describe different states of the battery, which together form a comprehensive evaluation system for battery status. The basic meaning of each state of the battery is shown in Table 1. Among the key parameters, SOC and SOH are fundamental. SOC indicates the current state of the battery, while SOH reflects its long-term health and capacity degradation. SOE and SOP are dynamic parameters that depend on SOC and SOH. SOT and SOS are constraints that limit other parameters, such as a decrease in SOP at high temperatures and a forced cut-off of charge and discharge when SOS is abnormal. SOF is a comprehensive evaluation parameter that integrates multiple parameters to determine whether a battery is usable for particular applications.

Table 1.
The basic meaning of each state of the battery.
3.1. SOC Estimation
The SOC of the battery is the ratio between the remaining capacity and the rated capacity under the same conditions at a certain discharge rate. The definition expression of SOC is given in Equation (1) [15].
where Qrem represents the remaining capacity of the battery with unit Ah, and Qmax is the maximum available capacity of the battery, which may vary due to factors such as aging and temperature. Therefore, in practical applications, the denominator of SOC should use the actual maximum capacity as much as possible, rather than the fixed nominal capacity, or adjust the nominal capacity in real time by increasing the capacity decay factor to ensure the accuracy of SOC estimation.
SOC estimation methods include direct estimation methods and indirect estimation methods, as shown in Figure 3. Direct estimation methods mainly include the discharge method, internal resistance (IR) method, open-circuit voltage (OCV) method, and ampere-hour (Ah) integration method. The discharge method is accurate, but it requires a large amount of experimental data and does not meet the online estimation requirements of EVs in actual driving, so it is difficult to apply in practice. The earliest used methods of SOC estimation are the IR method and the OCV method. The IR method has the problem that the relationship between IR and SOC is unstable due to the variable current discharge of the battery. The OCV method has a high estimation accuracy at the beginning and end of charging and discharging, but the accuracy will become worse during the charging and discharging process. At the same time, the battery must be left for a long time to measure the values of OCV, which contradicts its application in EVs, so it is rarely used alone in practice [16]. As shown in Equation (2), the Ah integration method is currently the most widely used in BMS, but the accuracy becomes worse as the cumulative error increases, so it requires high-precision current sensors and is susceptible to cumulative errors. It is commonly utilized together with other methods, like the OCV method [17], or it can be improved by incorporating the capacity (aging) and temperature correction coefficient to eliminate the cumulative error [18,19].
where SOC0 represents the initial state of SOC, and i is the current (negative for charging and positive for discharging) with unit A, and for more precise calculations, it is essential to account for the multiplication by charging and discharging efficiencies.
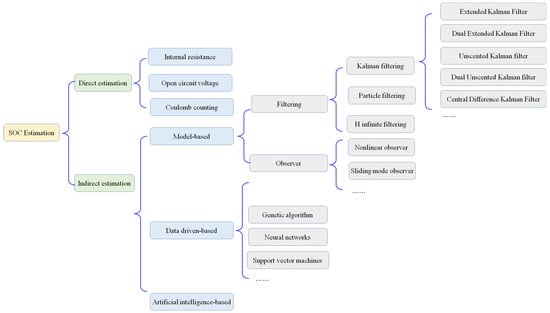
Figure 3.
SOC estimation methods.
Indirect estimation methods mainly include model-based observer/filter methods, data-driven methods, and artificial intelligence-based methods. The model-based observer/filter method based on the battery model is a research hotspot in the field of SOC estimation. The basic block diagram of model-based SOC estimation methods is shown in Figure 4. This method takes the error between the output voltage of the battery model and the measured voltage as the input of the observer or filter and feeds back the SOC estimation error, which is the estimated SOC value and the SOC value obtained by the measured current and ampere-hour integration method, to the battery model. This constantly revises the SOC estimation value. The estimation accuracy of the battery SOC is high due to its similarity to dual closed-loop control. The key premise of this method is to establish an accurate battery model. The type of battery model used is mainly divided into SOC estimation methods based on an electrochemical model and an equivalent circuit model (ECM). The observer/filter algorithm mainly adopts the nonlinear observer method, sliding mode observer (SMO), H∞ filter, particle filter, Kalman filter, and its improved algorithms, such as EKF and UKF. Zhang et al. [20] proposed a class of methods for SOC estimation based on the Lipschitz nonlinear observer. The observer has the advantages of simple structure and good estimation performance, which reduced the adverse impact of hysteresis and nonlinear factors on SOC estimation. Wang et al. [21] chose the particle filter algorithm to study battery SOC estimation and achieved good results because of the adaptability of the particle filter algorithm to non-Gaussian nonlinear systems. However, the Kalman filter method is suitable for various batteries and has a strong corrective effect on the initial estimation error. It has become the main method for studying SOC estimation in recent years. Xiong et al. [22] used genetic algorithms (GA) to identify Thevenin battery model parameters from the charging and discharging directions, respectively, and used the adaptive extended Kalman filter (AEKF) method to estimate the battery SOC. The results showed that the maximum error of SOC estimation accuracy was 2.53%. Sun et al. [23] developed an adaptive adjustment method for noise covariance using covariance matching within the framework of the UKF. They proposed an adaptive unscented Kalman filter (AUKF) to estimate the SOC of LIBs. This approach demonstrates improved accuracy compared to SOC estimation methods based on the EKF, UKF, and AEKF. Considering the inconsistency of the battery and the complex driving environment of EVs, He et al. [24] used statistical methods to improve the battery model and used the dual extended Kalman filter (dual-EKF) algorithm to achieve battery SOC estimation. To improve SOC estimation accuracy, Zhu et al. [25] proposed a joint estimation method in which the UFK is used to estimate SOC, and the recursive restricted least squares method is used to identify battery model parameters. The average absolute error is within 1.2% under different driving cycles and ambient temperatures. Shang et al. [26] established a model error prediction model based on a fuzzy neural network (NN) and used it to correct the EKF measurement noise covariance. This method effectively eliminates the SOC estimation error introduced by model errors and uncertain statistical characteristics of measurement noise. The estimation accuracy is within 1.2%, and it has good convergence and robustness.
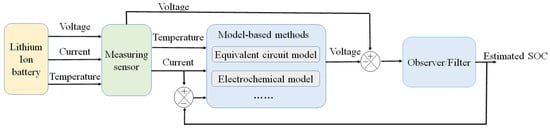
Figure 4.
Basic block diagram of model-based SOC estimation methods.
The Kalman filter method is not ideal for systems with weak nonlinearity and a Gaussian distribution in the initial state because it requires a lot of calculation. The drift of the internal operating point and interference noise has a great influence on the estimation accuracy. The environment in which the power battery is located is complex and changeable, and the above conditions are usually difficult to meet. Thus, the application of the Kalman filter is subject to some restrictions under the conditions of uncertainty in the system model and the statistical characteristics of noise.
Among them, data-driven methods mainly use fuzzy logic, GA, NN, and support vector regression (SVR). The basic block diagram of data-driven SOC estimation methods is shown in Figure 5. Ofoegbu [27] explored a data-driven SOC estimation of LIBs while discharging, using simple linear regression, ensemble methods, and feedforward neural networks (FFNNs), respectively, to ensure an accurate, low time complexity solution as compared to existing methods. However, the NN algorithm has a strong dependence on training data. Thus, the generalization is poor when the battery characteristics and capacity change. Chen et al. [28] came up with a synthetic method to estimate the SOC of LIBs that utilizes long short-term memory network (LSTM) modeling and adaptive H-infinity filter (AHIF). The experimental findings indicate that the estimate error of SOC can be limited to 2.1% in a diverse range of temperatures and aging states, demonstrating its high-precision estimation capacity and robustness. Chemali et al. [29] employed an innovative technique to estimate battery SOC with deep feedforward neural networks (DFFNN), in which battery measurements are directly linked to SOC. The SVR algorithm has good nonlinear approximation ability, fast convergence speed, and a globally optimal solution. Shi et al. [30] used cross-validation and grid search methods to identify model parameters of SVM to achieve battery SOC estimation. The results show that compared with the back propagation neural networks (BPNN), battery SOC estimation based on SVM performs better.
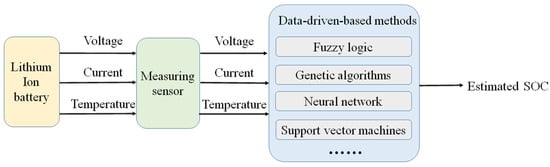
Figure 5.
Basic block diagram of data-driven SOC estimation methods.
The summary of different SOC estimation methods and their estimation errors is shown in Table 2. In summary, the existing SOC estimation methods are mostly based on the simplified battery model of the “large cell”, without considering the impact of battery inconsistency or the impact of vehicle operating environment, working conditions, and battery aging, resulting in low estimation accuracy and poor robustness. There is an urgent need to design a more effective, robust estimation method to suppress or eliminate various factors that affect the accuracy of SOC estimation to achieve accurate estimation of battery SOC throughout the life cycle.

Table 2.
Different SOC estimation methods and estimation errors.
3.2. SOE Estimation
Different from SOC, which measures the remaining charge relative to total capacity, SOE represents the remaining available energy (Wh) in a battery as a percentage of its total capacity under current operating conditions, which measures the remaining usable energy considering voltage variations under load. SOE is generally more effective at representing the energy capacity and available power level of a battery as an important component of state than SOC. The expression of the SOE definition is given in Equation (3) [31].
where Erem is the remaining discharge energy, and Etotal is the initial energy, which is determined through an energy testing procedure conducted on a new battery.
Unlike SOC, SOE not only considers the amount of charge but also takes into account the effects of voltage changes and energy efficiency. SOE estimation methods are similar to SOC estimation methods, with a focus on energy integration-based methods, ECM-based methods, data-driven methods, and hybrid methods. The expression of SOE integration is given in Equation (4) [32].
where SOE0 represents the initial state of SOE.
Unlike the Ah integration method of SOC, the energy integration method of SOE not only requires high-precision current sensors but also high-precision voltage sensors, usually combined with voltage correction, such as the OCV-SOE relationship, to improve accuracy.
Pei et al. [31] proposed a novel method for SOE estimation that relies on the online construction of the battery pack’s comprehensive OCV curve. In [32], a method is introduced that utilizes a wavelet-neural-network-based battery model and particle filter to estimate SOE. To simulate the dynamic electrical characteristics of batteries, the wavelet-neural-network battery model is employed. In [33], a Gaussian model-oriented battery model has been proposed and developed, and the estimator has been proposed with a central difference Kalman filter (CDKF) algorithm to achieve accurate battery SoE estimation. In [34], a new method based on the BPNN is presented for the SOE estimation. The SOE is introduced to replace the SOC to describe the residual energy of the battery in order to take into account the energy loss on the internal resistance, the electrochemical reactions, and the decrease in the OCV. Dong et al. [35] presents an online model-based estimation approach that can improve the accuracy and reliability of battery SOE estimation by considering uncertain dynamic load currents and environment temperatures. Correia et al. [36] use an SOE approach to calculate efficiency and round-trip efficiency of battery storage systems, in which efficiency results could also be relevant or important to other future works.
3.3. SOH Estimation
The SOH of a battery indicates its current condition relative to a new battery over its entire cycle life. Its value typically ranges from 0 to 1. There are many definitions of SOH, and there is a lack of uniformity in the concept. The current definition of SOH is mainly embodied in several aspects, such as capacity, peak power, internal resistance, and the number of remaining life cycles. Generally, capacity and power are used as indicators for judging SOH, so there are two estimation methods, including the capacity degradation method and the power degradation method. When it comes to estimating SOH or predicting the remaining useful life (RUL), capacity is the indicator that is most commonly used. When the maximum remaining capacity of a battery cannot meet its minimum performance requirements, that is, under standard conditions, when the maximum available capacity of the battery drops to 80% of its nominal capacity, the battery life can be considered terminated. At this time, SOH is defined as follows:
where Qnom is the nominal capacity of the battery.
The research approach of SOH estimation is to find suitable battery health indicators (HI) and establish a mapping relationship between HI and battery available capacity. As illustrated in Figure 6, the estimation methods for SOH are mostly divided into model-based and data-driven methods.
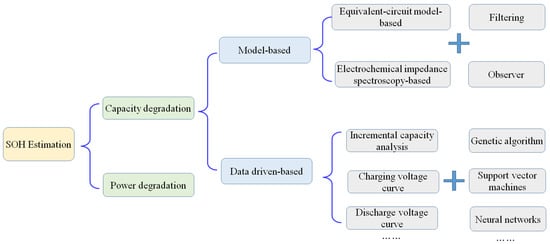
Figure 6.
SOH estimation methods.
Model-based SOH estimation methods are divided into equivalent-circuit model-based methods and electrochemical impedance spectroscopy (EIS)-based methods. The model-based method needs to first establish an accurate battery model to describe the internal model parameters such as OCV, diffusion capacitance, and battery impedance, and then use the filter or observer to estimate the battery SOH by establishing a mapping relationship between model parameters and available battery capacity. It has a clear physical meaning and high estimation accuracy, but it is complex and difficult to identify model parameters online. Kim et al. [37] regarded the capacity as the state of the battery system based on the established battery aging ECM and used the dual SMO to estimate the battery SOH. Zheng et al. [38] selected the Thevenin ECM as the basic battery model and achieved SOH estimation by using a dual Kalman filter based on the capacity degradation method. The experimental results showed that in the initial stage, the SOH estimated value has deviated from the true value, but the changing trend is consistent, and the error can be controlled by 1%. Liu et al. [39] employed the AUKF to estimate the IR of batteries in real-time, utilizing a state-space model of LIBs. The method incorporated a covariance adaptive matching technique to mitigate noise interference, enabling more accurate estimation. Subsequently, the SOH of the battery was determined by analyzing the relationship between IR and SOH, providing a comprehensive assessment of battery performance. However, the model obtained from historical conditions is difficult to apply to the complex and changeable real working conditions and environment of the vehicle, which makes real-time accuracy of SOH estimation extremely challenging.
The data-driven SOH estimation method does not need to establish an accurate battery model. Thus, it has a strong nonlinear mapping ability and good adaptability. Its model-free advantages have attracted more and more attention [40]. The methods need to fully utilize the big data of the battery’s historical operation, including voltage, current, and temperature measured by BMS, and then analyze the incremental capacity (IC) curve and discharge voltage (DV) curve. Finally, NN, SVR, and other methods are used to establish the mapping relationship between IC or DV curves and the available capacity of the battery. Taking the IC curve as an example, the IC analysis method has been an effective tool for battery SOH estimation in recent years. By dividing the charging capacity by the voltage at a constant charging current, the smooth voltage curve can be converted into an IC curve that is easy to identify the peak value. The peak position, amplitude, and envelope area of the IC curve can be used to predict battery SOH [41]. In [42], Zhou et al. proposed a practical way to calculate SoH for LIBs through Gaussian mixture regression (GMR) and IC analysis. However, since the peak of the IC curve is very sensitive to measurement noise, the robustness of this method is not ideal. Dong et al. [43] introduced a new capacity attenuation parameter to determine the SOH in real time and achieved the SOH estimation based on a support vector regression particle filter (SVR-PF). In [44], Wang et al. proposed a new method for monitoring battery degradation by combining significant health features with Gaussian process regression (GPR). Sun et al. [45] suggested a procedure known as a battery-physics-informed neural network (BPINN) to enhance the interpretability of the FFNN for SOH prediction. This method first extracts six features from the IC curve during battery discharge and uses the monotonic relationship between the peak features obtained from the IC curve and SOH as a constraint to enhance the training process of FFNN. However, the effectiveness and robustness of the data-driven method depend on the quality and quantity of training data, and the amount of calculation is large.
To a certain extent, SOH can reflect the RUL of batteries. RUL can be predicted based on the SOH estimation result. First, make the SOH variable, and then use predictive models, such as the capacity decay model and the impedance decay model, to realize RUL prediction. At present, SOH estimation and joint estimation of SOC and SOH have become hot issues in the research field of battery state estimation [46].
3.4. SOP/SOF Estimation
Whether the power battery is the sole or auxiliary power source, the peak power directly influences the power performance of the vehicle. The SOP is used to predict the maximum charge/discharge power of batteries under given operating conditions to ensure safe operation and optimize performance. How to limit the peak power of the battery has become an important function of BMS. The concept of SOP is often combined with SOF. SOF is a measurement that gauges whether a battery can meet particular performance requirements (like peak power output) in its current state, and it reflects the battery’s availability and reliability in practical applications. SOF evaluates the battery’s performance by combining parameters such as SOC, SOH, temperature, and load. The name and scope of the concept are slightly different, but the substance is similar. The battery state of peak power (SOP) is essential for the BMS to use the battery reasonably and extend the battery life. It is also the basis for the energy management system of EVs to optimize the power allocation; overall, it is essential to improve the overall performance of the vehicle. Currently, the SOP estimation methods mainly include the compound pulse method, model-based method, and data-driven method [47], as shown in Figure 7.
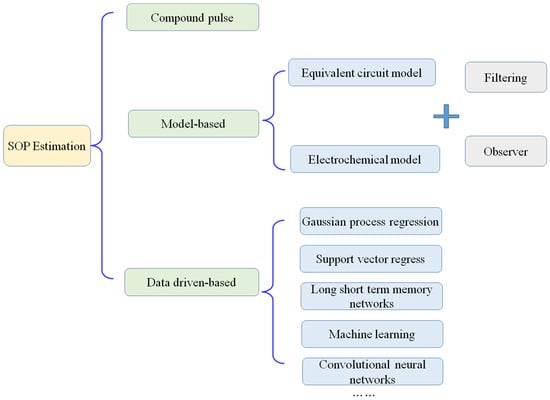
Figure 7.
SOP estimation methods.
Taking charge and discharge voltage, current, SOC, battery life, and operating temperature range as multi-parameter constraints, the multi-parameter constraint conditions can be constructed for the safe working range of power batteries, and the method of power battery SOP estimation can be studied. For example, when considering constraints such as battery SOC, voltage, and current limit specified by the manufacturer at the same time, the minimum charging current of the battery pack should be the maximum of the three, and the maximum discharge current should be the minimum of the three. It can be expressed as follows:
where and are the current limits under the highest and lowest SOC constraints; and are the current limits under the highest and lowest voltage constraints; and and are the battery cell current limits specified by the manufacturer.
Furthermore, considering the specified battery power constraints, the peak power of the series battery pack can be expressed as follows:
where and are the minimum charging power and maximum discharging power of the battery pack; and are the peak power limits of the battery cells specified by the battery manufacturer; and n is the number of batteries in the series.
The compound pulse method can estimate the instantaneous SOP of the battery through the values of OCV and IR under the current SOC based on the IR model of the battery. The IR model is simple; thus, the amount of calculation is small. However, the current changes very drastically during the actual operation of EVs, so that the estimation error is relatively large. Specifically, the estimated SOP is larger than the actual value because this method does not consider the battery charge and discharge current threshold and SOC limit. The model-based SOP estimation method is to establish an ECM of the battery, such as the Thevenin model and the second-order RC model, and estimate SOP by combining multiple parameters such as voltage, current, and SOC. Differently, the SOP estimation method based on the pseudo two-dimensional (P2D) electrochemical model calculates SOP from the perspective of internal chemical reactions in the battery. Liu et al. [48] established battery capacity–temperature and IR-temperature models to accurately predict the changes in battery-related parameters at different temperatures and used the multi-parameter constraint-based method and EKF to estimate the SOP. However, the above methods are based on a simple battery IR model, which can only be adapted to the power prediction under stable battery conditions. The power battery cannot be continuously charged or discharged during the actual operation of EVs, especially since the current and temperature of the battery change very sharply, and it is difficult to estimate the SOP in the dynamic charging and discharging process. The data-driven SOP estimation method mainly utilizes machine learning or deep learning models to directly learn the power characteristics of batteries from historical data, which is suitable for complex operating conditions. By analyzing the driving data of the power battery, Chen et al. [49] established a gray correlation analysis model to quantitatively analyze the influence of current, voltage, temperature, and other factors on the SOP of the battery and determine the gray correlation degree of the above factors to the SOP. It shows that the most significant impact on the SOP is the current (0.9637), followed by the voltage (0.7102), and the least impact is the temperature (0.6653). Jafari et al. [50] introduced a novel hybrid deep learning model that integrates convolutional neural networks (CNNs), long short-term memory (LSTM), and convolutional LSTM architectures. The results indicate that employing complex deep learning models optimized with PSO can significantly enhance SOP predictions in BMS. This advancement has the potential to improve the safety, reliability, and efficiency of battery operations.
In summary, most of the existing SOP estimation methods are based on battery characteristic parameters or models. Parameters such as temperature, voltage, current, and SOC are selected as the multi-parameter constraints for the safe operation of the battery, but the impacts of battery inconsistency, aging, and environment are not considered. This severely restricts the actual peak (maximum) power output of the power battery system.
SOP and SOF are both used to evaluate the dynamic performance of batteries, but their focus and application scenarios are different. SOP is the foundation of SOF. The evaluation of SOF usually relies on the power capability data provided by SOP [51,52]. The SOP estimation method is used by BMS to determine the maximum discharge power that the battery can provide currently, with the goal of preventing it from exceeding the limit. While SOF is used to determine whether the current maximum discharge power meets the driver’s demand for rapid acceleration power. If the demand is not met, SOF will issue a warning about power limitations.
3.5. SOT Estimation
The temperature has a significant influence on battery performance. Generally, the suitable working temperature of LIBs is 15 °C~35 °C, while the actual working temperature of EVs is −30 °C~50 °C. Therefore, the battery must be thermally managed; cooling is required at high temperatures, and heating is required at low temperatures [53,54]. Currently, only the surface temperature of the battery can be measured, and the internal temperature of the battery needs to be estimated using a thermal model. SOT generally extracts the battery core temperature value in the thermal model as the value of SOT estimation. In [55], a framework for estimating the state of thermal conditions in cylindrical LIBs was proposed, utilizing a square root cubature Kalman filter algorithm. This method enables precise online estimation of both internal and surface temperatures of the power battery, achieving a mean absolute error of less than 1.16 °C. Shen et al. [56] developed an SOT estimation framework, which accounts for multiple places temperature estimation and is concerned with a wide variation range and whole battery lifespan. Furthermore, an improved electrochemical–thermal model is established, which can accurately estimate the pole ear temperature and surface temperature with a maximum error (MAXE) of less than 1.10 °C. Li et al. [57] developed a method for SOC estimation utilizing the SOT to enhance battery thermal management. They proposed a lightweight, weight-clustered convolutional neural network combined with long short-term memory (WC-CNN-LSTM) to achieve accurate SOT and SOC estimations with minimal model complexity.
3.6. SOS Estimation
The battery SOS accurately assesses the battery safety status and gives the value of the safety risk level. Through the early warning of SOS, the battery can be prevented from working in high-risk areas, and the occurrence of safety accidents can be prevented. Compared with other state estimations, the research on SOS is still very scarce. However, the research on SOS has begun to attract the attention of researchers. Cabrera-Castillo et al. [58] introduced a definition and methodology for assessing the SOS of energy storage systems. This approach is based on the principle that safety is inversely related to the level of misuse. The proposed safety metric employs a scale similar to other common state indicators such as SOC, SOH, and SOF, ranging from 0, indicating complete unsafety, to 1, indicating full safety. Song et al. [59] provided a comprehensive overview of the definition and classification of battery safety, along with evaluation methods and influencing factors. They examined the safety boundaries of LIBs and analyzed the mechanisms by which nine factors—voltage, ambient temperature, current, mechanical deformation, external conditions, SOC, SOH, IR, and lithium plating—affect battery safety.
4. Multi-State Joint Estimation Scheme
The multi-time scale coupling problem arises from the complexity of battery dynamic behavior, such as significant differences in time scales of electrochemical reactions (μs~ms), polarization effects (s~min), hysteresis effects (min~h), and aging processes (days~years). Thus, the internal states of the battery, such as SOC, SOH, and SOP, have different time scales, as shown in Figure 8. They are strongly coupled and extremely sensitive to temperature and working conditions. SOC and SOP are state variables that change rapidly, while battery available capacity and SOH change slowly. If the same time scale is used, the estimated value of SOH will remain unchanged for a long time, which will cause calculation loss. If there is a slight difference in the estimated value of SOH in a short period, this will cause instability of the SOC estimation [60]. The traditional single-time-scale model is difficult to balance real-time performance and accuracy and needs to be solved through multi-time-scale decoupling and collaborative estimation.
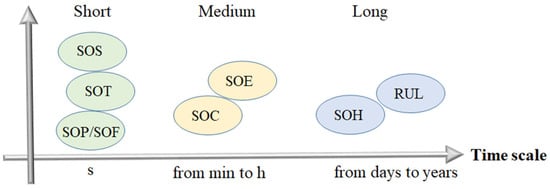
Figure 8.
Different time scales for different battery states.
The existing single-state islanding estimation methods are mostly for single-state estimation without considering the coupling relationship between each other; it is difficult to achieve accurate estimation during the full life cycle, as shown in Figure 9. The estimation error will become larger and larger as the battery ages in the actual operation of the vehicles. More challenging is that the industry has put forward higher requirements for battery state estimation: the absolute value of the estimated error of SOC, SOP, and SOH is 3% within the full life cycle and wide operating temperature range. The issue of accurate and coordinated estimation of batteries in multiple states remains extremely challenging internationally.
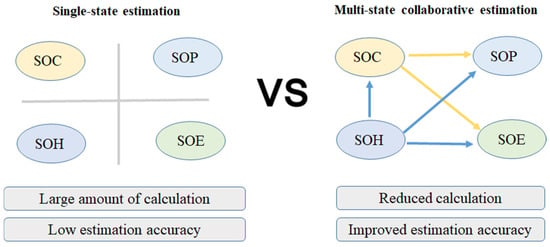
Figure 9.
Single-state and multi-state joint estimations.
One of the basic approaches for SOC-SOH-SOP joint estimation is shown in Figure 10. The implementation process of the method is as follows: First, based on the measured or obtained battery experimental big data, the influence of battery model parameters such as ohmic and polarization IR and OCV on the accuracy of state estimation is analyzed to determine which of them are the sensitive parameters. Second, data-driven methods can be used to study and establish the nonlinear mapping relationship between model-sensitive parameters and battery capacity, and the incremental analysis method can be used to track the peak value of the differential curve of the capacity and voltage at different stages of aging to realize the SOH estimation on the long-time scale. Third, based on the battery model and AUKF, the SOC estimation can be achieved under a short time scale (generally the same as the sampling interval) at different stages of aging. Fourth, the multi-parameter constraint conditions for the safe working range of power batteries can be constructed, such as charge and discharge voltage, current, SOC, SOH, and operating temperature range, and then the SOP estimation can be achieved. Finally, the SOC-SOH-SOP multi-state coordinated estimation can be obtained under multiple time scales, which can solve the problem of inaccurate state estimation caused by the environment, aging, and single-state estimation methods.
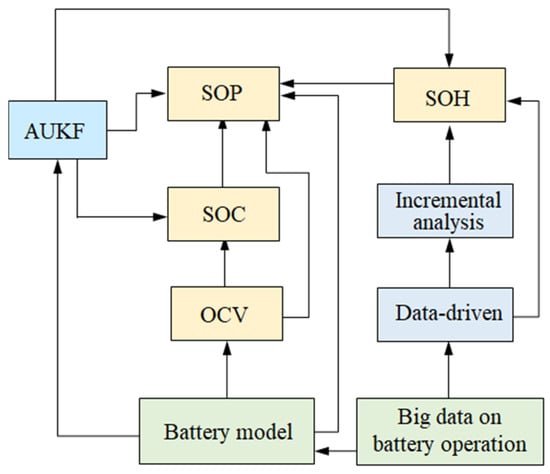
Figure 10.
SOC-SOH-SOP joint estimation.
Scholars have used different methods to study joint estimation between different states, as shown in Table 3, achieving better results and significantly improving estimation accuracy compared to single-state estimation. Li et al. [61] introduced a multi-time scale, multi-constraint SOP estimation method for LIBs utilizing H∞ filtering. The approach achieved a mean absolute relative error (MARE) of 1.17% for SOC estimation, while the MARE for SOP estimation across various time scales remained below 1.6%. These results demonstrate the method’s high accuracy and robustness in joint estimation tasks. Cheng et al. [62] proposed a joint estimation method for SOC and SOP of LIBs based on LSTM and used the coupling relationship between SOC and SOP to realize SOP estimation under multi-parameter constraints. Muh et al. [63] investigated a joint estimation approach for SOC and SOP using bidirectional LSTNM (BiLSTM). Their method considers the influence of the current battery state on one-step-ahead predictions of both SOC and SOP. The findings indicate that simultaneous estimation of SOC and SOP yields a significant improvement in accuracy—approximately 28.35% higher—compared to independent estimation methods. Qian et al. [64] proposed a hybrid neural network model, named CNN-SAM-LSTM, which integrates a convolutional neural network, a self-attention mechanism, and a long short-term memory neural network. This model is designed to jointly estimate the state of lithium-ion batteries, including state of charge (SOC), state of health (SOH), and state of energy (SOE). Lee et al. [65] studied the co-estimation of SOC and SOT in LIBs using a recursive least squares (RLS)-based heat generation model, which focused on analyzing battery heat generation prior to the implementation of thermal management strategies through a BMS. Liu et al. [66] trained a CNN-LSTM model to accomplish the joint estimation of battery SOC, SOH, and SOT, which can more comprehensively reflect the state of the battery compared to previous research. The result shows that the mean absolute error (MAE) of the CNN-LSTM model jointly estimating the SOC, SOH, and SOT is 2.9%, 4.8%, and 0.55 °C, which are lower than other data-driven models.

Table 3.
Different multi-state joint methods.
5. Discussion and Conclusions
From the research status mentioned above, it can be observed that there are still theoretical challenges that need to be addressed in battery state estimation. For example, how the nonlinear characteristics in battery dynamics affect the accuracy of state estimation, such as hysteresis effects, voltage relaxation, and capacity decay nonlinearity. The nonlinear characteristics of batteries significantly increase the complexity of state estimation, leading to the amplification of estimation errors in traditional linear models (such as ECMs) or simplified algorithms. Taking hysteresis effects as an example, the traditional OCV-SOC lookup table method may fail under hysteresis effects, and temperature changes and aging will further distort the OCV-SOC curve. Meanwhile, the hysteresis effects can lead to inaccurate measurement of instantaneous internal resistance, affecting SOP prediction. The future solution can be achieved by improving the battery model, describing different charge/discharge paths through differential equations, and establishing a bidirectional hysteresis model. Furthermore, the state estimation can be separated through multiple time scales, in which the hysteresis effect (slow dynamics) is decoupled from the polarization effect (fast dynamics).
Modeling, multi-state estimation, and RUL prediction of EV power battery systems are enduring research hotspots, especially with the development of artificial intelligence, big data, and internet of things technologies, which further promote the development and research of EV power battery-related technologies. The Kalman filtering method based on ECMs, for instance, has significant errors under complex operating conditions. In the future, multi-source information fusion models for complex and changeable battery operating conditions will gain significant attention. For example, the electrochemical–thermomechanical coupling model can be combined to improve the estimation accuracy under extreme working conditions, such as fast charging and low temperature. In addition, the multi-state collaborative estimation method of power battery will also be focused on. The combination of data-driven and physics-informed model fusion can further improve estimation accuracy, such as using physics-informed machine learning to achieve collaborative optimization of SOC-SOH-SOT joint estimation frameworks. Meanwhile, considering that complex algorithms (such as EChMs) are computationally heavy and difficult to run in real time, we can use edge AI chips to achieve lightweight algorithms through edge computing. It can not only improve the estimation accuracy of each state but also reduce the calculated amount of the controller through edge computing, which is of great significance to the BMS.
Future advancements in battery state estimation are expected to focus on achieving higher accuracy, real-time responsiveness, and adaptability. Combining electrochemical mechanisms, AI, and edge computing, it will finally achieve real-time and accurate estimation of battery life cycle and all working conditions.
Author Contributions
Conceptualization, Q.Z. and H.R.; methodology, Q.Z. and H.R.; software, Q.Z. and X.D.; validation, Q.Z. and X.D.; formal analysis, Q.Z. and H.R.; investigation, M.P. and Q.Z.; resources, Q.Z.; data curation, Q.Z. and M.P.; writing—original draft preparation, Q.Z. and M.P.; writing—review and editing, Q.Z. and D.Z.; visualization, Q.Z.; supervision, Q.Z. and D.Z.; project administration, Q.Z. and D.Z.; funding acquisition, Q.Z., X.D. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the National Natural Science Foundation of China, grant numbers 62203271 and U22A20245; in part by the China Postdoctoral Science Foundation 2023M742070 and GZC20231453; the Shandong Postdoctoral Science Foundation SDCX-ZG-202501012; and in part by the Natural Science Foundation of Xinjiang Uygur Autonomous Region, grant number 2022D01C462, which are gratefully acknowledged.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank the editors for the invitation and thank the anonymous reviewers and the editors for their helpful comments.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Ah | ampere-hour |
| AUKF | adaptive unscented Kalman filter |
| BiLSTM | bidirectional long short-term memory networks |
| BMS | battery management system |
| BPNN | back-propagation neural network |
| BPINN | battery physics-informed neural network |
| CDKF | central difference Kalman filter |
| CNN | convolutional neural networks |
| DOD | depth of discharge |
| DV | discharge voltage |
| Dual-EKF | dual extended Kalman filter |
| DFFNN | deep feedforward neural networks |
| EChM | electrochemical model |
| ECM | equivalent circuit model |
| EKF | extended Kalman filter |
| EV | electric vehicle |
| FFNN | feedforward neural network |
| FO | fractional-order |
| GA | genetic algorithms |
| GMR | Gaussian mixture regression |
| GPR | Gaussian process regression |
| HI | health indicator |
| IC | incremental capacity |
| LIB | lithium-ion battery |
| IR | internal resistance |
| LSTM | long short-term memory networks |
| MARE | mean absolute value relative error |
| NN | neural network |
| OCV | open-circuit voltage |
| P2D | pseudo two-dimensional |
| RLS | recursive least squares |
| RUL | remaining useful life |
| SMO | sliding mode observer |
| SOC | state of charge |
| SOE | state of energy |
| SOH | state of health |
| SOP | state of peak power |
| SOF | state of function |
| SOT | state of temperature |
| SOS | state of safety |
| SVR | support vector regression |
| SVR-PF | support vector regression particle filter |
| UKF | unscented Kalan filter |
References
- He, H.-W.; Xiong, R.; Chang, Y.-H. Dynamic Modeling and Simulation on a Hybrid Power System for Electric Vehicle Applications. Energies 2010, 3, 1821–1830. [Google Scholar] [CrossRef]
- Chen, H.; Liu, X.; Yu, J.; Okubo, K. Residual Performance Evaluation of Electric Vehicle Batteries: Focusing on the Analysis Results of a Social Survey of Vehicle Owners. Sustainability 2025, 17, 4685. [Google Scholar] [CrossRef]
- Kim, T.; Song, W.; Son, D.-Y.; Ono, L.K.; Qi, Y. Lithium-Ion Batteries: Outlook on Present, Future, and Hybridized Technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Zhang, T.; Sun, H. Research on Model Prediction of Remaining Service Life of Lithium-Ion Batteries Based on Chaotic Time Series. Electronics 2025, 14, 2280. [Google Scholar] [CrossRef]
- Zhang, Q.; Shang, Y.; Li, Y.; Cui, N.; Duan, B.; Zhang, C. A novel fractional variable-order equivalent circuit model and parameter identification of electric vehicle Li-ion batteries. ISA Trans. 2020, 97, 448–457. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.R.; Bharatiraja, C.; Udhayakumar, K.; Devakirubakaran, S.; Sekar, K.S.; Mihet-Popa, L. Advances in Batteries, Battery Modeling, Battery Management System, Battery Thermal Management, SOC, SOH, and Charge/Discharge Characteristics in EV Applications. IEEE Access 2023, 11, 105761–105809. [Google Scholar] [CrossRef]
- Jiao, S.; Zhang, G.; Zhou, M.; Li, G. A Comprehensive Review of Research Hotspots on Battery Management Systems for UAVs. IEEE Access 2023, 11, 84636–84650. [Google Scholar] [CrossRef]
- Singh, S.; More, V.; Batheri, R. Driving Electric Vehicles into the Future with Battery Management Systems. IEEE Eng. Manag. Rev. 2022, 50, 157–161. [Google Scholar] [CrossRef]
- Hasib, S.A.; Islam, S.; Chakrabortty, R.K.; Ryan, M.J.; Saha, D.K.; Ahamed, M.H.; Moyeen, S.I.; Das, S.K.; Ali, M.F.; Islam, M.R. A comprehensive review of available battery datasets, RUL prediction approaches, and advanced battery management. IEEE Access 2021, 9, 86166–86193. [Google Scholar] [CrossRef]
- Wang, X.; Liu, S.; Zhang, Y.; Lv, S.; Ni, H.; Deng, Y.; Yuan, Y. A Review of the Power Battery Thermal Management System with Different Cooling, Heating and Coupling System. Energies 2022, 15, 1963. [Google Scholar] [CrossRef]
- Zhang, C.; Kang, Y.; Duan, B.; Zhou, Z.; Zhang, Q.; Shang, Y.; Chen, A. An Adaptive Battery Capacity Estimation Method Suitable for Random Charging Voltage Range in Electric Vehicles. IEEE Trans. Ind. Electron. 2021, 69, 9121–9132. [Google Scholar] [CrossRef]
- Kampik, M.; Fice, M.; Sztymelski, K.; Oliwa, W.; Wieczorek, G. Examples of Problems with Estimating the State of Charge of Batteries for Micro Energy Systems. Energies 2025, 18, 2850. [Google Scholar] [CrossRef]
- Wilson, J.; Barthorpe, R.J.; Terzioglu, F. Alternative Sensing for State-of-Charge Estimation of Latent Heat Thermal Energy Storage. Energies 2025, 18, 2853. [Google Scholar] [CrossRef]
- Soyoye, B.D.; Bhattacharya, I.; Anthony Dhason, M.V.; Banik, T. State of Charge and State of Health Estimation in Electric Vehicles: Challenges, Approaches and Future Directions. Batteries 2025, 11, 32. [Google Scholar] [CrossRef]
- Plett, G.L. Review and Some Perspectives on Different Methods to Estimate State of Charge of Lithium-Ion Batteries. J. Automot. Saf. Energy 2019, 10, 249–272. [Google Scholar]
- Zhang, Q.; Cui, N.; Li, Y.; Duan, B.; Zhang, C. Fractional calculus based modeling of open-circuit voltage of lithium-ion batteries for electric vehicles. J. Energy Storage 2020, 27, 100945. [Google Scholar] [CrossRef]
- Li, Z.; Lu, L.G.; Ouyang, M.G. Comparison of Methods for Improving SOC Estimation Accuracy through an Ampere-hour Integration Approach. J. Tsinghua Univ. 2010, 8, 2193–2196. [Google Scholar]
- Luo, Y.; Qi, P.; Huang, H.; Wang, J.; Wang, Y.; Li, P. Study on battery SOC estimation by ampere-hour integral method with capacity correction. Automot. Eng. 2020, 42, 681–687. [Google Scholar]
- Wang, S.L.; Xiong, X.; Zou, C.Y.; Chen, L.; Jiang, C.; Xie, Y.X.; Stroe, D.I. An improved coulomb counting method based on dual open-circuit voltage and real-time evaluation of battery dischargeable capacity considering temperature and battery aging. Int. J. Energy Res. 2021, 45, 17609–17621. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Cui, N. Estimation of state-of-charge of lithium-ion battery: Nonlinear observer method. Control Theory Appl. 2012, 29, 1639–1644. [Google Scholar]
- Wang, L.; Wang, S.; Chen, L.; Zhang, L.; Liu, X. An improved particle filter method for lithium batteries SOC estimation. Chin. Battery Ind. 2018, 22, 120–123. [Google Scholar]
- Xiong, R.; Sun, F.; He, H. State-of-charge estimation of lithium-ion batteries in electric vehicles based on an adaptive extended Kalman filter. Gaojishu Tongxin/Chin. High. Technol. Lett. 2012, 22, 198–204. [Google Scholar]
- Sun, F.C.; Hu, X.S.; Zou, Y.; Li, S.G. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- He, Y.; Huang, D.; Liu, X. SOC Estimation of Battery Pack Based on Dual Kalman Filtering Algorithm at Different Temperatures. J. Power Supply 2018, 16, 112–118. [Google Scholar]
- Zhu, R.; Duan, B.; Zhang, J.; Zhang, Q.; Zhang, C. Co-estimation of model parameters and state-of-charge for lithium-ion batteries with recursive restricted total least squares and unscented Kalman filter. Appl. Energy 2020, 277, 115494. [Google Scholar] [CrossRef]
- Shang, Y.; Zhang, C.; Cui, N. State of charge estimation for lithium-ion batteries based on extended Kalman filter optimized by fuzzy neural network. Control Theory Appl. 2016, 33, 212–220. [Google Scholar]
- Ofoegbu, O.E. State of charge (SOC) estimation in electric vehicle (EV) battery management systems using ensemble methods and neural networks. J. Energy Storage 2025, 114, 115833. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, H.; Shu, X.; Zhang, Y.; Shen, J.; Liu, Y. Synthetic state of charge estimation for lithium-ion batteries based on long short-term memory network modeling and adaptive H-Infinity filter. Energy 2021, 228, 120630. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Shi, Q.S.; Zhang, C.H.; Cui, N.X. Estimation of battery state-of-charge using v-support vector regression algorithm. Int. J. Automot. Technol. 2008, 9, 759–764. [Google Scholar] [CrossRef]
- Pei, L.; Wu, Y.; Shen, X.; Yu, C.; Wen, Z.; Wang, T. Energy State Estimation for Series-Connected Battery Packs Based on Online Curve Construction of Pack Comprehensive OCV. Energies 2025, 18, 1772. [Google Scholar] [CrossRef]
- Dong, G.Z.; Zhang, X.; Zhang, C.B.; Chen, Z.H. A method for state of energy estimation of lithium-ion batteries based on neural network model. Energy 2015, 90, 879–888. [Google Scholar] [CrossRef]
- He, H.W.; Zhang, Y.Z.; Xiong, R.; Wang, C. A novel Gaussian model based battery state estimation approach: State-of-Energy. Appl. Energy 2015, 151, 41–48. [Google Scholar] [CrossRef]
- Liu, X.T.; Wu, J.; Zhang, C.B.; Chen, Z.H. A method for state of energy estimation of lithium-ion batteries at dynamic currents and temperatures. J. Power Sources 2014, 270, 151–157. [Google Scholar] [CrossRef]
- Dong, G.Z.; Chen, Z.H.; Wei, J.W.; Zhang, C.B.; Wang, P. An online model-based method for state of energy estimation of lithium-ion batteries using dual filters. J. Power Sources 2016, 301, 277–286. [Google Scholar] [CrossRef]
- Correia, A.F.M.; Moura, P.; de Almeida, A.T. Technical and Economic Assessment of Battery Storage and Vehicle-to-Grid Systems in Building Microgrids. Energies 2022, 15, 8905. [Google Scholar] [CrossRef]
- Kim, I.-S. A Technique for Estimating the State of Health of Lithium Batteries Through a Dual-Sliding-Mode Observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar]
- Deng, T.; Luo, W.; Li, Z.; Luo, J. Estimation state of health of electric vehicle battery by dual Kalman filter. Battery Bimon. 2018, 48, 95–99. [Google Scholar]
- Liu, S.-L.; Cui, N.-X.; Zhang, C.-H. State of health estimation of lithium-ion battery based on AUKF. Power Electron. 2017, 11, 122–124. [Google Scholar]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Yan, J. Prognostic health condition for lithium battery using the partial incremental capacity and gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Zhou, Z.; Duan, B.; Kang, Y.; Shang, Y.; Zhang, Q.; Zhang, C. Practical state of health estimation for LiFePO4 batteries based on Gaussian mixture regression and incremental capacity analysis. IEEE Trans. Ind. Electron. 2023, 70, 2576–2584. [Google Scholar] [CrossRef]
- Dong, H.; Jin, X.; Lou, Y.; Wang, C. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter. J. Power Sources 2014, 271, 114–123. [Google Scholar] [CrossRef]
- Wang, Z.; Yuan, C.; Li, X. Lithium Battery State-of-Health Estimation via Differential Thermal Voltammetry with Gaussian Process Regression. IEEE Trans. Transp. Electrif. 2021, 7, 16–25. [Google Scholar] [CrossRef]
- Sun, G.; Liu, Y.; Liu, X. A method for estimating lithium-ion battery state of health based on physics-informed machine learning. J. Power Sources 2025, 627, 235767. [Google Scholar] [CrossRef]
- Zuo, Y.; Hu, X.; Ma, H.; Li, S. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Sun, F.; Xiong, R.; He, H. Estimation of state-of-charge and state-of-power capability of lithium-ion battery considering varying health conditions. J. Power Sources 2014, 259, 166–176. [Google Scholar] [CrossRef]
- Liu, X.T.; He, Y.; Zeng, G.J.; Zheng, X.X. State-of-Power Estimation for Li-ion Battery Considering the Effect of Temperature. Trans. China Electrotech. Soc. 2016, 31, 155–163. [Google Scholar]
- Chen, H.; Yang, Z.; Li, X.; Qiao, P. Grey incidence analysis for factors influencing SOP of power battery. Chin. J. Power Sources 2019, 43, 1032–1033+1066. [Google Scholar]
- Jafari, S.; Byun, Y.C. AI-driven state of power prediction in battery systems: A PSO-optimized deep learning approach with XAI. Energy 2025, 331, 136764. [Google Scholar] [CrossRef]
- Reshma, P.; Manohar, V.J. Collaborative evaluation of SoC, SoP and SoH of lithium-ion battery in an electric bus through improved remora optimization algorithm and dual adaptive Kalman filtering algorithm. J. Energy Storage 2023, 68, 107573. [Google Scholar] [CrossRef]
- Raoofi, T.; Yildiz, M. Comprehensive review of battery state estimation strategies using machine learning for battery Management Systems of Aircraft Propulsion Batteries. J. Energy Storage 2023, 59, 106486. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, Y.; Hou, L.; Hu, J.; Shang, Y. In-situ analysis and estimation of temperature distribution for large-format lithium-ion batteries based on distributed optical fiber sensors. eTransportation 2025, 100425. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, L.; Wang, S.; Zhu, Y.; Hilal, A.; Shang, Y. An Integrated Heating–Charging Method for Lithium-Ion Batteries at Low Temperature. IEEE Trans. Transp. Electrif. 2025, 11, 8005–8017. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, Z.; Shen, S.; Zhang, Y.; Chen, Z.; Liu, Y. Accurate State of Temperature Estimation for Lithium-Ion Batteries Based on Square Root Cubature Kalman Filter. Appl. Therm. Eng. 2024, 242, 122452. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, Z.; Chen, Z.; Shu, X.; Liu, Y.; Shen, S.; Liu, Y.; Zhang, Y. Temperature estimation of multiple places for lithium-ion batteries based on improved electrochemical thermal modeling. IEEE Trans. Transp. Electrif. 2025, 11, 382–392. [Google Scholar] [CrossRef]
- Li, C.; Zhu, S.; Zhang, L.; Liu, X.; Li, M.; Zhou, H.; Zhang, Q.; Rao, Z. State of charge estimation of lithium-ion battery based on state of temperature estimation using weight clustered-convolutional neural network-long short-term memory. Green Energy Intell. Transp. 2025, 4, 100226. [Google Scholar] [CrossRef]
- Cabrera-Castillo, E.; Niedermeier, F.; Jossen, A. Calculation of the state of safety (SOS) for lithium ion batteries. J. Power Sources 2016, 324, 509–520. [Google Scholar] [CrossRef]
- Song, S.; LI, F.; Tang, X. Research progress on the safety-state assessment of lithium-ion batteries. Energy Storage Sci. Technol. 2023, 12, 3545–3555. [Google Scholar]
- Yin, X.; Song, Y.; Liu, W.; Liu, D. Multi-scale state joint estimation for lithium-ion battery. Chin. J. Sci. Instrum. 2018, 39, 118–126. [Google Scholar]
- Li, R.; Li, K.; Liu, P.; Zhang, X. Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter. Batteries 2023, 9, 191. [Google Scholar] [CrossRef]
- Cheng, W.; Yi, Z.; Liang, J.; Song, Y.; Liu, D. An SOC and SOP Joint Estimation Method of Lithium-ion Batteries in Unmanned Aerial Vehicles. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the Era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020; pp. 247–252. [Google Scholar]
- Muh, K.; Caliwag, A.; Jeon, I.; Lim, W. Co-Estimation of SoC and SoP Using BiLSTM. J. Korean Inst. Commun. Sci. 2021, 46, 314–323. [Google Scholar]
- Qian, C.; Guan, H.; Xu, B.; Xia, Q.; Sun, B.; Ren, Y.; Wang, Z. A CNN-SAM-LSTM hybrid neural network for multi-state estimation of lithium-ion batteries under dynamical operating conditions. Energy 2024, 294, 130764. [Google Scholar] [CrossRef]
- Lee, S.; Kang, E.; Kim, M.; Lee, S.; Song, M.; Lee, J.; Na, W.; Kim, J. Co-Estimation of SOC and SOT in Lithium-Ion Batteries Using an RLS-Based Heat Generation Model. In Proceedings of the 2025 IEEE Applied Power Electronics Conference and Exposition (APEC), Atlanta, GA, USA, 16–20 March 2025; pp. 3012–3017. [Google Scholar]
- Liu, Y.; Dai, P.; Chen, X. Joint Estimation of SOC, SOH and SOT for Battery Energy Storage System Based on CNN-LSTM. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 1884–1888. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).