Analysis of Heat Transfer and Fluid Flow in a Solar Air Heater with Sequentially Placed Rectangular Obstacles on the Fin Surface
Abstract
1. Introduction
2. Methodology
2.1. Description of the Model
2.2. Boundary Conditions and Solution Method
2.3. Grid Independence Test
2.4. Turbulence Model Selection
2.5. Performance Indices
3. Results and Discussion
3.1. Heat Transfer Performance
3.2. Fluid Friction
3.3. Thermo-Hydraulic Performance
3.4. Correlation Derivation
4. Conclusions
- (1)
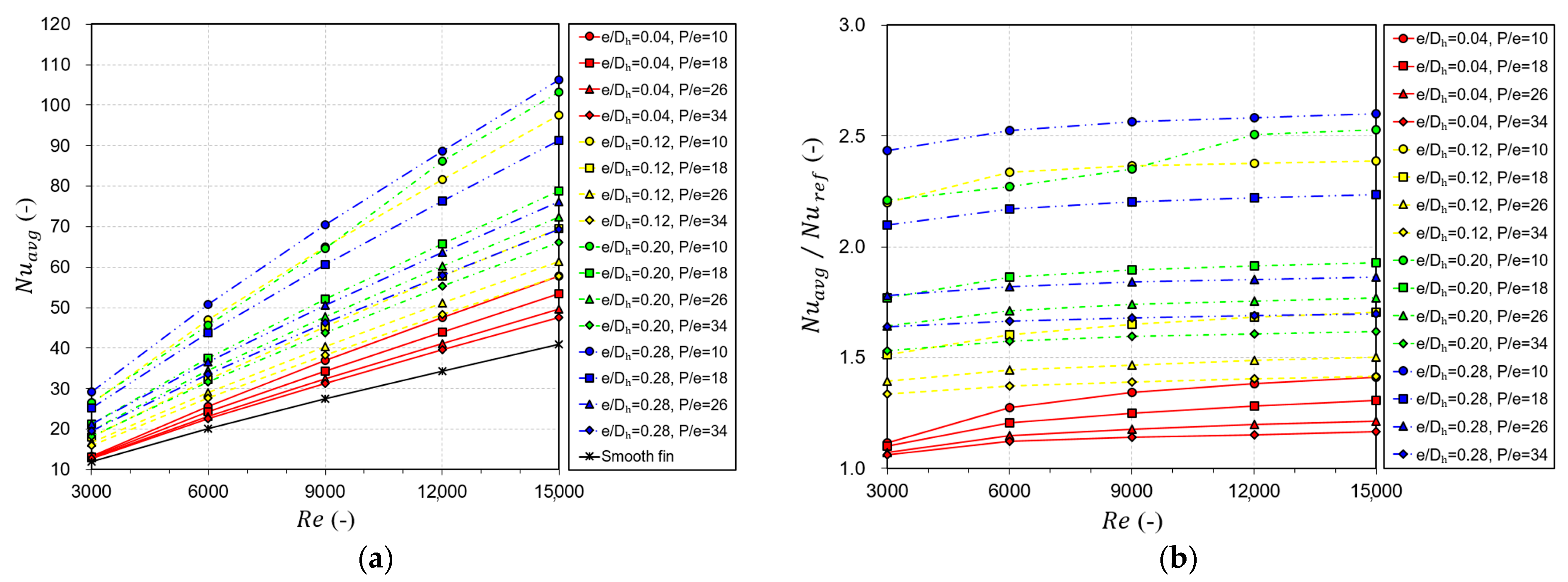
- An increase in was observed with higher relative obstacle height, lower relative obstacle pitch, and higher . The sequentially placed obstacles enhanced by 2.602 times for the case where a relative height of 0.28, a relative pitch of 10, and a of 15,000 were used.
- (2)
- Elevating the relative height and reducing the relative pitch led to an increment in , while had a comparatively smaller effect. The value of increased by 36.95 times compared to the smooth-fin case at a relative height of 0.28, a relative pitch of 10, and a of 3000.
- (3)
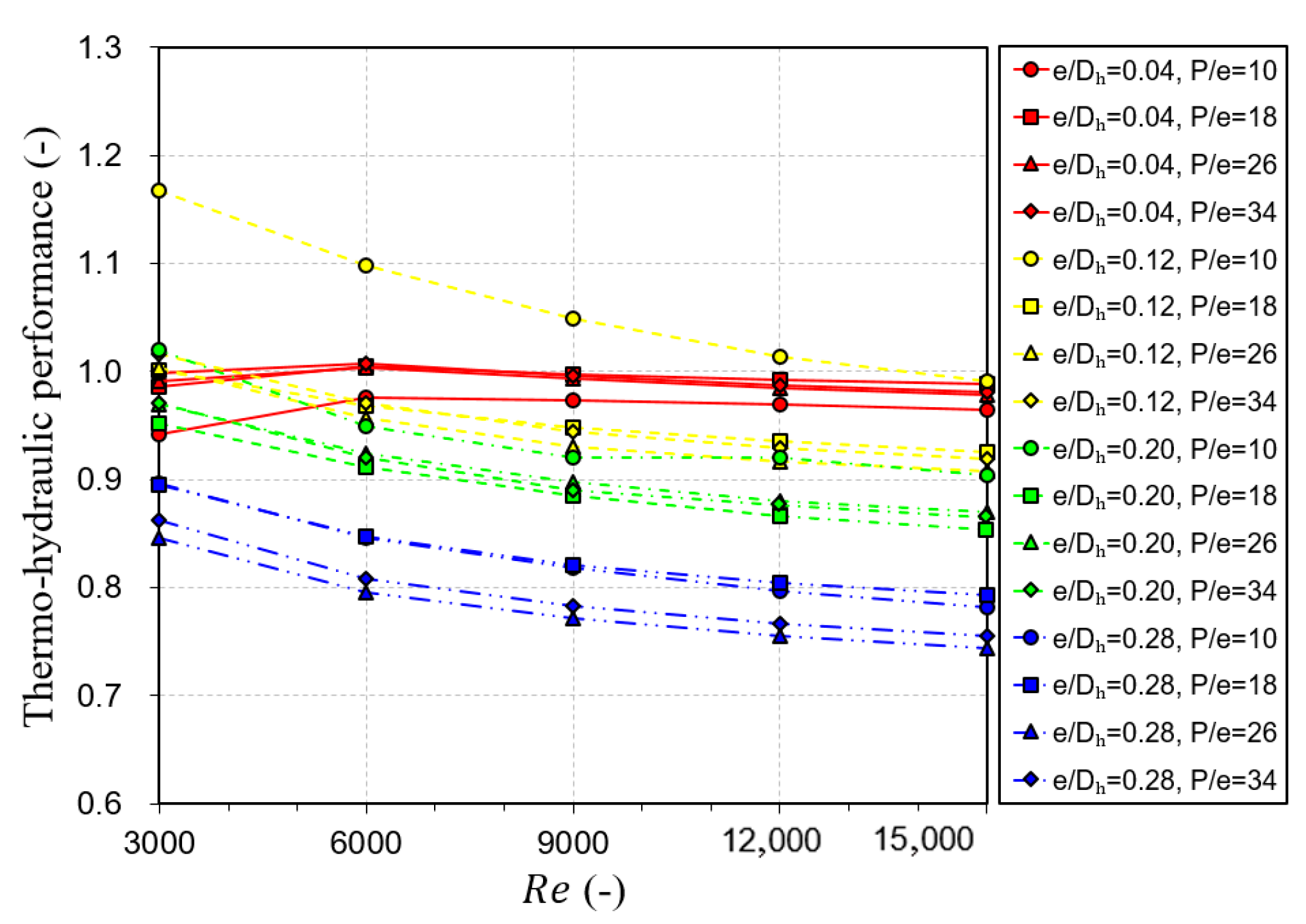
- The THP values varied from 0.744 to 1.167. The highest THP was achieved at a relative height of 0.12 and a relative pitch of 10, regardless of . Therefore, these conditions were deemed the most suitable for the obstacles when considering both thermal performance and flow resistance.
- (4)
- Correlations for , , and were derived as functions of relative height, relative pitch, and . The values of , , and were accurately predicted by the correlations with MAPEs of 5.08%, 4.55%, and 9.66%, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Surface area of the base fin (m2) | |
| Surface area of the side fin (m2) | |
| Total surface area of the fin (m2) | |
| Hydraulic diameter (m) | |
| Average friction factor (-) | |
| Friction factor for Gnielinski correlation (-) | |
| Smooth-finned air channel friction factor (-) | |
| Average convective heat transfer coefficient between the fin and the flowing air (W/m2·K) | |
| Convective heat transfer coefficient at the base surface of the fin (W/m2·K) | |
| Convective heat transfer coefficient at the side surface of the fin (W/m2·K) | |
| Thermal conductivity of the air (W/m·K) | |
| Length of the finned air channel (m) | |
| Average Nusselt number at the fin–air interface (-) | |
| Nusselt number on the fin base surface (-) | |
| Nusselt number for the smooth-finned air channel (-) | |
| Nusselt number on the fin side surface (-) | |
| Pressure drop (Pa) | |
| Prandtl number (-) | |
| Heat transfer rate at the base surface of the fin (W) | |
| Heat transfer rate at the side surface of the fin (W) | |
| Total fin-to-air heat transfer rate (W) | |
| Reynolds number (-) | |
| Temperature of the flowing air (°C) | |
| Temperature at the base surface of the fin (°C) | |
| Average temperature of the base and side of the fin (°C) | |
| Temperature on the side surface of the fin (°C) | |
| Velocity of the air (m/s) | |
| Greek symbol | |
| Air density (kg/m3) | |
References
- Chamoli, S.; Lu, R.; Xu, D.; Yu, P. Thermal performance improvement of a solar air heater fitted with winglet vortex generators. Sol. Energy 2018, 159, 966–983. [Google Scholar] [CrossRef]
- Singh, V.P.; Jain, S.; Karn, A.; Kumar, A.; Dwivedi, G.; Meena, C.S.; Dutt, N.; Ghosh, A. Recent Developments and Advancements in Solar Air Heaters: A Detailed Review. Sustainability 2022, 14, 12149. [Google Scholar] [CrossRef]
- Markam, B.; Maiti, S. Artificial enhancer for small-scale solar air heater—A comprehensive review. Clean. Energy Syst. 2023, 4, 100046. [Google Scholar] [CrossRef]
- Fakoor Pakdaman, M.; Lashkari, A.; Basirat Tabrizi, H.; Hosseini, R. Performance evaluation of a natural-convection solar air-heater with a rectangular-finned absorber plate. Energy Convers. Manag. 2011, 52, 1215–1225. [Google Scholar] [CrossRef]
- Fudholi, A.; Sopian, K.; Ruslan, M.H.; Othman, M.Y. Performance and cost benefits analysis of double-pass solar collector with and without fins. Energy Convers. Manag. 2013, 76, 8–19. [Google Scholar] [CrossRef]
- Priyam, A.; Chand, P. Thermal and thermohydraulic performance of wavy finned absorber solar air heater. Sol. Energy 2016, 130, 250–259. [Google Scholar] [CrossRef]
- Kabeel, A.E.; Hamed, M.H.; Omara, Z.M.; Kandeal, A.W. Influence of fin height on the performance of a glazed and bladed entrance single-pass solar air heater. Sol. Energy 2018, 162, 410–419. [Google Scholar] [CrossRef]
- Chand, S.; Chand, P.; Kumar Ghritlahre, H. Thermal performance enhancement of solar air heater using louvered fins collector. Sol. Energy 2022, 239, 10–24. [Google Scholar] [CrossRef]
- Karwa, R. Thermo-hydraulic performance of solar air heater with finned absorber plate forming multiple rectangular air flow passages in parallel under laminar flow conditions. Appl. Therm. Eng. 2023, 221, 119673. [Google Scholar] [CrossRef]
- Vengadesan, E.; Arunkumar, T.; Krishnamoorthi, T.; Senthil, S. Thermal performance improvement in solar air heating: An absorber with continuous and discrete tubular and v-corrugated fins. Therm. Sci. Eng. Prog. 2024, 48, 102416. [Google Scholar] [CrossRef]
- Elakrout, O.; Ghriss, O.; Bouabidi, A.; Garcia Castellanos, H.; Mohtaram, S.; Keçebaş, A.; Aryanfar, Y. Investigative analysis of the influence of diverse fin configurations on the performance of a dual pass solar air collector. Therm. Sci. Eng. Prog. 2024, 50, 102545. [Google Scholar] [CrossRef]
- Yang, M.; Yang, X.; Li, X.; Wang, Z.; Wang, P. Design and optimization of a solar air heater with offset strip fin absorber plate. Appl. Energy 2014, 113, 1349–1362. [Google Scholar] [CrossRef]
- Saravanan, A.; Parida, S.; Murugan, M.; Reddy, M.S.; Elumalai, P.V.; Kumar Dash, S. Thermal performance prediction of a solar air heater with a C-shape finned absorber plate using RF, LR and KNN models of Machine learning. Therm. Sci. Eng. Prog. 2023, 38, 101630. [Google Scholar] [CrossRef]
- Albdoor, A.K.; Obaid, Z.A.H.; Kamel, M.S.; Azzawi, I.D.J. Energy, exergy, economic and environmental analysis of a solar air heater integrated with double triangular fins: Experimental investigation. Int. J. Thermofluids 2024, 24, 100979. [Google Scholar] [CrossRef]
- Singh Bisht, V.; Kumar Patil, A.; Gupta, A. Review and performance evaluation of roughened solar air heaters. Renew. Sustain. Energy Rev. 2018, 81, 954–977. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A CFD (computational fluid dynamics) based heat transfer and fluid flow analysis of a solar air heater provided with circular transverse wire rib roughness on the absorber plate. Energy 2013, 55, 1127–1142. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A numerical investigation of square sectioned transverse rib roughened solar air heater. Int. J. Therm. Sci. 2014, 79, 111–131. [Google Scholar] [CrossRef]
- Yadav, A.S.; Bhagoria, J.L. A CFD based thermo-hydraulic performance analysis of an artificially roughened solar air heater having equilateral triangular sectioned rib roughness on the absorber plate. Int. J. Heat Mass Transf. 2014, 70, 1016–1039. [Google Scholar] [CrossRef]
- Gawande, V.B.; Dhoble, A.S.; Zodpe, D.B.; Chamoli, S. Experimental and CFD investigation of convection heat transfer in solar air heater with reverse L-shaped ribs. Sol. Energy 2016, 131, 275–295. [Google Scholar] [CrossRef]
- Singh, I.; Singh, S. CFD analysis of solar air heater duct having square wave profiled transverse ribs as roughness elements. Sol. Energy 2018, 162, 442–453. [Google Scholar] [CrossRef]
- Singh, I.; Vardhan, S.; Singh, S.; Singh, A. Experimental and CFD analysis of solar air heater duct roughened with multiple broken transverse ribs: A comparative study. Sol. Energy 2019, 188, 519–532. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, V. Unconventional solar air heater with triangular flow-passage: A CFD based comparative performance assessment of different cross-sectional rib-roughnesses. Renew. Energy 2021, 172, 1267–1278. [Google Scholar] [CrossRef]
- Boussouar, G.; Rostane, B.; Aliane, K.; Ravi, D.; Gęca, M.J.; Gola, A. Study of the Thermal Performance of Solar Air Collectors with and without Perforated Baffles. Energies 2024, 17, 3812. [Google Scholar] [CrossRef]
- Kumar, B.V.; Kanna, P.R.; Manikandan, G.; Taler, D.; Taler, J.; Sobota, T.; Nowak-Ocłoń, M. Investigation of Thermo-Hydraulic Performances of Artificial Ribs Mounted in a Rectangular Duct. Energies 2023, 16, 4404. [Google Scholar] [CrossRef]
- Khanlari, A.; Güler, H.Ö.; Tuncer, A.D.; Şirin, C.; Bilge, Y.C.; Yılmaz, Y.; Güngör, A. Experimental and numerical study of the effect of integrating plus-shaped perforated baffles to solar air collector in drying application. Renew. Energy 2020, 145, 1677–1692. [Google Scholar] [CrossRef]
- Alam, M.W.; Souayeh, B. Parametric CFD Thermal Performance Analysis of Full, Medium, Half and Short Length Dimple Solar Air Tube. Sustainability 2021, 13, 6462. [Google Scholar] [CrossRef]
- Choi, H.; Choi, K. Parametric study of a novel air-based photovoltaic-thermal collector with a transverse triangular-shaped block. Renew. Energy 2022, 201, 96–110. [Google Scholar] [CrossRef]
- Haldar, A.; Varshney, L.; Verma, P. Effect of roughness parameters on performance of solar air heater having artificial wavy roughness using CFD. Renew. Energy 2022, 184, 266–279. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.; Xie, S.; Xiao, Y. Thermo-hydraulic performance of solar air heater with built-in one-eighth sphere vortex generators. Appl. Therm. Eng. 2024, 245, 122837. [Google Scholar] [CrossRef]
- Singh, S.; Suman, S.; Mitra, S.; Kumar, M. Thermo-hydraulic performance enhancement of a solar air heater using rotating cylindrical turbulators. Appl. Therm. Eng. 2024, 236, 121748. [Google Scholar] [CrossRef]
- Mahanand, Y.; Senapati, J.R. Implementation of hybrid rib-turbulators on the thermal performance of solar air heater duct: A collective review. Sustain. Energy Technol. Assess. 2022, 52, 102345. [Google Scholar] [CrossRef]
- Hassan, A.; Nikbakht, A.M.; Fawzia, S.; Yarlagadda, P.; Karim, A. A Comprehensive Review of the Thermohydraulic Improvement Potentials in Solar Air Heaters through an Energy and Exergy Analysis. Energies 2024, 17, 1526. [Google Scholar] [CrossRef]
- Nidhul, K.; Yadav, A.K.; Anish, S.; Kumar, S. Critical review of ribbed solar air heater and performance evaluation of various V-rib configuration. Renew. Sustain. Energy Rev. 2021, 142, 110871. [Google Scholar] [CrossRef]
- Ghritlahre, H.K.; Verma, M.; Parihar, J.S.; Mondloe, D.S.; Agrawal, S. A detailed review of various types of solar air heaters performance. Sol. Energy 2022, 237, 173–195. [Google Scholar] [CrossRef]
- Choi, H.-U.; Moon, K.-A.; Kim, S.-B.; Choi, K.-H. CFD Analysis of the Heat Transfer and Fluid Flow Characteristics Using the Rectangular Rib Attached to the Fin Surface in a Solar Air Heater. Sustainability 2023, 15, 5382. [Google Scholar] [CrossRef]
- An, B.-H.; Choi, K.-H.; Choi, H.-U. Heat Transfer Augmentation and Friction Factor Due to the Arrangement of Rectangular Turbulators in a Finned Air Channel of a Solar Air Heater. Energies 2023, 16, 6891. [Google Scholar] [CrossRef]
- Diana, L.; Safitra, A.G.; Muhammad, G. Numerical Investigation of Airflow in a Trapezoidal Solar Air Heater Channel. In Proceedings of the 2019 International Electronics Symposium (IES), Surabaya, Indonesia, 27–28 September 2019; pp. 248–253. [Google Scholar]
- Al-Abbasi, O.; Sarac, B.; Ayhan, T. Experimental Investigation and CFD Modeling to Assess the Performance of Solar Air Humidifier. Int. J. Heat Technol. 2019, 37, 357–364. [Google Scholar] [CrossRef]
- Qader, B.S.; Supeni, E.E.; Ariffin, M.K.A.; Talib, A.R.A. RSM approach for modeling and optimization of designing parameters for inclined fins of solar air heater. Renew. Energy 2019, 136, 48–68. [Google Scholar] [CrossRef]
- Singh, S.; Singh, B.; Hans, V.S.; Gill, R.S. CFD (computational fluid dynamics) investigation on Nusselt number and friction factor of solar air heater duct roughened with non-uniform cross-section transverse rib. Energy 2015, 84, 509–517. [Google Scholar] [CrossRef]
- Singh, A.; Singh, S. CFD investigation on roughness pitch variation in non-uniform cross-section transverse rib roughness on Nusselt number and friction factor characteristics of solar air heater duct. Energy 2017, 128, 109–127. [Google Scholar] [CrossRef]
- Chaube, A.; Sahoo, P.K.; Solanki, S.C. Analysis of heat transfer augmentation and flow characteristics due to rib roughness over absorber plate of a solar air heater. Renew. Energy 2006, 31, 317–331. [Google Scholar] [CrossRef]
- Alam, T.; Kim, M.-H. Heat transfer enhancement in solar air heater duct with conical protrusion roughness ribs. Appl. Therm. Eng. 2017, 126, 458–469. [Google Scholar] [CrossRef]
- Kumar, S.; Verma, S.K. Heat transfer and fluid flow analysis of sinusoidal protrusion rib in solar air heater. Int. J. Therm. Sci. 2022, 172, 107323. [Google Scholar] [CrossRef]
- Wongcharee, K.; Changcharoen, W.; Eiamsa-ard, S. Numerical Investigation of Flow Friction and Heat Transfer in a Channel with Various Shaped Ribs Mounted on Two Opposite Ribbed Walls. Int. J. Chem. React. Eng. 2011, 9, A26. [Google Scholar] [CrossRef]
- Boulemtafes-Boukadoum, A.; Benzaoui, A. CFD based Analysis of Heat Transfer Enhancement in Solar Air Heater Provided with Transverse Rectangular Ribs. Energy Procedia 2014, 50, 761–772. [Google Scholar] [CrossRef]
- Kumar, R.; Goel, V.; Kumar, A. Investigation of heat transfer augmentation and friction factor in triangular duct solar air heater due to forward facing chamfered rectangular ribs: A CFD based analysis. Renew. Energy 2018, 115, 824–835. [Google Scholar] [CrossRef]
- Kim, S.-B.; Choi, H.-U. Numerical analysis of photovoltaic–thermal air collector with fins and rectangular turbulators. Therm. Sci. Eng. Prog. 2025, 59, 103393. [Google Scholar] [CrossRef]
- Choi, H.-U. Dynamic analysis of air-based photovoltaic–thermal system with fins and rectangular obstacles. Appl. Therm. Eng. 2025, 272, 126412. [Google Scholar] [CrossRef]
- Webb, R.L.; Eckert, E.R.G. Application of rough surfaces to heat exchanger design. Int. J. Heat Mass Transf. 1972, 15, 1647–1658. [Google Scholar] [CrossRef]
- Kumar, R.; Kumar, A.; Goel, V. Performance improvement and development of correlation for friction factor and heat transfer using computational fluid dynamics for ribbed triangular duct solar air heater. Renew. Energy 2019, 131, 788–799. [Google Scholar] [CrossRef]
- Gupta, A.D.; Varshney, L. Performance prediction for solar air heater having rectangular sectioned tapered rib roughness using CFD. Therm. Sci. Eng. Prog. 2017, 4, 122–132. [Google Scholar] [CrossRef]
- Choi, H.-U.; Choi, K.-H. CFD Analysis on the Heat Transfer and Fluid Flow of Solar Air Heater having Transverse Triangular Block at the Bottom of Air Duct. Energies 2020, 13, 1099. [Google Scholar] [CrossRef]
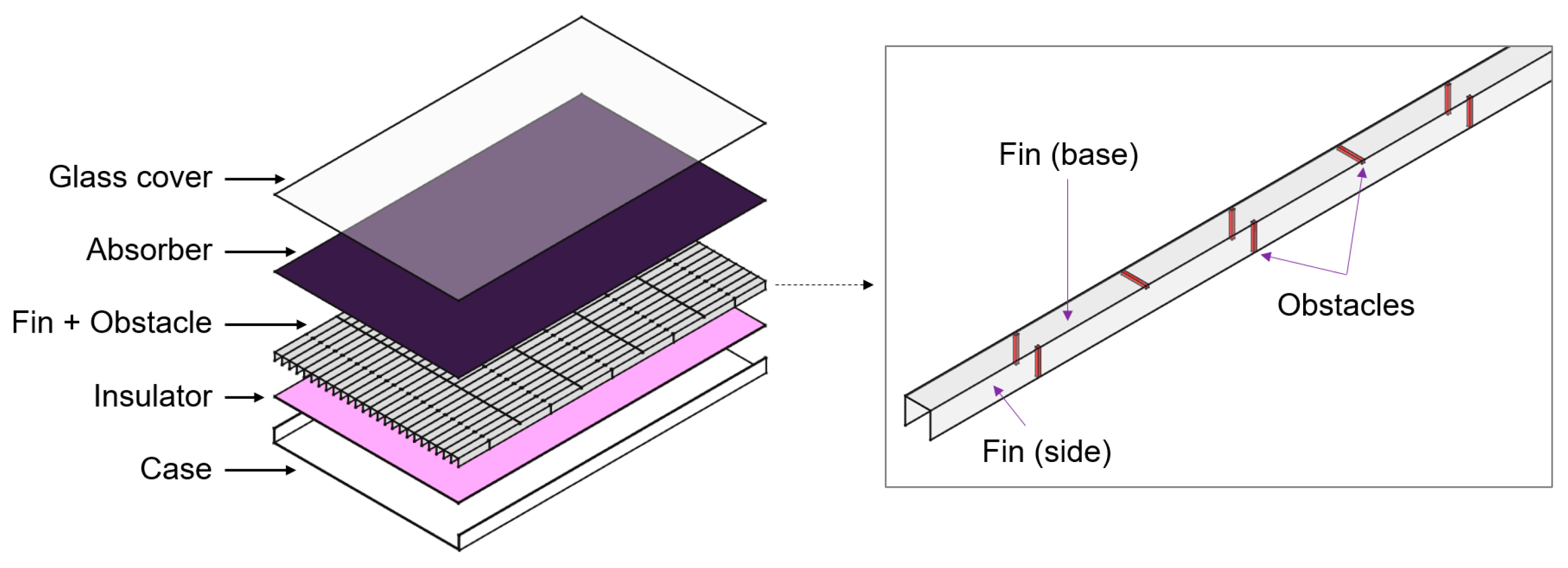
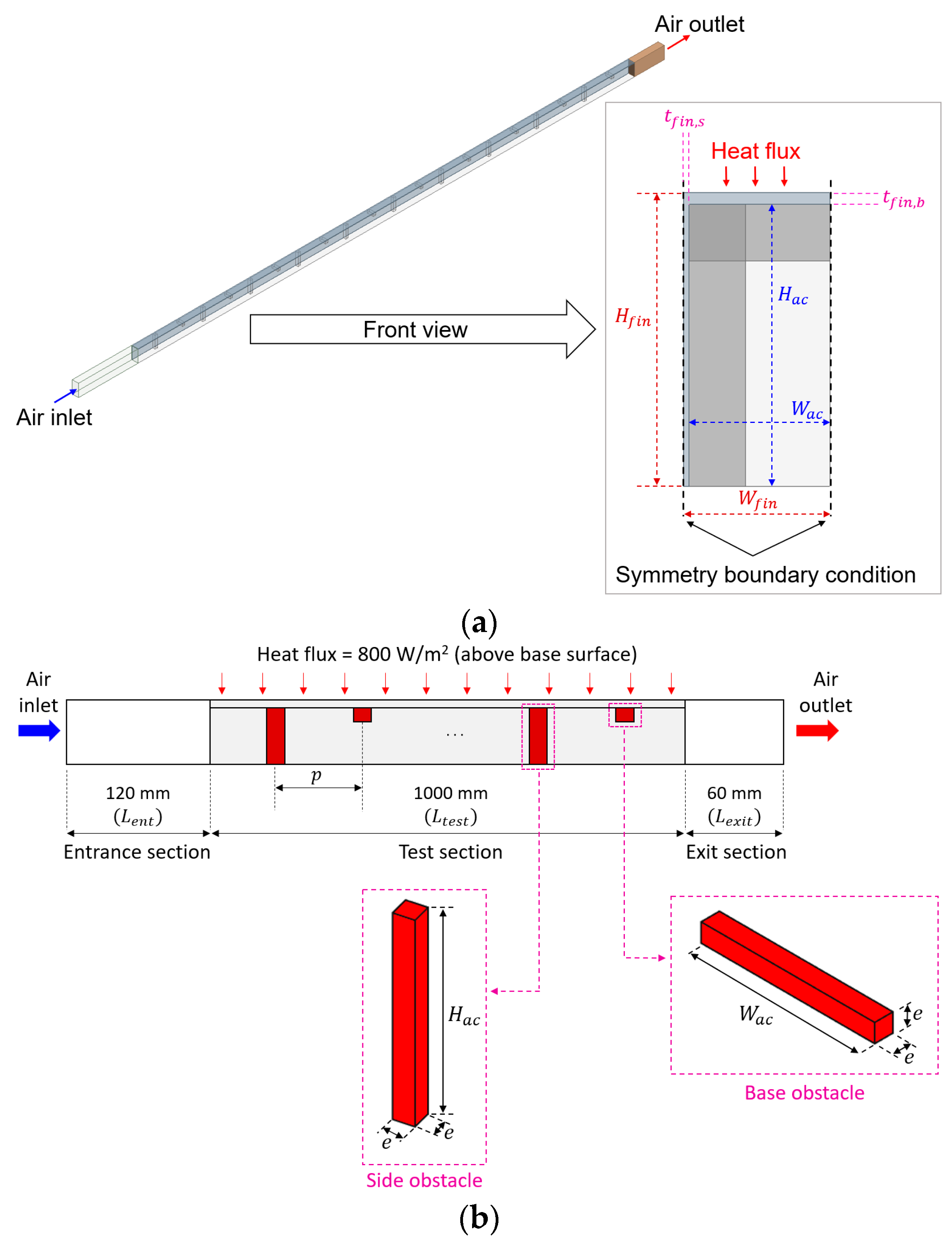

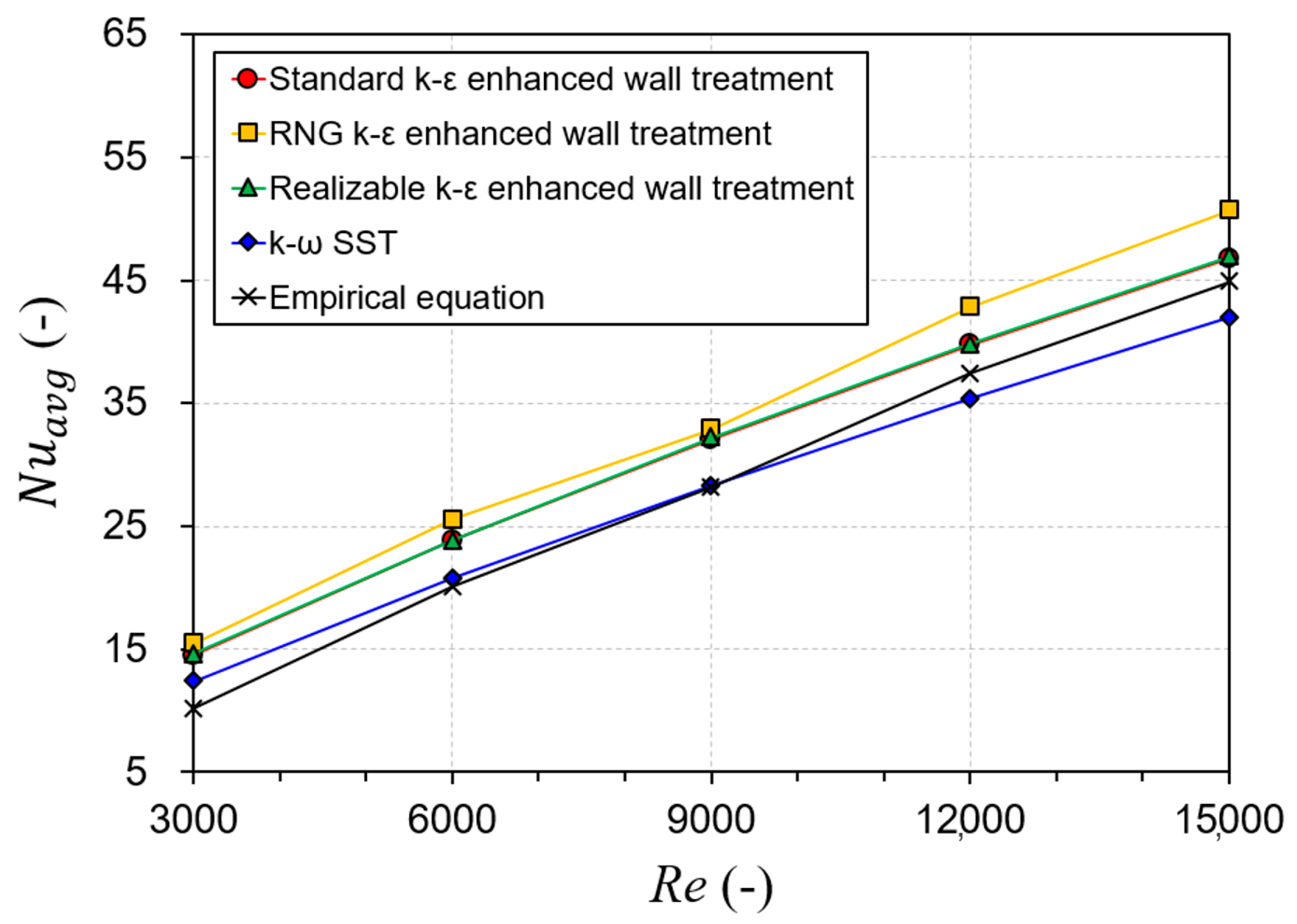
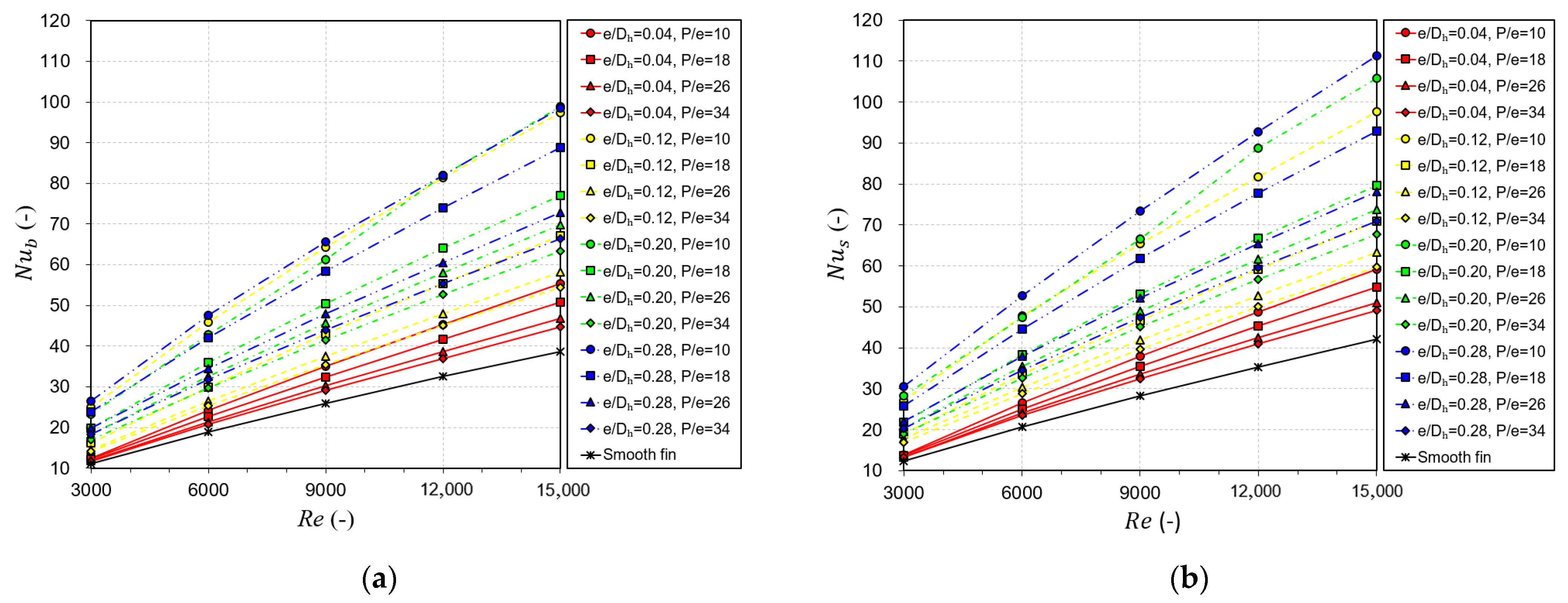
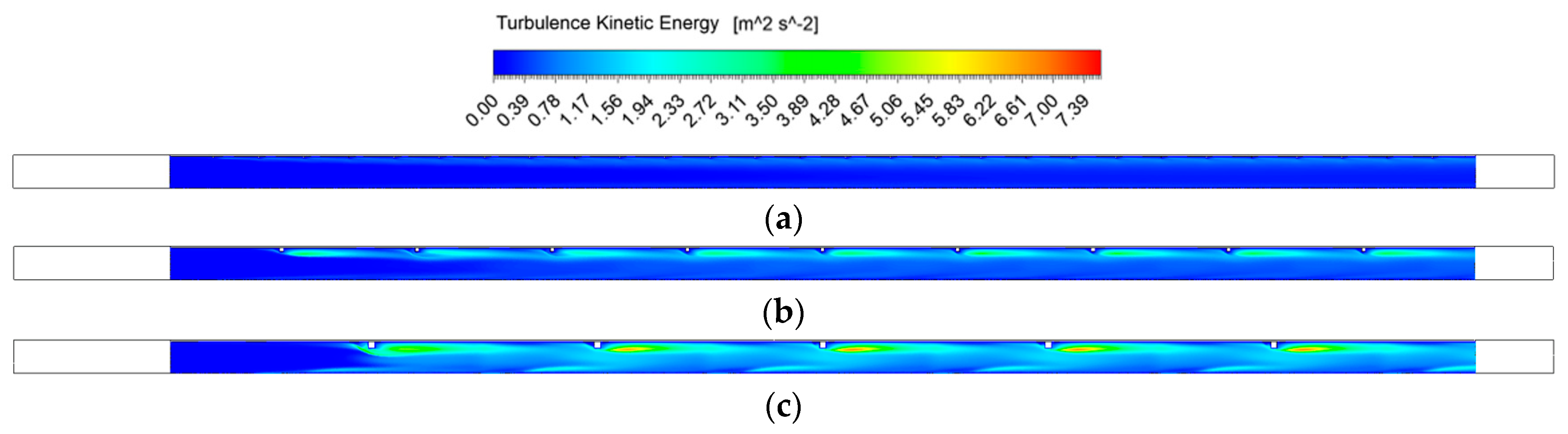


| Parameter | Nomenclature | Value |
|---|---|---|
| Length of entrance section (mm) | 120 | |
| Length of test section (mm) | 1000 | |
| Length of exit section (mm) | 60 | |
| Height of fin (mm) | 25 | |
| Width of fin (mm) | 12.5 | |
| Height of finned channel (mm) | 24 | |
| Width of finned channel (mm) | 12 | |
| Thickness of side fin (mm) | 0.5 | |
| Thickness of base fin (mm) | 1 | |
| Hydraulic diameter of finned channel (mm) | 24 | |
| Relative height (-) | 0.04, 0.12, 0.20, 0.28 | |
| Relative pitch (-) | 10, 18, 26, 34 |
| Boundary | Condition | Value |
|---|---|---|
| Top of base surface | Heat flux (W/m2) | 800 |
| Mid-plain of finned channel | Symmetry | - |
| Fin’s side surface | Symmetry | - |
| Other walls | Adiabatic | - |
| Inlet | Reynolds number (-) velocity (m/s) | 3000, 6000, 9000, 12,000, 15,000 1.683, 3.366, 5.048, 6.731, 8.414 |
| Outlet | Pressure (kPa) | 101.325 |
| Cell Number | (-) | (%) | (-) | (%) | (-) | (%) |
|---|---|---|---|---|---|---|
| 1,381,060 | 59.62 | - | 63.41 | - | 0.07045 | - |
| 2,779,150 | 59.25 | 0.62 | 58.24 | 8.16 | 0.08425 | 19.59 |
| 5,250,974 | 59.98 | 1.23 | 58.99 | 1.29 | 0.08430 | 0.06 |
| 6,622,861 | 59.89 | 0.14 | 59.29 | 0.51 | 0.08396 | 0.40 |
| 8,486,004 | 60.35 | 0.77 | 59.65 | 0.61 | 0.08408 | 0.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
An, B.-H.; Moon, K.-A.; Kim, S.-B.; Choi, H.-U. Analysis of Heat Transfer and Fluid Flow in a Solar Air Heater with Sequentially Placed Rectangular Obstacles on the Fin Surface. Energies 2025, 18, 3811. https://doi.org/10.3390/en18143811
An B-H, Moon K-A, Kim S-B, Choi H-U. Analysis of Heat Transfer and Fluid Flow in a Solar Air Heater with Sequentially Placed Rectangular Obstacles on the Fin Surface. Energies. 2025; 18(14):3811. https://doi.org/10.3390/en18143811
Chicago/Turabian StyleAn, Byeong-Hwa, Kwang-Am Moon, Seong-Bhin Kim, and Hwi-Ung Choi. 2025. "Analysis of Heat Transfer and Fluid Flow in a Solar Air Heater with Sequentially Placed Rectangular Obstacles on the Fin Surface" Energies 18, no. 14: 3811. https://doi.org/10.3390/en18143811
APA StyleAn, B.-H., Moon, K.-A., Kim, S.-B., & Choi, H.-U. (2025). Analysis of Heat Transfer and Fluid Flow in a Solar Air Heater with Sequentially Placed Rectangular Obstacles on the Fin Surface. Energies, 18(14), 3811. https://doi.org/10.3390/en18143811







