Hydroelectric Unit Fault Diagnosis Based on Modified Fractional Hierarchical Fluctuation Dispersion Entropy and AdaBoost-SCN
Abstract
1. Introduction
- The modified hierarchical entropy and fractional-order theory are incorporated into MFDE to boost its responsiveness to diverse fault signals and address the oversight of neglecting the high-frequency component of signals.
- Addressing the challenge of selecting the fractional order, the Euclidean distance is utilized to optimize the order, and a novel method for quantifying the complexity of time-series signals, termed MFHFDE, is introduced. The anti-noise performance and feature extraction capability of MFHFDE are analyzed, and it is demonstrated that MFHFDE surpasses traditional feature extraction methods such as HFDE, MFDE, and MDE.
- Utilizing the AdaBoost algorithm to assemble stochastic configuration networks, the AdaBoost-SCN strong classifier is established, which overcomes the problem of the weak generalization ability of SCN in the case of an unbalanced number of signal samples.
- The features extracted by MFHFDE are fed into the AdaBoost-SCN classifier. A novel fault diagnosis approach for hydroelectric units is proposed. The stability and superiority of this approach are confirmed via simulation experiments and contrasted against seven alternative models, such as HFDE-AdaBoost-SCN.
2. Related Theories
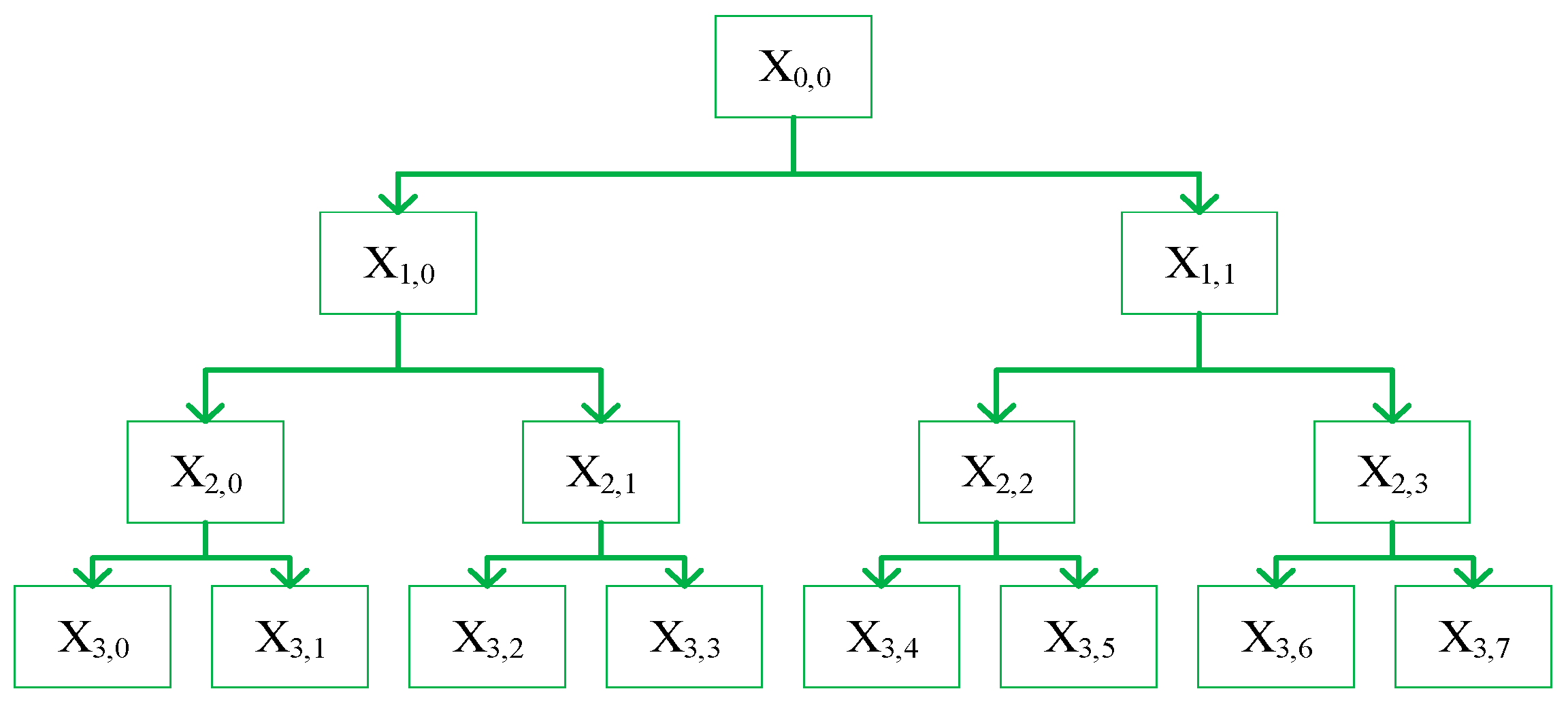
2.1. Hierarchical Fluctuation Dispersion Entropy
- Step 1:
- For the original time series , defines the operators and as:where N is the length of the time series; and represent the low-frequency and high-frequency components of the time series, respectively.
- Step 2:
- The matrix form of the operator for the k-th level can be represented as:where k is the decomposition level. If k is too small, the frequency band division of the time series will not be detailed enough to obtain sufficient low-frequency and high-frequency components. If k is too large, the computational efficiency will be low. According to Ref. [18], we set k to 4.
- Step 3:
- Construct vectors to represent non-negative integers:
- Step 4:
- The hierarchical component at e-th node in the k-th level can be obtained as:
- Step 5:
- Map to using the normal distribution function:where , , and represent the standard deviation and mean of the time series, respectively.
- Step 6:
- Each is assigned to an integer within the range of 1 to c using a linear transformation, as shown below:where represents the t-th element of the classified time series , c denotes the number of categories, and represents the integer part.
- Step 7:
- The embedding vector is calculated according to the embedding dimension m and the delay d.
- Step 8:
- The probability of each possible dispersion pattern is calculated as follows:where represents the number of times the embedding vector is mapped to each dispersion pattern .
- Step 9:
- The entropy value of the hierarchical fluctuation dispersion entropy can be obtained as:
2.2. Modified Fractional Hierarchical Fluctuation Dispersion Entropy
2.3. Stochastic Configuration Networks
- Step 1:
- Set initial input weights and biases as follows:where and are the input weight and bias of the s-th hidden node, respectively, and is the scaling factor for and . represents the maximum number of nodes in the hidden layer.
- Step 2:
- Use the sigmoid function to activate neurons in each layer. When the hidden layer node is S − 1, the output of SCN is given by:where represents the output weight of the s-th hidden node, is the input vector, and the network error can be calculated as follows:
- Step 3:
- Introduce a supervisory mechanism to randomly assign input weights and biases for node S as:where , ; r is the regularization parameter ranging from 0 to 1; μS = (1 − r)/S + 1; D represents the output dimension; is the output of the Sth hidden node.
- Step 4:
- Utilize the least squares method to calculate the hidden layer output weights and biases :Refer to the principles of setting SCN hyperparameters in Ref. [25]; the scaling factor for input weights and biases is set as {0.5, 1, 5, 10, 30, 50, 100, 150, 200, 250}, and the regularization parameter is set as {0.9, 0.99, 0.9999, 0.99999, 0.999999}.
2.4. AdaBoost-SCN
- ①
- Initialize the weights of training samples according to Equation (17) and set the number of weak classifiers M. Repeat steps ② to ⑤ for each round:
- ②
- Train the training samples based on the current weights of training samples to obtain the current weak classifier .
- ③
- Use the weak classifier to classify the training samples and obtain the classification error .
- ④
- Calculate the weight coefficient of based on the classification error as follows:
- ⑤
- Update the weights of the training samples based on the classification result of .
- ⑥
- Stop training after reaching the predetermined number of iterations. Generate the strong classifier by combining according to Equation (19):where is the strong classifier function.
3. MFHFDE Performance Analysis
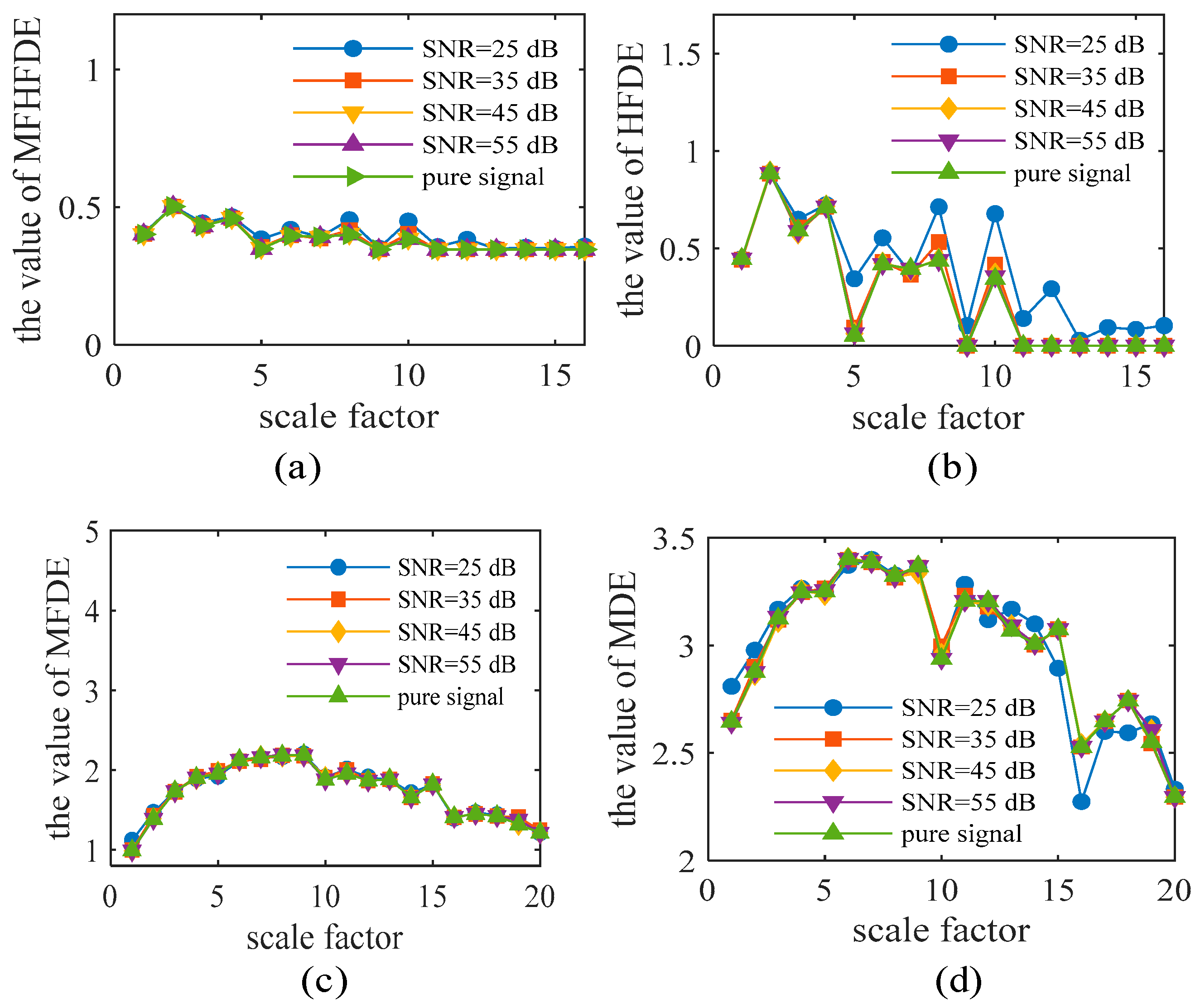
3.1. Analysis of MFHFDE’s Noise Immunity
3.2. MFHFDE Feature Extraction Capability
- (1)
- Simulation Experiment 1
- (2)
- Simulation Experiment 2
4. Experimental Analysis
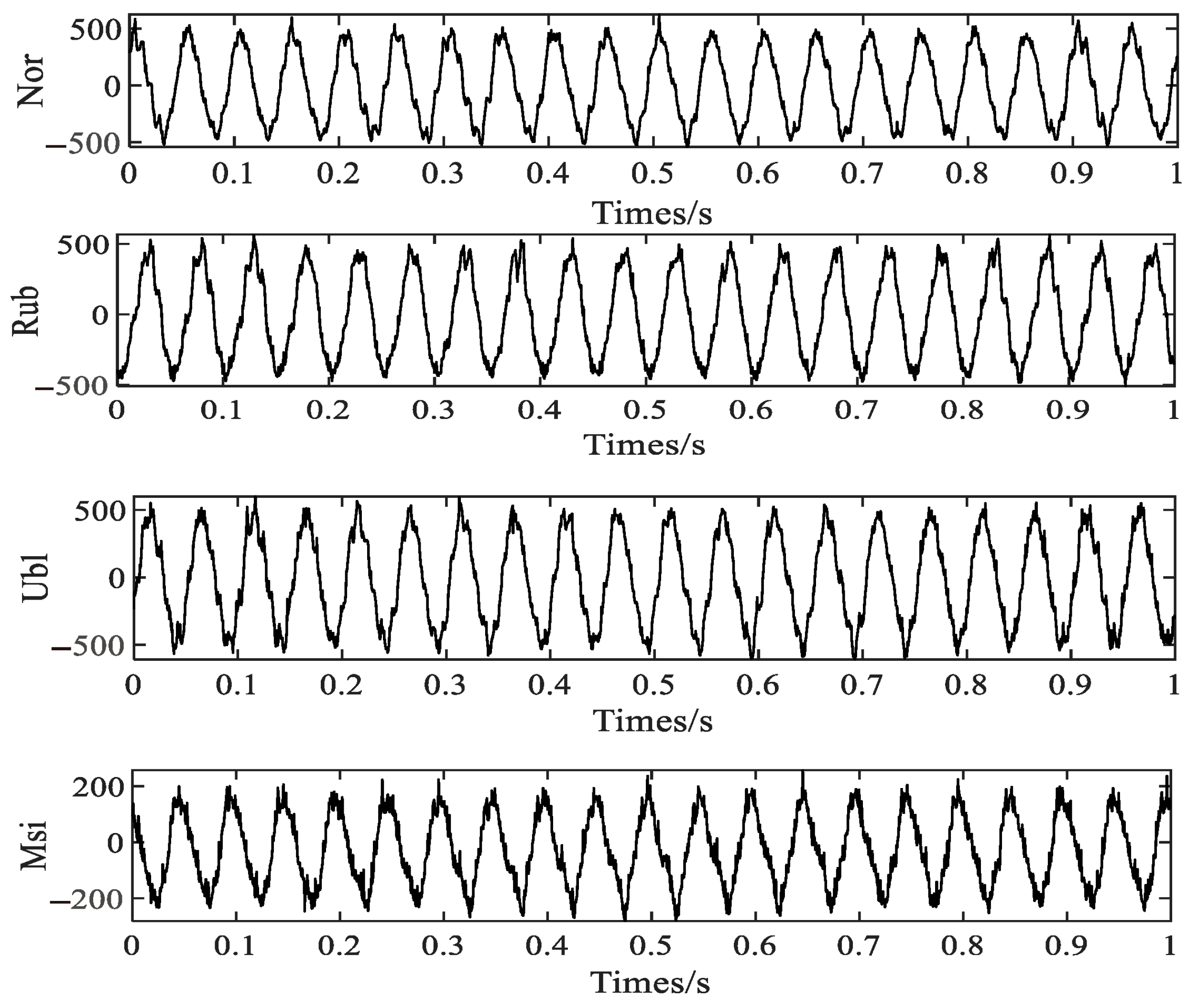
4.1. Vibration Data Acquisition on Rotor Test Bench
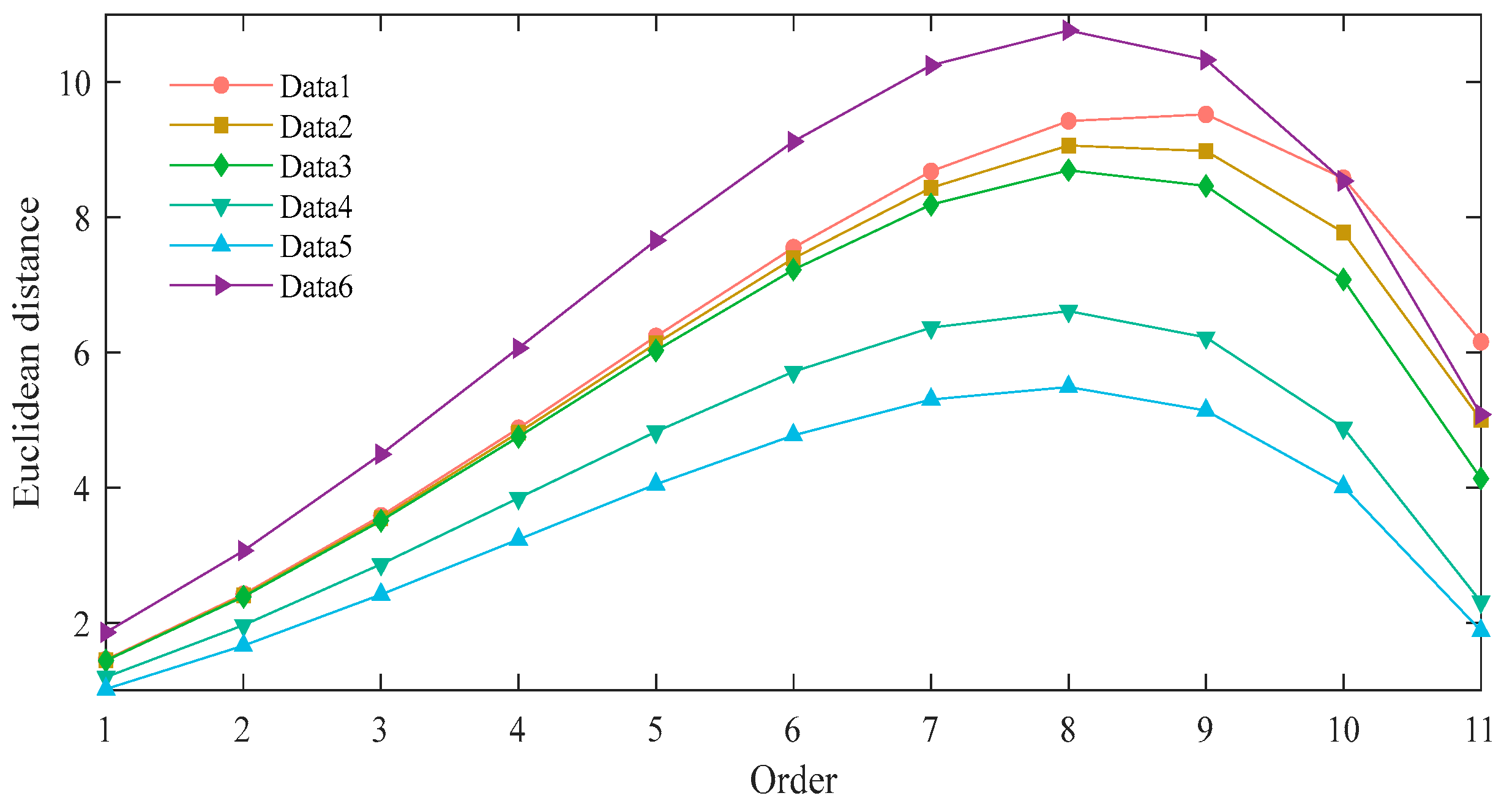
4.2. Selection of Euclidean Distance Optimization Algorithm Parameters
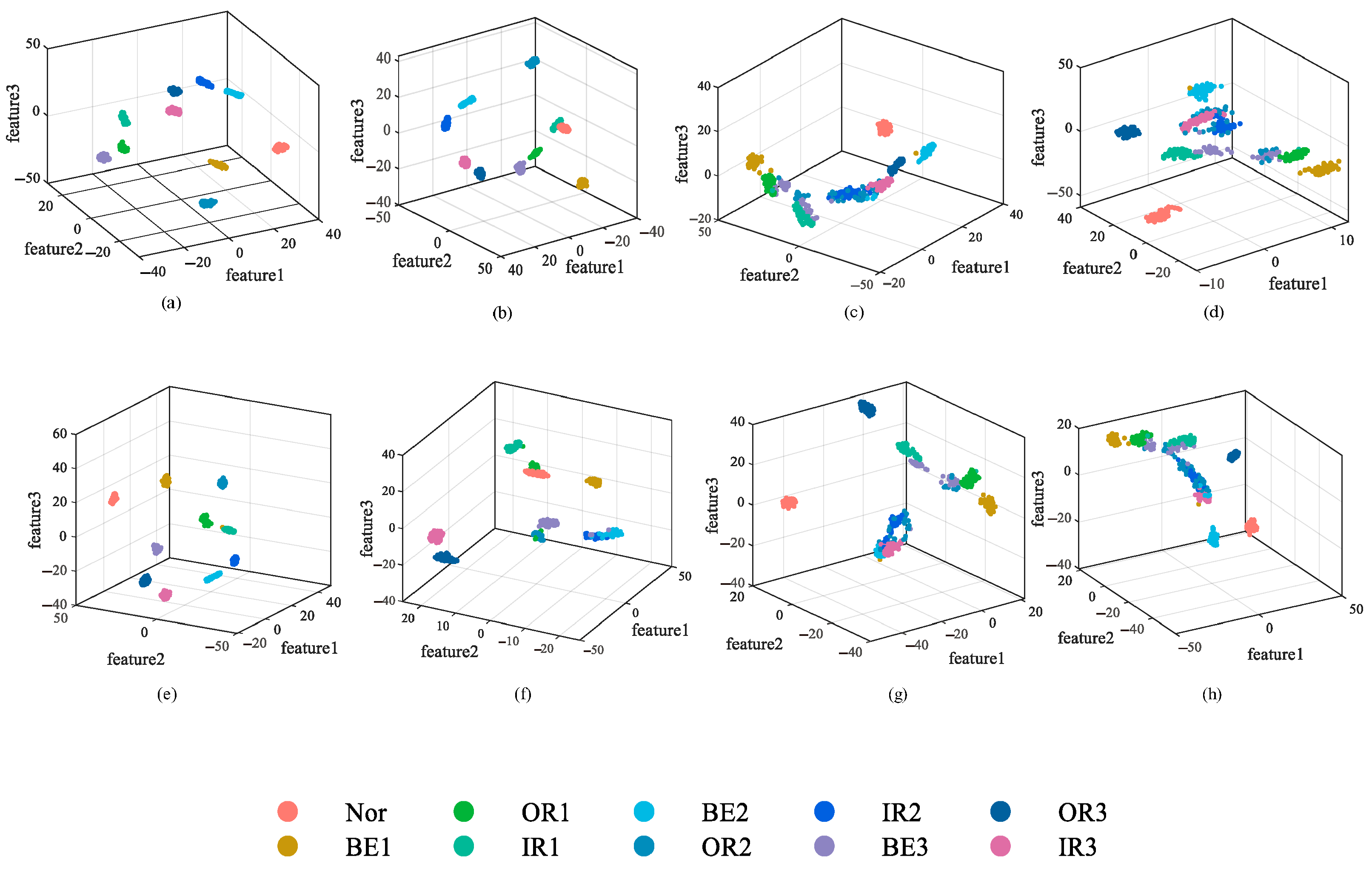
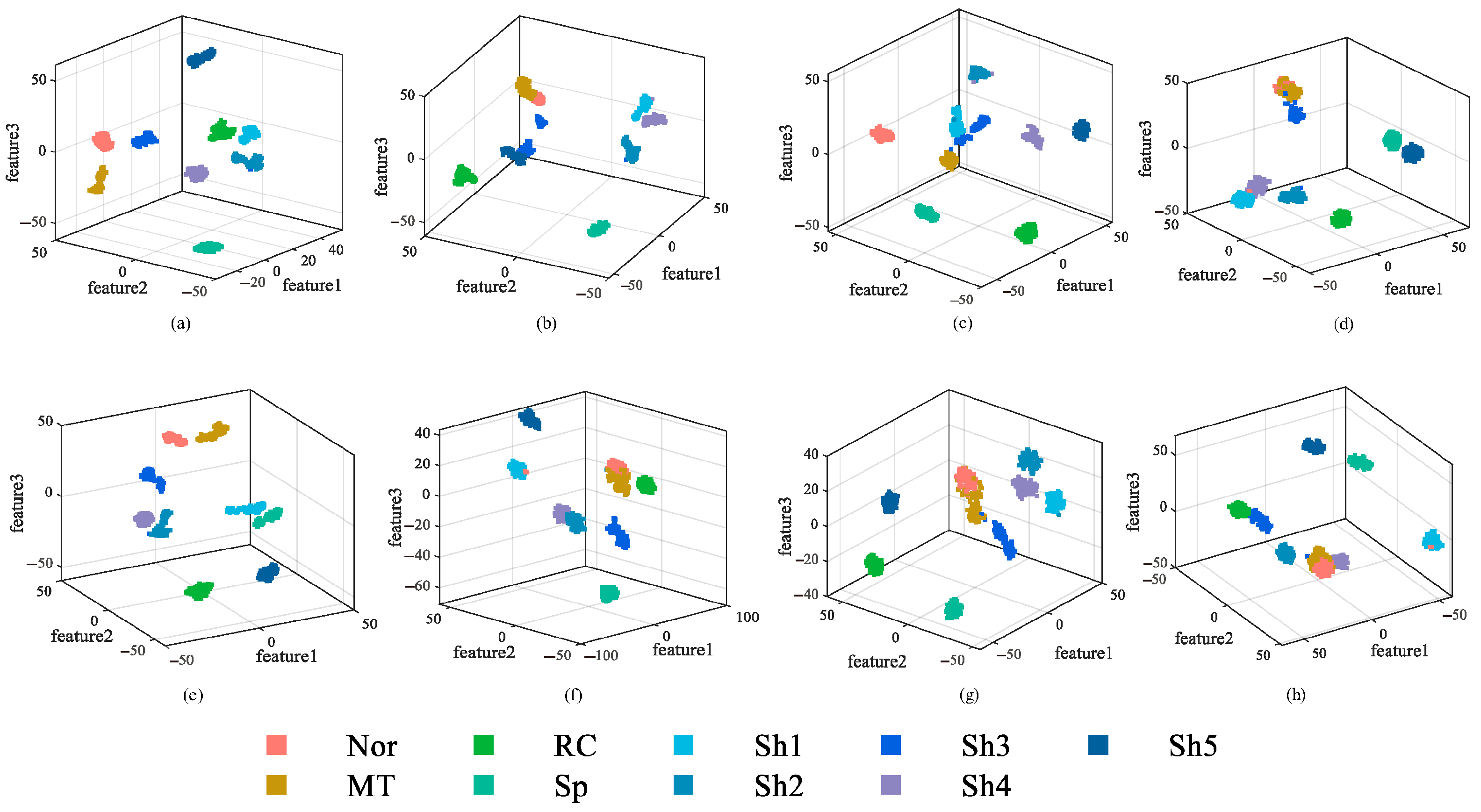
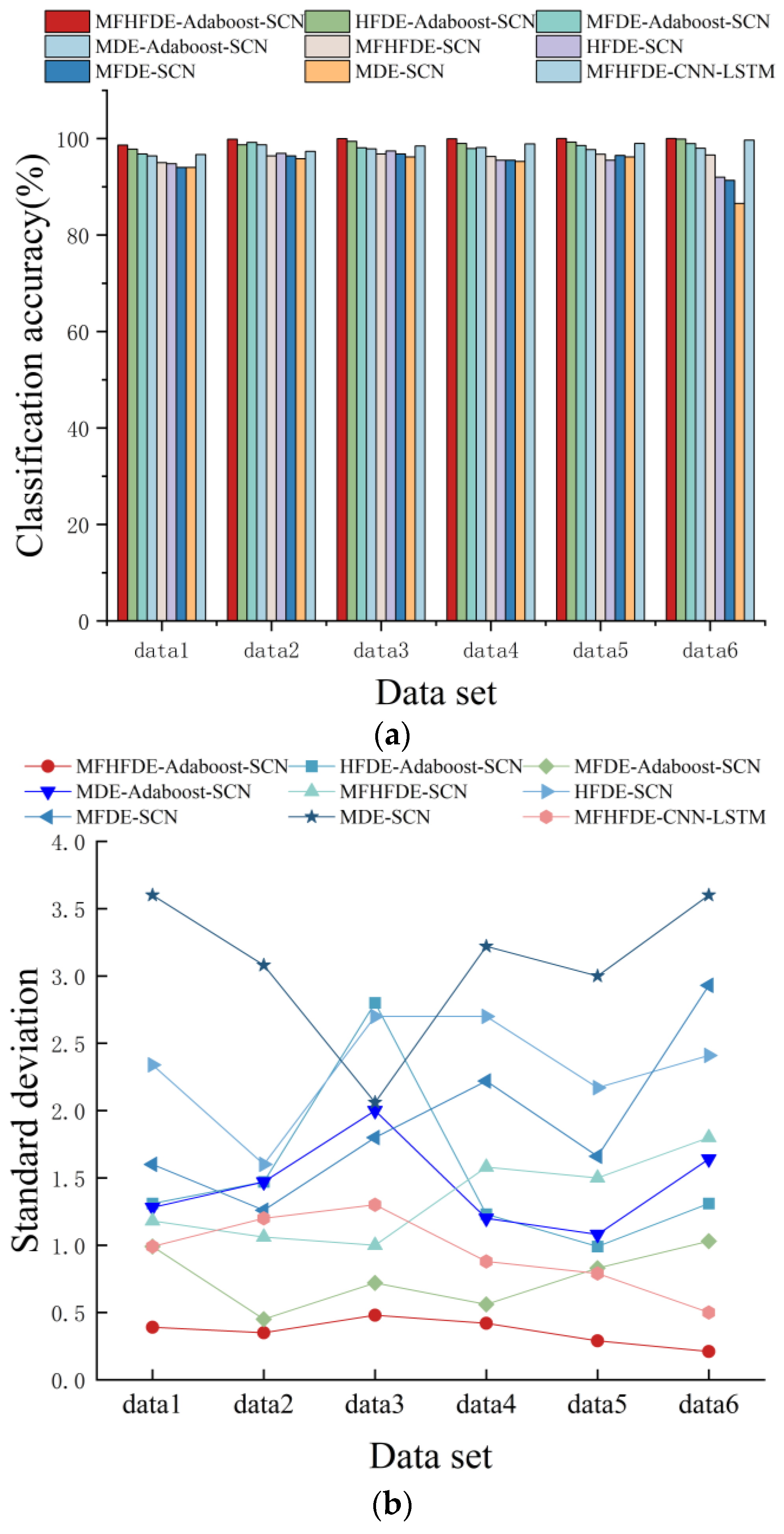
4.3. MFHFDE-AdaBoost-SCN Fault Recognition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, F.; Zhao, Z.; Hu, X.; Liu, D.; Kang, Z.; Ma, Z.; Xiao, P.; Yin, X.; Yang, J. Enhancing the safety of hydroelectric power generation systems: An intelligent identification of axis orbits based on a nonlinear dynamics method. Energy 2025, 324, 135864. [Google Scholar] [CrossRef]
- Rajabi, S.; Azari, M.S.; Santini, S.; Flammini, F. Fault diagnosis in industrial rotating equipment based on permutation entropy, signal processing and multi-output neuro-fuzzy classifier. Expert Syst. Appl. 2022, 06, 117754. [Google Scholar] [CrossRef]
- Sun, Y.; Cao, Y.; Li, P.; Xie, G.; Wen, T.; Su, S. Vibration-based fault diagnosis for railway point machines using VMD and multiscale fluctuation-based dispersion entropy. Chin. J. Electron. 2024, 33, 803–813. [Google Scholar] [CrossRef]
- Zhou, J.; Li, S.; Guo, J.; Wang, L.; Liu, Z.; Jin, T. Continuous hierarchical symbolic deviation entropy: A more robust entropy and its application to rolling bearing fault diagnosis. Mech. Syst. Signal Process 2025, 227, 112409. [Google Scholar] [CrossRef]
- Li, Y.; Mu, L.; Gao, P. Particle swarm optimization fractional slope entropy: A new time series complexity indicator for bearing fault diagnosis. Fractal Fract. 2022, 6, 345. [Google Scholar] [CrossRef]
- Azami, H.; Fernández, A.; Escudero, J. Multivariate multiscale dispersion entropy of biomedical times series. Entropy 2019, 21, 913. [Google Scholar] [CrossRef]
- Chawla, P.; Rana, S.B.; Kaur, H.; Singh, K. Diagnosis of autism spectrum disorder using EEMD and multiscale fluctuation based dispersion entropy with Bayesian optimized light GBM. Multimed. Tools Appl. 2024, 83, 65341–65362. [Google Scholar] [CrossRef]
- Tan, H.; Xie, S.; Liu, R.; Ma, W. Bearing fault identification based on stacking modified composite multiscale dispersion entropy and optimised support vector machine. Measurement 2021, 186, 110180. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Zheng, J.D.; Pan, H.Y. Use of generalized refined composite multiscale fractional dispersion entropy to diagnose the faults of rolling bearing. Nonlinear Dyn. 2020, 101, 1417–1440. [Google Scholar] [CrossRef]
- Liberti, L.; Lavor, C.; Maculan, N.; Mucherino, A. Euclidean distance geometry and applications. SIAM Rev. 2014, 56, 3–69. [Google Scholar] [CrossRef]
- Liao, G.-P.; Gao, W.; Yang, G.-J.; Guo, M.-F. Hydroelectric generating unit fault diagnosis using 1-D convolutional neural network and gated recurrent unit in small hydro. IEEE Sens. J. 2019, 19, 9352–9363. [Google Scholar] [CrossRef]
- Reza, H.B.; Dragan, M.; Srete, N.; Dragicevic, T. Support vector machine-based islanding and grid fault detection in active distribution networks. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2385–2403. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, S.; Zhang, J.; Jia, W. Parallel stochastic configuration networks for large-scale data regression. Appl. Soft Comput. 2021, 103, 107143. [Google Scholar] [CrossRef]
- Wang, W.Y.; Sun, C.D. The improved AdaBoost algorithms for imbalanced data classification. Inf. Sci. 2021, 563, 358–374. [Google Scholar] [CrossRef]
- Ma, J.; Li, S.; Qin, H.; Hao, A. Adaptive appearance modeling via hierarchical entropy analysis over multi-type features. Pattern Recognit 2020, 98, 107059. [Google Scholar] [CrossRef]
- Zhou, F.; Gong, J.; Yang, X.; Han, T.; Yu, Z. A new gear intelligent fault diagnosis method based on refined composite hierarchical fluctuation dispersion entropy and manifold learning. Measurement 2021, 186, 110136. [Google Scholar] [CrossRef]
- Li, W.; Shen, X.; Li, Y. A comparative study of multiscale sample entropy and hierarchical entropy and its application in feature extraction for ship-radiated noise. Entropy 2019, 21, 793. [Google Scholar] [CrossRef]
- Machado, J.T. Fractional order generalized information. Entropy 2014, 16, 2350–2361. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, P. Complexity analysis of time series based on generalized fractional order dual-embedded dimensional multivariate multiscale dispersion entropy. Fractals 2021, 29, 2150048. [Google Scholar] [CrossRef]
- Li, Y.; Tang, B.; Geng, B.; Jiao, S. Fractional order fuzzy dispersion entropy and its application in bearing fault diagnosis. Fractal Fract. 2022, 6, 544. [Google Scholar] [CrossRef]
- Mesquita, D.P.; Gomes, J.P.; Junior, A.H.S.; Nobre, J.S. Euclidean distance estimation in incomplete datasets. Neurocomputing 2017, 248, 11–18. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, X.; Wan, J.; Xiong, N. EDM-fuzzy: An Euclidean distance based multiscale fuzzy entropy technology for diagnosing faults of industrial systems. IEEE Trans. Ind. Inform. 2022, 17, 4046–4054. [Google Scholar] [CrossRef]
- Wang, D.; Li, M. Stochastic configuration networks: Fundamentals and algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef]
- Yang, S.; Ding, L.; Li, W.; Sun, W. Fishing risky behavior recognition based on adaptive transformer, reinforcement learning and stochastic configuration networks. Inf. Sci. 2024, 659, 120074. [Google Scholar] [CrossRef]
- Xiao, H.; Zhihuai, X.; Dong, L.; Wenli, Z.; Hai, W.; Wenjun, J. Vibration fault identification method of hydropower unit based on EEMD-SDCC Ⅰ-HMM. Vib. Shock. 2022, 41, 165–175+230. [Google Scholar]

| Method | Advantages | Limitations | Noise Robustness | Computational Cost | Reference |
|---|---|---|---|---|---|
| MPE | Simple computation | Ignores amplitude information | Low | 1.0 s | [2] |
| MDE | Captures amplitude information | Neglects signal fluctuations | Medium | 1.2 s | [4] |
| MFDE | Strong anti-interference, high stability | poor high-frequency adaptation | High | 2.5 s | [6] |
| MFHFDE (Proposed) | Combines hierarchical decomposition and fractional entropy | Higher computational cost | Best | 2.7 s |
| Index | Dataset Abbreviation | Number of Faults Imbalance | Imbalance Ratio |
|---|---|---|---|
| 1 | Data1 | 12 | 10 |
| 2 | Data2 | 24 | 5 |
| 3 | Data3 | 36 | 3.33 |
| 4 | Data4 | 72 | 2 |
| 5 | Data5 | 90 | 1.33 |
| 6 | Data6 | 120 | 1.00 |
| Model | Data1 | Data2 | Data3 | Data4 | Data5 | Data6 | Average Diagnosis Rate | |
|---|---|---|---|---|---|---|---|---|
| MFHFDE-Adaboost-SCN | 98.63 | 99.85 | 99.98 | 99.95 | 100 | 100 | 99.735 | 1 |
| HFDE-Adaboost-SCN | 97.8 | 98.7 | 99.43 | 99 | 99.28 | 99.88 | 99.015 | 2 |
| MFDE-Adaboost-SCN | 96.8 | 99.2 | 98.1 | 97.93 | 98.55 | 98.97 | 98.258 | 4 |
| MDE-Adaboost-SCN | 96.4 | 98.7 | 97.88 | 98.14 | 97.72 | 98 | 97.806 | 5 |
| MFHFDE-SCN | 95 | 96.42 | 96.8 | 96.28 | 96.75 | 96.6 | 96.308 | 6 |
| HFDE-SCN | 94.8 | 96.93 | 97.43 | 95.5 | 95.5 | 92 | 95.36 | 7 |
| MFDE-SCN | 94 | 96.42 | 96.8 | 95.5 | 96.5 | 91.33 | 95.092 | 8 |
| MDE-SCN | 94 | 95.8 | 96.2 | 95.25 | 96.2 | 86.55 | 94 | 9 |
| MFHFDE-CNN-LSTM | 96.67 | 97.33 | 98.45 | 98.88 | 99 | 99.68 | 98.335 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, X.; Xu, Z.; Lu, R.; Li, Y.; Li, B.; Wu, F.; Wang, B. Hydroelectric Unit Fault Diagnosis Based on Modified Fractional Hierarchical Fluctuation Dispersion Entropy and AdaBoost-SCN. Energies 2025, 18, 3798. https://doi.org/10.3390/en18143798
Xiong X, Xu Z, Lu R, Li Y, Li B, Wu F, Wang B. Hydroelectric Unit Fault Diagnosis Based on Modified Fractional Hierarchical Fluctuation Dispersion Entropy and AdaBoost-SCN. Energies. 2025; 18(14):3798. https://doi.org/10.3390/en18143798
Chicago/Turabian StyleXiong, Xing, Zhexi Xu, Rende Lu, Yisheng Li, Bingyan Li, Fengjiao Wu, and Bin Wang. 2025. "Hydroelectric Unit Fault Diagnosis Based on Modified Fractional Hierarchical Fluctuation Dispersion Entropy and AdaBoost-SCN" Energies 18, no. 14: 3798. https://doi.org/10.3390/en18143798
APA StyleXiong, X., Xu, Z., Lu, R., Li, Y., Li, B., Wu, F., & Wang, B. (2025). Hydroelectric Unit Fault Diagnosis Based on Modified Fractional Hierarchical Fluctuation Dispersion Entropy and AdaBoost-SCN. Energies, 18(14), 3798. https://doi.org/10.3390/en18143798








