Abstract
Linear passive electrical devices/components are usually characterized in the frequency domain by their impedance, i.e., the ratio of the voltage and current phasors. The use of the impedance concept does not raise particular concerns in low-frequency regimes; however, things become more complicated when it comes to rapid time-varying phenomena, mainly because the voltage depends not only on the position of the points between which it is defined but also on the choice of the integration path that connects them. In this article, based on first principles (Maxwell equations and Poynting vector flow considerations), we discuss the concept of impedance and define it unequivocally for a class of electrical devices/components with rotational symmetry. Two application examples are presented and discussed. One simple example concerns the per-unit-length impedance of a homogeneous cylindrical wire subject to the skin effect. The other, which is more elaborate, concerns a heterogeneous structure that consists of a dielectric disk sandwiched between two metal plates. For the lossless situation, the high-frequency impedance of this device (circular parallel plate capacitor) reaches zero when the frequency reaches a certain critical frequency fc; then, it becomes inductive and increases enormously when the frequency reaches another critical frequency at 1.6 fc. The influence of losses on the impedance of the device is thoroughly investigated and evaluated. Impedance corrections due to dielectric losses are analyzed using a frequency-dependent Debye permittivity model. The impedance corrections due to plate losses are analyzed by considering radial current distributions on the outer and inner surfaces of the plates, the latter exhibiting significant variations near the critical frequencies of the device.
1. Introduction
Two-terminal electrical devices, or components, that exhibit linear behavior are usually characterized in the frequency domain by their impedance, or harmonic impedance, which is defined by the ratio between the voltage and current (phasors) observed at the accessible terminals [1,2].
Using the concept of impedance does not pose particular difficulties for low-frequency applications, in which lumped-parameter models are commonly used for describing electric and magnetic field phenomena. The same is not true for high-frequency applications, in which the concepts of voltage and current lose their importance and are conveniently replaced by field quantities. Fortunately, however, for certain device geometries, impedances can still be defined and calculated accurately at very high frequencies, as long as the current and voltage of the device are defined unambiguously and carefully.
This work, which is essentially theoretical/tutorial in nature, deals with the high-frequency impedance of linear passive devices whose geometry is rotationally invariant, with an application focus on capacitors, important devices used for various purposes, such as filtering, tuning, phase shifting, coupling, noise suppression, bypass, etc. In particular, we address the issue of the inductive and resonant behavior of parallel-plate capacitors, which is a topic of interest associated with GHz technologies, IC packaging, microwave circuitry, etc. [3,4,5,6,7,8,9].
This paper is organized into five sections, the first of which is introductory and the last of which is conclusive. Table 1, below, lists the most important quantities and symbols that appear throughout the article.

Table 1.
Principal quantities and symbols.
Section 2 presents the basics, the nomenclature, and some considerations related to high-frequency impedance measurement.
In Section 3, we use first principles (Maxwell equations and Poynting theorems) to unambiguously define the current, voltage, and device impedance in the special case of rotationally symmetric devices, in which the magnetic field is purely azimuthal and the impedance definitions , and merge together into one. The subcase of circular cylindrical devices is examined, and Bessel functions are used to describe their electromagnetic field [1]. An example (cylindrical wire) from familiar skin effect theory is presented to show how a poor choice in the definition of the device voltage can lead to absurd results in the evaluation of the high-frequency impedance [9].
Section 4, which is the largest section, presents research work on the high-frequency impedance of a rotationally symmetric device consisting of a thin circular dielectric wafer sandwiched between two thick circular metal plates, with two external lead wires. The analysis window covers the frequency range of 0 to 15 GHz. Firstly, assuming that losses are absent, the device impedance is shown to exhibit a pattern of zeros and infinities, with alternating capacitive and inductive behaviors; afterward, the influence of dielectric losses is evaluated and, at last, the influence of plate losses on the device impedance is rigorously investigated. The impedance corrections due to dielectric losses are analyzed by considering a frequency-dependent complex permittivity described using a simple Debye model. The impedance corrections due to the finite conductivity of the plates are studied by considering the radial currents that flow along the outer and inner surfaces of the plates.
2. Background
Figure 1 is a schematic of the simplest closed circuit that describes the connection of a linear passive electromagnetic device, D, to an AC power source of frequency, the latter of which was provided with measurement equipment. The connection is established by a pair of wires of length l immersed in a dielectric medium (the air, for instance).
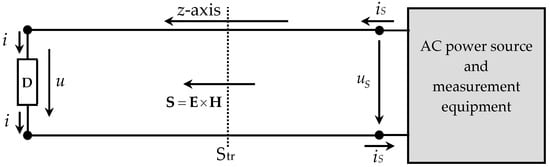
Figure 1.
A linear passive electromagnetic device, D, is fed by an AC power source. The connection is established by a pair of wires. The flow of energy from the source to D is electromagnetically described by the flux of the Poynting vector, , across the transverse plane, Str.
Since the circuit does not contain any nonlinear parts, the source voltage, , and source current, , are both sinusoidal. The same happens to the voltage, , and current, , at the device terminals, as follows:
where and represent the complex amplitudes (phasors) of the sinusoidal functions and . Regarding the notation in this work, overbars are used to denote complex quantities, asterisks are used to represent complex conjugation, capital letters are used to denote time-independent scalar quantities, and boldface letters are used to represent space vectors.
The intrinsic behavior of the linear device D, which is described by its constitutive equation, u = u(i), is independent of the source that feeds it; the relationship u = u(i) is physically definable even when u = i = 0. In the case of sinusoidal regimes of frequency ω, as in (1), the complex constitutive equation governing the device is as follows [2]:
where the frequency-dependent quantity is the well-known complex impedance, or harmonic impedance. For passive devices, the angle θ is an angle of the first or fourth quadrant, i.e., .
According to the abovementioned definition, adopted in this work, the voltage and current of the device are sinusoidal of the same frequency. However, the concept of impedance is still very useful for dealing with non-sinusoidal waveshapes using the superposition principle (Fourier analysis). Firstly, the spectrum of the current i(t) is obtained via the direct Fourier transform; secondly, the voltage spectrum is obtained through the product finally, voltage u(t) is computed by inverting its spectrum as follows:
As a parenthetical note, we may remark, based on (3), that the function
defines the voltage response of the device when it is excited by a Dirac pulse of current, whose spectrum is uniform, As. Do not confuse the clear meaning of z(t) in (4) with other unclear, debatable definitions of the type .
An important question that requires attention is related to the readings of the measurement equipment at the AC source port. Do they allow for the direct measurement of the device impedance ? In general, and especially at high frequencies, the answer is negative; the device and source voltages are unequal, , as are the device and source currents, . This is true even if the wires connecting the source to the device are assumed to be perfect electric conductors (PEC) with infinite conductivity. The pair of wires defines a transmission line (TL) of length l, whose current and voltage are functions of z, where and .
The complex impedance measured at the AC source port, , does not coincide with the device impedance, the reason for this is that the axial currents in the connecting wires create their own electromagnetic field (see Figure 2, which shows the electric and magnetic field lines around the wires in the transverse xy-plane). Measurements at the source port account for the whole electromagnetic field (EMF) of the entire circuitry observed by the source: the EMF of the device D, plus the EMF of the connection wires.
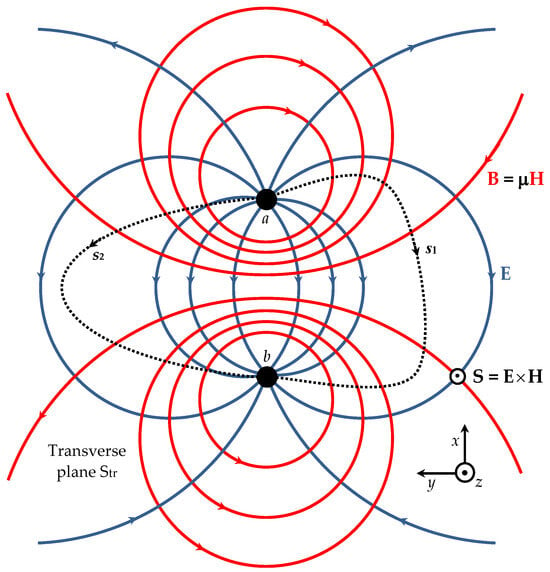
Figure 2.
EMF lines around the connecting wires (transverse cross-section). Axial currents in the wires produce a transverse H-field whose lines are tangential to the plane Str. The voltage between the wires a and b does not depend on the path joining them, provided that the trajectory is contained in Str.
At this point, an important remark concerning the correct interpretation of the concept of voltage—a frequent source of mistakes—is necessary. The voltage between two points a and b is defined by the line integral of the electric field from a to b, as follows:
The definition remains ambiguous until the integration path linking a to b is specified. Fortunately, in the present case (see Figure 2) such ambiguity is easily removed, as explained below.
The usual way of defining through a difference in potential is, in general, not applicable to high-frequency regimes, as the term in Maxwell equations grows in importance, and the E-field no longer behaves as a purely gradient field [1,2].
In our case, since the wire currents are purely axial (z-oriented), the magnetic field is purely transverse, and its field lines belong to the plane Str.
Based on (5), we define two voltages , from a to b, but along two different open paths, s1 and s2, respectively, both of which lie on the plane Str, where Next, Faraday’s induction law is applied to a closed clockwise path s, which is produced by the union of s1 and -s2, yielding the following result:
where Ss is a planar open surface bounded by s, traversed by zero magnetic flux, because In conclusion, irrespective of the specific shape of the integration path from a to b, the voltage between wires is uniquely defined, provided that the path stays in Str.
The flow of energy along the transmission structure, from the power source to the device D is electromagnetically described using the Poynting vector , and for AC regimes, it is described using its complex companion, the complex Poynting vector, [1,2]. The complex power varies along z and can be calculated from the flux of across the plane Str as follows:
If the two-wire line is uniform along the z-axis, the device impedance can be very approximately evaluated, using the information about the impedance measured at the source port , using the following relationship [1,2]:
where the complex frequency-dependent quantities and are intrinsic parameters of the transmission structure: the propagation constant and characteristic wave impedance, respectively. Derived from basic transmission line theory [1,2], the result in (8) shows that the relationship between and depends on the frequency and the length l of the transmission structure; only in the limit case will we have
3. Rotationally Symmetric Electromagnetic Devices
Notwithstanding the apparent simplicity of the system depicted in Figure 1, its rigorous theoretical analysis and its exact global solution are impossible tasks, even if all the conductors and dielectric media are assumed to be perfect. For example, in the TL, the wavefronts are parallel planar surfaces (Str), and the Poynting vector is parallel to the wires; however, near device D, the wavefront surfaces bend around, and the Poynting vector radially converges toward D. The transition between these two different types of wavefronts occurs in a region between the end of the TL and the periphery of the device. In the transition region, the field vectors have a distorted geometry, and exact analytical field solutions can hardly be found.
The practical impossibility of obtaining an exact analytical EMF solution should not make one quit, however. One should look for an approximate solution, making use of well thought out simplifying assumptions. The usual strategy for handling the difficulty consists of breaking down the system into its component parts, physically analyzing each part as rigorously as possible (taking advantage of peculiar geometries), and finally, combining the results. Fortunately, in most cases, the outcome will be satisfactory and adequate from an engineering viewpoint.
In this work, we analyze rotationally invariant two-terminal electromagnetic devices, that is, the bodies of revolution generated by the rotation around the z-axis of an arbitrary curvilinear path sab, drawn in the r-z plane, that unites the device terminals a and b, see Figure 3 (where three types of surfaces are identified: the closed surface SV, generated by 2π-rotation of sab defines the boundary surface of the device; the open surface Sax, on the r-z plane, bounded by the curve sab and the segment lab, defines the axial semi-section of the device; and the open surface Str, on the r-ϕ plane, defines the circular transverse cross-section of the device, whose radius ro varies along z).
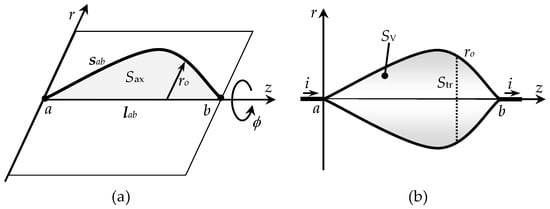
Figure 3.
The path sab, on the r-z plane, is ϕ-rotated in (a) to produce the rotationally symmetric device depicted in (b). The device is fed by lead wires connected at a and b; the distance lab is much smaller than the operating wavelength. SV is the device’s closed boundary, and Str is its transverse cross-section.
The device’s constitutive media are characterized by the usual parameters: conductivity σ, permittivity ε, and permeability μ, with the first two being combined in the frequency domain to produce a complex conductivity These constitutive parameters are allowed to vary with r and z, but not with ϕ, of course.
The simplest solution to Maxwell equations for problems with cylindrical geometry relies on ϕ-invariance, yielding an azimuthal magnetic field with circumferential field lines contained on the r-z transverse plane, Str, i.e.,
3.1. Current and Voltage Definitions
External lead wires connected at a and b permit the flow of current through the device and its energization. Assuming that the device is electrically short and that the boundary surface SV is a well-defined flux tube of the total current density vector, then the current intensity at a, b, and any transverse section Str(z), is practically the same and, therefore, can be unambiguously defined as follows:
where s(z) is the circumferential path of radius ro(z) that bounds Str(z).
The definition and calculation of the device’s voltage from a to b requires some care; it requires a clear specification of the chosen integration path and a sound justification for the choice made. This is because for high-frequency regimes, the E-field includes two contributions of different natures, one from the familiar scalar electric potential , and another from the vector magnetic potential [1,2], such that:
where denotes the magnetic flux linked with the path s, and is the Stokes’ unit normal. As a side note, observe that the equation in (11) is equivalent to .
Two appealing hypotheses for defining the device’s voltage are discussed below.
Hypothesis 1.
The voltage is defined by integrating the E-field from a to b along the peripheral curvilinear path sab contained on the plane on SV.
Hypothesis 2.
The voltage is defined by integrating the E-field from a to b along a straight line lab on the z-axis.
Both choices are clear and unambiguous; the first is more general in the sense that it holds for any value of , but the second is the simplest. Unfortunately, the two hypotheses produce conflicting results, as can be shown by applying Faraday’s induction law (11) to a closed clockwise path s made of the union of sab and -lab. Noting that the surface Sax, bound by s, is traversed by magnetic field lines antiparallel to , we find:
Next, we present an energy-based justification for choosing the hypothesis using the sab path. To begin, we emphasize that the assumption that the integration path remains on the plane is unnecessarily restrictive. Indeed, any planar or non-planar integration path from a to b, traced on the boundary surface SV of the device will always yield the same result for the voltage:
since SV is not crossed by magnetic field lines (H is tangential to SV).
Therefore, according to Faraday’s induction law, the contour integral of the E-field along any closed path drawn on SV must be zero , as if the E-field is purely conservative, which is exactly what happens with time-invariant regimes, where E is derivable from a simple scalar electric potential.
In short, with regard to line integrations or surface integrations carried out in the 2D curved subspace S, defined by all the points on SV, we can take and, from (14), sustain that:
We highlight that the domain of the potential function is exclusively the subspace S, S; the line integral in (15) cannot be evaluated along the straight segment lab, on the z-axis, whose points are outside of S.
The abovementioned result is key for the steps that follow.
The complex power at play in the whole volume V of the device can be evaluated using two approaches: employing the pair or employing the complex Poynting theorem [1,2] and calculating the inward flux of the complex Poynting vector across the closed boundary surface SV of the device. That is:
where ni denotes the inward unit vector normal to SV.
Next, we will show that equality
is ensured by the voltage definition in (15) with a path sab in S. To that end, we take and obtain:
where is the total current density vector, .
Substituting (18) into (17) yields:
where the second term on the right-hand side is identically zero (as can be verified by using the Gauss theorem and the property ).
The current density vector crosses SV, in and out of the device, at two arbitrarily small regions of area Sw around the points a and b, where the external lead wires meet the device, and the scalar potential is and , respectively. Therefore, from (19), we reach the following result:
where the definition of in (10) is used.
The conclusion in (20) proves that the definition of device voltage in (14) and (15), with integration paths on the device boundary surface SV is the correct one for time-varying regimes. The hypothesis in (12), with a straight path from a to b along the z-axis, although simple and appealing, fails to fit the energy criterion in (17) and leads to incorrect results, as we will see in the next section.
3.2. Impedance Definition
The correct definition of the device impedance should make use of the definitions of in (10) and (14), as follows:
where sab is an open path drawn on the boundary surface SV of the device, from terminal a to terminal b, and Str is a transverse section of the device.
Since our definition of meets the energy criterion in (17), we can be sure that the definition of impedance in (21) is coherent with other definitions based on energy considerations, namely:
3.3. Circular Cylindrical Devices
Circular cylindrical devices are an important subclass of rotationally symmetric electromagnetic devices. Their boundary surface Sv is a regular cylinder, with two equal circular tops, generated by the rotation around the z-axis of a [-shaped path sab; the device transverse sections Str are parallel equal circles of constant radius ro.
If, in addition, the parameters are kept unchanged along z, then we may assume that the EMF inside the device is practically z-invariant; otherwise, the definition of current in (10) would not hold. Taking and , Maxwell equations in cylindrical coordinates can be rewritten as:
Taking the r-derivative of the curl H equation in (23) yields:
By plugging from (23) into (24) leads to the following equation:
where, due to rotational symmetry, the medium parameters are allowed to vary radially, , μ(r). In general, in the case of inhomogeneous media, the differential equation for in (25) can only be solved numerically. However, for certain peculiar profiles of closed-form analytical solutions can still be found [10]. Naturally, the simplest situation occurs when the medium is homogeneous, in which case (25) is transformed into the Bessel equation:
where is the complex wavenumber. The solution of (26) is well-known [1,2], i.e.
where . The solution for is found by plugging (27) into (23), which yields:
where J0 and J1 in (27) and (28) are Bessel functions of the first kind of order 0 and 1, respectively.
3.4. Skin Effect Impedance
To conclude Section 3, aiming to illustrate the analysis conducted in Section 3.1 and Section 3.2 regarding the definition of voltage, we discuss well-known results regarding the per-unit-length skin effect impedance of a homogeneous circular cylindrical wire.
The wire of radius ro and indefinite length is made of a good conductor Then, by setting , the axial E-field in (28) becomes:
where δ is the skin depth or field penetration depth.
Next, we consider two neighboring points a and b, on the z-axis, at a distance lab, and with the help of (29), we evaluate the wire voltage between the transverse sections Str at z = a and z = b, using the two hypotheses in (12), as follows:
from where the per-unit-length impedance of the wire is calculated: for hypothesis 1 and for hypothesis 2:
The impedance expressions are different; they do not coincide even at low frequencies, when . In fact, taking into account the first two terms of the series expansions of J0 and J1 [11,12], we readily find:
where a negative imaginary part in is observed (X2 < 0), which, evidently, is a physical impossibility. Therefore, there can be no doubt that the device impedance calculated from the E-field integration along a direct straight path from a to b (r = 0) is a mistake and leads to incorrect results (as in [9]). The correct expression for the per-unit-length impedance of the circular cylindrical wire, which is widely reported in the literature [1,2,7], is in agreement with in (31), where the voltage is evaluated by integrating the E-field along a peripheral path on SV from a to b (r = ro).
Illustrative graphics of the real (R) and imaginary (X) parts of the impedances and , as a function of the frequency, are shown in Figure 4. Both impedances are normalized to their DC values, RDC. As expected, the positive real and imaginary parts of the impedance tend to one another and increase with the frequency, growing with f 1/2. Contrarily, the impedance , that decreases to zero when the frequency increases, displays a physically impossible behavior, showing frequency bands where its real or imaginary parts turn negative.
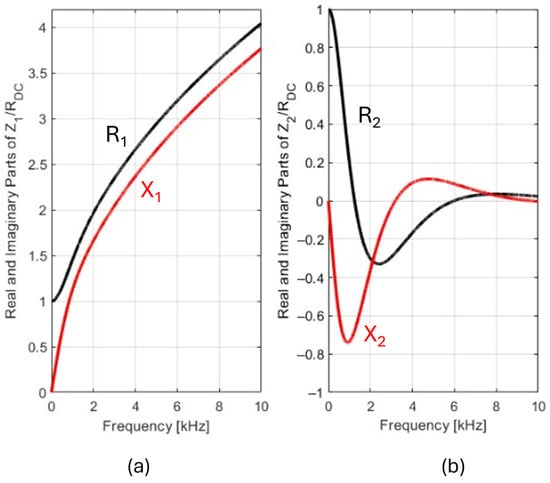
Figure 4.
Normalized wire impedance as a function of the frequency. Graphics of the real and imaginary parts of the per-unit-length impedance of a circular cylindrical copper wire with a radius of 5 mm. (a) Correct hypothesis: (b) Incorrect hypothesis: .
The relative error resulting from using the wrong impedance choice , instead of , can be calculated as follows:
Graphical results regarding the evolution of the impedance error (33) are presented in Figure 5. The error increases rapidly from zero to 120% in the frequency range of 0 to 1.2 kHz (where ), and as the frequency increases to higher values, the error stabilizes at 100% (when ).
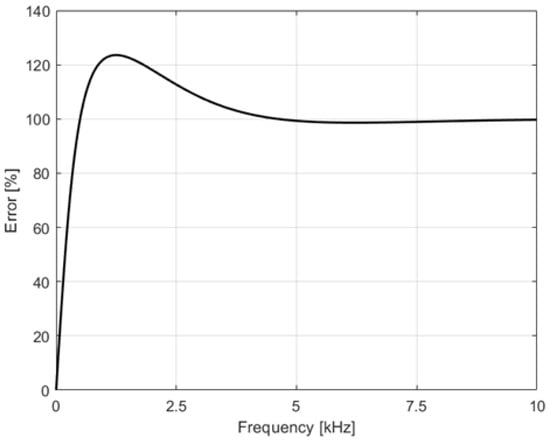
Figure 5.
Relative error incurred in the impedance calculation when the incorrect hypothesis is utilized. The error, in terms of a percentage, is defined in (33).
4. Circular Parallel Plate Capacitor
Figure 6 shows an axial section of the circular parallel plate capacitor, which consists of a thin circular dielectric wafer of thickness h and radius ro sandwiched between two metallic circular parallel plates of radius ro and thickness w.
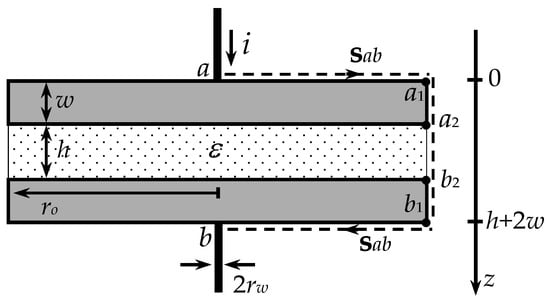
Figure 6.
Geometry of the circular parallel plate capacitor. To ensure that fringing field effects can be disregarded, the thickness of the dielectric layer is much smaller than its radius (h << ro). The device voltage is calculated by integrating the E-field along the peripheral path, aa1a2b2b1b.
The capacitor is connected externally at a and b through lead wires of radius rw. Its dielectric core is nonmagnetic, μ = μ0, and made of a good insulating material .
The low-frequency impedance of this structure tends asymptotically to zero as ω increases, as follows:
However, as we shall see, the results are rather different for high-frequency regimes.
Although they have different radius/length ratios, the circular parallel plate capacitor and the circular cylindrical wire are devices that essentially share the same geometrical description. Consequently, the results for the electromagnetic field in (27) and (28) should again apply, with the difference that while we had and for the cylindrical wire, we have and for the capacitor, that is, we have:
There is also another difference worth noting. In the case of the cylindrical wire, the boundary surface SV is fully conductive and establishes a well-defined flux tube for the current (conduction current). That is not exactly true in the case of the parallel plate capacitor, where fringing field effects take place around the plates, notably at the edges near the boundary r = ro; in other words, the displacement current flowing between the plates is not entirely contained in a well-defined cylindrical flux tube.
The subject of fringing field effects in capacitors is not easy to treat analytically; in some cases (electrostatics) it can be handled with the help of conformal mapping [1,13,14,15] but, in general, for fast time-varying regimes, analytical solutions are not available.
Electrostatic fringing field effects in parallel plate capacitors are responsible for the undesirable nonuniformity of the E-field between the plates, with nonuniformity being determined by two main factors: on the one hand, the dielectric core permittivity relative to the external medium permittivity and, on the other hand, the residual electric charge Qe on the edges and external faces of the capacitor plates.
Higher relative permittivity values lead to a strong confinement of the E-field inside the dielectric core and an increase in the electric charge Q on the internal faces of the capacitor plates and, therefore, imply a reduction of the Qe/Q ratio.
The second factor is essentially related to the geometry of the capacitor: the higher the h/ro ratio, the higher the Qe/Q ratio. This aspect has been a topic of interest since Maxwell’s time; various approaches for estimating the capacitance perturbed by fringing field effects are known, with the perturbation being typically expressed by a function of the type , where x is proportional to (see, for example, [15], table II).
Ordinarily, these effects are assumed to be negligible. We will adopt the same assumption, which is applicable when the dielectric wafer is very thin, h << ro, as needed to obtain high values of the capacitance CDC in (34).
In the following subsections, the rotationally symmetric device in Figure 5 will be analyzed by considering four possible situations regarding the absence/presence of losses, as well as the origin of the latter, whether they occur in the imperfect dielectric core or in the imperfect conducting plates. We will use the following combinations of superscripts and subscripts to identify the different results for the computed device impedance:
- concerns the combination of a perfect dielectric and a perfect conductor;
- concerns the combination of an imperfect dielectric and a perfect conductor;
- concerns the combination of a perfect dielectric and an imperfect conductor;
- concerns the combination of an imperfect dielectric and an imperfect conductor.
4.1. Base Lossless Case (PD-PC)
As a first step, we consider that losses are absent. The dielectric medium is a perfect electric insulator with real ε and σ = 0, and the capacitor plates are perfect electric conductors with .
The device voltage is calculated by integrating the E-field along the peripheral path aa1a2b2b1b, which is indicated by a broken line in Figure 6.
By plugging from (35) into (36), and dividing the latter by the current, we obtain the device impedance, as follows:
where v denotes the speed of light in the dielectric medium of permittivity ε. Note in (37) that the term tends toward 2 when , which confirms the low-frequency result in (34), valid when .
The result in (37) can be confirmed using the energy-based definition in (22) that involves the inward flux of the complex Poynting vector through the device’s boundary surface SV. In fact, we have:
where the E-field and the Poynting vector are zero in the circular PEC plates.
For the lossless case, the complex power is purely imaginary (reactive power), and from the complex Poynting theorem we must have:
The time-averaged magnetic energy stored in the dielectric volume is computed using in (35), yielding the following result:
Likewise, the time-averaged electric energy stored in the dielectric volume is computed using in (35), yielding the following result:
The interested reader may check Appendix A for details on integrals involving the squared Bessel functions such as those appearing in (40) and (41).
Finally, by subtracting the two energies, and employing (39), we find:
which confirms (37). We believe that the utilization of the energy formalism in (38)–(42) for evaluating the device impedance is a novel contribution, the advantage being that the concept of voltage is not involved.
We may confirm that, in the limit case ρ << 1, the general results for the time-averaged magnetic and electric energies in (40) and (41), yield the familiar low frequency results and . Let us check.
For ρ << 1, by using the first two terms of the series expansions of the Bessel functions, the following approximations apply:
By substituting (43) into (40) and (41) and considering we see that
The equations in (35) express the electric and magnetic fields in terms of the device current; however, if convenient, they can be rewritten in terms of the device voltage. All we have to do is replace with and use from (37). This yields the following field equations:
The frequency behavior of in (37) is determined by the zeros of the J0 and J1 Bessel functions, which are as follows [12,16]:
from where an ordered sequence of critical frequencies fk can be identified, the first of which is denoted by fc, that is:
where v0 is the free-space speed of light, and is the relative permittivity of the dielectric core of the capacitor. While the zeros of J0 (odd k) identify short-circuit conditions the zeros of J1 (even k) identify open-circuit conditions ; hence, we have:
The critical frequencies above, which are determined by the geometrical parameter ro, are resonance frequencies for which no energy can flow into the device; in fact, for the time-averaged values of the electric and magnetic energies stored in the dielectric core of the device are exactly balanced, , and the complex power is zero.
According to low-frequency analysis, it would be expected from (34) that the behavior of the device would always be capacitive, with its impedance decreasing monotonically to zero as the frequency increases to infinity, . Now, we realize that this is not true. The device impedance is capacitive in the range of 0 < f < fc, zero at f = fc, becomes inductive in the range of fc < f < f2, increases to infinity at f = f2fc, returns to capacitive behavior in the range of f2 < f < f3, and so on, repeatedly.
The modulus and angle of impedance, , in (37), for the lossless case (reference base case), are plotted against the frequency in Figure 7, considering the frequency window of 0–15 GHz and employing the following data:
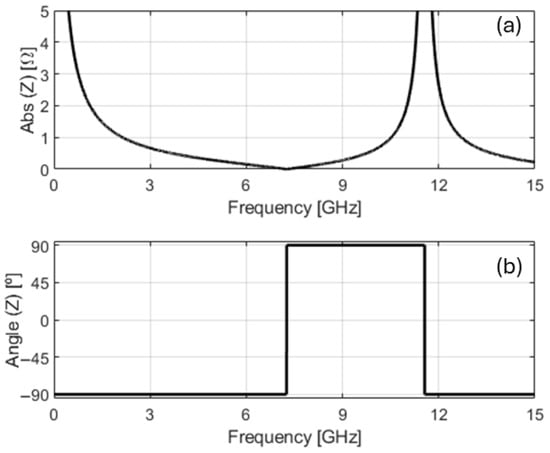
Figure 7.
Graphics of the modulus (a) and angle (b) of the impedance of a lossless circular parallel plate capacitor as a function of the frequency. The first two critical frequencies of the device (where the impedance angle jumps 180°) are f1 = 7.267 GHz and Z = 0, and f2 = 11.56 GHz and Note the device inductive behavior for f1 < f < f2.
As expected, it can be seen that the first critical frequencies are f1 = 7.257 GHz, where = 0, and f2 = 11.56 GHz, where The impedance angle jumps between two constant values, −90° and +90°.
If we had chosen to graph the device’s admittance, the singularity would appear at f1, and the zero would appear at f2.
4.2. Lossy Dielectric and Lossless Plates (ID-PC)
The inclusion of dielectric losses in impedance calculations is formally very simple; we only have to replace the (real) permittivity with a complex permittivity, adding to the first a new imaginary part Let us go back to the original concept of complex conductivity which was introduced in Section 3, and write:
where υ represents the so-called loss factor or loss angle.
Then, by using the complex in (37), we obtain the following result:
We emphasize that the argument of the Bessel functions is now complex (fourth quadrant). The zeros and infinite values mentioned in the analysis of the lossless case no longer appear. Resonance phenomena still occur at frequencies close to those in (47), but the flow of energy into the device is not zero: .
Although the insertion of into is technically simple, the specification of the complex function is not trivial. It depends on the physical–chemical composition of the medium responsible for the diverse polarization mechanisms (dipolar, ionic, atomic, and electronic) at play, each of which has its own signature and its own critical frequency. The real and imaginary parts of the analytic function are interdependent and, owing to causality, have to obey the Kramers–Kronig relationships [17].
Often, to make the analysis easier, the parameters and are assumed to be constant. Here, however, we will adopt a frequency-dependent model which, in any case, is the simplest of all, the Debye model [17]:
where denotes the relaxation frequency of the dielectric medium.
In this research, the following data are used: and fr = 400 GHz. Close to the device’s critical frequencies f1 and f2 the loss angle of the dielectric is about 15 mrad. Graphical results for the modulus and angle of the device’s impedance in (51) are shown in Figure 8 (solid lines labelled 1).
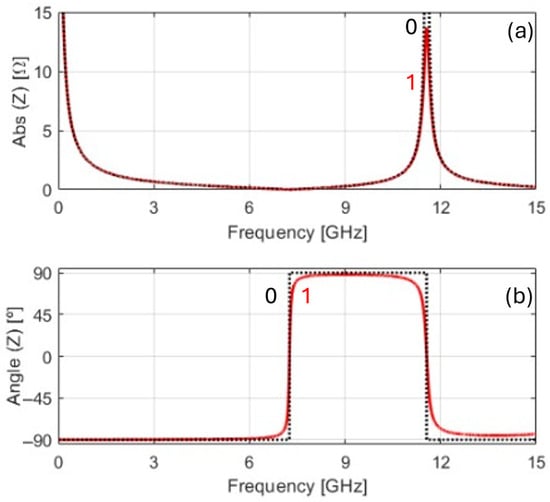
Figure 8.
Graphics of the modulus (a) and angle (b) of the impedance of the circular parallel plate capacitor as a function of the frequency, considering the presence of dielectric losses described by the Debye model in (52). The dotted curves with label 0 refer to the lossless case in Figure 7.
4.3. Lossless Dielectric and Lossy Plates (PD-IC)
The electric and magnetic fields are zero inside the capacitor’s PEC plates. Outside, just near the plates’ boundary surface, the tangential E-field remains zero. However, that is not true of the tangential magnetic field, which, according to will not be zero if a current sheet JS flows in an interface perpendicular to H. The subtraction of the tangential H fields on both sides of the current sheet must equate the intensity of the latter [1,8], that is: .
Let JS denote the linear current density (A/m) of the sheets of current flowing in the various parts of the plates. Due to symmetry, it will suffice to analyze one of the two plates, the left one in Figure 9, for 0 < z < w, whose closed boundary is
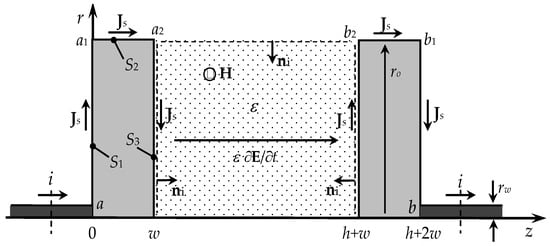
Figure 9.
Surface currents Js in the capacitor metal plates. They flow radially outward in S1, axially in S2, and radially inward in S3. When non-PEC plates are considered, these different types of surface currents originate losses characterized by different impedance contributions.
Consider a generic circle of radius r (0 < r < ro) in the circular interface S1, at z = 0, where a radial sheet of current exists Also, keep assuming that fringing field effects are negligible small (no electric charge on S1). Then, the EM field tangential to S1 is given as follows:
Consider the cylindrical interface S2 of radius ro and thickness w where an axial sheet of current exists Then, the EM field tangential to S2 is given as follows:
Finally, consider a circle of generic radius r (0 < r < ro) in the circular interface S3, at z = w, where a radial sheet of current exists Also, remember that S3 contains a radial distribution of electric charge characterized by a surface density εE(r), where E is the axial electric field in (35). Then, the EM field tangential to S3 is given as follows:
where Regarding the result in (55) for S3, which was obtained with the help of (35), we emphasize that the sheet of conduction current is radial inward at the periphery, with a density of but zero at the center. The reason that this happens is the gradual conversion of the plate conduction current sheet into axial displacement currents.
However, the conversion is not necessarily monotonic. Recalling that in (46) is the first zero of the Bessel function J1, it can be assured that if , then the current in S3 will, in fact, be inward radial, because the ratio , in (55), is positive for every possible value of r. Now, consider the case then for , the ratio is positive again; however, on the contrary, for smaller values of r, such that , the ratio turns negative, and the current will become outward radial.
The results for in (53)–(55) for the PEC case are key for the calculation of the electric field in the plates when losses are taken into account, i.e., when the plate conductivity σp is finite. The field penetration depth δ, and the surface resistance Rs of the conductive plates are defined as usual in skin effect analysis, through:
Although the plates are not PEC, we may still assume that the plate conductivity is high enough to guarantee that the new situation can be treated as a perturbation of the original PEC problem. In other words, we consider the following approximations:
- -
- The plates are thick, undergoing a strong skin effect, δ << w;
- -
- The H-field tangential to the boundaries S1, S2 and S3 is equal to the non-zero H-field in (53)–(55);
- -
- The zero E-field in (53)–(55) can be recalculated from the corresponding H-field in Sk using the following relationship, from skin effect theory [1]:
Therefore, along the various segments identified in Figure 9, we can write:
Next, we proceed with the evaluation of the device impedance, taking into account the perturbation caused by the skin effect on the lossy plates. We integrate the E-field along the peripheral path aa1a2b2b1b (Figure 9) and divide the result by . This yields:
The skin effect impedance perturbations above are easily determined from and , in (58), as follows:
The term in (59) is the voltage between the inner faces of the plates, between the peripheral points a2 and b2. Its calculation is more elaborate because we do not know the E-field between those points for the non-PEC case.
Consider the application of the complex Poynting theorem to the lossless dielectric wafer (dotted region in Figure 9) sandwiched between the lossy plates. Energy flows radially into the dielectric across the cylindrical surface of radius ro and length h (where is defined); flows in the axial direction toward the plates across the circular tops of radius ro at z = w and z = h + w; and is also stored in the dielectric volume in the form of electric and magnetic energy. Hence, we must have:
With regard to the right-hand side of (61), the term is the same as in (40); however, strictly speaking, the term is not the same as in (41).
The stored electric energy in (41), for the PEC plate case, was evaluated solely using the axial electric field: . However, when lossy plates are considered, a radial E-field component parallel to the plates must be added. The total E-field inside the dielectric medium is elliptically polarized, and consequently, its rms value will be such that . Nonetheless, for good conducting plates, the term is several orders of magnitude smaller than ; therefore, according to (39), we may say that the right-hand side of (61) is practically coincident with .
Therefore, we can rewrite (61) as follows:
or
The integral involving in (63) is not new; we encountered it in (40). By using this integral in (63), we obtain:
For the limit case ρ << 1, the term inside the large parentheses tends toward 1/4, and we find the low-frequency approximation .
The contributions in (60), together with in (64), fully characterize the frequency-dependent impedance corrections due to the presence of strong skin effect in the imperfect plates of the device. Adding them, we find:
where the influence of the frequency is conveyed in and .
Finally, from (59), the device impedance, with lossless dielectric but lossy plates, is computed as follows:
The abovementioned results for the impedance corrections, due to skin effect phenomena in the capacitor’s imperfect plates (supporting surface currents), are graphically represented in Figure 10.
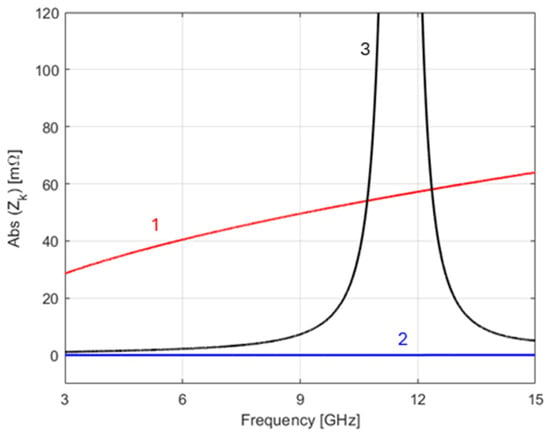
Figure 10.
Graphics of the modulus of the impedance corrections , associated to plate losses, as a function of the frequency in the range of 3–15 GHz. The angle of these impedances is not represented because it is constantly equal to π/4. Labels 1, 2, and 3 identify the impedance corrections and in (60), and in (64), respectively. These corrections refer to one plate (of a pair) and are obtained by considering that the dielectric is perfect, with ε = 10ε0.
For illustration purposes, we assume that both plates, made of aluminum, are 25 μm thick (w = h/20), and with regard to the radius of the lead wires, we used rw = w/5 = 5 μm. The frequency window of the analysis is 3–15 GHz, including the resonance frequencies f1 and f2. It should be emphasized that for this range of frequencies, the field penetration depth (δ in (56)) is of the order of 1 μm, and therefore, the plates with 25 μm of thickness can be considered thick plates.
The graphical plots in Figure 10 show that the impedance contribution Z2 (curve 2), proportional to w/ro, associated with the plate axial surface currents at r = ro, is negligible for as in [8]. In fact, for 15 GHz, we found that |Z 2|= 46 μΩ.
The contribution Z1 (curve 1), proportional to ln(ro/rw), associated with the radial surface currents at the outer face of the plate (z = 0), is critically dependent on the radius of the lead wire bonded to the plate. It is the dominant contribution for frequencies below the resonance frequency f2.
The contribution Z3 (curve 3), associated with the radial surface currents at the inner face of the plate at z = w, is extraordinarily large for frequencies close to f2 and theoretically infinite if the dielectric were lossless—an aspect disregarded in [8].
4.4. Lossy Dielectric and Lossy Plates (ID-IC)
The results in the previous section, which concern the contribution of the imperfect plates to the device impedance, were obtained by considering that the dielectric core of the device was a perfect dielectric (PD). Now, we remove this assumption, considering that the permittivity is complex, as in (52), and consequently, that κ and ρ become complex numbers. Now, we aim to find as follows:
where is obtained from (51).
We need not worry about alterations to the impedance contributions , in (60), because they do not depend on the dielectric medium; only does.
We may reuse (63) to calculate , but with some caution. Replacing κ with (and ρ with is essential but will not suffice; we also need to replace the squared real Bessel functions with the absolute value of the squared complex Bessel functions, as follows:
The calculation of the integral on the right-hand side of (68) is addressed in Appendix A and leads to the following simple result:
The result in (69) can be particularized for the case of ρ << 1 (via series expansions) and for the case of ρ >> 1 (via asymptotic expansions), yielding:
Using (69), the plate contribution in (67) to the device impedance becomes
Finally, by simultaneously considering the dielectric and plate imperfections, the device impedance is obtained from:
Graphical results for the modulus and angle of the device’s impedance in (72) against the frequency, for the full lossy case, are shown in Figure 11 (curves 2 in blue).
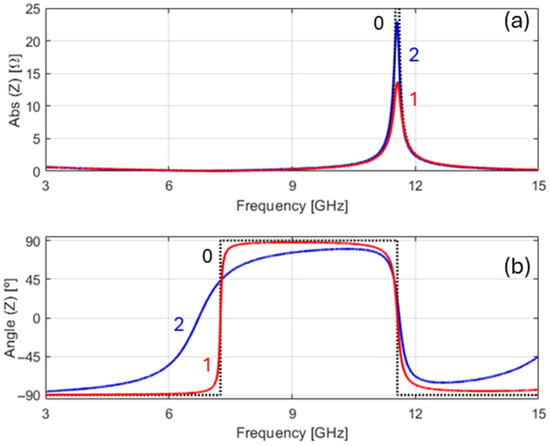
Figure 11.
Graphics of the modulus (a) and angle (b) of impedance of the circular parallel plate capacitor as a function of the frequency. Curves 2 (blue) refer to the full lossy case, with imperfect dielectric core and imperfect conducting plates. Curves 1 (red) refer to the imperfect dielectric case, but with perfect conductors. The dotted curves with the label 0 refer to the lossless case.
For comparison purposes, we also repeated the impedance plots for the other addressed cases, the ID/PC case (curves 1), and the PD/PC case (curves 0) in Figure 11. The results in Figure 11 show that the impedance peak at f = f2 has almost doubled from 14 Ω to about 23 Ω, owing to conductor imperfection. The most important mechanism responsible for this increase is the presence of radial currents on the inner faces of the capacitor plates.
The density of the radial surface currents JS(r) on the inner faces of the plates (surface S3 in Figure 9) was evaluated in (55) for the lossless dielectric case. The result in (55) can be easily generalized for the lossy case by substituting the real wavenumber , with its complex version , where the complex permittivity has already been defined in (52); then, for the ID/IC case, the radial surface current is given by:
and its rms value is defined as follows:
where the real function JN(r) represents the normalized surface current density, which is equal to 0 when r = 0 and equal to 1 when r = ro.
We computed and plotted the function JN against r/ro for three different frequencies: the resonance frequencies f1 and f2, and one in the middle f3 = (f1 + f2)/2. The results presented in Figure 12 clearly show that the surface current at f = f2 (blue curve) crowds near the circumference of radius r = ro/2, and that its intensity largely exceeds those of the other currents. If dielectric losses were much lower than those considered in the simulation (loss angle mrad), then the maximum of JN would increase to well over 50.
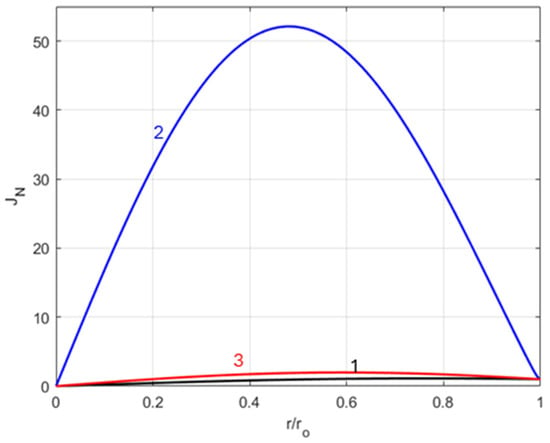
Figure 12.
Graphical plot of the rms value of the plate’s radial surface current density as a function of r/ro, for three different values of the frequency. The current density is normalized to its peripheral value . Curve 1 (black) was obtained for f = f1, curve 2 (blue) was obtained for f = f2, and curve 3 (red) was obtained for f = (f1 + f2)/2.
Table 2 provides a set of computed numerical values for the device’s complex impedance (inductive behavior) for the frequencies f1, f2, and (f1 + f2)/2, which are considered in the graph plots in Figure 12.

Table 2.
Device impedance for frequencies close to resonance.
5. Conclusions
This paper, essentially theoretical/tutorial in nature, deals with the high-frequency impedance of linear passive devices whose geometry is rotationally invariant, with special emphasis on one particular device: the circular parallel plate capacitor.
Firstly, by employing electromagnetic fundamentals, we discussed and unambiguously defined the concepts of current, voltage, and impedance, as applied in the case of rotationally symmetric devices, where the magnetic field is purely azimuthal.
Secondly, we applied those concepts to the investigation of the high-frequency impedance behavior of a circular parallel plate capacitor made of a thin dielectric wafer sandwiched between two thick metal plates in the frequency range of 0 to 15 GHz. To begin with, assuming a lossless scenario, we found that the device’s impedance was characterized by a repetitive pattern of singularities, zeros, and infinities along the frequency axis, with alternating capacitive and inductive behaviors. Subsequently, we added the influence of dielectric losses (using a Debye model) to smooth out the observed singularities. Finally, new research results were obtained regarding the influence of plate losses on the device’s impedance: we were able to conclude that the radial surface currents flowing on the internal faces of the capacitor contribute very significantly to increasing the overall impedance for frequencies close to resonance.
This work is based on a standard assumption: that the geometry of the capacitor (with h << ro) leads to negligible fringing field effects. This assumption requires validation. It is true that the topic of fringing fields has received a lot of attention in the past, but most of the literature has focused on analysis techniques (such as conformal mapping) that are applicable to electrostatic problems and not to high-frequency regimes. It would, therefore, be appropriate for future research to address the issue of the frequency dependence of fringing field effects. We doubt that explicit analytical results can be obtained, but we can hope that full-wave numerical approaches will be sufficient. A parallel research path is, of course, experimentation and measurement.
Funding
This work is funded by FCT/MECI through national funds and, when applicable, co-funded EU funds under award UID/50008: Instituto de Telecomunicações.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A
Integrals Involving Squared Bessel Functions
Definite integrals involving squared Bessel functions of the first kind, like
appear in (40), (41), and (63) for the orders of n = 0 and n = 1.
These squared Bessel functions are usually linked with the squared rms value of a given vector field expressed in the form of .
The calculation of Intn can be carried out with the help of the mathematical identities in (A2) and (A3) [11,12]:
yielding
and
The abovementioned results hold if the parameter in (A1) is real. If is complex, i.e., , we will have Consequently, with regard to the squared rms value of the field, we will have to replace F2 with . In other words, instead of (A1) we should consider (A6):
To compute , we utilize another mathematical identity [11,12]:
and make For n = 0, using (A3), we find that:
which permits the calculation of as follows:
For n = 1, from (A7) and (A3), we get:
which permits the calculation of as follows:
It is interesting to note that the results for in (A5) and (A11) converge to the same finite value when approaches zero, as follows:
References
- Simonyi, K. Foundations of Electrical Engineering; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Brandão Faria, J.A. Electromagnetic Foundations of Electrical Engineering; Wiley: Chichester, UK, 2008. [Google Scholar]
- Bahl, I. Lumped Elements for RF and Microwave Circuits; Artech House: London, UK, 2003. [Google Scholar]
- Poddar, R.; Brooke, M. Accurate high speed empirically based predictive modeling of deeply embedded gridded parallel plate capacitors fabricated in a multilayer LTCC process. IEEE Trans. Adv. Packag. 1999, 22, 26–31. [Google Scholar] [CrossRef]
- Li, Y.; Yew, T.; Chung, C.; Figueroa, D. Design and performance evaluation of microprocessor packaging capacitors using integrated capacitor-via-plane model. IEEE Trans. Adv. Packag. 2000, 23, 361–367. [Google Scholar] [CrossRef]
- Mellberg, A.; Stenarson, J. An evaluation of three simple scalable MIM capacitor models. IEEE Trans. Microw. Theory Tech. 2006, 54, 169–172. [Google Scholar] [CrossRef]
- Faria, J.A.B. Electromagnetic field approach to the modeling of disk-capacitor devices. Microw. Opt. Technol. Lett. 2006, 48, 1467–1472. [Google Scholar] [CrossRef]
- Deleniv, A.; Gevorgian, S. Modeling of conductor losses in capacitors with rectangular and circular plates. Int. J. RF Microw. Comput.-Aided Eng. 2009, 19, 170–176. [Google Scholar] [CrossRef]
- Han, S.; He, J.; Li, C. The electromagnetic field of a circular parallel plate capacitor excited by an AC current and AC voltage supply. Phys. Scr. 2024, 99, 125539. [Google Scholar] [CrossRef]
- Faria, J.A.B. Skin effect in inhomogeneous Euler-Cauchy tubular conductors. Prog. Electromagn. Res. 2011, 18, 89–101. [Google Scholar] [CrossRef]
- Bowman, F. Introduction to Bessel Functions; Dover: New York, NY, USA, 1958. [Google Scholar]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Chew, W.C.; Kong, J.A. Effects of fringing fields on the capacitance of circular microstrip disk. IEEE Trans. Microw. Theory Tech. 1980, 28, 98–104. [Google Scholar] [CrossRef]
- Sloggett, G.J.; Barton, N.G.; Spencer, S.J. Fringing field in disc capacitors. J. Phys. A Math. Gen. 1986, 19, 2725–2736. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, Z.; Yu, S.; Zsurzsan, T.G. Fringing effect analysis of parallel plate capacitors for capacitive power transfer application. In Proceedings of the 4th IEEE International Future Energy Electronics Conference, Singapore, 25–28 November 2019. [Google Scholar] [CrossRef]
- Finch, S. Bessel Functions Zeroes. Penn State University, PA, USA, 2003. Available online: https://citeseerx.ist.psu.edu (accessed on 2 June 2025).
- Orfanidis, S.J. Electromagnetic Waves and Antennas; Rutgers University: New Brunswick, NJ, USA, 2002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).