Numerical Investigation on Flow and Thermal Characteristics of Spray Evaporation Process in Boiler Desuperheater
Abstract
1. Introduction
2. Methods
2.1. Physical Models
2.2. Numerical Model Description
2.2.1. Continuous Phase Flow (Steam)
2.2.2. Dispersed Phase Flow (Water Droplets)
2.2.3. Heat and Mass Transfer Model
2.2.4. Simulation Strategy
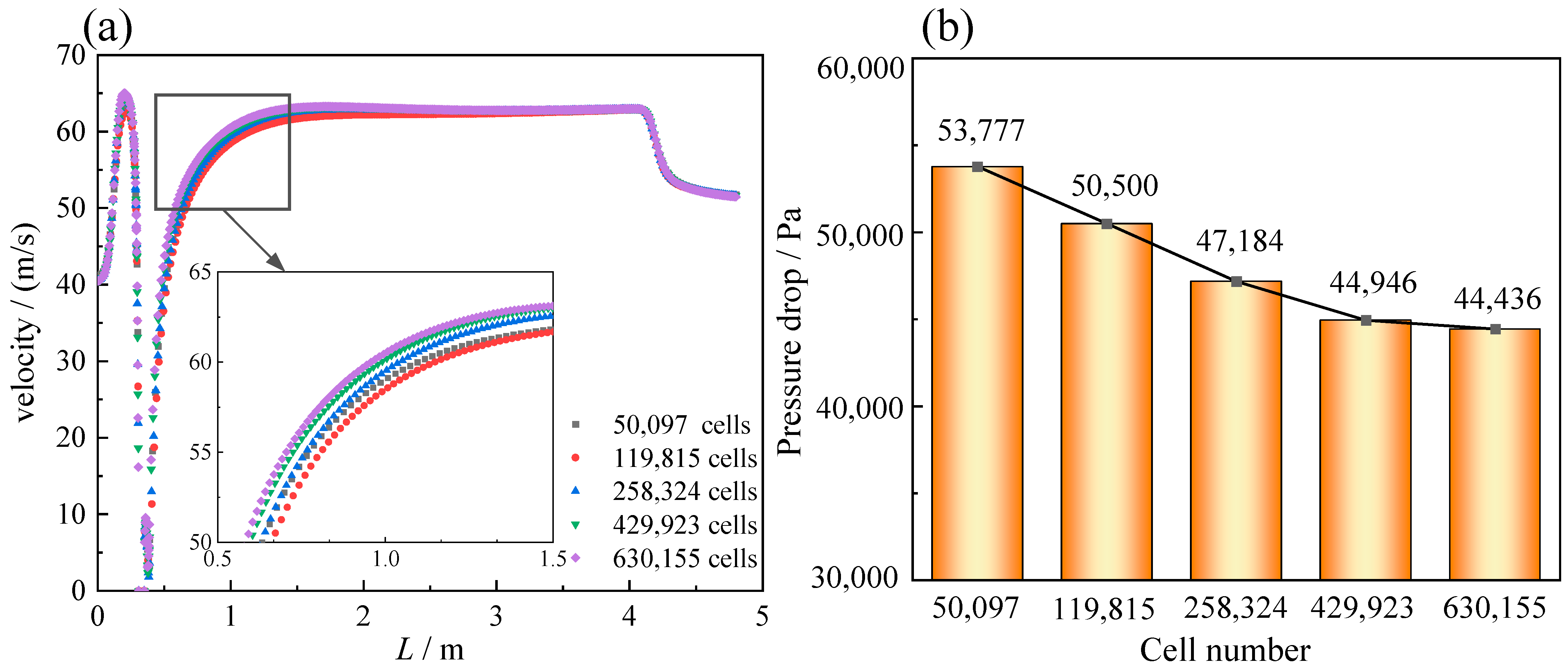
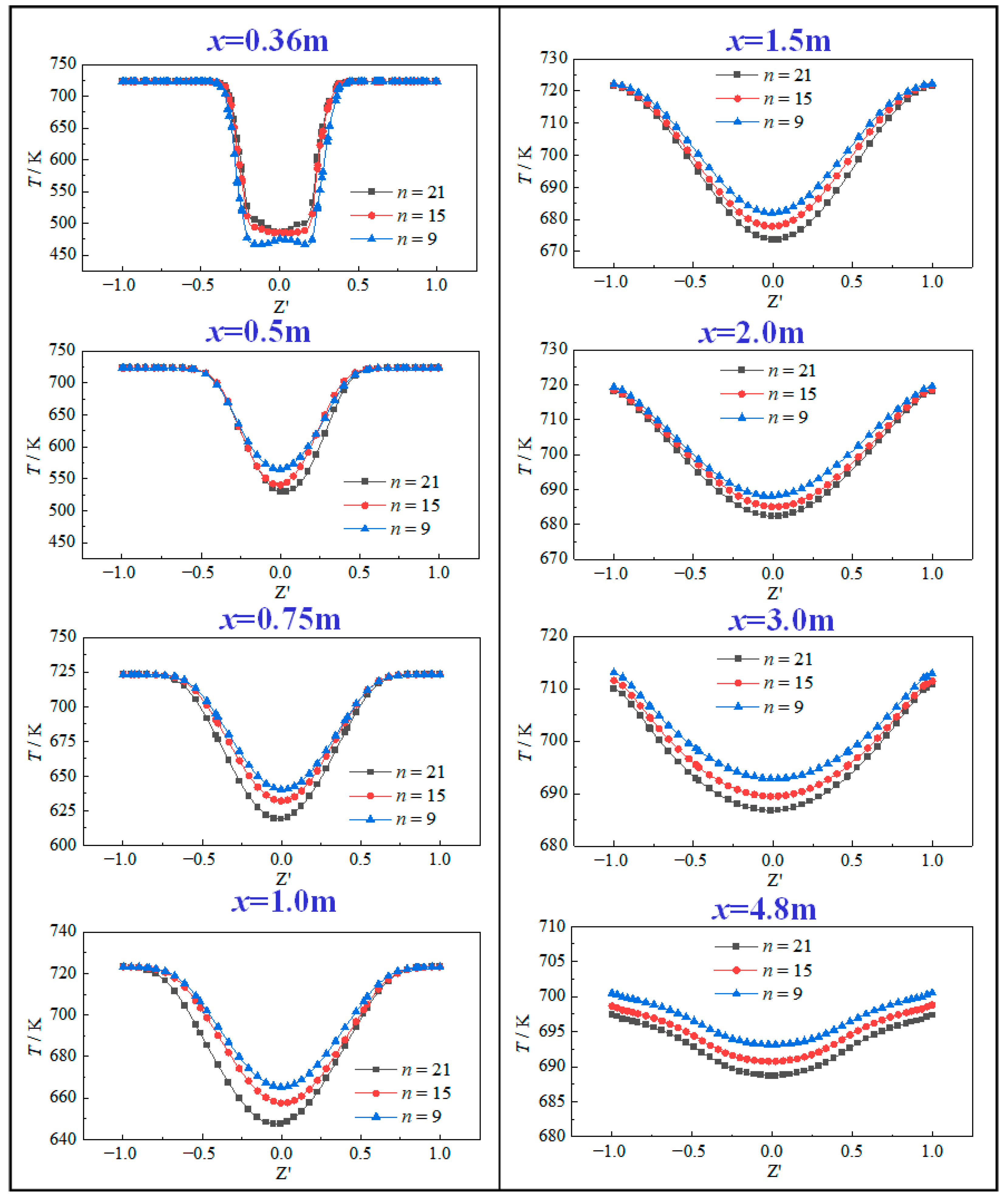
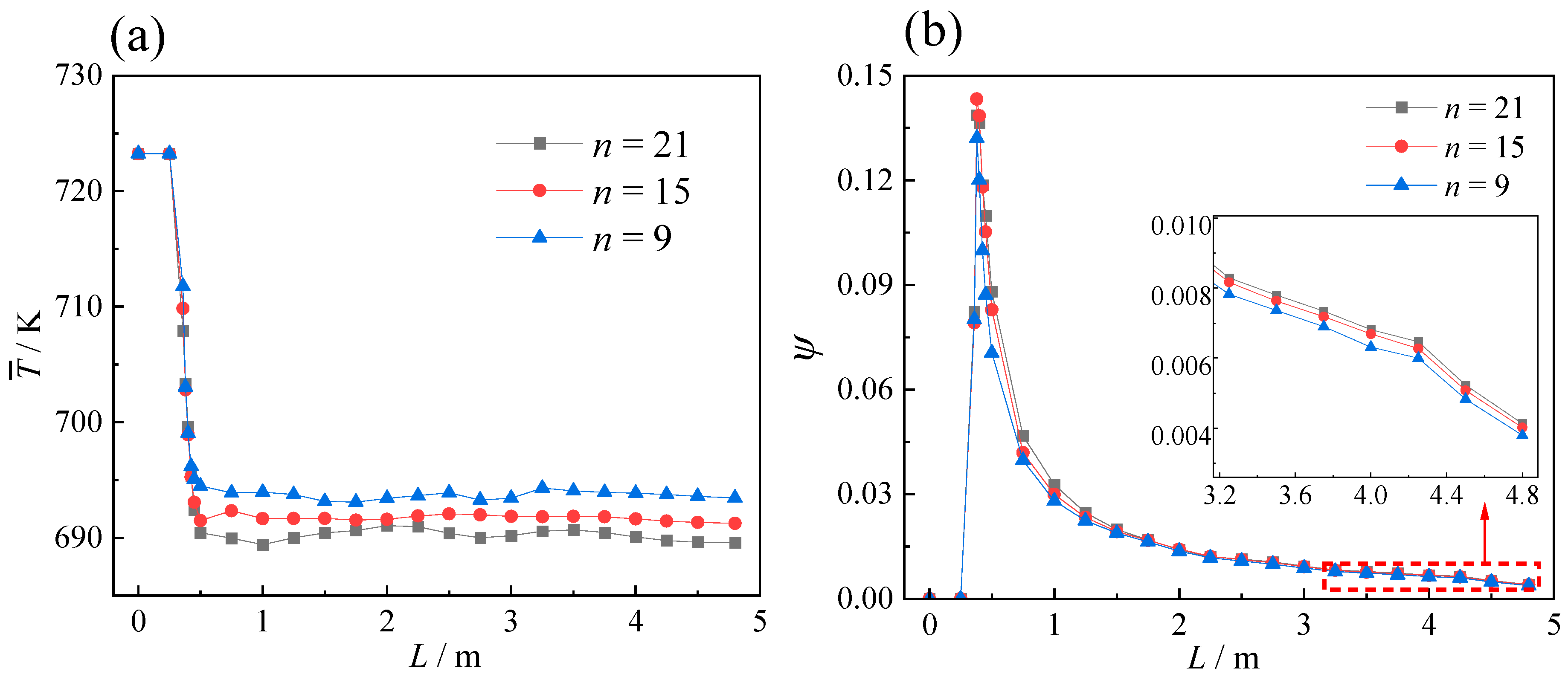
2.3. Grid Independence Test
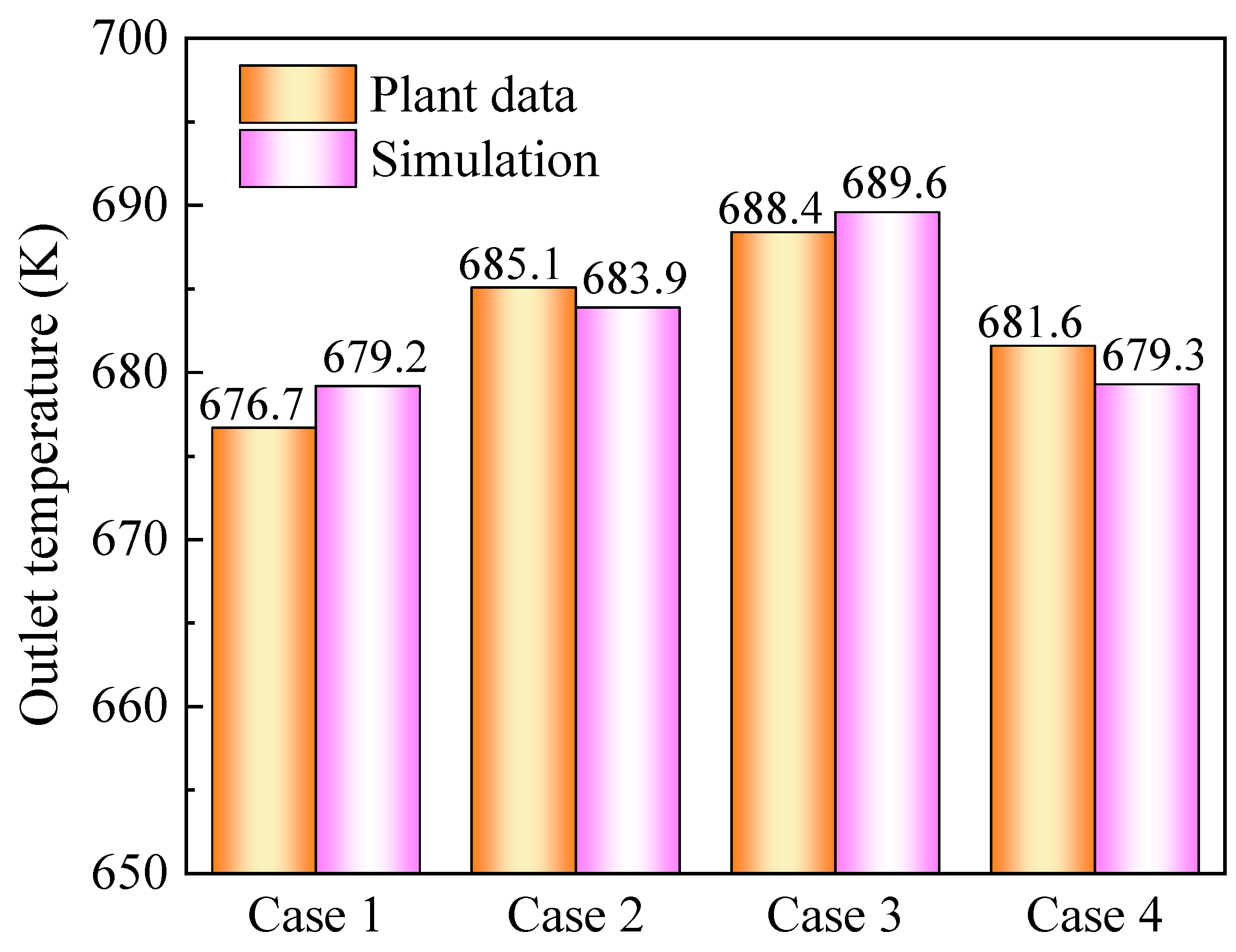
2.4. Model Validation
3. Results and Discussion
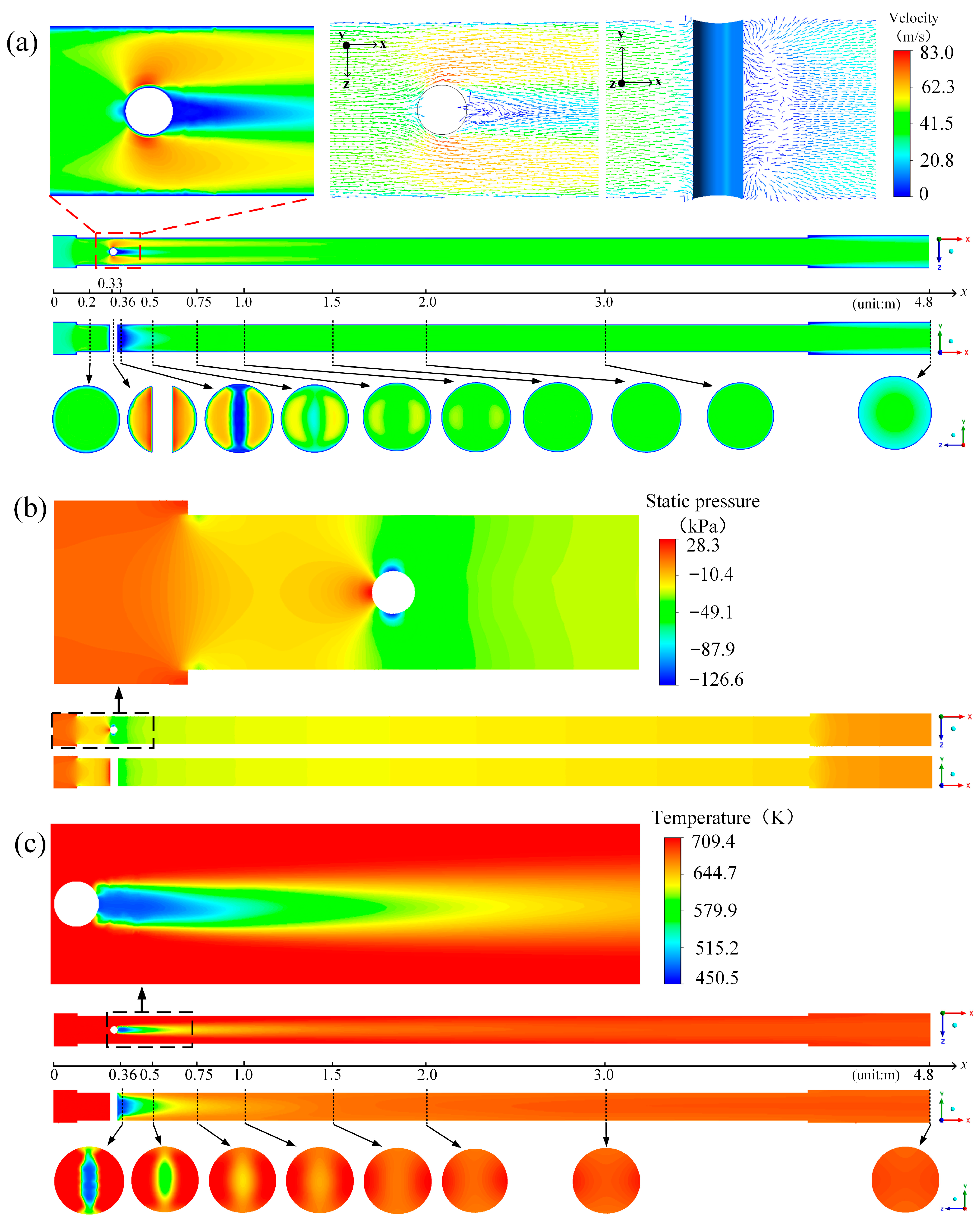
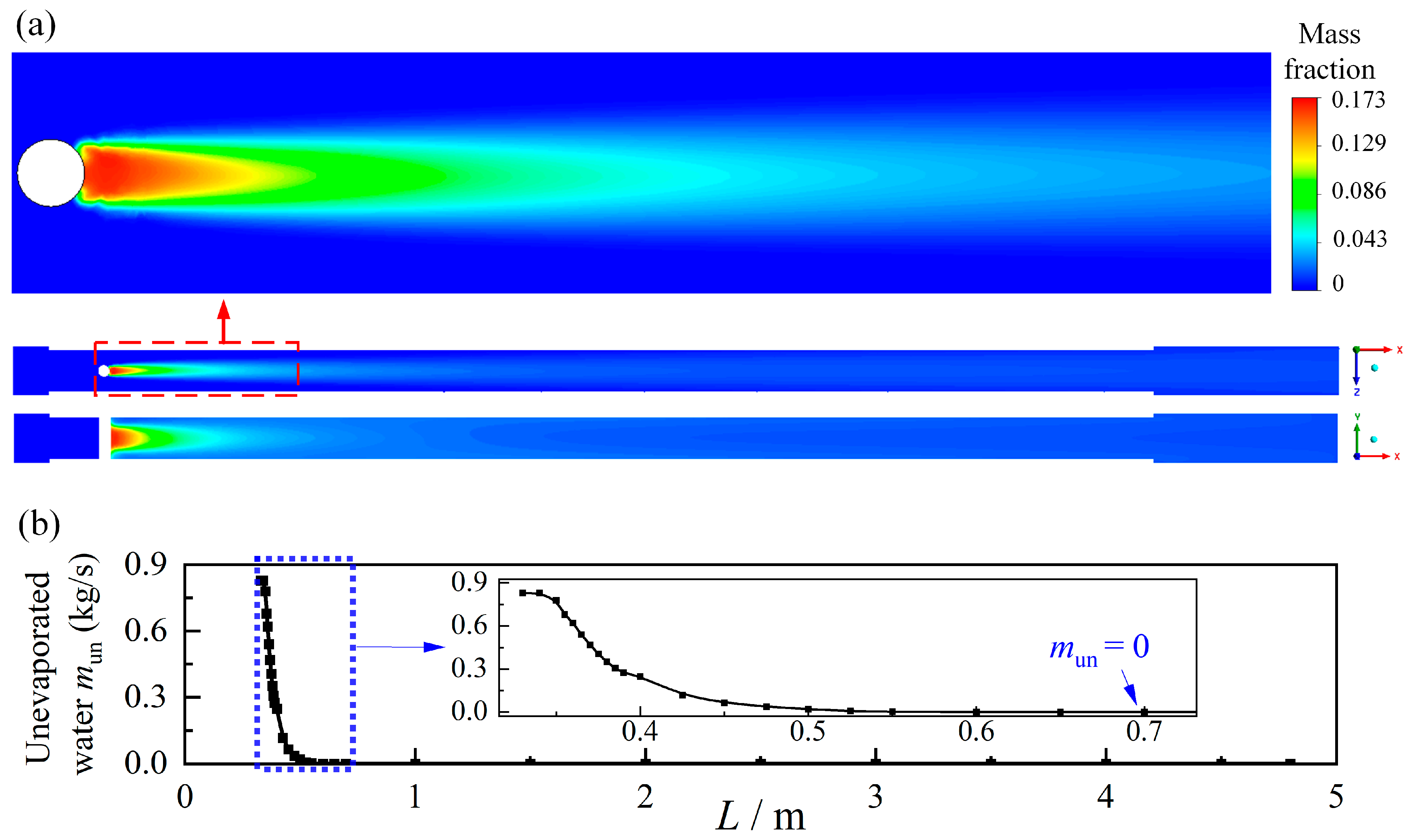
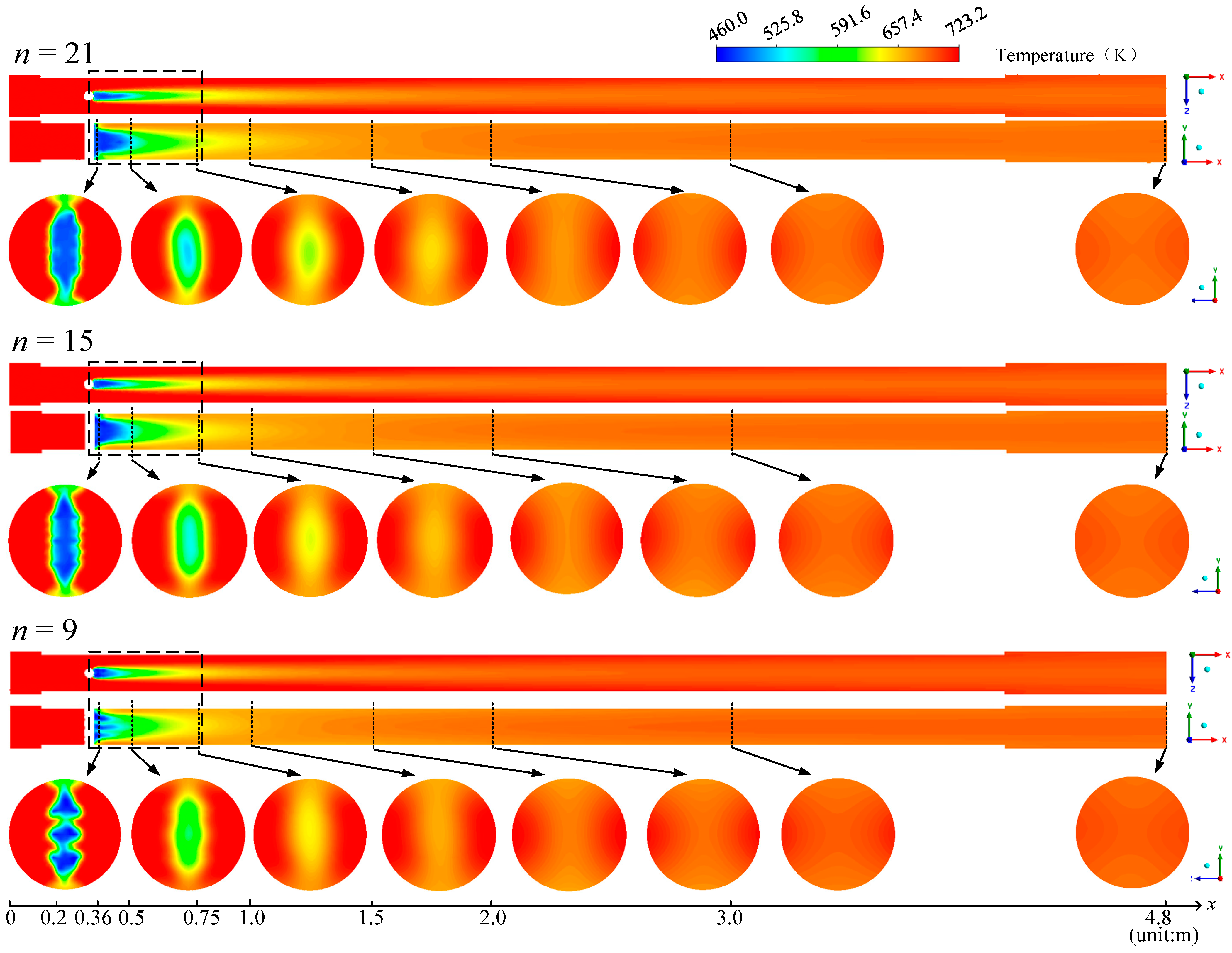
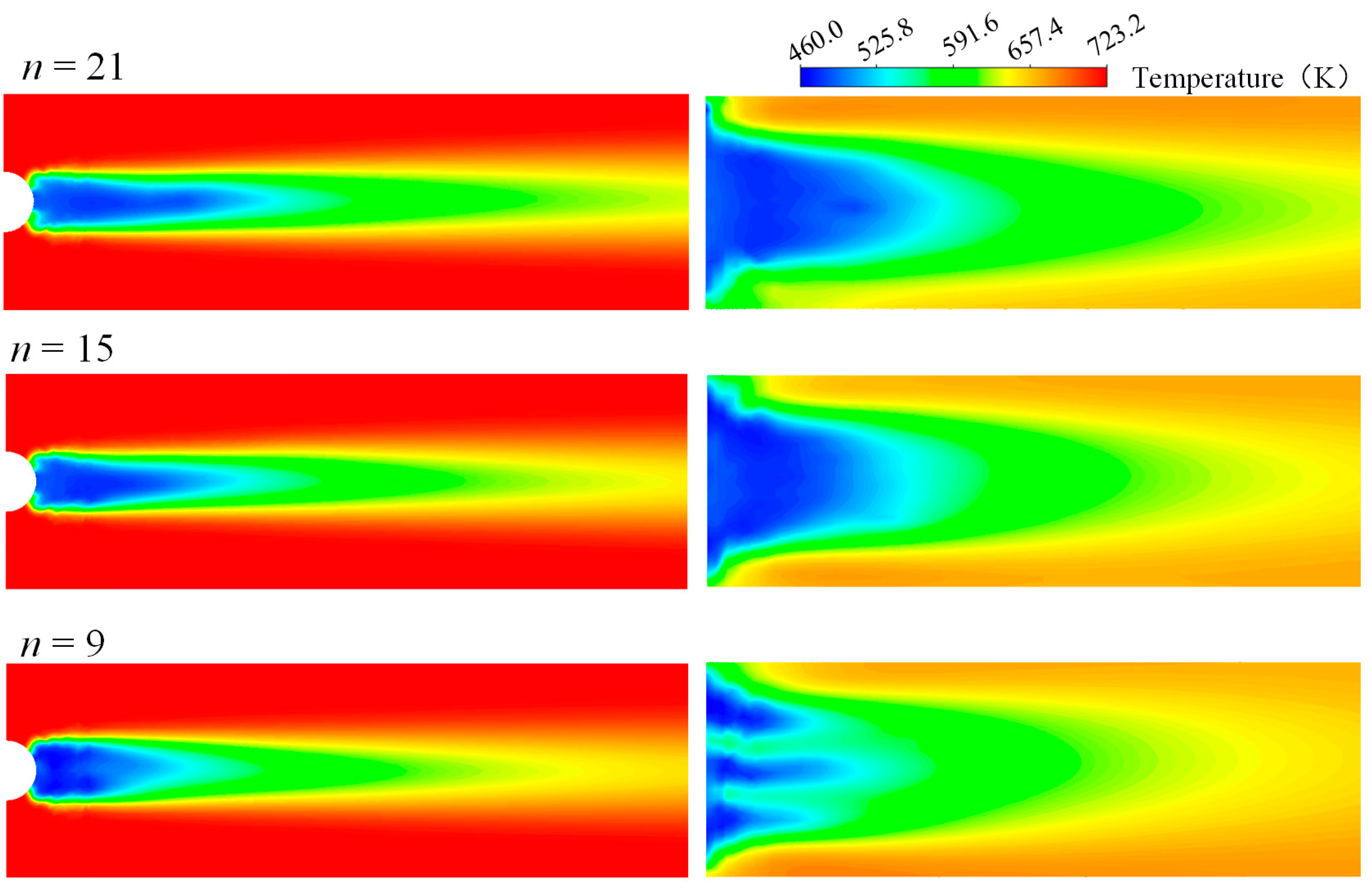
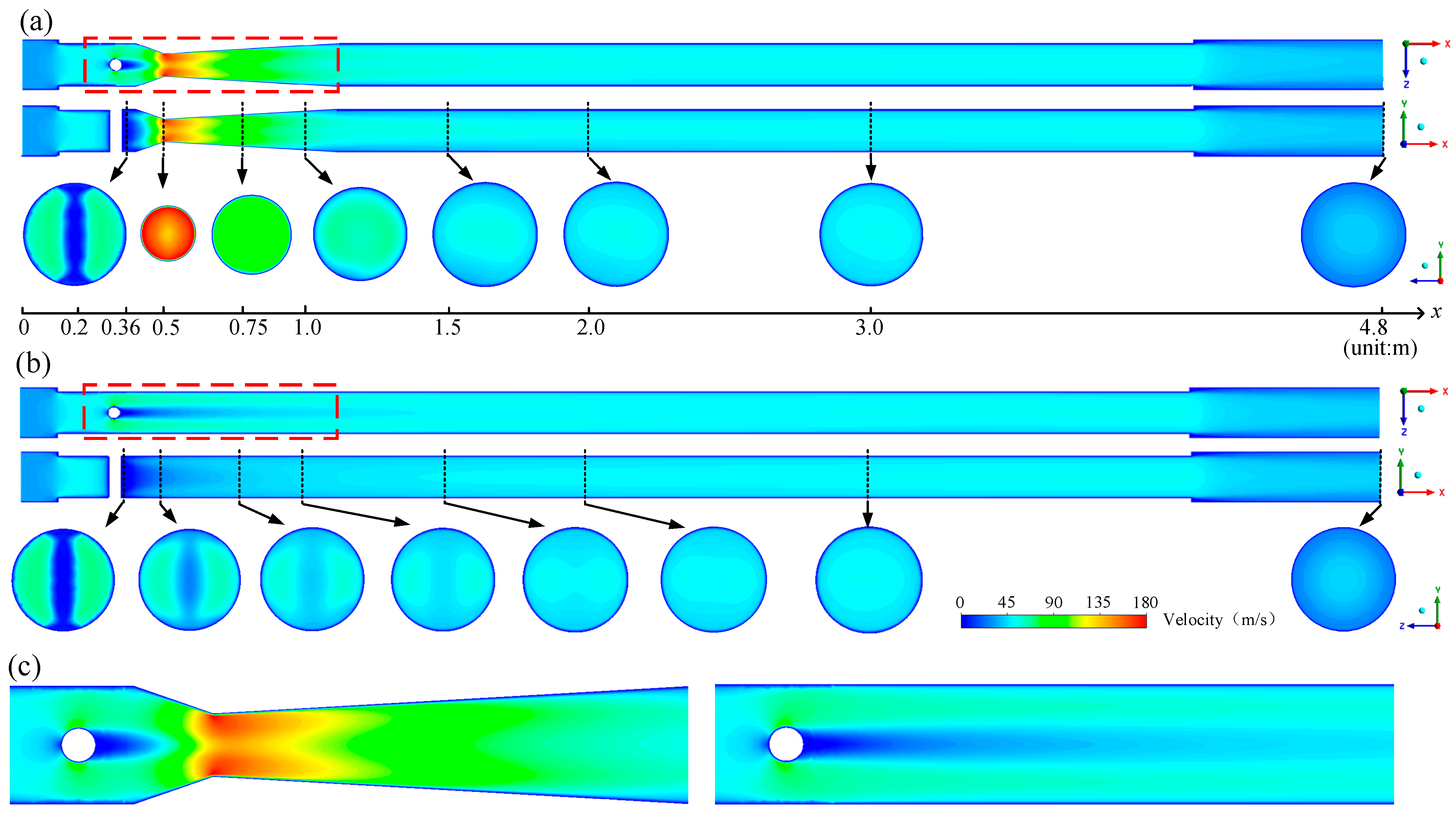
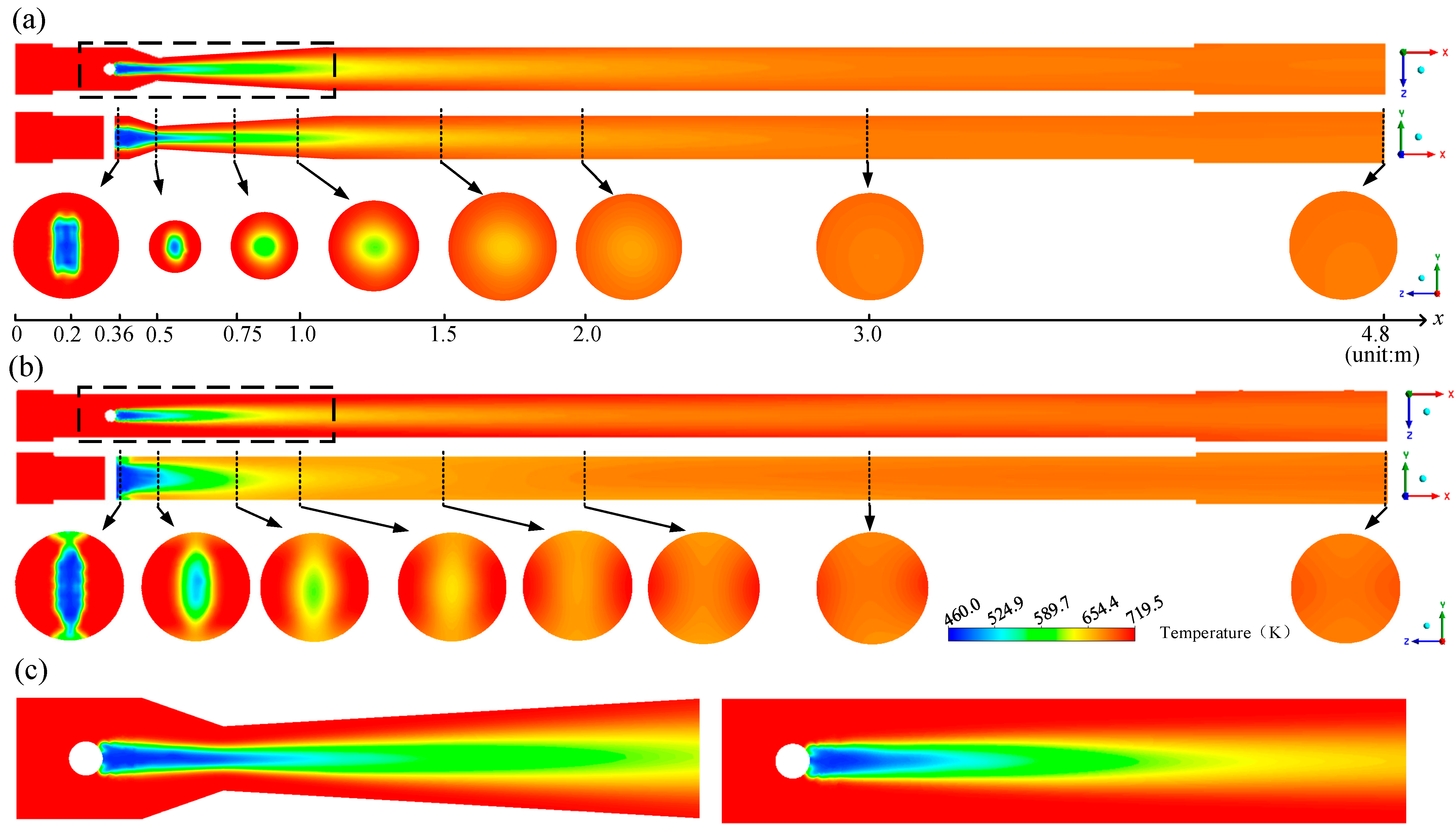
3.1. Analysis on Simulation Results of Case 2
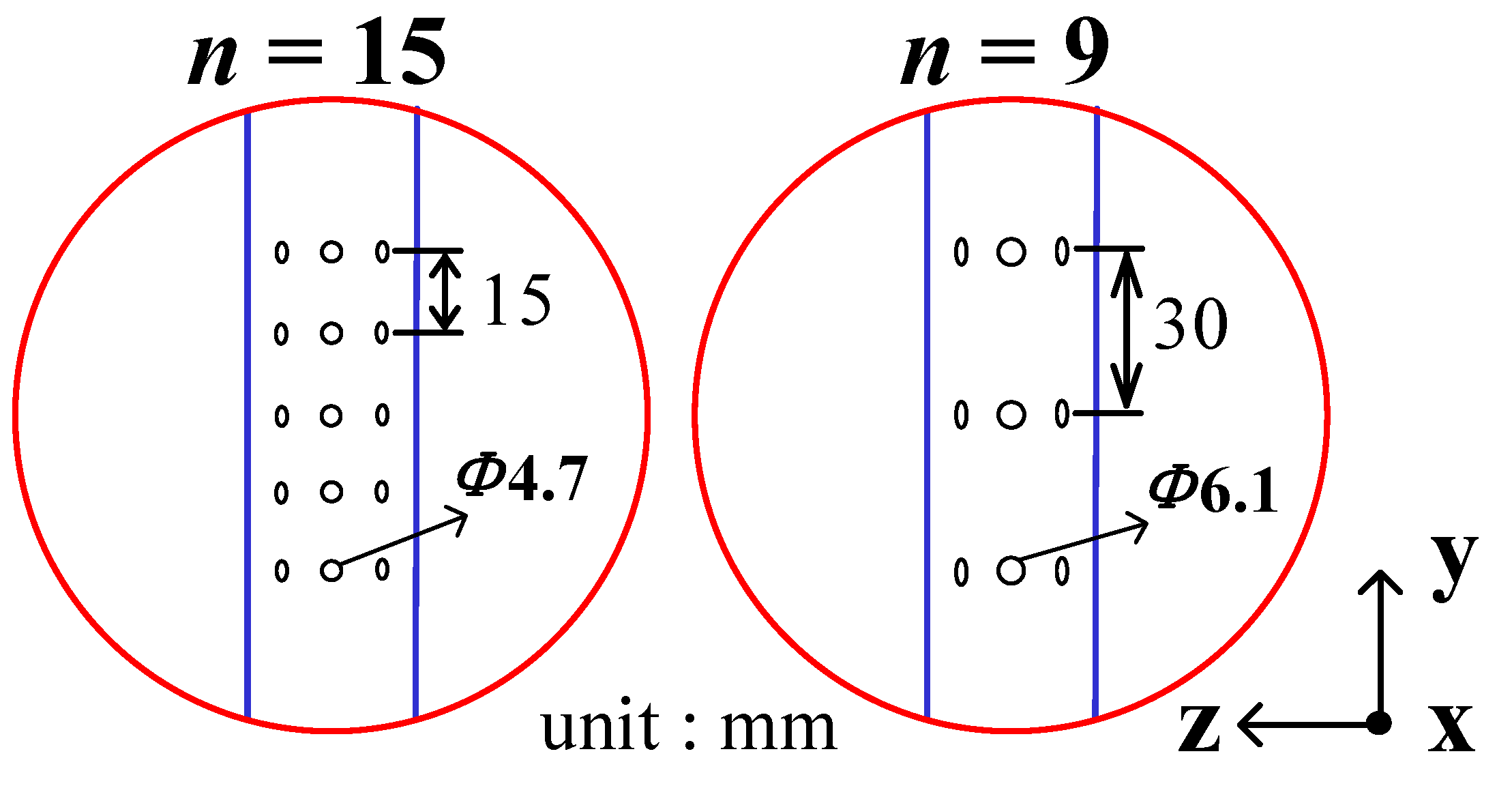
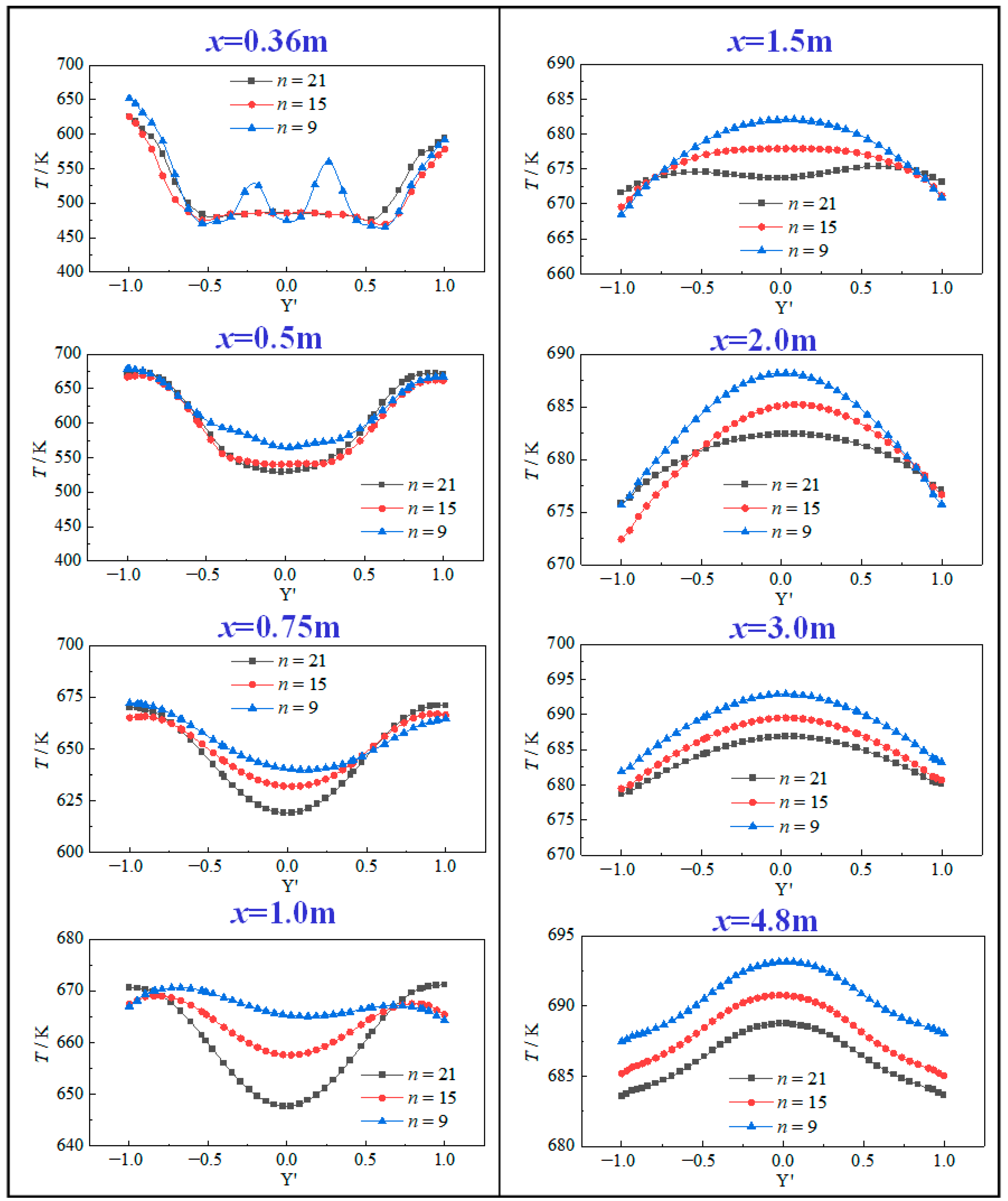
3.2. Influence of Orifice Dimensions
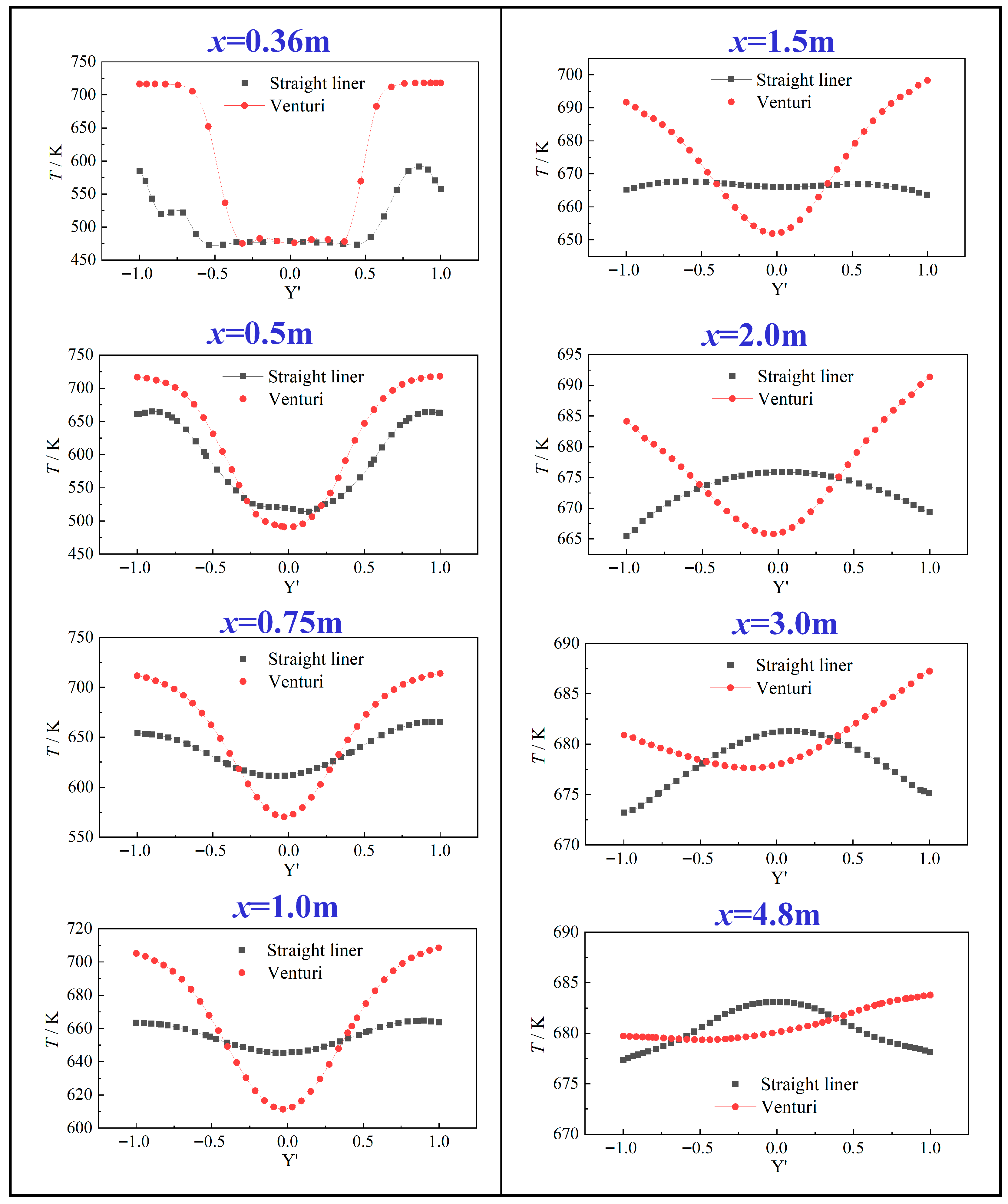
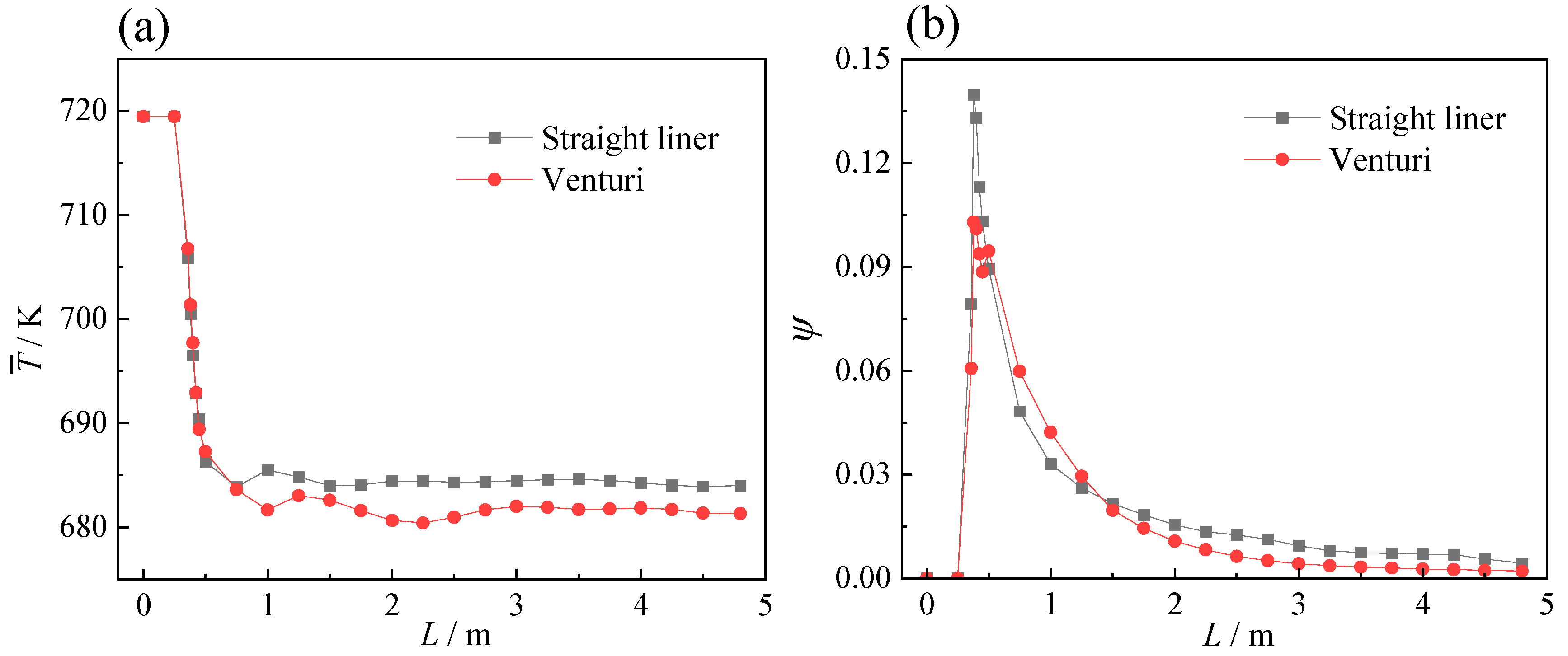
3.3. Influence of Structural Design
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sahajpal, S.; Shah, P.D. Thermal design of ammonia desuperheater-condenser and comparative study with HTRI. Procedia Eng. 2013, 51, 375–379. [Google Scholar] [CrossRef]
- Li, X.; Yu, X. Robust regulation for superheated steam temperature control based on data-driven feedback compensation. Appl. Energy 2022, 325, 119918. [Google Scholar] [CrossRef]
- Xu, Y.X.; Qian, J.Y.; Chen, L.L.; Jin, Z.J. The past, present and future of temperature and pressure reducing device. J. Mech. Electr. Eng. 2021, 38, 1081–1090, 1123. [Google Scholar]
- Schoonover, K.G.; Ren, W.M.; Ghiaasiaan, S.M.; Abdel-Khalik, S.I. Mechanistic modeling of desuperheater performance. ISA Trans. 1996, 35, 45–51. [Google Scholar] [CrossRef]
- Rahimi, E.; Torfeh, S.; Kouhikamali, R. Numerical study of counter-current desuperheaters in thermal desalination units. Desalination 2016, 397, 140–150. [Google Scholar] [CrossRef]
- Kouhikamali, R.; Hesami, H.; Ghavamian, A. Convective heat transfer in a mixture of cooling water and superheated steam. Int. J. Therm. Sci. 2012, 60, 205–211. [Google Scholar] [CrossRef]
- Grich, N.; Foudhil, W.; Harmand, S.; Ben Jabrallah, S. Numerical simulation of fog transport in a horizontal channel. MATEC Web Conf. 2020, 330, 01033. [Google Scholar] [CrossRef]
- Cho, B.; Choi, G.; Uruno, Y.; Kim, H.; Chung, J.; Kim, H.; Lee, K. One-dimensional simulation for attemperator based on commissioning data of coal-fired steam power plant. Appl. Therm. Eng. 2017, 113, 508–518. [Google Scholar] [CrossRef]
- Reitz, R.D. Modeling atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Ebrahimian, V.; Gorji-Bandpy, M. Two-dimensional modeling of water spray cooling in superheated steam. Therm. Sci. 2008, 12, 79–88. [Google Scholar] [CrossRef]
- Uruno, Y.; Chung, J.; Kim, H.; Lee, K. Three-dimensional simulation of droplet breakup and evaporation in attemperator. Int. J. Heat Mass Transf. 2022, 196, 123300. [Google Scholar] [CrossRef]
- Liang, H.Z.; Zhao, B.; Huang, C.; Song, H.; Jiang, X. Numerical simulation study on performance optimization of desuperheater. Energy Rep. 2021, 7, 2221–2232. [Google Scholar] [CrossRef]
- Zheng, J.; Lin, Y.J.; Zhao, D.; Wei, X.; Xia, Y.Q. Structure design and simulation analysis of new desuperheater. Chem. Eng. Mach. 2023, 50, 92–97. [Google Scholar]
- Faeth, G.M.; Hsiang, L.P.; Wu, P.K. Structure and breakup properties of sprays. Int. J. Multiph. Flow. 1995, 21, 99–127. [Google Scholar] [CrossRef]
- Taskiran, O.O.; Ergeneman, M. Trajectory based droplet collision model for spray modeling. Fuel 2014, 115, 896–900. [Google Scholar] [CrossRef]
- O’Rourke, P.J. Collective Drop Effects on Vaporizing Liquid Spray; Princeton University: Princeton, NJ, USA, 1981. [Google Scholar]
- Birouk, M.; Gökalp, I. Current status of droplet evaporation in turbulent flows. Prog. Energy Combust. Sci. 2006, 32, 408–423. [Google Scholar] [CrossRef]
- Hong, M.; Xu, G.; Lu, P.; Chen, F.; Sheng, G.; Zhang, Q. Numerical simulation on gas-droplet flow characteristics and spray evaporation process in CFB-FGD tower. Adv. Powder Technol. 2023, 34, 104008. [Google Scholar] [CrossRef]
- Afridi, M.I.; Qasim, M.; Khan, N.A.; Hamdani, M. Heat transfer analysis of Cu-Al2O3-water and Cu-Al2O3-kerosene oil hybrid nanofluids in the presence of frictional heating: Using 3-stage Lobatto IIIA formula. J. Nanofluids 2019, 8, 885–891. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Faeth, G.M. Spray Atomization and Combustion; Technical Report 1986-136; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 1986. [Google Scholar] [CrossRef]
- Chang, K.C.; Yang, J.C.; Wang, M.R. Grid-averaged Lagrangian equations of dispersed phase in dilute two-phase flow. AIAA J. 2003, 41, 1292–1303. [Google Scholar] [CrossRef]
- Feng, S.; Xiao, L.; Ge, Z.; Yang, L.; Du, X.; Wu, H. Parameter analysis of atomized droplets sprayed evaporation in flue gas flow. Int. J. Heat Mass Transf. 2019, 129, 936–952. [Google Scholar] [CrossRef]
- Ansys Help 2021/Fluent/Theory Guide. Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/corp/v211/en/flu_th/flu_th.html (accessed on 26 January 2021).[Green Version]
- Jeng, S.; Deng, Z. Numerical simulation of deformed droplet dynamics and evaporation. Recent Adv. Spray Combust. Spray Combust. Meas. Model Simul. 1996, 2, 305–328. [Google Scholar]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar][Green Version]
- Turner, M.R.; Sazhin, S.S.; Healey, J.J.; Crua, C.; Martynov, S.B. A breakup model for transient Diesel fuel sprays. Fuel 2012, 97, 288–305. [Google Scholar] [CrossRef]
- Palaszewski, S.J.; Jiji, L.M.; Weinbaum, S. A three-dimensional air-vapor-droplet local interaction model for spray units. ASME J. Heat. Transfer. 1981, 103, 514–521. [Google Scholar] [CrossRef]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops, Part I and Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Chaker, M.; Meher-Homji, C.B.; Mee, T., III. Inlet fogging of gas turbine engines: Part A-fog droplet thermodynamics, heat transfer and practical considerations. Turbo Expo Power Land Sea Air 2002, 36096, 413–428. [Google Scholar]
- Kuo, K.K.Y. Principles of Combustion; John Wiley and Sons: New York, NY, USA, 1986. [Google Scholar][Green Version]
- Liu, G.Q.; Ma, L.X.; Liu, J. Chemistry and Chemical Industry Physical Data Handbook; Chemical Industry Press: Beijing, China, 2002. [Google Scholar][Green Version]
- Lin, Q.; Li, Q.H.; Xu, P.; Zheng, R.Y.; Bao, J.J.; Li, L.; Tan, D.P. Transport mechanism and optimization design of LBM-LES coupling-based two-phase flow in static mixers. Processes 2025, 13, 1666. [Google Scholar] [CrossRef]






| Operating Pressure (MPa) | Mass Flow Rate (kg/s) | Inlet Temperature (K) | |||
|---|---|---|---|---|---|
| Steam | Water | Steam | Water | ||
| Case 1 | 10 | 29.33 | 1.50 | 721.55 | 476.10 |
| Case 2 | 26.06 | 0.83 | 709.38 | 474.56 | |
| Case 3 | 28.99 | 1.23 | 723.24 | 496.75 | |
| Case 4 | 27.16 | 1.16 | 719.45 | 475.87 | |
| Parameters | Steam | Water |
|---|---|---|
| Density/kg·m−3 | 34 | 860 |
| Specific heat capacity/J·(kg·K)−1 | 2760 | 4500 |
| Thermal conductivity/W·(m·K)−1 | 0.074 | 0.66 |
| Viscosity/Pa·s | 2.75 × 10−5 | 1.35 × 10−4 |
| Surface tense/N·m−1 | / | 0.037 |
| Boiling point/K | / | 584.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, B.; Du, B.; Wu, K.; Lin, Q.; Liu, B.; Cheng, M. Numerical Investigation on Flow and Thermal Characteristics of Spray Evaporation Process in Boiler Desuperheater. Energies 2025, 18, 3734. https://doi.org/10.3390/en18143734
Wang J, Liu B, Du B, Wu K, Lin Q, Liu B, Cheng M. Numerical Investigation on Flow and Thermal Characteristics of Spray Evaporation Process in Boiler Desuperheater. Energies. 2025; 18(14):3734. https://doi.org/10.3390/en18143734
Chicago/Turabian StyleWang, Jianqing, Baoqing Liu, Bin Du, Kaifei Wu, Qi Lin, Bohai Liu, and Minghui Cheng. 2025. "Numerical Investigation on Flow and Thermal Characteristics of Spray Evaporation Process in Boiler Desuperheater" Energies 18, no. 14: 3734. https://doi.org/10.3390/en18143734
APA StyleWang, J., Liu, B., Du, B., Wu, K., Lin, Q., Liu, B., & Cheng, M. (2025). Numerical Investigation on Flow and Thermal Characteristics of Spray Evaporation Process in Boiler Desuperheater. Energies, 18(14), 3734. https://doi.org/10.3390/en18143734







