A Comparative Study of Customized Algorithms for Anomaly Detection in Industry-Specific Power Data
Abstract
1. Introduction
2. Related Work
2.1. Overview of Outlier-Detection Techniques
2.1.1. Traditional Statistical-Based Methods
2.1.2. Machine Learning and Deep Learning-Based Methods
2.1.3. Case Studies of Industrial Power Data Analysis
2.1.4. Study Objectives and Contributions
3. Methodology
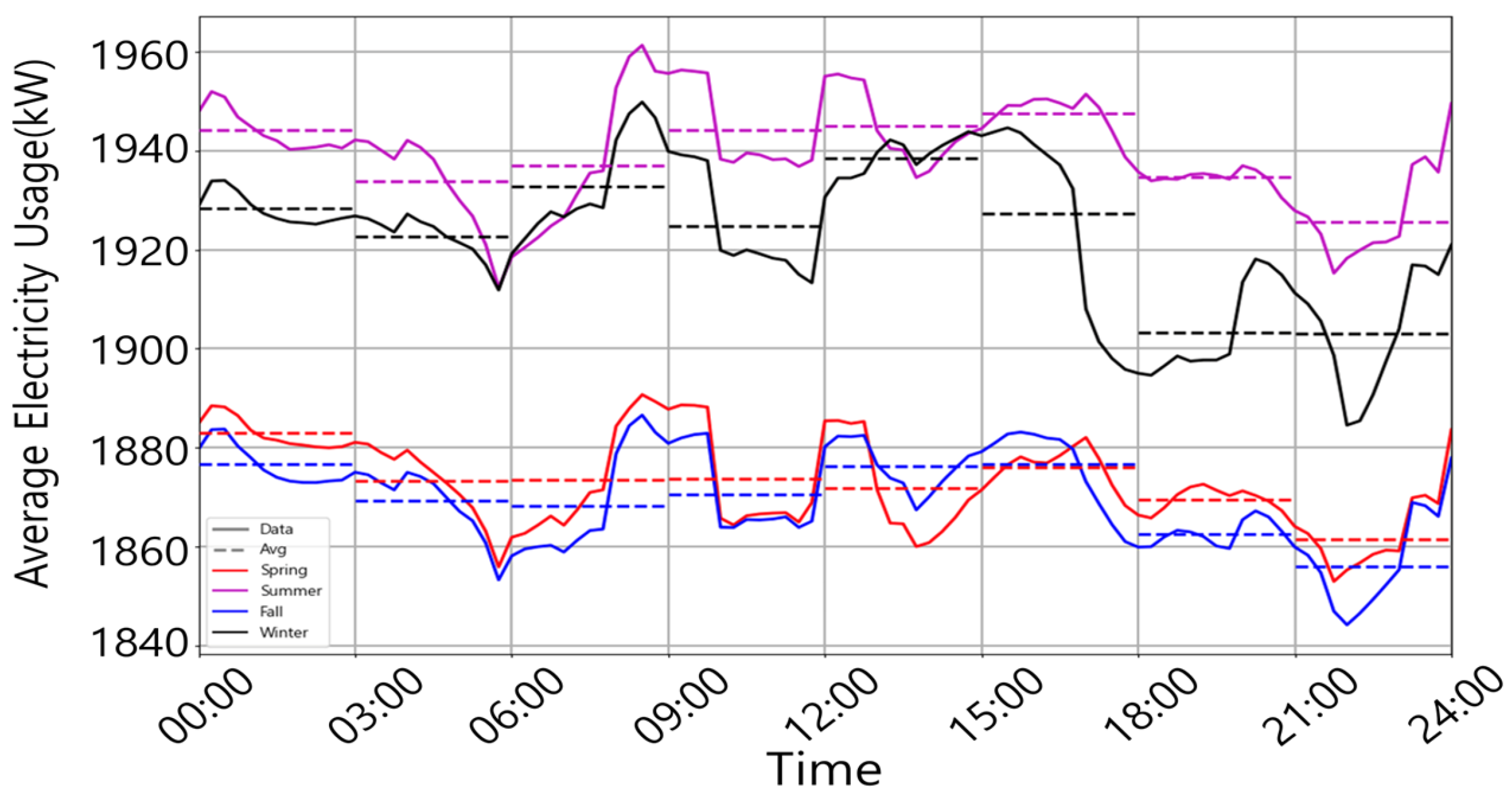
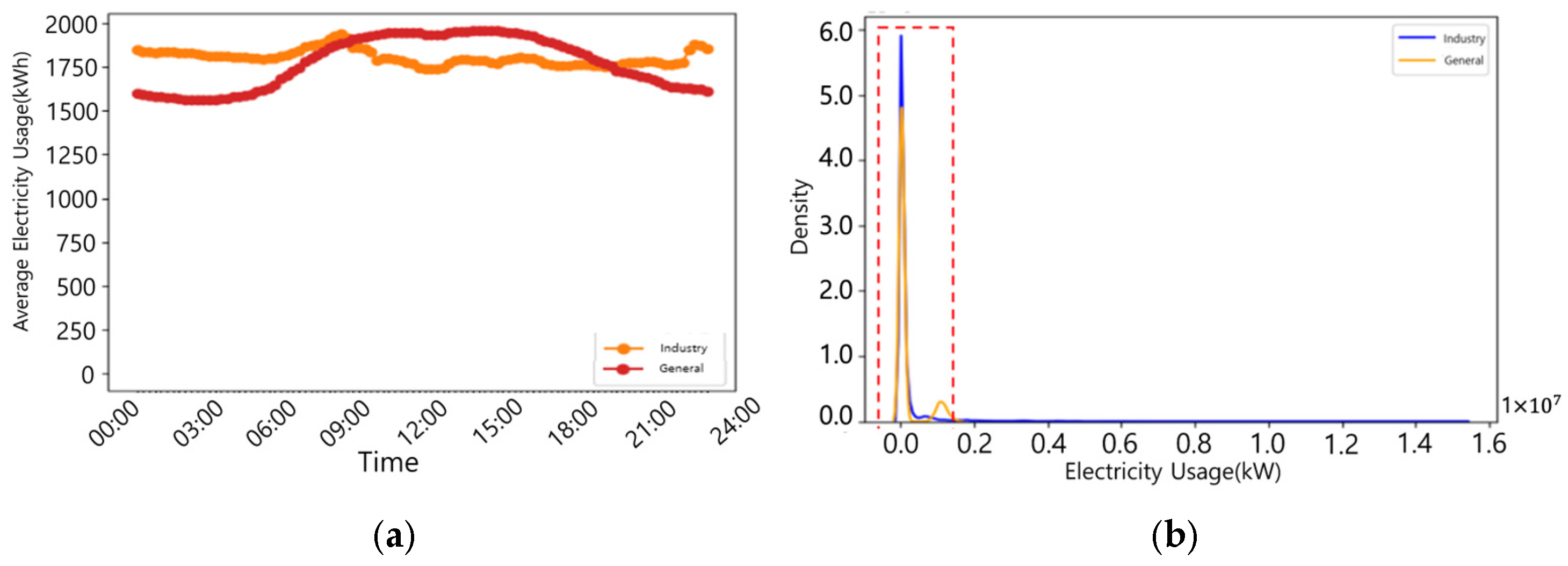
3.1. Dataset Composition and Characteristics
3.2. Comparison and Application of Outlier-Detection Algorithms
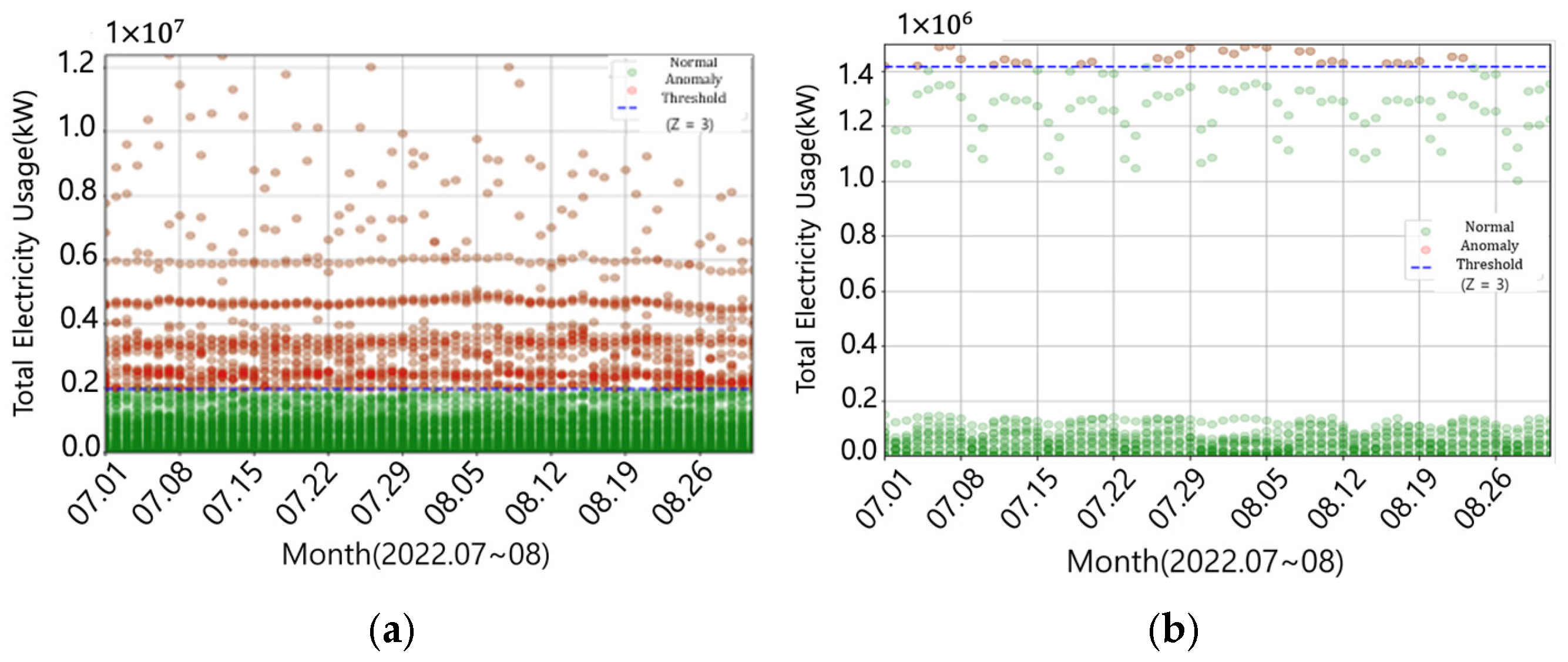
3.2.1. Z-Score-Based Outlier Detection
3.2.2. K-Means–Autoencoder Hybrid Mode
3.2.3. Isolation Forest–Autoencoder Hybrid Model
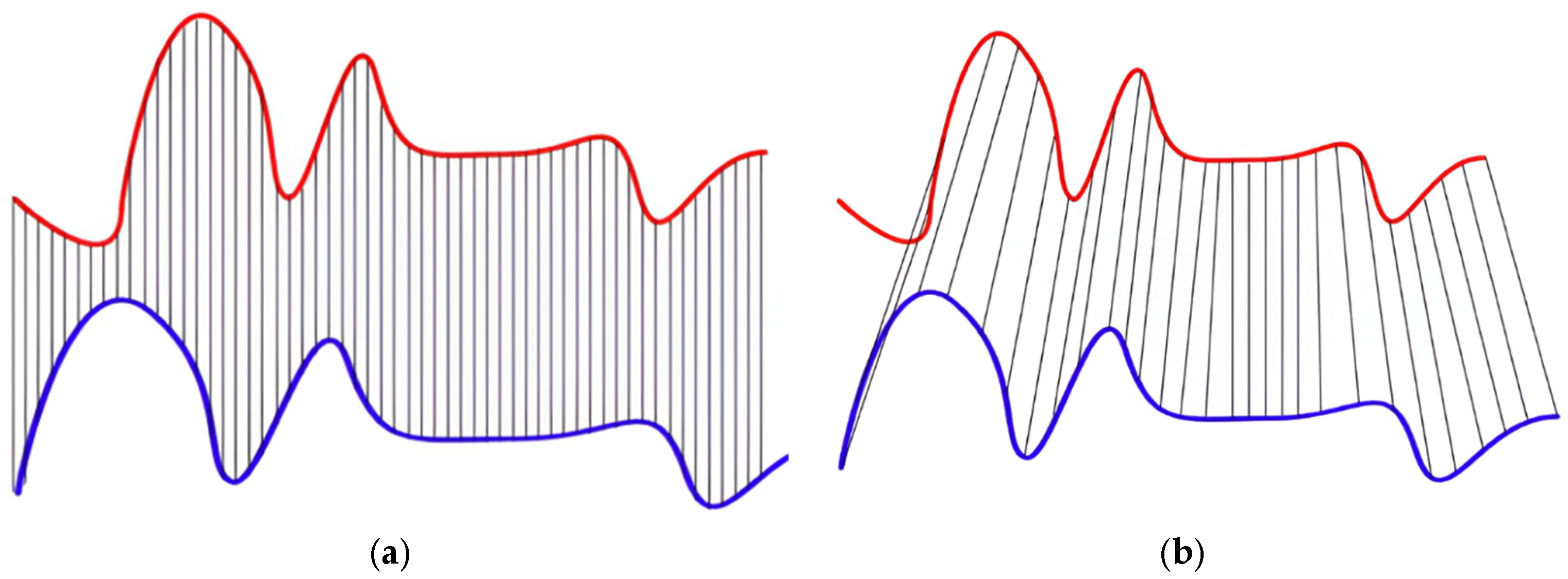
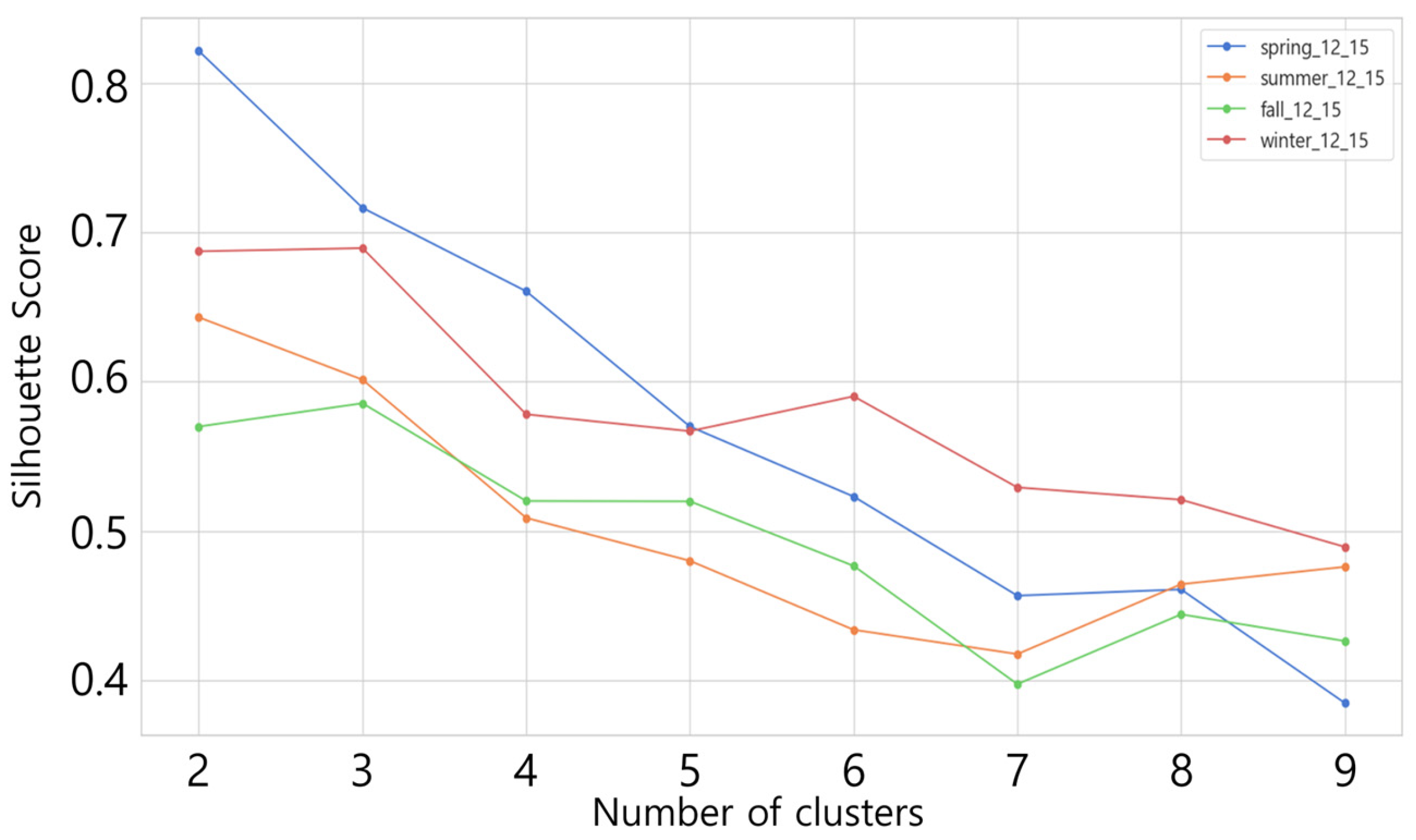
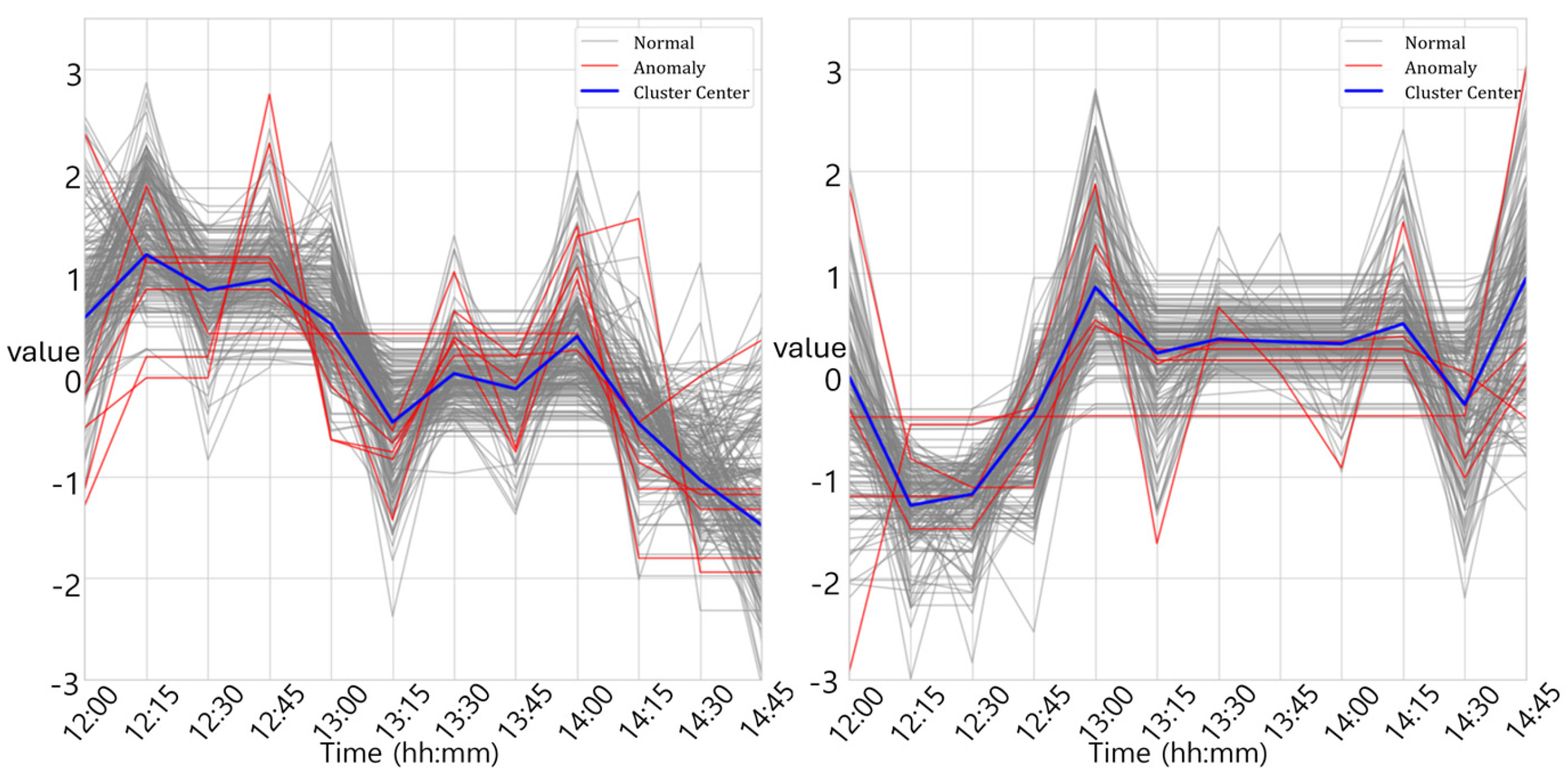
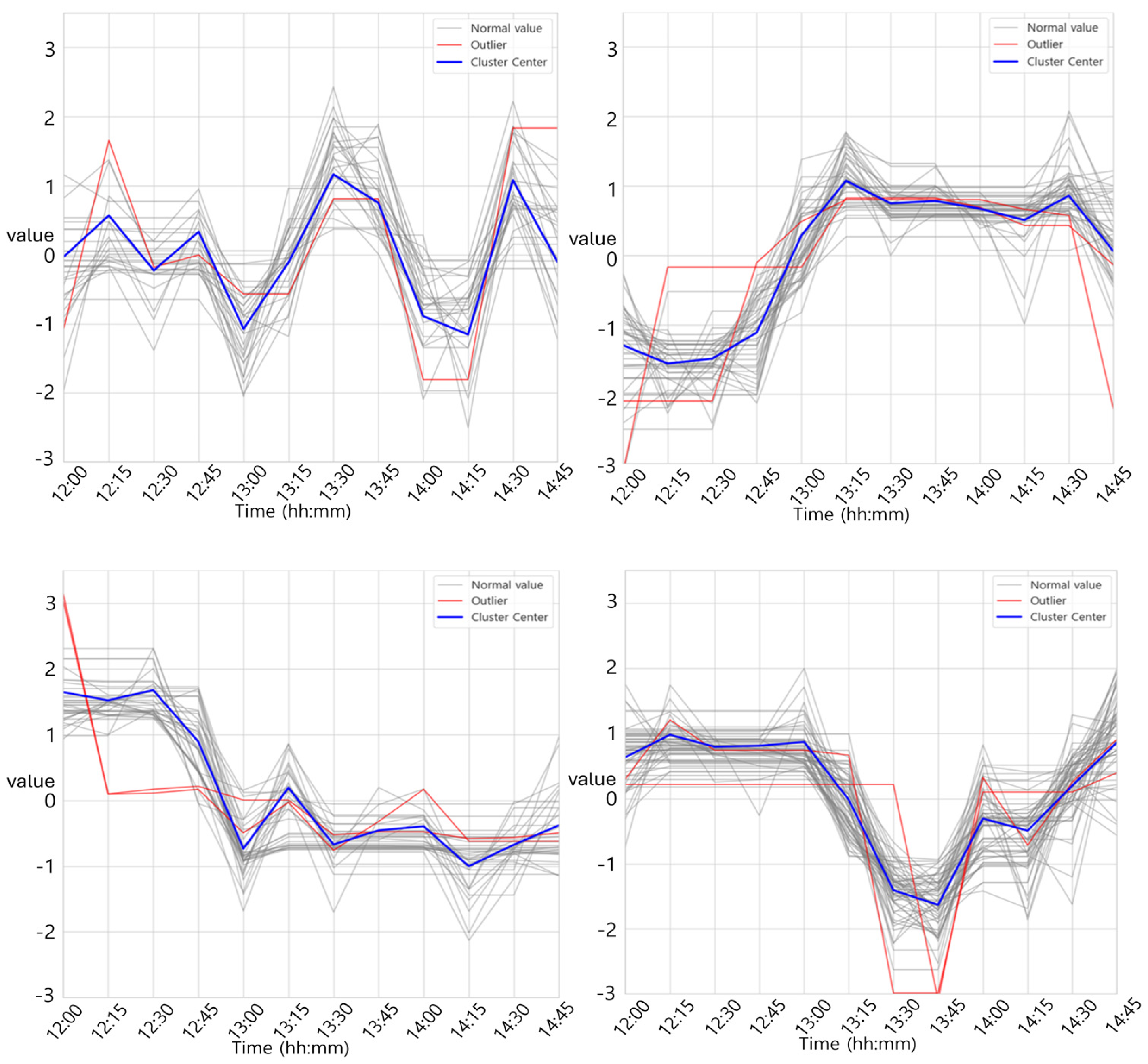
3.2.4. Application of DBA K-Means Clustering
3.3. Threshold Optimization and Evaluation Metrics
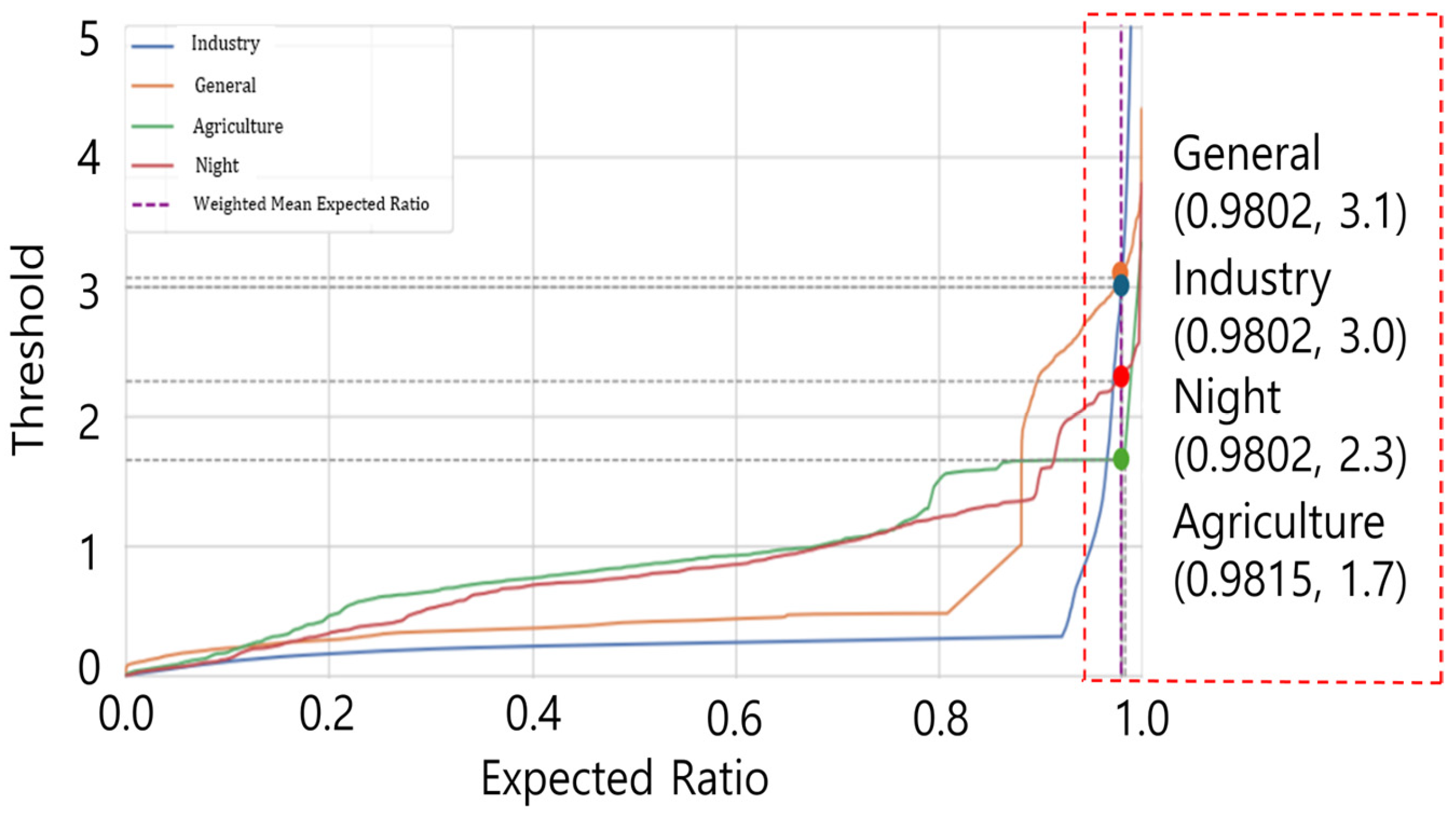
3.3.1. Z-Score Application
3.3.2. Contamination Optimization Method
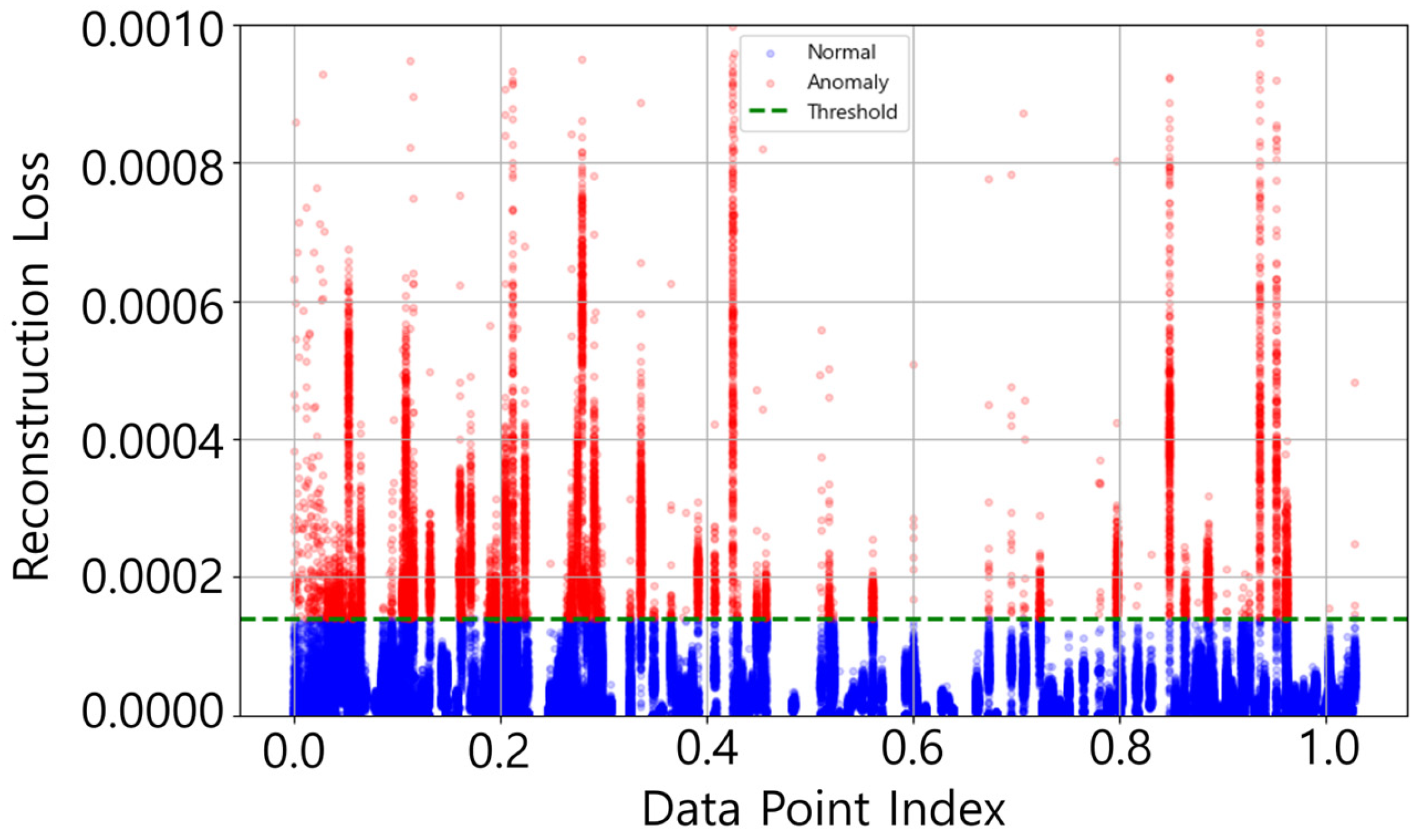
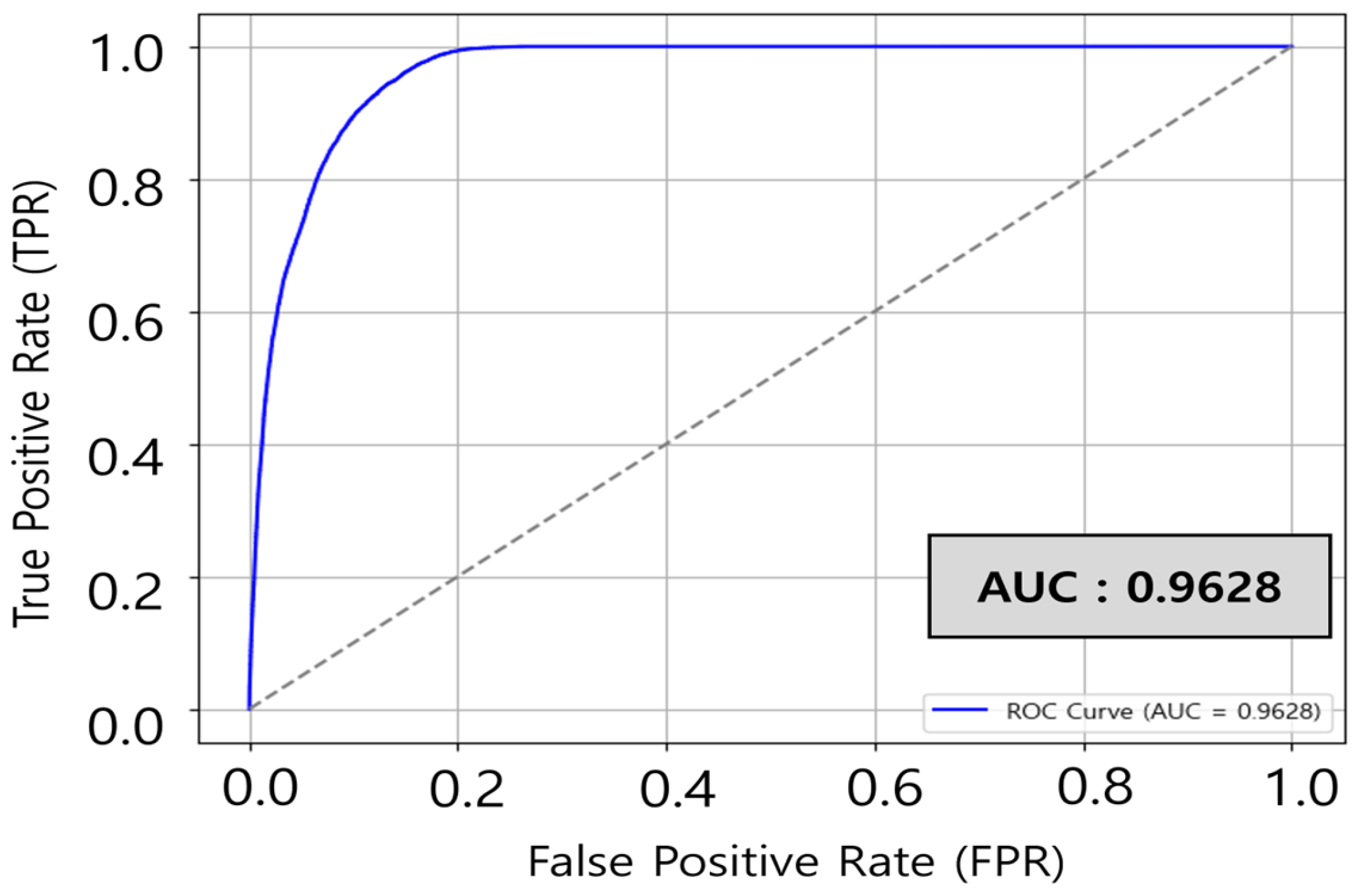
3.3.3. Use of AUC and Reconstruction Loss
3.3.4. Use of Silhouette Score
4. Conclusions
4.1. Industrial Outlier-Detection Performance Comparison
4.1.1. Metal Industry
4.1.2. Food Industry
4.1.3. Chemical Industry
4.2. Algorithm Performance Evaluation
4.3. Discussion on Model Selection and Limitations
5. Future Work
5.1. Research Summary and Key Findings
5.2. Industry-Specific Applicability and Deployment
5.3. Future Research Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Hyperparameter Configurations
| Parameter | Value |
|---|---|
| Encoder Architecture | |
| Input Layer | Input Features |
| Hidden Layer 1 | Dense(64), ReLU |
| Hidden Layer 2 | Dense(32), ReLU |
| Latent Space | Dense(16), ReLU |
| Decoder Architecture | |
| Hidden Layer 1 | Dense(32), ReLU |
| Hidden Layer 2 | Dense(64), ReLU |
| Output Layer | Dense(N), Sigmoid * * N = number of input features |
| Training Parameters | |
| Optimizer | Adam |
| Loss Function | Mean Squared Error |
| Epochs | 10 |
| Parameter | Value |
|---|---|
| n_clusters | Determined by Silhouette score |
| init | K-Means++ |
| metric | DTW |
| max_iter_barycenter | 3 |
| n_jobs | −1 |
| random_state | A fixed seed was used for reproducibility |
References
- Kim, D.S. International Trends and Korea’s Legal and Policy Responses for Achieving Carbon Neutrality through the Utilization of Biological Resources. J. Int. Econ. Law 2023, 21, 199–228. [Google Scholar]
- Korea Energy Economics Institute (KEEI). Monthly Energy Statistics 2024; KEEI: Ulsan, Republic of Korea, 2024. [Google Scholar]
- Lee, S.; Jin, H.; Nengroo, S.H.; Doh, Y.; Lee, C.; Heo, T.; Har, D. Smart metering system capable of anomaly detection by bi-directional LSTM autoencoder. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 7–9 January 2022. [Google Scholar]
- Ribeiro, D.; Matos, L.M.; Moreira, G.; Pilastri, A.; Cortez, P. Isolation forests and deep autoencoders for industrial screw tightening anomaly detection. Computers 2022, 11, 54. [Google Scholar] [CrossRef]
- Jamshidi, E.J.; Yusup, Y.; Kayode, J.S.; Kamaruddin, M.A. Detecting outliers in a univariate time series dataset using unsupervised combined statistical methods: A case study on surface water temperature. Ecol. Inform. 2022, 69, 101672. [Google Scholar] [CrossRef]
- Chadha, G.S.; Islam, I.; Schwung, A.; Ding, S.X. Deep convolutional clustering-based time series anomaly detection. Sensors 2021, 21, 5488. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhan, Q.; Yang, C.; Wang, J. Characterizing the spatio-temporal pattern of land surface temperature through time series clustering: Based on the latent pattern and morphology. Remote Sens. 2018, 10, 654. [Google Scholar] [CrossRef]
- Lee, S.; Nengroo, S.H.; Jin, H.; Doh, Y.; Lee, C.; Heo, T.; Har, D. Anomaly detection of smart metering system for power management with battery storage system/electric vehicle. ETRI J. 2023, 45, 650–665. [Google Scholar] [CrossRef]
- Xiong, Z.; Zhu, D.; Liu, D.; He, S.; Zhao, L. Anomaly detection of metallurgical energy data based on iForest-AE. Appl. Sci. 2022, 12, 9977. [Google Scholar] [CrossRef]
- Park, J.; Jin, T.; Lee, S.; Woo, J. Industrial electrification and efficiency: Decomposition evidence from the Korean industrial sector. Energies 2021, 14, 5120. [Google Scholar] [CrossRef]
- Lund, H.; Østergaard, P.A.; Connolly, D.; Mathiesen, B.V. Smart energy and smart energy systems. Energy 2017, 137, 546–555. [Google Scholar] [CrossRef]
- Lee, J.; Cho, Y. National-scale electricity peak load forecasting: Traditional, machine learning, or hybrid model? Energy 2022, 239, 122366. [Google Scholar] [CrossRef]
- Kamalov, F.; Sulieman, H. Time series signal recovery methods: Comparative study. In Proceedings of the 2021 International Symposium on Networks, Computers and Communications (ISNCC), Dubai, United Arab Emirates, 31 October–2 November 2021. [Google Scholar]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 3rd ed.; Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]
- Arthur; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Petitjean, F.; Ketterlin, A.; Gançarski, P. A global averaging method for dynamic time warping, with applications to clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Campos, G.O.; Zimek, A.; Sander, J.; Campello, R.J.G.B.; Micenková, B.; Schubert, E.; Assent, I.; Houle, M.E. On the Evaluation of Unsupervised Outlier Detection: Measures, Datasets, and an Empirical Study. Data Min. Knowl. Discov. 2016, 30, 891–927. [Google Scholar] [CrossRef]



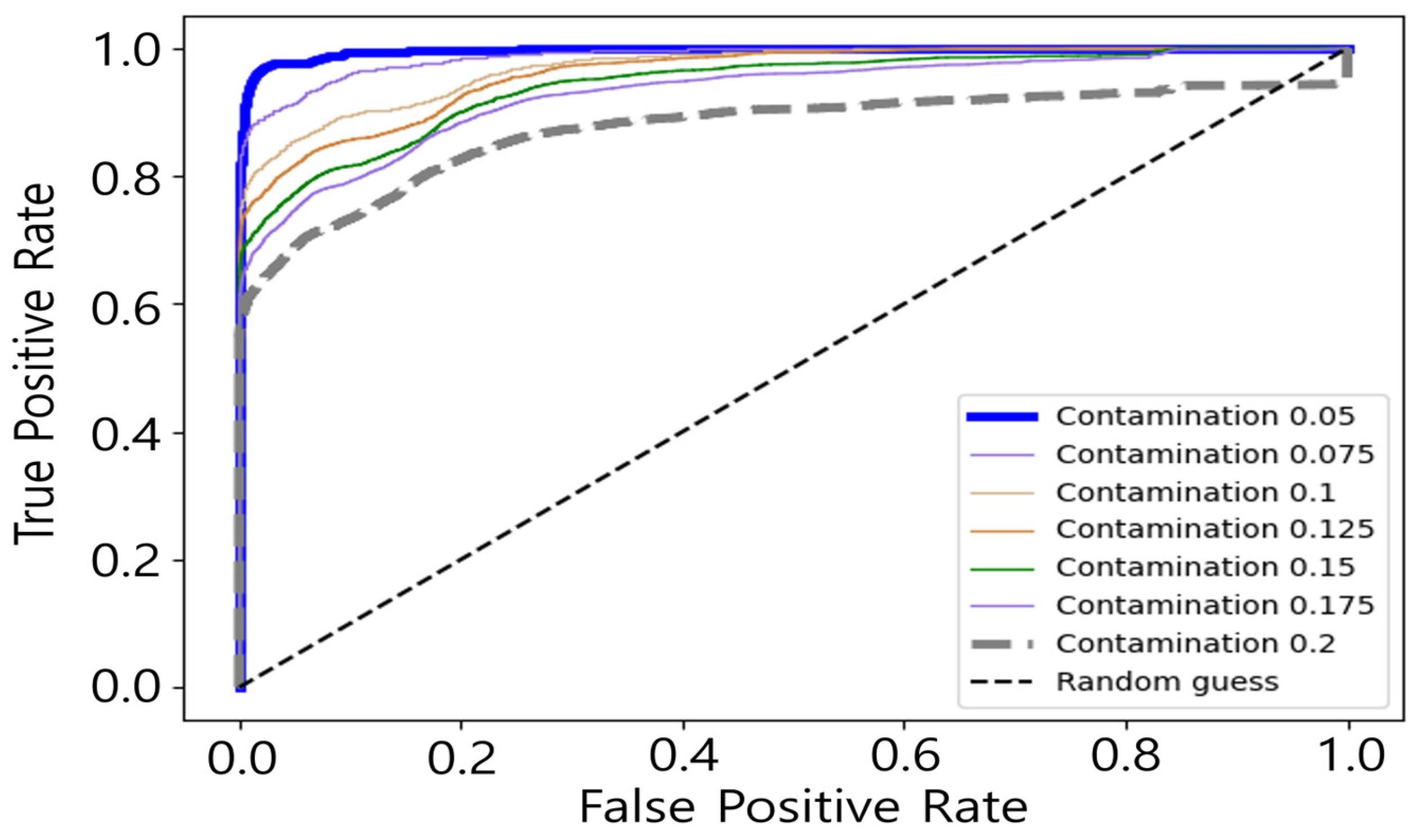

| Contamination | AUC | Reconstruction Loss Value |
|---|---|---|
| 0.050 | 0.9964 | 0.0055 |
| 0.075 | 0.9873 | 0.0148 |
| 0.100 | 0.9703 | 0.0380 |
| 0.125 | 0.9603 | 0.0286 |
| 0.150 | 0.9419 | 0.0300 |
| 0.175 | 0.9292 | 0.0282 |
| 0.200 | 0.8732 | 0.0212 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, M.; Jang, H.; Kwon, W.; Seo, J.; Park, S.; Park, B.; Park, J.; Yu, D.; Lee, S. A Comparative Study of Customized Algorithms for Anomaly Detection in Industry-Specific Power Data. Energies 2025, 18, 3720. https://doi.org/10.3390/en18143720
Jung M, Jang H, Kwon W, Seo J, Park S, Park B, Park J, Yu D, Lee S. A Comparative Study of Customized Algorithms for Anomaly Detection in Industry-Specific Power Data. Energies. 2025; 18(14):3720. https://doi.org/10.3390/en18143720
Chicago/Turabian StyleJung, Minsung, Hyeonseok Jang, Woohyeon Kwon, Jiyun Seo, Suna Park, Beomdo Park, Junseong Park, Donggeon Yu, and Sangkeum Lee. 2025. "A Comparative Study of Customized Algorithms for Anomaly Detection in Industry-Specific Power Data" Energies 18, no. 14: 3720. https://doi.org/10.3390/en18143720
APA StyleJung, M., Jang, H., Kwon, W., Seo, J., Park, S., Park, B., Park, J., Yu, D., & Lee, S. (2025). A Comparative Study of Customized Algorithms for Anomaly Detection in Industry-Specific Power Data. Energies, 18(14), 3720. https://doi.org/10.3390/en18143720






