Sensor-Reduced Active Power Decoupling Method for Single-Phase Rectifiers
Abstract
1. Introduction
2. Sensor-Reduced Control Strategy Based on Lyapunov Equation
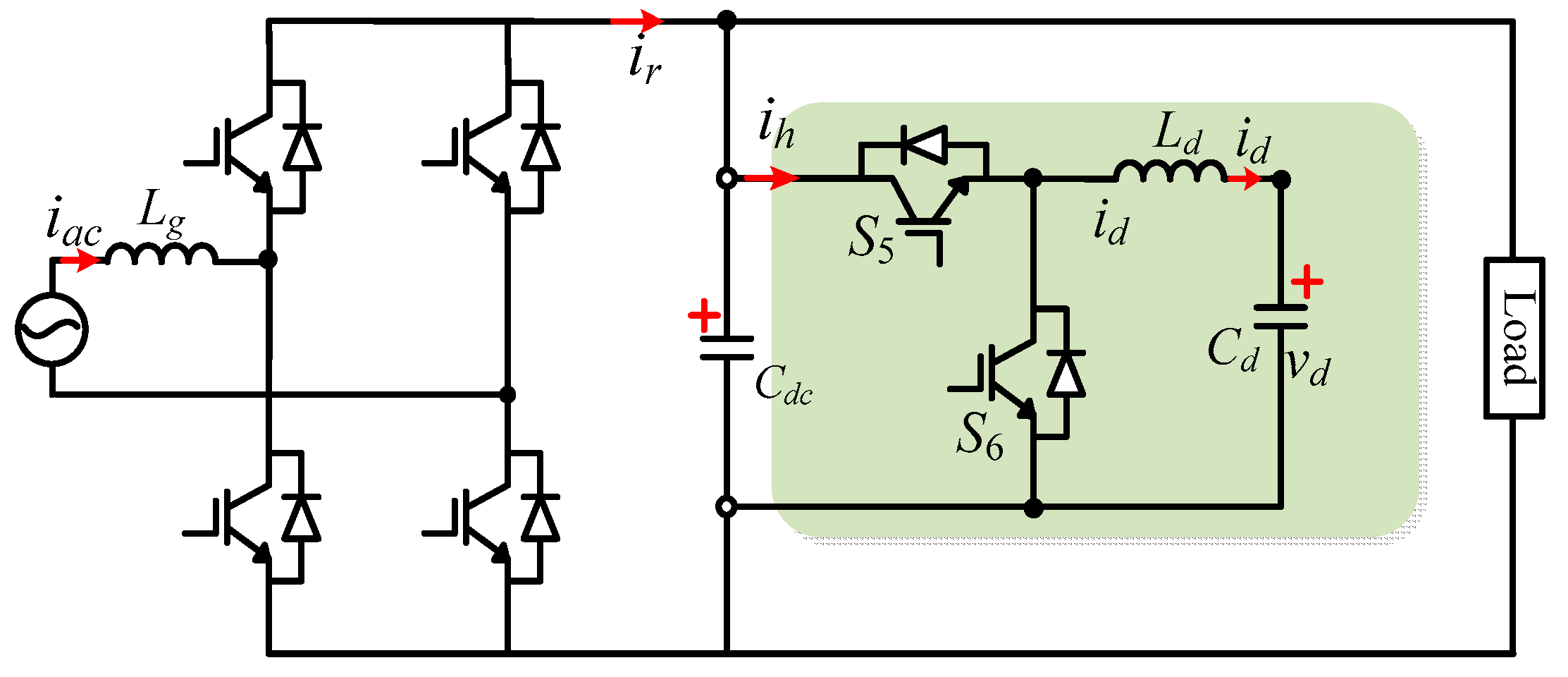
2.1. Operating Principle of Buck-Type Decoupling Circuit
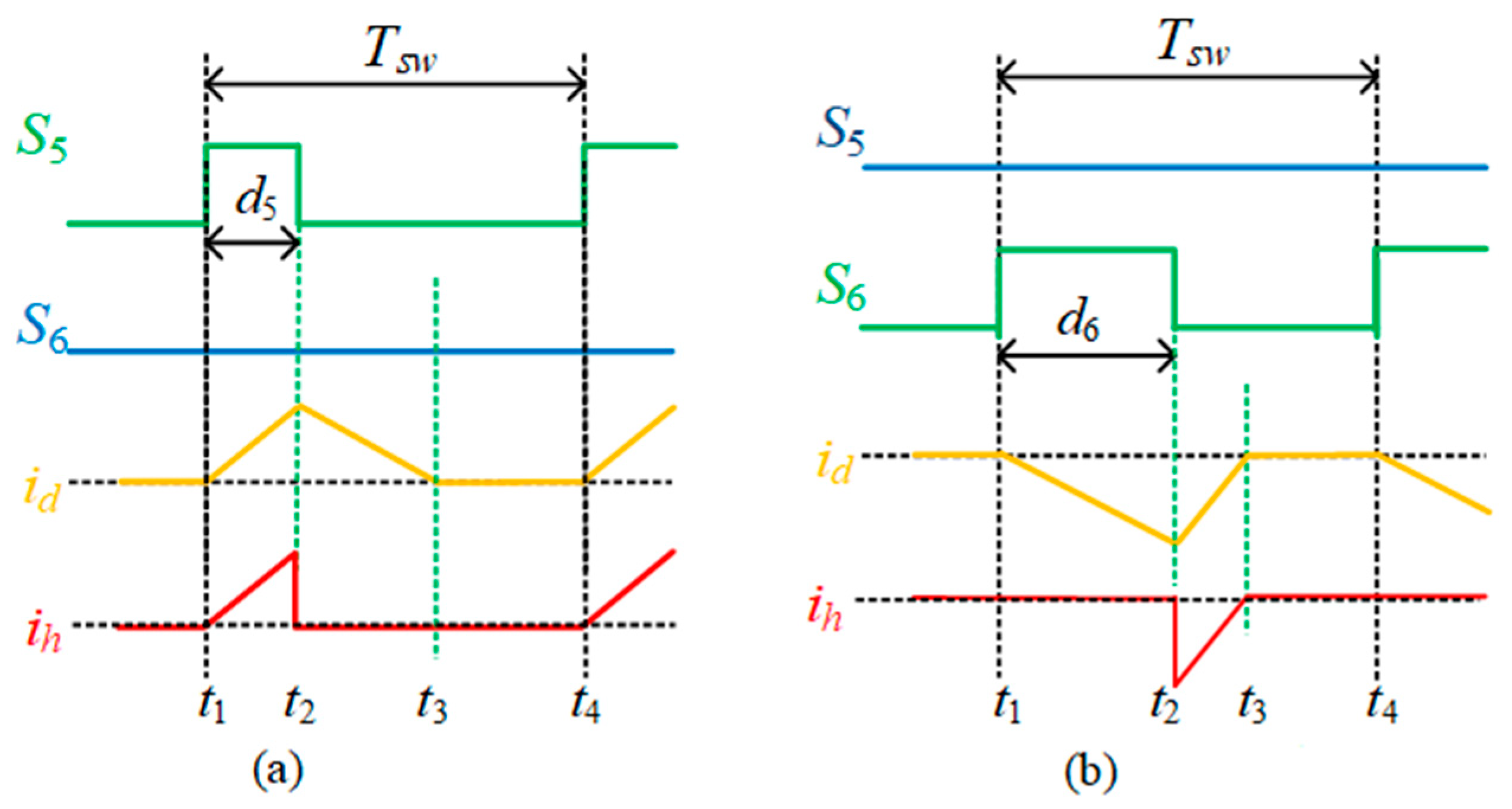
2.2. Stability-Conscious Sensor-Reduced Control Strategy Design
- (a)
- V(0) = 0;
- (b)
- V(x) > 0, x ≠ 0;
- (c)
- V(x) → ∞, ||x|| → ∞;
- (d)
- , x ≠ 0.
3. Current Reference Design and Control System Implementation
3.1. Virtual Impedance-Based Reference Current Design Methodology
3.2. Overall Structure of Sensor-Reduced Control
4. Qualitative and Quantitative Assessments
4.1. Qualitative Comparative Analysis
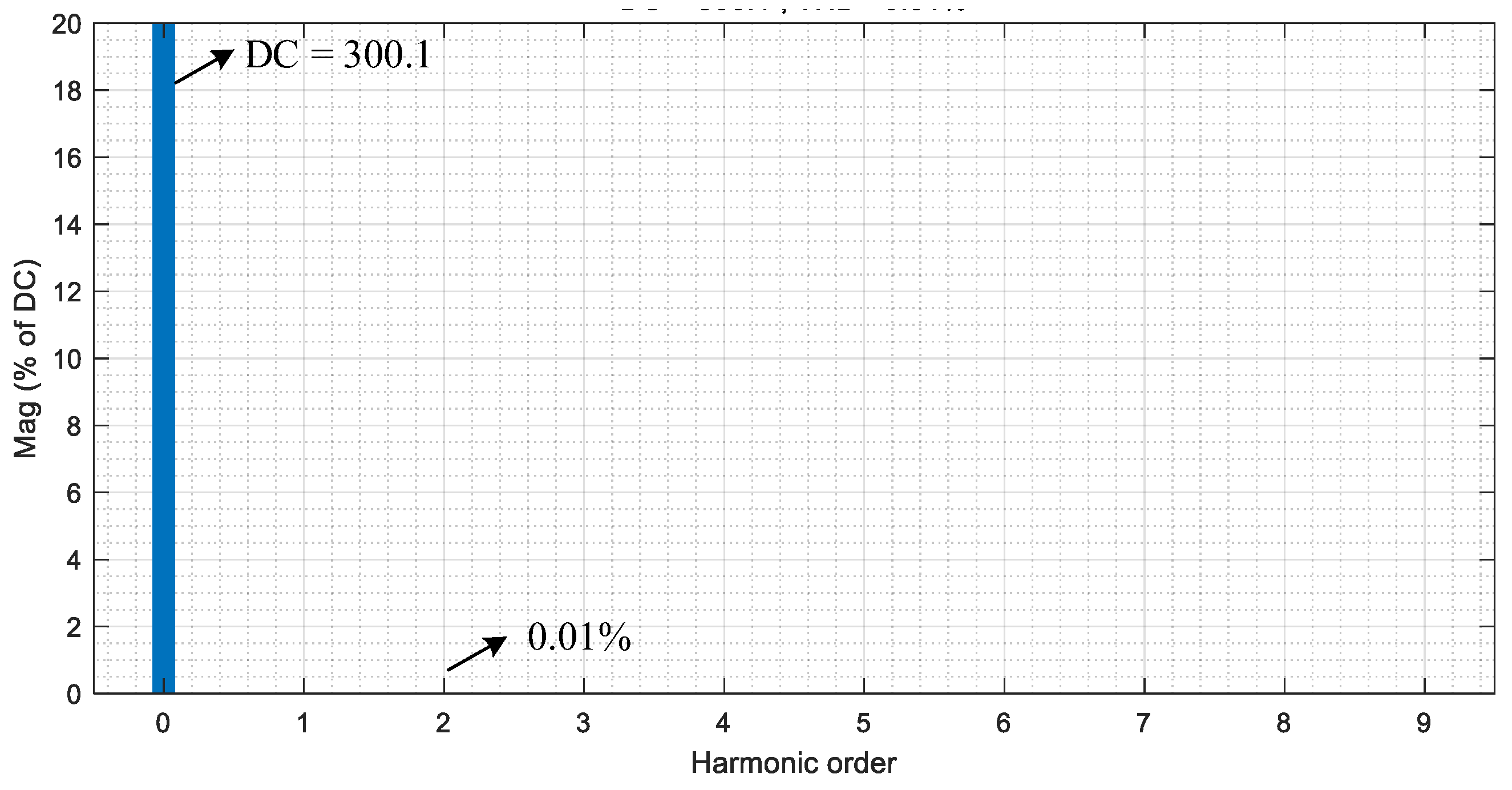
4.2. Simulation Verification and Analysis
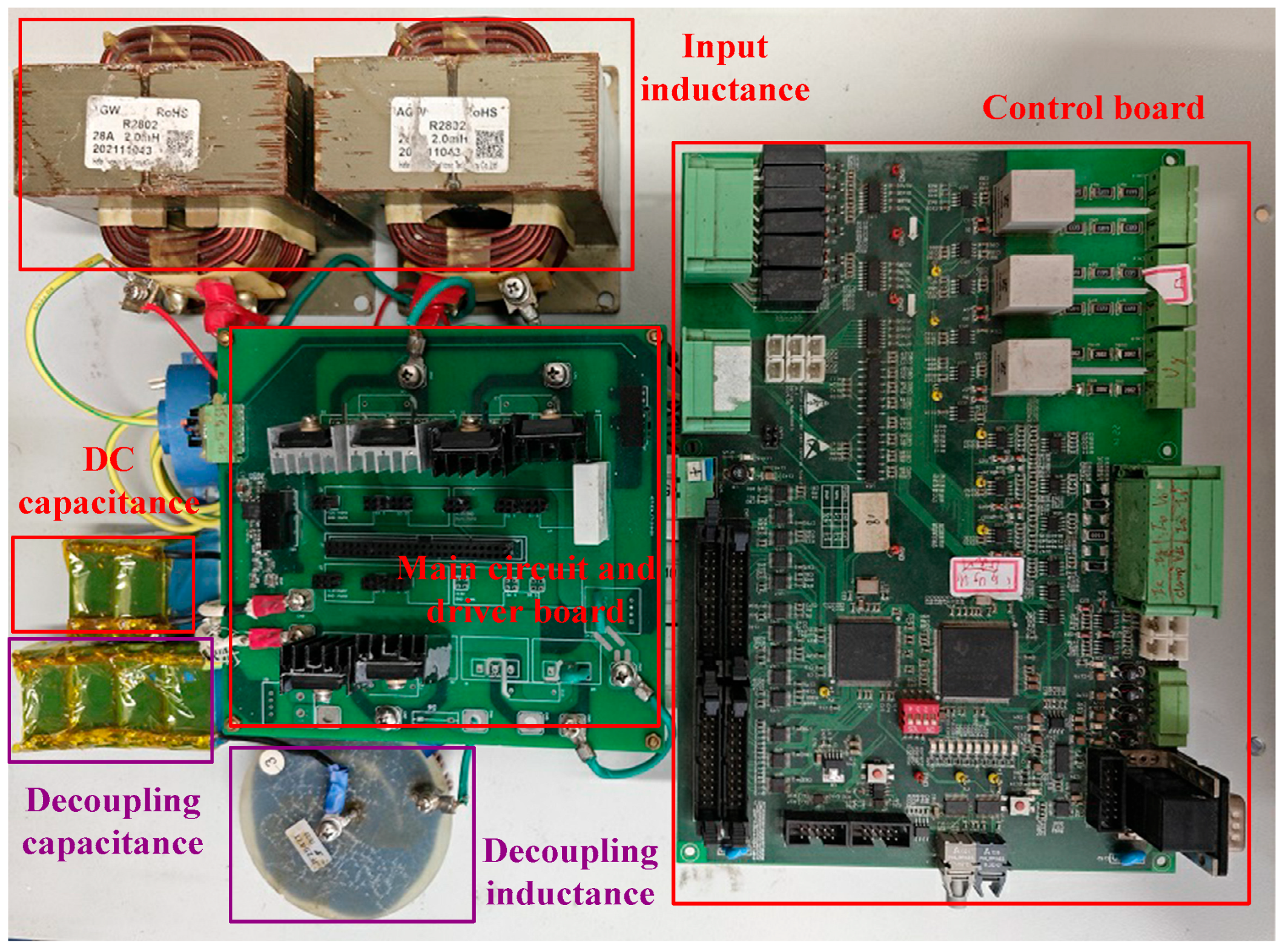
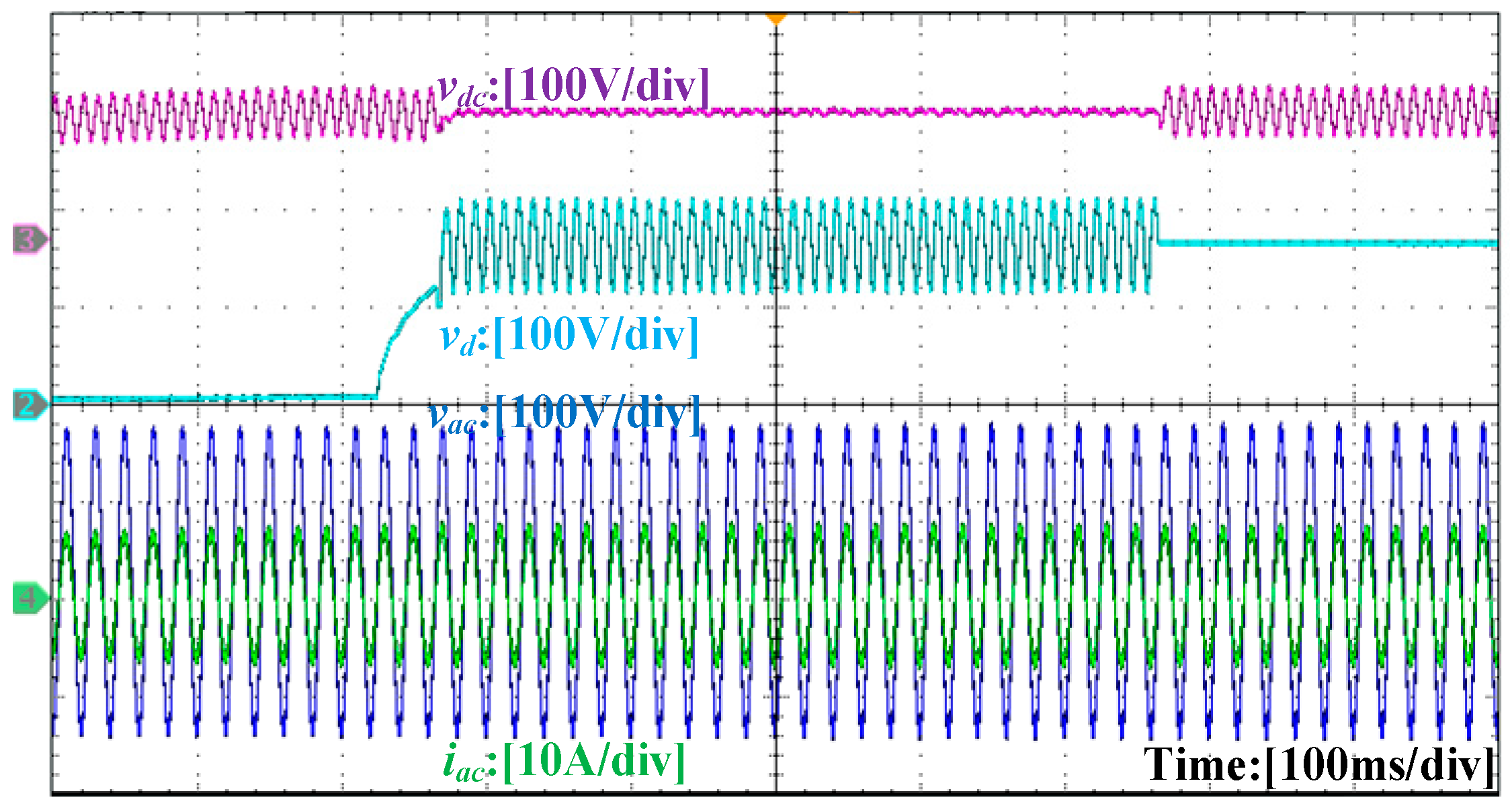
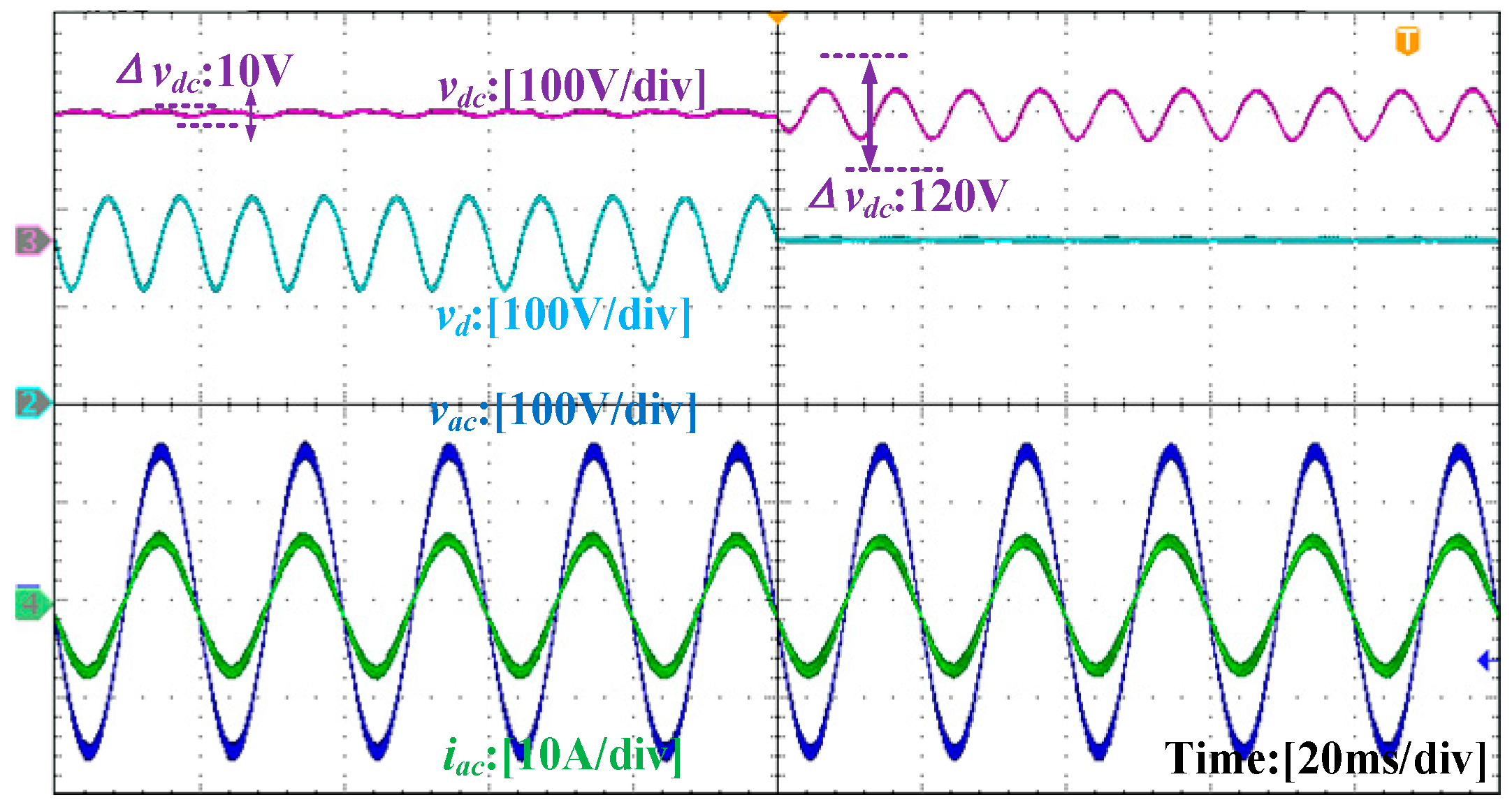
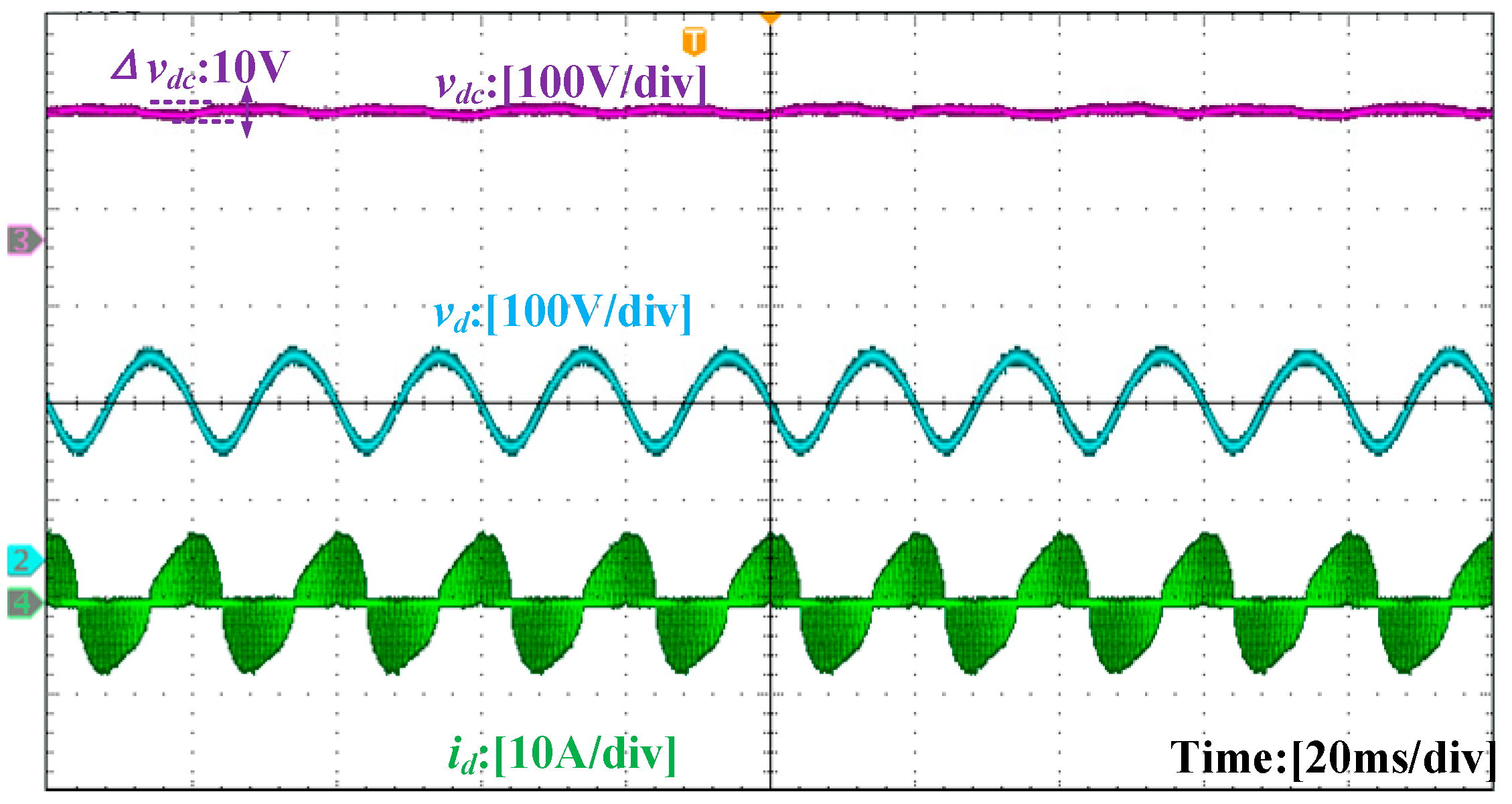
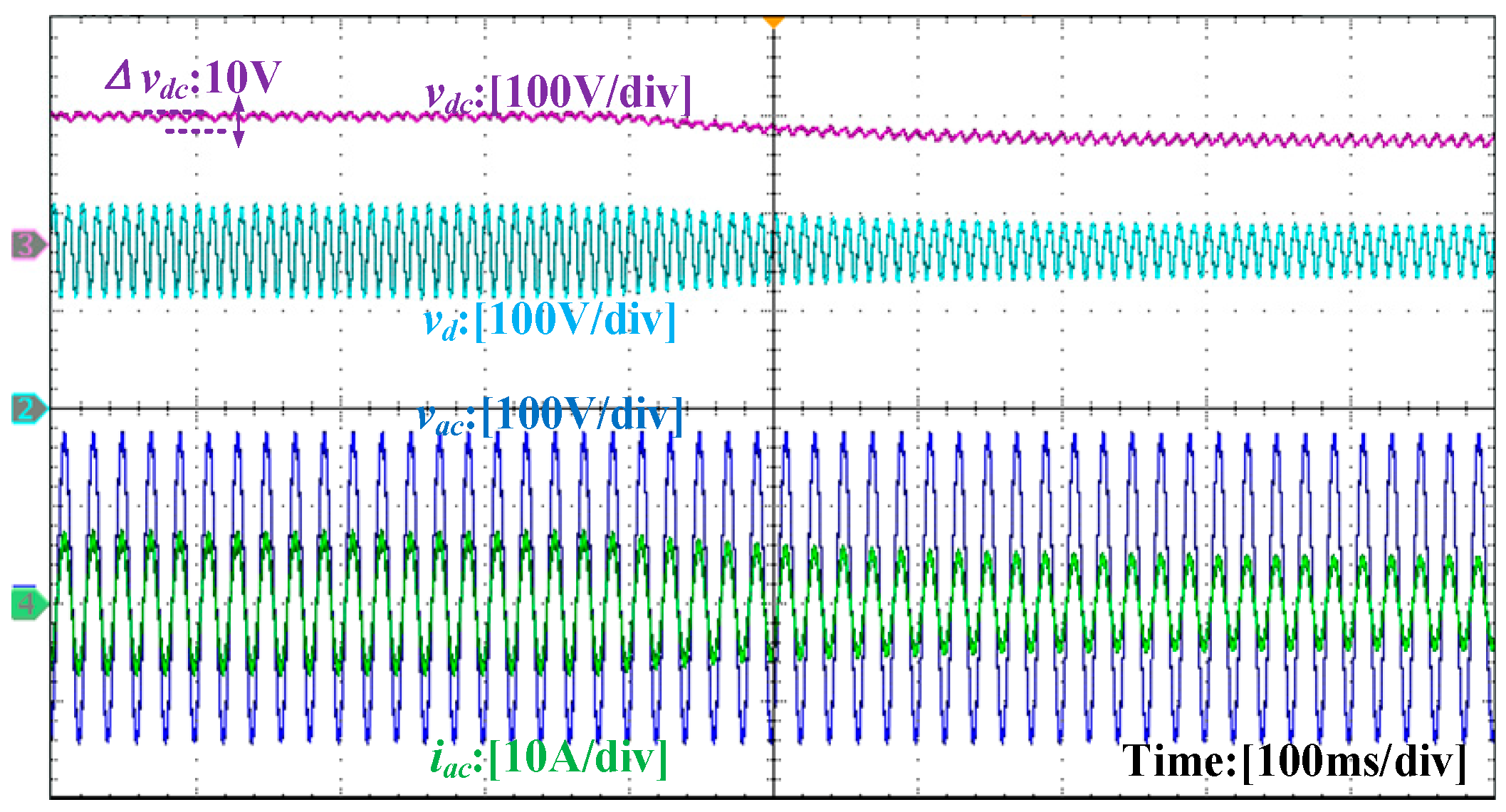
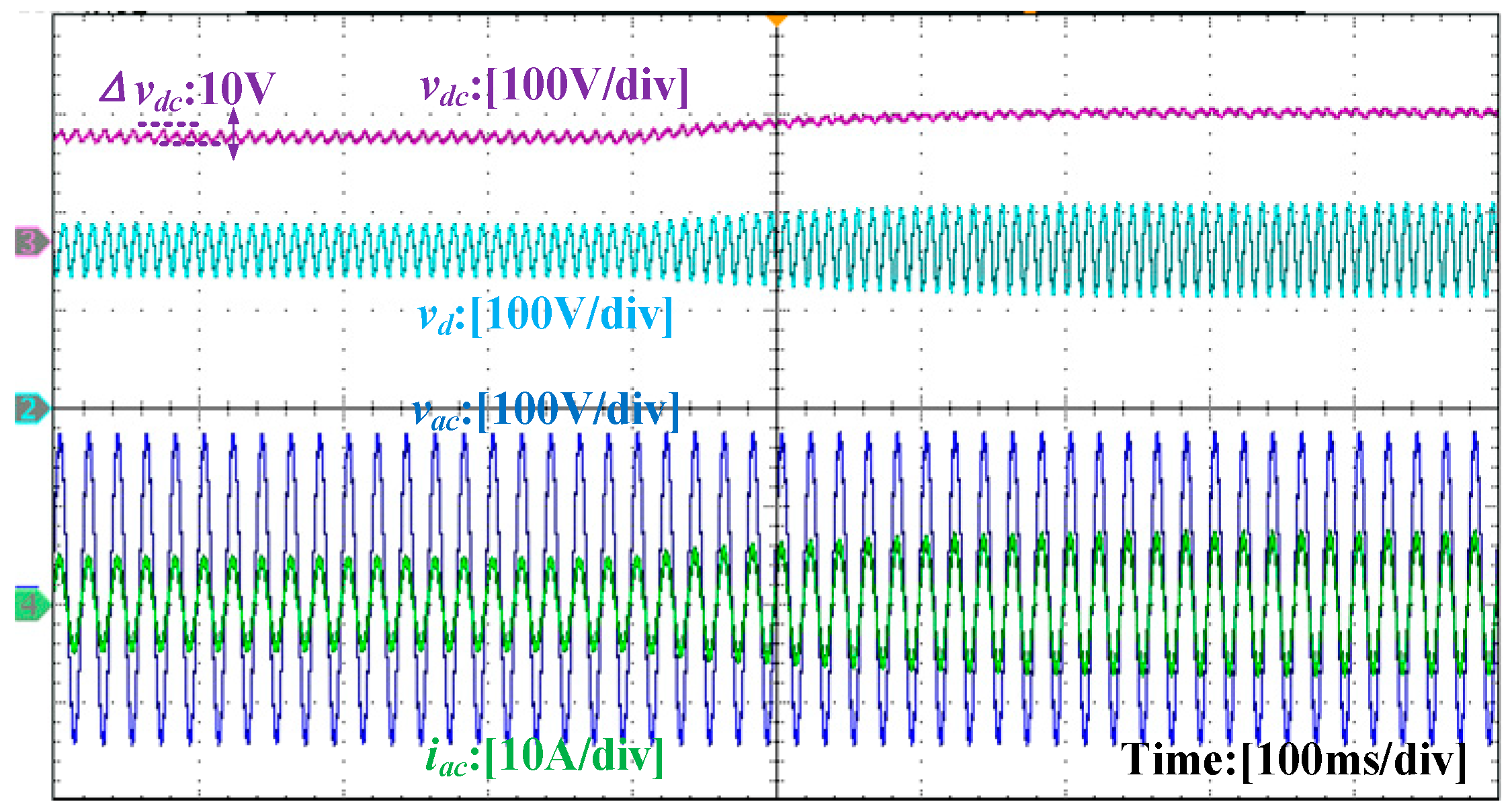
4.3. Experimental Verification and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Term |
| APD | Active Power Decoupling |
| MPPT | Maximum Power Point Tracking |
| LED | Light Emitting Diode |
| PF | Power Factor |
| THD | Total Harmonic Distortion |
| IEC | International Electrotechnical Commission |
| LMI | Linear Matrix Inequality |
| MMPC | Multiple Model Predictive Control |
| DCM | Discontinuous Conduction Mode |
| Symbol | Meaning |
| vac | Grid voltage |
| iac | Grid-side input current |
| Vac, Iac | Root-mean-square values of vac and iac |
| Pac | Grid-side instantaneous power |
| Prip | Second-order ripple power |
| Pdc | DC output power |
| ω | Grid angular frequency |
| vdc | DC bus voltage |
| Cdc | DC bus capacitor |
| Ld | Decoupling inductor |
| ih | Decoupling port current |
| ihref | Reference current of the decoupling port |
Appendix A
Derivation of Formula (13)
References
- Tian, H.; Chen, M.; Liang, G.; Xiao, X. Single-phase rectifier with reduced common-mode current, auto-PFC, and power decoupling ability. IEEE Trans. Power Electron. 2021, 37, 6873–6882. [Google Scholar] [CrossRef]
- Esteve, V.; Bellido, J.L.; Jordán, J. Optimal Design of a Single-Phase Bidirectional Rectifier. Energies 2024, 17, 1280. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, Z. A single-phase Vienna rectifier with wide output voltage range. IEEE Trans. Transp. Electrif. 2022, 8, 3884–3895. [Google Scholar] [CrossRef]
- Wang, H.; Liserre, M.; Blaabjerg, F. Toward reliable power electronics: Challenges, design tools, and opportunities. IEEE Ind. Electron. Mag. 2013, 7, 17–26. [Google Scholar] [CrossRef]
- Guo, B.; Su, M.; Sun, Y.; Wang, H.; Liu, B.; Zhang, X.; Pou, J.; Yang, Y.; Davari, P. Optimization design and control of single-stage single-phase PV inverters for MPPT improvement. IEEE Trans. Power Electron. 2020, 35, 13000–13016. [Google Scholar] [CrossRef]
- Wang, R.; Wang, F.; Boroyevich, D.; Burgos, R.; Lai, R.; Ning, P.; Rajashekara, K. A high power density single phase PWM rectifier with active ripple energy storage. IEEE Trans. Power Electron. 2011, 26, 1430–1443. [Google Scholar] [CrossRef]
- Sun, Y.; Liu, Y.; Su, M.; Xiong, W.; Yang, J. Review of active power decoupling topologies in single-phase systems. IEEE Trans. Power Electron. 2016, 31, 4778–4794. [Google Scholar] [CrossRef]
- Cui, Y.; Han, H.; Liu, Y.; Xu, G.; Su, M.; Xie, S. An efficiency-improved single-phase PFC rectifier with active power decoupling. IEEE Trans. Power Electron. 2022, 37, 10784–10796. [Google Scholar] [CrossRef]
- Xiong, J.; Zhang, J.; Xu, Z.; Din, Z.; Zheng, Y. Active power decoupling control for PWM converter considering sensor failures. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 2236–2245. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Sun, Y.; Su, M.; Xu, G.; Dan, H. Review and comparison of control strategies in active power decoupling. IEEE Trans. Power Electron. 2021, 36, 14436–14455. [Google Scholar] [CrossRef]
- Krein, P.T.; Balog, R.S. Cost-effective hundred-year life for single-phase inverters and rectifiers in solar and LED lighting applications based on minimum capacitance requirements and a ripple power port. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Washington, DC, USA, 5–19 February 2009. [Google Scholar]
- Yuan, H.; Li, S.; Tan, S.-C.; Hui, S.Y.R. Means of reducing number of sensors in single-phase power converters with an active power buffer. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition, New Orleans, LA, USA, 15–19 March 2020. [Google Scholar]
- Yuan, H.; Li, S.; Tan, S.-C.; Hui, S.Y.R. Sensor count reduction for single-phase converters with an active power buffer using algebraic observers. IEEE Trans. Power Electron. 2021, 68, 10666–10676. [Google Scholar] [CrossRef]
- Yuan, H.; Li, S.; Tan, S.-C.; Hui, R.S.-Y. Simplified algebraic estimation technique for sensor count reduction in single-phase converters with an active power buffer. IEEE Trans. Power Electron. 2021, 36, 11444–11455. [Google Scholar] [CrossRef]
- Yuan, H. Some control aspects of single-phase power converters with an active pulsating power buffer. In Proceedings of the 2022 IEEE 9th International Conference on Power Electronics Systems and Applications, Hong Kong, China, 20–22 September 2022; pp. 1–12. [Google Scholar]
- Farooqi, M.Z.; Singh, B.; Panigrahi, B.K. Reduced sensor based model predictive control of power decoupling circuit for on-board EV charger. IEEE Trans. Transp. Electrif. 2022, 9, 2104–2114. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Li, B.; Chen, N. Multifunction control strategy for single-phase AC/DC power conversion systems with voltage-sensorless power-decoupling function. IEEE Trans. Power Electron. 2020, 35, 13602–13620. [Google Scholar] [CrossRef]
- Wang, X.; Chen, M.; Li, B.; Zhu, G.; Chen, L.; Sun, X.; Zhang, D.; Hu, J. Control and modulation of a single-phase AC/DC converter with smooth bidirectional mode switching and symmetrical decoupling voltage compensation. IEEE Trans. Power Electron. 2022, 37, 3836–3853. [Google Scholar] [CrossRef]
- Shen, Y.; Zakzewski, D.; Hasnain, A.; Resalayyan, R.; Khaligh, A. Reduced sensor control approach for active power decoupling circuit in PV microinverter application. In Proceedings of the 2023 IEEE Energy Conversion Congress and Exposition, Nashville, TN, USA, 29 October–2 November 2023; pp. 13–18. [Google Scholar]
- Shen, Y.; Zakzewski, D.; Hasnain, A.; Resalayyan, R.; Khaligh, A. Sensorless control for DC-parallel active power decoupling in PV microinverters. IEEE Trans. Power Electron. 2023, 38, 14628–14637. [Google Scholar] [CrossRef]
- IEC 61000-3-2 ed 5.0; Electromagnetic Compatibility (EMC)-Part 3-2: Limit—Limits for Harmonic Current Emissions (Equipment Input Current ≤ 16 A per Phase. IEC: Geneva, Switzerland, 2018.
- Liu, Y.L.; Yuan, Y.H.; Wang, H.; Su, M.; Zhang, W.L. Cooperative control strategy for modular decoupling circuits. Trans. China Electrotech. Soc. 2024, 39, 3118–3128. [Google Scholar]



| Comparison Aspect | Capacitor Decoupling [6,7] | APD Method in [12,13,14,15] | APD Method in [16] | Proposed Method |
|---|---|---|---|---|
| Decoupling Principle | Passive filtering via large capacitors | Algebraic observer-based control | Voltage-sensorless modulated model predictive control | Lyapunov-based and virtual impedance control |
| Sensors | None | 3 Sensors | 1 Sensor | 1 Sensor |
| Reliability | Low | Medium | High | High |
| Complexity | Low | Medium | High | Medium |
| Volume | Large | Medium | Small | Small |
| DC Bus Ripple | >5% | <5% | <5% | <5% |
| Power Factor | 0.9~0.95 | >0.98 | >0.98 | >0.98 |
| THD | 10%~15% | <3% | <2% | <3% |
| Parameter | Symbol | Value |
|---|---|---|
| Grid voltage | vac | 110 VRMS |
| Grid frequency | fg | 50 Hz |
| Output power | Pdc | 600 W |
| DC bus voltage | Vdc | 300 V |
| DC-link capacitor | Cdc | 20 μF |
| Decoupling capacitor | Cd | 90 μF |
| Decoupling inductor | Ld | 0.5 mH |
| Switching frequency | fsw | 20 kHz |
| Proportional gain of PI1 | Kp1 | 0.8 |
| Integral gain of PI1 | Ki1 | 1.5 |
| Proportional gain of PI2 | Kp2 | 5 |
| Integral gain of PI2 | Ki2 | 8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Liu, S.; Cao, Q.; Wang, H. Sensor-Reduced Active Power Decoupling Method for Single-Phase Rectifiers. Energies 2025, 18, 3711. https://doi.org/10.3390/en18143711
Chen M, Liu S, Cao Q, Wang H. Sensor-Reduced Active Power Decoupling Method for Single-Phase Rectifiers. Energies. 2025; 18(14):3711. https://doi.org/10.3390/en18143711
Chicago/Turabian StyleChen, Ming, Shui Liu, Qinglong Cao, and Hui Wang. 2025. "Sensor-Reduced Active Power Decoupling Method for Single-Phase Rectifiers" Energies 18, no. 14: 3711. https://doi.org/10.3390/en18143711
APA StyleChen, M., Liu, S., Cao, Q., & Wang, H. (2025). Sensor-Reduced Active Power Decoupling Method for Single-Phase Rectifiers. Energies, 18(14), 3711. https://doi.org/10.3390/en18143711





