Effect of New Mesh Fins on the Heat Storage Performance of a Solar Phase Change Heat Accumulator

Abstract

In view of the problems of slow heat storage process and uneven temperature distribution in the existing phase change heat accumulator, a new type of mesh fin heat accumulator was designed and developed which increased the contact area between the phase change material (PCM) and the fins, enhanced the apparent thermal conductivity of the PCM, improved the heat storage efficiency of the heat accumulator, blocked the PCM, improved the natural convection erosion of the PCM on the upper and lower parts of the heat accumulator, and melted the PCM in each area more evenly. Fluent15.0 was used to numerically simulate the heat storage process of the mesh fins heat accumulator with the finite volume method. The composite PCM prepared by adding 10% mass fraction of expanded graphite to paraffin wax was used as the heat storage material. A 2D, non-steady-state model, incompressible fluid, and the pressure-based solution method were selected. The energy model and the solidification and melting model based on the enthalpy method were used to simulate and calculate the phase change process of PCM. The PISO algorithm was used. The influences of the structural parameters of the mesh fins on the heat storage condition of the heat accumulator were investigated by numerical simulation. The results showed that with the increase in the radius R of the mesh fin, the heat storage time decreased first and then increased. With the increases in vertical fin thickness c, mesh fins thickness δ, and vertical fins number N, the heat storage time decreased. The optimal mesh fin structure parameters were R = 33.5 mm, c = 3 mm, δ = 3 mm, and N = 8, and the heat storage time was 8086 s, which is 47.8% shorter than that of the concentric tube heat accumulator. Otherwise, with the increases in vertical fin thickness c, mesh fins thickness δ, and vertical fins number N, the PCM volume decreased, which shortened PCM melting time.

1. Introduction

In recent years, the development and utilization of solar energy has become a research hotspot around the world. Due to the uneven distribution of solar energy, low energy flow density, and intermittent sunshine, energy storage performance has become a key link in most solar energy applications [1]. Relevant scholars have proved through experiments that the concentric sleeve phase change heat accumulator has the highest heat storage efficiency, and with the increase in the amount of PCM, this advantage is more obvious [2,3,4]. However, due to the low thermal conductivity of PCM, the phase change heat storage process is faced with the problem of long heat storage time. One of the most efficient methods to enhance the heat transfer performance of the phase change heat storage process is using the fin structure to extend the heat transfer area, such as rectangular fins [5], annular fins [6], spiral fins [7], plate fins [8], and dendritic fins [9]. Relevant scholars have performed a lot of research on the structural design of phase change heat accumulators [10,11,12,13,14,15,16]. Ren et al. [17] designed and developed a snowflake-type finned heat accumulator. The melting time of snowflake fins was 45.6% shorter than that of traditional fins. Huang et al. [18] established a heat accumulator with tree-like fins. The results showed that the angle of the tree-like fins had a significant influence on the heat storage process, and the heat storage time was greatly shortened. Xu et al. [19] designed a biomimetic fin based on honeycomb and tree branch structures with detailed numerical simulations and internal natural convection analysis to investigate the effect of flow patterns on heat transfer efficiency. Marzouk et al. [20] numerically examined PCM melting in a rectangular enclosure with different fin geometries, including rectangular, constructal, and tree-shaped fins. Key performance indicators such as liquid fraction rate, melting time, and heat transfer rate were analyzed. Zhang et al. [21] developed a novel fin structure considering the laminar flow of liquid phase change materials, which established a robust design method for fin optimization in the shell-and-tube latent thermal energy storage unit. In the two-dimensional latent thermal energy storage unit, convection topology optimization was used to design and optimize the topological fin structure. The results showed that natural convection is a sufficient condition for the topological fin structure to be asymmetrical along the vertical direction. When natural convection was considered, the distribution of the fin structure along the gravity direction was asymmetrical and uneven, and the fins at the bottom of the latent thermal storage unit were wider, longer, and more branched. Mills et al. [22] investigated the melting behavior of phase change materials (PCMs) within an enclosure featuring tree-shaped internal fins, using both numerical simulations and experimental methods. The study utilized coconut oil as the PCM and applied it to an aluminum tree-shaped radiator. The heating direction and the power supplied to the heater were considered as key variables. The results indicated that heating from the bottom resulted in the lowest heater temperature, while heating from the top led to the highest temperature due to natural convection effects.

For most types of fins, the parameters affecting the heat transfer performance include fin number, length (diameter), thickness, angle, position, and arrangement. The optimization of fin structure includes parameter optimization and shape optimization. The parameter and shape of fins in a phase change heat storage system should be optimized as a whole, which considers the enhancing effect of fins on the heat conduction of PCM and its suppressing effect on the natural convection of liquid PCM. In general, rectangular fins usually show better performance than annular fins. The heat transfer performance of complex or innovative fins is generally better than that of rectangular fins at the same volume. However, rectangular fins are the most widely used fin type due to their simple structure, ease of manufacture, and low cost [15].

Although rectangular fins are the most widely used in the phase change heat storage process, the strengthening effect is greatly reduced when the number of fins is small. When the number of fins increases, although the heat storage time is significantly reduced, the temperature uniformity in the phase change material region is poor. Based on the advantages and disadvantages of differently shaped fins and considering the characteristics of the PCM itself, the liquid PCM will undergo natural convection, resulting in a large difference in the heat storage speed before and after heat storage and an uneven heat storage temperature. A new type of mesh fin heat accumulator that combines rectangular fin and annular fin was designed and developed, and it had a simple geometry structure, increased the contact area between the phase change material (PCM) and the fins, enhanced the apparent thermal conductivity of the PCM, and improved the heat storage efficiency of the heat accumulator. The mesh fins blocked the PCM, improved the erosion of natural convection on the upper and lower PCM of the accumulator, and made the PCM melt more evenly in each area. In order to have a deeper understanding of the temperature field inside the mesh fin heat accumulator and the heat storage process, the heat storage process of the mesh fin heat accumulator with different structural parameters was numerically simulated, and the influences of mesh fins, mesh fin radius R, vertical fin thickness c, mesh fin thickness δ, and vertical fin number N on the heat storage process were investigated.

2. Model Description

2.1. Physical Model

The three-dimensional structure diagram and two-dimensional cross-section diagram are shown in Figure 1. The mesh fins were composed of multiple longitudinal rectangular fins and an annular fin. In this case, the PCM was divided into multiple independent regions by the fins, as shown in Figure 1. There were five separate regions the PCM occupied (i.e., outside the mesh fin and four inner regions formed by the intersection of the vertical fins and mesh fin). Agyenim [23] established a horizontal concentric sleeve-type accumulator and an accumulator with vertical fins. It was proved by experiments that in the heat storage process of the accumulator, the axial temperature gradient of the PCM was very small, and the heat transfer was negligible. The heat transfer in the phase change heat accumulator was regarded as two-dimensional. Therefore, for the study of the strong heat transfer of the mesh fin phase change accumulator, a two-dimensional physical model was established, as shown in Figure 1b. The inner diameter of the heat exchange tube was d₀ = 25 mm, and the inner diameter of the heat storage cylinder was d₁ = 126 mm. The PCM was filled between the heat exchange tube and the heat storage cylinder. The PCM was a composite PCM with 10% mass fraction expanded graphite added to paraffin wax. The physical parameters of the composite PCM are shown in

Table 1. Physical parameters of the composite PCM.

State	Melting Point	Latent Heat of Phase Change	Density	Specific Heat Capacity	Thermal Conductivity
	K	(kJ·kg−1)	(kg·m−3)	(kJ·(kg·K)−1)	(W·(m·K)−1)
Solid State	327	235	900	1.828	1.568
Liquid State	329	235	880	1.918	1.458

[24]. Considering that the fin was a metal material, the thermal conductivity was high, and the thermal conductivity of paraffin was very low. After adding 10% expanded graphite, it can reach about 1.5 W/(m·K), which is much smaller than the thermal conductivity of the fin. Therefore, the heat exchange tube was simplified as a constant wall temperature surface. The heat accumulator shell was set as a thermal insulated surface due to the addition of thermal insulation materials on the outer wall surface.

2.2. Mathematical Model

In order to simplify the calculation, the following assumptions were made for the model [25,26]: (1) the composite PCM was pure and isotropic; (2) the wall thickness of the outer cylinder and the heat exchange between the outer cylinder wall and the surroundings were ignored; (3) the fluid in the liquid phase area of the PCM was incompressible Newtonian fluid; (4) considering the influence of natural convection in the accumulator, the natural convection was laminar flow; (5) the heat accumulator model ignored the wall thickness of the heat exchange tube and did not consider the heat transfer between the tube wall and the hot fluid and paraffin; and (6) the liquid PCM satisfied the Boussinesq hypothesis, that is, only the density change was considered in the buoyancy term.

The traditional enthalpy–porosity method was used to solve the heat storage process of the low-temperature device. The fins energy and simplified PCM governing equations were as follows:

(a)

Fins area

The fins were made of stainless steel; according to the Fourier heat conduction mechanism, the energy equation is as follows:

$${\rho }_s{C}_{p,s}{\displaystyle \frac{\partial T_s}{\partial t}}={\displaystyle \frac{\partial }{\partial x}}\left({\lambda }_s{\displaystyle \frac{\partial T_s}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left({\lambda }_s{\displaystyle \frac{\partial T_s}{\partial y}}\right)+{\displaystyle \frac{\partial }{\partial z}}\left({\lambda }_s{\displaystyle \frac{\partial T_s}{\partial z}}\right)+S_s$$

(1)

where ${\rho }_s$ is the density of the fins; $C_{p,s}$ is the isobaric specific heat capacity; $T_s$ is the temperature of the fins; ${\lambda }_s$ is the thermal conductivity; and $S_s$ is the solid inner heat source.

In this paper, the PCM heat accumulator was simplified to a two-dimensional model, and the energy equations was simplified as follows:

$${\displaystyle \frac{\partial T_s}{\partial t}}=a_s\left({\displaystyle \frac{{\partial }^2{T}_s}{\partial x^2}}+{\displaystyle \frac{{\partial }^2{T}_s}{\partial y^2}}\right)$$

(2)

where $a_s$ is the thermal diffusion coefficient.

(b)

PCM area

The influence of natural convection caused by gravity should also be considered in the PCM area. The two-dimensional governing equations should include the mass conservation equation, momentum conservation equation, and energy conservation equation. According to the enthalpy–porosity [25] method, the following can be obtained:

Mass conservation equation:

$${\displaystyle \frac{\partial u}{\partial x}}+{\displaystyle \frac{\partial v}{\partial y}}=0$$

(3)

Momentum conservation equation:

$${\rho }_P\left({\displaystyle \frac{\partial u}{\partial t}}+u{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial u}{\partial y}}\right)=-{\displaystyle \frac{\partial p}{\partial x}}+\eta \left({\displaystyle \frac{{\partial }^{2}u}{\partial x^2}}+{\displaystyle \frac{{\partial }^{2}u}{\partial y^2}}\right)+Su$$

(4)

$${\mathsf{\rho }}_{\mathrm{P}}\left({\displaystyle \frac{\mathrm{\partial }\mathrm{v}}{\mathrm{\partial }\mathrm{t}}}+\mathrm{u}{\displaystyle \frac{\mathrm{\partial }\mathrm{v}}{\mathrm{\partial }\mathrm{x}}}+\mathrm{v}{\displaystyle \frac{\mathrm{\partial }\mathrm{v}}{\mathrm{\partial }\mathrm{y}}}\right)=-{\displaystyle \frac{\mathrm{\partial }\mathrm{p}}{\mathrm{\partial }\mathrm{y}}}+{\mathsf{\eta }}_{\mathrm{P}}\left({\displaystyle \frac{{\mathrm{\partial }}^2\mathrm{v}}{\mathrm{\partial }{\mathrm{x}}^2}}+{\displaystyle \frac{{\mathrm{\partial }}^2\mathrm{v}}{\mathrm{\partial }{\mathrm{y}}^2}}\right)+\mathrm{S}\mathrm{v}$$

(5)

Source item:

$$Su=Au, Sv=Av+{\rho }_{ref}g\beta (T-T_{ref})$$

(6)

$$A=-\mathrm{C}{\displaystyle \frac{(1-\phi {)}^2}{{\phi }^3+\epsilon }}$$

(7)

where C is the mushy zone constant, which is generally 10⁴~10⁷ according to the different PCMs. In this paper, the PCM was paraffin. According to the experimental study, 10⁶ was the most reasonable [27]. β is the volume expansion coefficient; ρ_ref is the reference density; T_ref is the reference temperature; ε is infinitesimal, which is less than 0.001 and prevents the denominator from being 0; and φ is the liquid phase rate value.

$$\phi =\left\{\begin{array}{c}0 T_{\mathrm{P}\mathrm{C}\mathrm{M}}<T_{s,\mathrm{P}\mathrm{C}\mathrm{M}}\\ {\displaystyle \frac{T_{\mathrm{P}\mathrm{C}\mathrm{M}}-T_{s,\mathrm{P}\mathrm{C}\mathrm{M}}}{T_{l,\mathrm{P}\mathrm{C}\mathrm{M}}-T_{s,\mathrm{P}\mathrm{C}\mathrm{M}}}} \\ 1 T_{\mathrm{P}\mathrm{C}\mathrm{M}}>T_{l,\mathrm{P}\mathrm{C}\mathrm{M}}\end{array}\right.T_{l,\mathrm{P}\mathrm{C}\mathrm{M}}\le T_{\mathrm{P}\mathrm{C}\mathrm{M}}\le T_{s,\mathrm{P}\mathrm{C}\mathrm{M}}$$

(8)

where $T_{s,\mathrm{P}\mathrm{C}\mathrm{M}}$ and $T_{l,\mathrm{P}\mathrm{C}\mathrm{M}}$ are solid and liquid temperatures, respectively, and 0 and 1 denote solid and liquid states.

The energy equation is as follows:

$${\displaystyle \frac{\partial \left({\rho }_{p}h\right)}{\partial t}}+{\displaystyle \frac{\partial \left({\rho }_{p}uh\right)}{\partial x}}+{\displaystyle \frac{\partial \left({\rho }_{p}vh\right)}{\partial y}}=\mathrm{div}\left({\lambda }_P\mathrm{grad}{T}_p\right)+S_p$$

(9)

$$S_p=-\left({\displaystyle \frac{\partial (\rho \mathit{\Delta }H)}{\partial t}}+div(\rho \overrightarrow{u}\mathit{\Delta }H)\right)$$

(10)

$$h=h_{ref}+{\int }_{T_{ref}}^T{C_{p,}}_{P}dT$$

(11)

where h is the sensible enthalpy, and H is latent heat of PCM; λ_P is the thermal conductivity of PCM; and C_p,P is the specific heat capacity of PCM.

$${\lambda }_P={\lambda }_{s,P}(1-\phi )+{\lambda }_{1,P}\phi$$

(12)

$$C_{p,P}=C_{p,Ps}(1-\phi )+C_{p,P1}\phi$$

(13)

where λ_s,P is the thermal conductivity of solid PCM; λ_l,_P is the thermal conductivity of liquid PCM; C_p,Ps is the specific heat capacity of solid PCM; and C_p,Pl is the specific heat capacity of liquid PCM.

Because λ_s,P and λ_l,_P are constants, λ_s,P and λ_l,_P can be extracted from the differential equation in Equation (9).

After simplification, Equation (9) becomes the following:

$${\displaystyle \frac{\partial h}{\partial t}}+u{\displaystyle \frac{\partial h}{\partial x}}+v{\displaystyle \frac{\partial h}{\partial y}}={\displaystyle \frac{{\lambda }_p}{{\rho }_p}}\mathrm{div}\left(\mathrm{grad}{T}_p\right)+S_p$$

(14)

In Equation (10), $\rho$ represents the constants in the liquid and solid states; $\rho$ also can be extracted from the differential equation, and Equation (10) becomes:

$$S_p=-\rho \left({\displaystyle \frac{\partial (\mathit{\Delta }H)}{\partial t}}+div(\overrightarrow{u}\mathit{\Delta }H)\right)$$

(15)

On account of:

$$\overrightarrow{u}=u\left(x,y,t\right)\overrightarrow{i}+v\left(x,y,t\right)\overrightarrow{j}$$

(16)

$$\mathit{\Delta }H=\mathit{\Delta }H\left(x,y,t\right)$$

Therefore:

$$\begin{array}{ll}{S}_p& =-\rho \left({\displaystyle \frac{\partial \left(\mathit{\Delta }H\right)}{\partial t}}+div\left(u\left(x,y,t\right)\mathit{\Delta }H\left(x,y,t\right)\overrightarrow{i}+v\left(x,y,t\right)\mathit{\Delta }H\left(x,y,t\right)\overrightarrow{j}\right)\right)\\ & =-\rho \left({\displaystyle \frac{\partial \left(\mathit{\Delta }H\right)}{\partial t}}+div\left(u\left(x,y,t\right)\mathit{\Delta }H\left(x,y,t\right)\overrightarrow{i}+v\left(x,y,t\right)\mathit{\Delta }H\left(x,y,t\right)\overrightarrow{j}\right)\right)\\ & =-\rho \left({\displaystyle \frac{\partial \mathit{\Delta }H}{\partial t}}+{\displaystyle \frac{\partial \left(u\mathit{\Delta }H\right)}{\partial x}}+{\displaystyle \frac{\partial \left(v\mathit{\Delta }H\right)}{\partial y}}\right)\\ & =-\rho \left({\displaystyle \frac{\partial \mathit{\Delta }H}{\partial t}}+u{\displaystyle \frac{\partial \mathit{\Delta }H}{\partial x}}+\mathit{\Delta }H{\displaystyle \frac{\partial u}{\partial x}}+v{\displaystyle \frac{\partial \mathit{\Delta }H}{\partial y}}+\mathit{\Delta }H{\displaystyle \frac{\partial v}{\partial y}}\right)\end{array}$$

(17)

After simplification, the following equation can be obtained:

$$S_p=-\rho \left({\displaystyle \frac{\partial \mathit{\Delta }H}{\partial t}}+u{\displaystyle \frac{\partial \mathit{\Delta }H}{\partial x}}+v{\displaystyle \frac{\partial \mathit{\Delta }H}{\partial y}}\right)$$

(18)

2.3. Grid Independence Verification

The phase change area of the accumulator was meshed by Gambit 2.4, as shown in Figure 2, the grid spacing was designed with spacings of 1, 2, 3, and 4, and the discrete models with different grid numbers were obtained. In the case of the same conditions, except the grid spacing, the numerical simulation of the melting process of the PCM was carried out, respectively. The number of grids, the melting time, and calculation time of the PCM are shown in

Table 2. Grid independence verification.

Node Size	Grid Number	Melting Time of PCM/s	Computing Time/h
1	20,196	15,607	200
2	10,922	15,513	120
3	6344	14,701	110
4	1650	—	—

. When the grid spacing was 4, due to the small number of grids, the values of the temperature or liquid phase rate changed greatly and were difficult to be captured, and the calculations were easy to diverge. When the grid spacings were 2 and 3, the difference in calculation time was small, but the melting times of PCMs were quite different. When the grid spacings were 1 and 2, the melting times of the PCMs were very similar, but the calculation time of the grid spacing of 1 was 80 h more than that of the grid spacing of 2, and the calculation economy was poor. Therefore, the subsequent simulation of this paper used the grid spacing 2 to mesh the accumulator.

2.4. Time Step Independence Verification

When the grid spacing size was 2, the area-discretized accumulator model was imported into Fluent15.0 for simulation calculation. The unsteady time steps were set to 0.01 s, 0.05 s, 0.1 s, and 0.5 s, respectively. The melting process of PCM was numerically simulated. The time step, the melting time of PCM, and the calculation time are shown in

Table 3. Time step independence verification.

Time Step	Melting Time of PCM/s	Computing Time/h
0.01 s	15,619	297
0.05 s	15,600	163
0.1 s	15,513	120
0.5 s	—	—

. When the time step was 0.5 s, due to the large time step, the values of the temperature or the liquid phase rate change rate were difficult to numerically simulate and often diverged in the calculation process. When the time steps were 0.01 s and 0.05 s, the melting time of the PCM was closer, and the calculation time of the time step of 0.01 s was extremely long. When the time steps were 0.1 s and 0.05 s, the melting time of the PCM was relatively close, and the calculation time of the time step of 0.1 s was 43 h less than the calculation time of the time step of 0.05 s. Therefore, in the subsequent calculation of this paper, the time step of 0.1 s was selected to simulate the discretized accumulator.

2.5. Reliability Verification

In order to verify the reliability of the calculation method and model simplification in this study and the rationality of the hypothesis, the working conditions of reference [28] were selected. The experimental device and experimental thermocouple arrangement diagrams are shown in Figure 3. The physical model used in the experiment was a concentric sleeve phase change heat accumulator, and the PCM was paraffin with 10% expanded graphite. The inlet temperature of the thermal fluid in the accumulator was 70 °C, and the initial temperature of the PCM was 30 °C. Three monitoring points (measuring points 2, 5, and 7) in the experimental accumulator were taken, and the temperature of the monitor was set up at the corresponding experiment points. The simulation results were compared with the experimental results and are shown in Figure 4. The temperature curve of the monitoring point obtained by the heat accumulator model established in this paper was basically the same as the temperature curve of the corresponding monitoring point obtained by the experiment, and the numerical simulation results of the three monitoring points were in good agreement with the experimental temperature curve. The average error was less than 5%, which verified that the mathematical model and calculation method used in the numerical simulation of the melting and solidification processes of PCMs using Fluent15.0 software with the finite volume method were reliable.

3. Boundary Conditions and Fluent Settings

Fluent15.0 was used to numerically simulate the heat storage process of the mesh fin solar phase change heat accumulator with the finite volume method. Two-dimensional, non-steady-state model, incompressible fluid, and the pressure-based solution methods were selected. Due to the small density difference between the solid and liquid phases of paraffin, the PCM flow velocity generated by natural convection was also small, only 0.01 m/s, or even smaller. Therefore, the laminar flow model was selected. In order to reduce the residual error of the low-velocity flow field calculation process, the power law method was used to solve the problem. Considering the gravity option, the direction was the negative direction of the Y-axis, and the value was set at −9.8 m·s⁻². The energy model and the solidification and melting model based on the enthalpy method were used to simulate and calculate the phase change process of PCM. The natural convection flow state in the liquid phase area of the heat storage process was complex, and the PISO algorithm was used to solve the problem due to its obvious advantages in calculating the flow field with high transientity. The correction coefficient was 1, and the pressure and energy used a second-order discrete format. The pressure term was discretized by the PRESTO method.

The PCM was a composite PCM prepared by paraffin wax with 10% mass fraction of expanded graphite. The Boussinesq hypothesis was used for the density of 890 kg·m⁻³. The specific heat capacity and thermal conductivity of the PCM were a piecewise line, and the latent heat of the PCM was 235 kJ·kg⁻¹. Hot water was used to heat the PCM, and there was only a small temperature change at the inlet and outlet of the hot water. Therefore, the contact surface with the thermal fluid was set as a constant temperature surface of the temperature. The solidification and melting temperatures of paraffin wax used in this paper was between 327–329 K. For shell-and-tube heat exchangers, the temperature difference between hot and cold fluids was generally about 20 K, which not only ensured a good heat transfer rate, but also reduced the generation of useless energy. Therefore, the temperature of the hot source was selected as 343 K in this paper. In addition, as described in Section 2.1, the thermal conductivity of PCM was very low and was much lower than the thermal conductivity of the fins. Therefore, the fin was set to a uniform temperature of 343 K during the simulation process. The shell of the regenerator was set as an adiabatic wall surface, and the initial temperature of the PCM was 300 K using the patch function of Fluent15.0 software during the melting simulation calculation.

4. Results and Discussion

4.1. Effect of Mesh Fin on the Heat Storage Performance

It was obtained from references [24] that the heat storage time of the concentric sleeve-type phase change heat accumulator decreased first and then increased with the increase in the vertical fin height. When the vertical fin height was 28 mm, the heat storage time was the shortest. Therefore, the subsequent calculation of this paper was carried out at the vertical fin height value of 28 mm. 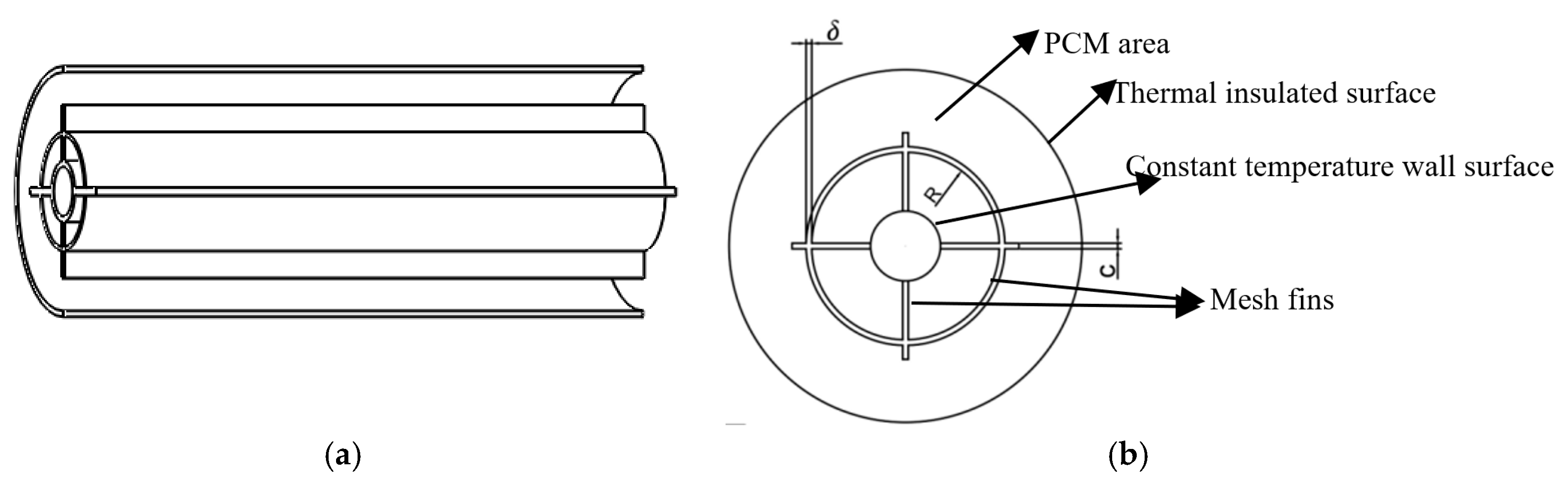In the numerical simulation model, as shown in Figure 1, the mesh fin radius was defined as R, the thickness was δ, the vertical fin thickness was c, and the number was N.

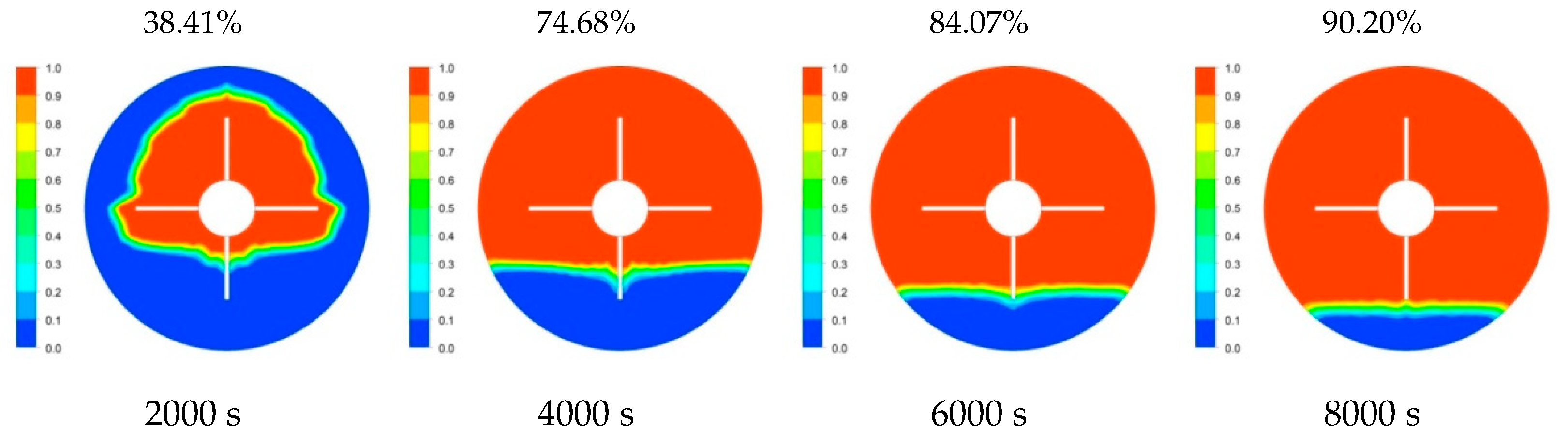
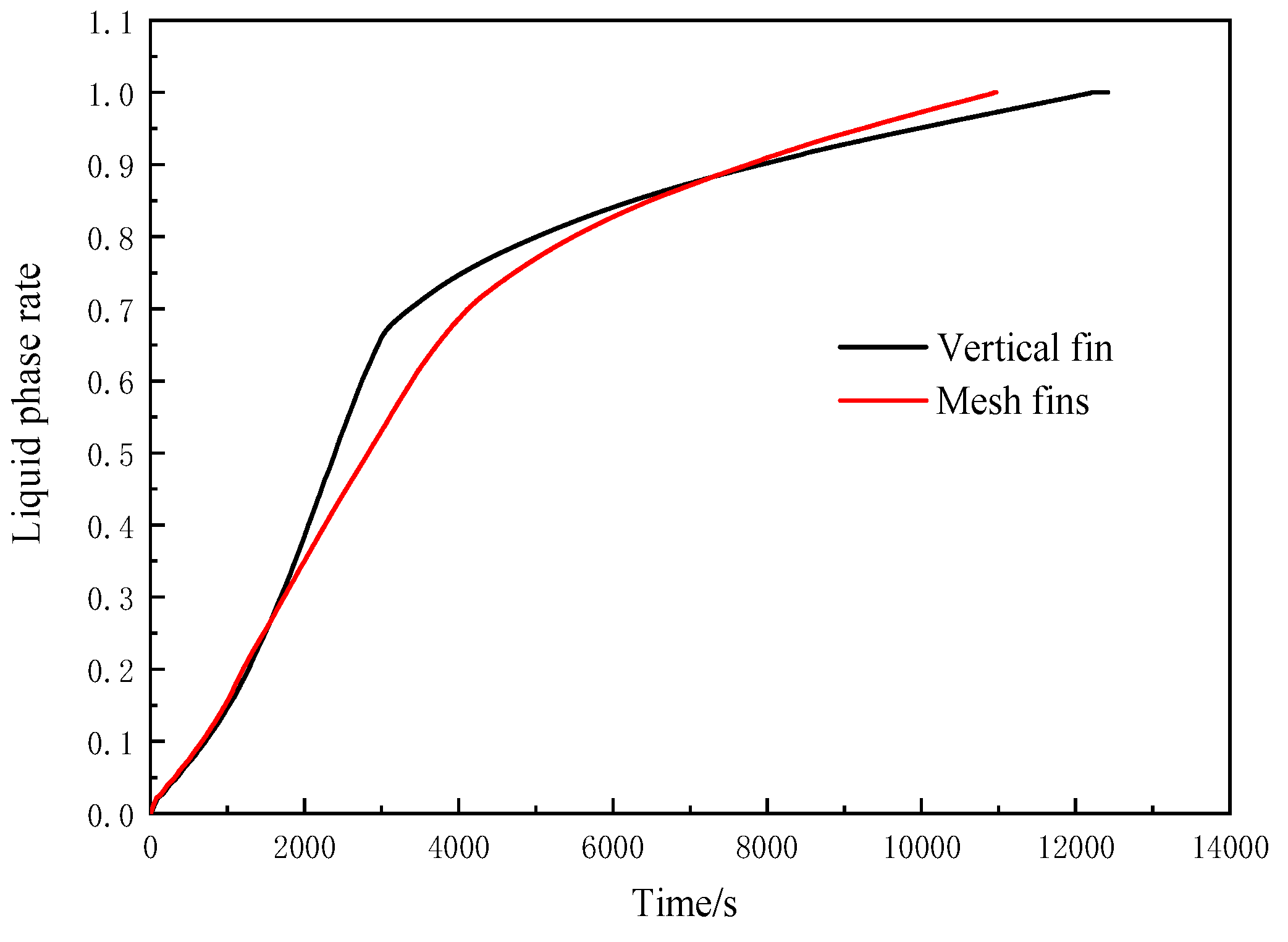
Solid–liquid phase cloud diagrams are shown in Figure 5 and Figure 6 at the vertical fin thickness c = 2 mm, the number of vertical fins N = 4, the mesh fin thickness δ = 2 mm, and the mesh fin radius R = 33.5 mm in the vertical fin accumulator (Figure 5) and the mesh fin accumulator (Figure 6) at the same operating parameters and initial conditions. The percentage of the material that melted at each time point is indicated in the upper right corner of the solid–liquid phase cloud diagrams. Liquid fraction curves of mesh fin heat accumulator and vertical fin heat accumulator are shown in Figure 7.

It can be seen from Figure 5, Figure 6 and Figure 7 that the liquid phase rate distribution curves and the solid–liquid phase area distributions on the cross-section of the two heat accumulators with different structures showed different representations at the same time. Before 2000 s, the volume average liquid phase rate curves of the two heat accumulators were basically the same, but the distribution areas were different. The liquid phase area of the vertical fin heat accumulator was closer to the upper wall. At 2000–4000 s, the liquid phase rate of the vertical fin changed more rapidly, and the liquid phase rate increased rapidly in the early stage and slowly in the later stage, while the liquid phase rate change curve of the mesh fin heat accumulator was more gentle and lower than the liquid phase rate of the vertical fin. The distribution of the liquid phase area on the cross-section of the two heat accumulators was completely different. At 4000 s, the PCM at the upper part of the vertical fin accumulators completely melted into the liquid phase, while the solid–liquid phase cross-section of the mesh fin heat accumulator presented a concave arc shape, and the height of the solid phase at the bottom of the vertical fin heat accumulator was greater than that of the mesh fin heat accumulator. At 4000–6000 s, the liquid phase rates of the two heat accumulators were similar, but the change rate of the liquid phase rate of the mesh fin heat accumulator was slightly faster than that of the vertical fin. When it reached 6000 s, the solid–liquid phase interfaces of the two heat accumulators with different structures were similar, but the solid phase area at the bottom of the mesh fin heat accumulator was obviously smaller than that of the vertical fin. In 6000–8000 s, the liquid phase rate curve of the mesh fin heat accumulator changed faster than that of the vertical fin heat accumulator. At 8000 s, the solid phase area of the mesh fin heat accumulator was much smaller than that of the vertical fin heat accumulator.

In the early stage of melting, thermal conductivity was the main method of heat transfer in the PCM area. For both mesh fin and vertical fin heat accumulators, the PCM around the fins first melted into liquid. Although the contact area between the mesh fins and the PCM was relatively large, due to the low thermal conductivity of paraffin, the change trends of the liquid phase ratio of the two heat accumulators were not much different in the early stage of melting. With the progress of melting, the liquid temperature around the fin was higher than that in other areas. Under the action of the gravity field, the liquid around the fin produced natural convection, which scoured the surrounding solid phase and accelerated the heat transfer in the whole phase change area. However, due to the blocking of the mesh fin, the natural convection of the liquid phase in the mesh fin heat accumulator could not be extended beyond the mesh fin, while the vertical fin did not have the influence of the mesh fin, and the natural convection of the liquid phase had a wider impact on the surrounding solid phase. Therefore, at 2000 s, the liquid phase area in the vertical fin heat accumulator was closer to the upper wall. With the extension of time, because of natural convection, the heat storage material in the upper part of the cross section of the vertical fin heat accumulator was quickly melted, while the natural convection blocked by the mesh fins in the mesh fin heat accumulator was small. At 4000 s, the solid–liquid phase distributions of the two different-structured heat accumulators were different. At 6000–8000 s, the PCM area entered the heat transfer mode dominated by heat conduction once again. The mesh fins had a large heat transfer area with the PCM, and the melting speed of the PCM of the mesh fin heat accumulator was much faster than that of the vertical fin in the later period. The melting speed of PCM in the mesh fin heat accumulator was much faster than that in the vertical fin heat accumulator. From Figure 7, it can be seen that the time of the full melting of the PCM in the mesh fin heat accumulator was shorter.

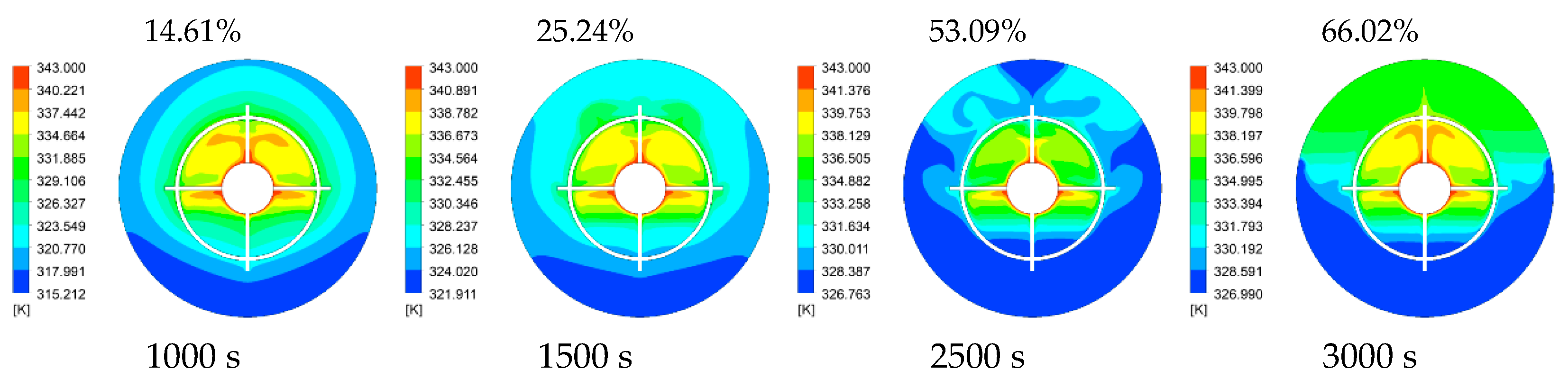
Figure 8 and Figure 9 are the temperature cloud diagrams of two differently structure heat accumulator sections at different times, obtained under the above simulation conditions. The percentage of the material that melted at each time point has been indicated in the upper right corner of the temperature cloud diagrams. It can be seen that in the heat storage process of the mesh fin heat accumulator and the vertical fin heat accumulator, the temperature distributions of the heat accumulator were basically the same, both of which were higher in the upper part of the heat accumulator and lower in the lower part of the heat accumulator. At 1000 s, under the influence of natural convection, the higher temperature area in the vertical fin heat accumulator was larger, but the average temperature was lower, and the high temperature area was about 334 K. The natural convection of the mesh fin heat accumulator was blocked by the mesh fin, and the strong natural convection occurred in the area surrounded by the mesh fin, while the natural convection outside the mesh fin was weak. Due to the high heat transfer performance of the mesh fins, the temperature in the local area inside the mesh fin was higher and reached about 340 K. At 1500 s, the area of natural convection in the vertical fin heat accumulator continued to expand, but the overall temperature decreased, and the temperature in most of the high-temperature areas was about 332 K, which indicated that the influence of natural convection made the local temperature distribution more uniform. For the mesh fins, due to the strong thermal conductivity and large contact area of the fins, the temperature rose rapidly in the area surrounded by the mesh fins, and most of the temperatures reached about 338 K. However, due to the weak effect of natural convection, the temperatures were low in the area outside the mesh fins, and most of them were only between 326–328 K. At 2500 s, the strong natural convection heat transfer mode of the vertical fin heat accumulator made the temperature of most of the upper PCM area rise to 343 K quickly, and the temperature difference in the upper part of the area was small, which led to the heat transfer mode in the PCM area from the natural convection heat storage mode to the heat conduction heat storage mode. However, the area of the solid phase area at the lower part of the heat accumulator section was still large, resulting in a small change in the temperature and solid–liquid phase area of the vertical fin heat accumulator between 2500 s and 3000 s. For the mesh fin heat accumulator at 2500 s, the temperature difference between the PCMs inside and outside the mesh fin was large, but both reached the liquid phase temperature. Therefore, the natural convection heat transfer effect was gradually enhanced, resulting in a large temperature change in the mesh fin heat accumulator between 2500 s and 3000 s, and the overall temperature of the mesh fin heat accumulator increased rapidly.

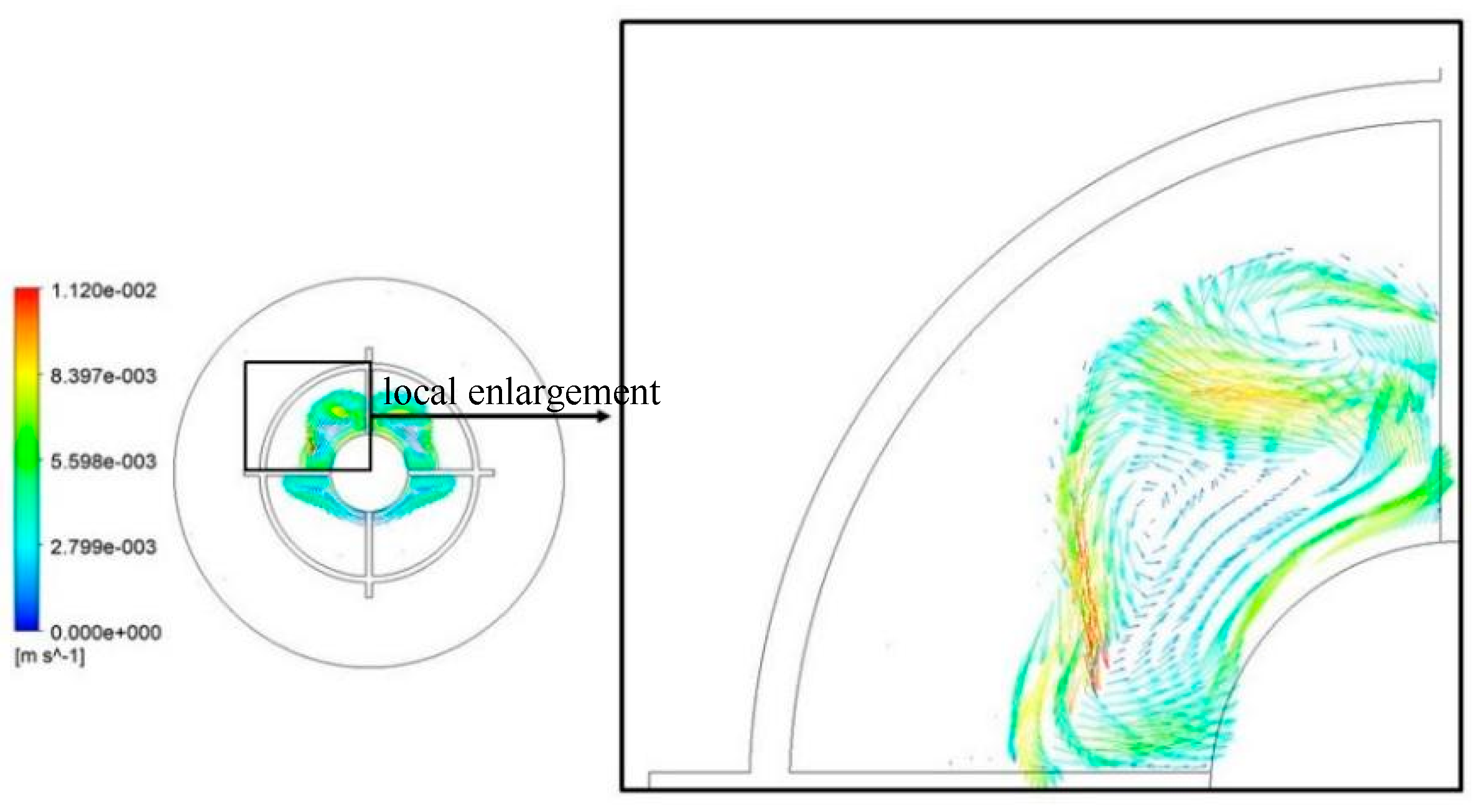
Figure 10 and Figure 11 are the velocity vector diagrams near the fins of two different heat accumulators at 500 s under the above simulation conditions. The natural convection intensity of the upper half of the heat accumulator section of the two structures was higher than that of the lower half, and the movements of the upper half of the vertical fin heat accumulator and the mesh fin heat accumulator were different. The PCM near the hot wall and the fin of the vertical fin heat accumulator absorbed heat, melted, and formed three vortex flows under the action of the gravity field, which caused natural convection heat transfer, so the solid–liquid interface moved to the left and upper parts of the heat accumulator. The PCM on the upper left side of the mesh fin heat accumulator melted to form approximately two vortex-like flow states. In addition, the fluid velocities of the PCM of the mesh fin were significantly higher than the flow velocities of the vertical fin. Therefore, at 500 s, in the vertical direction, the upward flow of the mesh fin had a stronger scouring ability and a higher swept surface.

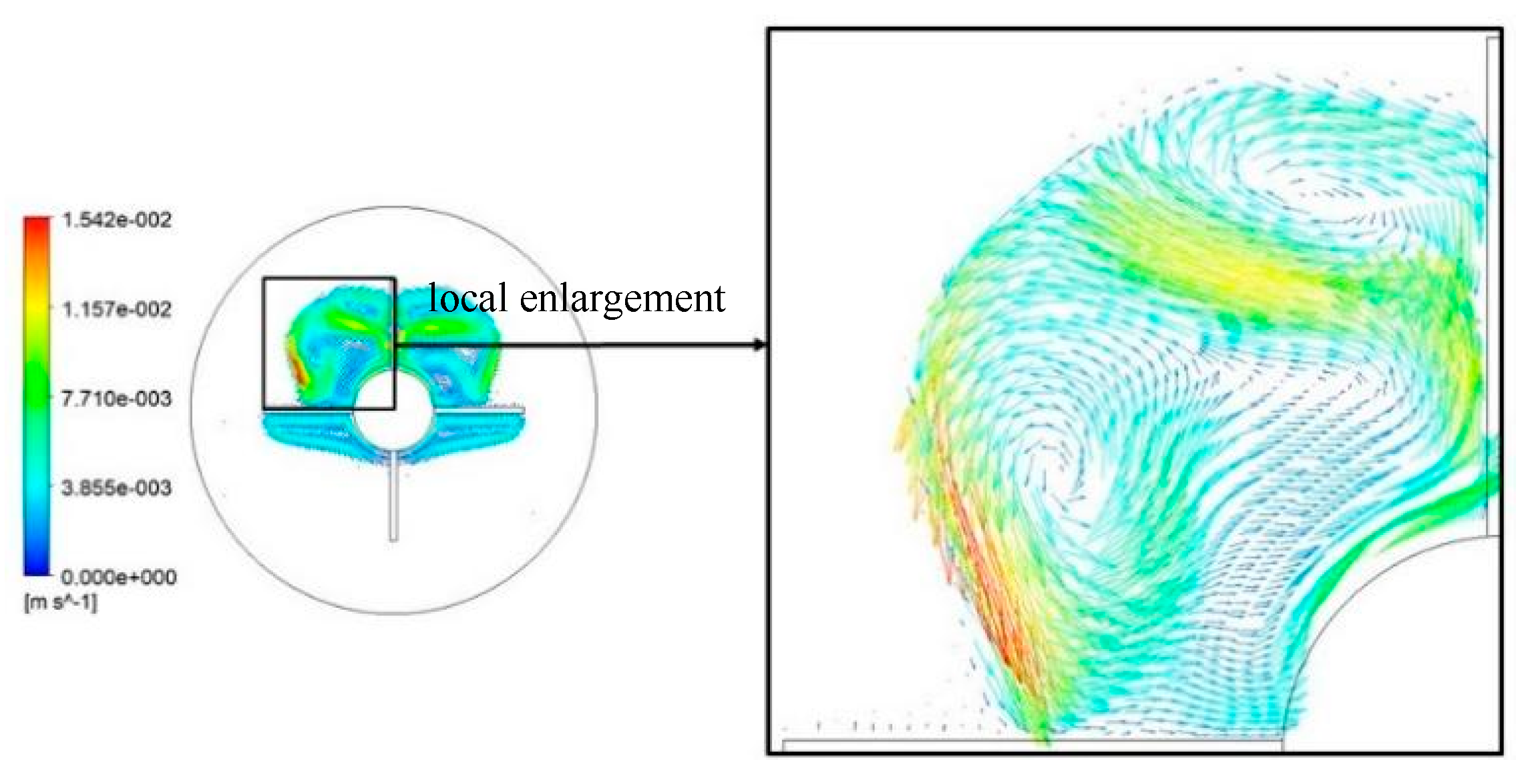
Figure 12 and Figure 13 are the velocity vector diagrams near the fins of two different heat accumulators at 1000 s under the above simulation conditions. Compared with 500 s, the natural convection-swept surface of the two vortex-like flows of the vertical fins gradually became larger. The flow velocities of the fluid were faster, which enhanced the natural convection heat transfer intensity of the vertical fin heat accumulator. At 1000 s, the solid–liquid interface of the mesh fin heat accumulator reached the mesh fin. Due to the blocking of the mesh fin, the natural convection could not diffuse outside the fin. The PCM outside the fin gradually melted and formed a weak natural convection under the heat conduction mode of the fin. The velocities of the fluid in the fin were also lower than that of the fluid at 500 s, so the natural convection heat transfer intensities inside and outside the mesh fin were reduced. This result is consistent with the results of the above-mentioned liquid phase rate distribution and liquid phase area distribution.

Figure 14 shows the liquid phase rate curve of the heat storage process of the mesh fin heat accumulator when the radii R of the mesh fin were 21.5 mm, 25.5 mm, 29.5 mm, 33.5 mm, and 37.5 mm, respectively, under the above simulation conditions. In the early stage of heat storage, the overall heat storage process took heat conduction as the main heat transfer mode, and the change trends of the liquid phase rate under different fin heights were basically the same. After 1000 s, the heat storage processes entered the natural convection-based heat transfer mode, the liquid phase rates increased rapidly, and when R = 21.5–33.5 mm, with the increase in R, the slopes of the liquid phase rate curve gradually increased, indicating that the heat storage speeds of the accumulator gradually accelerated. Then, the final heat storage times gradually became shorter with the increase in R. When R = 37.5 mm, the heat storage time increased, compared with other mesh fin radii.

When R was between 21.5–33.5 mm, the natural convection hindered by the upper mesh fins gradually increased with R, and the heat could not be timely transferred to the upper area of the accumulator. More heat was transferred to the lower part of the accumulator, which promoted the melting of the lower PCM and reduced the area of the PCM, depending on heat conduction heat transfer mode in the later stage. At the same time, the increase in the radius of the mesh fin increased the contact area between the fin and the PCM, which effectively improved the apparent thermal conductivity of the phase change area dominated by thermal conductivity in the later stage. When R = 37.5 mm, the mesh fin enhanced the blocking of natural convection, and the melting time of the PCM above the accumulator increased, but the solid–liquid interface of the PCM shifted downward almost unchanged; the heat gradually decayed along the radial direction of the vertical fin. When the radius of the mesh fin increased, although the heat transfer area in the PCM area increased, the energy transferred from the vertical fin to the mesh fin was also attenuated, resulting in an increase in the complete melting time of the PCM, compared to the accumulator with R = 33.5 mm.

4.2. Effect of Vertical Fin Thickness on the Heat Storage Performance

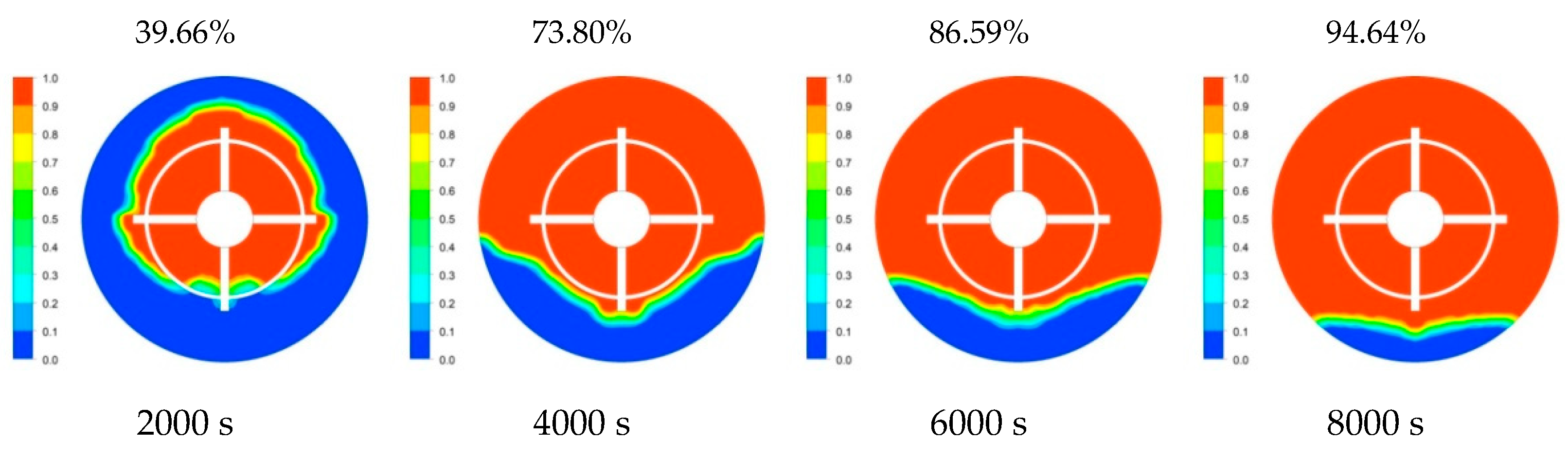
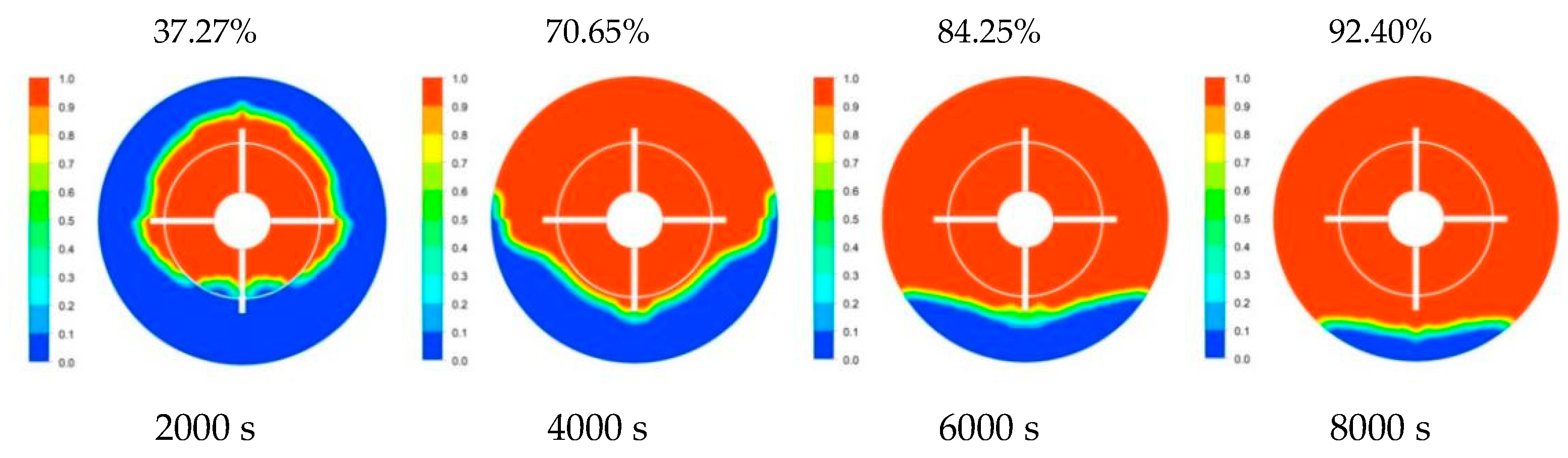
Figure 15, Figure 16 and Figure 17 show the solid–liquid phase cloud diagrams and the liquid phase rate curves at different times of the phase change heat accumulator when the radius of the mesh fin was R = 33.5 mm, the thickness of the mesh fin was δ = 2 mm, the number of vertical fins was N = 4, and the thicknesses of the vertical fin were c = 1 mm, 2 mm, 3 mm, and 4 mm, respectively. The percentage of the material that melted at each time point has been indicated in the upper right corner of the solid–liquid phase cloud diagrams.

From Figure 15 and Figure 16, it can be seen that the liquid phase distributions of the melting process of the PCM of the accumulator were basically similar when the vertical fin thicknesses were different. At 2000 s, the PCMs inside the area surrounded by mesh fins in the heat accumulator of c = 4 mm were all melted, while there were still more solid PCMs in the heat accumulator with c = 1 mm. At 4000 s, the PCMs on the upper and both sides of the mesh fin heat accumulator with c = 4 mm all melted, while there were still more solid PCMs on the upper part of the accumulator with c = 1 mm. After 6000 s, the solid–liquid interface of the accumulator with c = 4 mm was lower than that of the accumulator with c = 1 mm. The results showed that whether it was the heat transfer process dominated by heat conduction in the early stage or the heat transfer process dominated by natural convection heat transfer in the middle stage, with the increase in the thickness of the vertical fin, the heat storage rates of the heat accumulator were faster, and the times required were shorter.

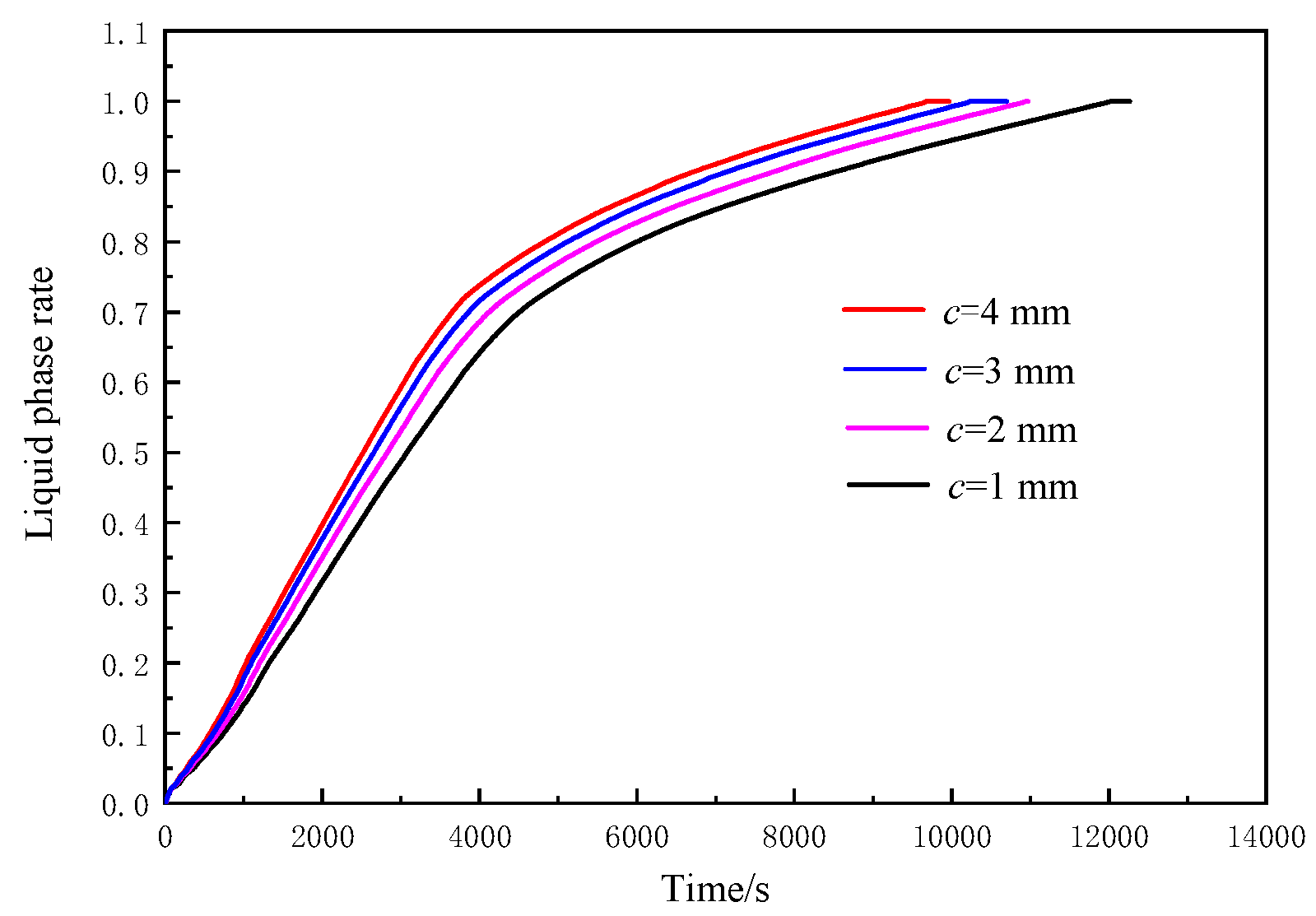
It can be seen from Figure 17 that when c = 1–4 mm, with the increase in fin thickness, the times of heat conduction mode dominated by heat conduction in the early stage were gradually shortened, and the whole heat storage process could enter the heat transfer process dominated by natural convection heat transfer more quickly. Before 4000 s, the heat storage processes were dominated by natural convection, so the liquid phase rate curves were steeper. After 4000 s, most of the area entered the heat storage process dominated by heat conduction, and the liquid phase rate curves were gentler, consistent with the above liquid phase rate cloud diagram results.

The analysis showed that when the thickness of the fin increased, the thermal resistance of heat conduction of the high-temperature wall through the fin decreased, the temperature difference between the fin from the bottom to the top decreased, and the temperatures at the top of the fin were relatively higher, resulting in greater temperature differences with the surrounding PCMs and a faster heat transfer speed. The PCM around the fin was easier to melt, and it entered the heat storage process dominated by the earlier natural convection heat transfer. In the process of heat conduction and heat storage in the later stage, the thickness of the fin increased, the apparent thermal conductivity inside the whole heat accumulator increased, the heat storage effect was better, and the time required was shorter. When the vertical fin thicknesses c were 1 mm, 2 mm, 3 mm, and 4 mm, respectively, the melting times of PCM were 12,027 s, 10,945 s, 10,238 s, and 9685 s, respectively, and the heat storage times were shortened by 8.9%, 6.6%, and 5.1%. Otherwise, with the increase in vertical fin thickness, the volume of PCM in the accumulator decreased, which also shortened the melting time of PCM (see Appendix A.1 for relevant calculations). The above melting time reduction ratio came from two aspects: fin-enhanced heat transfer and PCM volume reduction. It can be seen from the calculation that the proportions of melting time shortening caused by the increase in vertical fin thickness were 8.0%, 5.7%, and 4.2%.

4.3. Effect of Mesh Fin Thickness on the Heat Storage Performance

Figure 18, Figure 19 and Figure 20 show the liquid phase rate distribution cloud diagram and the liquid phase rate curve of the mesh fin heat accumulator with the mesh fin radius R = 33.5 mm, the vertical fin thickness c = 3 mm, the number of vertical fins N = 4, and the mesh fin thicknesses δ of 1 mm, 2 mm, 3 mm, and 4 mm, respectively. The percentage of the material that melted at each time point has been indicated in the upper right corner of the solid–liquid phase cloud diagrams.

It can be seen from Figure 18 and Figure 19 that before 4000 s, the melting morphologies of the PCMs of the heat accumulator with different mesh fin thicknesses were relatively the same. After 4000 s, the heat storage process of the heat accumulator with δ = 3 mm was faster than that of δ = 1 mm. The solid–liquid phase interface of the heat accumulator with δ = 3 mm was lower than that of the heat accumulator with δ = 1 mm, which indicated that the PCM of the heat accumulator with δ = 3 mm was melted faster than that of the heat accumulator with δ = 1 mm at this stage. In the later 6000 s and 8000 s, the heat accumulator entered the heat storage process dominated by heat conduction. The heat storage rate of the heat accumulator with δ = 3 mm was faster, and the solid phase area was smaller.

Before about 4000 s, the heat accumulators were in the natural convection heat storage state most of the time, and the slopes of the liquid phase rate curve were larger. After 4000 s, it entered the heat storage process dominated by heat conduction, and the slopes of the liquid phase rate curve became gentler. However, whether it was natural convection or the heat conduction-based heat storage process, the slope of the liquid phase rate curve of heat storage gradually increased with the increase in the thickness of the mesh fin. The thicker the fin thickness, the higher the liquid phase rate value of the heat accumulator at the same time. Whether it was the natural convection heat transfer or the later heat conduction process inside the heat accumulator, with the mesh fin thickness increase, the heat storage effect became better. According to the analysis, the increase in the thickness of the mesh fin increased the thermal conductivity of the heat storage material area, which played a strengthening role in the rapid entry into the natural convection heat transfer process and the later thermal conduction heat storage process. The simulation results showed that when the mesh fin thicknesses δ were 1 mm, 2 mm, 3 mm, and 4 mm, the melting times of the PCM were 10,446 s, 10,238 s, 9300 s, and 9200 s, respectively, and the heat storage times of the PCM were shortened by 2.1%, 9.1%, and 1.07%. Similarity, with the increase in mesh fin thickness, the volume of PCM in the accumulator decreased, which also shortened the melting time of PCM (see Appendix A.1 for relevant calculations). The above melting time reduction ratio came from two aspects: fin-enhanced heat transfer and PCM volume reduction. It can be seen from the calculation that the proportions of melting time shortening caused by the increase in mesh fin thickness were 1.7%, 8.7%, and 0.7%.

4.4. Effect of the Number of Vertical Fins on the Heat Storage Performance

Figure 21 and Figure 22 show the liquid phase rate distribution cloud diagrams and the liquid phase rate change curves of the phase change accumulator, with the radius of the mesh fin R = 33.5 mm, the thickness of the vertical fin c = 3 mm, the thickness of the mesh fin δ = 3 mm, and the numbers of vertical fins N = 4, 6, 8, and 10, respectively. The percentage of the material that melted at each time point has been indicated in the upper right corner of the solid–liquid phase cloud diagrams.

It can be seen from Figure 21, Figure 22 and Figure 23 that as the number of fins increased, the area of the liquid phase area gradually increased at the same time, and the required heat storage time was greatly reduced. In the early stage of melting, the slope of the liquid phase rate curve of the accumulator with N = 10 was higher than that of the liquid phase rate curve with N = 4. With the extension of time, the greater the number of fins, the faster the liquid phase rate increased. At 4000 s, the liquid phase rate of the accumulator with N = 4 was about 0.7, while the liquid phase rate of the accumulator with N = 10 reached 0.8.

In the initial stage of heat storage, the heat storage process was dominated by heat conduction. With the number of vertical fins increasing, the heat conduction process in the PCM area could be effectively strengthened. However, due to the blocking of fins, the natural convection heat storage process may be weakened. Due to the low flow rate of the liquid PCM in the initial stage, the natural convection heat transfer intensity was low. While the number of vertical fins increased, the heat storage caused by heat conduction was enhanced. Therefore, both heat conduction and natural convection played a certain role in heat storage. Therefore, at 2000 s, the upper natural convection heat storage and the lower heat conduction heat storage had an equivalent action in the mesh fin heat accumulator with N = 10. The PCMs around the fins were all melted into the liquid phase. With the extension of time, the internal temperature difference in the heat accumulator increased, the intensity of natural convection increased, and the upper PCM melted faster under the erosion of natural convection. The solid phase area of the accumulator with N = 10 was much smaller than that of the accumulator with N = 4.

Figure 24 and Figure 25 show the velocity contours of heat accumulators with N = 4 and N = 10 at different times under the above simulation conditions. The percentage of the material that melted at each time point has been indicated in the upper right corner of the velocity cloud diagrams. At 500 s, the internal velocities of the accumulator with N = 4 were up to 1.56 × 10⁻² m/s. In the area forming natural convection, most of the fluid velocities were about 7.79 × 10⁻³ m/s. The internal velocities of the accumulator with N = 10 were up to 1.18 × 10⁻² m/s, and most of the fluid velocities in the area forming natural convection were about 5.9 × 10⁻³ m/s.

In the initial stage of heat storage, because of the fins’ role of blocking natural convection, with the number of fins increasing, the effect of natural convection heat storage became worse. At 1000 s, the area surrounded by the mesh fins of the heat accumulator with N = 4 completely entered the natural convection heat storage state. However, due to the influence of the mesh fins, the fluid flow velocity decreased instead. In the heat accumulator with N = 10, the fins had a greater influence on the natural convection of the PCM. In the upper part, only two small areas surrounded by fins completely entered the strong natural convection state. The fins strengthened heat conduction, the temperature of the PCM around the fins was high, and the temperature differences inside the area separated by the fins were greater, which resulted in the flow velocities inside each area separated by the fins still increasing. At this stage, both heat conduction and natural convection had a certain contribution to heat storage. At 2000 s, the heat gradually diffused outside the fin, the PCM outside the fin gradually melted, and natural convection occurred under the action of the gravity field. The fluid velocities in the upper half of the heat accumulator with N = 4 were higher, and the natural convection was stronger, while the velocities in most areas of the lower half were close to 0. While the natural convection occurred in the upper half of the heat accumulator with N = 10, the PCM melted quickly under the influence of multi-fin heat conduction, and the heat storage of natural convection also occurred. The results are consistent with the results obtained from the curve of the liquid phase rate with time in Figure 21. At 3000 s, the PCM of the upper half of the accumulator with N = 4 melted completely, the natural convection intensity decreased, the velocities of the fluid gradually decreased, and it entered the heat storage process dominated by heat conduction. However, the PCM of the upper half of the accumulator with N = 10 still did not completely melt, and there was still natural convection heat storage. The heat conduction of the multi-fins strengthened the natural convection in the lower half of the accumulator again, and the area of the liquid phase area gradually increased. The results are consistent with the results of the liquid phase distribution cloud diagrams in Figure 21 and Figure 22.

The calculation results showed that when the numbers of vertical fins N were 4, 6, 8, and 10, the melting times of the PCM were 9300 s, 8852 s, 8086 s, and 7865 s, respectively, and the melting times of the PCM were shortened by 4.8%, 8.6%, and 2.7%. Otherwise, with the increase in the number of vertical fins, the volume of PCM in the accumulator decreased, which also shortened the melting time of PCM (see Appendix A.3 for relevant calculations). The above melting time reduction ratio came from two aspects: fin-enhanced heat transfer and PCM volume reduction. It can be seen from the calculation that the proportions of melting time shortening caused by the increase in mesh fin thickness were 3.4%, 7.2%, and 1.3%.

5. Conclusions

A new mesh fin heat accumulator was designed. This new design increased the contact area between the PCM and the fins, which, in turn, (i) enhanced the apparent thermal conductivity of the PCM, (ii) improved the heat storage efficiency of the heat accumulator, (iii) blocked the PCM, (iv) improved the natural convection erosion of the PCM on the upper and lower parts of the heat accumulator, and (v) helped the PCM in each area melt more evenly.

The heat storage process of the mesh fin heat accumulator with different structural parameters was numerically simulated by Fluent15.0. The paraffin with a mass fraction of 10% expanded graphite was used as the composite phase change heat storage material. The liquid PCM was based on the Boussinesq hypothesis. The density and specific heat capacity of the composite PCM were based on the piecewise-line hypothesis. The effects of mesh fins and mesh fin radius R, vertical fin thickness c, mesh fin thickness δ, and vertical fin number N on the heat storage process were investigated.

The liquid phase rate distribution curve and the solid–liquid phase distribution of the two heat accumulators with different structures showed different states at the same time. The fins increased the contact area with the PCM and increased the thermal conductivity of the PCM area while playing a certain role in blocking the thermal convection of the liquid phase material. In the early stage, the vertical fins melted faster than the PCMs of the mesh fin heat accumulator, and the melting speed was slow in the later stage; the time required for the mesh fin heat accumulator was shorter. With the increase in the mesh fin radius R, the heat storage time decreased first and then increased. When R = 33.5 mm, the heat storage time was the shortest.

With the vertical fin thickness c and the mesh fin thickness δ, the thermal resistance of the heat conduction through fins was reduced, the melting speed of the PCM was accelerated, and the heat storage time was gradually shortened, but the shortening trend was gradually slowed down. Increasing the number of vertical fins N not only increased the contact area between fins and PCM but also hindered the natural convection of melted PCMs to a certain extent. Therefore, when N exceeded a certain number, the heat storage time was not significantly shortened. Through the simulation results, the optimal mesh fin structure parameters were R = 33.5 mm, c = 3 mm, δ = 3 mm, and N = 8. The melting time of the PCM was 8086 s, which is 47.8% shorter than that of the concentric tube heat accumulator.

Naturally, with the thickness of the fins and the number of fins increasing, the PCM and the stored energy amount decreased. According to the calculation results, the proportion of the area occupied by the fin in the PCM area was about 8% under the optimal structural parameters. The increase in the fins had a certain effect on the capacity and heat storage of the PCM. In order to achieve the maximum heat storage efficiency of the accumulator, it was necessary to achieve the best balance between the heat storage time and the heat transfer enhancement of the fin.