Development and Performance Evaluation of Central Pipe for Middle-Deep Geothermal Heat Pump Systems
Abstract
1. Introduction
2. Methodology
2.1. Mathematical Models
2.1.1. Heat Transfer and Flow Models of Circulating Fluid
2.1.2. Heat Transfer Models for Central Pipe, Wellbore/Formation
2.1.3. Thermodynamic Cycle Models for Heat Pump
2.2. Solution of the Models
2.3. Validation of the Models
3. Results and Discussion
3.1. Optimization of Central Pipe Based on Response Surface Method
3.1.1. Work Condition and Orthogonal Experiments
3.1.2. Optimization of Central Pipe Base on Response Surface Method
3.2. Development a Novel Composite Central Pipe
3.2.1. Insulation Performance of the Composite Central Pipe
3.2.2. Tensile Performance of the Composite Central Pipe
3.3. Comparative Analysis with Existing Central Pipes
4. Conclusions
- (1)
- The transient heat transfer model, flow model, and heat pump thermodynamic cycle model developed in this study for the MD-GHP system demonstrated substantial capability to accurately characterize the energy transfer and conversion dynamics within the system, providing a robust framework for central pipe optimization design research;
- (2)
- The influence of various central pipe parameters on the COPs of an MD-GHP system with a well depth of 2700 m was analyzed and optimized using the response surface optimization method, which resulted in the identification of optimal central pipe parameters: an inner diameter of 88 mm, a thickness of 14 mm, and an effective thermal conductivity of 0.2 W/(m·K);
- (3)
- A novel composite central pipe, composed of HDPE, silica aerogels, and glass fiber tape, was designed and manufactured, with an effective thermal conductivity of 0.13 W/(m·K) and an axial tensile force of 29,000 N at 105 °C being achieved. Further, the single pipe can reach a length of 500 m. In addition, the production cost is only one-third that of existing vacuum-insulated central pipes;
- (4)
- The operational performance of the composite central pipe was compared with existing PE central pipes and vacuum-insulated central pipes using a numerical simulation method. It was found that the utilization of the composite central pipe results in an 11% and 7% increase in the system’s COPs compared to traditional PE central pipes and vacuum-insulated central pipes, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cp | Specific heat, J/(kg·°C) |
| ftp | The friction factor |
| g | Gravitational acceleration, 9.8 m/s2 |
| h | Enthalpy of the refrigerant, J/kg |
| wt | Circulating rate of water in geothermal well, kg/s |
| Lhp | Circulating rate of refrigerant in heat pump, kg/s |
| Lh | The mass flow rate of heating water, kg/s |
| P | Fluid pressure, Pa |
| QE | The heat release rate by refrigerant in condenser, W |
| QC | The heat absorption rate by refrigerant in evaporator, W |
| Qheatingload | Required district heating load, W |
| r | The wellbore radius, m |
| TFluid | The temperature of circulating fluid in geothermal well,·°C |
| Tin | Inlet temperature of circulating fluid,·°C |
| Tout | Outlet temperature of circulating fluid,·°C |
| Ts | The supply water temperature,·°C |
| Tb | The back water temperature,·°C |
| v | Velocity, m/s |
| Wpump | Power consumption of circulation pump, W |
| W | Power consumption of heat pump, W |
| Z | The depth of the wellbore, m |
| α | Convective heat transfer coefficient, J/(m2·s·°C) |
| λ | Thermal conductivity, J/(m·K) |
| η1 | The compressor isentropic efficiency |
| η2 | Mechanical efficiency of the compressor |
| ηC | Heat transfer efficiency of the condenser |
| ηE | Heat transfer efficiency of the evaporator |
| θ | The well angle to the horizontal line |
| ρ | Density, kg/m3 |
References
- Glassley, W.E. Geothermal Energy: Renewable Energy and the Environment; CRC Press: London, UK, 2015. [Google Scholar]
- Kazaz, O.; Abu-Nada, E. Innovative high-energy nanocomposite absorbers for superior solar-driven water desalination through broadband solar energy harvesting. Appl. Therm. Eng. 2025, 273, 126531. [Google Scholar] [CrossRef]
- Kamila, Z.; Kaya, E.; Zarrouk, S.J. Reinjection in geothermal fields: An updated worldwide review 2020. Geothermics 2021, 89, 101970. [Google Scholar] [CrossRef]
- Figueira, J.S.; Gil, A.G.; Vieira, A.; Michopoulos, A.K.; Boon, D.P.; Loveridge, F.; Cecinato, F.; Götzl, G.; Epting, J.; Zosseder, K.; et al. Shallow geothermal energy systems for district heating and cooling networks: Review and technological progression through case studies. Renew. Energy 2024, 236, 121436. [Google Scholar] [CrossRef]
- Sapinska-Sliwa, A.; Rosen, M.A.; Gonet, A.; Sliwa, T. Deep Borehole Heat Exchangers—A Conceptual and Comparative Review. Int. J. Air-Cond. Refrig. 2016, 24, 1630001. [Google Scholar] [CrossRef]
- Alimonti, C.; Soldo, E.; Bocchetti, D.; Berardi, D. The wellbore heat exchangers: A technical review. Renew. Energy 2018, 123, 353–381. [Google Scholar] [CrossRef]
- Anand, R.; Li, A.; Huang, W.; Chen, J.; Li, Z.; Ma, Q.; Jiang, F. Super-long gravity heat pipe for geothermal energy exploitation—A effective review. Renew. Sustain. Energy Rev. 2024, 193, 114286. [Google Scholar] [CrossRef]
- Nath, F.; Mahmood, N.; Ofosu, E.; Khanal, A. Enhanced geothermal systems: A critical review of recent advancements and future potential for clean energy production. Geoenergy Sci. Eng. 2024, 243, 213370. [Google Scholar] [CrossRef]
- Zhang, X. Numerical study of geothermal district heating from a ground heat exchanger coupled with a heat pump system. Appl. Therm. Eng. 2021, 185, 116335. [Google Scholar] [CrossRef]
- Du, Y.S.; Feng, Y.S.; Wu, X.L.; Shi, M.; Gao, P.J.; Tang, X.R.; Zhao, Y.; Wang, X.S.; Wang, Q.X.; Dong, X.Y.; et al. Research status and consideration of thermal insulation pipe technology for deep geothermal energy development. Drilling Eng. 2022, 49, 138–145. (In Chinese) [Google Scholar] [CrossRef]
- Śliwa, T.; Kotyza, J. Application of existing wells as ground heat source for heat pumps in Poland. Appl. Energy 2003, 74, 3–8. [Google Scholar] [CrossRef]
- Zhu, Z.; Miao, Y.; Li, D.; Lin, X.; Ra, J.; Sun, Y.; Yu, W. Pilot test and effect evaluation of thermal insulation tubing. Energy Conserv. Petrol. Ind. 2019, 9, 12–14. (In Chinese) [Google Scholar] [CrossRef]
- Afra, M.; Peyghambarzadeh, S.; Shahbazi, K.; Tahmassebi, N. Experimental study of implementing nano thermal insulation coating on the steam injection tubes in enhanced oil recovery operation for reducing heat loss. J. Pet. Sci. Eng. 2020, 189, 107012. [Google Scholar] [CrossRef]
- Gao, Q.; Jin, G.; Yu, H.; An, E.; Ghassemi, A.; Zhou, D.; Meng, H. Heat extraction from abandoned petroleum wells utilizing coaxial borehole heat exchanger in Ordos basin, China. Renew. Energy 2024, 230, 120806. [Google Scholar] [CrossRef]
- Dijkshoorn, L.; Speer, S.; Pechnig, R. Measurements and Design Calculations for a Deep Coaxial Borehole Heat Exchanger in Aachen, Germany. Int. J. Geophys. 2013, 14, 916541. [Google Scholar] [CrossRef]
- Li, C.; Guan, Y.; Yang, R.; Lu, X.; Xiong, W.; Long, A. Effect of inner pipe type on the heat transfer performance of deep-buried coaxial double-pipe heat exchangers. Renew. Energy 2020, 145, 1049–1060. [Google Scholar] [CrossRef]
- Deng, J.; Wei, Q.; Liang, M.; He, S.; Zhang, H. Does heat pumps perform energy efficiently as we expected: Field tests and evaluations on various kinds of heat pump systems for space heating. Energy Build. 2018, 182, 172–186. [Google Scholar] [CrossRef]
- Deng, J.; Wei, Q.; Liang, M.; He, S.; Zhang, H. Field test on energy performance of medium-depth geothermal heat pump systems (MD-GHPs). Energy Build. 2019, 184, 289–299. [Google Scholar] [CrossRef]
- Liu, B.; Wang, J.; Li, H.; Liu, J.; Wang, P.; Cai, W.; Sun, X.; Chen, C. In-situ test and numerical investigation on the long term performance of deep borehole heat exchanger coupled heat pump heating system. Case Stud. Therm. Eng. 2024, 61, 104855. [Google Scholar] [CrossRef]
- Xie, Y.Y. Research on the Potential and Model of Geothermal Heating in the Middle and DEEP Layers of Song Yuan. Ph.D. Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Song, X.; Zheng, R.; Li, G.; Shi, Y.; Wang, G.; Li, J. Heat extraction performance of a downhole coaxial heat exchanger geothermal system by considering fluid flow in the reservoir. Geothermics 2018, 76, 190–200. [Google Scholar] [CrossRef]
- Nian, Y.-L.; Cheng, W.-L. Evaluation of geothermal heating from abandoned oil wells. Energy 2018, 142, 592–607. [Google Scholar] [CrossRef]
- Moran, M.J. Fundamentals of Engineering Thermodynamics; John Wiley Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Li, H.; Wang, J.; Liu, S.; Tang, L.; Zhang, X.; Wang, P. Study on heat extraction capacity of deep coaxial borehole heat exchanger equipped with spiral-finned inner tube. Int. J. Heat Fluid Flow 2025, 116, 109946. [Google Scholar] [CrossRef]
- GB/T 10297; Test Method for Thermal Conductivity of Nonmetal Solid Materials—Hot-Wire Method. Standards Press of China: Beijing, China, 2015.
- GB/T 10296; Thermal Insulation-Determination of Steady-State Thermal Transmission Properties-Pipe Insulation Apparatus. Standards Press of China: Beijing, China, 2008.
- GB/T 8804; Thermoplastic Pipes—Determination of Tensile Properties. Standards Press of China: Beijing, China, 2013.
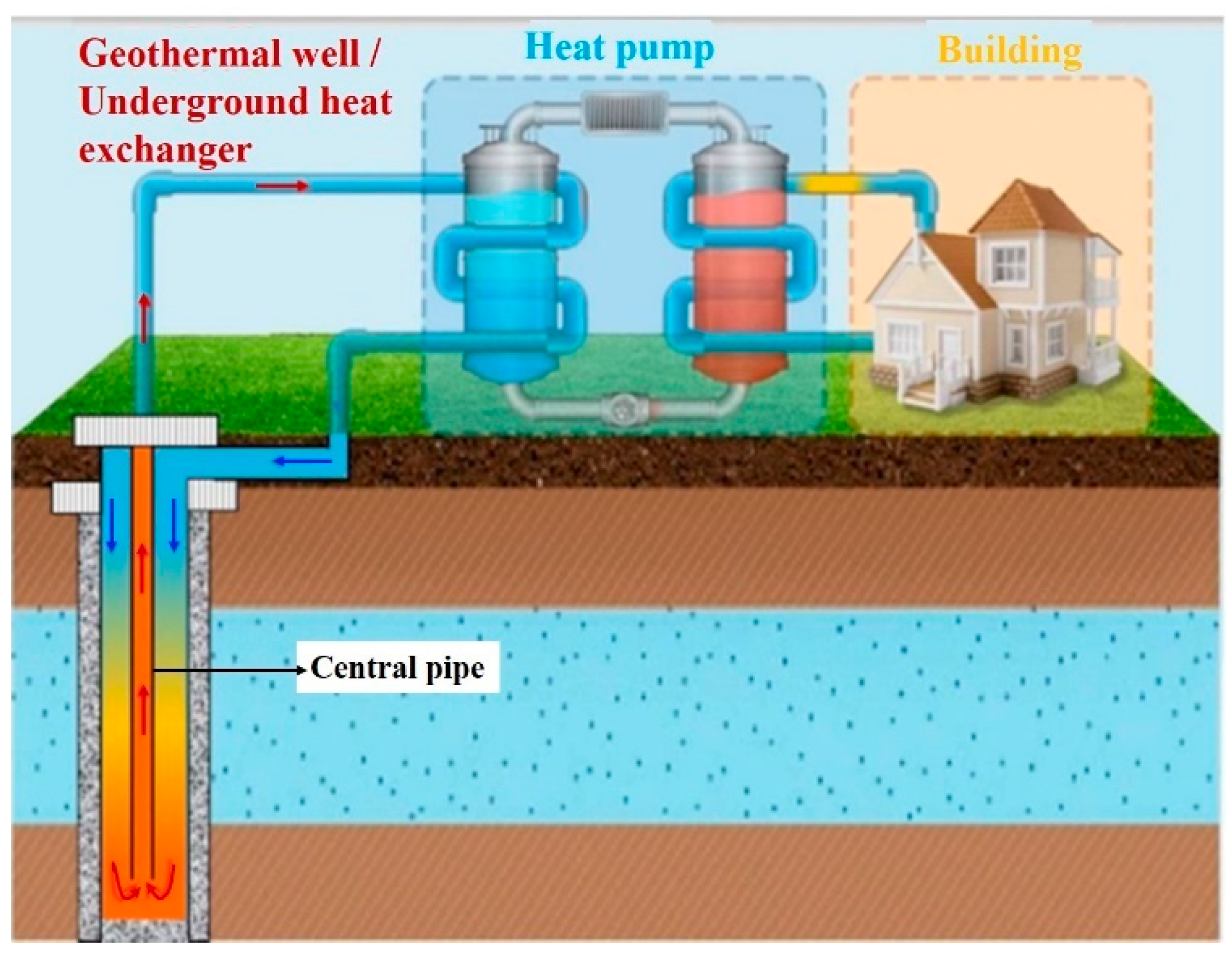
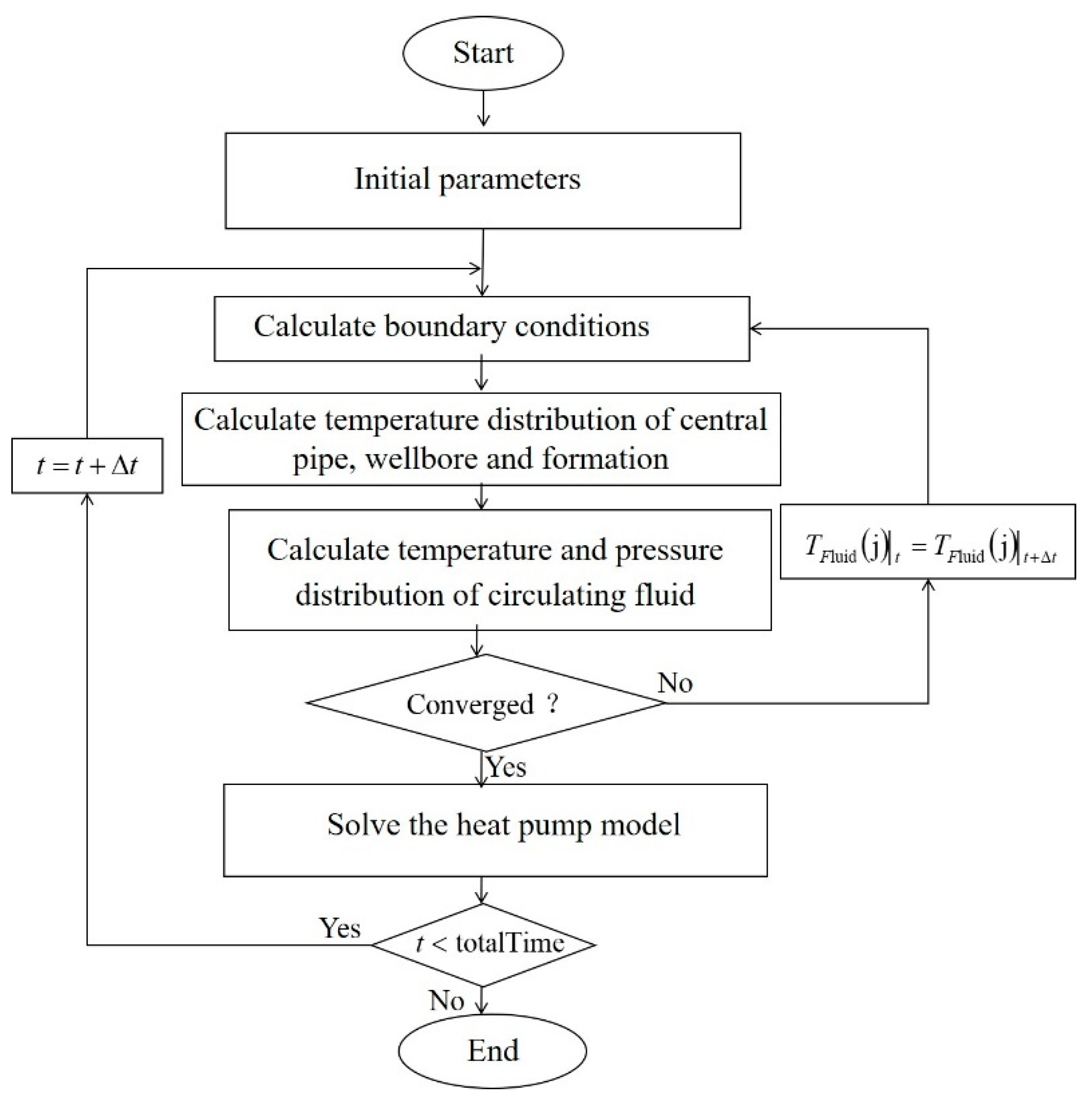
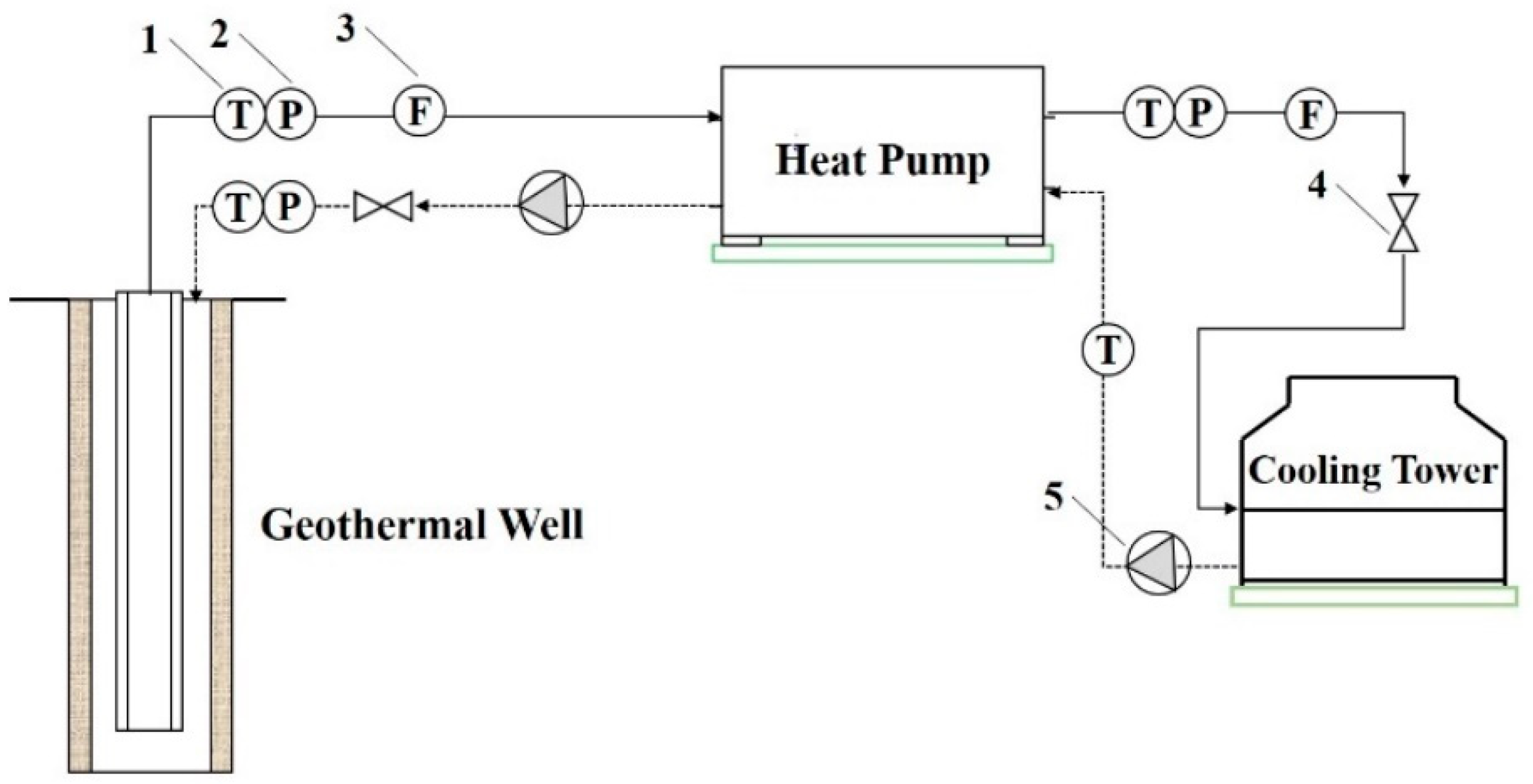
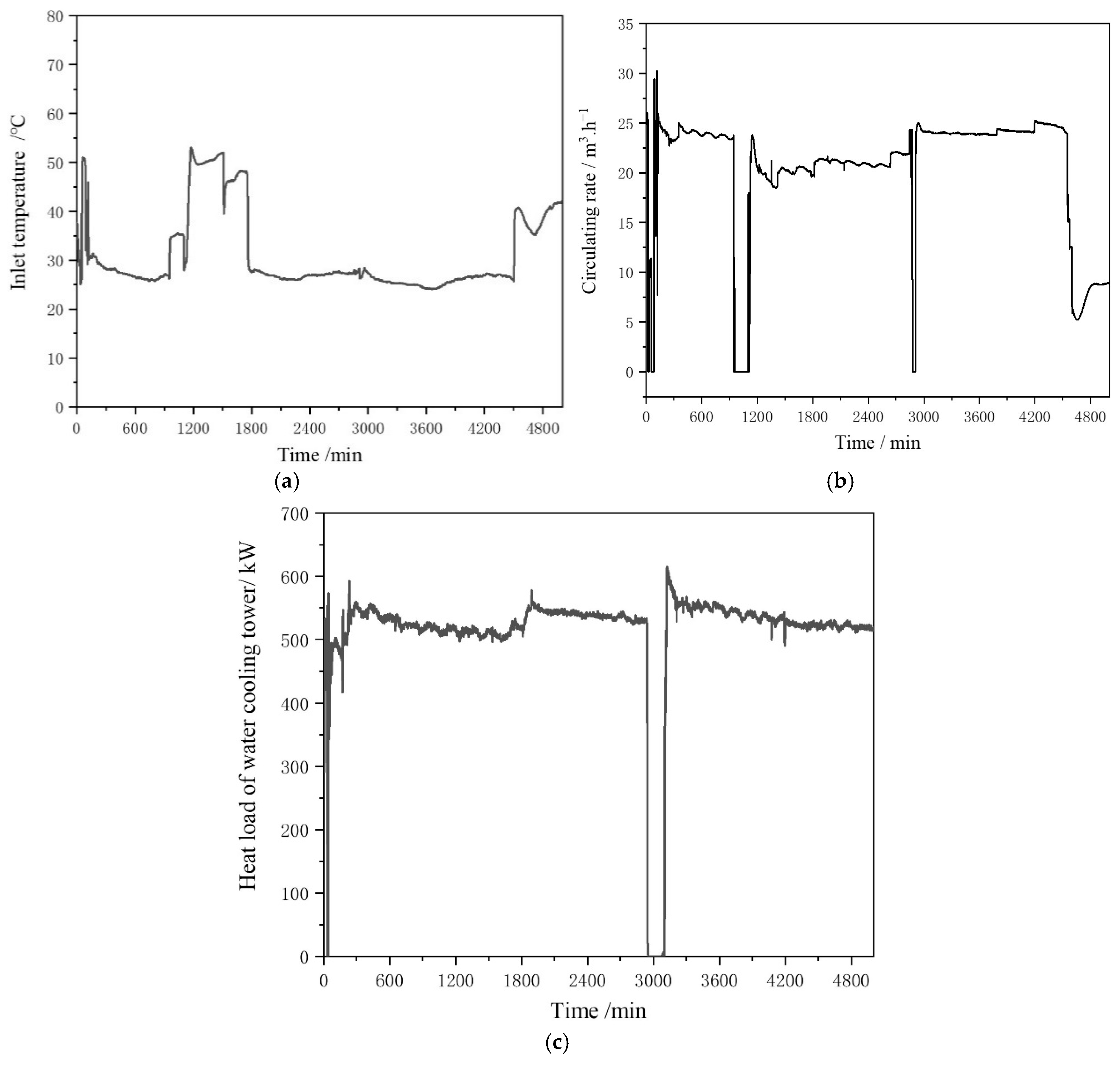

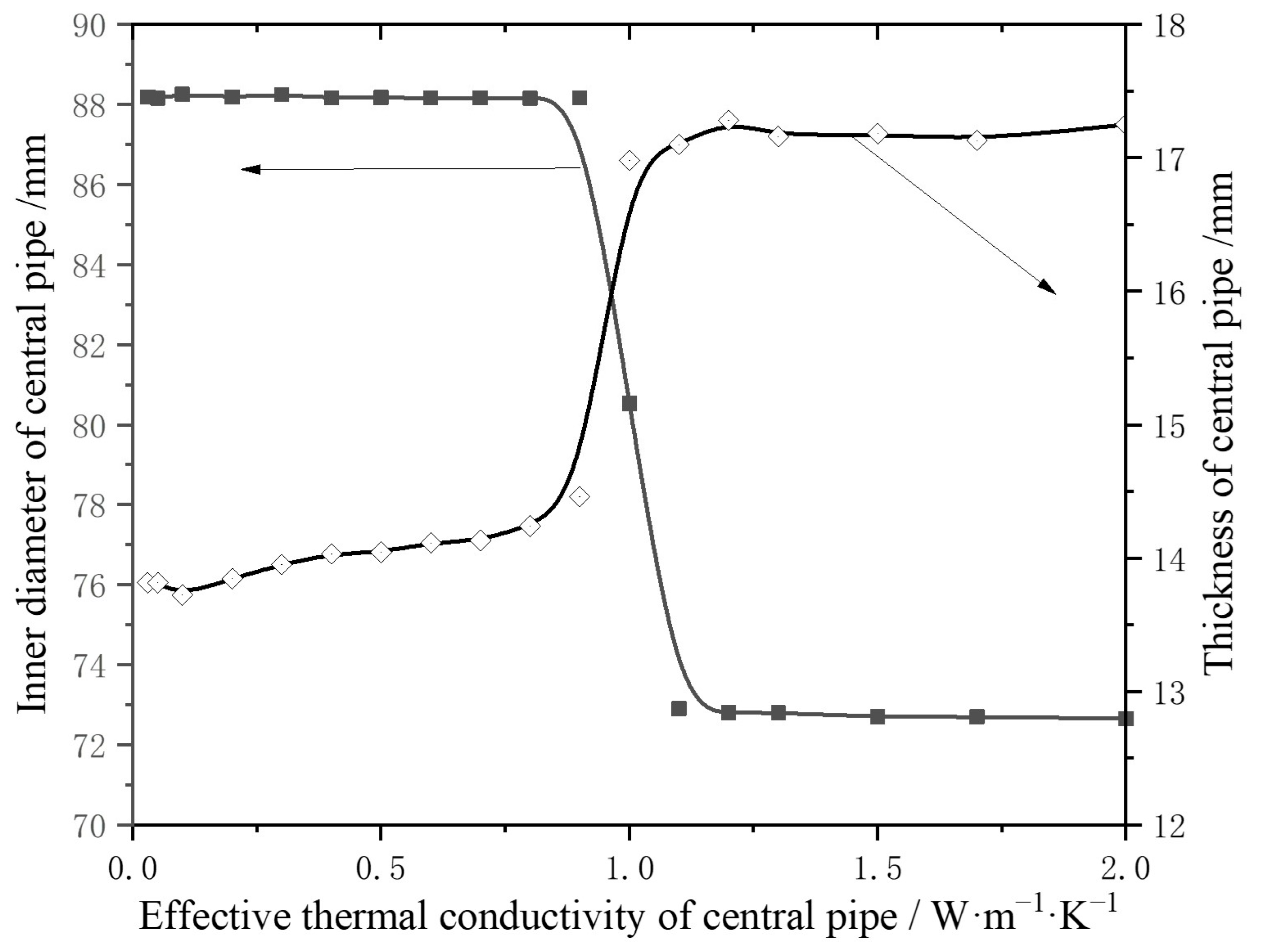




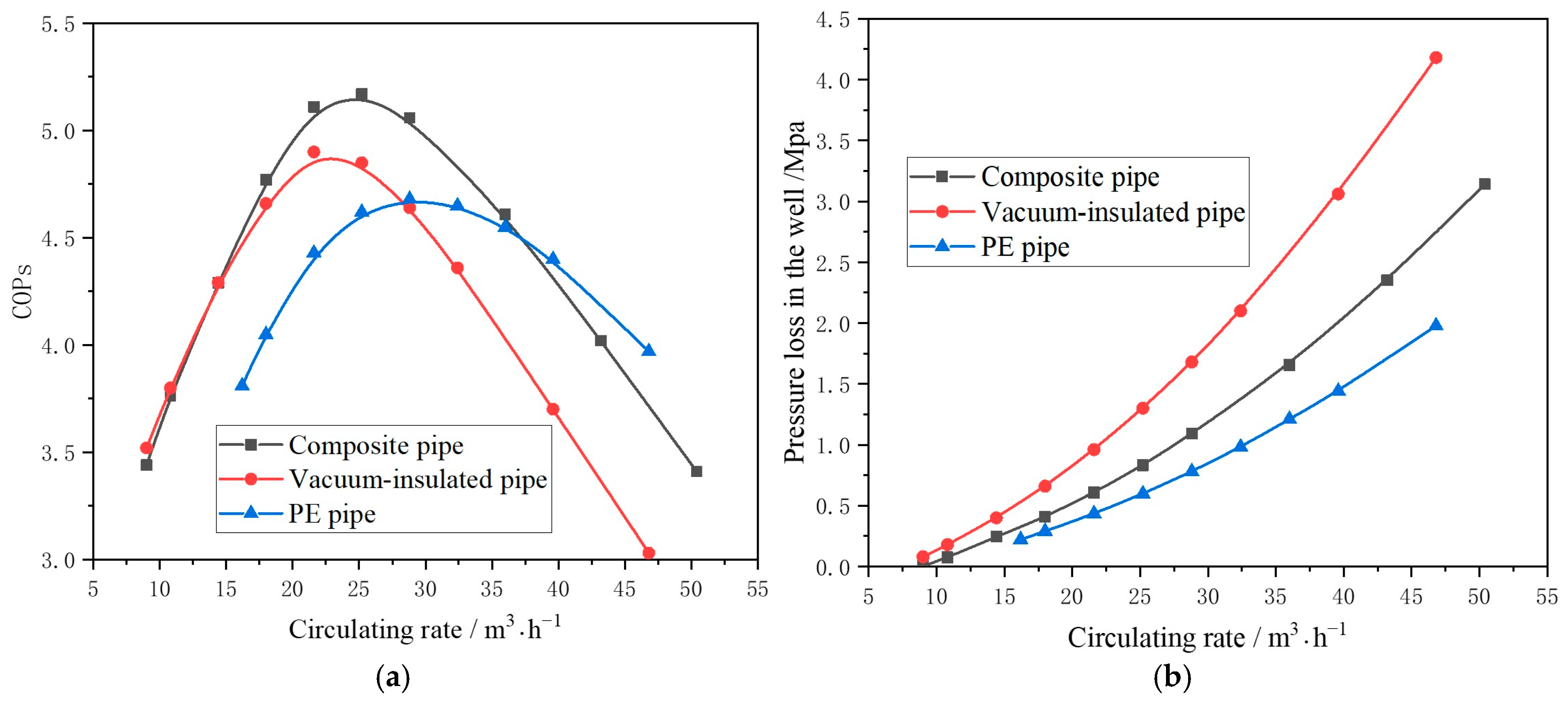
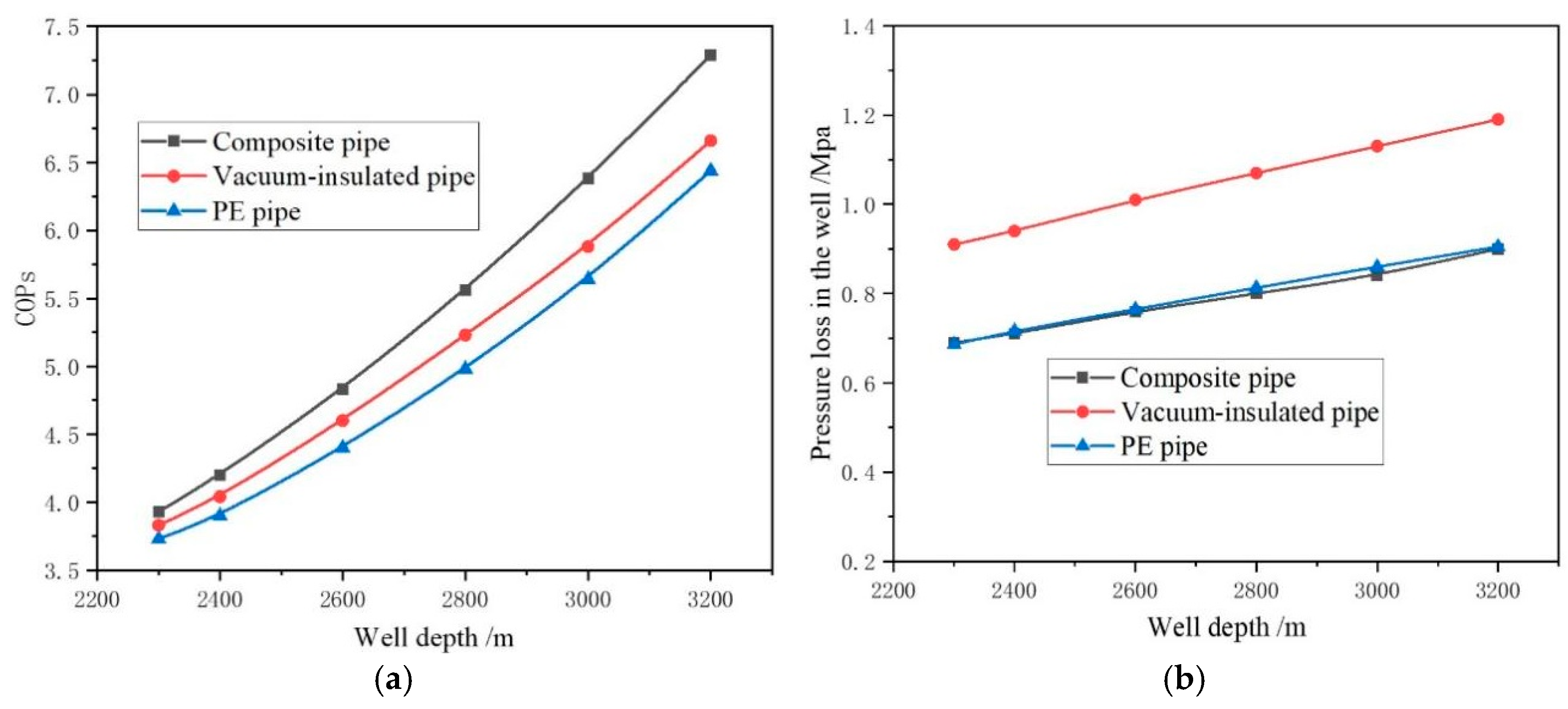
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Wellbore depth, m | 2700 | Measured formation temperature gradient, °C/100 m | 3.1 |
| Borehole diameter, mm | 222 | Circulating water flow, m3/h | 24 |
| Outer diameter of casing, mm | 177.8 | Heating load, kW | 400 |
| Inner diameter of casing, mm | 159.4 | Heating water temperature, °C | 45 |
| Cementing | Class G |
| Num. | dti | δt | λt | COPs (Calculated) | Num. | dti | δt | λt | COPs (Calculated) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 74 | 20 | 1.26 | 4.16 | 19 | 74 | 10 | 0.20 | 4.81 |
| 2 | 78 | 10 | 0.03 | 5.07 | 20 | 78 | 14 | 1.26 | 4.08 |
| 3 | 82 | 14 | 0.20 | 4.85 | 21 | 82 | 18 | 0.03 | 5.24 |
| 4 | 86 | 20 | 3.16 | 3.64 | 22 | 74 | 12 | 3.16 | 3.59 |
| 5 | 90 | 12 | 0.08 | 5.05 | 23 | 78 | 16 | 0.08 | 5.02 |
| 6 | 94 | 16 | 0.50 | 4.47 | 24 | 82 | 20 | 0.50 | 4.78 |
| 7 | 86 | 10 | 0.50 | 4.68 | 25 | 86 | 16 | 1.26 | 4.08 |
| 8 | 90 | 14 | 3.16 | 3.51 | 26 | 90 | 20 | 0.03 | 5.12 |
| 9 | 94 | 18 | 0.08 | 4.82 | 27 | 94 | 12 | 0.20 | 4.95 |
| 10 | 74 | 20 | 0.08 | 4.91 | 28 | 86 | 14 | 0.08 | 5.17 |
| 11 | 78 | 12 | 0.50 | 4.66 | 29 | 90 | 18 | 0.50 | 4.83 |
| 12 | 82 | 16 | 3.16 | 3.68 | 30 | 94 | 10 | 3.16 | 3.52 |
| 13 | 86 | 18 | 0.20 | 4.88 | 31 | 86 | 12 | 0.08 | 5.23 |
| 14 | 90 | 10 | 1.26 | 3.50 | 32 | 90 | 16 | 0.20 | 5.15 |
| 15 | 94 | 14 | 0.03 | 5.16 | 33 | 94 | 20 | 1.26 | 3.75 |
| 16 | 74 | 16 | 0.03 | 5.08 | 34 | 74 | 14 | 0.50 | 4.43 |
| 17 | 78 | 20 | 0.20 | 5.13 | 35 | 78 | 18 | 3.16 | 3.67 |
| 18 | 82 | 12 | 1.26 | 3.87 | 36 | 82 | 10 | 0.08 | 5.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Zhao, Z.; Guan, Z.; Lv, J.; Cui, L. Development and Performance Evaluation of Central Pipe for Middle-Deep Geothermal Heat Pump Systems. Energies 2025, 18, 3713. https://doi.org/10.3390/en18143713
Zhang X, Zhao Z, Guan Z, Lv J, Cui L. Development and Performance Evaluation of Central Pipe for Middle-Deep Geothermal Heat Pump Systems. Energies. 2025; 18(14):3713. https://doi.org/10.3390/en18143713
Chicago/Turabian StyleZhang, Xiong, Ziyan Zhao, Zhengrong Guan, Jiaojiao Lv, and Lu Cui. 2025. "Development and Performance Evaluation of Central Pipe for Middle-Deep Geothermal Heat Pump Systems" Energies 18, no. 14: 3713. https://doi.org/10.3390/en18143713
APA StyleZhang, X., Zhao, Z., Guan, Z., Lv, J., & Cui, L. (2025). Development and Performance Evaluation of Central Pipe for Middle-Deep Geothermal Heat Pump Systems. Energies, 18(14), 3713. https://doi.org/10.3390/en18143713






