Rock Physics Characteristics and Modeling of Deep Fracture–Cavity Carbonate Reservoirs

Abstract

The deep carbonate reservoirs in the Tarim Basin, Xinjiang, China, are widely developed with multi-scale complex reservoir spaces such as fractures, pores, and karst caves under the coupling of abnormal high pressure, diagenesis, karst, and tectonics and have strong heterogeneity. Among them, fracture–cavity carbonate reservoirs are one of the main reservoir types. Revealing the petrophysical characteristics of fracture–cavity carbonate reservoirs can provide a theoretical basis for the log interpretation and geophysical prediction of deep reservoirs, which holds significant implications for deep hydrocarbon exploration and production. In this study, based on the mineral composition and complex pore structure of carbonate rocks in the Tarim Basin, we comprehensively applied classical petrophysical models, including Voigt–Reuss–Hill, DEM (Differential Effective Medium), Hudson, Wood, and Gassmann, to establish a fracture–cavity petrophysical model tailored to the target block. This model effectively characterizes the complex pore structure of deep carbonate rocks and addresses the applicability limitations of conventional models in heterogeneous reservoirs. The discrepancies between the model-predicted elastic moduli, longitudinal and shear wave velocities (Vp and Vs), and laboratory measurements are within 4%, validating the model’s reliability. Petrophysical template analysis demonstrates that P-wave impedance (Ip) and the Vp/Vs ratio increase with water saturation but decrease with fracture density. A higher fracture density amplifies the fluid effect on the elastic properties of reservoir samples. The Vp/Vs ratio is more sensitive to pore fluids than to fractures, whereas Ip is more sensitive to fracture density. Regions with higher fracture and pore development exhibit greater hydrocarbon storage potential. Therefore, this petrophysical model and its quantitative templates can provide theoretical and technical support for predicting geological sweet spots in deep carbonate reservoirs.

1. Introduction

Carbonate rocks constitute only 20% of sedimentary rocks globally, yet carbonate reservoirs hold significant exploration potential, containing over 70% of global hydrocarbon resources and contributing to 60% of total production [1]. With the gradual development of shallow and medium-deep oil and gas resources, the exploration and development of deep and ultra-deep carbonate reservoirs have become a new direction and key area for the development of the oil and gas industry [2]. Under the coupling of abnormal high pressure, diagenesis, karst, and tectonics, deep carbonate reservoirs are widely developed with multi-scale complex reservoir spaces such as fractures, pores, and karst caves and have strong heterogeneity [3]. Fractures are elongated and narrow and formed by carbonate rocks under diagenesis and tectonics, and the density of the fractures is usually less than 0.1. The fracture development of carbonate rocks is controlled by the characteristics of its medium-brittle minerals and tectonic stresses (e.g., fault activity, differential compaction). Compared with clastic rocks, carbonate rocks are more prone to fracture formation during tectonic deformation, but their widely distributed nonfractured tight carbonate rocks also indicate that the degree of fracture development is closely related to the local stress field and diagenesis [3,4]. Although fractures have limited reservoir capacity for oil and gas, they are important seepage channels that greatly improve the flow capacity of oil and gas. The pores of carbonate reservoirs are usually divided into primary pores related to the rock structure formed during deposition and dissolved pores dissolved after deposition, and primary pores are usually not developed under strong compaction and cementation in deep and ultra-deep reservoirs [3,4,5]. Karst caves, predominantly formed by late-stage karstification, result from the dissolution-induced enlargement of pre-existing pores. The karst cave is an important space of the reservoir and has a good oil and gas storage capacity. Generally, carbonate reservoirs can be divided into fractured reservoirs, porous reservoirs, cavity reservoirs, and fracture–cavity reservoirs according to the different combinations of reservoir spaces. The deep and ultra-deep carbonate reservoirs in the Tarim Basin contain abundant oil and gas resources, among which the fracture–cavity carbonate reservoirs are an important part of production and development [3]. These kinds of reservoir karst caves or dissolution pores are connected with fractures to form the main reservoir space and permeability channel, which has great potential for exploration and development.

Petrophysical characteristics primarily describe the elastic properties of rocks and fluids, serving as a critical bridge between reservoir physical parameters (e.g., porosity, permeability) and seismic attributes. A thorough understanding of the petrophysical behavior of fracture–cavity carbonate reservoirs provides mechanistic insights and theoretical foundations for log interpretation and geophysical prediction in deep reservoirs, which is pivotal for advancing deep carbonate hydrocarbon exploration [5,6,7,8,9,10]. In terms of petrophysical modeling, traditional petrophysical models (such as the Xu–White [11] model) are based on the assumption of homogeneous pores and do not consider the multi-scale coupling effects of fractures and dissolution holes in ultra-deep carbonate rocks and the influence of a high-temperature and high-pressure environment on elastic parameters. In this study, Differential Effective Medium (DEM) theory was introduced to superimpose the contributions of dissolution holes and fractures step by step, which effectively solved the characterization problem of the complex pore structure of carbonate rocks. Generally, porosity is high, and elastic properties are mainly related to porosity, pore structure, cementation and diagenetic history, fluid type, etc. [8,9,10]. These models have certain limitations when applied to ultra-deep carbonate reservoirs. Deep carbonate reservoirs are subjected to intense compaction and cementation, and primary pores are usually not developed [3,4,5]. They are faced with a complex geological environment of abnormal pore pressure and stress field and present different petrophysical and elastic properties from those of the shallow layer [7]. The Xu–White model, designed for sandstone reservoirs, employs DEM theory to simulate elastic properties [11] but struggles with carbonates due to their intricate pore networks. To address this, Xu and Payne [12] integrated the Kuster–Toksöz (KT) model and DEM theory, developing the Xu–Payne model for carbonates. This model incorporates mineralogical components (e.g., calcite, dolomite, clay) and pore types (intergranular pores, karst cavities, fractures) but inadequately quantifies the volumetric partitioning of individual pore systems. Zhang et al. [13] extended the Xu–Payne model to accommodate carbonate reservoirs with diverse mineralogy and high clay content. Similarly, Sun et al. [14] applied a DEM–Gassmann integrated approach to calculate pore-type volume ratios in complex carbonates, and Zhao et al. [15] quantified pore distributions using well–seismic data fusion. In general, these models leverage equivalent medium theories to elucidate how complex pore structures modulate elastic properties [13,14,15], proving effective for medium- to high-porosity carbonates at shallow to moderate depths; however, there are issues such as dealing with complex lithology, describing reservoir spaces, and the imprecise characterization of the porosity volume fraction for each type of reservoir space. There is still a lack of systematic research on the petrophysical modeling of complex reservoir spaces in deep carbonate reservoirs.

Therefore, this study focuses on the mineral composition and complex pore structure of deep to ultra-deep fracture–cavity carbonate reservoirs in the Tarim Basin. The rock physics workflow involves four key steps: Firstly, the Voigt–Reuss–Hill (VRH) model was applied to estimate the elastic moduli of the mineral matrix, considering calcite, dolomite, and clay compositions. Secondly, fracture and cavity geometries were quantified using fracture density parameters. Then, the DEM–Hudson integrated model was employed to simulate the elastic properties of the dry rock skeleton, incorporating multi-scale pores and fractures. Moreover, Wood’s equation and Gassmann’s theory were combined to predict the elastic response of fluid-saturated rock. The proposed model was rigorously validated against extensive laboratory measurements and well log datasets. This study significantly advances the mechanistic understanding of heterogeneous carbonate reservoirs in the Tarim Basin while providing a transferable workflow to optimize hydrocarbon exploration in analogous deep-play basins worldwide, thereby bridging critical gaps between academic research and industrial applications.

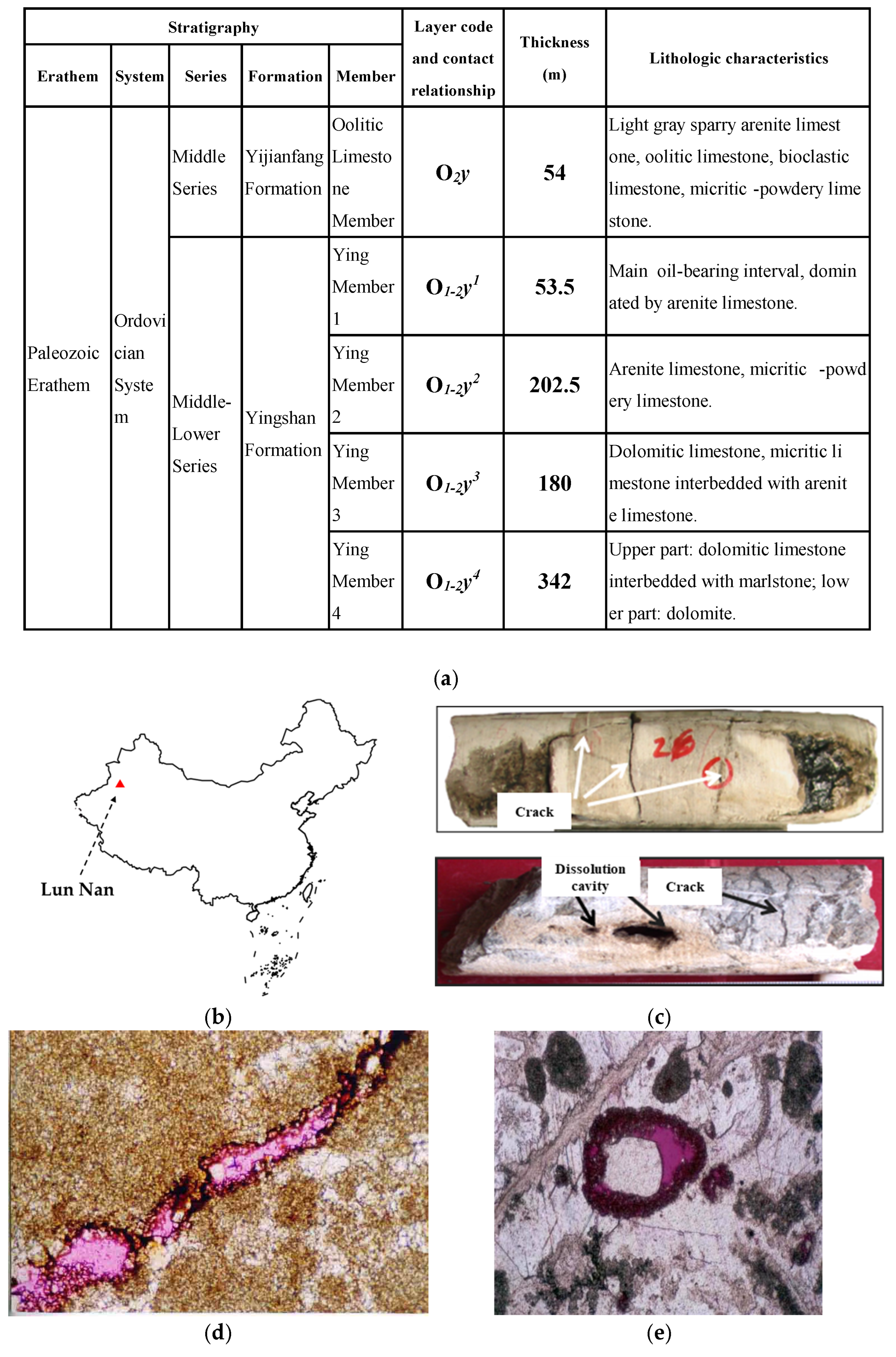
2. Basic Physical Characteristics of Reservoir Samples in Study Area

The Tarim Basin, China’s largest inland basin, is bounded by the South Tianshan Mountains to the north, Kunlun Mountains to the south, and Altun Mountains to the southeast. It represents a large, superimposed basin formed by the tectonic stacking of basins from multiple geological periods and diverse genetic origins. The basin’s interior comprises 12 tectonic units, categorized into 5 uplifts, 6 depressions, and 1 slope: Kuqa Depression, Tabei (North Tarim) Uplift, Awati Depression, Shuntuoguole Low Uplift, Manggar Depression, Bachu Uplift, Tazhong (Central Tarim) Uplift, Tadong (East Tarim) Uplift, Maigaiti Slope, Tanggubas Depression, Southwest Depression, and Southeast Depression [16]. Deep to ultra-deep carbonate fracture–cavity reservoirs are predominantly distributed in structural units such as the northern slope of the Tazhong Uplift, Shuntuoguole Low Uplift, northern slope of the Tabei Uplift, and Maigaiti Slope. This study area is located in the central part of the Lun Nan Uplift in the Tarim Basin, Xinjiang, China, covering an area of approximately 498.7 km². It is bordered to the east by the Lungudong gas field and to the south by the Tahe oilfield and is part of the rich hydrocarbon system of the Huan Lun Nan–Tahe–Halahatang depression. The sample was taken from a chamber located at a depth exceeding 6000 m. The main stratigraphy of the region includes the Quaternary, Neogene, Paleogene, Cretaceous, Jurassic, Triassic, Carboniferous, Ordovician, and Cambrian systems, with the Silurian, Devonian, and Permian systems generally missing. Controlled by ancient uplifts, the Ordovician system has undergone erosion and features the development of carbonate rock karst landforms, making it one of the primary oil-bearing strata in the Lunggu region. Under the coupled effects of abnormal high pressure, diagenesis, karstification, and tectonic activity, these reservoirs exhibit multi-scale heterogeneous pore systems—including fractures, dissolution-enhanced pores, and karst cavities—resulting in pronounced heterogeneity. Fracture–cavity carbonate reservoirs constitute a critical productive interval. Figure 1 displays representative core photographs and cast thin sections from deep carbonate reservoirs. Core observations highlight well-developed fracture networks dominated by high-angle (>60°) and subhorizontal fractures, alongside partially filled dissolution cavities with visible hydrocarbon staining on fracture surfaces and within cavities. Thin section analysis reveals a pore system dominated by intergranular and intragranular dissolution pores, interconnected by dissolution-enhanced microfractures. This interconnected pore–fracture network forms the primary storage space and permeability pathways, underpinning the reservoir’s exploration potential.

Figure 2a presents the porosity distribution of core samples from the study block, measured via helium porosimetry. Over 50% of samples exhibit porosities between 0.5 and 1.8%, with a median of 1.12% and an arithmetic mean of 1.6%. Figure 2b shows the permeability distribution obtained by pulse decay permeability measurements: more than half of samples have permeabilities < 0.1 mD (median = 0.05 mD), while the mean permeability reaches 4.82 mD, indicating a dual-porosity system where fractures locally enhance flow capacity. Figure 3 displays the mineral composition of carbonate samples analyzed by X-ray diffraction (XRD). The dominant mineral is calcite (97 wt%), with minor components including quartz, dolomite, clay, and pyrite.

Table 1. Mineral composition and petrophysical properties of reservoir samples.

Average Depth	Average Porosity	Average Permeability	Average Density	Main Mineral Content (%)
				Calcite	Dolomite	Quartz	Clay
7200 m	1.6%	4.82 mD	2.68 g·cm−3	96.66	1.58	1.18	0.58

summarizes the key petrophysical properties of the reservoir samples. In general, a high calcite content (96.66%) corresponds to a brittleness index (BI) of 55 ± 5 [9], favoring fracture development under tectonic stress. Fracture density strongly correlates with proximity to faults (R² = 0.76) [7], confirming tectonic control on fracture networks. Reservoir heterogeneity arises from complex fracture–cavity architectures. Seismically similar fracture–cave bodies show divergent internal fillings (e.g., clay vs. calcite cement), and fluid distributions (oil/water contacts) remain poorly constrained by current seismic techniques. To address these challenges, high-resolution petrophysical characterization integrating fracture–cavity geometry analysis, saturation-dependent rock physics modeling, and machine learning-driven seismic inversion is urgently required to improve prediction accuracy for undeveloped reserves.

3. Rock Physics Modeling Methods

The petrophysical heterogeneity of ultra-deep carbonate reservoirs arises from two primary factors: First, at depths exceeding 7000 m, elevated pressures and temperatures (>180 °C) induce mineral elastic modulus variations and fluid compressibility changes through pressure solution and thermal cracking. Second, strong compaction suppresses primary porosity, resulting in a dual-porosity system dominated by fractures (α < 0.01) and dissolution cavities (0.01 < α < 0.1), fundamentally distinct from shallow reservoirs with intergranular porosity. In the Tarim Basin’s ultra-deep carbonates, hydrocarbon accumulation relies on interconnected fracture–cavity networks formed by karstification and tectonic stress. Figure 4 conceptualizes these systems as ellipsoidal inclusions within an equivalent medium framework. Here, crack density (α)—defined as the short-to-long axis ratio of pores/cavities—quantifies pore geometry, with fractures (α ≪ 0.01) and cavities (α ≥ 0.01) differentiated by threshold α = 0.01 [17]. The elastic properties of carbonate rocks are characterized by three equivalent parameters: matrix, skeleton, and pore fluid. To model these properties, we developed a hierarchical workflow comprising four key steps:

(1)

Calculating the mineral matrix modulus via VRH averaging.

(2)

Calculating the dry rock frame modulus via DEM theory.

(3)

Conducting fluid substitution using Wood’s equation and Gassmann’s theory.

(4)

Demonstrating fracture–cavity coupling via Hudson’s model.

While the Xu–Payne model—designed for reservoirs with intergranular-dominated porosity (α > 0.1)—fails to capture fracture–cavity systems (α < 0.1) prevalent in ultra-deep carbonates [5], our approach addresses this limitation. By sequentially superimposing dissolution cavities (α = 0.1) and fractures (α = 0.001) through DEM modeling, we resolve the traditional model’s inadequacy in low-porosity reservoirs [14]. This stepwise incorporation of pore types enables the quantitative characterization of complex pore structures. As illustrated in Figure 5, the petrophysical modeling process involves three distinct stages:

(1)

The calculation of the matrix modulus of carbonate reservoirs.

(2)

The calculation of the skeletal modulus of dry rock in carbonate reservoirs.

(3)

The calculation of the modulus of fluid-saturated rocks [18].

Figure 4. Carbonate sample crack and dissolution pore model.

Figure 4. Carbonate sample crack and dissolution pore model.

Figure 5. Fracture–dissolution hole carbonate rock petrophysical modeling process.

Figure 5. Fracture–dissolution hole carbonate rock petrophysical modeling process.

3.1. Elastic Modulus of Rock Matrix

The equivalent elastic modulus and related parameters of rocks can be calculated using the Voigt–Reuss–Hill (VRH) averaging model, which requires input data on the volume fractions and elastic properties of individual mineral components [19]. The Voigt limit is sometimes referred to as the equal strain average, as it provides the ratio of average stress to average strain given the assumption of equal strain among the constituent components. The Reuss limit is sometimes referred to as the equal stress average, as it provides the ratio of average stress to average strain under the assumption of equal stress among the constituent components. The mathematical formulation is expressed as follows:

$$M_{VRH}={\displaystyle \frac{{\displaystyle \sum _{i=1}^N{f}_i{M}_i+{\displaystyle \sum _{i=1}^N\frac{f_i}{M_i}}}}{2}}$$

(1)

Let f_i and M_i denote the volume fraction and bulk/shear modulus of the i-th mineral component, respectively, Gpa. M_VRH is the bulk modulus or shear modulus of carbonate rock matrix minerals, Gpa.

3.2. Modulus of Elasticity of Rock Skeletons

For fracture–cavity carbonate reservoirs, the petrophysical properties are dominantly controlled by two types of pore systems: fractures and dissolution cavities. The Self-Consistent Approximation (SCA) model is unsuitable for modeling penny-shaped fractures (low-aspect-ratio cracks), whereas the Kuster–Toksöz (KT) model effectively describes fracture-dominated reservoirs with low porosity and known aspect ratios.

In modeling ultra-deep carbonate fracture–cavity systems, dissolution cavities exhibit a minimal impact on the rock matrix elastic moduli compared to fractures. To address this, we employ Differential Effective Medium (DEM) theory, progressively incorporating two inclusion phases—dissolution cavities (α ≥ 0.01) and fractures (α < 0.01)—into the solid mineral matrix to simulate the dry rock frame modulus. The coupled differential equations governing the equivalent elastic moduli (bulk modulus K*_(y)) and (shear modulus μ*_(y)) of the fracture–cavity carbonate reservoir are expressed as follows:

$$(1-y){\displaystyle \frac{d}{dy}}\left[K_{(y)}^{*}\right]={(K_2-K^{*})P}_{(y)}^{(*2)}$$

(2)

$$(1-\mathrm{y}){\displaystyle \frac{d}{dy}}\left[{\mu }_{(y)}^{*}\right]=\left({\mu }_2-{\mu }^{*}\right)Q_{(y)}^{(*2)}$$

(3)

The initial conditions are defined as the following:

$$K^{*}(0)=K_1 {\mu }^{*}(0)={\mu }_1$$

K₁ and μ₁ represent the bulk modulus and shear modulus of the host matrix (primary phase material); that is, when the content of dissolved pores and fractures is zero, these refer to the bulk modulus and shear modulus, unit: GPa. The inclusion phase (e.g., dissolution holes and fractures) is characterized by K₂ (bulk modulus) and μ₂ (shear modulus), and the addition of dissolution pores and fractures in the rock matrix affects the bulk modulus and shear modulus, unit: GPa. When the integral number of the containing object is y, the geometric factors P and Q need to be determined based on the medium environment with an equivalent modulus (K*, μ*), where the superscript *2 specifically refers to the equivalent modulus medium as the background of the inclusion when the parameter is calculated, which is dimensionless.

3.3. Modeling of Rock Anisotropy

Rock heterogeneity describes the spatial inhomogeneity of material properties such as elastic moduli and density. This manifests in the uneven distribution of pores, fractures, and mineral constituents within rock formations. Notably, fracture networks—defined by their spatial distribution (location, orientation, and density)—constitute a fundamental type of heterogeneity. The Hudson model (Hudson, 1981) [20] employs effective medium theory to upscale microscopic fracture heterogeneity into macroscopic anisotropic parameters. It achieves this by replacing the spatially variable fracture distribution with a homogeneous but anisotropic equivalent medium. Consequently, the model indirectly characterizes the original heterogeneous structure through its anisotropic representation.

The key fracture parameters required for the Hudson model include the following: (1) fracture density (ε), which controls the degree of heterogeneity, and (2) fracture orientation, which governs the spatial pattern of heterogeneity.

The model utilizes a perturbation approach: First-order approximation (Equation (4)) applies when ε < 0.1. Second-order correction (Equation (5)) becomes necessary at higher fracture densities (ε ≥ 0.1).

$$c_{ijkl}^{*}=c_{ijkl}^0+\epsilon \left[U_1{a}_{ijkl}^{(1)}+U_3{a}_{ijkl}^{(3)}\right]$$

(4)

$$c_{ijkl}^{*}=c_{ijkl}^0+\epsilon \left[U_1{a}_{ijkl}^{(1)}+U_3{a}_{ijkl}^{(3)}\right]+{\epsilon }^2\left[U_1{b}_{ijkl}^{(1)}+U_3{b}_{ijkl}^{(3)}\right]$$

(5)

$$U_1={\displaystyle \frac{4(\lambda +2\mu )}{3(\lambda +\mu )}},U_3={\displaystyle \frac{16(\lambda +2\mu )}{3(\lambda +4\mu )}}$$

(6)

$$\lambda =K-{\displaystyle \frac{2}{3}}\mu$$

(7)

$c_{ijkl}^0$ is the isotropic stiffness tensor of the intact matrix, ε is fracture density, U₁ and U₃ are the normal and tangential compliance parameters of fractures, $a_{ijkl}^{(1)}$ and $a_{ijkl}^{(3)}$ are fourth-order tensors dependent on fracture orientation (normal vector n), $b_{ijkl}^{(1)}$ and $b_{ijkl}^{(3)}$ are second-order perturbation tensors, λ is Lame’s constant, and K and μ are the bulk modulus and shear modulus of the dry rock frame, GPa.

3.4. Elastic Modulus Modeling for Fluid-Saturated Rocks

In a fluid suspension or mixture, Wood’s equation (Wood, 1955 [5]) provides accurate predictions of acoustic wave velocities when the scale of inhomogeneity is smaller than the wavelength. This formulation models the elastic behavior of mixed fluids under non-equilibrium pressure conditions, with the effective bulk modulus K_fl and density ρ of the fluid mixture characterized as follows:

$${\displaystyle \frac{1}{{{\displaystyle K}}_R}}={\displaystyle {\sum }_{i=1}^N\frac{{{\displaystyle f}}_i}{{{\displaystyle K}}_i}}$$

(8)

$$\rho ={\displaystyle {\sum }_{i=1}^N{f}_i{\rho }_i}$$

(9)

where f_i, K_i, and ρ_i represent the volume fraction, bulk modulus (GPa), and density of the i-th fluid component, respectively [19].

Gassmann’s equation demonstrates that pore fluids affect the bulk modulus of a rock but leave its shear modulus unchanged. This behavior arises from the fundamental mechanics of deformation: Volumetric deformation alters pore volume, inducing pore pressure changes that stiffen the rock matrix and increase the bulk modulus, which causes an increase in pore fluid pressure. Shear deformation, by contrast, preserves pore volume, making the shear modulus largely insensitive to fluid type or saturation. As a cornerstone of seismic petrophysics, Gassmann’s equation not only enables the simulation of elastic parameter variations under different fluid saturation scenarios but also enhances the interpretation of seismic data through fluid substitution modeling. The fluid substitution technique—predicting elastic property changes when altering pore fluid composition or saturation—remains one of Gassmann’s principal applications in hydrocarbon exploration.

$${\displaystyle \frac{{{\displaystyle K}}_S}{{{\displaystyle K}}_0-{{\displaystyle K}}_S}}={\displaystyle \frac{{{\displaystyle K}}_d}{{{\displaystyle K}}_0-{{\displaystyle K}}_d}}+{\displaystyle \frac{{{\displaystyle K}}_f}{\varphi \left({{\displaystyle K}}_0-{{\displaystyle K}}_f\right)}}$$

(10)

$${{\displaystyle \mu }}_s={{\displaystyle \mu }}_0$$

(11)

where K_d is the bulk modulus of dry rock, GPa; K_s is the bulk modulus of saturated rocks, GPa; K₀ is the bulk modulus of the matrix, GPa; K_f is the bulk modulus of fluid, GPa; μ_s is the shear modulus of saturated rock, GPa; μ₀ (GPa) is the shear modulus of dry rock; and φ is porosity.

Within the equivalent medium model, fractures and dissolution cavities are represented as ellipsoidal inclusions with varying aspect ratios to quantitatively characterize the complex pore structures of carbonate reservoirs [17]. Differential Effective Medium (DEM) theory was employed to model these two pore types. Given the low density of the rock matrix and high stiffness of dissolution cavities, the overall elastic behavior of the rock is predominantly governed by fracture content. To accurately capture this dependency, we adopted a sequential modeling approach: (1) first incorporating dissolution cavities into the matrix, followed by (2) superimposing fracture networks. The densities of these pore types (cavities and fractures) are quantified using Equation (12) [20].

$$C_r={\displaystyle \frac{3{\phi }_c}{4\times \pi \times {\alpha }_c}}$$

(12)

where α_c represents the aspect ratio of the dissolution hole or fracture, φ_c represents the porosity of the dissolution hole or fracture, and C_r represents the density of the dissolution hole or fracture.

Finally, according to Equation (13), we calculate the error between the calculated value and the true value obtained from the log.

$${\displaystyle \frac{\left|Predicted value-Well logging values\right|}{Well logging values}}\times 100\%=Error$$

(13)

The longitudinal wave and shear wave velocity of logging are obtained by acoustic logging. The speed of the wave is measured by emitting a sound wave using a sound transmitter in the well and then recording the propagation time of the wave through an acoustic receiver.

4. Results

Based on measured sample porosity data, initial dissolution porosity parameters were calibrated. Through the established petrophysical workflow, a 3D petrophysical template (Figure 6) was developed for fracture–cavity carbonate reservoirs. This template quantitatively links seismic-derived elastic parameters (Ip and Vp/Vs ratio) to reservoir properties (water saturation and fracture density). Seismic inversion-derived elastic parameters enable the characterization of reservoir properties, providing critical insights for hydrocarbon exploration. In Figure 6, the horizontal axis represents P-wave impedance, which exhibits high sensitivity to fracture density, and the vertical axis represents the Vp/Vs ratio, demonstrating stronger sensitivity to fluid. Dry cores display lower Vp/Vs ratios, water-saturated samples show elevated Vp/Vs ratios, and the disparity in Vp/Vs ratios between dry and water-saturated states diminishes as fracture density decreases [21]. The solid black line denotes water saturation ranging from 0% to 100%, while the pink dashed line illustrates the fracture density variation from 0 to 0.25. Under constant fracture density, both the Vp/Vs ratio and P-wave impedance increase with water saturation, as indicated by the trend in the solid black line in Figure 6. Under constant water saturation, an increase in fracture density leads to a reduction in both the Vp/Vs ratio and P-wave impedance, as indicated by the trend in the pink solid line in Figure 6.

Overall, both the P-wave impedance and Vp/Vs ratio exhibit positive correlations with water saturation but negative correlations with fracture density. A higher fracture density amplifies fluid effects on elastic properties. At low or zero fracture density, negligible fluid saturation eliminates differences between dry (gas-saturated) and water-saturated samples [22,23,24]. Higher water saturation reduces fracture density’s impact on the Vp/Vs ratio. At 80% water saturation, increased fracture density causes minimal Vp/Vs variation but significant P-wave impedance reduction [25,26,27,28]. Conversely, under low water saturation, fracture density strongly affects both Vp/Vs and Ip, as Vp/Vs is fluid-sensitive, while Ip is fracture-sensitive. Regions with higher fracture density correlate with enriched hydrocarbon reservoirs, enabling this petrophysical template to guide deep carbonate “sweet spot” prediction. These findings align with those of [5].

However, the model in Figure 6 primarily considers microfracture density and neglects dissolution pore variations. To address this, Differential Effective Medium (DEM) theory was applied to predict the skeletal elastic modulus by first adding dissolution porosity and then fracture porosity. Given the low overall porosity (<2%) and highly compacted matrix in the study area, the sequence of adding pores versus fractures has a minimal impact on equivalent elastic properties during DEM-based modeling [5]. Figure 7 presents a refined 5D petrophysical template that decouples the effects of fractures and dissolution pores on elastic parameters. The horizontal axis represents P-wave impedance, while the vertical axis shows the Vp/Vs ratio. Key trends include the following: The solid red line shows the water saturation, which varies from 0 to 80%. The green solid line shows the variation law of dissolved porosity, and its value changes from 0 to 2%. The solid blue line shows the fracture porosity, and its value varies from 0 to 2%. The sum of dissolution porosity and fracture porosity is 2%. Dissolution porosity and fracture porosity exhibit inverse trends: an increase in dissolution porosity reduces fracture porosity, while a decrease in dissolution porosity elevates fracture porosity. Similarly to Figure 6, under constant fracture porosity, increasing water saturation elevates both the Vp/Vs ratio and P-wave impedance (red solid line). Conversely, at fixed Sw, higher fracture porosity reduces Vp/Vs and Ip (blue solid line). Incorporating dissolution porosity, increased dissolution porosity (implying reduced fracture porosity) under constant Sw raises Vp/Vs and Ip (green curve). In general, water-saturated samples exhibit higher P-wave impedance and Vp/Vs ratios compared to dry samples. The Vp/Vs ratio is more sensitive to pore fluids, while Ip responds predominantly to fracture density. This model explicitly quantifies the distinct impacts of dissolution porosity and fracture density. The combined effects of fracture porosity, water saturation, and dissolution porosity govern the elastic properties, ultimately dictating the reservoir’s physical behavior.

In summary, the elastic properties of ultra-deep carbonate rocks are predominantly controlled by fractures, with fractures exerting a greater influence on rock elasticity than pores. Under constant total porosity, an increase in dissolution porosity reduces fracture porosity proportionally. Since wave velocities are highly sensitive to fractures but less responsive to stiffer pores, this leads to elevated P-wave (Vp) and S-wave (Vs) velocities. Although higher porosity slightly reduces rock density, the overall porosity remains low; thus, the velocity increase outweighs the density decrease, resulting in higher P-wave impedance as dissolution porosity increases (and fracture density decreases). Reduced fracture porosity significantly enhances Vp, thereby increasing the Vp/Vs ratio [29,30,31].

Additionally, rising water saturation (Sw) amplifies the Vp/Vs ratio. Water-saturated rocks exhibit consistently higher Vp/Vs ratios and Ip compared to dry rocks, with these parameters increasing progressively with Sw [32,33,34]. This phenomenon arises because pore fluids—largely incompressible—increase the bulk modulus and density of the rock while having a minimal impact on the shear modulus. Consequently, Vp rises significantly, whereas Vs remains relatively stable, driving the Vp/Vs ratio upward [21].

5. Discussion

This study integrates multiple petrophysical models—including Voigt–Reuss–Hill (VRH), Differential Effective Medium (DEM), Hudson, Wood, and Gassmann—to develop a fracture–dissolution pore petrophysical template for deep carbonate reservoirs in the Tarim Basin. The template explains the impacts of pore structure, fracture porosity, and fluid saturation on elastic moduli and velocity ratios (Vp/Vs). To validate the model’s reliability, predicted P- and S-wave velocities were compared against laboratory-measured data (Figure 8). The horizontal axis in Figure 8 represents measured elastic moduli and velocities, while the vertical axis shows model-predicted values. The red line denotes ideal 1:1 agreement between measurements and predictions. The results (Figure 9) demonstrate prediction errors below 4%, confirming the model’s accuracy.

Traditional models like the Xu–White and Kumar–Han approaches, designed primarily for shallow, homogeneous reservoirs, fail to characterize the dual fracture–dissolution pore systems in deep carbonates. In contrast, this study employs DEM–Hudson theory to simulate the progressive superposition of dissolution pores and fractures, effectively capturing the strong heterogeneity of ultra-deep carbonates and overcoming the limitations of conventional models. Compared to the DEM–Gassmann model by Sun et al. (2012) [14], this work further refines the fracture–pore coupling mechanism. By sequentially incorporating dissolution pores and fractures within the DEM framework, a five-dimensional petrophysical template is established, surpassing the constraints of traditional 2D templates. This advancement enables the comprehensive characterization of dissolution porosity, fracture porosity, water saturation, and other parameters, providing a robust theoretical foundation for reservoir parameter inversion.

The ultra-deep carbonate reservoirs in the Tarim Basin are controlled by “faulted karst bodies”, and the development degree of fractures and dissolution holes directly determines the reservoir and migration efficiency of oil and gas. The model in this paper shows that under the condition that the porosity of the study block is constant, the oil-bearing high-fracture-porosity area (such as the fault zone) has a high Vp/Vs ratio, while the gas-bearing areas of high fracture porosity have a low Vp/Vs ratio. In summary, petrophysical modeling and petrology scales are used to make use of seismic properties (e.g., wave impedance, VP/VS) to identify reservoir advantages in sweet spots, provided the key parameters [22].

Although the model showed good applicability in the deep carbonate rocks of the Tarim Basin, it still has the following limitations. The effects of temperature and pressure were not considered: For every 10 MPa increase in effective stress, the crack stiffness decreases by 8% [21], while high temperatures (>150 °C) reduce the calcite modulus by 12% [5]. Ultra-deep environments (>7000 m) may change the elastic modulus of minerals and pore fluid properties, but the current model does not consider the influence of temperature, which may underestimate the inelastic deformation of the actual reservoir. In addition, the pore structure was simplified to a certain extent, and the model considers the dissolved pores and fractures as idealized geometry, not taking into account fractures or dissolution holes. The connectivity of the network and the multi-scale coupling effect may affect the quantitative characterization of complex reservoir spaces [17].

6. Conclusions

(1). For the first time, the five parameters of dissolution porosity, fracture density, water saturation, the longitudinal and transverse wave velocity ratio, and wave impedance are co-characterized in the carbonate mineral composition and complex pore structure of the carbonate rocks in the study area of the Tarim Basin, breaking through the limitations of the traditional two-dimensional quantitative version. The DEM–Hudson model is used to realize the step-by-step superposition of dissolution pores and fractures, which solves the problem of multi-scale pore coupling and the strong heterogeneity characterization of ultra-deep and low-porosity reservoirs. Through the differential response of Vp/Vs and Ip, the occurrence law of fluids in fractures and dissolution pores is clarified. Based on the classical petrophysical theoretical models such as Voigt–Reuss–Hill, DEM (differential equivalent media), Hudson, Wood, and Gassmann, a fracture–cavity petrophysical model suitable for the study block is established, which effectively describes the complex pore structure of deep carbonate rocks. The applicability of the traditional model in heterogeneous reservoirs is solved. The error between the longitudinal and transverse wave velocity and elastic modulus predicted by the model and the measured data is less than 4%, which verifies the reliability of the model.

(2). The petrophysical template realizes the synergistic analysis and coupling of fracture porosity, dissolution porosity, and water saturation. The results show that with an increase in water saturation, the longitudinal and transverse wave velocity ratio and longitudinal wave impedance also increase with the same fracture density. Under the same water saturation condition, the fracture density increases, and the longitudinal and transverse wave velocity ratio and longitudinal wave impedance decrease. Overall, the longitudinal wave impedance and the longitudinal and transverse wave velocity ratio increase with an increase in water saturation and decrease with an increase in fracture density. The higher the fracture density, the greater the influence of the fluid in the fracture on the elastic properties of the reservoir sample. The larger the water saturation, the lesser the influence of fracture density on the velocity ratio of longitudinal and transverse waves. When the water saturation is low, the fracture density has a greater influence on the longitudinal and transverse wave velocity ratio and longitudinal wave impedance, and the longitudinal and transverse wave velocity ratio is more sensitive to the fluid, and the longitudinal wave impedance is more sensitive to the fracture density.

(3). The petrophysical model reveals the petrophysical characteristics of fracture–cavity carbonate reservoirs in the Tarim Basin, which can provide a theoretical basis for deep reservoir logging interpretation and geophysical prediction and is of great significance for deep oil and gas exploration and development. Of course, the model does not take into account the influence of temperature, and it is necessary to further combine high-temperature and high-pressure experiments with multi-scale digital core technology to improve the model parameter system and promote the efficient development of ultra-deep carbonate rock oil and gas resources.