A Method Based on CNN–BiLSTM–Attention for Wind Farm Line Fault Distance Prediction
Abstract
1. Introduction
2. Fault Location Principle for Cable–Overhead Hybrid Transmission Lines
2.1. Fault Data Extraction
2.2. Fault Section Location
- (1)
- An analysis of the wind farm configuration reveals that both the grid-connected step-up transformers and the collector line-connected step-up transformers of the wind turbines adopt Y-Δ connections. Under standard operational conditions, the system inherently lacks a zero-sequence current pathway.
- (2)
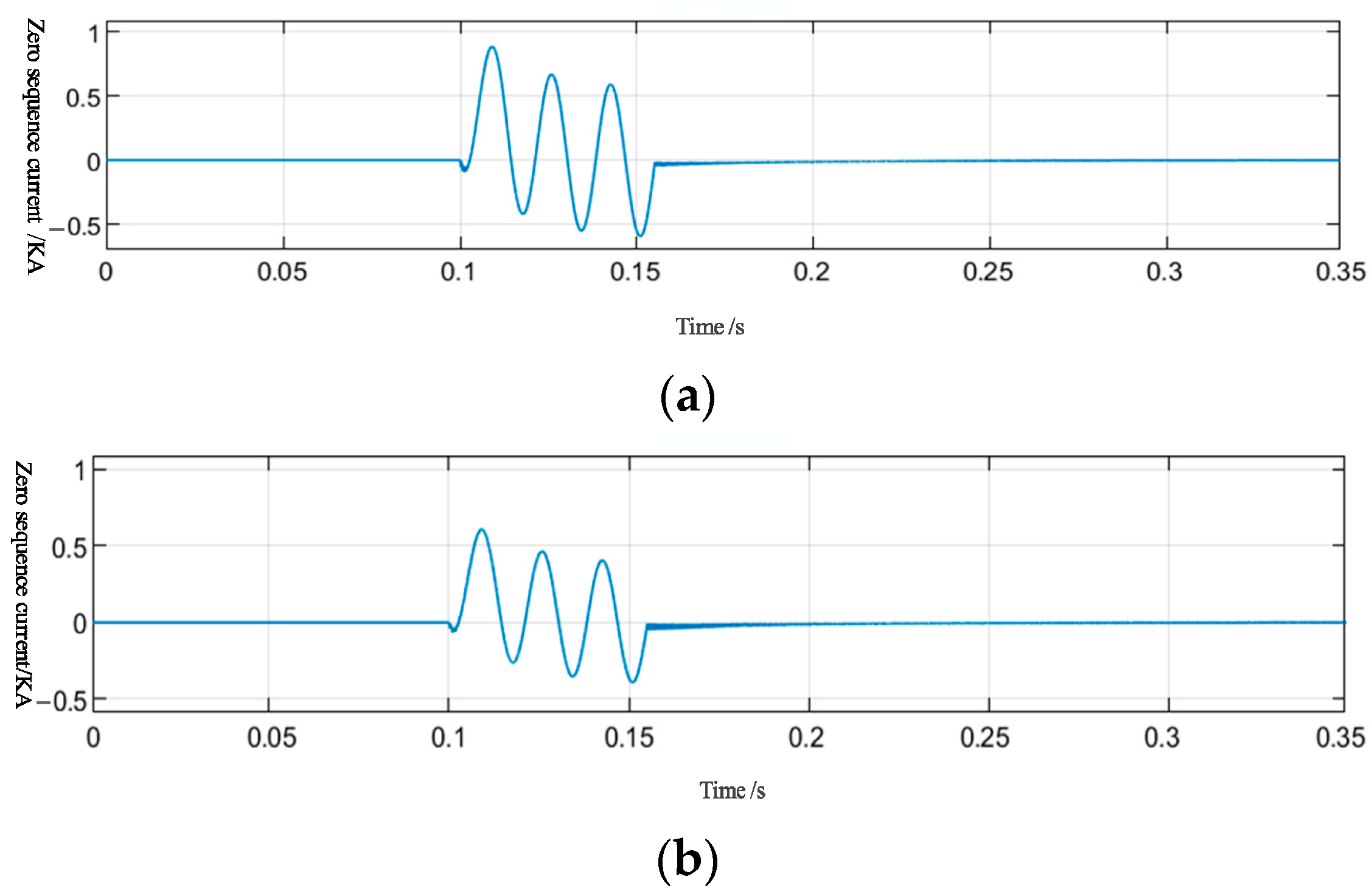
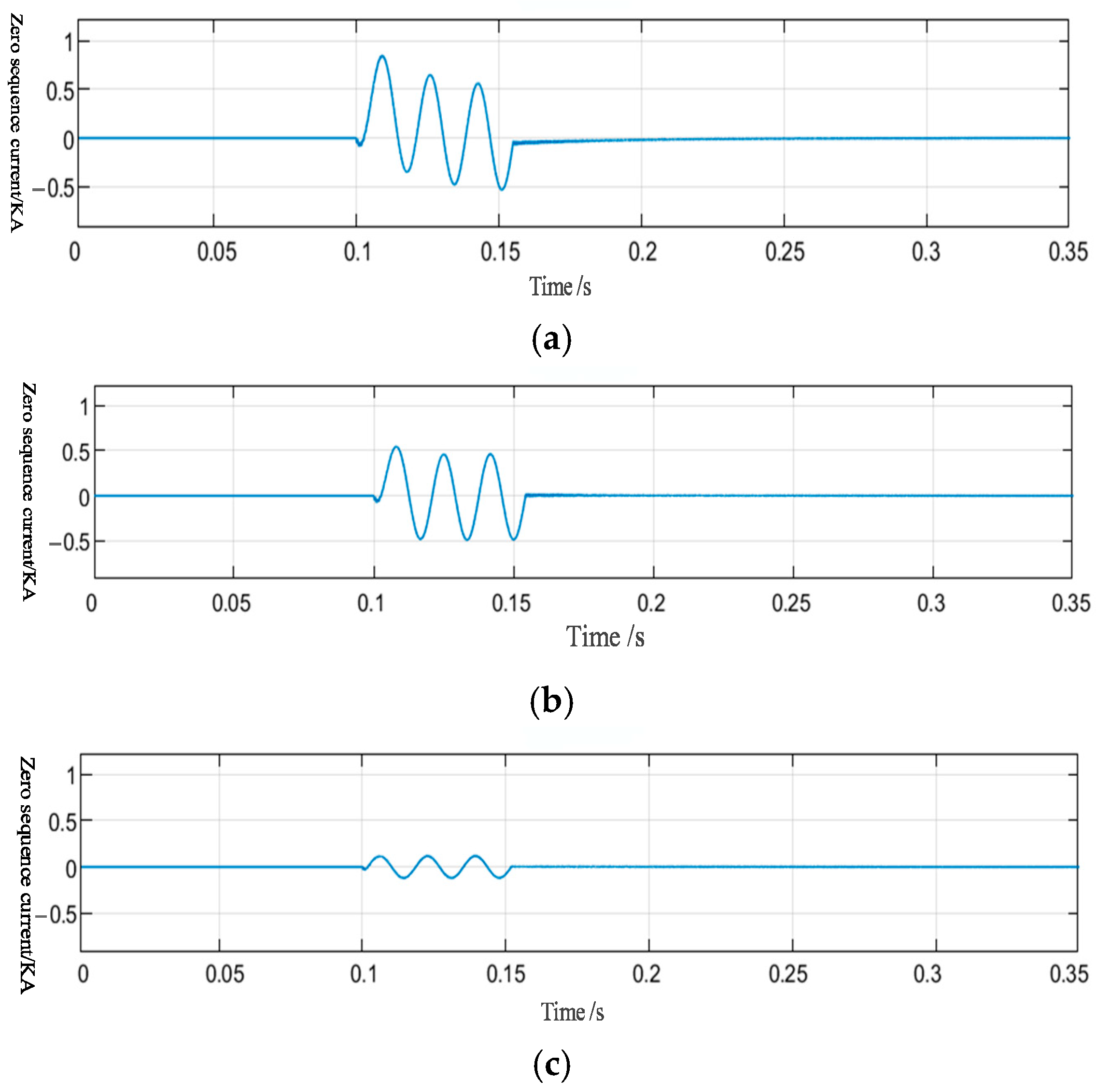
- During ground faults, zero-sequence currents propagate, originating at the fault locations and directed toward the main bus. If single-line-to-ground (SLG) faults occur at positions f1 to f5, the comparative results of the zero-sequence current measurements at each sectional monitoring point are as summarized in Table 1.
2.3. Fault Location
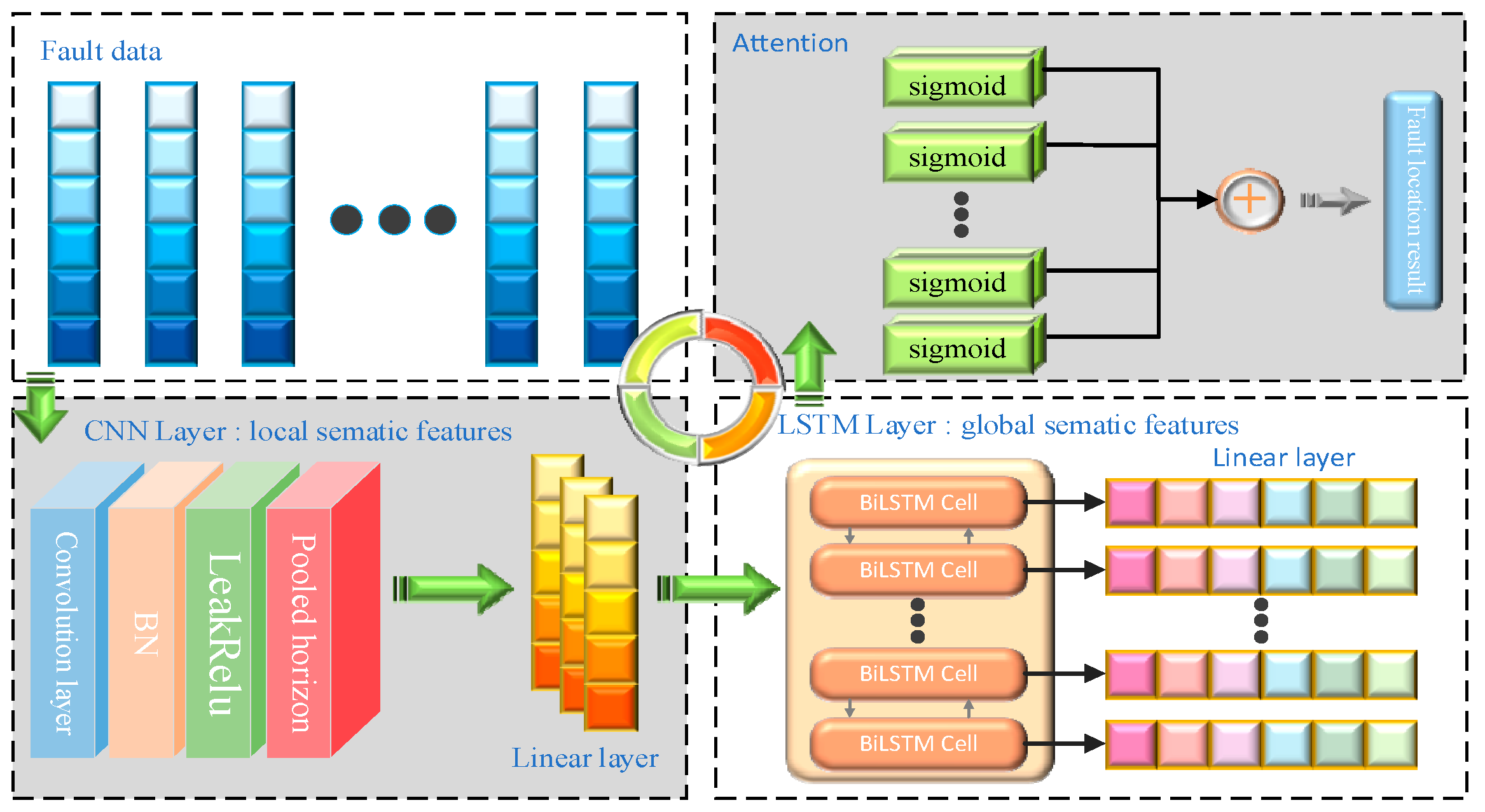
3. Fault Location Method Based on CNN–BiLSTM–Attention
Fault Location Process of CNN–BiLSTM–Attention Model
- (1)
- Fault sample data collection:
- (2)
- Data extraction and preprocessing:
- (3)
- Designing the structure of the CNN–BiLSTM–attention model:
- (1)
- The MSE quantifies the prediction accuracy through the arithmetic mean of the squared deviations between the model outputs and observed values , and it is mathematically defined asIn the formula, is the predicted fault distance; represents the actual fault distance; and n is the number of samples in the test set.
- (2)
- The mean absolute error (MAE) is the average value of the absolute error between the predicted value and the true value, with the formula
- (3)
- The mean absolute percentage error (MAPE) is the mean of the percentage of the absolute error to the true value and is given by the formula
- (4)
- Online fault location:
4. Simulation Verification
4.1. Construction of the Wind Farm Model and Generation of the Dataset
4.2. Experimental Results and Analysis
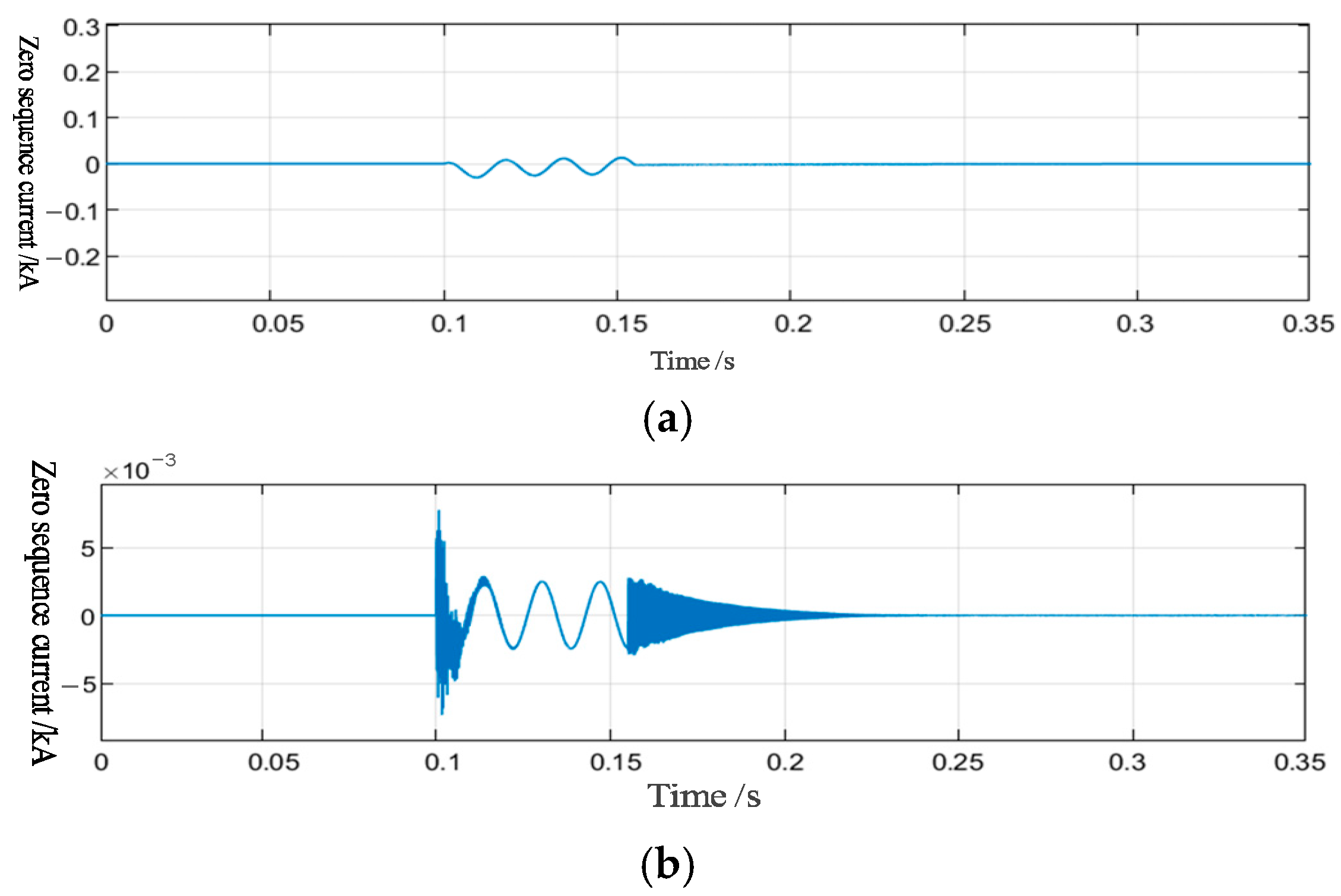
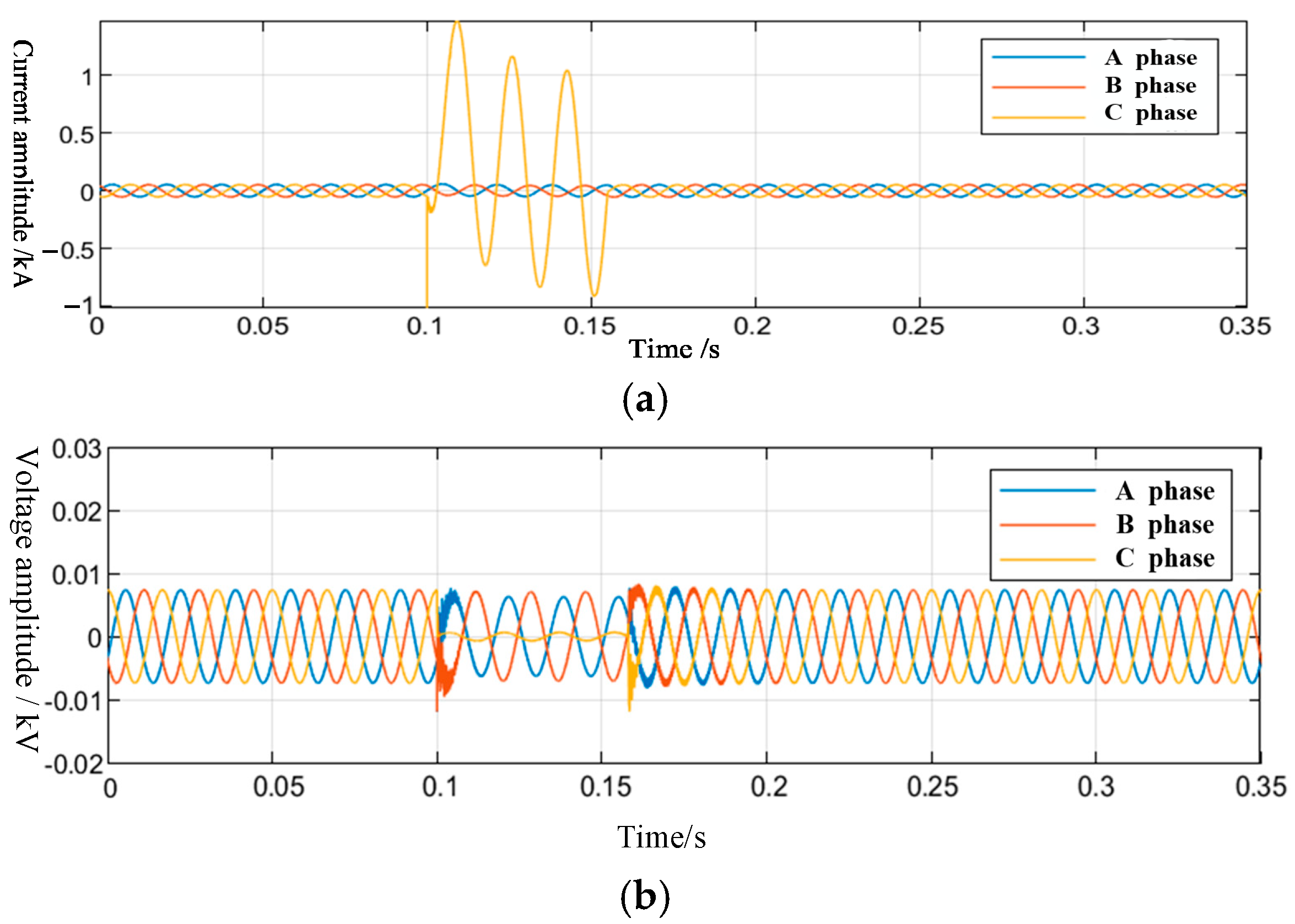
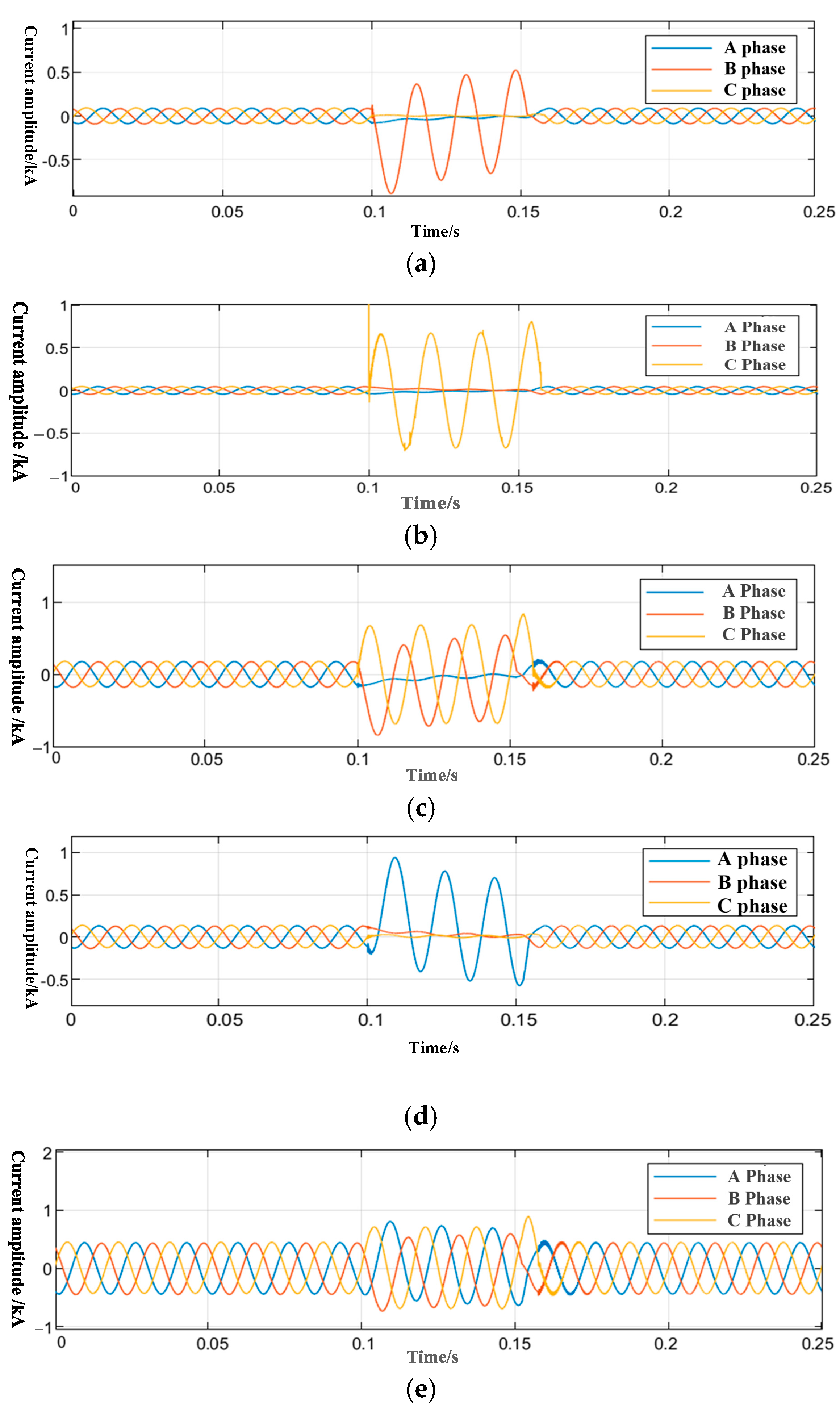
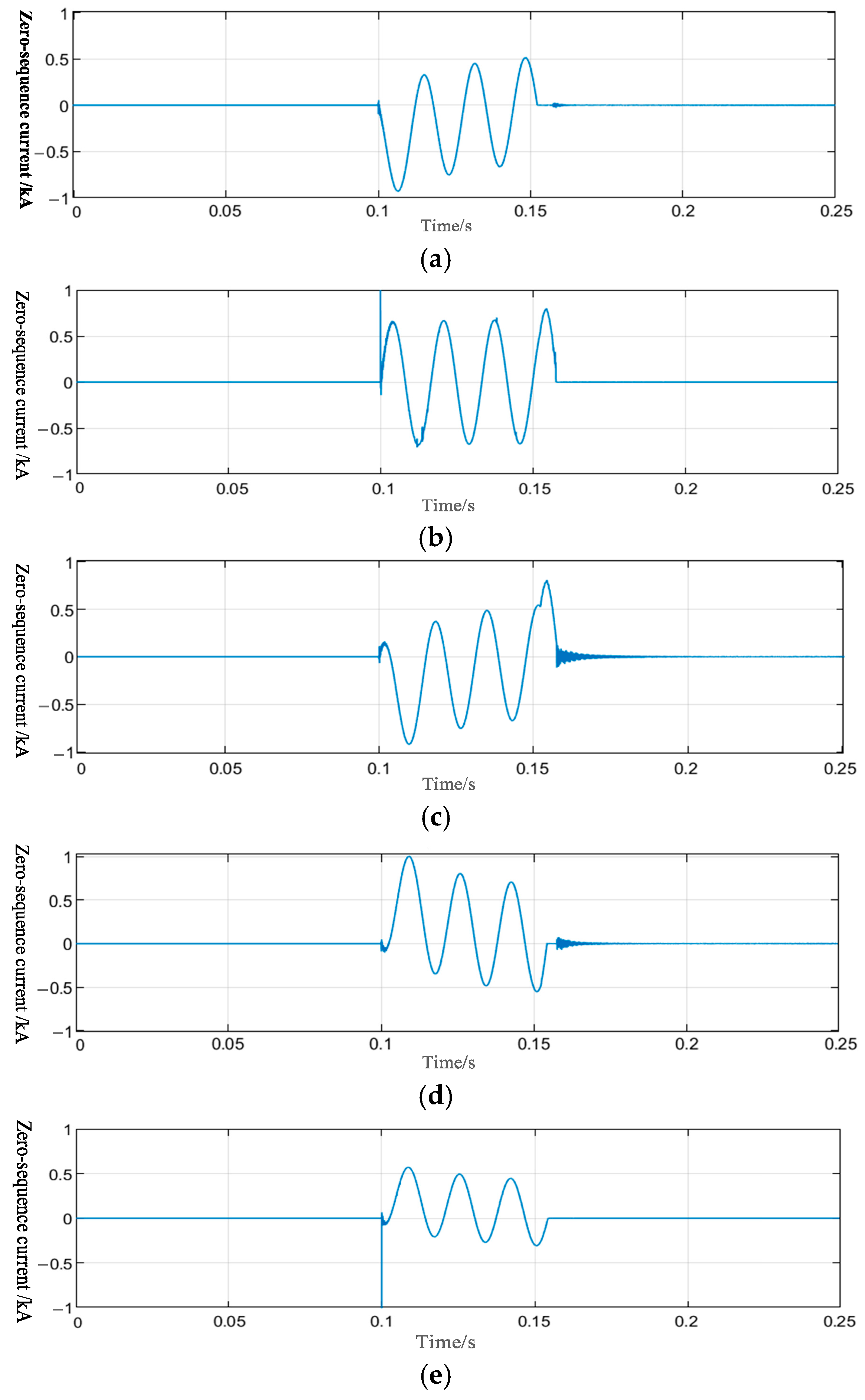
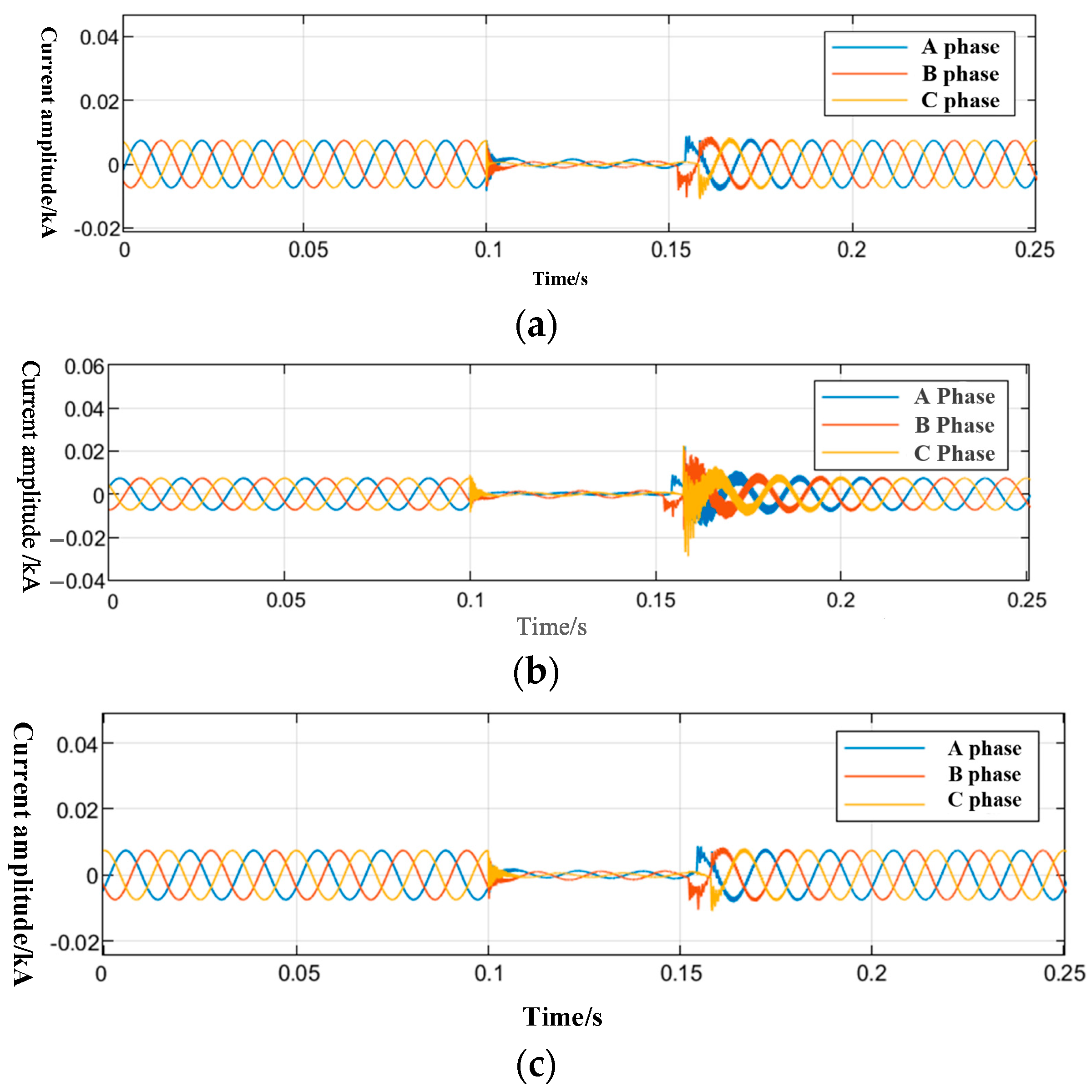
4.2.1. Characteristic Analysis of Grounding Faults in a Single Line
4.2.2. Characteristic Analysis of Simultaneous Grounding Faults in Different Lines
4.3. Fault Location Results Under Different Conditions
4.4. Fault Location of CNN–BiLSTM–Attention
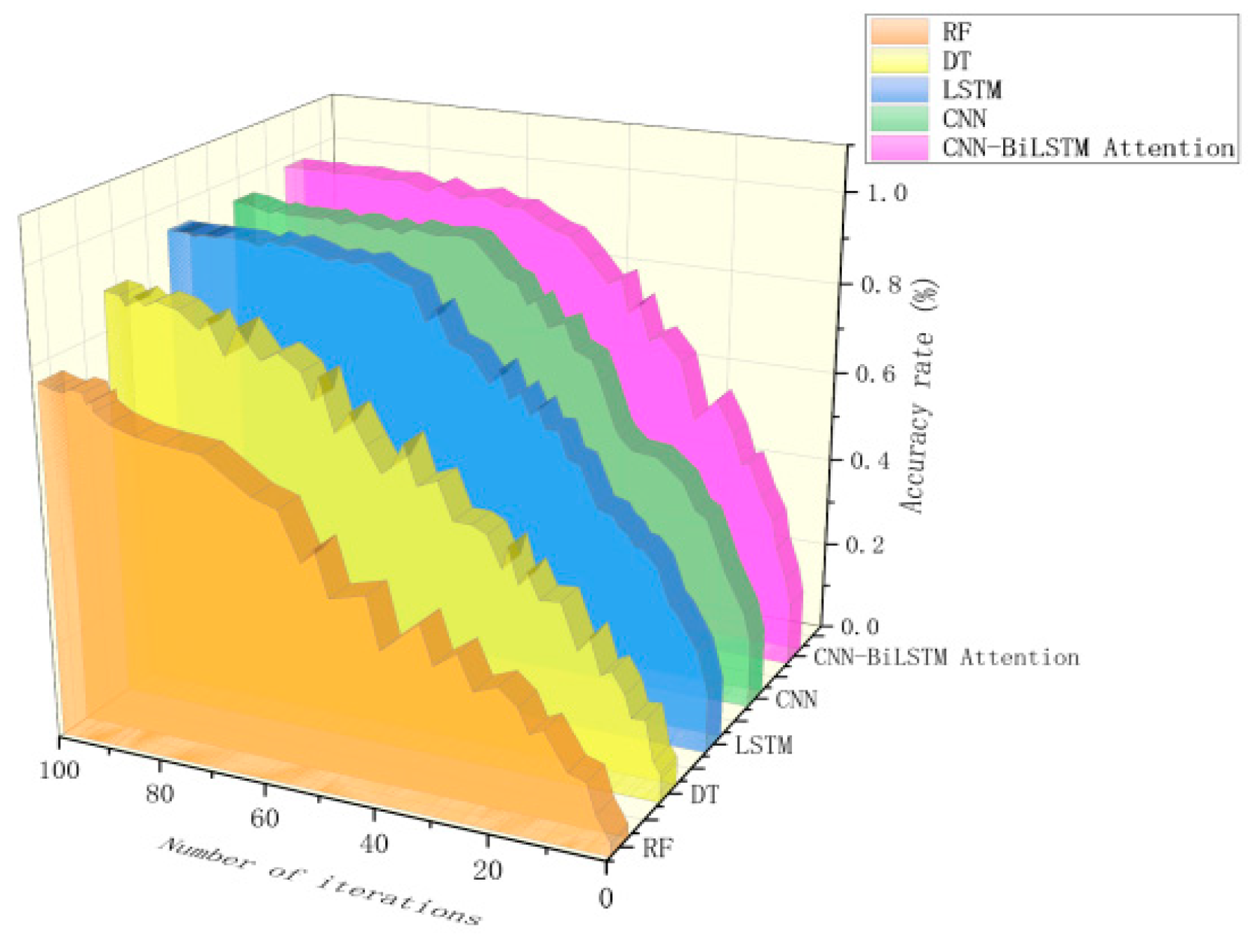
4.5. Ablation Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Ye, Y.; Ma, X.; Lin, X.; Xu, F.; Wang, C.; Ni, X.; Ding, C. Single-phase-to-ground fault section location in flexible resonant grounding distribution networks using soft open points. Int. J. Electr. Power Energy Syst. 2020, 122, 106198. [Google Scholar] [CrossRef]
- Li, Z.; Wheeler, P.; Watson, A.; Costabeber, A.; Wang, B.; Ren, Y. A Fast Diagnosis Method for Both IGBT Faults and Current Sensor Faults in Grid-Tied Three-Phase Inverters with Two Current Sensors. IEEE Trans. Power Electron. 2020, 35, 5267–5278. [Google Scholar] [CrossRef]
- Amatare, S.; Ojo, A. Predicting Customer Churn in Telecommunication Industry Using Convolutional Neural Network Model. IOSR J. Comput. Eng. 2021, 22, 54–59. [Google Scholar]
- Belagoune, S.; Bali, N.; Bakdi, A.; Baadji, B.; Atif, K. Deep Learning through LSTM Classification and Regression for Transmission Line Fault Detection, Diagnosis and Location in Large-Scale Multi-Machine Power Systems. Measurement 2021, 177, 109330. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, P.; Peng, X.; Wu, Z.; Yuan, H. Fault location of transmission line based on CNN-LSTM double-ended combined model. Energy Rep. 2022, 8, 781–791. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, L.; Lai, Y. Stock Price Prediction Using CNN-BiLSTM-Attention Model. Mathematics 2023, 11, 1985. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Q.; Liu, Y.; Tong, N.; Chen, S.; Zhang, C. Novel Fault Location Method for Power Systems Based on Attention Mechanism and Double Structure GRU Neural Network. IEEE Access 2020, 8, 75237–75248. [Google Scholar] [CrossRef]
- Chen, W.; Song, H.; Wu, H.; Tian, H.; Qi, Z. Neural network based on hybrid ac/dc hybrid power grid ac line fault location. J. Sichuan Electr. Power Technol. 2024, 47, 66–75. [Google Scholar]
- Yuan, S. Research on Single-Phase Grounding Short-Circuit Fault Location Method of Wind Farm Collector Line Based on Zero Sequence Network. Master’s Thesis, North China Electric Power University, Beijing, China, 2021; pp. 1–30. [Google Scholar]
- Peng, H. Wind Power Electricity Lines of Single-Phase Grounding Fault Location Method Research. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2022; pp. 1–24. [Google Scholar]
- Liu, F.; Renna, S.; Zhu, Y. Location of single-phase grounding fault section of wind farm collector wire based on FDM twin network. Renew. Energy 2023, 41, 401–410. [Google Scholar]
- Li, Z.; Zeng, X.; Xia, Y.; Wang, S.; Xi, Y. High voltage transmission line traveling wave fault location technology review. J. Chang. Univ. Sci. Technol. (Nat. Sci. Ed.) 2022, 19, 104–121. [Google Scholar]
- Huang, W. Fault Diagnosis Method of NPC-Type Three-Level Grid-Connected Inverter Based on Observer. Master’s Thesis, Hefei University of Technology, Hefei, China, 2023; pp. 1–25. [Google Scholar]
- Yang, L. Research on anomaly detection Algorithm of SCADA System based on Deep learning. Inf. Technol. Informatiz. 2024, 9–12. [Google Scholar]
- Zhao, J.; Hou, H.; Gao, Y.; Huang, Y.; Gao, S.; Lou, J. Single-phase ground fault location method for distribution network based on traveling wave time-frequency characteristics. Electr. Power Syst. Res. 2020, 186, 106401. [Google Scholar]
- Liang, J.; Jing, T.; Niu, H.; Wang, J. Two-terminal fault location method of distribution network based on adaptive convolution neural network. IEEE Access 2020, 8, 54035–54043. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. Traveling wave propagation characteristic-based LCC-MMC hybrid HVDC transmission line fault location method. IEEE Trans. Power Deliv. 2021, 37, 208–218. [Google Scholar] [CrossRef]
- Jalalt, S.M.; Miralizadeh, S.; Talavat, V.; Boalndi, T.G. A novel superimposed voltage energy-based approach for single phase to ground fault detection and location in distribution networks. IET Gener. Transm. Distrib. 2023, 17, 4215–4233. [Google Scholar] [CrossRef]
- Tavoosi, J.; Shirkhani, M.; Azizi, A.; Din, S.U.; Mohammadzadeh, A.; Mobayen, S. A hybrid approach for fault location in power distributed networks: Impedance-based and machine learning technique. Electr. Power Syst. Res. 2022, 210, 108073. [Google Scholar] [CrossRef]
- Lu, D.; Liu, Y.; Liao, Q.; Wang, B.; Huang, W.; Xi, X. Time-domain transmission line fault location method with full consideration of distributed parameters and line asymmetry. IEEE Trans. Power Deliv. 2020, 35, 2651–2662. [Google Scholar] [CrossRef]
- Xu, L.; Fan, S.; Zhang, H.; Xiong, J.; Liu, C.; Mo, S. Enhancing Resilience and Reliability of Active Distribution Networks through Accurate Fault Location and Novel Pilot Protection Method. Energies 2023, 16, 7547. [Google Scholar] [CrossRef]
- Shu, H.; Liu, X.; Tian, X. Single-ended fault location for hybrid feeders based on characteristic distribution of traveling wave along a line. Ower Delivery. IEEE Trans. Power Deliv. 2020, 36, 339–350. [Google Scholar] [CrossRef]
- Dong, J.; Zhu, Y.; Cui, N.; Jia, X.; Guo, L.; Qiu, R.; Shao, M. Estimating crop evapotranspiration of wheat-maize rotation system using hybrid convolutional bidirectional Long Short-Term Memory network with grey wolf algorithm in Chinese Loess Plateau region. Agric. Water Manag. 2024, 301, 108924. [Google Scholar] [CrossRef]
- Lu, G.; Liu, Y.; Wang, J.; Wu, H. CNN-BiLSTM-Attention: A multi-label neural classifier for short texts with a small set of labels. Inf. Process Manag. 2023, 60, 103320. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Z.; Chen, Q.; Liu, X.; Tu, J. CNN-BiLSTM Audible Noise Prediction for high-altitude multi-factor transmission lines based on multi-head attention mechanism. High Volt. Electr. Appar. 2024, 60, 160–169. [Google Scholar]
 indicates the system side;
indicates the system side;  indicates the main transformer;
indicates the main transformer;  indicates the grounding transformer.
indicates the grounding transformer.
 indicates the system side;
indicates the system side;  indicates the main transformer;
indicates the main transformer;  indicates the grounding transformer.
indicates the grounding transformer.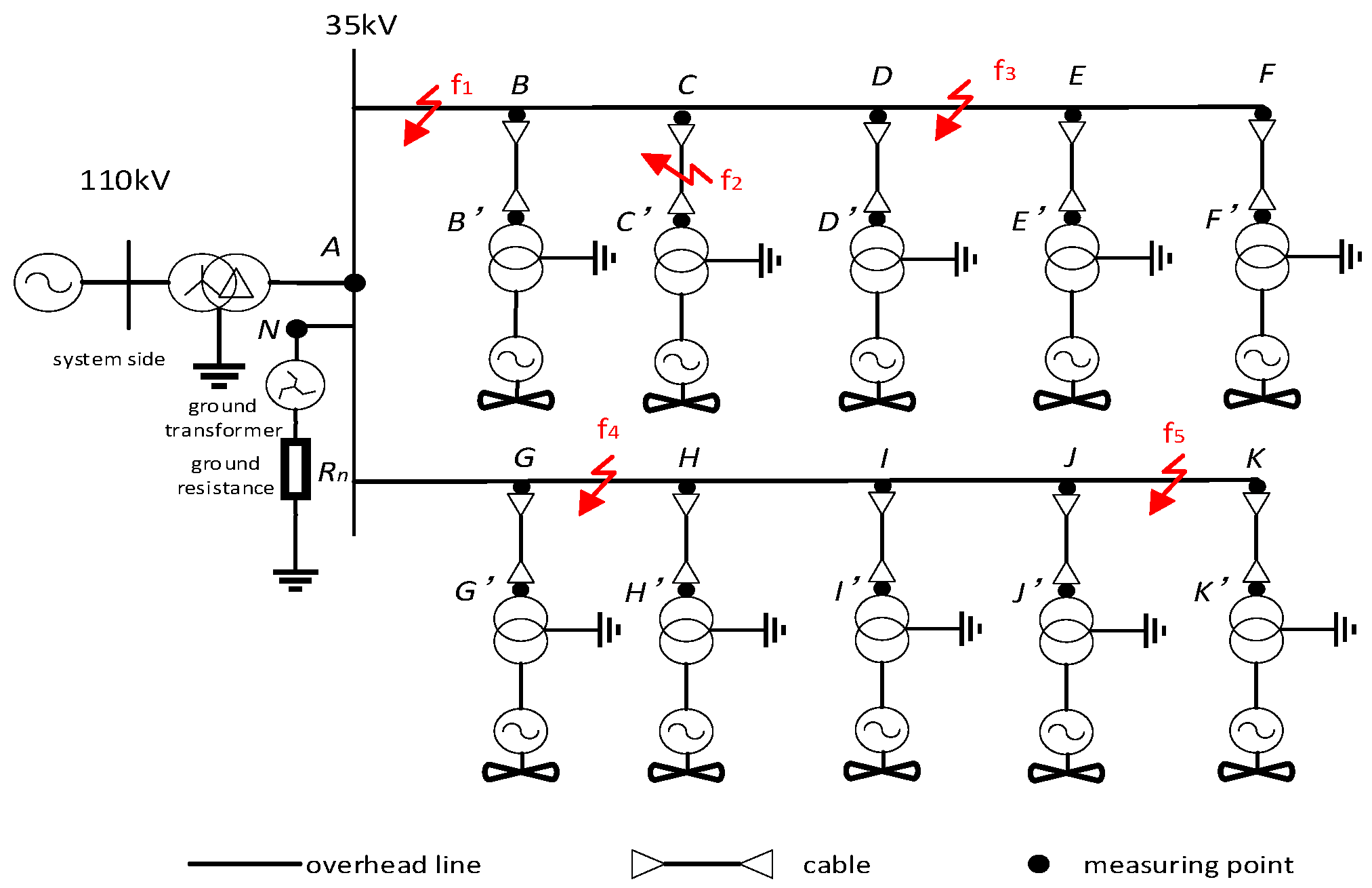





| Fault Point | f1 | f2 | f3 | f4 | f5 |
|---|---|---|---|---|---|
| Faulty section | A-B | C-C’ | D-E | G-H | J-K |
| Monitoring point where zero-sequence current is detected | A | A, B, C | A, B, C, D | A, G | A, J |
| Comparing zero-sequence current values of each measurement point |
| Name | Parameter Setting |
|---|---|
| Voltage level | 35 kV |
| Transformer connection method | Yg-D1 |
| Frequency | 50 Hz |
| Parameter | Numerical Value | Quantity |
|---|---|---|
| Fault type | AG, BG, CG | 3 |
| Transition resistor/Ω | 0.001, 0.01, 0.05, 0.1, 1, 10, 100, 200 | 8 |
| Initial phase angle/(°) | 1.5, 30, 60, 90, 181.5, 210, 240, 270 | 8 |
| Actual Fault Distance/km | Ground Resistance/Ω | Calculated Distance/km | Absolute Error/km | Percentage Error |
|---|---|---|---|---|
| 3.5 | 0.001 | 3.512 | 0.029 | 0.829% |
| 0.01 | 3.487 | 0.043 | 1.23% | |
| 0.05 | 3.534 | 0.074 | 2.10% | |
| 0.1 | 3.479 | 0.061 | 1.74% | |
| 1 | 3.448 | 0.084 | 2.41% | |
| 10 | 3.425 | 0.100 | 2.86% | |
| 100 | 3.607 | 0.116 | 3.32% |
| Model Structure | Argument | Value |
|---|---|---|
| CNN layer | Window size | 48 |
| Convolution kernel | 128 | |
| Convolution kernel 2 | 64 | |
| Maximum pooling length | 2 | |
| BiLSTM layer | BiLSTM unit 1 | 128 |
| BiLSTM unit 2 | 64 | |
| Fully connected layer | Output layer | One-dimensional vector |
| Dropout layer | Parameter: 0.2 | |
| Learning rate | 0.001 | |
| Model | MSE | MAE | MAPE |
|---|---|---|---|
| CNN | 0.163 | 0.399 | 7.977% |
| BiLSTM | 0.071 | 0.266 | 5.333% |
| CNN–BiLSTM–Attention | 0.059 | 0.233 | 4.657% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Gao, Q.; Liu, B.; Zhang, C.; Zhou, G. A Method Based on CNN–BiLSTM–Attention for Wind Farm Line Fault Distance Prediction. Energies 2025, 18, 3703. https://doi.org/10.3390/en18143703
Zhang M, Gao Q, Liu B, Zhang C, Zhou G. A Method Based on CNN–BiLSTM–Attention for Wind Farm Line Fault Distance Prediction. Energies. 2025; 18(14):3703. https://doi.org/10.3390/en18143703
Chicago/Turabian StyleZhang, Ming, Qingzhong Gao, Baoliang Liu, Chen Zhang, and Guangkai Zhou. 2025. "A Method Based on CNN–BiLSTM–Attention for Wind Farm Line Fault Distance Prediction" Energies 18, no. 14: 3703. https://doi.org/10.3390/en18143703
APA StyleZhang, M., Gao, Q., Liu, B., Zhang, C., & Zhou, G. (2025). A Method Based on CNN–BiLSTM–Attention for Wind Farm Line Fault Distance Prediction. Energies, 18(14), 3703. https://doi.org/10.3390/en18143703





