Mathematical Modeling and Analysis of the Mechanical Properties of a Nonferromagnetic Panel Under the Action of a Quasi-Steady Electromagnetic Field

Abstract

A physical and mathematical model and a methodology for studying the mechanical properties of a nonferromagnetic conductive panel under the action of a quasi-steady electromagnetic field are proposed. A two-dimensional thermomechanics problem is formulated for the considered panel of a rectangular cross-section. The initial relations for finding the determinant functions, namely, the components of the quasi-static stress tensor, are given. The thermomechanical problem was addressed using the author’s approach, which involves approximating the defining functions by cubic polynomials along the thickness direction. This approach enabled the transformation of the initial two-dimensional boundary value problems into one-dimensional formulations based on the integral characteristics of the defining functions. Using a finite integral transformation in the transverse coordinate, the expressions of all integral characteristics and determinant functions were obtained. On the basis of the proposed mathematical model, a computer analysis of all components of the quasi-static stress tensor and stress intensity in a tungsten panel depending on the dimensionless Fourier time, the Biot criterion, and the induction heating parameters was carried out. The thermomechanical behavior of the panel was analyzed using two modes of near-surface and in-depth induction heating of the panel by a homogeneous quasi-steady electromagnetic field.

1. Introduction

Modern electrical appliances, such as generators, transformers, inductors, and the magnetic coils of electric motors, widely use plate-conductive elements. During operation, these elements are exposed to external electromagnetic fields (EMFs), including quasi-steady fields, which can significantly influence their mechanical properties, operational longevity, and overall performance. Particular attention should be paid to the processes of technological heat treatment of electroconductive products that use induction heating.

Mathematical models, analytical and experimental approaches for describing and studying electromagnetic, thermal, and mechanical processes, are considered in many fundamental works, in particular [1,2,3,4,5,6].

Reference [1] offers an in-depth review of the principal electrical technologies used in process heating. In addition to addressing thermal stress phenomena, [2] includes contributions on related disciplines such as elasticity theory, thermal conductivity, and thermodynamics. Paper [3] is devoted to the construction of a two-dimensional physical and mathematical model to investigate the temperature behavior of a rectangular conductive strip subjected to induction heating by a quasi-steady electromagnetic field. A methodology for constructing solutions to the formulated problems of electrodynamics and thermal conductivity for the strip under consideration is proposed. This technique uses the approximation of the determining functions—the component of the magnetic field strength and temperature vector tangential to the band bases by cubic polynomials in the thickness variable. This approach enabled the transformation of the initial two-dimensional boundary value problems into one-dimensional formulations based on the integral characteristics of the defining functions. The solution to these one-dimensional problems is found by applying a finite integral transform in the transverse direction and the Laplace transform with respect to time. The qualitative and quantitative regularities of changes in time and in the cross-sectional area of both determinant functions for a strip made of stainless steel under the action of a quasi-steady electromagnetic field are analyzed numerically.

Papers [4,5] highlight the regularities of induction heating technology obtained on the basis of experimental studies.

Paper [6] considers the simulations of thermomechanical behavior in conductive solids exposed to high-temperature induction heating. The study examines how the frequency of the electric current influences the development of residual stresses in a cylindrical body. The analysis focuses on the induction treatment process, which entails heating the solid to a target temperature and subsequently cooling it. Particular attention is given to how different cooling conditions affect the resulting residual stress distribution.

In [7], a mathematical model describing the temperature field during high-frequency induction heating was proposed [7]. The model relies on solving a set of sequentially coupled equations of the electromagnetic and temperature fields. Computational simulations were performed using the appropriate software, and the results demonstrated a strong agreement between the model’s predictions and experimental data.

Reference [8] investigates the temperature distribution in a carbon steel plate during linear induction heating. This distribution was analyzed numerically using the electromagnetic and thermal coupling analysis. To validate the accuracy of the simulation results, the real process of induced deformation during linear heating was carried out. A strong correlation between the numerical predictions and experimental observations confirmed the reliability of the proposed approach.

Paper [9] proposes a model of the process of induction hardening of steel elements of complex shapes using induction heating. The induction contour hardening of gears is considered as an example. The results of modeling for coupled physical fields performed using software are presented.

Reference [10] addresses the challenge of efficiently solving coupled electromagnetic–thermal problems. To enhance computational performance, a semi-analytical modeling approach is introduced. This method combines an initial finite element analysis with the subsequent application of analytical electromagnetic formulations. The use of the proposed model is limited to simple geometric characteristics, such as flat or curved surfaces with a large ratio of curvature to skin-effect depth. Numerical and experimental verification of the model shows good agreement in predicting the temperature evolution, achieving higher accuracy than other known commercial software products.

In recent years, much attention has been paid to the synthesis of new structural materials that have a high melting point, high thermal and electrical conductivity, and increased mechanical strength. Papers [11,12,13,14] describe experimental methods for creating such new materials and investigate the effect of appropriate impurities in homogeneous materials and the new methods for their technological processing to improve thermomechanical properties.

These new materials, in particular those based on tungsten and copper matrix metal composites [14], usually have a heterogeneous structure, unlike the well-described homogeneous materials.

Despite the large number of theoretical and experimental studies devoted to electromagnetic, thermal, and mechanical processes in conductive bodies, most of them focus on one-dimensional models and stationary modes of EMF, in particular, modes of high-frequency induction heating by steady-state fields. However, the influence of a quasi-steady-state electromagnetic field on the thermophysical and mechanical properties of structural elements operating at elevated heating temperatures remains insufficiently studied.

This is due to the insufficient number of developed two-dimensional physical and mathematical models. Such two-dimensional models provide an opportunity for a deeper and more extended analysis of the thermomechanical behavior of plate elements under the action of a quasi-steady-state electromagnetic field. In contrast to the known models that use steady-state EMFs, the quasi-steady-state EMF takes into account the moment of switching on an inductor or a high-frequency oscillator and, to some extent, takes into account the transient mode of the change in time of the EMF, taking into account its output to steady-state electromagnetic oscillations.

Understanding and taking into account the interrelated effects of electromagnetic, temperature, and mechanical fields on the temperature regimes and thermal stress states of plate elements are important for predicting the performance and extending the service life of such elements in modern electrical and electromechanical systems. In these systems, electrically conductive elements such as electrodes, the plate elements of plasma processing structures, fusion reactor elements, and high-power electrical contacts are exposed to intense electromagnetic fields and high temperatures. Such studies are critical for both the temperature control and structural reliability of the material from which the conductive plate element is made.

Therefore, the purpose of this work is to fill the research gap by developing a comprehensive model of the thermomechanical behavior of nonferromagnetic panels, in particular, those made of tungsten, exposed to quasi-steady-state electromagnetic fields.

2. Formulation of the Thermomechanics Problem for an Electroconductive Panel

Consider a long conductive panel of a rectangular cross-section. In the rectangular Cartesian coordinate system ${Ox}_1{x}_2{x}_3$, the $O{x}_1$ axis coincides with the width $2d$, the $O{x}_3$axis with the thickness of the panel $2h$, and the panel is infinitely long along the $O{x}_2$ axis. The origin of the coordinate system is the point of symmetry of the rectangle.

The panel is exposed to an unsteady electromagnetic field (EMF), which causes induction heating. The temperature distribution in the panel is caused by the Joule heat, which has a non-stationary volumetric character. This temperature field creates a corresponding plane-deformed thermal stress state of the panel. To determine this state, it is necessary to formulate a two-dimensional problem of thermomechanics in stresses. This problem is complex and consists of three stages.

At the first stage, we use Maxwell’s equations to determine the EMF in the panel and the specific Joule heat density. The second stage involves determining the temperature distribution by solving the heat conduction equation, in which the heat source is Joule heat. At the third stage, we use the equations of the two-dimensional quasi-static thermoelasticity problem to find the components of the stress tensor that describe the thermal stress state of the panel. Let us illustrate this with this diagram.

The first two stages—the calculation of Joule heating and the temperature field—are examined in [3]. This work analyzes the temperature variation over Fourier time at characteristic points within the cross-section of a steel strip, considering different values of the Biot number for both near-surface and deep induction heating under a quasi-steady electromagnetic field. It also presents the temperature distribution across the strip’s cross-section in the steady-state heating regime.

The aim of this work is as follows:

• To build a two-dimensional physical and mathematical model for determining the thermal stress state of an electroconductive nonferromagnetic panel under the action of a non-stationary EMF.
• To develop a methodology for constructing a solution to the quasi-static problem of thermomechanics in the case of a plane-deformed state of the panel.
• To conduct a numerical analysis of the Fourier time evolution of the stress tensor components and stress intensity in a tungsten panel depending on the parameters of induction heating by quasi-steady-state EMF and different heat exchange conditions with the surrounding environment.

3. Determination of the Thermal Stress State of the Panel

Previous studies [3,5,6] have established that when an electroconductive body is subjected to induction heating by a quasi-steady electromagnetic field, the resulting stress state is primarily influenced by the generated Joule heat $Q$, with the effect of ponderomotive forces $\overrightarrow{F}$ being negligible. Consequently, under plane deformation driven solely by the temperature field $T(x_1,x_3,t)$, the governing equations for the two-dimensional quasi-static thermoelasticity problem are formulated as follows [3].

$$\begin{gathered} {\Delta }_1\left({\psi }^{\left(s\right)}+{\displaystyle \frac{\alpha ET}{1-\nu }}\right)=0; {\Delta }_1{\sigma }_{13}^{\left(s\right)}=-{\displaystyle \frac{{\partial }^2{\psi }^{\left(s\right)}}{\partial x_1\partial x_2}};{\Delta }_1={\displaystyle \frac{{\partial }^2}{\partial x_1^2}}+{\displaystyle \frac{{\partial }^2}{\partial x_3^2}}; {\displaystyle \frac{{\partial }^2{\sigma }_{11}^{\left(s\right)}}{\partial x_1}}={\displaystyle \frac{{\partial }^2{\sigma }_{13}^{\left(s\right)}}{\partial x_3}}; \\ {\sigma }_{33}^{\left(s\right)}={\psi }^{\left(s\right)}-{\sigma }_{11}^{\left(s\right)}; {\sigma }_{22}^{\left(s\right)}=\nu {\psi }^{\left(s\right)}-\alpha ET. \end{gathered}$$

(1)

Here, ${\sigma }_{11},{\sigma }_{22},{\sigma }_{13},{\sigma }_{33}$ denote the components of the quasi-static stress tensor ${\widehat{\sigma }}^{\left(s\right)}$, and ${\psi }^{\left(s\right)}={\sigma }_{11}+{\sigma }_{33}$ represents the sum of the normal stress components; $\alpha$ is the linear thermal expansion coefficient and $\nu$ is Poisson’s ratio; while $E$ stands for Young’s modulus.

Expressions

$${\displaystyle \frac{\partial {\psi }^{\left(s\right)\pm }}{\partial x_1}}+{\displaystyle \frac{\partial {\sigma }_{13}^{\left(s\right)\pm }}{\partial x_3}}=0, {\sigma }_{13}^{\left(s\right)\pm }=0, {\sigma }_{11}^{\left(s\right)\pm }={\psi }^{\left(s\right)\pm }$$

(2)

define the boundary conditions on the panel surfaces at $x_3=\pm h$ and the following expressions

$${\displaystyle \frac{\partial {\psi }_{\ast }^{\left(s\right)\pm }}{\partial x_3}}+{\displaystyle \frac{\partial {\sigma }_{\ast 13}^{\left(s\right)\pm }}{\partial x_1}}=0, {\sigma }_{\ast 13}^{\left(s\right)\pm }=0, {\sigma }_{\ast 33}^{\left(s\right)\pm }={\psi }_{\ast }^{\left(s\right)\pm }$$

(3)

describe the boundary conditions on the end surfaces at $x_1=\pm d$. These values are taken into consideration at the end sections of the panel $x_1=\pm d$, as indicated by the symbol $\ast$ in (3). In relations (1)‒(3), the dimensional Cartesian coordinates $x_1$, $x_3$are used.

To evaluate the thermomechanical response of the panel, the stress intensity is calculated using the known components of the stress tensor—${\sigma }_{11}\left(x_1,x_3,t\right), {\sigma }_{13}\left(x_1,x_3,t\right),$ ${\sigma }_{22}\left(x_1,x_3,t\right), \mathrm{a}\mathrm{n}\mathrm{d} {\sigma }_{33}\left(x_1,x_3,t\right)$—along with the temperature distribution $T\left(x_1,x_3,t\right)$. For the two-dimensional case under consideration, the stress intensity is expressed by the following formula:

$${\sigma }_i={\displaystyle \frac{1}{\sqrt{2}}}\sqrt{({\sigma }_{11}-{\sigma }_{22}{)}^2+({\sigma }_{22}-{\sigma }_{33}{)}^2+({\sigma }_{33}-{\sigma }_{11}{)}^2+6{\sigma }_{13}^2}.$$

(4)

4. Solution Methodology for 2D Initial Boundary Problems

The set of functions $\Phi \left(x_1,x_3,t\right)=\{{\sigma }_{11};{\sigma }_{13};{\sigma }_{22};{\sigma }_{33}\}$ varies with the spatial coordinates $x_1,x_3,$ and time $t$. These functions are approximated along the thickness direction using cubic polynomials expansions:

$$\Phi (x_1,x_3,t)=\sum _{j=1}^3{a}_{(j-1)}^{\Phi }(x_1,t)x_3^{j-1}.$$

(5)

The coefficients $a_{\left(j-1\right)}^{\Phi }\left(x_1,t\right)$ in the polynomials (5) are expressed through the integral characteristics ${\Phi }_s\left(x_1,t\right)$ of the functions $\Phi (x_1,x_3,t)$, defined as follows:

$${\Phi }_s\left(x_1,t\right)={\displaystyle \frac{2s-1}{2}}{\int }_{-1}^1\Phi \left(x_1,x_3,t\right)x_3^{s-1}d{x}_3 , \left(s=\mathrm{1,2}\right)$$

(6)

along with the boundary values ${\Phi }^{\pm }\left(x_1,t\right)$ of the functions on the surfaces $x_3=\pm h$. To derive the equations for determining the integral characteristics ${\Phi }_s\left(x_1,t\right)$, the governing Equation (1) involving ${\psi }^{\left(s\right)}$ and ${\sigma }_{13}$ are multiplied by $x_3^{s-1}$ and integrated over the thickness variable $x_3$, using definitions (5) and (6). This procedure yields a system of initial equations for ${\Phi }_s\left(x_1,t\right)\left(s=\mathrm{1,2}\right)$, which reduces the original two-dimensional problem to a set of one-dimensional equations in the coordinate $x_1$. These equations are solved by applying finite integral transforms in the $x_1$direction, in accordance with the boundary conditions specified at the ends of the panel $x_1=\pm d$. A detailed description of the method for finding the components of the stress tensor in the panel is described in [3].

5. Computational Analysis of Stress Tensor and Stress Intensity in an Electroconductive Panel Under Quasi-Steady Electromagnetic Heating

By applying the methodology described in [3] and the approach presented above, we derive expressions for the temperature and stress tensor components in a nonferromagnetic panel subjected to a uniform quasi-steady electromagnetic field. This field is characterized by the tangential values of the magnetic field intensity component $H_2\left(x_1,\hspace{0.33em}{x}_3,\hspace{0.33em}\tau \right)$on the panel surfaces at $x_3=\pm 1$ and $x_1=\pm d_{\ast }$, expressed as follows

$$H_2\left(x_1,\hspace{0.33em}\pm 1,\hspace{0.33em}\tau \right)=H_0\phi \left(\tau \right)e^{ib\tau }, H_2\left(\pm d,\hspace{0.33em}{x}_3,\hspace{0.33em}\tau \right)=H_0\phi \left(\tau \right)e^{ib\tau }$$

(7)

The dimensionless Cartesian coordinates are defined as $x_1^{\ast }=x_1/d_{\ast }$, $x_3^{\ast }=x_3/h$, with $d=d_{\ast }/h$ and $\tau =t/\left(\sigma \mu h^2\right)$, where t denotes time. In Expressions (7), the time-dependent function $\phi \left(\tau \right)$ is given by $\phi \left(\tau \right)=1-e^{\beta \tau }$.$\mathrm{H}\mathrm{e}\mathrm{r}\mathrm{e},i=\sqrt{-1}$ is the imaginary unit, and the parameter $b={\displaystyle \frac{1}{\left(2{\delta }_0^2\right)}}$, where ${\delta }_0={\left(2\omega \sigma \mu h^2\right)}^{-{\displaystyle \frac{1}{2}}}$, characterizes the penetration depth of the induction currents with frequency $\omega$ relative to the panel’s half-thickness $h$. In the expression $\beta ={\displaystyle \frac{ln\epsilon }{{\tau }_{\ast }}}$, the parameter ${\tau }_{\ast }$ denotes the dimensionless time required for electromagnetic oscillations at frequency $\omega$ to reach a steady-state amplitude $H_0$, where $\epsilon =0.001$.

The numerical experiment was performed for an electroconductive panel made of tungsten [15] (see

Table 1. The thermophysical and mechanical properties of tungsten.

Property	Value
Density (ρ)	19,250, kg/m3
Melting point	3695, K (≈3422 °C)
Boiling point	6203, K
Electrical conductivity (σ)	1.8 × 107, $\mathsf{\Omega }$/m
Thermal conductivity (λ)	173, W/(m·K)
Specific heat capacity (c)	134, J/(kg·K)
Young’s modulus (E)	411, GPa
Poisson’s ratio (ν)	0.28
Coefficient of Linear Expansion (α)	4.5 × 10−6, 1/K
Thermal diffusivity (κ)	6.7 × 10−5, m2/s

).

The panel has a thickness of $2h=2 \mathrm{m}\mathrm{m}$, and a width of $2d_{\ast }=40 \mathrm{m}\mathrm{m}$ (corresponding to a relative half-width $d=20$). Two values of the induction current penetration depth, given in relation to the panel’s half-thickness h, were calculated: near-surface heating is represented by parameter ${\delta }_0=0.1$, while in-depth heating is represented by ${\delta }_0=1$.

The surface heating of the panel under study is represented by the circular frequency of electromagnetic oscillations ${\omega }_1=2.2\times 10^{6}1/s$, while the in-depth heating is represented by the circular frequency of electromagnetic oscillations ${\omega }_2=2.2\times 10^{4}1/s$.

5.1. Analysis of Stress Tensor Components

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 show the change in Fourier time and in the cross-sectional area of the considered panel of the components ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$, ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$, ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$, and ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ of the quasi-static stress tensor at the value $Bi=1$ of the Biot criterion under induction heating by a quasi-steady-state EMF. The time variation in the Fourier data of the quasi-static stress tensor components was calculated at the characteristic points $M_1\hspace{0.33em}(0.25\hspace{0.33em}d,\hspace{0.33em}0.25)$, $M_2\hspace{0.33em}(0.5\hspace{0.33em}d,\hspace{0.33em}0.5)$, and $M_3\hspace{0.33em}(0.9\hspace{0.33em}d,\hspace{0.33em}0.9)$ of the cross-section of the tungsten panel under consideration. Figure 1, Figure 2, Figure 3 and Figure 4 show the data dependencies of the stress tensor components under the near-surface induction heating with ${\delta }_0=0.1$, and Figure 5, Figure 6, Figure 7 and Figure 8 show the dependencies of the data components under its in-depth heating with ${\delta }_0=1$.

When a panel with half-width $d=20$was exposed to near-surface induction heating by a quasi-steady electromagnetic field with ${\delta }_0=0.1$, the time-dependent behavior of the stress tensor components at characteristic points $M_1\hspace{0.33em}(0.25\hspace{0.33em}d,\hspace{0.33em}0.25)$, $M_2\hspace{0.33em}(0.5\hspace{0.33em}d,\hspace{0.33em}0.5)$, and $M_3\hspace{0.33em}(0.9\hspace{0.33em}d,\hspace{0.33em}0.9)$ was numerically analyzed.

The results showed that

• The stress tensor component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ takes on maximum compressive values at point $M_3$, which are approximately nine times greater than the maximum tensile values at points $M_1$ and $M_2$.
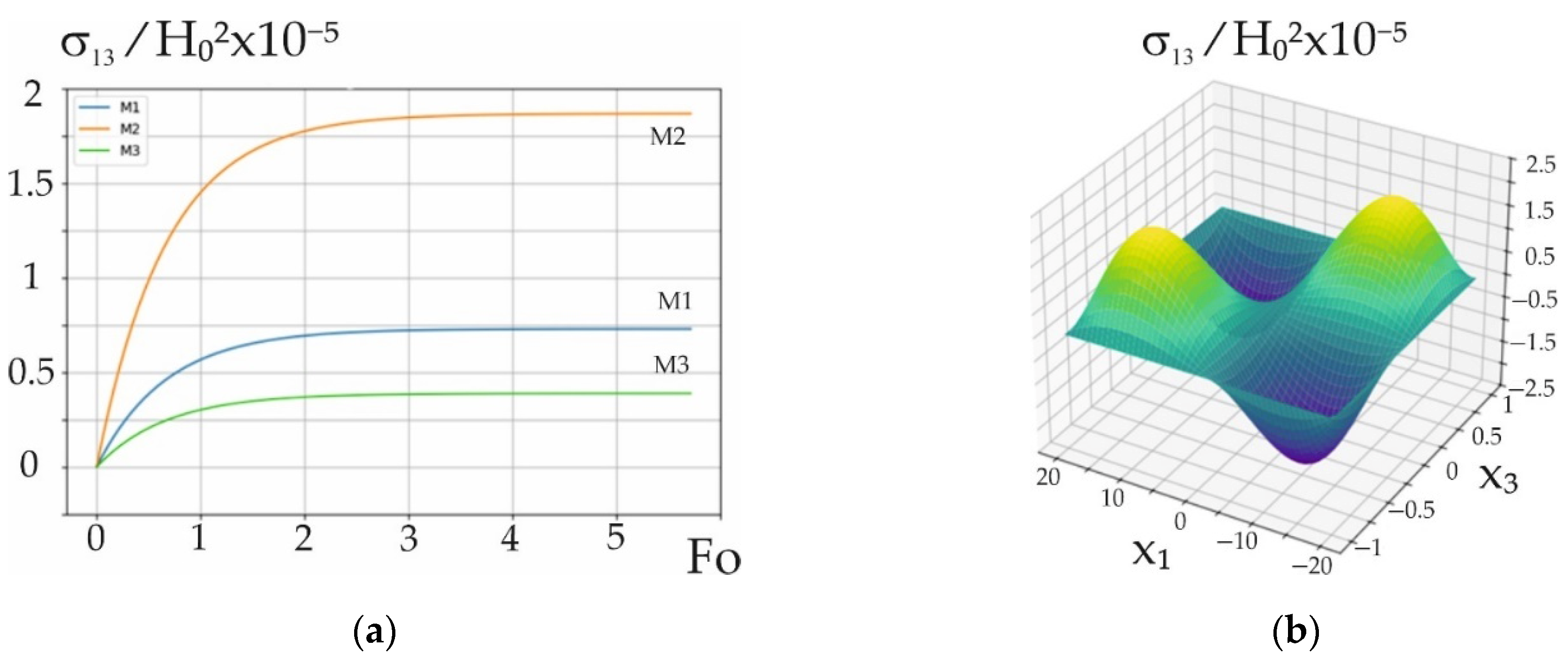
• The stress tensor component ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$ at all characteristic points has tensile values that are at maximum at point $M_2$ and are approximately five times smaller than the values of the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ at this point.
• The stress tensor component ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$ at all characteristic points has tensile values that are at maximum at point $M_1$ and are approximately four times larger than the same maximum tensile values of the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ at this point.
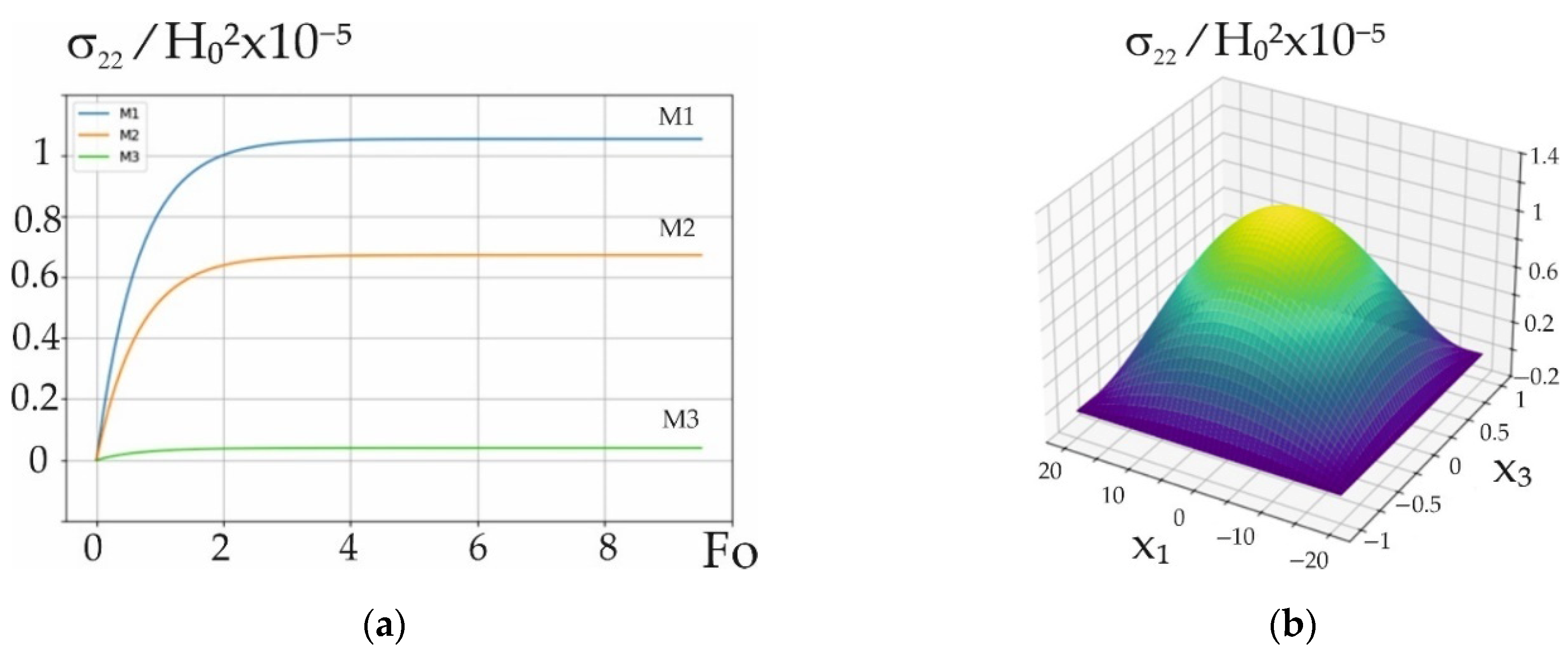
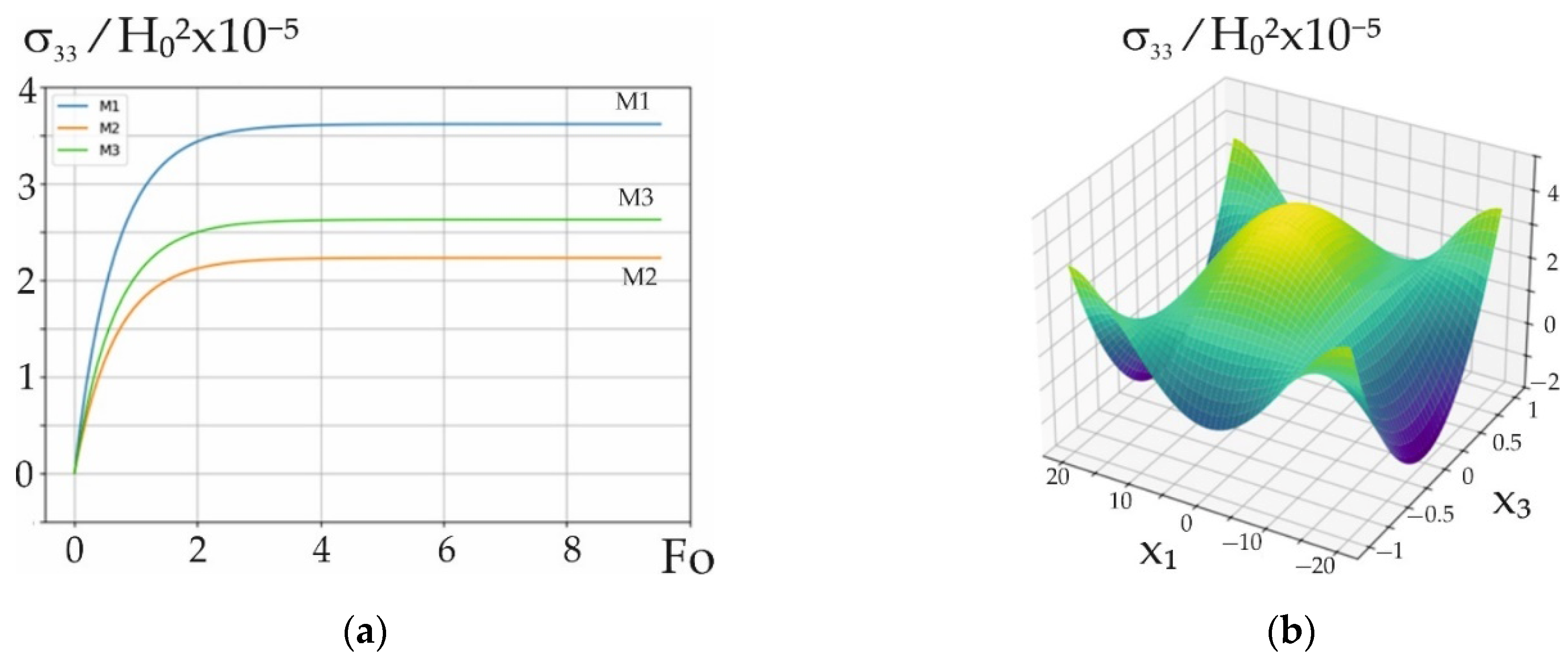
• The stress tensor component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ at all characteristic points has tensile values that are at maximum at point $M_1$ and are approximately three times larger than the same maximum tensile values of the component ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$ at this point.

It is determined that the maximum compressive stresses have the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ at point $M_3$, and the maximum tensile stresses have the component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$at point $M_1$.

Accordingly, the maximum compressive stresses of the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ at point $M_3$ are approximately two times smaller than the maximum tensile stresses of the component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ at point $M_1$.

The maximum values of shear stresses ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$ are approximately an order of magnitude smaller than the same values of normal stresses ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ and ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$and approximately two orders of magnitude smaller than the same values of normal stresses ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}.$

Analysis of the distribution of the stress tensor components over the cross-sectional area of the panel showed that

• The maximum values of the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ of the stress tensor are taken at points corresponding to the midpoints of the sides of the rectangle of the strip cross-section, and the maximum compressive values are taken at the corner points of this rectangle.
• The component ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$ takes on either the compressive or tensile maximum values of the same magnitude at opposite points on the diagonals of the cross-sectional rectangle.
• The component ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$ takes maximum values at the intersection point of the diagonals of the cross-sectional rectangle, and minimum values on the sides of this rectangle.
• The component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ takes on maximum tensile values at the intersection point of the diagonals of the cross-sectional rectangle and at its corner points and takes on maximum compressive values at the midpoints of the sides of the rectangle. Note that the maximum tensile values are approximately equal to the maximum compressive values of this component.

Let us present the results of the analysis of the change in time of the components of the stress tensor in the characteristic points $M_1\hspace{0.33em}(0.25\hspace{0.33em}d,\hspace{0.33em}0.25)$, $M_2\hspace{0.33em}(0.5\hspace{0.33em}d,\hspace{0.33em}0.5)$, and $M_3\hspace{0.33em}(0.9\hspace{0.33em}d,\hspace{0.33em}0.9)$ of a panel with half-width $d=20,$ subjected to in-depth induction heating by a quasi-steady electromagnetic field with ${\delta }_0=1$:

• The stress tensor component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ takes on maximum compressive values at point $M_3$, which are approximately 12 times larger than the maximum tensile values at points $M_1$ and $M_2$.
• The stress tensor component ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$ takes on maximum tensile values at point $M_2$, which are approximately five times larger than the same maximum tensile values at point $M_3$.
• The stress tensor component ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$ takes on maximum tensile values at point $M_1$, which are approximately 20 times larger than the same values at point $M_3$.
• The stress tensor component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ takes on maximum tensile values at point $M_1$, which are approximately 1.5 times larger than the same maximum tensile values at point $M_2$.

Analysis of the distribution of the stress tensor components over the cross-sectional area of the panel showed that

• The maximum tensile values of the component ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ of the stress tensor are taken at points corresponding to the midpoints of the sides of the cross-sectional rectangle, and the maximum compressive values are taken at the corner points of this rectangle.
• The component ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$ takes either compressive or tensile maximum values of the same magnitude at opposite points of the diagonals of the cross-sectional rectangle.
• The component ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$ takes maximum compressive values at the corner points of the cross-sectional rectangle and maximum tensile values at the intersection point of the diagonals of this rectangle.
• The component ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ takes maximum tensile values at the corner points and at the intersection of the diagonals of the cross-sectional rectangle, and maximum compressive values at the midpoints of its sides. Note that the maximum tensile values are approximately of the same order as the maximum compressive values of this component.

During in-depth heating, the maximum values of tensile stresses ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ are approximately 50 times smaller than the same values under near-surface induction heating. The qualitative nature of the change in compressive and tensile stresses under in-depth heating conditions is approximately the same as under near-surface heating conditions. Accordingly, the maximum values of the stress tensor components under in-depth heating conditions are significantly smaller than the same values under near-surface heating conditions. The stresses ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ are approximately 50 times smaller; the stresses ${\displaystyle \frac{{\sigma }_{13}}{H_0^2}}$, ${\displaystyle \frac{{\sigma }_{22}}{H_0^2}}$, and ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$ are approximately 40 times smaller. The largest in magnitude are compressive stresses ${\displaystyle \frac{{\sigma }_{11}}{H_0^2}}$ and tensile stresses ${\displaystyle \frac{{\sigma }_{33}}{H_0^2}}$.

5.2. Analysis of Stress Intensity

Figure 9 shows the time variation in the stress intensity ${\sigma }_i/H_0^2$during induction heating by the EMF at $Bi=1$ for both near-surface heating (Figure 9a) and in-depth heating (Figure 9b). Additionally, Figure 10 presents the spatial distribution of the stress intensity ${\sigma }_i/H_0^2$ over the cross-sectional area of the panel under consideration at $Bi=1$and $F_0=4$—corresponding to the moment when the stress intensity reaches its peak—for induction heating with penetration depths ${\delta }_0=\mathrm{0,1}$ (Figure 10a) and ${\delta }_0=1$ (Figure 10b).

The characteristic points $M_1\hspace{0.33em}(0.25\hspace{0.33em}d,\hspace{0.33em}0.25)$, $M_2\hspace{0.33em}(0.5\hspace{0.33em}d,\hspace{0.33em}0.5)$, and $M_3\hspace{0.33em}(0.9\hspace{0.33em}d,\hspace{0.33em}0.9)$ of the cross-section of the tungsten panel under consideration (curves M1-M3, respectively) were used to calculate the change in Fourier time of the stress intensities ${\sigma }_i/H_0^2$.

6. Conclusions

Based on the conducted analysis, the following key findings were established:

(1)

The highest stress intensity values in the panel during induction heating by a quasi-steady electromagnetic field occur near its edges. These peak values are strongly influenced by the dimensionless penetration depth parameter ${\delta }_0$ and the Biot number.

(2)

The stress intensity distribution at specific characteristic points (M1–M3) of the panel’s cross-section varies significantly with changes in $\delta$ ₀ and Bi.

(3)

At a fixed ${\delta }_0$, reducing the Biot number leads to a convergence in the stress intensity values at the selected points. Notably, when $Bi=0.01$, the stress values are almost the same. This behavior reflects a heating regime approaching thermally insulated boundary conditions on the panel’s lateral surfaces.

(4)

Under near-surface induction heating conditions (${\delta }_0=0.1$, $Bi=1)$ the maximum stress intensity ${\sigma }_i^{max}$ is approximately 40 times greater than that observed under in-depth heating (${\delta }_0=1$, $Bi=1$). Hence, near-surface heating is more effective for achieving higher stress levels in tungsten panels.

(5)

A tenfold reduction in the Biot number results in a tenfold increase in the time required for the stress intensity to reach a steady-state level, regardless of the induction heating mode.

(6)

For both near-surface and in-depth heating scenarios, the maximum stress intensity scales quadratically with the amplitude $H_0$ in the steady-state electromagnetic oscillations.

The numerical investigation of stress intensity behavior in a tungsten panel and the newly revealed dependencies on induction heating conditions and convective heat transfer parameters provide valuable insights. These findings have both theoretical and practical importance for engineering applications, particularly in predicting the load-bearing capacity of electroconductive plate structures subjected to quasi-steady electromagnetic fields.

The proposed two-dimensional physical and mathematical model and calculation scheme for studying the thermomechanical behavior of homogeneous nonferromagnetic conductive elements under the action of a quasi-stationary electromagnetic field also allows us to investigate the thermomechanical properties of conductive elements made of structurally heterogeneous materials, in particular, matrix metal composites based on tungsten and copper. To do this, experimenters need to determine the physical and mechanical characteristics of the newly created heterogeneous nonferromagnetic materials. These characteristics can be used to theoretically predict, based on the proposed physical and mathematical model, the thermomechanical behavior of plate elements made not only of homogeneous materials but also of structurally heterogeneous materials.