A Ladder-Type Carbon Trading-Based Low-Carbon Economic Dispatch Model for Integrated Energy Systems with Flexible Load and Hybrid Energy Storage Optimization
Abstract
1. Introduction
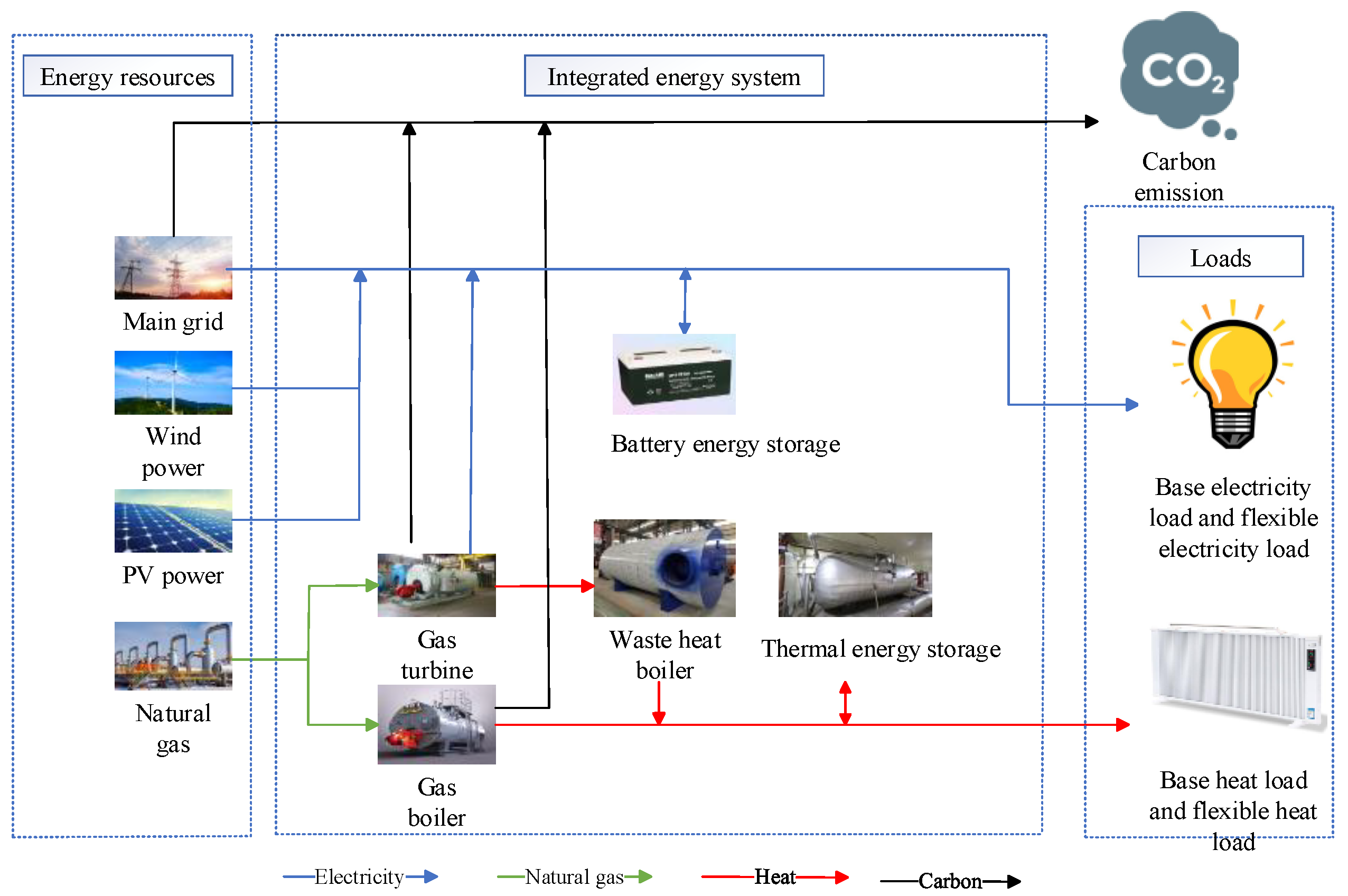
2. IES Structure and Ladder-Type Carbon Trading Mechanism
2.1. Structure of the IES
2.2. Carbon Credit Allowance Calculation Model
2.3. Actual Carbon Emissions Calculation Model
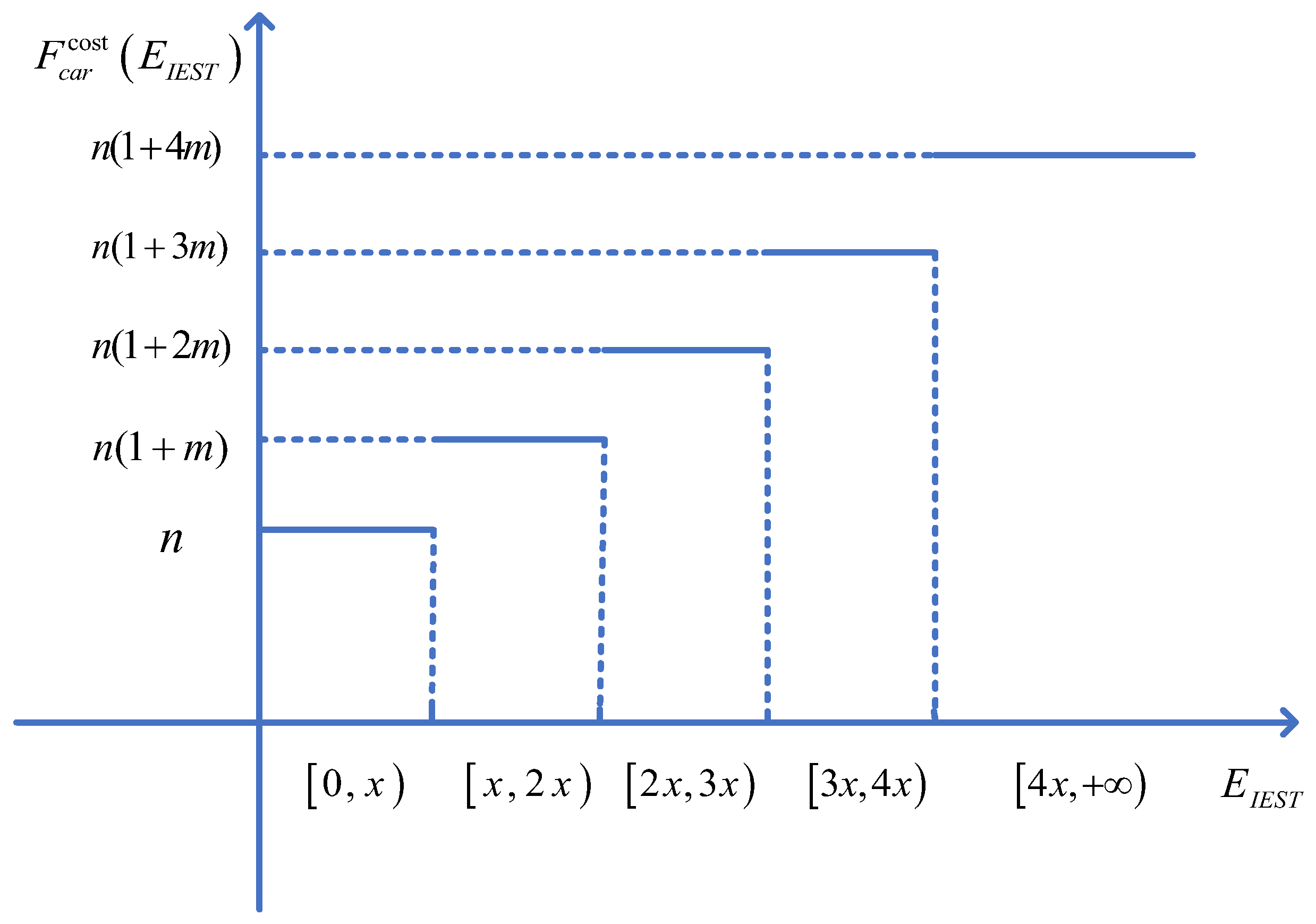
2.4. Ladder-Type Carbon Trading Mechanism
3. Low-Carbon Economic Dispatch Optimization Model for the IES
3.1. Mathematical Models for Flexible Loads
3.1.1. Shiftable Loads
3.1.2. Transferable Loads
3.1.3. Reducible Loads
3.2. Mathematical Models for Battery Energy Storage and Thermal Energy Storage Systems
3.3. Mathematical Models for GT, GB, WHB, and Wind and PV Power Generation Systems
3.4. Electrical and Thermal Power Balance Constraints
3.5. Objective Function of Low-Carbon Economic Dispatch Optimization Model for the IES
4. Case Studies
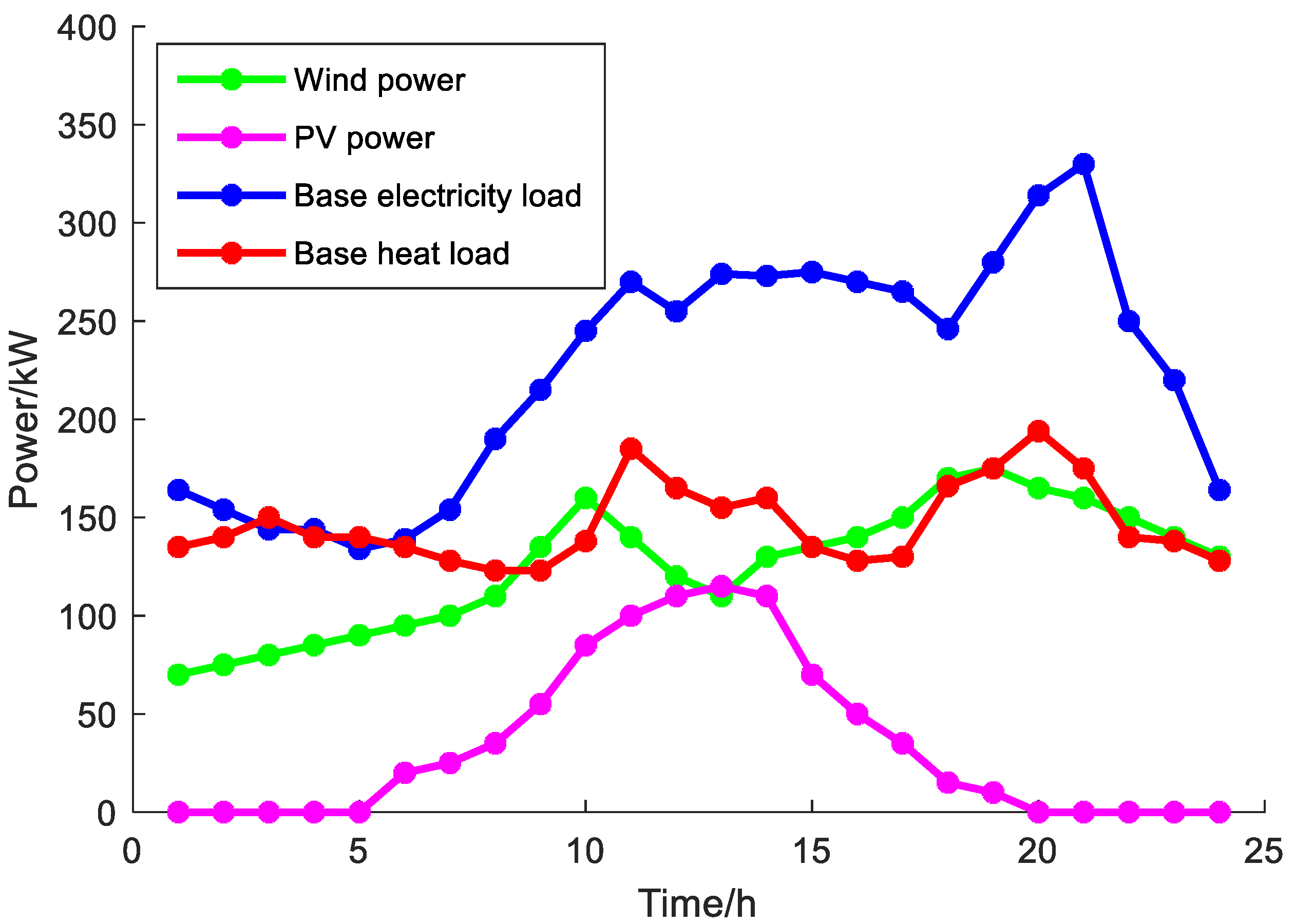
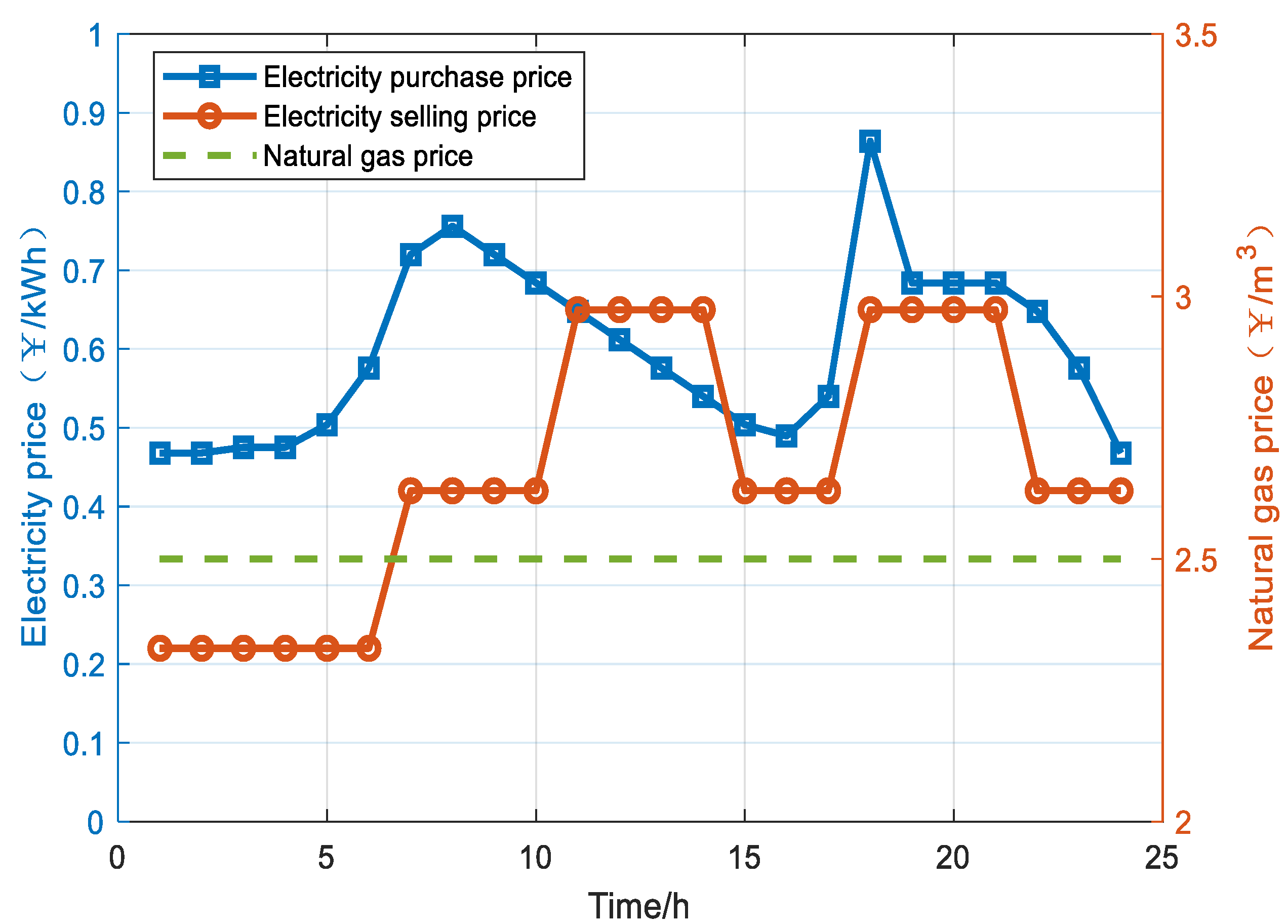
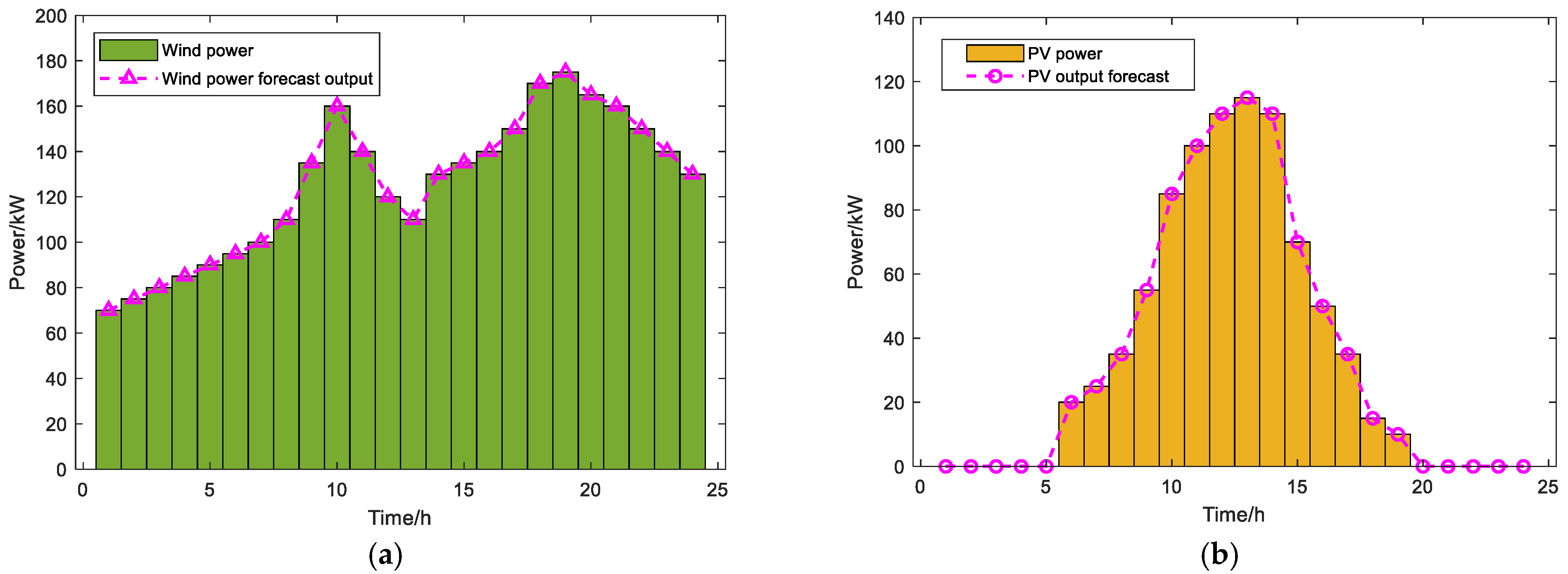
4.1. Parameter Settings
4.2. Results and Analysis
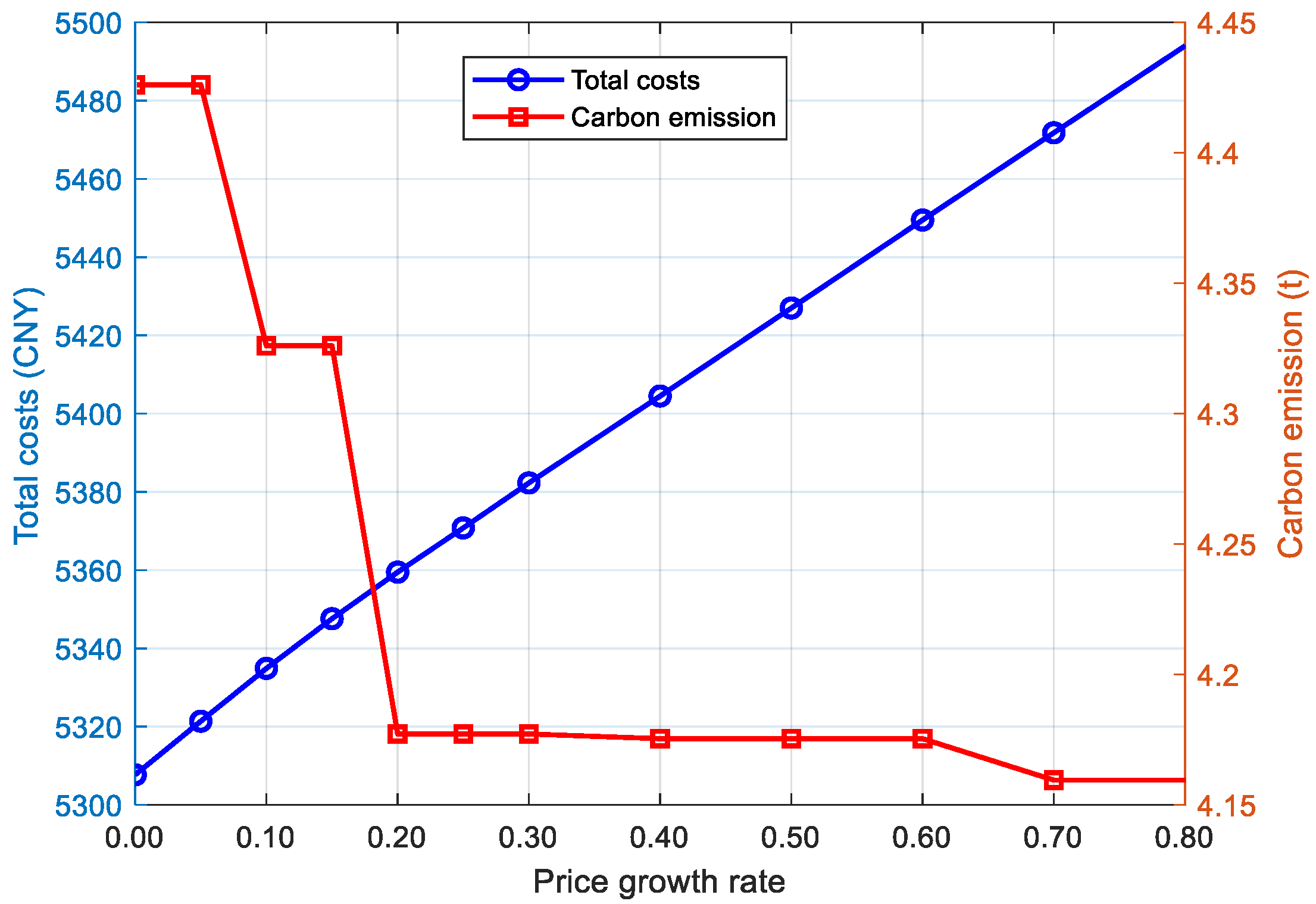
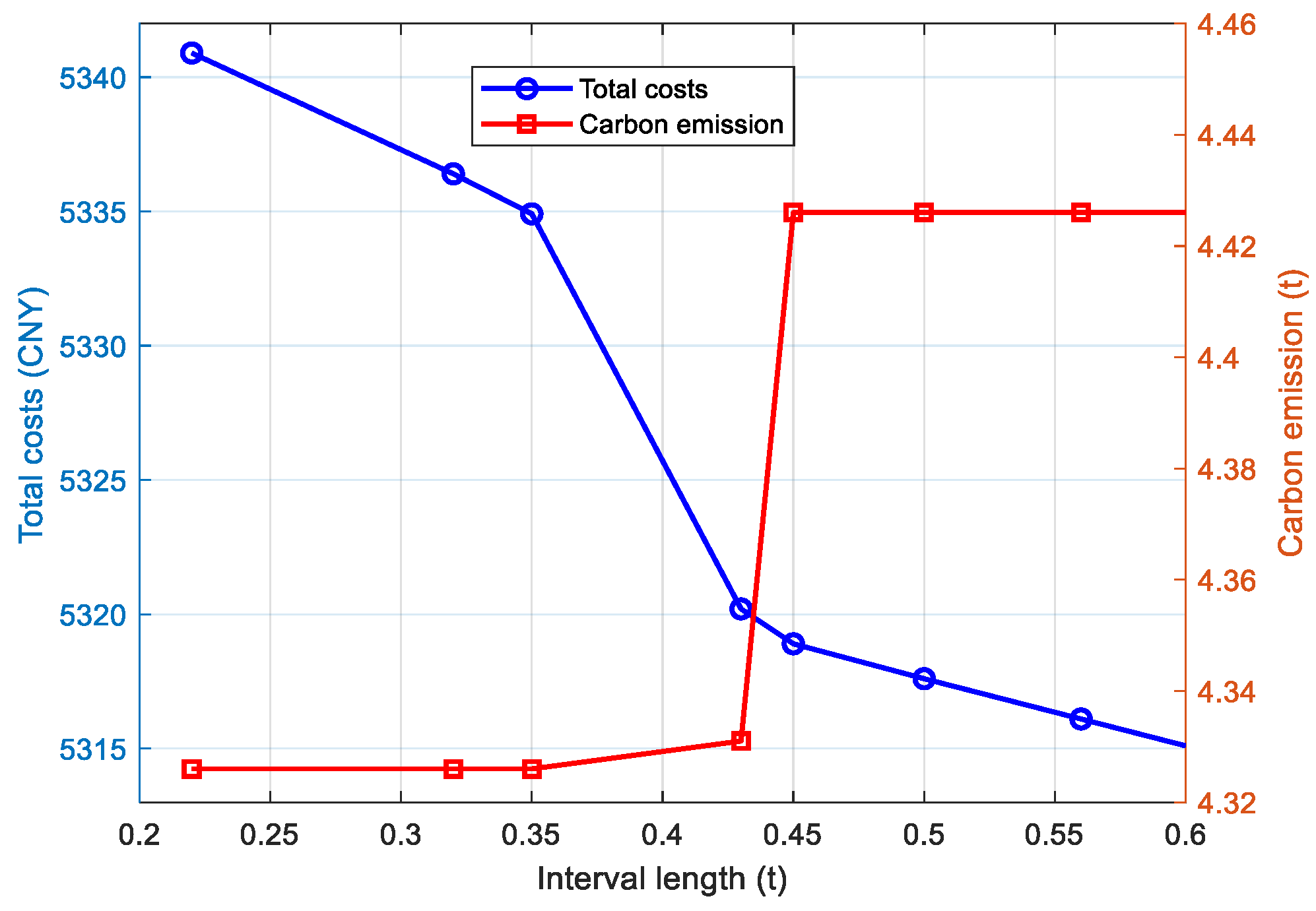
4.2.1. Sensitivity Analysis of Carbon Trading Parameters
- Impact of Carbon Trading Base Price (n)
- 2.
- Impact of Price Growth Rate (m)
- 3.
- Impact of Interval Length (x):
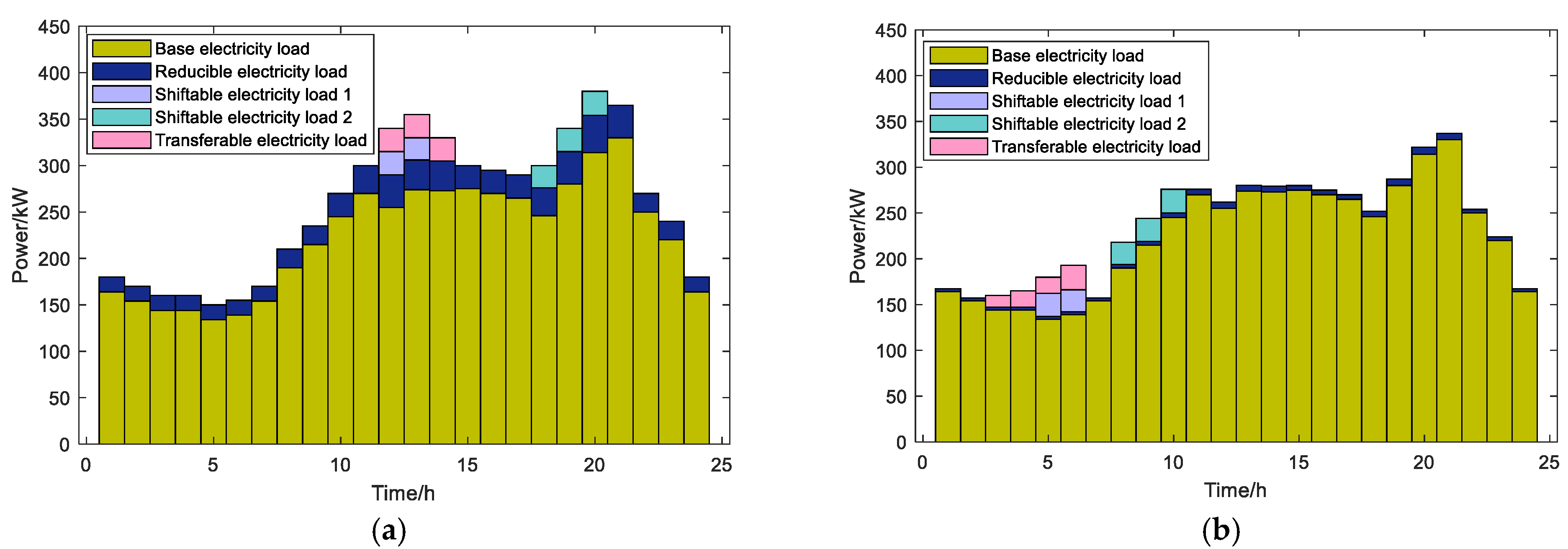
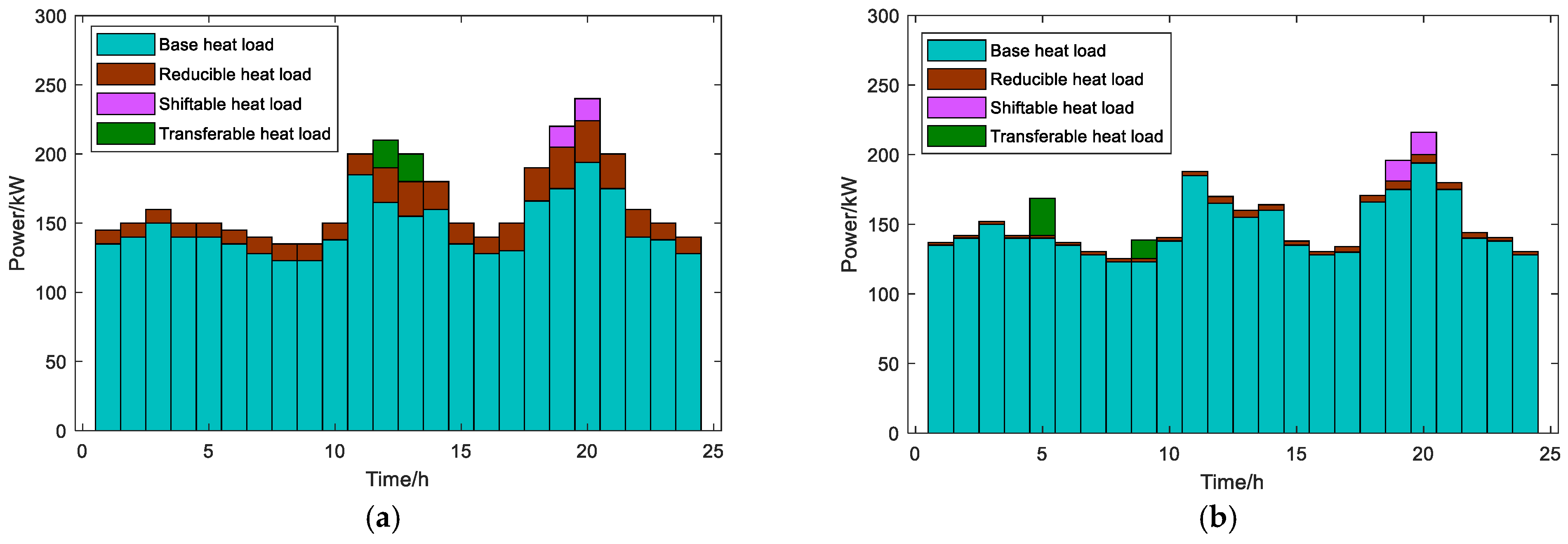
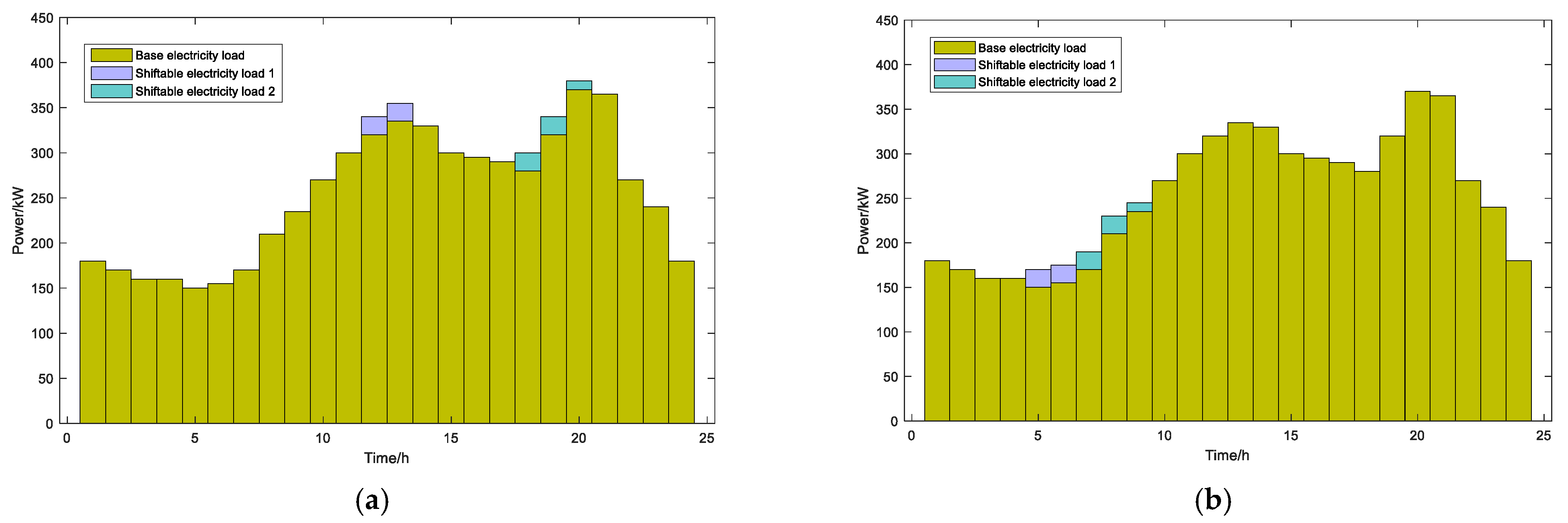
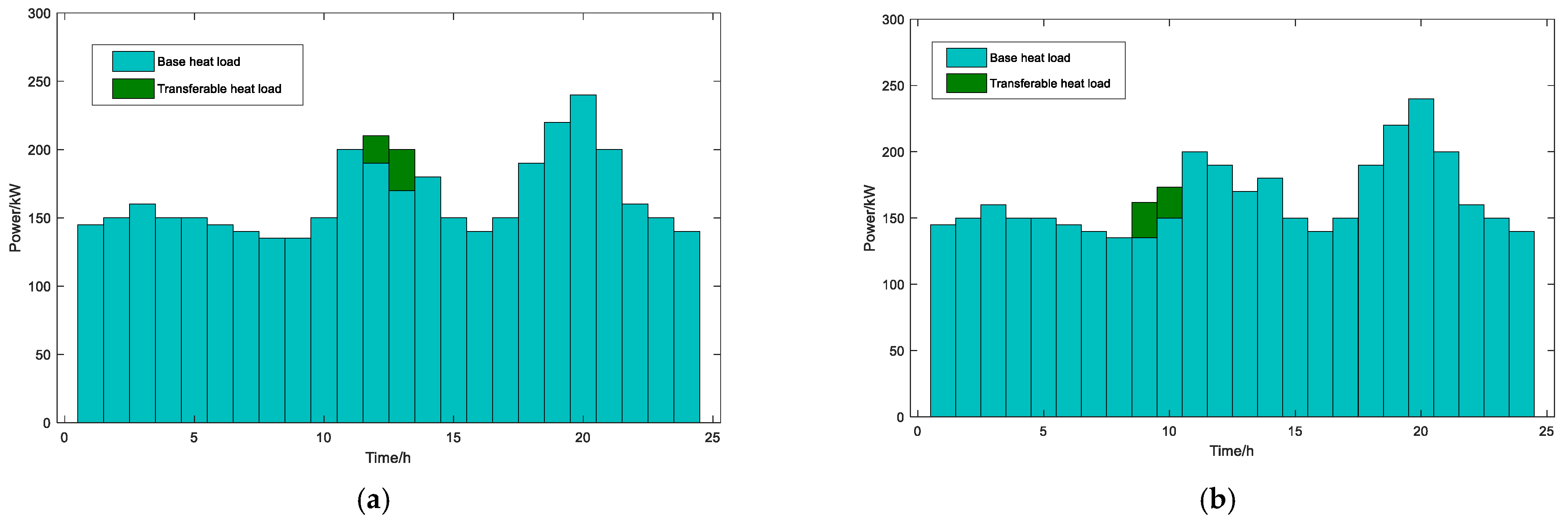
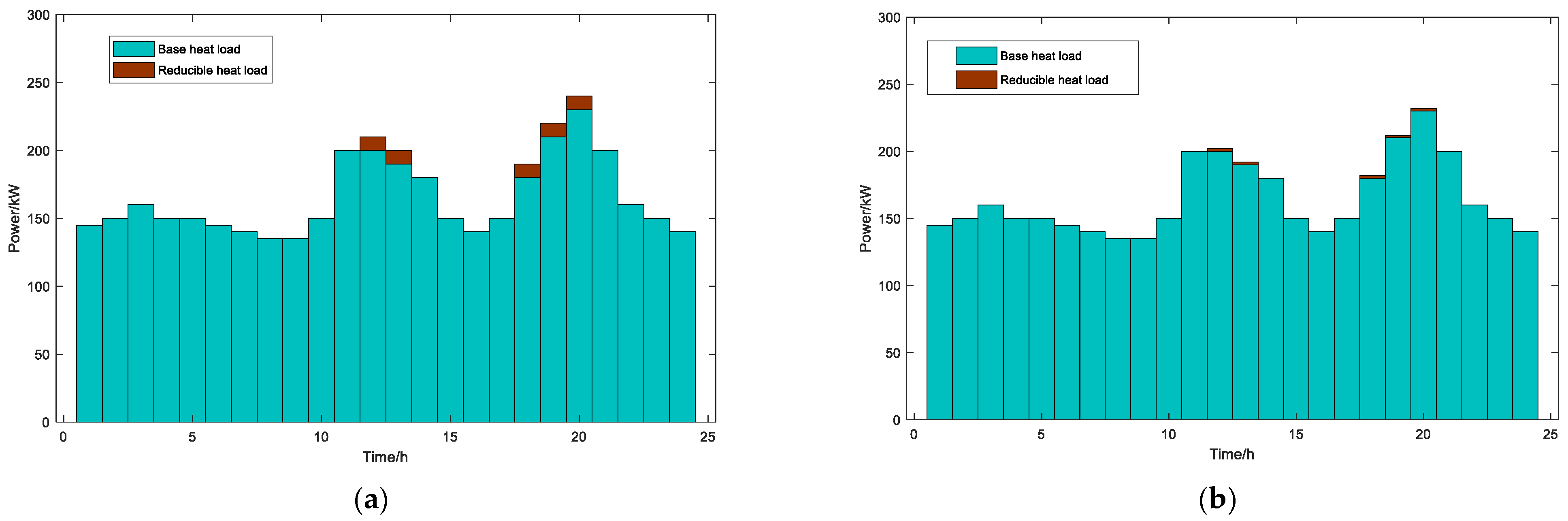
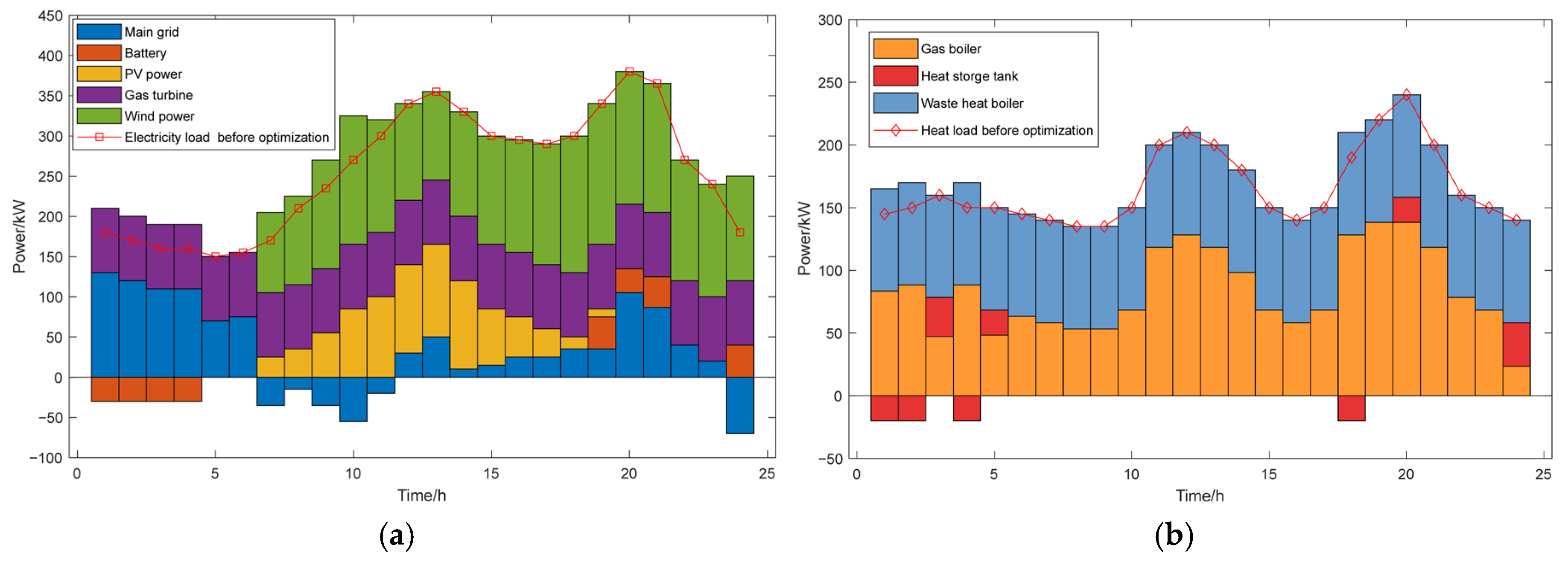
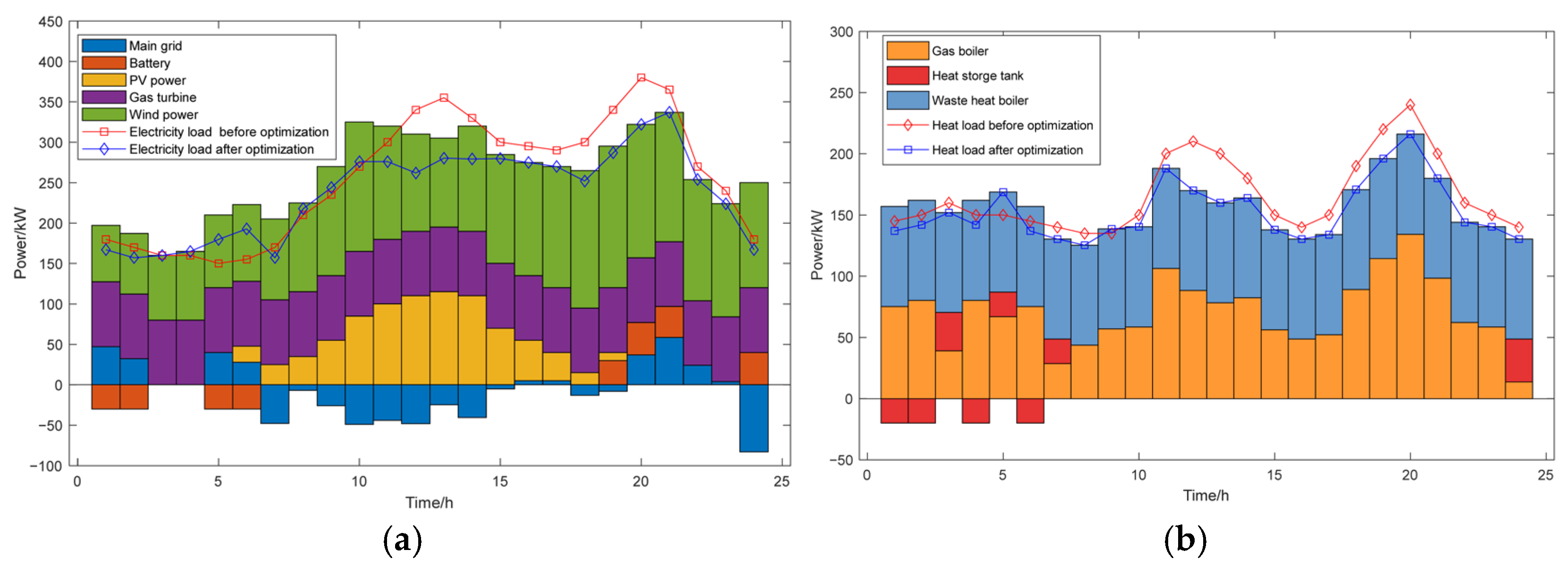
4.2.2. Optimal Scheduling Results Under Scenario 1
4.2.3. Comparative Analysis Across Scenarios
4.2.4. Impact of Hybrid Energy Storage System on System Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, J.; Chen, Z.; Hao, T.; Zhu, S.; Tang, Y.; Liu, H. Optimal intraday rolling operation strategy of integrated energy system with multi-storage. In Proceedings of the 2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 20–22 October 2018; pp. 1–5. [Google Scholar]
- Li, X.; Wang, W.; Wang, H. Hybrid time-scale energy optimal scheduling strategy for integrated energy system with bilateral interaction with supply and demand. Appl. Energy 2021, 285, 116458. [Google Scholar] [CrossRef]
- Wang, W.; Huang, S.; Zhang, G.; Liu, J.; Chen, Z. Optimal operation of an integrated electricity-heat energy system considering flexible resources dispatch for renewable integration. J. Mod. Power Syst. Clean Energy 2021, 9, 699–710. [Google Scholar] [CrossRef]
- Chen, W.; Chen, H.; Chen, J.; Chen, S.; Lin, X.; Li, Y. A Low-Carbon Economic Scheduling Model of Integrated Energy System Considering Ladder-Type Carbon Trading. In Proceedings of the 2022 IEEE 6th Conference on Energy Internet and Energy System Integration (EI2), Chengdu, China, 11–13 November 2022; pp. 2548–2551. [Google Scholar]
- Chen, J.; Ning, K.; Zhang, Q.; Xu, Q.; Chen, W.; Yu, X. Low-carbon optimization operation of integrated energy system considering ladder-type carbon trading and carbon capture. In Proceedings of the 2022 7th Asia Conference on Power and Electrical Engineering (ACPEE), Hangzhou, China, 15–17 April 2022; pp. 1916–1921. [Google Scholar]
- Zhang, G.; Liang, J.; Li, F.; Xie, C.; Han, L.; Zhang, Y. Low-carbon scheduling model of electricity-gas-heat integrated energy system considering ladder-type carbon trading mechanism, vehicles charging, and multimode utilization of hydrogen. IEEE Access 2024, 12, 132926–132938. [Google Scholar] [CrossRef]
- Fan, Y.; Chen, Y.; Cui, M. Electric-Hydrogen Integrated Energy System Optimization Considering Ladder-Type Carbon Trading Mechanism and User-Side Flexible Load. In Proceedings of the 2023 IEEE 6th International Electrical and Energy Conference (CIEEC), Hefei, China, 12–14 May 2023; pp. 1780–1784. [Google Scholar]
- Zhou, W.; Sun, Y.; Wang, J.; He, Y.; Wu, P.; Chen, L. Robust Optimal Dispatch of Park-level Integrated Energy System Considering Ladder-type Carbon Trading Mechanism. In Proceedings of the 2022 Power System and Green Energy Conference (PSGEC), Shanghai, China, 25–27 August 2022; pp. 38–43. [Google Scholar]
- Liu, Y.; Li, X.; Liu, Y. A low-carbon and economic dispatch strategy for a multi-microgrid based on a meteorological classification to handle the uncertainty of wind power. Sensors 2023, 23, 5350. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yan, Z.; Yao, Y.; Deng, Y.; Shao, C.; Zhang, Q. Coordinated low-carbon dispatching on source-demand side for integrated electricity-gas system based on integrated demand response exchange. IEEE Trans. Power Syst. 2023, 39, 1287–1303. [Google Scholar] [CrossRef]
- Li, Q.; He, M.; Tang, X.; Lee, W.-J.; Zhang, Z. Capacity configuration in integrated energy production unit considering ladder-type carbon trading under CCER quota. IEEE Trans. Ind. Appl. 2024, 61, 884–894. [Google Scholar] [CrossRef]
- Liu, S.; Ma, H.; Huang, C.; Mi, J.; Din, S.; Wang, J. Demand response-based operation optimization of a typical industrial and agricultural IES. In Proceedings of the 2023 IEEE 7th Conference on Energy Internet and Energy System Integration (EI2), Hangzhou, China, 15–18 December 2023; pp. 1065–1070. [Google Scholar]
- Ma, L.; Han, N.; Chen, S.; Gao, T. A study of day-ahead scheduling strategy of demand response for resident flexible load in smart grid. In Proceedings of the 2020 Management Science Informatization and Economic Innovation Development Conference (MSIEID), Guangzhou, China, 18–20 December 2020; pp. 197–200. [Google Scholar]
- Tu, J.; Zhou, M.; Cui, H.; Li, F. An equivalent aggregated model of large-scale flexible loads for load scheduling. IEEE Access 2019, 7, 143431–143444. [Google Scholar] [CrossRef]
- Wang, J.; Liu, J.; Zheng, Y.; Kong, X. Optimal Dispatch of Park-level Integrated Energy System with Flexible Loads and Equipment Variable Operating Conditions. In Proceedings of the 2024 IEEE 2nd International Conference on Power Science and Technology (ICPST), Dali, China, 9–11 May 2024; pp. 1735–1740. [Google Scholar]
- Wen, Y.; Luo, Y.; Dong, X.; Xie, X. Thermal and electrical demand response based on robust optimization. Electr. Power Syst. Res. 2023, 225, 109883. [Google Scholar] [CrossRef]
- Wu, M.; Yan, R.; Zhang, J.; Fan, J.; Wang, J.; Bai, Z.; He, Y.; Cao, G.; Hu, K. An enhanced stochastic optimization for more flexibility on integrated energy system with flexible loads and a high penetration level of renewables. Renew. Energy 2024, 227, 120502. [Google Scholar] [CrossRef]
- Liu, C.; Wang, C.; Yao, W.; Liu, C. Distributed Low-carbon Economic Dispatching for Multiple Park-level Integrated Energy Systems Based on Improved Shapley Value. IEEE Trans. Ind. Appl. 2024, 60, 8088–8102. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, P.; Ji, X.; Yang, M.; Ye, P. Low-Carbon Economic Dispatch of Integrated Energy Systems Considering Full-Process Carbon Emission Tracking and Low Carbon Demand Response. IEEE Trans. Netw. Sci. Eng. 2024, 11, 5417–5430. [Google Scholar] [CrossRef]
- Zhao, H.; Zhang, C.; Zhao, Y.; Wang, X. Low-carbon economic dispatching of multi-energy virtual power plant with carbon capture unit considering uncertainty and carbon market. Energies 2022, 15, 7225. [Google Scholar] [CrossRef]
- Cui, Y.; Zheng, J.; Wu, W.; Xu, K.; Ji, D.; Di, T. Framework and Outlooks of Multi-Source–Grid–Load Coordinated Low-Carbon Operational Systems Considering Demand-Side Hierarchical Response. Energies 2024, 17, 6208. [Google Scholar] [CrossRef]
- Li, J.; Yang, W.; Zhang, A.; Li, Q. Low-Carbon Optimal Operation of Park Integrated Energy System Considering Carbon Trading Mechanism. In Proceedings of the 2023 Panda Forum on Power and Energy (PandaFPE), Chengdu, China, 27–30 April 2023; pp. 1086–1091. [Google Scholar]
- Hu, J.; Liu, X.; Shahidehpour, M.; Xia, S. Optimal operation of energy hubs with large-scale distributed energy resources for distribution network congestion management. IEEE Trans. Sustain. Energy 2021, 12, 1755–1765. [Google Scholar] [CrossRef]







| Equipment | Parameter | Value |
|---|---|---|
| GB | /kW /kW | 0.35 0 150 |
| GT | /kW /kW /kW /kW | 0.35 0.10 0 80 15 15 |
| WHB | /kW /kW | 0.65 0 120 |
| Wind Power Generation System | /(CNY/kWh) /(CNY/kWh) | 0.50 0.20 |
| PV Power Generation System | /(CNY/kWh) /(CNY/kWh) | 0.62 0.30 |
| Electricity Energy Storage System | /kW /kW /kW /kW | 0.95 0.95 0.4 30 40 30 40 0.3 1 |
| Heat Energy Storage System | /kW /kW /kW /kW /kWh /kWh | 0.95 0.95 0.001 0.45 20 30 20 30 40 160 |
| Main Power Grid | /kW | 180 |
| Load Type | Original Operating Time | Original Load Power | Acceptable Operating Time | Unit Energy Compensation Cost |
|---|---|---|---|---|
| Shiftable electricity load 1 | 12:00~13:00 | 25,24 | 2:00~10:00 | 0.2 |
| Shiftable electricity load 2 | 18:00~20:00 | 24,25,26 | 7:00~10:00 | 0.2 |
| Shiftable heat load | 19:00~20:00 | 15,16 | 5:00~10:00 | 0.1 |
| Load Type | Original Operating Time | Original Load Power | Acceptable Operating Time | Lower and Upper Power Limits | Unit Energy Compensation Cost |
|---|---|---|---|---|---|
| Transferable electricity load | 12:00~14:00 | 25,25,25 | 3:00~10:00 | 8~26.7 | 0.3 |
| Transferable heat load | 12:00~13:00 | 20,20 | 5:00~10:00 | 8~26.7 | 0.2 |
| Load Type | Maximum Allowable Reduction Percentage | Unit Energy Compensation Cost |
|---|---|---|
| Reducible electricity load | 0.8 | 0.4 |
| Reducible heat load | 0.8 | 0.2 |
| Scenario 1 | Total Costs (CNY) | Carbon Trading Costs (CNY) | Operation Costs (CNY) | Renewable Energy Output (kW) | Carbon Emission (t) | Renewable Energy Curtailment (kW) | Renewable Energy Curtailment Rate (%) |
|---|---|---|---|---|---|---|---|
| Only shiftable load | 5654.65 | 282.50 | 5372.15 | 3765 | 4.80 | 85 | 2.21 |
| Only Transferable load | 5670.05 | 282.50 | 5387.55 | 3775 | 4.80 | 75 | 1.95 |
| Only reducible load | 5612.65 | 282.04 | 5330.61 | 3755 | 4.78 | 95 | 2.47 |
| Scenario | Total Costs (CNY) | Carbon Trading Costs (CNY) | Operation Costs (CNY) | Renewable Energy Output (kW) | Carbon Emission (t) | Renewable Energy Curtailment (kW) | Renewable Energy Curtailment Rate (%) |
|---|---|---|---|---|---|---|---|
| 1 | 5334.91 | 239.88 | 5095.03 | 3850.00 | 4.33 | 0 | 0.00 |
| 2 | 5665.74 | 282.49 | 5383.25 | 3835.00 | 4.80 | 15 | 0.40 |
| 3 | 5347.86 | - | 5347.86 | 3335.00 | 5.53 | 515 | 13.38 |
| Scenario 1 | Total Costs (CNY) | Carbon Trading Costs (CNY) | Operation Costs (CNY) | Renewable Energy Output (kW) | Carbon Emission (t) | Renewable Energy Curtailment (kW) | Renewable Energy Curtailment Rate (%) |
|---|---|---|---|---|---|---|---|
| With energy storage | 5334.91 | 239.88 | 5095.03 | 3850.00 | 4.33 | 0 | 0.00 |
| Without energy storage | 5463.25 | 268.20 | 5195.05 | 3770.00 | 4.65 | 80 | 2.08 |
| BESS Capacity (kWh) | Total Cost (CNY) | Carbon Trading Cost (CNY) | Renewable Energy Output (kW) | Renewable Energy Curtailment (kW) | Carbon Emissions (t) |
|---|---|---|---|---|---|
| 120 | 5368.84 | 243.71 | 3834 | 16 | 4.36 |
| 160 | 5379.07 | 242.44 | 3840 | 10 | 4.35 |
| 200 | 5334.91 | 239.88 | 3850 | 0 | 4.33 |
| TES Capacity (kWh) | Total Cost (CNY) | Carbon Trading Cost (CNY) | Renewable Energy Output (kW) | Renewable Energy Curtailment (kW) | Carbon Emissions (t) |
|---|---|---|---|---|---|
| 120 | 5420.53 | 248.15 | 3827 | 23 | 4.42 |
| 140 | 5394.67 | 245.93 | 3831 | 19 | 4.38 |
| 160 | 5368.84 | 243.71 | 3834 | 16 | 4.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, L.; Zhong, F.; Lai, C.S.; Zhong, B.; Xiao, Q.; Hsu, W. A Ladder-Type Carbon Trading-Based Low-Carbon Economic Dispatch Model for Integrated Energy Systems with Flexible Load and Hybrid Energy Storage Optimization. Energies 2025, 18, 3679. https://doi.org/10.3390/en18143679
Huang L, Zhong F, Lai CS, Zhong B, Xiao Q, Hsu W. A Ladder-Type Carbon Trading-Based Low-Carbon Economic Dispatch Model for Integrated Energy Systems with Flexible Load and Hybrid Energy Storage Optimization. Energies. 2025; 18(14):3679. https://doi.org/10.3390/en18143679
Chicago/Turabian StyleHuang, Liping, Fanxin Zhong, Chun Sing Lai, Bang Zhong, Qijun Xiao, and Weitai Hsu. 2025. "A Ladder-Type Carbon Trading-Based Low-Carbon Economic Dispatch Model for Integrated Energy Systems with Flexible Load and Hybrid Energy Storage Optimization" Energies 18, no. 14: 3679. https://doi.org/10.3390/en18143679
APA StyleHuang, L., Zhong, F., Lai, C. S., Zhong, B., Xiao, Q., & Hsu, W. (2025). A Ladder-Type Carbon Trading-Based Low-Carbon Economic Dispatch Model for Integrated Energy Systems with Flexible Load and Hybrid Energy Storage Optimization. Energies, 18(14), 3679. https://doi.org/10.3390/en18143679









