Experimental Study of an Evaporative Cooling System in a Rotating Vertical Channel with a Circular Cross-Section for Large Hydro-Generators
Abstract
1. Introduction
2. Basic Theory
3. Experimental Platform Design
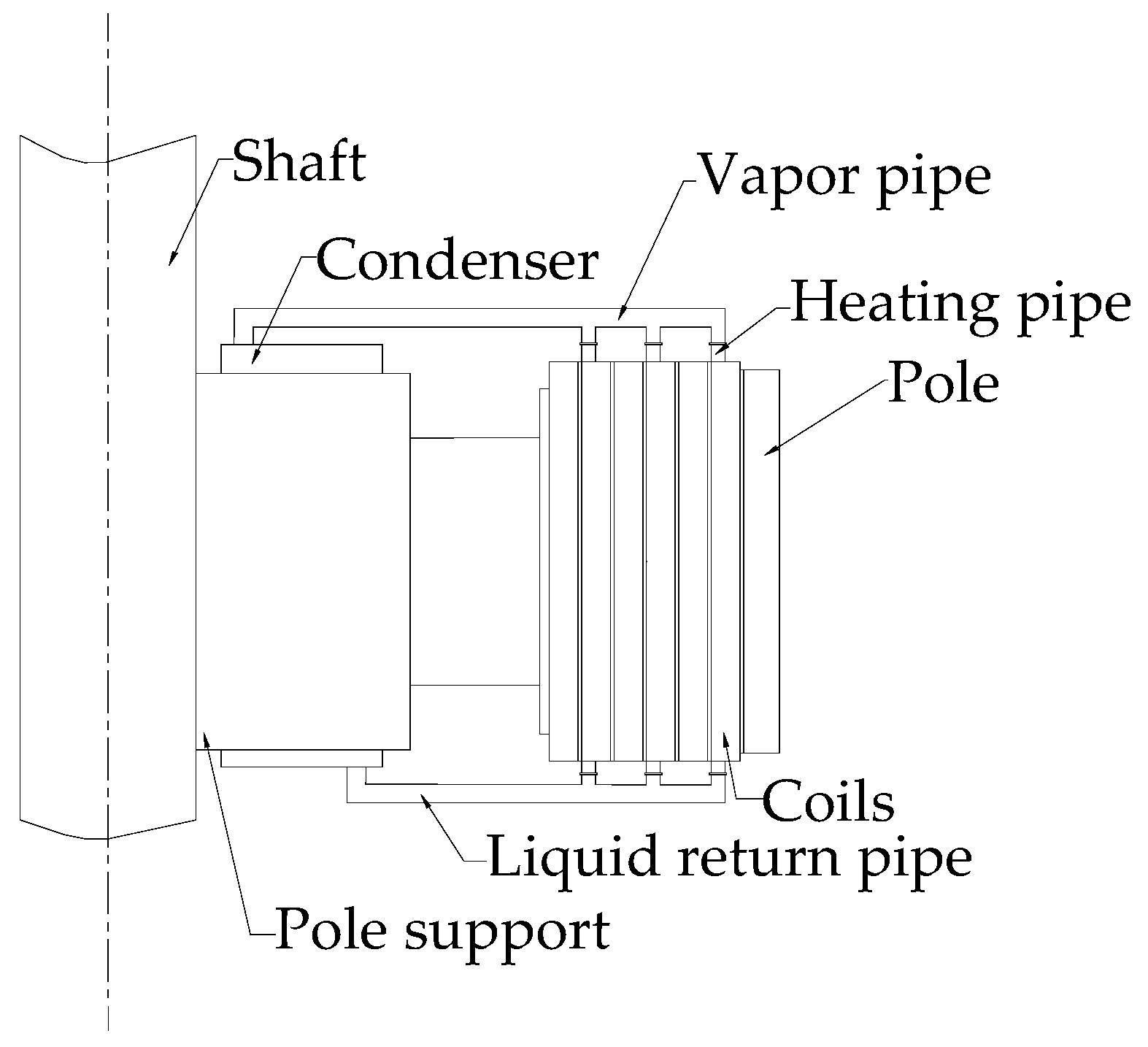
3.1. Basic Structure and Measurement Points
3.2. Experimental Conditions
4. Experimental Results and Discussion
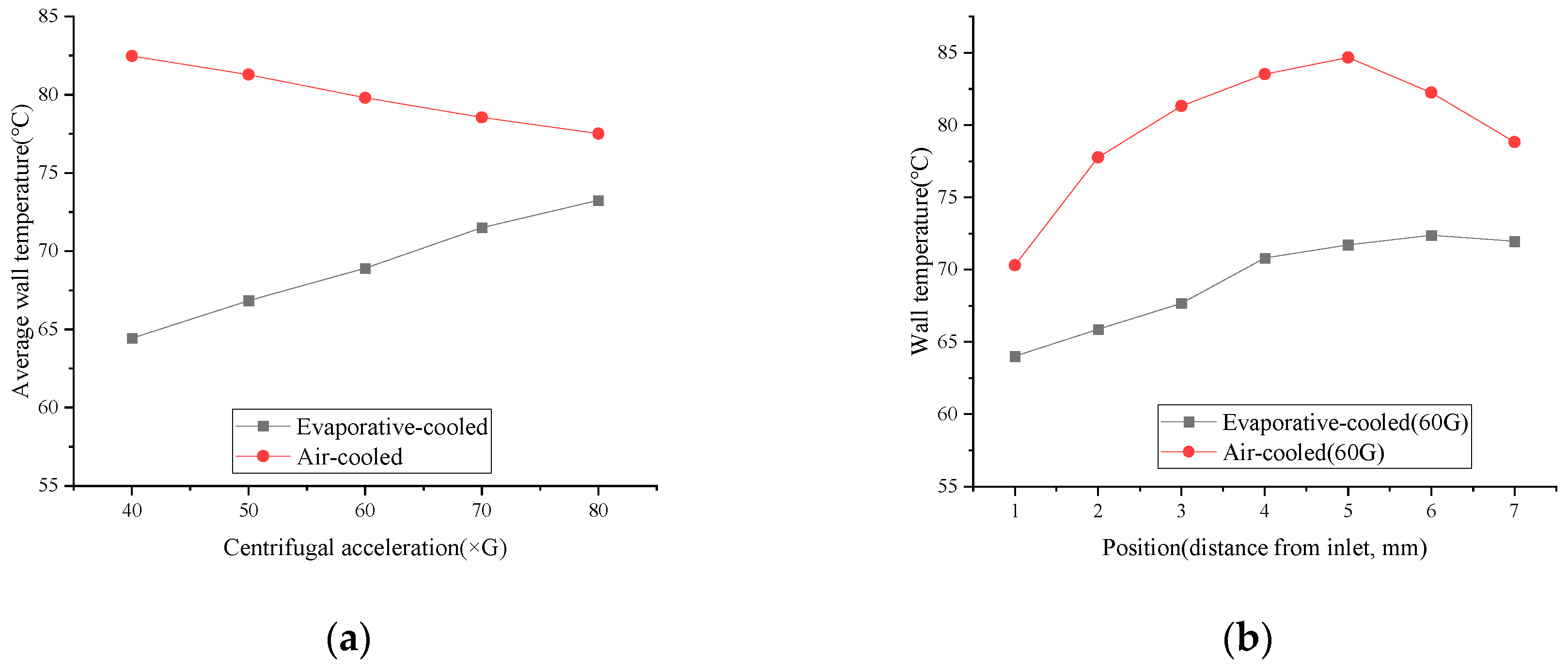
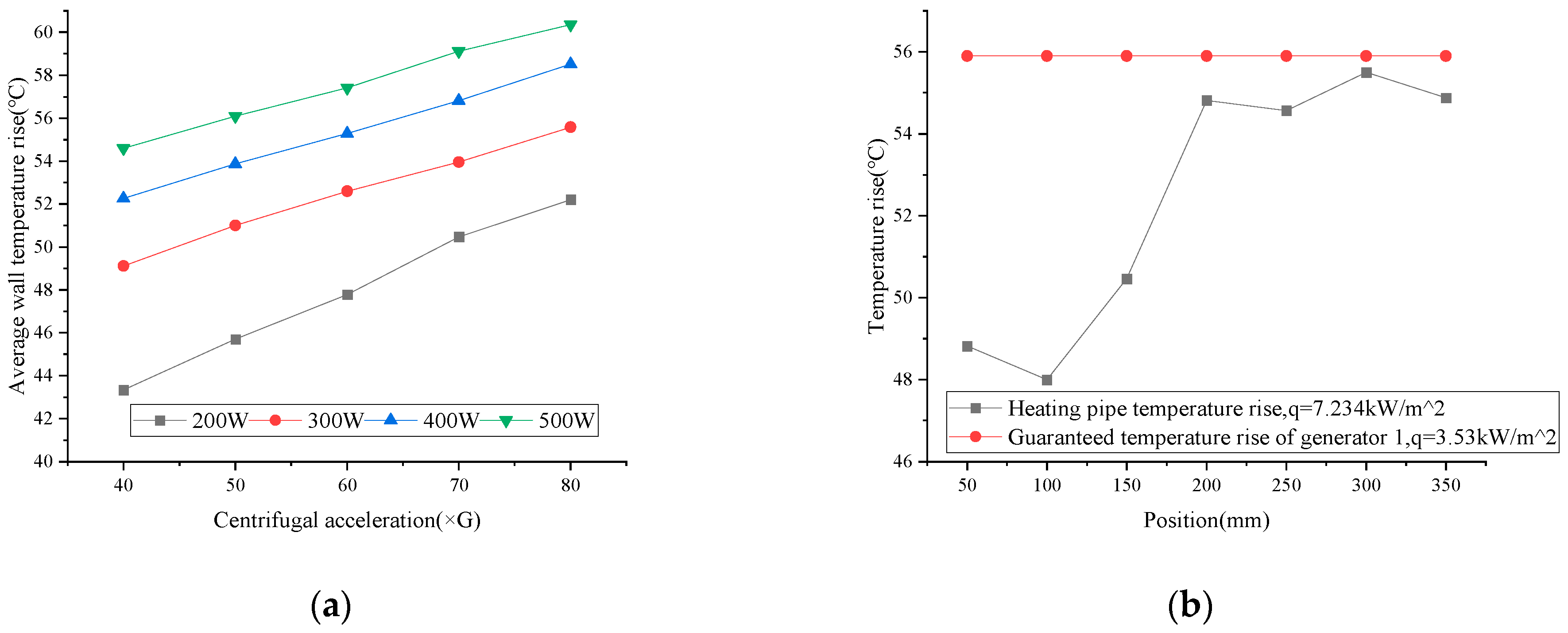
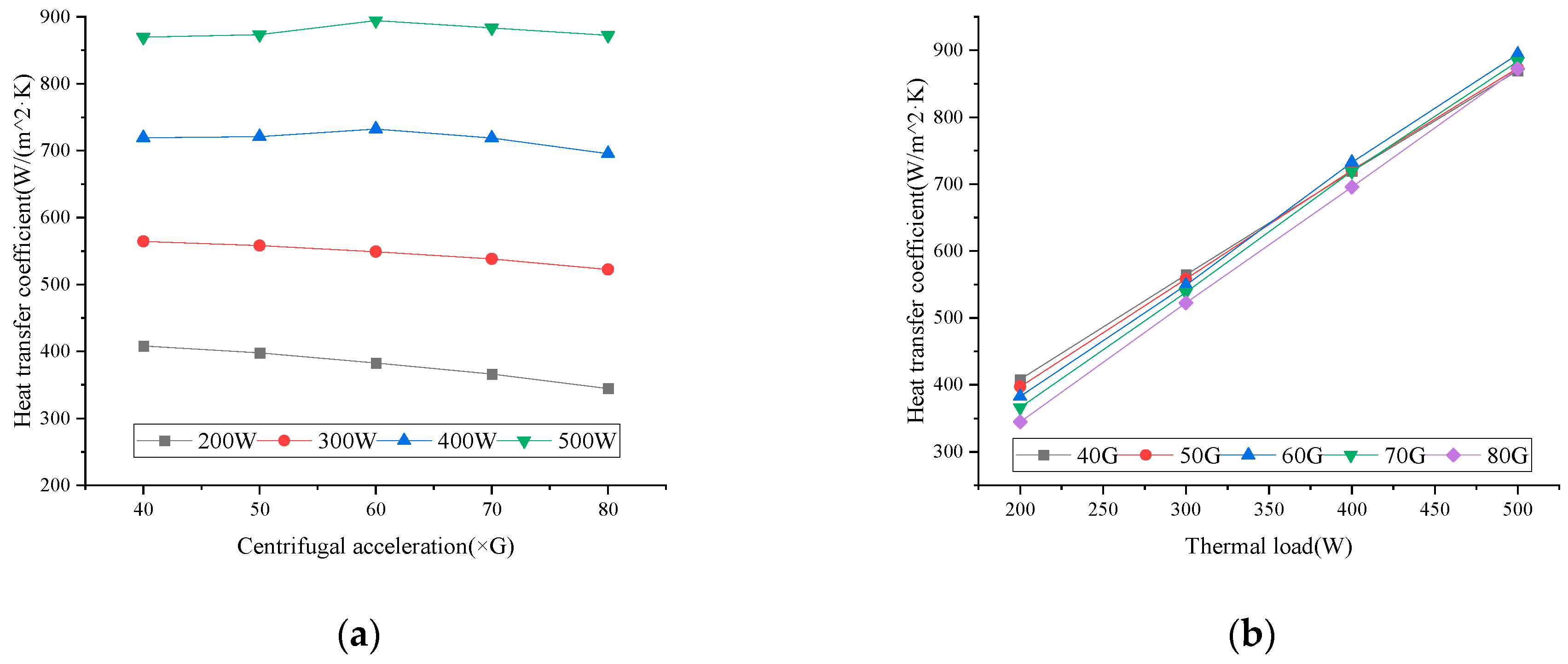
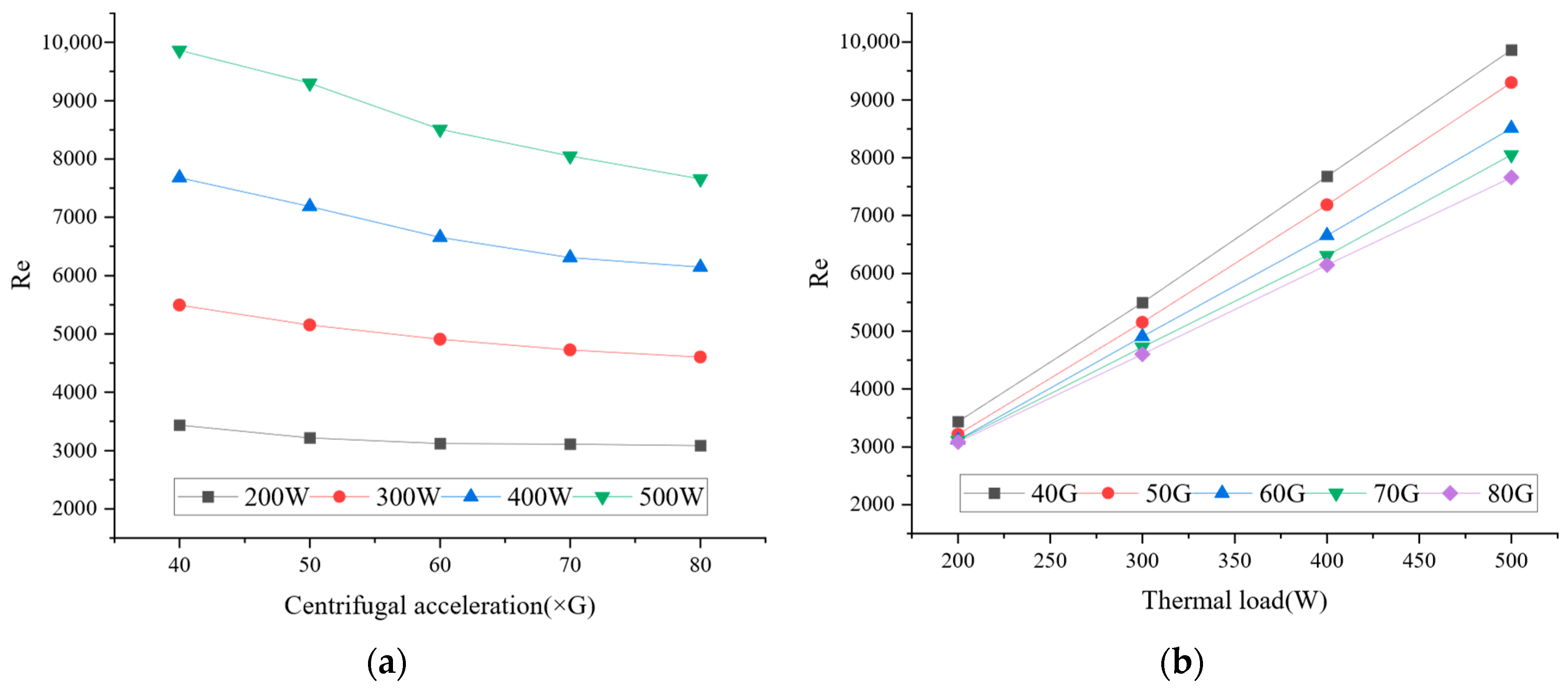
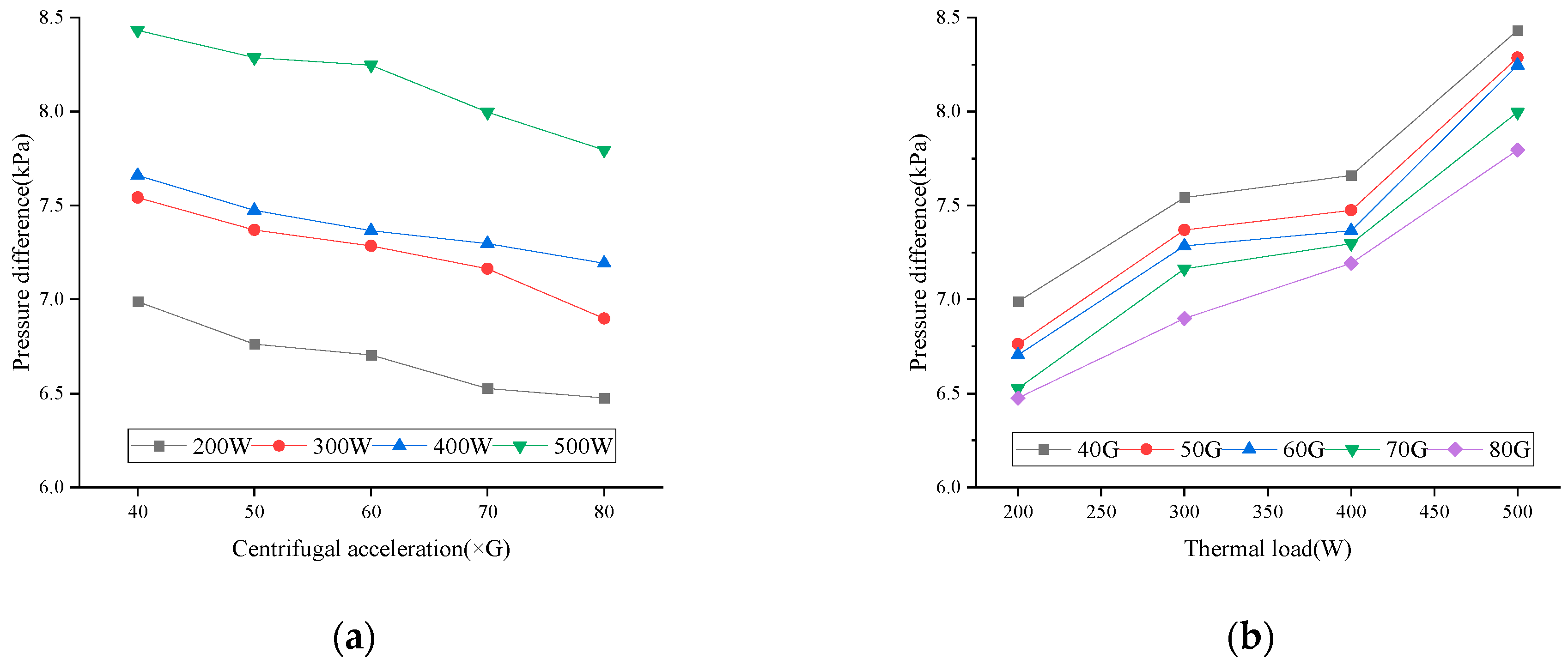
4.1. Experimental Results
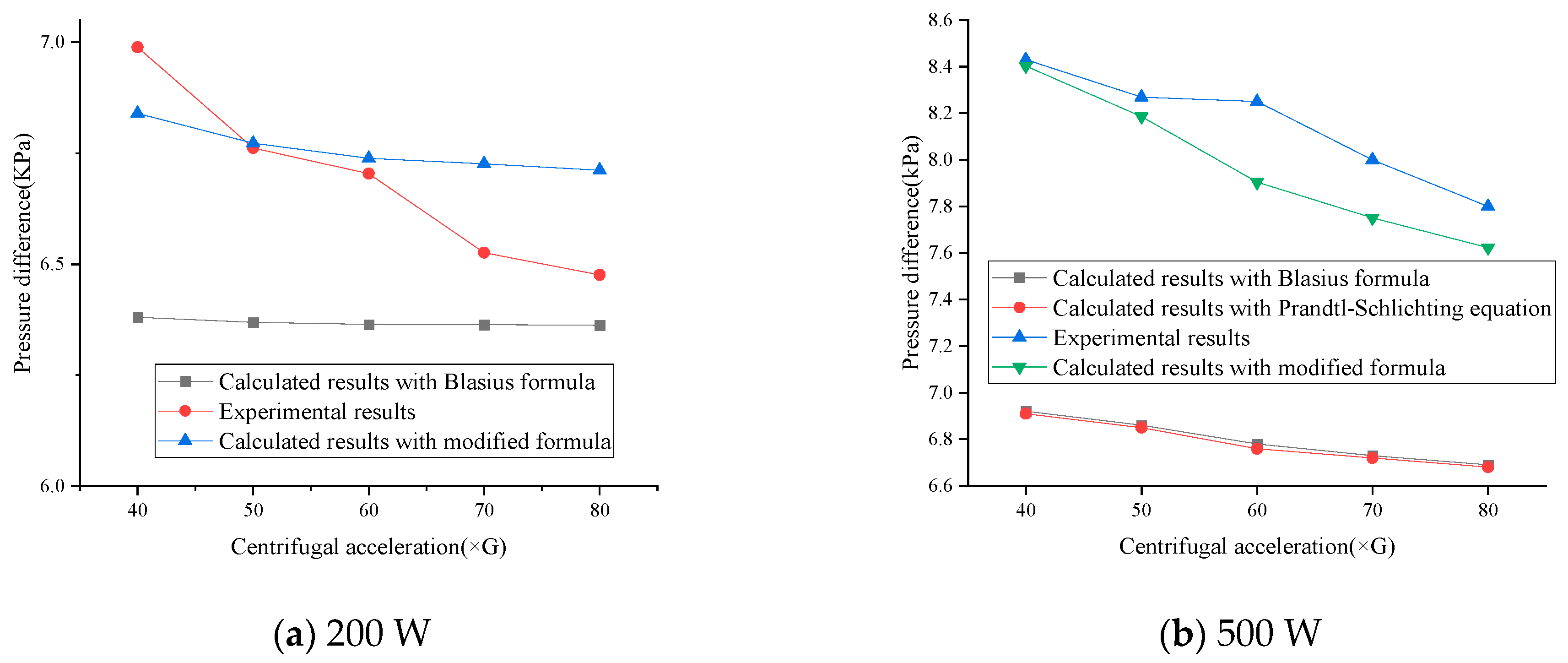
4.2. Friction Factor Modification and Experimental Verification
5. Conclusions
5.1. Key Findings
5.2. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ar(r) | centrifugal acceleration (m2/s) |
| c | flow rate (m/s) |
| D | diameter (m) |
| g | gravitation acceleration (m2/s) |
| kc | correction coefficient |
| L | length (m) |
| mass flow rate (kg/s) | |
| nN | rotating speed (r/min) |
| P | pressure (Pa) |
| ΔP | pressure difference (Pa) |
| q | electric heating power (W) |
| r | radius of rotation (m) |
| u | internal energy (W) |
| v | specific volume (m3/kg) |
| wi | internal work (W) |
| Greek letters | |
| ε | absolute roughness of pipeline inner wall (mm) |
| λ | friction factor |
| εc | modified friction factor |
| μ | viscosity (Pa·s) |
| ρ | density (kg/m3) |
| Subscripts and superscript | |
| 1 | heating pipe position |
| a | inlet |
| b | outlet |
References
- Zhu, D.; Guo, W.; Zhang, X. Study on simulation of fluid-solid thermal coupled fields for the ventilation and heat rejection system of hydrogenerator. J. Hydroelectr. Eng. 2009, 28, 5. [Google Scholar]
- Staton, D.A.; Cavagnino, A. Convection Heat Transfer and Flow Calculations Suitable for Electric Machines Thermal Models. IEEE Trans. Ind. Electron. 2008, 55, 3509–3516. [Google Scholar] [CrossRef]
- Li, W.; Zhou, F.; Hou, Y.; Cheng, S. Calculation of Rotor Temperature Field for Hydro-generator as well as the Analysis on Relevant Factors. Proc.-Chin. Soc. Electr. Eng. 2002, 22, 86–91. [Google Scholar]
- Lu, Y.P.; Li, W.L.; Ma, X.H.; Jin, H.Y. Numerical Simulation of Temperature Field in Rotor of Large Turbo Generator with Air-coolant. Proc. Chin. Soc. Electr. Eng. 2007, 27, 7–13. [Google Scholar]
- Zheng, X.; Zhang, T.; Liu, Y.; Luo, Y.; Li, D.; Wang, C. Research on High-efficient Cooling Technology in Rotor of 1000MW Hydro Generator. Hydropower Pumped Storage 2019, 5, 14–19. [Google Scholar]
- An, Z.; Qin, G.; Han, R.; Chi, S.; Jiang, B. The Demonstration and Calculation Analysis of Cooling Structure of Large Motor/Generator. Hydropower Pumped Storage 2017, 3, 1–5. [Google Scholar]
- Ding, D.; Li, Y.; Wang, T. Research on Ventilation System of High-head and High-speed Hydraulic Turbine Generator. Shanghai Medium Large Electr. Mach. 2016, 01, 24–26. [Google Scholar] [CrossRef]
- Ruan, L.; Chen, J.; Gu, G. Different Influence of Cooling Method to Stator Bar Insulation Characteristics in Pumped Storage Units. Trans. China Electrotech. Soc. 2017, 32, 246–251. [Google Scholar] [CrossRef]
- Yu, W. Make Choice of Cooling Means for Large Hydrogenerators. Large Electr. Mach. Hydraul. Turbine 2001, 7, 58–62. [Google Scholar]
- Schafer, D. The World’s Largest Fully Water Cooled Hydro Generators in the Bieudron Power Plant (Switzerland). In Proceedings of the IEEE International Electric Machines and Drives Conference (IEMDC 99), Seattle, WA, USA, 9–12 May 1999; pp. 827–829. [Google Scholar] [CrossRef]
- Zhao, D.; Jiang, R. Technical Renovation of 300MW Dual Water Internal Cooling Unit in Liujiaxia Hydropower Plant. Water Power 1999, 9, 15–17. [Google Scholar]
- Liu, F. The Study and Numerical Calculation on the Evaporative Cooling of Hydro-Generator; Hebei University of Technology: Tianjin, China, 2013. [Google Scholar]
- Li, D. Dissertation of Choosing Cooling Mode for Giant-scale Hydrogenerator. Water Power 2007, 33, 40–43. [Google Scholar]
- Wang, Y. Circulation Characteristics and Measuring Method of Evaporative Cooling System for the Rotor of Vertical Machine; Institute of Electrical Engineering, Chinese Academy of Sciences: Beijing, China, 2022. [Google Scholar]
- Zhang, J.; Zhong, S.; Zhang, X. Comparative Analysis of Cooling Methods for Hydroelectric Generators in the Three Gorges Underground Power Station. Mech. Electr. Tech. Hydropower Stn. 2017, 40, 47–50. [Google Scholar] [CrossRef]
- Yuan, J.; Gu, G.; Ruan, L.; Tian, X.; Duo, L.; Zhang, T. Applied Engineering Design of Three Gorges’ 840MVA Hydro-generator with Close Loop Self Circulating Evaporative Cooling System. In Proceedings of the 11th International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008. [Google Scholar]
- Gu, G.; Ruan, L. Applications and Developments of the Evaporative Cooling Technology in the Field of Hydrogenerators. Proc. Chin. Soc. Electr. Eng. 2014, 34, 5112–5119. [Google Scholar]
- Ruan, L.; Gu, G.; Tian, X.; Yuan, J. Experimental Research of New Coolant in Evaporative Cooling Technique of Large Generators. Adv. Technol. Electr. Eng. Energy 2002, 21, 21–24. [Google Scholar]
- Ruan, L.; Gu, G.; Tian, X. Experiment on Two-Phase Flowing Pressure Drop in the Evaporative Cooling System of Hydro-Generators. J. Tianjin Univ. 2005, 38, 27–30. [Google Scholar]
- Dong, H.; Ruan, L. Research on the Temperature Distribution of Stator Collector Ring in Evaporative Cooling Hydro-generator. In Proceedings of the 1st International Conference on Energy and Environmental Protection (ICEEP 2012), Hohhot, China, 23–24 June 2012; pp. 1622–1625. [Google Scholar] [CrossRef]
- Wang, Y.; Ruan, L. Self-Circulating Evaporative Cooling System of a Rotor and Its Experimental Verification. Processes 2022, 10, 934. [Google Scholar] [CrossRef]
- Zhao, S.; Wang, Y.; Yang, Z. Study on Heat Transfer Characteristics of Fully Immersed Evaporative Cooling for Excitation Winding of Vertical Hydrogenerator Rotor. Adv. Technol. Electr. Eng. Energy 2023, 42, 1–10. [Google Scholar]
- Zhu, K.; Li, R.; Yang, Z.; Hou, Z. Study on Vibration Characteristics of Evaporative Cooling Rotor of Vertical Hydro-generator. Adv. Technol. Electr. Eng. Energy 2024, 43, 104–112. [Google Scholar]
- Song, F.; Ewing, D.; Ching, C.Y. Experimental Investigation on the Heat Transfer Characteristics of Axial Rotating Heat Pipes. Int. J. Heat Mass Transf. 2004, 47, 4721–4731. [Google Scholar] [CrossRef]
- Hamdy, H.; Souad, H. Effect of Using Nanofluids on the Performance of Rotating Heat Pipe. Appl. Math. Model. 2015, 39, 4445–4462. [Google Scholar] [CrossRef]
- Yao, Q.; Song, B.; Zhao, M. Effects of Dynamic Load on the Heat Transfer Characteristics of Two-phase Pipe Boiling Flow. J. Aerosp. Power 2010, 25, 28–34. [Google Scholar] [CrossRef]
- Zhao, M. Experimental Research on Boiling Heat Transfer of Pipe Water Flow under Hi-G Condition. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2008. [Google Scholar]
- Luo, Z. Experimental Study of Flow Boiling Heat Transfer Characteristics of R245fa Under Hypergravity; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2023. [Google Scholar]
- Liu, Z.; Yu, Z.; Sun, W.; Zhang, K. Unsteady Numerical Calculation of Subcooled Boiling Heat Transfer in a Horizontal Pipe. J. Harbin Inst. Technol. 2023, 55, 39–45. [Google Scholar]
- Yan, Y. Experimental and Numerical Simulation of Heat Transfer Characteristics of R134A Flow in a Horizontal Smooth Tube; Xi’an University of Technology: Xi’an, China, 2023. [Google Scholar]
- Lei, H. CFD-VOF Simulation of Flow Boiling Process in a Square Channel; Ningxia University: Ningxia, China, 2024. [Google Scholar]
- Maurus, R.; Ilchenko, V.; Sattelmayer, T. Study of the Bubble Characteristics and the Local Void Fraction in Subcooled Flow Boiling Using Digital Imaging and Analysing Techniques. Exp. Therm. Fluid Sci. 2002, 26, 147–155. [Google Scholar] [CrossRef]
- Vlachou, M.C.; Lioumbas, J.S.; David, K.; Chasapis, D.; Karapantsios, T.D. Effect of Channel Height and Mass Flux on Highly Subcooled Horizontal Flow Boiling. Exp. Therm. Fluid Sci. 2017, 83, 157–168. [Google Scholar] [CrossRef]
- Jeon, S.S.; Kim, S.J.; Park, G.C. Numerical Study of Condensing Bubble in Subcooled Boiling Flow Using Volume of Fluid Model. Chem. Eng. Sci. 2011, 66, 5899–5909. [Google Scholar] [CrossRef]
- Wu, M.; Gao, N.; Miao, R.; Dong, Y.; Huang, N. Numerical Analysis of Boiling Vapor-liquid Distribution in a Central Orthogonal Rotating Pipe. Proc. Chin. Soc. Electr. Eng. 2020, 40, 1947–1953. [Google Scholar]
- Wang, S.; Dong, J.X.; Guo, H.Z.; Qiao, L.; Zhang, S.; Wang, J. Experimental Study on Condensation Friction Pressure Drop in Rotating Channels and Proposal of New Correlation. Therm. Sci. 2022, 26, 5253–5266. [Google Scholar] [CrossRef]
- Yu, S.; Cai, J.; Guo, C.; Gu, G. Cooling System Circulation Principle of Vertical Evaporative Cooling Motor. Sci. Sin. 2006, 49, 320–325. [Google Scholar]
- Yu, S. Study on the Void Fraction of Two-Phase Flow in the Evaporative Cooling Generator. Master’s Thesis, University of Chinese Academy of Sciences (UCAS), Beijing, China, 2003. [Google Scholar]
- Colebrook, C.F.; White, C.M. Experiments with Fluid Friction in Roughened Pipes. Proc. R. Soc. Lond. Ser. A-Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Moody, L.F. Friction Factors for Pipe Flow. Trans ASME 1944, 66, 671–678. [Google Scholar] [CrossRef]
- Allen, J.J.; Shockling, M.A.; Kunkel, G.J.; Smits, A.J. Turbulent Flow in Smooth and Rough Pipes. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2007, 365, 699–714. [Google Scholar] [CrossRef] [PubMed]








| ID | Sensor | Range | Accuracy |
|---|---|---|---|
| P1~P4 | Pressure sensor | −50–200 kPa | ±0.25% |
| T1~T4 | PT100 | 0–200 °C | ±0.25% |
| Tw | PT100 | −50–200 °C | ±0.15% |
| No. | Thermal Load (W) | Centrifugal Acceleration |
|---|---|---|
| 1 | 200 | 40 G |
| 2 | 300 | 40 G |
| 3 | 400 | 40 G |
| 4 | 500 | 40 G |
| 5 | 200 | 50 G |
| 6 | 300 | 50 G |
| 7 | 400 | 50 G |
| 8 | 500 | 50 G |
| 9 | 200 | 60 G |
| 10 | 300 | 60 G |
| 11 | 400 | 60 G |
| 12 | 500 | 60 G |
| 13 | 200 | 70 G |
| 14 | 300 | 70 G |
| 15 | 400 | 70 G |
| 16 | 500 | 70 G |
| 17 | 200 | 80 G |
| 18 | 300 | 80 G |
| 19 | 400 | 80 G |
| 20 | 500 | 80 G |
| Centrifugal Acceleration | Results Calculated with the Blasius Formula ΔPl (pa) | Results Calculated with the Prandtl–Schlichting Equation ΔPl (pa) | Experimental Results ΔPl (pa) |
|---|---|---|---|
| 40 G | 6922.08 | 6907.20 | 8432.44 |
| 50 G | 6858.90 | 6846.03 | 8286.61 |
| 60 G | 6775.00 | 6764.80 | 8247.06 |
| 70 G | 6729.59 | 6720.82 | 7997.14 |
| 80 G | 6691.82 | 6687.31 | 7796.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Ruan, L. Experimental Study of an Evaporative Cooling System in a Rotating Vertical Channel with a Circular Cross-Section for Large Hydro-Generators. Energies 2025, 18, 3681. https://doi.org/10.3390/en18143681
Li R, Ruan L. Experimental Study of an Evaporative Cooling System in a Rotating Vertical Channel with a Circular Cross-Section for Large Hydro-Generators. Energies. 2025; 18(14):3681. https://doi.org/10.3390/en18143681
Chicago/Turabian StyleLi, Ruiwei, and Lin Ruan. 2025. "Experimental Study of an Evaporative Cooling System in a Rotating Vertical Channel with a Circular Cross-Section for Large Hydro-Generators" Energies 18, no. 14: 3681. https://doi.org/10.3390/en18143681
APA StyleLi, R., & Ruan, L. (2025). Experimental Study of an Evaporative Cooling System in a Rotating Vertical Channel with a Circular Cross-Section for Large Hydro-Generators. Energies, 18(14), 3681. https://doi.org/10.3390/en18143681






