Thermodynamic Characteristics of Compressed Air in Salt Caverns of CAES: Considering Air Injection for Brine Drainage
Abstract
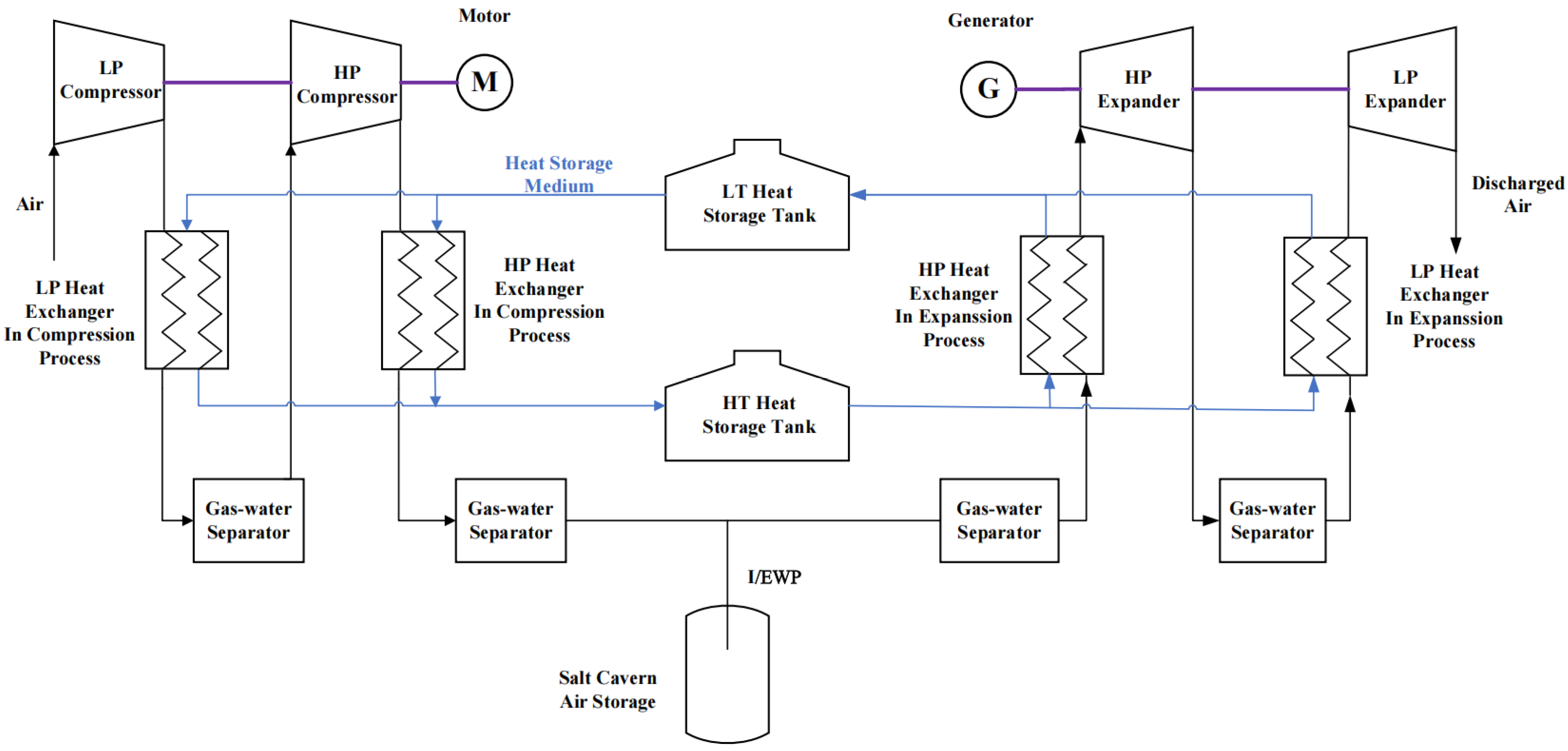
1. Introduction
2. Models and Governing Equations
2.1. Assumptions
- (1)
- Air leakage is not considered.
- (2)
- The volume of the cavern stays constant.
- (3)
- The air density, temperature, and pressure are uniform throughout the cavern space.
- (4)
- The density of brine is constant.
- (5)
- The airflow in the I/EWP and the flow of brine in the brine drainage pipe are assumed to be in a steady state.
- (6)
- The cross-sectional area of the I/EWP remains unchanged, and the airflow through the I/EWP is regarded as one-dimensional single-phase flow.
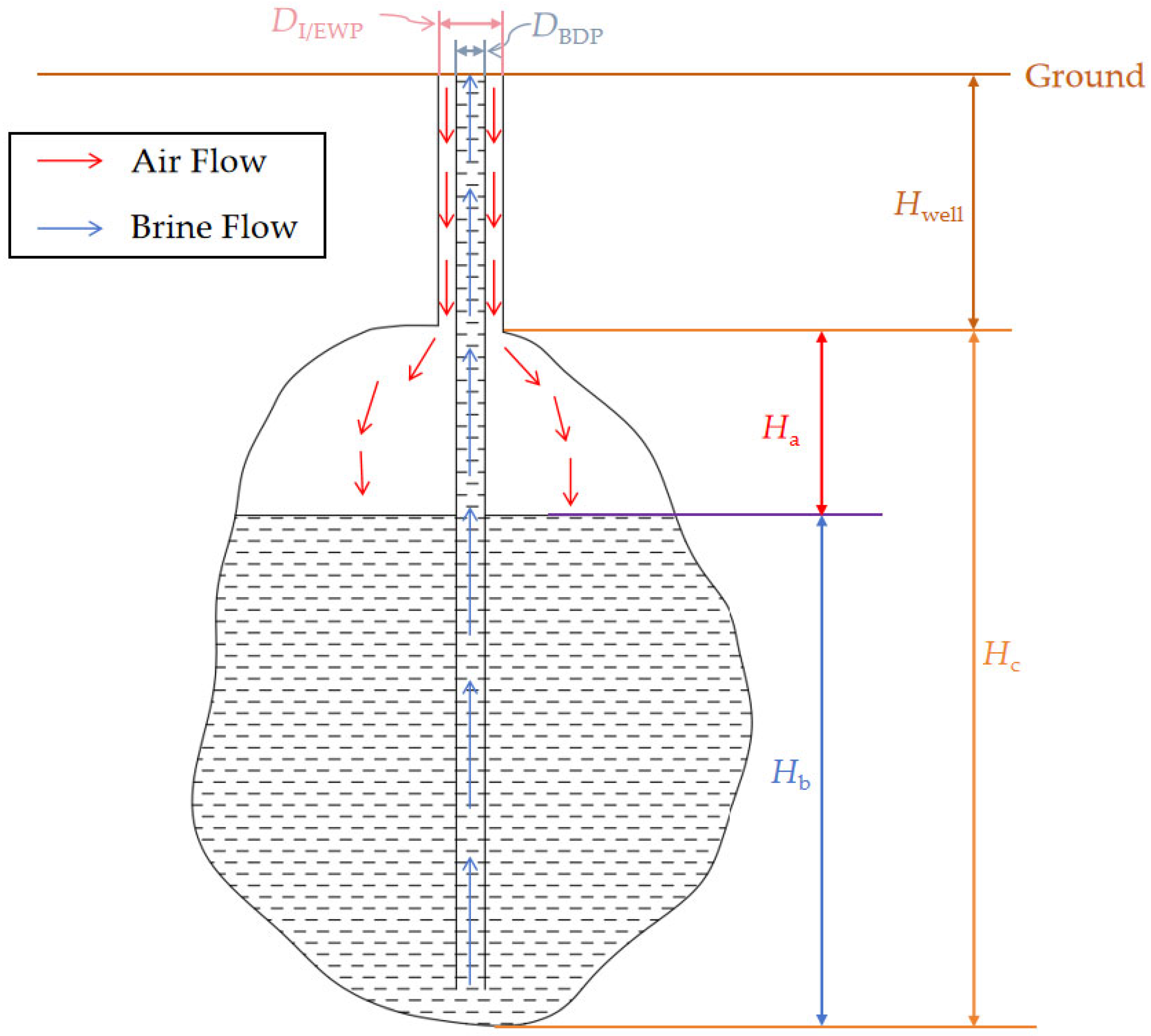
- (7)
- The radius of the air injection pipe is twice that of the brine drainage pipe (BDP). The impact on thermodynamic properties is obtained by equivalently replacing multiple BDPs with the same total cross-sectional area with a single BDP’s cross-sectional area.
- (8)
- The vaporization and condensation processes of brine are not considered.
2.2. Air Thermodynamics in Salt Cavern
2.3. Model of I/EWP Flow
2.4. Model of Air Injection for Brine Drainage
2.4.1. Air Injection and Pressure Increase Stage (AIPIS)
2.4.2. Pressure Increase and Brine Drainage Stage (PIBDS)
2.4.3. Halt Injection and Brine Drainage Stage (HIBDS)
2.4.4. Model Workflow and Parameter Settings
3. Results and Discussion
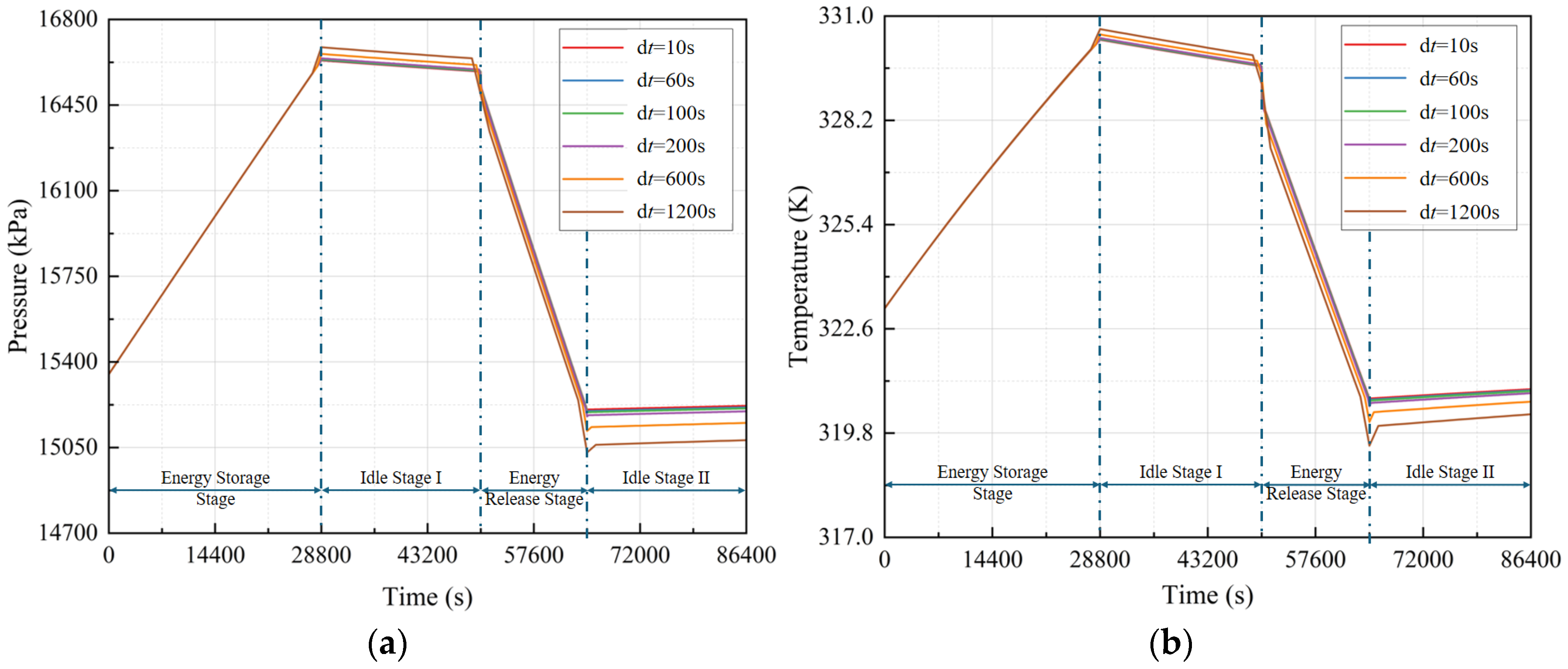
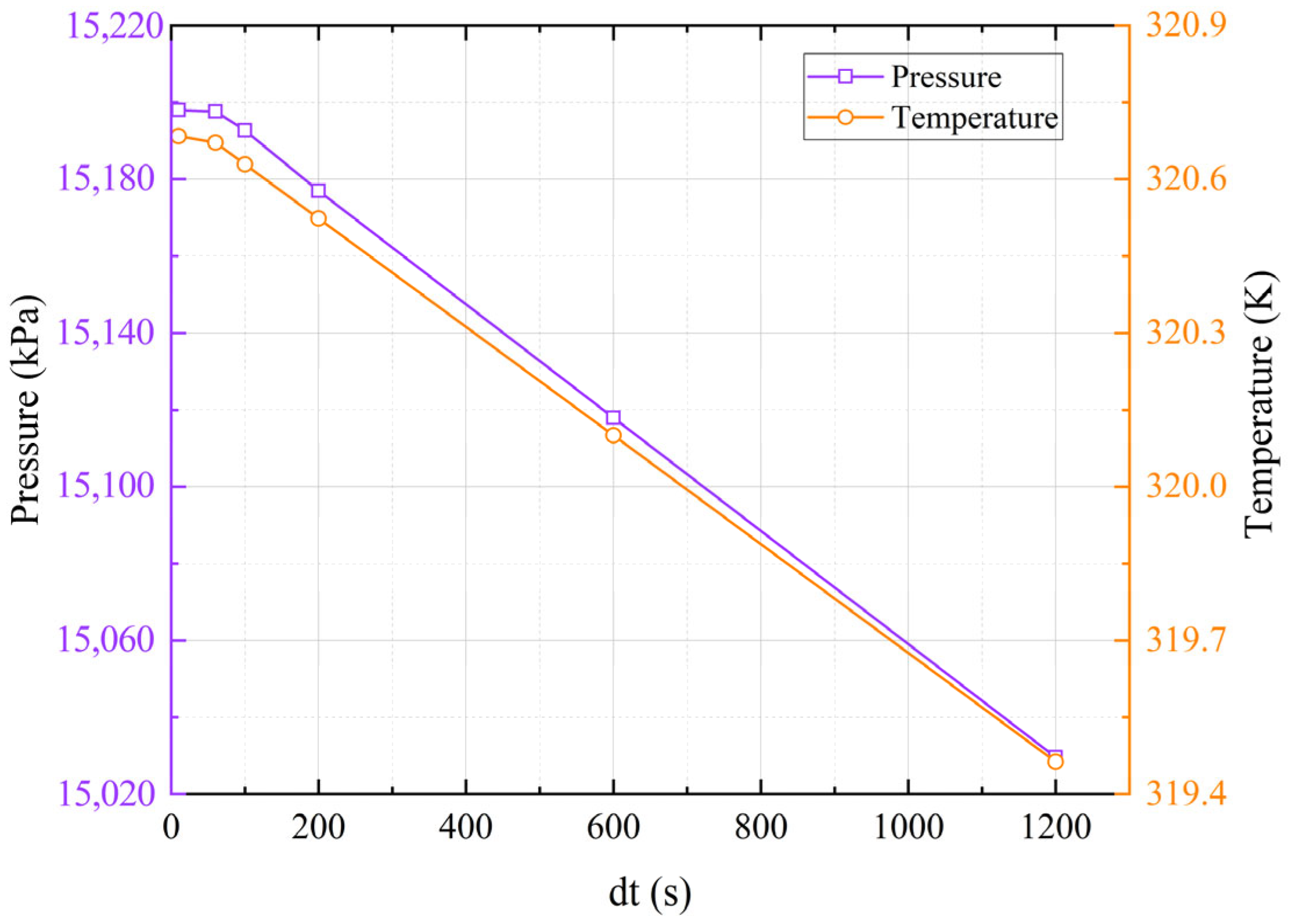
3.1. Verification of Time-Step Independence
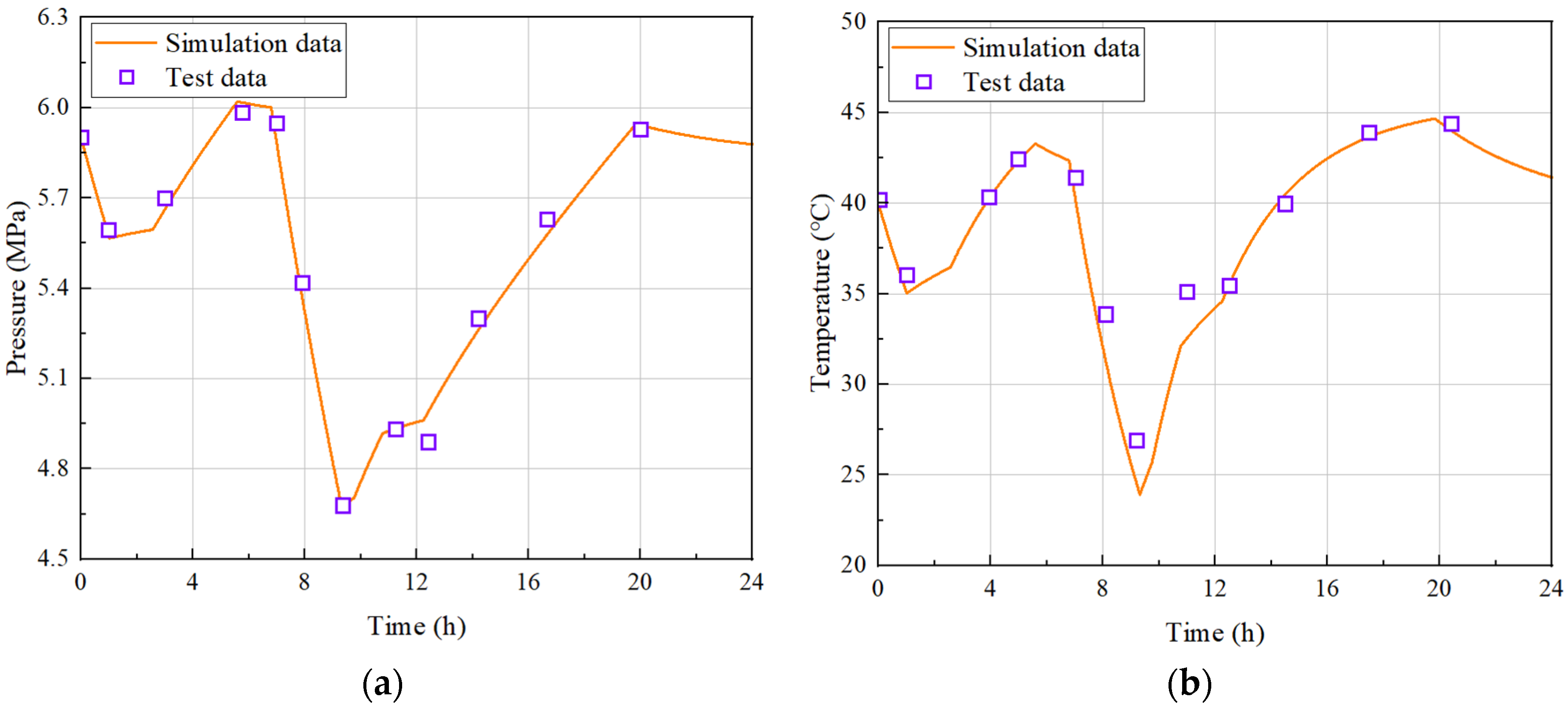
3.2. Validation of Cavern Thermodynamics
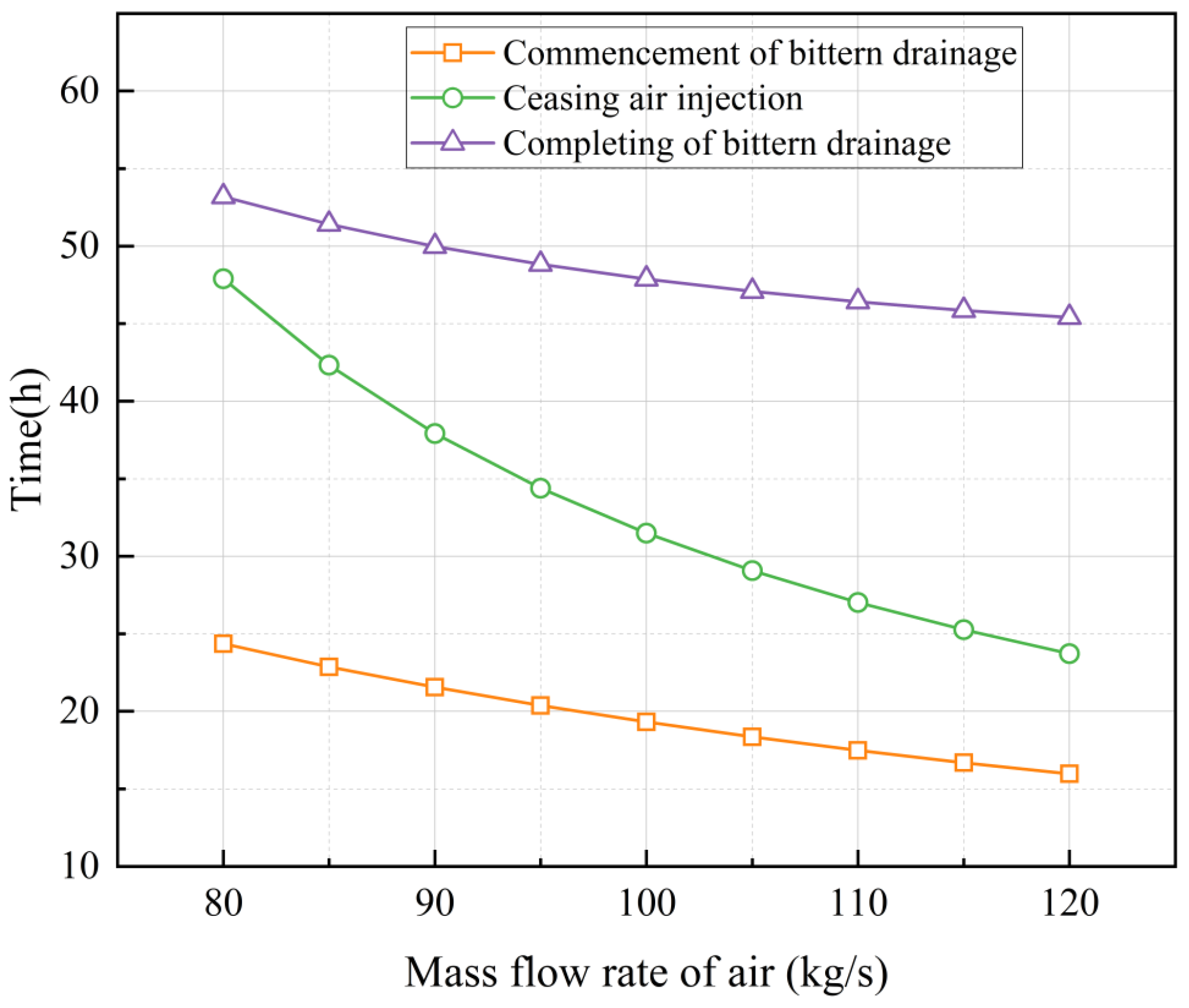
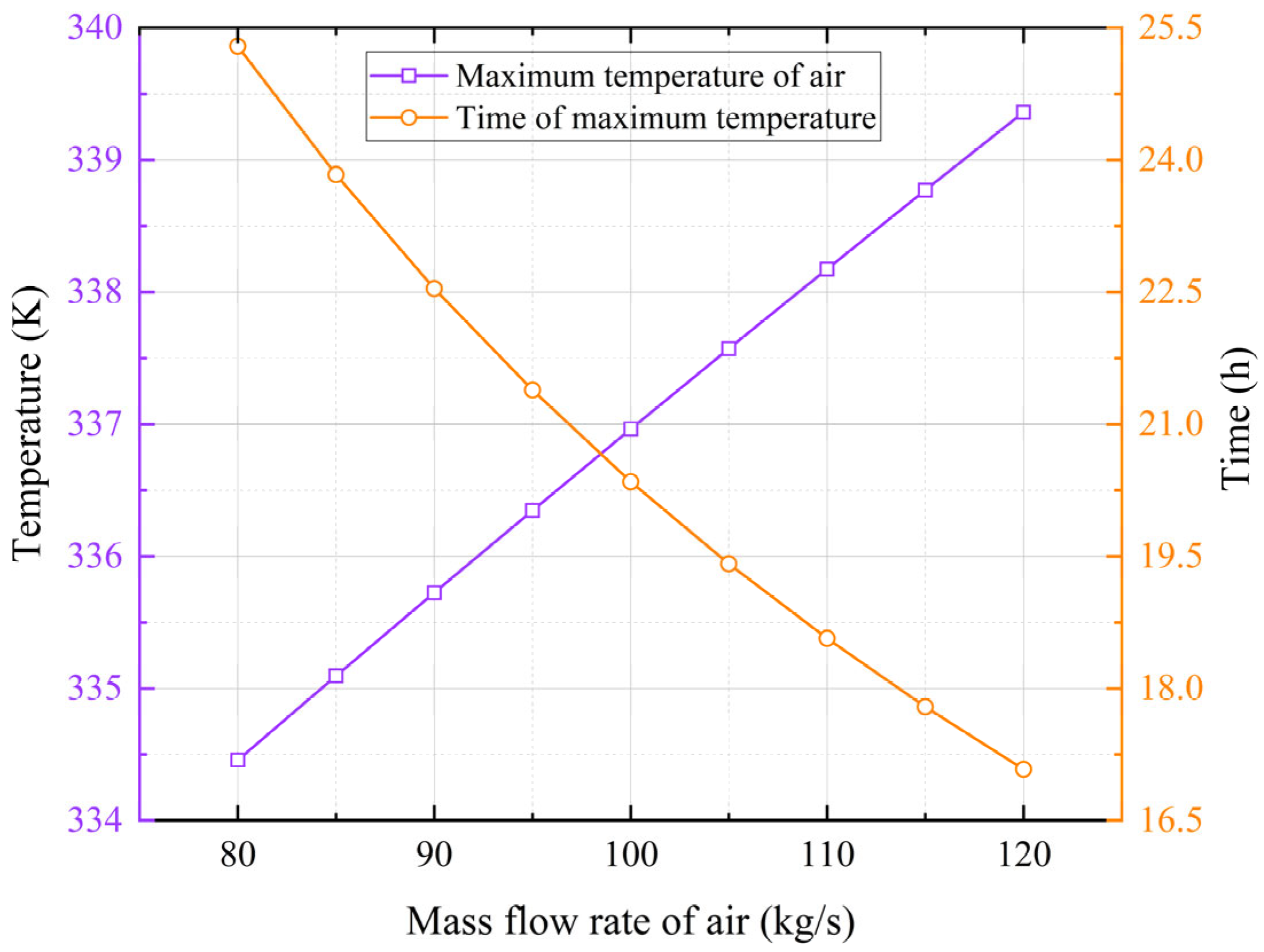
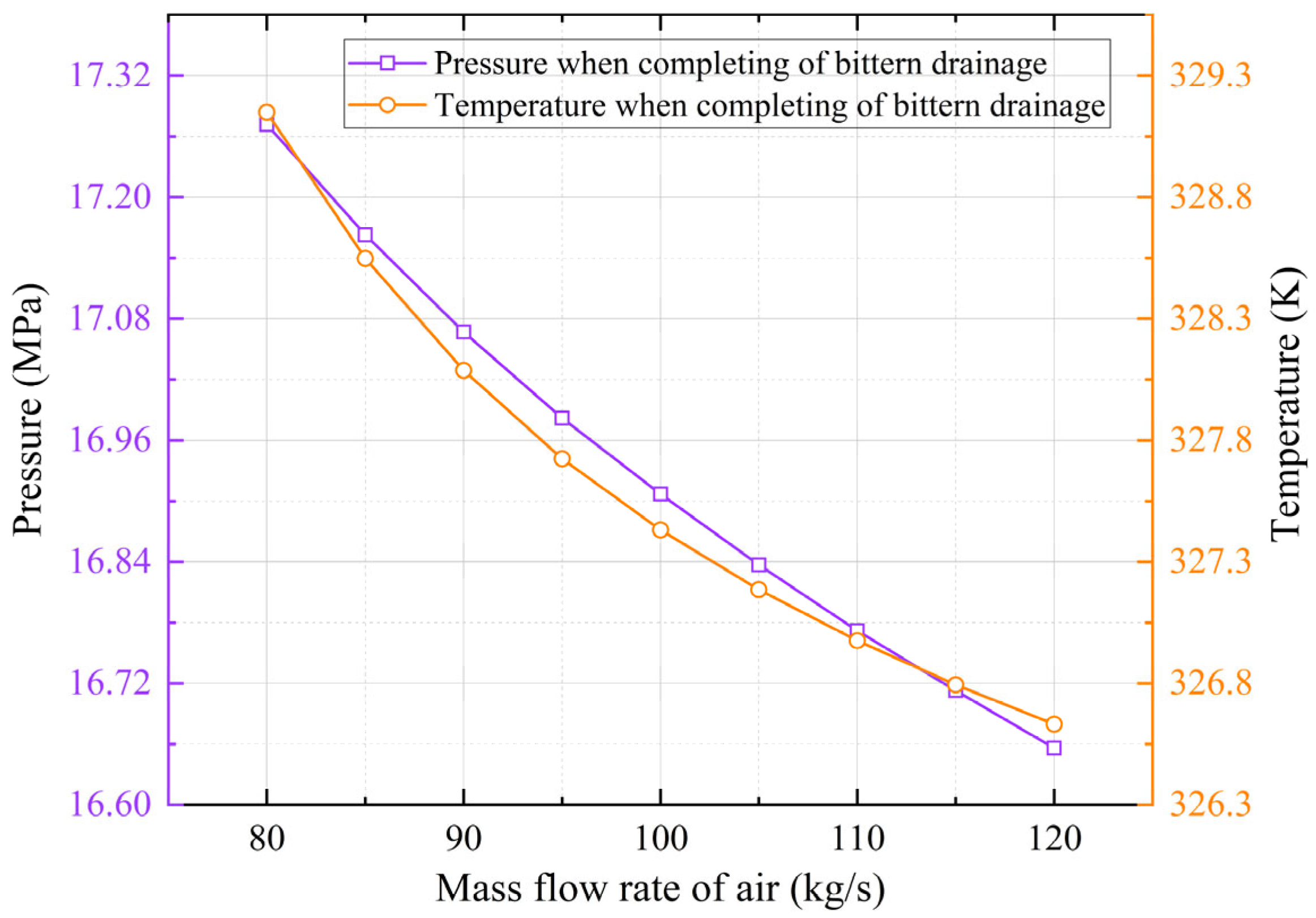
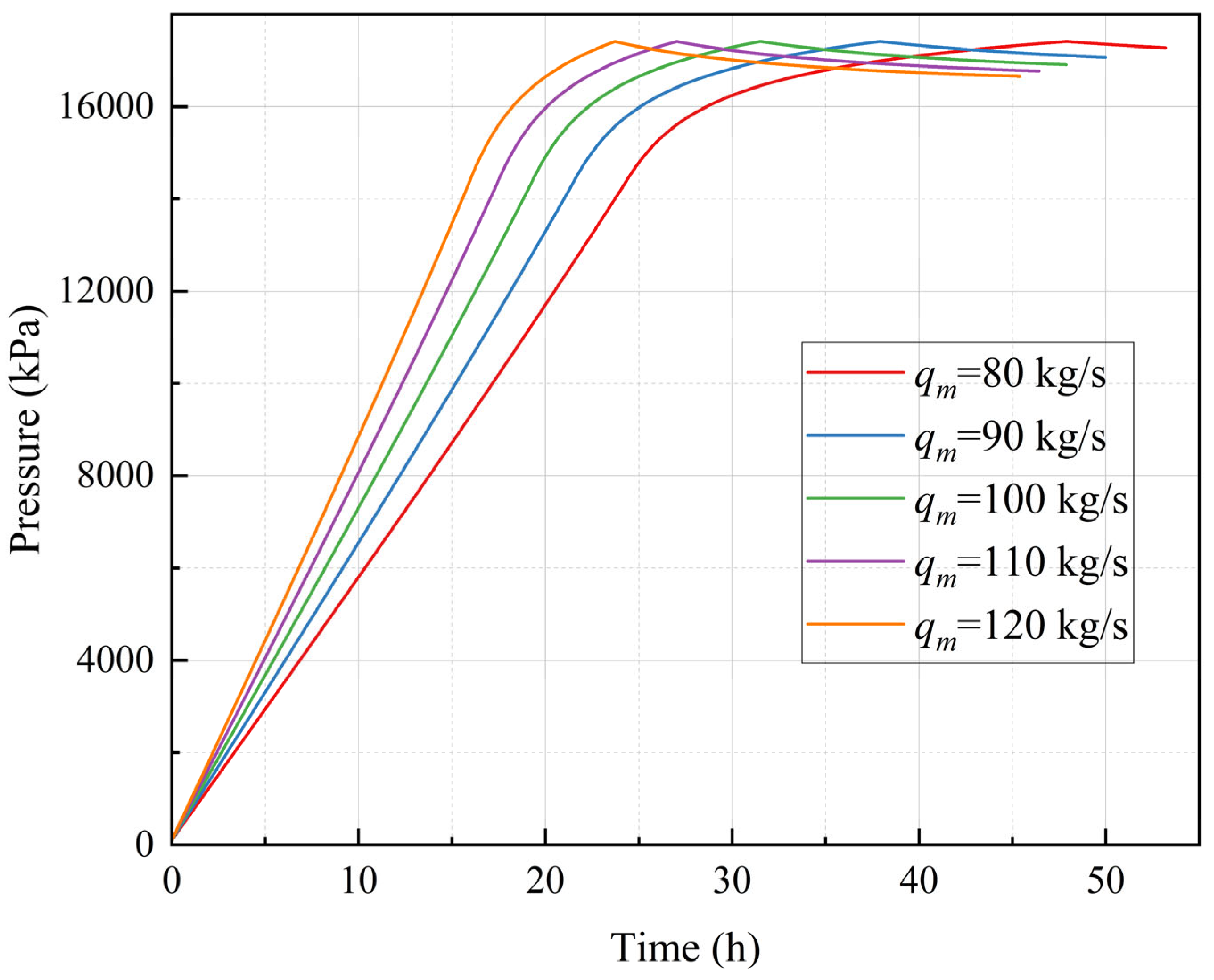
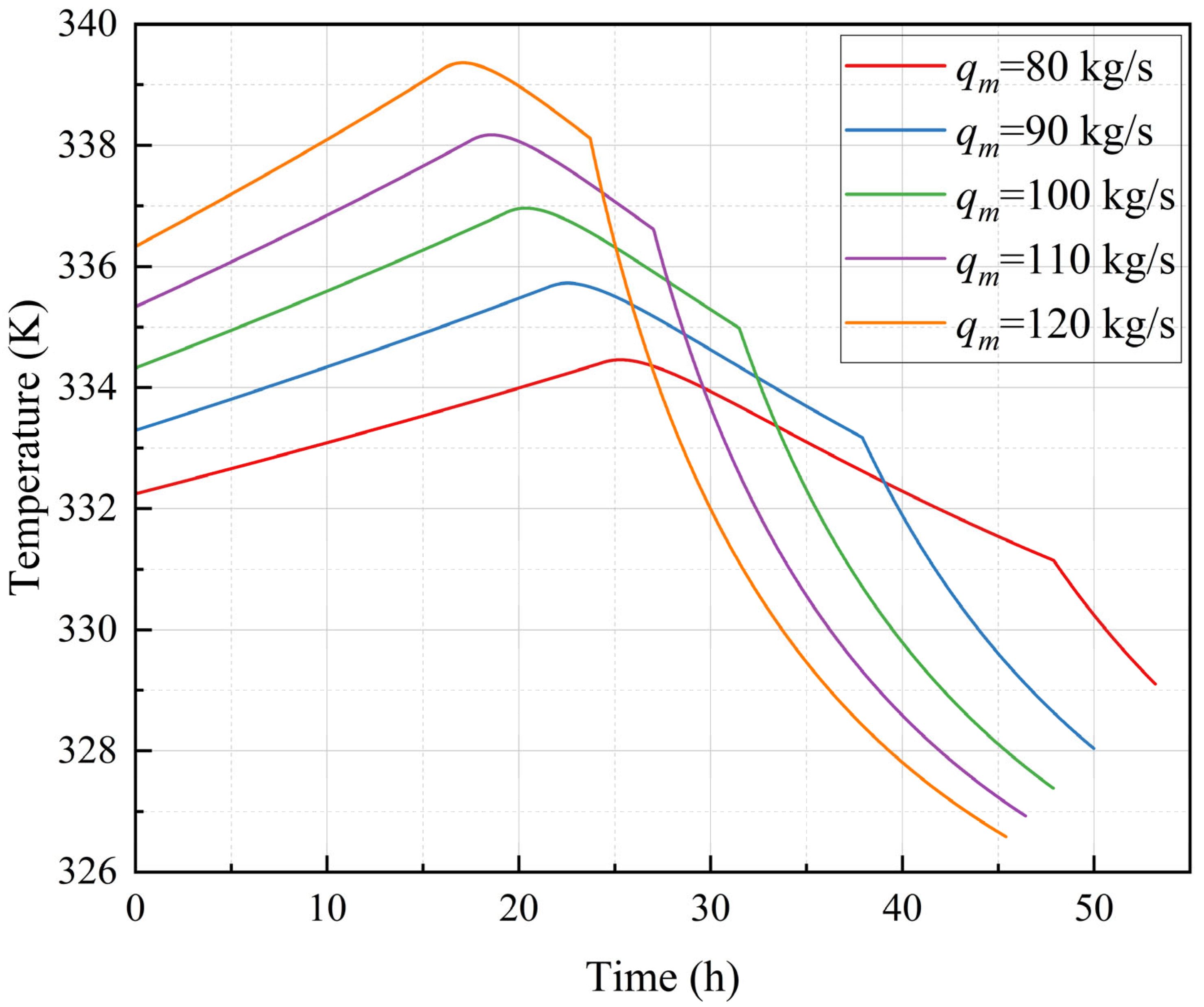
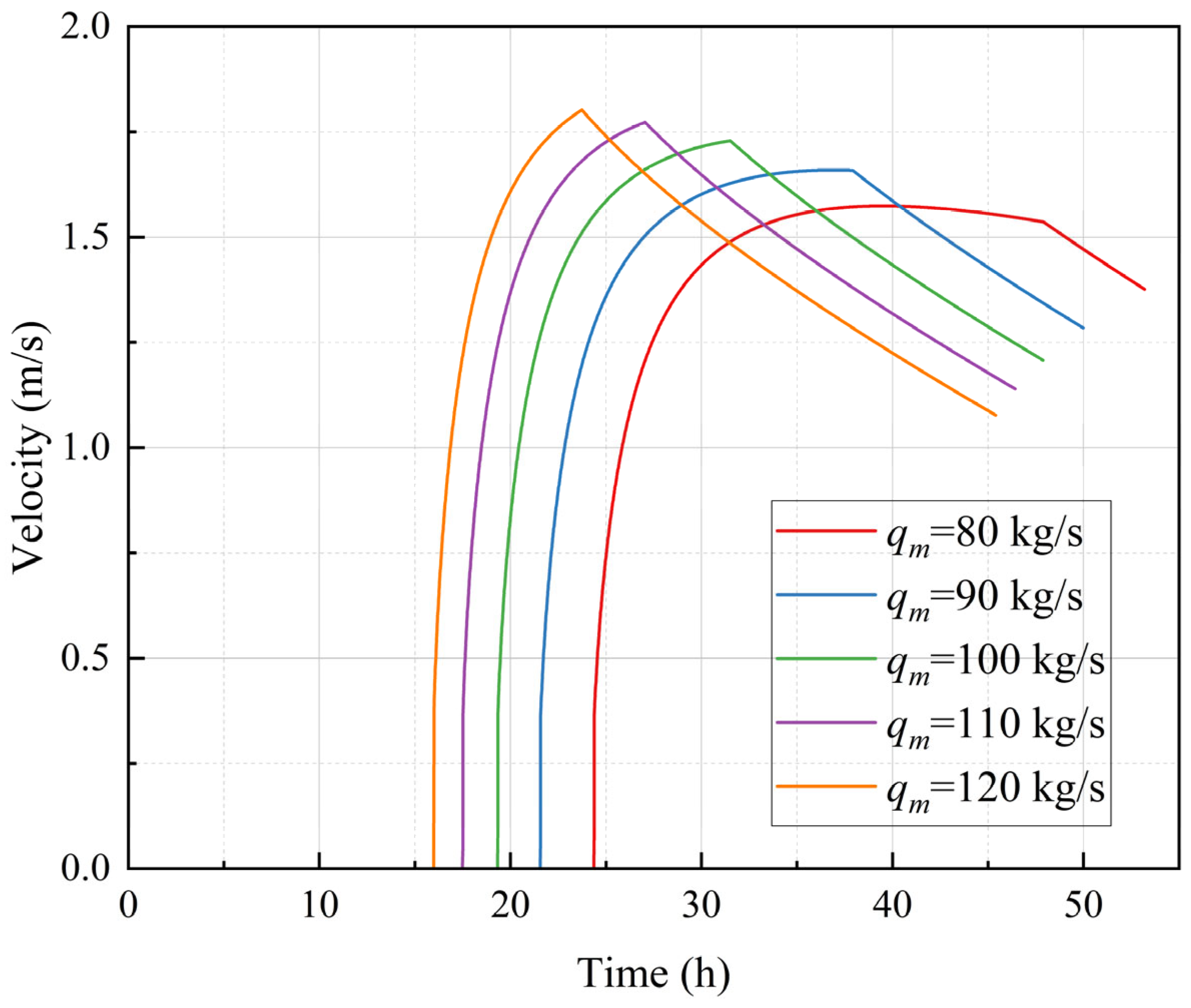
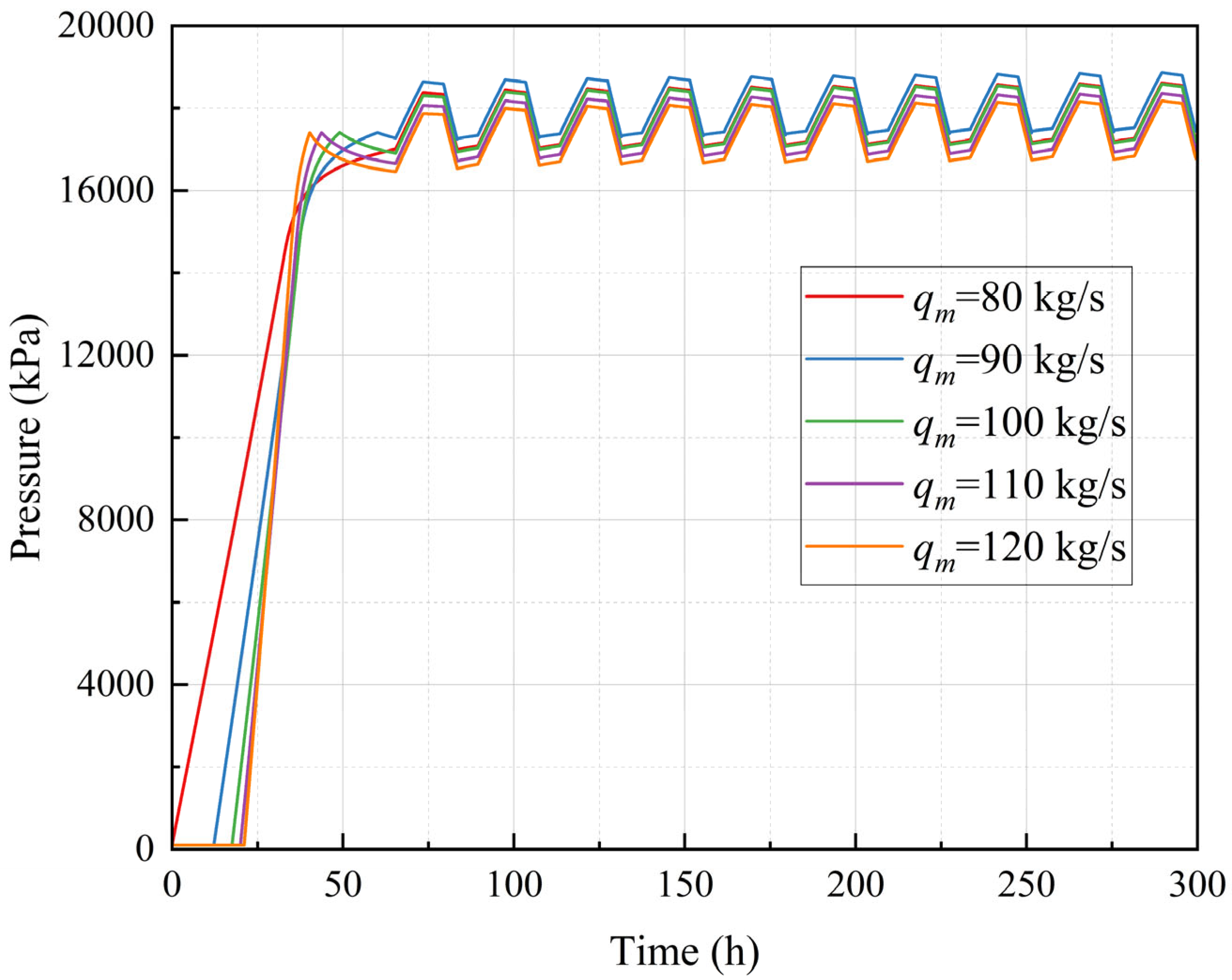
3.3. Influence of the Injection Flow Rates
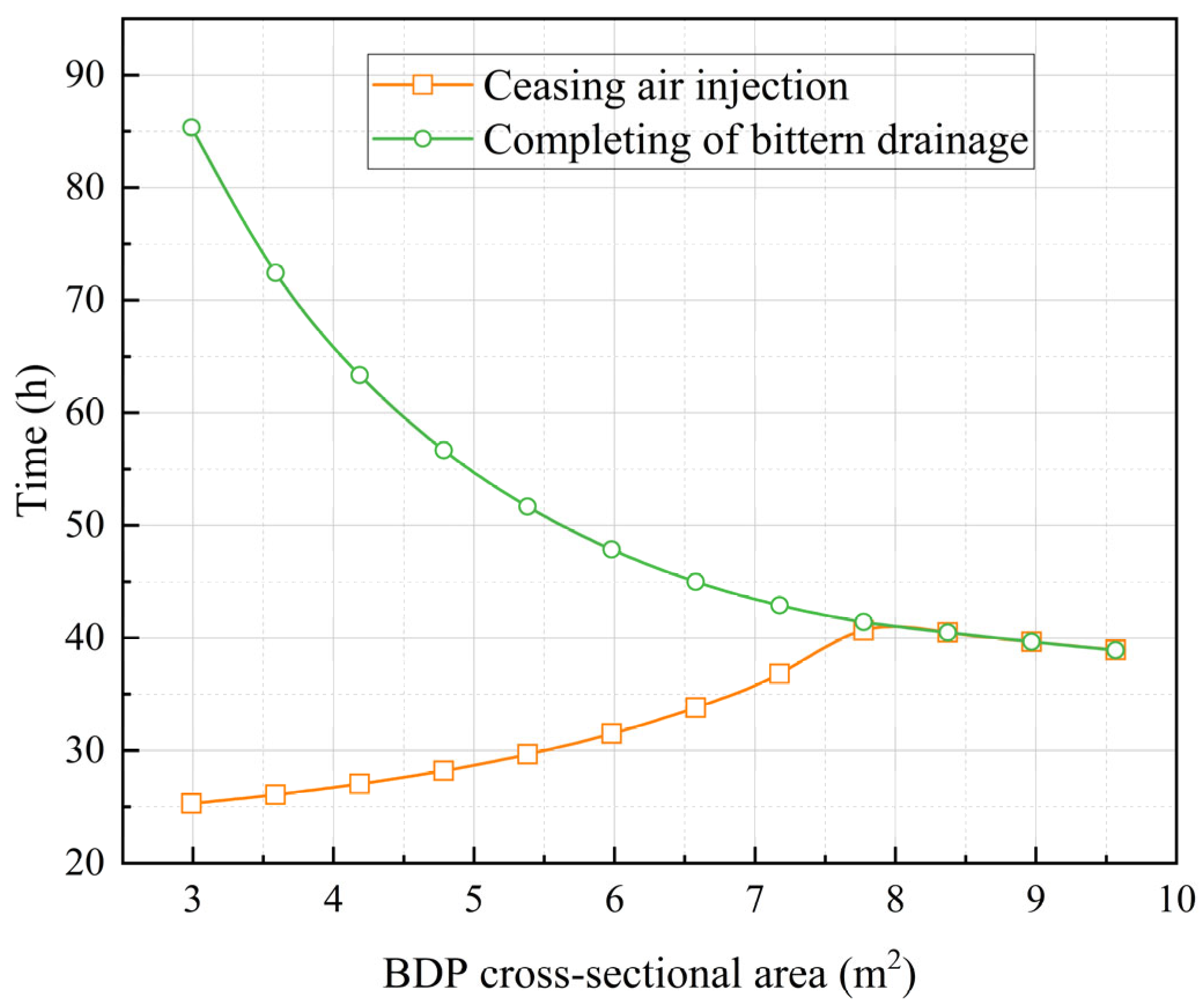
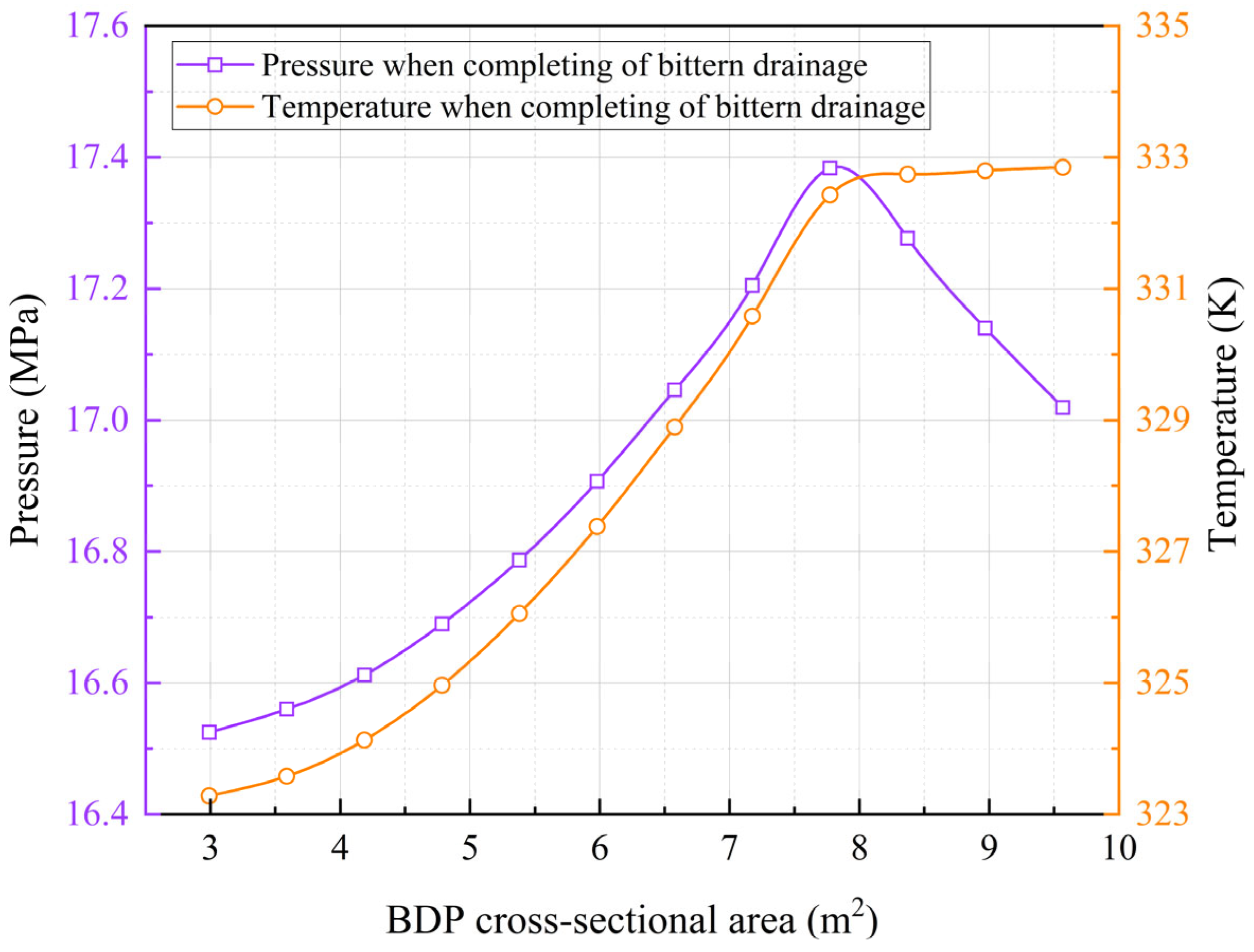
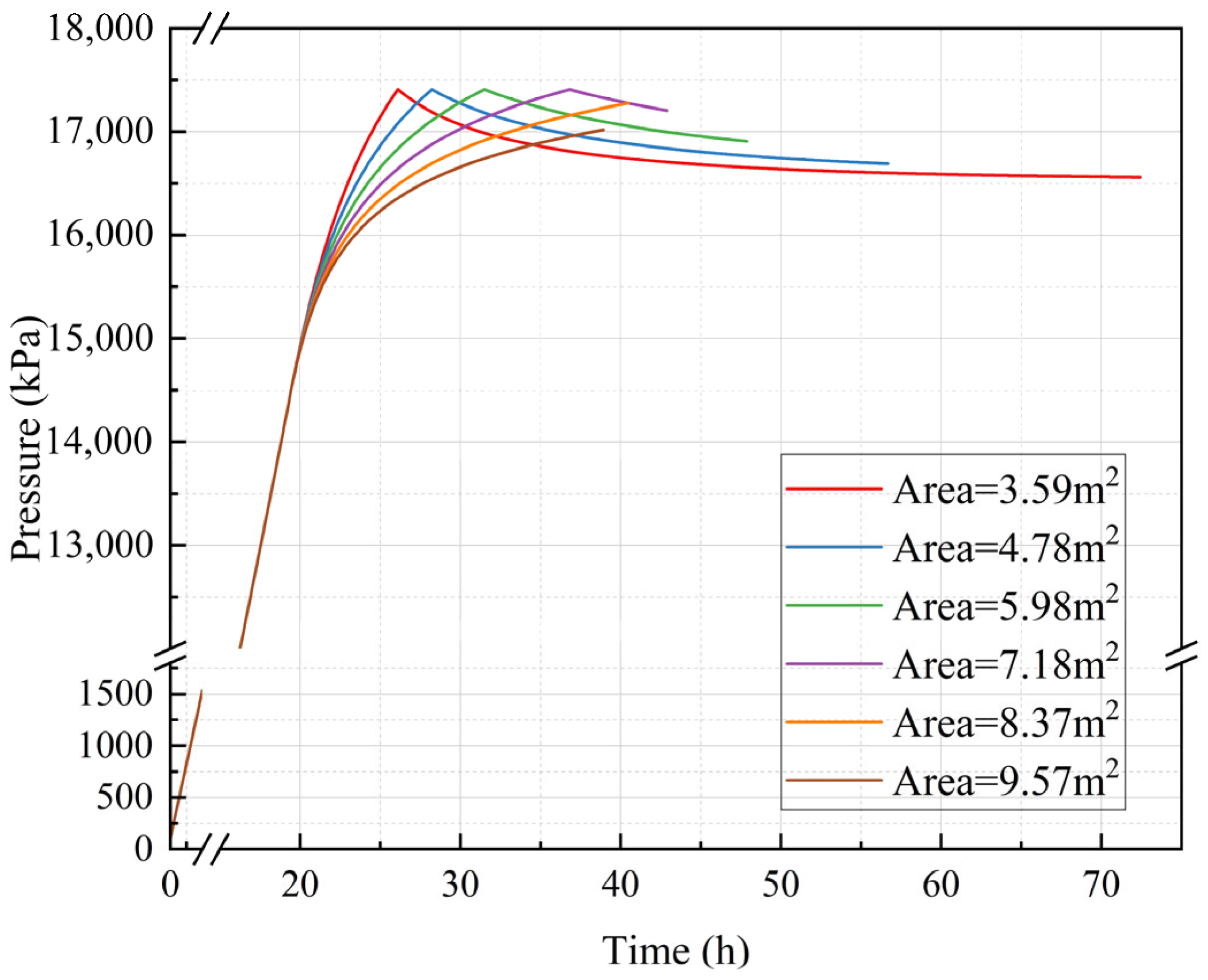
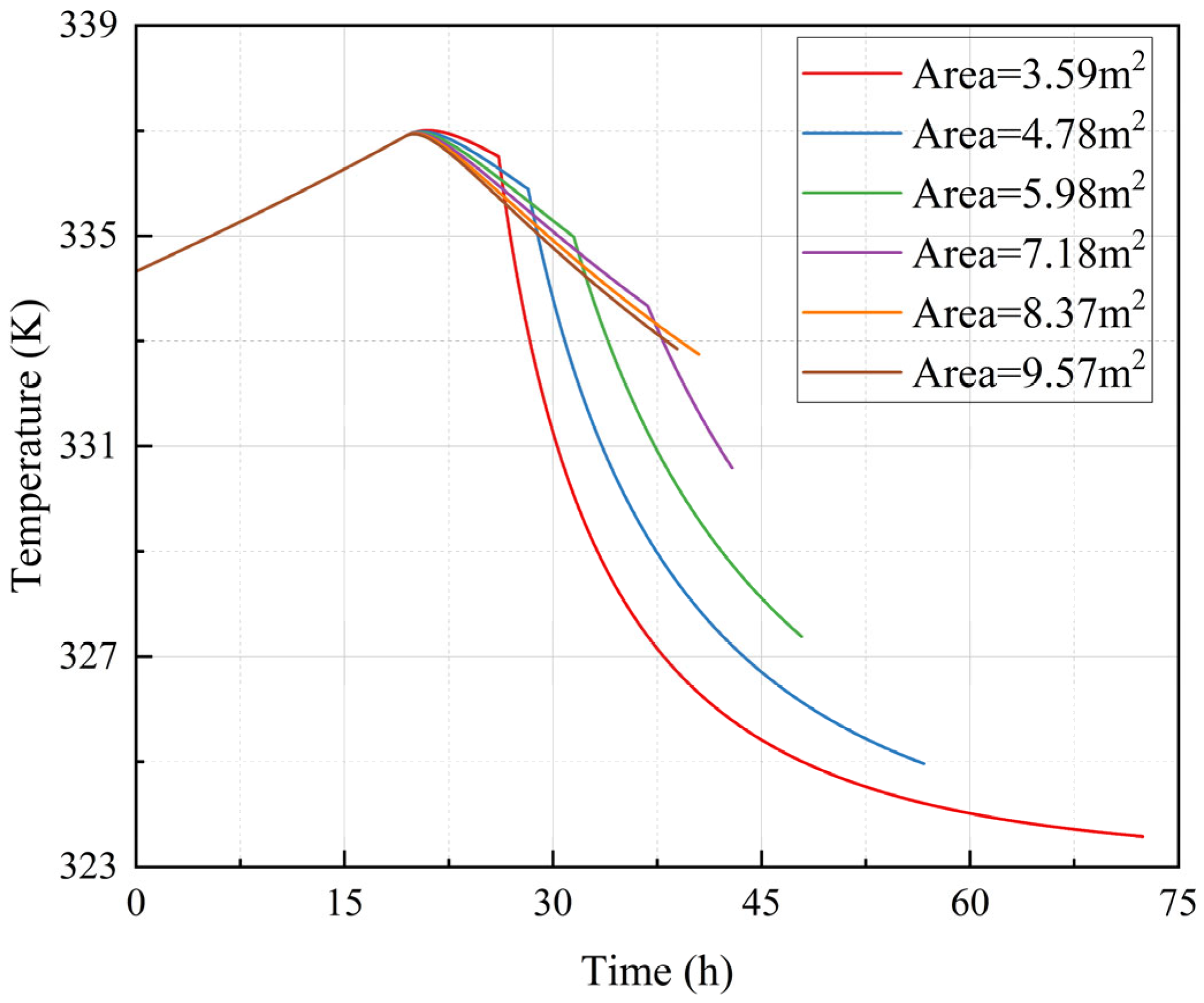
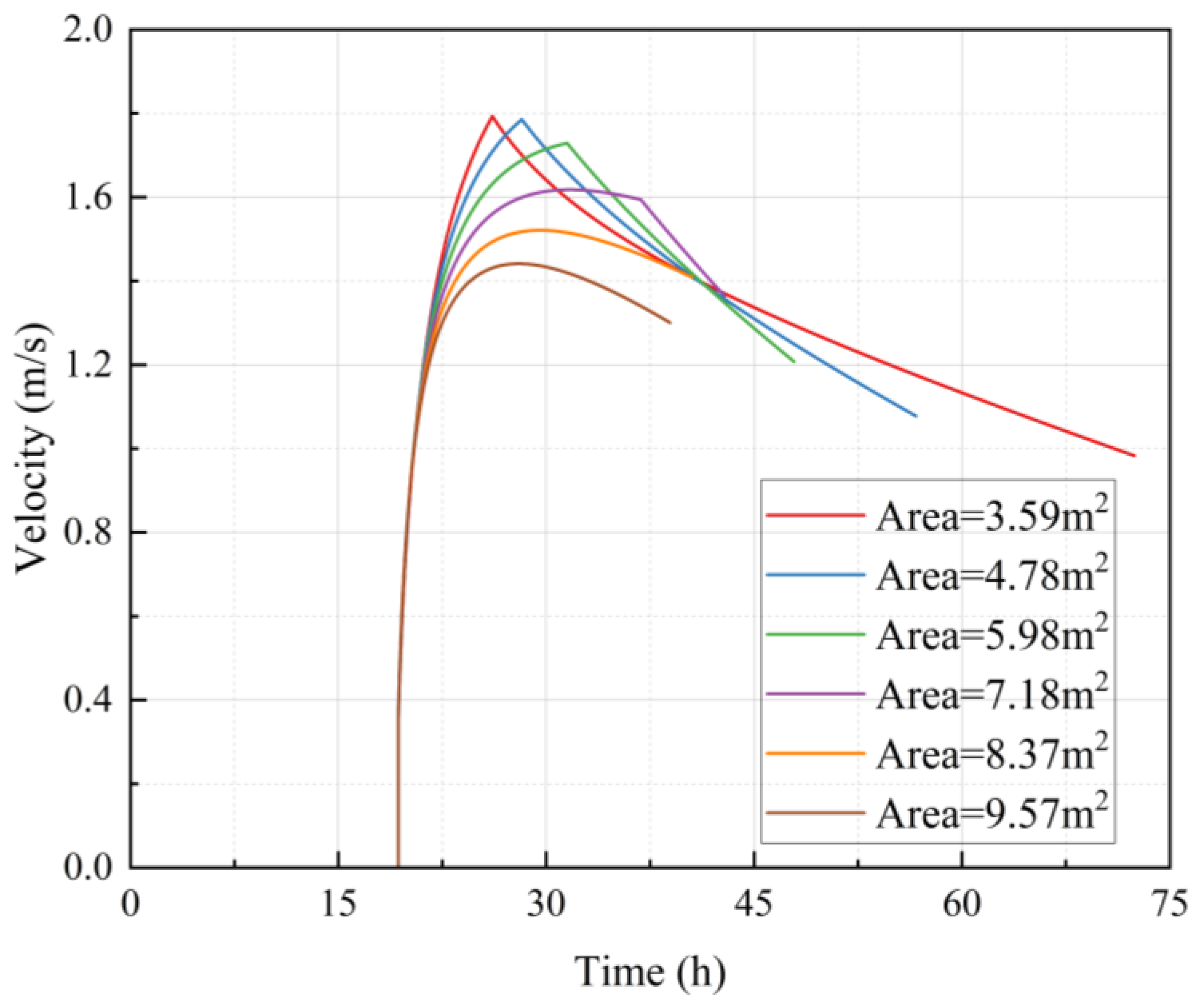
3.4. Influence of the BDP Cross-Sectional Area
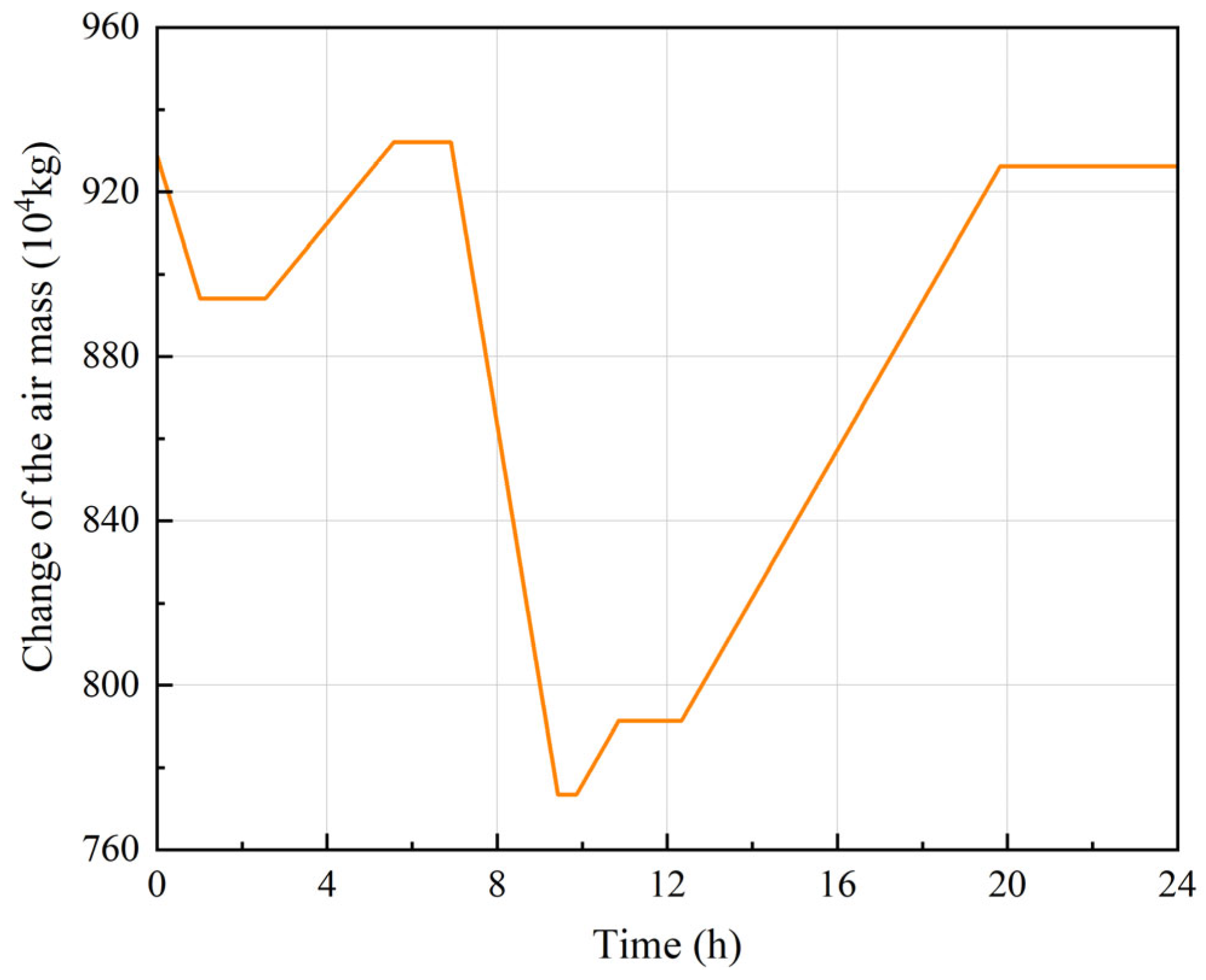
3.5. Effects on Operational Cycles
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CAES | Compressed air energy storage |
| ACAES | Adiabatic compressed air energy storage |
| BDP | Brine drainage pipeline |
| I/EWP | Injection/extraction well pipeline |
| AIPIS | Air injection and pressure increase stage |
| PIBDS | Pressure increase and brine drainage stage |
| HIBDS | Halt injection and brine drainage stage |
Nomenclature
| m | mass | U | heat transfer coefficient |
| u | internal energy | a | temperature gradient |
| t | time | b | surface temperature |
| h | specific enthalpy | tD | dimensionless time |
| T | temperature | α | thermal diffusivity |
| qm | mass flow rate | H | height |
| A | surface area | f | friction factor |
| ρ | density | V | volume |
| Cp | specific heat | subscript | |
| κ | thermal conductivity | in | injected air |
| r | radius | ca | cavern surface |
| P | pressure | rw | rock wall |
| v | velocity | out | withdrawn air |
| D | diameter | r | salt rock |
| ε | roughness | bd | brine drainage |
| Re | Reynolds number | a | air |
| μ | viscosity | b | brine |
| ΔQ | heat transfer | c | cavern |
References
- Nabat, M.H.; Habibzadeh, M.; Alsagri, A.S.; Arabkoohsar, A. An investigation and multi-criteria optimization of an innovative compressed air energy storage. J. Energy Storage 2024, 76, 109645. [Google Scholar] [CrossRef]
- Baniamerian, Z.; Garvey, S.; Rouse, J.; Cárdenas, B.; Pottie, D.L.; Barbour, E.R.; Bagdanavicius, A. How pressure affects costs of power conversion machinery in compressed air energy storage; Part I: Compressors and expanders. J. Energy Storage 2024, 89, 111791. [Google Scholar] [CrossRef]
- Bazdar, E.; Sameti, M.; Nasiri, F.; Haghighat, F. Compressed air energy storage in integrated energy systems: A review. Renew. Sustain. Energy Rev. 2022, 167, 112701. [Google Scholar] [CrossRef]
- Courtois, N.; Najafiyazdi, M.; Lotfalian, R.; Boudreault, R.; Picard, M. Analytical expression for the evaluation of multi-stage adiabatic-compressed air energy storage (A-CAES) systems cycle efficiency. Appl. Energy 2021, 288, 116592. [Google Scholar] [CrossRef]
- Razmi, A.R.; Soltani, M.; Ardehali, A.; Gharali, K.; Dusseault, M.B.; Nathwani, J. Design, thermodynamic, and wind assessments of a compressed air energy storage (CAES) integrated with two adjacent wind farms: A case study at Abhar and Kahak sites, Iran. Energy 2021, 221, 119902. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Xie, M.; Ye, K.; Mohtaram, S. Energy and exergy analysis of two modified adiabatic compressed air energy storage (A-CAES) system for cogeneration of power and cooling on the base of volatile fluid. J. Energy Storage 2021, 42, 103009. [Google Scholar] [CrossRef]
- Dreißigacker, V.; Belik, S. System Configurations and Operational Concepts for Highly Efficient Utilization of Power-to-Heat in A-CAES. Appl. Sci. 2019, 9, 1317. [Google Scholar] [CrossRef]
- Babaharra, O.; Choukairy, K.; Faraji, H.; Khallaki, K.; Hamdaoui, S.; Bahammou, Y. Thermal performance analysis of hollow bricks integrated phase change materials for various climate zones. Heat Transf. 2024, 53, 2148–2172. [Google Scholar] [CrossRef]
- Babaharra, O.; Choukairy, K.; Faraji, H.; Hamdaoui, S. Improved heating floor thermal performance by adding PCM microcapsules enhanced by single and hybrid nanoparticles. Heat Transf. 2023, 52, 3817–3838. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Li, Y.; Chen, H.; Wu, Y.; Wang, J.; Garvey, S.; Ding, Y. Dynamic simulation of Adiabatic Compressed Air Energy Storage (A-CAES) plant with integrated thermal storage—Link between components performance and plant performance. Appl. Energy 2017, 185, 16–28. [Google Scholar] [CrossRef]
- Saadat, M.; Shirazi, F.A.; Li, P.Y. Modeling and control of an open accumulator Compressed Air Energy Storage (CAES) system for wind turbines. Appl. Energy 2015, 137, 603–616. [Google Scholar] [CrossRef]
- Barbour, E.; Mignard, D.; Ding, Y.; Li, Y. Adiabatic Compressed Air Energy Storage with packed bed thermal energy storage. Appl. Energy 2015, 155, 804–815. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, K.; Li, X.; Xu, J. The thermodynamic effect of thermal energy storage on compressed air energy storage system. Renew. Energy 2013, 50, 227–235. [Google Scholar] [CrossRef]
- Zhang, C.; Yan, B.; Wieberdink, J.; Li, P.Y.; Van de Ven, J.D.; Loth, E.; Simon, T.W. Thermal analysis of a compressor for application to Compressed Air Energy Storage. Appl. Therm. Eng. 2014, 73, 1402–1411. [Google Scholar] [CrossRef]
- She, X.; Peng, X.; Nie, B.; Leng, G.; Zhang, X.; Weng, L.; Tong, L.; Zheng, L.; Wang, L.; Ding, Y. Enhancement of round trip efficiency of liquid air energy storage through effective utilization of heat of compression. Appl. Energy 2017, 206, 1632–1642. [Google Scholar] [CrossRef]
- Zhao, P.; Gao, L.; Wang, J.; Dai, Y. Energy efficiency analysis and off-design analysis of two different discharge modes for compressed air energy storage system using axial turbines. Renew. Energy 2016, 85, 1164–1177. [Google Scholar] [CrossRef]
- Zhou, S.-W.; Xia, C.-C.; Du, S.-G.; Zhang, P.-Y.; Zhou, Y. An Analytical Solution for Mechanical Responses Induced by Temperature and Air Pressure in a Lined Rock Cavern for Underground Compressed Air Energy Storage. Rock Mech. Rock Eng. 2015, 48, 749–770. [Google Scholar] [CrossRef]
- Zhou, S.-W.; Xia, C.-C.; Zhao, H.-B.; Mei, S.-H.; Zhou, Y. Numerical simulation for the coupled thermo-mechanical performance of a lined rock cavern for underground compressed air energy storage. J. Geophys. Eng. 2017, 14, 1382–1398. [Google Scholar] [CrossRef]
- Li, W.; Zhu, C.; Han, J.; Yang, C. Thermodynamic response of gas injection-and-withdrawal process in salt cavern for underground gas storage. Appl. Therm. Eng. 2019, 163, 114380. [Google Scholar] [CrossRef]
- Wu, D.; Wang, J.G.; Hu, B.; Yang, S.-Q. A coupled thermo-hydro-mechanical model for evaluating air leakage from an unlined compressed air energy storage cavern. Renew. Energy 2020, 146, 907–920. [Google Scholar] [CrossRef]
- Li, W.; Miao, X.; Yang, C. Failure analysis for gas storage salt cavern by thermo-mechanical modelling considering rock salt creep. J. Energy Storage 2020, 32, 102004. [Google Scholar] [CrossRef]
- Han, Y.; Cui, H.; Ma, H.; Chen, J.; Liu, N. Temperature and pressure variations in salt compressed air energy storage (CAES) caverns considering the air flow in the underground wellbore. J. Energy Storage 2022, 52, 104846. [Google Scholar] [CrossRef]
- Eparu, C.N.; Prundurel, A.P.; Doukeh, R.; Stoica, D.B.; Ghețiu, I.V.; Suditu, S.; Stan, I.G.; Rădulescu, R. Optimizing Underground Natural Gas Storage Capacity through Numerical Modeling and Strategic Well Placement. Processes 2024, 12, 2136. [Google Scholar] [CrossRef]
- Sun, X.; Ding, G.; Li, K.; Xin, C.; Wu, Z.; Gou, Y.; Ran, L.n.; Li, H.; Bai, S.; Wu, J.n. Research on the Influencing Factors of the Void Volume of Insoluble Sediment in Salt Cavern Gas Storage. Processes 2024, 12, 636. [Google Scholar] [CrossRef]
- Hagoort, J. Simulation of Production and Injection Performance of Gas Storage Caverns in Salt Formations. SPE Reserv. Eng. 1994, 9, 278–282. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Wang, J.; Hu, L.; Wu, X.; Yang, Y.; Gai, P.; Liu, Y.; Li, Y. The underground performance analysis of compressed air energy storage in aquifers through field testing. Appl. Energy 2024, 366, 123329. [Google Scholar] [CrossRef]
- Li, P.; Li, Y.; Shi, X.; Xie, D.; Ma, H.; Yang, C.; Daemen, J.J.K. Experimental and theoretical research on the debrining process in sediments for a gas storage salt cavern. Geoenergy Sci. Eng. 2023, 225, 211667. [Google Scholar] [CrossRef]
- Ge, X.; Li, Y.; Shi, X.; Chen, X.; Ma, H.; Yang, C.; Shu, C.; Liu, Y. Experimental device for the study of Liquid–Solid coupled flutter instability of salt cavern leaching tubing. J. Nat. Gas Sci. Eng. 2019, 66, 168–179. [Google Scholar] [CrossRef]
- Hafsi, Z. Accurate explicit analytical solution for Colebrook-White equation. Mech. Res. Commun. 2021, 111, 103646. [Google Scholar] [CrossRef]
- Wu, H.; Bai, B.; Li, X.; Liu, M.; He, Y. An explicit finite difference model for prediction of wellbore pressure and temperature distribution in CO2 geological sequestration. Greenh. Gases Sci. Technol. 2017, 7, 353–369. [Google Scholar] [CrossRef]
- Hasan, A.R.; Kabir, C.S. Heat Transfer During Two-Phase Flow in Wellbores: Part I—Formation Temperature. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 6–9 October 1991. [Google Scholar]
- Crotogino, F.; Mohmeyer, K.-U.; Scharf, R. Huntorf CAES: More than 20 years of successful operation. In Proceedings of the Solution Mining Research Institute (SMRI) Spring Meeting, Orlando, FL, USA, 22–24 April 2001. [Google Scholar]



| Parameters | Unit | Value |
|---|---|---|
| Average cavern radius, r | m | 50 |
| Cavern volume, Vca | m3 | 968,800 |
| Height of the cavern, Hca | m | 125 |
| Initial height of the brine, Hmax | m | 120 |
| Terminal height of the brine, Hmin | m | 2.5 |
| Height of the I/EWP, Hwell | m | 1200 |
| Heat transfer coefficient of cavern, hca | W/(m2·K) | 30 |
| Heat transfer coefficient at the gas–liquid interface, hb | W/(m2·K) | 45 |
| Upper limit of pressure, Pmax | MPa | 17.41 |
| Initial air pressure in the cavern, P0 | MPa | 0.2 |
| Initial air temperature in the cavern, T0 | K | 313.15 |
| Parameters | Unit | Value of Huntorf [32] |
|---|---|---|
| Average cavern radius, r | m | 20 |
| Cavern volume, Vca | m3 | 141,000 |
| Cavern surface area, Aca | m2 | 25,000 |
| Heat transfer coefficient of cavern, hca | W/(m2·K) | 30 |
| Initial air temperature in the cavern, T0 | K | 313.15 |
| Initial air pressure in the cavern, P0 | MPa | 5.9 |
| Injection temperature, Tin | K | 323.15 |
| Injection pressure, Pin | MPa | 7.2 |
| Injection mass rate, qmin | kg/s | 50 |
| Withdrawal mass rate, qmout | kg/s | 190 |
| Parameters | Unit | Value |
|---|---|---|
| Rated discharging power | MW | 350 |
| Rated charging power | MW | 245.27 |
| Round-trip efficiency | / | 71.35% |
| Energy storage capacity | MWh | 1400 |
| Average mass flow rate of air during generation period | kg/s | 752.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Wu, B.; Yin, Y.; Shao, L.; Li, R.; Jiang, X.; Sun, Y.; Huo, X.; Ling, C. Thermodynamic Characteristics of Compressed Air in Salt Caverns of CAES: Considering Air Injection for Brine Drainage. Energies 2025, 18, 3649. https://doi.org/10.3390/en18143649
Sun S, Wu B, Yin Y, Shao L, Li R, Jiang X, Sun Y, Huo X, Ling C. Thermodynamic Characteristics of Compressed Air in Salt Caverns of CAES: Considering Air Injection for Brine Drainage. Energies. 2025; 18(14):3649. https://doi.org/10.3390/en18143649
Chicago/Turabian StyleSun, Shizhong, Bin Wu, Yonggao Yin, Liang Shao, Rui Li, Xiaofeng Jiang, Yu Sun, Xiaodong Huo, and Chen Ling. 2025. "Thermodynamic Characteristics of Compressed Air in Salt Caverns of CAES: Considering Air Injection for Brine Drainage" Energies 18, no. 14: 3649. https://doi.org/10.3390/en18143649
APA StyleSun, S., Wu, B., Yin, Y., Shao, L., Li, R., Jiang, X., Sun, Y., Huo, X., & Ling, C. (2025). Thermodynamic Characteristics of Compressed Air in Salt Caverns of CAES: Considering Air Injection for Brine Drainage. Energies, 18(14), 3649. https://doi.org/10.3390/en18143649







