Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies
Abstract
1. Introduction
- A comprehensive small-signal stability assessment is presented for a bulk power system with mixed SG and IBR penetration, revealing how control strategies, parameter settings, and structural characteristics, including inertia and impedance, affect system stability.
- The study demonstrates the stabilizing role of supplementary grid assets (SCs and STATCOMs) and highlights the benefits of strategically distributing a sufficient number of voltage-source elements (SGs and GFMs) throughout the system to enable high penetration of passive assets, such as GFL IBRs.
2. Dynamical Models
2.1. Synchronous Generators
2.2. Inverter-Based Resources
2.2.1. Droop-Controlled Grid-Forming Inverters (Droop-GFM)
2.2.2. Virtual Oscillator-Controlled Grid-Forming Inverters (VOC-GFM)
2.2.3. Grid-Following Inverters (GFL)
2.3. Other Grid-Supporting Assets
2.3.1. Synchronous Condensers
2.3.2. STATCOMs
3. Description of Test System
3.1. Stability Analysis Method
3.2. Connecting Multiple Types of Generator at One Bus
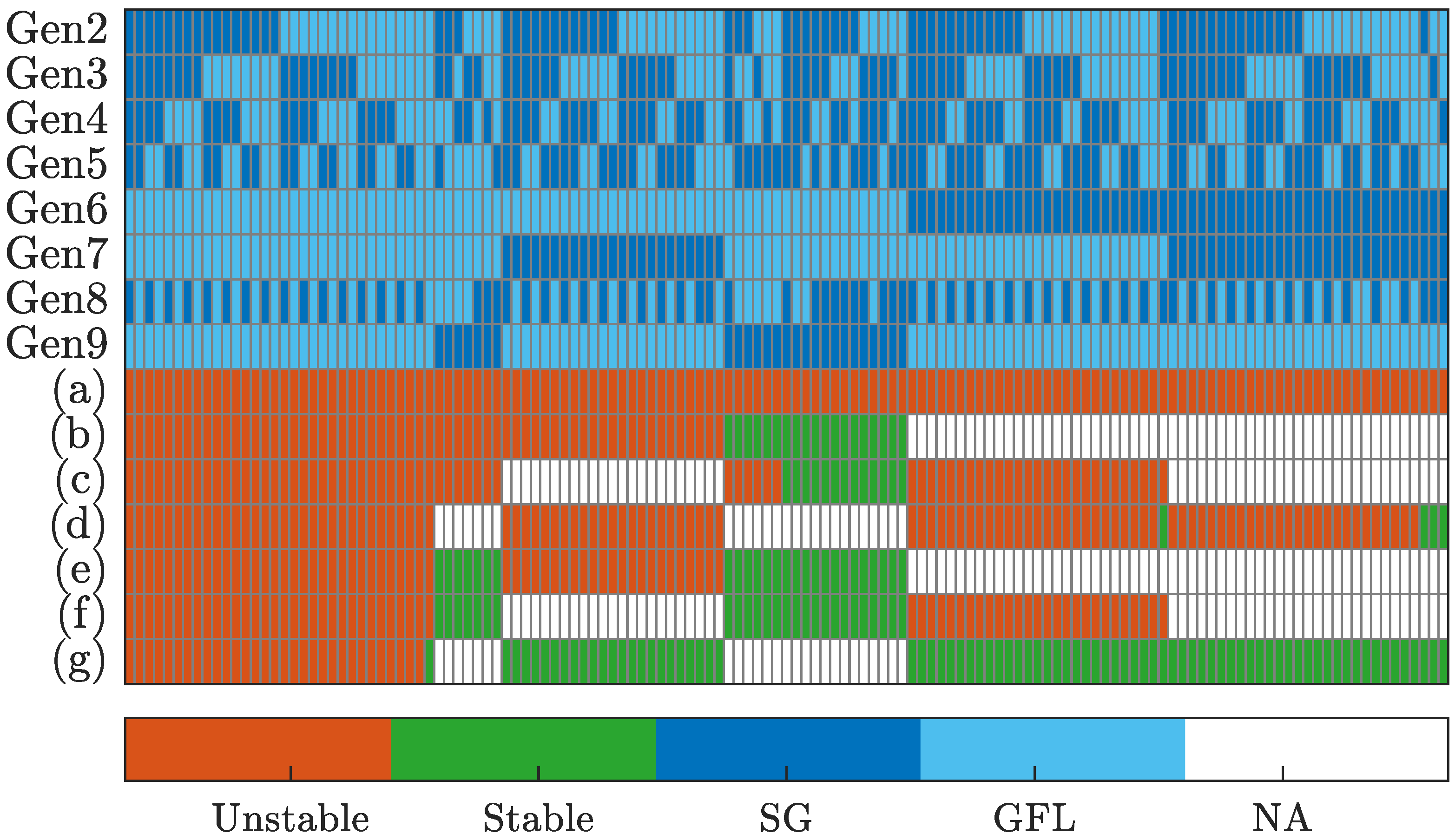
4. Case Studies and Discussion
4.1. Baseline Case—All Synchronous Generators
4.2. One-by-One Replacement of IBRs
4.2.1. Impact of GFL Inverter on Stability
4.2.2. Impact of GFL Inverter with Droop Control on Stability
4.2.3. Impact of GFM Inverters on Stability
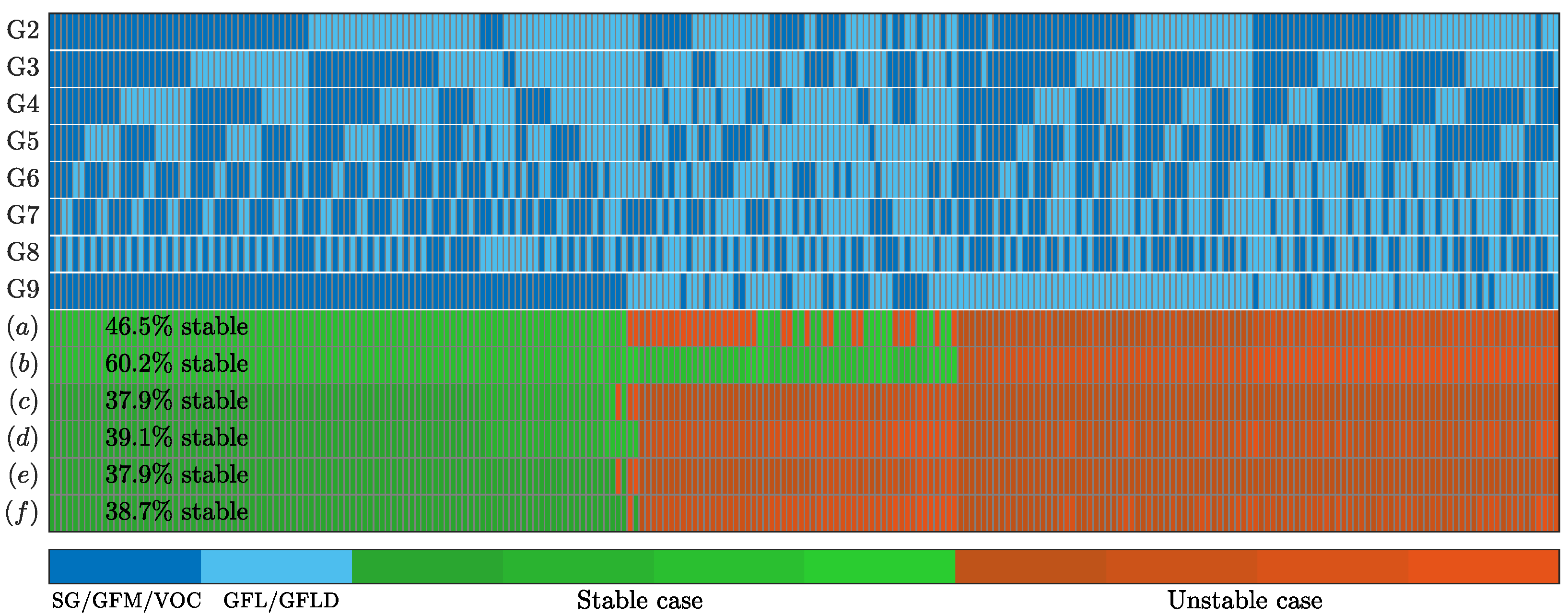
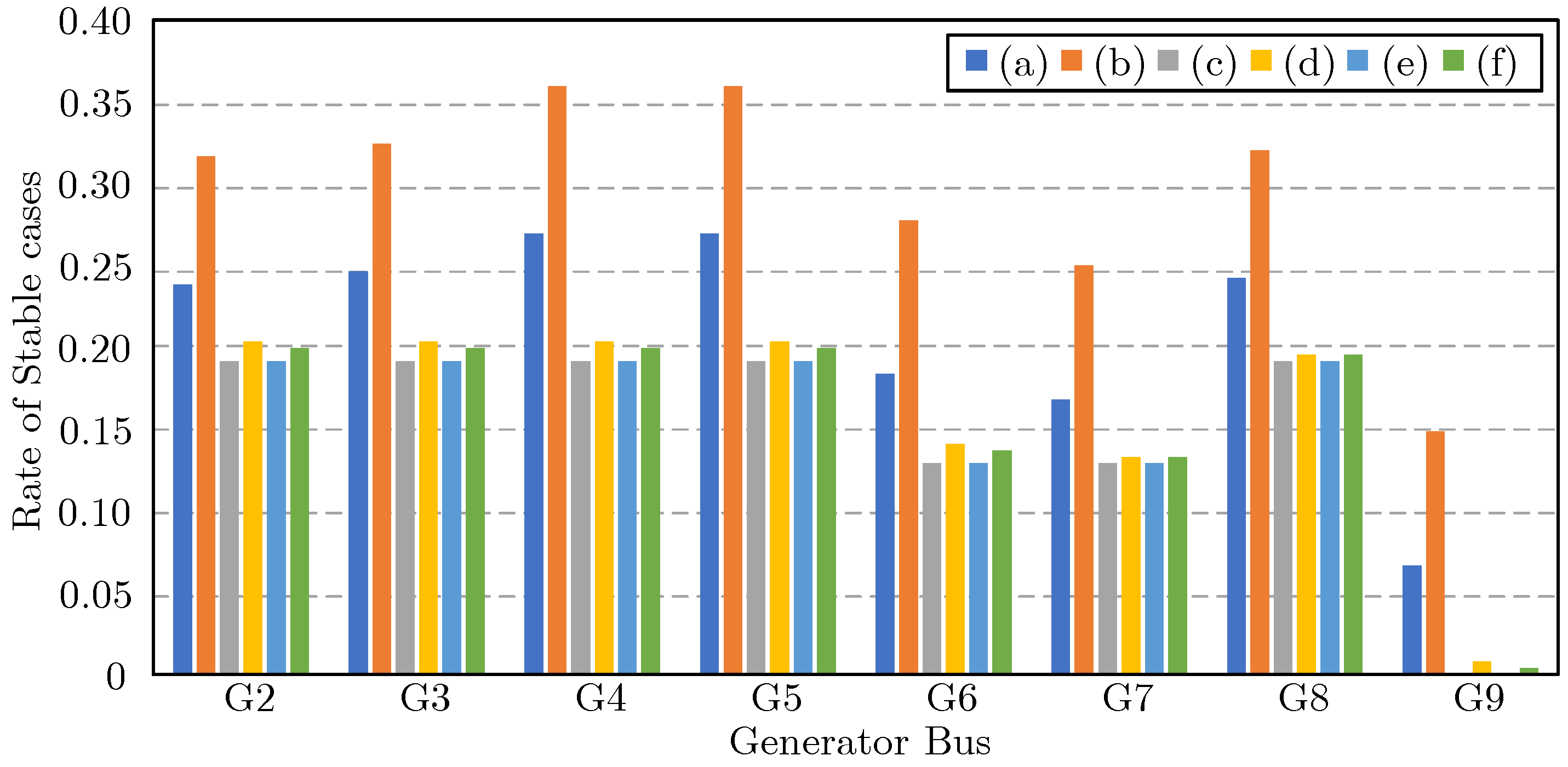
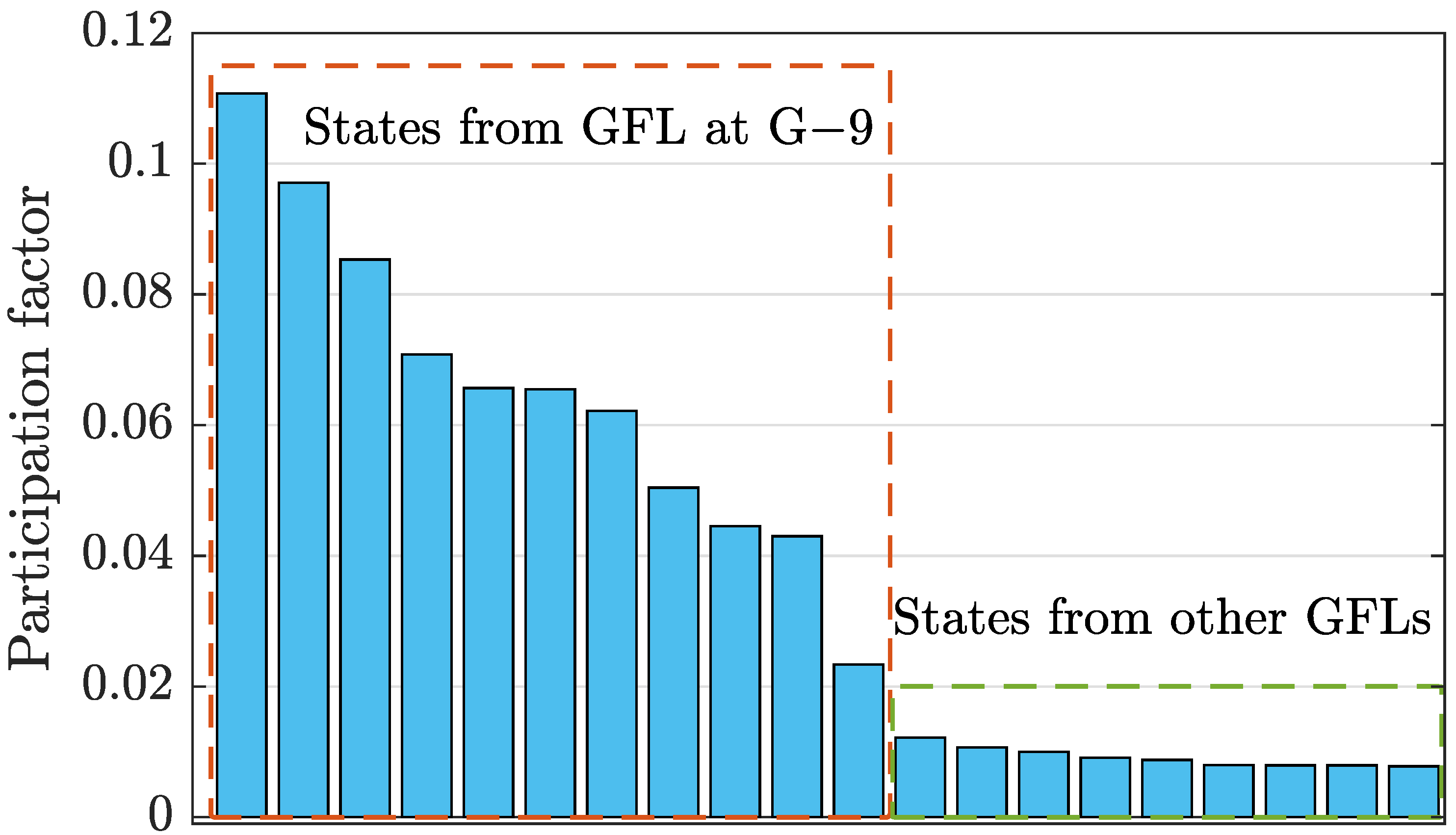
4.3. Identifying the Most Vulnerable Generator Bus in the Presence of IBRs
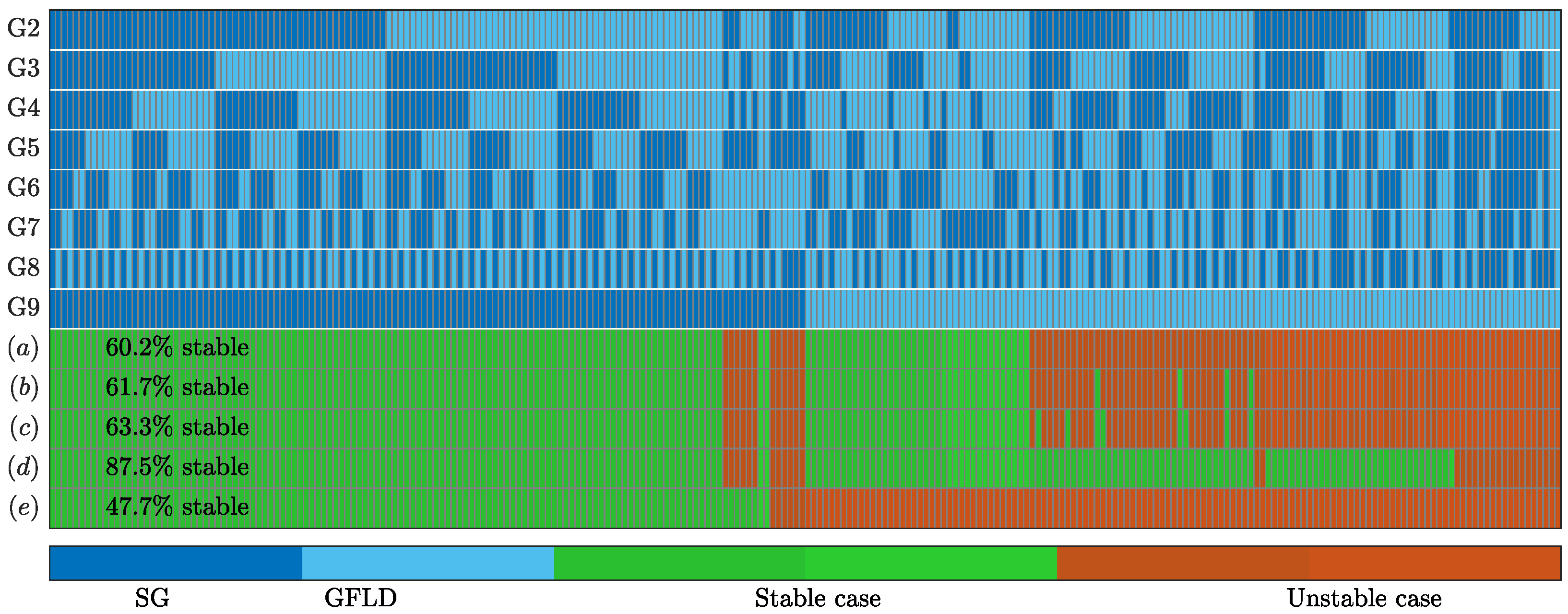
4.4. Stability at Different IBR Penetration Levels
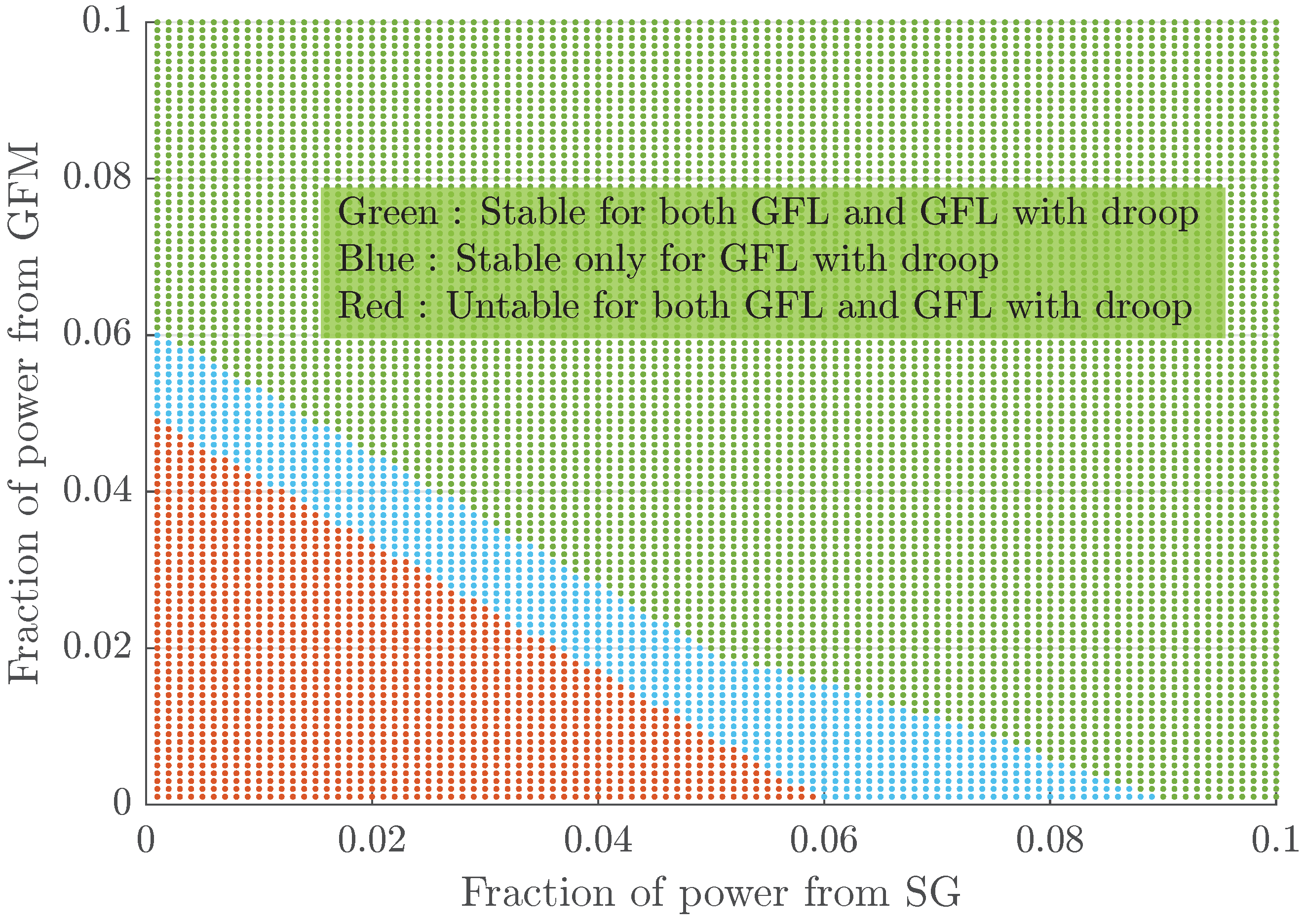
4.5. Fractional Replacement of SGs with IBRs
4.6. Impact of IBR Control Parameters on Stability
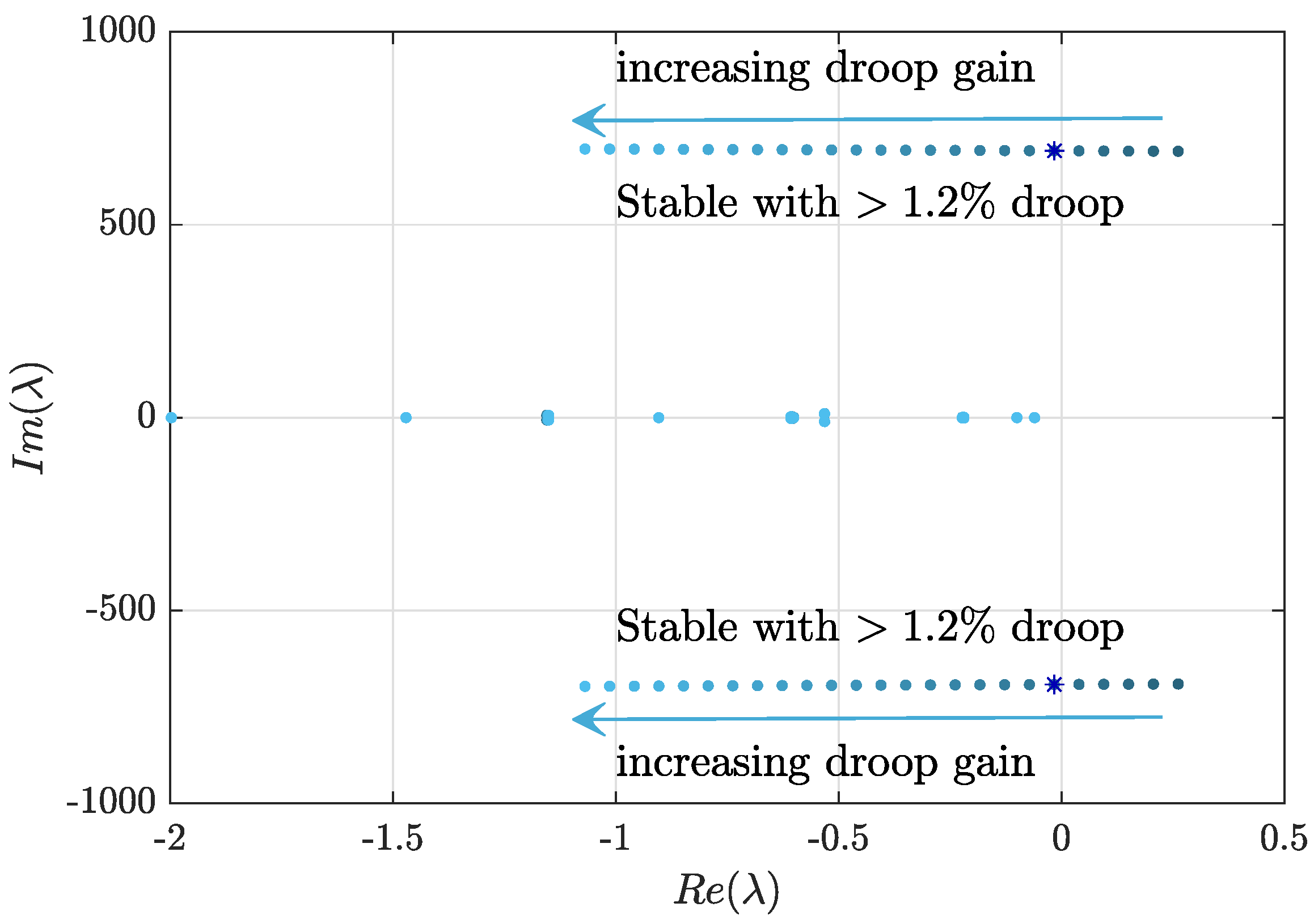
4.6.1. Effect of Droop Gain of GFLD Inverters
4.6.2. Impact of PLL Controller Parameters of GFLD Inverters on Stability
4.7. Impact of SG Inertia and Role of GFM Inverter
4.8. Impact of STATCOM and SC on Stability
4.9. Impact of Line Impedance on Stability
5. Conclusions and Future Works
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SG | Synchronous generator |
| IBR | Inverter-based resource |
| GFL | Grid-following inverter without droop |
| GFLD | Grid-following inverter with droop |
| Droop-GFM | Droop-controlled grid-forming inverter |
| VOC-GFM | Virtual oscillator control-based grid-forming inverter |
| SC | Synchronous condenser |
| STATCOM | Static synchronous compensator |
Appendix A
| Prated | 3 kV | Vrated | 208 V | Lf | 1 mH |
|---|---|---|---|---|---|
| F | H | ||||
| 1 | 430 | ||||
| Machine | H = , = 0, = = , = , = , = 5, = , D = 0 |
| AVR | = 0.01, = , = 200, = , = , = |
| PSS | = 1, = 10, = = 1, = = , = , = |
References
- Kroposki, B. UNIFI Specifications for Grid-Forming Inverter-Based Resources (v. 2); Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024.
- Chen, Y.; Shi, K.; Chen, M.; Xu, D. Data center power supply systems: From grid edge to point-of-load. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 11, 2441–2456. [Google Scholar] [CrossRef]
- Xu, S.; Xue, Y.; Chang, L. Review of power system support functions for inverter-based distributed energy resources-standards, control algorithms, and trends. IEEE Open J. Power Electron. 2021, 2, 88–105. [Google Scholar] [CrossRef]
- Huber, J.E.; Kolar, J.W. Applicability of solid-state transformers in today’s and future distribution grids. IEEE Trans. Smart Grid 2017, 10, 317–326. [Google Scholar] [CrossRef]
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Villegas Pico, H.N.; Seo, G.S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters; Technical Report; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2020.
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the Power Systems Computation Conference, Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar]
- Du, W.; Liu, Y.; Tuffner, F.K.; Huang, R.; Huang, Z. Model Specification of Droop-Controlled, Grid-Forming Inverters (GFMDRP_A); Technical Report; Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2021.
- Seo, G.S.; Colombino, M.; Subotic, I.; Johnson, B.; Gross, D.; Dörfler, F. Dispatchable virtual oscillator control for decentralized inverter-dominated power systems: Analysis and experiments. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 561–566. [Google Scholar]
- Awal, M.; Yu, H.; Husain, I.; Yu, W.; Lukic, S.M. Selective harmonic current rejection for virtual oscillator controlled grid-forming voltage source converters. IEEE Trans. Power Electron. 2020, 35, 8805–8818. [Google Scholar] [CrossRef]
- Du, W.; Achilles, S.; Ramasubramanian, D.; Hart, P.; Rao, S.; Wang, W.; Nguyen, Q.; Kim, J.; Zhang, Q.; Liu, H.; et al. Virtual Synchronous Machine Grid-Forming Inverter Model Specification (REGFM_B1); Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2024.
- Arghir, C.; Jouini, T.; Dörfler, F. Grid-forming control for power converters based on matching of synchronous machines. Automatica 2018, 95, 273–282. [Google Scholar] [CrossRef]
- Ali Khan, M.Y.; Liu, H.; Yang, Z.; Yuan, X. A comprehensive review on grid connected photovoltaic inverters, their modulation techniques, and control strategies. Energies 2020, 13, 4185. [Google Scholar] [CrossRef]
- Markovic, U.; Stanojev, O.; Aristidou, P.; Vrettos, E.; Callaway, D.; Hug, G. Understanding Small-Signal Stability of Low-Inertia Systems. IEEE Trans. Power Syst. 2021, 36, 3997–4017. [Google Scholar] [CrossRef]
- Ding, L.; Lu, X.; Tan, J. Comparative Small-Signal Stability Analysis of Grid-Forming and Grid-Following Inverters in Low-Inertia Power Systems. In Proceedings of the 47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar] [CrossRef]
- He, X.; Pan, S.; Geng, H. Transient Stability of Hybrid Power Systems Dominated by Different Types of Grid-Forming Devices. IEEE Trans. Energy Convers. 2022, 37, 868–879. [Google Scholar] [CrossRef]
- Johnson, B.; Sinha, M.; Ainsworth, N.; Dörfler, F.; Dhople, S. Synthesizing Virtual Oscillators to Control Islanded Inverters. IEEE Trans. Power Electron. 2015, 31, 6002–6015. [Google Scholar] [CrossRef]
- Siraj Khan, M.M.; Lin, Y.; Johnson, B.; Sinha, M.; Dhople, S. Stability Assessment of a System Comprising a Single Machine and a Virtual Oscillator Controlled Inverter with Scalable Ratings. In Proceedings of the 44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 4057–4062. [Google Scholar] [CrossRef]
- Johnson, B.; Rodriguez, M.; Sinha, M.; Dhople, S. Comparison of virtual oscillator and droop control. In Proceedings of the IEEE Workshop on Control and Modeling for Power Electronics, Stanford, CA, USA, 9–12 July 2017; pp. 1–6. [Google Scholar]
- Arévalo-Soler, J.; Sánchez-Sánchez, E.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Impact analysis of energy-based control structures for grid-forming and grid-following MMC on power system dynamics based on eigenproperties indices. Int. J. Electr. Power Energy Syst. 2022, 143, 108369. [Google Scholar] [CrossRef]
- Kenyon, R.W.; Hoke, A.; Tan, J.; Hodge, B.M. Grid-following inverters and synchronous condensers: A grid-forming pair? In Proceedings of the 2020 Clemson University Power Systems Conference, Clemson, SC, USA, 10–13 March 2020; pp. 1–7. [Google Scholar]
- Stiger, A.; Rivas, R.; Halonen, M. Synchronous condensers contribution to inertia and short circuit current in cooperation with STATCOM. In Proceedings of the IEEE PES GTD Grand International Conference and Exposition Asia, Bangkok, Thailand, 19–23 March 2019; pp. 955–959. [Google Scholar]
- Hu, W.; Su, C.; Fang, J.; Chen, Z. Comparison study of power system small signal stability improvement using SSSC and STATCOM. In Proceedings of the 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 1998–2003. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Zhang, S.; Peng, F.Z. Comparison of synchronous condenser and STATCOM for inertial response support. In Proceedings of the IEEE Energy Conversion Congress and Exposition, Pittsburgh, PA, USA, 14–18 September 2014; pp. 2684–2690. [Google Scholar] [CrossRef]
- Gross, D.; Colombino, M.; Brouillon, J.S.; Dörfler, F. The Effect of Transmission-Line Dynamics on Grid-Forming Dispatchable Virtual Oscillator Control. IEEE Trans. Control Netw. Syst. 2019, 6, 1148–1160. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Dazhong, M.; Xuguang, H. Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid 2020, 11, 2856–2866. [Google Scholar] [CrossRef]
- Li, D.; Yang, S.; Huang, W.; He, J.; Yuan, Z.; Yu, J. Optimal Planning Method for Power System Line Impedance Based on a Comprehensive Stability Margin. IEEE Access 2021, 9, 56264–56276. [Google Scholar] [CrossRef]
- Lin, Y.; Seo, G.S.; Vijayshankar, S.; Johnson, B.; Dhople, S. Impact of Increased Inverter-based Resources on Power System Small-signal Stability. In Proceedings of the IEEE Power & Energy Society General Meeting, Washington, DC, USA, 26–29 July 2021; pp. 1–5. [Google Scholar]
- Australian Energy Market Operator. Application of Advanced Grid-scale Inverters in the NEM. In White Paper; Australian Energy Market Operator: Victoria, Australia, 2021. [Google Scholar]
- Hiskens, I.A. IEEE PES Task Force on Benchmark Systems for Stability Controls; Technical Report; IEEE Power & Energy Society: Piscataway, NJ, USA, 2013. [Google Scholar]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Wiley Online Library: Hoboken, NJ, USA, 1998; Volume 101. [Google Scholar]
- Teodorescu, R.; Liserre, M.; Rodriguez, P. Grid Converters for Photovoltaic and Wind Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency Stability of Synchronous Machines and Grid-Forming Power Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef]
- Ali, Z.; Christofides, N.; Hadjidemetriou, L.; Kyriakides, E.; Yang, Y.; Blaabjerg, F. Three-phase phase-locked loop synchronization algorithms for grid-connected renewable energy systems: A review. Renew. Sustain. Energy Rev. 2018, 90, 434–452. [Google Scholar] [CrossRef]
- Bahrani, B. Power-synchronized grid-following inverter without a phase-locked loop. IEEE Access 2021, 9, 112163–112176. [Google Scholar] [CrossRef]
- Pai, M. Energy Function Analysis for Power System Stability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Zhao, J.; Zhang, Q.; Ziwen, L.; Xiaokang, W. A distributed black-start optimization method for global transmission and distribution network. IEEE Trans. Power Syst. 2021, 36, 4471–4481. [Google Scholar] [CrossRef]
- Sawant, J.; Seo, G.S.; Ding, F. Resilient Inverter-Driven Black Start with Collective Parallel Grid-Forming Operation. In Proceedings of the IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 16–19 January 2023; pp. 1–5. [Google Scholar]
- Du, W.; Chen, Z.; Schneider, K.P.; Lasseter, R.H.; Nandanoori, S.P.; Tuffner, F.K.; Kundu, S. A Comparative Study of Two Widely Used Grid-Forming Droop Controls on Microgrid Small-Signal Stability. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 963–975. [Google Scholar] [CrossRef]
- Lin, Y.; Johnson, B.; Gevorgian, V.; Purba, V.; Dhople, S. Stability assessment of a system comprising a single machine and inverter with scalable ratings. In Proceedings of the North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
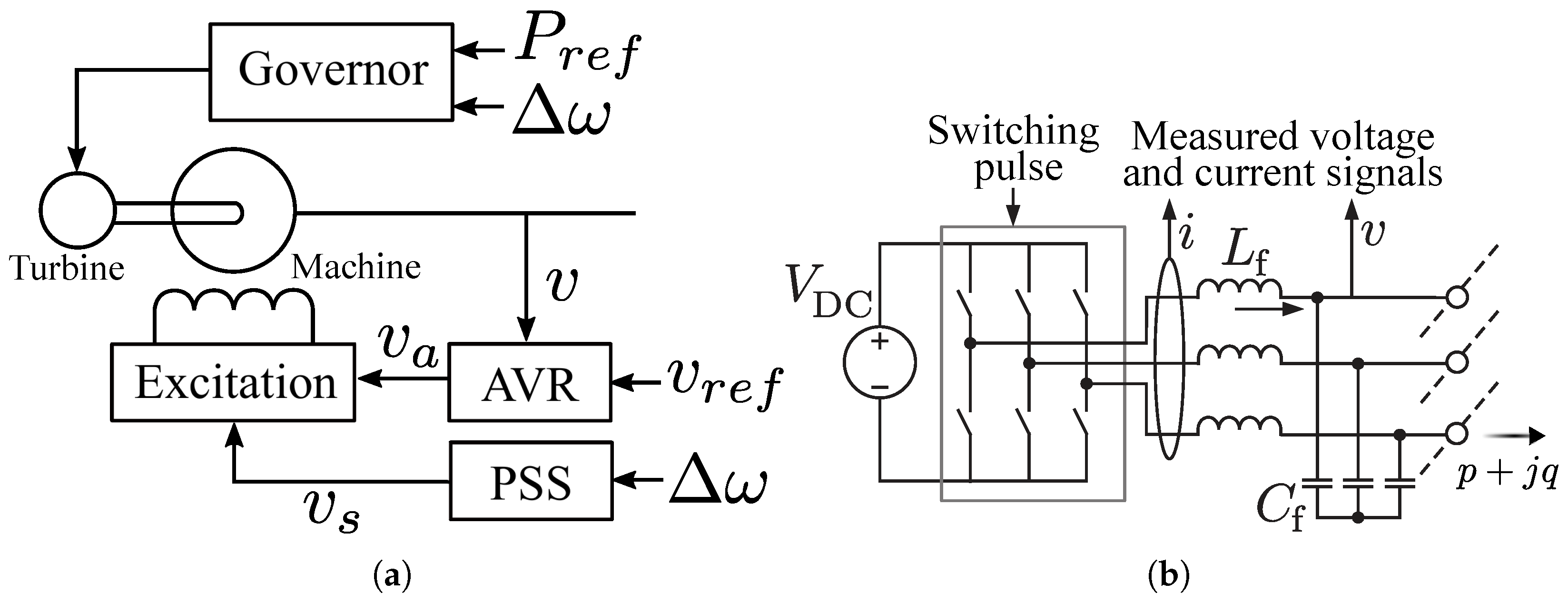
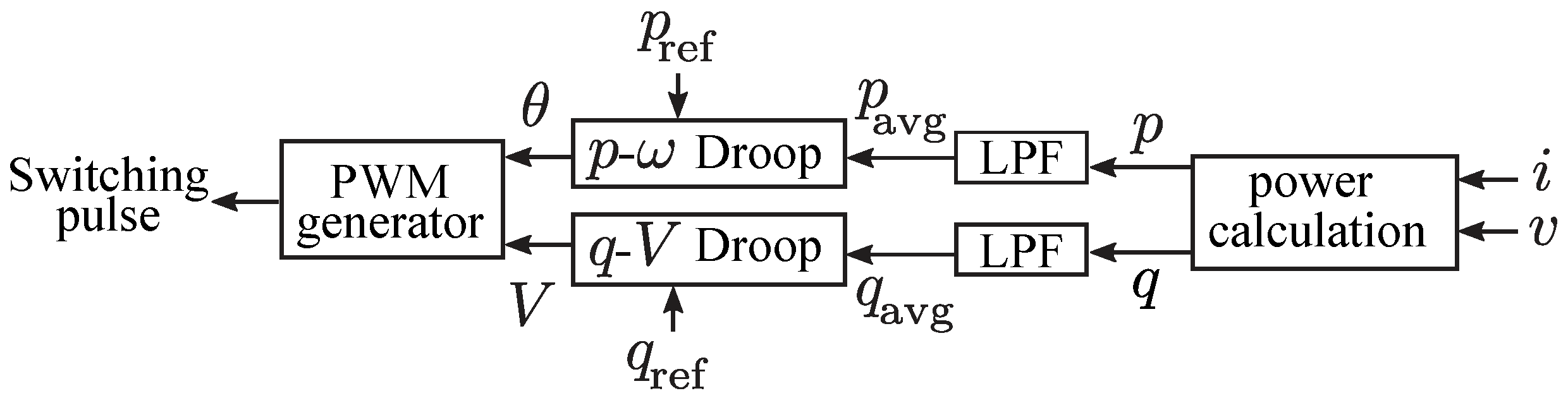
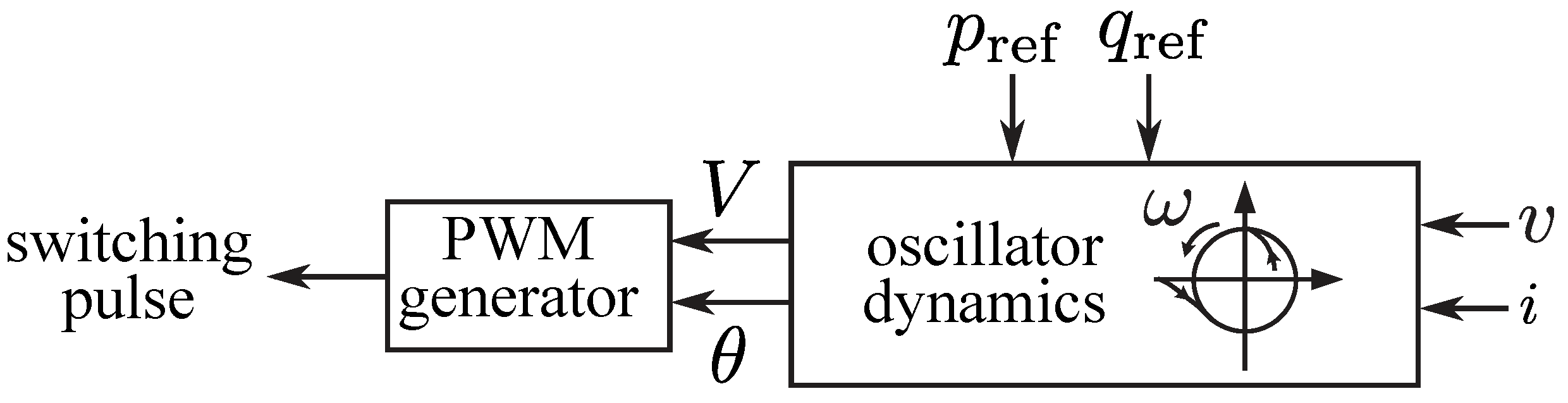
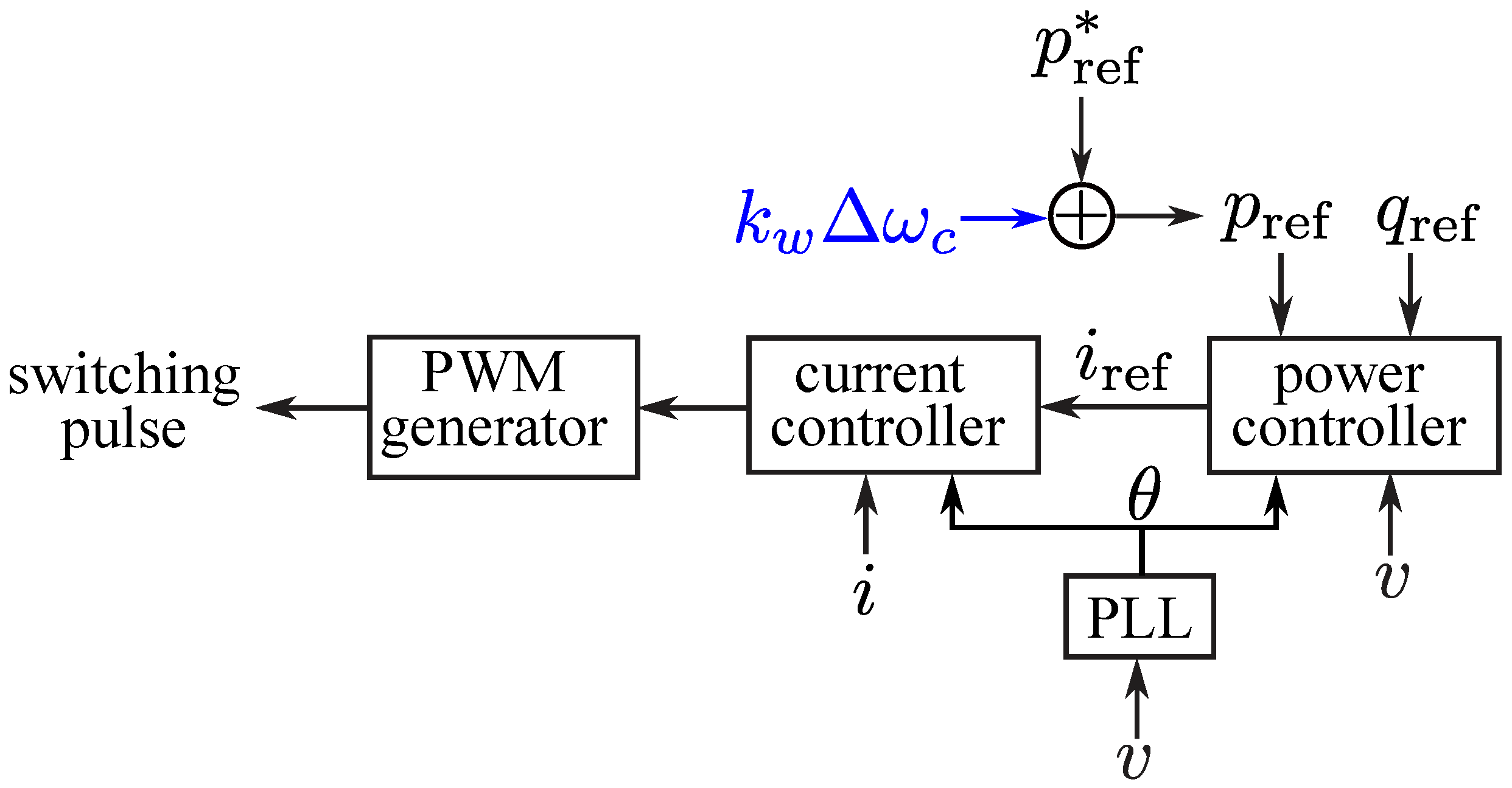




| Gen. Type | Grid Support Functionality | Notable Features |
|---|---|---|
| SG | Provides voltage and frequency regulation based on electro-mechanical coupling and provides rotational inertia. | Has been the foundation for legacy grids. Can stabilize a grid independently and provides support during contingencies in the grid. |
| GFM | Regulates the voltage and frequency based on the inverter terminal measurements with droop characteristics programmed. No mechanical inertia is present because this is a power electronics inverter-based resource. | Frequency-watt and voltage-VAR droops help multiple generators share loads and collectively maintain the grid. Backward compatible with SGs. Theoretically, small-signal stable at 100% IBR penetration level for a bulk grid. |
| GFL | Provides constant power/current at the inverter terminal. The terminal voltage and frequency depend on the rest of the grid. | Most popular control method for field-deployed IBRs. Cannot maintain grid stability alone for IBR penetration level. |
| GFLD | Provides constant power/current with droops on the active and reactive power references based on the frequency and voltage deviation from the nominal values. | Provides better grid support than normal GFL inverters; however, it might not firmly maintain grid stability alone, since there is no explicit control on the terminal voltage and frequency like a GFM inverter. Due to this, cannot ensure stability for a grid with IBR penetration. |
| SC | Provides only voltage-reactive power regulation and rotational inertia. | Provides grid support with voltage regulation and can contribute to frequency stability, since the mechanical inertia is present. |
| STATCOM | Provides reactive-power support and voltage regulation. No mechanical inertia is present because this is based on a power electronics inverter. | Can contribute to system stability using adaptive reactive-power provision. |
| Items | Takeaways |
|---|---|
| GFL and GFLD inverter | It is not practical to have a stable grid with the majority of SGs replaced with only grid-following inverters. The study reconfirms the need for voltage sources, i.e., GFM IBRs. Having grid-support functions in GFL IBRs improves the system stability, but it cannot guarantee system stability. |
| GFM inverter | It is critical to have GFM IBRs for stability in the IBR-dominant grid. However, having all IBRs with GFM control would not be necessary or practical, considering the additional engineering and cost needed. |
| Co-existence of SG, GFM, and GFL | Having voltage sources (SG or GFM) at fractional scales, distributed throughout the grid, would help retain system stability with the majority of IBRs run by conventional GFL controls, elucidating a practical approach for future grid stabilization. |
| SC and STATCOM | Having SC or STATCOM at nonvoltage source buses can improve stability in GFL-heavy grids, which confirms their effectiveness. They differ in grid stabilization due to their fundamental difference. |
| Other grid parameters | The role of machine inertia in system stability of high IBR penetration power systems is not clear, suggesting the necessity of further study. Network impedance affects system stability, especially in IBR-heavy grids, requiring attention in system planning and contingency analysis. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samanta, S.; Yang, B.; Seo, G.-S. Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies. Energies 2025, 18, 3645. https://doi.org/10.3390/en18143645
Samanta S, Yang B, Seo G-S. Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies. Energies. 2025; 18(14):3645. https://doi.org/10.3390/en18143645
Chicago/Turabian StyleSamanta, Sayan, Bowen Yang, and Gab-Su Seo. 2025. "Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies" Energies 18, no. 14: 3645. https://doi.org/10.3390/en18143645
APA StyleSamanta, S., Yang, B., & Seo, G.-S. (2025). Stability Analysis of Power Systems with High Penetration of State-of-the-Art Inverter Technologies. Energies, 18(14), 3645. https://doi.org/10.3390/en18143645







