Abstract
Reliable damage detection in operational offshore wind turbines (OWTs) remains challenging due to the inherent non-stationarity of environmental excitations and signal degradation from noise-contaminated partial measurements. To address these limitations, this study proposes a robust damage detection method for OWTs under non-stationary ambient excitations using partial measurements with strong noise resistance. The method is first developed for a scenario with known non-stationary ambient excitations. By reformulating the time-domain equation of motion in terms of non-stationary cross-correlation functions, structural stiffness parameters are estimated using partially measured acceleration responses through the extended Kalman filter (EKF). To account for the more common case of unknown excitations, the method is enhanced via the extended Kalman filter under unknown input (EKF-UI). This improved approach enables the simultaneous identification of the physical parameters of OWTs and unknown non-stationary ambient excitations through the data fusion of partial acceleration and displacement responses. The proposed method is validated through two numerical cases: a frame structure subjected to known non-stationary ground excitation, followed by an OWT tower under unknown non-stationary wind and wave excitations using limited measurements. The numerical results confirm the method’s capability to accurately identify structural damage even under significant noise contamination, demonstrating its practical potential for OWTs’ damage detection applications.
1. Introduction
Wind power has become one of the most rapidly advancing renewable energy technologies in recent years. Among its various forms, offshore wind energy offers distinct advantages by accessing stronger and more consistent wind resources than onshore alternatives, positioning it as a critical element in future sustainable energy systems [1]. Modern offshore wind turbines (OWTs) benefit from higher wind availability, enabling substantially increased full-load operating hours. This advantage has accelerated the deployment of larger-scale OWT installations. However, their expansion introduces significant structural safety concerns, as these turbines endure complex dynamic vibrations and extreme environmental conditions that can result in structural degradation and operational failures [2]. Consequently, improving operational reliability through advanced structural health monitoring (SHM) has become a key research focus to mitigate failure risks and ensure long-term performance [3].
In order to assess the integrity of OWTs, the application of vibration-based damage detection techniques is becoming increasingly necessary. The structural vibration induced by fluid–structure interactions, such as wind or wave loads, represents a complex dynamical phenomenon that has attracted extensive investigation in the engineering and physics research communities [4,5,6]. Although significant progress has been made in both time-domain [7,8,9,10] and frequency-domain [11,12,13] methods, several key challenges still demand urgent attention: (1) ambient vibration-based detection [14,15]; (2) noise-robust identification [16,17]; (3) accurate assessment using limited measurements [18,19,20]; and (4) reliable detection without excitation knowledge [21]. These challenges are further compounded by the inherent non-stationarity and nonlinearity of marine environmental loads (wind, wave loads, or earthquake) [22,23], which significantly limit the effectiveness of conventional stationary-based detection methods for OWT applications [24,25]. Consequently, the development of specialized damage detection methodologies capable of handling non-stationary excitations has become a pressing research priority for advancing OWT SHM systems.
Vibration monitoring in OWTs is significantly compromised by the complex interplay of environmental disturbances and operational noise sources (e.g., mechanical vibrations and electrical interference). This synergistic noise coupling fundamentally limits the effectiveness of conventional filtering approaches in structural response analysis [26]. Consequently, the development of advanced noise-robust techniques has emerged as a critical requirement for achieving reliable damage detection in OWT SHM systems. The cross-correlation function quantifies the correlation between two signals at different time lags [27]. When applied to the signal of dynamic random responses contaminated by noise, it effectively preserves the underlying signal correlation because noise and the dynamic response are statistically independent. This property gives the cross-correlation function a significant advantage in suppressing measurement noise. Based on the cross-correlation function of structural responses, numerous methods have been developed for modal parameter identification and structural damage detection [28,29,30]. However, most existing correlation-based approaches assume that the excitation is stationary broadband white noise [31], which severely limits their applicability in structural damage identification. Due to the complexity of non-stationary random processes, developing noise-robust methods for damage detection in OWTs under non-stationary ambient excitations remains an important challenge.
In addition, contemporary structural damage detection techniques face two significant implementation barriers. First, the predominant requirement for complete structural response data proves impractical for real-world engineering applications, where comprehensive instrumentation is often unfeasible. Second, the stochastic nature and inherent immeasurability of ambient excitations present fundamental challenges for operational damage assessment. The conventional extended Kalman filter (EKF) has demonstrated efficacy in structural dynamic parameter identification through its partial measurement capability [32]. However, its dependence on complete excitation information substantially restricts practical deployment. Recent decades have seen notable progress in simultaneous identification approaches for structural parameters and excitations [33,34,35], with the extended Kalman filter under unknown input (EKF-UI) method emerging as a particularly significant advancement [36]. This approach streamlines previous complex derivations while employing acceleration and displacement response fusion to effectively mitigate the drift in state and input estimation. The effectiveness of EKF-UI has been verified through tests and real-world engineering cases. For example, Li et al. [37] demonstrated the accuracy of EKF-UI in practical applications through a shaking table test on a five-story frame with rubber isolation bearings. Lei et al. [38] used the measured absolute acceleration responses of the Burbank Building in California, USA, during the 1991 Sierra Madre earthquake to successfully identify the unknown seismic input along with structural parameters using the EKF-UI based method. However, despite these developments, research addressing the damage detection of OWTs under unknown non-stationary ambient excitations remains conspicuously limited in the literature.
In view of the issues mentioned above, this paper presents a novel OWT damage detection method specifically designed for non-stationary ambient excitation scenarios, featuring enhanced noise immunity for high-noise environments and operational capability with partial structural measurements. Firstly, damage identification under known non-stationary ambient excitation is investigated. The equation of motion in the time-domain is transformed into the form of non-stationary cross-correlation functions. Then, following the EKF procedure, structural damage is estimated using partially measured acceleration responses. Secondly, considering the difficulties in measuring ambient excitations, the proposed method is improved to identify the structural damage under unknown non-stationary ambient excitation. Taking advantage of EKF-UI, the proposed method can simultaneously identify the structural physical parameters and the unknown non-stationary ambient excitations using partial acceleration and displacement responses. The effectiveness of the proposed method is firstly validated through a frame structure under known non-stationary ground excitation. Then, an OWT tower under unknown non-stationary wind and wave excitations is used to demonstrate the proposed method.
The rest of the paper is organized as follows: Section 2 gives a description of the proposed method, in which Section 2.1 is the equation of motion in the form of non-stationary cross-correlation functions; Section 2.2 and Section 2.3 present the identification method under known/unknown non-stationary ambient excitations, respectively, and the noise immunity of the proposed algorithm is thoroughly analyzed in Section 2.4. Then, corresponding numerical validations are investigated in Section 3. Finally, the conclusions and discussion are presented in Section 4.
2. The Proposed Method
2.1. Equation for Non-Stationary Cross-Correlation Function of Responses
For a linear structure with n degrees of freedom (DOFs) under known and unknown external inputs, the equation of motion can be expressed as
in which are vectors of structural displacement, velocity, and acceleration, respectively. represent the mass, damping, and stiffness matrices, respectively. denotes the vector of known excitations with influence matrix , and is the vector of unknown external input with influence matrix .
If and denote two stationary random processes, their cross-correlation is the function of time lag , expressed as
However, since the time-varying nature is the most distinctive characteristic of non-stationary random processes, the cross-correlation function between two such processes and depends not only on the time interval τ, but also on the selected reference time instant , as expressed in
Thus, when is a non-stationary random process, both sides of Equation (1) can be post-multiplied at the time instant by a reference acceleration response . Then, the expected values of each side are taken and Equation (1) is rewritten as
in which denotes the vector of cross-correlation function as
According to the studies in Ref. [28], the properties of the cross-correlation function can be derived for the non-stationary random processes and as
If the derivative of random process exists, the procedure can be extended to the general format as follows:
Thus, Equation (4) can be transformed into
Equation (8) shows the equation of motion in the form of the cross-correlation function under both known and unknown excitations that are non-stationary. For practical applications, can be determined as a fixed time instant; thus, there is only one variable in each cross-correlation function. It is worth noting that Equation (8) maintains a form analogous to the equation of motion in Equation (1), thereby permitting the application of time-domain system identification techniques for parameter estimation. For scenarios with known excitations, the EKF has demonstrated effectiveness in system identification using partial acceleration measurements. Building on this foundation, Section 2.2 presents a novel damage detection methodology that integrates cross-correlation functions with EKF for structural assessment under known non-stationary ambient excitations. Furthermore, for cases involving unknown external excitations, the EKF-UI approach becomes applicable through the fusion of partial acceleration and displacement measurements. Accordingly, Section 2.3 introduces an enhanced methodology combining cross-correlation functions with EKF-UI to enable system identification under unknown non-stationary ambient excitation conditions.
2.2. Structural Damage Detection Under Known Non-Stationary Ambient Excitations
For a linear structure under known excitations, Equation (8) can be rewritten as
An extended state vector is defined, in which is a l-dimensional vector of structural parameter. Then, Equation (9) can be transformed into the state equation as follows:
where and are damping and stiffness matrices containing the unknown parametric vector , respectively. is the model noise with zero mean and a covariance matrix .
Under the condition of partially observed structural acceleration responses, the discrete observation equation in the form of the cross-correlation function is
where is the vector of measurement at the time instant with being the sampling time interval. is the measurement noise vector with zero mean and a covariance matrix . Let and be the estimated and the predicted , respectively. Equations (10) and (11) can be linearized at and using Taylor series expansion to the first order, as follows:
For conventional EKF, the first procedure is the time update (prediction procedure):
with the prediction error covariance matrix derived as
Then, the second procedure is the measurement update, in which
where is the kalman gain matrix and given as
The correction error covariance matrix is derived as follows:
Thus, by taking the advantages of EKF and combining it with the cross-correlation function of partial acceleration responses, structural parameters can be identified under known non-stationary ambient excitations.
2.3. Structural Damage Detection Under Unknown Non-Stationary Ambient Excitations
A critical examination of Equation (16) reveals that precise excitation information is essential for reliable structural state estimation. This requirement presents significant practical limitations, as environmental excitations are often difficult or impossible to measure accurately in real-world applications, potentially compromising the effectiveness of conventional EKF-based system identification. To address this fundamental challenge, the present study employs a data fusion extended Kalman filter with unknown input (EKF-UI) methodology, thereby enabling robust damage detection under conditions of uncertain excitation inputs.
For a linear structure under unknown excitations in Equation (8), Equations (10)–(13) can be rewritten as
where is the cross-correlation function of unknown input.
Analogously, in the time update (prediction) procedure, the structural state is predicted as
Then, the structural state is estimated in the procedure of measurement update as
in which is the Kalman gain matrix and given as
Under the condition that the number of installed sensors is no less than the number of unknown inputs [36], can be estimated based on the least-squares estimation as
where .
The rest of the error covariance matrices can be expressed as follows:
where .
Finally, through the fusion of partially measured acceleration and displacement responses, the proposed method enables the simultaneous identification of both unknown non-stationary ambient excitations and structural parameters.
The limitation of the proposed method is that damage identification may fail when sensors are not installed at the locations of unknown excitations. This is due to the inherent constraints of the EKF-UI algorithm itself [36]. Additionally, since the least-squares estimation is used in Equation (26) for solving unknown excitations, the algorithm becomes inoperative when the number of sensors is fewer than that of the unknown loads. These limitations can be effectively managed through strategic accelerometer placement. Taking the damage identification of OWT towers as an example, the installation of accelerometers at both the base and top in field applications can effectively mitigate these limitations.
2.4. Influence of Measurement Noise
A comprehensive noise immunity analysis is performed to quantitatively evaluate the noise suppression capability of the cross-correlation function. Assuming two responses are polluted by random white noises, i.e., , where and are measured data polluted by noise, and are noisy-free responses, and are noise components, then the cross-correlation functions of the measured responses can be expressed as
For uncorrelated white noise, it is known that , and . Therefore,
where is a constant. The analysis of Equation (32) reveals that the cross-correlation function exhibits noise sensitivity only when . This finding suggests that setting effectively mitigates the influence of measurement noise by the cross-correlation analysis.
3. Numerical Validations
In this section, considering known or unknown non-stationary excitations, two numerical examples including a frame structure and an OWT, respectively, are provided for system identification to validate the effectiveness of the proposed synthesis algorithm.
3.1. Frame Structure Under Known Non-Stationary Ground Excitation
The numerical validation begins with a single-bay, two-story steel frame structure (seen in Figure 1) designed to emulate the key behavioral characteristics of frame-type support structures in OWTs. The frame-type support structure in the OWT represents a highly prevalent structural configuration, which has been extensively studied in Refs. [23,30,39]. The frame consists of four column elements, two beam elements, and four joints with a total of 12 DOFs. The parameters of each element are as follows: the cross-sectional area is , the linear density is , and , where and denote the Young’s modulus and the cross-sectional moment of inertia, respectively. The Rayleigh damping model is adopted and the first two damping ratios are assumed to be 0.01.
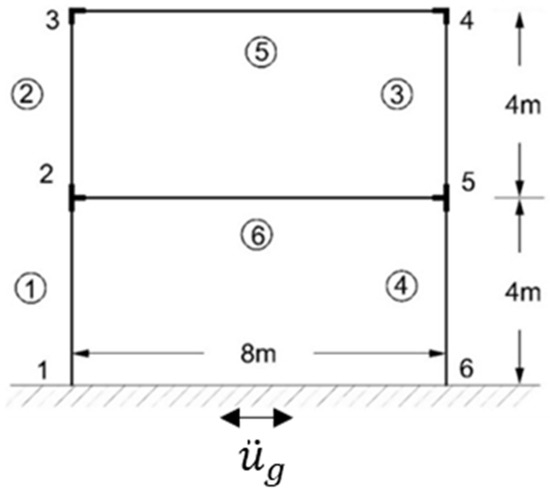
Figure 1.
One-bay two-story plane frame structure under known non-stationary ground excitation.
The ground motion excitation is simulated using the Kanai–Tajimi spectrum, which accounts for soil–structure interaction effects [40]. The power spectral density (PSD) function of this spectrum is expressed as
where is the spectral intensity to reflect the strength of an earthquake, and and are the predominant ground frequency and ground damping ratio, respectively. In this case, these parameters are set to be , , and respectively.
The stationary Kanai–Tajimi spectrum is transformed into a non-stationary process through amplitude modulation. This can be achieved as follows. Firstly, the baseline stationary time history signal is generated from the Kanai–Tajimi spectrum. Then, a modulation function that decays with time is applied and defined as
Finally, the resulting non-stationary excitation is then given by
in which denotes the ground acceleration. The temporal characteristics of the modulated excitation are presented in Figure 2 and Figure 3. Figure 2 displays the applied amplitude modulation function , and Figure 3 clearly demonstrates the non-stationary nature of the ground acceleration, with its amplitude decaying obviously over time.
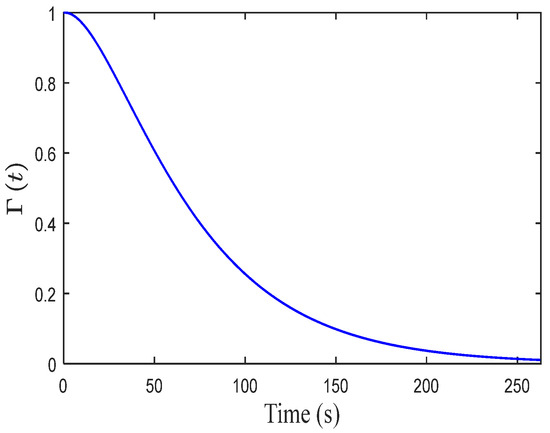
Figure 2.
Modulation function .
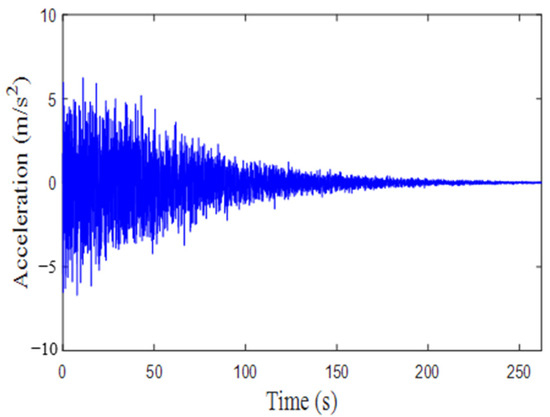
Figure 3.
Non-stationary ground excitation generated by the Kanai–Tajimi spectrum.
Given the practical challenges associated with angular acceleration measurements, the identification process utilizes only vertical and horizontal acceleration responses of the frame structure. The data acquisition system operates at a sampling frequency of 1000 Hz. To simulate realistic measurement conditions, all recorded responses are artificially contaminated by Gaussian white noise with 15% variance in root mean square (RMS) [10] as
where is the vector of the measured noisy acceleration response, is the vector of the noise-free acceleration response, denotes the standard deviation, and is a random standard normal distribution vector. For the system identification process, the horizontal acceleration response at Node 2 is designated as the reference signal, and the reference time moment is established at .
The numerical simulation implements structural damage through a reduction in the cross-sectional moment of inertia, with the stiffness coefficient serving as the primary indicator for both damage location and severity. Three distinct damage scenarios are investigated: (1) the baseline undamaged condition, (2) a single-element damage case (designated damaged scenario 1), and (3) a multiple-element damage case (damaged scenario 2). As presented in Table 1 and Figure 4, the method successfully identifies the stiffness parameters of damaged elements using only partial acceleration measurements under known non-stationary ground excitation. Notably, the approach maintains exceptional accuracy with identification errors within 1.15% despite 15% RMS noise contamination in the acceleration responses, demonstrating both high precision and remarkable noise robustness.

Table 1.
Identified stiffness coefficient of frame structure under known non-stationary ground excitation.
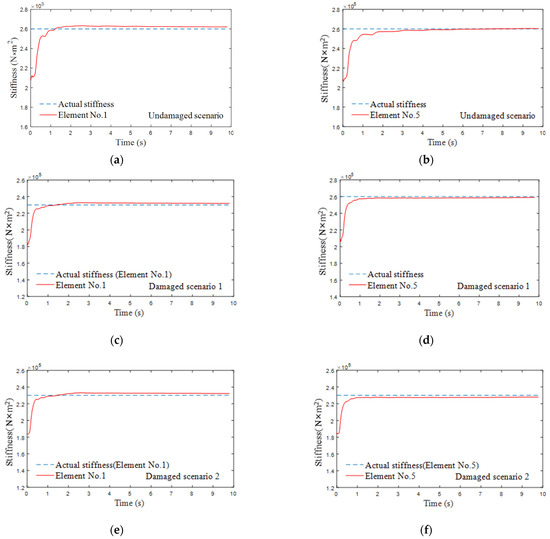
Figure 4.
Identified structural stiffness coefficient: (a) k1 in the undamaged scenario; (b) k5 in the undamaged scenario; (c) k1 in the damaged scenario 1; (d) k5 in the damaged scenario 1; (e) k1 in the damaged scenario 2; (f) k5 in the damaged scenario 2.
3.2. An OWT Tower Under Unknown Non-Stationary Wind and Wave Excitations
As shown in Figure 5a, an OWT tower from the National Renewable Energy Laboratory (NREL) technical report [41] is employed to validate the proposed method.
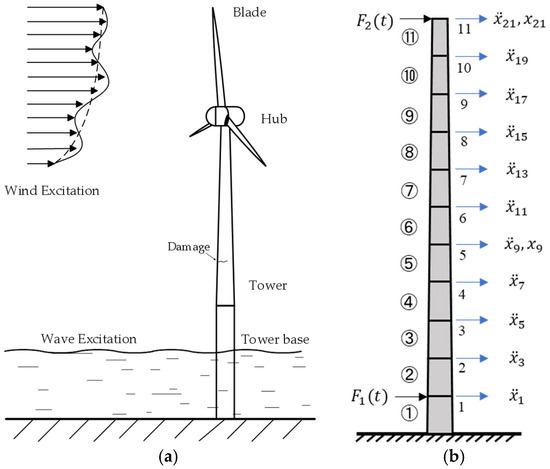
Figure 5.
OWT tower under unknown non-stationary wind and wave excitations: (a) sketch of the OWT; (b) simplified cantilever beam model and layout of sensors.
The tower is modeled as a one-dimensional cantilever beam, as illustrated in Figure 5b. The height of the tower is 87.6 m. The elastic modulus is set to E = 210 GPa. The effects of three blades are simplified as a concentrated force of 522.3 kN applied at the tower top [41]. The tower’s structural properties are defined by its geometric parameters: a base diameter of 6 m with a wall thickness of 0.027 m and a top diameter of 3.87 m with a wall thickness of 0.019 m. Both the radius and wall thickness vary linearly along the tower height. The effective density is adjusted to 8500 kg/m3 to account for the additional mass contributions from paint, bolts, welds, and flanges, which are not included in the nominal thickness data. The beam is discretized into 11 finite elements with 22 degrees of freedom (DOFs), including both translational and rotational DOFs at each node. Table 2 summarizes the length, unit length mass density, and bending stiffness EI for each element.

Table 2.
Geometric parameters of each element.
The structural analysis employs the Euler–Bernoulli beam formulation, for which the elemental stiffness matrix takes the following form:
Analogously, the local element mass matrix can be formulated using the consistent mass matrix approach:
Additionally, the Rayleigh damping model is used to estimate the damping matrix of the structure. According to [41], a structural damping ratio of 1% critical is set in all modes of the tower. The first natural frequency of the full system is 0.324 Hz. The OWT tower experiences combined wave and wind loading, both characterized as non-stationary ambient excitations. These environmental loads are modeled as concentrated horizontal forces and applied at nodes 1 and 11, respectively. These excitations are generated through a three-step process: first, a band-limited white noise signal with a 200 Hz cutoff frequency serves as the base excitation; second, this signal is processed through a linear filter system , where and ; finally, the filtered output is modulated by the amplitude modulation function to introduce non-stationary characteristics. The complete excitation signals are thus formulated as , where and .
For the OWT tower example, two conditions, including an undamaged baseline case and a damaged case, are examined. Considering that the damage severity in Section 3.1 is set at approximately 10% to represent relatively significant damage, herein, minor damage detection is conducted by implementing a 3% stiffness reduction in Element 3, following [39]. This configuration allows for the evaluation of the applicability of the proposed method in scenarios more representative of actual engineering conditions. The damage location is illustrated in Figure 5a.
Figure 5b illustrates the sensor configuration, comprising eleven accelerometers and two displacement transducers positioned at nodes 5 and 11 to monitor the dynamic response of the beam. The accelerometers are arranged evenly as far as possible to reduce the adverse impact of the sensor layout on the identification accuracy to the greatest extent. Thus, horizontal acceleration responses are measured throughout the structure, while displacement responses at the 9th and 21st DOFs are incorporated to mitigate the low-frequency drift in the identified excitations. The sampling frequency is 500 Hz, and the horizontal acceleration of node 1 serves as the reference signal for cross-correlation function computation, with the reference time set at . To investigate the effectiveness of the proposed method under different noise conditions, all measurements are intentionally contaminated with 5% and 15% RMS white noise.
For comparative analysis, traditional EKF-UI is implemented for damage identification alongside the proposed method. The identified stiffness coefficient of the third element under 5% RMS noise by using EKF-UI and the proposed method are presented in Figure 6 and Figure 7, respectively. Figure 6 shows that the results identified using EKF-UI significantly deviate from the exact values, despite convergence. In contrast, the identified stiffness coefficients in Figure 7 rapidly converge near the true values, showing markedly smaller errors than EKF-UI. The proposed method achieves accurate identification for both undamaged and damaged cases.
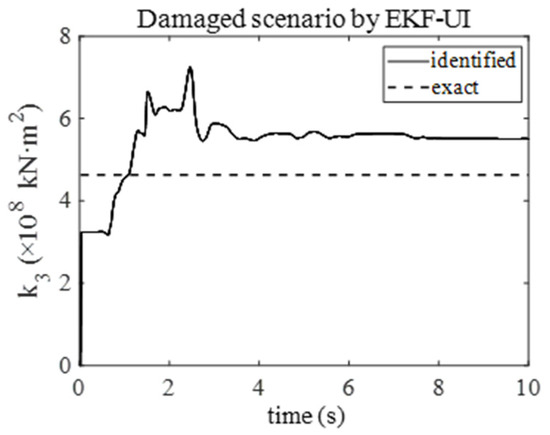
Figure 6.
Identified stiffness coefficient of the third element under 5% RMS noise by EKF-UI.
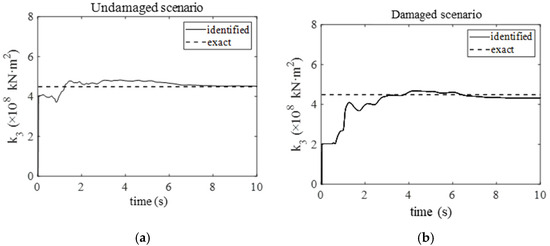
Figure 7.
Identified stiffness coefficient of the third element under 5% RMS noise (a) in the undamaged scenario; (b) in the damaged scenario.
Analogously, the identified stiffness coefficients of the third element under 15% RMS noise are presented in Figure 8 and Figure 9, respectively. As evidenced in Figure 8, the stiffness coefficients identified by EKF-UI exhibit persistent oscillations around zero, demonstrating its inability to maintain stable identification under 15% RMS noise. In contrast, Figure 9 demonstrates that the proposed method maintains high precision in stiffness coefficient estimation even under a high-level noise condition.
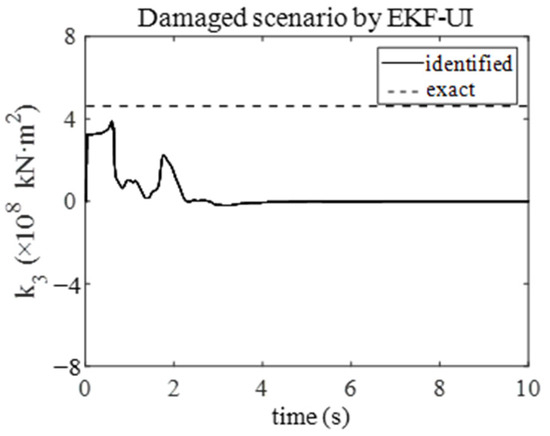
Figure 8.
Identified stiffness coefficient of the third element under 15% RMS noise by EKF-UI.
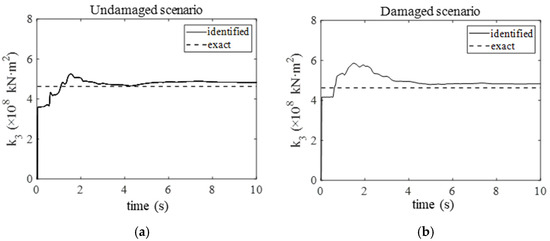
Figure 9.
Identified stiffness coefficient of the third element under 15% RMS noise: (a) in the undamaged scenario; (b) in the damaged scenario.
The sensitivity of the proposed method may be affected by the initial stiffness values since the method is derived from the EKF-UI frameworks. In the aforementioned case studies, the initial stiffness values are set at 85% of their true values. Then, the initial stiffness value is set to 70% of the exact value and the identification under 15% RMS noise is performed using the proposed approach. The corresponding results are presented in Figure 10. The increased deviation in initial values can lead to moderately slower convergence, but the final identification accuracy remains within acceptable limits.
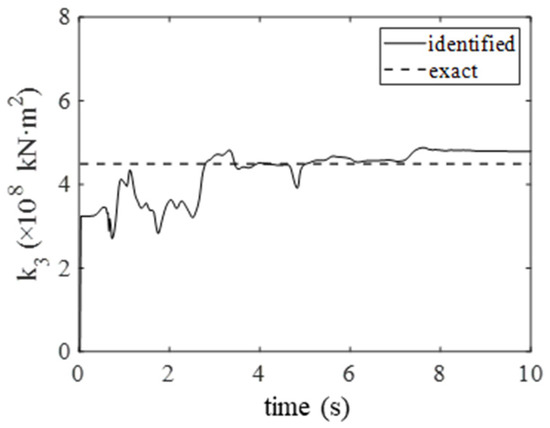
Figure 10.
Stiffness coefficient identified using different initial values.
Figure 11 and Figure 12 illustrate the successfully identified excitation characteristics represented as cross-correlation functions. As the time-domain equation of motion is transformed in terms of non-stationary cross-correlation functions, the final output is the identified cross-correlation function of unknown inputs rather than the excitations themselves, which is evidenced by Figure 11 and Figure 12. Since the structural damage assessment of OWT holds greater practical significance than load quantification in field applications, the accuracy or error range analysis for excitation recognition is not included herein. The final identified stiffness values are quantitatively summarized in Table 3. The runtime of the proposed method is 56.08 s, which is an acceptable computational effort. These results confirm the following:
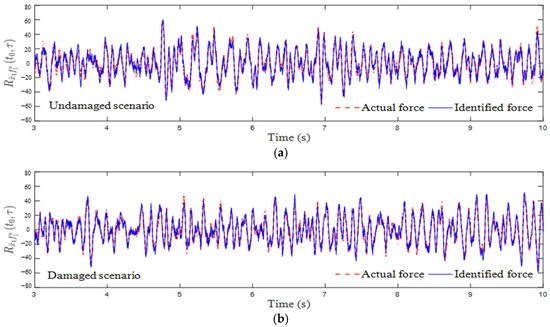
Figure 11.
Identified cross-correlation function of unknown input (a) in the undamaged scenario; (b) in the damaged scenario.
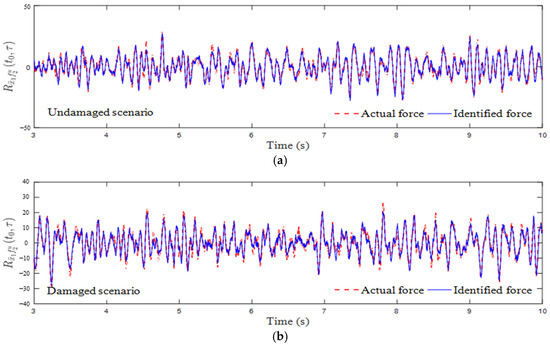
Figure 12.
Identified cross-correlation function of unknown input (a) in the undamaged scenario; (b) in the damaged scenario.

Table 3.
Identified stiffness coefficients of OWT tower under unknown non-stationary wind and wave excitations.
- (1)
- This developed approach can accurately detect the tower damage in operational OWTs through partial acceleration and displacement measurements, even under the challenging condition of concurrent unknown non-stationary wind and wave excitations.
- (2)
- The cross-correlation functions of the unknown excitations are accurately identified without observable drift phenomena.
- (3)
- Most notably, the method maintains reliable performance when processing raw measurement data contaminated with high-level noise (15% RMS), as evidenced by the satisfactory identification accuracy achieved without any signal preprocessing. This demonstrates the algorithm’s inherent noise robustness and practical applicability in real-world OWTs where measurement noise is unavoidable.
The proposed method represents non-stationary excitations using cross-correlation functions, making it applicable to various excitation types. In this numerical case, non-stationary wind and wave loads are generated through the amplitude modulation of white noise. Future work could explore more realistic excitations like time-varying wind fields and multi-component wave spectra to further validate the broader applicability. In addition, the current study does not address the impact of sensor placement configurations on identification accuracy. Subsequent research could enhance the proposed methodology by incorporating advanced sensor network optimization techniques.
4. Conclusions
Accurate damage detection in OWTs faces significant challenges owing to the combined effects of non-stationary environmental excitations and noise-polluted partial measurements. In this paper, a synthesis method based on the cross-correlation function and the EKF series algorithm is proposed for damage detection in OWTs under non-stationary ambient excitations. The proposed approach reformulates the time-domain equation of motion using non-stationary cross-correlation functions. When the non-stationary ambient excitations are known, structural parameters are identified through partial acceleration measurements using conventional EKF. For unknown excitation scenarios, the enhanced EKF-UI version enables the simultaneous identification of both structural damage and excitations through fused acceleration and displacement response data.
The method’s effectiveness is demonstrated through two numerical case studies: a frame structure subjected to known non-stationary ground excitation, and an OWT tower under unknown non-stationary wave and wind excitations. The stiffness coefficients can be identified accurately when the measured responses are contaminated by 15% RMS noise. The identification error of the first numerical example is limited to around 1.0%, and the largest identification error of the second numerical validation is 5.12%. These results are obtained using raw measurements without denoising preprocessing, confirming the method’s superior accuracy and exceptional noise resistance.
The innovation of this paper is that the proposed novel method combines the advantages of the cross-correlation function and the data-fusing EKF-UI algorithm. The damage detection of OWTs under unknown non-stationary ambient excitations can be conducted using partial structural responses. Furthermore, the proposed method has superiority in terms of accuracy and noise-resistance performance.
This study quantifies structural damage via element stiffness reduction. Future work should address realistic OWT damage mechanisms, e.g., progressive damage, by correlating stiffness reduction with localized failures like cracks, bolt loosening, corrosion, and fatigue fractures, which can better represent the operational damage conditions. A risk assessment method (CVaR) developed by Zhai et al. [42] may assist in dealing with uncertainty and noise pollution to improve the robustness and applicability of the proposed method. For real-world complex OWTs, a multi-agent energy system cooperative operation strategy based on asymmetric Nash game [43] could serve as a valuable reference framework. Such an approach would achieve multi-party cooperation and reasonable profit distribution in complex systems, which will help to strengthen the practical application background and comprehensive analysis of the proposed method. Further experimental verification on scaled OWT models will be conducted to verify the effectiveness of the proposed method, and related test results will be published in subsequent work.
Author Contributions
Conceptualization, N.Y. and W.Z.; methodology, N.Y.; validation, N.Y., P.H., H.Y., and Y.L.; writing—original draft preparation, N.Y.; writing—review and editing, N.Y., P.H., H.Y., Y.L., J.Z., and E.L.; supervision, N.Y. and W.Z.; funding acquisition, N.Y., W.Z., J.Z., and E.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation of China (52408322), the Fujian Provincial Natural Science Foundation of China (2023J05192), the Key Laboratory of Engineering Material & Structure Reinforcement (Sanming University), Fujian Province University (B170001-15), and Research on Key Technologies for High Large-Span Steel Beam Construction (GY-H-21160).
Institutional Review Board Statement
An IRB review of this research is not required.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
Contributions by the anonymous reviewers are strongly appreciated.
Conflicts of Interest
Author En Lin was employed by the company Fuzhou Urban and Rural Construction Group Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Wilk-Jakubowski, J.L.; Pawlik, L.; Wilk-Jakubowski, G.; Harabin, R. State-of-the-art in the use of renewable energy sources on the example of wind, wave energy, tidal energy, and energy harvesting: A review from 2015 to 2024. Energies 2025, 18, 1356. [Google Scholar] [CrossRef]
- Lee, G.N.; Ngo, D.V.; Lee, S.I.; Kim, D.H. Fatigue life convergence of offshore wind turbine support structure according to wind measurement period. Energies 2023, 16, 3199. [Google Scholar] [CrossRef]
- Jiang, C.H.; Chen, N.Z. G-Twin: Graph neural network-based digital twin for real-time and high-fidelity structural health monitoring for offshore wind turbines. Mar. Struct. 2025, 103, 103813. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; Algatheem, A.M.; El-Sapa, S. Magneto-slip interaction in the migration of two rigid spheres in infinite couple stress fluid. Chin. J. Phys. 2025, 95, 173–189. [Google Scholar] [CrossRef]
- Alotaibi, M.A.; El-Sapa, S. Effect of permeability on the interaction between two spheres translating through a couple stress fluid. Fluid Dyn. Res. 2025, 57, 015503. [Google Scholar] [CrossRef]
- El-Sapa, S.; Alsedais, N.S. Effect of slippage on a translational motion of two interacting non-concentric spheres squeezed by couple stress fluid. Indian J. Pure Appl. Math. 2024, 1–17. [Google Scholar] [CrossRef]
- Ou, Y.; Chatzi, E.N.; Dertimanis, V.K.; Spiridonakos, M.D. Vibration-based experimental damage detection of a small-scale wind turbine blade. Struct. Health Monit. 2016, 16, 79–96. [Google Scholar] [CrossRef]
- Xu, M.Q.; Li, J.; Wang, S.Q.; Yang, N.; Hao, H. Damage detection of wind turbine blades by Bayesian multivariate cointegration. Ocean Eng. 2022, 258, 111603. [Google Scholar] [CrossRef]
- Hoell, S.; Omenzetter, P. Sequential projection pursuit for optimised vibration based damage detection in an experimental wind turbine blade. Smart Mater. Struct. 2018, 27, 025007. [Google Scholar] [CrossRef]
- Yang, N.; Luo, S.J.; Lei, Y. Structural damage diagnosis based on the temporal moment of partially measured structural responses. J. Aerosp. Eng. 2021, 34, 04020106. [Google Scholar] [CrossRef]
- El-Kafafy, M.; Devriendt, C.; Guillaume, P.; Helsen, J. Automatic tracking of the modal parameters of an offshore wind turbine drivetrain system. Energies 2017, 10, 574. [Google Scholar] [CrossRef]
- Sarrafi, A.; Mao, Z.; Niezrecki, C.; Poozesh, P. Vibration-based damage detection in wind turbine blades using Phase-based Motion Estimation and motion magnification. J. Sound Vib. 2018, 421, 300–318. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P.Z. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Song, M.M.; Mehr, N.P.; Moaveni, B.; Hines, E.; Ebrahimian, H.; Bajric, A. One year monitoring of an offshore wind turbine: Variability of modal parameters to ambient and operational conditions. Eng. Struct. 2023, 297, 117022. [Google Scholar] [CrossRef]
- Zhang, P.; He, Z.J.; Cui, C.Y.; Ren, L.; Yao, R.Q. Operational modal analysis of offshore wind turbine tower under ambient excitation. J. Mar. Sci. Eng. 2023, 10, 1963. [Google Scholar] [CrossRef]
- Rosso, M.M.; Aloisio, A.; Melchiorre, J.; Huo, F.; Marano, G.C. Noise effects analysis on subspace-based damage detection with neural networks. Structures 2023, 54, 23–37. [Google Scholar] [CrossRef]
- Yu, Q.X.; Yu, H.B.; Zhou, L.; Meng, A.K.; Hu, X.Y.; Hou, X.D. Structural energy transfer to the elevated pile-cap foundation of an offshore wind turbine based on extracted transfer. J. Sound Vib. 2021, 512, 116388. [Google Scholar] [CrossRef]
- Yang, N.; Lei, Y.; Li, J.; Hao, H. Identification of gradually varying physical parameters based on discrete cosine transform using partial measurements. Struct. Control Health Monit. 2022, 29, e3111. [Google Scholar] [CrossRef]
- Xu, M.Q.; Guo, J.; Wang, S.Q.; Li, J.; Hao, H. Structural damage identification with limited modal measurements and ultra-sparse Bayesian regression. Struct. Control Health Monit. 2021, 28, e2729. [Google Scholar] [CrossRef]
- Iliopoulos, A.; Shirzadeh, R.; Weijtjens, W.; Guillaume, P.; Van Hemelrijck, D.; Devriendt, C. A modal decomposition and expansion approach for prediction of dynamic responses on a monopile offshore wind turbine using a limited number of vibration sensors. Mech. Syst. Signal Process. 2016, 68–69, 84–104. [Google Scholar] [CrossRef]
- Naseralavi, S.S.; Salajegheh, E.; Fadaee, M.J.; Salajegheh, J. A novel sensitivity-based method for damage detection of structures under unknown periodic excitations. J. Sound Vib. 2014, 333, 2776–2803. [Google Scholar] [CrossRef]
- Liu, Q.N.; Yan, Y.T.; Yang, Y.; Ma, L.; Qin, Z.H.; Bashir, M.; Yu, J.; Zhao, H.S. Influence of ground motion directionality on the dynamic behavior of a large-scale offshore wind turbine considering wind-earthquake coupling effects. Ocean Eng. 2025, 330, 121181. [Google Scholar] [CrossRef]
- Bai, J.L.; Jiao, C.Y.; Ai, F.W.; Wang, Y.H.; Yang, Q.S. Dynamic response of the jacket offshore wind turbines subjected to coupled wind, wave, and earthquake loads under scour conditions. Ocean Eng. 2025, 328, 120901. [Google Scholar] [CrossRef]
- Avendaño-Valencia, L.D.; Fassois, S.D. Stationary and non-stationary random vibration modelling and analysis for an operating wind turbine. Mech. Syst. Signal Process. 2014, 47, 263–285. [Google Scholar] [CrossRef]
- Orlando, A.; Pagnini, L.; Repetto, M.P. Structural response and fatigue assessment of a small vertical axis wind turbine under stationary and non-stationary excitation. Renew. Energy 2021, 170, 251–266. [Google Scholar] [CrossRef]
- Li, Y.; Wang, B.; Liu, Q.; Gao, S.; Lu, S.J. Application of converted displacement for modal parameter identification of offshore wind turbines with high-pile foundation. J. Ocean Univ. China 2022, 21, 1467–1478. [Google Scholar] [CrossRef]
- Blackman, R.B.; Tukey, J.W. The Measurement of Power Spectra; Dover: Mineola, NY, USA, 1958; pp. 42–58. [Google Scholar]
- Lei, Y.; Chen, F.; Zhou, H. An algorithm based on two-step Kalman filter for intelligent structural damage detection. Struct. Control Health Monit. 2012, 22, 694–706. [Google Scholar] [CrossRef]
- Panigrahi, S.K.; Patel, C.; Chourasia, A.; Bisht, R.S. Cross-correlation difference matrix based structural damage detection approach for building structures. J. Civ. Struct. Health Monit. 2024, 14, 1439–1453. [Google Scholar] [CrossRef]
- Li, W.; Huang, Y. A method for damage detection of a jacket platform under random wave excitations using cross correlation analysis and PCA-based method. Ocean Eng. 2020, 214, 107734. [Google Scholar] [CrossRef]
- Wang, L.X.; Li, X.Y.; Tan, Y.; Law, S.S. Long-term health monitoring of in-service bridge deck by covariance of covariance matrix of acceleration responses. Adv. Struct. Eng. 2015, 18, 2129–2149. [Google Scholar] [CrossRef]
- Hoshiya, M.; Saito, E. Structural identification by extended Kalman filter. J. Eng. Mech. 1984, 110, 1757–1771. [Google Scholar] [CrossRef]
- He, J.; Qi, M.C.; Tong, Z.H.; Hua, X.G.; Chen, Z.Q. An improved extended Kalman filter for parameters and loads identification without collocated measurements. Smart Struct. Syst. 2023, 31, 131–140. [Google Scholar]
- Yang, N.; Li, J.; Xu, M.Q.; Wang, S.Q. Real-time identification of time-varying cable force using an improved adaptive extended Kalman filter. Sensors 2022, 22, 4212. [Google Scholar] [CrossRef]
- Song, M.M.; Moaveni, B.; Ebrahimian, H.; Hines, E.; Bajric, A. Joint parameter-input estimation for digital twinning of the Block Island wind turbine using output-only measurements. Mech. Syst. Signal Process. 2023, 198, 110425. [Google Scholar] [CrossRef]
- Liu, L.J.; Su, Y.; Zhu, J.J.; Lei, Y. Data fusion based EKF-UI for real-time simultaneous identification of structural systems and unknown external inputs. Measurement 2016, 88, 456–467. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, Y.F.; Luo, Y.Z.; Qiu, S.F.; Sun, L.J. Seismic load identification for damper-added and base-isolated frame structures using EKF-UI algorithm and data fusion technique. J. Build. Eng. 2025, 104, 112426. [Google Scholar] [CrossRef]
- Lei, Y.; Qi, C.K.; Wang, S.Y. A smoothing EKF-UI-WDF method for simultaneous identification of structural systems and unknown seismic inputs without direct feedthrough. Struct. Control Health Monit. 2023, 2023, 6968598. [Google Scholar] [CrossRef]
- Xu, M.Q.; Wang, S.Q. Cross modal strain energy–based structural damage detection in the presence of noise effects. Adv. Mech. Eng. 2017, 9, 1687814017744122. [Google Scholar] [CrossRef]
- Tajimi, H. A statistical method of determining the maximum response of a building structure during an earthquake. In Proceedings of the 2nd World Conference on Earthquake Engineering, Tokyo, Japan, 11–18 July 1960. [Google Scholar]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5 MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009. [Google Scholar]
- Zhai, X.Y.; Li, Z.N.; Li, Z.M.; Xue, Y.X.; Chang, X.Y.; Su, J.; Jin, X.L.; Wang, P.; Sun, H.B. Risk-averse energy management for integrated electricity and heat systems considering building heating vertical imbalance: An asynchronous decentralized approach. Appl. Energy 2025, 383, 125271. [Google Scholar] [CrossRef]
- Ding, B.; Li, Z.N.; Li, Z.M.; Xue, Y.X.; Chang, X.Y.; Su, J.; Sun, H.B. Cooperative operation for multiagent energy systems integrated with wind, hydrogen, and buildings: An asymmetric Nash bargaining approach. IEEE Trans. Ind. Inform. 2025, 1–12. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).