Corrected Correlation for Turbulent Convective Heat Transfer in Concentric Annular Pipes
Abstract
1. Introduction
2. Physical Models and Numerical Methods
2.1. Problem Description
2.2. Governing Equations
- Conservation of mass equation (continuity equation)
- Momentum conservation equation (motion equation or Navier–Stokes equation)
- Energy conservation equation
- Turbulent kinetic energy k and its dissipation rate ε equationwhere σk and σε represent the turbulent Prandtl numbers for turbulent kinetic energy and its dissipation rate, which were set as constants in Fluent as C2 = 1.9, σT = 0.85, σk = 1.0, and σε = 1.2.
- Turbulent dynamic viscosity coefficientwhere represents the average rotation rate tensor in the angular velocity ωk rotating reference frame. Cµ is a function of the average strain rate and vorticity, in the boundary layer inertial bottom layer, Cµ = 0.09, and A0 = 4.04.
2.3. Boundary Conditions
2.4. Computational Models and Numerical Methods
2.5. Data Reduction
2.6. Grid Independence
3. Results and Discussion
3.1. Circular Pipe
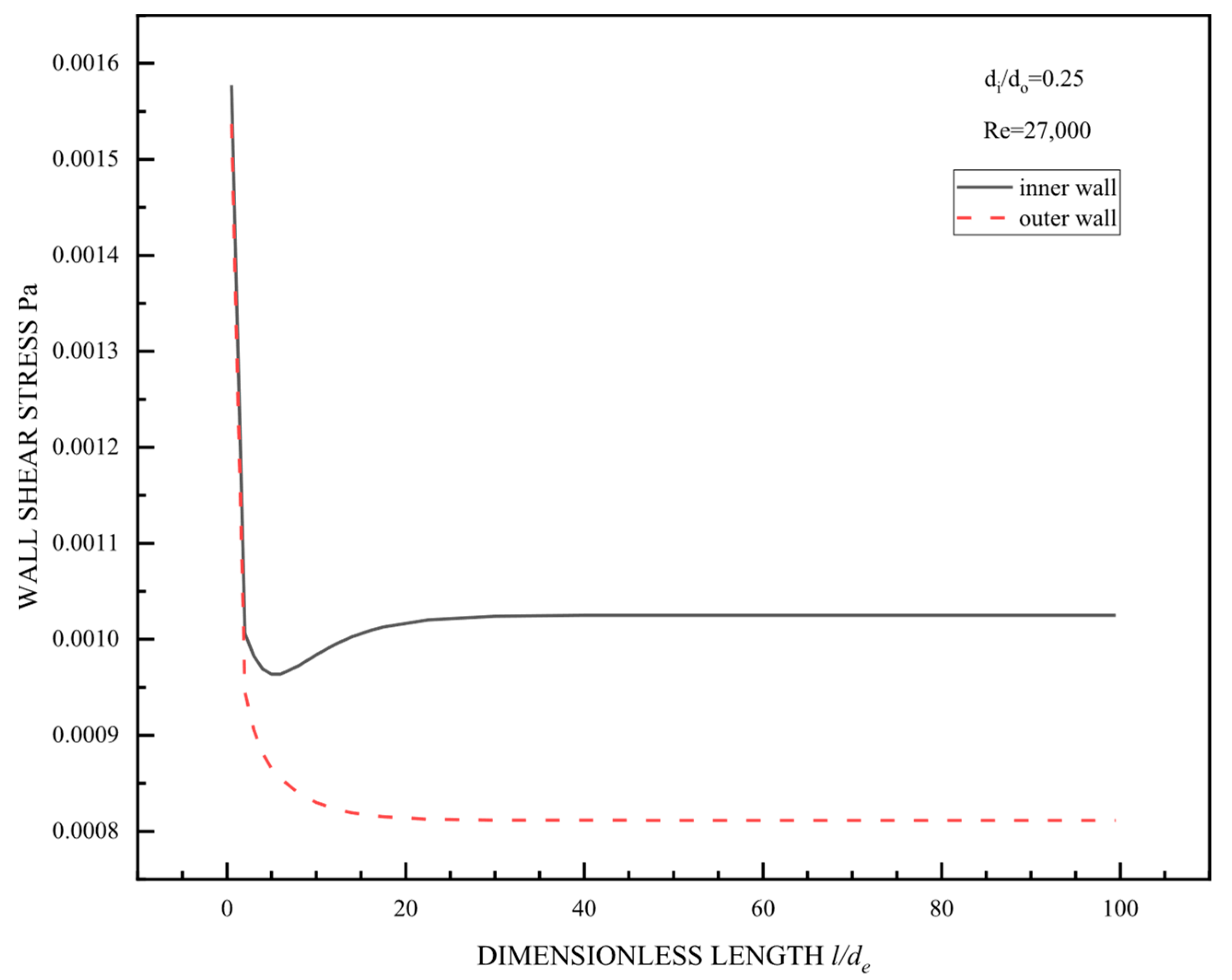
3.2. Concentric Annular Pipeline
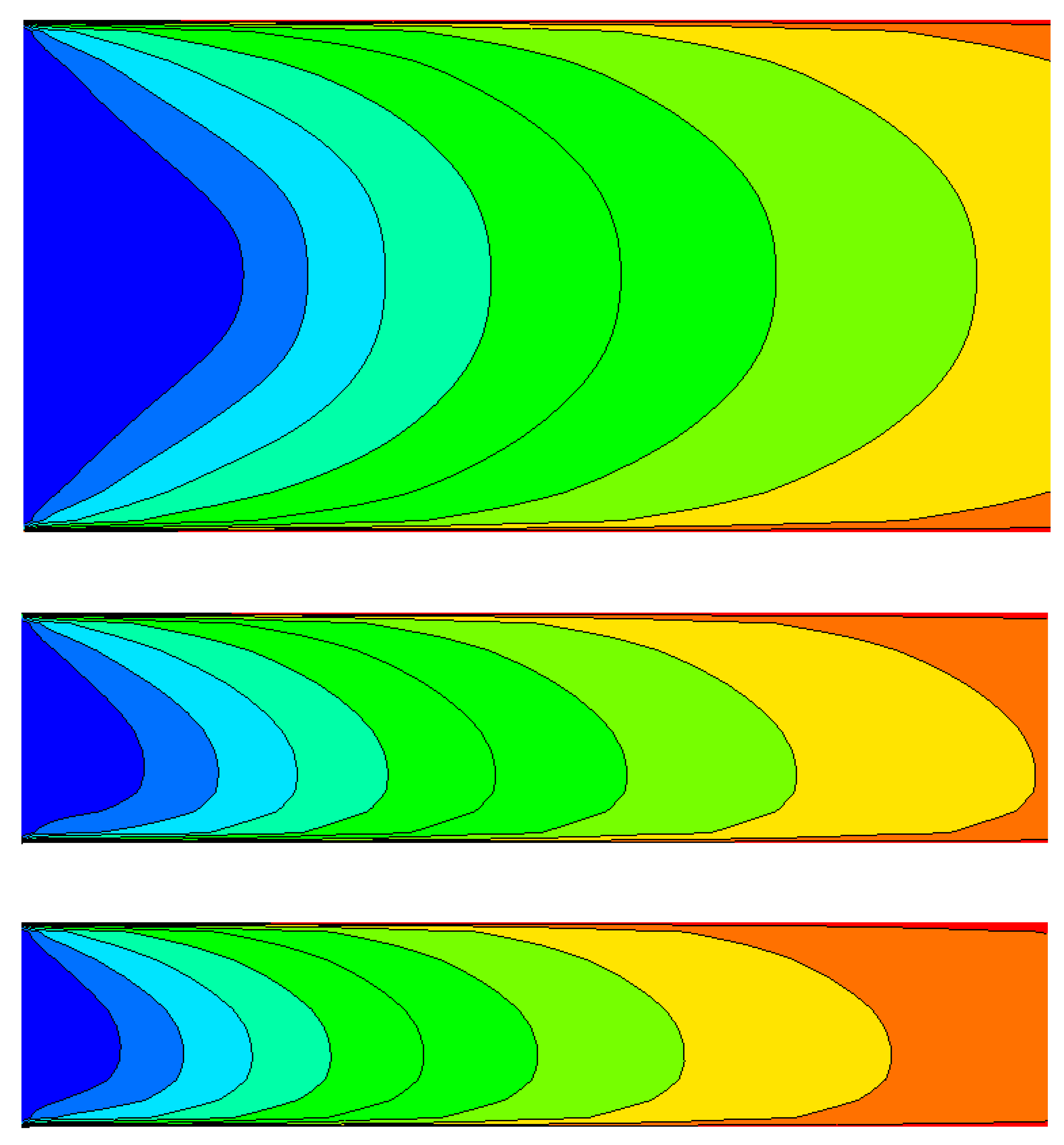
3.2.1. Flow Characteristics
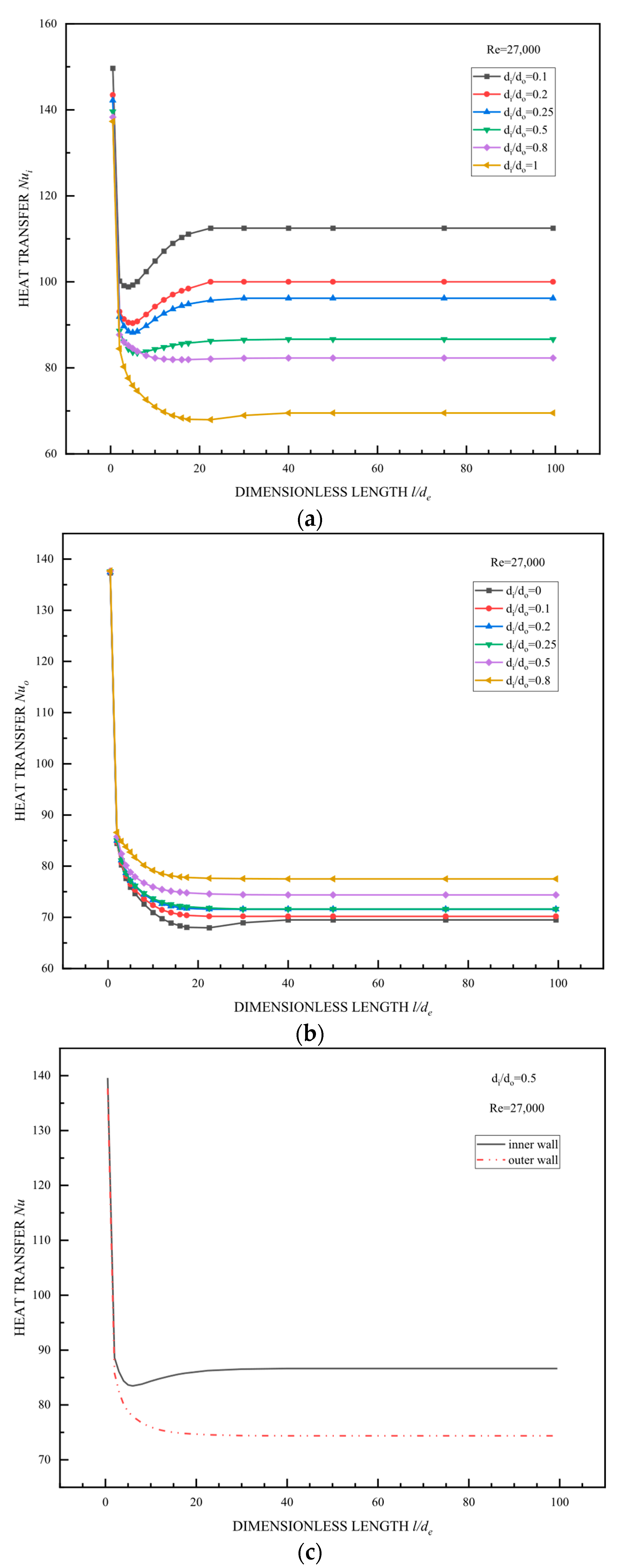
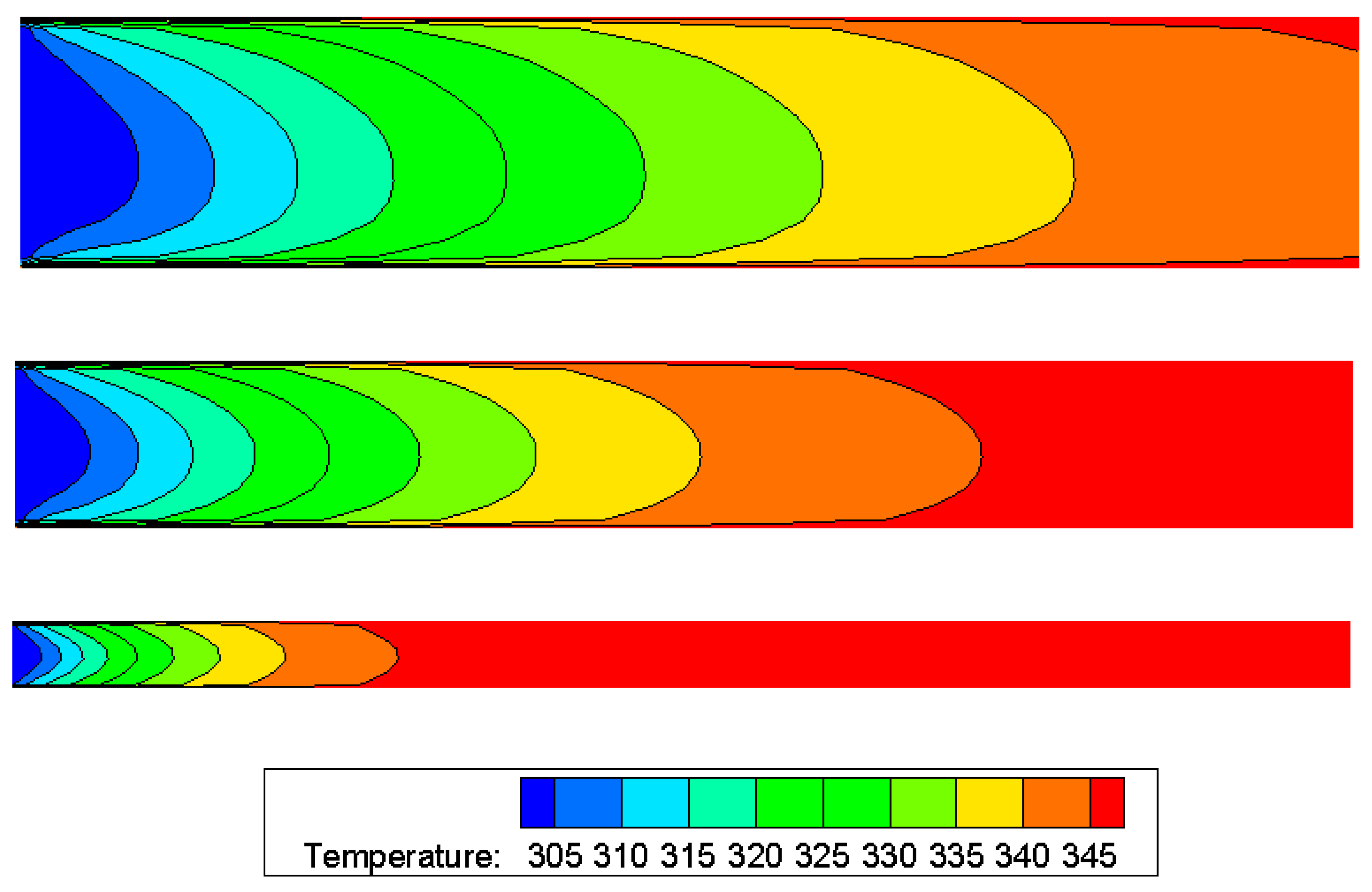
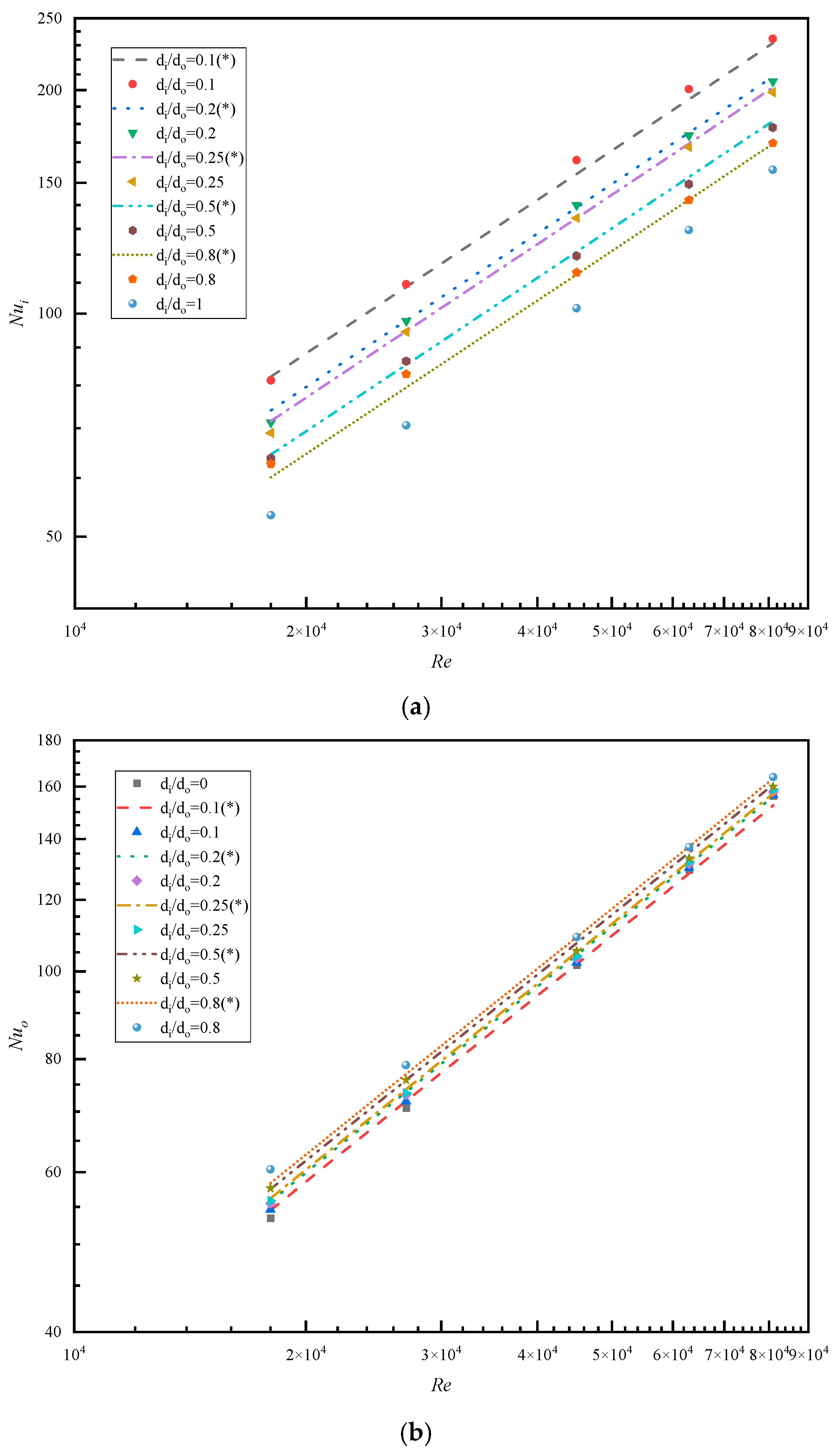
3.2.2. Heat Transfer Characteristics
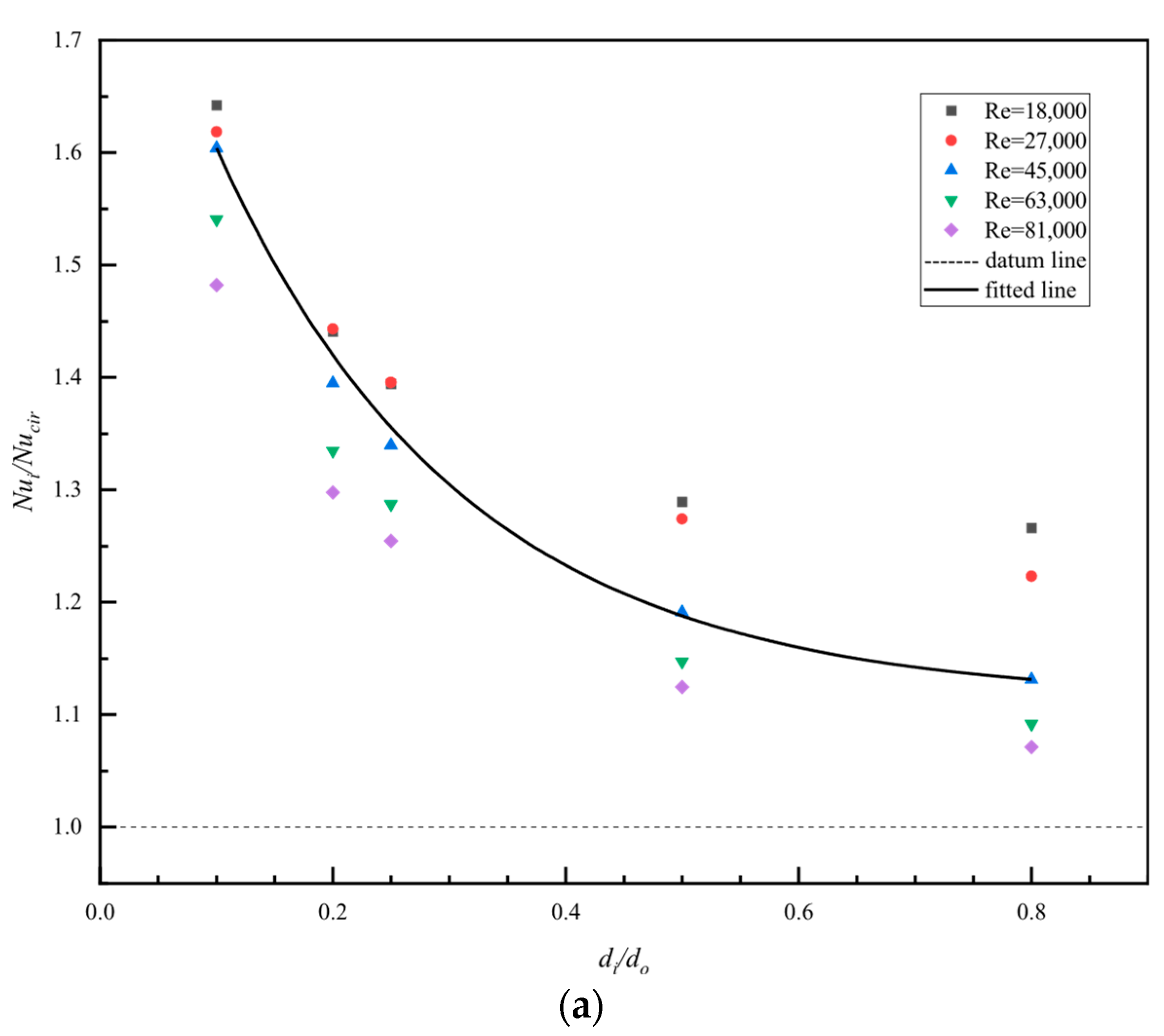
3.3. Comparison of the Heat Transfer Performance of All Pipelines
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, K.; He, Y.P.; Wu, D.Y. Calculation and Simulation Analysis of Resistance in Circular Pipelines. J. Chang. Inst. Technol. (Nat. Sci. Ed.) 2015, 16, 51–55. [Google Scholar]
- Lv, Y.J.; Peng, Y.S.; Ge, Z.H.; Zhao, P.H. The large eddy simulation study of turbulent heat transfer of liquid metal in a circular pipe. J. Univ. Sci. Technol. China 2015, 45, 917–922. [Google Scholar]
- Shah, R.K.; London, A.L. Laminar flow forced convection in ducts. In Advances in Heat Transfer; Supplement 1; Hartnett, J.P., Irvine, T.F., Eds.; Academic Press: New York, NY, USA, 1978; pp. 78–384. [Google Scholar]
- Yang, S.M.; Tao, W.Q. Heat Transfer, 4th ed.; Higher Education Press: Beijing, China, 2006; pp. 243–252. [Google Scholar]
- Dittus, F.W.; Boelter, L.M.K. Heat transfer in automobile radiators of the tubular type. Int. Commun. Heat Mass Transf. 1985, 1, 3–22. [Google Scholar] [CrossRef]
- Gnielinski, V. New equations for heat and mass transfer in turbulent pipe and channel flows. Int. Chem. Eng. 1976, 2, 359–368. [Google Scholar]
- Gnielinski, V. On heat transfer in tubes. Int. J. Heat Mass Transf. 2013, 63, 134–140. [Google Scholar] [CrossRef]
- Wang, P.; Yang, M.; Wang, Z.Y.; Xu, H.T. Numerical simulation of turbulent heat transfer of non-circular channel non-Newtonian fluid. J. Eng. Thermophys. 2014, 35, 2269–2273. [Google Scholar]
- Wang, P.; Yang, M.; Wang, Z.Y.; Xu, H.T. A new heat transfer correlation for turbulent flow of air with variable properties in noncircular ducts. ASME J. Heat Transf. 2014, 136, 101701-1–101701-08. [Google Scholar] [CrossRef]
- Yang, M.; Wang, X.M.; Wang, Z.Y.; Li, Z.; Zhang, Y.W. Correlation for turbulent convection heat transfer in elliptical tubes by numerical simulations. Front. Heat Mass Transf. 2018, 11, 7. [Google Scholar] [CrossRef]
- Qiao, L. Numerical Simulation of Turbulent Flow and Heat Transfer in a Rectangular Cross-Section Channel. Master’s Thesis, University of Shanghai for Science and Technology, Shanghai, China, 2015. [Google Scholar]
- Wang, S.S.; Xu, W.Q.; Hu, Y.H. Characterization of convective heat transfer and flow resistance in elliptical tubes. Ind. Heat. 2010, 39, 13–16. [Google Scholar]
- Yang, M.; Lu, H.T.; Zhao, Y.S.; Lu, T.K.; Dai, Z.H. Numerical experiments on turbulent convective heat transfer in a longitudinally swept tube bundle and its correlation equation. J. Univ. Shanghai Sci. Technol. 2017, 39, 110–113. [Google Scholar]
- Bagheri, E.; Wang, B.C. Direct numerical simulation of turbulent heat transfer in concentric annular pipe flows. Phys. Fluids 2021, 33, 055131. [Google Scholar] [CrossRef]
- Babus’Haq, R.F. Forced convection heat transfer from a pipe to air flowing turbulently inside it. Exp. Heat Transf. 1992, 59, 161–173. [Google Scholar] [CrossRef]
- Zhang, L.Y. Analytical Modeling and Characterization of Heat Transfer in a Coaxial Cased Medium-Depth Geothermal Heat Exchanger. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2024. [Google Scholar]
- Yin, Y.D.; Nong, Y.S.; Li, Y.Y.; Liu, S.J. Enhanced heat transfer and flow resistance characteristics of twisted tube coaxial casing heat exchangers. J. Chem. Eng. 2024, 75, 3528–3535. [Google Scholar]
- Li, W.J.; Yao, H.Q.; Zhao, S.W.; Zhang, W.K.; Sun, W.F.; Sun, Z.X. Analysis of heat transfer in porous cased heat exchangers with different arrangements. Build. Energy Effic. 2023, 51, 77–85. [Google Scholar]
- Huang, B. Research on Coupled Heat Transfer Characteristics of Cased Heat Exchanger with Inner Tube Filled with Porous Medium. Masteri’s Thesis, Huazhong University of Science and Technology, Wuhan, China, 2021. [Google Scholar]
- He, C.S. Research on prestressing technology of large-scale double-casing rapid cooling heat exchanger. China Boil. Press. Vessel. Saf. 2007, 35, 13–15. [Google Scholar]
- Boersma, B.-J.; Breugem, W.-P. Numerical simulation of turbulent flow in concentric annuli. Flow Turbul. Combust. 2011, 86, 113–127. [Google Scholar] [CrossRef]
- Bai, B.F.; Wang, Y.C.; Xiao, Z.J. Experimental study of forced flow and heat transfer in a concentric annular tube. Chem. Eng. 1998, 15, 14–19. [Google Scholar]
- Bao, L.L.; Xu, B.; Wang, Z.Y.; Li, B.J.; Luo, J.H. Analysis of heat transfer performance of medium-depth coaxial cased buried tube heat exchanger. Adv. Geophys. 2020, 35, 1217–1222. [Google Scholar]
- Liu, Z.; Liu, S.Y.; Gao, S. Research on the effect of tube diameter ratio on heat transfer performance of medium-depth buried tube heat exchanger. Electr. Power Explor. Des. 2021, 9, 67–73. [Google Scholar]
- Zhang, B.Z.; Chen, H.J.; Zhang, J.S. Flow field structure and heat transfer characteristics in a rotating annular section bent tube. J. Aerodyn. 2002, 20, 21–31. [Google Scholar]
- Dirker, J.; Meyer, J.P. Heat transfer coefficients in concentric annuli. Heat Transf. 2002, 124, 1001–1008. [Google Scholar] [CrossRef][Green Version]
- Shao, J.; Li, X.H.; Guo, Z.J.; Liu, R.J.; Tian, X.L. Study on the applicability of different turbulence models in numerical simulation of pipeline flow. Chem. Equip. Pip. 2016, 53, 66–71. [Google Scholar]
- Mohammad, H.Z.; Mona, Z.P.; Siamak, H.; Kambiz, V. Application of Porous-Embedded shell and tube heat exchangers for the Waste heat Recovery Systems. Appl. Therm. Eng. 2022, 211, 118452. [Google Scholar] [CrossRef]
- ANSYS, Inc. ANSYS Fluent Theory Guide [CP/OL]; ANSYS: Canonsburg, PA, USA, 2020. [Google Scholar]
- Jones, W.P.; Launder, B.E. The prediction of laminarization with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1972, 15, 301–311. [Google Scholar] [CrossRef]
- Jones, W.P.; Launder, B.E. The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence. Int. J. Heat Mass Transf. 1973, 16, 1119–1130. [Google Scholar] [CrossRef]
- Tao, W.Q. Numerical Heat Transfer, 2nd ed.; Xi’an Jiaotong University Press: Xi’an, China, 2001; pp. 227–370. [Google Scholar]
- Han, Z.Z. FLUENT—Fluid Engineering Simulation Case Studies and Analysis; Beijing Institute of Technology Press: Beijing, China, 2009; pp. 103–104. [Google Scholar]
- Tao, W.Q. Heat Transfer, 5th ed.; Higher Education Press: Beijing, China, 2019; pp. 230–231. [Google Scholar]
- Thermal Calculation Standard Method for Boiler Units; Beijing Boiler Factory Design Department, Translator; Machinery Industry Press: Beijing, China, 1976; pp. 47–75. [Google Scholar]
- Shah, R.K.; Joshi, S.D. Handbook of Single-Phase Convective Heat Transfer; Wiley-Interscience: New York, NY, USA, 1987; Chapter 5. [Google Scholar]
- Ghajar, A.J.; Tam, L.M. Heat transfer measurements and correlations in the transition region for a circular tube with three different inlet configurations. Exp. Therm. Fluid Sci. 1994, 8, 79–90. [Google Scholar] [CrossRef]
- Ji, W.T.; Zhang, D.C.; He, Y.L.; Tao, W.Q. Prediction of fully developed turbulent heat transfer of internal helically ribbed tubes--An extension of Gnielinski equation. Int. J. Heat Mass Transf. 2012, 55, 1375–1384. [Google Scholar] [CrossRef]

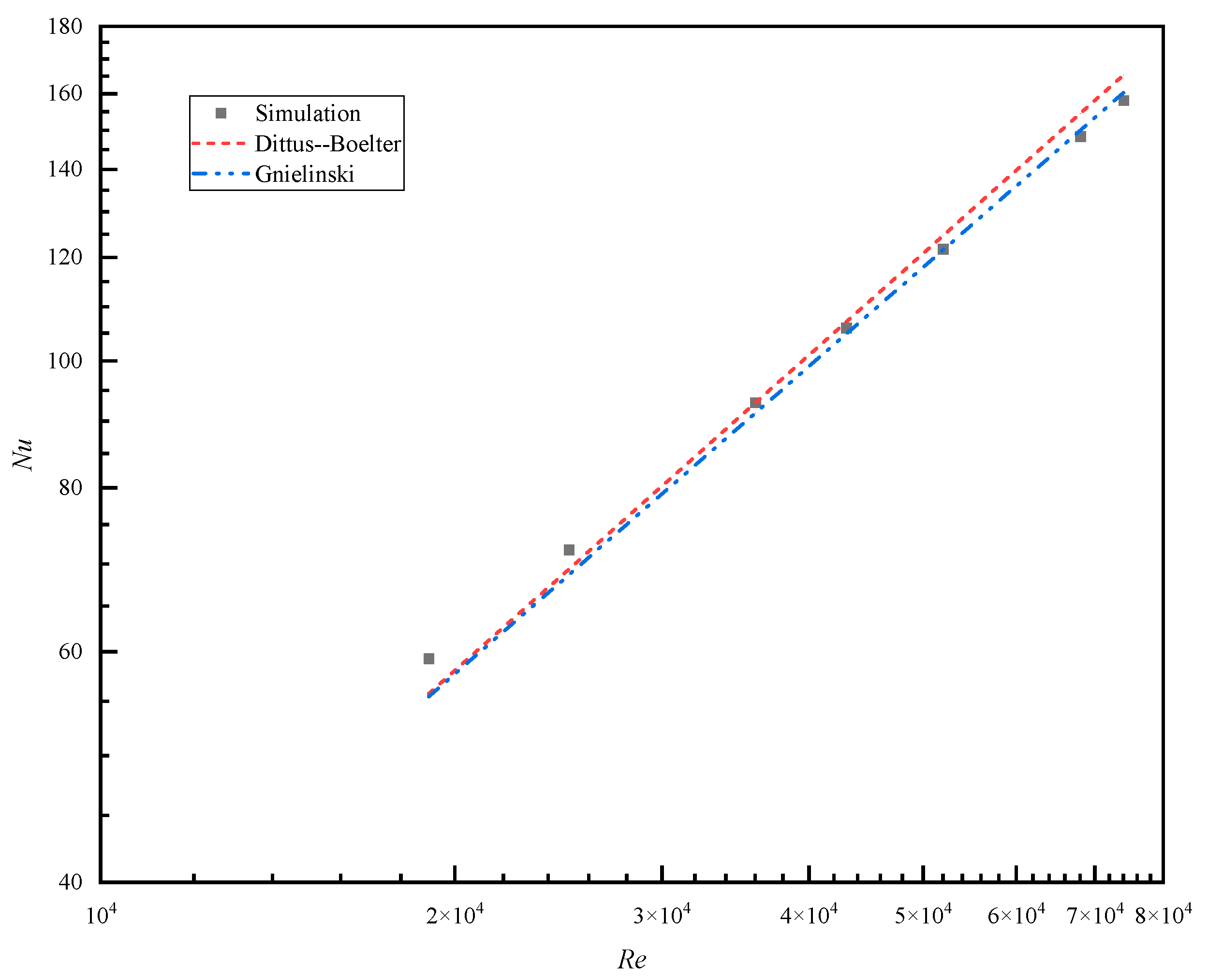
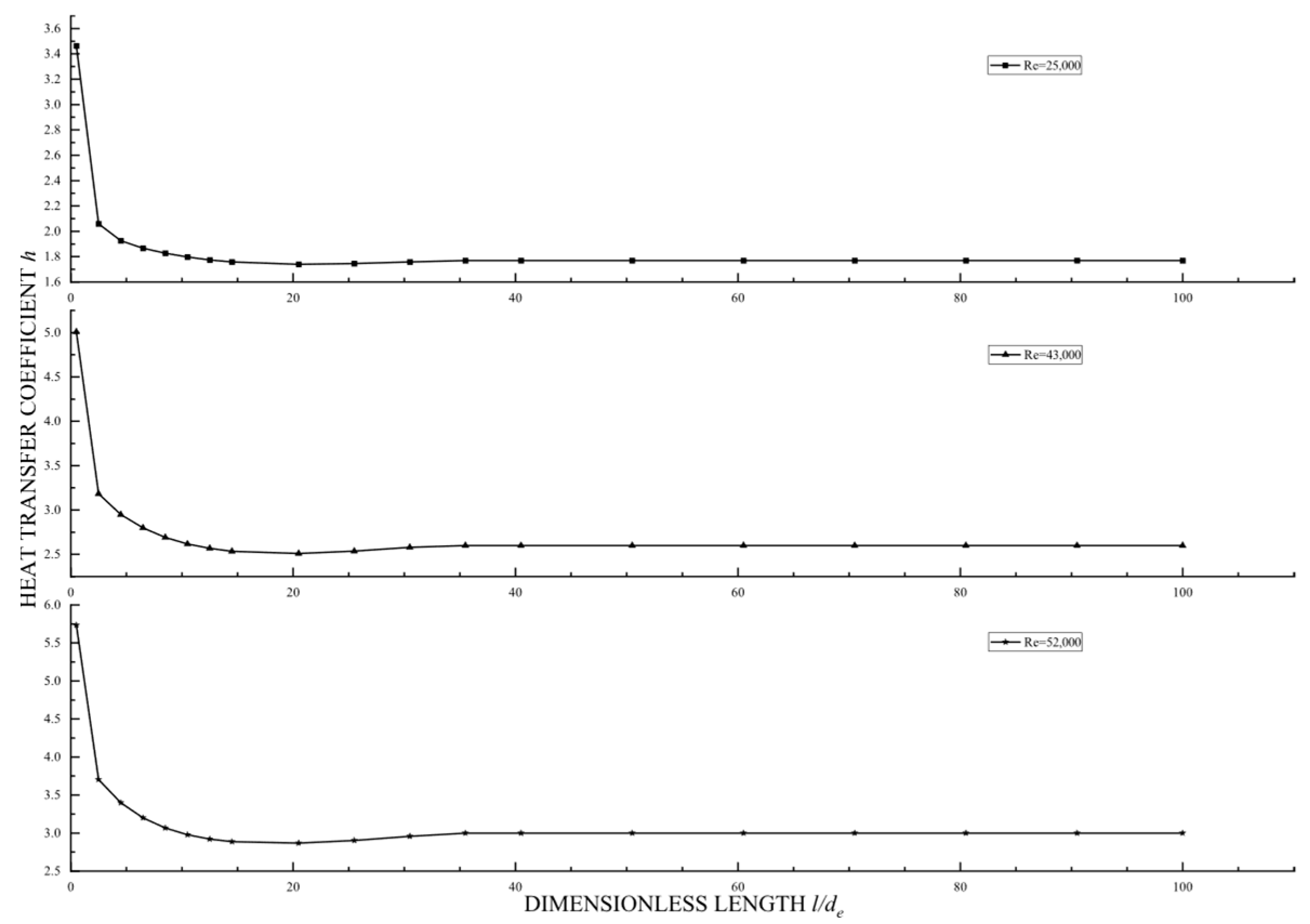
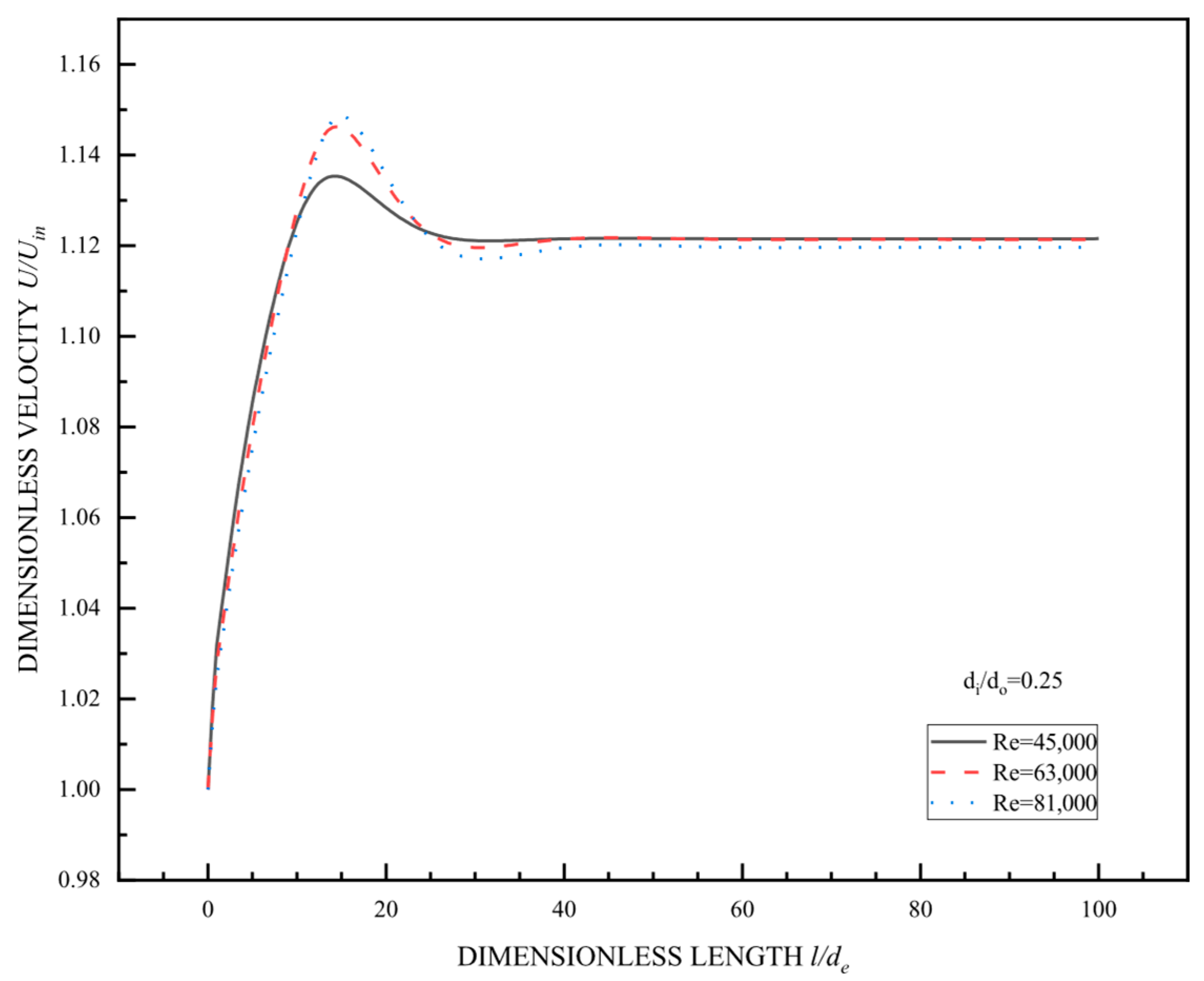
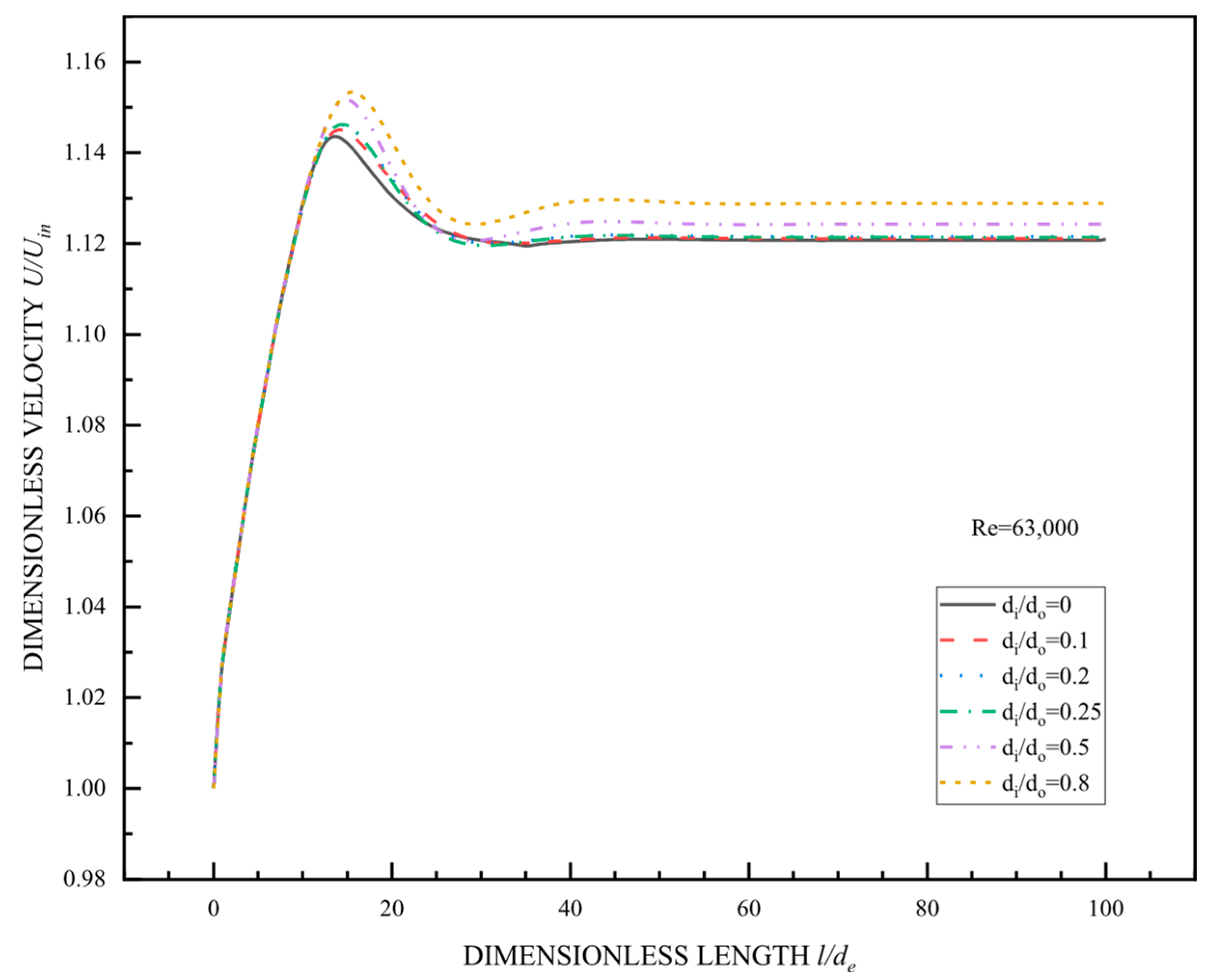

| Mesh Size | 1664 × 200 | 1876 × 200 | 2058 × 200 | 2230 × 200 | 2482 × 200 |
|---|---|---|---|---|---|
| 69.21 | 69.04 | 68.97 | 68.94 | 68.89 | |
| 55.93 | 55.87 | 55.84 | 55.83 | 55.82 |
| Mesh Size | 2058 × 100 | 2058 × 150 | 2058 × 200 | 2058 × 250 | 2058 × 300 |
|---|---|---|---|---|---|
| 68.98 | 68.98 | 68.97 | 68.96 | 68.96 | |
| 55.82 | 55.83 | 55.84 | 55.85 | 55.85 |
| Re | 19,000 | 25,000 | 36,000 | 43,000 | 52,000 | 68,000 | 74,000 |
|---|---|---|---|---|---|---|---|
| Inlet velocity (m/s) | 0.38 | 0.5 | 0.72 | 0.86 | 1.04 | 1.36 | 1.48 |
di/do | ||||||
| 0.1 | 0.2 | 0.25 | 0.5 | 0.8 | 1 | |
| 18,000 | 81.24 | 71.28 | 68.97 | 63.79 | 62.64 | 53.45 |
| 27,000 | 109.53 | 97.69 | 94.45 | 86.22 | 82.78 | 70.64 |
| 45,000 | 160.99 | 139.98 | 134.45 | 119.54 | 113.54 | 101.61 |
| 63,000 | 200.60 | 173.80 | 167.64 | 149.39 | 142.17 | 129.55 |
| 81,000 | 234.67 | 205.48 | 198.64 | 178.08 | 169.61 | 156.24 |
di/do | ||||||
| 0 | 0.1 | 0.2 | 0.25 | 0.5 | 0.8 | |
| 18,000 | 53.45 | 54.62 | 55.49 | 55.84 | 57.64 | 60.45 |
| 27,000 | 70.64 | 71.89 | 73.08 | 73.37 | 75.88 | 78.81 |
| 45,000 | 101.61 | 102.30 | 103.41 | 103.97 | 105.33 | 109.11 |
| 63,000 | 129.55 | 130.16 | 131.46 | 132.17 | 133.33 | 137.18 |
| 81,000 | 156.24 | 156.67 | 157.92 | 158.83 | 160.04 | 163.97 |
| D–B | 3.441 | −0.15 | −0.112 | 3.618 | 0.033 | −0.116 |
| Gnielinski | 2.704 | −0.15 | −0.085 | 2.843 | 0.033 | −0.089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wang, Z.; Yang, M. Corrected Correlation for Turbulent Convective Heat Transfer in Concentric Annular Pipes. Energies 2025, 18, 3643. https://doi.org/10.3390/en18143643
Xu J, Wang Z, Yang M. Corrected Correlation for Turbulent Convective Heat Transfer in Concentric Annular Pipes. Energies. 2025; 18(14):3643. https://doi.org/10.3390/en18143643
Chicago/Turabian StyleXu, Jinping, Zhiyun Wang, and Mo Yang. 2025. "Corrected Correlation for Turbulent Convective Heat Transfer in Concentric Annular Pipes" Energies 18, no. 14: 3643. https://doi.org/10.3390/en18143643
APA StyleXu, J., Wang, Z., & Yang, M. (2025). Corrected Correlation for Turbulent Convective Heat Transfer in Concentric Annular Pipes. Energies, 18(14), 3643. https://doi.org/10.3390/en18143643





