Multi-Level Asynchronous Robust State Estimation for Distribution Networks Considering Communication Delays

Abstract

With the hierarchical evolution of distribution network control architectures, distributed state estimation has become a focal point of research. To address communication delays arising from inter-level data exchanges, this paper proposes a multi-level, asynchronous, robust state estimation algorithm that accounts for such delays. First, a multi-level state estimation model is formulated based on the concept of a maximum normal measurement rate, and a hierarchical decoupling modeling approach is developed. Then, an event-driven broadcast transmission strategy is designed to unify boundary information exchanged between levels during iteration. A multi-threaded parallel framework is constructed to decouple receiving, computation, and transmission tasks, thereby enhancing asynchronous scheduling capabilities across threads. Additionally, a round-based synchronization mechanism is proposed to enforce fully synchronized iterations in the initial stages, thereby improving the overall process of asynchronous state estimation. Case study results demonstrate that the proposed algorithm achieves high estimation accuracy and strong robustness, while reducing the average number of iterations by nearly 40% and shortening the runtime by approximately 35% compared to conventional asynchronous methods, exhibiting superior estimation performance and computational efficiency under communication delay conditions.

1. Introduction

State estimation, as a critical supporting technology for monitoring and control in distribution network operations, analyzes system states by integrating various types of measurement data [1,2,3,4,5], thereby providing auxiliary support for core functions such as fault diagnosis [6], dispatch decision making [7], and energy management [8]. With the increasing integration of distributed energy resources and intelligent edge devices, the operational scale of distribution networks continues to expand, and the control architecture is evolving toward a hierarchical and collaborative framework [9,10]. In this context, traditional centralized state estimation methods are gradually revealing limitations in terms of data exchange, communication overhead, and computational efficiency [11,12].

In this context, state estimation algorithms are progressively evolving toward distributed architectures. Distributed state estimation features structural decoupling, parallel computation, and hierarchical coordination, making it well aligned with the needs of distribution networks characterized by wide geographical coverage and multi-level control structures. It has thus emerged as a key research focus and development direction in the field [13,14,15,16]. Reference [17] proposes a multi-area state estimation model using a generalized loss function, where matrix splitting is applied to achieve regional decomposition. Reference [18] constructs a multi-level estimation framework at the area level based on asynchronous measurements, enabling distributed state estimation via encrypted communication. These distributed estimation approaches are essentially built upon same-layer partitioned architectures, where global state estimation is achieved by parallel estimation of subregions. However, they do not address the issue of coordinated estimation in multi-level hierarchical structures.

To address the hierarchical structure and multi-level control characteristics of power system operations, several studies have proposed hierarchical state estimation frameworks featuring top-down coordination mechanisms to enable cross-level state fusion and coordinated estimation [19,20]. Existing efforts have primarily focused on inter-level modeling and coordination mechanisms between transmission and distribution systems. Reference [21] proposes a master–slave state estimation model that partitions the transmission and distribution systems into master and slave regions, where cross-level state fusion is achieved through coordinated variables. Reference [22] develops a multi-level estimation procedure based on hierarchical topology, wherein state estimation tasks are executed in parallel across different control levels. At the distribution network level, some preliminary investigations into multi-level state estimation strategies have also emerged. Reference [23] designs a hierarchical state estimation method for radial distribution networks, integrating SCADA and AMI data via regional decoupling. Reference [24] proposes a two-layer distributed state estimation approach that combines local estimation with boundary coordination and fusion. However, these methods essentially belong to intra-layer multi-stage estimation schemes, in which state estimation is first performed within individual subregions, followed by secondary estimation on tie-lines based on boundary states to complete the overall coordination [25,26]. A truly hierarchical state estimation framework, comparable to those used in transmission–distribution systems and capable of representing multi-level structures and enabling coordinated solving, has yet to be established.

On the other hand, communication conditions are a critical factor influencing the performance of state estimation, particularly in multi-level distributed architectures of distribution networks. Variations in communication paths and data update cycles across different levels often lead to asymmetric delays and response misalignments, which in turn affect the convergence speed and stability of state estimation algorithms [27,28]. To mitigate the dependence on synchronous communication mechanisms, some studies have introduced asynchronous estimation algorithms. Reference [29] proposes an online asynchronous state estimation algorithm based on the proximal point method. Reference [30] designed a local asynchronous convergence detection mechanism. In addition, several studies have attempted to reduce the impact of communication constraints by simplifying the treatment of communication delays. Reference [31] utilizes the correlations between measurement data to infer and compensate for missing measurements caused by communication interruptions. Reference [32] adopts a hybrid strategy that combines consensus and incremental updates to ensure convergence under heterogeneous communication scenarios. Although these approaches alleviate the adverse effects of communication delays to some extent, they fall short in fully addressing the challenges posed by the accumulated delays and inter-level response mismatches inherent in multi-level distribution network structures, which can ultimately compromise the convergence and stability of state estimation.

Building upon existing research, this paper further conducts a comparative analysis of representative state estimation methods for distribution networks developed in recent years, with a focus on differences in control architecture, communication mechanisms, hierarchical adaptability, and robustness, as summarized in

Table 1. Comparative analysis of different state estimation methods.

Method	Control Architecture	Communication Mode	Delay Adaptability	Hierarchical Adaptability
Centralized estimation (e.g., WLS)	Centralized control	Synchronous communication	Weak	Weak
Distributed synchronous estimation (e.g., synchronous ADMM)	Distributed control	Synchronous communication	Weak	Moderate
Distributed asynchronous estimation (e.g., asynchronous ADMM)	Distributed control	Asynchronous communication	Strong	Moderate
Graph neural network-based methods (e.g., GNN)	Data-driven control	Model training	Data-dependent	Weak
Filtering-based methods (e.g., UKF)	Recursive structure	Synchronous communication	Weak	Weak

.

In summary, although existing state estimation methods have achieved a certain degree of communication adaptability and distributed solving capability, they are mostly limited to same-layer architectures and lack systematic investigation into global state estimation under multi-level frameworks. To address this gap, this paper proposes an asynchronous robust state estimation algorithm that considers communication delays. The main contributions of this paper are as follows:

• A multi-level state estimation modeling method for distribution networks is proposed based on the concept of a maximum normal measurement rate, along with a decoupling analysis tailored to the structural characteristics of distribution systems.
• An event-driven broadcast transmission strategy and a synchronization initiation mechanism are designed to enhance the consistency of boundary information and the convergence stability during the initial estimation stage.
• A multi-threaded parallel mechanism is introduced, decoupling the receive–compute–transmit process, which structurally optimizes the state estimation algorithm under asynchronous conditions and significantly improves the computational efficiency and concurrent processing capability.

The remainder of this paper is organized as follows: Chapter 2 develops a decoupled model for multi-level state estimation in distribution networks and introduces the synchronous solution algorithm; Chapter 3 presents an enhanced asynchronous state estimation algorithm considering communication delays; Chapter 4 conducts comparative case studies to validate the effectiveness and advantages of the proposed method; Chapter 5 concludes the paper.

2. Modeling and Synchronous Solution Algorithm for Multi-Level State Estimation in Distribution Networks

2.1. Maximum Normal Measurement Rate Mathematical Model

The measurement normal rate can be used to reflect the reliability of measurement data, and its value is closely related to the uncertainty parameters of the measured results [33]. Based on the probabilistic characteristics of measurement values, the expanded uncertainty can be further derived to construct a confidence interval model. Specifically, assuming that the true value of a measurement Z_i falls within the interval [Z_i − V_i, Z_i + V_i] with a probability of pp, this confidence interval can statistically represent the credibility of the measurement result. The corresponding expression is:

$$P\left(\left|h_i(\overline{x})-Z_i\right|⩽V_i\right)=p$$

(1)

where $\overline{x}$ represents the theoretical system state; $h_i(\overline{x})$ represents the measurement function of point i under state $\overline{x}$; and V_i is the expanded uncertainty of point i corresponding to probability p.

For measurement points i with normal measurements during actual operation, the probability p is typically close to 1. Therefore, measurement points that satisfy Equation (2) can be regarded as normal points:

$$\left|h_i(x)-Z_i\right|⩽V_i$$

(2)

where x represents the system state obtained from state estimation.

To better evaluate the state estimation results at each point, the relative estimation deviation d_i of point i is defined based on Equation (2) as follows:

$$d_i={\displaystyle \frac{h_i(x)-Z_i}{V_i}}$$

(3)

According to Equation (3), a normal point satisfies |d_i| ≤ 1, while a point with abnormal measurement satisfies |d_i| > 1. Based on this, a point evaluation function is constructed as follows:

$$f\left(d_i\right)=\left|\begin{array}{cc}0& \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\left|d_i\right|⩽1\\ 1& \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}\left|d_i\right|>1\end{array}\right.$$

(4)

At this point, maximizing the measurement normal rate can be transformed into minimizing the sum of the evaluation functions of all points, thereby formulating a state estimation model with MNMR as the objective function:

$$\{\begin{array}{l}\underset{x}{min}{\displaystyle \sum _{i=1}^n}f(d_i)\\ \mathrm{s}.\mathrm{t}.\hspace{1em}{d}_i=\frac{h_i(\mathit{x})-Z_i}{U_i}\\ \hspace{1em}\hspace{1em} g(\mathit{x})=0\\ \hspace{1em}\hspace{1em} l(\mathit{x})\le 0\end{array}$$

(5)

where n represents the number of measurement points; g(x) represents the power flow constraints of the system; and l(x) represents the upper and lower bounds of system components, such as the transmission power limits of lines and output limits of generators.

The MNMR model proposed in Equation (5) exhibits strong robustness; regardless of the magnitude of deviation between the measurement data and the state estimation result, its weight in the objective function remains constant at 1. This reduces sensitivity to large deviations and significantly decreases the model’s responsiveness to abnormal measurement data, thereby enabling more stable identification of problematic measurements. However, since the point evaluation function is not continuously differentiable, the optimization problem becomes significantly more difficult to solve.

To address this issue, the point evaluation function is approximated using a sigmoid function, which preserves its evaluation capability while ensuring continuous differentiability. Specifically, it is defined as:

$$\left\{\begin{array}{l}f(d_i)=\delta (d_i)+\delta (-d_i)\\ \delta (d_i)={\displaystyle \frac{1}{1+{\mathrm{e}}^{\frac{2\eta }{\lambda -1}\left[-d_i+\left(1+\frac{\lambda -1}{2}\right)\right]}}}\end{array}\right.$$

(6)

where λ represents a positive constant and η represents an integer greater than 2.

2.2. Decoupled Model for Multi-Level State Estimation in Distribution Networks

In response to the distinctive operational characteristics of modern distribution networks, characterized by clear multi-level structures and refined control granularity, this paper proposes a generalized decoupled modeling framework for multi-level state estimation. The framework is organized into three representative hierarchical levels: the primary distribution network layer, the substation transformer layer, and the feeder layer, featuring a well-defined hierarchical structure and clear boundary coupling logic. 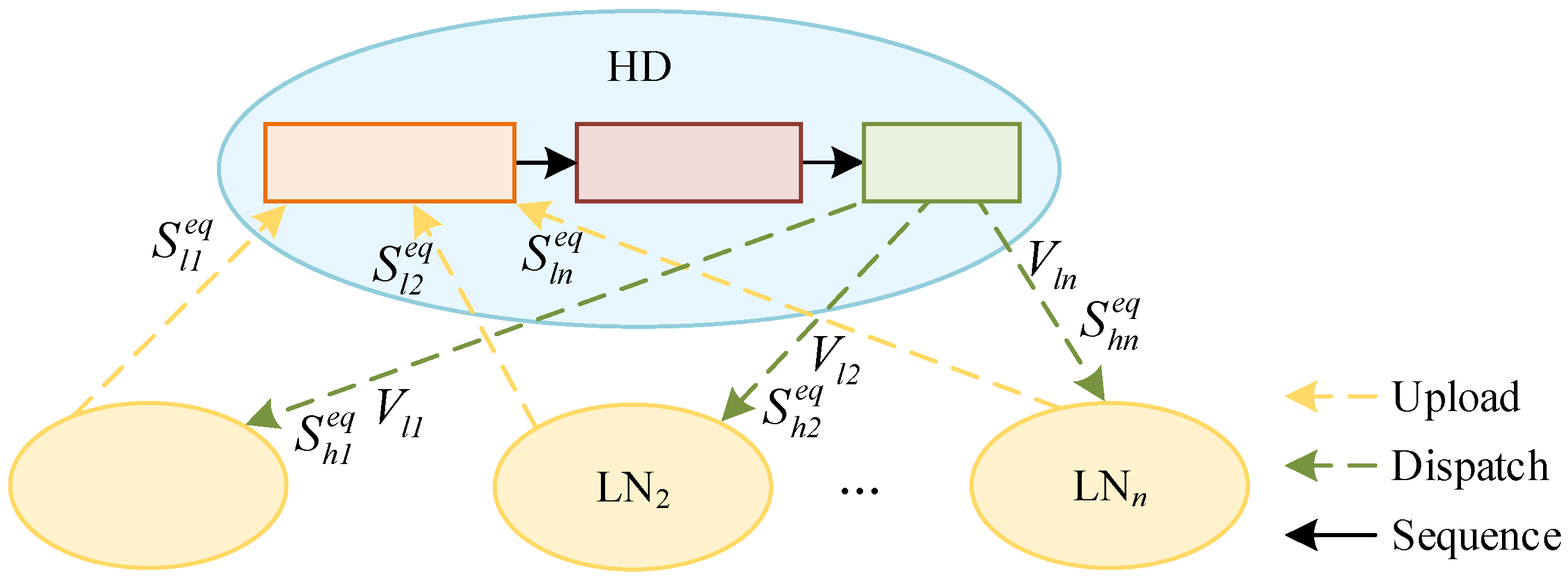Taking a two-level decoupling model as an example, as illustrated in Figure 1, the upper-level region HD (shown in blue) is connected to multiple lower-level region LDs (shown in yellow), which differ significantly in structure and operational attributes. Since different LD regions may fall under separate management entities, their topological structures, communication protocols, and data standards often vary considerably, making unified global modeling and data sharing difficult to implement directly. To address this, a distributed solution mechanism is introduced, allowing each LD region to perform independent modeling based on its own structural characteristics and measurement configuration, while interacting with the HD layer solely through boundary parameters.

The tie line between the HD layer and each LD is represented by r_hi,li, where h_i represents the node on the HD side and l_i represents the root node of LD_i. The voltage magnitude measurement at the root node is denoted as V_li. Considering the diverse topological configurations of distribution networks, such as radial and meshed structures, as well as nonlinear operational characteristics like three-phase imbalance, variables related to the tie line, including r_hi,li, and V_li, may be either scalars or vectors. When LD_i is connected to the HD layer via a single tie line, these variables are scalars; when LD_i has multiple tie lines or operates under three-phase unbalanced conditions, they are represented as vectors. In the subsequent analysis, no distinction is made between scalar and vector forms.

By incorporating the root node l_i of each LD into the HD layer, a complete HD region is formed. The state variables of this region include not only the original state variables of HD nodes, but also the state variables of each LD root node. To support this, equivalent pseudo-measurements are introduced, specifically the power flow measurements $S_{hi}^{\mathrm{eq}}$ and $S_{li}^{\mathrm{eq}}$ on both sides of the tie line connected to the root node of LD_i. Similarly, the complete set of state variables for each LD subregion can be obtained. Based on this, the measurements of the complete upper HD region and the complete lower LD subregions can be expressed as:

$$z_{\mathrm{EH}}={\left[\begin{array}{ccc}{z}_{\mathrm{HD}}& S_l^{\mathrm{eq}}& V_l\end{array}\right]}^T$$

(7)

$$z_{\mathrm{EL}}={\left[\begin{array}{ccc}{z}_{\mathrm{LD}}& S_h^{\mathrm{eq}}& V_l\end{array}\right]}^T$$

(8)

where EH represents the complete upper HD region and EL represents the complete lower LD subregions.

After decoupling, the global state estimation problem (5) can be decomposed into an EH subproblem and multiple EL_i subproblems:

$$\underset{{\mathit{x}}_{\mathrm{HD}}}{min}\sum _{i=1}^{n}f(d_i)=\sum _{i=1}^n(\delta (d_i)+\delta (-d_i))$$

(9)

$$\underset{{\mathit{x}}_{\mathrm{EL},i}}{min}\sum _{k=1}^{n}f(d_k)=\sum _{k=1}^n(\delta (d_k)+\delta (-d_k))$$

(10)

It can be observed that the state variables of node l_i, along with the line power flow measurements $S_{hi}^{\mathrm{eq}}$ and $S_{li}^{\mathrm{eq}}$, are involved in both subproblems, which naturally leads to an iterative process between the subproblems:

$$\left[S_{h1}^{\mathrm{eq}},\dots ,S_{hi}^{\mathrm{eq}},\dots ,S_{hn}^{\mathrm{eq}};V_{l1},\dots ,V_{li},\dots V_{ln}\right]={\mathrm{\Theta }}_{\mathrm{EH}}\left[S_{l1}^{\mathrm{eq}},\dots ,S_{li}^{\mathrm{eq}},\dots ,S_{ln}^{\mathrm{eq}}\right]$$

(11)

$$\left[S_{li}^{\mathrm{eq}}\right]={\mathrm{\Theta }}_{\mathrm{EL},i}\left[S_{hi}^{\mathrm{eq}};V_{li}\right]$$

(12)

Equation (11) describes the iterative process of the EH subproblem, where Θ_EH represents its iterative mapping; Equation (12) describes the iterative process of the EL_i subproblem, with Θ_EL,i denoting its iterative mapping. After each iteration, all state variables and equivalent pseudo-measurements are updated. By combining Equations (11) and (12), we obtain:

$$\left[S_{h,k+1}^{\mathrm{eq}};V_{l,k+1}\right]={\mathrm{\Theta }}_B\left[S_{h,k}^{\mathrm{eq}};V_{l,k}\right]$$

(13)

where ${\mathrm{\Theta }}_B={\mathrm{\Theta }}_{\mathrm{EH}}\left({\mathrm{\Theta }}_{\mathrm{EL},1}\left(·\right),{\mathrm{\Theta }}_{\mathrm{EL},2}\left(·\right),\dots ,{\mathrm{\Theta }}_{\mathrm{EL},n}\left(·\right)\right)$.

Equation (13) represents the fixed-point iterative form of multi-level state estimation in distribution networks. Compared with previous studies, the proposed model and iterative formulation are more aligned with engineering practice. In the solution of the two subproblems, the line power flow measurements on both sides of node l_i can be treated as node injection measurements and incorporated into the computation. This establishes a fixed-point iterative form for multi-level state estimation, enabling decoupled computation between the two parts. Each part can be solved using different estimation methods to accommodate the specific characteristics of measurement distribution, network topology, and other regional features.

2.3. Synchronous Algorithm for Multi-Level State Estimation in Distribution Networks

Equation (13) essentially represents the iterative form of the synchronous algorithm. Under the synchronous state estimation framework, the HD layer and each subregion LD_i are required to follow a centralized and strictly time-aligned synchronization mechanism. As shown in Figure 2, during each round of state estimation, the HD layer must synchronously receive boundary parameters from all LD_i subregions and can only proceed with its own state estimation after all data have been received. This synchronization strategy has the following inherent drawbacks: First, due to communication delays, the convergence process of the HD layer is constrained by the data arrival time of the slowest subregion. Second, for LD_i regions with complex topologies or limited computational capacity, the global synchronization cycle is further prolonged, leading to system-level asymmetric delay accumulation. Third, in the presence of data loss or timeout caused by communication delays, the HD layer may face the risk of divergence in state estimation due to incomplete parameters. As a result, traditional synchronous mechanisms severely limit the real-time performance and robustness of the system in multi-level state estimation scenarios.

3. Asynchronous Algorithm for Multi-Level State Estimation Considering Communication Delays

3.1. Asynchronous Algorithm for Multi-Level State Estimation

The multi-level state estimation problem in distribution networks can be abstracted into the fixed-point iterative form described by Equation (13), which can be solved using an asynchronous iterative approach to improve computational efficiency [34,35]. Given an initial value $\left[S_{h,0}^{\mathrm{eq}};V_{l,0}\right]$ for asynchronous iteration, the iterative sequence $\left[S_{h,k}^{\mathrm{eq}};V_{l,k}\right]$ for k = 0, 1… is generated based on the mapping Θ_B, and can be expressed as:

$$\left[S_{hi,k+1}^{\mathrm{eq}};V_{li,k+1}\right]=\left\{\begin{array}{cc}\left[S_{hi,k}^{\mathrm{eq}};V_{li,k}\right]& i\notin {\mathrm{\Phi }}_k\\ {\mathrm{\Theta }}_B\left[S_{hi,k}^{\mathrm{eq}};V_{li,k}\right]& i\in {\mathrm{\Phi }}_k\end{array}\right.$$

(14)

where Φ_k represents the set of LD regions whose updated values are successfully received by the HD layer without communication timeout during the (k+1)th iteration.

Equation (14) represents the basic iterative form of the asynchronous algorithm, in which the boundary state variables obtained in the (k+1)th iteration may vary depending on the communication conditions. By decoupling Equation (14), an asynchronous iterative form of the EH subproblem and the EL_i subproblems can be derived:

$$\left[S_{h,k+1}^{\mathrm{eq}};V_{l,k+1}\right]={\mathrm{\Theta }}_{\mathrm{EH}}\left[S_{l1,s_1\left(k\right)}^{\mathrm{eq}},\dots ,S_{li,s_i\left(k\right)}^{\mathrm{eq}},\dots ,S_{ln,s_n\left(k\right)}^{\mathrm{eq}}\right]$$

(15)

$$\left[S_{li,s_i\left(k\right)}^{\mathrm{eq}}\right]={\mathrm{\Theta }}_{\mathrm{EL},i}\left[S_{hi,s_i\left(k\right)}^{\mathrm{eq}};V_{li,s_i\left(k\right)}\right]$$

(16)

where s_i(k) represents the iteration index of the return value from the ith LD used by the HD layer in the (k+1)th iteration of the EH subproblem. This index is identical to that of the HD-issued value used in the corresponding computation of the EL_i subproblem.

There are two possible values for s_i(k): In the first case, s_i(k) = k, indicating that the LD received the value issued by the EH subproblem in the kth iteration, computed its EL_i subproblem accordingly, and the HD layer successfully received the return value in time. In the second case, $s_i\left(k\right)<k$, indicating that during the (k+1)th iteration of the EH subproblem, the HD layer either failed to receive the return value from the LD, or received outdated data.

Compared to Equation (13), the asynchronous iterative form primarily differs in the iteration index of the state variables used in each update, denoted as s_i(k). To improve the convergence speed, it is necessary to incorporate asynchronous-related constraints into the above asynchronous algorithm. When performing the next iteration of the EH subproblem, the HD layer must receive a sufficient number of updated return values from the LD regions. The minimum required number of such updates is denoted by the parameter S. To ensure convergence, the HD layer should also use return values from the LD regions in a timely manner, with the maximum allowable staleness denoted by the parameter τ. Based on these considerations, the iteration of the EH subproblem is subject to the following constraints:

$$\left\{\begin{array}{l}{s}_i\left(k\right)-s_i\left(k-\tau \right)>0\\ {\displaystyle \sum _{i=1}^n\mathrm{sgn}\left(s_i\left(k\right)-s_i\left(k-1\right)\right)}\ge S\\ s_i\left(k\right)\le k\end{array}\right.$$

(17)

When S = n or τ = 1, the first two constraints in Equation (17) reduce to $s_i\left(k\right)-s_i\left(k-1\right)>0$, meaning that updated data from every LD must be received in each successive iteration. In this case, the asynchronous state estimation degenerates into synchronous state estimation.

3.2. Broadcast Transmission Strategy

To address the issue of information synchronization lag inherent in synchronous mechanisms, traditional asynchronous state estimation relaxes the synchronization constraints by allowing the HD layer to initiate an iteration as soon as it receives updated data from at least S lower-level LD_i regions. This approach reduces the dependency of the upper-layer HD estimation process on the slowest LD region. However, in practical scenarios where communication delays and asynchronous triggers coexist, the data reporting frequencies across different LD_i regions often vary significantly. Some regions may have already completed multiple updates and transmitted new data, while others remain stalled at earlier iterations. As a result, the HD layer operates with input data that exhibit pronounced temporal heterogeneity. This heterogeneity introduces an accumulation of outdated information, which degrades the effectiveness of the estimation results and may even compromise the convergence performance of the algorithm.

To overcome this issue, this paper proposes an event-triggered broadcast transmission strategy. After each completion of the EH subproblem, the HD layer actively broadcasts the latest iteration index $\left[S_{h,k}^{\mathrm{eq}};V_{l,k}\right]$ to all LD_i regions. Regardless of whether a subregion has completed its current computation, each LD_i adopts the broadcasted result as the new starting point for subsequent estimation. This approach enables the dynamic calibration of the local state in each subregion.

Accordingly, after applying the broadcast transmission strategy, the second constraint in Equation (17) needs to be modified as follows:

$${\displaystyle \sum _{i=1}^n\mathrm{sgn}\left(s_i\left(k\right)-k\right)}\ge n-S$$

(18)

The remaining two constraint conditions remain the same as those in Equation (17). The modified constraint ensures that, during each iteration, the HD layer uses the latest S updated values from LD regions with iteration index k. For any LD subregion that has not provided an updated value for τ consecutive iterations, the HD layer must wait for its current update before proceeding to the next computation.

By actively issuing the latest iteration index after each upper-layer EH subproblem is solved, the proposed strategy effectively unifies the boundary state information between the HD layer and all LD_i regions. This ensures that each region performs subsequent estimation based on the most up-to-date boundary inputs, thereby avoiding error accumulation caused by version inconsistencies. As a result, the strategy significantly enhances data consistency and convergence stability in multi-level state estimation. Compared with traditional asynchronous strategies that rely on passive progression triggered by subregion updates, this mechanism introduces an explicit synchronization anchor, which effectively suppresses the risk of divergence caused by asynchronous communication and uneven feedback. Furthermore, the broadcast strategy imposes no strict dependency on the local estimation progress of lower-layer regions, demonstrating strong adaptability to communication constraints and excellent scalability. It is particularly well suited for large-scale distributed systems with complex structures and non-ideal communication conditions.

3.3. Multithreaded Parallel Mechanism

Under the broadcast transmission strategy, the upper-layer region is required to push the latest boundary state to all lower-layer regions during each iteration. This may lead to a surge in communication traffic within a short period, resulting in significant concurrent transmission pressure. Limited by the system thread architecture and processing capacity, such communication peaks may cause issues such as data reception delays and resource scheduling bottlenecks, thereby reducing the overall responsiveness of the estimation process. To mitigate these impacts, a multithreaded parallel mechanism can be employed to achieve structural decoupling between computation and communication tasks [36]. Alternatively, a predictor–corrector mechanism can be introduced to enhance the data update speed and parallel fault tolerance by performing feedforward prediction and corrective iteration on key variables [37]. This paper introduces a multithreaded parallel mechanism within both the HD layer and each LD_i region. By separating the execution channels for reception, computation, and transmission tasks, this mechanism decouples communication and computation processes, thereby enhancing the system’s processing capability and execution efficiency under high-concurrency conditions.

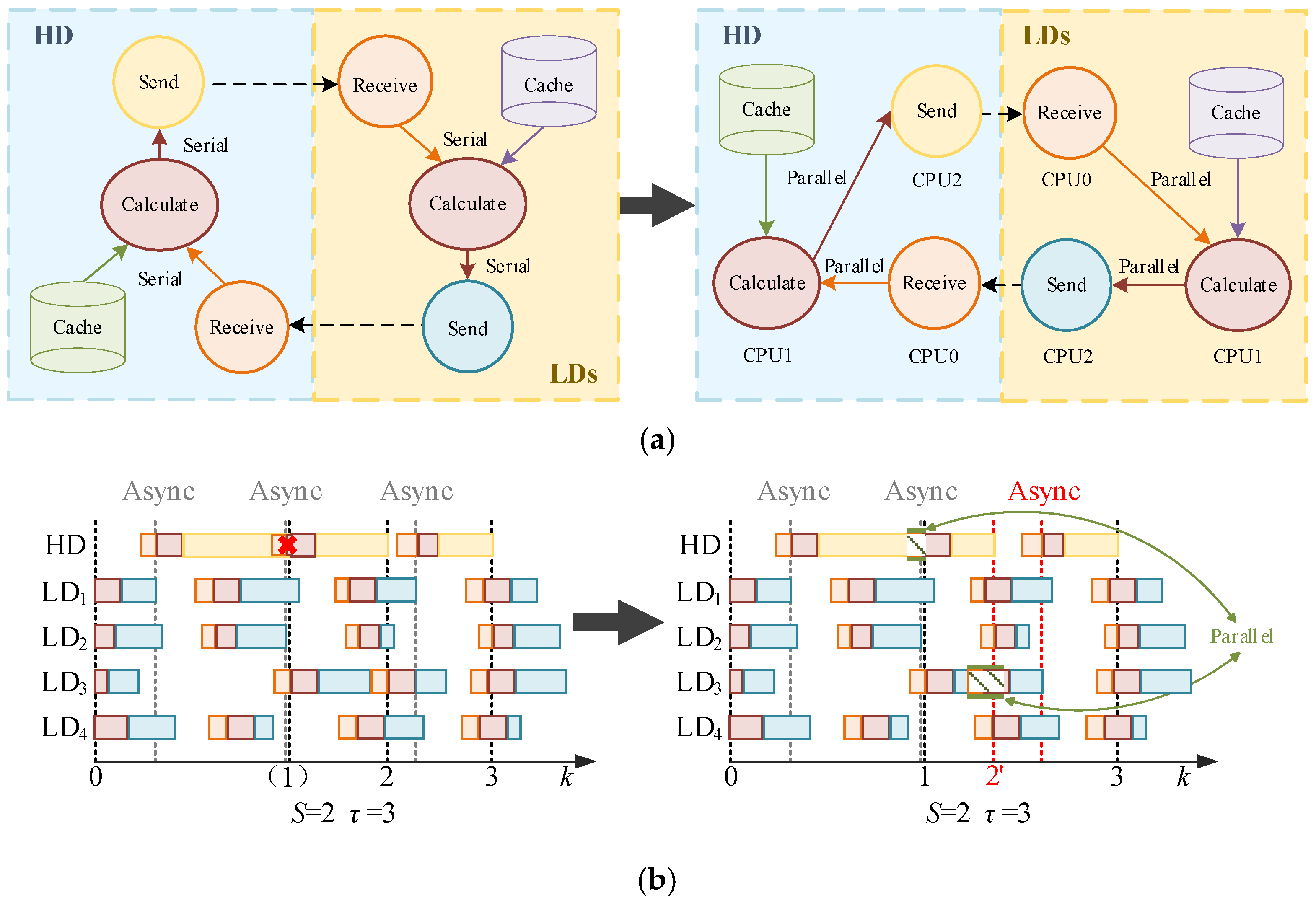
As illustrated in Figure 3a, the system deploys independent threads for reception, computation, and transmission. The reception thread continuously monitors and dynamically receives iteration data from other regions. The computation thread extracts the latest cached measurement information in real time and solves the corresponding EH or EL subproblem. Upon completion of the computation, the transmission thread promptly distributes the updated iteration sequence to the target regions. Dashed arrows represent inter-regional communication interactions, while solid arrows indicate the execution sequence of internal processes. These three types of threads operate collaboratively and are mutually decoupled, effectively alleviating resource idleness and execution blockages caused by concurrent broadcasting. This design significantly enhances the stability and execution efficiency of the asynchronous estimation algorithm under complex communication conditions.

Figure 3b illustrates the interaction process between the HD and each LD under asynchronous execution conditions, before and after the introduction of the parallel mechanism. Each rectangular block in the figure represents the execution time of a specific thread during the current iteration, with colors corresponding to the thread types shown in Figure 3a. For example, the yellow block for the HD indicates the operation time of its transmission thread. In the second iteration, due to reception delays at LD₃, the iteration sequence generated by the HD in the first round has not yet been delivered. As a result, the HD’s transmission thread continues occupying resources, and under the serial mechanism, conflicts occur with the reception thread in the current round, delaying the start of the HD’s next iteration, as marked by “x” in the figure. After introducing the parallel mechanism, the HD’s transmission from the previous round no longer blocks the reception in the new round, effectively avoiding resource conflicts. At k = 2, since LD₃ experiences delayed reception in the previous round, its new reception thread must wait for the previous transmission thread to finish before starting, which extends the HD’s broadcasting time. With the parallel mechanism, however, LD₃ can start its reception thread earlier, reducing the HD’s broadcast latency. Moreover, LD₃ completes its transmission earlier than LD₁ in the current round, allowing the HD to enter the next computation cycle earlier under the asynchronous trigger condition S = 2, thereby accelerating the overall scheduling progress and improving execution efficiency.

3.4. Synchronous Startup Mechanism

Meanwhile, to address the issue of significant disparities in response speeds among subregions during the initial phase of asynchronous estimation, where synchronizing the timing of boundary information feedback is difficult, the traditional asynchronous mechanism provides improved operational flexibility, but often causes premature computation to be triggered at the HD layer. Due to communication delays or computational lag in certain subregions during the initial iterations, the HD may begin calculations using incomplete or temporally inconsistent data. This can lead to the accumulation of estimation errors and adversely affect the overall convergence stability of the algorithm.

To mitigate the problem of error propagation during initial iterations, this paper proposes a synchronous bootstrapping mechanism. During the first k0k_0 iterations, the HD layer is required to execute the EH subproblem only after receiving the latest boundary states from all LD_i regions. This ensures that the system performs computations based on complete and synchronized data during the initialization phase, thereby enhancing the temporal consistency of the state estimation process.

Accordingly, after adopting the synchronous bootstrapping mechanism, an additional constraint must be introduced to enforce synchronous startup:

$$s_i(k)=\max (k,k_0),\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{1em}i=1,2,\dots ,n$$

(19)

When k < k₀, the HD layer must wait for updated results from all LD_i regions before proceeding to the next iteration. Once the initial synchronous window is exceeded, the system automatically switches to the asynchronous mode, where the EH subproblem can be triggered as long as responses from at least S regions are received.

This mechanism addresses the issue of insufficient data coverage in the early stages of the asynchronous mode by enforcing synchronous execution during the initial iterations. It effectively enhances the stability and reliability of early-stage state estimation, thereby providing favorable initial conditions for the subsequent asynchronous phase.

3.5. Improved Asynchronous State Estimation Algorithm Flow

The multi-level asynchronous state estimation algorithm proposed in this section is illustrated in Figure 4. The flow on the left side of the figure represents the process executed on the HD layer, while the right side shows the process running on all LD_i regions. At the start of the algorithm, each LD_i independently solves its EL subproblem based on local measurement data and sends the result to the HD layer. The HD continuously monitors the iteration data received from the LD_i regions. During the initial k₀ iterations, the HD must wait until all LD_i regions have returned their iteration values $S_{li,k}^{\mathrm{eq}}$ before triggering the EH subproblem computation, after which, the result $\left[S_{h,k+1}^{\mathrm{eq}};V_{l,k+1}\right]$ is broadcast to all LD_i regions. Once the iteration count exceeds k₀, the HD immediately solves the EH subproblem upon receiving iteration values $S_{li,k}^{\mathrm{eq}}$ from no fewer than S regions and confirming that the staleness of all LD_i values does not exceed the threshold τ; the resulting $\left[S_{h,k+1}^{\mathrm{eq}};V_{l,k+1}\right]$ is then broadcast to all LD_i regions. If these conditions are not satisfied, the HD continues polling for data until the triggering criteria are met. Each LD_i then proceeds to a new round of EL subproblem computation based on the received results. This process iterates until the voltage change at the boundary nodes between two consecutive iterations remains below a predefined convergence threshold, at which point, the algorithm terminates and outputs the final state estimation results.

4. Case Analysis

4.1. Case Setup

This chapter verifies the effectiveness of the proposed algorithm. The simulations were conducted on a computer equipped with an Intel Core i9-14900 CPU and 32 GB of available memory. The communication interactions were simulated programmatically in a local environment. The HD layer adopts the IEEE Case33 system with a nominal voltage of 12.66 kV, where nodes 4, 19, 24, and 25 are connected to the LD layers, with the original loads at these nodes set to zero. Each LD layer is modeled using a modified 18-bus system [38], with a nominal voltage of 0.4 kV and cable-type lines. The HD and each LD are connected via a distribution transformer with a rated capacity of 0.63 MVA. The transmission line impedance is set to 0.002 + j0.01 (in per unit), and the overall system configuration follows that shown in Figure 1. Communication delays are simulated using a normal distribution N(μ,σ²). The parameters for the MNMR model are set as λ = 2 and η = 3.

The measurement configuration is as follows: In the HD layer, measurements include the active power, reactive power, and voltage magnitude at the nodes, as well as the active and reactive power at injection points such as feeder inlets. In each LD layer, measurements include voltage magnitude at the nodes and active and reactive power at injection points such as feeder inlets.

To reflect the error characteristics of actual measurement devices, simulated measurement datasets are constructed by superimposing zero-mean Gaussian noise onto the true values obtained from power flow calculations in the HD and each LD region. For active and reactive power measurements at nodes, the standard deviation is set to σ = 0.01; for voltage magnitude measurements at nodes, σ = 0.004; for active and reactive power measurements at injection points, σ = 0.01; and for measurements related to boundary nodes, σ = 0.005. To generate bad data, a portion of the measurements is artificially perturbed using methods such as sign reversal, zeroing, or applying ±20% deviations from the original values. The proportion of bad data is set at 2%. The convergence error threshold is set to 10⁻⁶, and the error tolerance for boundary state variables is set to 10⁻⁴.

In this study, the voltage magnitudes, phase angles, and active and reactive power at the nodes are selected as state variables. The synchronous state estimation (S-SE) algorithm described in Section 2.3 and the traditional asynchronous state estimation (A-SE) algorithm described in Section 3.1 are used as benchmark methods to evaluate the estimation accuracy and convergence performance of the proposed improved asynchronous state estimation (HA-SE) algorithm. In addition, the runtime of each algorithm is adopted as an efficiency metric to assess the computational performance of the proposed method.

4.2. Analysis of State Estimation Results

To verify the estimation accuracy of the HA-SE algorithm, a comparison was conducted against the traditional WLS algorithm and the true values obtained from power flow calculations, with the asynchronous parameter set to S = 1 and τ = 3. The results are presented in

Table 2. Boundary node state estimation results.

Boundary Node		Parameter	True Value	WLS Algorithm	HA-SE Algorithm	Parameter	True Value	WLS Algorithm	HA-SE Algorithm
HD	4	V/p.u.	0.95291	0.95295	0.95294	P/MW	−0.40726	−0.41542	−0.41542
		θ/°	−1.72831	−1.76822	−1.76823	Q/MW	−0.13663	−0.13822	−0.13822
	19	V/p.u.	0.97574	0.97615	0.97614	P/MW	−0.40601	−0.40442	−0.40438
		θ/°	−1.77014	−1.76026	−1.76011	Q/MW	−0.13607	−0.13688	−0.13687
	24	V/p.u.	0.95164	0.951852	0.95184	P/MW	−0.40734	−0.40083	−0.40080
		θ/°	−1.94983	−1.90388	−1.90375	Q/MW	−0.13666	−0.14047	−0.14048
	25	V/p.u.	0.94849	0.94889	0.94887	P/MW	−0.40752	−0.40510	−0.40509
		θ/°	−2.02008	−1.99429	−1.99429	Q/MW	−0.13674	−0.13920	−0.13918
LD	4	V/p.u.	0.95291	0.95295	0.95295	P/MW	0.40726	0.41487	0.41486
		θ/°	−1.72831	−1.76822	−1.76823	Q/MW	0.13663	0.13839	0.13839
	19	V/p.u.	0.97574	0.97615	0.97614	P/MW	0.40601	0.40316	0.40311
		θ/°	−1.77014	−1.76026	−1.76011	Q/MW	0.13607	0.13820	0.13819
	24	V/p.u.	0.95164	0.95185	0.95184	P/MW	0.40734	0.40158	0.40155
		θ/°	−1.94983	−1.90388	−1.90375	Q/MW	0.13666	0.13896	0.13896
	25	V/p.u.	0.94849	0.94889	0.94888	P/MW	0.40752	0.40617	0.40616
		θ/°	−2.02008	−1.99429	−1.99429	Q/MW	0.13674	0.13744	0.13742

. As shown, the HA-SE algorithm yields estimation results for the voltage magnitude, phase angle, active power, and reactive power, which are highly consistent with both the WLS algorithm and the true values. Most deviations are controlled within 0.001, demonstrating excellent accuracy. With the introduction of boundary variable interaction, the voltage magnitudes at the boundary nodes of the upper HD and lower LD layers are nearly identical, indicating strong consistency between the hierarchical estimation results. In addition, the active power injected at the HD boundary nodes is negative, while the corresponding LD boundary injections are positive, with their sum approaching zero, which conforms to power flow conservation. These findings confirm that the proposed algorithm possesses high estimation accuracy and strong engineering applicability.

To further evaluate the robustness of the proposed algorithm under abnormal measurement scenarios, varying proportions of outlier data were introduced into the test cases, and the robust estimation capabilities of the WLS and HA-SE algorithms were compared. The maximum voltage deviation and overall deviation results for both algorithms are presented in

Table 3. Robust state estimation comparison.

Bad Data Ratio/%	WLS Algorithm		HA-SE Algorithm
	Maximum Voltage. Deviation/p.u.	Overall Voltage Deviation/p.u.	Maximum Voltage Deviation/p.u.	Overall Voltage Deviation/p.u.
0	0.0125	0.2397	0.0122	0.2323
3	0.0144	0.2697	0.0125	0.2482
6	0.0163	0.2921	0.0131	0.2523
10	0.0192	0.3246	0.0139	0.2571
14	0.0224	0.3603	0.0144	0.2684

. Here, the overall voltage deviation refers to the total deviation between the estimated and true voltage values across all nodes, reflecting the algorithm’s global estimation error level. As the proportion of abnormal data increases from 0% to 14%, the WLS algorithm demonstrates greater sensitivity to outliers, with the overall deviation rising rapidly from 0.2397 to 0.3603 and the maximum deviation increasing significantly, indicating a notable decline in estimation stability. In contrast, the HA-SE algorithm exhibits much smaller variation in the overall deviation, increasing only from 0.2323 to 0.2684 under the same conditions, and maintains more stable estimation performance. These results indicate that the HA-SE algorithm possesses stronger robustness in the presence of abnormal measurements. The proposed multi-level decoupled structure and asynchronous coordinated iteration mechanism effectively suppress the propagation of local anomalies, thereby enhancing the stability and robustness of state estimation and ensuring the safe operation of the system in complex environments.

Furthermore, this section compares the boundary consistency of state estimation results obtained using the S-SE, A-SE, and HA-SE algorithms. With asynchronous parameters fixed, the boundary node state estimation results of each algorithm are tested and recorded, as shown in

Table 4. State estimation results of different algorithms.

Algorithm	Maximum Mismatch of Boundary Voltage Magnitude/p.u.	Maximum Mismatch of Boundary Voltage Phase Angle/°	Maximum Mismatch of Boundary Active Power/MW	Maximum Mismatch of Boundary Reactive Power/MW	Maximum Deviation of Node Voltage/p.u.
Independent computation	0.0011	0.0844	0.0269	0.0341	0.0125
S-SE	1.2161 × 10−9	9.1948 × 10−8	0.0018	0.0013	0.0122
A-SE	6.4501 × 10−9	9.1948 × 10−8	0.0018	0.0018	0.0122
HA-SE	2.1709 × 10−9	9.1319 × 10−8	0.0013	0.0013	0.0122

. The mismatch value refers to the deviation between the HD and LD layer estimation results for the same boundary node; smaller values indicate better coordination achieved by the algorithm under the multi-layer decoupling framework. As shown in Table 4, when each layer performs fully independent computation without any information exchange, the mismatch at boundary nodes increases significantly, and the overall error level is much higher than that of the other three algorithms. This indicates that such an approach is not suitable for coordinated operation in multi-layer distribution networks. The S-SE algorithm, leveraging a globally synchronized triggering mechanism and consistently utilizing the latest exchanged results at each iteration, significantly reduces mismatch values, and achieves strong boundary consistency. The A-SE algorithm, based on a traditional asynchronous triggering strategy, improves iterative efficiency but suffers from notable boundary inaccuracies due to the lag in lower-layer iteration sequences. In contrast, the proposed HA-SE algorithm optimizes the traditional asynchronous triggering strategy and achieves superior performance in terms of the voltage magnitude, phase angle, and power metrics. The mismatch values are significantly lower than those of the A-SE algorithm and nearly identical to those of the S-SE algorithm, confirming the effectiveness of the HA-SE method in enhancing coordination consistency under asynchronous estimation.

4.3. Algorithm Performance Under Communication Delays

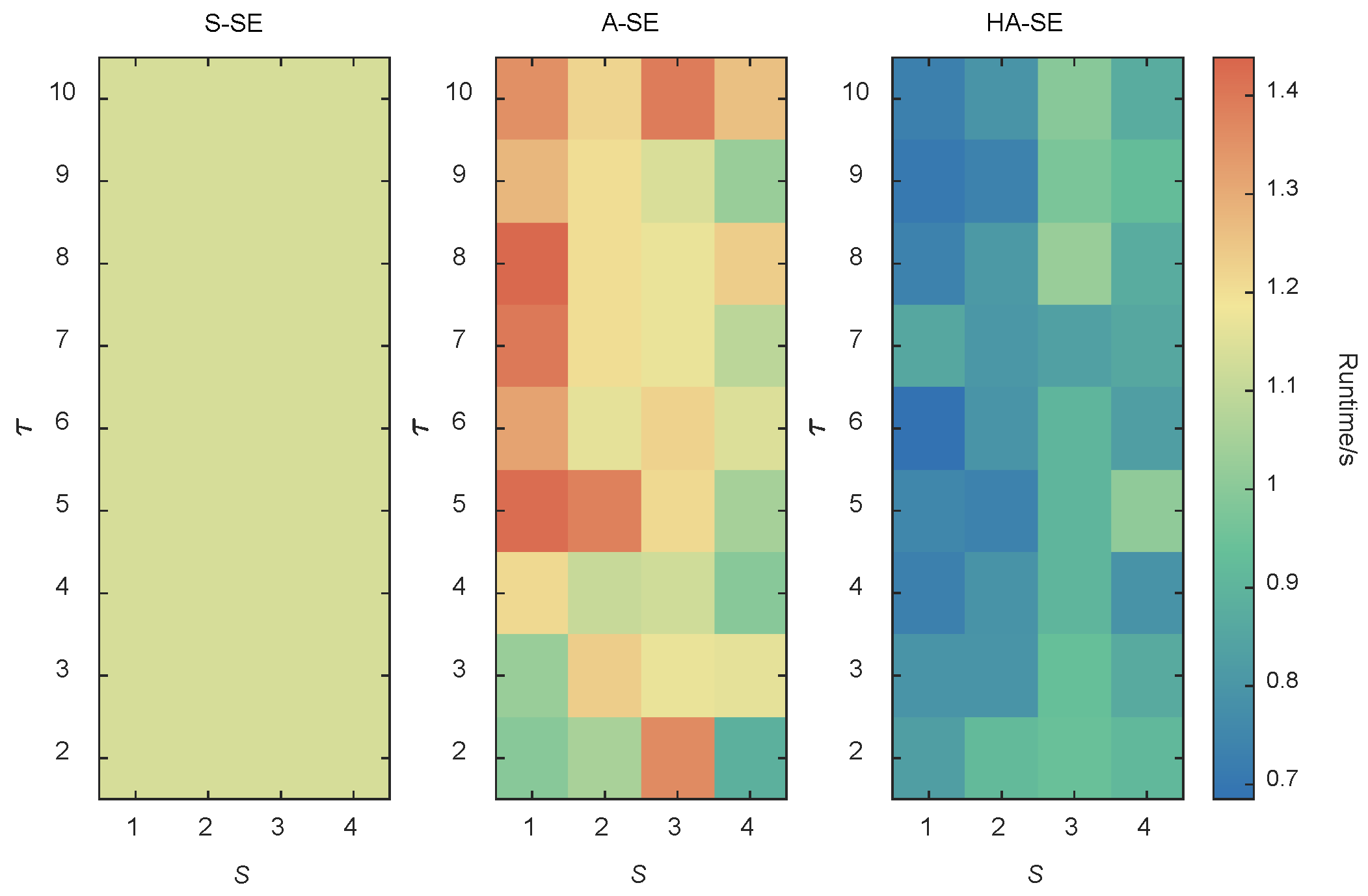
Based on the consideration of random communication delays, this section presents a comparative analysis of the runtime and parameter sensitivity of the three algorithms. Figure 5 shows the runtime comparison under different asynchronous parameter settings. It can be observed that the runtime of the S-SE algorithm remains steady at approximately 1.16 s, unaffected by changes in asynchronous parameters, which reflects the operational stability of its synchronous mechanism. In contrast, the runtime of the A-SE algorithm is more sensitive to parameter variations, fluctuating between 0.95 and 1.45 s. This indicates that although the A-SE algorithm adopts an asynchronous mechanism that can reduce waiting time to some extent, it may also suffer from resource contention or computational disorder, ultimately resulting in lower overall efficiency compared to the S-SE algorithm. By comparison, the HA-SE algorithm consistently achieves runtimes between 0.70 and 1.05 s across various parameter settings. It not only demonstrates lower computational costs, but also frequently achieves optimal or near-optimal runtimes close to 0.7 s under multiple parameter combinations, highlighting its robustness and stability. This suggests that the HA-SE algorithm is less prone to being trapped in local optima and is more capable of finding global or near-global solutions, thereby enabling efficient and stable state estimation under diverse and heterogeneous communication conditions. Overall, the proposed HA-SE algorithm significantly improves operational efficiency and exhibits superior and more stable performance.

Furthermore,

Table 5. Performance comparison of the three algorithms.

Algorithm	Average Iteration Count	Average Runtime/s	Minimum Runtime/s
S-SE	12.22	1.137	1.137
A-SE	23.86	1.230	0.997
HA-SE	14.37	0.833	0.685

presents the average number of iterations, average runtime, and minimum runtime of the three algorithms under various asynchronous parameter settings. The comparison shows that the A-SE algorithm exhibits significantly higher iteration counts and runtime in most parameter combinations compared to both the S-SE and the proposed HA-SE algorithm, highlighting its drawbacks in terms of slow convergence and low computational efficiency. However, under certain specific parameter settings, the minimum runtime of the A-SE algorithm is slightly better than that of the S-SE algorithm, indicating that it possesses some efficiency potential under favorable conditions. Nevertheless, this potential is highly dependent on the precise tuning of the asynchronous parameters, making it less stable and controllable in practical applications.

In contrast, the HA-SE algorithm demonstrates a significantly lower average iteration count than the A-SE algorithm and is only slightly higher than that of the S-SE algorithm. This indicates that the HA-SE algorithm effectively mitigates the accumulation of asynchronous communication errors and enhances convergence stability in the early stages through its broadcast transmission strategy and synchronous bootstrapping mechanism. As a result, it significantly improves the convergence performance and overall stability of asynchronous state updates. Regarding runtime, the HA-SE algorithm outperforms both the S-SE and A-SE algorithms in terms of both average and minimum values, demonstrating a clear advantage in execution efficiency. This improvement is primarily attributed to the multithreaded parallel mechanism, which enables the decoupled and concurrent execution of receiving, computation, and transmission tasks, greatly enhancing thread resource utilization and system computational throughput.

To further account for the diversity of topologies in practical distribution networks, the possibility of non-radial configurations is considered. In addition to the commonly observed radial structure, the connections between LD and HD layers may exhibit ring or meshed characteristics, where a single LD region can be connected to the HD system through multiple tie lines. To reflect such cases, a more representative system model is constructed. The HD layer adopts the IEEE 69-bus distribution system from MATPOWER [39], while the LD layer remains composed of four regions: Two of these are based on the previously modified 18-bus systems, and the other two are derived from a modified case16ci system [40], with the voltage level set to 0.4 kV and a base power of 1 MVA. This paper uses MATPOWER 8.0, which was developed by the Power Systems Engineering Research Center (PSERC) at Cornell University, Ithaca, NY, USA.

In terms of connection configuration, the two 18-bus LDs are connected to nodes 28 and 46 of the HD system, respectively. The two 16-bus LDs are connected to the HD system through multiple feeders: one group is connected to nodes 52, 53, and 59, while the other group is connected to nodes 13, 14, and 68.

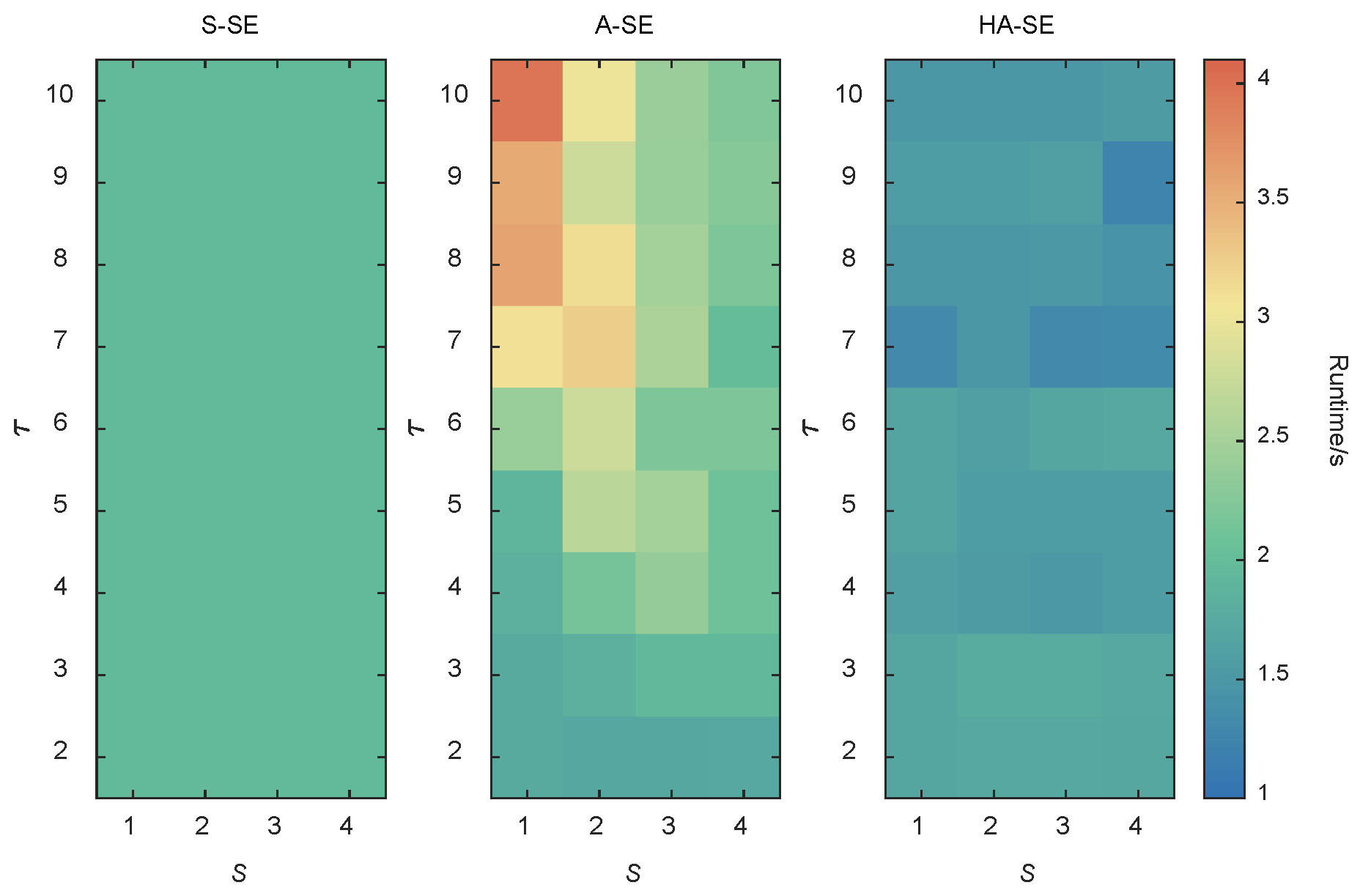
Figure 6 illustrates the runtime performance of the three algorithms under different asynchronous parameter configurations. It can be observed that the A-SE algorithm is highly sensitive to asynchronous parameters, resulting in significant fluctuations in runtime. In contrast, the proposed HA-SE algorithm exhibits relatively stable runtime across various parameter settings, with limited sensitivity to parameter perturbations, further validating the stability of its performance.

A performance comparison of the HA-SE, S-SE, and A-SE algorithms was also conducted, with

Table 6. Performance comparison of the three algorithms under ring topology configuration.

Algorithm	Average Iteration Count	Average Runtime/s	Minimum Runtime/s
S-SE	14.94	1.955	1.955
A-SE	31.46	2.408	1.717
HA-SE	16.21	1.575	1.189

presenting the average number of iterations and runtime results under different parameter settings. Although the system includes LD subsystems with ring structures, the observed trends remain consistent with those in the earlier radial LD scenarios. The A-SE algorithm still exhibits a relatively high average iteration count, whereas the proposed HA-SE algorithm, benefiting from asynchronous scheduling and boundary state broadcasting, achieves iteration counts comparable to the S-SE algorithm. Moreover, HA-SE outperforms both benchmark methods in terms of average and minimum runtime, demonstrating superior computational efficiency and concurrent control capability.

Based on the above results, it can be concluded that the proposed HA-SE algorithm not only achieves a good balance between estimation accuracy and convergence performance, but also demonstrates excellent computational efficiency. It effectively overcomes the efficiency bottlenecks and stability issues associated with traditional A-SE algorithms in complex communication environments, thereby exhibiting superior practicality and significant potential for engineering applications and deployment.

5. Conclusions

This paper proposes an asynchronous robust state estimation algorithm tailored for the multi-level structure of distribution networks. The main findings are as follows: First, in terms of estimation accuracy and robustness, the proposed algorithm achieves high estimation precision under multi-layer asynchronous conditions. It demonstrates excellent boundary consistency and strong robustness against outliers, reflecting superior accuracy and reliability in state estimation. Second, under the influence of communication delays and uneven asynchronous update frequencies, the algorithm incorporates a broadcast transmission strategy and a synchronous bootstrapping mechanism to address the issue of insufficient data coverage in the early estimation stages. This enhances the consistency of boundary information and stabilizes the convergence process, significantly reducing the number of iterations compared to traditional asynchronous methods. Finally, regarding computational efficiency, the algorithm adopts a multithreaded parallel mechanism that decouples the tasks of receiving, computation, and transmission. Across various asynchronous parameter configurations, it reduces the average runtime by approximately 30–50% compared to synchronous and conventional asynchronous methods, thereby validating its superior execution efficiency while maintaining estimation accuracy.

Future research can be pursued in several directions: First, the communication modeling capabilities can be extended by incorporating non-Gaussian delay characteristics to improve the algorithm’s adaptability in complex network environments. Second, the proposed method can be validated in practical engineering scenarios by integrating real-world distribution network topologies and measurement data. Third, for real-time applications, the asynchronous scheduling and iterative mechanisms can be further optimized to enhance the algorithm’s online operation and rapid response performance.