Abstract
This paper analyzes the possibility of using averaged models to analyze the distribution of power losses in the components of a DC-DC converter including a power module. An electrothermal averaged model of a buck converter including the IGBT module was formulated. This model takes into consideration conduction and switching losses in the mentioned components, the self-heating phenomenon in each component, and mutual thermal coupling between their sub-components. It is designed for SPICE software (version PSPICE A/D 17.4). Its correctness was verified experimentally, and the results obtained were compared with the results of analyses performed with the use of PLECS software and the IGBT module model proposed by the manufacturer. The proposed model’s results show very good accuracy. Through the use of the proposed model, the dependences of the components of power losses and the case temperature of the IGBT module and the inductor on parameters describing the control signal and load of this converter were determined. The distribution of power losses in the converter components was analyzed for selected operating conditions of the buck converter. On the basis of the results obtained, some recommendations were formulated for designers of such DC-DC converters.
1. Introduction
DC-DC converters are an important part of switch-mode power supplies [1,2,3]. They are used in both low- and high-power supply systems. The structures of DC-DC converters are described in many papers [1,4]. They include both isolated and non-isolated DC-DC converters. Each of these converters contains such components as transistors, diodes, inductors and capacitors. The number of these components and the values of their parameters may be different, but each of them is a source of power losses in the converter under consideration [5,6,7].
A very important parameter of switch-mode power supplies is their energy efficiency [8]. As demonstrated in the results from the papers [9,10,11], the value of this parameter depends on the input voltage, load current, frequency and duty cycle of the control signal. In the components of DC-DC converters, there are conduction and switching losses [12,13].
The first of these types is related to the DC characteristics of these components. For transistors and diodes, conduction losses are the result of the voltage drop on the device operating in forward mode. In turn, for capacitors and inductors, they are the effect of the occurrence of parasitic resistances of these components [14,15]. Switching losses are related to the turning on and turning off of transistors and diodes or to hysteresis losses in the cores contained in inductors and transformers [16]. Both groups of losses depend on the construction of the mentioned components and their junction temperature [11,17].
The junction temperature of semiconductor devices and passive components is higher than the ambient temperature due to the self-heating phenomenon and mutual thermal coupling between converter components placed on a common base [18,19,20]. Thermal coupling occurs, among others, between diodes and IGBTs placed in the power module [10,21] and between the winding and the core of each inductor [22,23]. A change in the junction temperature of particular components causes a change in the values of parameters characterizing power losses in these components [11,24].
The design stage of a power electronic converter requires computer simulations to control power losses in its components and to manage its thermal performance. Such simulations need appropriate software and models of all the components of the system in a form acceptable in the used software. The commonly used programs for the circuit-level analysis of power electronic systems are SPICE [25,26] and PLECS [27]. However, it is reported in many papers that due to significant differences in electrical and thermal time constants, the simulation duration is not acceptable. In the case of switch-mode power supplies, dedicated methods for increasing the speed of transient analysis simulations [28,29,30] or averaged models are used, which allow the computation of the characteristics of such systems in a steady state using DC analysis [9,10,17] or simplified transient simulations [31]. Averaged models of selected power electronic converters are described, among others, in [4,5,9,32,33]. Typically, in such models, losses in the system components are omitted [4,5] or described in a very simple form using linear resistors and omitting switching losses.
Self-heating phenomena and mutual thermal couplings can be included in computer analyses if special electrothermal models are used [19,34,35]. These models are typically based on the classical Cauer or Foster network, with the parameter estimation procedure based on 3D FEM modeling [36,37] or transient thermal impedance measurements [38]. In [10], an averaged electrothermal model of a half-bridge converter including an IGBT module was formulated. The described model takes into account thermal phenomena occurring both in this module and in passive components.
The aim of the research presented in this paper is to formulate an averaged electrothermal model of a buck DC-DC converter including an IGBT module and to analyze the influence of the operating conditions of this converter on the losses in its components and their junction temperatures. New formulas describing dynamic power losses in semiconductor devices and in the inductor cores are proposed. Additionally, a method of taking into account the influence of power losses in the core and switching losses in semiconductor devices on the energy efficiency of the modeled DC-DC converter is proposed. The elaborated model has the form of subcircuits for SPICE software. The model was verified experimentally, and the obtained results of simulations were compared with the results obtained in PLECS using the model proposed by the producer of the IGBT module. The characteristics of the converter under test in the steady state were determined using the elaborated model and the model designed for PLECS software, illustrating the influence of selected factors on power losses in each component and their junction temperature, as well as the converter’s energy efficiency. It is shown that the use of the proposed averaged model makes it possible to obtain more accurate computation results and a shorter calculation time than those obtained using PLECS software. Through the use of the formulated model, the dependence of power losses in each component was calculated using DC analysis in different operating conditions. Also, the distribution of power losses in the analyzed converter was computed and discussed.
2. Tested Buck Converter
The investigations were carried out for a non-isolated buck converter. A diagram of it is shown in Figure 1.
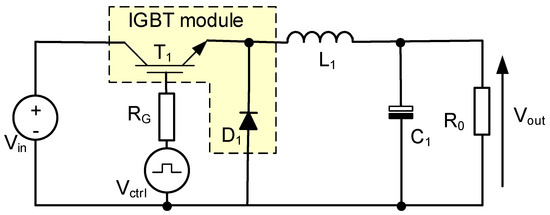
Figure 1.
Diagram of the tested non-isolated buck DC-DC converter.
The considered converter contains four components. The first of them is an IGBT module, FF50R12RT4. Two IGBTs and two diodes connected in an inverter branch are included in this module. Only one diode and one transistor from this module are used. The gate of the transistor is connected with an external source of the control signal Vctrl via a resistor RG of resistance 56 Ω. The energy storage component is an inductor L1 of inductance equal to 1.412 mH. This inductor contains a ferrite core. The capacitor C1 has a capacitance equal to 10 mF. The resistor R0 is a load of the tested DC-DC converter, whereas the voltage source Vin represents the power supply of this converter.
The transistors contained in the applied IGBT module are characterized by the following allowable parameter values: The maximum collector current amounts to 50 A, and the maximum collector–emitter voltage is 1200 V [39]. The diode in this model is characterized by a maximum forward current of 50 A, and the repetitive peak reverse voltage is equal to 1200 V. The maximum permissible power dissipated in the module is 285 W. The dimensions of the module case are 94 × 34 × 30 mm. The junction–case thermal resistance is 0.53 K/W for the transistor and 0.84 K/W for the diode. The signal controlling the transistor gate is generated using a function generator and a gate driver, IR2125. To the case of the considered module, a thermocouple was glued, and it was used to measure its temperature. The temperatures of the inductor winding and core were measured using an infrared thermometer.
During the measurements, the ambient temperature was kept constant and its value was 30 °C ± 0.5 °C. The value of the temperature was measured with the use of a classical thermometer. The RMS values of voltages and currents at the input and output of the tested DC-DC converters were measured using a power analyzer. An oscilloscope was used to control the values of switching frequency and the duty cycle.
3. Form of the Elaborated Model
The developed model of the buck converter belongs to the group of averaged electrothermal models described, e.g., in [10,17]. Such a type of model can be used to rapidly compute the characteristics of the modeled DC-DC converter in the steady state using DC analysis. Electrothermal models take into account both electrical and thermal phenomena. The proposed model has the network form designed for SPICE software. Its circuit representation is shown in Figure 2.

Figure 2.
Circuit representation of the averaged electrothermal model of the buck DC-DC converter.
All the voltages and currents in the considered network correspond to the average values of these quantities in the steady state. The converter under test is supplied from a voltage source Vin, and its load is a resistor R0. There are external components of the modeled converter.
The proposed model consists of three blocks: electrical model, power model and thermal model. In the electrical model, the controlled voltage sources ET and ER and the current source GD represent the main circuit of the averaged diode–transistor switch. The concept for the formulation of this part of the model is described, e.g., in [10]. This model is used to compute the average values of the diode current (current source GD) and the IGBT voltage (voltage sources ET and ER) in the converter operating both in CCM (Continuous Conduction Mode) and DCM (Discontinuous Conduction Mode). These voltages and currents depend on the junction temperature TjT of the transistor and temperature TjD of the diode, respectively. The model uses piece-wise linear DC characteristics of the diode and the transistor. In the description of these characteristics, the linear dependences of the forward voltage and series resistance of these semiconductor devices on their junction temperature are used [10].
The output voltage and current of the controlled sources used in the main circuit of the averaged diode–transistor switch are described as follows:
The values of parameters describing characteristics of the IGBT (VIGBT and RIGBT) and of the diode (VD and RD) are computed in the Aided block using the controlled voltage sources EViGBT, ERIGBT and ERD and a voltage source Vd. The dependence of the considered parameters on the junction temperature of these devices is considered.
The inductor L1 and resistor RL, representing the resistance of its winding, are connected in series. Resistance RL depends linearly on the winding temperature TL [23]. Resistor RC1 corresponds to the ESR of capacitor C1.
The block denoted as CCM/DCM is used to detect the mode of operation of the analyzed DC-DC converter. The equivalent duty cycle of the control signal Veu is computed in this block using a controlled voltage source Eeu. This parameter is used in descriptions of the output voltage of the voltage sources ET and ER, as well as of the output current of the current source GD, according to the formulas given in [10]. The value of Veu is not lower than the actual duty cycle of the control signal d [4,5,10]. The other elements occurring in the block CCM/DCM (controlled current source Ga, voltage source Va, resistor Ra and controlled voltage source Ex) are used to compute voltage Veu.
In addition to the components corresponding to the actual components of the modeled converter, the electrical model contains additional RS and IP components that represent additional loss components in the modeled DC-DC converter. The resistor RS represents the parasitic resistance of the connections in the converter. The controlled current source IP models an additional component of the converter input current resulting from switching losses in semiconductor devices and core losses in the inductor. The current of this source is given as follows:
where Pcore—the power dissipated in the core; PD_sw—the switching losses in the diode; and PIGBT_sw—the switching losses in the transistor. All the mentioned components of power losses are computed in the power model.
The power model is used to compute conduction and switching power losses in the components of the tested DC-DC converter. The controlled voltage sources ED_sw, ET_sw and Ecore are used to compute switching power losses in the diode PD_sw, in the transistor PIGBT_sw and in the core Pcore, respectively. In turn, the controlled voltage sources ED_DC, ET_DC and EPL are used to compute conduction power losses in diode PD_DC, in transistor PIGBT_DC and in inductor PL, respectively.
In the thermal model, the junction temperatures TjD of the diode and TjT of the IGBT, as well as the temperature of the inductor winding TL, the inductor core Tcore, and the case of the IGBT module TTh, are computed using the controlled voltage sources ETD, ETT, ETL, ETcore and ETth, respectively. This model contains only the controlled voltage sources without any RC network, because the presented model is designated for use in DC analysis.
The module case temperature Tth and the junction temperatures of the diode TjD and IGBT TjT are calculated using the following formulas:
where Ta denotes the ambient temperature, RthT is the thermal resistance of the IGBT, RthD is the thermal resistance of the diode, and Rthm is the mutual thermal resistance between the thermocouple and the IGBT and between the thermocouple and the diode. In turn, PD_DC and PIGBT_DC denote the conduction power losses in the diode and the IGBT, whereas PD_sw and PIGBT_sw are the switching power losses in these devices.
The form of Equation (7) shows that the module case temperature Tth is higher than Ta only due to the power dissipated in the semiconductor devices included in the IGBT module.
Switching losses are described using the following equations:
where f0 denotes the frequency value for which the values of parameters PD_sw0 and PIGBT_sw0 were determined, and ITav is the average value of the IGBT collector current, whereas α, αfD, αfT, αIT and ITav0 are the model parameters.
Conduction power losses in semiconductor devices are described using the following formulas:
where IDav denotes the average value of the diode current. The values of IDav and ITav are calculated in the electrical model. The values of voltages VD and VIGBT and resistances RD and RIGBT are calculated in the Aided block, whereas voltage Veu is computed in the block CCM/DCM.
The inductor winding temperature TL is the sum of three components: temperature Ta; the product of the thermal resistance of the winding and the power lost in the winding; and the product of the mutual thermal resistance between the core and winding Rthc-w and the power lost in the core Pcore. In turn, the core temperature Tcore is the sum of three components: temperature Ta; the product of the thermal resistance of the core Rthcore and the power Pcore; and the product of Rthc-w and the power lost in the winding PL.
The power PL is calculated as the product of the square of the average value of the inductor current and the resistance of its winding RL. In turn, power Pcore is described as follows:
where k is a model parameter.
The values of the model parameters describing the electrical properties of the transistor and diode were determined based on the static characteristics of these devices published by the manufacturer or derived from the measurements performed by the user. The values of the VD and RD parameters were obtained from the approximation of the characteristics of the diode operating in forward mode, and the values of the VIGBT and RIGBT parameters from the approximation of the output characteristics of the transistor corresponding to a high value of the control voltage VGE. The inductance of inductor L1 and its series resistance RL were measured using an RLC bridge. The values of resistance RC1 and the capacitance C1 of the capacitor are determined in a similar manner.
The values of the thermal resistances of the transistor RthT and diode RthD and the mutual thermal resistance Rthm between these devices were measured using the indirect electrical method described in [38]. In turn, the thermal resistances of the core Rthcore and the mutual thermal resistance between the core and the inductor winding Rthc-w were measured using the method described in [22].
The values of the coefficients appearing in the description of individual power loss components in semiconductor devices and in the inductor core were determined based on the approximation of the measured characteristics of the tested DC-DC converter. The PD_sw0 coefficient is determined for a selected value of the converter operating frequency f0 based on the measured value of the diode junction temperature and the ambient temperature at known values of PD_DC power and thermal resistance of this device. The αfD coefficient is calculated based on the measured values of PD_sw power for two values of frequency f.
The value of the coefficient PIGBT_sw0 is determined for a selected frequency value f0 and the average value of the transistor current ITav0 based on the measured value of the transistor junction temperature and the ambient temperature at known values of PIGBT_DC power and thermal resistance of this device. Based on the measured values of PIGBT_sw power for two values of frequency f and two values of transistor current ITav, values of the coefficients α, αTf and αIT are determined. The value of the coefficient k is determined based on the measured value of the inductor core temperature Tcore at a fixed temperature value Ta and fixed values of the frequency f and the duty cycle d of the control signal and the supply voltage of converter Vin.
4. Results
Through the use of the buck converter model presented in the previous section, a series of simulations of the considered converter was performed. The influence of supply voltage, load resistance and parameters of the control signal on the converter characteristics was considered. Then, simulations in identical conditions were performed in PLECS software using the model of the IGBT module proposed by its creator [40] and the models of the capacitor and the inductor containing their series resistances. The thermal model of the module was extended by the elements responsible for heat transport from the case to the ambient environment. In the case of the inductor, core losses were omitted, because the parameters describing its B(H) dependence are out of the range formally acceptable by PLECS. The magnetic force in saturation cannot be higher than the product of the coercive magnetic force and the number 20. For the used ferromagnetic core, the value of the coercive magnetic force is 50 A/m, whereas the saturation magnetic force amounts to 4 kA/m.
It is worth noting that PLECS makes it possible to model the nonlinearity of the magnetization curve, but it is impossible to take into account the influence of the core losses on the characteristics of the tested switched-mode power converters in a simple manner [41]. As described in [42], the possibility of building complex magnetic components in a special magnetic circuit domain based on the permeance–capacitance analogy was not explored in this paper.
The steady-state results of these simulations are shown in the figures below. In each of these figures, the solid lines denote the simulation results obtained using the averaged electrothermal model and DC analysis, and the dashed lines represent the simulation results obtained using PLECS software, whereas the points indicate the measurement results.
Section 4.1 includes characteristics showing the influence of the control signal parameters and load resistance on the converter output voltage, energy efficiency and temperature of selected components of the tested converter. Section 4.2 presents the calculated dependences of the components of power losses in the converter components on the output current and frequency. In Section 4.3, the distribution of power losses in the tested converter in selected operating conditions is analyzed.
4.1. Characteristics of the Buck Converter
Figure 3, Figure 4, Figure 5 and Figure 6 present the results of the tests carried out at the input voltage Vin = 325 V and the control signal frequency f = 20 kHz. These tests were carried out in a wide range of load current Iout changes at selected values of the control signal duty cycle d.
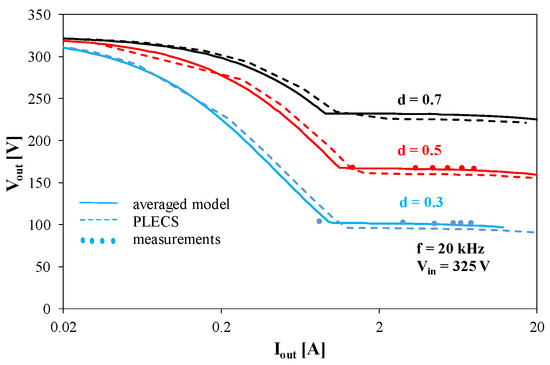
Figure 3.
Output characteristics of the tested converter operating at f = 20 kHz.

Figure 4.
Dependence of the IGBT module temperature (solid lines) and the IGBT junction temperature (dashed lines) on the converter output current at f = 20 kHz.
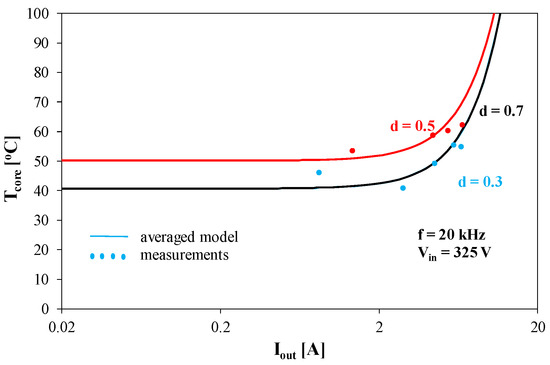
Figure 5.
Dependence of the inductor core temperature on the output current of the tested converter operating at f = 20 kHz.
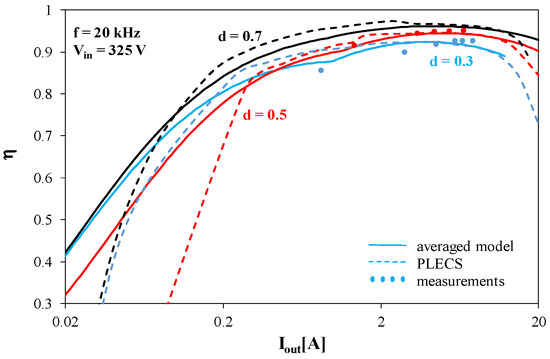
Figure 6.
Dependence of the energy efficiency of the tested DC-DC converter on its output current at f = 20 kHz.
Figure 3 illustrates the influence of the duty cycle d on the output characteristics of the considered converter.
Figure 3 shows that the proposed model provides a good match between the calculations performed using SPICE and PLECS and the measurement results. The discrepancies between the results of measurement and computations do not exceed 2% for the proposed model and 8% for the PLECS model. An increase in the d coefficient value causes an increase in the output voltage Vout of the tested converter. For the used values of load current Iout, the tested converter operates in both CCM and DCM. The critical current below which the converter operates in DCM is about 1 A and decreases with an increase in the parameter d. For high Iout current values, a drop in the Vout voltage value is visible. This is caused by voltage drops on the converter components.
Figure 4 presents the dependence of the temperature of the IGBT module (solid lines) and the junction temperature of the transistor included in this module (dashed lines) on current Iout.
The junction and case temperatures of the considered IGBT module increase with an increase in the coefficient d. The values of TjT are higher than the values of TTh for all considered converter operating conditions. The values of temperature Tth obtained with the PLECS computations are underestimated by some Celsius degrees for low values of Iout and overestimated for high values of this current. The values of temperature Tth obtained using the averaged model differ from the measurement results by no more than 5 °C. The values of parameter d weakly influence the values of temperature Tth.
Figure 5 shows the inductor core temperature Tcore as a function of current Iout. The results of computations performed in PLECS software are not presented in this figure, because the thermal properties of the inductor core were not included in the available model of this device.
The presented curves show that at low values of Iout current, the core temperature does not depend on the value of this current, because the main reason for the increase in the core temperature is a hysteresis loss proportional to the converter input voltage of 325 V. The curves Tcore(Iout) obtained for d = 0.3 and d = 0.7 overlap. The influence of the d factor value on Tcore temperature is visible in this operating range. For higher values of Iout current, an increase in the Tcore temperature value is visible as a function of this current. This is caused by an increase in losses in the inductor winding and mutual thermal couplings between the winding and the inductor core [22].
Figure 6 illustrates the influence of current Iout on the energy efficiency η of the converter. For the computations performed using SPICE software and for the measurements, the value of η is calculated as the quotient of the power dissipated in the load and the power taken from the power supply. In contrast, due to the specific operation of PLECS, in which each component of the losses is calculated separately and used only to compute the device junction temperature, the other manner of calculation of η is used. These calculations were performed using the following formula:
where Pinavg denotes the average value of the input power of the tested DC-DC converter, whereas ΣPloss denotes the sum of average values of the power losses in the converter components. The sum contains conduction and switching losses in the diode and in the transistor, as well as the power losses in the inductor winding and the core. The core losses are calculated using Formula (12).
The dependences η(Iout) obtained using the measurements and computations have maximums at Iout equal to about 6 A. The value of this maximum increases when the coefficient d increases and reaches as much as 96% at d = 0.7. The decrease in energy efficiency in the range of high currents is related to an increase in losses in semiconductor devices. The dependences η(Iout) obtained using PLECS software are consistent with the measurement results only for high values of the output current, whereas in the range of low values of Iout, the calculated values of energy efficiency are underestimated. The obtained results suggest that the model of the tested DC-DC converter implemented in PLECS software describes the power losses in a simplified form. In contrast, the results obtained using the considered averaged model fit well with the measurement results.
Figure 7, Figure 8, Figure 9 and Figure 10 present the results of the tests carried out at the input voltage Vin = 325 V and the control signal duty cycle d = 0.5. These tests were performed for different values of switching frequency f at selected values of load resistance R0.

Figure 7.
Dependence of the IGBT module temperature (solid lines) and the IGBT junction temperature (dashed lines) on frequency at d = 0.5.

Figure 8.
Dependence of the inductor core temperature on frequency at d = 0.5.
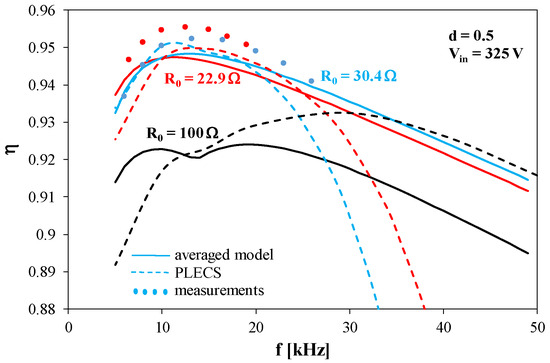
Figure 9.
Dependence of the converter energy efficiency on frequency at d = 0.5.

Figure 10.
Dependence of the IGBT module temperature (solid lines) and the IGBT junction temperature (dashed lines) on input voltage at d = 0.5 and R0 = 25 Ω.
Figure 7 shows the dependence of the IGBT module temperature and the transistor junction temperature on frequency.
As can be seen, both temperatures considered increase as a function of frequency and decrease as a function of load resistance R0. Similarly, the difference between temperatures TjT and TTh increases with increasing switching frequency, even reaching 20 °C. It is worth noting that with an identical value of load resistance, the temperature value of the IGBT module increases by as much as 120 °C when changing the frequency from 5 to 40 kHz. Of course, the increase in Tth due to an increase in frequency decreases with an increase in R0. For high values of frequency, the results of calculations performed using PLECS software are overestimated in comparison with the results obtained using SPICE software, even by 100 °C.
Figure 8 shows the effect of frequency on the inductor core temperature.
With an increase in frequency, the inductor core temperature decreases monotonically. It is worth noting that a change in the load resistance value in the considered range results in only a small change in the Tcore temperature value, visible especially in the higher-frequency range. The presented characteristics cannot be obtained using PLECS software because the properties of the inductor core in this software are omitted.
Figure 9 presents the dependence of the energy efficiency of the considered converter on frequency.
The dependences η(f) obtained from the measurements and calculations have a maximum. With an increase in resistance R0, the frequency at which this maximum is observed increases. The value of energy efficiency increases for lower values of resistance R0. The efficiency rapidly decreases in the range of low frequency due to the DCM operation of the tested converter. The considered dependences obtained using PLECS software show a fast decrease in the range of high frequency and low load resistance. The obtained results suggest that the switching losses in semiconductor devices are overestimated.
Analyses were also carried out to illustrate the influence of the input voltage on the temperatures of individual components of the converter under consideration, its energy efficiency and the power lost in these components. The results of these considerations are presented in Figure 10, Figure 11 and Figure 12. The calculations were carried out for selected values of frequency f, with d = 0.5 and R0 = 25 Ω.

Figure 11.
Dependence of the core temperature on the input voltage at d = 0.5 and R0 = 25 Ω.

Figure 12.
Dependence of energy efficiency on the input voltage of the converter at d = 0.5 and R0 = 25 Ω.
Figure 10 shows the dependence of the IGBT module temperature Tth and temperature TjT on Vin voltage.
Both temperature TjT and temperature TTh increase as a function of voltage Vin. The changes in the values of these temperatures with an increase in voltage Vin in the considered range are the biggest for the highest of the considered converter switching frequencies. In these conditions, they even exceed 100 °C. The values of temperature Tth obtained using PLECS show much greater changes than the values of this temperature obtained using the proposed averaged model implemented in SPICE. The differences between the results obtained using both the considered models even exceed 100 °C.
Figure 11 shows the effect of frequency on the dependence of the core temperature on the input voltage.
The obtained Tcore(Vin) dependencies are increasing functions. An increase in frequency results in a decrease in Tcore. For the lowest of the considered frequency values, the change in the core temperature value with changes in Vin voltage in the considered range exceeds as much as 100 °C. This means that in order to limit the core temperature, it is advantageous to set a higher value of the converter operating frequency.
Figure 12 presents the dependence of the energy efficiency of the considered converter on the input voltage for selected values of frequency.
It can be seen in Figure 12 that for each of the considered switching frequency values, one can find the voltage value Vin for which the dependence η(Vin) takes the highest value. According to the results obtained using SPICE, this optimal voltage value Vin increases with increasing frequency. In contrast, the dependence η(Vin) obtained using PLECS shows the opposite tendency, because this software overestimates the switching losses in semiconductor devices.
The results of the investigations presented in this section show that the proposed averaged electrothermal model of a buck converter makes it possible to obtain good accuracy in modeling characteristics that describe the electrical and thermal properties of this converter. Therefore, this model is used in the subsequent portion of this article to analyze the distribution of power losses between semiconductor and magnetic components of this DC-DC converter.
4.2. Dependence of the Components of Power Losses on Operating Conditions
On the basis of the electrothermal DC analyses of the tested DC-DC converter performed using the averaged electrothermal model of this converter, the components of power losses were computed. The dependences of these power losses on the converter operating conditions are presented in this subsection. All presented results of computations correspond to the steady state.
In all the figures in this subsection, the solid lines denote the loss components related to switching, and the dashed lines indicate the loss components related to conduction. The particular loss components are marked with the following symbols: PL—inductor winding losses; Pcore—inductor core losses; PD_DC—diode conduction losses; PIGBT_DC—transistor conduction losses; PD_sw—diode switching losses; and PIGBT_sw—transistor switching losses.
Figure 13 and Figure 14 present the influence of current Iout on the above-mentioned components of power losses. The results shown in Figure 13 correspond to d = 0.3, whereas the results presented in Figure 14 correspond to d = 0.5. The computations were performed for f = 20 kHz.

Figure 13.
Dependences of the components of power losses in the buck converter on its output current at f = 20 kHz and d = 0.3.
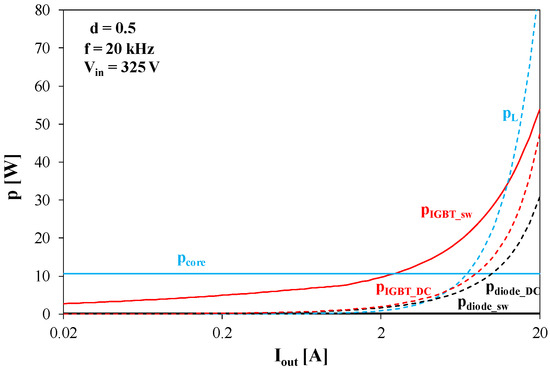
Figure 14.
Dependences of the components of power losses in the buck converter on its output current at f = 20 kHz and d = 0.5.
Through an analysis of the graphs presented in Figure 13 and Figure 14, it can be seen that the switching losses, PD_sw, of the diode are much lower than the other loss components. The losses Pcore in the core have a fixed value over the entire range of Iout current changes, and their value is higher for a higher value of the d coefficient. In the range of low Iout current values, the core losses are the dominant component of the losses in the tested converter. The conduction losses PD_DC of the diode and PIGBT_DC of the transistor, as well as the losses in the inductor winding PL, increase with an increase in Iout current. It is worth noting that the conduction losses in the diode and the transistor have similar values. The switching losses PIGBT_sw in the transistor increase as a function of Iout current and at Iout values exceeding several amps are the dominant component of the losses in the converter. Through a comparison of the results presented in Figure 13 and Figure 14, it can be seen that an increase in the value of the duty cycle d causes a significant increase in the value of all the loss components and, in particular, an increase in the share of losses in the inductor winding and conduction losses of semiconductor devices in the total losses in the converter.
Figure 15 and Figure 16 present the influence of f on the considered components of power losses. The results presented in Figure 15 refer to the operation of the converter with load resistance R0 = 22.9 Ω, whereas the results in Figure 16 refer to operation at R0 = 100 Ω.
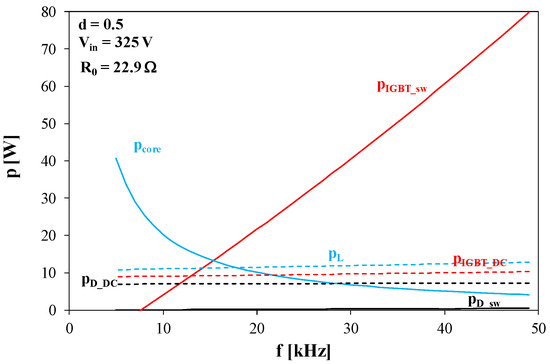
Figure 15.
Dependences of the components of power losses in the buck converter on frequency at R0 = 22.9 Ω and d = 0.5.

Figure 16.
Dependences of the components of power losses in the buck converter on frequency at R0 = 100 Ω and d = 0.5.
In both the figures, it can be seen that the dominant components of power losses are Pcore and PIGBT_sw. The power Pcore decreases as a function of f, and its value practically does not depend on the value of R0. In turn, the power PIGBT_sw linearly increases as a function of frequency, and an increase in the value of R0 results in a decrease in the nominal value of PIGBT_sw. The conduction losses of semiconductor devices and the losses in the inductor winding PL practically do not change as a function of frequency, but their values decrease with an increase in resistance R0. Switching losses in the diode are at a negligible level.
The influence of Vin voltage on the components of power losses is shown in Figure 17 for frequency f = 10 kHz and in Figure 18 for frequency f = 40 kHz.

Figure 17.
Dependences of the components of power losses in the buck converter on the input voltage at f = 10 kHz, R0 = 25 Ω and d = 0.5.
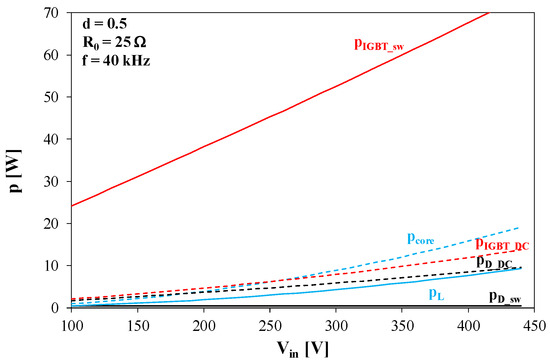
Figure 18.
Components of the power losses in the buck converter with the input voltage at f = 40 kHz, R0 = 25 Ω and d = 0.5.
In Figure 17 and Figure 18, it is shown that an increase in Vin voltage causes an increase in all the components of power losses. At the lowest of the considered switching frequencies, the dominant component of the power losses is Pcore, while for the highest of these frequencies, the dominant component is the switching losses of the transistor. The remaining components of the losses do not change significantly with the changes in frequency. The presented dependences indicate that the supply voltage is a factor that significantly affects the power losses in the individual components of the converter, and this affects its energy efficiency.
4.3. Power Loss Distribution at Selected Operating Conditions
To illustrate the influence of the operating point on the participation of each component of the power losses in the total power losses in the tested buck converter, the pie diagrams shown below were created. Figure 19 shows the distribution of power losses in the tested buck converter operating at different values of Vin and f. The presented results were obtained at load resistance R0 = 15 Ω and d = 0.5.
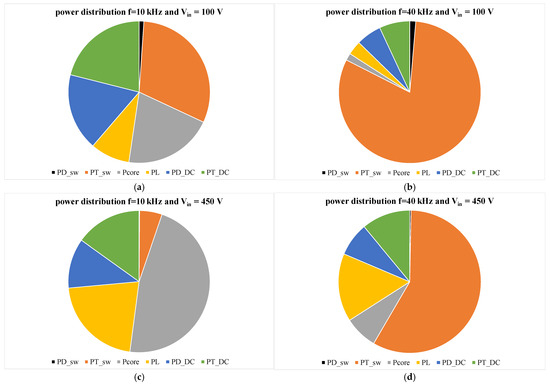
Figure 19.
Distribution of the power losses in the tested DC-DC converter in selected operating conditions: (a) f = 10 kHz and Vin = 100 V, (b) f = 40 kHz and Vin = 100 V, (c) f = 10 kHz and Vin = 450 V, (d) f = 40 kHz and Vin = 450 V.
As can be seen, the distribution of losses in particular converter components changes with a change in the frequency and input voltage. In each of the considered cases, switching losses in the diode are negligible. At a low value of Vin voltage and low frequency (Figure 19a), the most important losses are the transistor switching losses, but the conduction losses of semiconductor devices and the losses in the inductor core together constitute over 60% of the total losses in the converter. With an increase in f (Figure 19b), the transistor switching losses constitute over 80% of all the losses in the converter. At a high value of Vin, at low values of f (Figure 19c), almost half of the losses in the converter are Pcore power, while at a high switching frequency (Figure 19d), less than a half of the losses are PT_sw power.
Through a comparison of the results presented in Figure 19, it can be concluded that in the analyzed DC-DC converter operating at high frequency, switching losses in the transistor dominate. At low frequencies, Pcore values are of significant importance. An increase in the input voltage value results in an increase in Iout, which translates into an increase in the share of conduction losses in the semiconductor devices and in the inductor.
5. Conclusions
This paper proposes the use of an averaged electrothermal model of a buck converter in calculations of power losses in the components of this converter. The use of this model allows the determination of the characteristics of the DC-DC converter under consideration, taking into account self-heating and mutual thermal couplings between the dies in the IGBT module. It was shown that these characteristics are consistent with the characteristics obtained from the measurements. The characteristics computed using PLECS software, presented for comparison, show that this software makes it possible to properly compute the values of the tested converter output voltage and the temperature of the module; however, the models of the inductors used in this software are too simple. Therefore, the power losses and η of the tested converter should be calculated taking into account the proposed description of the core losses.
The main advantages of the proposed averaged electrothermal model are high accuracy and short computation time. Through the use of this model, the characteristics of the tested converter can be obtained using fast DC analysis. The use of PLECS necessitates transient analysis, which makes it possible to obtain only coordinates of one point in the characteristics after each analysis. This means that the use of the proposed averaged model makes it possible to obtain more accurate results in a shorter time period than PLECS software.
In the previous sections, the results of the research illustrating the influence of selected factors on power losses in individual components of the buck converter were presented. The analyses carried out showed that in different operating conditions of the DC-DC converter under consideration, different loss components determine its energy efficiency. For example, for fixed values of frequency and input voltage and low load current values, the greatest power losses occur in the inductor core, while for high values of this current, the IGBT transistor switching losses and semiconductor device conduction losses dominate, which increase as a function of this current. In turn, for a fixed value of load resistance, losses in the inductor core decrease as a function of frequency, and the transistor switching losses increase as a function of frequency. The remaining loss components practically do not depend on frequency. The value of the converter input voltage is also of significant importance. All the power loss components increase with an increase in this voltage.
It is also worth noting that the presented method of analyzing the properties of the considered class of DC-DC converters allows for a very simple determination of the converter operating conditions (frequency, input voltage, load current) at which there will be no risk of excessive temperature increase in individual components of the converter and at which it will be possible to obtain an acceptable value of energy efficiency. The short time duration of simulations, counted in single milliseconds, is also important. It ensures high calculation efficiency.
The presented results and analysis method may be useful for designers of switched-mode power converters. They can also be a tool with which to analyze the influence of selected factors on the properties of such a system and other DC-DC converters. Through the use of the proposed averaged electrothermal model of a buck converter, it is possible to rapidly select a device, the properties of which significantly limit its energy efficiency.
Author Contributions
Conceptualization (K.G. and P.G.); methodology (K.G. and P.G.); investigation (K.G. and P.G.); writing—original draft preparation (K.G. and P.G.); writing—review and editing (K.G. and P.G.); visualization (K.G.); supervision (K.G.). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The presented experimental data can be made available on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Rashid, M.H. Power Electronic Handbook; Academic Press: Cambridge, MA, USA; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Billings, K.; Morey, T. Switch-Mode Power Supply Handbook; McGraw-Hill Companies: New York, NY, USA, 2011. [Google Scholar]
- Kazimierczuk, M. Pulse-Width Modulated DC-DC Power Converters; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Ericson, R.; Maksimovic, D. Fundamentals of Power Electronics; Springer Nature: Cham, Switzerland, 2020. [Google Scholar]
- Basso, C. Switch-Mode Power Supply SPICE Cookbook; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Wei, K.; Lu, D.D.-C.; Zhang, C.; Siwakoti, Y.; Soon, J.L.; Yao, Q. Modeling and Analysis of Thermal Resistances and Thermal Coupling between Power Devices. IEEE Access 2019, 66, 4302–4308. [Google Scholar] [CrossRef]
- Forouzesh, M.; Siwakoti, Y.P.; Gorji, S.A.; Blaabjerg, F.; Lehman, B. Step-Up DC-DC converters: A comprehensive review of voltage-boosting techniques, topologies, and applications. IEEE Trans. Power Electron. 2017, 32, 9143–9178. [Google Scholar] [CrossRef]
- Sabetfar, T.; Hosseinpour, M.; Seifi, A.; Heydari-Doostabad, H. Switched Capacitor Non-Isolated Step-up DC-DC Converter with Low Voltage Stress of Devices and High Efficiency. IEEE Trans. Power Electron. 2025; early access. [Google Scholar]
- Martínez-Caballero, L.; Kot, R.; Milczarek, A.; Malinowski, M. Converter Averaging Approach for Modeling a Residential Supply Subsystem. In Proceedings of the 2023 IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14–16 June 2023. [Google Scholar]
- Górecki, K.; Górecki, P. Electrothermal averaged model of a half-bridge DC-DC converter containing a power module. Electronics 2024, 13, 3662. [Google Scholar] [CrossRef]
- Górecki, K. Influence of parasitic elements and operating conditions of semiconductor switches on power losses and the junction temperature of these switches. Energies 2023, 16, 5803. [Google Scholar] [CrossRef]
- Li, Y.; Ruan, X.; Zhang, L.; Dai, J.; Jin, Q. Optimized Parameters Design and Adaptive Duty-Cycle Adjustment for Class e DC-DC Converter with on-off Control. IEEE Trans. Power Electron. 2019, 34, 7728–7744. [Google Scholar] [CrossRef]
- Ayachit, A.; Kazimierczuk, M.K. Averaged small-signal model of PWM DC-DC converters in CCM including switching power loss. IEEE Trans. Circuits Syst. II—Exp. Briefs 2019, 66, 262–266. [Google Scholar] [CrossRef]
- Vipin, V.B.; Mohan, N. Sensitivity Analysis of the High-Frequency-Link MMC to DC Link Voltage Ripples in a Back-to-Back Connected MMC-Based Power Electronic Transformer. IEEE Trans. Power Electron. 2025, 40, 8691–8708. [Google Scholar] [CrossRef]
- Van Dijk, E.; Spruijt, H.J.N.; O’Sullivan, D.M.; Klaassens, J.B. PWM-Switch Modeling of DC-DC Converters. IEEE Trans. Power Electron. 1995, 10, 659–665. [Google Scholar] [CrossRef]
- Bakri, R.; Corgne, G.; Margueron, X. Thermal Modeling of Planar Magnetics: Fundamentals, Review and Key Points. IEEE Access 2023, 11, 41654–41679. [Google Scholar] [CrossRef]
- Górecki, P. Electrothermal Averaged Model of a Diode–IGBT Switch for a Fast Analysis of DC–DC Converters. IEEE Trans. on Power Electronics 2022, 37, 13003–13013. [Google Scholar] [CrossRef]
- Schweitzer, D.; Ender, F.; Hantos, G.; Szabo, P.G. Thermal transient characterization of semiconductor devices with multiple heat-sources—Fundamentals for a new thermal standard. Microelectron. J. 2015, 46, 174–182. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.D.-C.; Siwakoti, Y.P. Electro-Thermal Modeling of a Boost Converter Considering Device Self-heating. In Proceedings of the 2020 IEEE Applied Power Electronics Conference and Exposition (APEC), New Orleans, LA, USA, 15–19 March 2020. [Google Scholar]
- Azer, P.; Rodriguez, R.; Guo, J.; Gareau, J.; Bauman, J.; Ge, H.; Bilgin, B.; Emadi, A. Time-Efficient Integrated Electrothermal Model for a 60-kW Three-Phase Bidirectional Synchronous DC-DC Converter. IEEE Trans. Ind. Appl. 2020, 56, 654–668. [Google Scholar] [CrossRef]
- Qian, C.; Gheitaghy, A.M.; Fan, J.; Tang, H.; Sun, B.; Ye, H.; Zhang, G. Thermal Management on IGBT Power Electronic Devices and Modules. IEEE Access 2017, 6, 12868–12884. [Google Scholar] [CrossRef]
- Górecki, K.; Detka, K.; Górski, K. Compact thermal model of the pulse transformer taking into account nonlinearity of heat transfer. Energies 2020, 13, 2766. [Google Scholar] [CrossRef]
- Górecki, K.; Górecki, P. SPICE-aided nonlinear electrothermal modeling of an IGBT module. Electronics 2023, 12, 4588. [Google Scholar] [CrossRef]
- Zhang, Y.; Si, J.; Wang, X.-T.; Li, J.; Zhao, H. Stability Analysis of Buck Converter Based on Passivity-Based Stability Criterion. App. Sci. 2024, 14, 1755. [Google Scholar] [CrossRef]
- Rashid, M.H. Spice for Power Electronics and Electric Power; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Kimhi, D.; Ben-Yaakov, S.A. SPICE Model for Current Mode PWM Converters Operating Under Continuous Inductor Current Conditions. IEEE Trans. Power Electron. 1991, 6, 281–286. [Google Scholar] [CrossRef]
- Allmeling, J.H.; Hammer, W.P. PLECS—Piece-wise Linear Electrical Circuit Simulation for Simulink. In Proceedings of the IEEE 1999 International Conference on Power Electron and Drive Systems PEDS’99, Hong Kong, China, 27–29 July 1999. [Google Scholar]
- Catalano, A.P.; Riccio, M.; Codecasa, L.; Magnani, A.; Romano, G.; d’Alessandro, V.; Maresca, L.; Rinaldi, N.; Breglio, G.; Irace, A. Model-Order Reduction Procedure for Fast Dynamic Electrothermal Simulation of Power Converters. Applications in Electronics Pervading Industry, Environment and Society. Lect. Notes Electr. Eng. 2017, 512, 81–87. [Google Scholar]
- Ceccarelli, L.; Kotecha, R.; Iannuzzo, F.; Mantooth, A. Fast Electro-thermal Simulation Strategy for SiC MOSFETs Based on Power Loss Mapping. In Proceedings of the IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018. [Google Scholar]
- Bryant, A.; Parker-Allotey, N.A.; Hamilton, D.; Swan, I.; Mawby, P.A.; Ueta, T.; Nishijima, T.; Hamada, K. A Fast Loss and Temperature Simulation Method for Power Converters, Part I: Electrothermal Modeling and Validation. IEEE Trans. Power Electron. 2012, 27, 248–257. [Google Scholar] [CrossRef]
- Cheng, T.; Lu, D.; Siwakoti, Y. A MOSFET SPICE Model with Integrated Electro-Thermal Averaged Modeling, Aging, and Lifetime Estimation. IEEE Access 2021, 9, 5545–5554. [Google Scholar] [CrossRef]
- Vorperian, V. Simplified analysis of PWM converters using model of PWM switch: Continuous conduction mode. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 490–496. [Google Scholar] [CrossRef]
- Vorperian, V. Simplified analysis of PWM converters using model of PWM switch. II. Discontinuous conduction mode. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 497–505. [Google Scholar] [CrossRef]
- Bryant, B.; Kazimierczuk, M.K. Voltage-Loop Power-Stage Transfer Functions with MOSFET Delay for Boost PWM Converter Operating in CCM. IEEE Trans. Ind. Electron. 2007, 54, 347–353. [Google Scholar] [CrossRef]
- Wu, R.; Wang, H.; Pedersen, K.B.; Ma, K.; Ghimire, P.; Iannuzzo, F.; Blaabjerg, F. A temperature-dependent thermal model of IGBT modules suitable for circuit-level simulations. IEEE Trans. Ind. Appl. 2016, 52, 3306–3314. [Google Scholar] [CrossRef]
- d’Alessandro, V.; Codecasa, L.; Catalano, A.P.; Scognamillo, C. Circuit-Based Electrothermal Simulation of Multicellular SiC power MOSFETs using FANTASTIC. Energies 2020, 13, 4563. [Google Scholar] [CrossRef]
- Bahman, A.S.; Ma, K.; Blaabjerg, F. A novel 3D thermal impedance model for high power modules considering multi-layer thermal coupling and different heating/cooling conditions. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition—APEC, Charlotte, NC, USA, 15–19 March 2015; pp. 1209–1215. [Google Scholar]
- Górecki, K.; Górecki, P.; Zarębski, J. Measurements of parameters of the thermal model of the IGBT module. IEEE Trans. Instrum. Meas. 2019, 68, 4864–4875. [Google Scholar] [CrossRef]
- Technical Information IGBT Module FF50R12RT4, Infineon. 2013. Available online: https://www.infineon.com/dgdl/Infineon-FF450R12KE4-DS-v02_02-EN.pdf?fileId=db3a3043156fd57301161a1705031df8 (accessed on 2 July 2025).
- PLECS Model of FF50R12RT4 Module. Available online: https://www.infineon.com/dgdlc/en?dcId=8a8181663431cb50013431cb500b0000&downloadTitle=Infineon-FF50R12RT4-PLECS-SimulationModels-v01_00-EN.zip&download=L2RnZGwvSW5maW5lb24tRkY1MFIx MlJUNC1QTEVDUy1TaW11bGF0aW9uTW9kZWxzLXYwMV8wMC1FTi56aXA/ZmlsZUlkPTU1NDZkNDYyNzNhNTM2N mYwMTczZjFhMmM5MTEwMzViJmRhPXQ= (accessed on 2 July 2025).
- Introduction to the PLECS Magnetic Domain, Tutorial Version 1.0, PLEXIM. Available online: https://plexim.com/sites/default/files/tutorials_categorized/plecs/magnetic_domain.pdf (accessed on 2 July 2025).
- Magnetics. Designing Complex Magnetic Components. PLEXIM. Available online: https://www.plexim.com/products/plecs/magnetic (accessed on 2 July 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).