Novel Data-Driven PDF Modeling in FGM Method Based on Sparse Turbulent Flame Data
Abstract
1. Introduction
2. Modeling Methodology
- When reaches its minimum value of 0, = 0. In this case, there are no turbulent fluctuations at this point in the flow field, indicating laminar flow conditions.
- When reaches its maximum value of 1, approaches infinity. For mixture fraction , it indicates that the local mixture exists in either pure fuel or pure oxidizer states. The probability of each state is determined by the value of . For progress variable , it indicates that the local mixture exists in either unburnt or burnt states, which means the flame is infinitely thin.
- When equals either 0 or 1, must be 0. Under these conditions, the physical states are the same regardless of the value of .
2.1. Conditional PDF
2.2. Machine Learning Methods
2.2.1. Random Forest
2.2.2. XGBoost
2.2.3. Support Vector Regression
2.2.4. Gaussian Process Regression
2.2.5. Deep Neural Network
3. Dataset for Machine Learning
3.1. Sandia CO/H2/N2 Jet Flame
3.2. Sydney Swirling Flame
3.3. Data Processing
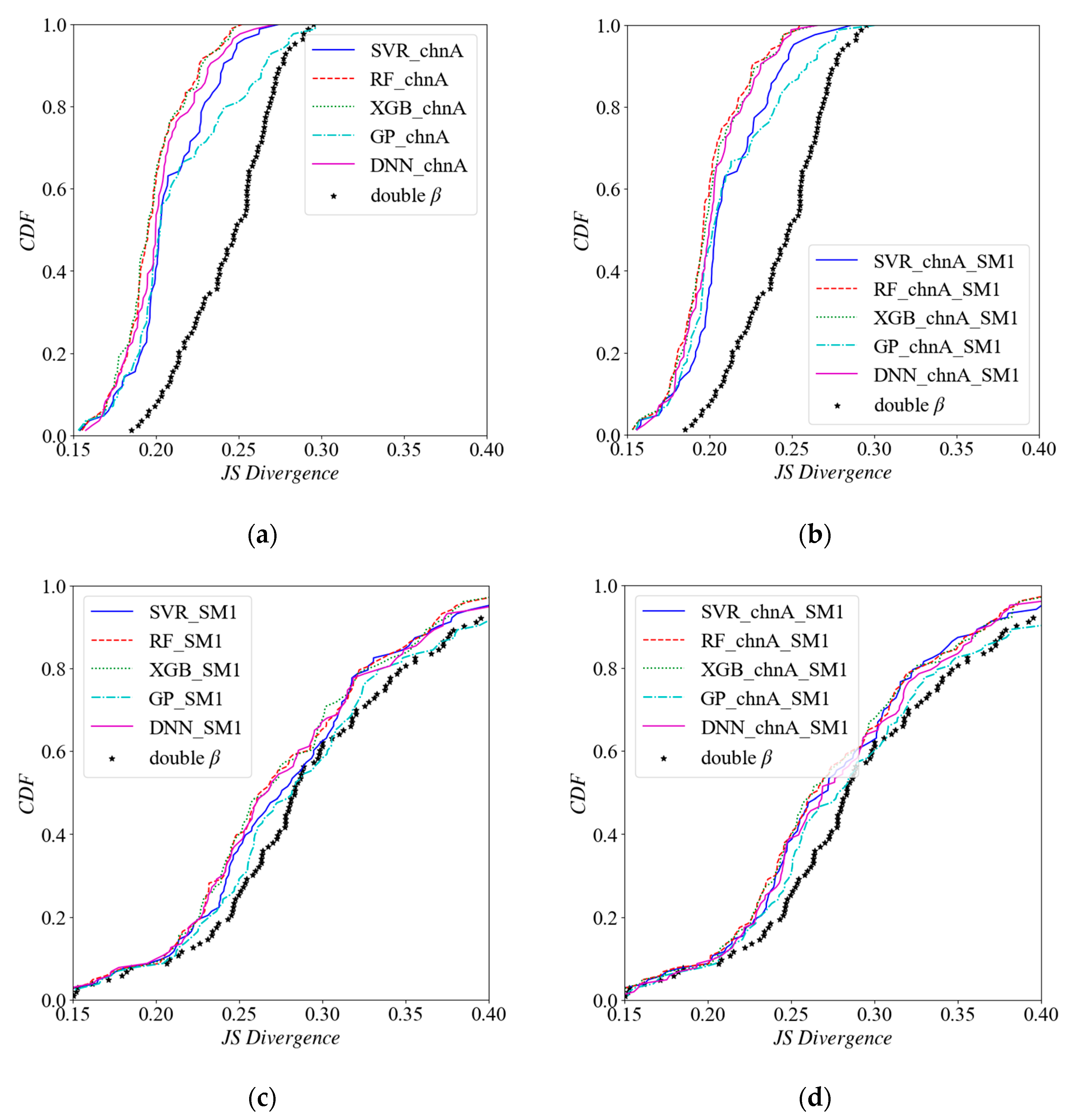
4. Result Analysis
4.1. Direct Comparison of Model Predictions
4.2. Comparison of Joint PDF
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pope, S.B. Small Scales, Many Species and the Manifold Challenges of Turbulent Combustion. Proc. Combust. Inst. 2013, 34, 1–31. [Google Scholar] [CrossRef]
- van Ojien, J.A.; de Goey, L.P.H. Modelling of Premixed Laminar Flames Using Flamelet-Generated Manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef]
- Zhang, G.; Wu, Y.; Wu, J.; Zhang, Y.; Zhang, H. State of the Art and Challenges of Flamelet Method in Gas Turbine Combustor Simulation. J. Tsinghua Univ. (Sci. Technol.) 2023, 63, 505–520. [Google Scholar]
- Pierce, C.D.; Moin, P. Progress-Variable Approach for Large-Eddy Simulation of Non-Premixed Turbulent Combustion. J. Fluid Mech. 2004, 504, 73–97. [Google Scholar] [CrossRef]
- Peters, N. Laminar Diffusion Flamelet Models in Non-Premixed Turbulent Combustion. Prog. Energy Combust. Sci. 1984, 10, 319–339. [Google Scholar] [CrossRef]
- Cook, A.W.; Riley, J.J. A Subgrid Model for Equilibrium Chemistry in Turbulent Flows. Phys. Fluids 1994, 6, 2868–2870. [Google Scholar] [CrossRef]
- Ramaekers, W.J.S.; Albrecht, B.A.; van Oijen, J.A.; de Goey, L.P.H. The Application of Flamelet Generated Manifolds in Partailly-Premixed Flames. In Proceedings of the Fluent Benelux User Group Meeting, Wavre, Belgium, 6–7 October 2005. [Google Scholar]
- Vreman, A.W.; Albrecht, B.A.; van Oijen, J.A.; de Goey, L.P.H. Premixed and Nonpremixed Generated Manifolds in Large-Eddy Simulation of Sandia Flame D and F. Combust. Flame 2008, 153, 394–416. [Google Scholar] [CrossRef]
- Grout, R.W.; Swaminathan, N.; Cant, R.S. Effects of Compositional Fluctuations on Premixed Flames. Combust. Theory Model. 2009, 13, 823–852. [Google Scholar] [CrossRef]
- Zhang, W.; Karaca, S.; Wang, J.; Huang, Z.; van Oijen, J. Large Eddy Simulation of the Cambridge/Sandia Stratified Flame with Flamelet-Generated Manifolds: Effects of Non-Unity Lewis Numbers and Stretch. Combust. Flame 2021, 227, 106–119. [Google Scholar] [CrossRef]
- Popov, P.P. Alternatives to the Beta Distribution in Assumed PDF Methods for Turbulent Reactive Flow. Flow Turbul. Combust. 2022, 108, 433–459. [Google Scholar] [CrossRef]
- Salehi, M.M.; Bushe, W.K.; Shahbazian, N.; Groth, C.P.T. Modified Laminar Flamelet Presumed Probability Density Function for LES of Premixed Turbulent Combustion. Proc. Combust. Inst. 2013, 34, 1203–1211. [Google Scholar] [CrossRef]
- Ghadimi, M.; Atayizadeh, H.; Salehi, M.M. Presumed Joint-PDF Modelling for Turbulent Stratified Flames. Flow Turbul. Combust. 2021, 107, 405–439. [Google Scholar] [CrossRef]
- Darbyshire, O.R.; Swaminathan, N. A Presumed Joint Pdf Model for Turbulent Combustion with Varying Equivalence Ratio. Combust. Sci. Technol. 2012, 184, 2036–2067. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Z.; Ye, T.; Cheng, M.; Zhao, M. Large Eddy Simulation of Turbulent Stratified Combustion Using Dynamic Thickened Flame Coupled Tabulated Detailed Chemistry. Appl. Math. Model. 2018, 62, 476–498. [Google Scholar] [CrossRef]
- Ruan, S.; Swaminathan, N.; Darbyshire, O. Modelling of Turbulent Lifted Jet Flames Using Flamelets: A Priori Assessment and a Posteriori Validation. Combust. Theory Model. 2014, 18, 295–329. [Google Scholar] [CrossRef]
- Chen, Z.X.; Doan, N.A.K.; Ruan, S.; Langella, I.; Swaminathan, N. A Priori Investigation of Subgrid Correlation of Mixture Fraction and Progress Variable in Partially Premixed Flames. Combust. Theory Model. 2018, 22, 862–882. [Google Scholar] [CrossRef]
- Jaganath, V.; Stoellinger, M. Transported and Presumed Probability Density Function Modeling of the Sandia Flames with Flamelet Generated Manifold Chemistry. Phys. Fluids 2021, 33, 045123. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine Learning: Trends, Perspectives, and Prospects. Science 80 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. Perspective: Materials Informatics and Big Data: Realization of the “Fourth Paradigm” of Science in Materials Science. APL Mater. 2016, 4, 053208. [Google Scholar] [CrossRef]
- Afanaseva, O.V.; Tulyakov, T.F. Comparative Analysis of Image Segmentation Methods in Power Line Monitoring Systems. Int. J. Eng. Trans. A Basics 2026, 39, 1–11. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden Fluid Mechanics: Learning Velocity and Pressure Fields from Flow Visualizations. Science 80 2020, 367, 1026–1030. [Google Scholar] [CrossRef]
- An, J.; Chen, Y.; Su, X.; Zhou, H.; Ren, Z. Applications and Prospects of Machine Learning in Turbulent Combustion and Engines. J. Tsinghua Univ. 2023, 63, 462–472. [Google Scholar]
- Liu, J.; Liu, G.; Wu, J.; Zhang, G.; Wu, Y. Prediction of Flame Type and Liftoff Height of Fuel Jets in Turbulent Hot Coflow Using Machine Learning Methods. Combust. Sci. Technol. 2025, 197, 1760–1782. [Google Scholar] [CrossRef]
- Zeng, J.; Cao, L.; Xu, M.; Zhu, T.; Zhang, J.Z.H. Complex Reaction Processes in Combustion Unraveled by Neural Network-Based Molecular Dynamics Simulation. Nat. Commun. 2020, 11, 5713. [Google Scholar] [CrossRef]
- Ji, W.; Deng, S. Autonomous Discovery of Unknown Reaction Pathways from Data by Chemical Reaction Neural Network. J. Phys. Chem. A 2021, 125, 1082–1092. [Google Scholar] [CrossRef]
- Mirgolbabaei, H.; Echekki, T. A Novel Principal Component Analysis-Based Acceleration Scheme for LES-ODT: An a Priori Study. Combust. Flame 2013, 160, 898–908. [Google Scholar] [CrossRef]
- Malik, M.R.; Coussement, A.; Echekki, T.; Parente, A. Principal Component Analysis Based Combustion Model in the Context of a Lifted Methane/Air Flame: Sensitivity to the Manifold Parameters and Subgrid Closure. Combust. Flame 2022, 244, 112134. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, S.; Wu, Y.; Zhang, G.; Li, X.; Zhang, H. FlamePINN-1D: Physics-Informed Neural Networks to Solve Forward and Inverse Problems of 1D Laminar Flames. Combust. Flame 2025, 273, 113964. [Google Scholar] [CrossRef]
- Song, M.; Tang, X.; Xing, J.; Liu, K.; Luo, K.; Fan, J. Physics-Informed Neural Networks Coupled with Flamelet/Progress Variable Model for Solving Combustion Physics Considering Detailed Reaction Mechanism. Phys. Fluids 2024, 36, 103616. [Google Scholar] [CrossRef]
- Chen, Z.X.; Iavarone, S.; Ghiasi, G.; Kannan, V.; D’Alessio, G.; Parente, A.; Swaminathan, N. Application of Machine Learning for Filtered Density Function Closure in MILD Combustion. Combust. Flame 2021, 225, 160–179. [Google Scholar] [CrossRef]
- Henry de Frahan, M.T.; Yellapantula, S.; King, R.; Day, M.S.; Grout, R.W. Deep Learning for Presumed Probability Density Function Models. Combust. Flame 2019, 208, 436–450. [Google Scholar] [CrossRef]
- Gitushi, K.M.; Ranade, R.; Echekki, T. Investigation of Deep Learning Methods for Efficient High-Fidelity Simulations in Turbulent Combustion. Combust. Flame 2022, 236, 111814. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Wu, Y.; Zhang, R.; Guo, H.; Yue, G. A Data Driven Conditional Presumed PDF Generation Method for FGM with Random Forest Model. Combust. Sci. Technol. 2025, 00, 1–27. [Google Scholar] [CrossRef]
- Minamoto, Y.; Swaminathan, N.; Cant, R.S.; Leung, T. Reaction Zones and Their Structure in MILD Combustion. Combust. Sci. Technol. 2014, 186, 1075–1096. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A. Support Vector Method for Function Approximation, Regression Estimation, and Signal Processing. In Proceedings of the 10th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 3 December 1996; pp. 281–287. [Google Scholar]
- O’Hagan, A. Curve Fitting and Optimal Design for Prediction. J. R. Stat. Soc. B 1978, 40, 1–24. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 7, ISBN 026218253X. [Google Scholar]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial Neural Networks: A Tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Barlow, R.S.; Fiechtner, G.J.; Carter, C.D.; Chen, J.Y. Experiments on the Scalar Structure of Turbulent CO/H2/N2 Jet Flames. Combust. Flame 2000, 120, 549–569. [Google Scholar] [CrossRef]
- Al-Abdeli, Y.M.; Masri, A.R. Stability Characteristics and Flowfields of Turbulent Non-Premixed Swirling Flames. Combust. Theory Model. 2003, 7, 731–766. [Google Scholar] [CrossRef]
- Masri, A.R.; Kalt, P.A.M.; Barlow, R.S. The Compositional Structure of Swirl-Stabilised Turbulent Nonpremixed Flames. Combust. Flame 2004, 137, 1–37. [Google Scholar] [CrossRef]
- Masri, A.R.; Bilger, R.W.; Dibble, R.W. Turbulent Nonpremixed Flames of Methane near Extinction: Probability Density Functions. Combust. Flame 1988, 73, 261–285. [Google Scholar] [CrossRef]
- Ma, L. Computational Modeling of Turbulent Spary Combustion. Doctoral Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Lin, J. Divergence Measures Based on the Shannon Entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]

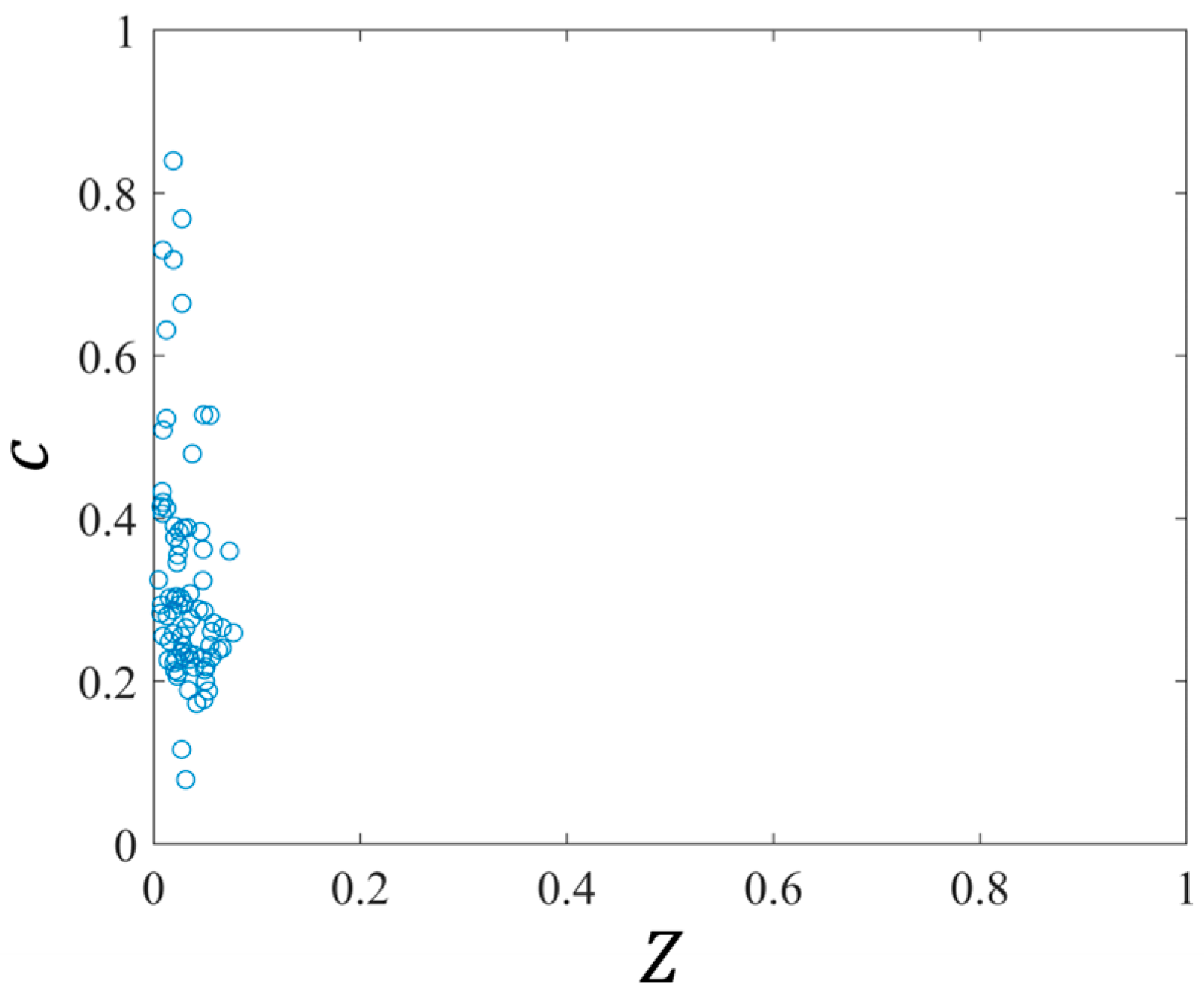
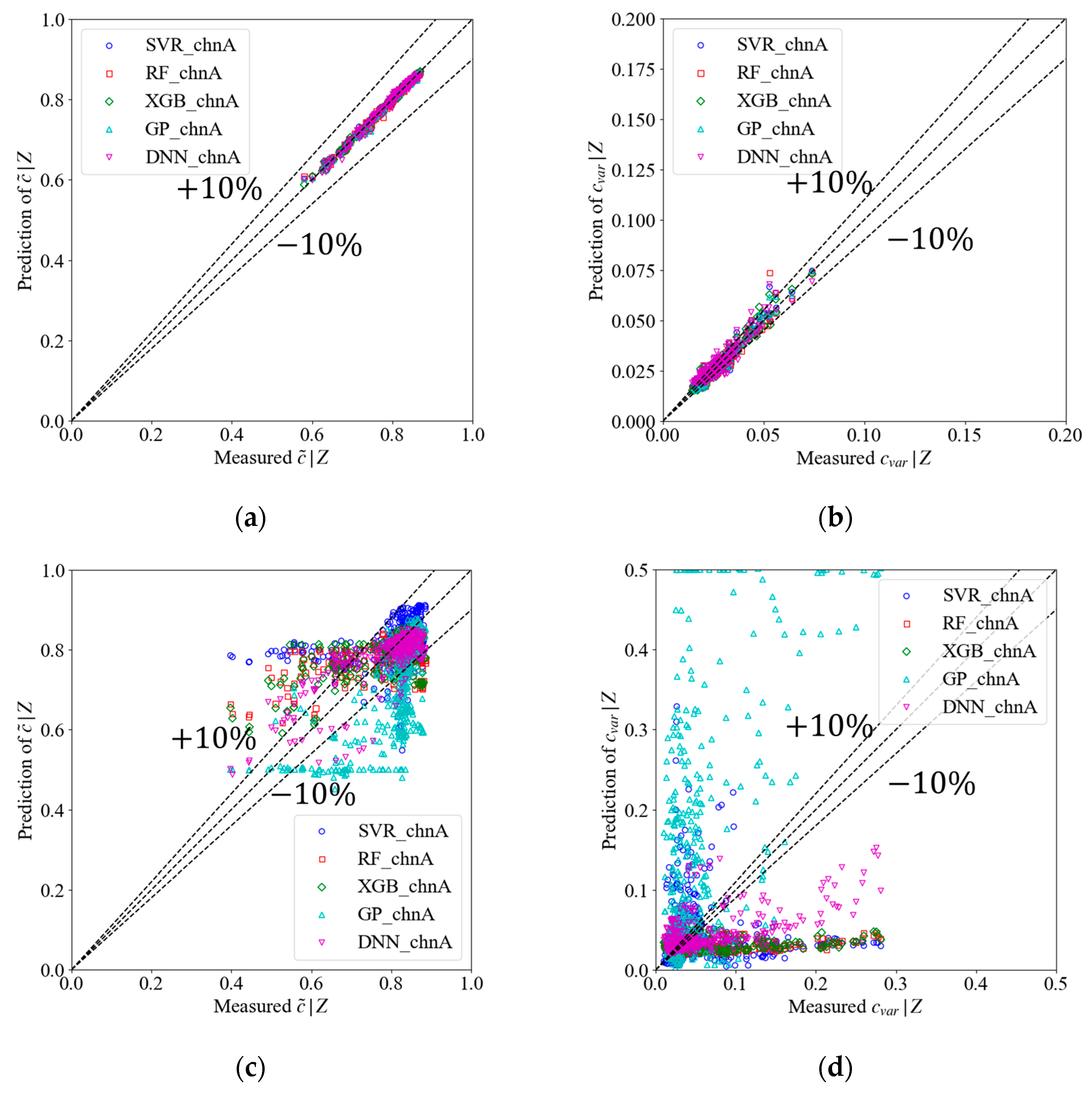




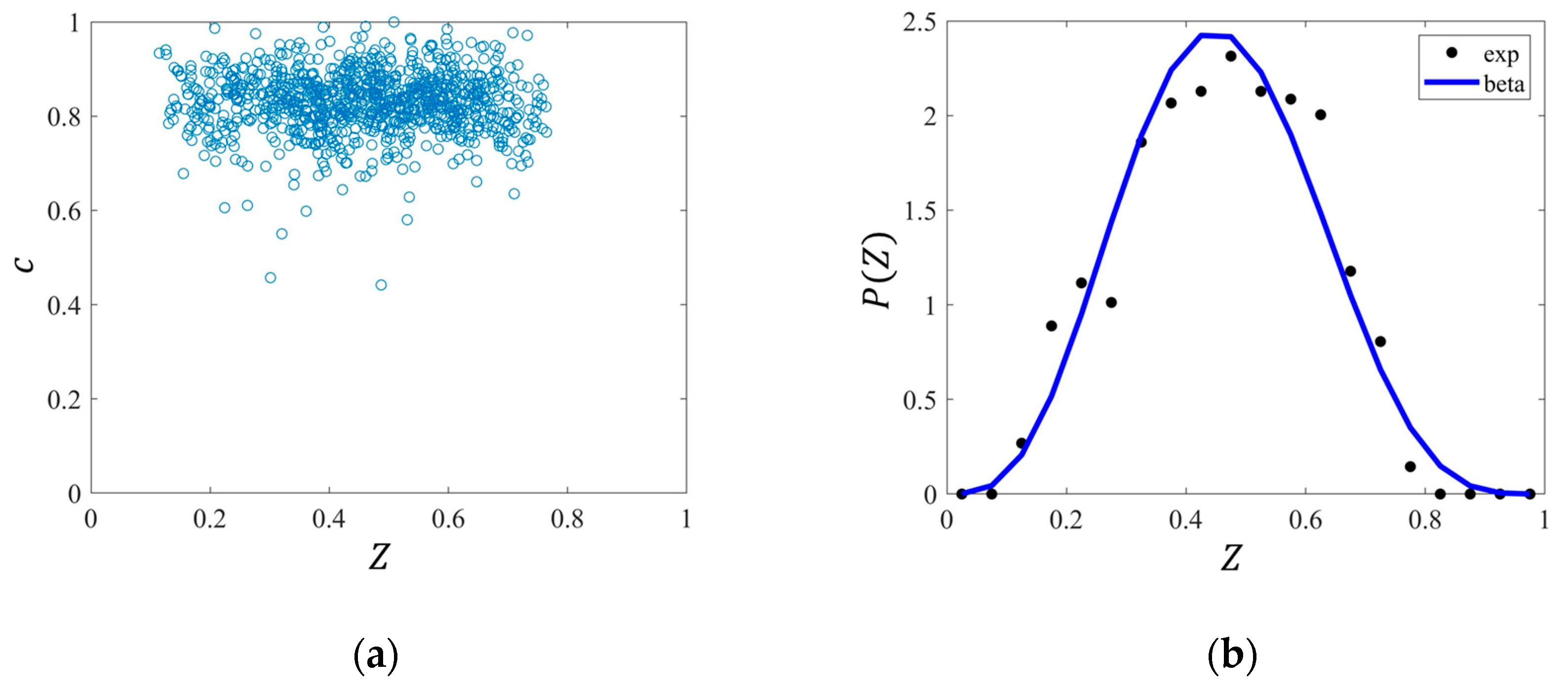


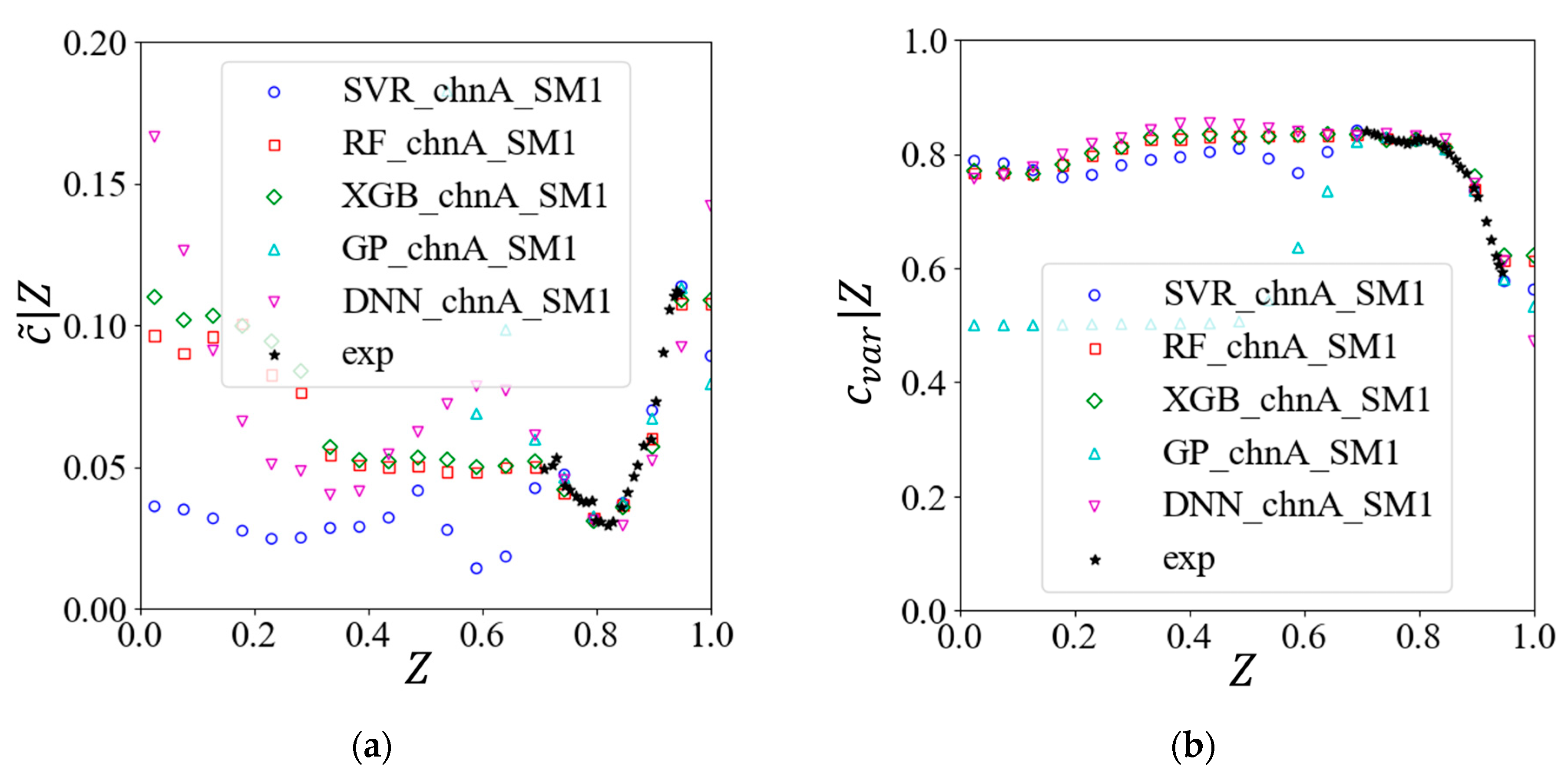

| Nozzle ID (mm) | Nozzle OD (mm) | (m/s) | |
|---|---|---|---|
| 4.58 | 6.34 | 76.0 1.5 | ~16,700 |
| (m/s) | (m/s) | (m/s) | (m/s) | ||
|---|---|---|---|---|---|
| 32.7 | 38.2 | 20 | 19.1 | 7200 | 75,900 |
| Models’ Name | ML Methods | Training Set |
|---|---|---|
| SVR_chnA | Support Vector Regression | chnA’s training set |
| RF_chnA | Random Forest | chnA’s training set |
| XGB_chnA | XGBoost | chnA’s training set |
| GP_chnA | Gaussian Process Regression | chnA’s training set |
| DNN_chnA | Deep neural network | chnA’s training set |
| SVR_SM1 | Support Vector Regression | SM1’s training set |
| RF_SM1 | Random Forest | SM1’s training set |
| XGB_SM1 | XGBoost | SM1’s training set |
| GP_SM1 | Gaussian Process Regression | SM1’s training set |
| DNN_SM1 | Deep neural network | SM1’s training set |
| SVR_chnA_SM1 | Support Vector Regression | fusional training set |
| RF_chnA_SM1 | Random Forest | fusional training set |
| XGB_chnA_SM1 | XGBoost | fusional training set |
| GP_chnA_SM1 | Gaussian Process Regression | fusional training set |
| DNN_chnA_SM1 | Deep neural network | fusional training set |
| Table Sets | Metrics Type | SVR | RF | XGB | GPR | DNN |
|---|---|---|---|---|---|---|
| chnA | max error for | 3.4% | 1.9% | 3.2% | 2.4% | 3.1% |
| ratio of error < 10% for | 100% | 100% | 100% | 100% | 100% | |
| max error of | 29.5% | 19.2% | 27.5% | 15.8% | 32.2% | |
| ratio of error < 10% for | 91.9% | 98.0% | 97.7% | 97.2% | 77.5% | |
| SM1 | max error of | 2.9% | 8.2% | 11.4% | 2.4% | 8.1% |
| ratio of error < 10% for | 100% | 100% | 99.5% | 100% | 100% | |
| max error of | 50.4% | 22.8% | 39.1% | 22.5% | 70.1% | |
| ratio of error < 10% for | 84.4% | 95.2% | 94.1% | 90.5% | 65.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Liu, J.; Wu, Y.; Yue, G. Novel Data-Driven PDF Modeling in FGM Method Based on Sparse Turbulent Flame Data. Energies 2025, 18, 3546. https://doi.org/10.3390/en18133546
Zhang G, Liu J, Wu Y, Yue G. Novel Data-Driven PDF Modeling in FGM Method Based on Sparse Turbulent Flame Data. Energies. 2025; 18(13):3546. https://doi.org/10.3390/en18133546
Chicago/Turabian StyleZhang, Guihua, Jiayue Liu, Yuxin Wu, and Guangxi Yue. 2025. "Novel Data-Driven PDF Modeling in FGM Method Based on Sparse Turbulent Flame Data" Energies 18, no. 13: 3546. https://doi.org/10.3390/en18133546
APA StyleZhang, G., Liu, J., Wu, Y., & Yue, G. (2025). Novel Data-Driven PDF Modeling in FGM Method Based on Sparse Turbulent Flame Data. Energies, 18(13), 3546. https://doi.org/10.3390/en18133546






