A Method for Modeling Time Delay-Related Measurement Errors, Applicable in Power and Energy Monitoring and in Fault Detection Algorithms for Energy Grids
Abstract
1. Introduction
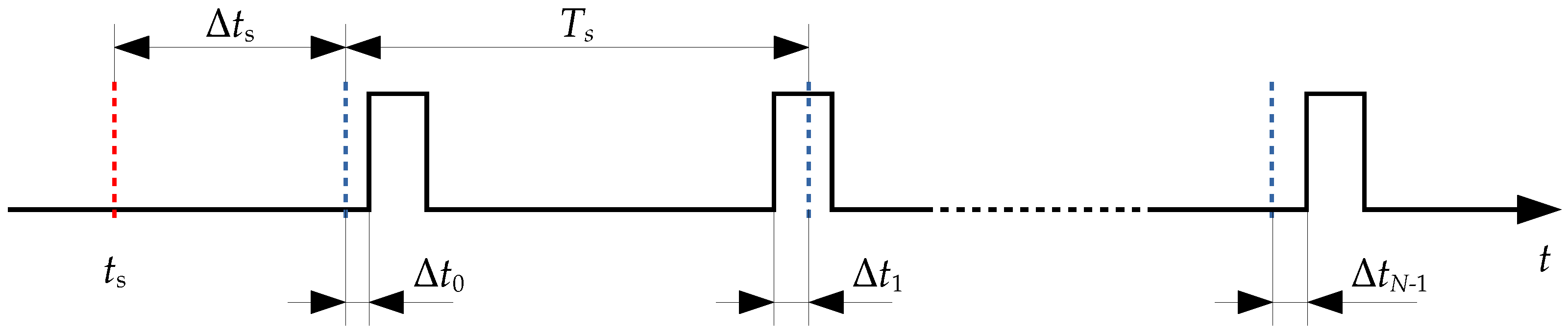
2. Time-Related Error Model
- , the delay in starting the measurement relative to the time , at which the measurement should begin;
- , the difference in the processing time of the i-th signal sample relative to the time expected based on the sampling period .
2.1. Error Signal Related to Measurement Initiation Delay
2.2. Error Signal Related to Sampling Period Fluctuation
2.3. Delay-Related Error Signal Variance
2.4. The Case of a Non-Zero Expected Value of Sampling Period Fluctuation
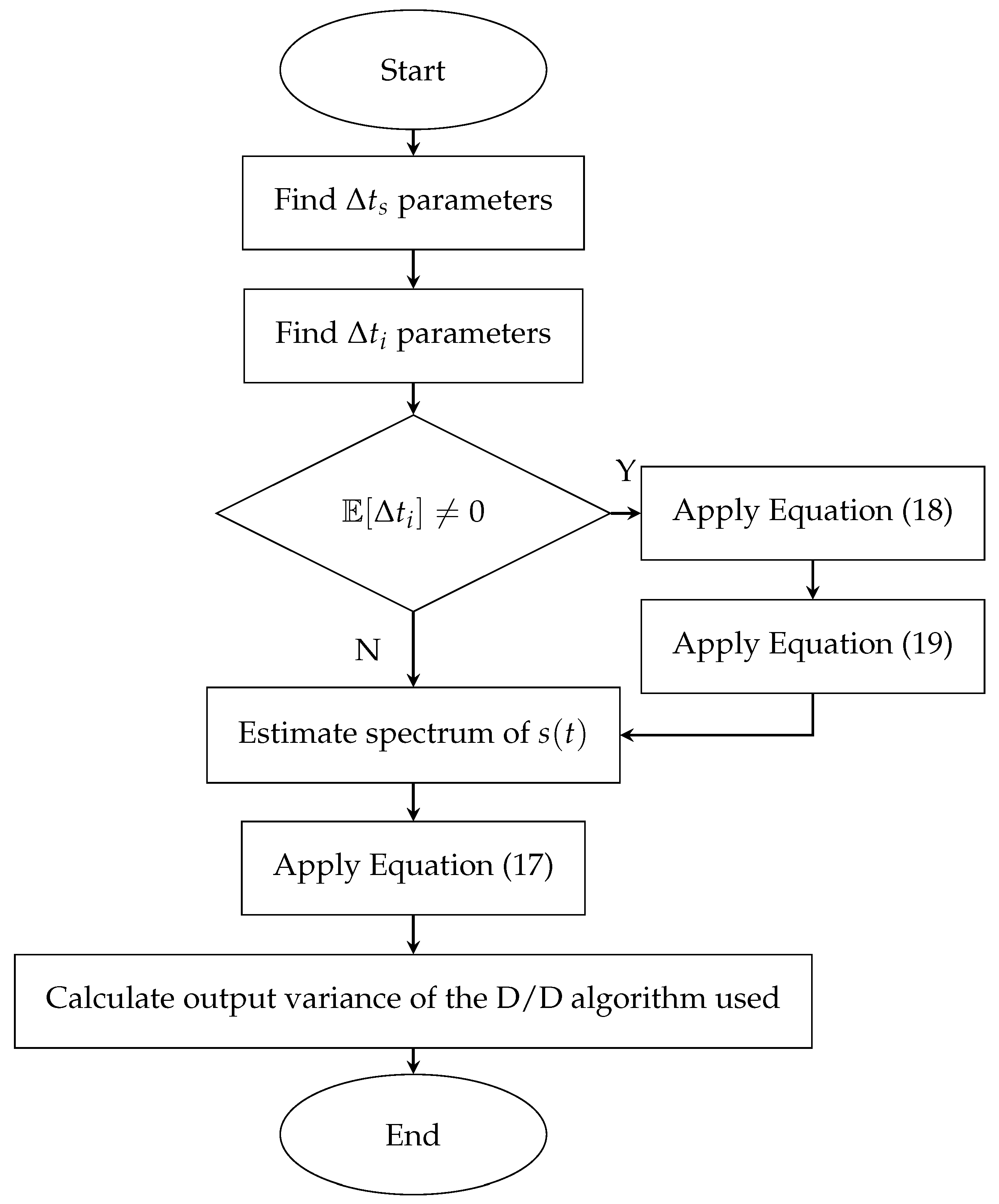
3. Verification of the Proposed Method
- Randomize the initial phase of the signal , where ;
- Generate a vector N of successive samples of quantity based on Equation (1);
- Randomize the value of the quantity according to the given parameters of the distribution of this quantity;
- Randomize a vector of N successive values of the quantity according to the given parameters of the distribution of this quantity;
- Generate a vector of N consecutive samples of the signal based on Equation (2);
- Calculate the realization values of the error signal according to Equation (3);
- Calculate the variance value of the error signal based on Equation (20);
- Estimate the variance value of the error signal based on Equation (17);
- Calculate the relative error of the estimated variance value based on Equation (21).
3.1. Case of Delay in Initiation of the Measurement Process
3.2. The Case with Sampling Period Fluctuation
3.3. The Case with Multiple Delay Sources
3.4. Experiments Conclusions
4. Example Applications of the Proposed Method
- Whether the measurement chain performs multiple tasks that might be mutually exclusive;
- The typical execution time of the algorithm responsible for detecting the phenomenon that initiates the measurement process;
- The nature of the distribution of the measurement process initiation delay time;
- Whether the S/H system continues to track the input signal after the initiation of A/D processing or whether tracking is performed continuously without interruption.
- How the processing of subsequent samples from the A/D converter input is initiated;
- The resolution and stability of the clock signal used to measure the sampling time.
5. Conclusions
- Proposing a uniform and universal model of error signals related to delays;
- Indication of an analytical method for determining the variance value of the discussed error signals for selected parameters of the distribution of delay realizations;
- Indication of the component properties of the error signal related to delays, important from the point of view of analyzing the impact of the D/D processing algorithm on these signals;
- Indication of possible sources and genesis for the discussed error signals;
- Verification of the effectiveness of the proposed method in relation to the Monte Carlo method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| List of Symbols | |
| Measurement chain input quantity | |
| Voltage representation of the | |
| Digital representation of the | |
| N | Number of input quantities of the used DSP algorithm |
| Sampling period | |
| Sampling frequency | |
| Initiation of the measurement process in the ideal situation | |
| Delay of the measurement process initiation | |
| The difference in the processing time of the i-th signal sample | |
| Course of the a quantity in the ideal case | |
| Course of the a quantity in the real case |
| Error signal of the a quantity caused by phenomenon b | |
| Amplitude of the k-th harmonic of the a signal | |
| Phase of the k-th harmonic of the a signal | |
| Pulsation of the k-th harmonic of the a signal | |
| Variance of the a signal | |
| Abbreviations | |
| A/A | Analog-to-analog |
| A/D | Analog-to-digital converter |
| D/D | Digital-to-digital |
| DFT | Discrete Fourier Transform |
| DSP | Digital signal processing |
| S/H | Sample-and-hold |
| WT | Wavelet Transform |
Appendix A
Appendix A.1. The Case with Uniform Distribution
Appendix A.2. The Case of Normal Distribution
Appendix A.3. The Case of the Gamma Distribution
References
- Agarwal, S.; Sharma, S.; Rahman, M.H.; Vranckx, S.; Maiheu, B.; Blyth, L.; Janssen, S.; Gargava, P.; Shukla, V.K.; Batra, S.; et al. Air quality forecasting using artificial neural networks with real time dynamic error correction in highly polluted regions. Sci. Total Environ. 2020, 735, 139454. [Google Scholar] [CrossRef] [PubMed]
- Volosnikov, A.S. Measurement System Based on Nonrecursive Filters with the Optimal Correction of the Dynamic Measurement Error. Meas. Tech. 2023, 65, 720–728. [Google Scholar] [CrossRef]
- Roj, J. Estimation of the artificial neural network uncertainty used for measurand reconstruction in a sampling transducer. IET Sci. Meas. Technol. 2014, 8, 23–29. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet Tour of Signal Processing, 3rd ed.; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Akujuobi, C.M. Wavelets and Wavelet Transform Systems and Their Applications; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Durak, L.; Arikan, O. Short-time Fourier transform: Two fundamental properties and an optimal implementation. IEEE Trans. Signal Process. 2003, 51, 1231–1242. [Google Scholar] [CrossRef]
- Alegria, F. Using digital methods in active power measurement. Acta IMEKO 2023, 12, 1–8. [Google Scholar] [CrossRef]
- Pandey, S. Analog Multiplier Based Single Phase Power Measurement. J. Electr. Electron. Syst. 2016, 5, 2332-0796. [Google Scholar] [CrossRef]
- Unser, M.; Aldroubi, A. A review of wavelets in biomedical applications. Proc. IEEE 1996, 84, 626–638. [Google Scholar] [CrossRef]
- Hasan, O. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy. Expert Syst. Appl. 2009, 36, 2027–2036. [Google Scholar] [CrossRef]
- Yan, R.; Gao, R.X.; Chen, X. Wavelets for fault diagnosis of rotary machines: A review with applications. Signal Process. 2014, 96, 1–15. [Google Scholar] [CrossRef]
- Siddique, M.F.; Ahmad, Z.; Ullah, N.; Kim, J. A Hybrid Deep Learning Approach: Integrating Short-Time Fourier Transform and Continuous Wavelet Transform for Improved Pipeline Leak Detection. Sensors 2023, 23, 8079. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Z.; Huang, G.; Wang, F.; Wang, P.; Liang, J. Power Grid Faults Diagnosis Based on Improved Synchrosqueezing Wavelet Transform and ConvNeXt-v2 Network. Electronics 2025, 14, 388. [Google Scholar] [CrossRef]
- Altaie, A.S.; Abderrahim, M.; Alkhazraji, A.A. Transmission Line Fault Classification Based on the Combination of Scaled Wavelet Scalograms and CNNs Using a One-Side Sensor for Data Collection. Sensors 2024, 24, 2124. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Gu, Z.; Park, J.H.; Xie, X.; Sun, W. Distributed Cooperative Voltage Control of Networked Islanded Microgrid via Proportional-Integral Observer. IEEE Trans. Smart Grid 2024, 15, 5981–5991. [Google Scholar] [CrossRef]
- STMicroelectronics. Application Note AN1636; STMicroelectronics: Geneva, Switzerland, 2003; Available online: https://www.st.com/resource/en/application_note/an1636-understanding-and-minimising-adc-conversion-errors-stmicroelectronics.pdf (accessed on 30 May 2025).
- Arpaia, P.; Baccigalupi, C.; Martino, M. Metrological characterization of high-performance delta-sigma ADCs. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Topór-Kaminski, T.; Jakubiec, J. Uncertainty modelling method of data series processing algorithms. In Proceedings of the 10th International Symposium on Development in Digital Measuring Instrumentation and 3rd Workshop on ADC Modelling and Testing, IMEKO, Naples, Italy, 17–18 September 1998; Volume 2, pp. 631–636. [Google Scholar]
- Baker, B.C. Optimize Your SAR ADC Design; Texas Instruments Inc.: Dallas, TX, USA, 2019. [Google Scholar]
- Jakubiec, J. Błędy i Niepewności Danych w Systemie Pomiarowo-Sterującym; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2010. (In Polish) [Google Scholar]
- Wymysło, M. Badanie związków między błędami opóźnień a innymi błędami w systemie pomiarowo-sterującym w oparciu o definicję współczynnika korelacji. Przegląd Elektrotechniczny 2016, 92, 217–220. (In Polish) [Google Scholar] [CrossRef]
- Wymysło, M. Współbieżna realizacja zadań programowych jako przyczyna powstawania opóźnień w systemie pomiarowo-sterującym. Zesz. Nauk. Wydział Elektrotechniki Autom. Politech. Gdańskiej 2016, 49, 129–132. (In Polish) [Google Scholar]
- Wymysło, M.; Jakubiec, J. Przedziałowa postać wyniku pomiaru jako podstawa wyrażania niedokładności w systemach pomiarowo-sterujących. Zesz. Nauk. WydziałU Elektrotechniki Autom. Politech. Gdańskiej 2018, 59, 73–78. (In Polish) [Google Scholar] [CrossRef]
- Zakharov, I.P.; Vodotyka, S.V.; Shevchenko, E.N. Methods, Models, and Budgets for Estimation of Measurement Uncertainty During Calibration. Meas. Tech. 2011, 54, 387–399. [Google Scholar] [CrossRef]
- Rovera, G.D.; Siccardi, M.; Römisch, S.; Abgrall, M. Time Delay Measurements: Estimation of the Error Budget. Metrologia 2019, 56, 035004. [Google Scholar] [CrossRef]
- Huang, Z.G.; Qiao, C.J.; Ma, C.; Zhao, S. The Analysis and Correction of Time-Delay in the Precise Acoustic Measurement System. Appl. Mech. Mater. 2013, 333–335, 236–242. [Google Scholar] [CrossRef]
- Choi, M.; Choi, J.; Chung, W.K. State estimation with delayed measurements incorporating time-delay uncertainty. IET Control Theory Appl. 2012, 6, 2351–2361. [Google Scholar] [CrossRef]
- Tarasov, V.N. Mathematical Model of Delay Based on a System with Gamma Distribution. Phys. Wave Process. Radio Syst. 2021, 24, 62–67. [Google Scholar] [CrossRef]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; JCGM: Sèvres, France, 2008; Available online: https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf (accessed on 30 May 2025).
- Laplante, P.A. The certainty of uncertainty in real-time systems. IEEE Instrum. Meas. Mag. 2004, 7, 44–50. [Google Scholar] [CrossRef]
- Bandyszak, T.; Weyer, T.; Daun, M. Uncertainty Theories for Real-Time Systems. In Handbook of Real-Time Computing; Tian, Y., Levy, D.C., Eds.; Springer Nature: Berlin/Heidelberg, Germany, 2022; pp. 99–132. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Propagation of Distributions Using a Monte Carlo Method; JCGM: Sèvres, France, 2008; Available online: https://www.bipm.org/documents/20126/2071204/JCGM_101_2008_E.pdf (accessed on 30 May 2025).
- Janssen, H. Monte-Carlo based uncertainty analysis: Sampling efficiency and sampling convergence. Reliab. Eng. Syst. Saf. 2013, 109, 123–132. [Google Scholar] [CrossRef]
- Saleh, R.; Wilton, S.; Mirabbasi, S.; Hu, A.; Greenstreet, M.; Lemieux, G.; Pande, P.P.; Grecu, C.; Ivanov, A. System-on-chip. Proc. IEEE 2006, 94, 1050–1069. [Google Scholar] [CrossRef]
- Renesas Electronics Corporation. Application Note AN-815—Understanding Jitter Units; Renesas Electronics Corporation: Tokyo, Japan, 2020; Available online: https://www.renesas.com/en/document/apn/815-understanding-jitter-units (accessed on 30 May 2025).
- Reay, D.S. Digital Signal Processing Using the ARM Cortex M4; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Jakubiec, J.; Roj, J. Error Analysis of Analytical and Neural Real-Time Reconstruction of Analog Signals; Wydawnictwo Politechniki Śląskiej: Gliwice, Poland, 2024. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Willsky, A.S.; Nawab, S.H. Signals & Systems, 2nd ed.; Pearson: London, UK, 2013. [Google Scholar]
- Ruhm, K.H. Deterministic, Nondeterministic Signals; Institute for Dynamic Systems and Control: Zurich, Switzerland, 2008. [Google Scholar]
- Kampik, M.; Roj, J.; Dróżdż, L. Error Model of a Measurement Chain Containing the Discrete Wavelet Transform Algorithm. Appl. Sci. 2024, 14, 3461. [Google Scholar] [CrossRef]
- Dróżdż, L.; Roj, J. Origin and properties of own error signals of the discrete wavelet transform algorithms. Int. J. Electron. Telecommun. 2024, 70, 643–648. [Google Scholar] [CrossRef]
- Kampik, M.; Roj, J.; Dróżdż, L. Estimation of the resultant expanded uncertainty of the output quantities of the measurement chain using the discrete wavelet transform algorithm. Appl. Sci. 2024, 14, 3691. [Google Scholar] [CrossRef]
- Horalek, V. Analysis of basic probability distributions, their properties and use in determining type B evaluation of measurement uncertainties. Measurement 2013, 46, 16–23. [Google Scholar] [CrossRef]
- Grimmett, G.; Stirzaker, D. Probability and Random Processes, 4th ed.; Oxford University Press: Oxford, UK, 2020. [Google Scholar]
- Kuo, H.H. White Noise Distribution Theory; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar] [CrossRef]
- Oppenheim, A.V.; Schafer, R.W. Discrete-Time Signal Processing, 3rd ed.; Pearson: London, UK, 2009. [Google Scholar]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms and Applications, 5th ed.; Pearson: London, UK, 2021. [Google Scholar]
- Jakubiec, J.; Konopka, K. The error based model of a single measurement result in uncertainty calculation of the mean value of series. In Proceedings of the Problems and Progress in Metrology: PPM’15, Gliwice, Poland, 7–10 June 2015; Volume 20, pp. 75–78. [Google Scholar]
- Dróżdż, L. Time Related Error Parameters Estimation Example on GitHub. 2025. Available online: https://github.com/Kuszki/Octave-Uncertainty-TREU-Example (accessed on 30 May 2025).
- Ahmad, K.A. Wavelet Packets and Their Statistical Applications; Springer: Singapore, 2018. [Google Scholar]
- Averbuch, A.Z.; Neittaanmäki, P.; Zheludev, V.A. Spline and Spline Wavelet Methods with Applications to Signal and Image Processing; Springer: Berlin/Heidelberg, Germany, 2019; Volume 3. [Google Scholar]
- Wang, J. On Spline Wavelets. In Wavelets and Splines; Chen, G., Lai, M.-J., Eds.; Nashboro Press: Des Peres, MO, USA, 2006; pp. 456–483. [Google Scholar]
- ARM Limited. CMSIS-DSP—Embedded Compute library for Cortex-M and Cortex-A. 2024. Available online: https://arm-software.github.io/CMSIS-DSP (accessed on 30 May 2025).
- STMicroelectronics. Datasheet DS10314; STMicroelectronics: Geneva, Switzerland, 2017; Available online: https://www.st.com/resource/en/datasheet/stm32f411ce.pdf (accessed on 30 May 2025).
- Atmel. ATmega32/L Datasheet; Atmel: San Jose, CA, USA, 2011; Available online: https://ww1.microchip.com/downloads/en/DeviceDoc/doc2503.pdf (accessed on 30 May 2025).
- Kampik, M.; Roj, J.; Dróżdż, L. A Method for Estimating the Resultant Expanded Uncertainty Value Based on Interval Arithmetic. Appl. Sci. 2024, 14, 7334. [Google Scholar] [CrossRef]
- Koliander, G.; El-Laham, Y.; Djurić, P.M.; Hlawatsch, F. Fusion of probability density functions. Proc. IEEE 2022, 110, 404–453. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, J.; Jiang, C.; Huang, Z.L. A new uncertainty propagation method considering multimodal probability density functions. Struct. Multidiscip. Optim. 2019, 60, 1983–1999. [Google Scholar] [CrossRef]
- Dieck, R.H. Measurement Uncertainty: Methods and Applications; ISA: Singapore, 2017. [Google Scholar]
- Yang, L.; Guo, Y. Combining pre-and post-model information in the uncertainty quantification of non-deterministic models using an extended Bayesian melding approach. Inf. Sci. 2019, 502, 146–163. [Google Scholar] [CrossRef]
- Urbanski, M.K.; Wąsowski, J. Fuzzy approach to the theory of measurement inexactness. Measurement 2003, 34, 67–74. [Google Scholar] [CrossRef]
- Dróżdż, L. Reductive Interval Arithmetic Method Application Example on GitHub. 2024. Available online: https://github.com/Kuszki/Octave-Uncertainty-RIA-Example (accessed on 30 May 2025).
- Roj, J.; Dróżdż, L. Propagation of Random Errors by the Discrete Wavelet Transform Algorithm. Electronics 2021, 10, 764. [Google Scholar] [CrossRef]
- Eaton, J.W. GNU Octave Official Website. 2024. Available online: https://octave.org (accessed on 30 May 2025).
- Osgood, B. The Fourier Transform and Its Applications; Stanford University: Stanford, CA, USA, 2007. [Google Scholar]
- Tassaddiq, A.; Qadir, A. Fourier Transform and Distributional Representation of the Generalized Gamma Function with Some Applications. Appl. Math. Comput. 2011, 218, 1084–1088. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Qadir, A. Fourier Transform and Distributional Representation of the Gamma Function Leading to Some New Identities. Int. J. Math. Math. Sci. 2004, 2004, 2091–2096. [Google Scholar] [CrossRef]
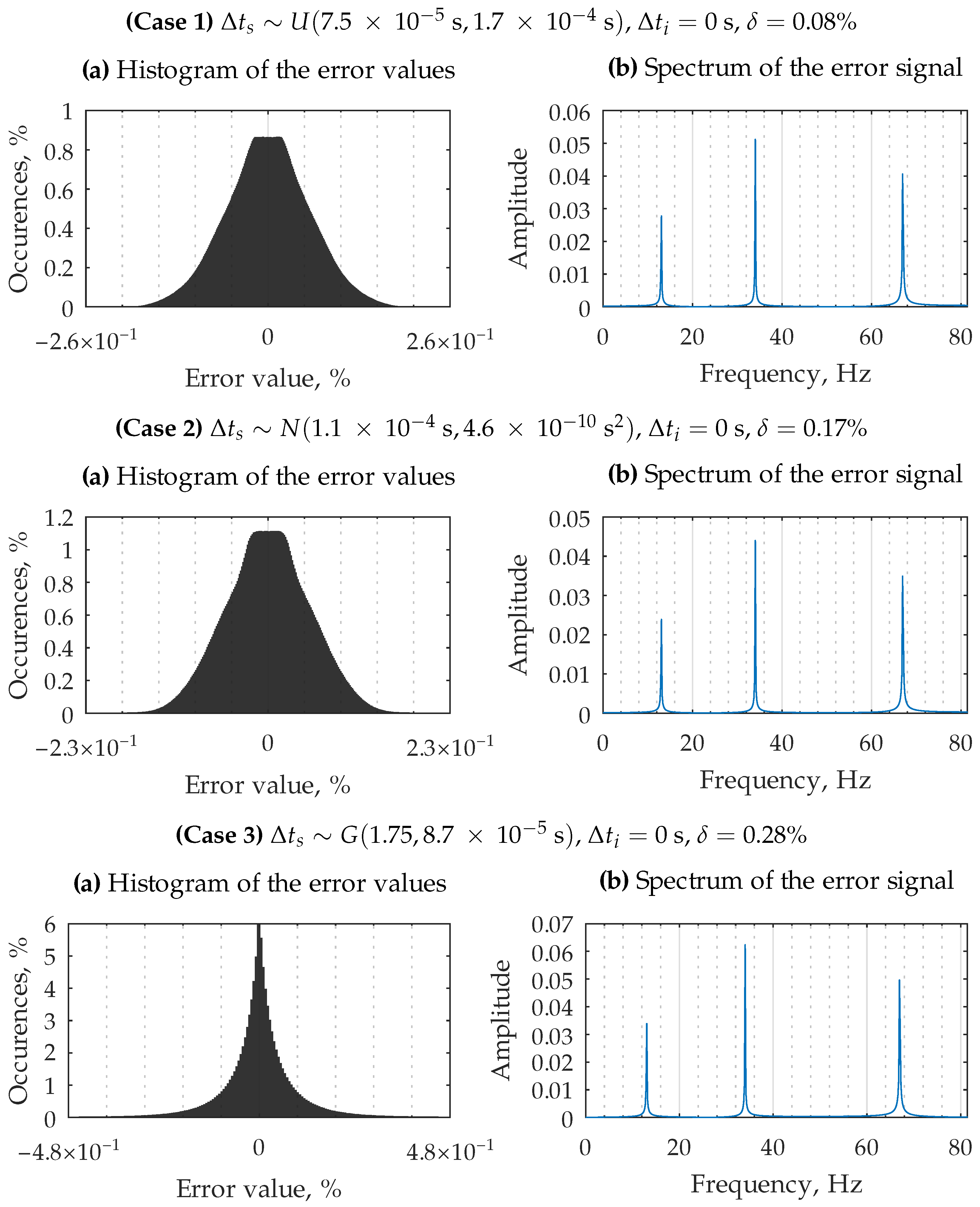
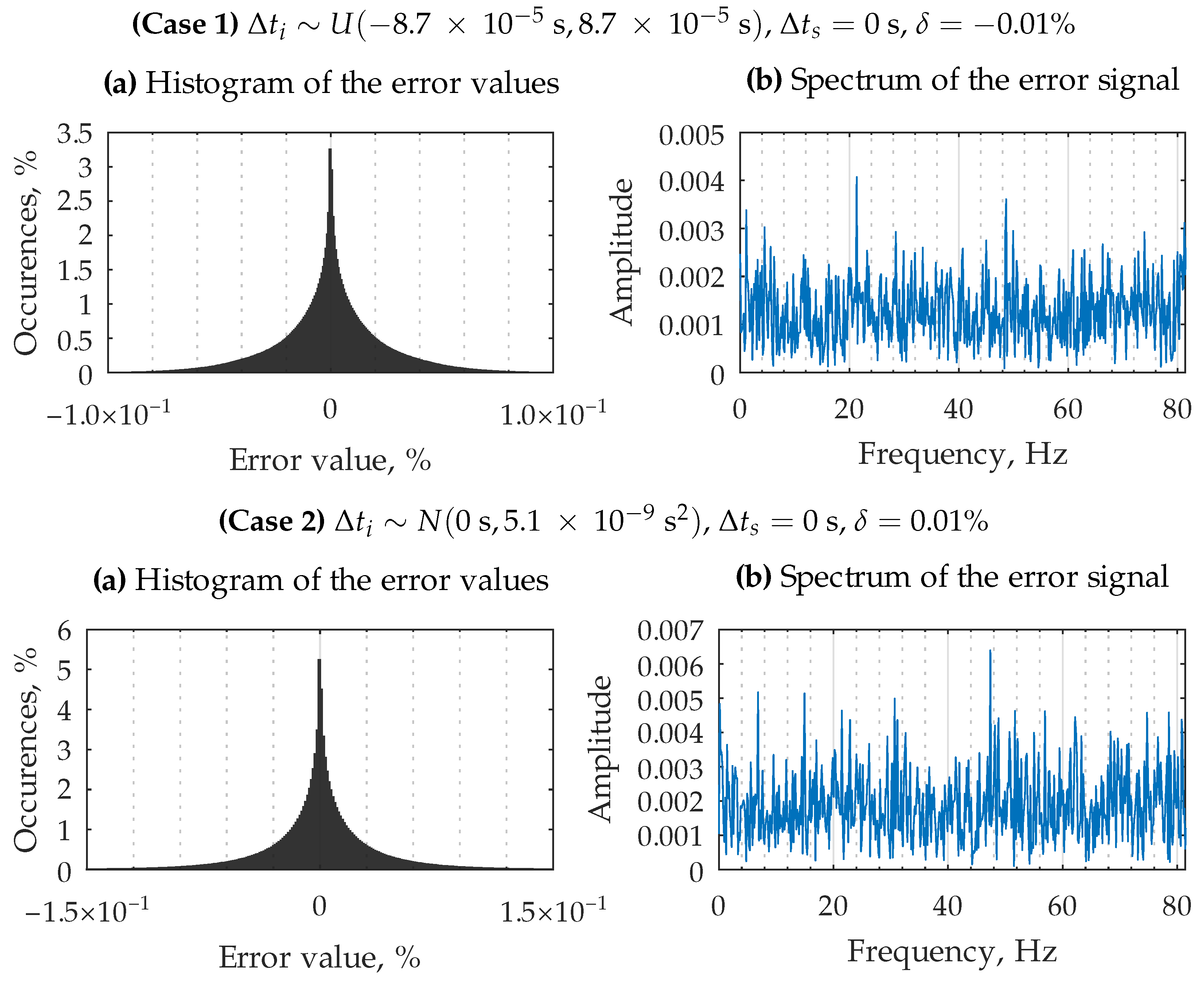
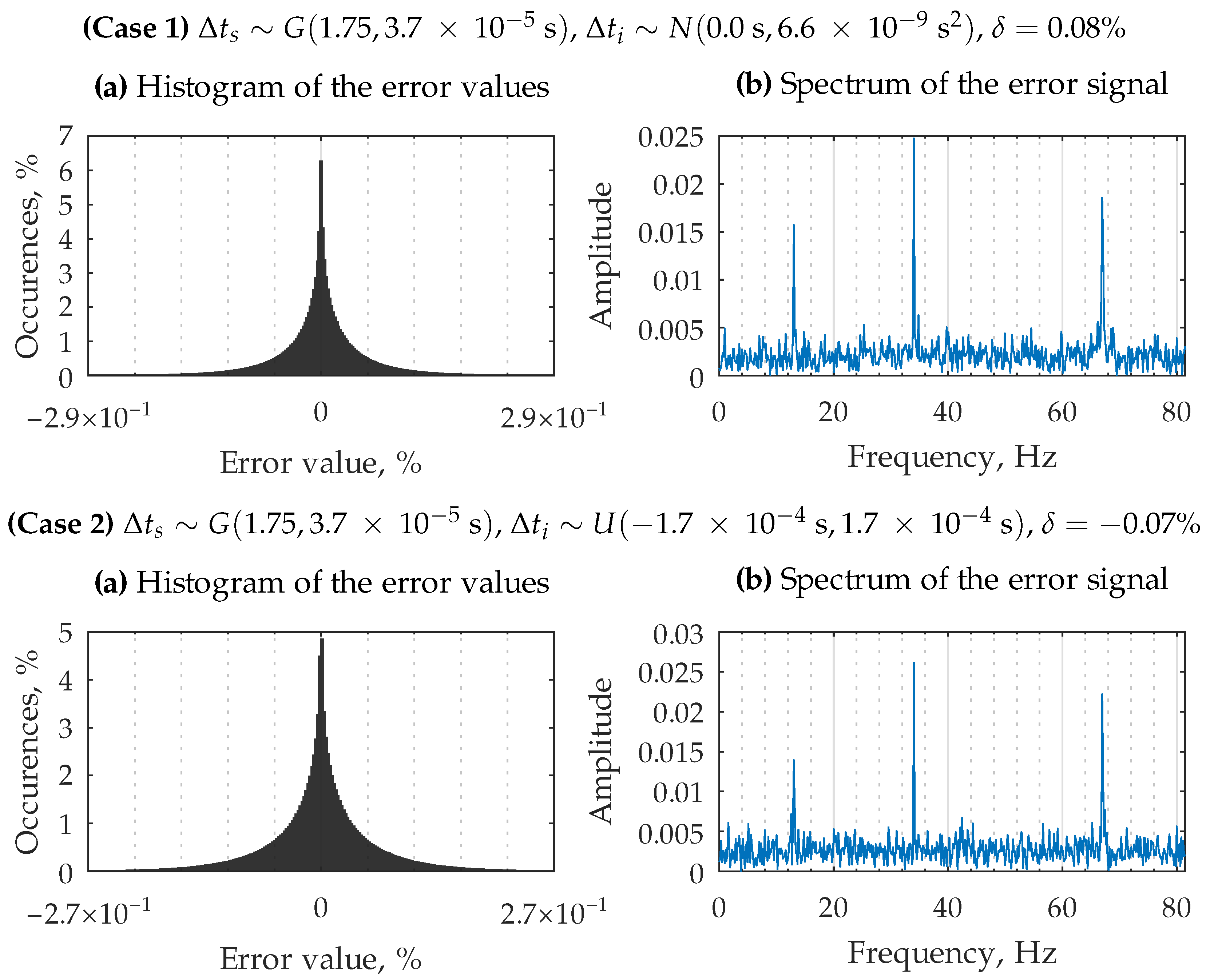
| Experiment Parameters | Error (21), | Compute Time, s | ||
|---|---|---|---|---|
| Equation (17) | Monte Carlo | |||
| 0.08 | 1.9 × 10−5 | 10 | ||
| 0.17 | 1.8 × 10−5 | 10 | ||
| 0.28 | 1.8 × 10−5 | 10 | ||
| −0.01 | 1.9 × 10−5 | 11 | ||
| 0.01 | 1.7 × 10−5 | 12 | ||
| 0.08 | 3.4 × 10−5 | 13 | ||
| −0.07 | 3.5 × 10−5 | 11 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kampik, M.; Dróżdż, Ł.; Roj, J. A Method for Modeling Time Delay-Related Measurement Errors, Applicable in Power and Energy Monitoring and in Fault Detection Algorithms for Energy Grids. Energies 2025, 18, 3524. https://doi.org/10.3390/en18133524
Kampik M, Dróżdż Ł, Roj J. A Method for Modeling Time Delay-Related Measurement Errors, Applicable in Power and Energy Monitoring and in Fault Detection Algorithms for Energy Grids. Energies. 2025; 18(13):3524. https://doi.org/10.3390/en18133524
Chicago/Turabian StyleKampik, Marian, Łukasz Dróżdż, and Jerzy Roj. 2025. "A Method for Modeling Time Delay-Related Measurement Errors, Applicable in Power and Energy Monitoring and in Fault Detection Algorithms for Energy Grids" Energies 18, no. 13: 3524. https://doi.org/10.3390/en18133524
APA StyleKampik, M., Dróżdż, Ł., & Roj, J. (2025). A Method for Modeling Time Delay-Related Measurement Errors, Applicable in Power and Energy Monitoring and in Fault Detection Algorithms for Energy Grids. Energies, 18(13), 3524. https://doi.org/10.3390/en18133524






