A Robust Low-Carbon Optimal Dispatching Method for Power System Distribution Based on LCA Carbon Emissions
Abstract
1. Introduction
2. LCA Carbon Emissions Assessment
2.1. Carbon Emission Analysis Methodology Based on Life Cycle Assessment
2.2. Systematic Carbon Life Cycle Assessment
3. System Modeling
3.1. Objective Function
- (1)
- The cost objective:
- (2)
- Carbon emission target
3.2. Restrictive Condition
- (1)
- Crew constraints
- (2)
- System power constraints
- (3)
- Wind and light output constraints
- (4)
- Electrochemical energy storage constraints
- (5)
- Load reduction constraints
- (6)
- Distributed robust constraint

4. Distributed Robust Optimization
4.1. Uncertainty Parameterization
4.2. Model Transformation
- (1)
- Linear transformation of the objective function
- (2)
- Approximate methods for combining Bonferroni and CVaR
5. Calculus Analysis
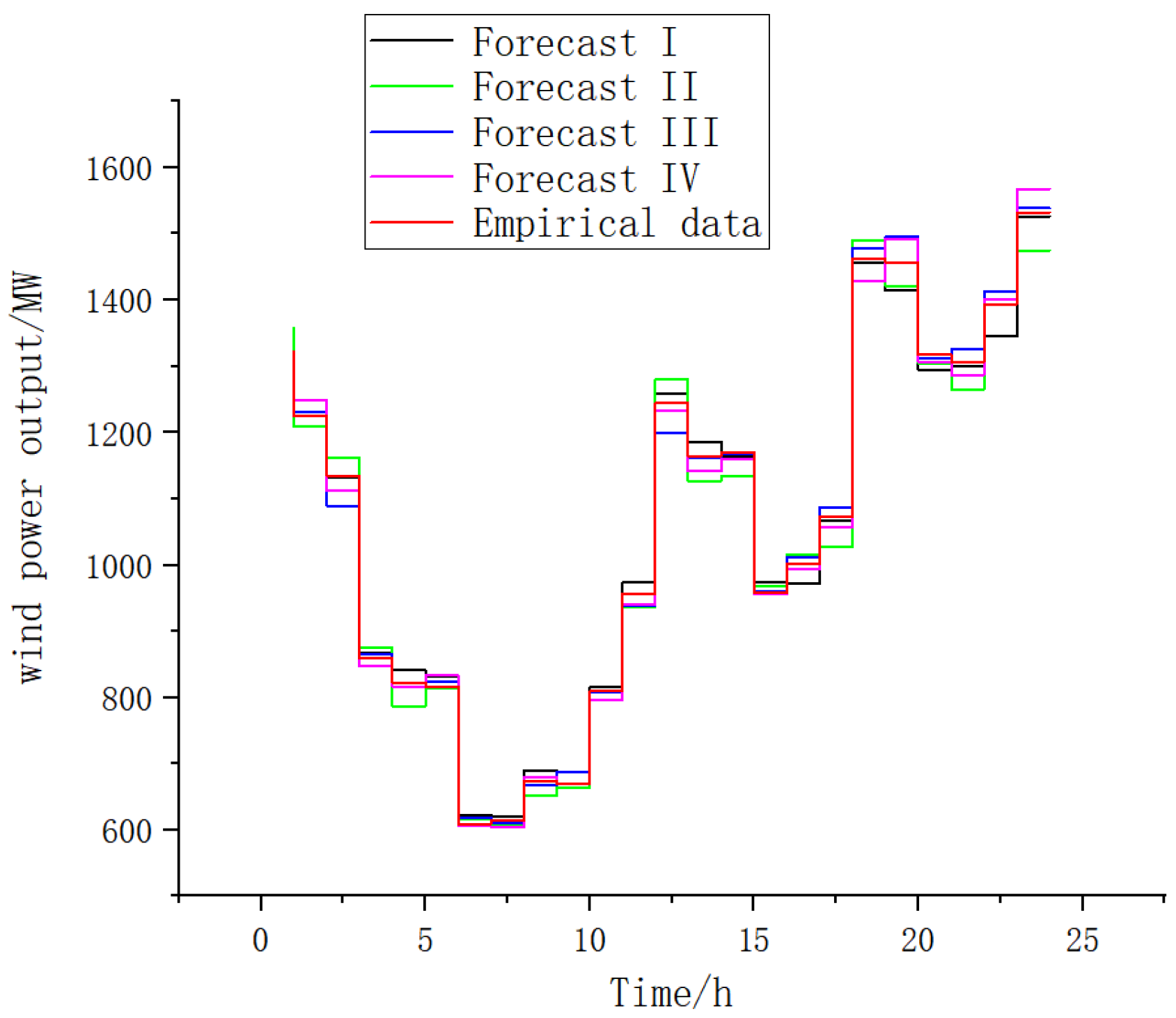
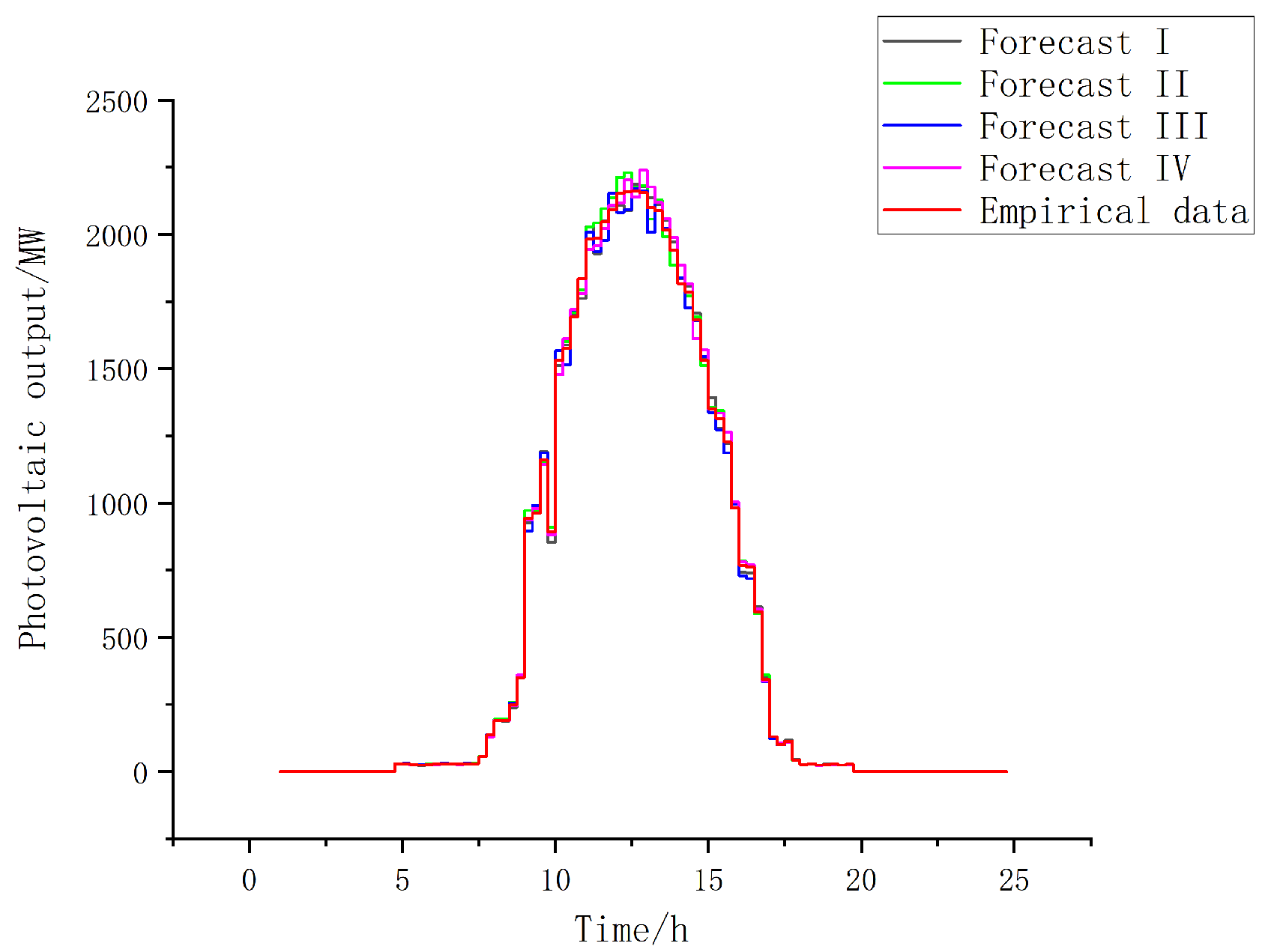
5.1. Example Data
5.2. Comparative Analysis
- (1)
- Optimization results
- 1:
- Carbon trading, load shedding;
- 2:
- Carbon trading, no load shedding;
- 3:
- No carbon trading, load shedding;
- 4:
- No carbon trading, no load shedding.
- (2)
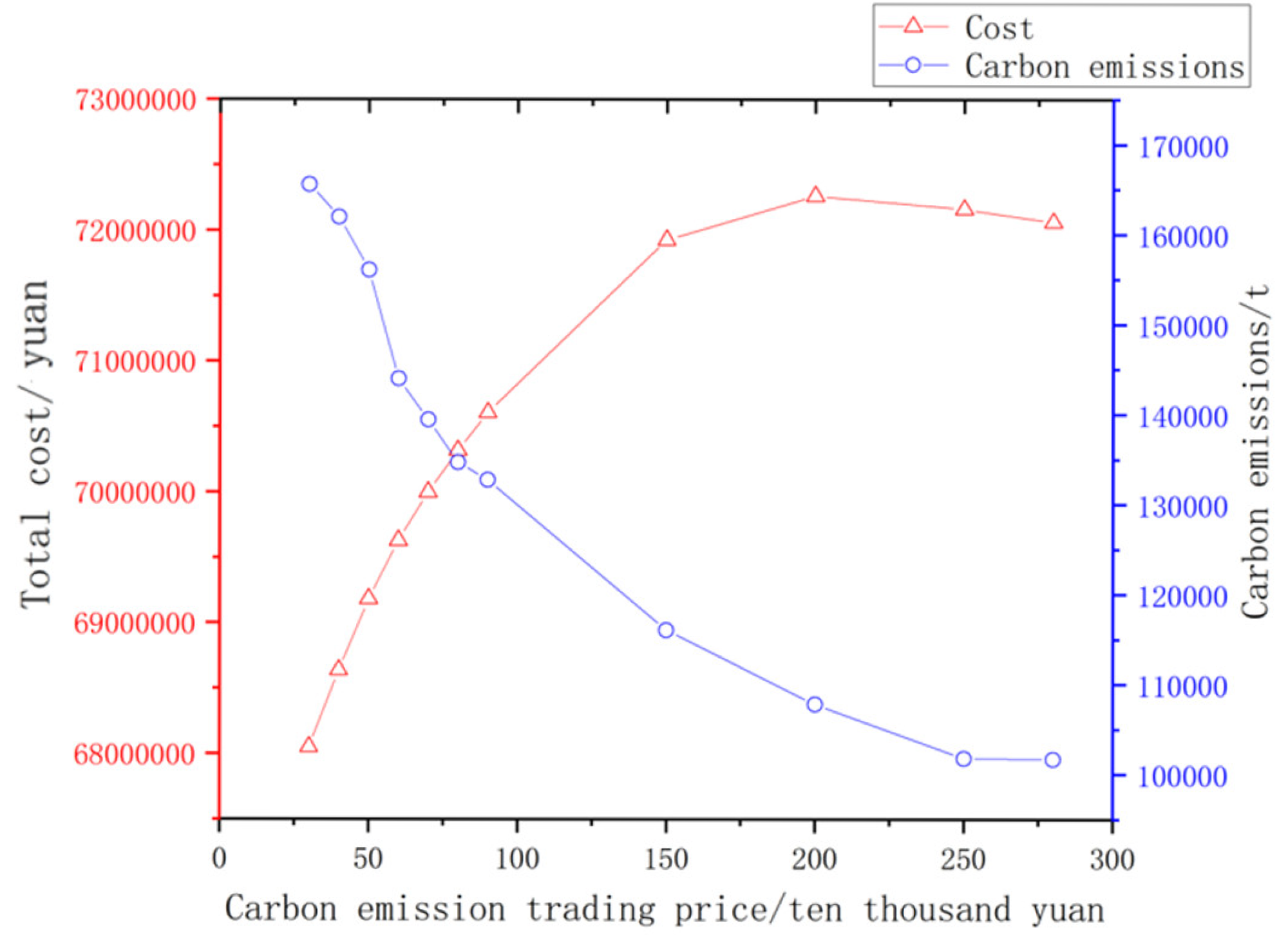
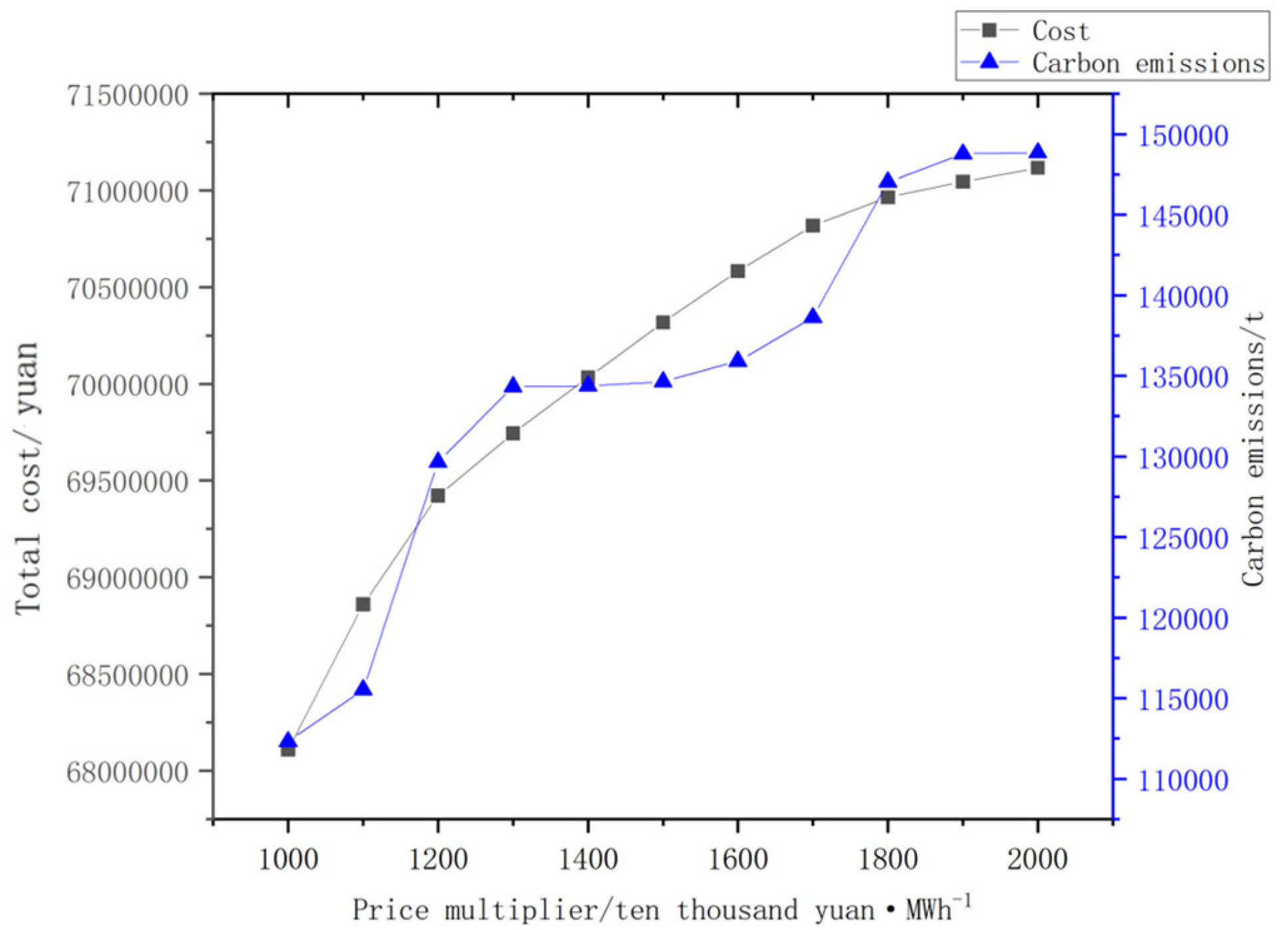
- Sensitivity analysis of carbon reduction measures
- (3)
- Comparison of Optimization Methods
6. Conclusions
- (1)
- When carbon trading and load shedding are present in the optimization scenarios, they can effectively reduce carbon emissions but will increase the cost of operating the system by approximately 125 CNY per ton of carbon emissions reduced using carbon trading and 80 CNY per ton of carbon emissions reduced using load shedding.
- (2)
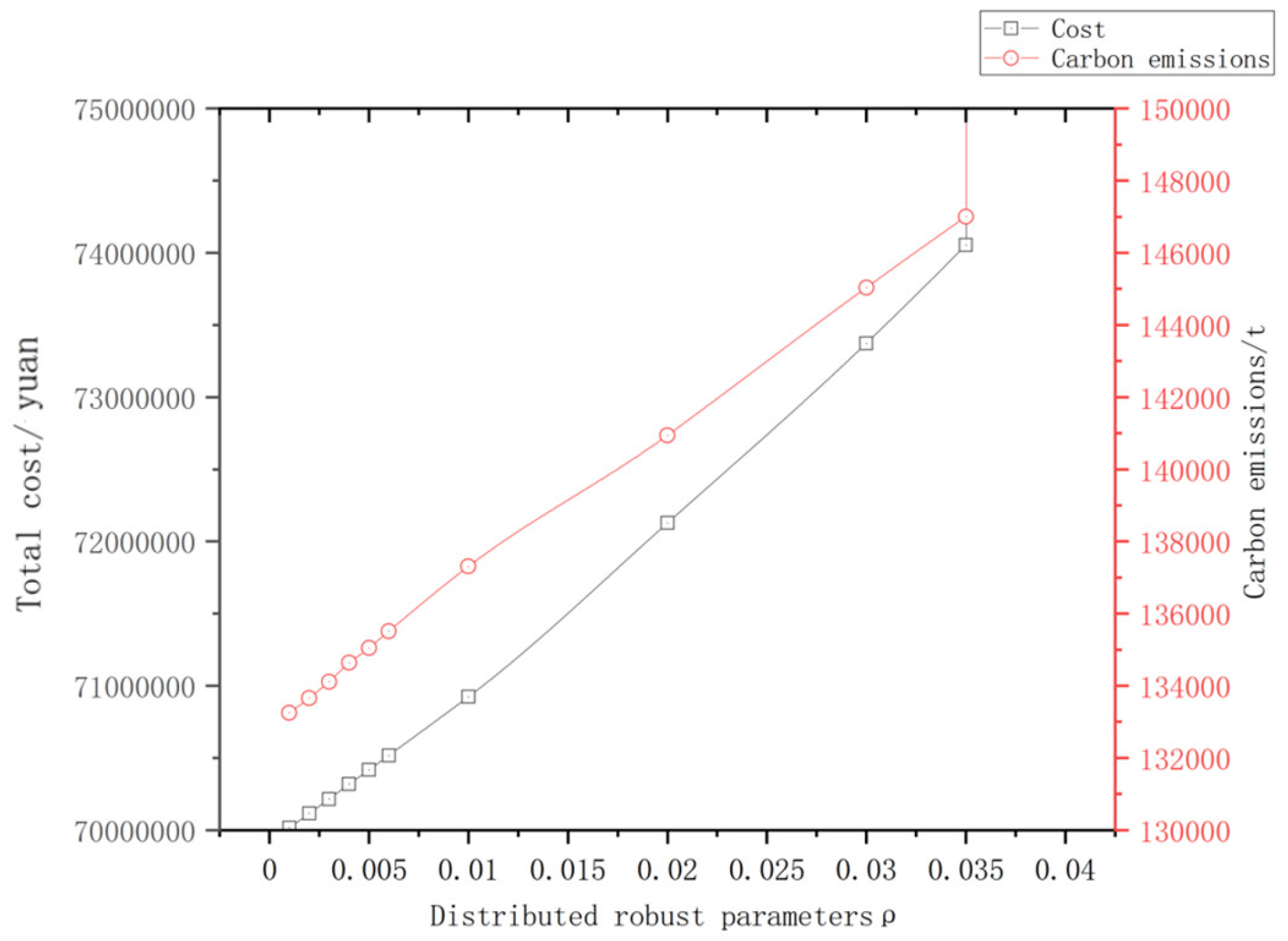
- With the enhancement of carbon trading price, the total operating cost of the system first rises and then falls; the enhancement of load shedding price will lead to an increase in carbon emissions, and when the cost of load shedding is too high, it will no longer be adopted as a way of emission reduction; within a certain range, the distribution robustness parameter d has a small impact on the system cost and carbon emissions, and the reasonable adjustment of this parameter is conducive to the promotion of the system’s economic and low-carbon operation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.; Lan, X.; Ye, J.; Huang, H.; Xu, Y.; Ji, A.; Hu, X. The goal and path of source network load storage coordination and interaction to help the construction of a new power system. J. Phys. Conf. Ser. 2023, 2636, 012013. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, X.; Zhong, J.; Ma, N. Low carbon multi-objective scheduling of integrated energy system based on ladder light robust optimization. Int. Trans. Electr. Energy Syst. 2020, 30, e12498. [Google Scholar] [CrossRef]
- Meng, Z.; Dong, F.; Chi, L. Optimal dispatch of integrated energy system with P2G considering carbon trading and demand response. Environ. Sci. Pollut. Res. Int. 2023, 30, 104284–104303. [Google Scholar] [CrossRef] [PubMed]
- Babahammou, R.H.; Merabet, A.; Miles, A. Technical modelling and simulation of integrating hydrogen from solar energy into a gas turbine power plant to reduce emissions. Int. J. Hydrogen Energy 2024, 59, 343–353. [Google Scholar] [CrossRef]
- PraveenKumar, S.; Kumar, A. Thermodynamic, environmental and economic analysis of solar photovoltaic panels using aluminium reflectors and latent heat storage units: An experimental investigation using passive cooling approach. J. Energy Storage 2025, 112, 115487. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Z. Low carbon economic dispatching model for a virtual power plant connected to carbon capture system considering green certificates-carbon trading mechanism. Sustain. Energy Technol. Assess. 2023, 60, 103575. [Google Scholar] [CrossRef]
- Su, Z.; Yang, L. Peak shaving strategy for renewable hybrid system driven by solar and radiative cooling integrating carbon capture and sewage treatment. Renew. Energy 2022, 197, 1115–1132. [Google Scholar] [CrossRef]
- Boré, A.; Dziva, G.; Chu, C.; Huang, Z.; Liu, X.; Qin, S.; Ma, W. Achieving sustainable emissions in China: Techno-economic analysis of post-combustion carbon capture unit retrofitted to WTE plants. J. Environ. Manag. 2023, 349, 119280. [Google Scholar] [CrossRef]
- Li, M.; Qin, J.; Han, Z.; Niu, Q. Low-carbon economic optimization method for integrated energy systems based on life cycle assessment and carbon capture utilization technologies. Energy Sci. Eng. 2023, 11, 4238–4255. [Google Scholar] [CrossRef]
- Talaie, M.; Jabari, F.; Foroud, A.A. Modeling and economic dispatch of a novel fresh water, methane and electricity generation system considering green hydrogenation and carbon capture. Energy Convers. Manag. 2024, 302, 118087. [Google Scholar] [CrossRef]
- Kumar, T.R.; Beiron, J.; Biermann, M.; Harvey, S.; Thunman, H. Plant and system-level performance of combined heat and power plants equipped with different carbon capture technologies. Appl. Energy 2023, 338, 120927. [Google Scholar] [CrossRef]
- Li, M.; Gao, H.; Abdulla, A.; Shan, R.; Gao, S. Combined effects of carbon pricing and power market reform on CO2 emissions reduction in China’s electricity sector. Energy 2022, 257, 124739. [Google Scholar] [CrossRef]
- Wang, H.-r.; Feng, T.-T.; Zhong, C. Effectiveness of CO2 cost pass-through to electricity prices under “electricity-carbon” market coupling in China. Energy 2023, 266, 126387. [Google Scholar] [CrossRef]
- Ma, X.; Pan, Y.; Zhang, M.; Ma, J.; Yang, W. Impact of carbon emission trading and renewable energy development policy on the sustainability of electricity market: A stackelberg game analysis. Energy Econ. 2024, 129, 107199. [Google Scholar] [CrossRef]
- Ou, Z.; Yang, K.; Lou, Y.; Peng, S.; Li, P.; Zhou, Q. Consider Carbon Emission Flow Analysis of Power System with Regards to Power Loss and Wind Power Uncertainty. J. Phys. Conf. Ser. 2023, 2584, 012107. [Google Scholar] [CrossRef]
- Wang, G.; Ma, H.; Wang, B.; Alharbi, A.M.; Wang, H.; Ma, F. Multi-Objective Optimal Power Flow Calculation Considering Carbon Emission Intensity. Sustainability 2023, 15, 16953. [Google Scholar] [CrossRef]
- Chen, S.; Sun, B.; He, Z.; Wu, Z. Calculation method of carbon emission flow in power system based on the theory of power flow calculation. In Proceedings of the 2015 6th International Conference on Manufacturing Science and Engineering, Begawan, Brunei, 1–2 June 2015. [Google Scholar]
- Huang, J.; Duan, W.; Zhou, Q.; Zeng, H. Methodology for carbon emission flow calculation of integrated energy systems. Energy Rep. 2022, 8, 1090–1097. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Lee, Y.K. Two-Layer Robust Distributed Predictive Control for Load Frequency Control of a Power System under Wind Power Fluctuation. Energies 2023, 16, 4714. [Google Scholar] [CrossRef]
- Li, J.; Xiao, Y.; Lu, S. Optimal configuration of multi microgrid electric hydrogen hybrid energy storage capacity based on distributed robustness. J. Energy Storage 2024, 76, 109762. [Google Scholar] [CrossRef]
- Zhao, X.; Xu, Q.; Yang, Y.; Zhou, G. Distributed distributionally robust optimization of distribution network incorporating novel battery charging and swapping station. Int. J. Electr. Power Energy Syst. 2024, 155 Pt B, 109643. [Google Scholar] [CrossRef]
- Li, M.; Furifu, C.; Ge, C.; Zheng, Y.; Lin, S.; Liu, R. Distributed Robust Optimal Dispatch for the Microgrid Considering Output Correlation between Wind and Photovoltaic. Energy Eng. 2023, 120, 1775–1801. [Google Scholar] [CrossRef]
- Wang, J.; Wu, H.; Duan, H.; Zillante, G.; Zuo, J.; Yuan, H. Combining life cycle assessment and Building Information Modelling to account for carbon emission of building demolition waste: A case study. J. Clean. Prod. 2018, 172, 3154–3166. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, Z.; Zhang, W.; Borhani, T.N.; Li, R.; Zhang, Z. Life cycle assessment f combustion-based electricity generation technologies integrated with carbon capture and storage: A review. Environ. Res. 2022, 207, 112219. [Google Scholar] [CrossRef] [PubMed]
- Ordoudis, C.; Nguyen, V.A.; Kuhn, D.; Pinson, P. Energy and reserve dispatch with distributionally robust joint chance constraints. Oper. Res. Lett. A J. Oper. Res. Soc. Am. 2021, 49, 291–299. [Google Scholar] [CrossRef]


| Generators | Maximum Output MW | Minimum Output MW | Coal or Gas Consumption Parameters a | Coal Consumption Parameters b | Coal or Gas Consumption Parameters c |
|---|---|---|---|---|---|
| coal burner 1 | 1000 | 300 | 0.0015 | 0.27 | 15.23 |
| coal burner 2 | 1000 | 300 | 0.0015 | 0.27 | 15.23 |
| coal burner 3 | 600 | 180 | 0.0023 | 0.274 | 11.71 |
| coal burner 4 | 600 | 180 | 0.0023 | 0.274 | 11.71 |
| coal burner 5 | 600 | 180 | 0.0023 | 0.274 | 11.71 |
| coal burner 6 | 450 | 135 | 0.00336 | 0.293 | 8.88 |
| coal burner 7 | 450 | 135 | 0.00336 | 0.293 | 8.88 |
| coal burner 8 | 450 | 135 | 0.00336 | 0.293 | 8.88 |
| coal burner 9 | 200 | 70 | 0.00426 | 0.321 | 5.14 |
| coal burner 10 | 200 | 70 | 0.00426 | 0.321 | 5.14 |
| coal burner 11 | 150 | 45 | 0.00558 | 0.332 | 3.54 |
| coal burner 12 | 150 | 45 | 0.00558 | 0.332 | 3.54 |
| gas engine 1 | 300 | 80 | 0.00217 | / | 6.88 |
| gas engine 2 | 300 | 80 | 0.00217 | 3.14 | |
| gas engine 3 | 120 | 50 | 0.00217 | 3.14 | |
| gas engine 4 | 120 | 50 | 0.00247 | 2.54 | |
| wind turbine | 1500 | 0 | / | ||
| photovoltaic unit | 2000 | 0 | |||
| Load Shedding/MW | Prices/CNY·MWh−1 |
|---|---|
| 0–200 | 250 |
| 200–500 | 360 |
| 500–700 | 430 |
| 700–800 | 550 |
| Carbon Trading Volume/t | Prices/CNY·t−1 |
|---|---|
| 40 | |
| 60 | |
| 90 |
| Scenarios | Costs/CNY | Carbon Footprint/t |
|---|---|---|
| 1 | 71,317,876.86 | 134,636.42 |
| 2 | 70,758,017.43 | 148,848.16 |
| 3 | 66,856,792.55 | 170,248.98 |
| 4 | 65,987,341.52 | 181,174.54 |
| Methodologies | Costs/CYN | Carbon Emissions/t |
|---|---|---|
| Distributed robustness | 70,015,652 | 133,253.2 |
| robustness | 70,919,230 | 136,447.4 |
| Stochastic optimization | 69,833,879 | 133,945.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xi, P.; Yang, C.; Xu, X.; Li, H.; Lu, S.; Li, J. A Robust Low-Carbon Optimal Dispatching Method for Power System Distribution Based on LCA Carbon Emissions. Energies 2025, 18, 3522. https://doi.org/10.3390/en18133522
Xi P, Yang C, Xu X, Li H, Lu S, Li J. A Robust Low-Carbon Optimal Dispatching Method for Power System Distribution Based on LCA Carbon Emissions. Energies. 2025; 18(13):3522. https://doi.org/10.3390/en18133522
Chicago/Turabian StyleXi, Peng, Chenguang Yang, Xiaobin Xu, Hangtian Li, Shiqiang Lu, and Jinchao Li. 2025. "A Robust Low-Carbon Optimal Dispatching Method for Power System Distribution Based on LCA Carbon Emissions" Energies 18, no. 13: 3522. https://doi.org/10.3390/en18133522
APA StyleXi, P., Yang, C., Xu, X., Li, H., Lu, S., & Li, J. (2025). A Robust Low-Carbon Optimal Dispatching Method for Power System Distribution Based on LCA Carbon Emissions. Energies, 18(13), 3522. https://doi.org/10.3390/en18133522






