Dynamic Identification Method of Distribution Network Weak Links Considering Disaster Emergency Scheduling
Abstract
1. Introduction
2. The Real-Time Failure Rate Index of Distribution Network Lines
2.1. Batts Typhoon Model
2.2. Distribution Network Line Fault Model During Typhoon
2.2.1. Wind Load on Overhead Line Conductors
2.2.2. Wind Load on Overhead Line Poles
2.2.3. Total Load of Overhead Line Poles
2.2.4. Failure Rate of Overhead Line Poles
2.2.5. Overhead Line Failure Rate
2.2.6. Failure Rate of Overhead Line Based on Monte Carlo Simulation
3. The Index of Line Degree and Line Betweenness Based on Complex Network Theory
3.1. Improved Bus Degrees
3.2. Line Degrees
3.3. Line Betweenness
4. Load Loss Index
4.1. Objective Function
4.2. Constraints
4.2.1. Energy Storage Operation Constraints
4.2.2. Gas Turbine Operating Constraints
4.2.3. Bus Power Balance Constraints
4.2.4. Power Flow Equality Constraints
4.2.5. Voltage Constraints
4.2.6. Line Capacity Constraints
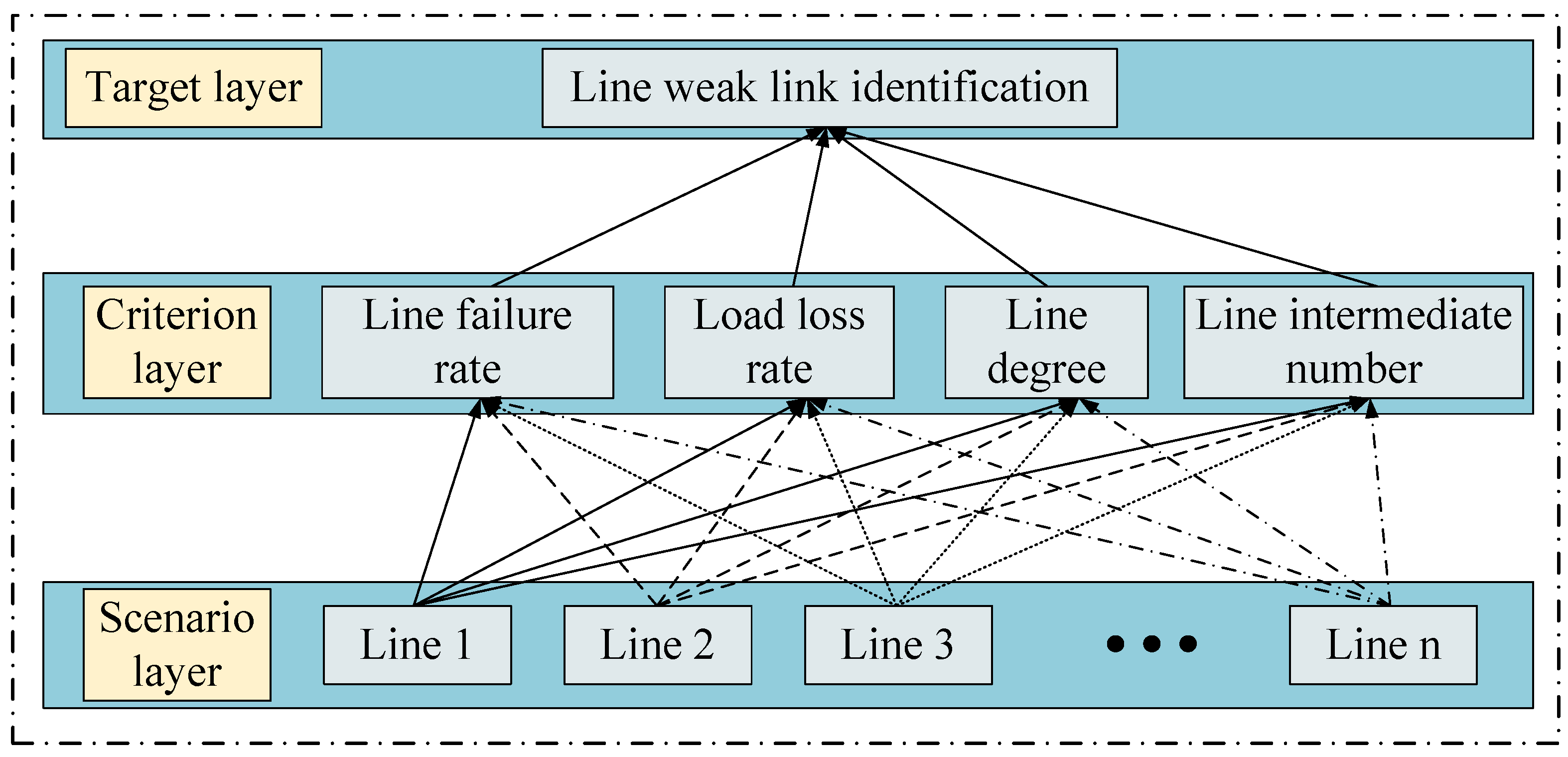
5. Distribution Network Weak Link Identification Comprehensive Index
5.1. Aggregative Index
5.2. Analytic Hierarchy Process
5.2.1. Establishing the Hierarchical Structure Model
5.2.2. Comparison Matrix Construction
5.2.3. Weight Matrix Calculation and Consistency Check
5.3. Entropy Weight Method
5.3.1. Index Proportion Calculation
5.3.2. Entropy Index Value Calculation
5.3.3. Entropy Weight Calculation
5.3.4. Subjective and Objective Comprehensive Weight Calculation
5.4. TOPSIS Method Comprehensive Weight Analysis
5.4.1. Original Matrix Standardization
5.4.2. Weighted Index Evaluation Matrix Calculation
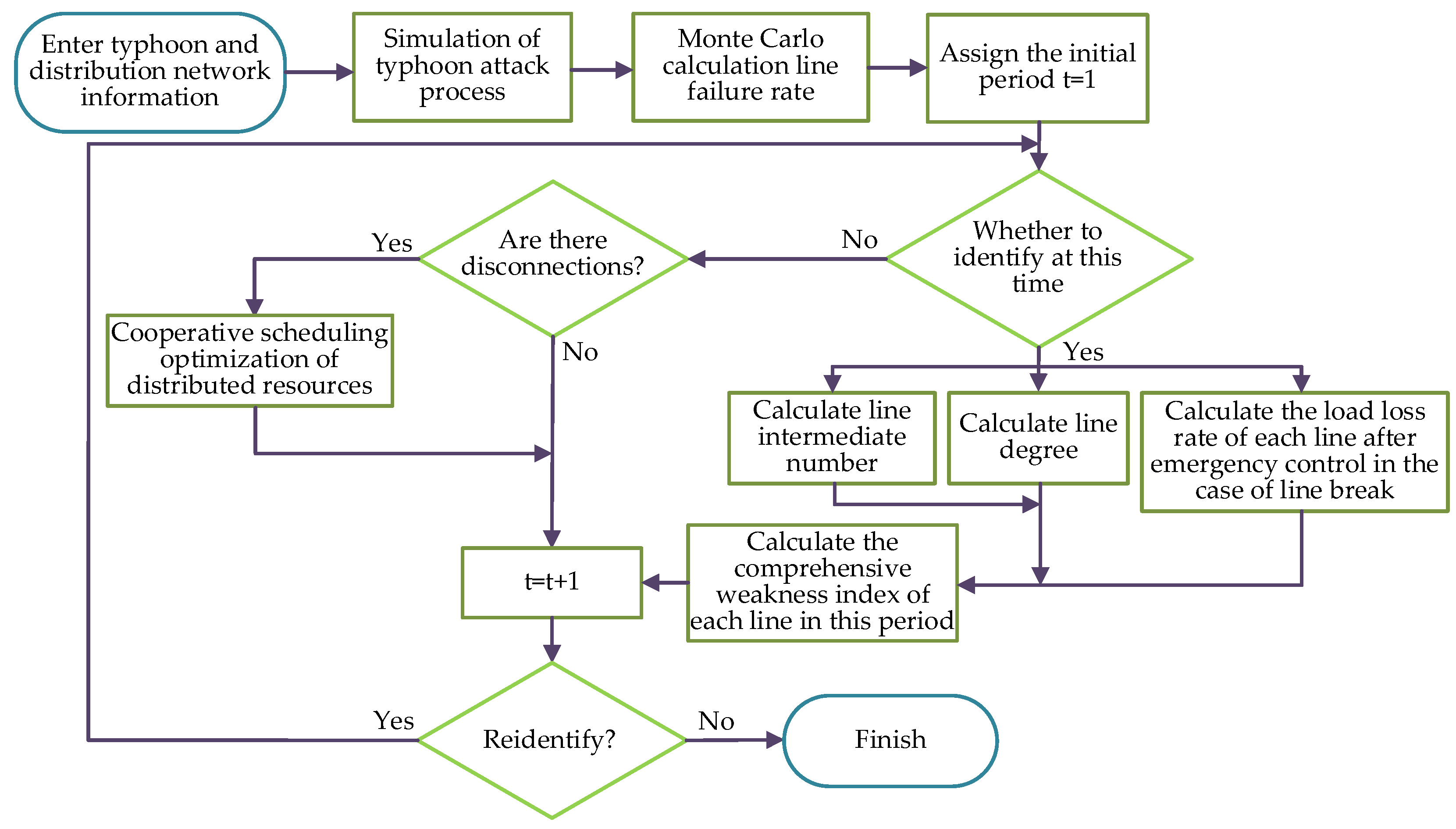
5.5. Solving Process of Identification Model
6. Case Study
6.1. Introduction of the Case
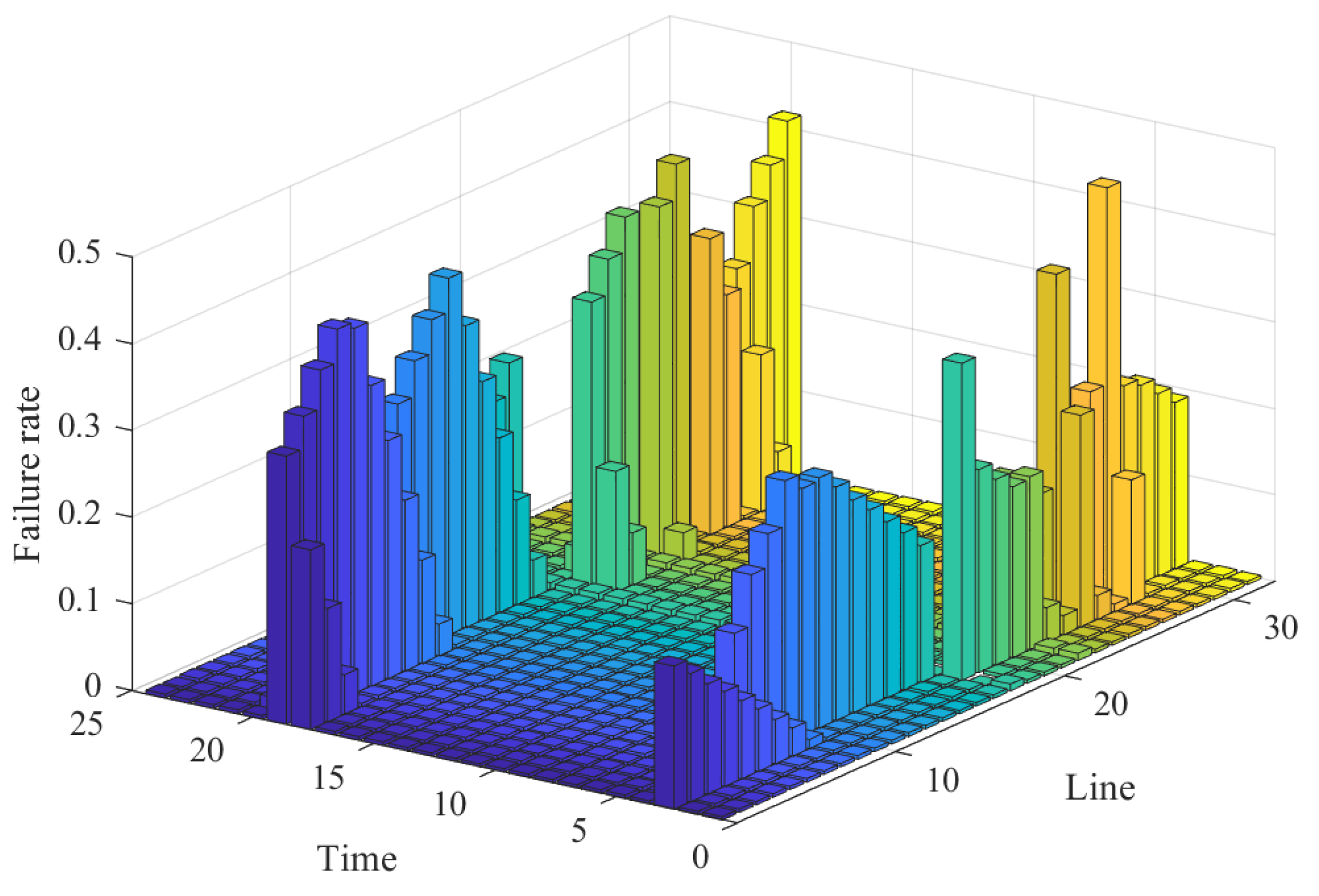
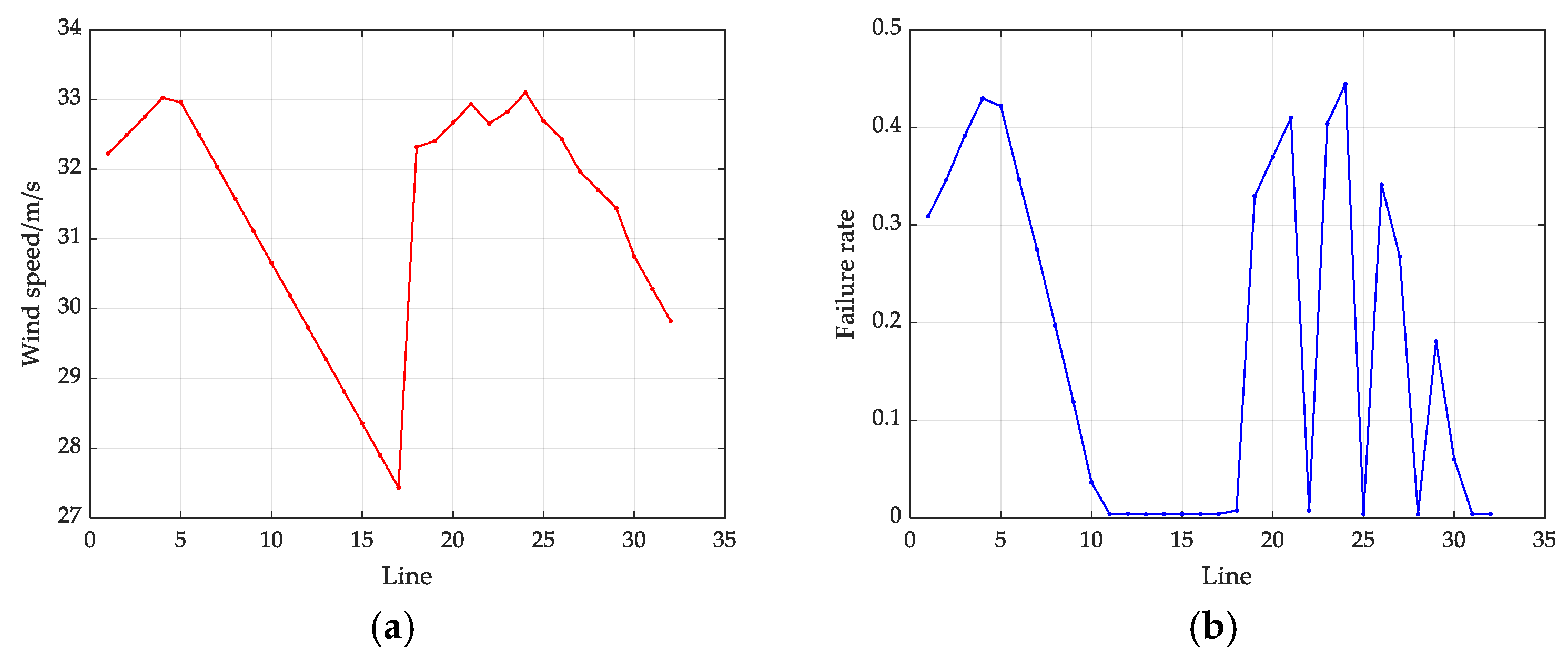
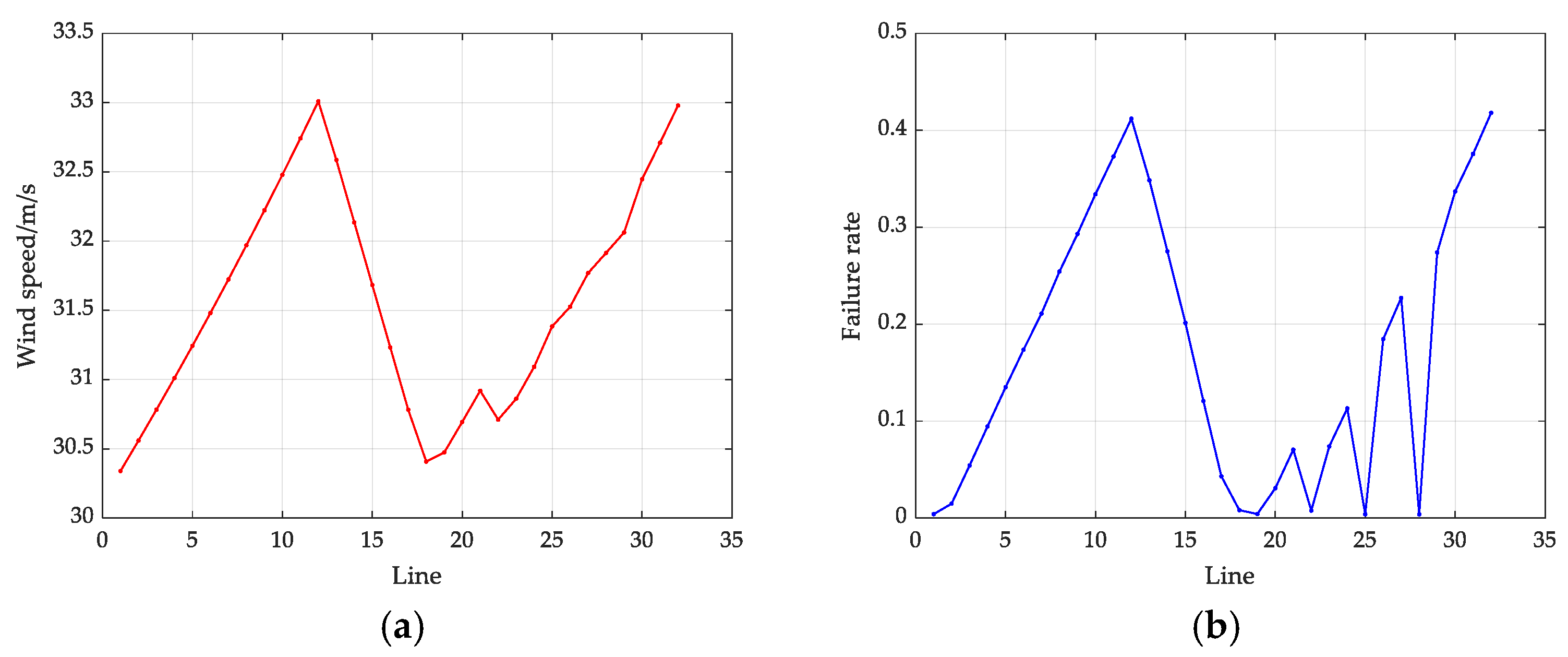
6.2. Real-Time Failure Rate Change Diagram of Each Line
6.3. Identification and Analysis of Weak Links in Distribution Network During Existing Line Failures
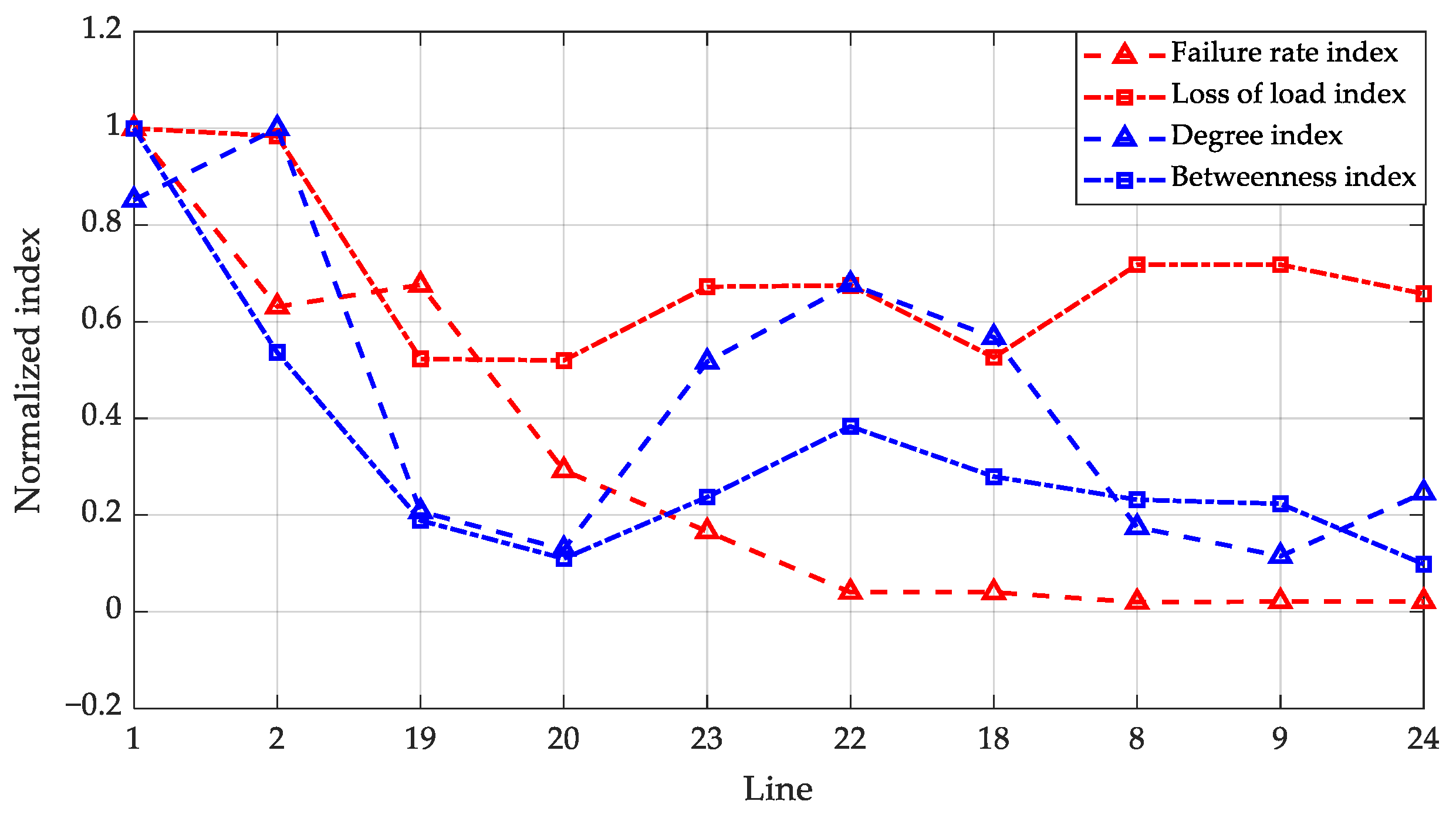
6.3.1. Analysis of Identification Results of Line Weak Links
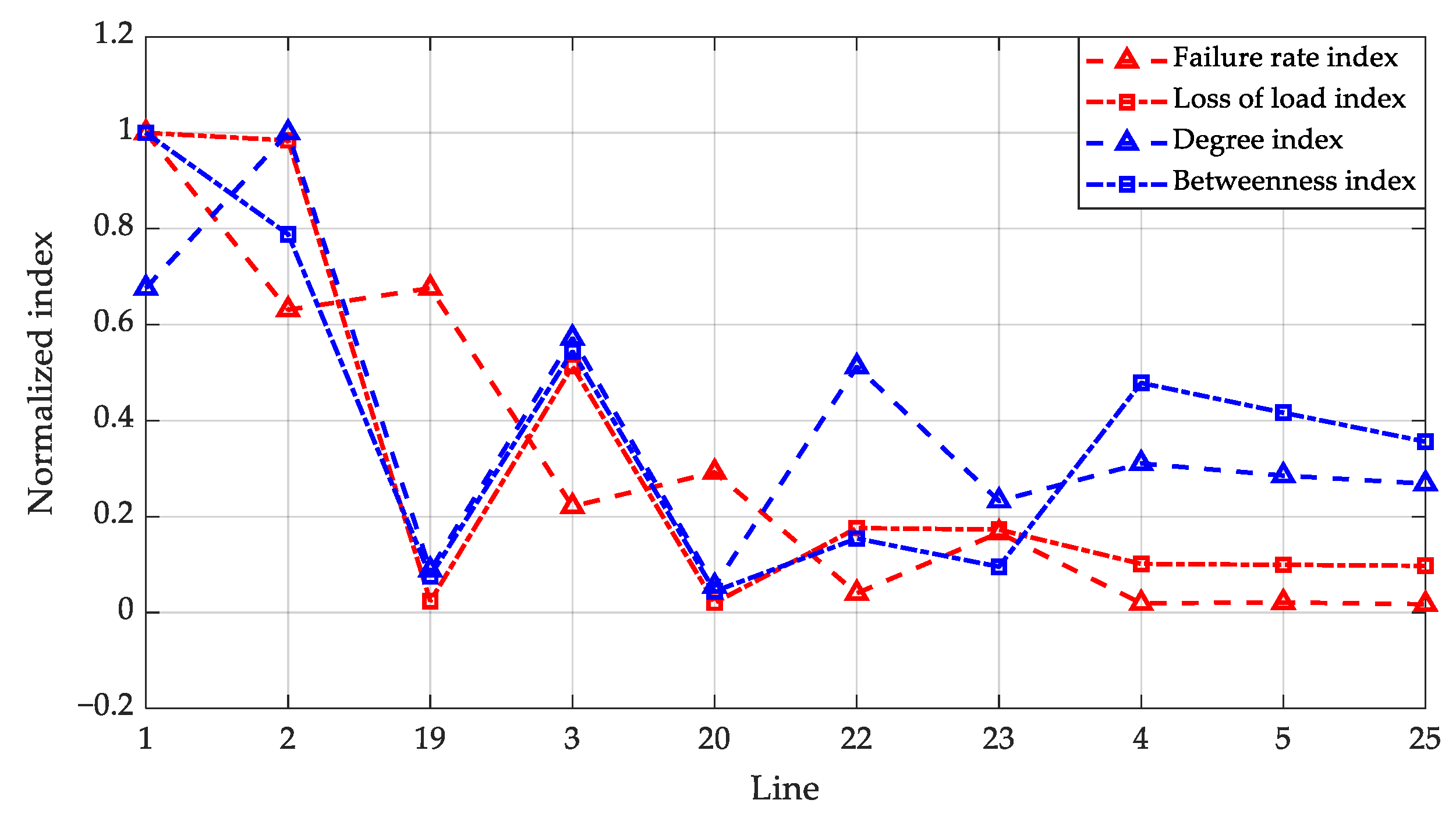
6.3.2. Analysis of Each Index of Line Weakness
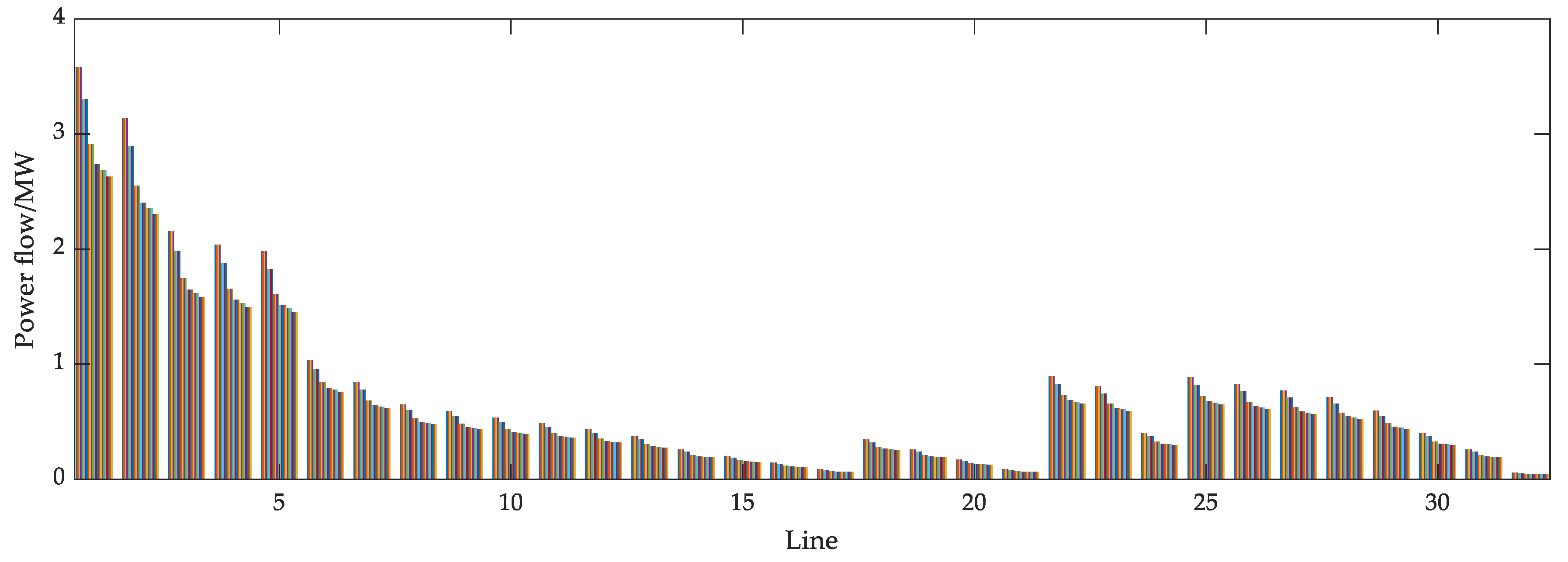
6.3.3. Power Flow Change of Each Line During the Identification Period
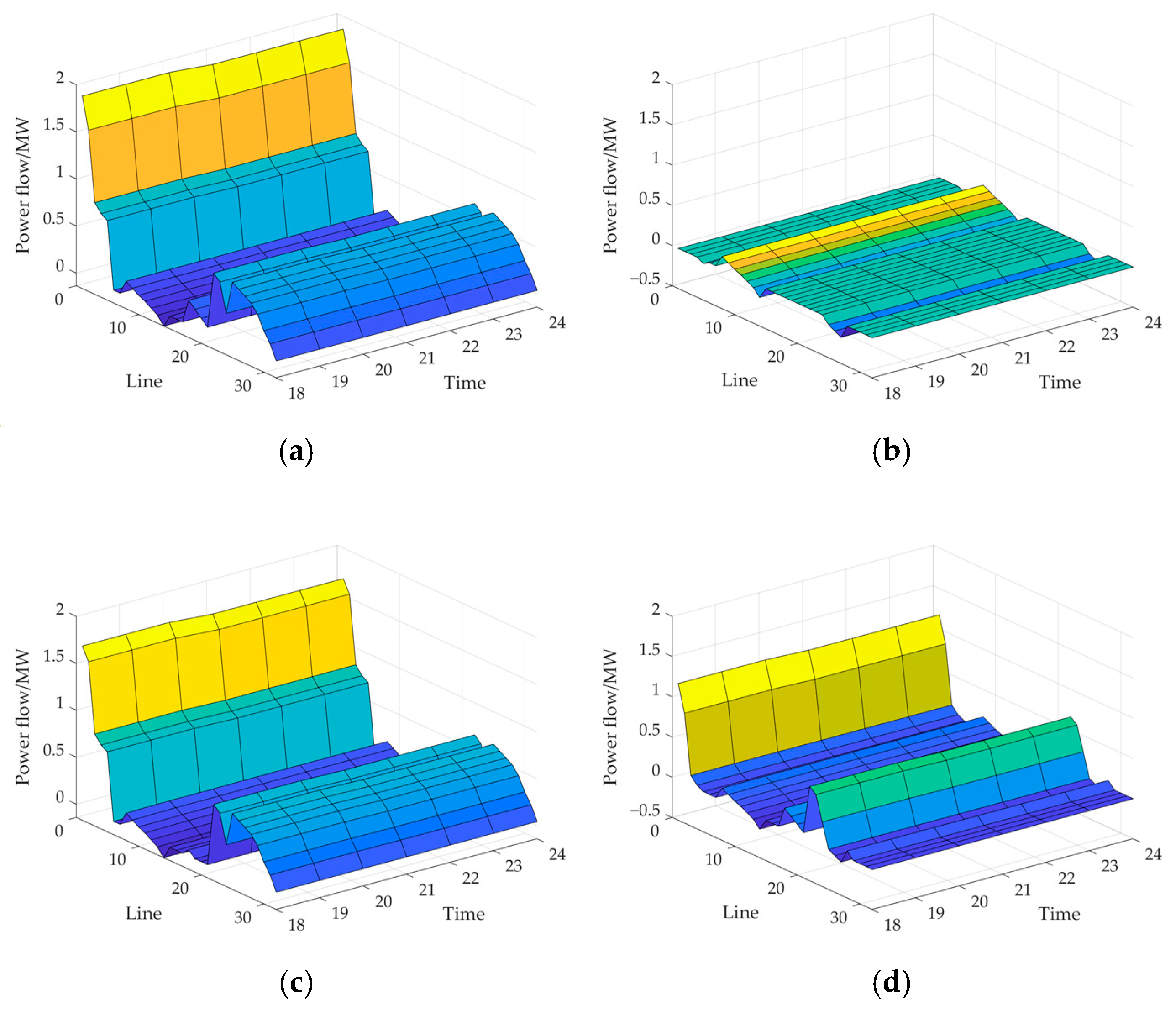
6.3.4. The Output Change of Each Distributed Resource After the Identification Period
6.4. Comparison of Identification Results of Weak Links Under Different Failure Conditions
6.5. Comparison of Identification Results of Weak Links in Different Identification Periods
7. Conclusions
- (1)
- The Batts typhoon model can be used to simulate the whole process of a typhoon impacting the distribution network, and the wind speed variation characteristics of each point in the distribution network can be obtained. Based on the overhead line and pole wind load model, the Monte Carlo method can be effectively applied to the calculation of the failure rate of distribution network lines, taking into account the random characteristics of line failure.
- (2)
- The subjective and objective comprehensive evaluation method combining AHP, entropy weight, and TOPSIS can not only unify the size of each index value, but also assign a comprehensive weight according to the change characteristics of each index value, which is very suitable for the identification of weak links in the distribution network using multiple indexes.
- (3)
- The results show that the model proposed in this paper can effectively realize the dynamic identification of distribution network weak links under the consideration of distributed resource emergency power supply, the identification results can be dynamically changed according to different fault situations and different time periods, and the identification results can give more comprehensive early warning information considering the failure rate, distribution network structure, and load loss.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, F.; Xie, R.; Yang, B.; Guo, L.; Ma, P.; Shi, J.; Ye, M.; Song, W. Detection and identification of cyber and physical attacks on distribution power grids with pvs: An online high-dimensional data-driven approach. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 1282–1291. [Google Scholar] [CrossRef] [PubMed]
- Zolanvari, M.; Teixeira, M.A.; Gupta, L.; Gupta, L.; Khan, K.M.; Jain, R. Machine learning-based network vulnerabilityanalysis of industrial internet of things. IEEE Internet. Things J. 2019, 6, 6822–6834. [Google Scholar] [CrossRef]
- Wang, M.; Xiang, Y.; Wang, L.; Yu, D.; Jiang, J. Critical line identification for hypothesized multiple line attacks against power systems. In Proceedings of the 2016 IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016; pp. 1–5. [Google Scholar]
- Adebayo, I.G.; Jimoh, A.A.; Yusuff, A.A. Detection of weak bus through fast voltage stability index and inherent structural characteristics of power system. In Proceedings of the 4th International Conference on Electric Power and Energy Conversion Systems (EPECS), Sharjah, United Arab Emirates, 24–26 November 2015; pp. 1–5. [Google Scholar]
- Liu, Y.; Li, Z.; Wei, W.; Zheng, J.; Zhang, H. Data-driven dispatchable regions with valid boundaries for renewable power generation: Concept and construction. IEEE Trans. Sustain. Energy 2022, 13, 882–891. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Wu, L.; Lu, P.; Zhang, S. Transmission line overload risk assessment for power systems with wind and load-power generation correlation. IEEE Trans. Smart Grid 2015, 6, 1233–1242. [Google Scholar] [CrossRef]
- Hu, A.; Fan, X.; Huang, D.; Zhang, F.; Shi, S. Risk assessment of distribution lines in typhoon weather considering socio-economic factors. Energies 2023, 16, 6664. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; He, J.; He, L.; Ye, Z.; Liu, Z. Renewable energy real-time carrying capacity assessment method and response strategy under typhoon weather. Energies 2024, 17, 1401. [Google Scholar] [CrossRef]
- Li, G.; Zhang, P.; Luh, P.B.; Li, W.; Bie, Z.; Serna, C.; Zhao, Z. Risk analysis for distribution systems in the northeast U.S. under wind storms. IEEE Trans. Power Syst. 2014, 29, 889–898. [Google Scholar] [CrossRef]
- Bjarnadottir, S.; Li, Y.; Stewart, M.G. Hurricane risk assessment of power distribution poles considering impacts of a changing climate. J. Infrastruct. Syst. 2013, 19, 12–24. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Lei, S.; Wang, Z.; Wu, F.; Hou, Y. Markov decision process-based resilience enhancement for distribution systems: An approximate dynamic programming approach. IEEE Trans. Smart Grid 2020, 11, 2498–2510. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.; Wu, Q.; Terzija, V. A numerical approach for hybrid simulation of power system dynamics considering extreme icing events. IEEE Trans. Smart Grid 2018, 9, 5038–5046. [Google Scholar] [CrossRef]
- Yang, H.; Chung, C.Y.; Zhao, J.; Dong, Z. A probability model of ice storm damages to transmission facilities. IEEE Trans. Power Deliv. 2013, 28, 557–565. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, W.; Liu, Y.; Xin, Y.; Wu, Q. Quantitative resilience assessment for power transmission systems under typhoon weather. IEEE Access 2018, 6, 40747–40756. [Google Scholar] [CrossRef]
- Arroyo, J.M. Bilevel programming applied to power system vulnerability analysis under multiple contingencies. IET Gener. Transm. Distrib. 2010, 4, 178–190. [Google Scholar] [CrossRef]
- Wang, C.; Ju, P.; Wu, F.; Lei, S.; Pan, X. Sequential steady-state security region-based transmission power system resilience enhancement. Renew. Sustain. Energy Rev. 2021, 151, 111533. [Google Scholar] [CrossRef]
- Sun, P.; Dong, Y. On vulnerability analysis of nodes against cross-domain cascading failures propagation in active distribution network cyber-physical system. In Proceedings of the 7th International Conference on Dependable Systems and Their Application(DSA), Xi’an, China, 29 November 2020; pp. 355–363. [Google Scholar]
- Chen, K.; Zheng, N.; Cai, Q.; Li, Y.; Lin, C.; Li, L. Cyber-physical power system vulnerability analysis based on complex network theory. In Proceedings of the 6th Asia Conference on Power and Electrical Engineering(ACPEE), Chongqing, China, 8–11 April 2021; pp. 482–486. [Google Scholar]
- Darestani, Y.M.; Shafieezadeh, A.; DesRoches, R. Effects of adjacet spans and correlated failure events on sysyem-level hurricane reliability of power distribution lines. IEEE Trans. Power Del. 2018, 33, 2305–2314. [Google Scholar] [CrossRef]
- Poudel, S.; Ni, Z.; Sun, W. Electrical distance approach for searching vulnerable branches during contingencies. IEEE Trans. Smart Grid 2018, 9, 3373–3382. [Google Scholar] [CrossRef]
- Liu, H.; Wang, C.; Ju, P.; Li, H. A sequentially preventive model enhancing power system resilience against extreme-weather-triggered failures. Renew. Sustain. Energy Rev. 2022, 156, 111945. [Google Scholar] [CrossRef]
- Gupta, S.; Kazi, F.; Wagh, S.; Singh, N. Analysis and prediction of vulnerability in smart power transmission system: A geometrical approach. Int. J. Electr. Power Energy Syst. 2018, 94, 77–87. [Google Scholar] [CrossRef]
- Shafieezadeh, A.; Begovic, M.M.; DesRoches, R. Age-dependent fragility models of utility wood poles in power distribution networks against extreme wind hazards. IEEE Trans. Power Deliv. 2014, 29, 131–139. [Google Scholar] [CrossRef]
- Chen, W. Quantitative decision-making model for distribution system restoration. IEEE Trans. Power Syst. 2010, 25, 313–321. [Google Scholar] [CrossRef]
- Huang, Y.; Jiang, Y.; Wang, J. Adaptability evaluation of distributed power sources connected to distribution network. IEEE Access 2021, 9, 42409–42423. [Google Scholar] [CrossRef]
- Liu, N.; Zhang, J.; Zhang, H.; Liu, W. Security assessment for communication networks of power control systems using attack graph and MCDM. IEEE Trans. Power Del. 2010, 25, 1492–1500. [Google Scholar] [CrossRef]
- Wen, J.; Lin, S.; Qu, X.; Xiao, Q. A TOPSIS-based vulnerability assessment method of distribution network considering network topology and operation status. IEEE Access 2023, 11, 94358–94370. [Google Scholar] [CrossRef]
- Batts, M.E.; Cordes, M.R.; Russell, L.R.; Shaver, J.R.; Simiu, E. Hurricane wind speeds in the United States. J. Struct. Div. 1980, 106, 2001–2006. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of 66kV and Below Overhead Electrical Power Line; Ministry of Housing and Urban-Rural Development of the People’s Republic of China: Beijing, China, 2010. [Google Scholar]
- Baran, M.E.; Wu, F.F. Network reconfiguration in distribution systems for loss reduction and load balancing. IEEE Trans. Power Del. 1989, 4, 1401–1407. [Google Scholar] [CrossRef]
- Dolatabadi, S.H.; Ghorbanian, M.; Siano, P.; Hatziargyriou, N.D. An enhanced IEEE 33 bus benchmark test system for distribution system studies. IEEE Trans. Power Syst. 2021, 36, 2565–2572. [Google Scholar] [CrossRef]





| Comparative Scale | Significance | Comparative Scale | Significance |
|---|---|---|---|
| 1 | Pairwise comparisons are equally important | 7 | Pairwise is more important than the former |
| 3 | Pairwise is slightly more important than the former | 9 | Pairwise is more important than the former |
| 5 | Pairwise is obviously more important than the former | The importance is somewhere in the middle |
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 |
| Rank | Line | Index Value | Rank | Line | Index Value |
|---|---|---|---|---|---|
| 1 | 1 | 0.1975 | 17 | 24 | 0.0195 |
| 2 | 2 | 0.1611 | 18 | 29 | 0.0182 |
| 3 | 19 | 0.0922 | 19 | 30 | 0.0113 |
| 4 | 3 | 0.0814 | 20 | 14 | 0.0086 |
| 5 | 20 | 0.0451 | 21 | 31 | 0.0074 |
| 6 | 22 | 0.0387 | 22 | 10 | 0.0058 |
| 7 | 23 | 0.0372 | 23 | 12 | 0.0055 |
| 8 | 4 | 0.0346 | 24 | 13 | 0.0054 |
| 9 | 5 | 0.0315 | 25 | 11 | 0.0053 |
| 10 | 25 | 0.0285 | 26 | 32 | 0.0040 |
| 11 | 26 | 0.0254 | 27 | 21 | 0.0039 |
| 12 | 8 | 0.0253 | 28 | 16 | 0.0037 |
| 13 | 9 | 0.0250 | 29 | 17 | 0.0037 |
| 14 | 18 | 0.0235 | 30 | 7 | 0.0036 |
| 15 | 27 | 0.0229 | 31 | 15 | 0.0035 |
| 16 | 28 | 0.0209 | 32 | 6 | 0 |
| Rank | Line | Index Value | Rank | Line | Index Value |
|---|---|---|---|---|---|
| 1 | 1 | 0.1435 | 17 | 26 | 0.0215 |
| 2 | 2 | 0.1006 | 18 | 25 | 0.0208 |
| 3 | 19 | 0.0821 | 19 | 21 | 0.0206 |
| 4 | 20 | 0.0425 | 20 | 5 | 0.0204 |
| 5 | 23 | 0.0425 | 21 | 16 | 0.0202 |
| 6 | 22 | 0.0419 | 22 | 17 | 0.0202 |
| 7 | 18 | 0.0348 | 23 | 30 | 0.0202 |
| 8 | 8 | 0.0304 | 24 | 7 | 0.0201 |
| 9 | 9 | 0.0297 | 25 | 29 | 0.0201 |
| 10 | 24 | 0.0279 | 26 | 28 | 0.0201 |
| 11 | 14 | 0.0245 | 27 | 32 | 0.0201 |
| 12 | 10 | 0.0233 | 28 | 4 | 0.0201 |
| 13 | 11 | 0.0230 | 29 | 15 | 0.0201 |
| 14 | 13 | 0.0229 | 30 | 31 | 0.0201 |
| 15 | 12 | 0.0229 | 31 | 3 | 0 |
| 16 | 27 | 0.0225 | 32 | 6 | 0 |
| Rank | Line | Index Value | Rank | Line | Index Value |
|---|---|---|---|---|---|
| 1 | 2 | 0.1203 | 17 | 9 | 0.0267 |
| 2 | 1 | 0.1127 | 18 | 25 | 0.0238 |
| 3 | 3 | 0.0815 | 19 | 18 | 0.0186 |
| 4 | 4 | 0.0559 | 20 | 28 | 0.0173 |
| 5 | 5 | 0.0542 | 21 | 30 | 0.0123 |
| 6 | 24 | 0.0517 | 22 | 14 | 0.0067 |
| 7 | 23 | 0.0514 | 23 | 10 | 0.0065 |
| 8 | 26 | 0.0461 | 24 | 31 | 0.0057 |
| 9 | 21 | 0.0445 | 25 | 13 | 0.0038 |
| 10 | 20 | 0.0419 | 26 | 11 | 0.0037 |
| 11 | 19 | 0.0390 | 27 | 12 | 0.0036 |
| 12 | 27 | 0.0388 | 28 | 32 | 0.0022 |
| 13 | 8 | 0.0337 | 29 | 17 | 0.0015 |
| 14 | 7 | 0.0327 | 30 | 15 | 0.0015 |
| 15 | 22 | 0.0320 | 31 | 16 | 0.0015 |
| 16 | 29 | 0.0284 | 32 | 6 | 0 |
| Rank | Line | Index Value | Rank | Line | Index Value |
|---|---|---|---|---|---|
| 1 | 2 | 0.0810 | 17 | 5 | 0.0303 |
| 2 | 1 | 0.0791 | 18 | 4 | 0.0297 |
| 3 | 3 | 0.0561 | 19 | 22 | 0.0290 |
| 4 | 32 | 0.0441 | 20 | 7 | 0.0261 |
| 5 | 12 | 0.0439 | 21 | 15 | 0.0251 |
| 6 | 31 | 0.0419 | 22 | 23 | 0.0221 |
| 7 | 11 | 0.0411 | 23 | 25 | 0.0216 |
| 8 | 9 | 0.0407 | 24 | 24 | 0.0215 |
| 9 | 30 | 0.0396 | 25 | 18 | 0.0169 |
| 10 | 13 | 0.0393 | 26 | 16 | 0.0160 |
| 11 | 10 | 0.0382 | 27 | 28 | 0.0157 |
| 12 | 8 | 0.0376 | 28 | 21 | 0.0099 |
| 13 | 29 | 0.0367 | 29 | 17 | 0.0061 |
| 14 | 27 | 0.0341 | 30 | 19 | 0.0059 |
| 15 | 14 | 0.0338 | 31 | 20 | 0.0058 |
| 16 | 26 | 0.0312 | 32 | 6 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, W.; Lan, L.; Shen, L.; Shi, D.; Wang, C. Dynamic Identification Method of Distribution Network Weak Links Considering Disaster Emergency Scheduling. Energies 2025, 18, 3519. https://doi.org/10.3390/en18133519
Ji W, Lan L, Shen L, Shi D, Wang C. Dynamic Identification Method of Distribution Network Weak Links Considering Disaster Emergency Scheduling. Energies. 2025; 18(13):3519. https://doi.org/10.3390/en18133519
Chicago/Turabian StyleJi, Wenlu, Lan Lan, Lu Shen, Dahang Shi, and Chong Wang. 2025. "Dynamic Identification Method of Distribution Network Weak Links Considering Disaster Emergency Scheduling" Energies 18, no. 13: 3519. https://doi.org/10.3390/en18133519
APA StyleJi, W., Lan, L., Shen, L., Shi, D., & Wang, C. (2025). Dynamic Identification Method of Distribution Network Weak Links Considering Disaster Emergency Scheduling. Energies, 18(13), 3519. https://doi.org/10.3390/en18133519






