Balancing Solar Energy, Thermal Comfort, and Emissions: A Data-Driven Urban Morphology Optimization Approach
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.2.1. Single-Factor Studies
1.2.2. Comprehensive Multi-Factor Analysis of Urban Morphology
1.2.3. Machine Learning-Based Approaches and Optimization Strategies
1.3. Research Gap and Objectives
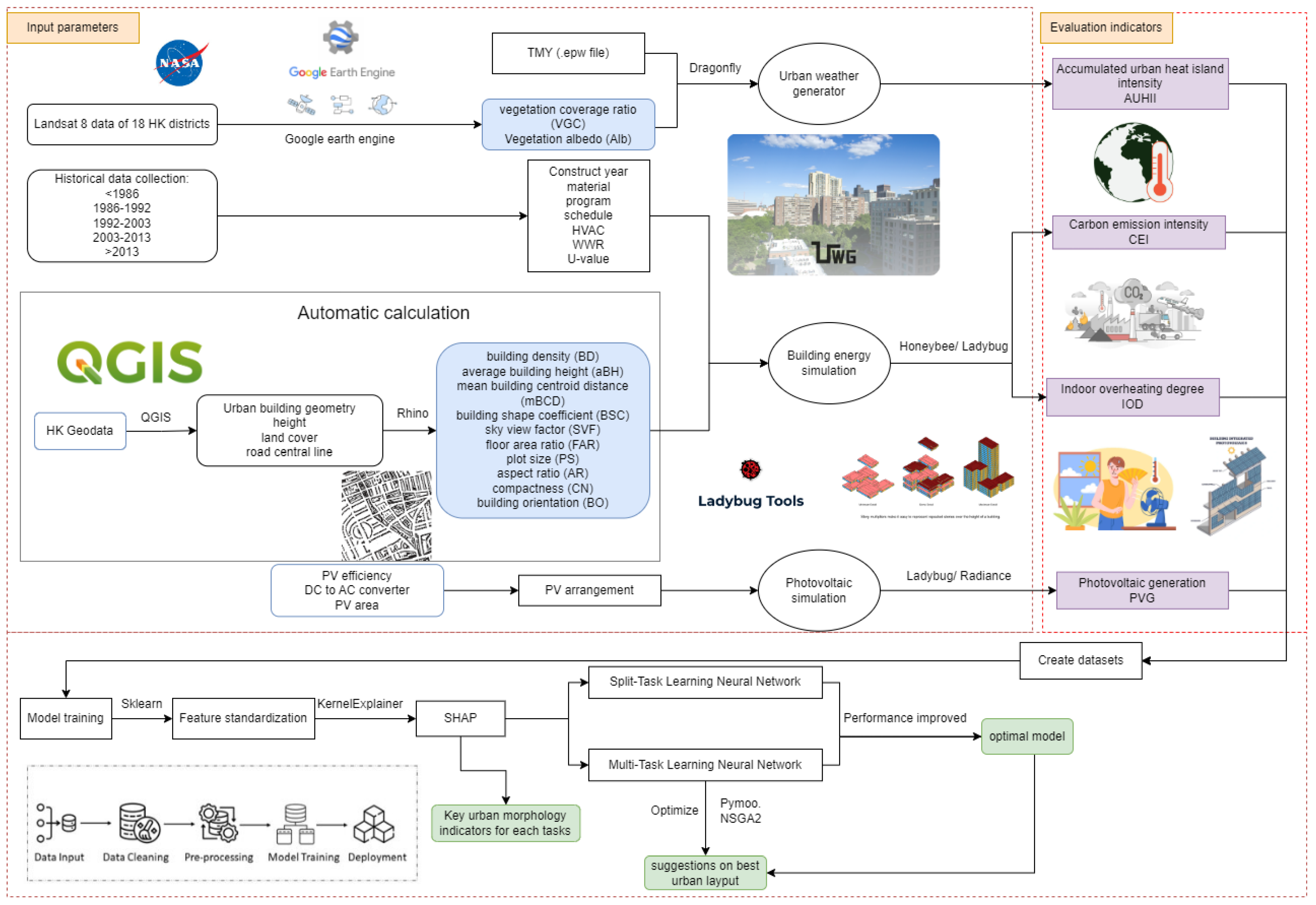
2. Methodology
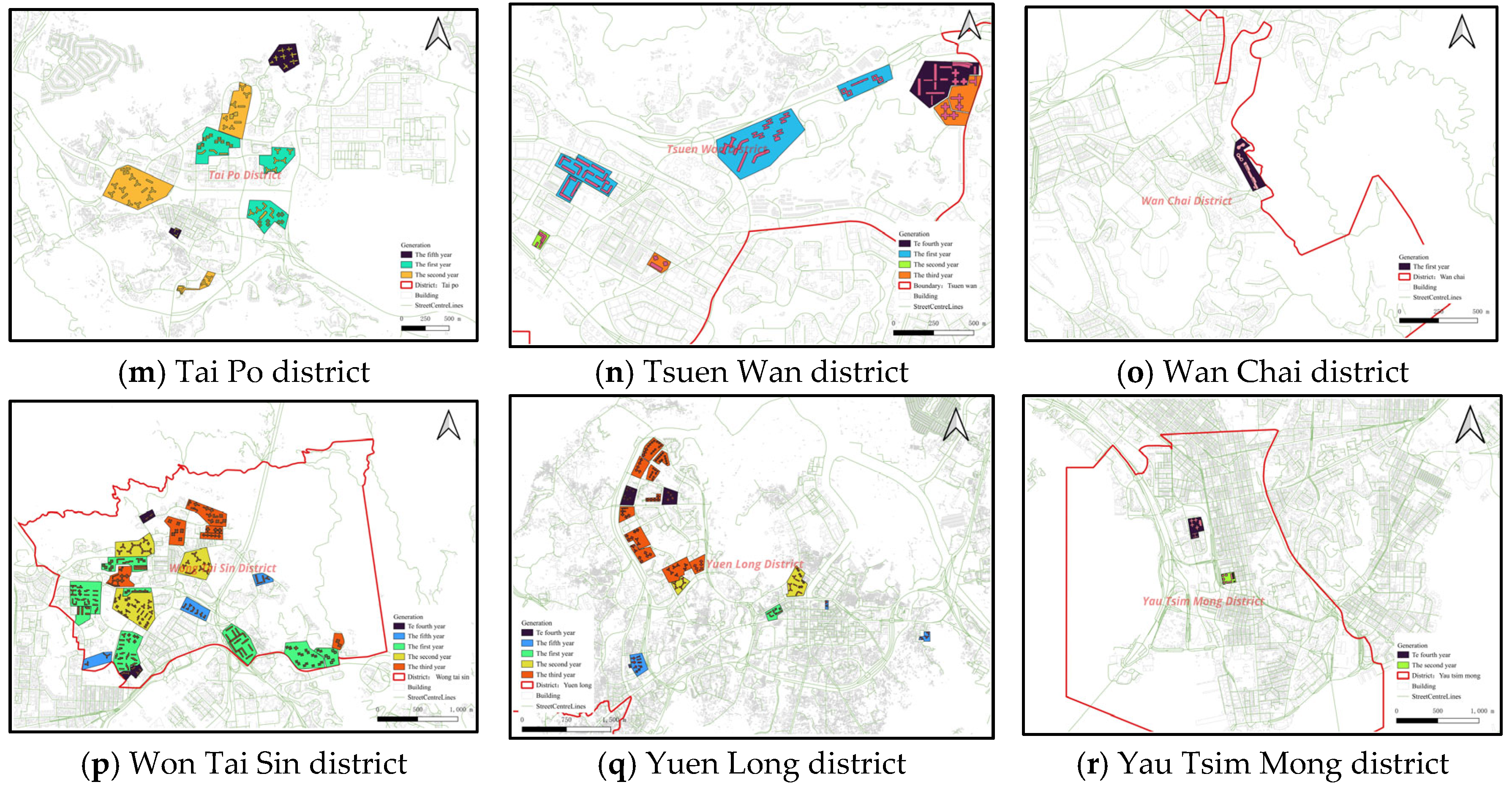
2.1. Study Area and Data Sources
2.2. Urban Morphology Indicators and Targets
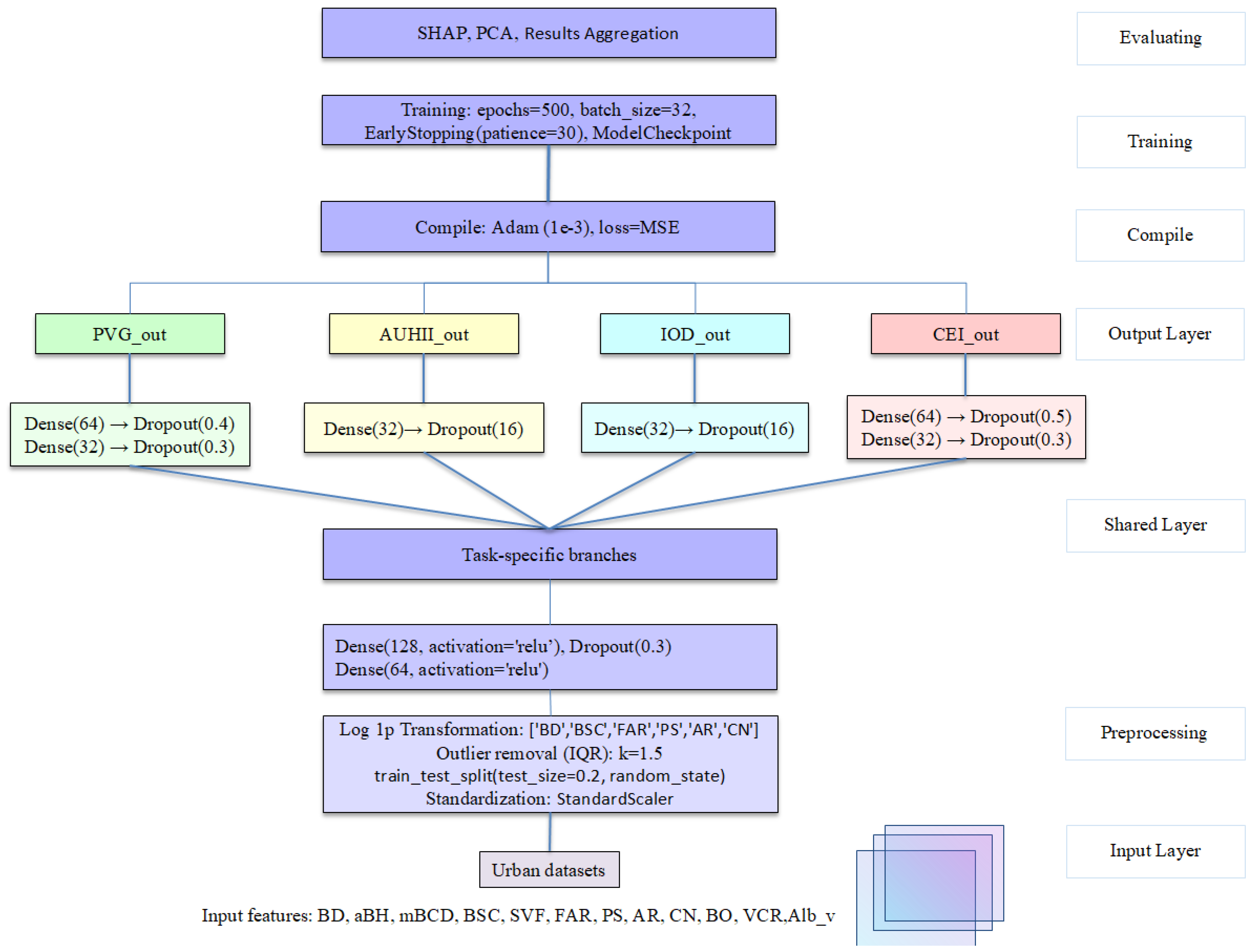
2.3. Development of ANN-Based Multi-Task Learning Model
2.4. Evaluation Criteria and SHAP Explanation
2.5. Framework
3. Results and Discussion
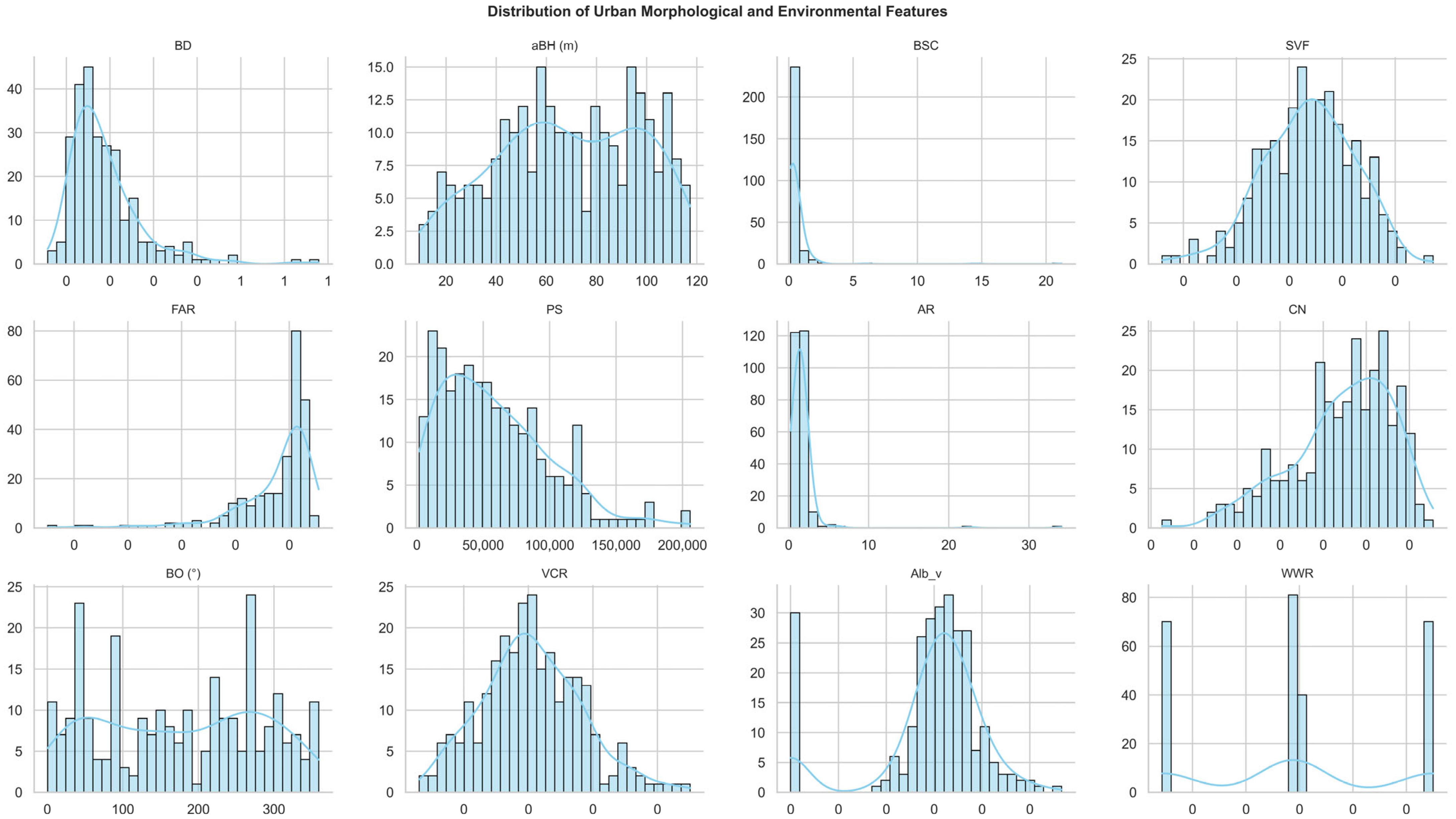
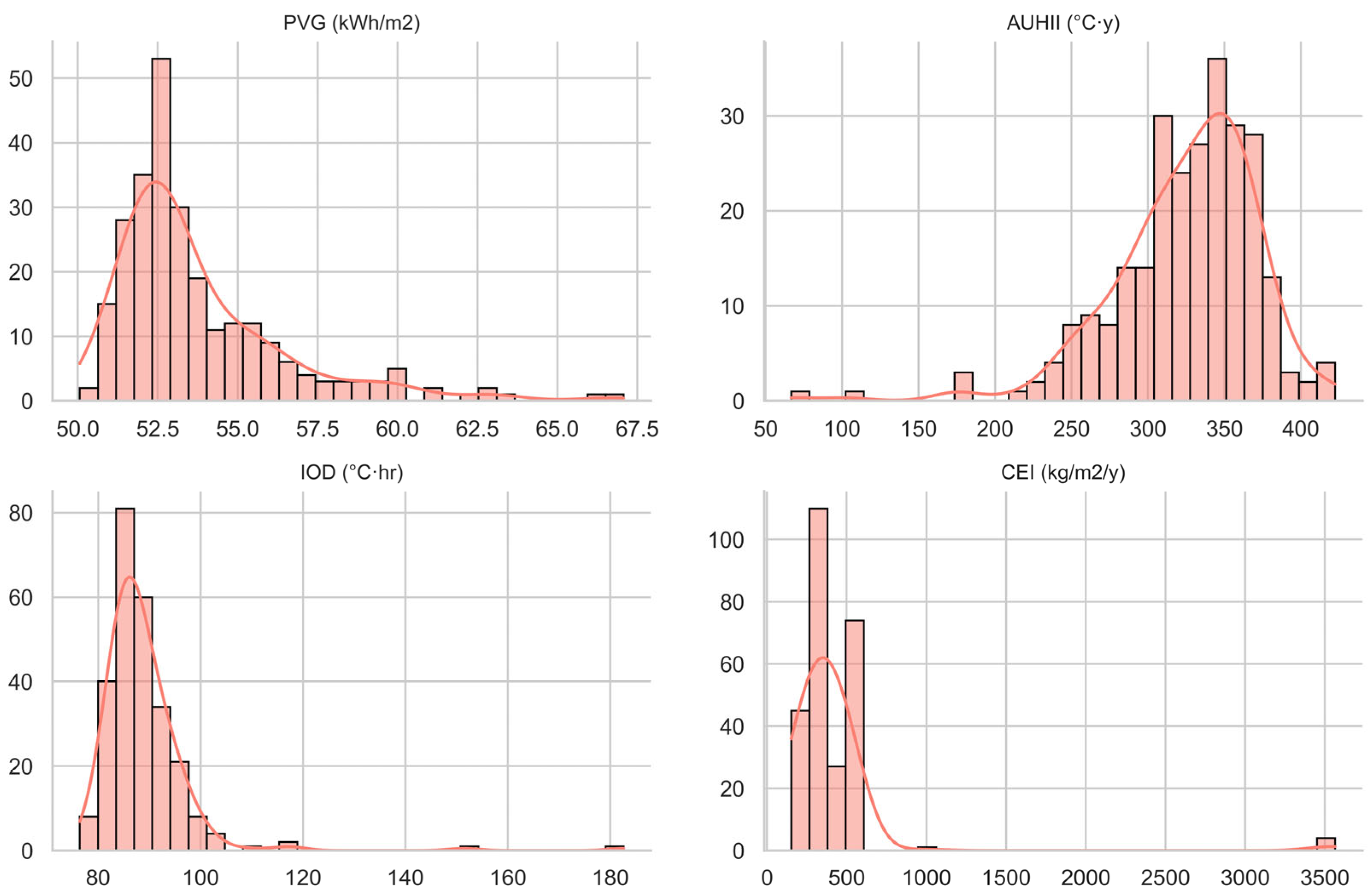
3.1. Urban Morphology Input Parameters
3.2. Model Performance
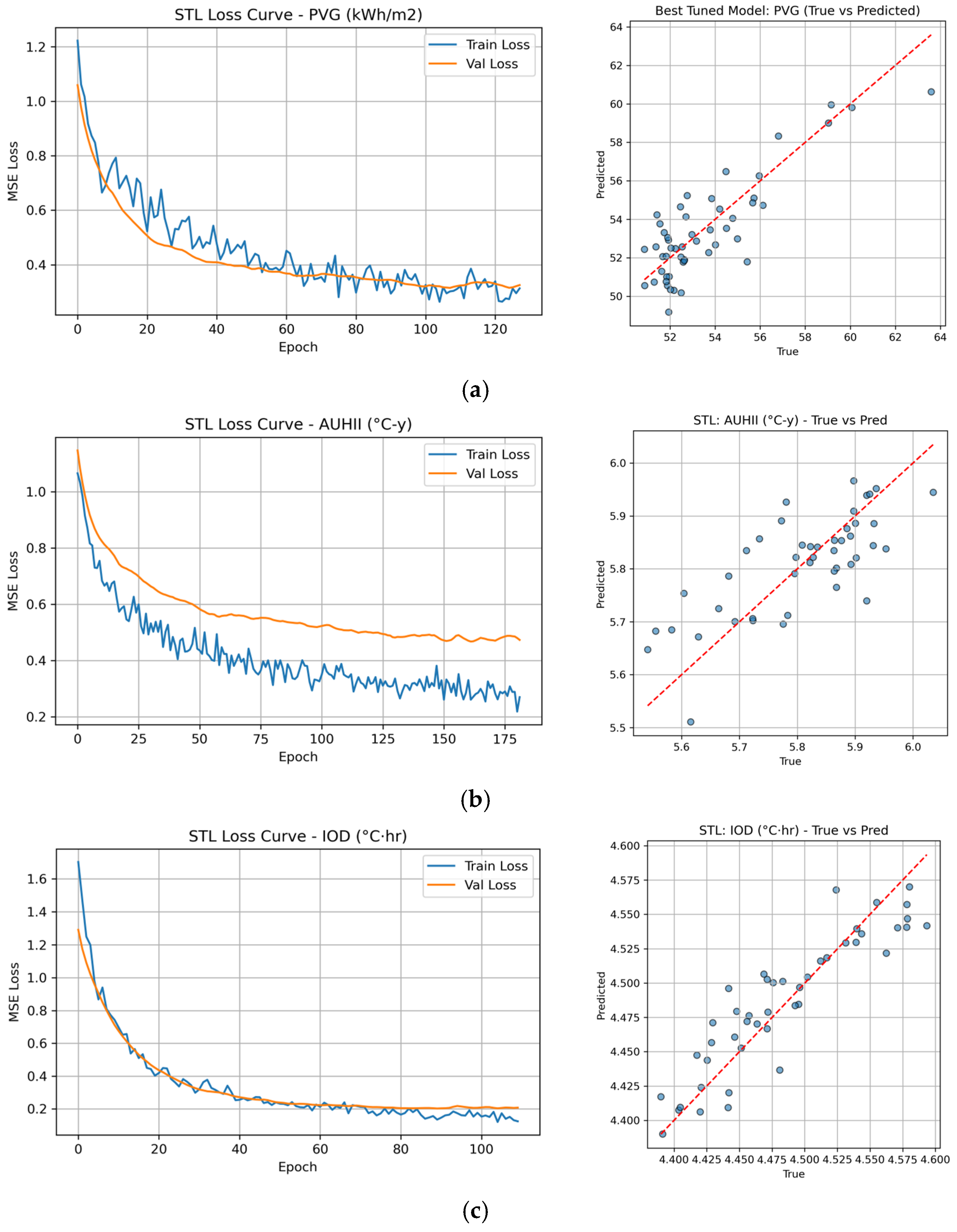
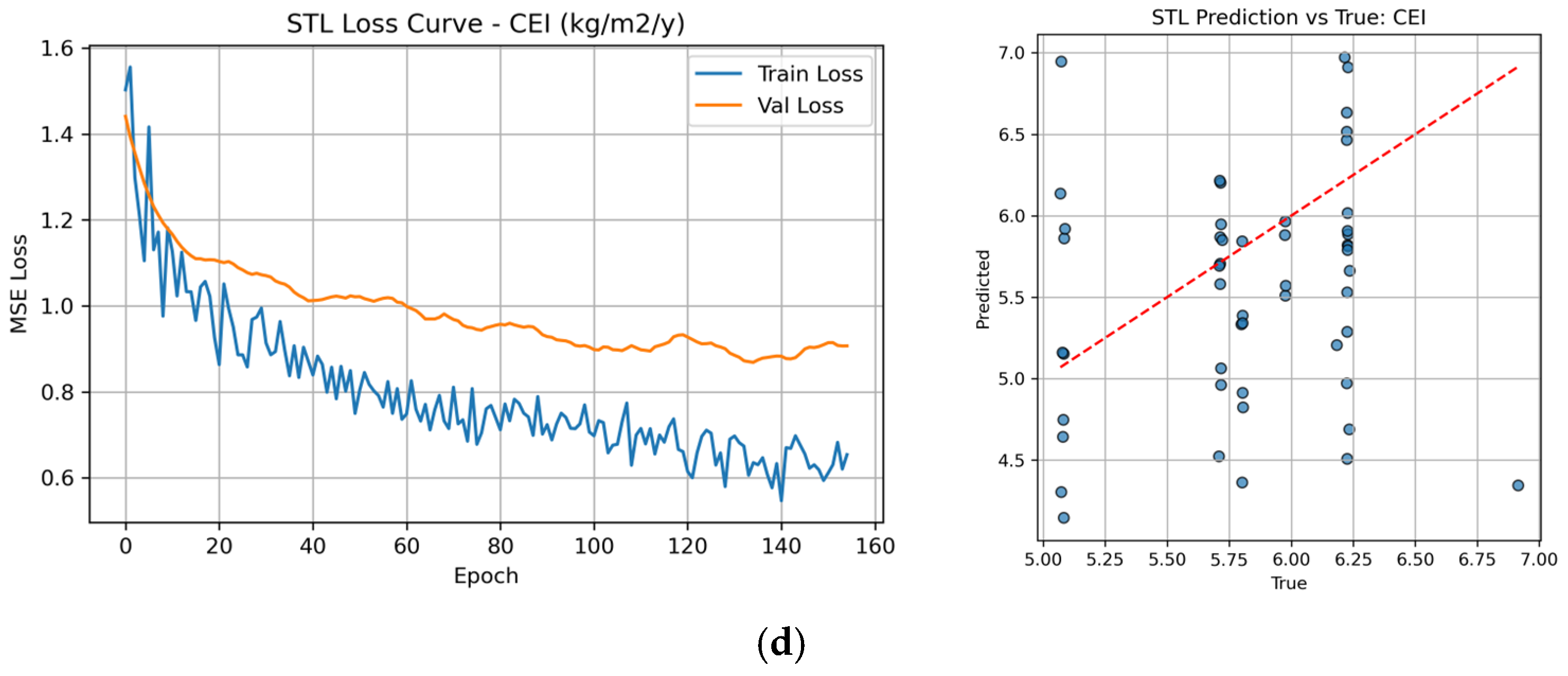
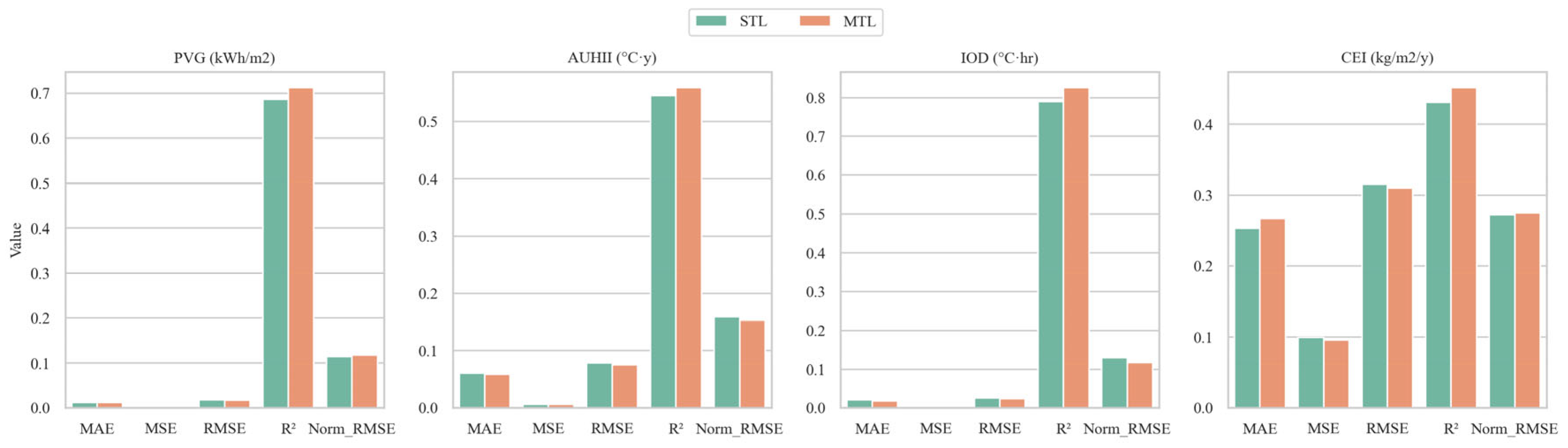
3.2.1. Single-Task Learning Model
3.2.2. Multi-Task Learning Model
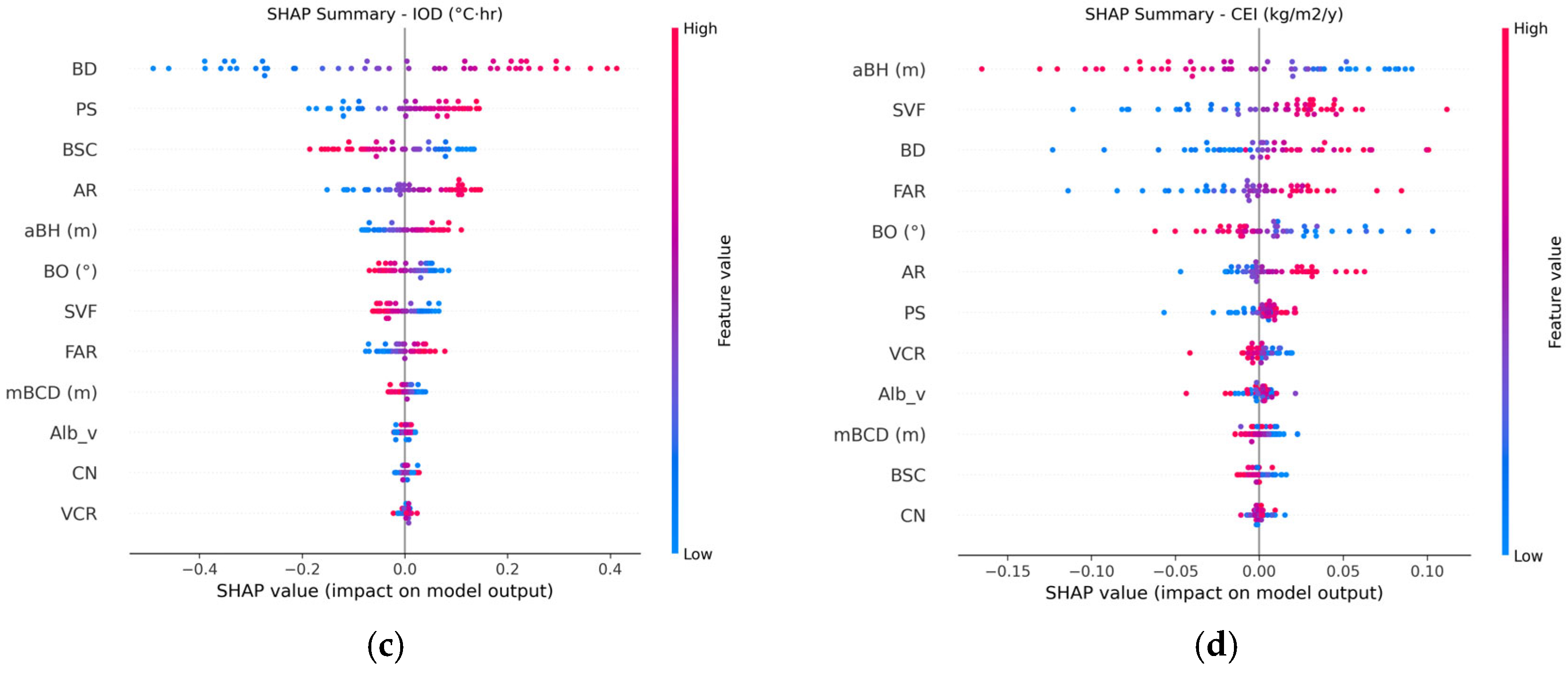
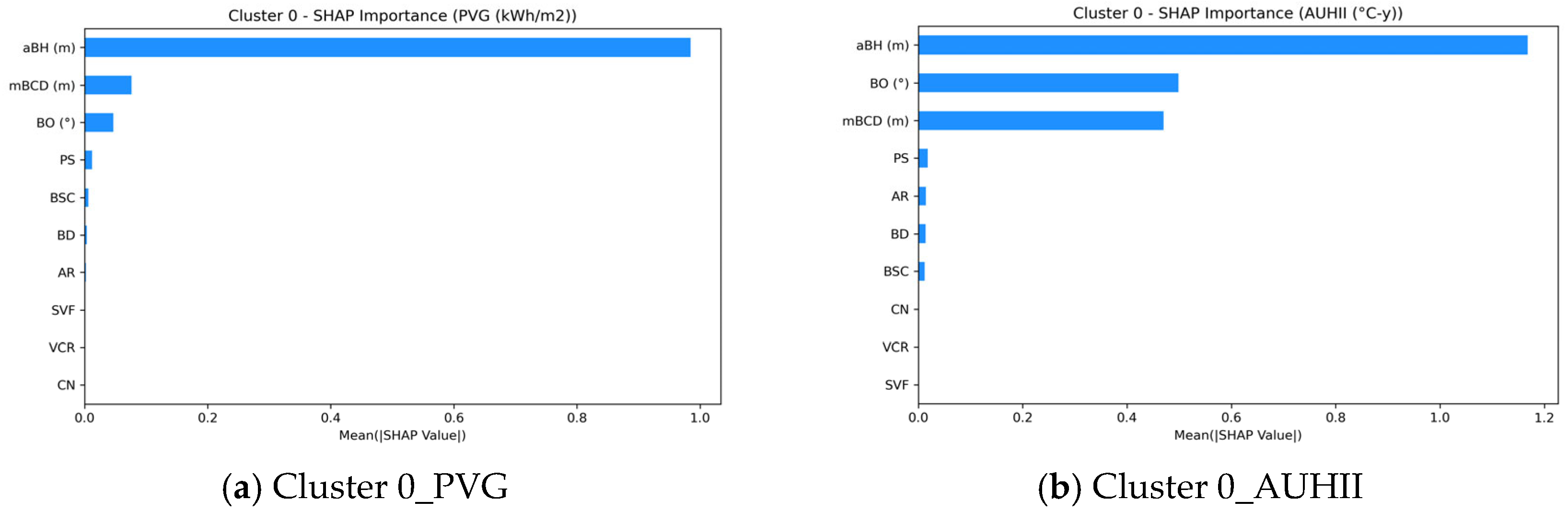
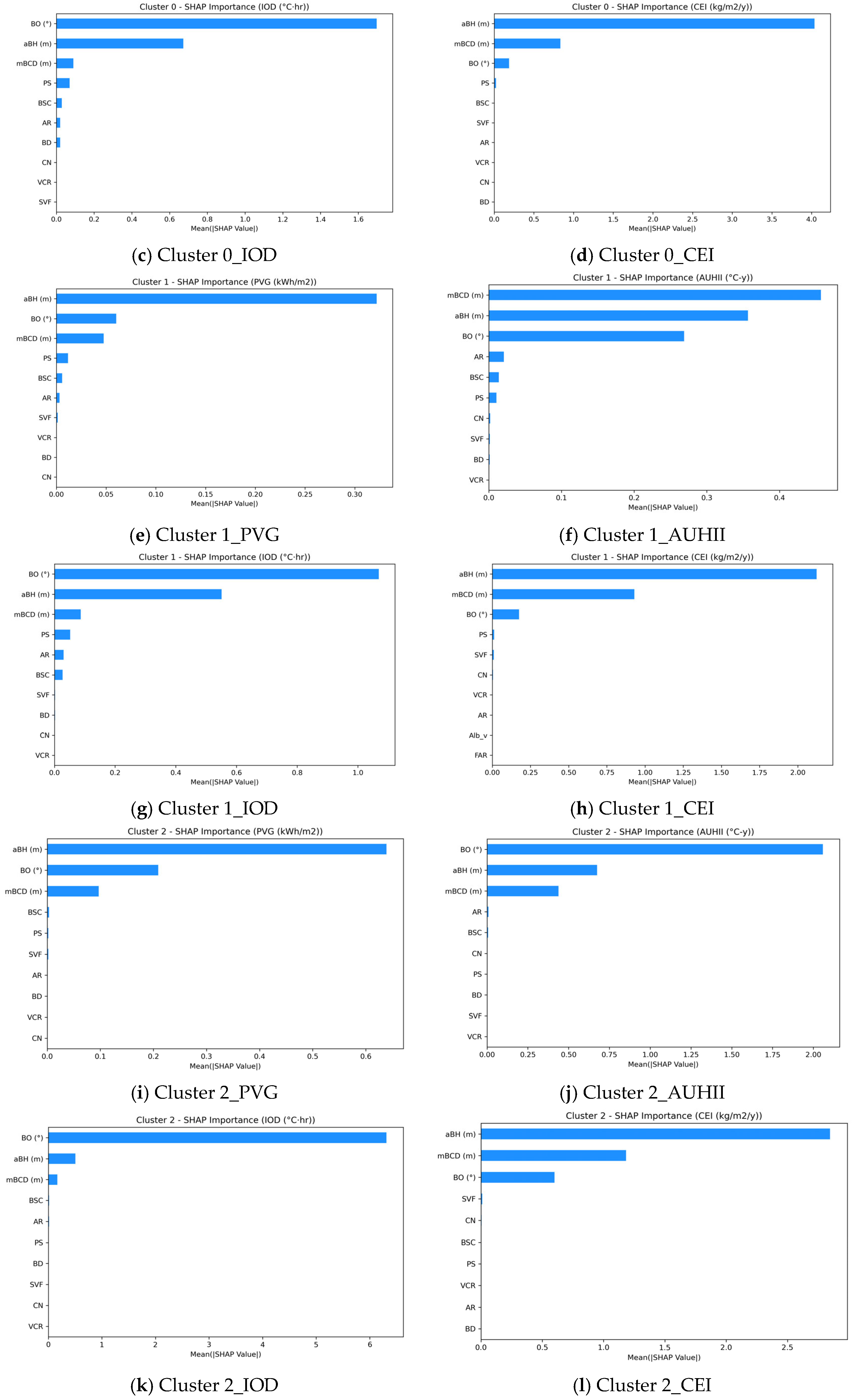
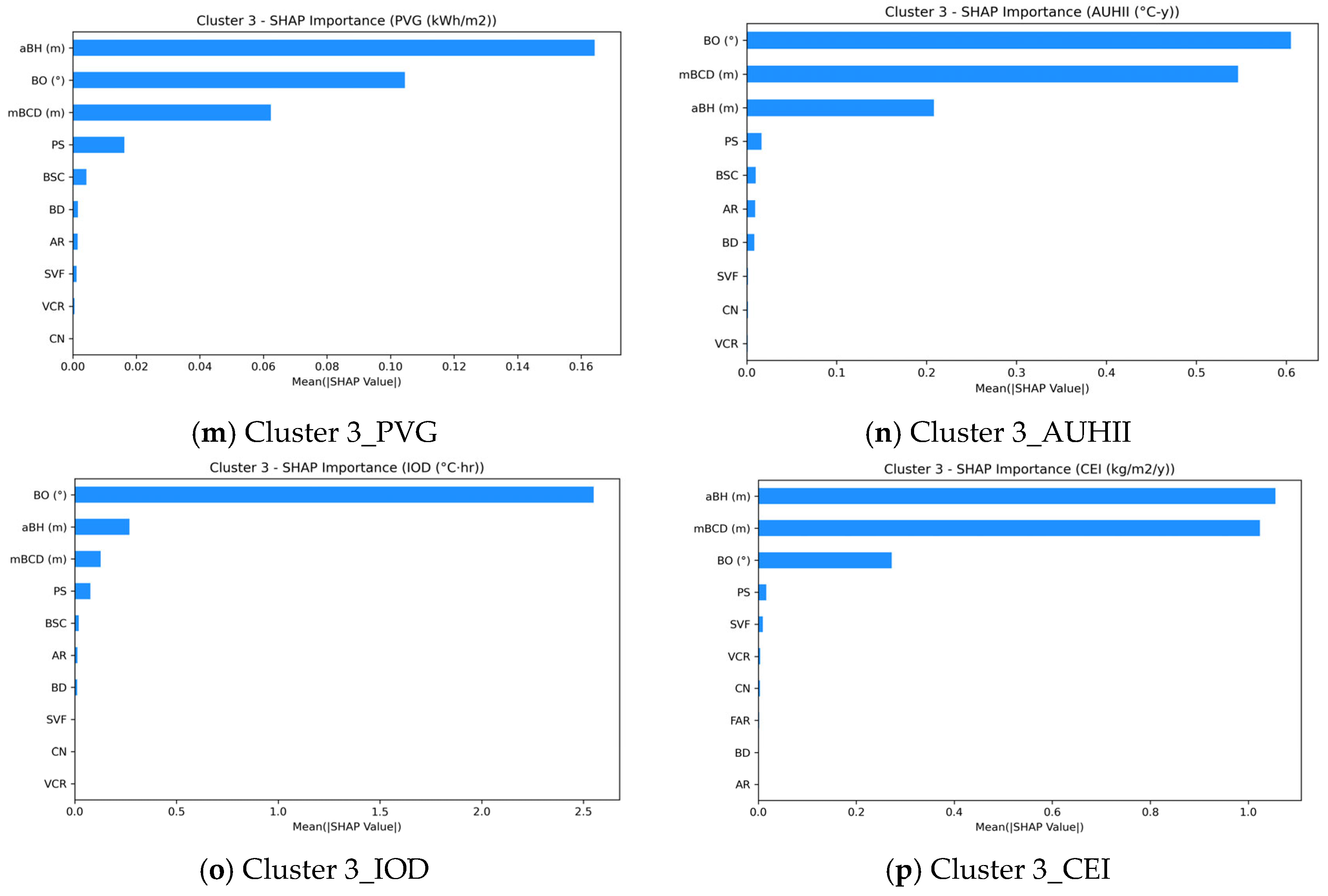
3.3. SHAP-Based Feature Importance and Interactions
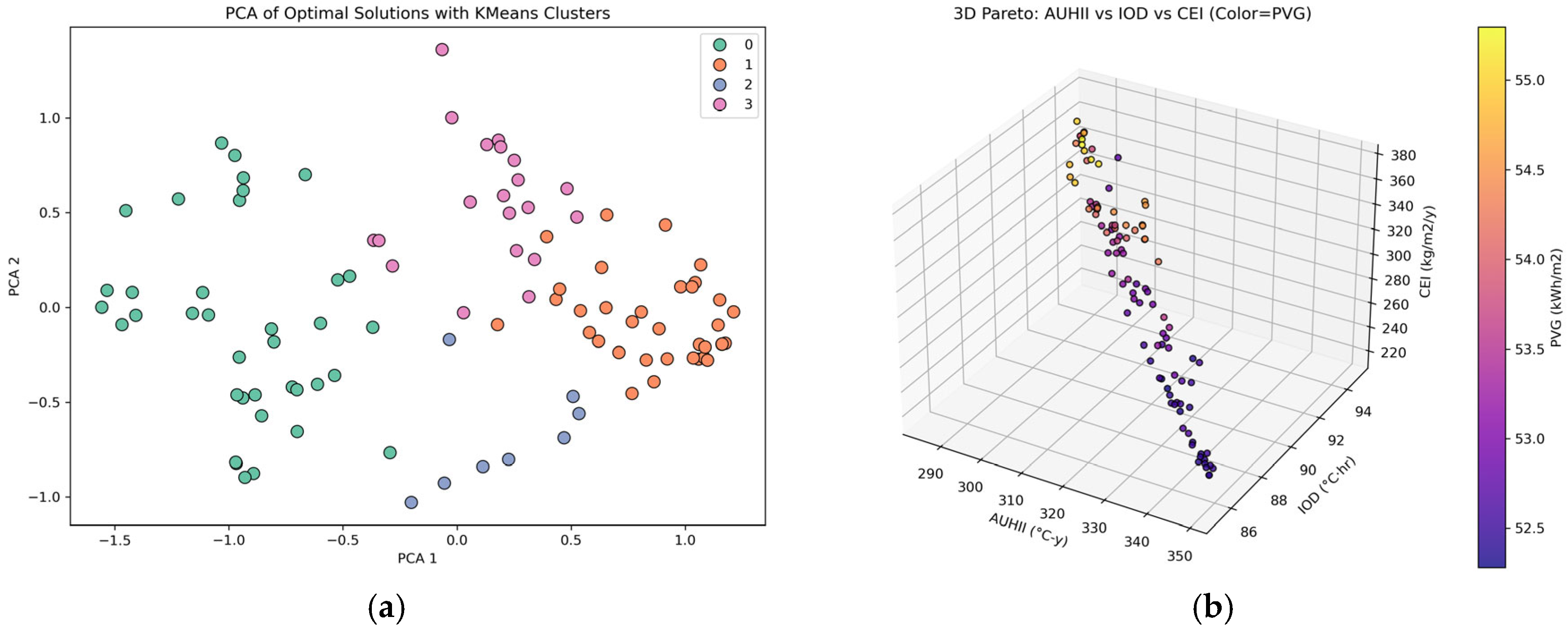
3.4. Optimization Results and Pareto Fronts
4. Conclusions
- (1)
- Quantitative evaluation demonstrated that the MTL model achieved high predictive accuracy across all targets, with R2 values reaching 0.712 for PVG, 0.559 for AUHII, 0.825 for IOD, and 0.451 for CEI. Compared with STL models, MTL improved performance by efficiently leveraging shared representations, particularly for tasks with strong underlying correlations such as AUHII and IOD.
- (2)
- The SHAP-based analysis identified average building height (aBH), building density (BD), and building orientation (BO) as the dominant morphological factors, explaining up to 65% of the total predictive variance across tasks. Specifically, a higher aBH increased PVG by enhancing rooftop solar access but simultaneously exacerbated AUHII and IOD under dense urban conditions, reflecting clear trade-offs among environmental goals.
- (3)
- Among the identified configurations, Cluster 3 demonstrated the most robust and transferable urban morphology strategy for integrated sustainability. It featured mid-to-high building heights (aBH = 72.11 m), moderate inter-building distances (mBCD = 109.92 m), and east-southeast orientations (BO = 183°). This morphology consistently achieved superior outcomes across multiple objectives, with the highest PVG (55.26 kWh/m2), the lowest CEI (359.76 kg/m2/y), and competitive AUHII (294.1 °C·y) and IOD (92.7 °C·h) values. These results suggest that urban blocks combining moderate height, sufficient spacing, and optimized orientation can effectively balance energy efficiency, thermal comfort, and carbon reduction goals, offering valuable guidance for sustainable urban development across diverse climatic and urban contexts.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| aBH | Average building height |
| ANN-MTL | Artificial neural network-based multi-task learning |
| Alb_v | Vegetation albedo |
| AR | Aspect ratio |
| AUHII | Accumulated urban heat island intensity (°C∙y) |
| BD | Building density |
| BO | Building orientation |
| BSC | Building shape coefficient |
| CEI | Carbon emission intensity (kg/m2/y) |
| CN | Compactness |
| COP | The coefficient of performance |
| FAR | Floor area ratio |
| FiT | Feed-in tariff |
| FST-GCN | Functional–spatial–temporal GCN |
| GIS | Geographic Information System |
| GNN-GA | GNN plus Genetic Algorithm |
| GCN-LSTM | Graph convolution network (GC) embedded long short-term memory network (LTSM) |
| GEE | Google Earth Engine |
| HK Geodata | Hong Kong geospatial data |
| HVAC | Heating, ventilation, and air conditioning |
| IOD | Indoor overheating degree (°C·h) |
| IQR | Interquartile range method |
| LCZs | Local climate zones |
| Ab | Total building footprint area |
| Hi | Height of building i |
| dij | Distance between centroids of buildings i and j |
| Av | Total building volume |
| At | Total sky hemisphere area |
| N | Number of plots/buildings/weather stations |
| W | Width of street canyon |
| Angle of building i | |
| Es | The solar energy received by the building surface within a specific time period |
| The urban temperature at time-step t | |
| Hourly heat index | |
| N | Total number of time-steps |
| GFA | Gross floor area |
| The carbon sink factors | |
| LST | Land surface temperature |
| mBCD | Mean building centroid distance |
| ML | Machine learning |
| MTL | Multi-task learning |
| MSE | Mean squared error |
| NDCs | Nationally determined contributions |
| NSGA-II | Non-dominated sorting genetic algorithm II |
| PCA | Principal component analysis |
| PS | Plot size |
| PV | Photovoltaics |
| PVG | Photovoltaic generation (kWh/m2) |
| UHII | Urban heat island intensity |
| UHR | Urban heat resilience |
| VCR | Vegetation coverage ratio |
| WWR | Window-to-wall ratios |
| RMSE | Root mean square error |
| R2 | Coefficient of determination |
| SHAP | SHapley Additive exPlanations |
| SHGC | Solar heat gain coefficient |
| STL | Single-task learning |
| SVF | Sky view factor |
| TMY | Typical meteorological year |
| At | Total study area |
| nb/np | Total number of buildings/number of plots |
| Ae | Total exterior surface area |
| Ao | Obstructed sky area |
| Af | Total floor area |
| L | Length of street canyon |
| P | Perimeter of building footprints |
| S | Active area |
| Ƞ | Efficiency of the PV system |
| The rural temperature at time-step t | |
| Critical heat index threshold | |
| EUI | Energy use intensity |
| Electrical power carbon emissions factor |
References
- Global Climate Highlights 2024|Copernicus. Available online: https://climate.copernicus.eu/global-climate-highlights-2024?utm_source=chatgpt.com (accessed on 26 April 2025).
- State of the Global Climate. 2024. Available online: https://wmo.int/publication-series/state-of-global-climate-2024 (accessed on 26 April 2025).
- Record-Breaking Annual Growth in Renewable Power Capacity. 2025. Available online: https://www.irena.org/News/pressreleases/2025/Mar/Record-Breaking-Annual-Growth-in-Renewable-Power-Capacity?utm_source=chatgpt.com (accessed on 26 April 2025).
- CAT 2035 Climate Target Update Tracker. Available online: https://climateactiontracker.org/climate-target-update-tracker-2035/ (accessed on 26 April 2025).
- China’s New Renewable Energy Plan: Key Insights for Businesses. China Briefing News 2024. Available online: https://www.china-briefing.com/news/chinas-new-renewable-energy-plan-key-insights-for-businesses/ (accessed on 26 April 2025).
- Hong Kong’s Climate Action Plan 2050-Climate Change Laws of the World. Available online: https://climate-laws.org/documents/hong-kong-s-climate-action-plan-2050_b5b6 (accessed on 17 May 2025).
- Yuan, Y.; Santamouris, M.; Xu, D.; Xiaolei, G.; Li, C.; Cheng, W.; Su, L.; Xiong, P.; Fan, Z.; Wang, X.; et al. Surface urban heat island effects intensify more rapidly in lower income countries. Npj Urban Sustain. 2025, 5, 11. [Google Scholar] [CrossRef]
- World Population by Year. Worldometer. Available online: http://www.worldometers.info/world-population/world-population-by-year/ (accessed on 26 April 2025).
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Zuo, M.; Li, M.; Li, H.; Chen, T. Discovering morphological impact discrepancies on thermal environment among urban functional zones using essential urban land use categories and machine learning. Urban Clim. 2025, 61, 102423. [Google Scholar] [CrossRef]
- Natanian, J.; Auer, T. Beyond nearly zero energy urban design: A holistic microclimatic energy and environmental quality evaluation workflow. Sustain. Cities Soc. 2020, 56, 102094. [Google Scholar] [CrossRef]
- Yuan, B.; Zhou, L.; Hu, F.; Wei, C. Effects of 2D/3D urban morphology on land surface temperature: Contribution, response, and interaction. Urban Clim. 2024, 53, 101791. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, W.; Shao, Y.; Wang, N.; Yu, Z.; Li, H.; Hu, Q. The impacts and thresholds detection of 2D/3D urban morphology on the heat island effects at the functional zone in megacity during heatwave event. Sustain. Cities Soc. 2025, 118, 106002. [Google Scholar] [CrossRef]
- Hong, T.; Yim, S.H.L.; Heo, Y. Interpreting complex relationships between urban and meteorological factors and street-level urban heat islands: Application of random forest and SHAP method. Sustain. Cities Soc. 2025, 126, 106353. [Google Scholar] [CrossRef]
- Zhu, S.; Yan, Y.; Zhao, B.; Wang, H. Assessing the impact of adjacent urban morphology on street temperature: A multisource analysis using random forest and SHAP. Build. Environ. 2025, 267, 112326. [Google Scholar] [CrossRef]
- Liu, Q.; Hang, T.; Wu, Y. Unveiling differential impacts of multidimensional urban morphology on heat island effect across local climate zones: Interpretable CatBoost-SHAP machine learning model. Build. Environ. 2025, 270, 112574. [Google Scholar] [CrossRef]
- Zhang, L.; Cao, M.; Li, N.; Luo, L.; Chen, Y.; Li, Z. Machine learning prediction of heating and cooling loads based on Athenian residential buildings’ simulation dataset. Energy Build. 2025, 342, 115808. [Google Scholar] [CrossRef]
- Jia, L.-R.; Li, Q.-Y.; Chen, X.; Lee, C.-C.; Han, J. Indoor Thermal and Ventilation Indicator on University Students’ Overall Comfort. Buildings 2022, 12, 1921. [Google Scholar] [CrossRef]
- Kim, S.W.; Brown, R.D. Development of a micro-scale heat island (MHI) model to assess the thermal environment in urban street canyons. Renew. Sustain. Energy Rev. 2023, 184, 113598. [Google Scholar] [CrossRef]
- Tian, P.; Cai, M.; Sun, Z.; Liu, S.; Wu, H.; Liu, L.; Peng, Z. Effects of 3D urban morphology on CO2 emissions using machine learning: Towards spatially tailored low-carbon strategies in Central Wuhan, China. Urban Clim. 2024, 57, 102122. [Google Scholar] [CrossRef]
- Li, Y.; Schubert, S.; Kropp, J.P.; Rybski, D. On the influence of density and morphology on the Urban Heat Island intensity. Nat. Commun. 2020, 11, 2647. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.; Cho, S.; Chow, D.H.C. Urban morphology indicators and solar radiation acquisition: 2011–2022 review. Renew. Sustain. Energy Rev. 2024, 199, 114548. [Google Scholar] [CrossRef]
- Morales, R.D.; Audenaert, A.; Verbeke, S. Thermal comfort and indoor overheating risks of urban building stock - A review of modelling methods and future climate challenges. Build. Environ. 2025, 269, 112363. [Google Scholar] [CrossRef]
- Hamdy, M.; Carlucci, S.; Hoes, P.-J.; Hensen, J.L.M. The impact of climate change on the overheating risk in dwellings—A Dutch case study. Build. Environ. 2017, 122, 307–323. [Google Scholar] [CrossRef]
- Shi, Q.; Luo, W.; Xiao, C.; Wang, J.; Zhu, H.; Chen, X. Investigating urban-scale building thermal resilience under compound heat waves and power outage events based on urban morphology analysis. Build. Environ. 2025, 276, 112747. [Google Scholar] [CrossRef]
- Lei, L.; Shao, S.; Liang, L. An evolutionary deep learning model based on EWKM, random forest algorithm, SSA and BiLSTM for building energy consumption prediction. Energy 2024, 288, 129795. [Google Scholar] [CrossRef]
- Oukawa, G.Y.; Krecl, P.; Targino, A.C. Fine-scale modeling of the urban heat island: A comparison of multiple linear regression and random forest approaches. Sci. Total Environ. 2022, 815, 152836. [Google Scholar] [CrossRef]
- Tang, H.; Chai, X.; Chen, J.; Wan, Y.; Wang, Y.; Wan, W.; Li, C. Assessment of BIPV power generation potential at the city scale based on local climate zones: Combining physical simulation, machine learning and 3D building models. Renew. Energy 2025, 244, 122688. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.; Jiang, F.; Zhang, S.; Tan, Y. Assessing the impacts of urban morphological factors on urban building energy modeling based on spatial proximity analysis and explainable machine learning. J. Build. Eng. 2024, 85, 108675. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Yu, S.; Qin, H.; Xu, Z. AI-Driven urban planning optimization: A graph neural network and genetic algorithm framework for tackling peak-hour challenges. Sustain. Cities Soc. 2025, 126, 106407. [Google Scholar] [CrossRef]
- Zhang, J.; Wan, Y.; Tian, M.; Li, H.; Chen, K.; Xu, X.; Yuan, L. Comparing multiple machine learning models to investigate the relationship between urban morphology and PM2.5 based on mobile monitoring. Build. Environ. 2024, 248, 111032. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, J.; Bai, B. Unveiling nonlinear effects of built environment attributes on urban heat resilience using interpretable machine learning. Urban Clim. 2024, 56, 102046. [Google Scholar] [CrossRef]
- Yang, C.; Li, S.; Gou, Z. Spatiotemporal prediction of urban building rooftop photovoltaic potential based on GCN-LSTM. Energy Build. 2025, 334, 115522. [Google Scholar] [CrossRef]
- Xu, Z.; Yi, Z.; Wang, Y.; Wang, D.; Zhang, L.; Huo, H. Estimating near-surface air temperature in urban functional zones in China using spatial-temporal attention. Build. Environ. 2025, 276, 112860. [Google Scholar] [CrossRef]
- Erdem Okumus, D.; Akay, M. Quantitative assessment of non-stationary relationship between multi-scale urban morphology and urban heat. Build. Environ. 2025, 272, 112669. [Google Scholar] [CrossRef]
- Li, L.; Sun, S.; Zhong, L.; Han, J.; Qian, X. Novel spatiotemporal nonlinear regression approach for unveiling the impact of urban spatial morphology on carbon emissions. Sustain. Cities Soc. 2025, 125, 106381. [Google Scholar] [CrossRef]
- GovHK: Feed-in Tariff. Available online: https://www.gov.hk/en/residents/environment/sustainable/renewable/feedintariff.htm (accessed on 24 April 2025).
- C40 Good Practice Guides: Hong Kong-Energy Saving Plan 2015-2025+. C40 Cities. Available online: https://www.c40.org/case-studies/c40-good-practice-guides-hong-kong-energy-saving-plan-2015-2025/ (accessed on 17 May 2025).
- GovHK: Climate Change. Available online: https://www.gov.hk/en/residents/environment/global/climate.htm (accessed on 24 April 2025).
- Google Earth Engine. Available online: https://earthengine.google.com (accessed on 26 April 2025).
- Chan, A.L.S.; Chow, T.T.; Fong, S.K.F.; Lin, J.Z. Generation of a typical meteorological year for Hong Kong. Energy Convers. Manag. 2006, 47, 87–96. [Google Scholar] [CrossRef]
- Common Spatial Data Infrastructure (CSDI) Portal for Government. Available online: https://portal.csdi.gov.hk/csdi-webpage/ (accessed on 24 April 2025).
- Login-BRAVO. Available online: https://bravo.bd.gov.hk/login.action (accessed on 24 April 2025).
- List of Public Housing Estates in Hong Kong. Wikipedia. 2025. Available online: https://en.wikipedia.org/wiki/List_of_public_housing_estates_in_Hong_Kong (accessed on 10 March 2025).
- Wang, L.; Cheng, J.C.; Mazan, W.; Jacoby, S. Standard Block and Modular Dwelling Designs in Hong Kong’s Public Housing. Architecture 2024, 4, 89–111. [Google Scholar] [CrossRef]
- Xue, C.Q.L.; Hui, K.C.; Zang, P. Public buildings in Hong Kong: A short account of evolution since the 1960s. Habitat Int. 2013, 38, 57–69. [Google Scholar] [CrossRef]
- Standard 90.1. Available online: https://www.ashrae.org/technical-resources/bookstore/standard-90-1 (accessed on 9 December 2023).
- Electrical and Mechanical Services Department (EMSD). Code of Practice for Energy Efficiency of Building Services Installation (BEC 2024); EMSD: Hong Kong, China, 2024. Available online: https://www.emsd.gov.hk/beeo/en/pee/BEC_2024_ENG.pdf (accessed on 30 December 2024).
- Electrical and Mechanical Services Department (EMSD). Codes & Technical Guidelines: Buildings Energy Efficiency Ordinance–EMSD. Available online: https://www.emsd.gov.hk/beeo/en/mibec_beeo_codtechguidelines.html (accessed on 24 June 2025).
- Landsat 8-9 OLI/TIRS Collection 2 Level 1 Data Format Control Book | U.S. Geological Survey. Available online: https://www.usgs.gov/media/files/landsat-8-9-olitirs-collection-2-level-1-data-format-control-book (accessed on 24 April 2025).
- Bian, C.; Cheung, K.L.; Chen, X.; Lee, C.C. Integrating microclimate modelling with building energy simulation and solar photovoltaic potential estimation: The parametric analysis and optimization of urban design. Appl. Energy 2025, 380, 125062. [Google Scholar] [CrossRef]
- Torbarina, L.; Ferkovic, T.; Roguski, L.; Mihelcic, V.; Sarlija, B.; Kraljevic, Z. Challenges and Opportunities of Using Transformer-Based Multi-Task Learning in NLP Through ML Lifecycle: A Position Paper. Nat. Lang. Process. J. 2024, 7, 100076. [Google Scholar] [CrossRef]
- Meyer, J. Multi-Task and Transfer Learning in Low-Resource Speech Recognition. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, September 2019. [Google Scholar]
- Zhai, Z.; Chen, F.; Yu, H.; Hu, J.; Zhou, X.; Xu, H. PS-MTL-LUCAS: A partially shared multi-task learning model for simultaneously predicting multiple soil properties. Ecol. Inform. 2024, 82, 102784. [Google Scholar] [CrossRef]
- Welcome to the SHAP Documentation—SHAP Latest Documentation. Available online: https://shap.readthedocs.io/en/latest/ (accessed on 26 April 2025).
- shap.KernelExplainer—SHAP Latest Documentation. Available online: https://shap.readthedocs.io/en/latest/generated/shap.KernelExplainer.html (accessed on 26 April 2025).
- Hu, Y.-S.; Lo, K.-Y.; Hsieh, I.-Y.L. AI-driven short-term load forecasting enhanced by clustering in multi-type university buildings: Insights across building types and pandemic phases. J. Build. Eng. 2025, 104, 112417. [Google Scholar] [CrossRef]
- Spatial without Compromise · QGIS Web Site. Available online: https://qgis.org/ (accessed on 26 April 2025).
- Costantino, D.; Grimaldi, A.; Pepe, M. 3D MODELLING OF BULDINGS AND URBAN AREAS USING GRASSHOPPER AND RHINOCERSOS. Geogr. Tech. 2022, 17, 167–176. [Google Scholar] [CrossRef]
- Castrejon-Esparza, N.M.; González-Trevizo, M.E.; Martínez-Torres, K.E.; Santamouris, M. Optimizing urban morphology: Evolutionary design and multi-objective optimization of thermal comfort and energy performance-based city forms for microclimate adaptation. Energy Build. 2025, 115750. [Google Scholar] [CrossRef]
- La Gatta, V.; Sperlì, G.; De Cegli, L.; Moscato, V. From single-task to multi-task: Unveiling the dynamics of knowledge transfers in disinformation detection. Inf. Sci. 2025, 696, 121735. [Google Scholar] [CrossRef]
- Abdulnassar, A.A.; Nair, L.R. Performance analysis of K-means with modified initial centroid selection algorithms and developed K-means9+ model. Meas. Sens. 2023, 25, 100666. [Google Scholar] [CrossRef]
- Feng, W.; Chen, J.; Yang, Y.; Gao, W.; Zhao, Q.; Xing, H.; Yu, S. The Impact of Building Morphology on Energy Use Intensity of High-Rise Residential Clusters: A Case Study of Hangzhou, China. Buildings 2024, 14, 2245. [Google Scholar] [CrossRef]
- Chew, L.W.; Norford, L.K. Pedestrian-level wind speed enhancement with void decks in three-dimensional urban street canyons. Build. Environ. 2019, 155, 399–407. [Google Scholar] [CrossRef]
- Aydin, E.E.; Ortner, F.P.; Peng, S.; Yenardi, A.; Chen, Z.; Tay, J.Z. Climate-responsive urban planning through generative models: Sensitivity analysis of urban planning and design parameters for urban heat island in Singapore’s residential settlements. Sustain. Cities Soc. 2024, 114, 105779. [Google Scholar] [CrossRef]
- Gao, X.; Yu, H.; Li, L.; Yu, J. A county-level analysis of spatiotemporal variation and human causes of urban heat islands in the Guangdong-Hong Kong-Macao Greater Bay Area. City Environ. Interact. 2025, 26, 100194. [Google Scholar] [CrossRef]
- Ngamsiriudom, T.; Tanaka, T. Making an urban environmental climate map of the Bangkok Metropolitan Region, Thailand: Analysis of air temperature, wind distributions, and spatial environmental factors. World Dev. Sustain. 2023, 3, 100105. [Google Scholar] [CrossRef]
- Llorin, A.G.A.; Olaguera, L.M.P.; Cruz, F.A.T.; Villarin, J.R.T. Improved WRF simulation of surface temperature and urban heat island intensity over Metro Manila, Philippines. Atmospheric Res. 2024, 310, 107644. [Google Scholar] [CrossRef]
- Singh, M.; Sharston, R.; Murtha, T. Critical evaluation of the spatiotemporal behavior of UHI, through correlation analyses based on multi-city heterogeneous dataset. Sustain. Cities Soc. 2024, 110, 105576. [Google Scholar] [CrossRef]
- Kong, J.; Zhao, Y.; Strebel, D.; Gao, K.; Carmeliet, J.; Lei, C. Understanding the impact of heatwave on urban heat in greater Sydney: Temporal surface energy budget change with land types. Sci. Total Environ. 2023, 903, 166374. [Google Scholar] [CrossRef]




| Generation | First | Second | Third | Fourth | Fifth |
|---|---|---|---|---|---|
| Year | Before 1986s | 1986–1992 | 1992–2003 | 2003–2012 | 2012–present |
| Building type | Slab, Cruciform Block, Trident | Trident, Harmony | Concord, Harmony | Concord, Trident | Cruciform |
| U_value of roof | 0.58–1.13 | 0.58 | 0.58 | 0.55–0.58 | 1.8 |
| U_value of wall | 2.16–3.33 | 2.88–3.33 | 2.75–2.88 | 2.75–3.85 | 1.9 |
| U_value of floor | 2.48 | 2.48 | 2.48 | 2.48 | 2.48 |
| U_value of windows | 1.13–5.75 | 5.75 | 5.75 | 5.75–5.78 | 5.8 |
| SHGC | 0.37–0.72 | 0.57 | 0.681 | 0.6–0.775 | 0.82 |
| WWR | 0.304–0.382 | 0.305–0.4 | 0.65 | 0.148 | 0.143 |
| COP | 2.5–5 | 2.5 | 2.5 | 2.4–2.5 | 3 |
| People density (W/m2) | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 |
| Lighting density (W/m2) | 46.395 | 15 | 15–19 | 19 | 15 |
| Equipment density (W/m2) | 543.53 | 142 | 142 | 142 | 100 |
| Cooling (°C) | 25 | 25 | 24–26 | 20–29 | 25 |
| Infiltration (ACH) | 1.5 | 1.5 | 0.5 | 0.5 | 0.3–0.6 |
| Indicator | Abbreviation | Formula | Description |
|---|---|---|---|
| Building density | BD | BD = Ab/At | Ab: Total building footprint area At: Total study area |
| Average building height | aBH | aBH = ()/nb | Hi: Height of building i nb: Total number of buildings |
| Mean building centroid distance | mBCD | mBCD = ()/(nb(nb − 1)) | dij: Distance between centroids of buildings i and j |
| Building shape coefficient | BSC | BSC = Ae/Ab | Ae: Total exterior surface area. Av: Total building volume. |
| Sky view factor | SVF | SVF = 1 − (Ao/At) | Ao: Obstructed sky area. At: Total sky hemisphere area. |
| Floor area ratio | FAR | FAR = Af/At | Af: Total floor area. At: Total study area |
| Plot size | PS | PS = At/np | At: Total study area np: Number of plots |
| Aspect ratio | AR | AR = L/W | L: Length of street canyon W: Width of street canyon |
| Compactness | CN | CN = Ab/P2 | Ab: Total building footprint area P: Perimeter of building footprints |
| Building orientation | BO | BO = ()/nb | : Orientation angle of building i nb: Total number of buildings |
| Vegetation coverage ratio | VCR | NDVImean: Mean NDVI of the study area NDVImin: Bare-soil reference NDVI NDVImax: Full-vegetation reference NDVI | |
| Vegetation albedo | Alb_v | Alb_v = | : The surface reflectivity of different bands : The weighting coefficient of each band |
| Target | Metric | STL_Mean | MTL_Mean | Test | p_Value |
|---|---|---|---|---|---|
| PVG (kWh/m2) | R2 | 0.687 ± 0.018 | 0.712 ± 0.015 | paired t-test | 0.0125 (*) |
| AUHII (°C·y) | R2 | 0.546 ± 0.022 | 0.559 ± 0.019 | paired t-test | 0.0499 (*) |
| IOD (°C·h) | R2 | 0.789 ± 0.010 | 0.825 ± 0.008 | paired t-test | 0.0035 (*) |
| CEI (kg/m2/y) | R2 | 0.430 ± 0.050 | 0.451 ± 0.045 | paired t-test | 0.9537 |
| Parameters | Cluster 0 | Cluster 1 | Cluster 2 | Cluster 3 |
|---|---|---|---|---|
| BD | 0.29 | 0.30 | 0.36 | 0.37 |
| aBH (m) | 97.86 | 74.24 | 74.23 | 72.11 |
| mBCD (m) | 107.81 | 123.99 | 109.31 | 109.92 |
| PS | 10.97 | 10.91 | 10.90 | 11.52 |
| AR | 0.93 | 1.12 | 0.93 | 0.93 |
| BO (°) | 274 | 276 | 268 | 183 |
| PVG (kWh/m2) | 52.51 | 52.85 | 54.42 | 55.26 |
| AUHII (°C∙y) | 346.0 | 331.2 | 304.8 | 294.1 |
| IOD (°C·h) | 87.0 | 86.8 | 90.7 | 92.7 |
| CEI (kg/m2/y) | 216.92 | 290.75 | 337.87 | 359.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bian, C.; Hu, P.; Li, C.Y.; Lee, C.C.; Chen, X. Balancing Solar Energy, Thermal Comfort, and Emissions: A Data-Driven Urban Morphology Optimization Approach. Energies 2025, 18, 3421. https://doi.org/10.3390/en18133421
Bian C, Hu P, Li CY, Lee CC, Chen X. Balancing Solar Energy, Thermal Comfort, and Emissions: A Data-Driven Urban Morphology Optimization Approach. Energies. 2025; 18(13):3421. https://doi.org/10.3390/en18133421
Chicago/Turabian StyleBian, Chenhang, Panpan Hu, Chun Yin Li, Chi Chung Lee, and Xi Chen. 2025. "Balancing Solar Energy, Thermal Comfort, and Emissions: A Data-Driven Urban Morphology Optimization Approach" Energies 18, no. 13: 3421. https://doi.org/10.3390/en18133421
APA StyleBian, C., Hu, P., Li, C. Y., Lee, C. C., & Chen, X. (2025). Balancing Solar Energy, Thermal Comfort, and Emissions: A Data-Driven Urban Morphology Optimization Approach. Energies, 18(13), 3421. https://doi.org/10.3390/en18133421








