Multi-Objective Optimization of Gas Storage Compressor Units Based on NSGA-II
Abstract
1. Introduction
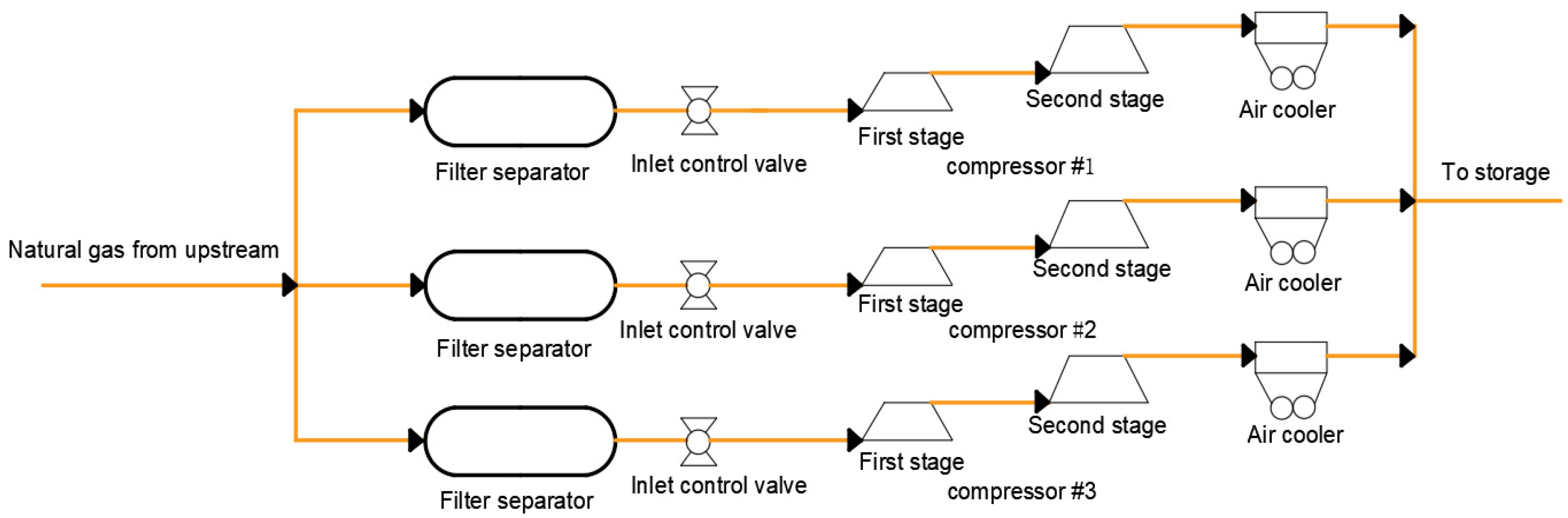
2. Basic Information of Gas Storage Facility
2.1. Basic Parameters of Compressors
2.2. Basic Parameters of Air Coolers
2.3. Natural Gas Composition
3. System Optimization Models
3.1. Compressor Mechanism Model
3.1.1. Thermodynamic Model
- Within the study period, the system operates under steady-flow conditions, and there are no performance differences among cylinders of the same stage.
- The natural gas undergoes an isenthalpic process when passing through various throttling valves, with no performance losses.
- Since the reciprocating compressor is not equipped with an intercooler, the discharge pressure and temperature of the first-stage compressor are considered as the intake pressure and temperature of the second-stage compressor, while inter-stage pressure losses are ignored.
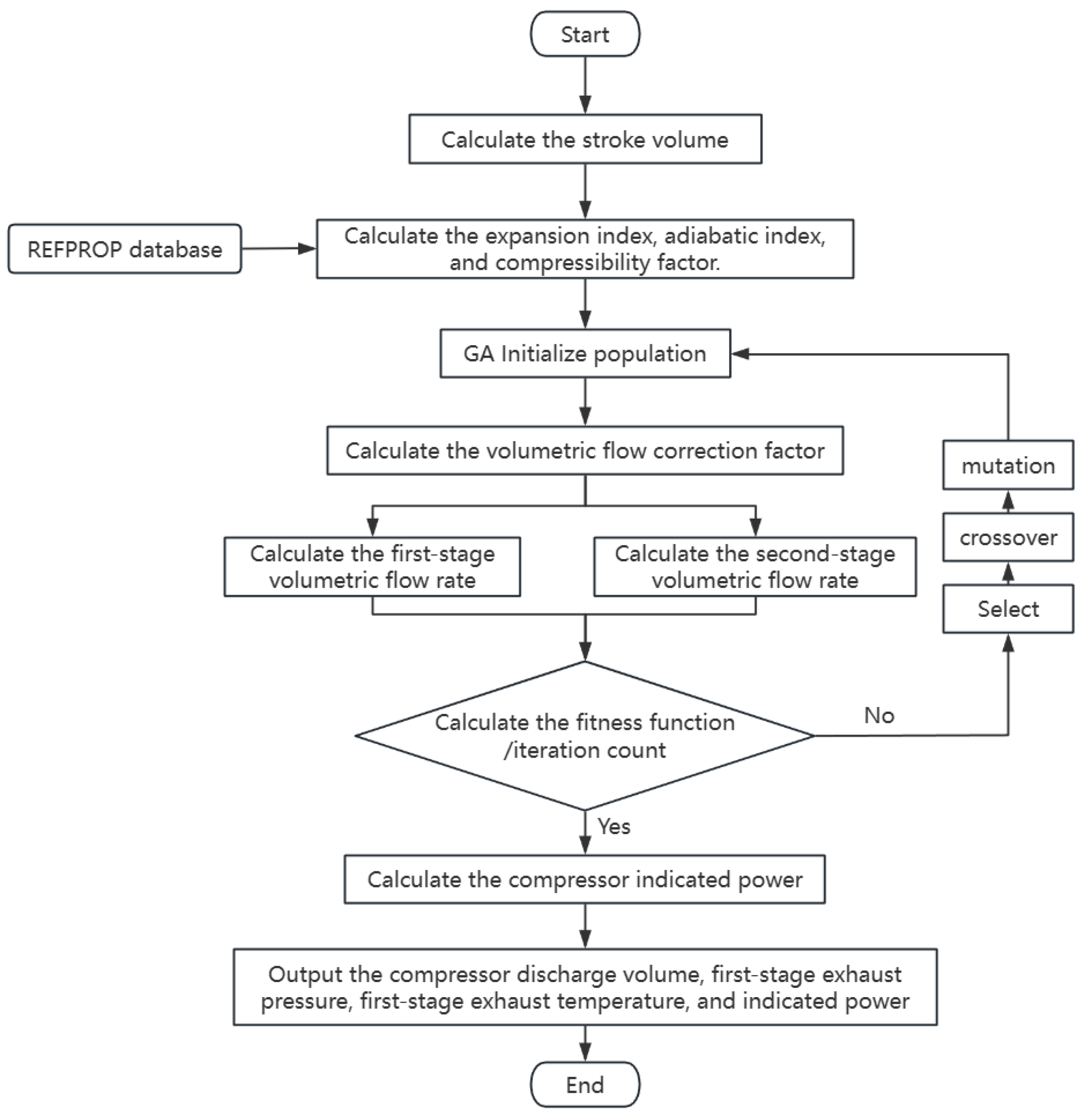
3.1.2. GA-BP Model
- Initialize the population
- 2.
- Fitness function
- 3.
- Genetic operations
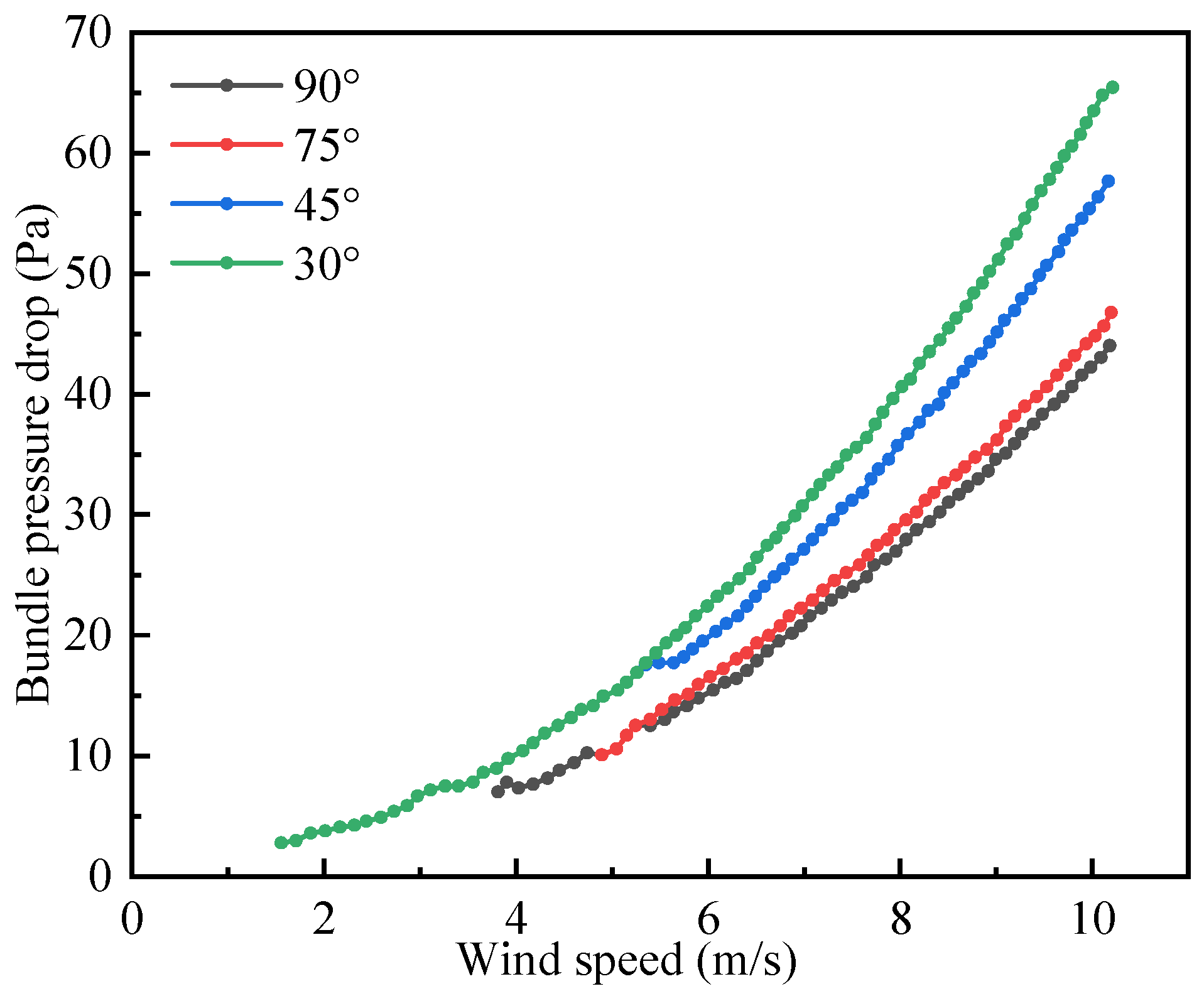
3.2. Air Cooler Flow and Heat Transfer Model
3.2.1. Flow Model
- Since the fan speed is relatively low, the variation in air density is negligible, and it can be treated as an incompressible fluid [18].
- The airflow over the air cooler is steady. In forced ventilation, the airflow generated by the fan passes entirely through the fins.
- The airflow generated by the fan is uniform, and the effects of the environment and structure on the fan airflow are neglected.
3.2.2. Heat Transfer Model
- The entire heat transfer process is in a steady state.
- The contact thermal resistance between the fins and the tubes is neglected [23].
- The effect of thermal radiation from the environment is ignored, and the thermal conductivity of the fins is considered constant.
- The natural gas inside the heat exchanger is assumed to flow uniformly through all tube bundles.
- The airflow provided by the fan is uniform, and the position of the tube bundles has no significant impact on the heat exchange performance.
- The air velocity is constant, meaning that variations in forced convection heat transfer outside the tubes are minimal. This allows for reasonable simplifications of the heat exchange process to facilitate data fitting and calculations.
3.3. NSGA-II Optimization Model
3.3.1. Objective Function
- Gas injection volume of the compressor:
- 2.
- Total power of the gas injection process:
3.3.2. Constraints
- Compressor power consumption:
- 2.
- Compressor speed:
- 3.
- Fan cooler speed:
- 4.
- Process parameter range:
3.3.3. NSGA-II Model Parameters
- Introduced non-dominated sorting and crowding distances to evaluate the quality of individuals, allowing the algorithm to better handle multi-objective optimization problems.
- Used a selection strategy based on the non-dominated sorting and crowding distances, enabling the algorithm to select better individuals.
- Maintained population diversity through the crowding distance, allowing the algorithm to find a broader range of solutions. An elitist strategy was used to ensure that excellent individuals from the previous generation are retained.
4. Results and Discussion
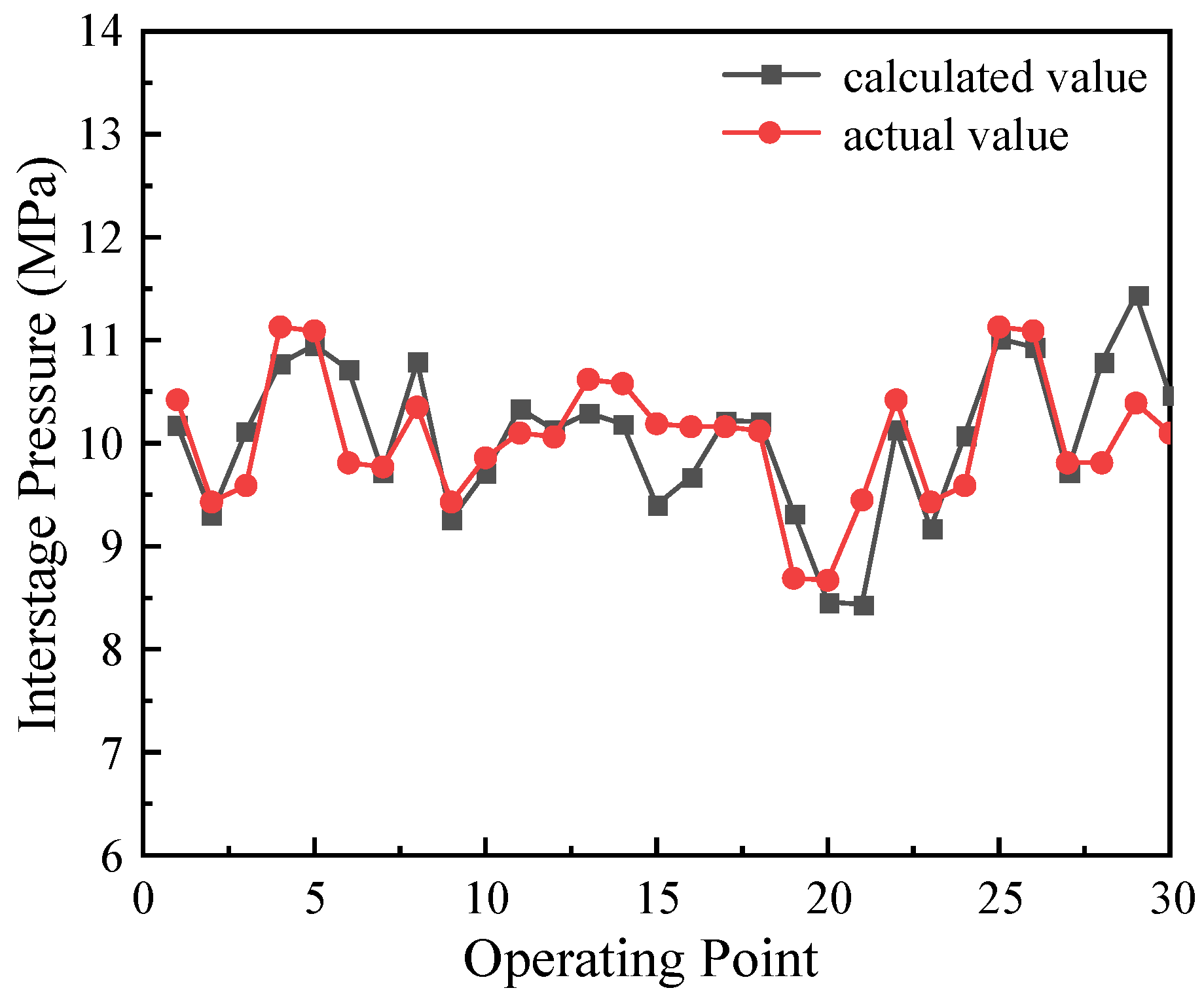
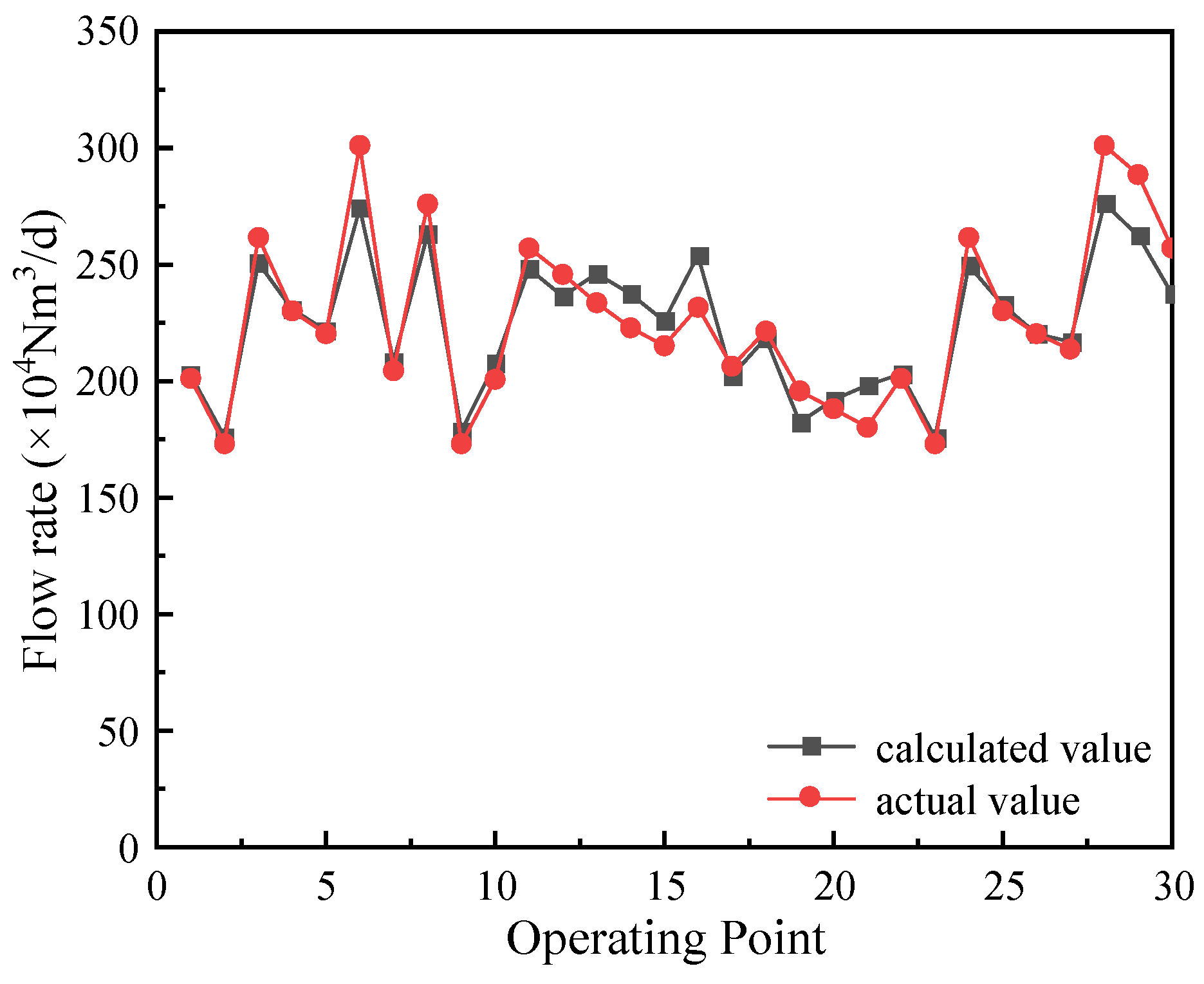
4.1. Validation of the Compressor Thermodynamic Model
4.2. Thermodynamic Performance Analysis of the Compressor
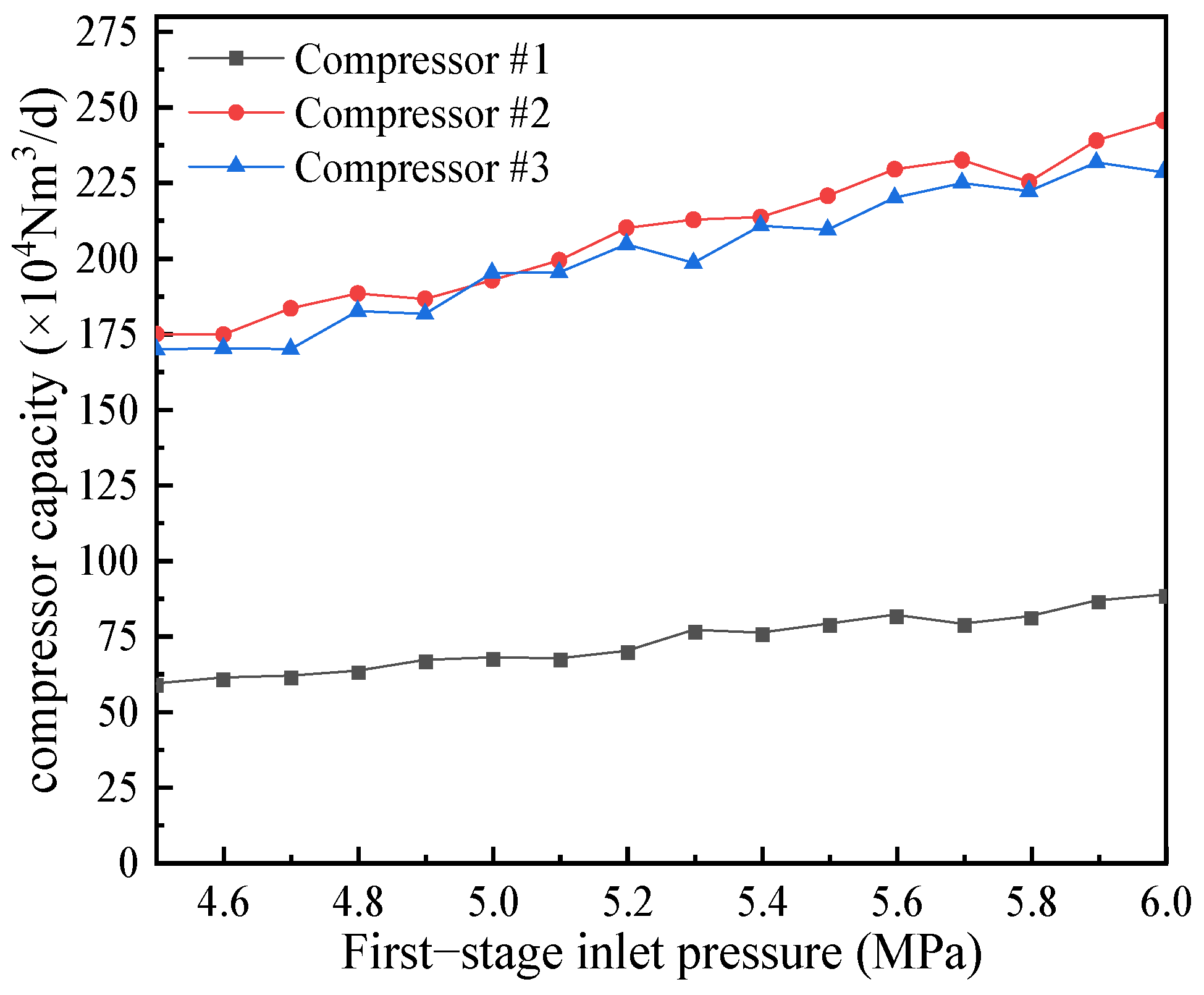
4.2.1. Effect of First-Stage Inlet Pressure
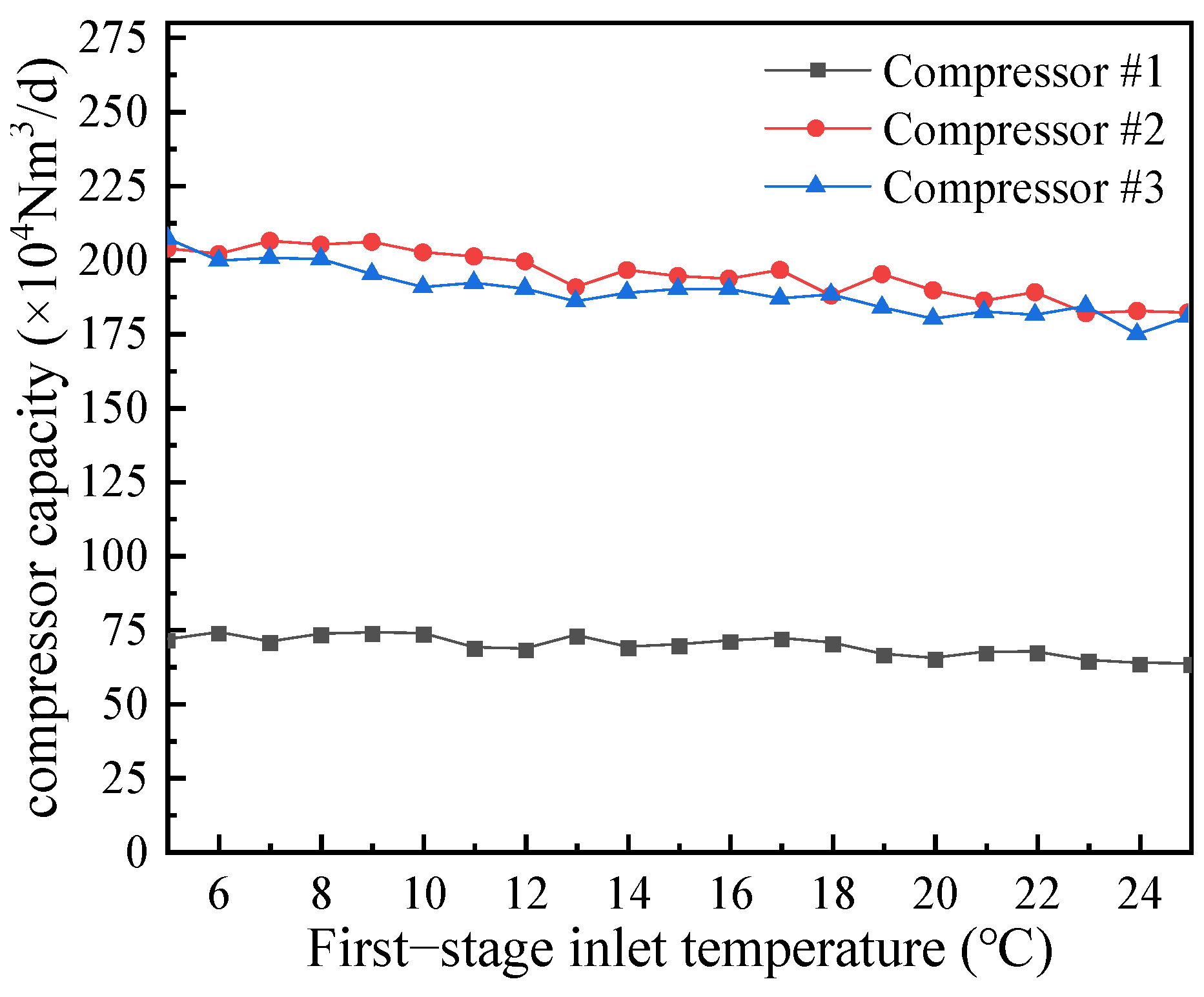
4.2.2. Effect of First-Stage Temperature
4.2.3. Effect of Second-Stage Discharge Pressure
4.3. NSGA-II Optimization Results
4.3.1. High-Pressure-Ratio Operation
4.3.2. Medium-Pressure-Ratio Operation
4.3.3. Low-Pressure-Ratio Operation
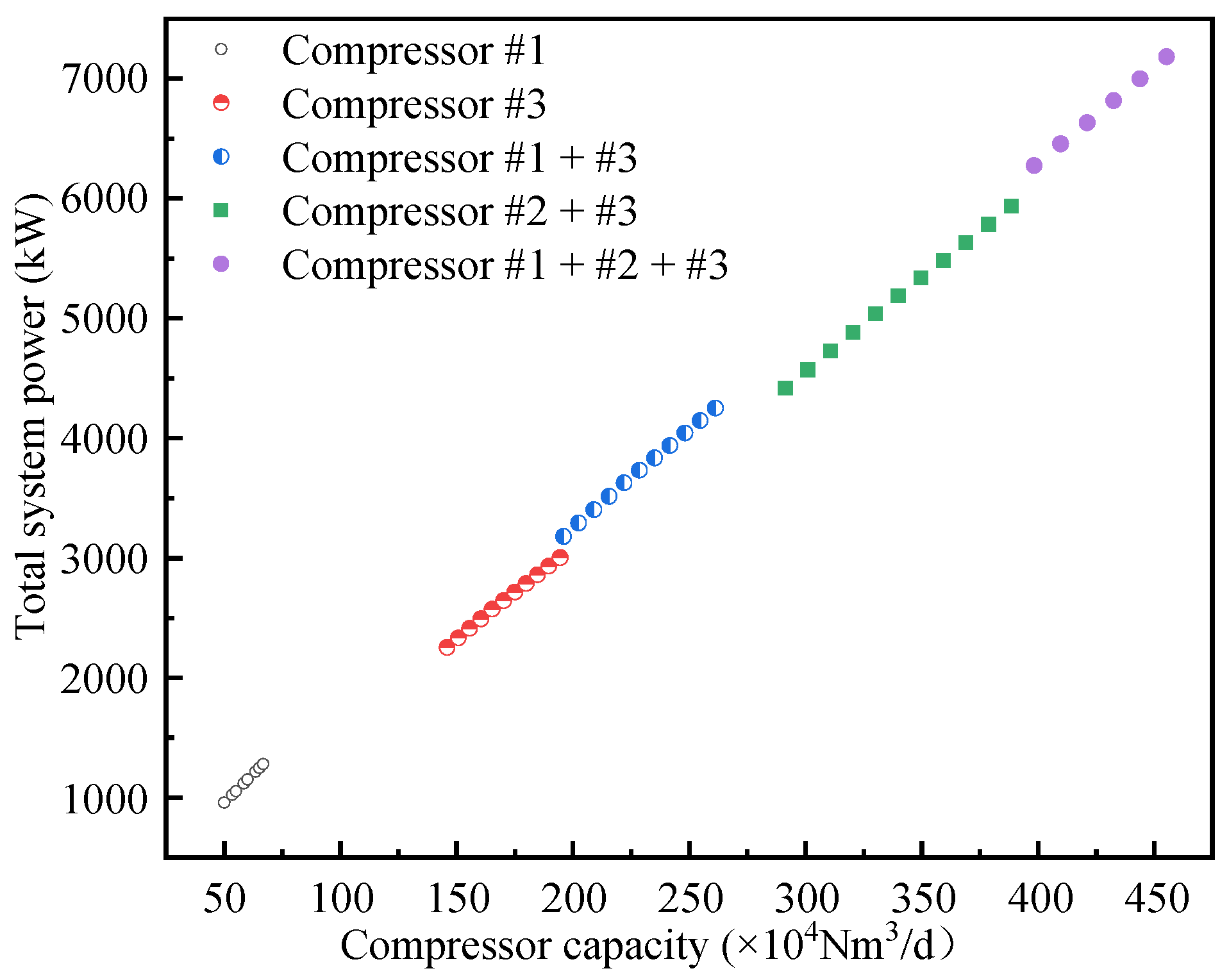
4.4. Compressor Unit Operation Plan
5. Conclusions
- A thermodynamic model for reciprocating compressors and a flow–heat transfer model for air coolers were developed, establishing a quantitative relationship between the air volume, power consumption, and fan speed of the air coolers. The energy consumption characteristics of air coolers were revealed, showing a significant nonlinear relationship between compressor power and speed. As the compressor speed approaches its maximum, the power consumption of the air coolers increases more rapidly.
- The effects of suction pressure, suction temperature, and discharge pressure on compressor performance were analyzed. The results indicate that increasing the suction pressure while reducing the suction temperature and discharge pressure can enhance the compressor’s gas handling capacity and reduce energy consumption.
- A multi-objective optimization model based on the NSGA-II algorithm was proposed for the three compressors in the gas storage facility. The objective functions were maximizing gas injection volume and minimizing total energy consumption, with decision variables including compressor and air cooler speeds. Constraints such as compressor operating limits and process requirements were incorporated. The algorithm classified compressor operation conditions into high, medium, and low compression ratios for optimization. The results show that an optimal startup sequence exists: as the daily gas injection volume increases, Compressor #1, #3, and then #2 should be sequentially activated, with parallel operation utilized when necessary to achieve optimal energy efficiency. It was also noted that compressors should avoid operating within certain partial gas injection ranges whenever possible.
- The optimal matching speeds of air coolers and compressors under different conditions and rotational speeds were determined. This study found that reducing the air cooler speed appropriately can significantly save energy while ensuring the maximum outlet temperature requirement for gas injection is met. The energy-saving potential increases as the compression ratio decreases. Under the studied conditions, adjusting air cooler speeds at high compression ratios offers an energy-saving potential of 2%, whereas at low compression ratios, this potential can reach up to 8%.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
| Suction Pressure (0.1 MPa) | k Value | k = 1.4 |
|---|---|---|
| 1.5 | m = 1 + 0.5(k − 1) | m = 1.2 |
| 1.5~4 | m = 1 + 0.62(k − 1) | m = 1.25 |
| 4~10 | m = 1 + 0.75(k − 1) | m = 1.3 |
| 10~30 | m = 1 + 0.88(k − 1) | m = 1.35 |
| >30 | m = k | m = 1.4 |
Appendix A.2
| Equipment Load (%) | Fan Efficiency (%) | Motor Power Factor (%) |
|---|---|---|
| 50 | 94.8 | 76.8 |
| 75 | 94.9 | 83.4 |
| 100 | 94.5 | 85.2 |
| Energy Consumption Equipment | Parameters |
|---|---|
| Compressor oil injector pump motor | 361 W/380 V/3 PH/50 Hz |
| Compressor pre-lubrication oil pump motor | 3.75 KW/380 V/3 PH/50 Hz |
| Crankcase heater | 2 × 2 KW/220 V/1 PH/50 Hz |
| Oil injector tank heater | 3 × 150 W/220 V/1 PH/50 Hz |
| Compressor packing cooling water pump | 0.75 KW/380 V/3 PH/50 Hz |
| Drive motor space heater | 82 W/220 V/1 PH/50 Hz |
| UCP (UPS power supply) | 1.87 KW/220 V/1 PH/50 Hz |
| Electric trace heating | 8 W/220 V/50 Hz |
References
- Li, Q.; Li, Q.; Wu, J.; Li, X.; Li, H.; Cheng, Y. Wellhead Stability During Development Process of Hydrate Reservoir in the Northern South China Sea: Evolution and Mechanism. Processes 2025, 13, 1630. [Google Scholar] [CrossRef]
- Li, Q.; Wu, J.; Li, Q.; Wang, F.; Cheng, Y. Sediment Instability Caused by Gas Production from Hydrate-Bearing Sediment in Northern South China Sea by Horizontal Wellbore: Sensitivity Analysis. Nat. Resour. Res. 2025, 34, 1667–1699. [Google Scholar]
- Ding, G.; Wei, H. Review on 20 years’ UGS construction in China and the prospect. Oil Gas Storage Transp. 2020, 39, 25–31. [Google Scholar]
- Ma, X.; Zheng, D.; Wei, G.; Ding, G.; Zheng, S. Development directions of major scientific theories and technologies for underground gas storage. Nat. Gas Ind. 2022, 42, 93–99. [Google Scholar]
- Hong, H.; Jiang, Z.; Ma, W.; Xiong, W.; Zhang, J.; Liu, W.; Wang, Y. Design of an IMCPID Optimized Neural Network for Stepless Flow Control of Reciprocating Mechinery. Appl. Sci. 2021, 11, 7785. [Google Scholar] [CrossRef]
- Ma, J.; Ding, X.; Horton, W.T.; Ziviani, D. Development of an automated compressor performance mapping using artificial neural network and multiple compressor technologies. Int. J. Refrig. 2020, 120, 66–80. [Google Scholar] [CrossRef]
- Wang, F.; Li, X.; Chen, X.; Wang, W.; Gong, J. Prediction method for compressor real energy head characteristics based on deep learning network. Oil Gas Storage Transp. 2020, 39, 459–466. [Google Scholar]
- Chen, J.; Tan, Y. Determination of Optimal Running Scheme about Injection Process of the Natural Gas Storage Reservoirs. Oil Gas Storage Transp. 2002, 06, 3–4+7–10. [Google Scholar]
- Yang, Y.; Li, S.B.; Chen, Z.W.; Chen, J.W.; Li, P. Optimization measures to maintain economical operation of electrically driven compressor during gas injection in underground gas storage. Nat. Gas Explor. Dev. 2017, 40, 102–106. [Google Scholar]
- Wu, K.; Tian, Y.; Yang, Y. Optimization of start-up/shutdown scheme of compressor in gas storage period of gas storage at tiered pricing for electricity. Petrochem. Ind. Technol. 2017, 24, 75–77. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Wang, A.; Xiao, Y.; Liu, C.; Zhao, Y.; Sun, S. Multi-objective optimization of building energy consumption and thermal comfort based on SVR-NSGA-II. Case Stud. Therm. Eng. 2024, 63, 105368. [Google Scholar] [CrossRef]
- Ye, L.; Li, C.; Wang, C.; Zheng, J.; Zhong, K.; Wu, T. A multi-objective optimization approach for battery thermal management system based on the combination of BP neural network prediction and NSGA-II algorithm. J. Energy Storage 2024, 99, 113212. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, P. NSGA-II algorithm based control parameters optimization strategy for megawatt novel nuclear power systems. Energy 2025, 316, 134444. [Google Scholar] [CrossRef]
- Huber, M.L.; Lemmon, E.W.; Bell, I.H.; McLinden, M.O. The NIST REFPROP database for highly accurate properties of industrially important fluids. Ind. Eng. Chem. Res. 2022, 61, 15449–15472. [Google Scholar] [CrossRef]
- Qu, Z. Principle of Reciprocating Compressor; Xi’an Jiaotong University Press: Xi’an, China, 2019. [Google Scholar]
- Sun, L. Heat Exchanger Process Design; China Petrochemical Press: Beijing, China, 2015. [Google Scholar]
- Duvenhage, K.; Kröger, D.G. The influence of wind on the performance of forced draught air-cooled heat exchangers. J. Wind. Eng. Ind. Aerodyn. 1996, 62, 259–277. [Google Scholar] [CrossRef]
- Dong, Z.; Chen, F.; Yu, Y.; Chen, L. Analysis on Relationship between Air Aftercooler Power and Total Power of the Compressor Unit in Long-distance Pipeline Compressor Station. Nat. Gas Oil 2009, 27, 51–54+68. [Google Scholar]
- Zhang, S.; Yang, W.; Gao, X.; Chen, F. Compressor Station Gas Temperature Circular Rise Simulation and Analysis. Nat. Gas Oil 2019, 37, 36–41. [Google Scholar]
- Liu, S.; Li, G.; Tong, L.; Xu, Q.; Zhang, J.; Zou, W. Setting program of air cooler in gas compressor stations. Oil Gas Storage Transp. 2019, 38, 228–234. [Google Scholar]
- Yang, S.; Tao, W. Heat Transfer; Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Wang, C.; Chi, K. Heat transfer and friction characteristics of plain fin-and-tube heat exchangers, part I: New experimental data. Int. J. Heat Mass Transf. 2000, 43, 2681–2691. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, J.H.; Luo, S.; Sun, J.H.; Liang, G.C.; Peng, C. Optimization of Gas Injection and Production in Gas Storage Based on Large Depleted Gas Reservoir with Consideration of Safe and Stable Operation. Spec. Oil Gas Reserv. 2021, 28, 76–82. [Google Scholar]
- Blank, J.; Deb, K. Pymoo: Multi-objective optimization in python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Yu, Y.; Sun, S. Compressor Engineering Manual; China Petrochemical Press: Beijing, China, 2012. [Google Scholar]






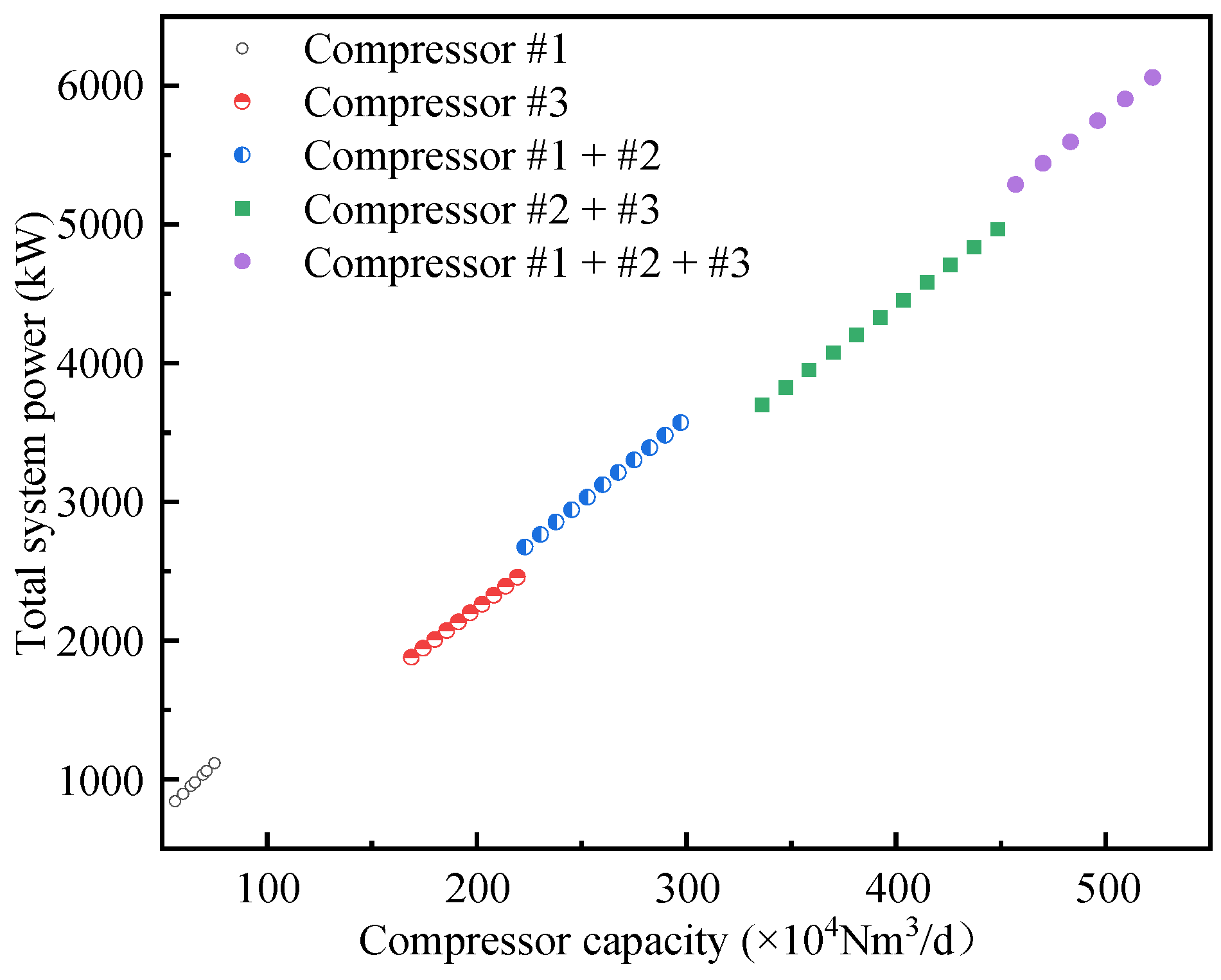
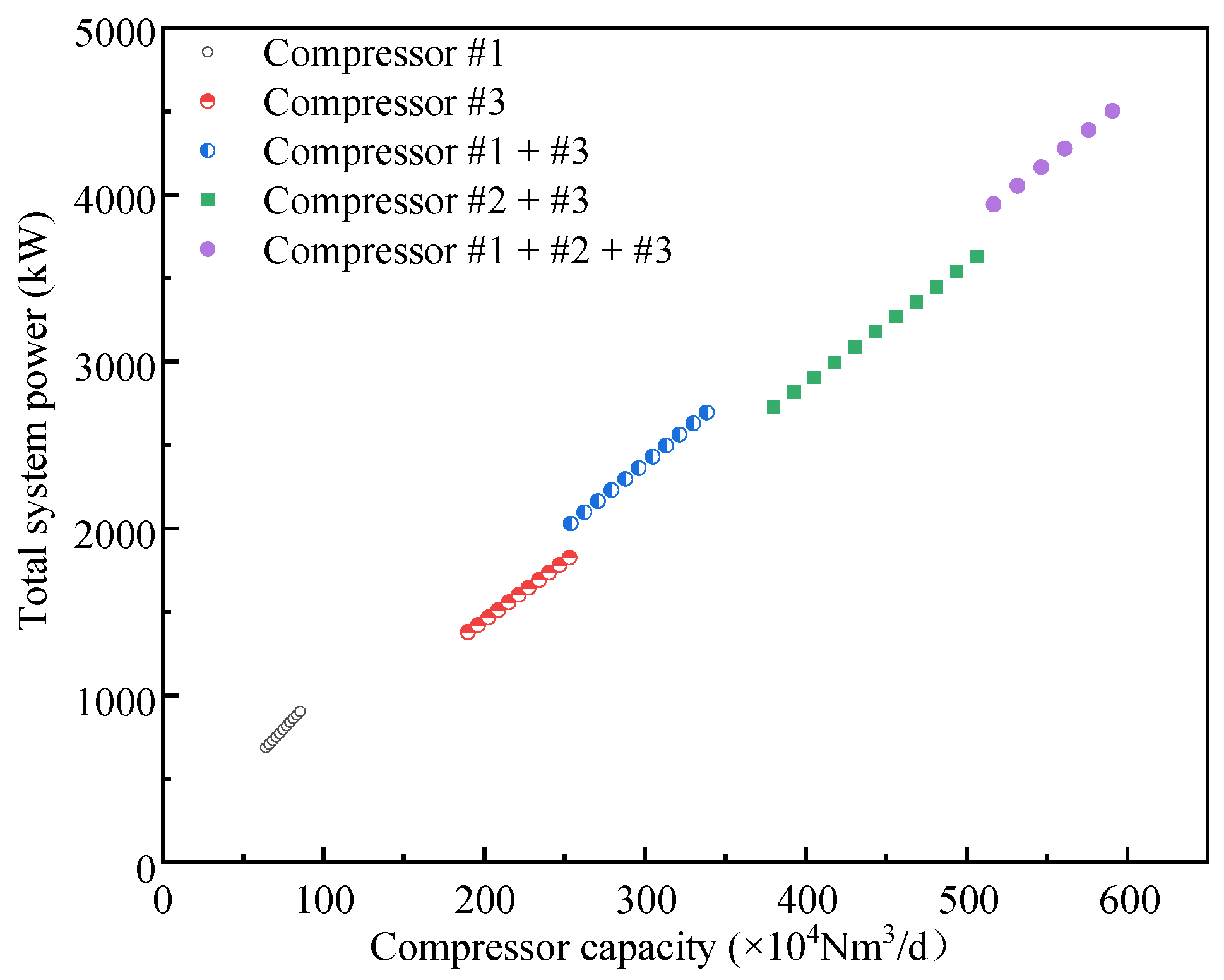
| No. | #1 | #2 | #3 |
|---|---|---|---|
| Rated Flow (×104 m3/d) | 80 | 180 | 180 |
| Suction Pressure (MPa) | 4.5~7.5 | 4.5~7.5 | 4.5~7.5 |
| Rated Discharge Pressure (MPa) | 6.9~17 | 6.9~17 | 6.9~17 |
| Actual Speed (r/min) | 750~1000 | 750~1000 | 750~1000 |
| Stages | 2 | 2 | 2 |
| Number of Cylinders | 3 | 6 | 6 |
| Rated Power (kW) | 1324 | 3531 | 3532 |
| No. | #1 | #2 | #3 |
|---|---|---|---|
| Fan Diameter (inches) | 120 | 180 | 180 |
| Number of Blades (pieces) | 6 | 8 | 8 |
| Number of Fans (pieces) | 2 | 2 | 2 |
| Blade Angle (°) | 12 | 12 | 12 |
| Piping Layout Method | Crossflow | Crossflow | Crossflow |
| Pipe Diameter (mm) | 15.9 | 15.9 | 15.9 |
| Pipe Length (m) | 9.1 | 17.7 | 17.7 |
| Finned Surface Area Ratio | 15.9 | 15.9 | 15.9 |
| Number of Tube Rows | 3 | 3 | 3 |
| Motor Rated Speed (r/min) | 1450 | 1450 | 1500 |
| Motor Rated Power (kW) | 15 | 55 | 45 |
| Composition | Mole Fraction (%) |
|---|---|
| Methane | 96.1 |
| Ethane | 1.74 |
| Propane | 0.58 |
| Isobutane | 0.28 |
| Isopentane | 0.03 |
| N-hexane | 0.09 |
| Nitrogen | 0.56 |
| Carbon dioxide | 0.62 |
| Input Parameters | Structural Parameters | Output Parameters |
|---|---|---|
| First-Stage Suction Pressure First-Stage Suction Temperature Second-Stage Discharge Pressure Second-Stage Discharge Temperature | First-Stage Piston Stroke First-Stage Cylinder Diameter Second-Stage Piston Stroke Second-Stage Cylinder Diameter Piston Rod Diameter | Discharge Volume First-Stage Discharge Pressure First-Stage Discharge Temperature First-Stage Indicated Power Second-Stage Indicated Power |
| Operating Condition | Daily Gas Injection Volume Range (×104 Nm3) | Compressor Start up Plan |
|---|---|---|
| High Pressure Ratio | <66 | Compressor #1 |
| 67~140 | No optimal energy-saving plan; Compressor #3 can be started to shorten the operation time of Compressor #1 | |
| 145~194 | Compressor #3 | |
| 195~261 | Compressor #1 and #3 | |
| 291~388 | Compressor #2 and #3 | |
| >398 | Compressor #1, #2, and #3 | |
| Medium Pressure Ratio | <74 | Compressor #1 |
| 74~168 | No optimal energy-saving plan; Compressor #2 can be started to shorten the operation time of Compressor #1 | |
| 168~219 | Compressor #3 | |
| 223~297 | Compressor #1 and #3 | |
| 339~447 | Compressor #2 and #3 | |
| >456 | Compressor #1, #2, and #3 | |
| Low Pressure Ratio | <85 | Compressor #1 |
| 85~190 | No optimal energy-saving plan; Compressor #2 can be started to shorten the operation time of Compressor #1 | |
| 190~253 | Compressor #3 | |
| 254~338 | Compressor #1 and #3 | |
| 379~505 | Compressor #2 and #3 | |
| >516 | Compressor #1, #2, and #3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Fan, L.; Lu, J.; He, M.; Qian, S.; Wei, Q.; Wang, G.; Bai, H.; Zhou, H.; Liu, Y.; et al. Multi-Objective Optimization of Gas Storage Compressor Units Based on NSGA-II. Energies 2025, 18, 3377. https://doi.org/10.3390/en18133377
Zhao L, Fan L, Lu J, He M, Qian S, Wei Q, Wang G, Bai H, Zhou H, Liu Y, et al. Multi-Objective Optimization of Gas Storage Compressor Units Based on NSGA-II. Energies. 2025; 18(13):3377. https://doi.org/10.3390/en18133377
Chicago/Turabian StyleZhao, Lianbin, Lilin Fan, Jun Lu, Mingmin He, Su Qian, Qingsong Wei, Guijiu Wang, Haoze Bai, Hu Zhou, Yongshuai Liu, and et al. 2025. "Multi-Objective Optimization of Gas Storage Compressor Units Based on NSGA-II" Energies 18, no. 13: 3377. https://doi.org/10.3390/en18133377
APA StyleZhao, L., Fan, L., Lu, J., He, M., Qian, S., Wei, Q., Wang, G., Bai, H., Zhou, H., Liu, Y., & Chang, C. (2025). Multi-Objective Optimization of Gas Storage Compressor Units Based on NSGA-II. Energies, 18(13), 3377. https://doi.org/10.3390/en18133377





