A Review of Digital Twinning Applications for Floating Offshore Wind Turbines: Insights, Innovations, and Implementation

Abstract

This paper presents a comprehensive literature review on the digital twinning of floating offshore wind turbines (FOWTs). In this study, the digital twin (DT) is defined as a dynamic virtual model that accurately mirrors a physical system throughout its lifecycle, continuously updated with real-time data and use simulations, machine learning, and analytics to support informed decision-making. The recent advancements and major issues have been introduced, which need to be addressed before realizing a FOWT DT that can be effectively used for life extension and operation and maintenance planning. This review synthesizes relevant literature reviews focused on modeling FOWT and its specific components along with the latest research. It specifically focuses on the structural, mechanical, and energy production components of FOWTs within the DT framework. The state of the art DT for FOWT, or large scale operational civil and energy infrastructure, is not yet matured to perform real-time update of digital replicas of these systems. The main barriers include real-time coupled modeling with high fidelity, the design of sensor networks, and optimization methods that synergize the sensor data and simulations to calibrate the model. Based on the literature survey provided in this paper, one of the main barriers is uncertainty associated with the external loads applied to FOWT. In this review paper, a robust method for inverse analysis in the absence of load information has been introduced and validated by using simulated experiments. Furthermore, the regulatory requirements have been provided for FOWT life extension and the potential of DT in achieving that.

1. Introduction

As the urgency to diversify energy sources intensify, the deployment of sustainable energy infrastructure has become a critical focus. Floating offshore wind turbines (FOWTs) are reliable energy sources with significant potential for large-scale deployment. These structures offer significant advantages in regions where fixed-bottom offshore wind turbines (OWTs) are constrained by depth limitations (typically over 60 m). FOWTs enable the exploitation of stronger and more consistent wind resources found offshore. Additional advantages include less installation noise, fewer geotechnical issues due to soil–structure interaction, reduced costs in deep areas, access to much wider potential wind farm areas, and minimized visual impact from coastal areas [1].

Moreover, the deployment of FOWTs in deep-water zones offers the potential to access higher wind speeds and more consistent wind patterns compared to their onshore and shallow-water counterparts [2]. However, the dynamic and harsh marine environment poses significant risks to the structural integrity and longevity of floating structures, particularly due to stringent regulatory requirements for energy infrastructure certification [3].

On average, the number of planned turbine installations is more than 100 per farm. Therefore, routine on-site inspections are not logistically and financially feasible. Also, the on-site inspections are costly, and they present significant difficulties in terms of the safety conditions of the workers. Therefore, there is a demand for strategies that can provide remote feedback based on the actual condition of FOWTs. A contender that can provide this situational awareness would be a digital twin (DT). DTs can be utilized to monitor FOWT health and substitute or complement mandatory inspections. This is essential to ensure not only regulatory compliance, but also the safety, reliability, and economic viability of FOWTs [4].

1.1. Global Floating Offshore Wind Development

Over the past decade, FOWTs have gained traction in major global markets such as the UK, EU, Norway, China, Japan, South Korea, and the United States. Early pilot projects (e.g., Hywind Scotland and Fukushima Forward) demonstrated feasibility in deep waters. At the same time, recent initiatives like the UK’s Green Volt and Norway’s Hywind Tampen signal a shift toward commercial-scale deployments [5,6,7].

The EU [8,9], Norway [7,10], South Korea [11], Japan [12], and the U.S. have each set ambitious deployment targets ranging from 14 to 30 GW by 2030, with China leading turbine manufacturing and scaling domestic capacity [13,14,15,16]. In the U.S., federal and state-level planning, such as BOEM’s call areas and Maine’s 12-turbine pilot project, has increased interest in floating wind platforms on both the Atlantic and Pacific coasts [17,18,19]. The University of Maine is leading the design efforts with its patented VolturnUS [20] transformational floating concrete hull technology, inspired by the structure of an upside-down bridge [18].

Despite regional policy and engineering readiness differences, FOWTs across these geographies share common challenges: deep water deployment, dynamic environmental loads, and complex regulatory environments. These challenges highlight the need for more adaptive, real-time, and data-integrated design and operation strategies, which are areas where digital twinning technologies can provide substantial value.

1.2. FOWT Levelized Cost of Energy Reduction Strategies

The levelized cost of energy (LCOE) is used to assess the economic viability of a design, which represents the lifetime cost of an energy source per unit of energy generated [21]. The National Renewable Energy Laboratory (NREL) estimates that by 2030, LCOE from floating offshore wind in Oregon could decrease to USD 0.06–0.088/kWh, a significant reduction compared to the average LCOE of USD 0.0882/kWh for Oregon in 2020 [22]. Musial et al. (2021) predicted that the LCOE for floating offshore wind will decline from approximately USD160/MWh in 2020 to USD 60–105/MWh by 2030 [23]. Currently, there are three full-scale operational floating wind farms globally, located in Scotland and Portugal [24]. The global pipeline for floating offshore wind energy more than tripled in 2020, with an expected increase of up to 70 GW of floating offshore wind capacity that could be operational by 2040 [25].

1.2.1. Construction and Installation

The construction, installation, and logistics phases offer significant potential for the reduction in LCOE [13]. The logistics process begins with site modeling and phased design planning. This supports milestone tracking and cost control. Port infrastructure has a critical role: Manufacturing ports, ideally near the wind farm, serve as deployment hubs, while mobilization ports are used when nearby manufacturing is unavailable. Some state-of-the-art FOWT platform designs include concrete platforms [20] that reduce the need for mobilization ports. Vessel selection also impacts cost [26]. Thus, a balance among LCOE, deployment duration, safety, and environmental impact is required [21].

1.2.2. Operations and Maintenance

FOWT operations and maintenance (O&M) include major barriers to the scalability of offshore wind farms. O&M accounts for roughly 20–35% of total lifecycle costs due to harsh sea conditions, limited accessibility, and complex logistics [27,28,29]. O&M costs include both visible (transport, labor, and parts) and invisible components such as production losses (PL) from performance degradation.

FOWTs present unique O&M challenges since many vessels used in fixed-bottom maintenance cannot operate beyond 50 m water depth [25]. This makes cost-effective and reliable maintenance strategies even more critical. Maintenance approaches can be categorized into five types: reactive, preventive, condition-based, predictive, and prescriptive. Among them, predictive and prescriptive strategies (backed by real-time monitoring and modeling) are preferable because they reduce downtime and improve turbine lifespan [30,31].

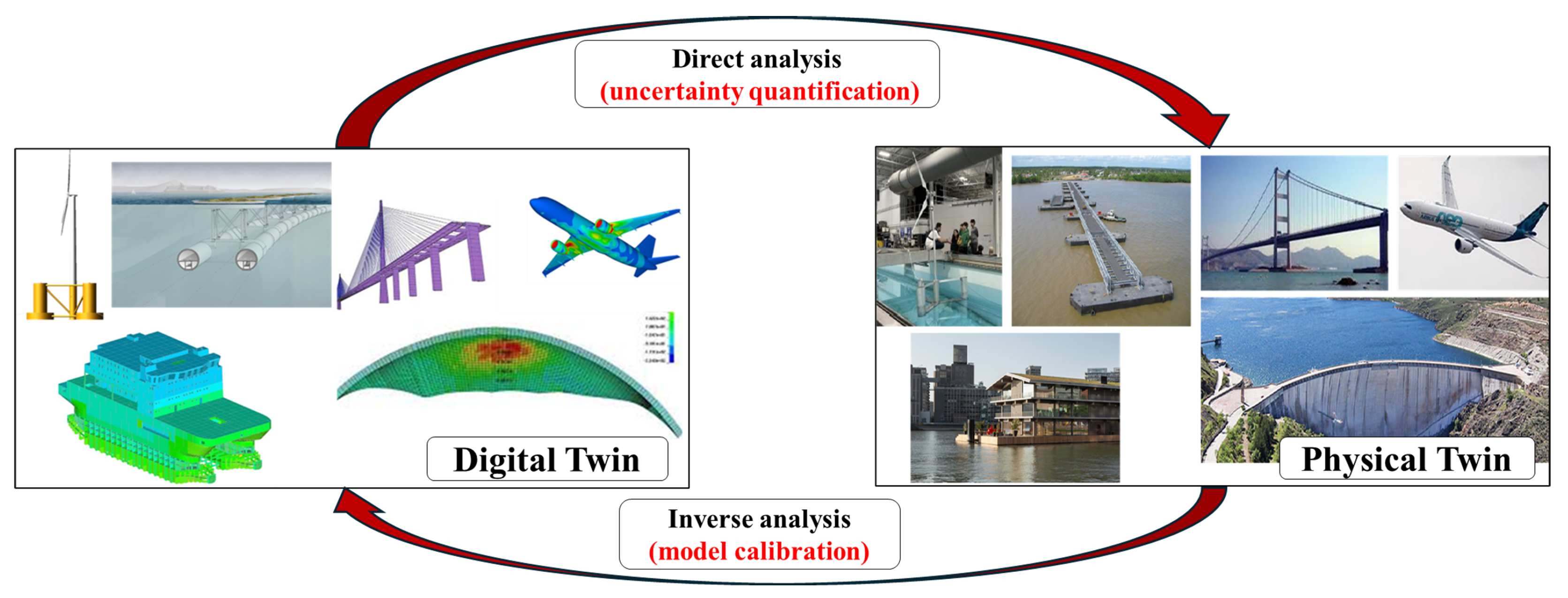
DTs are reliable solutions for predictive maintenance since they virtually replicate the physical system (see Figure 1) and support real-time monitoring, diagnostics, and performance forecasting. DTs support condition monitoring (CM) and structural health monitoring (SHM) in structural applications. Hence, DTs improve reliability and provide valuable information for life-cycle decisions.

While early-phase FOWT deployment continues to advance, end-of-life strategies such as decommissioning or life extension remain underexplored. In the U.S., regulatory frameworks are still under development, with the National Oceanic and Atmospheric Administration (NOAA) and Bureau of Ocean Energy Management (BOEM) expected to provide environmental and operational guidance [32,33,34].

1.2.3. DTs for FOWT Life Extension and LCOE Reduction

The BOEM and Bureau of Safety and Environmental Enforcement (BSEE) regulate the design, installation, and operation of offshore renewable energy projects in the U.S., as outlined in CFR Parts 285 and 585 [32,33]. These regulations require “accepted industry practices,” though the term remains undefined [4]. To fill this gap, the American Clean Power Association (ACP) released the Offshore Compliance Recommended Practices OCRP-1-2022 [35], which references International Electrotechnical Commission (IEC), International Organization for Standardization (ISO), and European standards to define best practices for offshore wind.

Standards from the IEC, Det Norske Veritas (DNV), the American Bureau of Shipping (ABS), and OCRP-1-2022 support continuous or periodic assessments throughout a typical 25–30-year FOWT design life. These standards assume high safety margins due to harsh ocean conditions that often lead to conservative designs. Increased investment in early-stage design and planning has been shown to reduce lifetime cost and associated risks [36]. For example, an extension of five years for turbine design life raises capital expenditure (CAPEX) by 4–6% but can reduce LCOE overall.

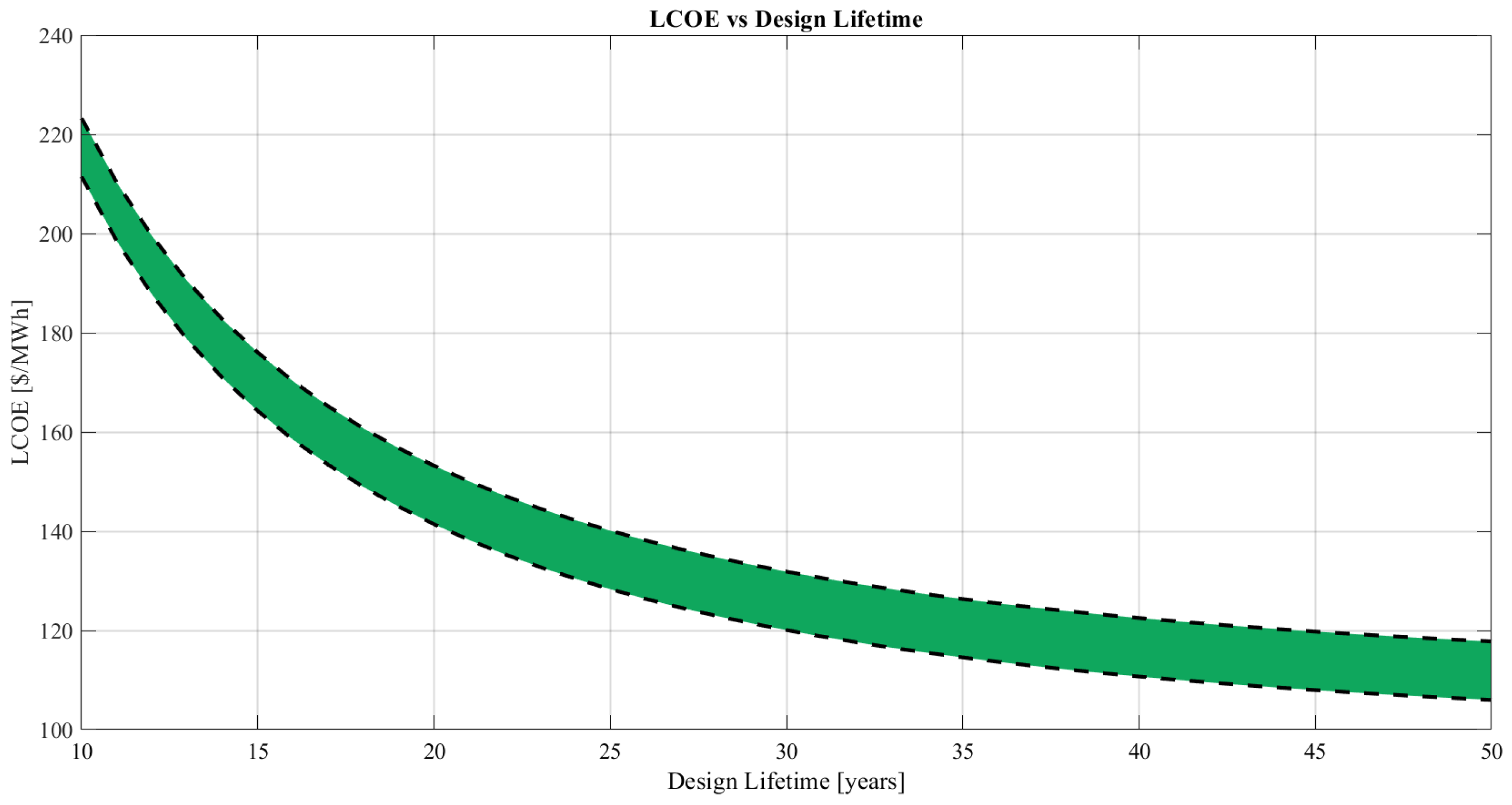
DTs and continuous monitoring could support life extension strategies beyond the five-year threshold [37]. To illustrate this potential, Figure 2 shows estimated LCOE trends for the Gulf of Maine using DOE and NREL data [38,39].

DTs can support control retrofitting by monitoring shifts in structural dynamics, such as tower first-aft mode (1FA) or drivetrain torsional modes. This allows the adaptive tuning of control algorithms. They can also track changes in the power curve to inform upgrades. Astolfi et al. [40] show that control redesign, based on operational and numerical data, can improve performance by 1% without hardware changes.

In related sectors, repowering has emerged as a cost-effective life extension method [41]. Full repowering replaces entire turbines, while partial repowering includes updates for select components (often without permitting). Both approaches are incentivized by the production tax credit (PTC) [42]. Notable examples include the Mendota Hills project in Illinois, which increased capacity from 50 MW to 76 MW [43], and the Jeffers Wind project in Minnesota, which upgraded 20 turbines to produce 197,000 MWh annually [44,45].

Internationally, life extension standards vary. Germany uses DNVGL-SE-0263 for wind turbine life extension certification based on structural inspection and performance modeling [46]. Denmark’s Executive Order 73 mandates blade and structural inspections at the end of design life and requires cost–benefit analysis to justify continued operation [47].

The combination of digital twinning technologies with proven repowering strategies may allow U.S. FOWTs to extend beyond 25 years, reduce O&M costs, improve efficiency, and create new job markets.

1.2.4. Design Validation via DT

As conventional scaled modeling in controlled laboratory environments often fails to replicate the real-world environmental conditions, the DT adaptation for FOWT’s design validation can be a viable solution. Along with some unique challenges to FOWT (e.g., the inability to employ Froude and Reynolds’ scaling laws simultaneously), physical testing methods struggle with scaling effects, limited data fidelity, and unrealistic environmental conditions that result in discrepancies between the experimental results and actual operational performance [48]. DTs can bridge this gap by the integration of data-driven simulations and full-scale operation data [49]. This technology allows for real-time SHM [50], and it can allow for improving the economic viability and scalability of FOWTs as a result of enhanced structural dynamics and fatigue life estimation [37].

1.3. Objectives and Main Contributions

At the time of this paper, digital twinning for FOWTs is in early development stage, and while various approaches exist for digital twinning and SHM, this review primarily emphasizes Kalman filter (KF) variants. This focus is due to their real-time capabilities, early adoption in FOWT studies, and their demonstrated maturity and robustness under uncertainty. Hence, it reflects prevailing trends in the literature and the authors’ own research experience. The authors acknowledge that the interest in alternative methods, such as operational modal analysis (OMA) [51] and deep learning techniques [52], have started to increase and represent valuable avenues for future work.

There are four main objectives of this paper to synthesize the current state-of-the-art in digital twinning for structural, mechanical, and energy-related components of FOWTs: to identify recent innovations in filtering and inverse analysis methods suitable for real-time applications; to examine practical challenges involved in DT deployment in harsh offshore environments; and to highlight areas where further research is urgently needed to support scalable DT implementation.

This is a central question of this review: How can digital twinning enhance life extension, operation, and maintenance of FOWTs, and what technical and practical barriers must be addressed to realize its full potential?

In response, this paper offers various contributions. First, it comprehensively reviews the current literature on digital twinning in FOWTs, organized around core subsystems such as the tower, mooring system, drivetrain, and energy production units. Second, it identifies key barriers to widespread DT adoption, which include the lack of real-time coupled modeling strategies, challenges in sensor network design, and the need for robust data-simulation integration frameworks. Third, it highlights the role of KF variants and other inverse analysis techniques in real-time diagnostics, control, and state estimation. Fourth, the paper outlines practical implementation issues (e.g., sensor reliability, edge computing) and discusses their implications for offshore deployment.

Furthermore, a proof-of-concept study is provided in this paper to offer a detailed example for a FOWT DT. In this case study, the focus is on the integration of KF, augmented Kalman filter (AKF), and Universal filter (UF) into DTs for FOWTs. A case study from the recent literature has been used as a base, and these filters are applied to estimate mooring forces and platform motions under hydrodynamic loads.

2. Research Methodology and Meta-Analysis of Literature Trends

This study conducted a targeted literature search focused on digital twinning applications for FOWTs to ensure a comprehensive and structured review. The primary database used was Google Scholar, which provides broad access to peer-reviewed journals and conference proceedings across engineering, energy systems, and structural health monitoring domains.

Search queries included combinations of terms such as “digital twin,” “floating offshore wind turbine,” “marine structure”, “offshore structure,” “floating platform”, “structural health monitoring,” “Kalman filter,” “machine learning,” “inverse modeling,” and more. The search was limited to works published between 2019 and early 2025 to reflect the most recent advancements. Only peer-reviewed journal articles and conference papers written in English were considered.

The screening process involved title and abstract reviews for relevance, followed by full-text reviews of shortlisted papers. Selected works were categorized based on their primary contribution areas such as structural components (e.g., blades, tower, foundation), mechanical systems (e.g., drivetrain, mooring), wave motions, energy production, damage identification, fault detection, monitoring techniques, inverse estimation strategies, and DT frameworks. Papers were selected not only for technical depth but also for their representativeness of recent research trends and relevance to the FOWT domain.

This methodology informed the structure of the literature review in subsequent sections and ensured that the selection of sources was aligned with the scope and objectives of this paper.

3. Existing Relevant Review Papers and Literature Gap

Digital twinning has gained significant traction across various engineering sectors such as construction, oil and gas, marine energy, and offshore wind. In this section, general reviews of DTs in related fields are summarized. Then, the focus is narrowed to reviews directly related to FOWTs, in order to highlight their relevance and gaps specific to this domain.

In [53], the authors provided a basic overview of DTs in dynamic systems and discussed system identification, uncertainty quantification, and real-time data integration, elements critical to structural engineering applications, while [54] reviewed DT applications in the oil and gas sector, with an emphasis on safety and operational reliability in harsh environments similar to offshore wind.

Moreover, Pezeshki et al. [55] offered a focused review of SHM strategies in offshore structures and discussed DT integration for real-time monitoring, a key requirement for FOWT reliability.

Schneider et al. [56] presented a machine learning-based approach to monitor the environmental impacts of offshore wind farms. Their work underlines how DTs can incorporate spatial and temporal environmental variability into offshore asset management.

Among the most relevant and recent contributions, Chen et al. [37] conducted a dedicated review of DTs in FOWTs. They analyzed modeling strategies combining physics-based simulations with machine learning to enhance real-time state estimation and structural performance assessment. Majidi Nezhad et al. [57] reviewed DT applications in marine renewable energy systems with an emphasis on surrogate modeling and data synchronization, both of which are crucial for the real-time digital twinning of floating wind platforms.

Several broader review papers, while not focused exclusively on FOWTs, are also worth mentioning: Opoku et al. [58] reviewed DTs in the construction sector, with emphasis on lifecycle modeling and multi-domain data integration, which are challenges that similarly affect FOWT projects. Chen et al. [59] provided a maritime-focused DT overview centered on predictive maintenance and OMA, both highly relevant to SHM in offshore wind. Lv et al. [60] emphasized life-cycle management and sustainability in marine DT applications and highlighted the potential for performance-driven DTs in floating systems. Brönner et al. [61] discussed DTs in ocean governance and environmental modeling and framed DTs as tools for ecosystem integration and regulatory support, which is an increasingly important aspect of offshore wind development.

Despite recent progress, the field still lacks a comprehensive synthesis that links component-level digital twin models (e.g., tower, mooring, drivetrain) to integrated, system-wide strategies for FOWTs. This review addresses that gap by focusing on structural health monitoring (SHM), inverse estimation methods, and the role of Kalman-type filtering (alongside innovative alternative methods) in real-time diagnostics and control. The structure of the paper reflects this focus: First, the core components of digital twinning algorithms are introduced; then, the existing literature on DTs for key FOWT subsystems is reviewed; and finally, a proof-of-concept case study is presented to demonstrate practical application.

4. Core Components of the Digital Twinning Algorithms

In this study, the mainstream definition of a DT eloquently defined by International Business Machines Corporation (IBM) has been adopted. According to IBM, the main components of a DT [62] are as follows:

• A system in the real world and instruments on it that measure some quantities of interest;
• A digital replica or a computational model of the system;
• A method, such as a system identification algorithm, that can use sensor data and calibrate the digital replica. To develop and execute a successful DT for the FOWT, to facilitate O&M and life extension and similar demands, the probabilistic framework depicted in Figure 3 can be used.

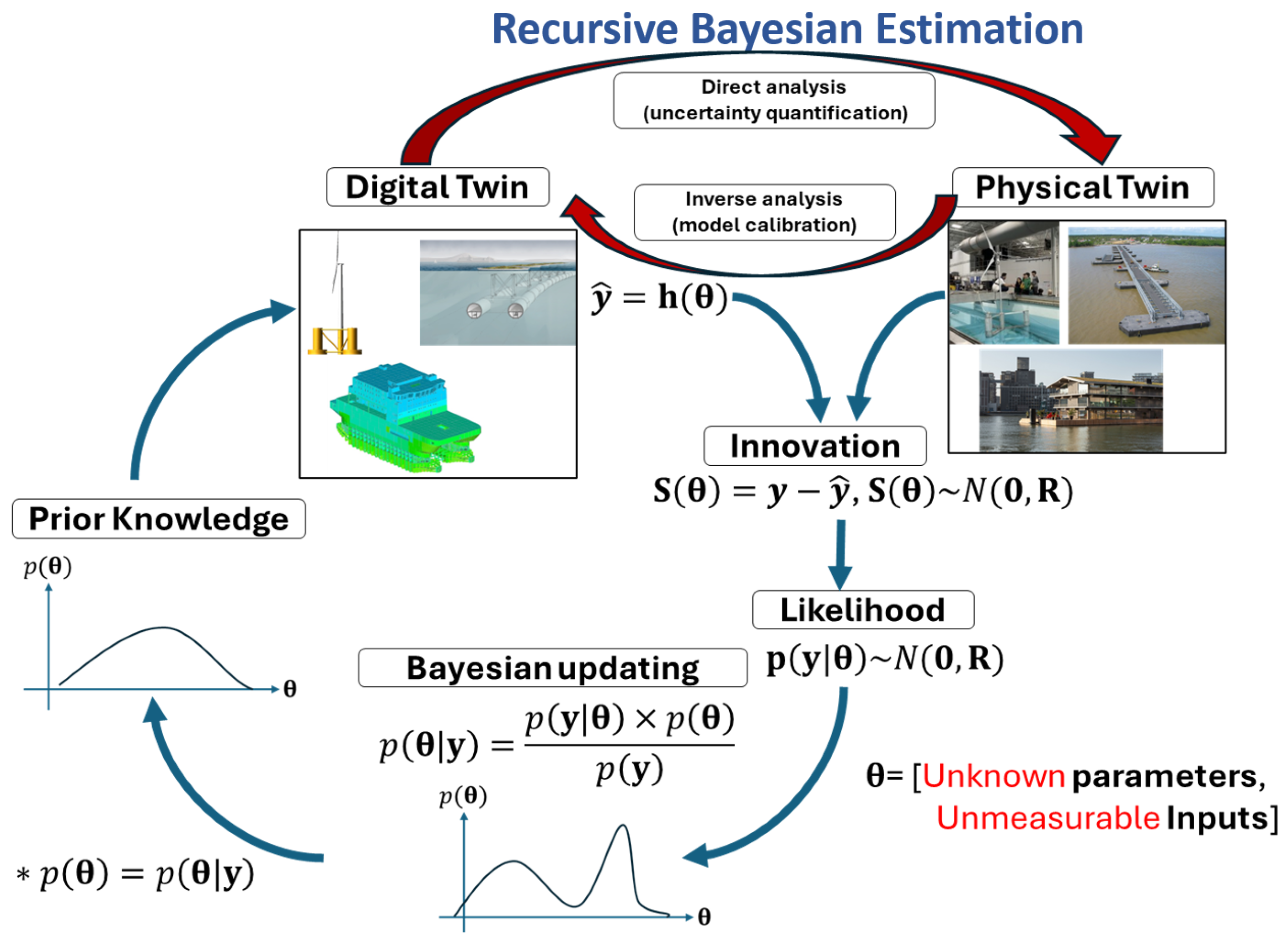
The probabilistic digital twinning framework (Figure 3) uses Bayesian inference to improve model accuracy and quantify uncertainty. It allows for a bidirectional connection between the DT and its physical twin (PT). PT is the real-world system that is being monitored. It can be an experimental scaled model [63], a larger scale field model [64], or a full-scale FOWT [65]. Discrepancies between measured and predicted responses are used to update the model via Bayesian updating. Bayesian updating refines prior knowledge and improves the estimation of unmeasured inputs, such as environmental loads.

This framework supports both uncertainty quantification and inverse analysis for model calibration. For advanced filtering, it is important to distinguish core components of a DT: the algorithm type (deterministic vs. stochastic), the processing method (batch vs. sequential), and the model formulation (linear vs. nonlinear). These distinctions guide how data are handled and how real-time updates are incorporated.

4.1. Sensors and Physical Models for FOWT DTs

Real-time monitoring in FOWT DTs relies on advanced sensor networks that continuously feed measured data into computational models for real-time system updates and decision-making. In general, key sensor categories include but are not limited to the following:

• Supervisory control and data acquisition (SCADA) systems, which monitor and control blade pitch angles, rotor speed, and power output to optimize energy generation [66].
• Motion sensors (e.g., GPS and inclinometers) that track platform displacements and rotations in six degrees of freedom (6-DoF).
• Strain gauges and accelerometers that measure structural loads, deformations, and vibrational responses critical for fatigue and damage assessments [67].
• Environmental sensors (e.g., LiDARs and SoDARs) that capture wind profiles, wave heights, and hydrodynamic conditions to inform boundary conditions and update DT models [48]. Beyond sensing, LiDAR data has been used to design advanced feedforward controllers for tower load alleviation and generator speed regulation [68,69].

Some of these listed sensors (e.g., SCADA and inclinometers) are standard, while others (e.g., LiDAR, SoDAR and strain gauges) are less frequently installed due to their higher cost and uncertain short-term return on investment. Martinez-Luengo and Shafiee [70] conducted a detailed cost–benefit analysis and showed that while SHM systems increase CAPEX, their ability to reduce OPEX through fewer inspections and better risk management often offsets the initial costs. Their findings support selective, risk-informed sensor deployment rather than universal instrumentation, which is a practice increasingly adopted in OWF strategies.

Additionally, it should be noted that while LiDAR and SoDAR systems are valuable tools for site assessment, power curve certification, and even certain control strategies, they offer only partial snapshots of the inflow wind field (typically limited to rotor-effective wind speed and shear). As such, they cannot provide full real-time spatial wind reconstruction. This limits their role in feedforward DTs or estimators. Moreover, standardized certification guidelines for their integration in DT-based monitoring or control frameworks are not yet established.

Diagnostic DT models integrate unsupervised learning techniques to process sensor data. This allows early detection of structural degradation and enhances operational reliability [71]. As digital twinning applications advance for FOWTs, multi-source sensor fusion will further improve prediction accuracy and model resilience [67].

While these sensors form the backbone of digital twinning in FOWT systems, sensor deployment and maintenance in offshore environments present substantial challenges and limitations [29]. The harsh marine environment exposes sensors and electronics to corrosion, biofouling, and mechanical fatigue, which shorten service life and increase maintenance needs [72,73]. Offshore systems also face constraints in power supply, bandwidth, and communication reliability, with frequent interruptions and delays in data transmission. Sensor drift, noise, and calibration difficulties further degrade data quality [74]. Moreover, real-time data processing is often limited by reliance on satellite communication or the need for robust edge computing systems [75].

To address these challenges, sensor networks must be robust and have redundant and fail-safe designs. The incorporation of edge-level pre-processing, onboard filtering, and hybrid edge-cloud computing architectures can reduce data volume and latency without any reduction in responsiveness [67]. Additionally, standardized data protocols and modular integration strategies can also improve system-wide compatibility and long-term maintainability.

4.2. Computational Modeling for FOWT DT

DTs for FOWTs rely heavily on computational models that can intake real-time data and predict system behavior. These models form the core of DTs for online estimation, control, and diagnostic capabilities. As FOWTs experience complex dynamic forces from wind, waves, currents, and operational conditions, adequate structural analysis is critical for structural reliability and integrity.

Computational models range from simplified linear representations for control applications to fully coupled nonlinear simulations that capture aero–hydro–elastic interactions. Numerical simulations, which include computational fluid dynamics (CFD) and finite element (FE) models, provide a preliminary way to assess structural performance under various conditions. However, it is critical to achieve a balance between model accuracy and computational efficiency. High-fidelity models are computationally expensive, while simplified models may lack precision.

There are several numerical simulation methods and tools available for FOWTs with different fidelity ranks. In general, FOWT numerical models employ multi-body dynamics (MBD) modeling approach. For MBD models, the FOWT structure is generally represented by a system of rigid or flexible bodies connected through various joints. Rigid body models (e.g., Bagherian et al. [76] facilitate real-time simulations but lack strain modeling, while flexible models capture strain fields for more detailed structural analysis but require more computational power. These models can be linearized or nonlinear.

Several commercial (e.g., OrcaFlex [77]) and open-source tools (e.g., OpenFAST [78]) facilitate coupled numerical simulations. Regulatory guidance, such as ABS guidelines [79], provides methodologies for modeling strategies and performance validation.

4.2.1. Linearized Models

Linearized computational models are commonly used in digital twin frameworks for FOWTs due to their balance between simplicity and performance. These models reduce the complexity of nonlinear aero–hydro–elastic interactions by approximating system dynamics around operating points. This enables efficient real-time analysis and controller design. Techniques such as frequency-domain linearization and state-space modeling allow stability assessments, reduced-order modeling, and controller tuning [80]. Tools like OpenFAST include linearization modules specifically for FOWTs, facilitating eigenanalysis and disturbance modeling [81]. While linearized models may oversimplify some interactions, they are often sufficient for early-stage DT development or control-oriented applications [82,83].

4.2.2. Nonlinear Models

Nonlinear models are essential for simulations of the full dynamic complexity of FOWTs, especially for DTs that aim for high-fidelity state estimation or damage detection. Unlike linear models, they account for time-varying loads, geometric nonlinearities, and environmental disturbances. Studies have shown that advanced filtering methods such as extended Kalman filters (EKF), unscented Kalman filters (UKF), and particle filters (PF) and hybrid approaches like the hybrid interacting particle Kalman filter (H-IPKF) can handle such nonlinearities in digital twin applications [84,85,86,87].

In addition to fully linear or nonlinear models, intermediate approaches have been explored for control-oriented DTs. Linear parameter-varying (LPV) models offer a structured way to assimilate nonlinearities while a linear model form is maintained. This allows gain-scheduled control design. Zhao and Nagamune [88] applied switching LPV control to a semi-submersible FOWT and demonstrated improved performance over baseline and H∞ controllers. Another notable direction is the use of low-order parametric models that preserve key nonlinear dynamics and remain computationally efficient. Lemmer et al. [89] developed a multibody-based reduced-order model (ROM) tailored for concept-level FOWT design. This approach allows fast simulations and is especially useful for early-stage optimization.

These approaches allow DTs to assimilate real-time data and adapt to variable operational conditions. Thus, they are particularly valuable for SHM and inverse load estimation.

4.3. Data-Driven Modeling in FOWT Digital Twins

Data-driven modeling is a fundamental aspect of FOWT DTs since it enables the integration of real-world sensor data into predictive models. Unlike purely physics-based approaches, data-driven methods refine the model’s behavior based on observed responses. Thus, they improve adaptability under variable conditions. These algorithms can be broadly categorized by how they handle uncertainty (deterministic vs. stochastic) and how they update models over time (batch vs. sequential).

4.3.1. Deterministic Algorithms

Deterministic algorithms assume fully known system dynamics and minimal or no uncertainty. They are often used when environmental conditions are well-characterized or when future behavior can be accurately predicted based on current states. A notable example is the use of phase-resolved wave models to forecast future wave elevations at the float in irregular sea states [90]. Such models offer computational efficiency but may lack robustness in the presence of real-world uncertainties.

4.3.2. Stochastic Algorithms

Stochastic algorithms explicitly model uncertainty, incorporating probabilistic representations of measurement noise, environmental variability, and unmodeled dynamics. KF and its variants are core tools in stochastic DTs, as they allow the system to update information about structural states based on uncertain data. These methods have been applied to SHM in FOWTs [82,91], wave response modeling [52,92], and mooring force prediction [85], among others. Stochastic techniques are well suited for offshore environments since they enhance the resilience of DTs to data imperfections [56].

4.3.3. Batch Processing

Batch processing involves data accumulation over a period and retrospective model updating. Though not generally suitable for real-time applications, this approach can be used for periodic recalibration of DTs. For example, Katsidoniotaki et al. [93] built a DT for a wave energy converter using 25 CFD simulations based on a design of experiments (DoE) strategy. This is an example of pre-processing in batch mode before live deployment.

4.3.4. Sequential Algorithms

Sequential (or online) processing continuously updates the model as new data arrive. This is critical for real-time DT applications such as SHM and anomaly detection in FOWTs. KF and KF variants inherently operate sequentially since they update state estimates at each time step [94,95]. Sequential processing is useful for real-time control and decision-making since it allows a DT to respond immediately to changes in environmental conditions or structural behavior.

4.4. System Identification and State Estimation for FOWT DTs

System identification and state estimation are critical for digital twinning. Identification refers to building models from data, while estimation uses models to infer unmeasured states or inputs. Both support real-time monitoring, fault detection, and control adaptation in FOWT DTs.

Identification techniques can be categorized as parametric or non-parametric. Parametric models assume a known structure and estimate specific parameters (useful for targeting properties like damping or stiffness). Non-parametric models capture system behavior directly from data, which is useful when unknown or complex dynamics and uncertainty are present.

Estimation methods such as KFs, Luenberger observers, and robust estimators rely on these models to infer quantities like mooring loads or platform motions. The following subsections outline key approaches for model estimation and state reconstruction.

4.4.1. Stochastic Linear and Nonlinear Sequential System Identification

System identification methods may be linear [96] or nonlinear [97]. The choice depends on the system’s complexity and the desired level of model fidelity. Linear approaches are often sufficient for control design and near-equilibrium analysis, where input–output relationships can be reasonably approximated. However, for FOWTs that operate in dynamic offshore environments with strong nonlinearities, more advanced nonlinear techniques are typically required.

DTs rely on sequential system identification [98] that enables continuous refinement of model parameters as new sensor data become available. This is typically achieved through stochastic filtering methods such as the KF for linear systems, and its nonlinear extensions (EKF, UKF, PF, and H-IPKF) for nonlinear systems. These filters allow the DT to track structural states as they evolve in real-time and account for uncertainties in both measurements and model predictions.

4.4.2. Kalman Filters for Linear or Weakly Nonlinear and Gaussian Uncertainties

As mentioned earlier, Kalman filtering techniques are widely used in digital twinning to estimate structural states in real-time under uncertain or partially observed conditions. For systems that are linear or weakly nonlinear with Gaussian noise, the EKF is commonly applied. It approximates nonlinear dynamics by linearizing the state-space model at each time step. While EKF is computationally efficient and effective for mild nonlinearities, it suffers from reduced accuracy and potential instability in highly nonlinear regimes due to its reliance on Jacobian calculations.

To address these limitations, the unscented Kalman filter (UKF) was developed using a sigma-point approach, which approximates state distributions directly rather than through model linearization [94]. This derivative-free method improves estimation accuracy and numerical robustness, particularly in the presence of measurement.

A notable work [95] compares EKF and UKF. The author’s main goal was to formulate a multi-rate KF framework that can work with sensors with different sampling rates. They demonstrate that UKF offers superior accuracy in state estimation and robustness to noise in nonlinear systems, which makes it ideal for real-time applications.

These KF variants may provide a computational backbone for real-time state estimation in FOWT DTs for adaptive monitoring, fault detection, and control under uncertain and dynamic offshore conditions.

4.4.3. Particle Filters for Nonlinear Non-Gaussian Uncertainties

In DTs for FOWTs, PFs can be useful for system state estimation in scenarios where system dynamics are highly nonlinear and uncertainties are non-Gaussian. Unlike Kalman filters, which assume near-Gaussian state distributions, PFs use a Monte Carlo sampling approach to approximate the posterior distribution directly [99]. This makes them suitable for complex offshore environments where structural responses may exhibit multimodal or heavy-tailed distributions.

However, PFs can be computationally expensive, particularly for high-dimensional systems [100]. To address this, various enhancements have been developed to improve convergence and reduce the computational burden, including improved resampling schemes and smoothing algorithms [101,102,103,104,105,106]. An extensive review of classical filtering and smoothing methods for nonlinear systems with known inputs can be found in [107].

Importantly, many real-world applications, such as FOWTs, face uncertainty not only in system states but also in external inputs (e.g., unmeasured wave forces or wind disturbances). Recent filtering frameworks account for unknown inputs by jointly estimating states and inputs in a unified stochastic framework [108,109,110]. These input-augmented PF methods are particularly relevant for DTs that operate with partial sensing or noisy offshore data.

PF applications for FOWT DTs can be a promising solution for robust, real-time monitoring and model correction in FOWTs under uncertain and nonlinear environmental conditions where conventional estimators fall short.

4.4.4. Minimum-Variance Unbiased Filters: No Assumptions on Unknown Loads and Their Statistics

In early research, Kitanidis [111] introduced a recursive filtering approach designed to yield unbiased, minimum-variance estimates of inputs and states in linear systems. While effective, this method did not achieve global optimality with respect to mean square error and was specifically tailored for systems without direct feedthrough with no priori assumptions about the input. To address systems with direct feedthrough, Hou and Patton [112] developed an optimal filter framework for output-only state estimation. However, their filter did not use all the available measurement data, which reduced its ability to make the best use of the observations [112]. Hsieh [113] later refined the original Kitanidis filter to enhance its practical applicability. An extension for output-only estimation in systems with direct feedthrough was also proposed by Darouach et al. [114]. Gillijns–De Moor [115] contributed an unbiased minimum-variance estimator for joint input and state estimation that was globally optimal for systems without direct feedthrough; they later proposed their formulation to accommodate direct feedthrough cases [116]. Building upon this, Hsieh [117] introduced a filter capable of handling input and state estimation under more relaxed rank conditions, showing that in the case of full-rank direct feedthrough matrices, the filters proposed by [112,114,116] are fundamentally equivalent to [117]. In structural dynamics applications, Lourens et al. [118] applied the Gillijns–De Moor filter designed for systems with direct feedthrough [116]. They focused on cases involving dense sensor networks combined with reduced-order structural models. Their study addressed numerical problems that appeared when the number of sensors exceeded the order of the model. Lourens [119] proposed an augmented Kalman filter (AKF) to estimate unknown forces in structural systems. It was shown that using acceleration-only data could lead to numerical instability. This issue was attributed to unobservability problems in the formulation of the augmented system. Maes et al. [120] contributed analytical conditions necessary for the invertibility of linear systems, which are relevant for various input–state estimation strategies. A generalized framework accommodating both the presence and absence of direct feedthrough was presented by Yong et al. [121], integrating and extending previous filtering techniques [115,116]. Maes et al. [122] demonstrated that applying minimum-variance unbiased (MVU) filtering via instantaneous system inversion, as proposed in [116], can become ill-posed in certain system identification settings. Song [123] used unscented transform and created a nonlinear extension of the MVU filter presented by [116] for the estimation of unknown inputs, states, and system parameters in dynamic systems through the generalized minimum-variance unbiased (GMVU) joint input–state estimation technique and the unscented minimum-variance unbiased (UMVU) estimation scheme, and the authors present significant improvements in computational efficiency.

4.4.5. Stochastic Smoothing for Mitigating Ill-Posedness

This ill-posedness problem mentioned in the previous subsection significantly affects the input reconstruction quality and notably amplifies the measurement (observation) noise. The source of this issue is linked to the delayed reaction of the response of the system to the inputs when the acceleration measurement is not collocated with the points at which dynamic loads are exerted on. Accordingly, Maes et al. [120] describes the development of a smoothing method which yields delayed estimations but with high fidelity and considerably lower level of estimation noise; the developed smoothing algorithm applies to any system with direct feedthrough in its state-space equations and the algorithm was validated by an application in structural system identification. Fang et al. [124] proposed smoothing algorithms for the state and input estimation of nonlinear systems based on the linearization of system equations. Maes et al. [122] extended the smoothing algorithm in [120] to the nonlinear system and used it for joint input–state–parameter estimation in structural dynamics. They concluded that the adaptation of the smoothing algorithm can significantly reduce the estimation error, especially in cases where data originate from sensors that are not collocated with the estimated inputs.

5. Digital Twinning of Structural, Mechanical, and Energy Production Components of FOWTs

This section aims to provide a comprehensive review of the Kalman filtering and SHM applications for the FOWT structural and mechanical elements such as tower, mooring system, blades, nacelle, gears, and transmission systems as well as the work on fault detection and damage identification and energy production. For improved readability and a structured overview, this literature review is organized by major FOWT sub-components and their relevant digital twinning applications. As FOWT is in its early development stage, the research toward its DT is also in early development; therefore, when appropriate, component DTs for OWTs that potentially can be readily adopted for FOWTs (e.g., gearboxes) are also referred to.

5.1. Tower

This section explores advanced methodologies for the estimation of tower loads and fatigue in wind turbines, with a focus on digital twinning technologies and related techniques. The research presented spans various approaches, which include the KF, reduced-order modeling, and data-driven virtual sensing.

Branlard et al. [82] introduced a DT concept for the real-time load and fatigue estimation of land-based turbines using OpenFAST [78] linearizations combined with a KF. This study validated the approach with SCADA data from a GE 1.5-MW turbine. Approximately 10% accuracy has been achieved in the estimation of damage equivalent loads. This is an initial attempt at a proof of concept. The authors highlight the potential of DTs for monitoring and the optimization of wind turbine operations.

In a follow-up study, Branlard et al. [84] extended this concept, and the authors incorporated a reduced mechanical model based on the Rayleigh–Ritz method, and they adopted the AKF. This model not only increased computational efficiency but also enhanced the accuracy of load estimations since it includes additional states (e.g., forces) in the state vector. The study emphasized the practicality of this approach for real-time fatigue life estimation under more realistic conditions.

This study has been followed by Branlard et al. [48], where the authors developed a DT for a full-scale prototype (TetraSpar) with an AKF for state estimation. The filter was augmented to include aerodynamic torque, which improves the accuracy of structural load estimations. The study demonstrated that the DT could estimate damage equivalent loads with errors that range between 5% to 15%, which presents a good potential for structural health monitoring in offshore environments.

Tarpø et al. [125] introduced a data-driven virtual sensing technique using principal component analysis (PCA) to estimate dynamic strain in offshore wind turbines. This method was validated with real-life data from an offshore wind turbine near Sprogø, Denmark. The researchers developed a system that could estimate strain over two months with high precision from a small training dataset. The study presents the technique’s potential to replace physical strain gauges with virtual sensors, and it provides robust monitoring for fatigue damage in wind turbines.

Zhao et al. [126] presented a DT for an offshore wind turbine on a monopile using a reduced-prder modeling (ROM) approach. The study employed the static condensation reduced basis element (scRBE) method, which allowed for a significant reduction in computational effort with high accuracy. Although the DT performed well under static conditions, limitations of the method in dynamic scenarios were highlighted. However, this approach still provides fast and accurate load and stress analysis in monopile-supported turbines under certain conditions.

Song et al. [127] focused on the joint estimation of dynamic input loads and unknown model parameters. The authors utilized a recursive Bayesian inference framework and a window-based EKF in the DT of a turbine at the Block Island Wind Farm. This approach allowed for accurate predictions of acceleration and strain data. The study highlighted the importance of accurate input load estimation for tower fatigue assessment for the structural integrity of offshore wind turbines.

5.2. Mooring and Motion Control

This section explores the advancements in DT technologies for the prediction and monitoring of mooring loads in FOWTs.

Walker et al. [128] developed a DT for mooring line tension estimation with a data-driven model based on kernel regularized least squares (KRLS). The authors utilized real operational data from the Hywind Pilot Park. This approach demonstrated accurate predictions of mooring line tensions.

Although it is not FOWT-focused, it is worth mentioning Katsidoniotaki et al. [93], where the authors created a DT for the prediction of extreme loads on the mooring system of a point-absorber wave energy converter (WEC) in extreme wave conditions. The DT demonstrated a 90.36% accuracy with a significantly small computation time compared to traditional CFD simulations. Such a DT may be applied to a FOWT structure in the future.

In a different approach, Yung et al. [85] employed a physics-based model with an AKF to estimate mooring forces in FOWTs. Moreover, the authors developed a multiple-model adaptive estimation (MMAE) algorithm to adapt the system to different sea states in real-time.

Alkarem et al. [129] presented a DT model developed to mitigate the motion of FOWTs caused by wave actions. The authors proposed an active control system (ACS) based on a mass-spring damper system, re-tuned in real-time to respond to current and forecasted sea conditions. They employed OpenFAST [78] for simulations and a scale model in laboratory tests. The study compares two wave prediction controllers, the current sea-state controller (CSSC) and future sea-state controller (FSSC). The FSSC showed improved performance in mitigating the wave-induced motion. The research demonstrates a proof of concept for the employment of DTs to enhance FOWT stability.

This study was extended by Ammerman et al. [86] with the co-authorship of Alkarem, where the authors demonstrated an experimental validation of a Kalman filter designed to estimate the state of a floating offshore wind turbine (FOWT) platform. OpenFAST [78] was employed for the numerical model and linearized model extraction. The validation was performed on a 1:70 scale model of the UMaine VolturnUS-S platform. The authors focused on hydrodynamic excitations and structural responses and they utilized the KF with five selected measurements. With the assumption that the input loads are known, they achieved accurate estimations of system states, (e.g., surge, heave, and tower base bending moment) even without the direct measurements. The results demonstrated robustness across a range of sea conditions, which improves the state estimation in comparison to a baseline state-space model.

Moreover, Alkarem et al. [130] presented a predictive digital twin for FOWTs that incorporates a wave prediction–reconstruction (WRP) model to enhance real-time system state predictions. The proposed framework incorporates a multivariate long short-term memory (MLSTM) recurrent neural network (RNN) model to predict the future states of the FOWT based on both past system data and wave forecast information. This way, the authors can demonstrate future forecasting rather than assuming the loads are known. Again, the authors used a 1:70 scale model of the UMaine VolturnUS-S platform. The integration of WRP capabilities improved the prediction accuracy by 50% compared to baseline models, especially under extreme wave conditions.

Cao et al. [52] explored the use of deep neural operators, such as DeepONet and Fourier neural operator (FNO), to predict the real-time responses of mooring systems under irregular waves. The authors presented the potential of advanced machine learning techniques for the improvement of predictive accuracy and efficiency of DTs for offshore structures.

Yin et al. [131] developed a bi-directional long short-term memory (Bi-LSTM) model to predict the wave-induced motions of a semi-submersible FOWT platform. The authors generated wave and motion data from ANSYS AQWA, and the model is trained to forecast surge, heave, and pitch motions up to 10 s in advance. Various hyperparameters (neurons, layers, and optimizers) are optimized. It was found that a one-layer Bi-LSTM with the Adam optimizer provides the highest accuracy ($R^2$ above 90% in most cases) under unseen wave conditions and noisy environments.

5.3. Blades, Nacelle, Gears, and Transmission Systems

This section explores the application of digital twinning technologies in the monitoring and optimization of key wind turbine components, including blades, drivetrains, planetary gears, bearings, and transmission systems.

Vettori et al. [132] focused on input–state estimation for wind turbine blades with an adaptive-noise AKF. This method, validated with experimental data, demonstrated enhanced accuracy in blade dynamics prediction under uncertain loading conditions, which is essential for real-time monitoring.

The high-fidelity modeling of gear faults is also critical in DT implementations for drivetrain systems. For instance, Li et al. [133] proposed a precise numerical method to estimate the time-varying mesh stiffness in spiral bevel gears with spalling defects, offering insights into how contact mechanics and load redistribution affect dynamic behavior.

Also regarding drivetrain monitoring, Mehlan et al. [134] developed a virtual sensor within a digital twinning framework to monitor fatigue damage in wind turbine gearboxes. With the integration of high-fidelity models with data from condition monitoring systems, the study achieved reliable load estimations that are crucial for the predictive maintenance and life-cycle extension of drivetrain components.

Li et al. [135] advanced fault diagnosis techniques with their approach in virtual and real data combination in a DT, particularly for complex subsystems such as bearings and gearboxes. This method showed high accuracy in composite fault diagnosis and provided significant improvements in fault management within wind turbines.

In contrast, Pujana et al. [136] introduced a hybrid-model-based DT for drivetrains, which integrates physics-based models with stochastic elements to generate synthetic failure data, which enhanced the accuracy of failure detection.

Moreover, Yucesan et al. [137] and Wang et al. [138] contributed to the field with studies that focus on the main bearing fatigue and large-scale offshore wind power systems, respectively. The work of Yucesan et al. [137] combined reduced-order models with neural networks to monitor grease degradation in bearings. On the other hand, Wang et al. [138] utilized real-time simulation and 3D visualization technologies in a DT system for flexible direct transmission systems. This enables the effective remote management and predictive maintenance of offshore wind farms.

Another notable study is from Lu et al. [139], where the authors propose a hybrid digital twin framework that integrates simulation and deep learning to predict thermal errors in CNC machine tool spindles. Their method, DT-LSTM, combines a physics-based DT model with an LSTM network and particle swarm optimization to enhance accuracy and robustness. Although focused on manufacturing systems, this hybrid approach is highly relevant to component-level digital twins in FOWTs, especially for temperature-sensitive subsystems such as drivetrains or generators, where internal thermal effects impact performance and health monitoring.

5.4. Fault Detection and Damage Identification

This section is dedicated to the discussion of several key studies that have developed and validated digital twinning frameworks for fault detection and damage identification. These include advanced technologies such as deep learning, FEA, and optimal sensor placement to enhance the safety, reliability, and operational efficiency of offshore wind structures.

In SHM, damage identification and fault detection are related but distinct terms, though they are often used interchangeably in some contexts. In general, fault detection is a broader term that indicates an abnormal condition without classification of the nature of the problem (e.g., aerodynamic degradation due to ice accretion, erosion, or blade contamination), while damage identification is more specific and involves diagnosis and assessment of the damage. Fault detection refers to the process of identification of an abnormal event that has occurred within a system. It indicates that there may be a fault or failure present. It is generally the first step in a fault management process and involves recognition of the existence of a deviation from normal operation or design parameters. For DTs, fault detection would typically involve monitoring the system performance data and capturing the behavior when it deviates from expected norms, which indicates a potential fault.

On the other hand, damage identification goes a step further by not only the identification of something wrong (as in fault detection) but also the characterization and, possibly, quantification of the nature of the damage. This may include the location, type, and severity of the damage within a structure. Damage identification often involves data acquisition from sensors (such as strain gauges or accelerometers) in combination with a DT to detect, localize, and assess the extent of physical damage to the structure.

One notable study by Dang et al. [140] introduced a cloud-based DT framework for real-time SHM via deep learning. This framework, validated on both scaled and full-scale bridge models, demonstrated a high accuracy in damage detection. This is important for proactive maintenance and, hence, the extension of the service life of structures.

In 2023, Mousavi et al. [141] focused on a DT-based framework for damage detection in FOWTs under various loading conditions. This framework successfully integrated a numerical model with deep learning techniques to accurately detect damage even in complex environmental scenarios. Zhang et al. [142] presented a framework that combines reduced-order and full-order models to efficiently analyze the dynamic responses of offshore structures. Wang et al. [143] developed a DT for offshore jacket platforms that incorporates an optimal sensor placement (OSP) strategy and Bayesian-based damage identification, which proved effective even under noisy conditions.

Additionally, studies have explored digital twinning applications in fault diagnosis, such as Wang et al. [144], where a fault diagnosis method for wind turbine planetary gears was developed using a combination of empirical mode decomposition and machine learning models, and, Hu et al. [91], where a transferable diagnosis method for incipient fault detection in wind turbines was introduced, which presented high accuracy and robustness across different turbine models.

5.5. Energy Production

The integration of digital twinning technology into FOWTs has brought significant advancements in energy production optimization and the increased accuracy of real-time wind speed predictions.

In addition to wind speed prediction, Kim et al. [66] have developed a physics-based output prediction model (P-bOPM) for a 10 MW FOWT that has been developed to improve energy output forecasting. This model integrates real-time data and simulations to account for the dynamic interactions among wind, waves, and turbine responses. The study highlighted the high accuracy of the model and its ability to provide real-time updates. This significantly improves the operational flexibility and reliability of offshore wind power systems.

Another notable development presented by Li et al. [135] is the predictable multi-turbines spatiotemporal correlations framework (PMTSTCF), which utilizes the correlations among multiple wind turbines within a farm to enhance wind speed forecasts. Combined with digital twinning and internet of things (IoT) technologies, this framework demonstrated improved prediction accuracy over traditional models. Data from a wind farm in China have been used to validate it. This advancement allows for more precise forecasting, which is important for energy output maximization in wind farms.

These studies present that the combination of digital twinning technology with advanced modeling frameworks and real-time data integration may be instrumental in the performance optimization and energy production of FOWTs.

5.6. Operational Modal Analysis and Alternative DT and SHM Techniques for OWTs and FOWTs

While this paper emphasizes Kalman-type methods due to their current prevalence in FOWT digital twin research, other SHM techniques, particularly operational modal analysis (OMA), are also gaining traction and offer complementary strengths. This section highlights recent OMA-based studies relevant to FOWT applications.

OMA techniques have traditionally been used in structural diagnostics of civil and offshore infrastructure, and their adoption in FOWTs is increasing. Kim et al. [51] demonstrated a coupled simulation and OMA-based methodology for detecting damage in FOWT towers and blades using numerical-sensor signals. Their results showed that curvature mode shapes (CMS) were more sensitive than displacement mode shapes for identifying local damage, even under complex floating dynamics. This supports the relevance of OMA, particularly frequency domain decomposition (FDD), as a complementary or alternative approach to filtering-based methods for modal characterization and fault detection in FOWT systems.

One critical challenge for OMA in wind turbines is the presence of harmonic excitations (e.g., 1P, 3P, 6P) due to rotor rotation. These harmonics can mask structural modes or complicate their identification using output-only methods. To address this, linear time-periodic (LTP) models have been proposed as a suitable framework. Allen et al. [145] applied output-only modal analysis tailored to LTP systems and demonstrated its effectiveness on simulated wind turbine data. Ehlers et al. [146] also investigated sensor placement and state estimation strategies for wind turbines and concluded that sensors in the rotating frame do not necessarily improve observability, an insight valuable for DT sensor network design.

SHM techniques are also being extended to components beyond the tower. Anastasiadis et al. [147] developed and validated multiple vibration-based approaches for detecting stiffness reductions in synthetic mooring lines of the OO-Star Wind Floater. Their method addressed variations due to changing environmental and operational conditions. The authors showed that transmittance function-based models combined with carefully selected damage-sensitive features can detect degradation levels as low as 10% while minimizing false positives.

Modal characterization is also important for platform and tower dynamics. Serrano-Antoñanazas et al. [148] proposed a simulation-based power spectral density (PSD) approach to isolate vibration frequencies associated with specific degrees of freedom (DOFs). Their study identified the first tower bending mode aligning with the 3P rotor frequency (0.605 Hz) and highlighted the importance of active damping strategies.

Zhang et al. [75] presented an SHM system for OWTs using a Raspberry Pi-based platform running a hybrid KF-RDT-SSI algorithm. Their approach combined filtering and stochastic subspace identification (SSI) to extract modal parameters accurately under noisy conditions, which can be a promising path for decentralized DT implementation.

Most notably, OMA has now been validated in full-scale floating wind environments. Pimenta et al. [149] applied the SSI-COV method to experimental data from the WindFloat Atlantic project and successfully extracted tower modal properties under operational conditions. Their results show how floating platform motions and blade pitch affect tower dynamics. They affirm the viability of output-only OMA for dynamic characterization in floating systems.

A related study by the same authors [150] used SSI-COV to identify modal frequencies and damping ratios in the OC4-DeepCwind semi-submersible and UMaine-Hywind spar platforms. Their work confirmed that OMA methods can reliably track changes in FOWT dynamic behavior across variable environmental conditions, which supports their integration into continuous SHM and DT systems.

Together, these studies demonstrate that OMA-based and data-driven SHM methods also provide valuable tools for the digital twinning of FOWTs. While Kalman-type filters dominate current practice, output-only modal identification techniques such as SSI-COV, FDD, and vector autoregressive (VAR)-based models are increasingly validated and represent alternative pathways for high-fidelity structural diagnostics.

6. A Proof-of-Concept Study for FOWT

The literature reveals that a limited number of studies have focused on the stochastic estimation of either state or joint input–state for offshore structures. This study conducts an inverse estimation analysis for joint input–state estimation with different filtering techniques. As mentioned, KF, one of the earliest developed algorithms used to estimate the state of certain unobserved locations of a structure, utilizes models in state space, which accounts for process and measurement uncertainty [151]. The Kalman gain is derived via the minimization of the covariance of the state estimation error, which provides the optimal estimator for linear systems. However, Kalman-type filters, whether linear or nonlinear, have limitations as they require the input to be completely known [87,152,153]. Inputs such as mooring forces on mooring lines, drag forces on turbine platforms, wind loads on structures, and vehicular traffic loads on bridges are often unknown. These inputs cannot be measured directly or are cost prohibitive.

To address the input estimation problem, Lourens et al. developed a novel output-only input–state estimation algorithm for linear systems, known as the augmented Kalman filter (AKF) [119]. On the other hand, Eftekhar Azam et al. [154,155] introduced a technique called the dual Kalman filter (DKF), which addresses the issue of observability in the AKF when using pure acceleration measurements. Both AKF and DKF use a random walk model for the unknown inputs; hence, a tuning process for additional hyperparameters is necessary. However, these filters do not guarantee the optimality of input estimates [119,154,155]. Given that input statistics are often completely unknown, Gillijns and de Moor developed a minimum-variance unbiased (MVU) filter for the joint input and state estimation of linear systems without direct feed-through. This is referred to here as GDF-WNDF, which operates without acceleration measurements [115]. In the same year, Gillijns and De Moor introduced an algorithm capable of direct feedthrough (GDF-WDF), which can also work with pure acceleration measurements [116]. These filters provide optimal estimation, but GDF-WDF requires a full-rank feedthrough matrix, which means that the number of acceleration measurements must be at least equal to the number of unknown inputs.

To address the limitations of these MVU-based filters, Ebrahimzadeh Hassanabadi et al. introduced the Universal filter (UF), which is also based on MVU principles [156]. The UF can handle all scenarios, including systems without direct feedthrough, those with direct feedthrough, and those with rank-deficient feedthrough matrices.

6.1. Scope

Forward analyses of the FOWT response to wind and wave in the time domain leads to an aero–servo–hydro–elastic simulation [157]. However, when dealing with inverse analyses performed for the digital twinning of the FOWT structure, the aerodynamic, hydrodynamic, and servo forces can be assumed as unknown loads. This substantially simplifies the computational model used for a DT of FOWT, without any sacrifice in the accuracy of the state estimation. As mentioned above, in a first step toward the development of DTs for a fixed bottom wind turbine, recently, NREL researchers used an AKF and a linearized 2 DOF model of a jacket wind turbine extracted from OpenFAST [78] for wind load estimation [84].

Also previously mentioned in the literature review above, Yung et al. performed numerical simulations on the OC4 DeepCWind [158] floating platform. Moreover, the authors developed a multiple-model adaptive estimation (MMAE) algorithm to adapt the system to different sea states in real-time. Yung et al. [85] utilized the augmented Kalman filter (AKF), which provided good results for weak nonlinear scenarios. Although the results were promising, the authors highlighted the need for a new model based on advanced Kalman filter models to involve more complex load cases, which can help the estimation of restoring forces and predict wave elevations.

Here, a proof of concept is provided by evaluation of the performances of the AKF and the UF. The methodology provided by Yung et al. [85] has been used as a foundational case study to be used for the proof of concept, with the addition of UF application for the estimation of the hydrodynamic motions and mooring forces of a FOWT platform.

6.2. Methodology

As mentioned earlier, the KF, AKF, and UF have been employed in this study to estimate the hydrodynamic motions and mooring forces of a FOWT platform, more specifically, the UMaine VolturnUS-S reference platform (sketch is provided at Figure 4) Developed for the IEA Wind 15-Megawatt Offshore Reference Wind Turbine [20].

The OpenFAST [78] simulation tool has been used to develop numerical models to capture the coupled dynamics of the FOWT that arise from hydrodynamic loads. A sea state condition provided by Yung et al. (2023) [85] has been used. For simplicity, the MMAE algorithm has been ignored.

Then, inverse analysis for the state-space model identification has been made with the utilization of the MATLAB (version R2023b) System Identification Toolbox for the state space (A, B, C, and D) matrices’ extraction from the model to develop a state-space model.

Finally, previously mentioned filtering techniques (KF, AKF, and UF) have been implemented to estimate the states and inputs of the FOWT system, which targets the 6-DoF motion of the platform and the mooring line loads at the fairlead.

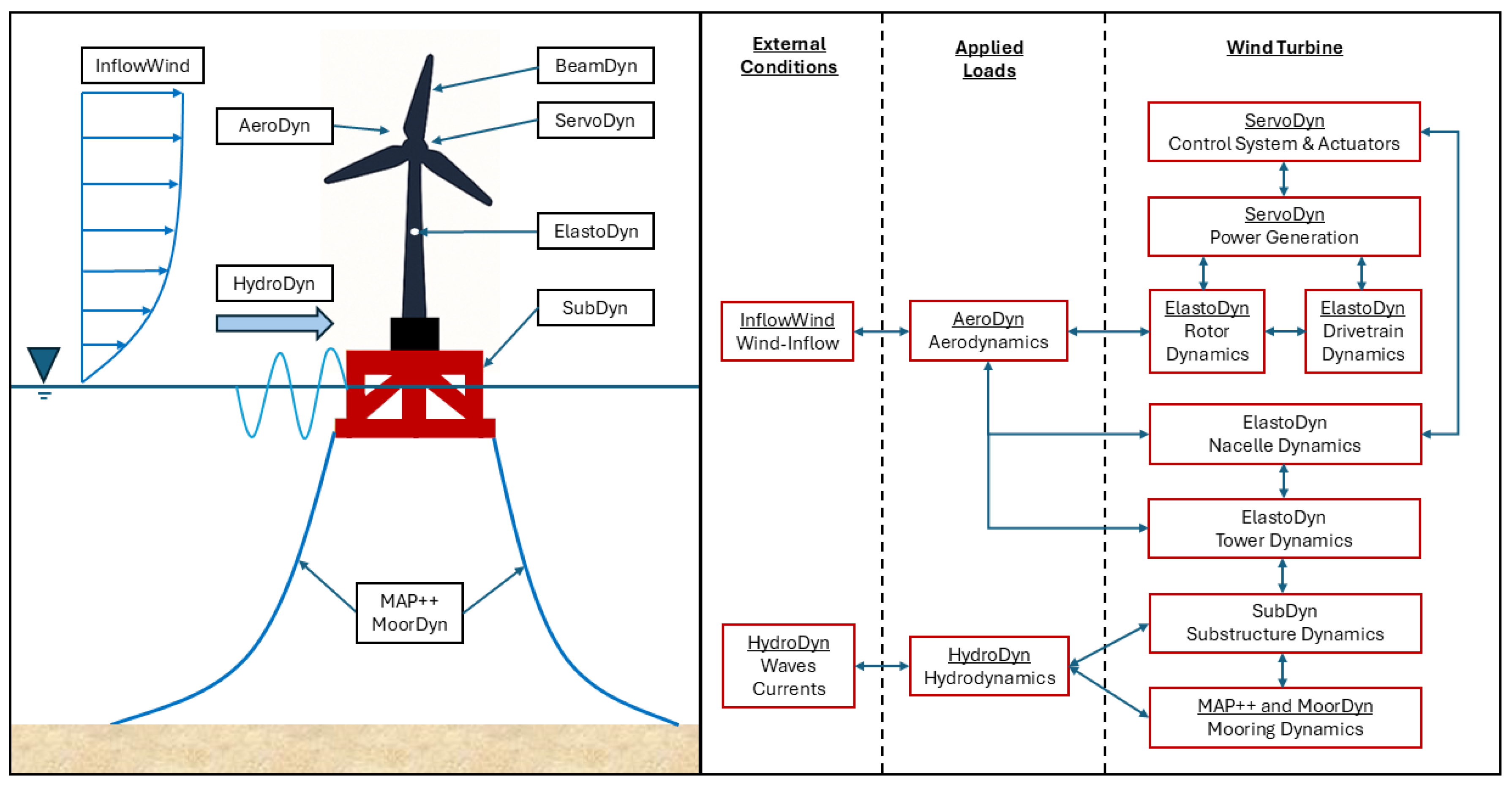
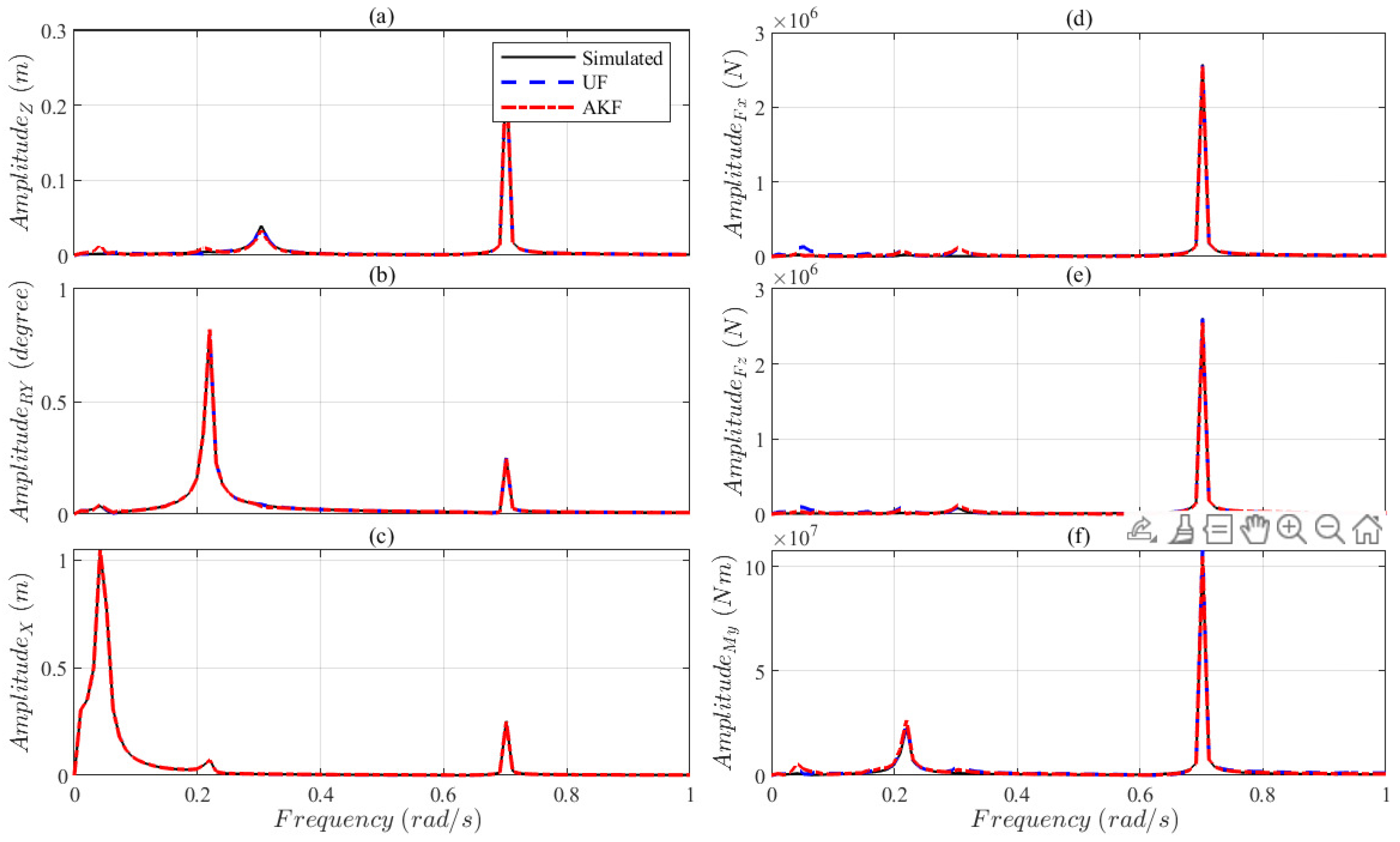
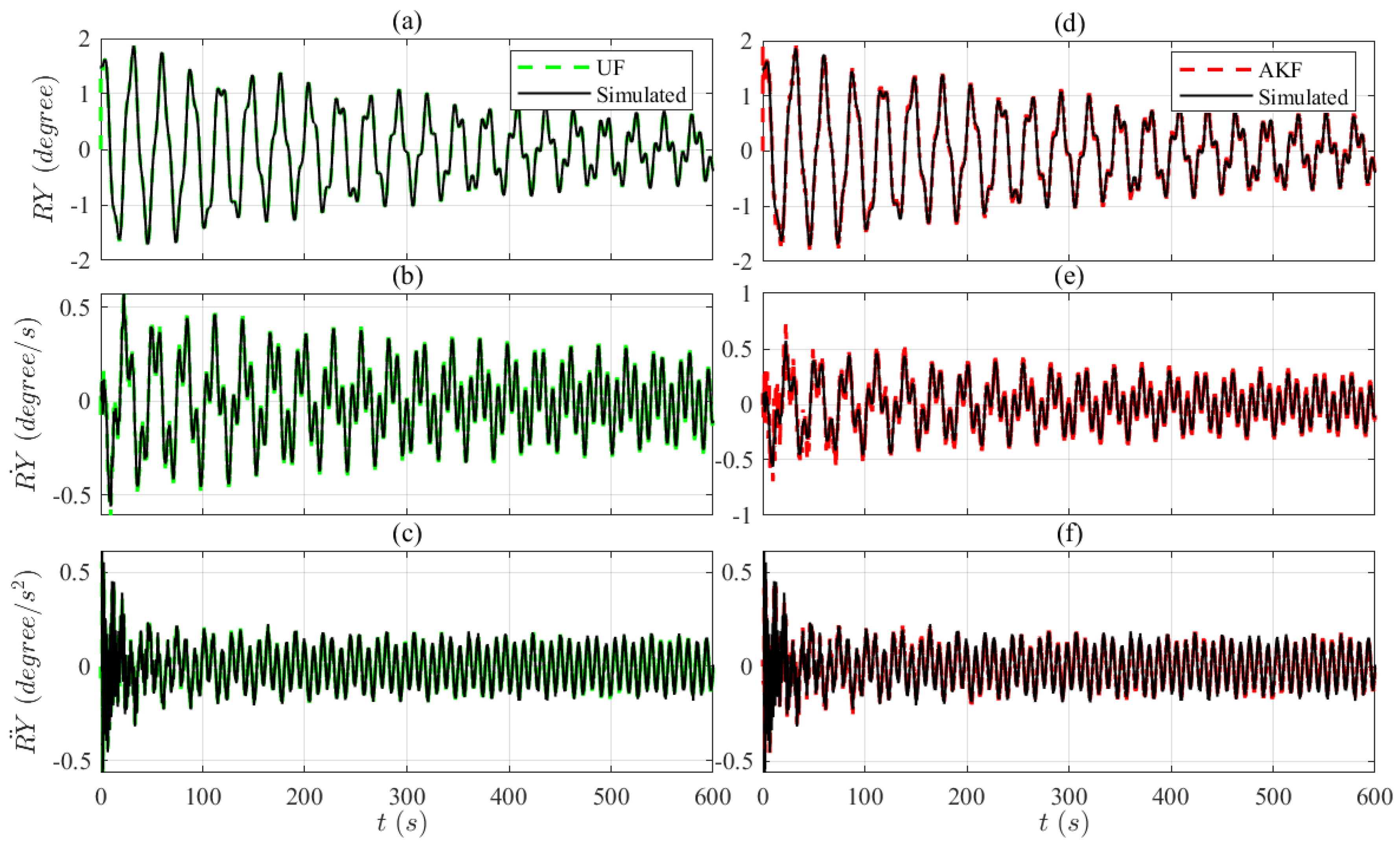
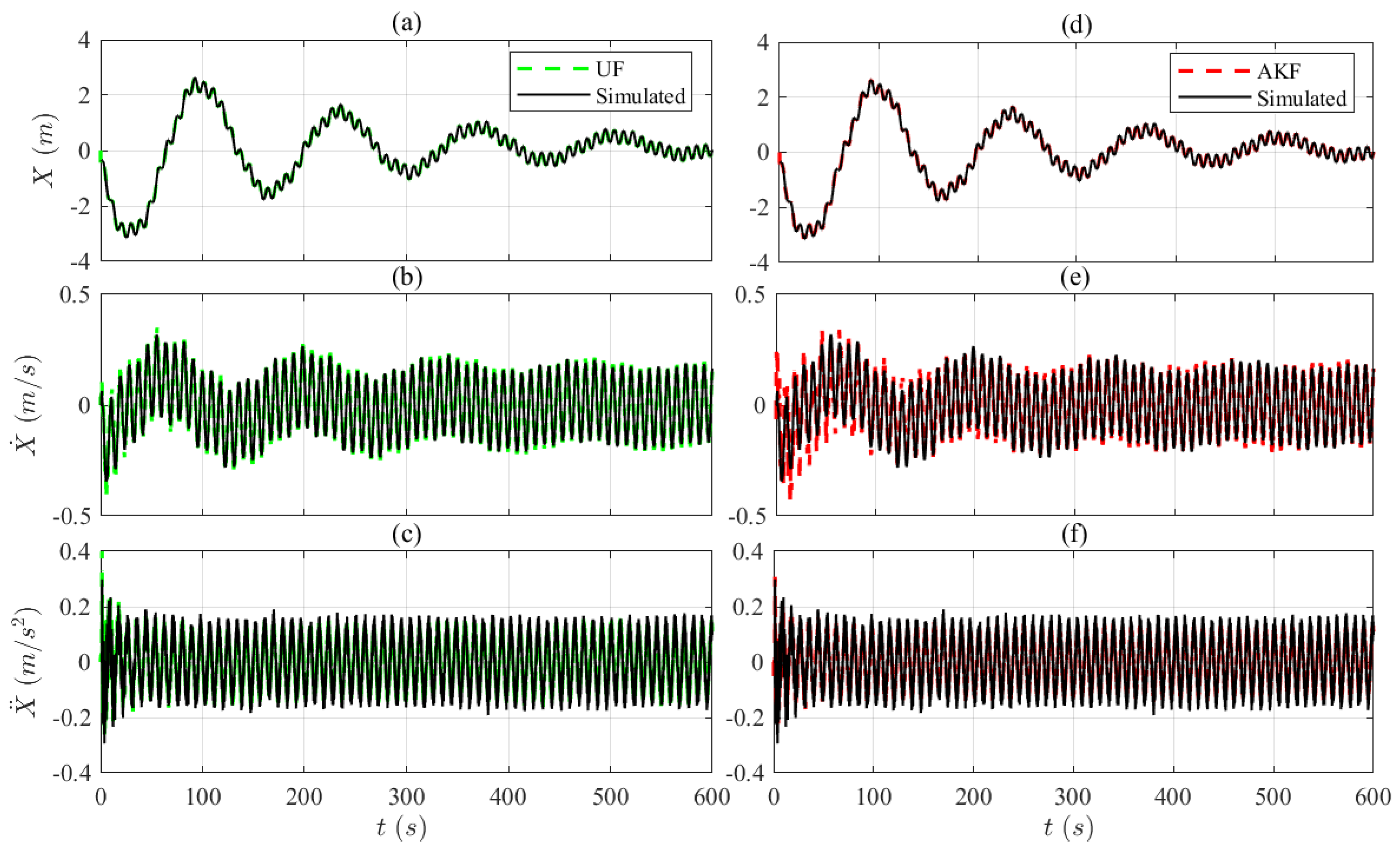
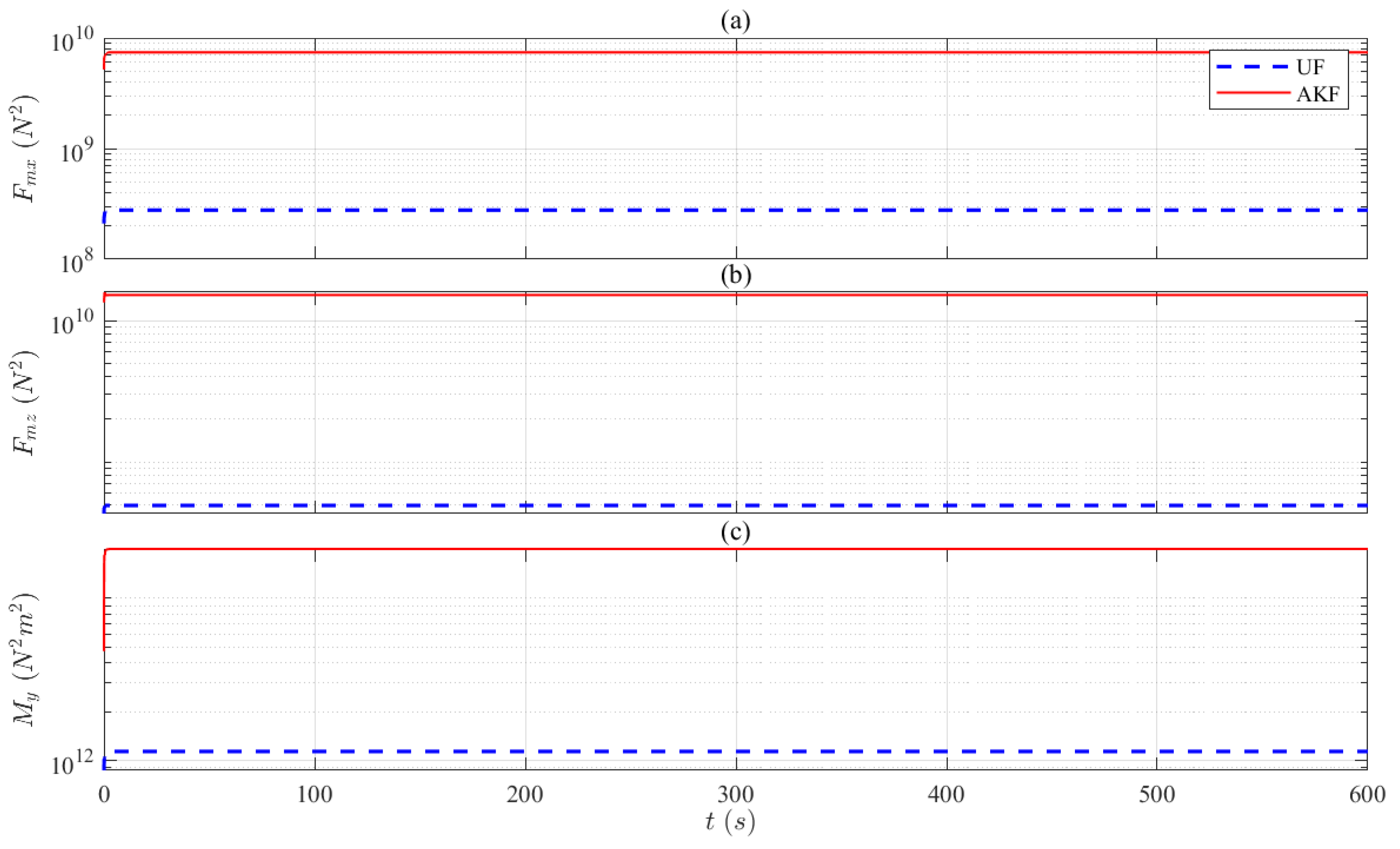
6.3. Simulated Experiments: OpenFAST Simulations

OpenFAST (previously known as FAST) is an open-source wind turbine simulation tool developed by the US National Renewable Energy Laboratory. OpenFAST is defined as a “glue code” that incorporates several sub-modules (Figure 5) to enable the coupled nonlinear aero–hydro–servo–elastic time and frequency domain simulations. It can run extensive numbers of nonlinear time-domain simulations in real-time and extract linearized models for the wind system response, modal analysis, control co-design, and aeroelastic instability studies [78].

As mentioned above, one of the sea state conditions provided by Yung et al. [85] has been used for OpenFAST [78] hydrodynamic simulations where the JONSWAP spectrum was employed with the wave height set to 2 [m] and the wave period set to 8.93 [s].

6.4. FOWT Digital Twin Problem Definition

A finite element model, such as a numerical model, offers advantages in the creation of a DT of a physical structure. This model is based on the linear second-order dynamic equation of motion with $n_s$ degrees of freedom (DOF). The equation includes the mass matrix ${\mathbf{M}}_s\in {\mathbb{R}}^{n_s\times n_s}$, stiffness matrix ${\mathbf{K}}_s\in {\mathbb{R}}^{n_s\times n_s}$, and damping matrix ${\mathbf{C}}_s\in {\mathbb{R}}^{n_s\times n_s}$. Here, the subscript s represents the system. The external force $\mathbf{p}\left(t\right)$ is also included. The dynamic equation is defined as follows:

$${\mathbf{M}}_s\ddot{\mathbf{u}}\left(t\right)+{\mathbf{C}}_s\dot{\mathbf{u}}\left(t\right)+{\mathbf{K}}_s\mathbf{u}\left(t\right)={\mathbf{S}}_p\mathbf{p}\left(t\right)$$

(1)

In the given equation, $\ddot{\mathbf{u}}\left(t\right)$, $\dot{\mathbf{u}}\left(t\right)$, and $\mathbf{u}\left(t\right)$ represent the acceleration, velocity, and displacement vectors, respectively, at specified DOF. In this study platform displacement is defined as $\mathbf{u}\left(t\right)={\left[ZRYRXXYRZ\right]}^T$, as shown in Figure 4. For offshore wind turbines, the mass matrix ${\mathbf{M}}_s$ accounts for both the structural mass and the added mass caused by the surrounding fluid movement. The damping matrix ${\mathbf{C}}_s$ also includes similar considerations. These additional terms complicate the problem, making it necessary to use system identification techniques with multi-input and multi-output systems, which are discussed later in this study. To implement the filtering algorithm, the model must be reformulated into state-space form. This process begins with the continuous form in the time domain, as shown below:

$$\begin{array}{cc}\hfill \dot{\mathbf{x}}\left(t\right)& ={\mathbf{A}}_s\mathbf{x}\left(t\right)+{\mathbf{B}}_s\mathbf{p}\left(t\right)+\mathbf{w}\left(t\right),\hfill \\ \hfill {\mathbf{A}}_s& =\left[\begin{array}{cc}{\mathbf{0}}_{n_s\times n_s}& {\mathbf{I}}_{n_s\times n_s}\\ -{\mathbf{M}}_s^{-1}{\mathbf{K}}_s& -{\mathbf{M}}_s^{-1}{\mathbf{C}}_s\end{array}\right],{\mathbf{B}}_s\hfill & \hfill =\left[\begin{array}{c}{\mathbf{0}}_{n_s\times n_p}\\ {\mathbf{M}}_s^{-1}{\mathbf{S}}_p\end{array}\right]\end{array}$$

(2)

Here, $\mathbf{x}\left(t\right)={\left[\begin{array}{cc}\mathbf{u}\left(t\right)& \dot{\mathbf{u}}\left(t\right)\end{array}\right]}^T\in {\mathbb{R}}^n$ represents the state vector. The system matrices ${\mathbf{A}}_s\in {\mathbb{R}}^{n\times n}$ and ${\mathbf{B}}_s\in {\mathbb{R}}^{n\times n_p}$ denote the state and input matrices, respectively. Additionally, ${\mathbf{S}}_p\in {\mathbb{R}}^{n_s\times n_p}$ is a boolean matrix called the input influence matrix, where $n_p$ represents the total number of applied inputs on the structure. The term $\mathbf{w}\left(t\right)\in {\mathbb{R}}^n$ accounts for modeling uncertainty and is referred as process noise. Here, $n=2n_s$ defines the total number of states. Since measurement data are typically stored in discrete form, the discretized process equation is presented below:

$${\mathbf{x}}_k={\mathbf{A}}_{k-1}{\mathbf{x}}_{k-1}+{\mathbf{B}}_{k-1}{\mathbf{p}}_{k-1}+{\mathbf{w}}_{k-1}$$

(3)

In this paper, ${\mathbf{x}}_k$ represents the fictitious state, which assists in the output vector estimation (as discussed in the system identification section). The matrices ${\mathbf{A}}_{k-1}$ and ${\mathbf{B}}_{k-1}$ are the discretized state and input matrices, respectively, and remain time-invariant throughout this study. These matrices can be obtained with the MATLAB System Identification Toolbox.

A sparsely measured system output is stored in the observation vector ${\mathbf{y}}_k\in {\mathbb{R}}^{n_m}$, which may include the displacement, velocity, and acceleration of the system. In general, displacement and acceleration sensors are common for field operations, while velocity sensors are less common. However, all three types of measurements can be obtained with the help of computer vision techniques [159]. The measurement vector is related to the state and input through the output matrix ${\mathbf{C}}_k$ and the feedforward matrix ${\mathbf{D}}_k$, which can be represented as follows:

$${\mathbf{y}}_k={\mathbf{C}}_k{\mathbf{x}}_k+{\mathbf{D}}_k{\mathbf{p}}_k+{\mathbf{v}}_k$$

(4)

In the process and measurement equations (refer to Equation (3) and Equation (4) respectively), the noise vectors ${\mathbf{w}}_{k-1}\sim N(0,{\mathbf{Q}}_{k-1})$ and ${\mathbf{v}}_k\sim N(0,{\mathbf{R}}_k)$ represent zero-mean white Gaussian noise (WGN), respectively. These noise vectors are uncorrelated $(\mathbb{E}\left({\mathbf{w}}_i{\mathbf{v}}_j^T\right)=0)$ at any time step and are independent of the initial estimated state. The covariance matrices are defined as follows:

$${\mathbf{Q}}_{k-1}\stackrel{\Delta }{=}\mathbb{E}\left[{\mathbf{w}}_{k-1}{\mathbf{w}}_{k-1}^T\right],{\mathbf{R}}_k\stackrel{\Delta }{=}\mathbb{E}\left[{\mathbf{v}}_k{\mathbf{v}}_k^T\right]$$

(5)

In this study, all system matrices $({\mathbf{A}}_{k-1},{\mathbf{B}}_{k-1},{\mathbf{C}}_k,{\mathbf{D}}_k)$ are extracted from the MATLAB System Identification Toolbox with the utilization of a multi-input, multi-output dataset. The toolbox also provides the covariance of the measurement noise ${\mathbf{R}}_k$. Here, only the process noise covariance matrix ${\mathbf{Q}}_{k-1}$ is tuned with the grid search algorithm. Within the next section, the system identification technique and the identification of the system matrix with MATLAB are discussed.

6.5. System Identification

In this paper, input and output data are extracted from the OpenFAST (version 3.5.1) [78] software (details of the number of inputs and outputs are discussed in the Section 6.6). To simulate noisy data, the measurement data are contaminated with $1\%$ of the root mean square (RMS) value of the true data. The input and output data are then stored in an object class named data (though any other name can be used).

Using the MATLAB System Identification Toolbox [160,161], the following steps are followed to estimate a state-space model:

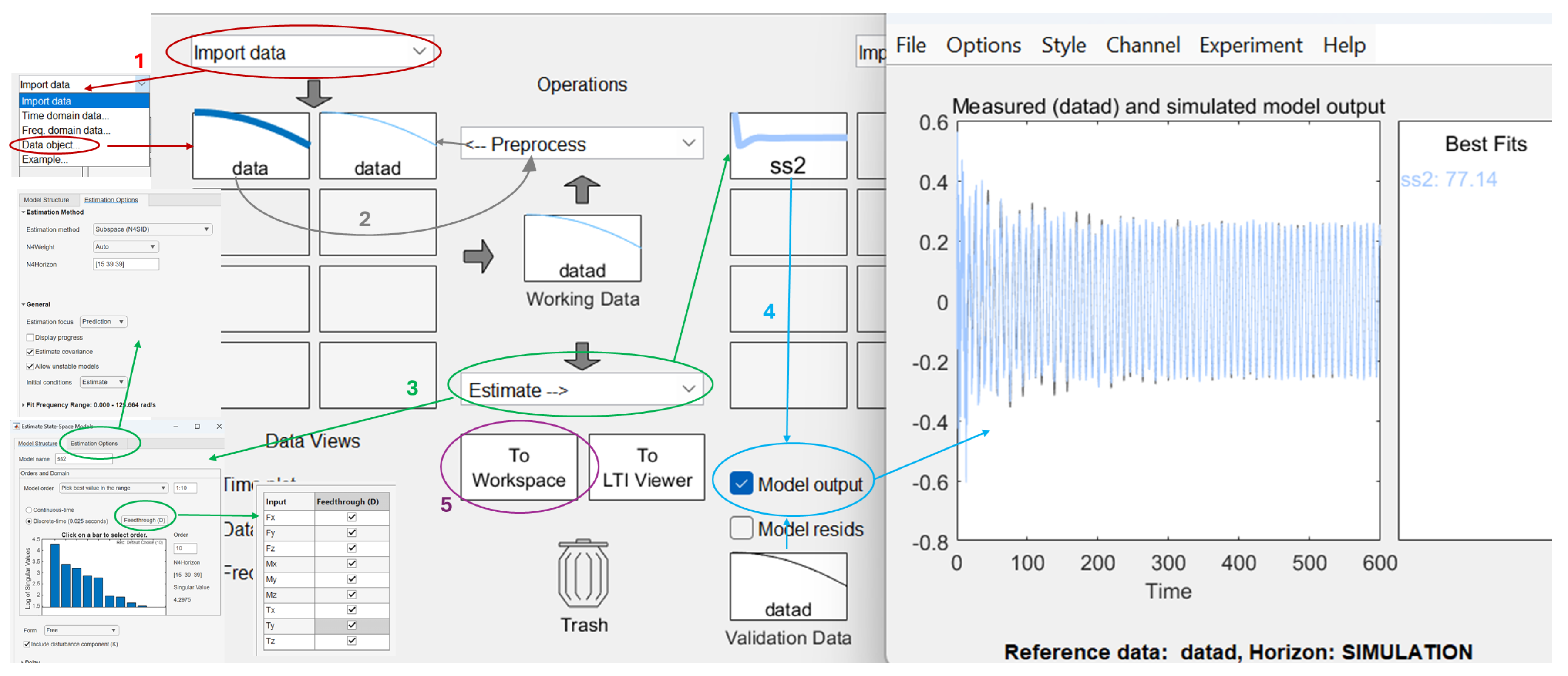
• Step 1: Import data. Launch the System Identification Toolbox GUI and use the “Import Data” option to load the data object. Set the initial time to zero. (Red arrow in Figure 6)
• Step 2: Preprocess data. Go to the “Operations” tab and apply the “Remove Mean” function to make the dataset zero mean (producing datad). Move this to the working data section. (Gray symbol in Figure 6)
• Step 3: Estimate the model.

  -

  Select “Estimate” → “State-space models”.

  -

  Set the domain to “discrete” and enable “Feedthrough” for all inputs.

  -

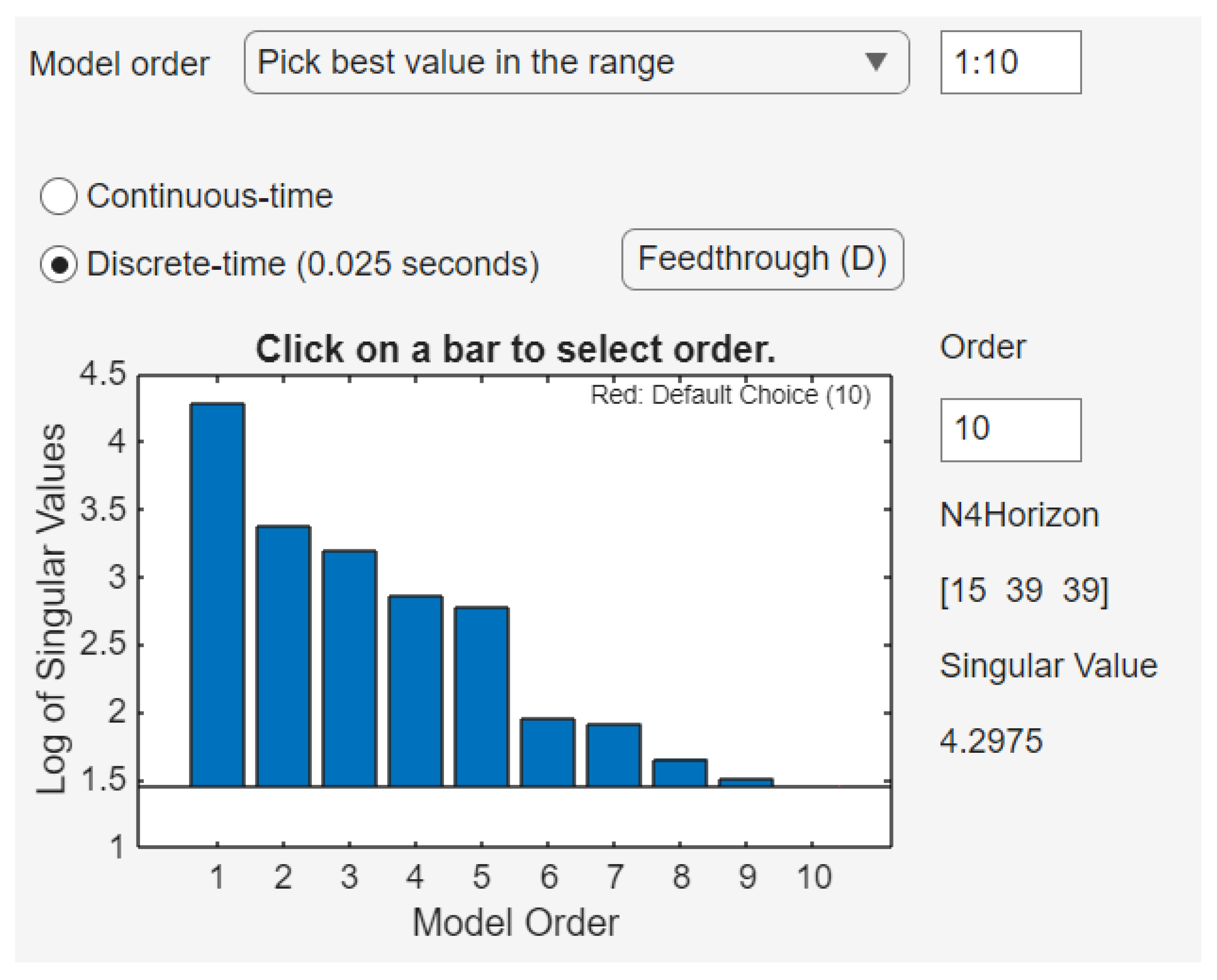
  Use singular value decomposition (SVD) to choose the appropriate model order.

  -

  Leave the state-space matrices $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$, $\mathbf{D}$, and $\mathbf{K}$ set to “free”.

  -

  Enable “Include Disturbance” and set the initial condition to zero.

  (Green arrow in Figure 6)
• Step 4: Evaluate the model. Once estimated, compare the simulated model (ss2) to the preprocessed data (datad) using “Model Views”. Evaluate output prediction accuracy. (Celestial light blue indicator in Figure 6)
• Step 5: Export the model. If performance is acceptable, extract the model to the MATLAB workspace and save it in the desired directory.

The estimation uses the N4SID (numerical subspace state space system identification) algorithm with focus set to “prediction.” A well-conditioned basis is automatically chosen. For further reference, see the System Identification Toolbox User’s Guide [161].

6.5.1. Kalman Filter

In real-world scenarios, it is often impractical to measure real-time responses at all critical locations of structures. Therefore, studies focus on the estimation of the states such as displacement, velocity, acceleration, and strain at unobserved locations. The KF is a widely recognized state estimation filter used for this purpose. It operates under the assumption that all system matrices $({\mathbf{A}}_{k-1},{\mathbf{B}}_{k-1},{\mathbf{C}}_k,$ and ${\mathbf{D}}_k)$ and the applied inputs that excite the structure $\mathbf{p}\left(t\right)$ are fully known and characterized. This allows the Kalman filter to predict and estimate the states of interest based on available measurements and system dynamics [151].

As a stochastic framework, it deals with the mean ${\widehat{\mathbf{x}}}_{k|k}$ and covariance of the state estimation error ${\mathbf{P}}_{k|k}^{\mathbf{x}}$. The framework for the KF begins with the assumption that the initial state ${\widehat{\mathbf{x}}}_{0|0}$ and their covariance ${\mathbf{P}}_{0|0}^{\mathbf{x}}$ are known. The filter operates in two major steps. The first step is the time update (also known as the prediction step), where the state at the $k^{th}$ step is predicted using the measurement and input from the ${k-1}^{th}$ step. This step assumes that the system is observable, which means that the rank of the observability matrix $obsv({\mathbf{C}}_{k-1},{\mathbf{A}}_{k-1})$ should be equal to the number of states n, where $obsv$ is the MATLAB function for observability matrix [162]. The formulation of the prediction state is represented as follows:

$${\widehat{\mathbf{x}}}_{k|k-1}={\mathbf{A}}_{k-1}{\widehat{\mathbf{x}}}_{k-1|k-1}+{\mathbf{B}}_{k-1}{\mathbf{p}}_{k-1}$$

(6)

$$\begin{array}{cc}\hfill {\mathbf{P}}_{k|k-1}^{\mathbf{x}}& =\mathbf{E}\left[\begin{array}{c}\left({\mathbf{x}}_k-{\widehat{\mathbf{x}}}_{k|k-1}\right){\left({\mathbf{x}}_k-{\widehat{\mathbf{x}}}_{k|k-1}\right)}^T\end{array}\right]\hfill \\ \hfill & ={\mathbf{A}}_{k-1}\mathbf{E}\left[\left({\mathbf{x}}_{k-1}-{\widehat{\mathbf{x}}}_{k-1|k-1}\right){\left({\mathbf{x}}_{k-1}-{\widehat{\mathbf{x}}}_{k-1|k-1}\right)}^T\right]{\mathbf{A}}_{k-1}^T+\mathbf{E}\left[\begin{array}{c}{\mathbf{w}}_{k-1}{\mathbf{w}}_{k-1}^T\end{array}\right]\hfill \\ \hfill & ={\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T+{\mathbf{Q}}_{k-1}\hfill \end{array}$$

(7)

After the time update, the predicted state is corrected via the measurement dataset in the measurement update step. This process begins with the residual (or innovation) ${\mathbf{ϵ}}_k$ calculation, which is

$$\begin{array}{cc}\hfill {\mathbf{ϵ}}_k& ={\mathbf{y}}_k-{\widehat{\mathbf{y}}}_k\hfill \\ \hfill & ={\mathbf{C}}_k{\mathbf{x}}_k+{\mathbf{D}}_k{\mathbf{p}}_k+{\mathbf{v}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}-{\mathbf{D}}_k{\mathbf{p}}_k\hfill \\ \hfill & ={\mathbf{C}}_k({\mathbf{x}}_k-{\widehat{\mathbf{x}}}_{k|k-1})+{\mathbf{v}}_k\hfill \end{array}$$

(8)

The updated state ${\widehat{\mathbf{x}}}_{k|k}$ can be expressed as a function of the Kalman gain ${\mathbf{K}}_k$ (a state gain matrix) and the predicted state ${\widehat{\mathbf{x}}}_{k|k-1}$ as follows:

$${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k{\mathbf{ϵ}}_k$$

(9)

The Kalman gain is calculated by the process of covariance ${\mathbf{P}}_{k|k}^{\mathbf{x}}$ minimization. Briefly, this study provides only the formulations of the Kalman gain ${\mathbf{K}}_k$ and ${\mathbf{P}}_{k|k}^{\mathbf{x}}$, which are as follows:

$${\mathbf{K}}_k={\mathbf{P}}_{k|k-1}{\mathbf{C}}_k^T{\left({\mathbf{P}}_k^{\mathbf{ϵ}}\right)}^{†}$$

(10)

$${\mathbf{P}}_{k|k}=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{C}}_k){\mathbf{P}}_{k|k-1}$$

(11)

where ${\mathbf{P}}_k^{\mathbf{ϵ}}=\mathbb{E}\left[{\mathbf{ϵ}}_k{{\mathbf{ϵ}}_k}^T\right]={\mathbf{C}}_k{\mathbf{P}}_{k|k-1}{\mathbf{C}}_k^T+{\mathbf{R}}_k$, and ${\left[\right]}^{†}$ represents the pseudo-inverse. The pseudo-inverse is used to truncate the singular values. This prevents ill-conditioning during the inversion process. In linear problems, the Kalman gain is always the optimal gain. The operational process of the KF is illustrated in Algorithm 1. In this study, the KF is used to evaluate the accuracy of the system matrices extracted with the MATLAB System Identification Toolbox [161] for the first sea state.

Algorithm 1 KF algorithm for state estimation

1: procedure KF(${\mathbf{A}}_{k-1},{\mathbf{B}}_{k-1},{\mathbf{C}}_k,{\mathbf{D}}_k,{\mathbf{y}}_k,{\mathbf{p}}_{k-1},{\mathbf{Q}}_{k-1},{\mathbf{R}}_k$)  ▹ known state-space matrices and measurement   2:     Initialize state ${\widehat{\mathbf{x}}}_{0|0}$, and estimated error covariance of state ${\mathbf{P}}_{0|0}^{\mathbf{x}}$                                ▹ Initial guess   3:     for <each $k^{th}$ measurement ${\mathbf{y}}_k$> do                                    ▹ start loop with $t_k$, where $k=1,2,3...N$   4:         Prediction stage:   5:         ${\widehat{\mathbf{x}}}_{k|k-1}={\mathbf{A}}_{k-1}{\widehat{\mathbf{x}}}_{k-1|k-1}+{\mathbf{B}}_{k-1}{\mathbf{p}}_{k-1}$                                                                              ▹ Predicted state   6:         ${\mathbf{P}}_{k|k-1}^{\mathbf{x}}={\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1|k-1}{\mathbf{A}}_{k-1}^T+{\mathbf{Q}}_{k-1}$                                                          ▹ Predicted state covariance   7:         Update stage:   8:         ${\mathbf{ϵ}}_k={\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}-{\mathbf{D}}_k{\mathbf{p}}_k$   9:         ${\mathbf{P}}_k^{\mathbf{ϵ}}={\mathbf{C}}_k{\mathbf{P}}_{k|k-1}{\mathbf{C}}_k^T+{\mathbf{R}}_k$ 10:         ${\mathbf{K}}_k={\mathbf{P}}_{k|k-1}{\mathbf{C}}_k{\left({\mathbf{P}}_k^{\mathbf{ϵ}}\right)}^{†}$                                                                                                   ▹ Kalman gain 11:         ${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k{\mathbf{ϵ}}_k$                                                                                                 ▹ Updated state 12:         ${\mathbf{P}}_{k|k}=(\mathbf{I}-{\mathbf{K}}_k{\mathbf{C}}_k){\mathbf{P}}_{k|k-1}$                                                                        ▹ Updated state covariance 13:     end for 14: end procedure

6.5.2. Augmented Kalman Filter

In this section, a brief explanation of the AKF is provided. All the notations introduced in the previous section are carried forward into this section and the following sections. The AKF incorporates the unknown inputs into the state vector, denoted as ${\widehat{\mathbf{x}}}_k^a$, where the superscript a refers to the augmented state. The new state vector is represented by the following equation [119]:

$${\widehat{\mathbf{x}}}_k^a={\left[\begin{array}{cc}{\widehat{\mathbf{x}}}_k& {\widehat{\mathbf{p}}}_k\end{array}\right]}^T$$

(12)

The transition of the unknown input is governed by an identity matrix for time transition, i.e., ${\widehat{\mathbf{p}}}_{k+1}={\mathbf{I}}_{n_p}{\widehat{\mathbf{p}}}_k$, where ${\mathbf{I}}_{n_p}$ refers to the identity matrix with respective size. However, to enable the filter to adjust the unknown input value, a fictitious noise ${\mathbf{v}}_k^{\mathbf{p}}$ with statistics ${\mathbf{v}}_k^{\mathbf{p}}\stackrel{\Delta }{=}N(0,{\mathbf{Q}}_k^{\mathbf{p}})$ is introduced into the relevant process equation:

$${\widehat{\mathbf{p}}}_{k+1}={\widehat{\mathbf{p}}}_k+{\mathbf{v}}_k^{\mathbf{p}}$$

(13)

The covariance ${\mathbf{Q}}_k^{\mathbf{p}}$ of this fictitious noise is adjusted using grid search optimization. Once the unknown input is augmented into the system, the state-space model is redefined and cast into its augmented form. Matrices associated with the augmented formulation are distinguished by a superscript ‘a’. The system matrices become

$${\mathbf{A}}_{k-1}^a=\left[\begin{array}{cc}{\mathbf{A}}_{k-1}& {\mathbf{B}}_{k-1}\\ {\mathbf{0}}_{m\times 2ns}& {\mathbf{I}}_{m\times m}\end{array}\right],{\mathbf{C}}_k^a=\left[\begin{array}{cc}{\mathbf{C}}_k& {\mathbf{D}}_k\end{array}\right]$$

(14)

Moreover, the comprehensive formulation of this method is encapsulated in Algorithm 2 for the implementation of the AKF.

Algorithm 2 AKF algorithm for input and state estimation

1: procedure AKF(${\mathbf{A}}_{k-1}^a,{\mathbf{C}}_k^a,{\mathbf{y}}_k,{\mathbf{Q}}_{k-1}^a,{\mathbf{R}}_k$)    ▹ known state-space matrices and measurement   2:     Initialize state ${\widehat{\mathbf{x}}}_{0|0}^a$, and estimated error covariance of state ${\mathbf{P}}_{0|0}^a$             ▹ Initial guess   3:     for <each $k^{th}$ measurement ${\mathbf{y}}_k$> do                  ▹ start loop with $t_k$, where $k=1,2,3...N$   4:         Prediction stage:   5:         ${\widehat{\mathbf{x}}}_{k|k-1}^a={\mathbf{A}}_{k-1}^a{\widehat{\mathbf{x}}}_{k-1|k-1}^a$                                                            ▹ Predicted augmented state   6:         ${\mathbf{P}}_{k|k-1}^a={\mathbf{A}}_{k-1}^a{\mathbf{P}}_{k-1|k-1}^a{\mathbf{A}}_{k-1}^{aT}+{\mathbf{Q}}_{k-1}^a$                               ▹ Predicted augmented covariance   7:         Update stage:   8:         ${\mathbf{K}}_k={\mathbf{P}}_{k|k-1}^a{\mathbf{C}}_k^{aT}{({\mathbf{C}}_k^a{\mathbf{P}}_{k|k-1}^a{\mathbf{C}}_k^{aT}+{\mathbf{R}}_k)}^{†}$                                                              ▹ Kalman gain   9:         ${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k({\mathbf{y}}_k-{\mathbf{C}}_k^a{\widehat{\mathbf{x}}}_{k|k-1}^a)$                                          ▹ Updated augmented state 10:         ${\mathbf{P}}_{k|k}^a={\mathbf{P}}_{k|k-1}^a-{\mathbf{K}}_k{\mathbf{C}}_k^a{\mathbf{P}}_{k|k-1}^a$                              ▹ Updated covariance of augmented state 11:     end for 12: end procedure

6.5.3. Universal Filter

The UF operates in three main steps that use measurements: input estimation, state prediction, and state update [156]. The UF begins by the estimation of the biased prior state ${\widehat{\mathbf{x}}}_{k|k-1}^b$ of the true state:

$${\widehat{\mathbf{x}}}_{k|k-1}^b={\mathbf{A}}_{k-1}{\widehat{\mathbf{x}}}_{k-1|k-1}$$

(15)

Then, the initial state prediction, an unbiased minimum-variance estimate of the real input ${\mathbf{p}}_k$, denoted ${\widehat{\mathbf{p}}}_k$, is derived. This estimation fuses the biased prior state ${\widehat{\mathbf{x}}}_{k|k-1}^b$ with the current observation ${\mathbf{y}}_k$, as illustrated in the equation below:

$${\widehat{\mathbf{p}}}_k={\mathbf{G}}_k({\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}^b)$$

(16)

In the above Equation (16), ${\mathbf{G}}_k$ represents the input gain calculated using the weighted least squares method [115,156]. Subsequently, the unbiased prior state ${\widehat{\mathbf{x}}}_{k|k-1}$ is estimated in the prediction step and the posterior state ${\widehat{\mathbf{x}}}_{k|k}$ in the measurement step; both are formulated below:

$$\begin{array}{cc}\hfill {\widehat{\mathbf{x}}}_{k|k-1}& ={\widehat{\mathbf{x}}}_{k|k-1}^b+{\mathbf{B}}_{k-1}{\widehat{\mathbf{p}}}_k\hfill \\ \hfill {\widehat{\mathbf{x}}}_{k|k}& ={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k({\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}-{\mathbf{D}}_k{\widehat{\mathbf{p}}}_k)\hfill \end{array}$$

(17)

The unbiasedness of the input and state is proved in the detailed mathematical form in the given paper by Ebrahimzadeh Hassanabadi et al. (2023) [156]. All the estimation error vectors are defined below:

$$\begin{array}{cc}\hfill {\tilde{\mathbf{p}}}_k& ={\mathbf{p}}_k-{\mathbf{G}}_k({\varsigma }_k{\mathbf{p}}_k+{\mathbf{ϵ}}_k)\hfill \\ \hfill {\tilde{\mathbf{x}}}_{k|k-1}& ={\mathbf{A}}_{k-1}{\tilde{\mathbf{x}}}_{k-1}+{\mathbf{G}}_{k-1}{\tilde{\mathbf{p}}}_k+{\mathbf{w}}_{k-1}\hfill \\ \hfill {\tilde{\mathbf{x}}}_k& ={\tilde{\mathbf{x}}}_{k|k-1}-{\mathbf{K}}_k({\mathbf{C}}_k{\tilde{\mathbf{x}}}_{k|k-1}+{\mathbf{D}}_k{\tilde{\mathbf{p}}}_k+{\mathbf{v}}_k)\hfill \end{array}$$

(18)

where, ${\mathbf{\varsigma }}_k={\mathbf{C}}_k{\mathbf{B}}_{k-1}+{\mathbf{D}}_k$, $\mathrm{rank}\left({\mathbf{\varsigma }}_k\right)\ge$ number of unknown inputs $n_p$. Last but not least, ${\mathbf{ϵ}}_k={\mathbf{C}}_k({\mathbf{A}}_{k-1}{\tilde{\mathbf{x}}}_{k-1}+{\mathbf{w}}_{k-1})+{\mathbf{v}}_k$.

For the proof of minimum variance, we need all the covariance matrices used in the algorithm, starting with the covariance of error ${\mathbf{ϵ}}_k$:

$$\begin{array}{cc}\hfill {\mathbf{P}}_k^{\mathbf{ϵ}}& =\mathrm{Cov}\left({\mathbf{ϵ}}_k\right)\hfill \\ \hfill & ={\mathbf{C}}_k({\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T+{\mathbf{Q}}_{k-1}){\mathbf{C}}_k^T+{\mathbf{R}}_k\hfill \end{array}$$

(19)

Importantly, the noise components are assumed to be uncorrelated with the initial state error; thus, $\mathbb{E}\left[{\mathbf{v}}_1{\tilde{\mathbf{x}}}_0^T\right]=0$ and $\mathbb{E}\left[{\mathbf{w}}_0{\tilde{\mathbf{x}}}_0^T\right]=0$. This assumption allows for the simplification of the error covariance calculations by also eliminating $\mathbb{E}\left[{\mathbf{v}}_k{\tilde{\mathbf{x}}}_{k-1}^T\right]=0$ and $\mathbb{E}\left[{\mathbf{w}}_{k-1}{\tilde{\mathbf{x}}}_{k-1}^T\right]=0$ from the final formula. The covariance of the prior state and input estimation error can be expressed, respectively as below:

$$\begin{array}{cc}\hfill {\mathbf{P}}_k^{\mathbf{p}}& ={\mathbf{G}}_k{\mathbf{P}}_k^{\mathbf{ϵ}}{\mathbf{G}}_k^T\hfill \\ \hfill {\mathbf{P}}_{k|k-1}^{\mathbf{x}}& ={\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{B}}_{k-1}^T+{\mathbf{Q}}_{k-1}\hfill \\ \hfill & +{\mathbf{A}}_{k-1}{\mathbf{P}}_k^{\mathbf{xp}}{\mathbf{B}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{px}}{\mathbf{A}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{pw}}+{\mathbf{P}}_k^{\mathbf{wp}}{\mathbf{B}}_{k-1}^T\hfill \end{array}$$

(20)

In the above equation,

$$\begin{array}{cc}\hfill {\mathbf{P}}_k^{\mathbf{xp}}& =-{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T{\mathbf{C}}_k^T{\mathbf{G}}_k^T\hfill \\ \hfill {\mathbf{P}}_k^{\mathbf{pw}}& =-{\mathbf{G}}_k{\mathbf{C}}_k{\mathbf{Q}}_{k-1}\hfill \end{array}$$

(21)

Finally, the error covariance matrix of the posterior state can be accurately expressed as

$${\mathbf{P}}_{k|k}^{\mathbf{x}}={\mathbf{K}}_k{\mathsf{\Psi }}_k{\mathbf{K}}_k^T-{\mathbf{{\rm Y}}}_k^T{\mathbf{K}}_k^T-{\mathbf{K}}_k{\mathbf{{\rm Y}}}_k+{\mathbf{P}}_{k|k-1}^{\mathbf{x}}$$

(22)

where

$${\mathbf{{\rm Y}}}_k={\mathbf{C}}_k{\mathbf{P}}_{k|k-1}^{\mathbf{x}}+{\mathbf{D}}_k{\mathbf{P}}_{k|k-1}^{\mathbf{px}}+{\mathbf{P}}_{k|k-1}^{\mathbf{vx}}$$

(23)

In the Equation (23), ${\mathsf{\Psi }}_k$ matrix is a function of ${\mathbf{{\rm Y}}}_k$, the covariance of measurement noise ${\mathbf{R}}_k$, the input error estimation ${\mathbf{P}}_k^{\mathbf{p}}$, and the different cross-covariance among the input error, prior state error, and measurement noise. This can be formulated as below:

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_k& ={\mathbf{C}}_k{\mathbf{{\rm Y}}}_k^T+{\mathbf{D}}_k({\mathbf{P}}_{k|k-1}^{\mathbf{px}}{\mathbf{C}}_k^T+{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{D}}_k^T+{\mathbf{P}}_k^{\mathbf{pv}})+{\mathbf{P}}_{k|k-1}^{\mathbf{vx}}{\mathbf{C}}_k^T+{\mathbf{P}}_k^{\mathbf{vp}}{\mathbf{D}}_k^T+{\mathbf{R}}_k\hfill \end{array}$$

(24)

The values of all covariance matrices discussed in the Equation (24) can be defined through the following expressions:

$$\begin{array}{cc}\hfill {\mathbf{P}}_{k|k-1}^{\mathbf{px}}& ={\mathbf{P}}_k^{\mathbf{px}}{\mathbf{A}}_{k-1}^T+{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{B}}_{k-1}^T+{\mathbf{P}}_k^{\mathbf{pw}}\hfill \\ \hfill {\mathbf{P}}_{k|k-1}^{\mathbf{vx}}& ={\mathbf{P}}_k^{\mathbf{vp}}{\mathbf{B}}_{k-1}^T\hfill \\ \hfill {\mathbf{P}}_k^{\mathbf{pv}}& =-{\mathbf{G}}_k{\mathbf{R}}_k\hfill \end{array}$$

(25)

Considering the equation ${\mathbf{\varsigma }}_k{\mathbf{p}}_k={\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k-1}-{\mathbf{\epsilon }}_k$, the weighted least squares method is employed to minimize the covariance matrix of the error term ${\mathbf{\epsilon }}_k$. This approach aims to reduce the variance of the estimation error. According to this technique, the input gain can be calculated by taking the inverse of the latter expression; thereby, the formula for the input gain ${\mathbf{G}}_k$ is derived and, then, the input error covariance ${\mathbf{P}}_k^{\mathbf{p}}$ is derived:

$$\begin{array}{cc}\hfill {\mathbf{G}}_k& ={\left[{\mathbf{\varsigma }}_k^T{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}{\mathbf{\varsigma }}_k\right]}^{†}{\mathbf{\varsigma }}_k{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}\hfill \\ \hfill {\mathbf{P}}_k^{\mathbf{p}}& ={\left[{\mathbf{\varsigma }}_k^T{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}{\mathbf{\varsigma }}_k\right]}^{†}\hfill \end{array}$$

(26)

The optimal value of the Kalman gain ${\mathbf{K}}_k$ is determined by the minimization of the trace of the state estimation error covariance, as previously defined in Equation (22). Numerical instability can arise due to rank deficiency or infinitesimally small singular values in ${\mathsf{\Psi }}_k$. To address this issue, a state tolerance value may be applied to keep the singular values greater than the tolerance value, thereby maintaining system stability:

$${\mathbf{K}}_k={\mathbf{{\rm Y}}}_k^T{\mathbf{U}}_k{\left({\mathbf{U}}_k^T{\mathsf{\Psi }}_k{\mathbf{U}}_k\right)}^{†}{\mathbf{U}}_k^T$$

(27)

where ${\mathbf{U}}_k$ is the left singular matrix of the decomposed ${\mathsf{\Psi }}_k$. In this study, all the system matrices (${\mathbf{A}}_{k-1}$, ${\mathbf{B}}_{k-1}$, ${\mathbf{C}}_{k-1}$, ${\mathbf{D}}_{k-1}$) and the hyperparameters (${\mathbf{Q}}_{k-1}$, ${\mathbf{R}}_k$) are assumed to be time-invariant. Hyperparameters are tuned using the grid search optimization algorithm.

This filter can handle all cases from a direct feedthrough point of view, such as systems with direct feedthrough, without direct feedthrough, and rank-deficient cases. For implementation as computer code, an algorithm is presented in Algorithm 3.

Algorithm 3 MVU-based UF algorithm for input and state estimation

1: procedure UF(${\mathbf{A}}_{k-1},{\mathbf{B}}_{k-1},{\mathbf{C}}_k,{\mathbf{D}}_k,{\mathbf{y}}_k,{\mathbf{Q}}_{k-1},{\mathbf{R}}_k$)    ▹ known state-space matrices and measurement   2:     Initialize ${\widehat{\mathbf{x}}}_{0|0}$, ${\mathbf{P}}_{0|0}^{\mathbf{x}}$                                                                                                      ▹ Initial guess   3:     for <each $k^{th}$ measurement ${\mathbf{y}}_k$> do                              ▹ start loop with $t_k$, where $k=1,2,3...N$   4:         ${\mathbf{\varsigma }}_k={\mathbf{C}}_k{\mathbf{B}}_{k-1}+{\mathbf{D}}_k$   5:         ${\mathbf{P}}_k^{\mathbf{ϵ}}={\mathbf{C}}_k({\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T+{\mathbf{Q}}_{k-1}){\mathbf{C}}_k^T+{\mathbf{R}}_k$   6:         ${\mathbf{P}}_k^{\mathbf{p}}={\left[{\mathbf{\varsigma }}_k^T{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}{\mathbf{\varsigma }}_k\right]}^{†}$                                                                                ▹ Input error covariance   7:         ${\mathbf{G}}_k={\left[{\mathbf{\varsigma }}_k^T{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}{\mathbf{\varsigma }}_k\right]}^{†}{\mathbf{\varsigma }}_k{\left({\mathbf{P}}_k^{\mathbf{\epsilon }}\right)}^{†}$                                                                                        ▹ Input gain   8:         ${\mathbf{P}}_k^{\mathbf{xp}}=-{\mathbf{P}}_{k-1|k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T{\mathbf{C}}_k^T{\mathbf{G}}_k^T$   9:         ${\mathbf{P}}_k^{\mathbf{pw}}=-{\mathbf{G}}_k{\mathbf{C}}_k{\mathbf{Q}}_{k-1}$ 10:         ${\mathbf{P}}_{k|k-1}^{\mathbf{x}}={\mathbf{A}}_{k-1}{\mathbf{P}}_{k-1}^{\mathbf{x}}{\mathbf{A}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{B}}_{k-1}^T+{\mathbf{Q}}_{k-1}+{\mathbf{A}}_{k-1}{\mathbf{P}}_k^{\mathbf{xp}}{\mathbf{B}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{px}}{\mathbf{A}}_{k-1}^T+{\mathbf{B}}_{k-1}{\mathbf{P}}_k^{\mathbf{pw}}+{\mathbf{P}}_k^{\mathbf{wp}}{\mathbf{B}}_{k-1}^T$ 11:         ${\mathbf{P}}_{k|k-1}^{\mathbf{px}}={\mathbf{P}}_k^{\mathbf{px}}{\mathbf{A}}_{k-1}^T+{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{B}}_{k-1}^T+{\mathbf{P}}_k^{\mathbf{pw}}$ 12:         ${\mathbf{P}}_k^{\mathbf{pv}}=-{\mathbf{G}}_k{\mathbf{R}}_k$ 13:         ${\mathbf{P}}_{k|k-1}^{\mathbf{vx}}={\mathbf{P}}_k^{\mathbf{vp}}{\mathbf{B}}_{k-1}^T$ 14:         ${\mathbf{{\rm Y}}}_k={\mathbf{C}}_k{\mathbf{P}}_{k|k-1}^{\mathbf{x}}+{\mathbf{D}}_k{\mathbf{P}}_{k|k-1}^{\mathbf{px}}+{\mathbf{P}}_{k|k-1}^{\mathbf{vx}}$ 15:         ${\mathsf{\Psi }}_k={\mathbf{C}}_k{\mathbf{{\rm Y}}}_k^T+{\mathbf{D}}_k({\mathbf{P}}_{k|k-1}^{\mathbf{px}}{\mathbf{C}}_k^T+{\mathbf{P}}_k^{\mathbf{p}}{\mathbf{D}}_k^T+{\mathbf{P}}_k^{\mathbf{pv}})+{\mathbf{P}}_{k|k-1}^{\mathbf{vx}}{\mathbf{C}}_k^T+{\mathbf{P}}_k^{\mathbf{vp}}{\mathbf{D}}_k^T+{\mathbf{R}}_k$ 16:         ${\mathbf{K}}_k={\mathbf{{\rm Y}}}_k^T{\mathbf{U}}_k{\left({\mathbf{U}}_k^T{\mathsf{\Psi }}_k{\mathbf{U}}_k\right)}^{†}{\mathbf{U}}_k^T$                                                                                    ▹ Kalman gain 17:         Biased estimated state ${\widehat{\mathbf{x}}}_{k|k-1}^b={\mathbf{A}}_{k-1}{\widehat{\mathbf{x}}}_{k-1|k-1}$ 18:         Estimated input ${\widehat{\mathbf{p}}}_k={\mathbf{G}}_k({\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}^b)$ 19:         Prior estimated state ${\widehat{\mathbf{x}}}_{k|k-1}={\widehat{\mathbf{x}}}_{k|k-1}^b+{\mathbf{B}}_{k-1}{\widehat{\mathbf{p}}}_k$ 20:         Posterior estimated state ${\widehat{\mathbf{x}}}_{k|k}={\widehat{\mathbf{x}}}_{k|k-1}+{\mathbf{K}}_k({\mathbf{y}}_k-{\mathbf{C}}_k{\widehat{\mathbf{x}}}_{k|k-1}-{\mathbf{D}}_k{\widehat{\mathbf{p}}}_k)$ 21:         State covariance ${\mathbf{P}}_k^{\mathbf{x}}={\mathbf{K}}_k{\mathsf{\Psi }}_k{\mathbf{K}}_k^T-{\mathbf{{\rm Y}}}_k^T{\mathbf{K}}_k^T-{\mathbf{K}}_k{\mathbf{{\rm Y}}}_k+{\mathbf{P}}_{k|k-1}^{\mathbf{x}}$ 22:     end for 23: end procedure

6.6. Results and Discussion

The wind turbine platform displacements are extracted from the OpenFAST [78] software. With the displacement data, the velocity and acceleration are calculated via the central difference formulation, which allows to combine the displacement, velocity, and acceleration to serve as the measurement data. The UF does not perform well with only displacement data [156]. Additionally, the AKF encounters observability issues when only acceleration data are present, which is why both velocity and acceleration data are included.

In this study, six inputs are extracted from OpenFAST [78]. The platform has six DOFs: heave (Z), pitch (RY), roll (RX), surge (X), sway (Y), and yaw (RZ). The displacement, velocity, and acceleration for all DOFs are stored with 1% added root mean square (RMS) noise. Data preparation for system identification is performed for the first of seven sea states. A multi-input, multi-output system is created as an IDDATA object.

Using the System Identification Toolbox, an optimized state-space model with 10 fictitious states, denoted as $x_k$, is extracted (details provided in the System Identification Toolbox section). The model order determined by the toolbox is presented in Figure 7.

Based on the platform setup and applied wave motion, it was found that the measurements for three DOFs—heave, pitch, and surge—are significant, while the others primarily contain noise and relatively small values. To validate the accuracy and functionality of this state-space model, the KF was applied using known loads, with the initial state value assumed to be ${\widehat{\mathbf{x}}}_{0|0}=0$ and the state covariance ${\mathbf{P}}_{0|0}^{\mathbf{x}}=1\times {10}^{-20}$. The hyperparameters ${\mathbf{Q}}_{k-1}=1\times {10}^{-5}$ and $3.6\times {10}^{-5}\times {\mathbf{R}}_k$ are optimized via grid search optimization, where ${\mathbf{R}}_k$ is obtained from the System Identification Toolbox, and used for this analysis. The results for the first sea state reported in Figure 8 were compared with simulated results from OpenFAST [78], which demonstrated that the model is capable of output estimation of the quantities.

After confirming the performance of model, input–state estimation was performed using both AKF and UF (see Figure 9). For the first sea state, all six displacements, velocities, and accelerations were assumed to be known measurements. First, the hyperparameters of UF, such as ${\mathbf{Q}}_{k-1}=5\times {10}^{-5}$, were optimized using a grid search algorithm, and ${\mathbf{R}}_k$ was taken as the exact value extracted from the System Identification (SI) Toolbox. The initial conditions were set to ${\widehat{\mathbf{x}}}_{0|0}=0$ and ${\mathbf{P}}_{0|0}^{\mathbf{x}}=1\times {10}^{-30}$. The tolerance values for singular value decomposition (SVD) during the estimation were set to $1\times {10}^{-50}$ for the input and $1\times {10}^{-5}$ for the state.

The same process was applied to AKF; however, AKF required additional tuning of hyperparameters for the input in the process model, resulting in more parameters needing adjustment compared to UF. The optimized hyperparameters for AKF were ${\mathbf{Q}}_{\mathbf{x}}=2.34\times {10}^{-7}$ and ${\mathbf{Q}}_{\mathbf{p}}=1\times {10}^{13}$, and ${\mathbf{R}}_k$ was the same value as extracted from the SI Toolbox. The initial conditions for AKF were set to ${\widehat{\mathbf{x}}}_{0|0}=0$, ${\mathbf{P}}_{0|0}^{\mathbf{x}}=1\times {10}^{-20}$, and ${\mathbf{P}}_{k-1|0}^{\mathbf{p}}=1\times {10}^{10}$.

The estimated forces are shown in Figure 9. The left column of the figures presents the results from UF, while the right column displays the results from AKF. Both are compared with the simulated inputs extracted from OpenFAST [78]. The filters perform with nearly the same efficiency, which aligns with the findings of Ebrahimzadeh Hassanabadi’s study [156].

It was observed that when the excitation frequency and the first natural frequency of the structure are approximately close, both filters estimate the input with nearly the same accuracy (frequency is shown in Figure 10).

In Figure 11, the heave displacement, velocity, and acceleration are presented, and it is evident that UF performs slightly better than AKF in all the estimated heave DOF quantities. Although the differences are slight, they are not very noticeable. This is due to the assumption in AKF that inputs are fictitious, leading to less accurate input estimations, which, in turn, affects state estimation accuracy. Figure 12 for pitch response and Figure 13 for surge response show a similar pattern, with UF slightly outperforming AKF in the estimation of pitch and surge displacement, velocity, and acceleration.

Finally, it is necessary to evaluate the covariances. Figure 14 presents the covariances of inputs such as $F_{mx}$, $F_{mz}$, and $M_y$. It was observed that after approximately 1 s, the covariances converge to constant values for both UF and AKF. This convergence indicates that the input gain has reached its optimal value. Additionally, UF consistently exhibits lower covariance values compared to AKF, suggesting that input estimation is more accurate with UF. As discussed earlier, this study uses a fictitious state model, making it essential to check the convergence of state covariances. If convergence is achieved, the Kalman gain reaches its optimal value, indicating optimal state estimation. There are 10 fictitious states, so there are 10 corresponding covariances. However, for clarity, only the covariance of the first state is reported in Figure 15. The results show that convergence is reached after approximately 1 s, and the covariance from UF is significantly lower than that from AKF, further demonstrating that state estimation is more accurate with UF.

6.7. Limitations and Assumptions of the Case Study

While general challenges and limitations of FOWT DTs have been discussed in earlier sections, it is crucial to outline the specific assumptions and limitations pertinent to the AKF and UF applied in this proof-of-concept study.

The AKF operates under several key assumptions. It postulates a fictitious model for the unknown input, which is then augmented to the state vector. This approach necessitates specifying an initial estimated state (${\widehat{\mathbf{x}}}_{0|0}^{\mathbf{a}}$) and its error covariance (${\mathbf{P}}_{0|0}^{\mathbf{a}}$) for the augmented system, along with initial mean and error covariance values for the fictitious input at $t=0$. Like many filtering methods, AKF assumes that both modeling and measurement uncertainties adhere to a zero-mean white Gaussian noise distribution. Furthermore, hyperparameter tuning is required for the fictitious input model, as well as for the standard process and measurement noise covariances. Despite its capabilities, AKF faces several limitations. It performs optimally only if the feedthrough matrix is full rank or absent, and it can fail with rank-deficient feedthrough matrices, particularly when the number of unknown inputs exceeds the available acceleration measurement data. This can also lead to unobservability issues if measurements are limited or solely based on acceleration data. The reliance on a fictitious input model can add complexity and may not always accurately reflect real-world input dynamics, and the need to tune additional hyperparameters for this fictitious input can increase the computational burden.

In contrast, the UF offers a distinct approach since no assumptions are present on a specific model for the unknown input, which often represents a more realistic scenario for unmeasured loads. To initiate its recursive loop, UF primarily requires an initial estimated state (${\widehat{\mathbf{x}}}_{0|0}$) and its error covariance (${\mathbf{P}}_{0|0}^{\mathbf{x}}$). Its methodology is rooted in the minimum-variance principle for Kalman gain calculation, and the input gain is computed using the weighted least squares method. Similar to AKF, UF assumes modeling and measurement uncertainties to be zero-mean white Gaussian noise. However, one notable limitation of the UF is that hyperparameter tuning for the modeling and measurement uncertainties (${\mathbf{Q}}_k,{\mathbf{R}}_k$) is still required, which can pose a significant challenge in practical applications.

7. Conclusions

This review has explored the current landscape of digital twinning in the context of FOWTs with a particular focus on SHM, inverse modeling techniques, and filtering-based estimation strategies. While DT has made substantial progress in adjacent fields like manufacturing and onshore wind, its application to floating platforms remains in an emergent stage. The reviewed literature shows critical advancements in the use of KF-variants, unscented filters, and machine learning-enhanced models, but practical implementation is still limited by challenges in sensor deployment, environmental variability, and real-time model updating.

A key insight from this review is the increased emphasis on probabilistic, real-time monitoring frameworks, particularly those that allow joint state and input estimation without full knowledge of environmental forcing. The shift from purely physics-based modeling toward hybrid approaches (integration of reduced-order models, data-driven filters, and adaptive control strategies) reflects the field’s push toward real-world deployability. Kalman-type filters remain dominant, but their limitations have motivated the development of more frameworks such as minimum-variance unbiased filters, smoothing algorithms, and OMA methods.

Across structural components (i.e., towers, mooring systems, drivetrain subsystems, and blades) DTs show strong potential to reduce operational costs, extend service life, and improve safety. However, the lack of standardization, sensor interoperability, and validation against full-scale systems remains a significant barrier. Most implementations to date have relied on simulations, scaled lab models, or isolated case studies. There is a pressing need for more integrated, system-level demonstrations of DT in the field, especially under variable sea states and sensor degradation scenarios.

This review also identified a gap in holistic system integration. Few studies connect component-level twins to a full floating platform, and even fewer include real-time control or predictive maintenance in the loop.

Furthermore, while filtering algorithms are well-documented in academic studies, practical deployment under communication delays, power constraints, and harsh offshore conditions is rarely addressed in depth.

In conclusion, DTs hold immense promise for how FOWTs are monitored, maintained and controlled. However, this will require not just algorithmic innovation, but also thoughtful integration with sensing hardware, regulatory standards, and real-world constraints. This review aims to serve as a foundation and catalyst for that next stage of research.

8. Future Directions

As digital twinning for FOWTs evolves, several technical and implementation barriers remain. Future work should address both foundational challenges and emerging opportunities. The following key directions are identified:

8.1. Experimental Validation

Laboratory Testing: Controlled lab-scale experiments allow detailed investigation of coupled dynamic responses. However, their scalability is limited due to challenges in the creation of the combined effects of wind, wave, and current loading, along with known scaling law inconsistencies. Future efforts should focus on enhanced hybrid modeling frameworks that combine experimental and numerical data to improve transferability.

Field-Scale Validation: Real-world testing provides unmatched insights into environmental complexity but comes with high logistical and financial burdens. Sensor maintenance, data quality, and harsh conditions are major constraints. There is a pressing need for demonstration-scale projects to validate DT frameworks under realistic offshore scenarios.

8.2. Model Development and Integration

Real-Time Physics-Based DTs: Physics-based DTs are critical for the dynamic analysis of FOWT behavior and SHM. However, high-fidelity models are often too computationally expensive for real-time use. Future research should focus on model reduction, efficient solvers, and adaptive fidelity approaches that maintain accuracy without reduced speed.

Supervised and Physics-Informed Machine Learning: Supervised ML models support applications like anomaly detection and fatigue life estimation but require large, high-quality labeled datasets—difficult to obtain in offshore settings. Physics-informed ML (PIML) can address data scarcity since physical constraints will be embedded into learning processes. Research should explore hybrid architectures to improve reliability under sparse or noisy data conditions.

8.3. Key Technical Challenges

Digital Twinning under Uncertainty: The accurate representation of wind and wave conditions is a persistent challenge. Approaches that infer or estimate unknown environmental loads (i.e., advanced filtering, smoothing, or inverse modeling techniques) must be developed further.

Modeling Errors and Drift: Discrepancies between the DT and PT are inevitable due to modeling simplifications, parameter drift, or degradation. Adaptive filters and ensemble modeling strategies can help mitigate these errors, but improved correction algorithms remain an open research area.

Sparse Sensor Networks: Cost and practical limitations often lead to sparse instrumentation on FOWTs. This restricts observability and hinders DT accuracy. New work is needed in data fusion, virtual sensing, and time-series reconstruction methods (e.g., LSTM networks) to reconstruct missing states and inputs.

Scalability for Large Farms: Most DT frameworks are developed at the individual turbine level. Scaling up to entire floating wind farms introduces challenges in data handling, coordination, and computational cost. Modular, distributed, and edge-based DT architectures may help address this.

8.4. System-Level Opportunities

End-to-End DT Architectures: Future systems should integrate sensing, filtering, control, and lifecycle forecasting into a unified DT pipeline. Modular and interoperable frameworks will allow adaptation to varying turbine designs and environmental conditions.

Lifecycle Applications: Beyond operations and maintenance, DTs offer value in repowering, regulatory certification, and end-of-life decisions. Standardizing DT-supported life extension methodologies could unlock long-term cost savings.

Benchmarking and Method Comparison: While KFs are widely used, the systematic benchmarking of estimation techniques—including particle filters, smoothing, and deep learning models—is lacking. Public datasets and shared test cases would facilitate this.

8.5. Strategic Research Priorities

In light of these observations, future research should prioritize the following:

• Field-scale validation of digital twinning frameworks for FOWTs, especially for state/input estimation under uncertain external loads.
• Robust sensor fusion techniques that can operate under intermittent connectivity or sensor failure.
• Standardized benchmarking datasets and protocols to evaluate and compare filtering methods in offshore environments.
• Cross-disciplinary collaboration among civil, electrical, and control engineers to work on system-level DT design from the outset.

Future research focus on these areas will accelerate the practical deployment of DTs in floating wind and ensure that the field moves beyond theoretical frameworks into fully functional offshore systems. Collaboration across academia, industry, and regulatory bodies will be essential to achieving scalable, cost-effective solutions.