Abstract
Improving the energy efficiency of buildings is a critical pathway in mitigating greenhouse gas emissions and fostering sustainable urban development. This study introduces a simulation-based multi-objective optimization framework designed to enhance both the thermal and economic performance of residential buildings. A representative single-family dwelling located in Patras, Greece, served as a case study to demonstrate the application and scalability of the proposed methodology. The optimization simultaneously minimized two conflicting objectives: the building’s annual thermal energy demand and the cost of construction materials. The computational process was implemented using MATLAB’s Multi-Objective Genetic Algorithm, supported by a modular Excel interface that enables the dynamic customization of design parameters and climatic inputs. A parametric analysis across four optimization scenarios was conducted by systematically varying the key algorithmic hyperparameters—population size, mutation rate, and number of generations—to assess their impact on convergence behavior, Pareto front resolution, and solution diversity. The results confirmed the algorithm’s robustness in producing technically feasible and non-dominated solutions, while also highlighting the sensitivity of optimization outcomes to hyperparameter tuning. The proposed framework is a flexible, reproducible, and computationally tractable approach to supporting early-stage, performance-driven building design under realistic constraints.
1. Introduction
The building and construction sector accounts for approximately 40% of global primary energy consumption and over 30% of total greenhouse gas (GHG) emissions, positioning it as a key contributor to climate change and the urban heat island effect [1,2]. In response, considerable effort has been directed toward developing strategies that reduce operational energy demands while addressing the broader environmental and thermal challenges of urbanization. These strategies range from passive design interventions—such as thermal insulation, natural ventilation, and solar shading—to advanced solutions incorporating renewable energy systems, cool and phase-change materials, and hybrid control mechanisms [3,4,5,6,7,8,9,10].
A central driver of these advancements is the integration of computational tools for simulating and optimizing building energy performance. Physics-based simulation models enable detailed thermal analysis by incorporating envelope characteristics, occupancy schedules, and site-specific climatic conditions [11,12,13,14,15]. When combined with optimization algorithms, these models support the systematic evaluation of design alternatives across multiple, often conflicting objectives. Concurrently, machine learning (ML) techniques have emerged as powerful data-driven tools for pattern recognition, energy forecasting, and system control. Supervised, unsupervised, and reinforcement learning methods offer capabilities for adaptive control, anomaly detection, and demand prediction with increasing accuracy and autonomy [16,17,18,19,20,21,22]. Together, simulation and ML-based frameworks facilitate robust, dynamic, and intelligent building energy management, accounting for environmental, behavioral, and operational complexities [23,24,25,26].
Optimization frameworks in this domain commonly target objectives such as minimizing energy consumption, reducing costs, and mitigating environmental impacts, while satisfying thermal comfort requirements and regulatory constraints. Design variables often span envelope configuration, insulation levels, glazing ratios, HVAC operational parameters, and material choices [27,28]. These frameworks serve as essential tools for navigating tradeoffs among energy efficiency, economic viability, and occupant comfort, supporting data-informed, performance-driven design decisions [29].
This study aimed to evaluate the effectiveness of a simulation-based multi-objective optimization framework for improving both the energy and economic performance of residential buildings, using a single-family dwelling in Patras, Greece, as a case study. Building on the review presented in Section 2, this study focused on minimizing two conflicting objective functions—the annual thermal energy demand and construction material cost—under realistic climatic and architectural constraints. The proposed approach integrates MATLAB’s [30] Multi-Objective Genetic Algorithm into a modular Excel version 16.0 interface, enabling dynamic scenario generation and scalability for diverse use cases. A key aspect of the investigation is the sensitivity analysis of optimization hyperparameters, specifically, the population size, number of generations, and mutation rate, with respect to their influence on the convergence quality and Pareto front resolution. The overarching objective is to provide a reproducible, adaptable framework that supports informed design decision-making in the early stages of residential project development.
The novelty of this work lies in its structured application of a flexible simulation–optimization platform, capable of accommodating diverse design inputs and boundary conditions through a modular Excel–MATLAB version R2022 interface. Unlike many conventional studies limited by static configurations or narrow performance criteria, this study explores the influence of varying hyperparameter settings on the quality of optimization results. This enables a deeper understanding of how algorithmic configurations shape solution space coverage and Pareto front quality. The methodological flexibility ensures that the approach can be readily adapted for different building typologies, climates, and performance objectives. By bridging algorithmic precision and practical design workflows, this study advances the integration of optimization techniques into real-world building design processes.
This paper is structured as follows: Section 2 presents a comprehensive review of simulation-based optimization techniques in energy-efficient building design. Section 3 details the methodological framework, including the case study context, model setup, definition of objectives and design parameters, and optimization implementation. Section 4 reports and discusses the optimization results, with particular attention given to the influence of hyperparameter settings on solution quality and decision-support potential. Finally, Section 5 concludes the paper with a summary of key findings and recommendations for further research.
2. Simulation-Based Approaches to Multi-Objective Energy Optimization in Buildings
The ongoing effort to lower energy consumption in buildings has been significantly aided by advancements in Building Performance Simulation (BPS) tools. These tools simulate the complex time-dependent behavior of building systems and have played a key role in enabling energy-conscious design, enhancing indoor comfort conditions, and supporting the adoption of sustainable construction strategies. With improvements in computational capabilities and the emergence of sophisticated optimization algorithms, the field has transitioned from simple parametric studies to fully integrated simulation–optimization environments. Such environments combine simulation platforms with advanced search techniques, promoting a more structured and data-informed approach to designing high-performance buildings.
Traditional approaches to evaluating building performance often utilize parametric analyses, which involve varying a single input parameter at a time to observe its individual effect. While these studies have provided initial guidance, they are limited by assumptions of linearity, an inability to reflect interactions between multiple parameters, and a lack of computational efficiency. Critically, they rarely identify truly optimal configurations. In response to these shortcomings, Simulation-Based Optimization (SBO) techniques have emerged as a more robust alternative. SBO methods combine simulation tools—such as EnergyPlus [31] or TRNSYS [32]—with optimization algorithms that iteratively search for superior design solutions. This integration supports the resolution of complex, multi-objective design problems, where tradeoffs must be made between energy use, occupant comfort, environmental performance, and cost considerations [33,34,35].
2.1. Classification of Simulation-Based Optimization Methods
SBO methods comprise a wide array of algorithmic methods, which can be classified according to their approach to navigating the search space and managing problem constraints. The choice of a suitable optimization technique is largely dictated by the specific features of the problem at hand—such as the number of decision variables, the type of variables involved (e.g., continuous, discrete, or hybrid), and the mathematical properties of the objective functions, including whether they are linear or non-linear, convex or non-convex [11,36,37,38,39].
Deterministic optimization techniques—such as Linear Programming (LP), Non-Linear Programming (NLP), and Integer Programming (IP)—use formal mathematical models to derive optimal solutions [40,41,42,43]. These methods are typically efficient and well-suited to problems with convex structures and clearly defined constraints. However, their applicability in practical building design is limited, as real-world scenarios often involve non-linear behavior, intricate constraints, and a mix of continuous and discrete variables.
Metaheuristic and evolutionary algorithms—including Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), Simulated Annealing (SA), and Ant Colony Optimization (ACO)—have demonstrated strong performance in the context of building design optimization [44,45,46,47,48]. Drawing inspiration from natural and biological systems, these approaches are particularly effective in exploring large, complex search spaces with multiple local optima. Unlike gradient-based methods, they do not require derivative information, which makes them well-suited to non-linear problems. Their ability to escape local minima is especially beneficial in optimizing various building parameters, such as thermal insulation, HVAC configurations, lighting strategies, and occupancy-related controls.
Gradient-based methods, such as gradient descent and conjugate gradient methods, utilize derivative information to guide the search toward optimal solutions [16,17,49]. While these algorithms are generally efficient when applied to smooth and continuously differentiable problems, their effectiveness is often limited in building optimization contexts [36,40]. This is due to challenges like entrapment in local optima and high sensitivity to initial parameter values, which are common due to the highly non-linear nature of building energy models.
Stochastic and direct-search techniques—including dynamic programming, tabu search, and pattern search—investigate the solution space using probabilistic strategies or predefined heuristic rules [18,19,20,21]. These approaches are known for their robustness and simplicity in implementation [50]. However, they often demand significant computational resources, particularly when applied to large-scale optimization problems involving multiple interrelated objectives.
Among the various optimization approaches, multi-objective evolutionary algorithms—especially the Non-Dominated Sorting Genetic Algorithm II (NSGA-II)—have gained widespread adoption in building performance studies [36,51]. Their strength lies in generating Pareto-optimal solution sets, which enable designers to assess tradeoffs between conflicting objectives, such as minimizing energy consumption while maintaining thermal comfort, without committing to a single optimal outcome [36,44,47].
2.2. Integration of Simulation and Optimization: Methods and Applications
SBO methods for building performance typically rely on two fundamental components: (a) a dynamic simulation tool capable of accurately modeling building behavior across various design alternatives and (b) an optimization algorithm that systematically explores possible configurations to identify those that satisfy predefined performance criteria.
The combined use of simulation and optimization facilitates informed decision-making during both the early design phase and building retrofit processes. It enables a thorough investigation of the design space across a wide range of applications, including the optimization of the building envelope, HVAC systems, daylight utilization, spatial layout, and construction material choices [25,26,52]. Common design variables targeted in optimization studies include the building geometry, insulation levels, glazing characteristics, window-to-wall ratios, HVAC operating parameters, and passive design elements like shading devices or thermal mass [29,53,54]. The performance criteria, or objective functions, often focus on indicators such as the annual energy use, thermal comfort (e.g., PMV, hours of discomfort), Life-Cycle Cost (LCC), and carbon dioxide (CO2) emissions—or a weighted combination of these. In multi-objective settings, Pareto-based methods such as NSGA-II are widely used to explore tradeoffs among competing goals and provide a range of balanced solutions [12,44,47,55].
SBO has seen extensive application in both newly constructed and existing buildings, consistently contributing to enhanced energy efficiency, occupant comfort, and reduced environmental impacts. Empirical research emphasizes the critical role of the building envelope—especially insulation and glazing—in determining thermal performance [22,24,25]. Additionally, SBO approaches provide valuable guidance in selecting design solutions that align with budgetary limits, regulatory requirements, and broader sustainability objectives.
Although SBO methods have demonstrated considerable effectiveness, they are not without limitations. One of the primary challenges is the high computational cost associated with coupling dynamic simulations with sophisticated optimization algorithms. Additional difficulties arise from modeling uncertainties, the variability of occupant behavior, and the need to simplify real-world complexities for practical implementation [53,56,57]. As a result, achieving a balance between model accuracy and usability often requires the careful selection and limitation of the design parameters included in the analysis. Despite these challenges, a broad body of literature affirms that SBO serves as a powerful tool for performance-orientated building design. When applied appropriately, it allows architects, engineers, and decision-makers to uncover optimal or near-optimal solutions that successfully balance energy efficiency, occupant comfort, cost considerations, and environmental impact [55,57,58,59].
2.3. Real-World Case Studies
Simulation-based optimization has been widely applied in real-world building design and retrofit scenarios, providing a structured approach to enhancing energy efficiency, minimizing life-cycle costs, and improving indoor environmental quality. Numerous case studies have demonstrated the effective integration of building performance simulation tools—such as EnergyPlus, TRNSYS, or bespoke thermal models—into optimization algorithms, particularly evolutionary and multi-objective techniques like Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), and their hybrid variants [10,58,60,61,62,63,64,65].
Across diverse climates and building types, studies commonly target variables such as the envelope composition, insulation thickness, window characteristics, and HVAC system parameters. Objective functions frequently include energy consumption, thermal comfort metrics (e.g., PMV, discomfort hours), life-cycle cost (LCC), environmental impact indicators (e.g., CO2 emissions), and visual comfort, often framed in multi-objective contexts using Pareto-based methods [57,58,64,65,66,67,68]. Reported outcomes demonstrate energy savings ranging from 20% to 70% and LCC reductions of up to 25%, with payback periods between 2 and 5 years depending on the climatic and economic context [64,69,70].
For instance, in [58], an NSGA-II approach was applied to optimize energy use, cost, and environmental impact for school buildings in France, achieving well-distributed Pareto fronts across four objectives. Similarly, in [62,71], GA-based multi-objective models were used to optimize envelope components in Canadian buildings, showing the effectiveness of the method in identifying low-cost, low-energy solutions. Studies in Turkey [69,70] explored insulation thickness optimization under varying fuel prices and climates, demonstrating substantial savings in heating demand and short payback times.
Despite their effectiveness, these simulation-based frameworks often face practical challenges: high computational demand, complex model configuration, and sensitivity to algorithmic settings [53,65,72]. Moreover, many approaches rely on fixed configurations or static design assumptions, limiting their flexibility for iterative, early-stage design exploration.
In this context, the current study contributes a novel, lightweight optimization framework that integrates MATLAB’s NSGA-II algorithm into a modular Excel interface. This structure allows for the rapid prototyping and user-friendly customization of design parameters, enabling practitioners to test multiple envelope-material configurations and assess performance tradeoffs. Furthermore, unlike most existing studies, this research explicitly evaluates the influence of hyperparameter tuning—such as population size, mutation rate, and generation count—on solution quality and convergence behavior. This sensitivity analysis offers insights into the stability and adaptability of the optimization framework and enhances its relevance for early-phase residential design under realistic constraints.
3. Methodology
This section describes the methodological approach adopted to evaluate how simulation-based multi-objective optimization can improve both energy efficiency and construction cost in residential buildings. A real-world case study involving a detached single-family house located in Patras, Greece, is used to demonstrate the combined use of climatic data, detailed building parameters, optimization modeling, and computational tools.
3.1. Climatic Context and Building Description
The residential building examined in this study is located in the city of Patras, western Greece (38.25° N latitude, 21.73° E longitude), with elevations ranging from 0 to 100 m above sea level. According to the Köppen–Geiger classification, Patras falls within the climatic zone, characterized by hot, dry summers and mild, wet winters.
To support accurate energy modeling, particularly heating demand estimation, the study uses long-term climatic data in the form of Heating Degree Days (HDD), provided by the National Observatory of Athens (NOA) [73].
HDD is a well-established climatic indicator used to estimate space-heating requirements. It is defined as the cumulative sum of the differences between a base outdoor temperature (typically 18 °C) and the mean daily outdoor temperature for each day when the latter is lower than the base. HDD can be expressed as follows [74].
where is the base (reference) indoor temperature [°C], usually 18 °C, is the average outdoor air temperature on the day i, N is the total number of days in the month, and (+) denotes the positive part of the function ensuring that only days when < contribute to the HDD total.
The dataset includes monthly values for the period from 2010 to 2021, calculated with a base indoor temperature of 18 °C. Table 1 summarizes the monthly HDD values for Patras, totaling 766 HDD annually [75].

Table 1.
Monthly Heating Degree Days (HDD) for Patras (2010–2021).
Although the climate of Patras is characterized by hot summers in addition to mild winters, the current study focuses solely on the heating period and thus only considers Heating Degree Days (HDD) in the energy demand calculation. Cooling Degree Days (CDD), which quantify the need for air conditioning to maintain indoor thermal comfort during warm periods, are equally important for accurately estimating annual energy performance in Mediterranean climates. However, the exclusion of CDD from this study is a deliberate simplification aimed at reducing the model complexity and computational load, given the scope of the optimization framework and the focus on winter thermal performance and construction cost trade-offs.
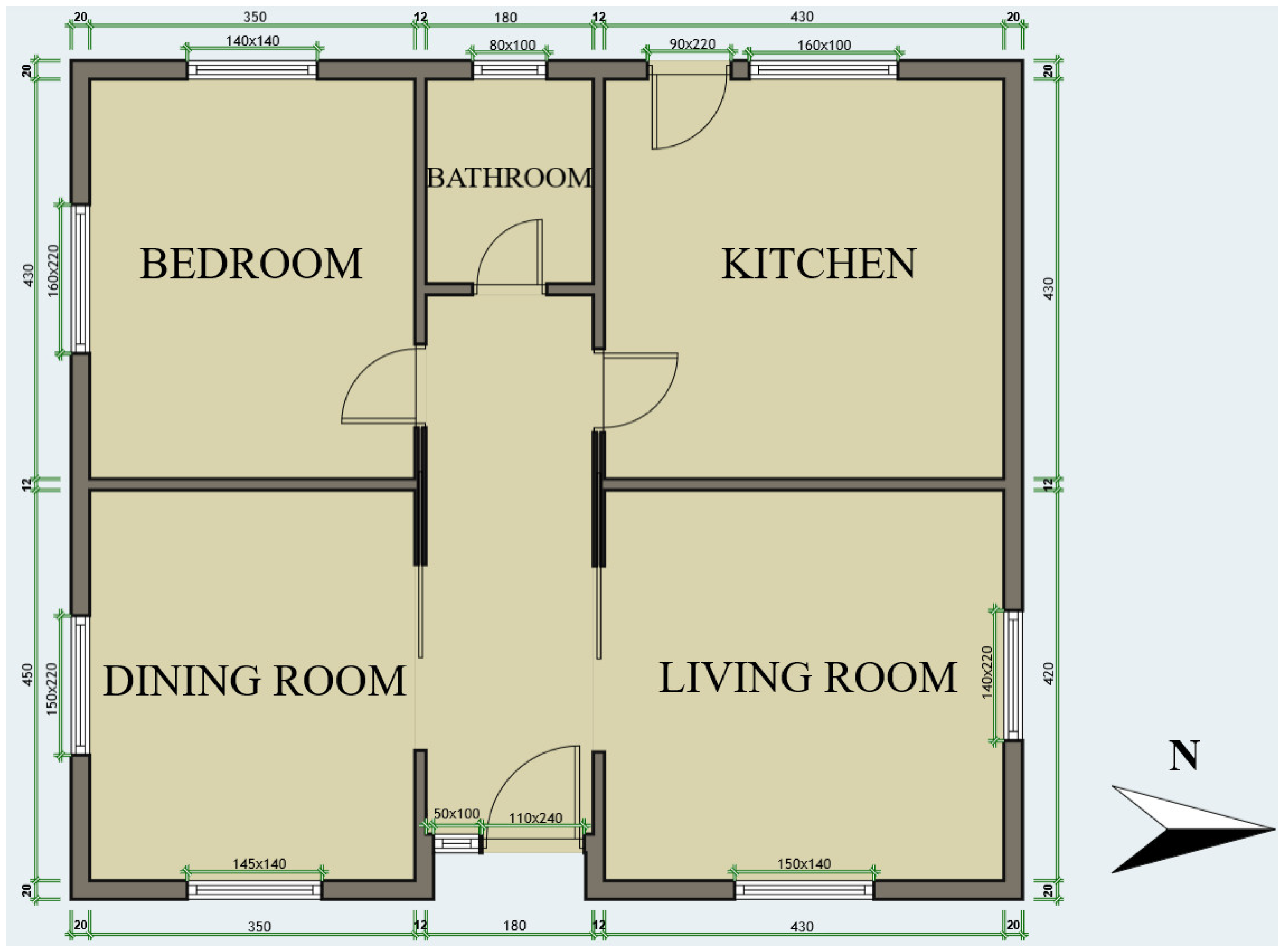
The building under analysis is a single-story, detached residential unit representative of low-rise housing in Greece. It includes five functional spaces: the kitchen, living room, dining area, bedroom, and bathroom (Figure 1). Each space is naturally ventilated and illuminated, and the structure has two external doors. The internal ceiling height is uniformly 2.75 m. Geometric modeling was carried out using simplified envelope data. Table 2 provides the surface areas of the building’s elements.

Figure 1.
Architectural floor plan of the single-family residential building used as the case study, including spatial layout and zoning relevant to thermal performance evaluation.

Table 2.
Surface areas of building elements.
3.2. Optimization Framework
An SBO framework was employed to simultaneously reduce the energy consumption and material costs. The optimization was conducted in MATLAB using the Global Optimization Toolbox, specifically through the gamultiobj function. This function implements a Multi-Objective Genetic Algorithm (MOGA), which is well-suited for addressing continuous, non-linear, and multi-modal optimization problems. The algorithm progresses by evolving a population of candidate solutions using genetic operators such as selection, crossover, mutation, and elitism. Critical parameters—including the number of individuals per generation, total generations, and mutation probability—are specified by the user.
In this study, typical settings involved 100 to 150 individuals per generation across 50 to 75 generations, with mutation rates ranging from 0.03 to 0.05. The result is a Pareto front that illustrates the tradeoffs among competing design objectives. For greater flexibility and ease of use, the optimization algorithm was integrated with a modular Microsoft Excel interface. This linkage enables users to modify input parameters—such as design variables, material specifications, and building features—without directly editing the MATLAB source code.
3.2.1. Objective Functions
The optimization targets two competing objectives: (1) minimizing the building’s annual thermal energy demand and (2) reducing the cost of construction materials.
The first objective function, denoted as and expressed in kWh/year, represents the heating energy required to maintain indoor thermal comfort. It is influenced by the thermal properties of the building envelope and the prevailing climatic conditions at the building location. The thermal demand () values are estimated using HDD data and the overall thermal transmittance of the building, represented by a weighted-average U-value (), along with adjustment factors accounting for orientation, building height, and heating duration. The calculation is based on a simplified steady-state heat transfer model based that employes the HDD concept to approximate the cumulative temperature difference between indoor and outdoor environmental conditions over the heating season [74]. The thermal demand () is thus calculated as a function of geometrical and operational factors affecting heat losses [73,74]:
where HDD is the annual heating degree days, is the weighted-average U value of the entire building envelope, is the total surface area of the building, accounts for heat losses due to infiltration and ventilation, and , , and are adjustment multipliers for orientation, heating duration, and height.
The second objective function is the material cost of construction (in €), which represents the total cost of key building components such as insulation, glazing, and wall assemblies. The construction material cost, denoted as (in €), can be expressed as follows [73]:
represents the cost of the building’s foundations, as well as the beams and columns of the structure, assuming that they are made of reinforced concrete. For simplification, this cost is assumed to be fifteen thousand euros (EUR 15,000), which is considered reasonable for a residential building with a living area of around 80 m2. Among the other symbols, is the specific cost of the roof (in EUR/m2), is the specific cost of the floor (in EUR/m2), is the specific cost of the walls (in EUR/m2), is the area of the internal walls (included to account for the total material cost), is the specific cost of the insulation applied to the building (in EUR/m2), is the cost of the doors, and is the specific cost of the windows (in EUR/m2). Finally, is the total insulated area (in m2), including the exterior walls, the roof and the floor:
Equation (2) is based on a bottom–up construction cost estimation approach, widely used in early-stage building design and life-cycle cost analyses [29,73].
Additional construction expenses—such as labor, permits, and administrative costs—were excluded from the analysis due to their significant regional variability and lack of standardization. The selected objectives reflect key priorities in the early design phase of residential buildings, where tradeoffs between energy performance and financial feasibility must be carefully balanced. Reducing thermal energy demand supports environmentally sustainable design and enhances indoor comfort, while limiting material costs is essential in ensuring that energy-efficient solutions remain both economically viable and broadly implementable.
3.2.2. Design Variables
The optimization process considers twelve design variables that characterize both the thermal performance and material costs of the building envelope. These variables are grouped into two main categories: (a) U-values, representing the thermal transmittance of the roof, floor, external walls, windows, doors, and insulation layers, and (b) unit costs of materials for building surfaces (in EUR/m2) and doors (in EUR/unit).
Each material complies with standardized thermal performance values defined by the Technical Chamber of Greece, ensuring alignment with national building energy regulations. Cost data were collected from regional suppliers in Patras, with the flexibility to adapt the dataset for alternative scenarios. To maintain consistency, each thermal transmittance value is directly linked to a corresponding material cost. Combinations deemed unrealistic or non-compliant are penalized during the optimization run. The material palette includes various types of insulation—such as EPS, XPS, GEPS, mineral wool, and polyurethane—as well as variations in wall assemblies, glazing systems, and structural components for floors, roofs, and doors.
Table 3 summarizes the set of design variables used in the multi-objective optimization, along with their respective symbols, units, and descriptions.

Table 3.
Summary of the design variables used in the optimization process, including thermal transmittance (U-values) and associated material costs for various envelope components. Each variable is defined by its symbol, its unit, and a brief description.
4. Results and Discussion
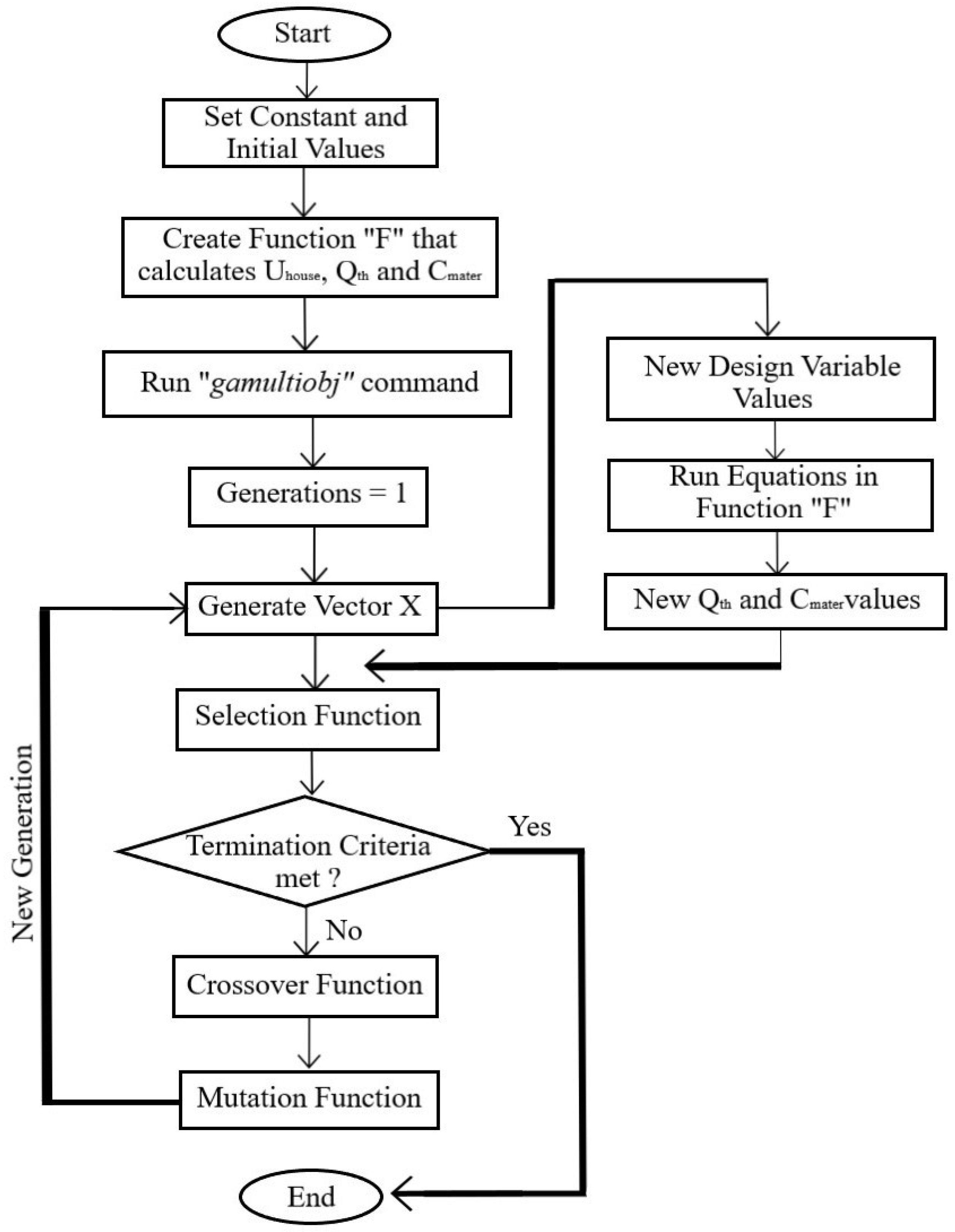
This section presents a critical evaluation of the results obtained from the simulation-based multi-objective optimization framework, aiming to assess the effectiveness of the MATLAB-based algorithm in navigating the design space and identifying robust Pareto-optimal solutions. An emphasis is placed on the influence of key algorithmic hyperparameters—namely, population size, maximum number of generations, and mutation rate—on convergence dynamics, the diversity of solutions, and the resolution of the Pareto front. Figure 2 presents the flow chart of the optimization process for this case study.
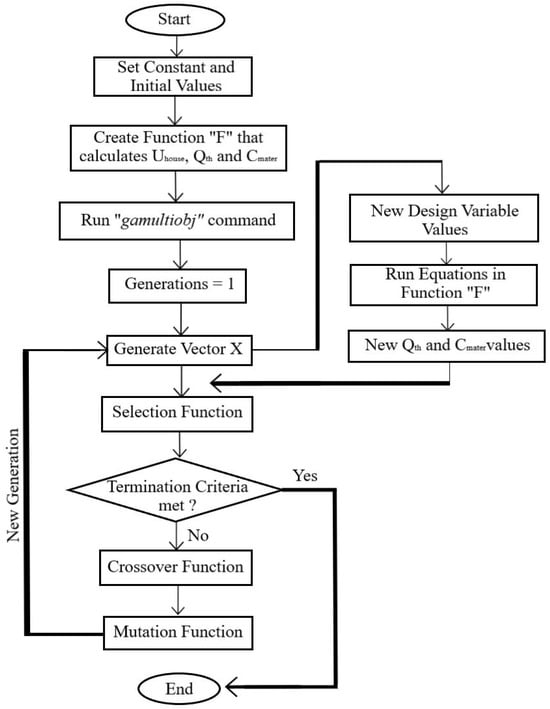
Figure 2.
Schematic flowchart of the simulation-based multi-objective optimization process.
To enable a systematic analysis, four optimization scenarios were executed, each defined by a distinct configuration of the hyperparameters. In each scenario, only one parameter was varied at a time, thereby isolating and enabling the evaluation of its specific impact on the behavior and efficiency of the optimization process.
The specific values assigned in each scenario are summarized in Table 4.

Table 4.
Hyperparameter values for each scenario.
The performance of the optimization process is assessed by analyzing the structure of the Pareto front and the density of solution points across the objective space. In multi-objective optimization, a well-formed Pareto front is typically smooth and continuous, allowing for the identification of high-quality, non-dominated solutions. Discontinuities, jagged edges, or sparsely populated regions may indicate inadequate convergence or limited search space exploration.
The optimization outcomes are illustrated through a series of comparative diagrams, each representing the tradeoff landscape between the two conflicting objectives: the annual thermal energy demand and construction material cost. The shape, density, and continuity of the Pareto front are employed as qualitative indicators of the algorithm’s exploratory capacity and optimization performance.
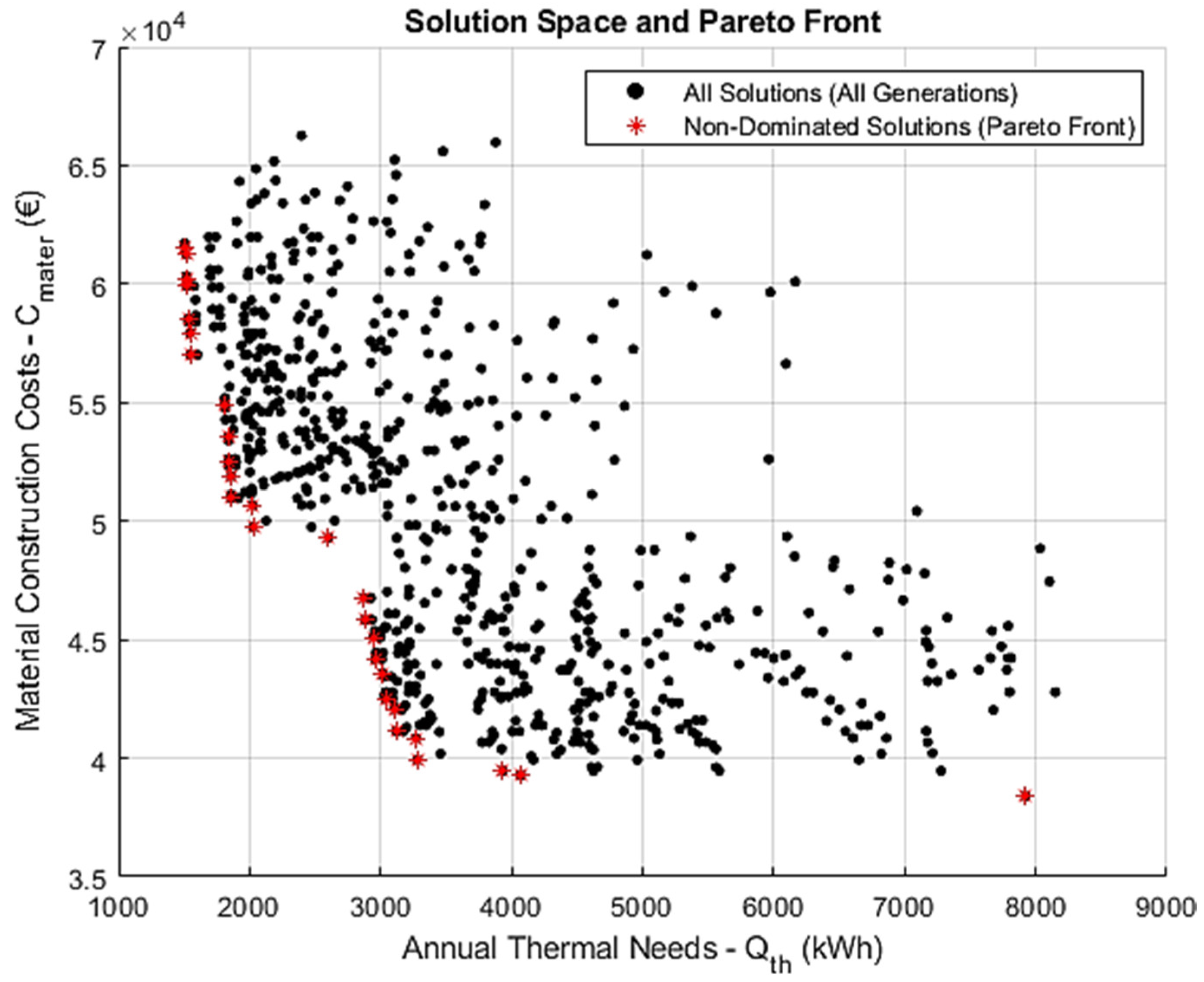
In Scenario 1 (Figure 3), which corresponds to the lowest-resolution configuration—comprising a population size of 100, a maximum of 50 generations, and a relatively high mutation rate of 0.10—the algorithm successfully generates a broad set of feasible solutions. Nonetheless, the resulting Pareto front displays discernible discontinuities along both objective axes (i.e., material cost and annual thermal energy demand), indicating the incomplete exploration of the design space. Despite these irregularities, the Pareto front generally preserves the expected concave (hyperbolic) profile characteristic of bi-objective optimization problems.
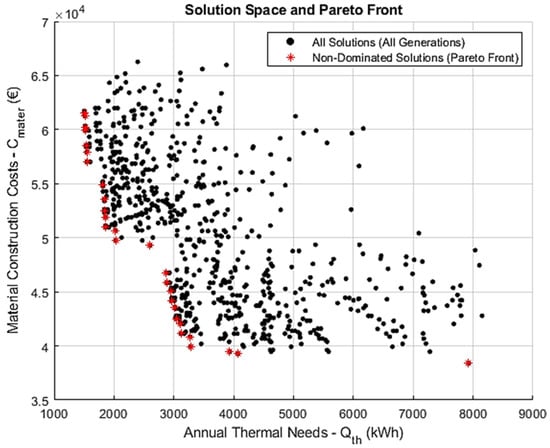
Figure 3.
Pareto front and solution space for Scenario 1, using 50 generations, a population size of 100, and a mutation rate of 0.1. The sparse distribution and limited front coverage reflect suboptimal diversity and search performance.
The distribution of objective function values remains within technically acceptable bounds, affirming the basic validity of the optimization process under this minimal configuration.
However, the observed gaps and uneven density of solutions emphasize the sensitivity of the algorithm’s performance to hyperparameter selection—particularly the role of the mutation rate and computational budget in achieving adequate search space coverage.
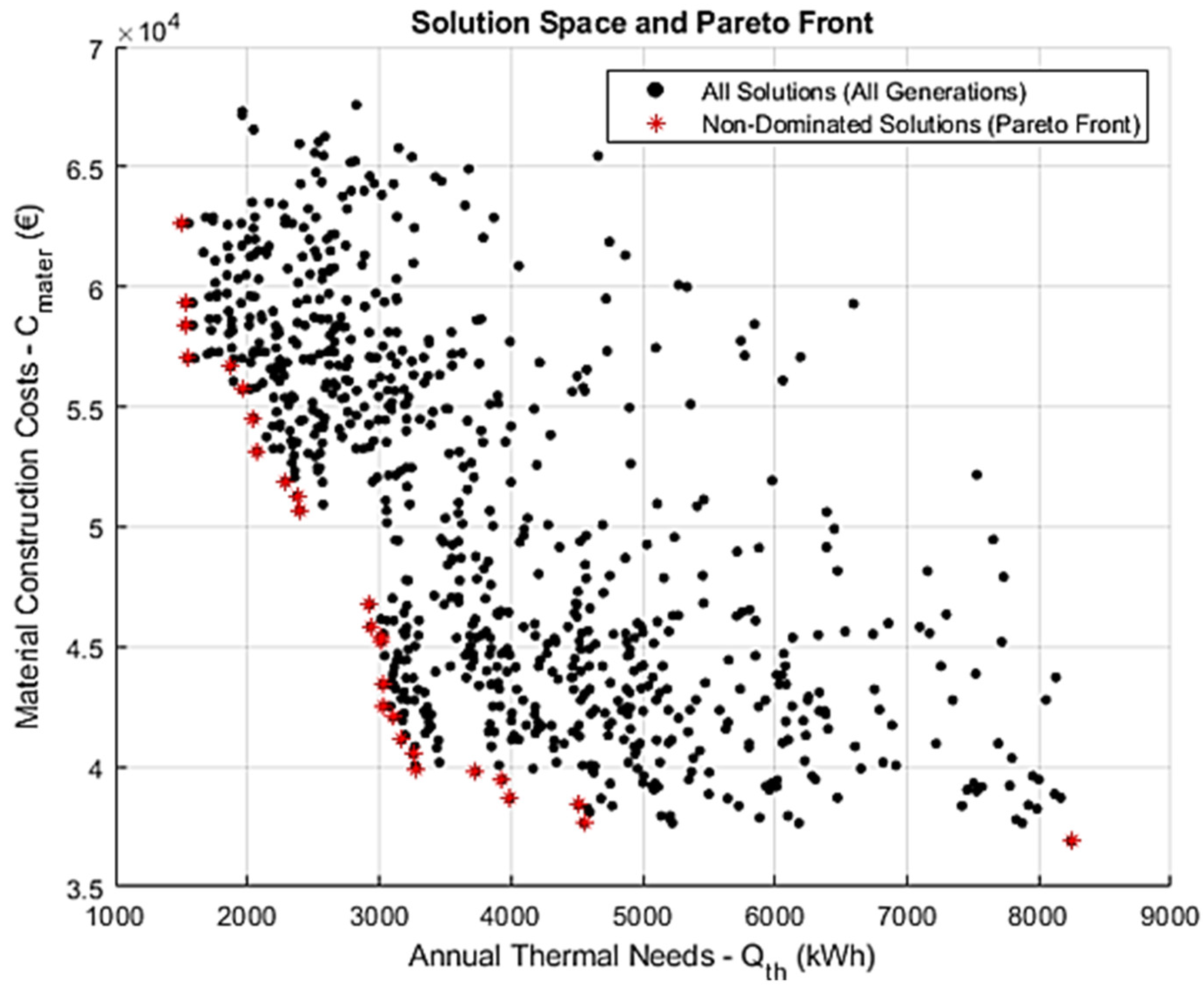
Scenario 2 investigates the effect of reducing the mutation rate from 0.10 to 0.04 while keeping the population size and number of generations constant at 100 and 50, respectively. This lower mutation rate constrains the magnitude of variation introduced between generations, resulting in smaller incremental changes within the design variable space. While such fine-tuning is generally conducive to improved accuracy, it also slows the algorithm’s capacity to explore the solution space effectively.
The resulting diagram (Figure 4) bears a superficial resemblance to that of Scenario 1; however, a more detailed examination reveals a more jagged and fragmented Pareto front, along with a sparser distribution of solutions across the objective space.
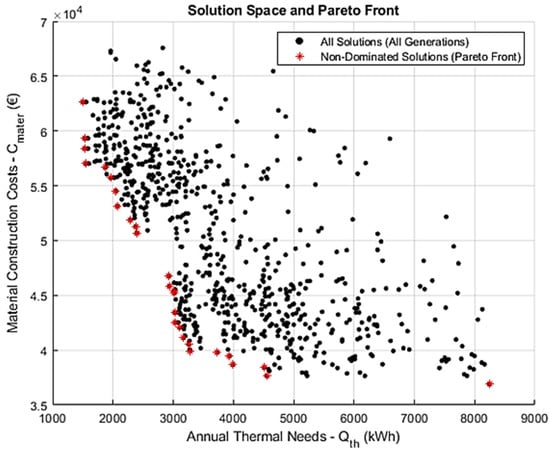
Figure 4.
Pareto front and solution space for Scenario 2, with 50 generations, a population size of 100, and a reduced mutation rate of 0.04. Improved solution clustering and front continuity indicate enhanced search stability.
These patterns point to diminished search space coverage and reduced convergence performance under the current computational constraints. Importantly, the observed limitations are not solely attributable to the lower mutation rate.
Rather, the effectiveness of a reduced mutation rate typically relies on extended search efforts—namely, an increased number of generations and/or larger population sizes—to counterbalance the slower evolutionary dynamics.
In this configuration, the restricted number of generations impeded the algorithm’s ability to fully leverage the benefits of a more conservative mutation strategy. Consequently, Scenario 2 illustrates the inherent tradeoff between the search precision and convergence rate when calibrating mutation-related hyperparameters.
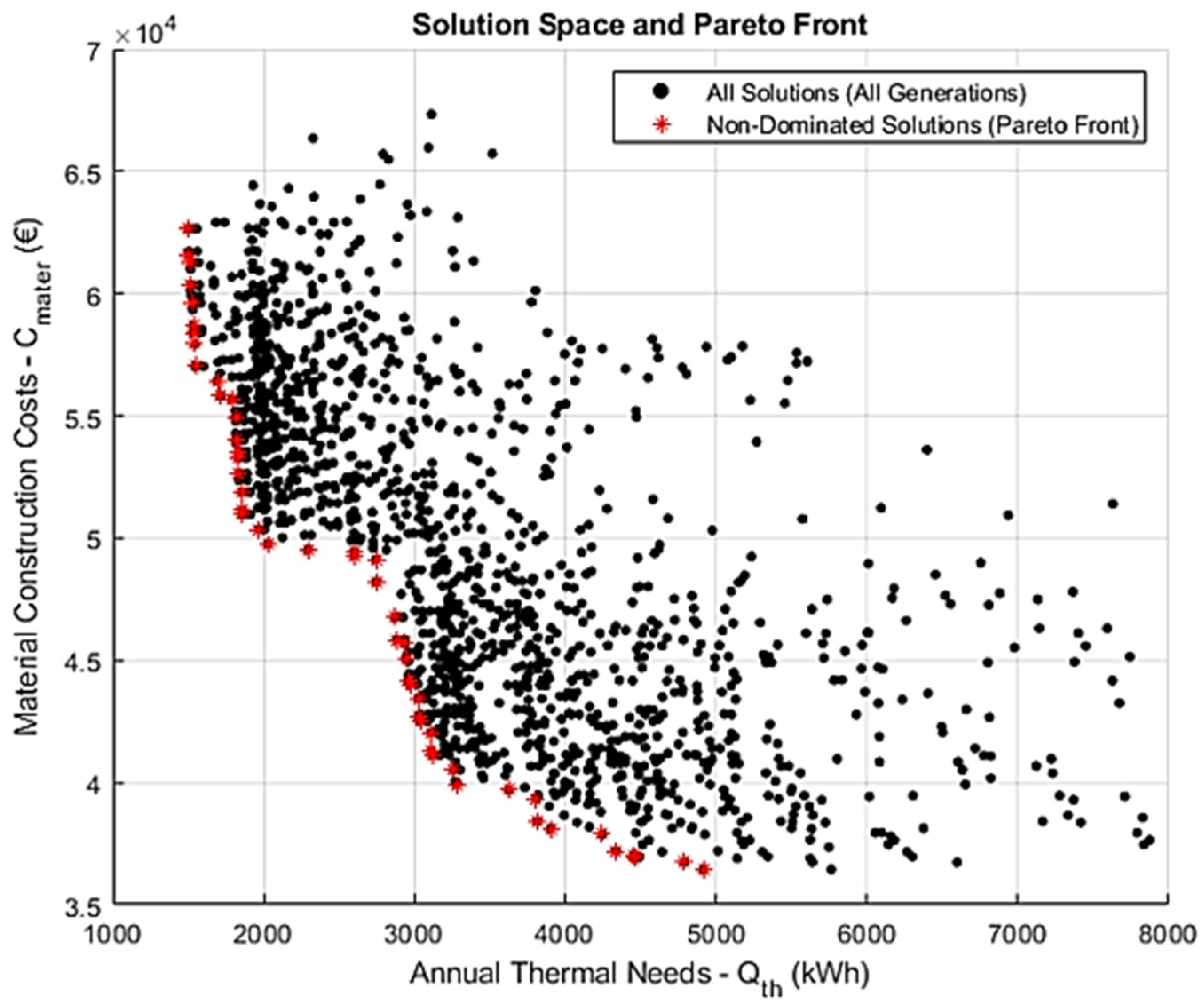
Scenario 3 isolates the influence of population size by increasing it from 100 to 200, while holding both the number of generations (50) and the mutation rate (0.04) constant—identical to the configuration used in Scenario 2. This modification aims to assess how a larger population affects solution diversity, convergence behavior, and the overall quality of the Pareto front. As illustrated in Figure 5, expanding the population size markedly improves the resolution and uniformity of the search space. The resulting Pareto front is smoother and more densely populated and exhibits fewer discontinuities compared to Scenario 2. The tradeoff surface between thermal energy demand and construction material cost appears more continuous, reflecting improved exploration and convergence characteristics. These enhancements align with theoretical expectations: a larger population enables broader sampling of the design space within each generation, increasing the likelihood of identifying non-dominated solutions and reducing the risk of premature convergence. The comparative findings underscore the fact that population size plays a critical role in enhancing both the diversity and robustness of the optimization outcomes—particularly under the conditions of a low mutation rate and limited generational depth.
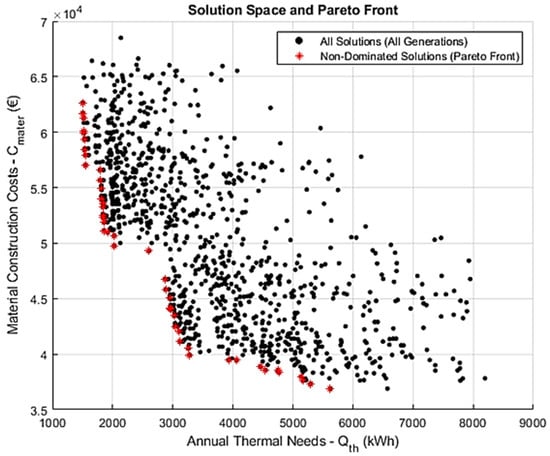
Figure 5.
Pareto front and solution space for Scenario 3, applying 50 generations, a population size of 200, and a mutation rate of 0.04. The higher population size contributes to broader exploration and a denser front.
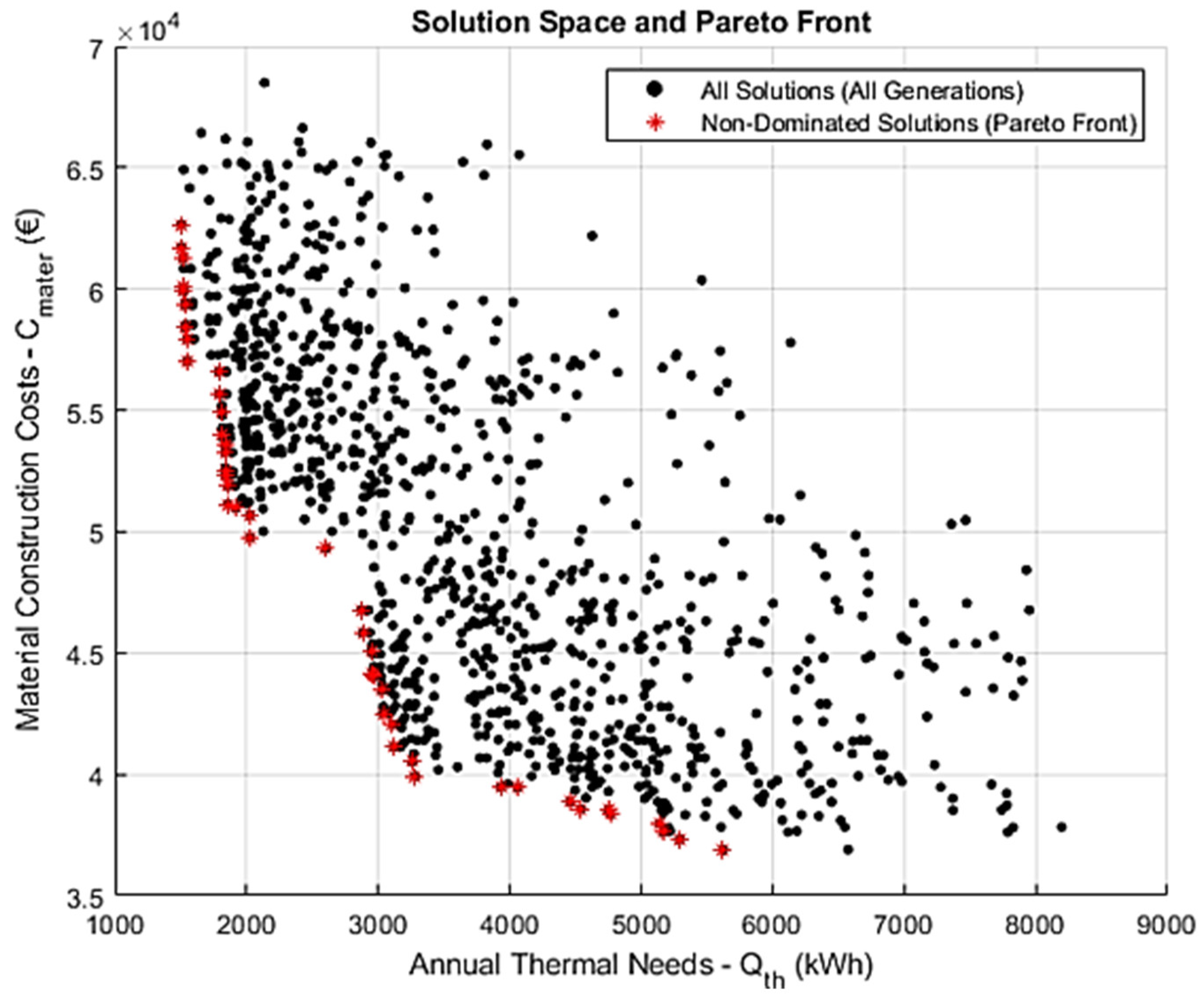
Scenario 4 represents the highest-resolution configuration explored in this study, combining an expanded population size (200) with an increased number of generations (100) and a low mutation rate (0.04). This setup was designed to maximize both the breadth and depth of the evolutionary search, thereby improving the algorithm’s ability to identify high-quality Pareto-optimal solutions. While this configuration entails a higher computational cost, it provides greater opportunities for both the exploration of the design space and the refinement of convergence behavior. As shown in Figure 6, the resulting Pareto front exhibits the highest level of continuity and density among all tested scenarios. The solution space is thoroughly covered, with minimal discontinuities and a well-distributed set of non-dominated solutions. The tradeoff curve maintains a generally concave (hyperbolic) shape, although minor irregularities persist, consistent with those observed in previous scenarios. These deviations may be attributed to two factors. First, the discretization of design variables—stemming from the use of a finite set of material options—can inherently limit the smoothness of the Pareto front. Second, even with extended evolutionary cycles, low mutation rates may constrain the algorithm’s ability to traverse sparsely populated regions of the solution space, particularly when separated by large performance gaps. Nevertheless, the consistency of these anomalies across all scenarios suggests they are not artifacts of algorithmic failure but rather intrinsic features of the optimization landscape defined by the problem’s structure and variable granularity.
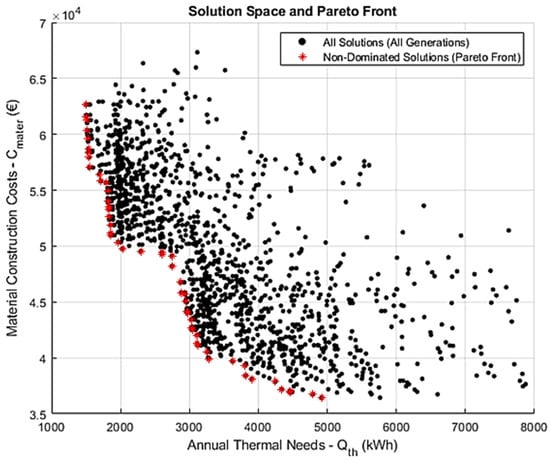
Figure 6.
Pareto front and solution space for Scenario 4, with extended settings of 100 generations, a population size of 200, and a mutation rate of 0.04. This configuration yields the most continuous and comprehensive front, demonstrating the benefit of a deeper search in capturing diverse optimal solutions.
A comparative analysis was carried out to assess the effect of varying NSGA-II hyperparameters on the outcome of the multi-objective optimization. The four configurations, detailed in Table 4, differ in population size, generation count, and mutation rate. Scenario 1 served as the baseline and yielded 28 non-dominated solutions with relatively limited front coverage. In Scenario 2, reducing the mutation rate to 0.04 resulted in a modest increase to 38 solutions, indicating improved stability in the search process. Scenario 3, with an increased population size (200), produced 49 non-dominated solutions, reflecting an enhanced exploration capability.
The highest number of non-dominated solutions (65) was achieved in Scenario 4, which also involved the largest population and the highest number of generations. This configuration produced the most continuous and well-distributed Pareto front, demonstrating the significant impact of hyperparameter tuning on both solution quality and diversity.
Table 5 presents the hyperparameter values used in each scenario, along with the corresponding number of Pareto-optimal solutions, execution time, and key observations regarding optimization performance.

Table 5.
Summary of hyperparameter configurations and their impact on the number and quality of non-dominated solutions.
The optimization process employed MATLAB’s built-in implementation of the NSGA-II algorithm, which uses default genetic operators, including tournament selection for parent selection and simulated binary crossover for offspring generation. These settings were kept unchanged across all scenarios to ensure consistency and comparability in the results.
In addition to optimization performance metrics, the execution time was recorded for each scenario to provide insights into the computational complexity of the process. As shown in the updated Table 5, the runtime increased substantially with more computationally intensive hyperparameter configurations: Scenario 1 was completed in approximately 7 min, Scenario 2 in 15 min, Scenario 3 in 30 min, and Scenario 4 in about 90 min. This trend highlights the trade-off between the computational effort and solution quality. While larger populations and extended generation counts improved the coverage and continuity of the Pareto front, they also imposed higher computational costs. These findings are particularly relevant for real-world applications, where the scalability and feasibility of optimization strategies are often constrained by the available computational resources.
A defining feature of multi-objective optimization is the existence of tradeoffs between conflicting objectives. In this study, the dual goals of minimizing annual thermal energy demand and construction material cost illustrate this tension. These objectives are inherently at odds—reducing energy demand often requires higher-performance (and therefore costlier) materials, while minimizing cost may compromise thermal efficiency. The optimization process yields a Pareto front, which represents the set of non-dominated solutions. Each point on this front offers a unique compromise between the two objectives, and any solution not on the front is suboptimal, being outperformed in at least one criterion by a Pareto-optimal alternative.
Navigating the Pareto front empowers decision-makers—whether architects, engineers, or investors—to select solutions that align with project-specific priorities, such as budget constraints or sustainability goals. Moving along the front quantifies the tradeoffs: for instance, a shift toward lower thermal demand typically incurs increased material cost, and vice versa. While no single solution on the Pareto front is universally optimal, the concept of a utopia point—a theoretical minimum for both objectives—can serve as a reference. Selecting the Pareto solution nearest to this point (e.g., using Euclidean distance) provides a structured approach for identifying balanced tradeoffs when the simultaneous minimization of both objectives is unattainable. Overall, the Pareto front acts as a robust decision-support mechanism, facilitating the transparent, data-driven evaluation of alternatives. The algorithmic framework presented—reinforced by sensitivity analysis across multiple hyperparameter configurations—demonstrates both effectiveness and adaptability for performance-based building design under competing objectives.
5. Concluding Remarks and Future Directions
This study presented a simulation-based multi-objective optimization framework aimed at improving both the thermal and economic performance of residential buildings. A representative single-family dwelling in Patras, Greece, was used as a case study to demonstrate the applicability and flexibility of the proposed methodology. The framework integrates a steady-state, physics-based simulation model with a Multi-Objective Genetic Algorithm (MOGA) implemented in MATLAB and coupled with a modular Excel interface, enabling dynamic input management and the efficient exploration of design alternatives. The optimization process targeted two inherently conflicting objectives: minimizing the building’s annual thermal energy demand and reducing construction material costs.
A parametric sensitivity analysis was conducted to evaluate the impact of key algorithmic hyperparameters—the population size, mutation rate, and number of generations—on the optimization of performance. The results highlighted the importance of hyperparameter tuning in shaping the structure and resolution of the resulting Pareto fronts. Larger population sizes and extended generation counts improved the search space coverage and solution diversity, while lower mutation rates enhanced the local search accuracy but required greater computational effort to avoid premature convergence. Conversely, configurations with reduced computational depth or higher mutation rates yielded less refined Pareto fronts, emphasizing the tradeoffs between computational efficiency and solution quality.
The proposed framework exhibited robustness in generating technically feasible and diverse non-dominated solutions, offering valuable decision-support capabilities for early-stage building design. The integration of a modular Excel–MATLAB interface further enhances the system’s adaptability, allowing for the straightforward customization of design parameters, material databases, and climatic inputs across a wide range of residential design scenarios. While the study focused on a single residential building in Patras, the modularity of the framework enables its application to other building typologies and climatic contexts with minimal adjustments. Broader implementation across varied climates and use cases would further validate its practical relevance and scalability.
It is acknowledged that the thermal model employed—based on Heating Degree Days (HDD)—was selected to balance simplicity with computational tractability for optimization purposes. Nevertheless, further validation against dynamic simulation platforms (e.g., EnergyPlus or TRNSYS) and empirical building performance data would strengthen the credibility of the approach. This remains a valuable direction for future work.
Beyond its academic significance, the proposed optimization framework is intended to support practical decision-making in early-stage building design. Its modular Excel–MATLAB interface allows practitioners to define project-specific inputs such as material properties, thermal transmittance values, unit costs, and climatic data without requiring deep programming knowledge. The tool is particularly suited to the preliminary design phases, where the rapid assessment of alternative solutions is critical. By generating diverse Pareto-optimal design options, the framework enables architects and engineers to identify cost-effective solutions that balance energy efficiency and construction feasibility, ultimately supporting more informed and sustainable design practices.
In addition to methodological validation, the incorporation of input uncertainty analysis is identified as a critical next step. Future work could integrate stochastic elements—such as fluctuating material prices or interannual climatic variability—into the optimization process. Methods such as Monte Carlo simulation or probabilistic sensitivity analysis would enable the quantification of the robustness of optimal solutions and provide confidence intervals for decision-makers.
The further development of the framework may also involve expanding the optimization objectives to include additional performance indicators, such as life-cycle environmental impacts, embodied carbon, or occupant thermal comfort metrics. Moreover, the integration of real-time operational data and the coupling of the optimization engine with machine learning algorithms hold significant potential for improving predictive accuracy, enabling adaptive control strategies, and enhancing decision support capabilities in both new and existing residential energy systems.
Author Contributions
Conceptualization, A.R. and G.M.; methodology, D.M., and A.R.; software, D.M.; validation, D.M. and A.G.; formal analysis, D.M. and S.M.; investigation, D.M. and A.R.; resources, G.M.; data curation, A.G. and A.A.; writing—original draft preparation, D.M., G.M. and J.A.P.; writing—review and editing, G.M. and J.A.P.; visualization, D.M.; supervision, A.R., S.M. and G.M.; project administration, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ACO | Ant Colony Optimization |
| BPS | Building Performance Simulation |
| GA | Genetic Algorithm |
| GHG | Greenhouse Gas |
| HDD | Heating Degree Days |
| HVAC | Heating, Ventilation and Air Conditioning |
| IP | Integer Programming |
| LCC | Life-Cycle Cost |
| LP | Linear Programming |
| ML | Machine Learning |
| MOGA | Multi Objective Genetic Algorithm |
| NLP | Non-linear Programming |
| NOA | National Observatory of Athens |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| PMV | Predicted Mean Vote |
| PSO | Particle Swarm Optimization |
| SA | Simulated Annealing |
| SBO | Simulation-Based Optimization |
References
- International Energy Agency. Global Status Report for Buildings and Construction; License: CC BY 4.0.; International Energy Agency: Paris, France, 2019; Available online: https://www.iea.org/reports/global-status-report-for-buildings-and-construction-2019 (accessed on 3 February 2025).
- Santamouris, M.; Vasilakopoulou, K. Present and future energy consumption of buildings: Challenges and opportunities towards decarbonization. E-Prime—Adv. Electr. Eng. Electron. Energy 2021, 1, 100002. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Souliotis, M.; Papadaki, M.; Halkos, G.; Paravantis, J.; Makridis, S.; Papaefthimiou, S. Applications of earth-to-air heat exchangers: A holistic review. Renew. Sustain. Energy Rev. 2022, 155, 111921. [Google Scholar] [CrossRef]
- Mihalakakou, G.; Souliotis, M.; Papadaki, M.; Menounou, P.; Dimopoulos, P.; Kolokotsa, D.; Paravantis, J.A.; Tsangrassoulis, A.; Panaras, G.; Giannakopoulos, E.; et al. Green roofs as a nature-based solution for improving urban sustainability: Progress and perspectives. Renew. Sustain. Energy Rev. 2023, 180, 113306. [Google Scholar] [CrossRef]
- Chwieduk, D.A. Towards modern options of energy conservation in buildings. Renew. Energy 2017, 101, 1194–1202. [Google Scholar] [CrossRef]
- Cao, X.; Dai, X.; Liu, J. Building energy-consumption status worldwide and the state-of-the-art technologies for zero-energy buildings during the past decade. Energy Build. 2016, 128, 198–213. [Google Scholar] [CrossRef]
- Tombazis, A.N.; Preuss, S.A. Design of passive solar building in urban areas. Sol. Energy 2001, 70, 311–318. [Google Scholar] [CrossRef]
- Athienitis, A.K. Thermal Analysis and Design of Passive Solar Buildings, 1st ed.; Routledge: London, UK, 2001. [Google Scholar] [CrossRef]
- Kappou, S.; Souliotis, M.; Papaefthimiou, S.; Panaras, G.; Paravantis, J.A.; Michalena, E.; Hills, J.M.; Vouros, A.P.; Dimenou, K.; Mihalakakou, G. Review Cool Pavements: State of the Art and New Technologies. Sustainability 2022, 14, 5159. [Google Scholar] [CrossRef]
- Giannadakis, A.; Romeos, A.; Kalogirou, I.; Dimopoulos, D.I.; Trachanas, G.P.; Marinakis, V.; Mihalakakou, G. Energy performance analysis of a passive house building. Energy Sources Part B Econ. Plan. Policy 2025, 20, 2455114. [Google Scholar] [CrossRef]
- Nielsen, T.R. Optimization of Buildings with Respect to Energy and Indoor Environment. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2003. Byg Rapport No. R-036. [Google Scholar]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Rothlauf, F. Design of Modern Heuristics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Wetter, M. GenOpt—A Generic Optimization Program. Seventh Int. IBPSA Conf. 2001, 7, 601–608. [Google Scholar] [CrossRef]
- Hwang, C.L.; Masud, A.S. Multiple Objective Decision Making—Methods and Applications; Springer: Berlin/Heidelberg, Germany, 1979. [Google Scholar]
- Qian, N. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.I.; Hamed, E.T.; Chilmeran, H.T.S. A Modified Bat Algorithm with Conjugate Gradient Method for Global Optimization. Int. J. Math. Math. Sci. 2020, 2020, 4795793. [Google Scholar] [CrossRef]
- Nayak, S. Fundamentals of Optimization Techniques with Algorithms, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Chelouah, R.; Siarry, P. Tabu search applied to global optimization. Eur. J. Oper. Res. 2000, 123, 256–270. [Google Scholar] [CrossRef]
- Hooke, R.; Jeeves, T.A. “Direct Search” Solution of Numerical and Statistical Problems. J. ACM 1961, 8, 212–229. [Google Scholar] [CrossRef]
- Kolda, T.G.; Lewis, R.M.; Torczon, V. Optimization by Direct Search: New Perspectives on Some Classical and Modern Methods. Soc. Ind. Apllied Math. 2003, 45, 385–482. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Gero, J.S.; D’Cruz, N.; Radford, A.D. Energy in context: A multicriteria model for building design. Build. Environ. 1983, 18, 99–107. [Google Scholar] [CrossRef]
- Heiselberg, P.; Brohus, H.; Hesselholt, A.; Rasmussen, H.; Seinre, E.; Thomas, S. Application of sensitivity analysis in design of sustainable buildings. Renew. Energy 2009, 34, 2030–2036. [Google Scholar] [CrossRef]
- Huang, Y.; Niu, J.L. Optimal building envelope design based on simulated performance: History, current status and new potentials. Energy Build. 2016, 117, 387–398. [Google Scholar] [CrossRef]
- Gan, V.J.L.; Lo, I.M.C.; Ma, J.; Tse, K.T.; Cheng, J.C.P.; Chan, C.M. Simulation optimisation towards energy efficient green buildings: Current status and future trends. J. Clean. Prod. 2020, 254, 120012. [Google Scholar] [CrossRef]
- Deb, C.; Zhang, F.; Yang, J.; Lee, S.E.; Shah, K.W. A review on time series forecasting techniques for Building energy consumption. Renew. Sustain. Energy Rev. 2017, 74, 902–924. [Google Scholar] [CrossRef]
- Shi, G.; Liu, D.; Wei, Q. Prediction of energy consumption in office buildings based on echo state network. In Proceedings of the 2016 12th World Congress on Intelligent Control and Automation (WCICA), Guilin, China, 12–15 June 2016; Volume 2016-Septe, pp. 895–899. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- MATLAB; Version R2024a; MathWorks: Natick, MA, USA, 2024; Available online: https://www.mathworks.com (accessed on 20 October 2024).
- U.S. Department of Energy. Energy Plus: Weather Data. 2024. Available online: https://energyplus.net/weather (accessed on 4 May 2025).
- Klein, S.A. TRNSYS 18: A Transient System Simulation Program. 2017. Available online: http://sel.me.wisc.edu/trnsys (accessed on 4 May 2025).
- Wright, J.A.; Loosemore, H.A.; Farmani, R. Optimization of building thermal design and control by multi-criterion genetic algorithm. Energy Build. 2002, 34, 959–972. [Google Scholar] [CrossRef]
- Attia, S.; Hamdy, M.; O’Brien, W.; Carlucci, S. Assessing gaps and needs for integrating building performance optimization tools in net zero energy buildings design. Energy Build. 2013, 60, 110–124. [Google Scholar] [CrossRef]
- Al Mindeel, T.; Spentzou, E.; Eftekhari, M. Energy, thermal comfort, and indoor air quality: Multi-objective optimization review. Renew. Sustain. Energy Rev. 2024, 202, 114682. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Branke, J.S.R.; Deb, K.; Miettinen, K. Multi-Objective Optimization: Interactive and Evolutionary Approaches, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Professional: Boston, MA, USA, 1989. [Google Scholar]
- Taveres-Cachat, E.; Goia, F. Exploring the impact of problem formulation in numerical optimization: A case study of the design of PV integrated shading systems. Build. Environ. 2021, 188, 107422. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer Series in Operations Research and Financial Engineering; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Chanas, S.; Zieliński, P. On the equivalence of two optimization methods for fuzzy linear programming problems. Eur. J. Oper. Res. 2000, 121, 56–63. [Google Scholar] [CrossRef]
- Swann, W.H. A survey of non-linear optimization techniques. FEBS Lett. 1969, 2, S39–S55. [Google Scholar] [CrossRef]
- Wolsey, L. Integer Programming; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar] [CrossRef]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing: Natural Computing Series, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Kegl, M.; Butinar, B.J.; Kegl, B. An efficient gradient-based optimization algorithm for mechanical systems. Numer. Methods Biomed. Eng. 2002, 18, 363–371. [Google Scholar] [CrossRef]
- Yang, X.-S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Asadi, E.; Silva, M.G.; Antunes, C.H.; Dias, L.; Glicksman, L. Multi-objective optimization for building retrofit: A model using genetic algorithm and artificial neural network and an application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Attia, S.; Hamdy, M.; O’Brien, W.; Carlucci, S. Computational optimisation for zero energy buildings design: Interviews results with twenty eight international experts. In Proceedings of the BS 2013 13th Conference of International Building Performance Simulation Association, Chambéry, France, 26–28 August 2013; pp. 3698–3705. [Google Scholar] [CrossRef]
- Arani, S. Optimizing Energy Performance of Building Renovation Using Traditional and Machine Learning Approaches. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2020. [Google Scholar]
- Russell, A.D.; Arlani, G.A. Objective functions for optimal building design. Comput. Des. 1981, 13, 327–338. [Google Scholar] [CrossRef]
- Benaddi, F.Z.; Boukhattem, L.; Tabares-Velasco, P.C. Multi-objective optimization of building envelope components based on economic, environmental, and thermal comfort criteria. Energy Build. 2024, 305, 113909. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-objective optimization of the building energy performance: A simulation-based approach by means of particle swarm optimization (PSO). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- Sharif, S.A.; Hammad, A. Simulation-Based Multi-Objective Optimization of institutional building renovation considering energy consumption, Life-Cycle Cost and Life-Cycle Assessment. J. Build. Eng. 2019, 21, 429–445. [Google Scholar] [CrossRef]
- Chantrelle, F.P.; Lahmidi, H.; Keilholz, W.; El Mankibi, M.; Michel, P. Development of a multicriteria tool for optimizing the renovation of buildings. Appl. Energy 2011, 88, 1386–1394. [Google Scholar] [CrossRef]
- Evins, R.; Pointer, P.; Vaidyanathan, R.; Burgess, S. A case study exploring regulated energy use in domestic buildings using design-of-experiments and multi-objective optimization. Build. Environ. 2012, 54, 126–136. [Google Scholar] [CrossRef]
- Ferrara, M.; Fabrizio, E.; Virgone, J.; Filippi, M. A simulation-based optimization method for cost-optimal analysis of nearly Zero Energy Buildings. Energy Build. 2014, 84, 442–457. [Google Scholar] [CrossRef]
- Sahu, M.; Bhattacharjee, B.; Kaushik, S.C. Thermal design of air-conditioned building for tropical climate using admittance method and genetic algorithm. Energy Build. 2012, 53, 1–6. [Google Scholar] [CrossRef]
- Wang, W.; Rivard, H.; Zmeureanu, R. An object-oriented framework for simulation-based green building design optimization with genetic algorithms. Adv. Eng. Inform. 2005, 19, 5–23. [Google Scholar] [CrossRef]
- Junghans, L.; Darde, N. Hybrid single objective genetic algorithm coupled with the simulated annealing optimization method for building optimization. Energy Build. 2015, 86, 651–662. [Google Scholar] [CrossRef]
- Bichiou, Y.; Krarti, M. Optimization of envelope and HVAC systems selection for residential buildings. Energy Build. 2011, 43, 3373–3382. [Google Scholar] [CrossRef]
- Sarmas, E.; Dimitropoulos, N.; Strompolas, S.; Mylona, Z.; Marinakis, V.; Giannadakis, A.; Romaios, A.; Doukas, H. A web-based Building Automation and Control Service. In Proceedings of the 2022 13th International Conference on Information, Intelligence, Systems & Applications (IISA), Corfu, Greece, 18–20 July 2022; p. 22095409. [Google Scholar] [CrossRef]
- Juan, Y.K.; Gao, P.; Wang, J. A hybrid decision support system for sustainable office building renovation and energy performance improvement. Energy Build. 2010, 42, 290–297. [Google Scholar] [CrossRef]
- Penna, P.; Prada, A.; Cappelletti, F.; Gasparella, A. Multi-objectives optimization of Energy Efficiency Measures in existing buildings. Energy Build. 2015, 95, 57–69. [Google Scholar] [CrossRef]
- Khani, A.; Khakzand, M.; Faizi, M. Multi-objective optimization for energy consumption, visual and thermal comfort performance of educational building (case study: Qeshm Island, Iran). Sustain. Energy Technol. Assess. 2022, 54, 102872. [Google Scholar] [CrossRef]
- Bolattürk, A. Optimum insulation thicknesses for building walls with respect to cooling and heating degree-hours in the warmest zone of Turkey. Build. Environ. 2008, 43, 1055–1064. [Google Scholar] [CrossRef]
- Bolattürk, A. Determination of optimum insulation thickness for building walls with respect to various fuels and climate zones in Turkey. Appl. Therm. Eng. 2006, 26, 1301–1309. [Google Scholar] [CrossRef]
- Wang, W.; Zmeureanu, R.; Rivard, H. Applying multi-objective genetic algorithms in green building design optimization. Build. Environ. 2005, 40, 1512–1525. [Google Scholar] [CrossRef]
- Hamdy, M.; Nguyen, A.T.; Hensen, J.L.M. A performance comparison of multi-objective optimization algorithms for solving nearly-zero-energy-building design problems. Energy Build. 2016, 121, 57–71. [Google Scholar] [CrossRef]
- National Observatory of Athens (NOA). Institute for Environmental Research and Sustainable Development. Available online: https://www.iersd.noa.gr/en/ (accessed on 4 May 2025).
- Kreider, J.F.; Rabl, A. Heating and Cooling of Buildings: Design for Efficiency; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Karagiannidis, A.; Lagouvardos, K.; Kotroni, V.; Galanaki, E. Analysis of Current and Future Heating and Cooling Degree Days over Greece Using Observations and Regional Climate Model Simulations. Environ. Sci. Proc. 2023, 26, 149. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).