Abstract
Hybrid electric vertical take-off and landing (HEVTOL) flying vehicles serve as effective platforms for efficient transportation, forming a cornerstone of the emerging low-altitude economy. However, the current lack of co-optimization methods for powertrain component sizing and energy controller design often leads to suboptimal HEVTOL performance. To address this, this paper proposes a hierarchical manifold-enhanced Bayesian evolutionary optimization (HM-BEO) approach for HEVTOL systems. This framework employs lightweight manifold dimensionality reduction to compress the decision space, enabling Bayesian optimization (BO) on low-dimensional manifolds for a global coarse search. Subsequently, the approximate Pareto solutions generated by BO are utilized as initial populations for a non-dominated sorting genetic algorithm III (NSGA-III), which performs fine-grained refinement in the original high-dimensional design space. The co-optimization aims to minimize fuel consumption, battery state-of-health (SOH) degradation, and manufacturing costs while satisfying dynamic and energy management constraints. Evaluated using representative HEVTOL duty cycles, the HM-BEO demonstrates significant improvements in optimization efficiency and solution quality compared to conventional methods. Specifically, it achieves a 5.3% improvement in fuel economy, a 7.4% mitigation in battery SOH degradation, and a 1.7% reduction in system manufacturing cost compared to standard NSGA-III-based optimization.
1. Introduction
To address growing concerns about greenhouse gas emissions and increasing demand for advanced air mobility, the development of hybrid electric vertical take-off and landing (HEVTOL) flying vehicles has expanded rapidly worldwide [1]. Combining electric power and range extenders, it represents a promising architecture that enables longer ranges and higher payload capacities compared to purely electric variants [2]. Efficient powertrain sizing and an energy management system (EMS) are critical for maximizing the performance of these complex systems with multiple power sources and diverse driving/flight phases, while minimizing operational costs [3]. HEVTOL performance is also influenced by control strategy boundary conditions, which depend on propulsion system component parameters [4]. Therefore, coordinating propulsion system design and energy management while recognizing their interdependencies is essential [5]. The combined effects of component parameters and EMS determine HEVTOL operational performance across different flight envelopes [6]. Effective co-optimization of component sizing and energy management requires appropriate scaling of critical electrical and range extender components alongside optimal control parameter selection [7].
Co-optimization techniques for powertrain design have been extensively researched and refined over the past decade for various powertrain systems [8]. However, directly applying these methods to high-dimensional HEVTOL design problems faces challenges [9], particularly the computational costs associated with evaluating complex multi-physics models [10]. Traditional approaches often neglect or simplify dynamic behaviors, potentially leading to suboptimal performance under real-world flight conditions [11]. For instance, the Willans line method, which uses linear transfer functions to represent input–output power relationships, is commonly employed for engine and motor sizing [12]. This approach simplifies engine fuel consumption and motor electrical loss models by assuming operation within high-efficiency regions [13]. Furthermore, Zhou et al. developed an HEV intelligent sizing system by combining a chaos-enhanced accelerated particle swarm optimization (CAPSO) algorithm with the Willans line method [14]. He et al. used the Willans line method to create proportionally scaled engine fuel consumption maps for optimizing hybrid systems in UAVs [15]. However, the methods ignore the dynamic characteristics and inertia of power machines during operation, potentially reducing model accuracy and creating discrepancies between optimized and actual performance [16]. Thus, developing a hybrid powertrain co-design framework interfacing with surrogate models such as a Bayesian model is essential for accurately capturing dynamic behaviors [12]. In practical hybrid powertrain co-design, multiple performance objectives are typically considered rather than focusing on a single one [17]. The inherent strong nonlinearities and complex constraints of hybrid powertrains often result in interacting and conflicting multi-objective functions. Traditional optimization methods design different weighting factors and combine objective functions into a single one based on specific requirements [18]. However, changing design requirements necessitate redesigning objective functions and restarting optimization processes, leading to significant computational burdens and complexity.
To this end, multi-objective evolutionary algorithms (MOEAs) and non-dominated concepts provide Pareto solution sets, offering designers flexibility in selecting parameter combinations based on design criteria [19]. Current multi-objective optimization techniques, such as the non-dominated sorting genetic algorithm-III (NSGA-III), have been widely adopted for propulsion system co-design [7]. Additionally, Bayesian optimization (BO) has gradually been applied to engineering optimizations due to its efficient exploration capabilities under expensive cost functions [20]. Deb et al. introduced the reference point-based NSGA-III for handling high-dimensional, multi-variable multi-objective problems [21]. He et al. applied NSGA-III to optimize engine displacement, battery pack count, and supercapacitor quantity based on cost-power ratios, energy consumption, and emissions [22]. However, traditional niching strategies in NSGA and its variants may overemphasize diversity, potentially hindering convergence and exposing issues with fixed evolutionary operators that require further investigation [23]. Furthermore, dynamic programming (DP) is frequently used as the control strategy for iterative hybrid powertrain co-optimization [24]. Nevertheless, DP requires prior knowledge of driving conditions and struggles with real-time applications due to high computational demands. Thus, establishing and implementing co-optimization under real-time control is crucial [25]. Li et al. proposed a method to minimize HEV operational costs through rule-based (RB) strategies, including optimized thresholds for specific driving cycles and power split device gear ratios [26]. Although RB strategies are computationally efficient and suitable for real-time applications, achieving desired control effects remains challenging due to heavy reliance on practical engineering experience [27]. Moreover, when facing high-dimensional hybrid system design problems under both ground-driving and flying scenarios, directly applying traditional NSGA-III or BO methods risks encountering the curse of dimensionality, slow convergence and local optimality [28].
Some preliminary studies have emerged that address powertrain optimization of HEVTOLs. However, these works often rely on heuristic or simplified optimization methodologies, which are particularly insufficient in the joint design of component sizing and energy management controllers [29]. For instance, Jung et al. demonstrate the feasibility of controller verification in UAVs, illustrating the challenges in reliable onboard energy controllers [30]. Likewise, Ruan et al. provide a broad overview of propulsion strategies for mobile systems but also reveal the fragmented treatment of system-level optimization across different domains [31]. For ground-based systems, Stefan et al. [32] and Bao et al. [33] focused on the trade-off between battery capacity and mission energy demands, showcasing the importance of optimal hybridization. Meanwhile, Parkar et al. introduced a metaheuristic co-optimization framework, yet still faced convergence inefficiencies in high-dimensional spaces [34]. Based on this, Pardhi et al. incorporated environmental lifecycle factors into the sizing problem, moving closer to multi-objective, multi-domain design formulations [35]. Collectively, these works highlight the value of co-optimizing powertrain architecture and control strategies. However, current solutions often suffer from limited scalability, weak convergence under complex constraints, and insufficient handling of high-dimensional design space gaps, which motivate the development of more structured, hierarchy-enhanced, and dimension-reduced optimization frameworks as proposed in this work [36]. To the best of the authors’ knowledge, no existing work has yet proposed a unified multi-objective optimization framework that simultaneously addresses component sizing and energy management controller calibration for HEVTOLs.
This gap limits the ability of current methodologies to efficiently solve high-dimensional, tightly coupled design problems, thereby falling short of meeting the engineering demands for rapid and high-performance HEVTOL system development. Therefore, this paper proposes a novel hierarchical optimization framework, HM-BEO, integrating lightweight manifold dimensionality reduction with Bayesian coarse search and evolutionary refinement, maintaining optimization accuracy while significantly improving computational efficiency. Compared to conventional methods, this approach ensures high-accuracy modeling of dynamic constraints while substantially enhancing co-optimization quality. Key contributions include: (1) a unified co-optimization framework for HEVTOL component sizing and energy controller calibration, explicitly formulating the design problem as a constrained multi-objective optimization task over a high-dimensional space, targeting real-world metrics such as fuel consumption, battery degradation, and system cost; (2) a hierarchical optimization scheme combining low-dimensional Bayesian global search with NSGA-III-based refinement, which efficiently balances exploration and exploitation across design stages and mitigates the curse of dimensionality; (3) comprehensive validation on representative HEVTOL duty cycles, demonstrating superior convergence, optimization quality, and engineering applicability over traditional single-layer or decoupled optimization methods.
The remainder of this paper is organized as follows: Section 2 describes the hybrid powertrain configuration and energy management strategy. Section 3 formulates the Pareto-based co-optimization problem and details the proposed methodology. Section 4 presents and analyzes co-optimization results of powertrain sizing and controller design, validating the effectiveness of the algorithms. Conclusions are provided in Section 5.
2. Powertrain Modeling and Control Strategy
The hybrid electric flying vehicle studied in this paper adopts a coaxial twelve-rotor layout, with each rotor driven by an independent motor. The system is equipped with a dual-engine range extender system consisting of two internal combustion engines (ICEs) and two sets of electric generators, providing continuous energy replenishment during flight. The two sets of power generation units will adopt the same parameters to ensure systematic symmetry and reliability. All motors and generators are connected to a central DC bus via DC/AC and AC/DC converters, and the battery is connected in parallel to the DC bus via a DC/DC converter for energy storage and auxiliary power supply. During the flight mission, the battery and the range extender system jointly provide power output to the rotor motors. The DC bus serves as a unified energy scheduling platform between various energy sources and loads, supporting multi-source dynamic switching and load balancing.
2.1. Vehicle Dynamics Model
Figure 1 depicts the flying vehicle schematic, showing (actual flight speed), (angle between flight direction and horizontal), , , , (thrust, lift, air resistance, acceleration), and (gravity). From flight aerodynamics, the total flight power of the flying vehicle is computed using the formula:
where and are the power for vertical and horizontal motion. Effective vertical and horizontal velocities are and . According to [37], for vertical motion (climbing and descending) at velocity is given by:
where is rotor disk radius, is rotor disk area. Horizontal power comprises parasitic power and induced power needed to overcome parasitic and lift-induced drag. These power components are calculated by:
where is blade chord length, number of blades, angular velocity, and is solved by the following equation [37]:
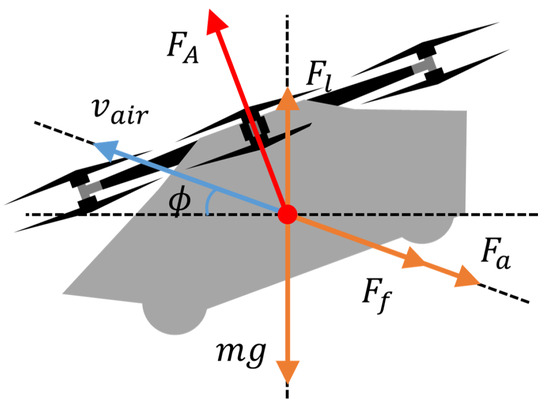
Figure 1.
Dynamics model of the HEVTOL.
2.2. Powertrain Model
The engine fuel consumption model and the motor/generator model are detailed below. The engine efficiency model is derived through a fitting process based on experimental data collected from heavy-duty engine tests, and the engine efficiency is a function of engine power, as illustrated in Figure 2, where the black data points represent the test data and the red line specifically fits the highest efficiency points observed. The motor/generator efficiency is approximated as a constant value of to reflect the performance of current high-efficiency electric machines.
where denotes the engine fuel consumption rate, is the engine power, and refers to the lower heating value of the fuel. Additionally, and represent the electrical and mechanical power of the motor/generator, respectively. Furthermore, the coefficient k is defined as −1 when it operates as a motor, indicating a power loss, and 1 when it functions as a generator, representing power generation from mechanical to electrical energy with corresponding efficiency.
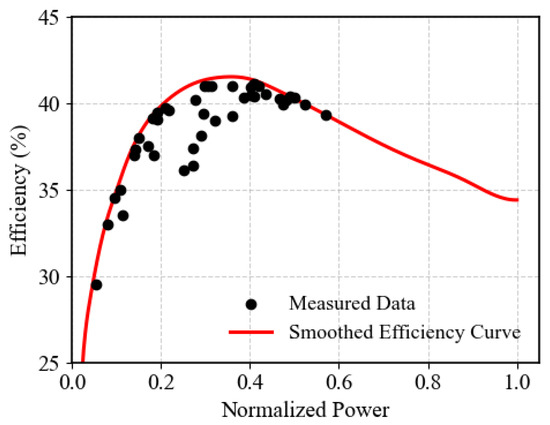
Figure 2.
The efficiency curve of the engine with normalized output power index.
Considering repeated charge and discharge cycles accelerate battery aging and shorten its lifespan. The large capacity of HEVTOL batteries can also lead to high replacement costs when batteries are excessively aged. Therefore, battery capacity loss has a significant economic impact on HEVTOL performance. To extend battery life, battery state of health (SOH) loss is incorporated as a key objective function. In this work, a thermoelectric coupling model is developed, parameterized as shown in Figure 3. Assuming that charging and discharging have equal effects on battery aging, the battery capacity loss can be expressed as a function of the charge/discharge rate , battery temperature , and SOC. R is the molar gas constant, and Ah represents the accumulated charge.
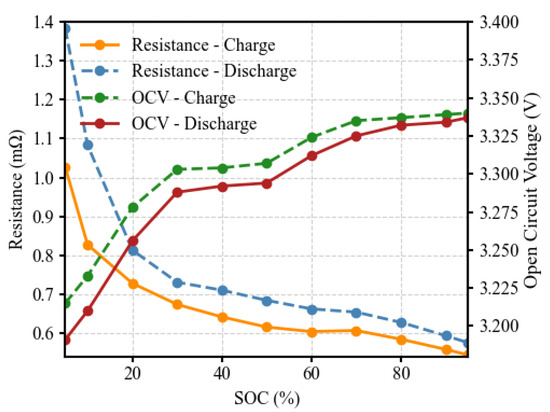
Figure 3.
Open circuit voltage and resistance during battery charging and discharging.
The battery capacity loss , effective total Ah-throughput , and SOH are described by the following equations [7]:
where the coefficients and are defined as: and
The total Ah-throughput is defined from the beginning to the end of the battery’s life, given a nominal current :
where indicates the end of the battery’s life.
The severity factor is defined as the ratio of the theoretical total Ah-throughput to the practical total Ah-throughput [7]:
The battery life is determined when the battery capacity degrades to 80
where the nominal variables used are , , and °C.
The effective total Ah-throughput can be calculated by integrating the severity factor and the absolute value of the battery current [7]:
When equals the nominal total Ah-throughput , the battery’s lifespan is considered terminated. For generality, the initial SOH for each driving cycle is set to 100%. The SOH is then defined by:
2.3. Energy Controller Model
The HEVTOL in this paper is equipped with the mainstream adaptive equivalent consumption minimization strategy (A-ECMS) energy management system. However, its system control parameters and calibrations are to be jointly determined with component sizing. A-ECMS is an optimization-based control method that uses an equivalence factor (EF) to convert electrical energy consumption into equivalent fuel consumption. The total power demand at time t is denoted by , and the system begins with an initial state-of-charge . The optimization process is subject to physical bounds on power, torque, and speed, along with an SOC tracking tolerance . To reduce computational complexity, the control input is limited to battery output power . Engine power is then determined via:
Consequently, the engine’s fuel consumption rate becomes a function of , as the engine operates along its optimal operating line (OOL). The objective is to minimize the cumulative fuel consumption over a drive cycle, as formulated in Equation (13) [38].
To enforce SOC constraints over time, a Hamiltonian function is defined as:
where p is the co-state variable, and is the SOC rate of change. The equivalence factor is introduced based on the co-state p and the engine efficiency estimate , typically set to half of peak thermal efficiency:
Substituting into the Hamiltonian, the formulation becomes:
Since a fixed EF has limitations in adaptability, A-ECMS adopts a proportional-integral (PI) controller to dynamically update the EF [5].
where represents the EF at time t; is the initial EF value, which will be determined via optimization; and and are the proportional and integral gains, respectively. The overall operation mechanism of A-ECMS is depicted as shown in Figure 4.
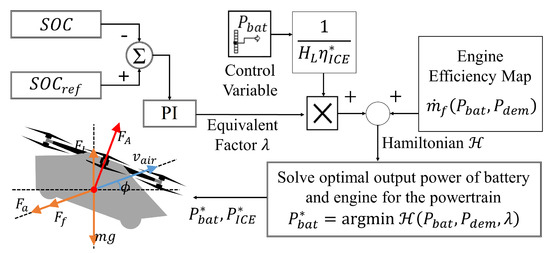
Figure 4.
The principle of adaptive-equivalent consumption minimization strategy for energy management controller.
3. Co-Optimization of HEVTOL Powertrain Sizing and Energy Management System
To address computational burdens and convergence challenges in traditional methods for high-dimensional design spaces, this paper proposes a hierarchical manifold-enhanced Bayesian-evolutionary optimization (HM-BEO) approach, as illustrated in Figure 5. The methodology comprises three key phases: (1) lightweight manifold discovery—initially identifies latent low-dimensional structures through manifold learning of randomized design variable samples, effectively reducing optimization space dimensionality; (2) manifold-projected Bayesian optimization—constructs Gaussian process (GP) surrogate models within the reduced manifold subspace for Bayesian optimization, enabling rapid global exploration to generate preliminary approximate Pareto solutions; (3) surrogate-guided NSGA-III refinement—maps Bayesian-optimized solutions back to the original space as initial populations and then applies NSGA-III for local multi-objective evolutionary refinement of Pareto frontiers. This hierarchical architecture synergistically combines Bayesian optimization’s global search efficiency with NSGA-III’s diversity preservation in local search, while manifold dimensionality reduction effectively mitigates the curse of dimensionality.
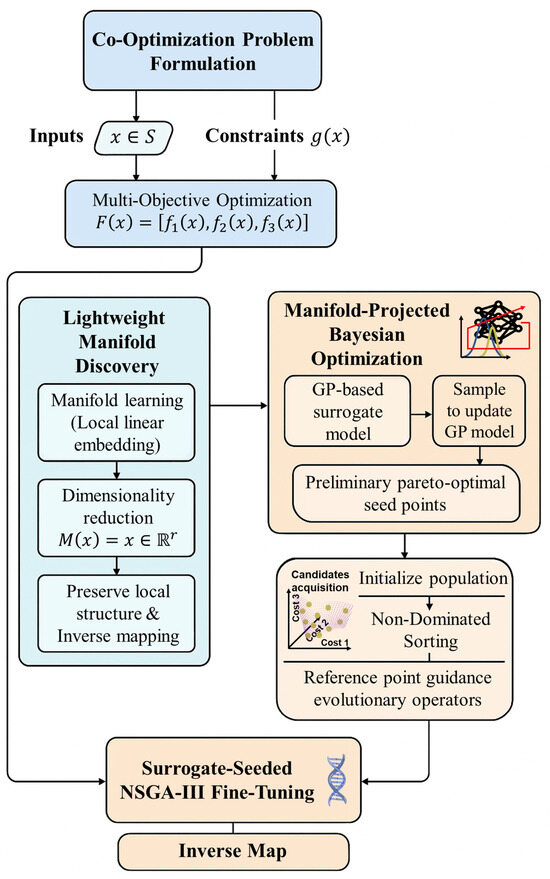
Figure 5.
The overall design of the hierarchical manifold-enhanced Bayesian evolutionary optimization for the HEVTOL powertrain sizing and energy management system.
3.1. Problem Formulation
This study focuses on the co-optimization of hybrid electric propulsion system component sizing and energy management strategy. Let the optimization parameters collectively form a decision vector , aiming to simultaneously minimize fuel consumption, battery SOH degradation, and component manufacturing costs. Specifically, we define three optimization objectives: corrected fuel consumption , battery SOH loss , and system component cost , comprehensively addressing both operational and manufacturing cost minimization requirements. The optimization variables include powertrain parameters (maximum ICE power , maximum generator power , maximum motor power ) and control strategy parameters (A-ECMS coefficients , , and ). The parameter ranges are specified in Table 1, which is determined based on extensive manufacturing experience gained from industry and a comprehensive review of relevant configuration and sizing settings derived from existing literature [37].

Table 1.
Variable definitions for HEVTOL powertrain and controller co-optimization.
The objective functions are formulated as follows. The corrected fuel consumption combines actual engine fuel consumption with battery SOC consumption equivalent:
where denotes the fuel-SOC conversion factor. Battery SOH degradation , derived from the electro-thermal coupled battery model in Section 2, is defined as:
where and represent initial and final battery health states, denotes effective discharge capacity, and is the nominal capacity.
The system component cost incorporates ICE, generator, motor, and battery costs (with battery capacity pre-calibrated based on acceleration time and range requirements):
In this study, we assume that only size-dependent direct material costs are considered in the cost model, while other costs such as R&D, integration, and control systems, whose values are weakly correlated with component sizing, are excluded. Component cost models are specified as [7]:
where , , and represent ICE, generator, and motor costs, respectively, while includes battery pack and management system costs, with coefficients sourced from Electric Power Research Institute (EPRI) standards [39]. The co-optimization problem is formulated as a multi-objective optimization problem, where denotes the feasible design space, subject to constraints [7]:
where represents the i-th constraint function encompassing dynamics, component performance, and control system stability limits. Pareto optimality is defined as: x is Pareto-optimal if no other satisfies
The non-dominated solution set is:
where indicates dominates x across all objectives. This formulation establishes an integrated optimization framework for HEVTOL propulsion system design and control strategy.
3.2. Lightweight Manifold Discovery
To alleviate the curse of dimensionality in the combined decision space of HEVTOL component sizing and energy management control parameter optimization, a lightweight manifold reduction approach is introduced in this work. Based on an initial sampling set , the underlying low-dimensional manifold structure is identified. The dimension reduction mapping is defined as:
where r denotes the dimension of the reduced manifold. The method employed is local linear embedding (LLE), aiming to preserve the linear relationships within local neighborhoods of the data. Firstly, the reconstruction weights are computed by minimizing the following, where denotes the k-nearest neighbors of point . The reconstruction weights are subject to the normalization constraint:
Subsequently, the low-dimensional embeddings are obtained by preserving the same reconstruction relationships:
To ensure that the dimensionality reduction does not destroy the local structures of the original data, the local preservation error is defined as:
Finally, an inverse mapping is constructed to approximately reconstruct the original space x using locally weighted regression:
where denotes the weighting coefficients determined by the distance between z and . The above manifold reduction process, built upon local linearity preservation, ensures that the intrinsic nonlinear correlations among decision variables are retained in the reduced manifold subspace, thereby enabling subsequent optimization to be conducted within a structurally sound low-dimensional space and significantly reducing the complexity and computational burden of HEVTOL system design optimization.
3.3. Manifold-Projected Bayesian Optimization
After obtaining the low-dimensional manifold subspace that characterizes the HEVTOL powertrain co-design parameter search space, a BO strategy is employed for global coarse exploration. For each objective , a Gaussian process surrogate model is constructed:
where denotes the mean function and denotes the covariance function, defined using the squared exponential kernel:
where is the signal variance and is the characteristic length scale. The GP predictive mean and variance at a query point are given by the following, where Z denotes the set of existing sampled points, represents the observed objective values, and is the noise variance.
Based on the GP predictions, the expected improvement (EI) acquisition function is defined as follows, where is the best observed objective value so far. Substituting the GP predictions yields the closed-form EI expression [7]:
where and are the cumulative distribution function and probability density function of the standard normal distribution, respectively. In the case of multiple objectives, a weighted summation of EI values is adopted:
where are the weighting factors for each objective. At each iteration, the point maximizing is selected for high-fidelity evaluation and the GP models are subsequently updated. Bayesian Optimization dynamically balances exploration and exploitation through GP-predicted uncertainty, enabling rapid identification of promising regions in the manifold subspace with minimal function evaluations and providing high-quality seed solutions for subsequent evolutionary search.
3.4. Surrogate-Seeded NSGA-III Fine-Tuning
To further refine the optimal combination of co-design parameters and to escape local optima, the preliminary Pareto-optimal solutions obtained from the Bayesian optimization phase are inversely mapped back to the original design space , forming an initial population for NSGA-III evolutionary optimization. The population P and corresponding objective function evaluations are defined as:
where denotes the population size. The individuals are ranked into different Pareto fronts based on non-dominated sorting. An individual dominates another individual if:
To maintain diversity, the objectives are normalized:
where and are preliminary sampling extrema. Predefined reference points are distributed uniformly in the normalized objective space:
The perpendicular distance from each individual to the nearest reference point is calculated as:
Selection is performed based on proximity to reference points, ensuring uniform coverage along the Pareto front. Mutation is performed as:
where is a perturbation sampled from a polynomial distribution, and denotes the bounds of . The detailed implementation steps are listed in Algorithm 1, showing each stage of the HM-BEO pipeline. Through the guided initial population seeding, non-dominated sorting, and reference point association, NSGA-III fine-tunes the initial Pareto set uniformly and efficiently explores local improvements via genetic operators, ultimately forming a dense, diverse, and high-performance solution set of optimal component sizing and control parameters for HEVTOL applications.
| Algorithm 1: Pseudocode of hierarchical manifold Bayesian evolutionary optimization | |
| I: Manifold Discovery | |
| 1 | Generate M samples using Latin Hypercube Sampling |
| 2 | for each sample do |
| 3 | Identify K-nearest neighbors |
| 4 | Solve local linear reconstruction weights |
| 5 | end for |
| 6 | Learn low-dimensional embedding preserving reconstruction |
| 7 | Train inverse mapping (e.g., RBF regression) |
| 8 | Store manifold dataset |
| II: Manifold-Guided Bayesian Optimization | |
| 9 | Fit GP models for each objective on latent variables z |
| 10 | for to do |
| 11 | Compute multi-objective acquisition function (e.g., Expected Improvement) |
| 12 | Select maximizing acquisition |
| 13 | Map to and evaluate |
| 14 | Add to dataset and update GP |
| 15 | end for |
| 16 | Select top-N seeds for fine-tuning |
| III: NSGA-III-Based Local Refinement | |
| 17 | Map to as initial population |
| 18 | for to do |
| 19 | Evaluate objectives for all individuals in |
| 20 | Apply crossover and mutation to produce |
| 21 | Merge and , select next via NSGA-III selection |
| 22 | end for |
| 23 | Return final Pareto front |
4. Results and Discussion
This section presents a comparative analysis between the proposed HM-BEO co-optimization framework, built upon scalable component efficiency maps, and two benchmark methods: NSGA-III and standard genetic algorithm (GA) [40]. The optimization and validation processes are conducted under realistic ground cruising cycles and aerial flight scenarios (taking-off, cruising, and landing phases) for HEVTOL operations, using a population size of 90 and a maximum of 60 generations. Further validation is carried out under real-world HEVTOL driving cycles (integrating both terrestrial and aerial modes, see Figure 6), comparing the original A-ECMS strategy with the HM-BEO-optimized HEVTOL parameters. The employed drive cycles are illustrated in Figure 7. Furthermore, this paper adopts MATLAB R2024a for deploying our optimization algorithms, including the HM-BEO framework, while the physical model of the HEVTOL powertrain and its energy management system were built and simulated in Simulink.
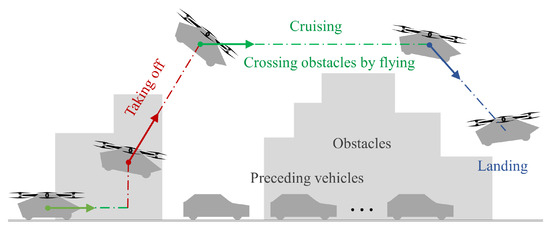
Figure 6.
Scenario setting of a typical driving condition for HEVTOLs.
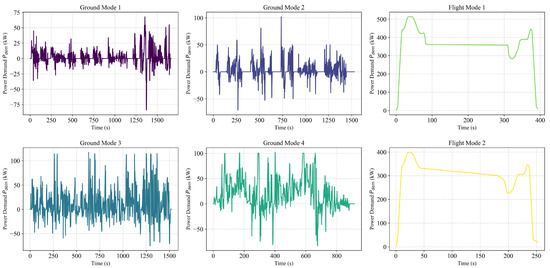
Figure 7.
The employed drive cycles integrating both terrestrial and aerial modes.
4.1. Results of Pareto-Based Co-Optimization
Figure 8 illustrates the evolution of the Pareto optimization results for both the state-of-the-art NSGA-III and the proposed HM-BEO methods. It can be observed that HM-BEO achieves a superior Pareto distribution at early generations, outperforming NSGA-WM even at the final generation, indicating significant improvements in convergence speed and solution quality due to the introduction of manifold dimensionality reduction and hierarchical optimization mechanisms [41].
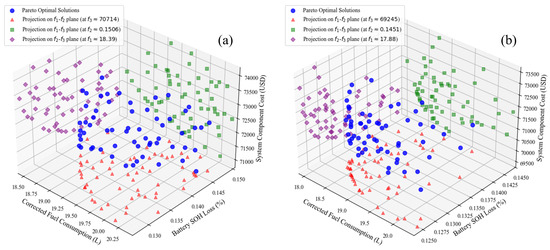
Figure 8.
Evolution of Pareto optimization results: (a) for NSGA-III and (b) for HM-BEO.
By comparing the final generations, HM-BEO yields parameter configurations with reduced operational cost and component sizing cost compared to the NSGA-III approach, where the projected Pareto fronts realizes the superior multi-objective optimization capabilities of the HM-BEO framework. For each method, four representative solutions are selected for analysis: the solutions that individually optimize each objective function, including minimum fuel consumption (-optimal), minimum battery degradation (-optimal), minimum component cost (-optimal), as well as a trade-off solution that balances all three objectives. Detailed results are presented in Table 2 and Table 3. These results summarize the optimization outcomes obtained using NSGA-III and HM-BEO, respectively.

Table 2.
Performance of representative solutions under NSGA-III optimization.

Table 3.
Performance of representative solutions under HM-BEO optimization.
From the NSGA-III results, we observe that the -optimal solution achieves the lowest fuel consumption with , but at the expense of a relatively higher emission index () and battery degradation cost (). In contrast, the -optimal solution significantly reduces emissions () but increases both fuel consumption and battery cost. The trade-off solution offers a balanced configuration, moderately improving all three objectives, making it a strong candidate for practical deployment. Comparatively, HM-BEO delivers similar trends, but with subtle differences in control parameter configurations.
Notably, the trade-off solution in HM-BEO shows a slightly better performance in emission reduction () than the NSGA-III counterpart, while maintaining comparable fuel consumption and battery cost. This indicates that HM-BEO may offer improved control adaptability in highly constrained environments. Overall, both algorithms demonstrate the ability to generate diverse Pareto-optimal solutions with meaningful variations in parameter tuning, offering flexibility in controller design depending on application priorities. The detailed results regarding the three compared optimization methods are depicted in a summary, as shown in Figure 9.
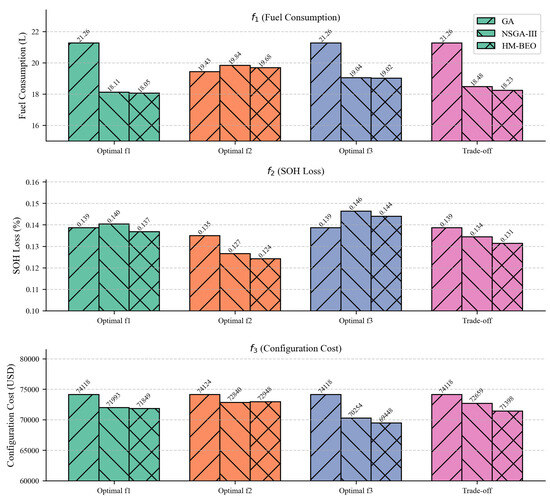
Figure 9.
Comparisons of the specific Pareto solutions generated from GA, NSGA-III and HM-BEO.
4.2. Pareto Front Evolution and Convergence Analysis
To quantitatively evaluate convergence behavior and solution diversity, we adopt the inverted generational distance (IGD) metric [42], defined as:
where P is the reference Pareto front, Q is the solution set generated by the algorithm, and denotes the Euclidean distance from point a to its nearest neighbor in Q [43].
Figure 10 shows the IGD trends for standard GA, NSGA-III and HM-BEO throughout the optimization process. HM-BEO consistently maintains a lower IGD, indicating better convergence and distribution quality across generations. Notably, IGD values for all the methods stabilize around generations 40 and 50, marking Pareto front convergence. HM-BEO converges significantly earlier, further validating the effectiveness of the hierarchical strategy and manifold-based dimensionality reduction in accelerating convergence.
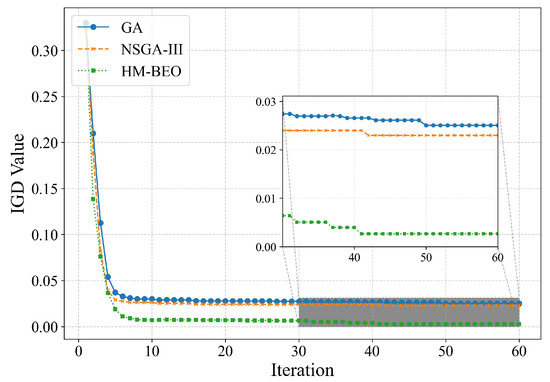
Figure 10.
The dynamics of IGD value during optimization with GA, NSGA-III and HM-BEO.
Table 4 and Figure 11 summarize the comparative performance of the optimized energy management strategies in terms of fuel consumption, battery SOH degradation, and SOC variation. The A-ECMS optimized by the NSGA-III method consumes the most fuel (19.47 L after correction [22]) and results in the greatest battery wear (0.27% SOH loss), with a final SOC of 30.77%. The HM-BEO optimized A-ECMS, however, demonstrates clear improvements in all metrics, reducing fuel usage to 18.44 L after correction while also mitigating SOH degradation and achieving a higher final SOC. The dynamic programming approach, considered a benchmark for optimal control, achieves the best performance with the lowest fuel consumption (17.76 L after correction) and minimal SOH loss (0.25%). Its final SOC is also well-balanced at 34.04%, indicating an effective energy distribution throughout the driving cycle. These results collectively highlight the effectiveness of optimization in improving energy efficiency and battery longevity in hybrid energy management systems.

Table 4.
Summary of fuel consumption, SOH degradation, and SOC variations under different energy management strategies and global optimization.
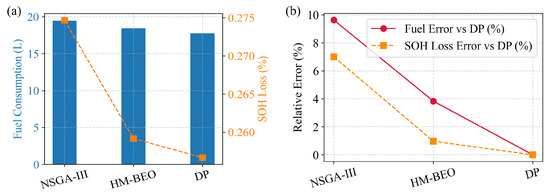
Figure 11.
Comparisons of fuel consumption and SOH degradation between the optimized A-ECMS energy management strategies and the globally optimal DP results: (a) shows the absolute values while (b) presents the relative errors.
The optimized energy controller derived via HM-BEO reduces fuel consumption by 5.3%, mitigates battery SOH degradation by 7.4%, and achieves more stable SOC behavior compared to the original method. Therefore, the HM-BEO framework outperforms traditional methods not only in final Pareto front quality but also in convergence speed and robustness. The control strategies optimized under HM-BEO demonstrate superior performance in fuel efficiency, battery preservation, and thermal management, highlighting the engineering applicability and scalability of the proposed methodology for complex hybrid powertrain systems.
5. Conclusions
This paper addresses the challenges of high-dimensional complexity, dynamic constraints, and energy management coupling in HEVTOL propulsion system design by proposing a novel hierarchical manifold-enhanced Bayesian evolutionary optimization framework. Leveraging manifold-based dimensionality reduction with Bayesian evolutionary search, the proposed approach significantly enhances optimization efficiency and system-level performance. Key contributions include:
- The lightweight manifold-based dimensionality reduction framework is proposed for joint component sizing and energy management parameterization in HEVTOL systems, effectively compressing the high-dimensional design space and improving optimization efficiency.
- A hybrid optimization strategy combining global Bayesian exploration and refined NSGA-III evolution is designed, enabling efficient escape from local optima while ensuring strict adherence to dynamic constraints. The HM-BEO framework achieves faster convergence compared to NSGA-III, as evidenced by IGD trends.
- Comprehensive validation under real-world driving scenarios confirms the engineering applicability of the optimized strategy, with the HM-BEO-derived control parameters reducing fuel consumption by 5.3%, mitigating battery SOH degradation by 7.4%, and reducing system manufacturing costs by 1.7% compared to traditional NSGA-III-based optimization. These improvements highlight the framework’s effectiveness in enhancing energy efficiency, battery longevity, and system cost-efficiency for flying vehicles.
Author Contributions
Methodology, C.L. and N.L.; Software, C.L. and N.L.; Validation, C.L.; Data curation, C.L.; Writing—original draft, C.L.; Writing—review & editing, N.L. and H.Z.; Supervision, C.C. and H.Z.; Funding acquisition, C.C. and H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 52302410), research and development of autonomous driving domain controller and its algorithm (Grant No. 2023Z070), and the China Postdoctoral Science Foundation (Grant No. 2024T170489).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The assistance of the interns at Beijing Tsintelink Technology Co., Ltd. in model development and coding is gratefully acknowledged, and the code will be made available upon request for research purposes.
Conflicts of Interest
Authors Chenghao Lyu and Nuo Lei were employed by the Tsintelink Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K.; Li, M. A novel deep reinforcement learning-based predictive energy management for fuel cell buses integrating speed and passenger prediction. Int. J. Hydrogen Energy 2025, 100, 456–465. [Google Scholar] [CrossRef]
- Chen, C.; Wang, J.; Xu, Q.; Wang, J.; Li, K. Mixed platoon control of automated and human-driven vehicles at a signalized intersection: Dynamical analysis and optimal control. Transp. Res. Part C Emerg. Technol. 2021, 127, 103138. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Geng, J.; Hao, H.; Liu, Z. Comprehensive assessment for different ranges of battery electric vehicles: Is it necessary to develop a battery electric vehicle with an ultra-long range? iScience 2023, 26, 106654. [Google Scholar] [CrossRef]
- Qing, H.; Feng, Y.; Zhang, C.; Gao, J.; Chen, H.; Hao, D.; Yu, P.; Simonovic, M. Parallel structure-based decentralized model predictive control of vehicle PEMFC anode circulation system. Energy 2025, 324, 135767. [Google Scholar] [CrossRef]
- Jin, N.; Jia, F.; Dai, L.; Liu, H.; Wang, T.; Hu, P. A Hierarchical Energy Management Strategy for PHEVs: Optimizing SOC Trajectory Tracking Performance Using Adaptive Initial Equivalent Factor Strategy (AIEFS). Energy 2025, 318, 134816. [Google Scholar] [CrossRef]
- Yi, F.; Shu, X.; Zhou, J.; Zhang, J.; Feng, C.; Gong, H.; Zhang, C.; Yu, W. Remaining useful life prediction of PEMFC based on matrix long short-term memory. Int. J. Hydrogen Energy 2025, 111, 228–237. [Google Scholar] [CrossRef]
- Lei, N.; Zhang, H.; Wang, H.; Wang, Z. An Improved Co-Optimization of Component Sizing and Energy Management for Hybrid Powertrains Interacting With High-fidelity Model. IEEE Trans. Veh. Technol. 2023, 72, 15585–15596. [Google Scholar] [CrossRef]
- He, R.; Ping, Y.; Li, T.; Zhang, Y.; Chen, R. Phase Transition of n-Heptane/Ethanol Blends from Subcritical to Supercritical Conditions. Int. J. Heat Mass Transf. 2022, 185, 122405. [Google Scholar] [CrossRef]
- Zhou, J.; Shu, X.; Zhang, J.; Yi, F.; Jia, C.; Zhang, C.; Kong, X.; Zhang, J.; Wu, G. A deep learning method based on CNN-BiGRU and attention mechanism for proton exchange membrane fuel cell performance degradation prediction. Int. J. Hydrogen Energy 2024, 94, 394–405. [Google Scholar] [CrossRef]
- Chen, C.; Cai, M.; Wang, J.; Li, K.; Xu, Q.; Wang, J.; Li, K. Cooperation Method of Connected and Automated Vehicles at Unsignalized Intersections: Lane Changing and Arrival Scheduling. IEEE Trans. Veh. Technol. 2022, 71, 11351–11366. [Google Scholar] [CrossRef]
- Lu, D.; Yi, F.; Hu, D.; Li, J.; Yang, Q.; Wang, J. Online optimization of energy management strategy for FCV control parameters considering dual power source lifespan decay synergy. Appl. Energy 2023, 348, 121516. [Google Scholar] [CrossRef]
- Wang, Z.; Sasse, J.P.; Trutnevyte, E. Home or workplace charging? Spatio-temporal flexibility of electric vehicles within Swiss electricity system. Energy 2025, 320, 135452. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K. Superior energy management for fuel cell vehicles guided by improved DDPG algorithm: Integrating driving intention speed prediction and health-aware control. Appl. Energy 2025, 394, 126195. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, W.; Cash, S.; Olatunbosun, O.; Xu, H.; Lu, G. Intelligent sizing of a series hybrid electric power-train system based on Chaos-enhanced accelerated particle swarm optimization. Appl. Energy 2017, 189, 588–601. [Google Scholar] [CrossRef]
- He, C.; Jia, Y.; Ma, D. Optimization and Analysis of Hybrid Electric System for Distributed Propulsion Tilt-Wing UAV. IEEE Access 2020, 8, 224654–224667. [Google Scholar] [CrossRef]
- Jia, C.; Liu, W.; He, H.; Chau, K. Deep reinforcement learning-based energy management strategy for fuel cell buses integrating future road information and cabin comfort control. Energy Convers. Manag. 2024, 321, 119032. [Google Scholar] [CrossRef]
- Chen, C.; Xu, Q.; Cai, M.; Wang, J.; Wang, J.; Li, K. Conflict-Free Cooperation Method for Connected and Automated Vehicles at Unsignalized Intersections: Graph-Based Modeling and Optimality Analysis. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21897–21914. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Hao, H.; Liu, Z. Comparative analysis for different vehicle powertrains in terms of energy-saving potential and cost-effectiveness in China. Energy 2023, 276, 127564. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, N.; Wang, Z. Ammonia-hydrogen propulsion system for carbon-free heavy-duty vehicles. Appl. Energy 2024, 369, 123505. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Hao, H.; Liu, Z. Opportunities, Challenges and Strategies for Developing Electric Vehicle Energy Storage Systems under the Carbon Neutrality Goal. World Electr. Veh. J. 2023, 14, 170. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point-Based Nondominated Sorting Approach, Part I: Solving Problems With Box Constraints. IEEE Trans. Evol. Comput. 2014, 18, 577–601. [Google Scholar] [CrossRef]
- He, Y.; Wang, C.; Zhou, Q.; Li, J.; Makridis, M.; Williams, H.; Lu, G.; Xu, H. Multiobjective component sizing of a hybrid ethanol-electric vehicle propulsion system. Appl. Energy 2020, 266, 114843. [Google Scholar] [CrossRef]
- Chen, M.; Li, B.; Bian, Y.; Zhuang, W.; Evangelou, S.; Pan, X.; Chen, B. Intersection Signal-Vehicle Coupled Coordination With Mixed Autonomy Vehicles. IEEE Trans. Transp. Electrif. 2024, 11, 668–681. [Google Scholar] [CrossRef]
- Zhang, H.; Fan, Q.; Liu, S.; Li, S.E.; Huang, J.; Wang, Z. Hierarchical energy management strategy for plug-in hybrid electric powertrain integrated with dual-mode combustion engine. Appl. Energy 2021, 304, 117869. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, S.; Lei, N.; Fan, Q.; Li, S.E.; Wang, Z. Learning-based supervisory control of dual mode engine-based hybrid electric vehicle with reliance on multivariate trip information. Energy Convers. Manag. 2022, 257, 115450. [Google Scholar] [CrossRef]
- Li, Y.; Lu, X.; Kar, N.C. Rule-Based Control Strategy With Novel Parameters Optimization Using NSGA-II for Power-Split PHEV Operation Cost Minimization. IEEE Trans. Veh. Technol. 2014, 63, 3051–3061. [Google Scholar] [CrossRef]
- Sun, H.; Li, S.; Li, B.; Chen, M.; Zhang, S.; Zhuang, W.; Yin, G.; Chen, B. Spatial–temporal transformer-based ecological car-following strategy for connected electric vehicles in dynamic environments. Energy 2025, 317, 134673. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, B.; Lei, N.; Li, B.; Li, R.; Wang, Z. Integrated Thermal and Energy Management of Connected Hybrid Electric Vehicles Using Deep Reinforcement Learning. IEEE Trans. Transp. Electrif. 2024, 10, 4594–4603. [Google Scholar] [CrossRef]
- Li, K.; Zhou, J.; Jia, C.; Yi, F.; Zhang, C. Energy sources durability energy management for fuel cell hybrid electric bus based on deep reinforcement learning considering future terrain information. Int. J. Hydrogen Energy 2024, 52, 821–833. [Google Scholar] [CrossRef]
- Wen, Y.; Chu, Z.; Srivastava, A.; Teng, F.; Chen, B. Resilient Microgrid Scheduling With Synthetic Inertia From Electric Vehicles Within a Network of Charging Stations. IEEE Trans. Control Syst. Technol. 2024, 33, 775–787. [Google Scholar] [CrossRef]
- He, R.; Ping, Y.; Li, T. Evaporation and condensation characteristics of n -heptane and multi-component diesel droplets under typical spray relevant conditions. Int. J. Heat Mass Transf. 2020, 163, 120162. [Google Scholar] [CrossRef]
- Milićević, S.; Blagojević, I.; Milojević, S.; Bukvić, M.; Stojanović, B. Numerical Analysis of Optimal Hybridization in Parallel Hybrid Electric Powertrains for Tracked Vehicles. Energies 2024, 17, 3531. [Google Scholar] [CrossRef]
- Bao, H.; Knights, P.; Kizil, M.; Nehring, M. Energy Consumption and Battery Size of Battery Trolley Electric Trucks in Surface Mines. Energies 2024, 17, 1494. [Google Scholar] [CrossRef]
- Parkar, O.; Snyder, B.; Rahi, A.; Anwar, S. Modified Particle Swarm Optimization Based Powertrain Energy Management for Range Extended Electric Vehicle. Energies 2023, 16, 5082. [Google Scholar] [CrossRef]
- Pardhi, S.; El Baghdadi, M.; Hulsebos, O.; Hegazy, O. Optimal Powertrain Sizing of Series Hybrid Coach Running on Diesel and HVO for Lifetime Carbon Footprint and Total Cost Minimisation. Energies 2022, 15, 6974. [Google Scholar] [CrossRef]
- Jia, C.; He, H.; Zhou, J.; Li, J.; Wei, Z.; Li, K. Learning-based model predictive energy management for fuel cell hybrid electric bus with health-aware control. Appl. Energy 2024, 355, 122228. [Google Scholar] [CrossRef]
- Ruan, S.; Ma, Y.; Wei, Z.; Zhang, C.; Xiang, C. Data-Driven Cooperative Differential Game Based Energy Management Strategy for Hybrid Electric Propulsion System of a Flying Car. IEEE Trans. Intell. Transp. Syst. 2024, 25, 14770–14784. [Google Scholar] [CrossRef]
- Zhang, H.; Lei, N.; Liu, S.; Fan, Q.; Wang, Z. Data-driven predictive energy consumption minimization strategy for connected plug-in hybrid electric vehicles. Energy 2023, 283, 128514. [Google Scholar] [CrossRef]
- Wu, X.; Cao, B.; Li, X.; Xu, J.; Ren, X. Component sizing optimization of plug-in hybrid electric vehicles. Appl. Energy 2011, 88, 799–804. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Huang, P.; Han, W.; Lyu, Y.; Xu, M.; Zhao, D. Dynamics as Prompts: In-Context Learning for Sim-to-Real System Identifications. IEEE Robot. Autom. Lett. 2025, 10, 3190–3197. [Google Scholar] [CrossRef]
- Xiongbo, D.; Chu, X.; Wang, R.; Chen, Z.; Zhou, F.; Abdellatief, T. The performance and emissions characteristics of the gasoline spark ignition engine fuelled with green and renewable methanol and hydrogen. Renew. Energy 2024, 240, 122184. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, B.; Lei, N.; Li, B.; Chen, C.; Wang, Z. Coupled velocity and energy management optimization of connected hybrid electric vehicles for maximum collective efficiency. Appl. Energy 2024, 360, 122792. [Google Scholar] [CrossRef]
- Chen, B.; Li, X.; Evangelou, S.; Lot, R. Joint Propulsion and Cooling Energy Management of Hybrid Electric Vehicles by Optimal Control. IEEE Trans. Veh. Technol. 2020, 69, 4894–4906. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).