A Real-Time Investigation of an Enhanced Variable Step PO MPPT Controller for Photovoltaic Systems Using dSPACE 1104 Board
Abstract
1. Introduction
1.1. Reasoning and Motivation
1.2. Literature Review
- This study presents a newly improved variable-step current perturbation Perturb and Observe (IVSCP-PO) MPPT controller strategy.
- It provides a dynamic adjustment of step size based on simultaneous changes in power, voltage, and current for precise tuning and faster convergence.
- It incorporates a drift avoidance mechanism to prevent loss of tracking locus during rapid changes in atmospheric conditions, enhancing accuracy and stability.
- It effectively tracks the MPP under sudden changes in insolation conditions, overcoming the limitations of traditional and improved PO algorithms.
- Extensive comparison with the traditional PO approach under various scenarios demonstrates superior performance in convergence speed, MPP fluctuation, accuracy, and tracking efficiency.
- It is experimentally validated using a real-time test bench system with the dSPACE DS1104 board, providing practical evidence of the approach’s effectiveness beyond simulations.
2. An Overview of the Components of the Photovoltaic System
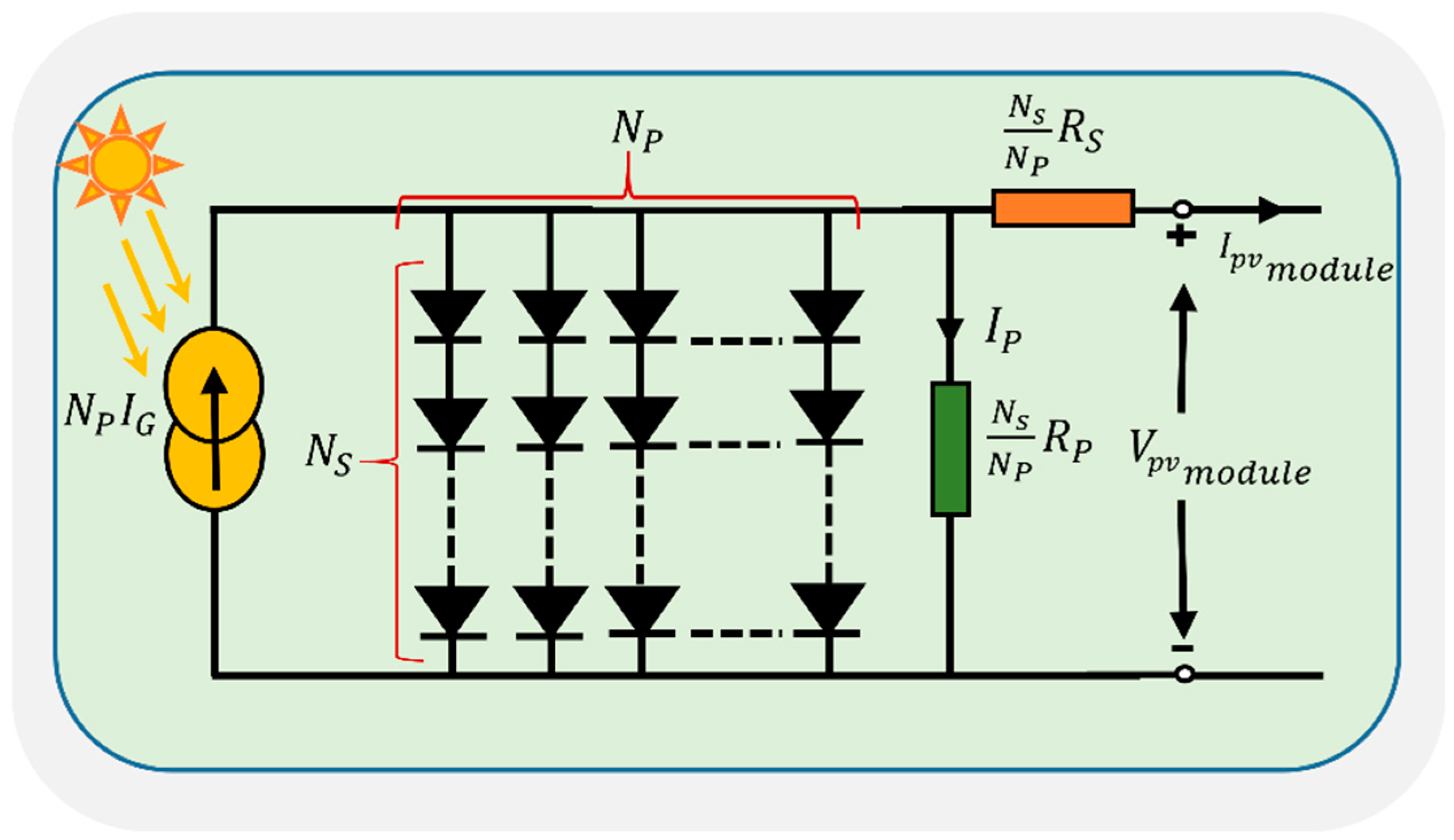
2.1. Mathematical Model of Solar Photovoltaic Cell Equivalent Circuit
2.2. Maximum Power Point System
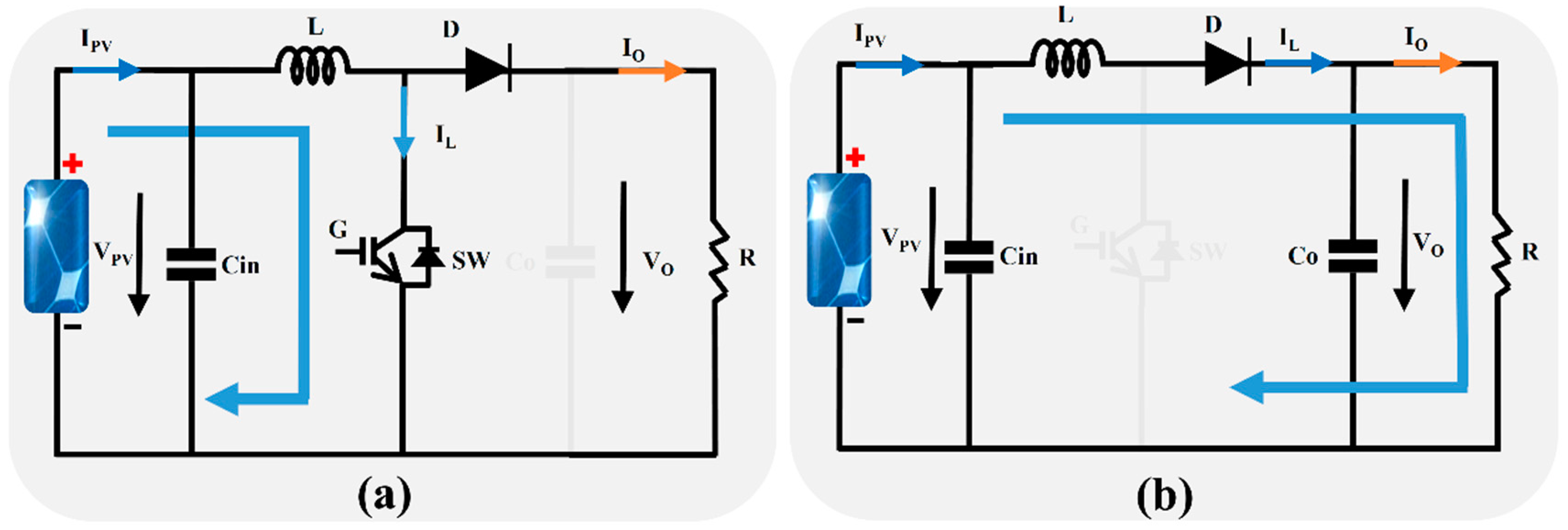
2.2.1. DC-DC Converter
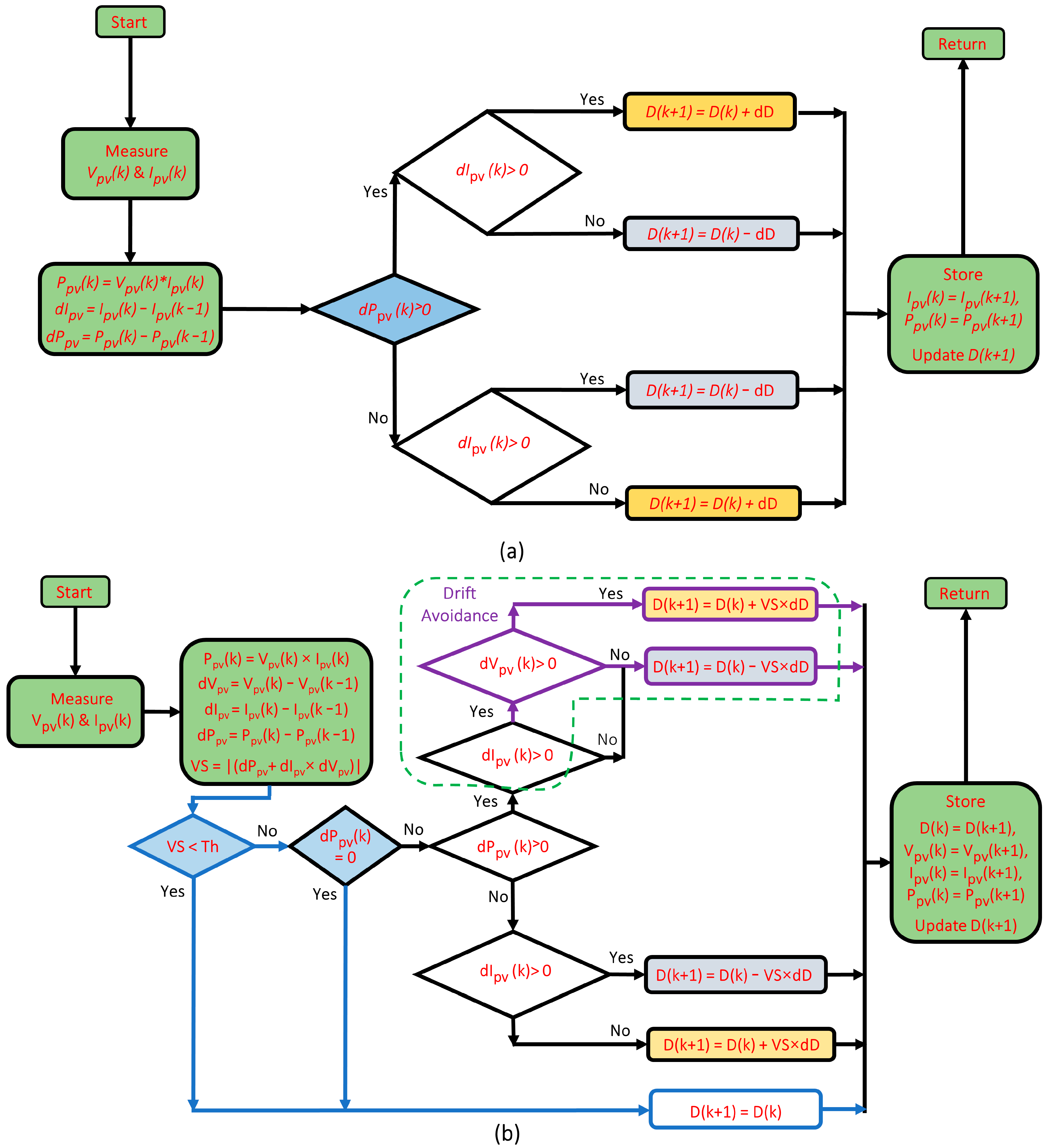
2.2.2. Classical and Amended PO MPPT Controllers
- (a)
- Classical PO MPPT algorithm
- (b)
- Proposed IVSCP-PO MPPT controller
3. Results and Discussions
3.1. Simulation-Based Investigation
3.1.1. Variable Atmospheric Circumstances
First Investigation during the Rapid Shift in Solar Intensity
Second Investigation under Rapid Shift in Temperature
Third Investigation under Gradient Insolation Situations
3.2. Experimental-Based Investigation
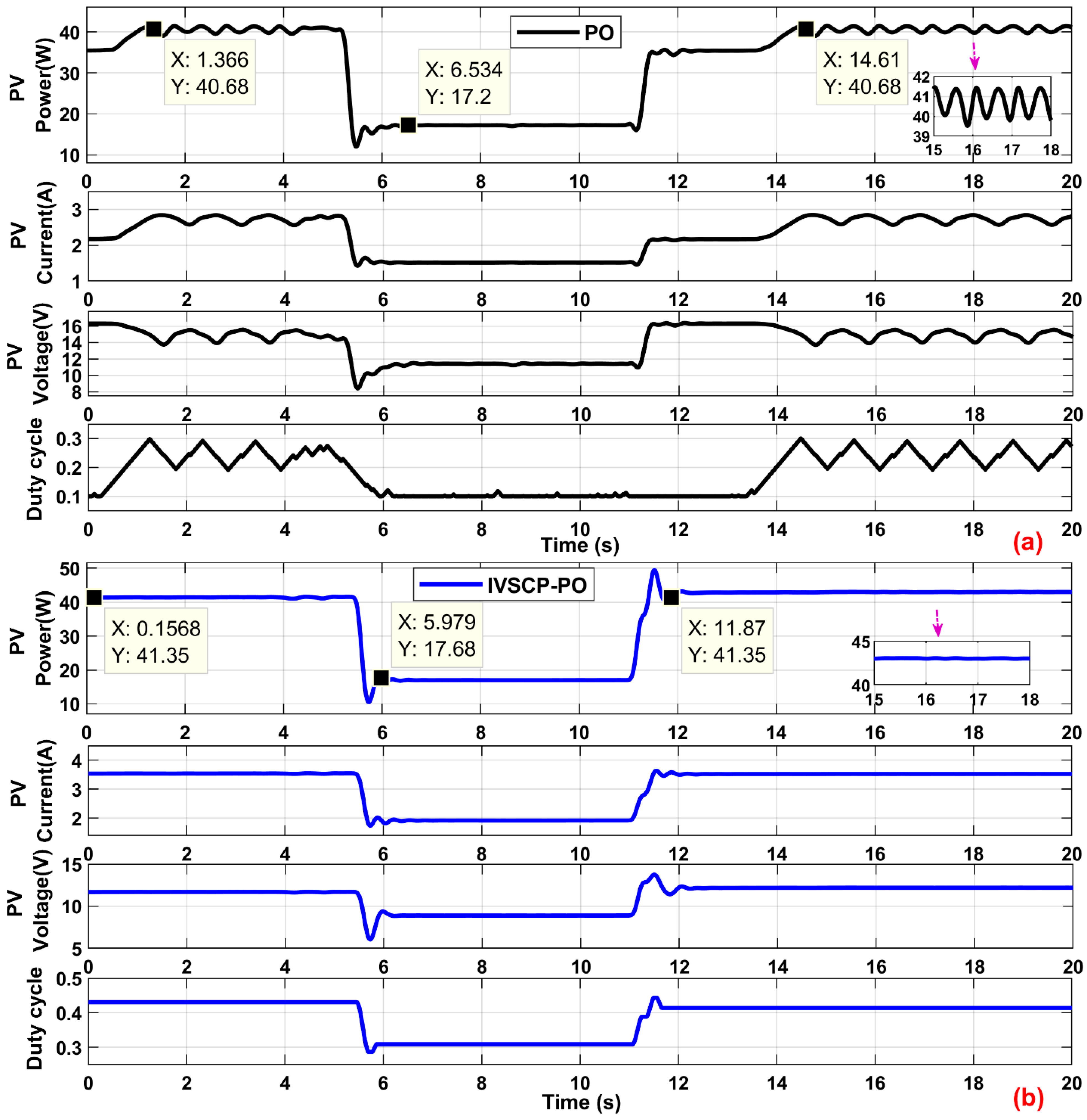
3.2.1. Static Atmospheric Circumstances
3.2.2. Variable Atmospheric Circumstances
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Y.; Wang, H.; Lian, J. Review of integrated installation technologies for offshore wind turbines: Current progress and future development trends. Energy Convers. Manag. 2022, 255, 115319. [Google Scholar] [CrossRef]
- Bouabdalli, E.M.; Jouad, M.; Touhtouh, S.; Chellakhi, A.; Hajjaji, A. Synthesis, structural, and optical behavior of erbium-doped silicophosphate glasses for photonics applications. Luminescence 2024, 39, e4802. [Google Scholar] [CrossRef]
- Ahmadi, S.; Tostado-Véliz, M.; Ghadimi, A.A.; Miveh, M.R.; Jurado, F. A novel interval-based formulation for optimal scheduling of microgrids with pumped-hydro and battery energy storage under uncertainty. Int. J. Energy Res. 2022, 46, 12854–12870. [Google Scholar] [CrossRef]
- Mouncef, E.M.; Mostafa, B. Battery total capacity estimation based on the sunflower algorithm. J. Energy Storage 2022, 48, 103900. [Google Scholar] [CrossRef]
- Hsu, R.Y.; Lai, Y.L.; Chou, Y.H.; Syu, W.J. Improving Carrier Transport Behavior in a Bilayer ETL for Enhanced Efficiency of Perovskite Solar Cells: An Investigation. Energies 2024, 17, 871. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, L.; Zhang, C. Research Progress of Semi-Transparent Perovskite and Four-Terminal Perovskite/Silicon Tandem Solar Cells. Energies 2024, 17, 1833. [Google Scholar] [CrossRef]
- Fatima, Q.; Haidry, A.A.; Hussain, R.; Zhang, H. Device Simulation of a Thin-Layer CsSnI3-Based Solar Cell with Enhanced 31.09% Efficiency. Energy Fuels 2023, 37, 7411–7423. [Google Scholar] [CrossRef]
- Huda, A.; Kurniawan, I.; Purba, K.F.; Ichwani, R.; Aryansyah; Fionasari, R. Techno-economic assessment of residential and farm-based photovoltaic systems. Renew. Energy 2024, 222, 119886. [Google Scholar] [CrossRef]
- El Kassar, R.; Al Takash, A.; Faraj, J.; Khaled, M.; Ramadan, H.S. Phase change materials for enhanced photovoltaic panels performance: A comprehensive review and critical analysis. Energy Built Environ. 2024. [Google Scholar] [CrossRef]
- Bouabdalli, E.M.; El Jouad, M.; Garmim, T.; Louardi, A.; Hartiti, B.; Monkade, M.; Touhtouh, S.; Hajjaji, A. Elaboration and characterization of Ni and Al co-doped SnO2 thin films prepared by spray pyrolysis technique for photovoltaic applications. Mater. Sci. Eng. B 2022, 286, 116044. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y.; Mchaouar, Y. Optimization of Power Extracting from Photovoltaic Systems Based on a Novel Adaptable Step INC MPPT Approach. IFAC-PapersOnLine 2022, 55, 508–513. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Farahani, M.; Shamsi-nejad, M.A.; Najafi, H.R. Design and construction of a digital solar array simulator with fast dynamics and high performance. Sol. Energy 2020, 196, 319–326. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y. An Improved Maximum Power Point Approach for Temperature Variation in PV System Applications. Int. J. Photoenergy 2021, 2021, 9973204. [Google Scholar] [CrossRef]
- Yang, B.; Zhu, T.; Wang, J.; Shu, H.; Yu, T.; Zhang, X.; Yao, W.; Sun, L. Comprehensive overview of maximum power point tracking algorithms of PV systems under partial shading condition. J. Clean. Prod. 2020, 268, 121983. [Google Scholar] [CrossRef]
- Nguimfack-Ndongmo, J.D.D.; Harrison, A.; Alombah, N.H.; Kuate-Fochie, R.; Asoh, D.A.; Kenné, G. Adaptive terminal synergetic-backstepping technique based machine learning regression algorithm for MPPT control of PV systems under real climatic conditions. ISA Trans. 2024, 145, 423–442. [Google Scholar] [CrossRef] [PubMed]
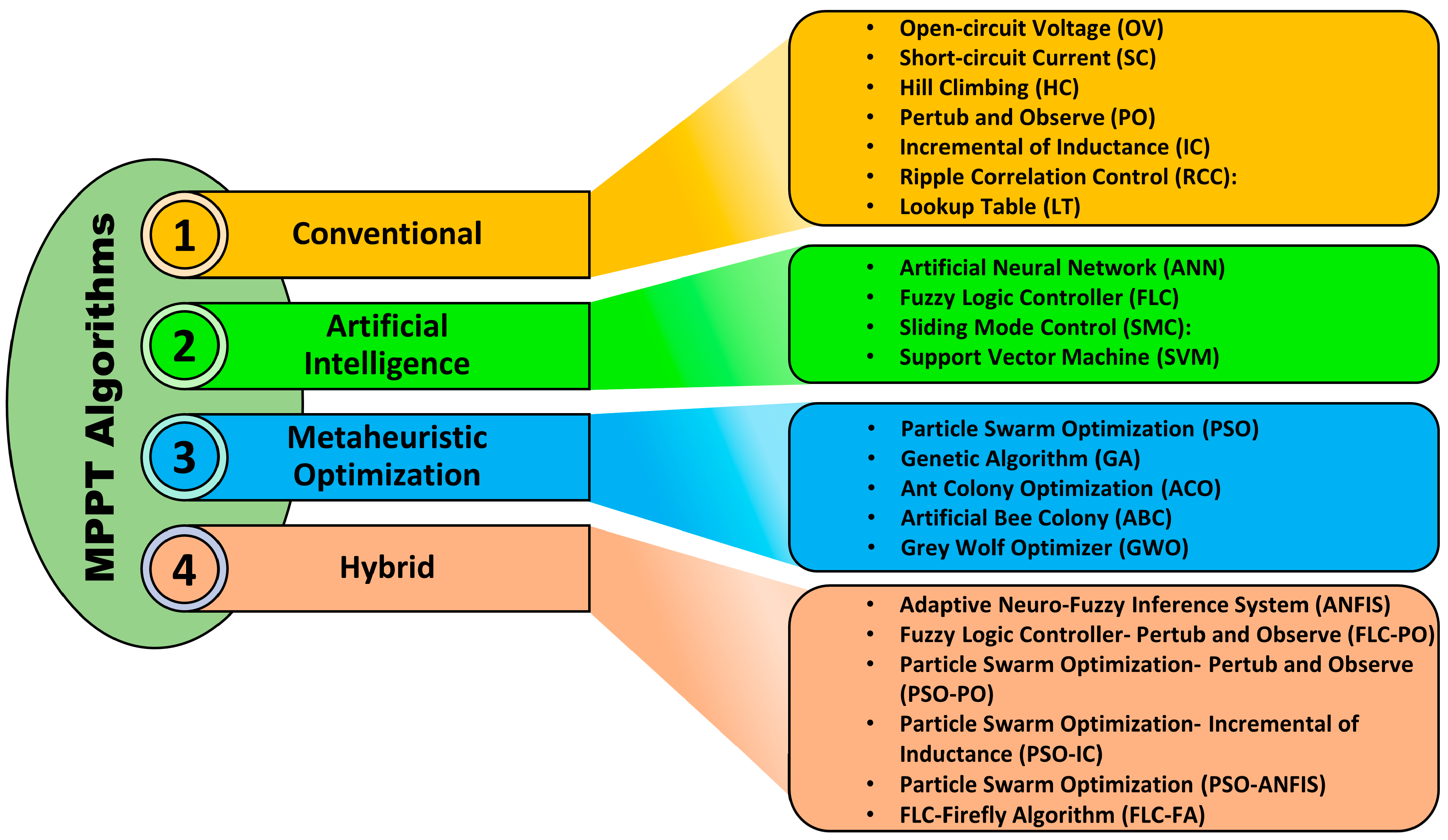
- Boubaker, O. MPPT techniques for photovoltaic systems: A systematic review in current trends and recent advances in artificial intelligence. Discov. Energy 2023, 3, 9. [Google Scholar] [CrossRef]
- Harrison, A.; Nfah, E.M.; De Dieu Nguimfack Ndongmo, J.; Alombah, N.H. An Enhanced P&O MPPT Algorithm for PV Systems with Fast Dynamic and Steady-State Response under Real Irradiance and Temperature Conditions. Int. J. Photoenergy 2022, 2022, 6009632. [Google Scholar] [CrossRef]
- Sameera; Tariq, M.; Rihan, M.; Ayan, M. A comprehensive review on the application of recently introduced optimization techniques obtaining maximum power in the solar PV System. Renew. Energy Focus 2024, 49, 100564. [Google Scholar] [CrossRef]
- Jately, V.; Azzopardi, B.; Joshi, J.; Venkateswaran, V.B.; Sharma, A.; Arora, S. Experimental Analysis of hill-climbing MPPT algorithms under low irradiance levels. Renew. Sustain. Energy Rev. 2021, 150, 111467. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y. An Innovative Fast-Converging Speed MPPT Approach without Oscillation for Temperature Varying in Photovoltaic Systems Applications. Energy Sources Part A Recover. Util. Environ. Eff. 2022, 44, 2674–2696. [Google Scholar] [CrossRef]
- Behera, P.K.; Pattnaik, M. Design and real-time implementation of wind–photovoltaic driven low voltage direct current microgrid integrated with hybrid energy storage system. J. Power Sources 2024, 595, 234028. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y.; Doubabi, H. An Enhanced Incremental Conductance MPPT Approach for PV Power Optimization: A Simulation and Experimental Study. Arab. J. Sci. Eng. 2024. [Google Scholar] [CrossRef]
- Ali, M.N.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M.F. An Efficient Fuzzy-Logic Based Variable-Step Incremental Conductance MPPT Method for Grid-Connected PV Systems. IEEE Access 2021, 9, 26420–26430. [Google Scholar] [CrossRef]
- Fapi, C.B.N.; Wira, P.; Kamta, M.; Tchakounté, H.; Colicchio, B. Simulation and dSPACE Hardware Implementation of an Improved Fractional Short-Circuit Current MPPT Algorithm for Photovoltaic System. Appl. Sol. Energy (Engl. Transl. Geliotekhnika) 2021, 57, 93–106. [Google Scholar] [CrossRef]
- Bollipo, R.B.; Mikkili, S.; Bonthagorla, P.K. Hybrid, Optimization, Intelligent and Classical PV MPPT Techniques: Review. CSEE J. Power Energy Syst. 2020, 7, 9–33. [Google Scholar]
- Abidi, H.; Sidhom, L.; Chihi, I. Systematic Literature Review and Benchmarking for Photovoltaic MPPT Techniques. Energies 2023, 16, 3509. [Google Scholar] [CrossRef]
- Ibrahim, M.H.; Ang, S.P.; Dani, M.N.; Rahman, M.I.; Petra, R.; Sulthan, S.M. Optimizing Step-Size of Perturb & Observe and Incremental Conductance MPPT Techniques Using PSO for Grid-Tied PV System. IEEE Access 2023, 11, 13079–13090. [Google Scholar] [CrossRef]
- Guerra, M.I.S.; de Araújo, F.M.U.; Dhimish, M.; Vieira, R.G. Assessing maximum power point tracking intelligent techniques on a pv system with a buck–boost converter. Energies 2021, 14, 7453. [Google Scholar] [CrossRef]
- Jamshidi, F.; Salehizadeh, M.R.; Yazdani, R.; Azzopardi, B.; Jately, V. An Improved Sliding Mode Controller for MPP Tracking of Photovoltaics. Energies 2023, 16, 2473. [Google Scholar] [CrossRef]
- Baatiah, A.O.; Eltamaly, A.M.; Alotaibi, M.A. Improving Photovoltaic MPPT Performance through PSO Dynamic Swarm Size Reduction. Energies 2023, 16, 6433. [Google Scholar] [CrossRef]
- Chao, K.H.; Rizal, M.N. A hybrid mppt controller based on the genetic algorithm and ant colony optimization for photovoltaic systems under partially shaded conditions. Energies 2021, 14, 2902. [Google Scholar] [CrossRef]
- Gong, L.; Hou, G.; Huang, C. A two-stage MPPT controller for PV system based on the improved artificial bee colony and simultaneous heat transfer search algorithm. ISA Trans. 2023, 132, 428–443. [Google Scholar] [CrossRef]
- Aguila-Leon, J.; Vargas-Salgado, C.; Chiñas-Palacios, C.; Díaz-Bello, D. Solar photovoltaic Maximum Power Point Tracking controller optimization using Grey Wolf Optimizer: A performance comparison between bio-inspired and traditional algorithms. Expert Syst. Appl. 2023, 211, 118700. [Google Scholar] [CrossRef]
- Raj, R.D.A.; Naik, K.A. Priority queue-based switching matrix algorithm for adaptive neuro-fuzzy inference system assisted MPPT controlled PV system. Energy Convers. Manag. 2023, 293, 117519. [Google Scholar] [CrossRef]
- Liu, H.; Khan, M.Y.A.; Yuan, X. Hybrid Maximum Power Extraction Methods for Photovoltaic Systems: A Comprehensive Review. Energies 2023, 16, 5665. [Google Scholar] [CrossRef]
- Mohanty, S.; Subudhi, B.; Ray, P.K. A Grey Wolf-Assisted Perturb & Observe MPPT Algorithm for a PV System. IEEE Trans. Energy Convers. 2017, 32, 340–347. [Google Scholar] [CrossRef]
- Harrison, A.; Dieu Nguimfack-Ndongmo, J.D.; Alombah, N.H.; Aloyem Kazé, C.V.; Kuate-Fochie, R.; Asoh, D.A.; Nfah, E.M. Robust nonlinear MPPT controller for PV energy systems using PSO-based integral backstepping and artificial neural network techniques. Int. J. Dyn. Control 2023, 12, 1598–1615. [Google Scholar] [CrossRef]
- Ajiatmo, D.; Robandi, I. A Hybrid fuzzy logic controller-firefly algorithm (FLC-FA) based for MPPT photovoltaic (PV) system in solar car. In Proceedings of the 2016 IEEE International Conference on Power and Renewable Energy, ICPRE, Shanghai, China, 21–23 October 2016. [Google Scholar] [CrossRef]
- Padmanaban, S.; Priyadarshi, N.; Bhaskar, M.S.; Holm-Nielsen, J.B.; Ramachandaramurthy, V.K.; Hossain, E. A Hybrid ANFIS-ABC Based MPPT Controller for PV System with Anti-Islanding Grid Protection: Experimental Realization. IEEE Access 2019, 7, 103377–103389. [Google Scholar] [CrossRef]
- El Marghichi, M.; Dangoury, S. Electrical parameters identification for three diode photovoltaic based on the manta ray foraging optimization with dynamic fitness distance balance. Optik 2024, 296, 171548. [Google Scholar] [CrossRef]
- Magableh, M.A.K.; Radwan, A.; Mohamed, Y.A.R.I. A Novel Hybrid Approach Based on Analytical and Metaheuristic Algorithms for Parameters and Dynamic Resistance Estimation of a PV Array. IEEE Trans. Power Syst. 2023, 38, 5459–5474. [Google Scholar] [CrossRef]
- Mouncef, E.; Hilali, A.; Loulijat, A.; Essounaini, A.; Chellakhi, A. Modelling photovoltaic modules with enhanced accuracy using particle swarm clustered optimization. Acta IMEKO 2024, 13, 1–10. [Google Scholar] [CrossRef]
- Changmai, P.; Deka, S.; Kumar, S.; Babu, T.S.; Aljafari, B.; Nastasi, B. A Critical Review on the Estimation Techniques of the Solar PV Cell’s Unknown Parameters. Energies 2022, 15, 7212. [Google Scholar] [CrossRef]
- Castro, R.; Silva, M. Experimental and theoretical validation of one diode and three parameters–based pv models. Energies 2021, 14, 2140. [Google Scholar] [CrossRef]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y. A novel theta MPPT approach based on adjustable step size for photovoltaic system applications under various atmospheric conditions. Energy Syst. 2022, 15, 89–114. [Google Scholar] [CrossRef]
- Rai, N.; Abbadi, A.; Hamidia, F.; Douifi, N.; Samad, B.A.; Yahya, K. Biogeography-Based Teaching Learning-Based Optimization Algorithm for Identifying One-Diode, Two-Diode and Three-Diode Models of Photovoltaic Cell and Module. Mathematics 2023, 11, 1861. [Google Scholar] [CrossRef]
- Abdelkhalek, C.; Said, E.B.; Younes, A. A novel MPPT tactic for PV systems with fast-converging speed and zero oscillation. In Proceedings of the 2020 5th International Conference on Renewable Energies for Developing Countries, REDEC, Marrakech, Morocco, 29–30 June 2020. [Google Scholar] [CrossRef]
- Farajdadian, S.; Hajizadeh, A.; Soltani, M. Recent developments of multiport DC/DC converter topologies, control strategies, and applications: A comparative review and analysis. Energy Rep. 2024, 11, 1019–1052. [Google Scholar] [CrossRef]
- Nandish, B.M.; Pushparajesh, V.; Marulasiddappa, H.B. DC-DC power converter topologies for sustainable applications. In Power Converters, Drives and Controls for Sustainable Operations; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar] [CrossRef]
- Jana, S.; Kumar, N.; Mishra, R.; Sen, D.; Saha, T.K. Development and implementation of modified MPPT algorithm for boost converter-based PV system under input and load deviation. Int. Trans. Electr. Energy Syst. 2020, 30, e12190. [Google Scholar] [CrossRef]
- Rashid, M.H. Power Electronics: Circuits, Devices, and Applications; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Chellakhi, A.; El Beid, S.; Abouelmahjoub, Y. An improved adaptable step-size P&O MPPT approach for standalone photovoltaic systems with battery station. Simul. Model. Pract. Theory 2022, 121, 102655. [Google Scholar] [CrossRef]
- Altwallbah, N.M.M.; Radzi, M.A.M.; Azis, N.; Shafie, S.; Zainuri, M.A.A.M. New perturb and observe algorithm based on trapezoidal rule: Uniform and partial shading conditions. Energy Convers. Manag. 2022, 264, 115738. [Google Scholar] [CrossRef]
- Taibi, D.; Amieur, T.; Laamayad, T.; Sedraoui, M. Improvement of the Standard Perturb & Observe MPPT control strategy by the proposed Fuzzy Logic Mechanism for a Cascade Regulation of a PMSM-based PV pumping system. Arab. J. Sci. Eng. 2023, 48, 6631–6647. [Google Scholar] [CrossRef]
- Ali, A.I.M.; Mousa, H.H.H.; Ramadan, H.; Kamel, S. An Enhanced P & O MPPT Algorithm With Concise Search Area for Grid-Tied PV Systems. IEEE Access 2023, 11, 79408–79421. [Google Scholar] [CrossRef]
- Kermadi, M.; Mekhilef, S.; Salam, Z.; Ahmed, J.; Berkouk, E.M. Assessment of maximum power point trackers performance using direct and indirect control methods. Int. Trans. Electr. Energy Syst. 2020, 30, e12565. [Google Scholar] [CrossRef]
- Kollimalla, S.K.; Mishra, M.K. A novel adaptive p&o mppt algorithm considering sudden changes in the irradiance. IEEE Trans. Energy Convers. 2014, 29, 602–610. [Google Scholar] [CrossRef]
- Wang, S.C.; Pai, H.Y.; Chen, G.J.; Liu, Y.H. A Fast and Efficient Maximum Power Tracking Combining Simplified State Estimation with Adaptive Perturb and Observe. IEEE Access 2020, 8, 155319–155328. [Google Scholar] [CrossRef]
- Mohammadinodoushan, M.; Abbassi, R.; Jerbi, H.; Ahmed, F.W.; Abdalqadir kh ahmed, H.; Rezvani, A. A new MPPT design using variable step size perturb and observe method for PV system under partially shaded conditions by modified shuffled frog leaping algorithm—SMC controller. Sustain. Energy Technol. Assess. 2021, 45, 101056. [Google Scholar] [CrossRef]
- Ahmed, J.; Salam, Z. A Modified P and O Maximum Power Point Tracking Method with Reduced Steady-State Oscillation and Improved Tracking Efficiency. IEEE Trans. Sustain. Energy 2016, 7, 1506–1515. [Google Scholar] [CrossRef]
- Femia, N.; Petrone, G.; Spagnuolo, G.; Vitelli, M. Optimization of perturb and observe maximum power point tracking method. IEEE Trans. Power Electron. 2005, 20, 963–973. [Google Scholar] [CrossRef]
- Manjunath, M.G.; Vyjayanthi, C.; Modi, C.N. Adaptive step size based drift-free P&O algorithm with power optimiser and load protection for maximum power extraction from PV panels in stand-alone applications. IET Renew. Power Gener. 2021, 15, 1270–1285. [Google Scholar] [CrossRef]
- Manoharan, P.; Subramaniam, U.; Babu, T.S.; Padmanaban, S.; Holm-Nielsen, J.B.; Mitolo, M.; Ravichandran, S. Improved Perturb and Observation Maximum Power Point Tracking Technique for Solar Photovoltaic Power Generation Systems. IEEE Syst. J. 2021, 15, 3024–3035. [Google Scholar] [CrossRef]



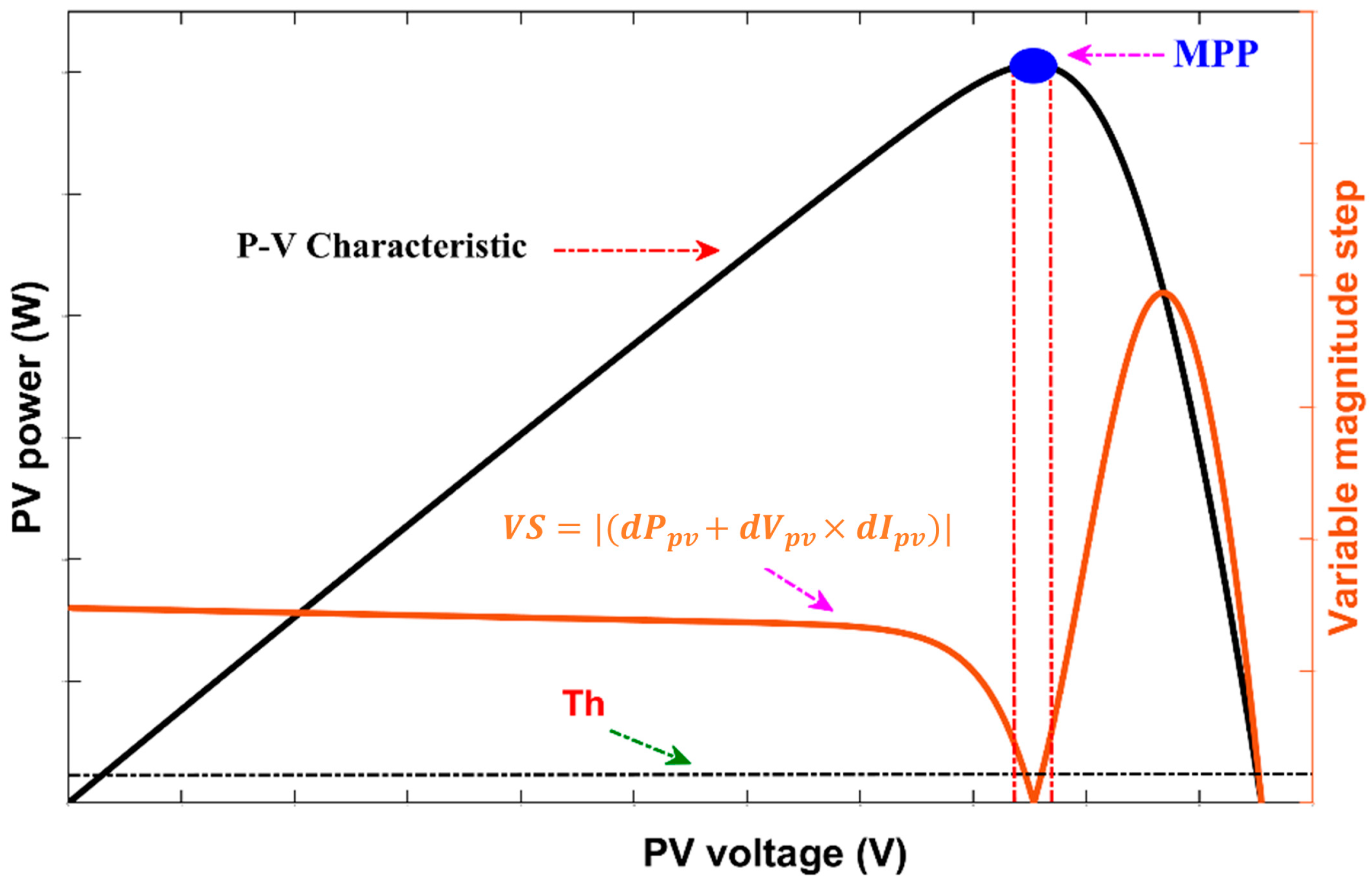



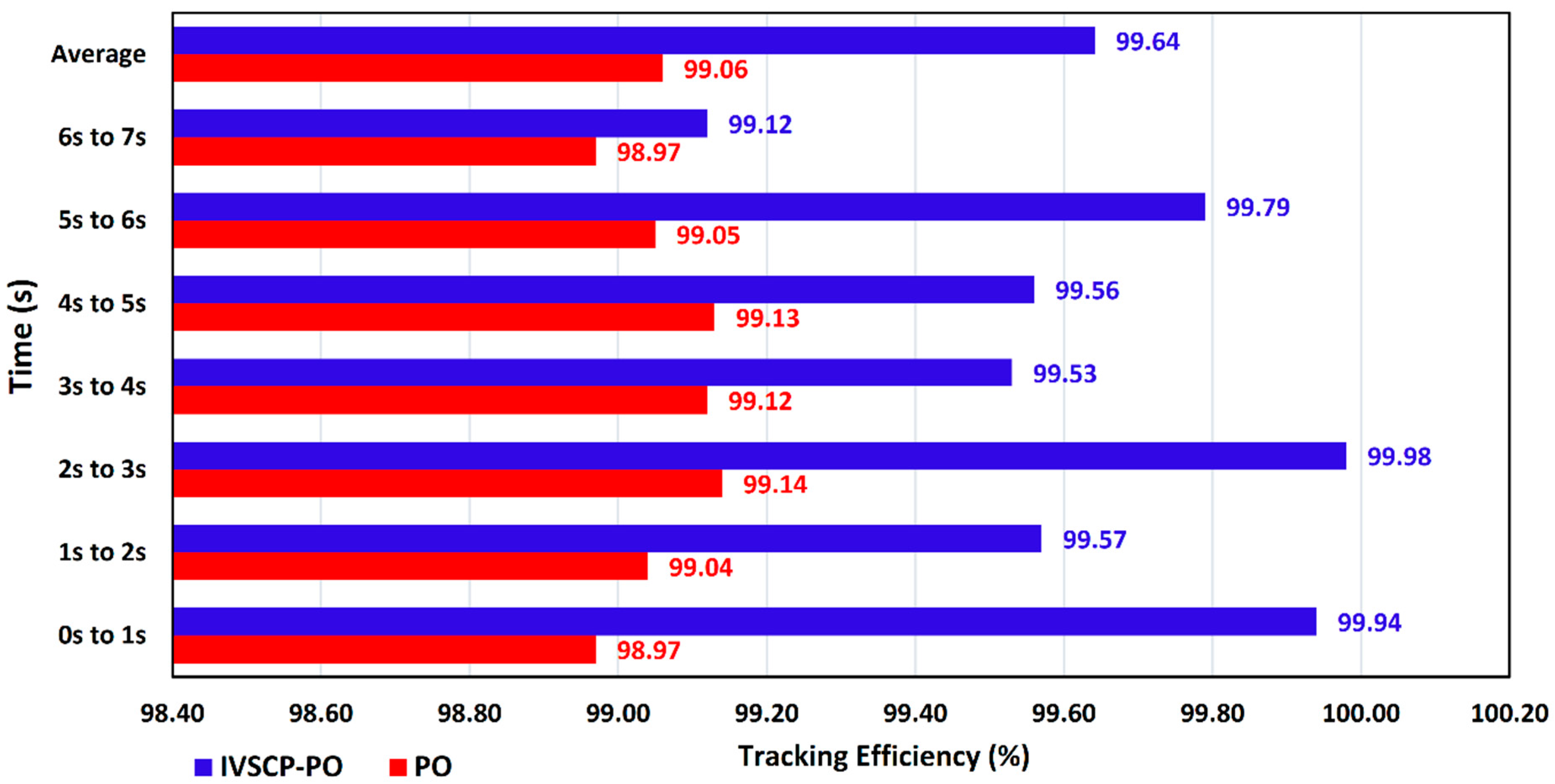
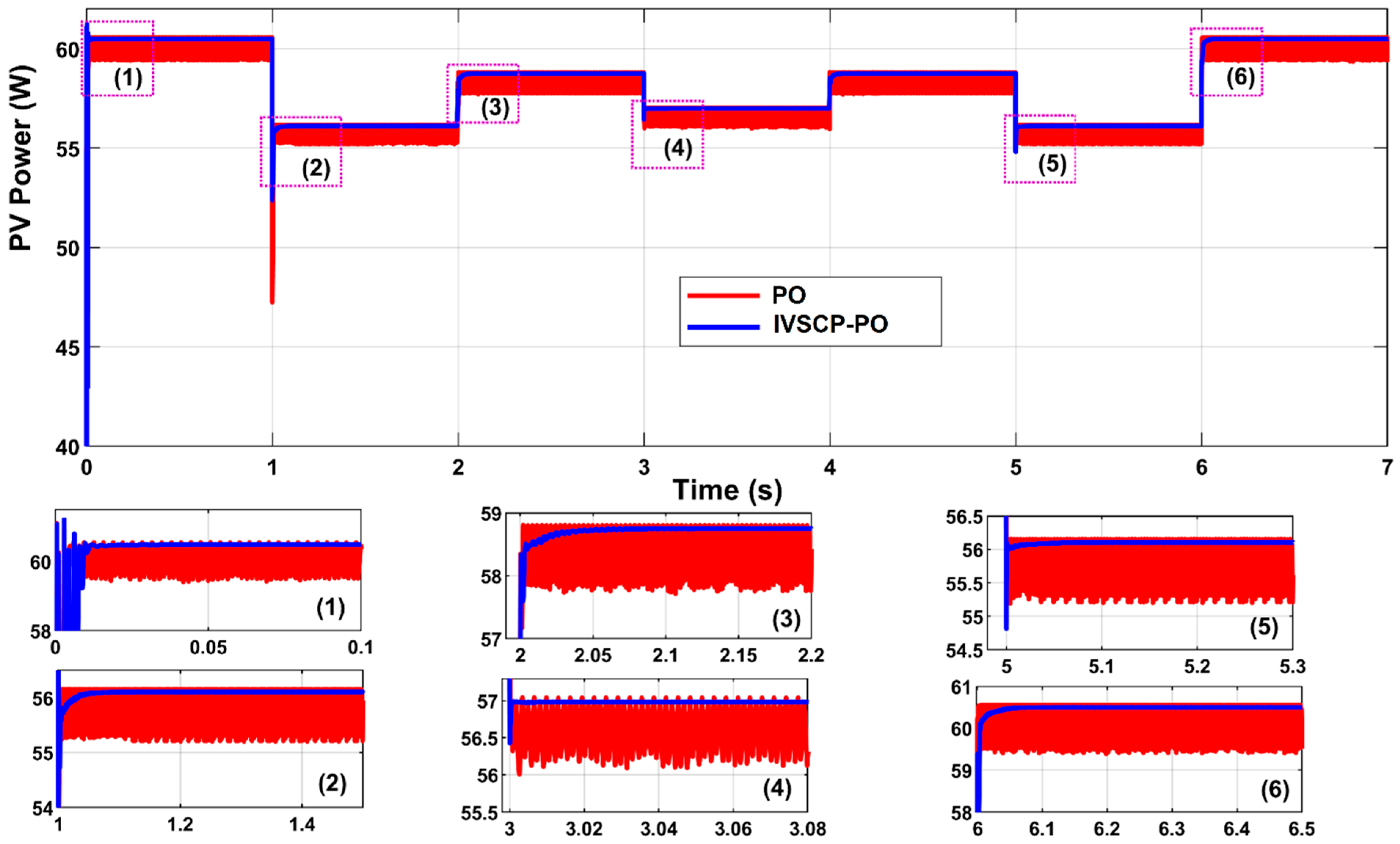
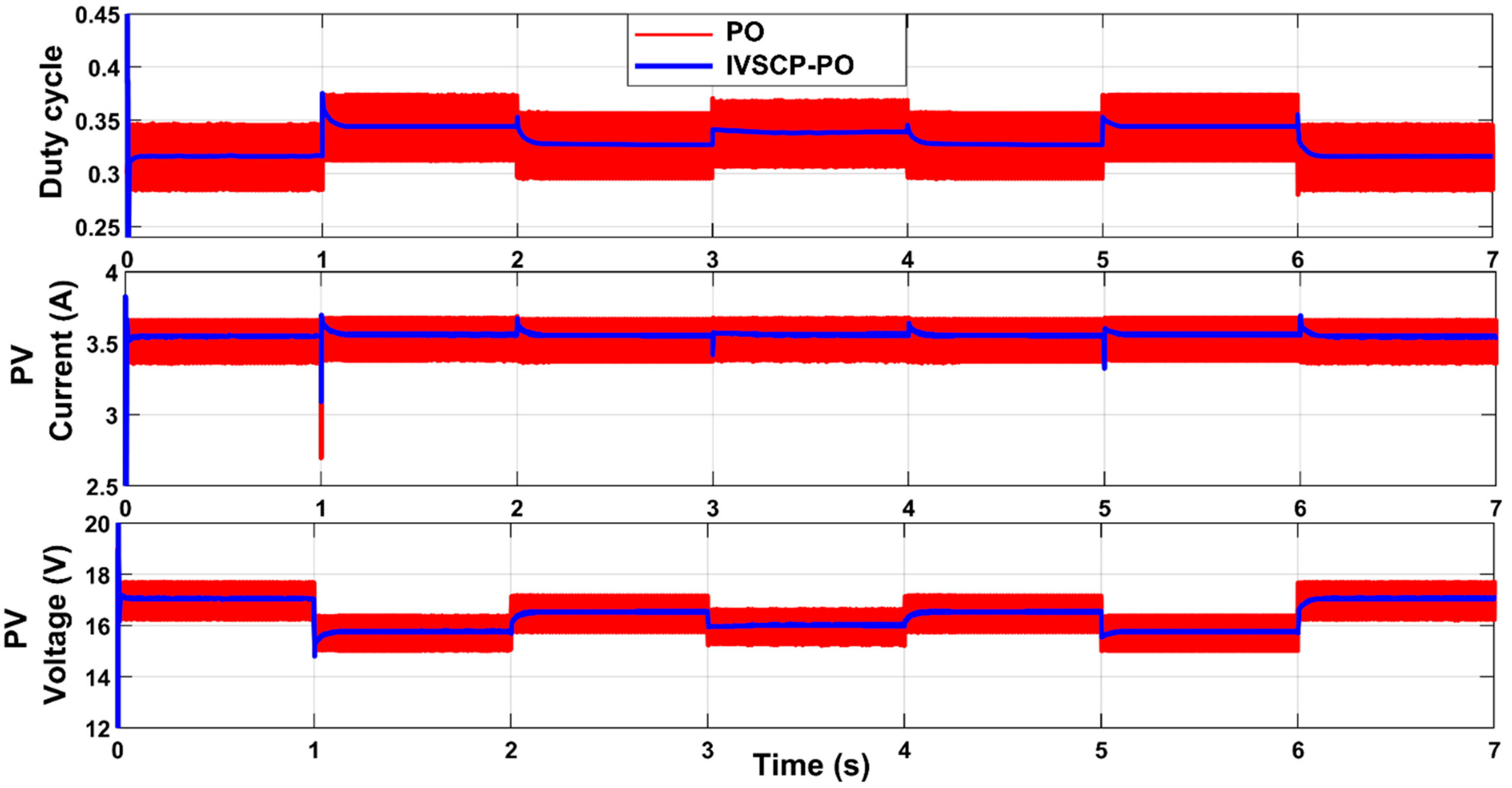
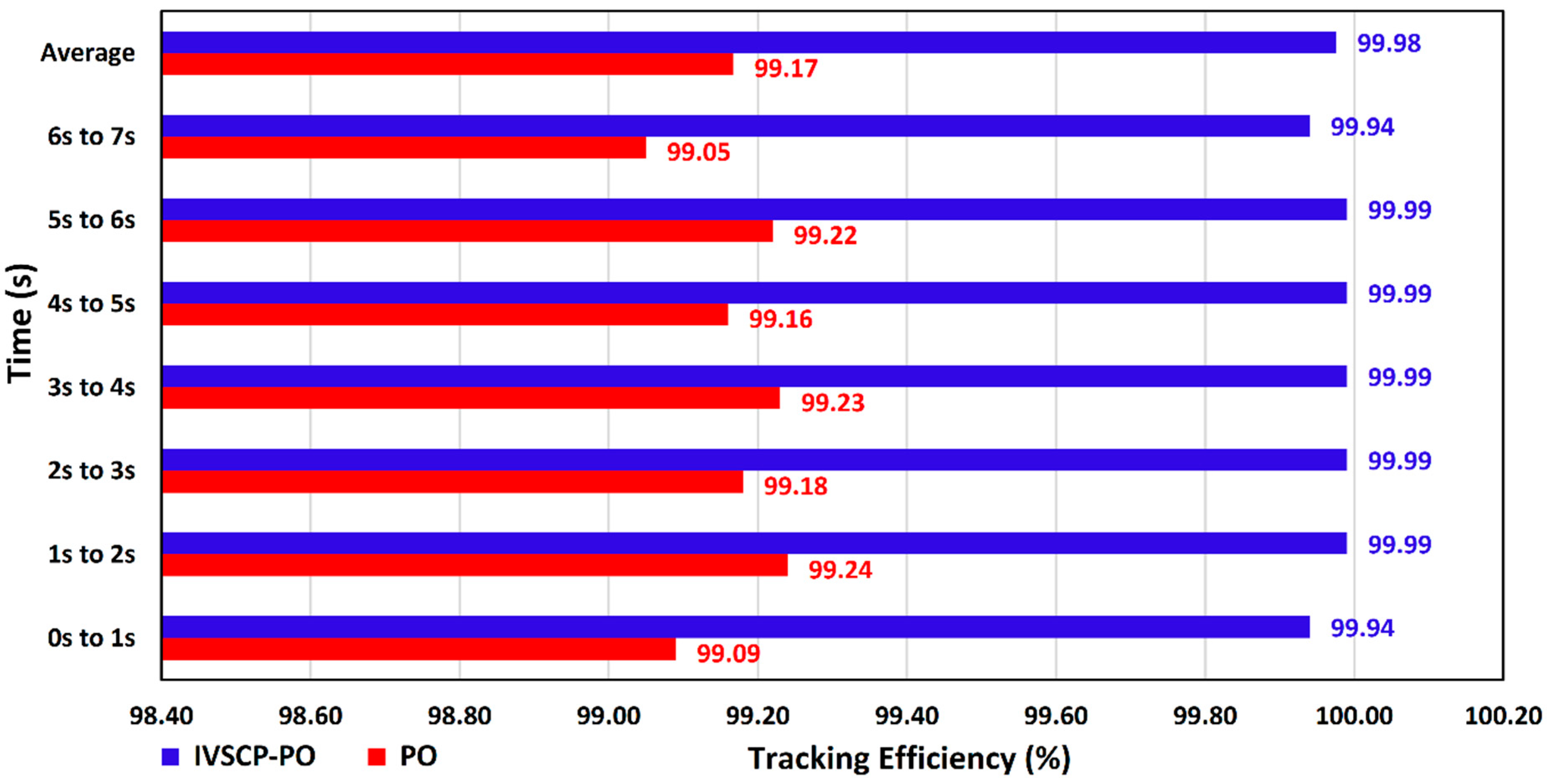
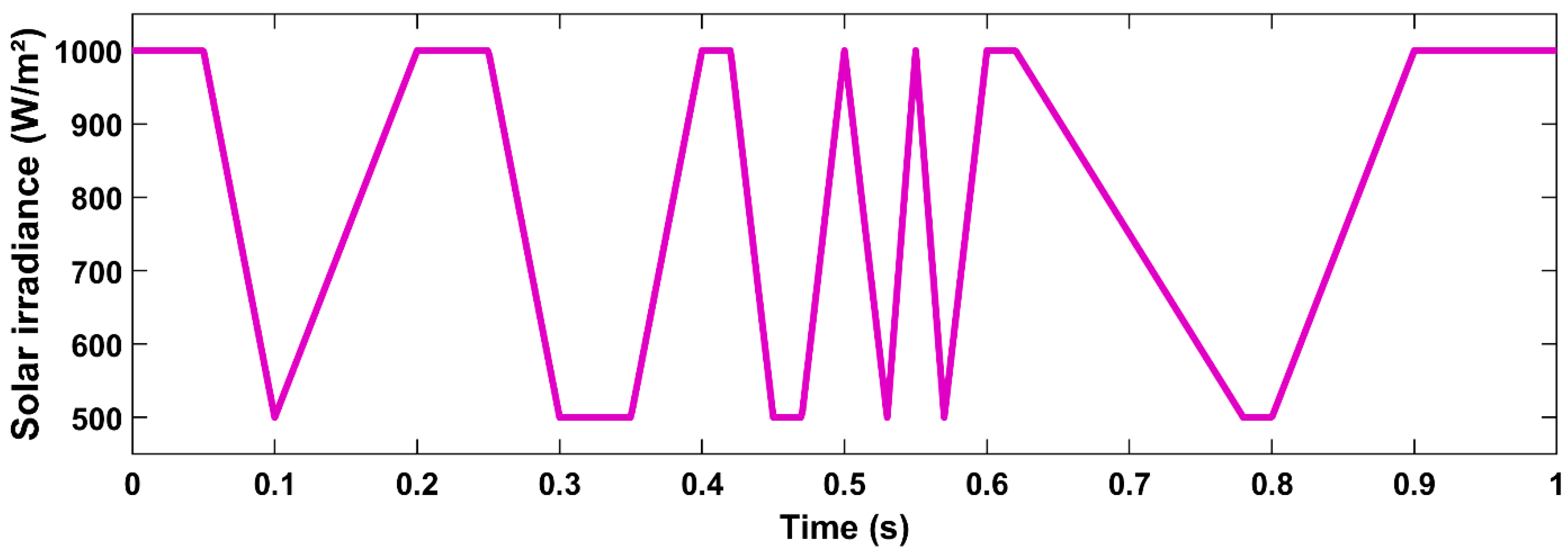
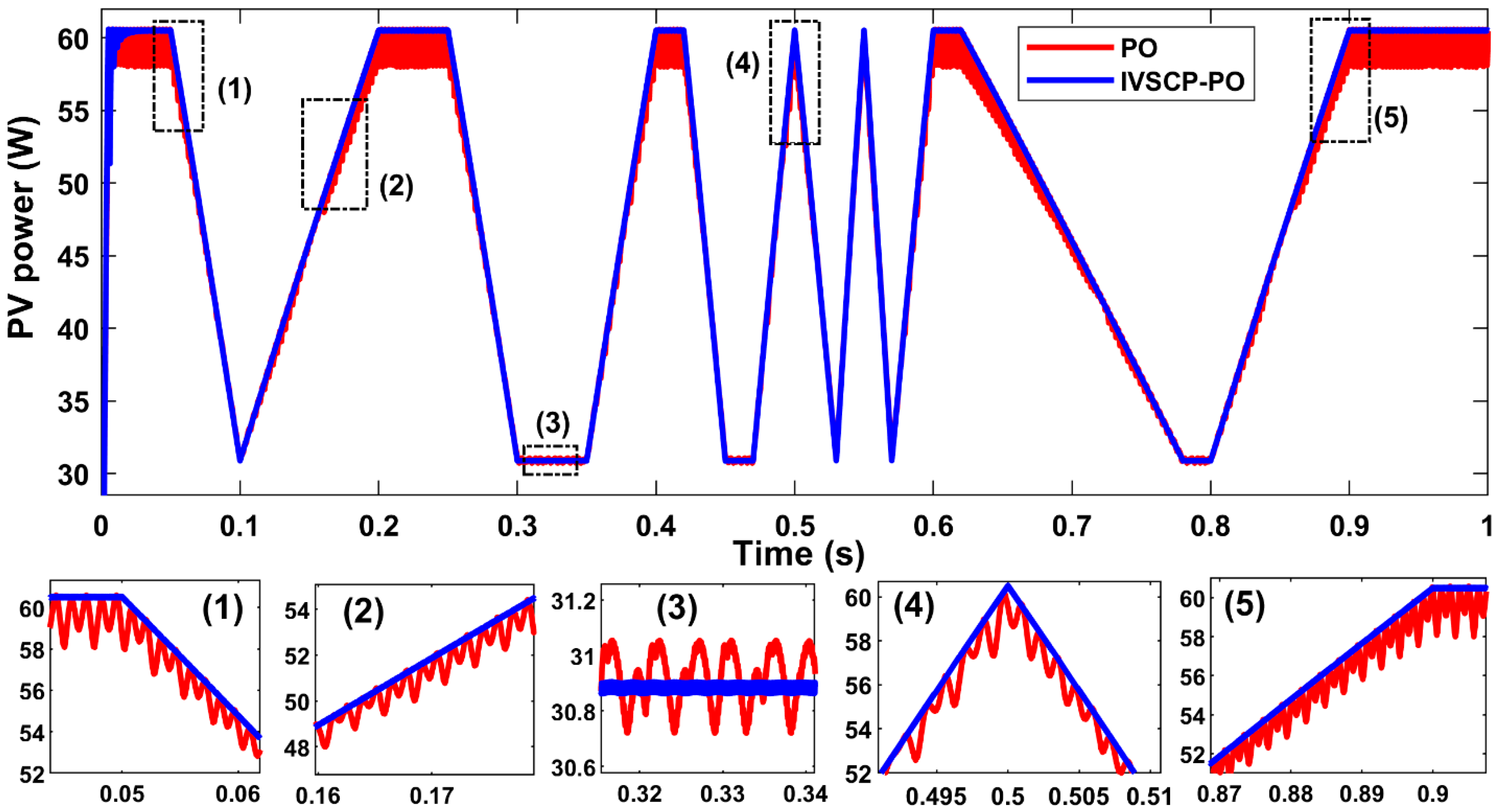


| Parameters | Rate |
|---|---|
| Photovoltaic array | |
| Power at MPP | 60 W |
| Voltage at MPP | 17.6 V |
| Current at MPP | 3.4 A |
| Open circuit voltage | 21.2 V |
| Short circuit current | 3.04 A |
| DC-DC Boost converter | |
| Input capacitance (CIN) | 1000 μF |
| Output capacitance (COUT) | 470 μF |
| Inductance (L) | 165 μH |
| Frequency (f) | 30 kHz |
| Load | |
| Resistor | 10 Ω |
| Parameters | MPPT Approaches | |||||||
|---|---|---|---|---|---|---|---|---|
| [59] | [60] | [61] | [62] | [63] | [64] | [53] | Proposed (IVSCP-PO) | |
| Year | 2020 | 2021 | 2016 | 2005 | 2021 | 2020 | 2022 | 2024 |
| Converter type | Boost | Buck | Buck-Boost | Boost | Boost | Boost | Buck | Boost |
| Average tracking time (seconds) | 0.6 | 0.15 | 0.27 | 0.04 | 0.14 | 0.036 | 0.003 | 0.002 |
| Converging velocity | Low | Medium | High | Low | Medium | Medium | High | Very High |
| Average efficiency of tracking (%) | 99.2 | 99 | 98.8 | 99.5 | - | 96 | 99.60 | 99.85 |
| Fluctuations | Medium | Low | Low | High | low | Low | Low | Zero |
| Implementation complexity | Medium | Medium | low | low | Complex | Medium | Low | Low |
| Experimental Verification | No | No | Yes | Yes | Yes | Yes | No | Yes |
| Parameters | Description | Rate |
|---|---|---|
| PV module | ||
| MPP | PMPP | 60 W |
| Tolerance of output PV power | ±5 | |
| Voltage at MPP | VMPP | 17.6 V |
| Current at MPP | IMPP | 3.4 A |
| Voltage of open circuit | VOC | 21.2 V |
| Current of short circuit | ISC | 4.2 A |
| Boost converter | ||
| Input capacitance | CIN | 1000 × 10−6 F, 100 V |
| Output capacitance | COUT | 470 × 10−6 F, 400 V |
| Inductance | L | 165 × 10−6 H |
| MOSFET | P30 N60 E | - |
| MOSFET driver | MCP 1406 | - |
| Switching Frequency | f | 30 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chellakhi, A.; El Beid, S. A Real-Time Investigation of an Enhanced Variable Step PO MPPT Controller for Photovoltaic Systems Using dSPACE 1104 Board. Energies 2025, 18, 3343. https://doi.org/10.3390/en18133343
Chellakhi A, El Beid S. A Real-Time Investigation of an Enhanced Variable Step PO MPPT Controller for Photovoltaic Systems Using dSPACE 1104 Board. Energies. 2025; 18(13):3343. https://doi.org/10.3390/en18133343
Chicago/Turabian StyleChellakhi, Abdelkhalek, and Said El Beid. 2025. "A Real-Time Investigation of an Enhanced Variable Step PO MPPT Controller for Photovoltaic Systems Using dSPACE 1104 Board" Energies 18, no. 13: 3343. https://doi.org/10.3390/en18133343
APA StyleChellakhi, A., & El Beid, S. (2025). A Real-Time Investigation of an Enhanced Variable Step PO MPPT Controller for Photovoltaic Systems Using dSPACE 1104 Board. Energies, 18(13), 3343. https://doi.org/10.3390/en18133343







