Insight into the Creep Damage Evolution in Water-Immersed Coal Pillars: Experiment and Numerical Model Investigation
Abstract
1. Introduction
2. Research Methodology
2.1. Creep Experiments of Water-Immersed Coal
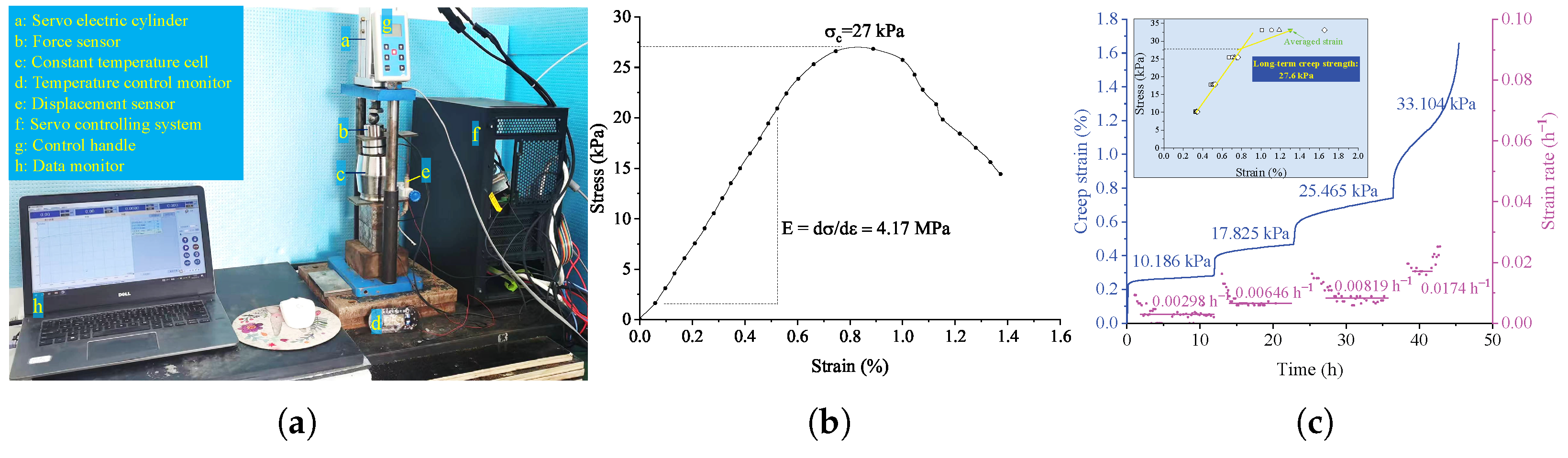
2.1.1. Experiment Materials and Apparatus
2.1.2. Creep Experiment Procedure
2.2. Similarity Model Test of a Coal Pillar
2.2.1. Generalized Similarity Model
2.2.2. Similarity Ratio and Materials
2.2.3. Model Test Procedure
2.3. Numerical Modeling of a Coal Pillar
2.3.1. Numerical Model Setup
2.3.2. Boundary Conditions
2.4. Parameters Assign
3. Experiment Result Analysis
3.1. Creep Behavior of Water-Immersed Coal
3.2. Evolution of Creep Damage in a Coal Pillar
4. Mechanism of Creep Damage in a Coal Pillar
4.1. Stress Evolution in the Coal Pillar
4.2. Theoretical Analysis of the Creep Damage of a Coal Pillar
- When , the coal mass supporting stress is the peak stress , where K is the peak stress concentration coefficient.
- When , the coal mass supporting stress is the residual strength of the coal mass .
- When the distance x from the coal wall of the goaf approaches infinity, the supporting stress is the original rock stress .
5. Discussion
6. Conclusions
- Water immersion significantly affects the long-term mechanical properties of coal, leading to material softening and a reduction in creep strength. Initial instantaneous strain increases with immersion time, from 0.16% for non-immersed samples to 0.25% for 8-week-immersed samples, with final strain reaching 1.15% in the latter, compared to 0.78% in the former.
- The combined approach of similarity modeling and numerical simulation effectively captures the creep damage processes in coal pillars. On day 3, new fractures formed above the coal pillar sidewall, with damaged sections extruding into the goaf. By day 15, further creep failure triggered overburden fracture interactions and slight deformation. By day 30, damage progressed to the pillar’s core, with creep-driven fractures continuously propagating centrally, accompanied by overburden rock movement.
- During the creep damage process, the trapezoidal stress distribution along a coal pillar undergoes significant changes, characterized by increasing concentrated and bearing stresses within the pillar.
- Redistributed concentrated stress, exceeding the long-term strength of coal, drives damage propagation toward the pillar’s center, resulting in continuous creep damage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, C.; Wang, F.; Bai, Q. Underground space utilization of coalmines in China: A review of underground water reservoir construction. Tunn. Undergr. Space Technol. 2021, 107, 103657. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, D.; Zhang, J.; Liang, B. Study on the strength deterioration characteristic and damage model of coal pillar dams with repeated water immersion in underground reservoirs. Sci. Rep. 2024, 14, 6338. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Liu, F.; Kou, M.; Li, M. A review of stability of dam structures in coal mine underground reservoirs. Water 2024, 16, 1856. [Google Scholar] [CrossRef]
- Fan, J.; Li, Z.; Feng, G.; Zhang, H.; Qi, C.; Zhang, J. Failure analysis of coal pillars and overburden from underground water reservoir under the mining-water invasion coupling effect. Eng. Fail. Anal. 2023, 151, 107406. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, Q.; Liu, W. Evaluation of long-term tightness of the coal pillar dam of underground reservoir and protection countermeasures. Energies 2023, 15, 7229. [Google Scholar] [CrossRef]
- Li, Y.; Yao, Q.; Li, X.; Zheng, C. Creep characteristics and long-term strength of underground water reservoirs’ coal pillar dam specimens under different osmotic pressures. J. Clean. Prod. 2024, 452, 141901. [Google Scholar] [CrossRef]
- Chen, Y.; Hao, X.; Xue, D.; Li, Z.; Ma, X. Creep behavior and permeability evolution of coal pillar dam for under-ground water reservoir. Int. J. Coal Sci. Technol. 2023, 10, 11. [Google Scholar] [CrossRef]
- Danesh, N.N.; Chen, Z.; Connell, L.D.; Kizil, M.S.; Pan, Z.; Aminossadati, S.M. Characterisation of creep in coal and its impact on permeability: An experimental study. Int. J. Coal Geol. 2017, 173, 200–211. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Y.; Han, P.; Bai, Q. Coal pillar failure analysis and instability evaluation methods: A short review and prospect. Eng. Fail. Anal. 2022, 138, 106344. [Google Scholar] [CrossRef]
- Wu, W.D.; Bai, J.B.; Wang, X.Y.; Yan, S.; Wu, S.X. Numerical study of failure mechanisms and control techniques for a gob-side yield pillar in the Sijiazhuang coal mine, China. Rock Mech. Rock Eng. 2019, 52, 1231–1245. [Google Scholar] [CrossRef]
- Qu, X.; Chen, Y.; Yin, D. Experimental study on progressive failure characteristics of strip coal pillar models under different roof and floor conditions. Case Stud. Constr. Mater. 2023, 18, e02147. [Google Scholar] [CrossRef]
- Yang, H.; Liu, W. Microscopic Damage Mechanism of Coal Sample Under Uniaxial Compression Test Under Different Creep Pre-damage. Geotech. Geol. Eng. 2020, 38, 1675–1687. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, J.; Spearing, A.; Chai, J.; Dong, C. Experimental study of the creep properties of coal considering initial damage. Int. J. Rock Mech. Min. Sci. 2021, 139, 104629. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, B.; Huang, W.; Li, Z.; Zhang, X.; Zhang, L.; Wu, Y. The nonlinear creep behavior and creep damage constitutive model of coal rock. Arab. J. Geosci. 2023, 16, 193. [Google Scholar] [CrossRef]
- Wang, D.; Wang, E.; Feng, X.; Wei, M.; Li, D.; Liu, Q.; Li, B.; Zhang, X. Triaxial creep damage–catastrophe instability characteristics and a nonlinear constitutive model of gas-bearing coal. Bull. Eng. Geol. Environ. 2022, 81, 437. [Google Scholar] [CrossRef]
- Yang, S.Q.; Xu, P.; Ranjith, P.G. Damage model of coal under creep and triaxial compression. Int. J. Rock Mech. Min. Sci. 2015, 80, 337–345. [Google Scholar] [CrossRef]
- Guo, J.; Zong, D.; Ma, L. Creep damage characteristics and constitutive model of pre-damage coal. Eng. Fail. Anal. 2024, 158, 108002. [Google Scholar] [CrossRef]
- Jia, W.; Zhou, H.; Xie, S.; Wang, Y.; Hu, X.; Zhang, L. Pore-pressure and stress-coupled creep behavior in deep coal: Insights from real-time NMR analysis. Int. J. Min. Sci. Technol. 2024, 34, 77–90. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, D.; Huang, S. Creep characteristics and creep model of coal based on pore water pressure. Processes 2023, 11, 638. [Google Scholar] [CrossRef]
- Danesh, N.N.; Chen, Z.; Aminossadati, S.M.; Kizil, M.S.; Pan, Z.; Connell, L.D. Impact of creep on the evolution of coal permeability and gas drainage performance. J. Nat. Gas Sci. Eng. 2016, 33, 469–482. [Google Scholar] [CrossRef]
- Zhou, H.W.; Zhang, L.; Wang, X.Y.; Rong, T.; Wang, L. Effects of matrix-fracture interaction and creep deformation on permeability evolution of deep coal. Int. J. Rock Mech. Min. Sci. 2020, 127, 104236. [Google Scholar] [CrossRef]
- Li, X.; Liu, X.; Tan, Y.; Rong, T.; Wang, L. Creep constitutive model and numerical realization of coal-rock combination deteriorated by immersion. Minerals 2022, 11, 292. [Google Scholar] [CrossRef]
- Wang, L.; Cheng, J.; Yang, H.; Yang, Y.; Wu, Y.; Jia, Z.; Zhang, Y.; Xue, D. Characterization of multi-step creep behavior and fractional derivative modeling for a water-saturated coal. Mech. Time-Depend. Mater. 2024, 28, 2771–2791. [Google Scholar] [CrossRef]
- Li, Y.; Zheng, D.; Zhang, S.; Dang, J.; Zhang, H.; Hou, J. Study on mechanical characteristics and energy accumulation and release law of coal samples with different saturation and creep damage. Int. J. Coal Prep. Util. 2024, 44, 1477–1504. [Google Scholar] [CrossRef]
- Yao, Q.; Li, Y.; Li, X.; Yu, L.; Zheng, C. Permeation–strain characteristics and damage constitutive model of coal samples under the coupling effect of seepage and creep. Int. J. Rock Mech. Min. Sci. 2024, 127, 105729. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, F.; Yang, G. Experimental study on creep characteristics of infiltrated coal-rock under load. Arch. Appl. Mech. 2023, 93, 1331–1349. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Wang, X.; Wang, L.; Su, T.; Wei, Q.; Deng, T. A triaxial creep model for deep coal considering temperature effect based on frac-tional derivative. Acta Geotech. 2023, 17, 1739–1751. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, H.; Wang, X.; Zhao, J.; Ju, Y.; Deng, T. On permeability evolution of coal induced by temperature, creep, and matrix–fracture interaction. Energy Fuels 2022, 36, 1470–1481. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Hu, K.; Xie, S.; Jia, W.; Song, L. A Fractional Creep Model for Deep Coal Based on Conformable Derivative Con-sidering Thermo-Mechanical Damage. Processes 2024, 12, 1121. [Google Scholar] [CrossRef]
- Deng, H.; Zhou, H.; Li, L. Fractional creep model of temperature-stress-time coupled damage for deep coal based on temperature-equivalent stress. Results Phys. 2022, 39, 105765. [Google Scholar] [CrossRef]
- Li, G.; Yan, G.; Kong, S.; Bai, X.; Du, C.; Li, J.; Zhang, J. Study on the Creep of Damage-Containing Anthracite: Theory and Experiment. Appl. Sci. 2023, 13, 8691. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, E.; Ding, Z. Research on the creep model of deep coal roadway and its numerical simulation re-production. Int. J. Environ. Res. Public Health 2022, 19, 15920. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Xu, J.; Li, C. Similar simulation test study on permeability evolution mechanism of fault sliding fracture zone. Arab. J. Geosci. 2022, 15, 548. [Google Scholar] [CrossRef]
- Zhao, N.; Wei, S.; Wang, L.; Sun, J. Simulation analysis of the evolution law of creep rupture crack extension in X-fractured rock body. Sci. Rep. 2024, 14, 14843. [Google Scholar] [CrossRef]
- Gutiérrez-Ch, J.G.; Senent, S.; Zeng, P.; Jimenez, R. DEM simulation of rock creep in tunnels using Rate Process Theory. Comput. Geotech. 2022, 142, 104559. [Google Scholar] [CrossRef]
- Wang, X.Y.; Wang, X.; Zhang, X.C.; Zhu, S.-F. Creep damage characterization of UNS N10003 alloy based on a numerical simulation using the Norton creep law and Kachanov–Rabotnov creep damage model. Nucl. Sci. Tech. 2019, 30, 65. [Google Scholar] [CrossRef]
- Li, J.H. Experimental study of water storage soaking of coal mine underground reservoir to coal pillar dam body strength. Coal Min. Technol 2018, 23, 15–17. [Google Scholar]
- Ai, T.; Wu, S.; Zhang, R.; Gao, M.; Zhou, J.; Xie, J.; Ren, L.; Zhang, Z. Changes in the structure and mechanical properties of a typi-cal coal induced by water immersion. Int. J. Rock Mech. Min. Sci. 2021, 138, 104597. [Google Scholar] [CrossRef]
- Song, B.; Zhai, X.; Ma, T.; Wang, B.; Hao, L.; Zhou, Y. Effect of water immersion on pore structure of bituminous coal with different metamorphic degrees. Energy 2023, 274, 127449. [Google Scholar] [CrossRef]
- Sinha, S.; Walton, G. Modeling the behavior of a coal pillar rib using bonded block models with emphasis on ground-support interaction. Int. J. Rock Mech. Min. Sci. 2021, 148, 104965. [Google Scholar] [CrossRef]
- Sun, X.; Lu, M.; Li, C. Optimization of staggered distance of coal pillars in multiseam mining: Theoretical analysis and numerical simulation. Energy Sci. Eng. 2021, 9, 357–374. [Google Scholar] [CrossRef]
- Li, H.; Xu, D.; Li, G.; Wei, S.; Wu, B. Feasibility Study on the Construction of Underground Reservoirs in Coal Goaf—A Case Study from Buertai Coal Mine, China. Sustainability 2024, 16, 9912. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, T.; Ran, J.; Du, Y.; Zhang, H.; Jiang, H. Model test on creep deformation and failure characteristics of soft rock roadways. Eng. Fail. Anal. 2022, 141, 106670. [Google Scholar] [CrossRef]
- Arora, K.; Gutierrez, M. Viscous-elastic-plastic response of tunnels in squeezing ground conditions: Analytical modeling and experimental validation. Int. J. Rock Mech. Min. Sci. 2021, 146, 104888. [Google Scholar] [CrossRef]
- Gong, Y.F.; Zhu, C.Y.; Zhu, G.W. Analysis of physical parameters of materials similar to coal and rock mass based on geophysical model construction of mines. Appl. Geophys. 2023, 20, 116–129. [Google Scholar] [CrossRef]
- Yang, Y.; Yue, H.; Zhao, Y.; Zhang, S.; Zhang, J.; Wang, Z.; Yang, W. Experimental study on ratio optimization of similar materials for underground mining of Shendong coalfield: A case study of Shangwan coal mine. Processes 2023, 11, 1352. [Google Scholar] [CrossRef]
- Yi, S.; Zhang, Y.; Yi, H.; Li, X.; Wang, X.; Wang, Y.; Chu, T. Study on the instability activation mechanism and defor-mation law of surrounding rock affected by water immersion in goafs. Water 2022, 14, 3250. [Google Scholar] [CrossRef]
- Kolditz, O.; Bauer, S.; Bilke, L.; Böttcher, N.; Delfs, J.O.; Fischer, T.; Zehner, B. OpenGeoSys: An open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012, 67, 589–599. [Google Scholar] [CrossRef]
- Chen, X.; Liu, Z.; Li, T.; Ma, J.; Hu, J. Microstructural Evolution and Damage Mechanism of Water-Immersed Coal Based on Physicochemical Effects of Inorganic Minerals. Materials 2024, 17, 5579. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, X.; Gao, Y.; Shao, Z.; Zhang, Y.; Liu, X. The influence of water immersion on the physical and chemical structure of coal. Combust. Sci. Technol. 2022, 194, 1136–1154. [Google Scholar] [CrossRef]
- Xia, H.; Zhang, H.; Zhang, J. Research on damage mechanism and mechanical characteristics of coal rock under water immersion. Sustainability 2023, 15, 13095. [Google Scholar] [CrossRef]
- Innocente, J.C.; Paraskevopoulou, C.; Diederichs, M.S. Estimating the long-term strength and time-to-failure of brittle rocks from laboratory testing. Int. J. Rock Mech. Min. Sci. 2021, 147, 104900. [Google Scholar] [CrossRef]
- Bu, Q.; Tu, M.; Fu, B. Research on the redistribution law of lateral mining stress and the bearing characteristics of section coal pillar in extra-thick fully mechanized top-coal caving mining. Shock Vib. 2021, 2021, 4355977. [Google Scholar] [CrossRef]
- Zhang, R.F.; Shen, W.L.; Zhang, Y.; Li, B.B.; Zhu, R.R. Study on Stress Weakening of Surrounding Rock in Lower Coal Roadway of Close Distance Coal Seam Based on Average Stress Concentration Difference. Coal Technol. 2023, 42, 20–25. [Google Scholar]
- Galav, A.; Singh, G.S.P.; Sharma, S.K. A numerical modeling approach for assessment of seepage characteristics and performance of protective water barrier pillars in underground coal mines. Sustainability 2022, 39, 2047–2063. [Google Scholar] [CrossRef]
- Yi, H.; Ji, Z.; Liu, J.; Zhuo, Z.; Yi, S.; Shi, X. Insight into the mechanical degradation of coal corroded by concentrated brine solution. Geomech. Energy Environ. 2024, 38, 100547. [Google Scholar] [CrossRef]
- Huang, S.; Zhao, G.; Meng, X.; Cheng, X.; Gu, Q.; Liu, G.; Zhu, S. Development of cement-based grouting material for reinforcing narrow coal pillars and engineering applications. Processes 2022, 10, 2292. [Google Scholar] [CrossRef]









| LCC Quantities | Similitude Relations | Ratios |
|---|---|---|
| Length | 200 | |
| Density | 1.5 | |
| Acceleration | 1 | |
| Time | 14.14 | |
| Stress | 300 | |
| Elastic modulus | 300 | |
| Strength | 300 | |
| Strain | 1 | |
| Viscosity | 4242.6 |
| Stratum ID | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio (-) | Cohesion (MPa) | Friction Angle () | Tensile Strength (MPa) |
|---|---|---|---|---|---|---|
| 2461 | 8.75 | 0.26 | 1.2 | 30 | 0.605 | |
| 2460 | 19.5 | 0.2 | 2.75 | 38 | 1.84 | |
| 2580 | 5.99 | 0.2 | 4 | 37 | 1.2 | |
| 2487 | 13.5 | 0.123 | 2.06 | 40 | 1.13 | |
| 1400 | 5.3 | 0.32 | 1.25 | 32 | 0.15 | |
| 2560 | 7.07 | 0.22 | 5 | 34 | 1.5 | |
| 2540 | 4.01 | 0.25 | 2 | 35 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yi, S.; Chen, Z.; Guo, Q.; Cai, X.; Guo, X.; Yi, H. Insight into the Creep Damage Evolution in Water-Immersed Coal Pillars: Experiment and Numerical Model Investigation. Energies 2025, 18, 3340. https://doi.org/10.3390/en18133340
Li X, Yi S, Chen Z, Guo Q, Cai X, Guo X, Yi H. Insight into the Creep Damage Evolution in Water-Immersed Coal Pillars: Experiment and Numerical Model Investigation. Energies. 2025; 18(13):3340. https://doi.org/10.3390/en18133340
Chicago/Turabian StyleLi, Xueliang, Sihai Yi, Zheng Chen, Qingbiao Guo, Xiangjun Cai, Xin Guo, and Haiyang Yi. 2025. "Insight into the Creep Damage Evolution in Water-Immersed Coal Pillars: Experiment and Numerical Model Investigation" Energies 18, no. 13: 3340. https://doi.org/10.3390/en18133340
APA StyleLi, X., Yi, S., Chen, Z., Guo, Q., Cai, X., Guo, X., & Yi, H. (2025). Insight into the Creep Damage Evolution in Water-Immersed Coal Pillars: Experiment and Numerical Model Investigation. Energies, 18(13), 3340. https://doi.org/10.3390/en18133340






