Shear Wave Velocity in Geoscience: Applications, Energy-Efficient Estimation Methods, and Challenges
Abstract
1. Introduction
2. Conventional Applications
3. New Applications
4. Energy-Efficient and Cost-Effective Approaches
4.1. Geophysical Methods
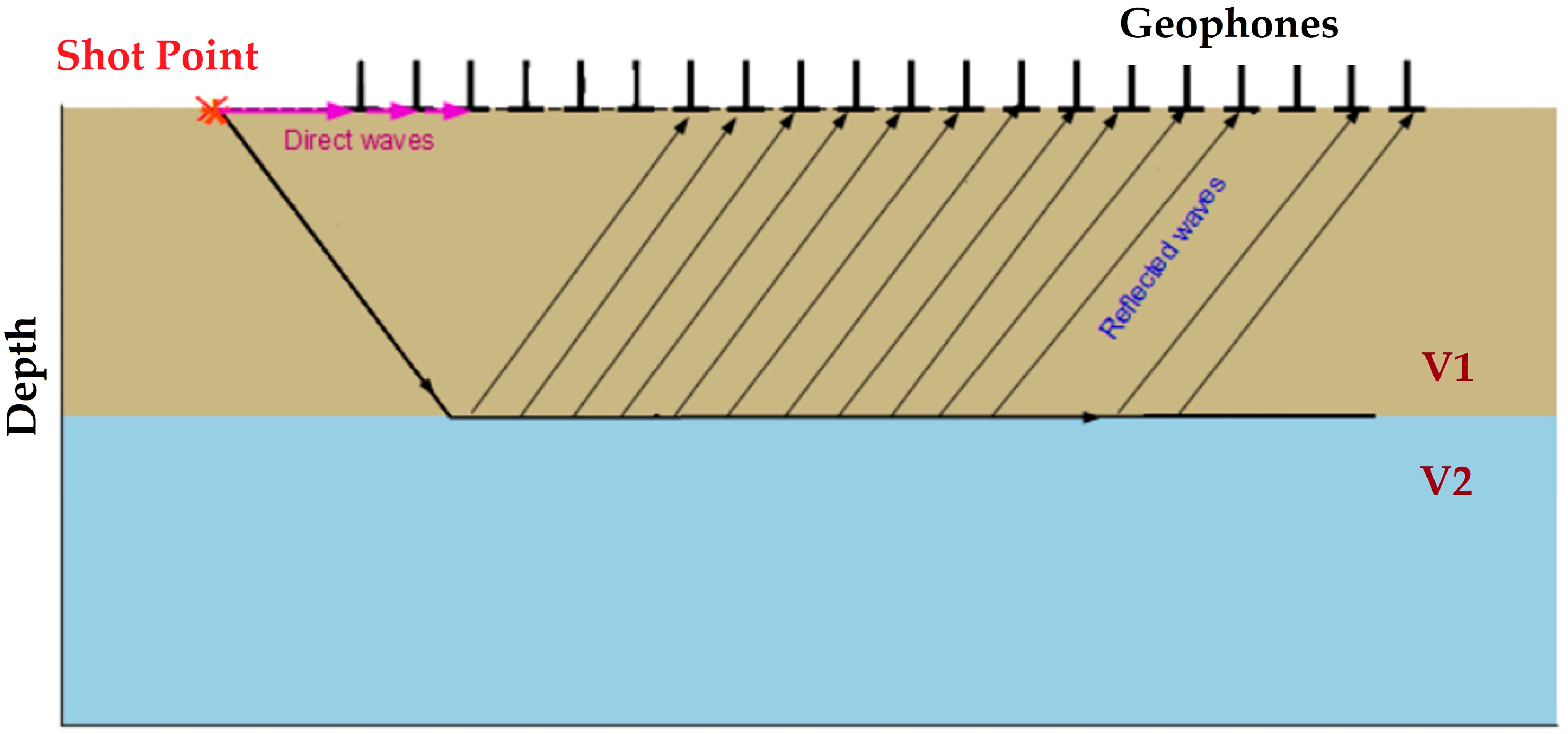
4.1.1. Seismic Refraction Techniques
4.1.2. Surface Wave Analysis
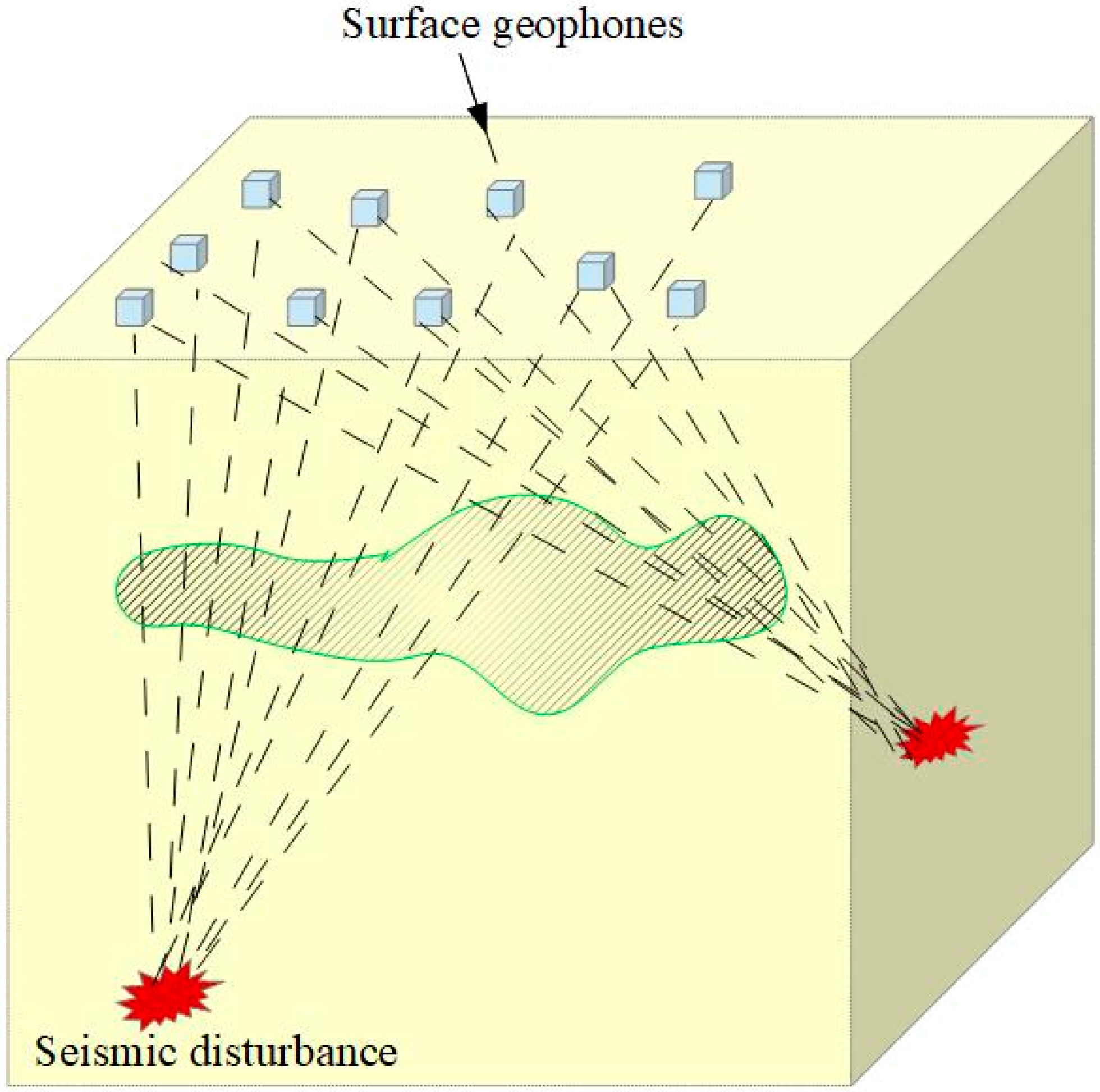
4.1.3. Seismic Tomography
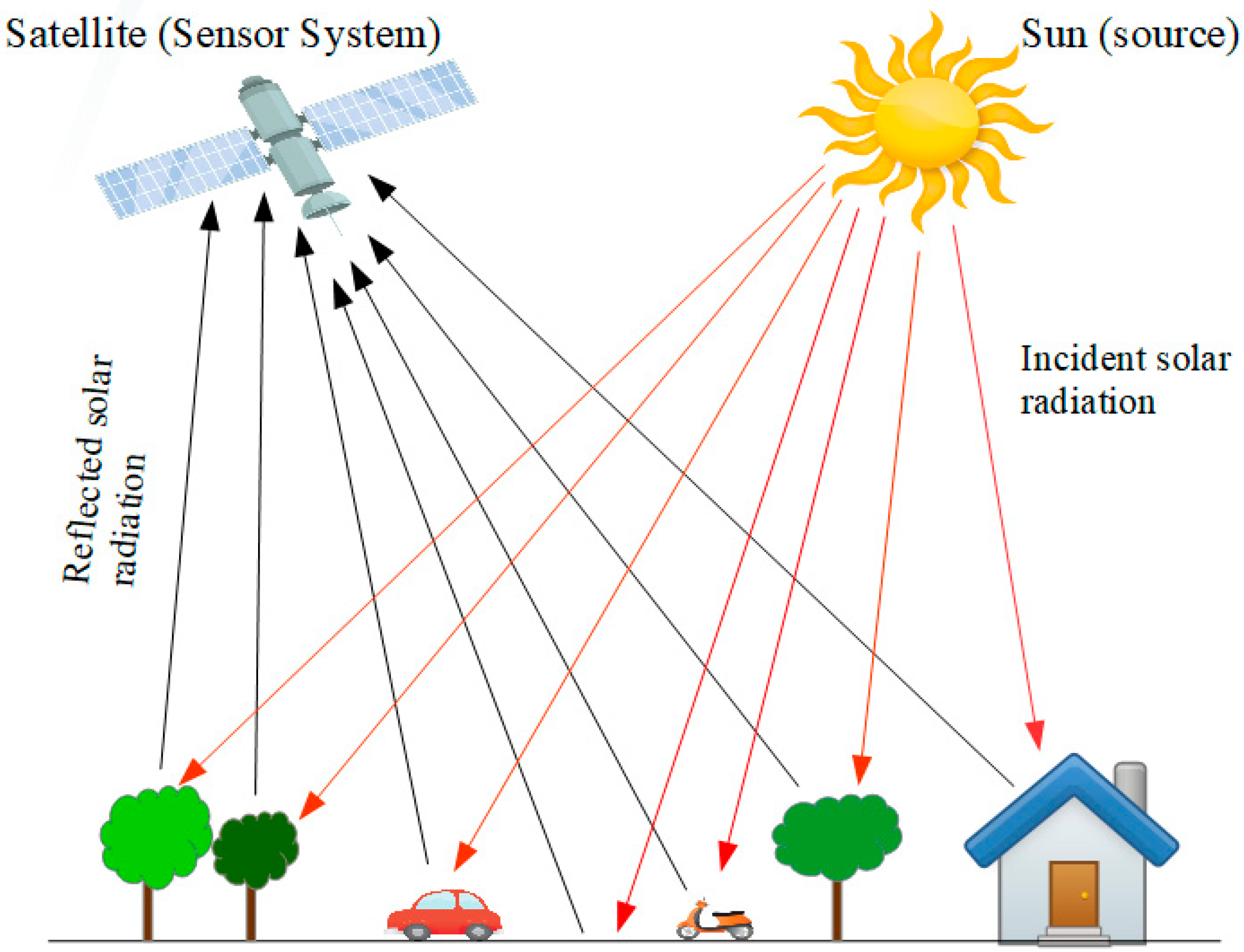
4.2. Remote Sensing
4.3. Machine Learning and Data-Driven Techniques
5. Challenges of Vs Measurement
5.1. Data Availability and Quality
5.2. Spatial and Temporal Variability
5.3. Non-Unique Relationships
5.4. Anisotropy and Inhomogeneity
5.5. Integration of Multiple Data Sources
5.6. Interpretability and Uncertainty Quantification
5.7. Standardization and Collaboration
5.8. Scale Effects
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACOFIS | Ant Colony–Fuzzy Inference System |
| AdaBoost | Adaptive Boosting |
| AI | Artificial Intelligence |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN-LM | Artificial Neural Network–Levenberg–Marquardt |
| ANN | Artificial Neural Network |
| Bi-LSTM | Bidirectional Long Short-Term Memory |
| BPNN | Backpropagation Neural Network |
| BPANN | Backpropagation Artificial Neural Network |
| BRR | Bayesian Ridge Regression |
| CatBoost | Categorical Boosting |
| CCS | Carbon Capture and Storage |
| CNN | Convolutional Neural Network |
| COA | Cuckoo Optimization Algorithm |
| CSA | Coupled Simulated Annealing |
| CTGAN | Conditional Generative Adversarial Network |
| CT | Computed Tomography |
| CVAE | Conditional Variational Autoencoders |
| DL | Deep Learning |
| DNN | Deep Neural Network |
| DTS | Delta-T Shear (Shear Wave Slowness) |
| DTP | Delta-T Compressional (Compressional Wave Slowness) |
| EGS | Enhanced Geothermal System |
| ELM | Extreme Learning Machine |
| FL | Fuzzy Logic |
| FWI | Full-Waveform Inversion |
| GA | Genetic Algorithm |
| GEP | Gene Expression Programming |
| GNN | Graph Neural Networks |
| GCN-BiGRU | Graph Convolutional Network with Bidirectional Gated Recurrent Units |
| GPR | Gaussian Process Regression |
| IRIS | Incorporated Research Institutions for Seismology |
| KNN | K-Nearest Neighbors |
| LB | Laplacian Boosting |
| LiDAR | Light Detection and Ranging |
| LIME | Local Interpretable Model-Agnostic Explanations |
| LR | Linear Regression |
| LSSVM | Least Squares Support Vector Machine |
| LSTM | Long Short-Term Memory |
| LSSVM-COA | Least Squares Support Vector Machine–Cuckoo Optimization Algorithm |
| LSSVM-CSA | Least Squares Support Vector Machine–Coupled Simulated Annealing |
| LSSVM-GA | Least Squares Support Vector Machine–Genetic Algorithm |
| LSSVM-PSO | Least Squares Support Vector Machine–Particle Swarm Optimization |
| MAE | Mean Absolute Error |
| MELM | Multilayer Extreme Learning Machine |
| MELM-COA | Multilayer Extreme Learning Machine–Cuckoo Optimization Algorithm |
| ML | Machine Learning |
| MLP | Multilayer Perceptron |
| MLR | Multiple Linear Regression |
| MIV | Mean Impact Value |
| MASW | Multichannel Analysis of Surface Waves |
| MSE | Mean Squared Error |
| NF | Neuro-Fuzzy |
| NFS | Neuro-Fuzzy System |
| NN | Neural Network |
| NSGA-II | Non-Dominated Sorting Genetic Algorithm II |
| OSGeo | Open-Source Geospatial Foundation |
| PINNs | Physics-Informed Neural Networks |
| PSO | Particle Swarm Optimization |
| R2 | Coefficient of Determination |
| RF | Random Forest |
| RFR | Random Forest Regression |
| RMSE | Root Mean Squared Error |
| SASW | Spectral Analysis of Surface Waves |
| SHAP | SHapley Additive exPlanations |
| SPT-N | Standard Penetration Test—N Value |
| SRT | Seismic Refraction Tomography |
| SVR | Support Vector Regression |
| UAV-based | Unmanned Aerial Vehicle-based |
| VelProfES | Velocity Profile Estimation System |
| Vs | Shear Wave Velocity |
| Vp | Compressional Wave Velocity |
| XAI | Explainable Artificial Intelligence |
| XGBoost | Extreme Gradient Boosting |
References
- Moss, R.E.S. Quantifying measurement uncertainty of thirty-meter shear-wave velocity. Bull. Seismol. Soc. Am. 2008, 98, 1399–1411. [Google Scholar] [CrossRef]
- Foti, S.; Hollender, F.; Garofalo, F.; Albarello, D.; Asten, M.; Bard, P.Y.; Comina, C.; Cornou, C.; Cox, B.; Di Giulio, G.; et al. Guidelines for the good practice of surface wave analysis: A product of the InterPACIFIC project. Bull. Earthq. Eng. 2018, 16, 2367–2420. [Google Scholar] [CrossRef]
- Shafiee, A.; Azadi, A. Shear-wave velocity characteristics of geological units throughout Tehran City, Iran. J. Asian Earth Sci. 2007, 29, 105–115. [Google Scholar] [CrossRef]
- Incorporated Research Institutions for Seismology (IRIS). S-Wave Motion—Animation. Available online: https://www.iris.edu/hq/inclass/animation/swave_motion (accessed on 19 February 2025).
- L’Heureux, J.S.; Long, M. Relationship between shear-wave velocity and geotechnical parameters for Norwegian clays. J. Geotech. Geoenvironmental Eng. 2017, 143, 04017013. [Google Scholar] [CrossRef]
- Sundararajan, N.; Seshunarayana, T. Shear wave velocities in the estimation of earthquake hazard over alluvium in a seismically active region. J. Geol. Soc. India 2018, 92, 259–264. [Google Scholar] [CrossRef]
- Parolai, S.; Richwalski, S.M.; Milkereit, C.; Fäh, D. S-wave velocity profiles for earthquake engineering purposes for the Cologne area (Germany). Bull. Earthq. Eng. 2006, 4, 65–94. [Google Scholar] [CrossRef]
- Jamiolkowski, M. Role of geophysical testing in geotechnical site characterization. Soils Rocks 2012, 35, 117–137. [Google Scholar] [CrossRef]
- Anbazhagan, P.; Sitharam, T.G. Site characterization and site response studies using shear wave velocity. J. Seismol. Earthq. Eng. 2008, 10, 53–67. [Google Scholar]
- Li, X.Y.; Zhang, Y.G. Seismic reservoir characterization: How can multicomponent data help? J. Geophys. Eng. 2011, 8, 123. [Google Scholar] [CrossRef]
- Rezaee, M.R.; Ilkhchi, A.K.; Barabadi, A. Prediction of shear wave velocity from petrophysical data utilizing intelligent systems: An example from a sandstone reservoir of Carnarvon Basin, Australia. J. Pet. Sci. Eng. 2007, 55, 201–212. [Google Scholar] [CrossRef]
- Mourad, M.; Tsuji, T.; Ikeda, T.; Ishitsuka, K.; Senna, S.; Ide, K. Mapping aquifer storage properties using s-wave velocity and insar-derived surface displacement in the Kumamoto area, Southwest Japan. Remote Sens. 2021, 13, 4391. [Google Scholar] [CrossRef]
- Pugin, A.J.M.; Pullan, S.E.; Hunter, J.A.; Oldenborger, G.A. Hydrogeological prospecting using P-and S-wave landstreamer seismic reflection methods. Near Surf. Geophys. 2009, 7, 315–328. [Google Scholar] [CrossRef]
- Hedtmann, N.; Alber, M. Investigation of water-permeability and ultrasonic wave velocities of German Malm aquifer rocks for hydro-geothermal energy. In Proceedings of the ISRM EUROCK, Ostrava, Czech Republic, 20–22 June 2017. [Google Scholar]
- Sharifi-Mood, M.; Olsen, M.J.; Gillins, D.T.; Mahalingam, R. Performance-based, seismically-induced landslide hazard mapping of Western Oregon. Soil Dyn. Earthq. Eng. 2017, 103, 38–54. [Google Scholar] [CrossRef]
- Shukla, R.; Ranjith, P.; Haque, A.; Choi, X. A Review of Studies on CO2 Sequestration and Caprock Integrity. Fuel 2010, 89, 2651–2664. [Google Scholar] [CrossRef]
- Peuchen, J.; De Ruijter, M.R.; Hospers, B.; Assen, R.L. Shear wave velocity integrated in offshore geotechnical practice. In Proceedings of the SUT Offshore Site Investigation and Geotechnics, London, UK, 26–28 November 2002. [Google Scholar]
- Hosseini, K.; Matthews, K.J.; Sigloch, K.; Shephard, G.E.; Domeier, M.; Tsekhmistrenko, M. SubMachine: Web-based tools for exploring seismic tomography and other models of Earth’s deep interior. Geochem. Geophys. Geosystems 2018, 19, 1464–1483. [Google Scholar] [CrossRef]
- Nejad, M.M.; Momeni, M.S.; Manahiloh, K.N. Shear wave velocity and soil type microzonation using neural networks and geographic information system. Soil Dyn. Earthq. Eng. 2018, 104, 54–63. [Google Scholar] [CrossRef]
- Lee, M.W. A simple method of predicting S-wave velocity. Geophysics 2006, 71, F161–F164. [Google Scholar] [CrossRef]
- Putra, D.P.N.; Utama, W.; Garini, S.A.; Indriani, R.F. Geological Mapping Optimisation Using Satellite Gravity, Satellite Imagery, and Seismic Shear Velocity (Vs30) to Monitor Lithological Condition in Geothermal Area of Mount Salak, West Java. BIO Web Conf. 2024, 89, 02001. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J. Data-driven S-wave velocity prediction method via a deep-learning-based deep convolutional gated recurrent unit fusion network. Geophysics 2021, 86, M185–M196. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B.; Fumal, T.E. Equations for estimating horizontal response spectra and peak acceleration from western North American earthquakes: A summary of recent work. Seismol. Res. Lett. 1997, 68, 128–153. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, N. Dependencies of shear wave velocity and shear modulus of soil on saturation. J. Eng. Mech. 2016, 142, 04016083. [Google Scholar] [CrossRef]
- Thitimakorn, T.; Channoo, S. Shear wave velocity of soils and NEHRP site classification map of Chiang Rai City, Northern Thailand. Electron. J. Geotech. Eng. 2012, 17, 2891–2904. [Google Scholar]
- Uma Maheswari, R.; Boominathan, A.; Dodagoudar, G.R. Use of surface waves in statistical correlations of shear wave velocity and penetration resistance of Chennai soils. Geotech. Geol. Eng. 2010, 28, 119–137. [Google Scholar] [CrossRef]
- Baxter, C.D.; Bradshaw, A.S.; Green, R.A.; Wang, J.H. Correlation between cyclic resistance and shear-wave velocity for providence silts. J. Geotech. Geoenvironmental Eng. 2008, 134, 37–46. [Google Scholar] [CrossRef]
- Yunmin, C.; Han, K.; Ren-peng, C. Correlation of shear wave velocity with liquefaction resistance based on laboratory tests. Soil Dyn. Earthq. Eng. 2005, 25, 461–469. [Google Scholar] [CrossRef]
- Rodriguez-Marek, A.; Bray, J.D.; Abrahamson, N.A. A geotechnical seismic site response evaluation procedure. In Proceedings of the 12WCEE 2000: 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Oh, T.M.; Bang, E.S.; Cho, G.C.; Park, E.S. Estimation of undrained shear strength for saturated clay using shear wave velocity. Mar. Georesources Geotechnol. 2017, 35, 236–244. [Google Scholar] [CrossRef]
- Oloruntobi, O.; Butt, S. The shear-wave velocity prediction for sedimentary rocks. J. Nat. Gas Sci. Eng. 2020, 76, 103084. [Google Scholar] [CrossRef]
- Kováčik, J.; Emmer, Š. Correlation between shear wave velocity and porosity in porous solids and rocks. J. Powder Technol. 2013, 1, 643167. [Google Scholar] [CrossRef]
- Korneev, V. Slow waves in fractures filled with viscous fluid. Geophysics 2008, 73, N1–N7. [Google Scholar] [CrossRef]
- Hussien, M.N.; Karray, M. Shear wave velocity as a geotechnical parameter: An overview. Can. Geotech. J. 2015, 53, 252–272. [Google Scholar] [CrossRef]
- Azhar, A.S.B.; Latiff, A.H.A.; Lim, L.H.; Gödeke, S.H. Groundwater investigation of a coastal aquifer in Brunei Darussalam using seismic refraction. Environ. Earth Sci. 2019, 78, 220. [Google Scholar] [CrossRef]
- Jarvis, K.D.; Knight, R.J. Aquifer heterogeneity from SH-wave seismic impedance inversion. Geophysics 2002, 67, 1548–1557. [Google Scholar] [CrossRef]
- Sayers, C.M. Elastic wave velocities in a granitic geothermal reservoir. Geophys. Prospect. 2022, 71, 114–124. [Google Scholar] [CrossRef]
- Lou, M.; Rial, J.A. Characterization of geothermal reservoir crack patterns using shear-wave splitting. Geophysics 1997, 62, 487–494. [Google Scholar] [CrossRef]
- Wawerzinek, B.; Buness, H.; von Hartmann, H.; Tanner, D.C. S-wave experiments for the exploration of a deep geothermal carbonate reservoir in the German Molasse Basin. Geotherm. Energy 2021, 9, 6. [Google Scholar] [CrossRef]
- Mendrinos, D.; Karytsas, C.; Karytsas, S.; Poletto, F.; Farina, B.; Barison, E. Correlations of Seismic Velocities and Elastic Moduli with Temperature in Superhot and Enhanced Geothermal Systems. Clean Technol. 2022, 4, 440–457. [Google Scholar] [CrossRef]
- Del Gaudio, V.; Muscillo, S.; Wasowski, J. What we can learn about slope response to earthquakes from ambient noise analysis: An overview. Eng. Geol. 2014, 182, 182–200. [Google Scholar] [CrossRef]
- Chen, Y.; Irfan, M.; Uchimura, T.; Wu, Y.; Yu, F. Development of elastic wave velocity threshold for rainfall-induced landslide prediction and early warning. Landslides 2019, 16, 955–968. [Google Scholar] [CrossRef]
- Qureshi, M.U.; Yamada, S.; Towhata, I. A simplified technique for slope stability assessment based on in-situ S-wave velocity measurement. In Earthquake-Induced Landslides: Proceedings of the International Symposium on Earthquake-Induced Landslides, Kiryu, Japan, 2012; Springer: Berlin/Heidelberg, Germany, 2013; pp. 871–881. [Google Scholar]
- Feng, Z.Y.; Lu, Y.R.; Shen, Z.R. A numerical simulation of seismic signals of coseismic landslides. Eng. Geol. 2021, 289, 106191. [Google Scholar] [CrossRef]
- Fjaer, E.; Holt, R.M.; Horsrud, P.; Raaen, A.M. Petroleum Related Rock Mechanics; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Blake, O.O.; Faulkner, D.R.; Worden, R.H.; Armitage, P.J.; Espie, A.A. Effect of thermal shock on the permeability and seismic wave velocity of the caprock and reservoir during CO2 injection. Int. J. Greenh. Gas Control 2022, 118, 103691. [Google Scholar] [CrossRef]
- Gholami, R.; Raza, A.; Iglauer, S. Leakage risk assessment of a CO2 storage site: A review. Earth-Sci. Rev. 2021, 223, 103849. [Google Scholar] [CrossRef]
- Ringrose, P.S.; Mathieson, A.S.; Wright, I.W.; Selama, F.; Hansen, O.; Bissell, R.; Saoula, N.; Midgley, J. The In Salah CO2 storage project: Lessons learned and knowledge transfer. Energy Procedia 2013, 37, 6226–6236. [Google Scholar] [CrossRef]
- Nadim, F.; Kvalstad, T.J. Risk assessment and management for offshore geohazards. In Proceedings of the ISGSR2007 First International Symposium on Geotechnical Safety & Risk, Shanghai, China, 18–19 October 2007. [Google Scholar]
- Ten Brink, U.S.; Lee, H.J.; Geist, E.L.; Twichell, D. Assessment of tsunami hazard to the US East Coast using relationships between submarine landslides and earthquakes. Mar. Geol. 2009, 264, 65–73. [Google Scholar] [CrossRef]
- Zhao, M.; Gao, Z.; Wang, P.; Du, X. Response spectrum method for seismic analysis of monopile offshore wind turbine. Soil Dyn. Earthq. Eng. 2020, 136, 106212. [Google Scholar] [CrossRef]
- Brithish Geological Survey. Offshore Seismic Hazard in UK Waters. Available online: https://www.earthquakes.bgs.ac.uk/hazard/hazard_offshore.html (accessed on 24 January 2025).
- Gao, W.; Grand, S.P.; Baldridge, W.S.; Wilson, D.; West, M.; Ni, J.F.; Aster, R. Upper mantle convection beneath the central Rio Grande rift imaged by P and S wave tomography. J. Geophys. Res. Solid Earth 2004, 109, B03305. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, H.; Yang, Y. Shear wave velocity structure of the crust and upper mantle in Southeastern Tibet and its geodynamic implications. Sci. China Earth Sci. 2020, 63, 1278–1293. [Google Scholar] [CrossRef]
- Mainprice, D.; Tommasi, A.; Couvy, H.; Cordier, P.; Frost, D.J. Pressure sensitivity of olivine slip systems and seismic anisotropy of Earth’s upper mantle. Nature 2005, 433, 731–733. [Google Scholar] [CrossRef]
- Butler, R.; Tsuboi, S. Antipodal seismic reflections upon shear wave velocity structures within Earth’s inner core. Phys. Earth Planet. Inter. 2021, 321, 106802. [Google Scholar] [CrossRef]
- Mussett, A.E.; Khan, M.A. Looking into The Earth: An Introduction to Geological Geophysics; University Press: Cambridge, NY, USA, 2000; 470p. [Google Scholar]
- Sarkar, R.; Kolathayar, S.; Drukpa, D.; Choki, K.; Rai, S.; Tshering, S.T.; Yuden, K. Near-surface seismic refraction tomography and MASW for site characterization in Phuentsholing, Bhutan Himalaya. SN Appl. Sci. 2021, 3, 394. [Google Scholar] [CrossRef]
- U.S. Environmental Protection Agency (EPA). Seismic Refraction. Available online: https://www.epa.gov/environmental-geophysics/seismic-refraction (accessed on 18 April 2024).
- Nazarian, S. In Situ Determination of Elastic Moduli of Soil Deposits and Pavement Systems by Spectral-Analysis-of-Surface-Waves Method (Shear Velocity, Propagation, Liquefaction, Non-Destructive, Earthquake). Ph.D. Thesis, The University of Texas, Austin, TX, USA, 1984. [Google Scholar]
- Boore, D.M. Determining subsurface shear-wave velocities: A review. In Proceedings of the Third International Symposium on the Effects of Surface Geology on Seismic Motion, Grenoble, France, 30 August–1 September 2006; pp. 67–85. [Google Scholar]
- Jones, R. In-situ measurement of the dynamic properties of soil by vibration methods. Geotechnique 1958, 8, 1–21. [Google Scholar] [CrossRef]
- Abbiss, C.P. Shear wave measurements of the elasticity of the ground. Geotechnique 1981, 31, 91–104. [Google Scholar] [CrossRef]
- SAGE. Available online: https://www.iris.edu/hq/files/programs/education_and_outreach/aotm/7/SeismicTomography_Background.pdf (accessed on 11 September 2024).
- Li, Y.; Wu, Q.; Pan, J.; Sun, L. S-wave velocity structure of northeastern China from joint inversion of Rayleigh wave phase and group velocities. Geophys. J. Int. 2012, 190, 105–115. [Google Scholar] [CrossRef]
- Pilz, M.; Parolai, S.; Picozzi, M.; Bindi, D. Three-Dimensional Shear Wave Velocity Imaging by Ambient Seismic Noise Tomography. Geophys. J. Int. 2012, 189, 501–512. [Google Scholar] [CrossRef]
- Manu-Marfo, D.; Aoudia, A.; Pachhai, S.; Kherchouche, R. 3D Shear Wave Velocity Model of the Crust and Uppermost Mantle beneath the Tyrrhenian Basin and Margins. Sci. Rep. 2019, 9, 3609. [Google Scholar] [CrossRef]
- Louie, J.N. Faster, better: Shear-wave velocity to 100 meters depth from refraction microtremor arrays. Bull. Seismol. Soc. Am. 2001, 91, 347–364. [Google Scholar] [CrossRef]
- Ellefsen, K.J.; Tuttle, G.J.; Williams, J.M.; Lucius, J.E. S-wave refraction survey of alluvial aggregate (No. 2005-5012). Open-File Rep. Kansas Geol. Surv. 2005, 36, 11. [Google Scholar]
- Boiero, D. Surface Wave Analysis for Building Shear Wave Velocity Models. Ph.D. Thesis, Politecnico di Torino, Torino, Italy, 2009. [Google Scholar]
- Fichtner, A.; Kennett, B.L.; Tsai, V.C.; Thurber, C.H.; Rodgers, A.J.; Tape, C.; Rawlinson, N.; Borcherdt, R.D.; Lebedev, S.; Priestley, K.; et al. Seismic tomography 2024. Bull. Seismol. Soc. Am. 2024, 114, 1185–1213. [Google Scholar] [CrossRef]
- Wikipedia Contributors. Seismic Interferometry. Wikipedia. Available online: https://en.wikipedia.org/wiki/Seismic_interferometry?utm_source=chatgpt.com (accessed on 23 May 2025).
- Wolf, J.; Becker, T.W.; Garnero, E.; Liu, K.H.; West, J.D. Comprehensive global data set of uniformly processed shear-wave splitting measurements. Geophys. J. Int. 2025, 241, 863–875. [Google Scholar] [CrossRef]
- Zerafa, C.; Galea, P.; Sebu, C. Synergizing Deep Learning and Full-Waveform Inversion: Bridging Data-Driven and Theory-Guided Approaches for Enhanced Seismic Imaging. arXiv 2025, arXiv:2502.17585. [Google Scholar] [CrossRef]
- Earp, S.; Curtis, A.; Zhang, X.; Hansteen, F. Probabilistic neural network tomography across Grane field (North Sea) from surface wave dispersion data. Geophys. J. Int. 2020, 223, 1741–1757. [Google Scholar] [CrossRef]
- Miller, R.D.; Bradford, J.H.; Holliger, K. (Eds.) Advances in Near-Surface Seismology and Ground-Penetrating Radar; Society of Exploration Geophysicists, American Geophysical Union, Environmental and Engineering Geophysical Society: Tulsa, OK, USA, 2010. [Google Scholar]
- Wikipedia contributors. Subsurface mapping by ambient noise tomography. Wikipedia. Available online: https://en.wikipedia.org/wiki/Subsurface_mapping_by_ambient_noise_tomography?utm_source=chatgpt.com (accessed on 4 June 2025).
- U.S. Geological Survey (USGS). What Is Remote Sensing and What Is It Used For? Available online: https://www.usgs.gov/faqs/what-remote-sensing-and-what-it-used (accessed on 31 December 2024).
- Yusroni, S.A.; Kemalasari, V.T.; Putra, D.P.N. Identification of Land Cover Changes from Landsat 8 Oli Satellite Imagery Using Normalized Difference Vegetation Index (NDVI) Method (Study Case: Surabaya). J. Mar. Sci. Technol. 2021, 2, 5–10. [Google Scholar] [CrossRef]
- Avtar, R.; Komolafe, A.A.; Kouser, A.; Singh, D.; Yunus, A.P.; Dou, J.; Kumar, P.; Gupta, R.D.; Johnson, B.A.; Minh, H.V.T.; et al. Assessing sustainable development prospects through remote sensing: A review. Remote Sens. Appl. Soc. Environ. 2020, 20, 100402. [Google Scholar] [CrossRef] [PubMed]
- Ejemeyovwi, D.O.; Achima, B.T.; Ogwu, C. Remote Sensing Satellite Systems and Capabilities in Mapping Environmental Resources. KIU J. Soc. Sci. 2023, 9, 117–124. [Google Scholar] [CrossRef]
- Retallack, A.; Finlayson, G.; Ostendorf, B.; Clarke, K.; Lewis, M. Remote sensing for monitoring rangeland condition: Current status and development of methods. Environ. Sustain. Indic. 2023, 19, 100285. [Google Scholar] [CrossRef]
- Eskandari, A.; Hosseini, M.; Nicotra, E. Application of Satellite Remote Sensing, UAV-Geological Mapping, and Machine Learning Methods in the Exploration of Podiform Chromite Deposits. Minerals 2023, 13, 251. [Google Scholar] [CrossRef]
- Rizki, M.K.; Lubis, A.M.; Handayani, L.; Mukti, M.M.; Anggono, T.; Gaol, K.L.; Sudrajat, Y. Gravity Anomaly Evaluation of the Geothermal Field Distribution Around the Seismo-Volcanic Area of Toba Lake. J. Phys. Conf. Ser. 2022, 2377, 012042. [Google Scholar] [CrossRef]
- Setyawan, A.; Khusna, L.M.; Suseno, J.E.; Rina, D.I.; Yulianto, T.; Aribowo, Y. Detecting hot spring manifestations based on gravity data satellite on mountain Lawu. J. Phys. Conf. Ser. 2021, 1943, 012034. [Google Scholar] [CrossRef]
- Flechtner, F.; Reigber, C.; Rummel, R.; Balmino, G. Satellite Gravimetry: A Review of Its Realization. Surv. Geophys. 2021, 42, 1029–1074. [Google Scholar] [CrossRef]
- Noeker, M.; Karatekin, Ö. The wedge-pentahedra method (WPM): Topographic reduction of local terrain in the context of solar system surface gravimetry and robotic exploration. Front. Space Technol. 2022, 3, 982873. [Google Scholar] [CrossRef]
- Kadhim, N.; Mourshed, M.; Bray, M. Advances in remote sensing applications for urban sustainability. Euro-Mediterr. J. Environ. Integr. 2016, 1, 7. [Google Scholar] [CrossRef]
- Ghione, F.; Köhler, A.; Dichiarante, A.M.; Aarnes, I.; Oye, V. Vs30 and depth to bedrock estimates from integrating HVSR measurements and geology-slope approach in the Oslo area, Norway. Front. Earth Sci. 2023, 11, 1242679. [Google Scholar] [CrossRef]
- Wróbel, M.; Stan-Kłeczek, I.; Marciniak, A.; Majdański, M.; Kowalczyk, S.; Nawrot, A.; Cader, J. Integrated Geophysical Imaging and Remote Sensing for Enhancing Geological Interpretation of Landslides with Uncertainty Estimation—A Case Study from Cisiec, Poland. Remote Sens. 2022, 15, 238. [Google Scholar] [CrossRef]
- Holland, C.W.; Dettmer, J.; Dosso, S.E. Remote sensing of sediment density and velocity gradients in the transition layer. J. Acoust. Soc. Am. 2005, 118, 163–177. [Google Scholar] [CrossRef]
- Abbas, A.; Vantassel, J.P.; Cox, B.R.; Kumar, K.; Crocker, J. A frequency-velocity CNN for developing near-surface 2D vs images from linear-array, active-source wavefield measurements. Comput. Geotech. 2023, 156, 105305. [Google Scholar] [CrossRef]
- Feng, G.; Zeng, H.H.; Xu, X.R.; Tang, G.Y.; Wang, Y.X. Shear wave velocity prediction based on deep neural network and theoretical rock physics modeling. Front. Earth Sci. 2023, 10, 1025635. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, H.; Sun, L.; Wang, J. Remote sensing techniques for detecting internal solitary waves: A comprehensive review and prospects. IEEE Geosci. Remote Sens. Mag. 2024, 12, 46–78. [Google Scholar] [CrossRef]
- Rajabi, M.; Bohloli, B.; Ahangar, E.G. Intelligent approaches for prediction of compressional, shear and Stoneley wave velocities from conventional well log data: A case study from the Sarvak carbonate reservoir in the Abadan Plain (Southwestern Iran). Comput. Geosci. 2010, 36, 647–664. [Google Scholar] [CrossRef]
- Asoodeh, M.; Bagheripour, P. Prediction of compressional, shear, and Stoneley wave velocities from conventional well log data using a committee machine with intelligent systems. Rock Mech. Rock Eng. 2012, 45, 45–63. [Google Scholar] [CrossRef]
- Maleki, S.; Moradzadeh, A.; Riabi, R.G.; Gholami, R.; Sadeghzadeh, F. Prediction of shear wave velocity using empirical correlations and artificial intelligence methods. NRIAG J. Astron. Geophys. 2014, 3, 70–81. [Google Scholar] [CrossRef]
- Bagheripour, P.; Gholami, A.; Asoodeh, M.; Vaezzadeh-Asadi, M. Support vector regression-based determination of shear wave velocity. J. Pet. Sci. Eng. 2015, 125, 95–99. [Google Scholar] [CrossRef]
- Nourafkan, A.; Kadkhodaie-Ilkhchi, A. Shear wave velocity estimation from conventional well log data by using a hybrid ant colony–fuzzy inference system: A case study from Cheshmeh–Khosh oilfield. J. Pet. Sci. Eng. 2015, 127, 459–468. [Google Scholar] [CrossRef]
- Ataee, O.; Hafezi Moghaddas, N.; Lashkari Pour, G.R.; Abbari Nooghabi, M.J. Predicting shear wave velocity of soil using multiple linear regression analysis and artificial neural networks. Sci. Iran. 2018, 25, 1943–1955. [Google Scholar] [CrossRef]
- Anemangely, M.; Ramezanzadeh, A.; Amiri, H.; Hoseinpour, S.A. Machine learning technique for the prediction of shear wave velocity using petrophysical logs. J. Pet. Sci. Eng. 2019, 174, 306–327. [Google Scholar] [CrossRef]
- Wang, P.; Peng, S. On a new method of estimating shear wave velocity from conventional well logs. J. Pet. Sci. Eng. 2019, 180, 105–123. [Google Scholar] [CrossRef]
- Azadpour, M.; Saberi, M.R.; Javaherian, A.; Shabani, M. Rock physics model-based prediction of shear wave velocity utilizing machine learning technique for a carbonate reservoir, southwest Iran. J. Pet. Sci. Eng. 2020, 195, 107864. [Google Scholar] [CrossRef]
- Lian, J.; John, P.C.; Brian, R.; Pablo, G. Rock physics modelling using machine learning. In SEG Technical Program Expanded Abstracts 2020; Society of Exploration Geophysicists: Houston, TX, USA, 2020; pp. 2530–2534. [Google Scholar] [CrossRef]
- Khatibi, S.; Aghajanpour, A. Machine learning: A useful tool in geomechanical studies, a case study from an offshore gas field. Energies 2020, 13, 3528. [Google Scholar] [CrossRef]
- Wang, J.; Cao, J.; Yuan, S. Shear wave velocity prediction based on adaptive particle swarm optimization optimized recurrent neural network. J. Pet. Sci. Eng. 2020, 194, 107466. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, Y.; Zhang, Y.; Qiu, J.; Wu, S. The adoption of deep neural network (DNN) to the prediction of soil liquefaction based on shear wave velocity. Bull. Eng. Geol. Environ. 2021, 80, 5053–5060. [Google Scholar] [CrossRef]
- Jeong, J.; Park, E.; Emelyanova, I.; Pervukhina, M.; Esteban, L.; Yun, S.T. Application of conditional generative model for sonic log estimation considering measurement uncertainty. J. Pet. Sci. Eng. 2021, 196, 108028. [Google Scholar] [CrossRef]
- Olayiwola, T.; Sanuade, O.A. A data-driven approach to predict compressional and shear wave velocities in reservoir rocks. Petroleum 2021, 7, 199–208. [Google Scholar] [CrossRef]
- Miah, M.I. Improved prediction of shear wave velocity for clastic sedimentary rocks using hybrid model with core data. J. Rock Mech. Geotech. Eng. 2021, 13, 1466–1477. [Google Scholar] [CrossRef]
- Kim, J. Synthetic shear sonic log generation utilizing hybrid machine learning techniques. Artif. Intell. Geosci. 2022, 3, 53–70. [Google Scholar] [CrossRef]
- Wong, W.K.; Nuwara, Y.; Juwono, F.H.; Motalebi, F. Sonic waves travel-time prediction: When machine learning meets geophysics. In Proceedings of the 2022 International Conference on Green Energy, Computing and Sustainable Technology (GECOST), Sousse, Tunisia, 2–4 October 2022; pp. 159–163. [Google Scholar] [CrossRef]
- Mehrad, M.; Ramezanzadeh, A.; Bajolvand, M.; Hajsaeedi, M.R. Estimating shear wave velocity in carbonate reservoirs from petrophysical logs using intelligent algorithms. J. Pet. Sci. Eng. 2022, 212, 110254. [Google Scholar] [CrossRef]
- Laalam, A.; Mouedden, N.; Ouadi, H.; Chemmakh, A.; Merzoug, A.; Boualam, A.; Djezzar, S.; Aihar, A.; Berrehal, B.E. Prediction of Shear Wave Velocity in the Williston Basin Using Big Data Analysis and Robust Machine Learning Algorithms. In Proceedings of the 56th U.S. Rock Mechanics/Geomechanics Symposium, Santa Fe, NM, USA, 26–29 June 2022. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Ma, Q.; Zhang, X.; Zhou, H. Automatic prediction of shear wave velocity using convolutional neural networks for different reservoirs in Ordos Basin. J. Pet. Sci. Eng. 2022, 208, 109252. [Google Scholar] [CrossRef]
- Jiang, R.; Ji, Z.; Mo, W.; Wang, S.; Zhang, M.; Yin, W.; Wang, Z.; Lin, Y.; Wang, X.; Ashraf, U. A Novel Method of Deep Learning for Shear Velocity Prediction in a Tight Sandstone Reservoir. Energies 2022, 15, 7016. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, D.; Li, H.; Gao, J. S-wave velocity prediction using physical model-driven Gaussian process regression: A case study of tight sandstone reservoir. Geophysics 2023, 88, D85–D93. [Google Scholar] [CrossRef]
- Kheirollahi, H.; Manaman, N.S.; Leisi, A. Robust estimation of shear wave velocity in a carbonate oil reservoir from conventional well logging data using machine learning algorithms. J. Appl. Geophys. 2023, 211, 104971. [Google Scholar] [CrossRef]
- Cova, D.; Liu, Y. Shear wave velocity prediction using bidirectional recurrent gated graph convolutional network with total information embeddings. Front. Earth Sci. 2023, 11, 1101601. [Google Scholar] [CrossRef]
- Akinyemi, O.D.; Elsaadany, M.; Siddiqui, N.A.; Elkurdy, S.; Olutoki, J.O.; Islam, M.M. Machine learning application for prediction of sonic wave transit time-A case of Niger Delta basin. Results Eng. 2023, 20, 101528. [Google Scholar] [CrossRef]
- Mustafa, A.; Tariq, Z.; Iqbal, A.; Naeem, M. A Data-Driven Intelligent Approach to Predict Shear Wave Velocity in Shale Formations. In Proceedings of the 57th U.S. Rock Mechanics/Geomechanics Symposium, Atlanta, GA, USA, 25–28 June 2023. [Google Scholar] [CrossRef]
- Khalilidermani, M.; Knez, D. Comparing Artificial Intelligence Algorithms with Empirical Correlations in Shear Wave Velocity Prediction. Appl. Sci. 2023, 13, 13126. [Google Scholar] [CrossRef]
- Fu, X.; Wei, Y.; Su, Y.; Hu, H. Shear Wave Velocity Prediction Based on the Long Short-Term Memory Network with Attention Mechanism. Appl. Sci. 2024, 14, 2489. [Google Scholar] [CrossRef]
- Gomaa, S.; Shahat, J.S.; Aboul-Fotouh, T.M.; Khaled, S. Neural Network Model for Predicting Shear Wave Velocity Using Well Logging Data. Arab. J. Sci. Eng. 2024, 50, 4721–4730. [Google Scholar] [CrossRef]
- Dehghani, M.; Jahani, S.; Ranjbar, A. Comparing the performance of machine learning methods in estimating the shear wave transit time in one of the reservoirs in southwest of Iran. Sci. Rep. 2024, 14, 4744. [Google Scholar] [CrossRef] [PubMed]
- Joshi, A.; Raman, B.; Mohan, C.K.; Cenkeramaddi, L.R. A new machine learning approach for estimating shear wave velocity profile using borelog data. Soil Dyn. Earthq. Eng. 2024, 177, 108424. [Google Scholar] [CrossRef]
- Yılmaz, B.; Türkmen, M.; Meral, S.; Akagündüz, E.; Tileylioglu, S. Deep Learning-Based Average Shear Wave Velocity Prediction Using Accelerometer Records. arXiv 2024, arXiv:2408.14962. [Google Scholar] [CrossRef]
- Leisi, A.; Shad Manaman, N. Three-Dimensional Shear Wave Velocity Prediction by Integrating Post-Stack Seismic Attributes and Well Logs: Application on Asmari Formation in Iran. J. Pet. Explor. Prod. Technol. 2024, 14, 2399–2411. [Google Scholar] [CrossRef]
- Castagna, J.P.; Batzle, M.L.; Eastwood, R.L. Relationships between compressional-wave and shear-wave velocities in clastic silicate rocks. Geophysics 1985, 50, 571–581. [Google Scholar] [CrossRef]
- Rajabi, M.; Hazbeh, O.; Davoodi, S.; Wood, D.A.; Tehrani, P.S.; Ghorbani, H.; Mehrad, M.; Mohamadian, N.; Rukavishnikov, V.S. Predicting shear wave velocity from conventional well logs with deep and hybrid machine learning algorithms. J. Petrol. Explor. Prod. Technol. 2023, 13, 19–42. [Google Scholar] [CrossRef]
- Entezari, I.; Sharp, J.; Mayne, P.W. A data-driven approach to predict shear wave velocity from CPTu measurements. In Cone Penetration Testing 2022; CRC Press: Boca Raton, FL, USA, 2022; pp. 374–380. [Google Scholar]
- Chala, A.T.; Ray, R. Uncertainty Quantification in Shear Wave Velocity Predictions: Integrating Explainable Machine Learning and Bayesian Inference. Appl. Sci. 2025, 15, 1409. [Google Scholar] [CrossRef]
- IRIS. Available online: https://ds.iris.edu/ds/nodes/dmc/ (accessed on 4 June 2025).
- OpenTopography. Available online: https://portal.opentopography.org/dataCatalog (accessed on 4 June 2025).
- OSGeo Foundation. Available online: https://www.osgeo.org/ (accessed on 1 June 2025).
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2005. [Google Scholar]
- Rai, C.S.; Hanson, K.E. Shear-wave velocity anisotropy in sedimentary rocks: A laboratory study. Geophysics 1988, 53, 800–806. [Google Scholar] [CrossRef]
- Valcke, S.L.A.; Casey, M.; Lloyd, G.E.; Kendall, J.M.; Fisher, Q.J. Lattice preferred orientation and seismic anisotropy in sedimentary rocks. Geophys. J. Int. 2006, 166, 652–666. [Google Scholar] [CrossRef]
- Kaderali, A.; Stanoev, T. On anisotropy and inhomogeneity parameter estimation using traveltimes. arXiv 2020, arXiv:2012.03393. [Google Scholar] [CrossRef]
- Toro, G.R. Uncertainty in shear-wave velocity profiles. J. Seismol. 2022, 26, 713–730. [Google Scholar] [CrossRef]
- Bernard, R.W.; Jason, T.D.; Thomas, S. Guidelines for Estimation of Shear Wave Velocity Profiles; PEER Report 2012/08; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2012. [Google Scholar]
- Sehizadeh, M.; Nasseri, M.H.; Young, R.P. The scaling effect on rock behaviour by comparing compressional wave velocities measured in the lab and field. Adv. Geosci. 2018, 45, 167–176. [Google Scholar] [CrossRef]
- Khalilidermani, M.; Knez, D. Shear Wave Velocity Applications in Geomechanics with Focus on Risk Assessment in Carbon Capture and Storage Projects. Energies 2024, 17, 1578. [Google Scholar] [CrossRef]
- Bekdaş, G.; Aydın, Y.; Işıkdağ, U.; Nigdeli, S.M.; Hajebi, D.; Kim, T.-H.; Geem, Z.W. Shear Wave Velocity Prediction with Hyperparameter Optimization. Information 2025, 16, 60. [Google Scholar] [CrossRef]
- Nath, F.; Asish, S.M.; Ganta, D.; Debi, H.R.; Aguirre, G.; Aguirre, E. Artificial Intelligence Model in Predicting Geomechanical Properties for Shale Formation: A Field Case in Permian Basin. Energies 2022, 15, 8752. [Google Scholar] [CrossRef]
- Al-Anazi, A.; Gates, I.D. A Support Vector Machine Algorithm to Classify Lithofacies and Model Permeability in Heterogeneous Reservoirs. Eng. Geol. 2010, 114, 267–277. [Google Scholar] [CrossRef]
- Zhou, Y.; Gu, Z.; He, C.; Yang, J.; Xiong, J. An Improved Decline Curve Analysis Method via Ensemble Learning for Shale Gas Reservoirs. Energies 2024, 17, 5910. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, L.; Yu, X.; Azzolina, N.A.; Wan, X.; Smith, S.A.; Bosshart, N.W.; Sorensen, J.A.; Ling, K. Progress of Gas Injection EOR Surveillance in the Bakken Unconventional Play—Technical Review and Machine Learning Study. Energies 2024, 17, 4200. [Google Scholar] [CrossRef]
- Ali, N.; Fu, X.; Chen, J.; Hussain, J.; Hussain, W.; Rahman, N.; Iqbal, S.M.; Altalbe, A. Advancing Reservoir Evaluation: Machine Learning Approaches for Predicting Porosity Curves. Energies 2024, 17, 3768. [Google Scholar] [CrossRef]
- Rezaee, R.; Ekundayo, J. Permeability Prediction Using Machine Learning Methods for the CO2 Injectivity of the Precipice Sandstone in Surat Basin, Australia. Energies 2022, 15, 2053. [Google Scholar] [CrossRef]
- Zhang, H.; Mi, B.; Xi, C.; Liu, Y.; Guan, B.; Ning, L. Extraction of surface-wave phase velocities from ambient noise in the presence of local noise sources based on matched-field processing. J. Appl. Geophys. 2022, 204, 104755. [Google Scholar] [CrossRef]
- García-Martín, E.; Rodrigues, C.F.; Riley, G.; Grahn, H. Estimation of energy consumption in machine learning. J. Parallel Distrib. Comput. 2019, 134, 75–88. [Google Scholar] [CrossRef]
- Anand, A.; Deb, C. The potential of remote sensing and GIS in urban building energy modelling. Energy Built Environ. 2023, 5, 957–969. [Google Scholar] [CrossRef]
| Technique | Advantages | Disadvantages | Depth Range | Spatial Resolution |
|---|---|---|---|---|
| Seismic Refraction | Provides depth-dependent shear wave velocity profile High-resolution estimation of Vs Cost-effective and efficient Non-intrusive and minimal site disturbance | Requires controlled seismic sources Limited to near-surface applications Sensitive to geophone spacing and array design | Under 100 m | high |
| Surface Wave Analysis | Estimates shear wave velocity variations with depth Cost-effective and efficient Minimal disturbance to the site | Requires long-wavelength surface waves Extracting reliable dispersion curves is tough Appropriate inversion methods are crucial | 10–100 m | intermediate |
| Seismic Tomography | Provides detailed subsurface velocity models Captures Vs variations in complex settings High-resolution estimation of Vs | Requires seismic data from multiple receivers Computational complexity Sensitivity to initial model assumptions | Meters to a few kilometers | low |
| Technique | Advantages | Disadvantages |
|---|---|---|
| Remote Sensing | Cost-effective and energy-efficient Provides spatially extensive information Non-intrusive and reduces fieldwork requirements Enables monitoring of temporal variations | Relies on correlations with surface features Requires ground truth data for calibration and validation Uncertainties due to atmospheric and geometric effects Correlations may vary with regional geological conditions |
| Reference | AI Model | Error Estimation |
|---|---|---|
| Rezaee et al. (2007) [11] | NFS | MSE = 0.001 |
| Rajabi (2010) [95] | GA, FL, NF | MSE = 0.0153, 0.0084, 0.0184 |
| Asoodeh and Bagheripour (2012) [96] | FL, ANN, NF | MSE = 0.0081, 0.0068, 0.0078 |
| Maleki et al. (2014) [97] | SVR, BPNN | R2 = 0.97, 0.94 |
| Bagheripour et al. (2015) [98] | SVR | R2 = 0.9716 |
| Nourafkan et al. (2015) [99] | ACOFIS | MSE = 0.0033, R2 = 0.9590 |
| Anemangely et al. (2019) [101] | LSSVM-COA, LSSVM-PSO, LSSVM-GA | R2 = 0.929, 0.877, 0.868 |
| Wang and Peng (2019) [102] | ELM, ANN | RMSE = 0.0795, 0.0913 |
| Azadpour et al. (2020) [103] | ML | R2 = 0.941 |
| Lian et al. (2020) [104] | SVM, RF, MLP | Average R2 for ML models = 0.64 |
| Khatibi and Aghajanpour (2020) [105] | NN | R2 = 0.9555 |
| Olayiwola and Sanuade (2021) [109] | LSSVM | R2 = 0.9991 |
| Miah (2021) [110] | LSSVM-CSA | R2 = 0.96 |
| Wong et al. (2022) [112] | ANN, MLR | R2 = 0.86 (ANN), 0.36 (MLR) |
| Mehrad et al. (2022) [113] | CNN, MELM, LSSVM | R2 = 0.825, 0.826, 0.815 |
| Laalam et al. (2022) [114] | XGBoost, RFR, LR, AdaBoost, BRR | R2 = 0.55 to 0.92, XGBoost outperforms others |
| Zhang et al. (2022) [115] | CNNs | R2 = 0.957 |
| Kheirollahi et al. (2023) [118] | MLR, ELM, ANN | R2 = 0.99 (ANN), 0.96 (MLR, ELM) |
| Cova and Liu (2023) [119] | GCN-BiGRU | R2 = 0.947 |
| Akinyemi et al. (2023) [120] | LR, KNN, SVR, RFR, XGBoost, CatBoost, BPANN | R2 = 0.92 to 0.94 (CatBoost had best result) |
| Khalilidermani and Knez (2023) [122] | GEP | R2 = 0.972 |
| Mustafa et al. (2023) [121] | ANN | R2 = 0.96 |
| Fu et al. (2024) [123] | NN | MAE = 38.89, LSTM MAE = 45.35 |
| Gomaa et al. (2024) [124] | ANN | R2 = 0.58 |
| Dehghani et al. (2024) [125] | ANN, LR, RF, LB, SVM | R2 = 0.8780, 0.8471, 0.8470, 0.9495, 0.8583, 0.7975 |
| Leisi and Shad Manaman (2024) [128] | ANN | RMSE = 0.94 |
| Technique | Advantages | Disadvantages |
|---|---|---|
| ML and Data-Driven Approaches | Captures complex relationships in data Offers high prediction accuracy Can handle non-linear relationships Utilizes available data effectively Allows for incorporation of multiple data points | Requires large, labeled datasets May suffer from overfitting Interpretability of results may be challenging Performance dependent on data quality |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalilidermani, M.; Knez, D.; Zamani, M.A.M. Shear Wave Velocity in Geoscience: Applications, Energy-Efficient Estimation Methods, and Challenges. Energies 2025, 18, 3310. https://doi.org/10.3390/en18133310
Khalilidermani M, Knez D, Zamani MAM. Shear Wave Velocity in Geoscience: Applications, Energy-Efficient Estimation Methods, and Challenges. Energies. 2025; 18(13):3310. https://doi.org/10.3390/en18133310
Chicago/Turabian StyleKhalilidermani, Mitra, Dariusz Knez, and Mohammad Ahmad Mahmoudi Zamani. 2025. "Shear Wave Velocity in Geoscience: Applications, Energy-Efficient Estimation Methods, and Challenges" Energies 18, no. 13: 3310. https://doi.org/10.3390/en18133310
APA StyleKhalilidermani, M., Knez, D., & Zamani, M. A. M. (2025). Shear Wave Velocity in Geoscience: Applications, Energy-Efficient Estimation Methods, and Challenges. Energies, 18(13), 3310. https://doi.org/10.3390/en18133310






