Fast Identification of LiNMC Cells for Railway Applications
Abstract
1. Introduction
- Size of the Storage System: The size of storage systems is relatively large; correspondingly, the development of full-scale prototypes and their testing is relatively expensive.
- Production Scale: With respect to other sectors, such as the automotive sector, the scale of production is relatively modest. Thus, the costs of product development and assessment cannot be justified by large production scales.
- Required Life and Safety levels: The operational life of rolling stock is typically over 25–30 years, with associated mileages of 107 km (30 million kilometers should be a statistically feasible estimation). The current life of batteries is limited both in terms of equivalent cycles [10] and calendar [11] aging. Therefore, batteries with a lifespan corresponding to approximately 8–10 years are often required, along with a corresponding mileage of several million kilometers.
- Operational Stress Conditions: The inertia of rolling stock is typically relatively important with respect to motion resistances. Thus, to ensure an acceptable level of autonomy, the size of the battery is relatively small. At the same time, peak traction demand and regenerative braking are quite demanding, as power and energy are transferred during both phases due to the train’s high inertia. As an example, for a Hitachi Blues BEMU (battery electric multiple unit), the size of the DC-DC controller used to interface the battery with the traction and braking loads is approximately three times greater than the nominal power of the battery [12,13,14]; this means that it is possible to charge and discharge the battery pack with a peak performance that is near or about 3C. Moreover, thermal and fire protection specifications are even more demanding, as the battery is not only subjected to high charge and discharge rates but also unfavorable conditions when the train is not in operation.
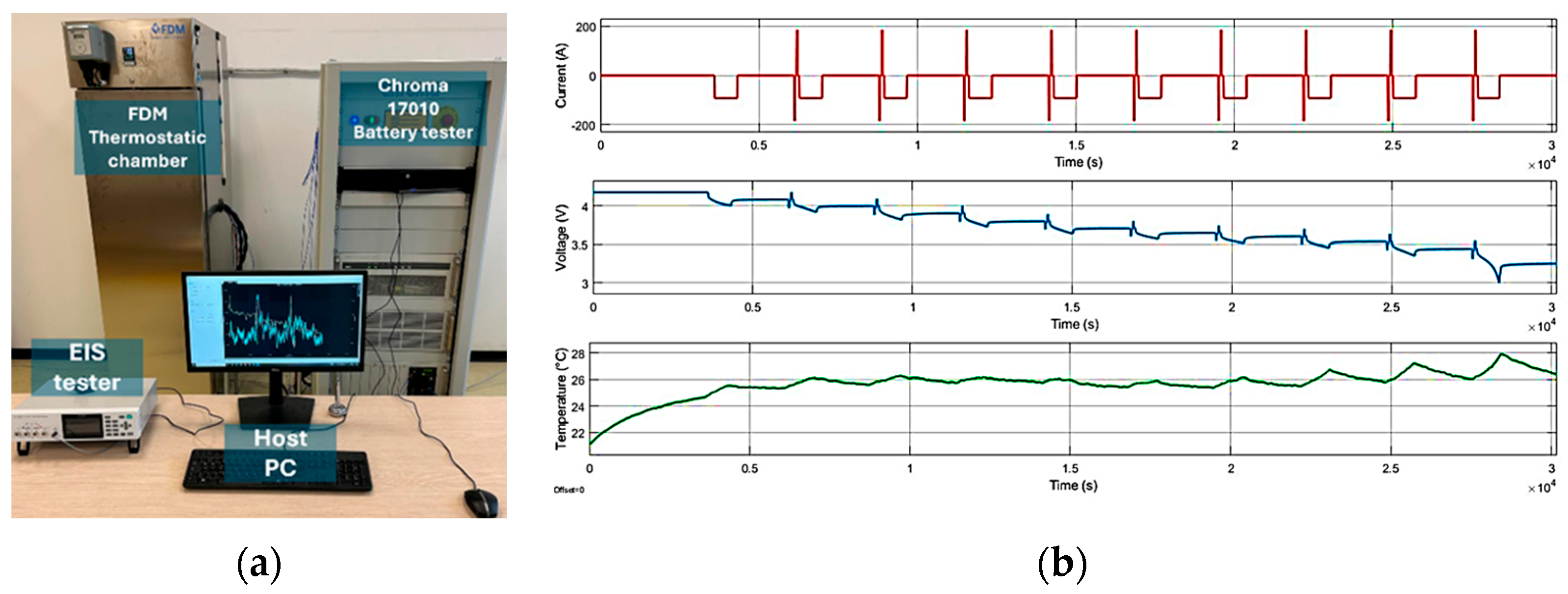
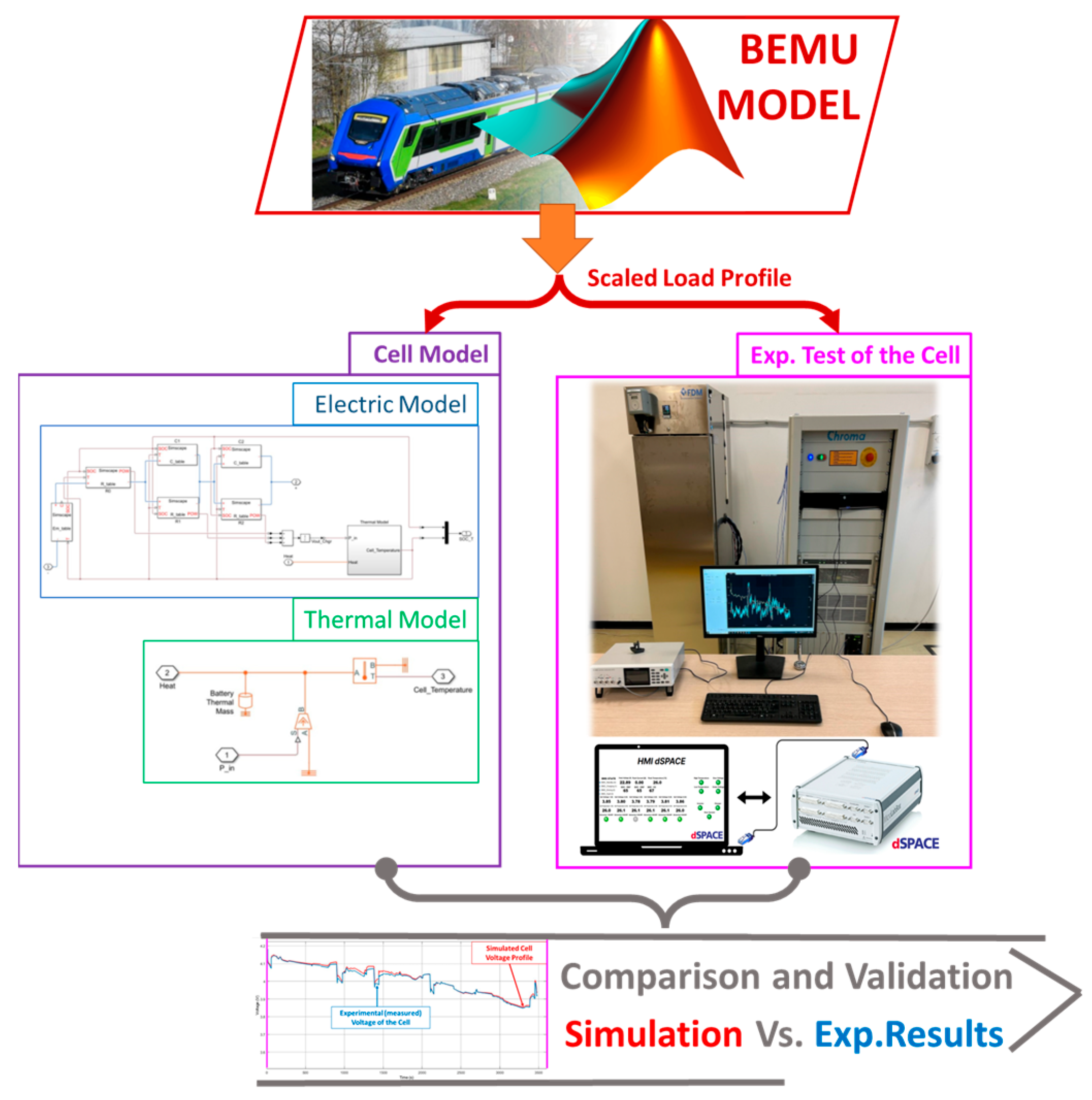
- Cell Identification with a Lumped Thermal–Electric Model: Using the testing devices of Florence University, the behavior of SOC and temperature are identified.
- BMS SIL Testing: The identified model is then used to implement a battery module model with its BMS. Moreover, the SIL testing of the BMS module is implemented.
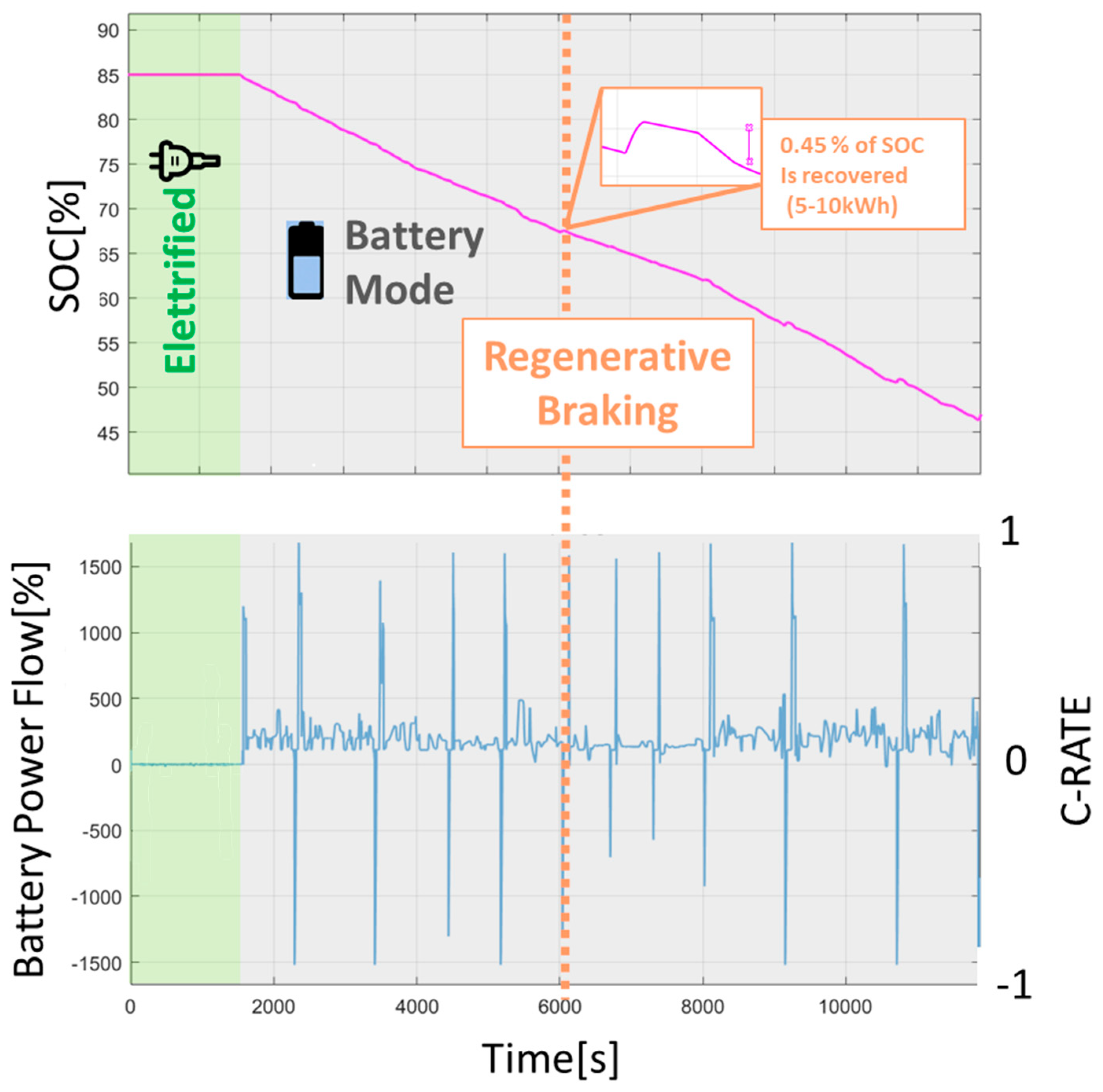
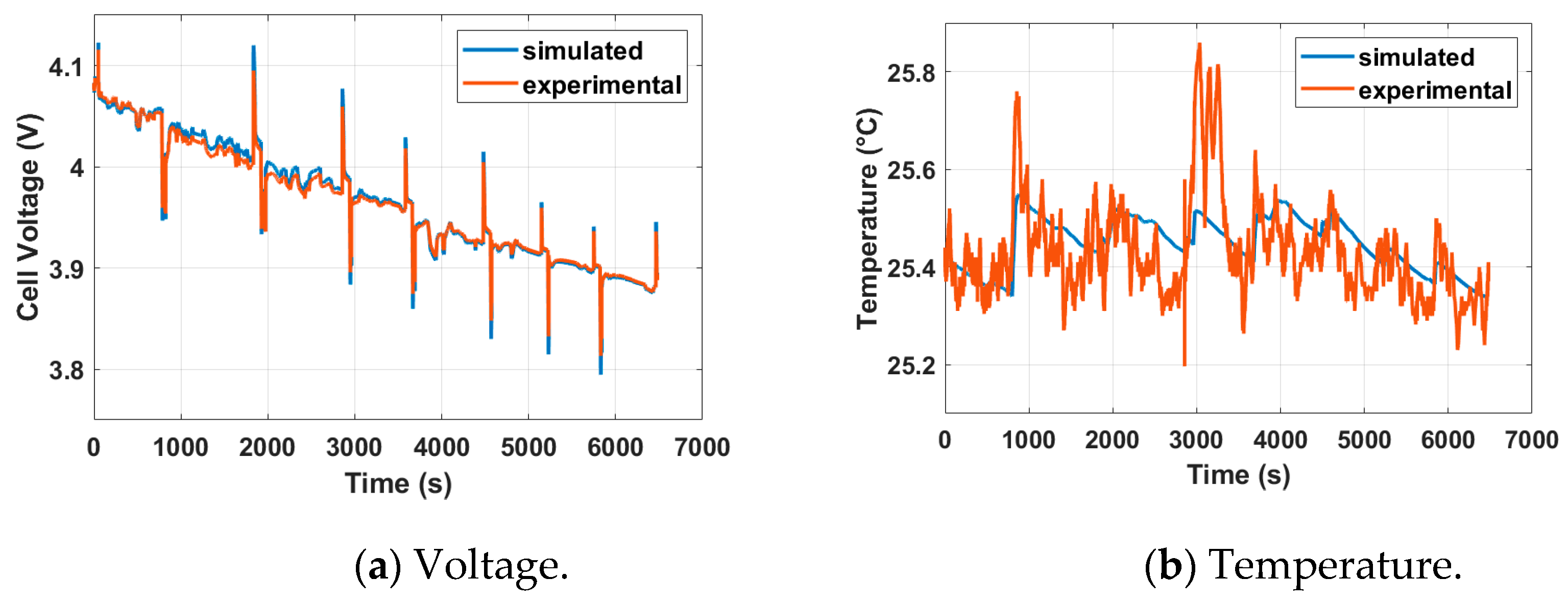
- Application of a Scaled Railway Mission Profile and Validation: A scaled mission profile of the BEMU train is applied to both the tested and simulated cells. A comparison between the experimental and simulated responses of the cell is used to further validate the identified model.
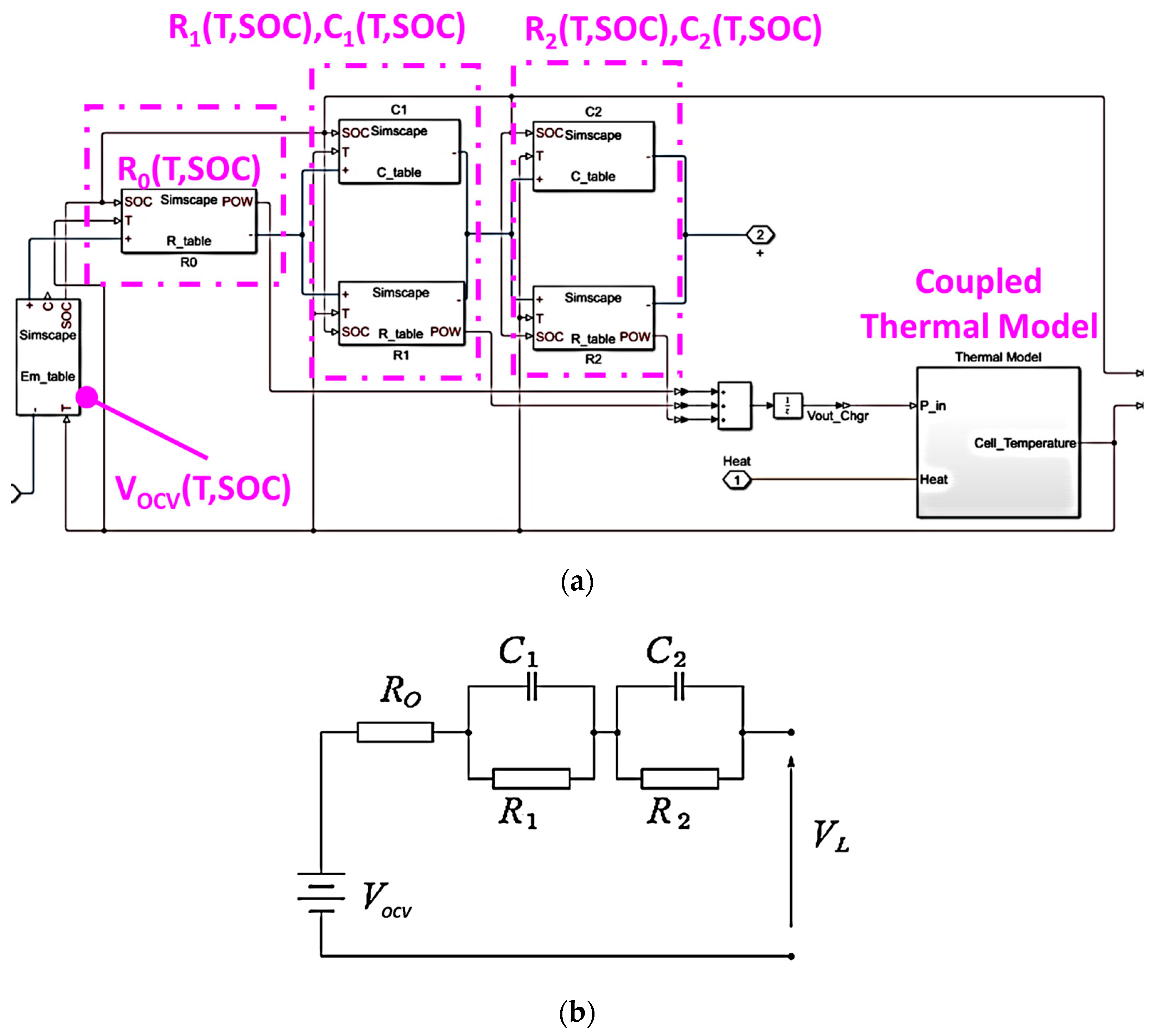
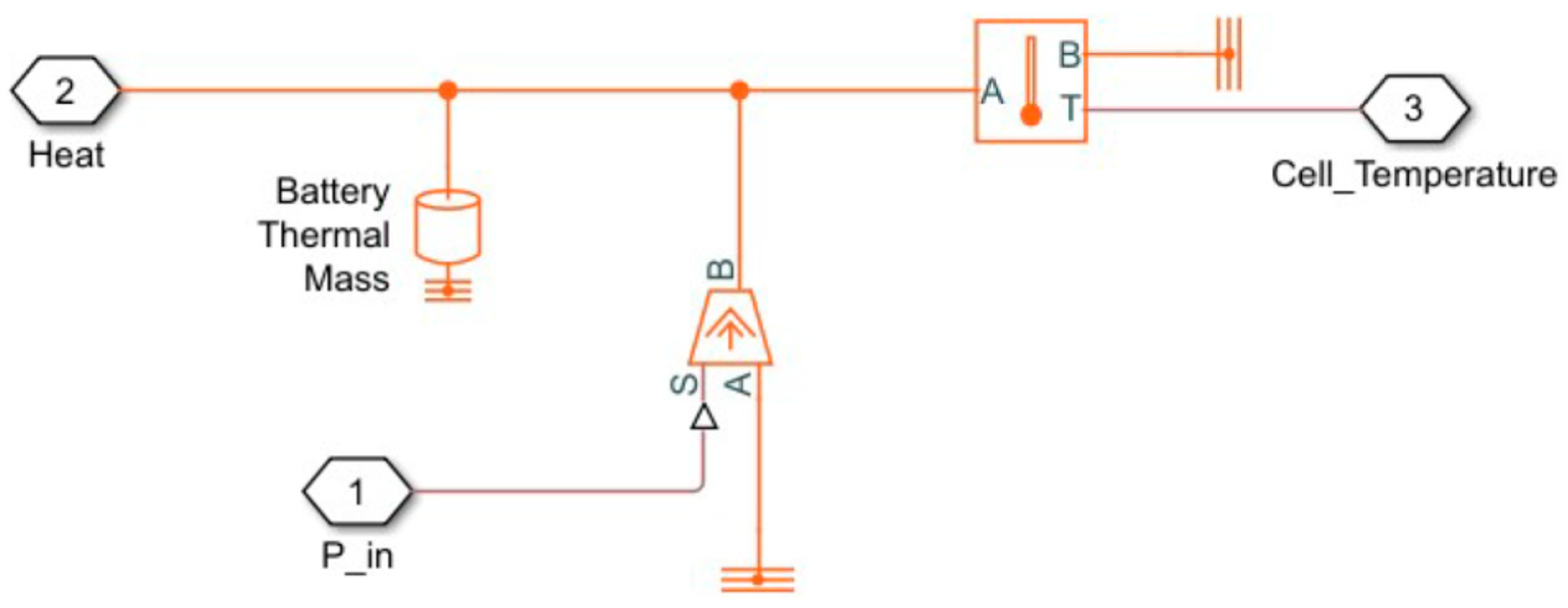
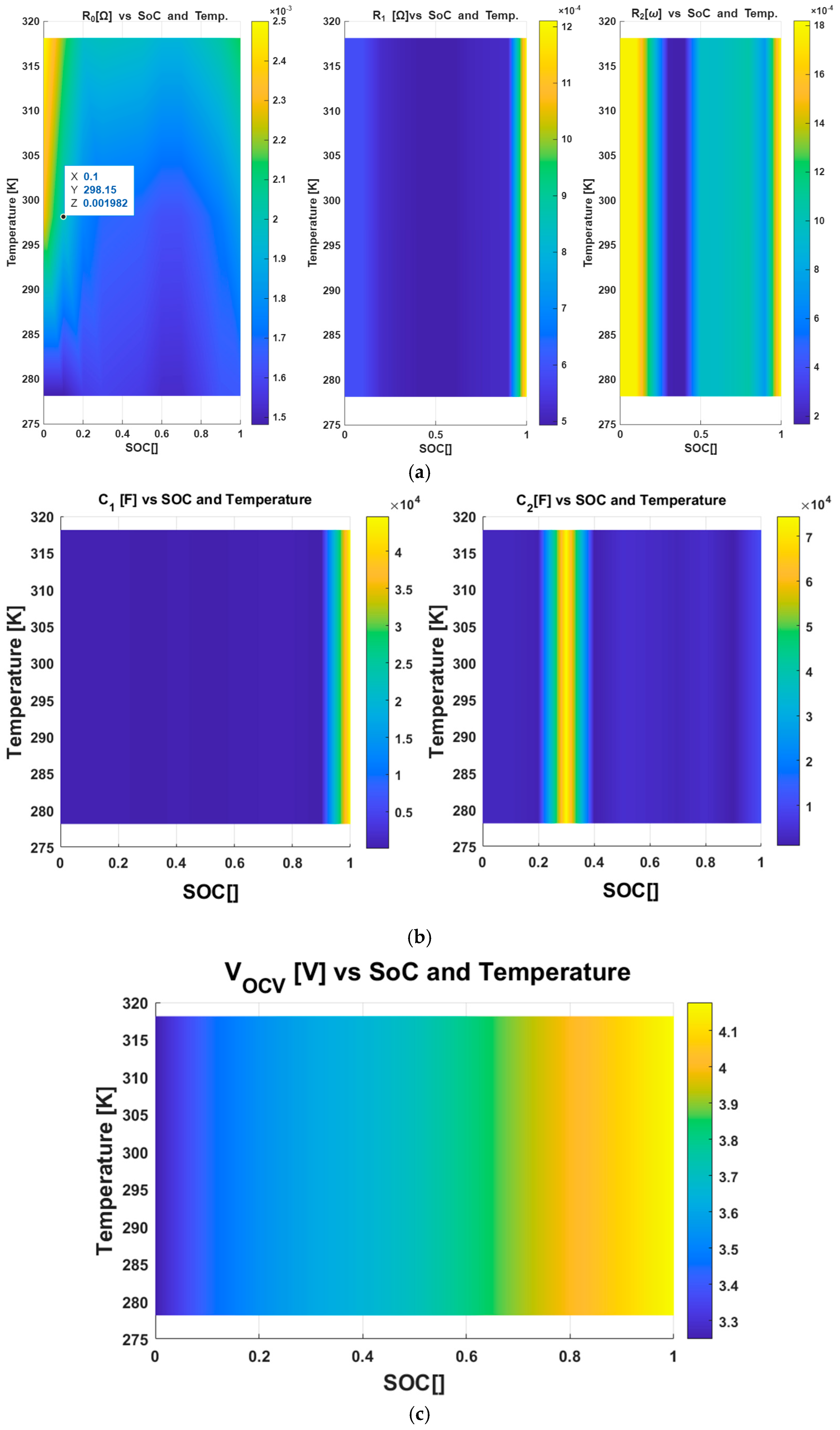
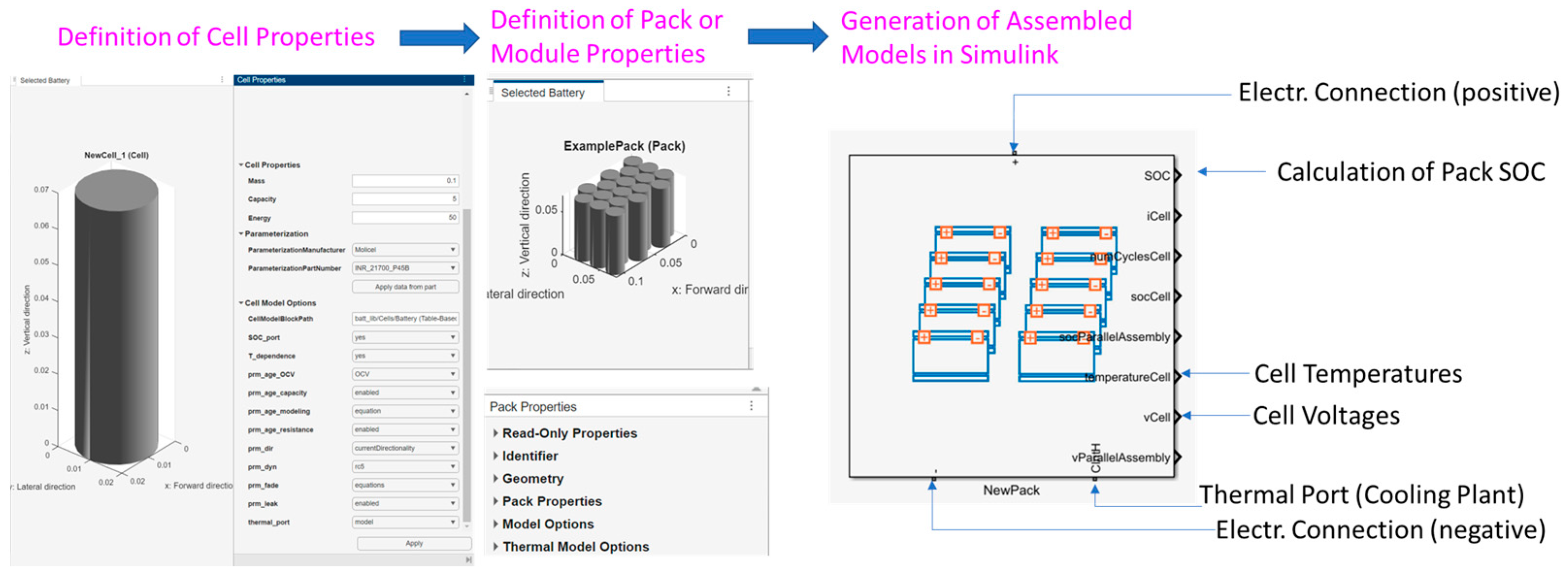
2. Cell Identification with a Lumped Thermal–Electric Model
- Ri and Ii are the i-th resistances and corresponding currents, respectively;
- T and Tamb are the temperatures of the cell and the surrounding environment;
- mcell, cp, hconv, and Acell are thermal parameters of the cell (mass, mean specific heat, thermal exchange coefficient, and corresponding surface).
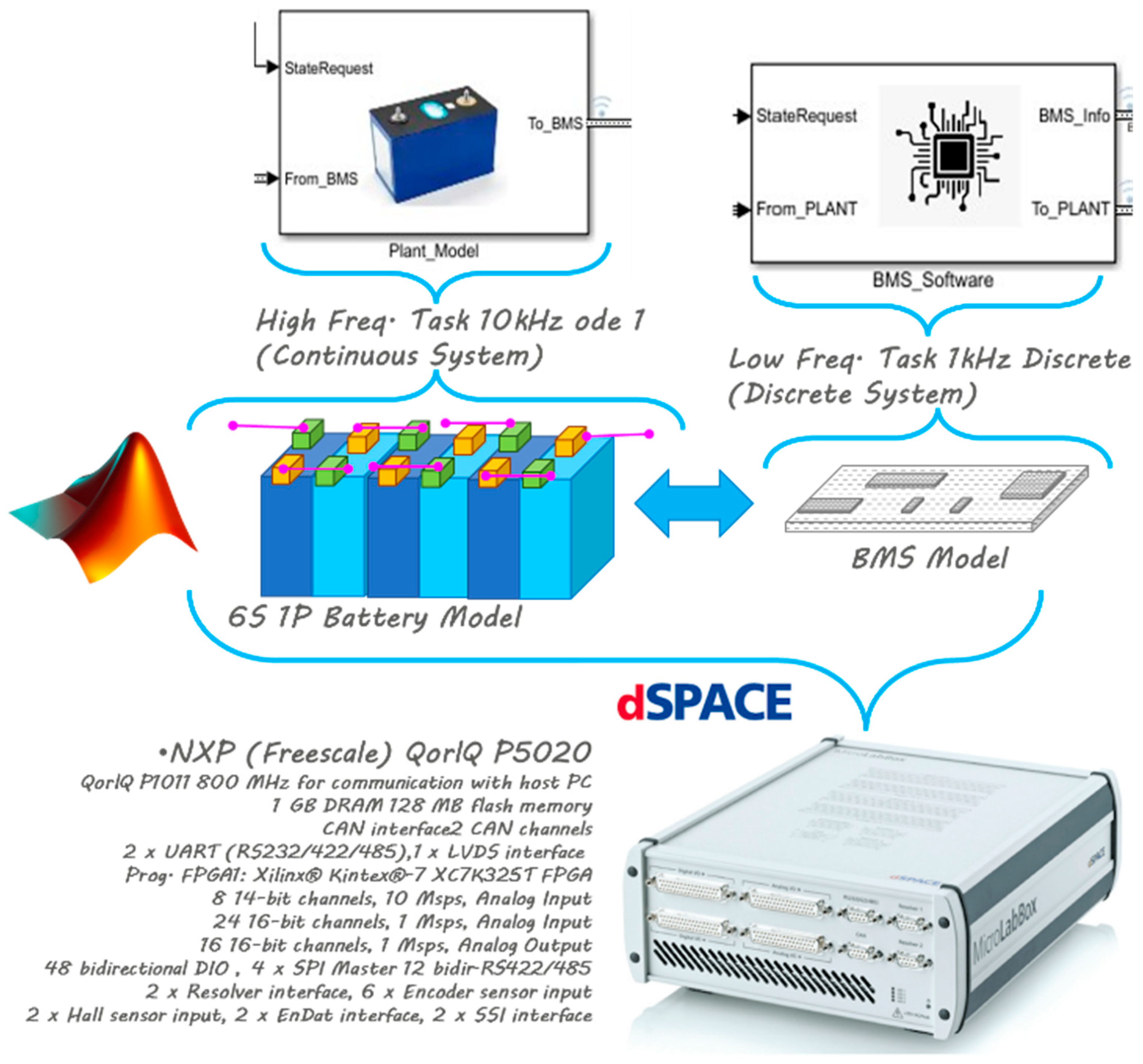
3. SIL Testing of a Simulated BMS
- Safety and Protection: Protection against the maximum current according to the cell’s state is implemented. Allowable currents are estimated from the SOC and temperature measurements through tabulated functions. The voltage and temperature of cells are also monitored.
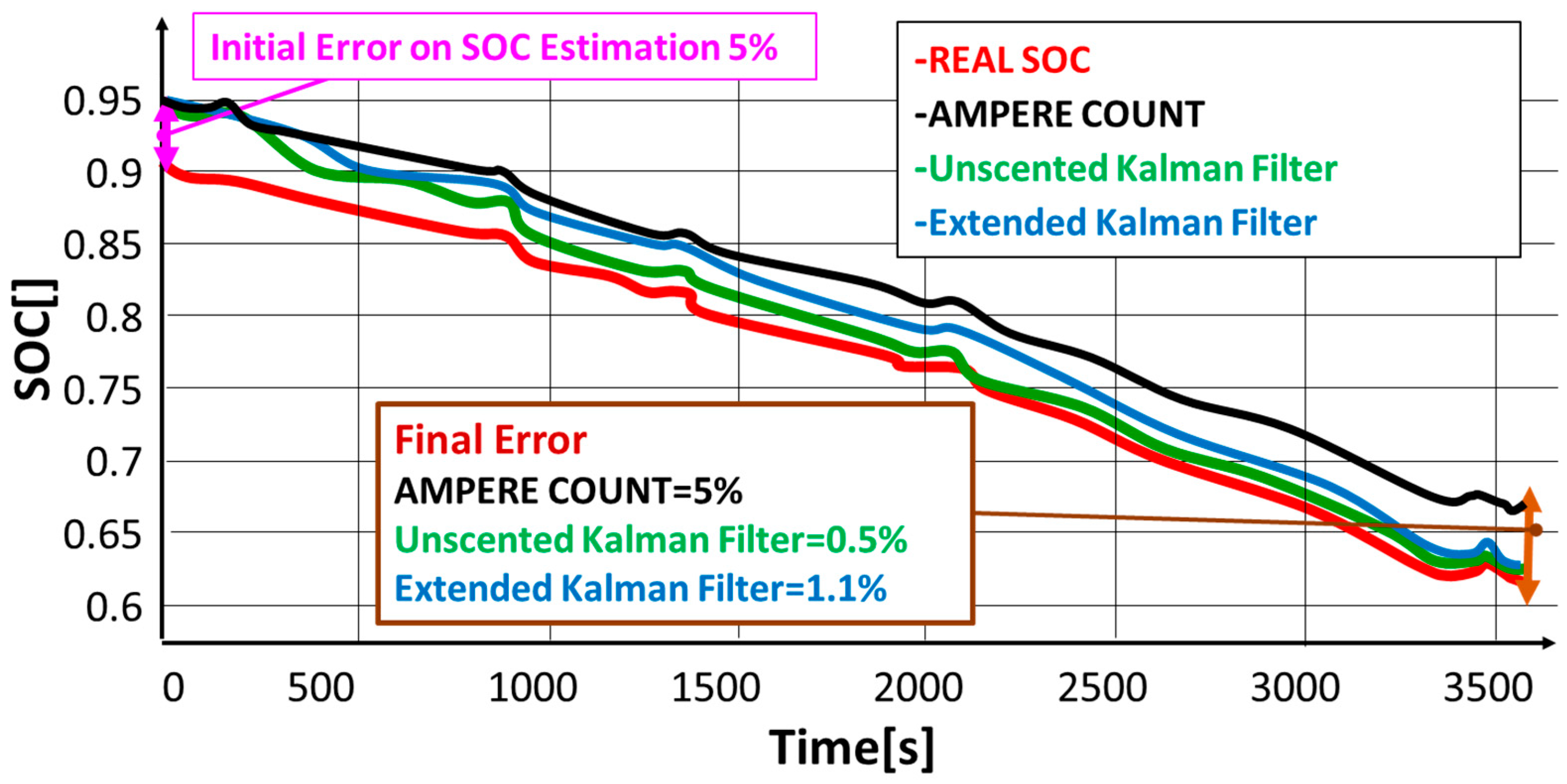
- SOC Estimation: Battery state function (2) is assumed, where the modeled states are the battery’s SOC and the voltage differences measured across two RC groups, V1 and V2 (2):
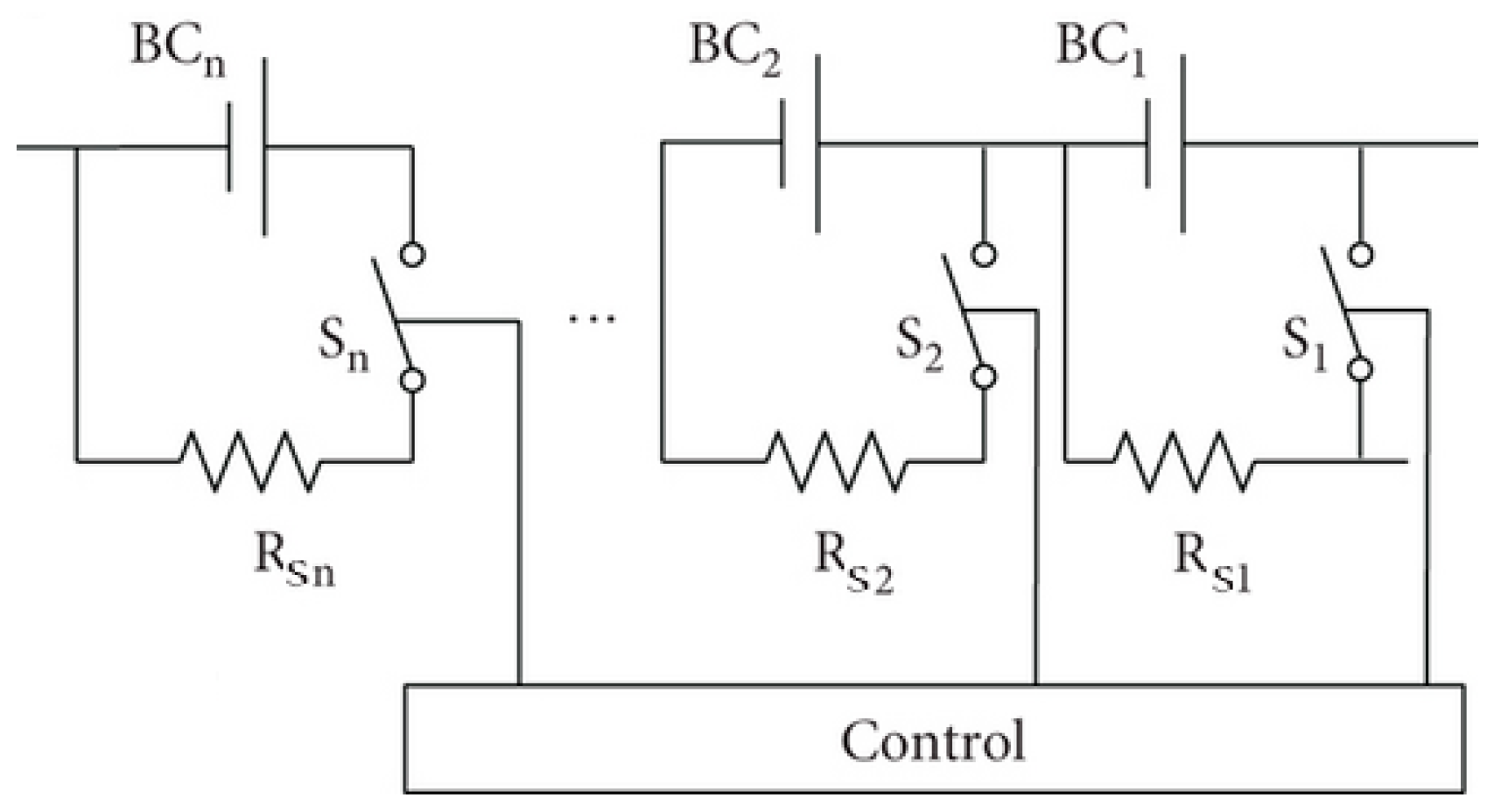
- Cell Balancing: Differential aging and natural construction tolerance result in cell unbalancing [21]. For this reason, the BMS is often integrated with a balancing circuit that can be used actively or passively to restore the system. In this study, a model of a passive resistive balancing circuit, taken from the authors of [22], is implemented. The cells are balanced through commutated shunt resistors according to the circuit scheme described in Figure 7. When balancing is activated, the connected cells (Figure 6) are discharged on passive resistors (Rsi) that are connected or disconnected, acting on the controlled relay/contact Si. The activation logic is relatively simple: During balancing, the maximum voltage of a cell, Vcell_ref (lower than 4.2 [V]), is defined, and if this threshold is exceeded, the cell is shunted and discharged by the corresponding resistor. To avoid excessive chattering with respect to the controlled contact, hysteresis (of about 0.02 [V]) is introduced in the commutation logic.
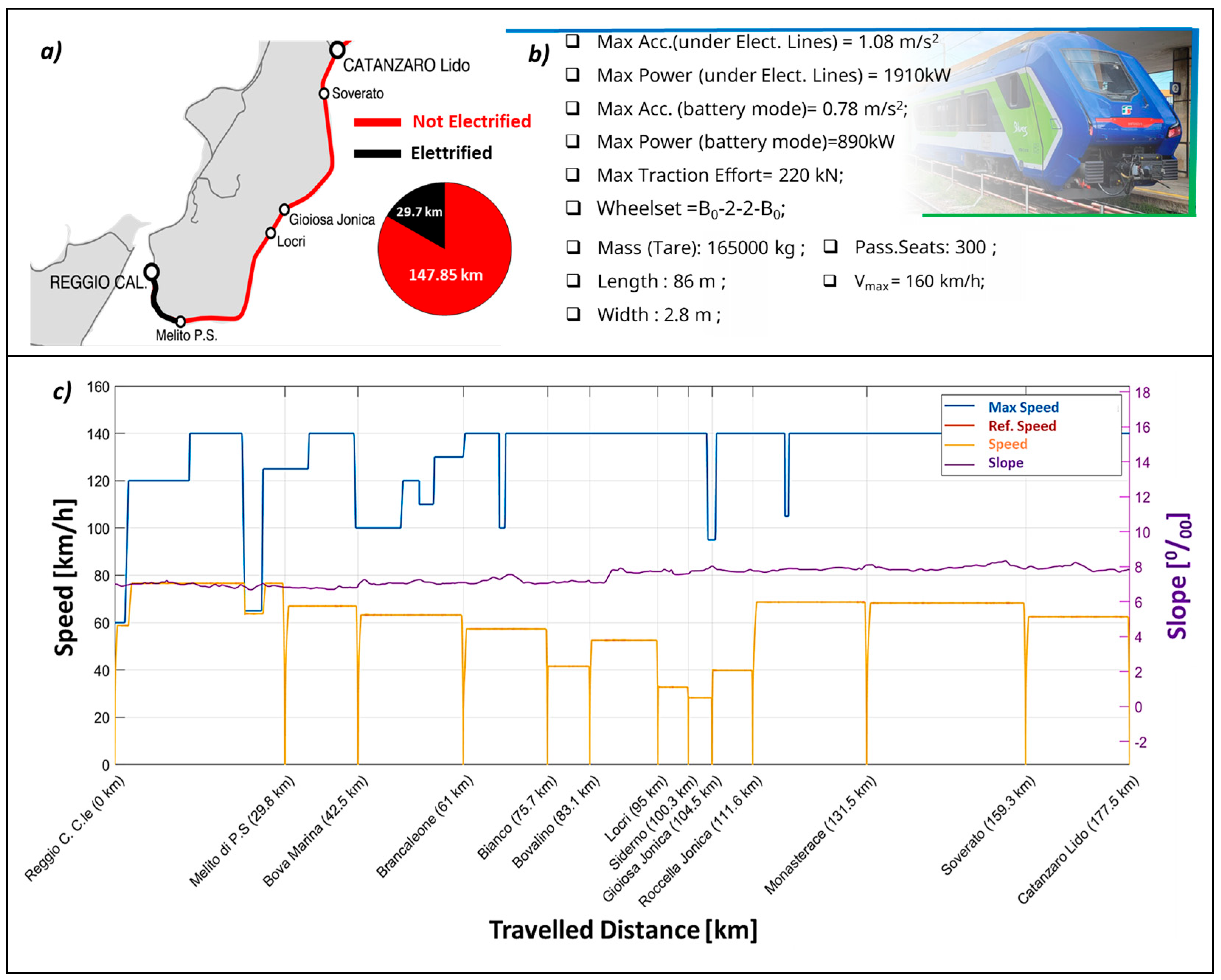
4. Application of a Scaled Railway Mission Profile and Validation
Sizing of Battery Pack and Generation of the Scaled Test Profile
5. Conclusions
- The proposed SIL-HIL testing procedure is innovative for the proposed railway application at the academic level, or at least in terms of the currently available literature.
- Moreover, the application of scaled testing for both batteries and BMSs is relatively uncommon in railway applications.
- The performed research is innovative not only in its proposed applications but also in the customizations that make the railway applications significantly different from conventional automotive or industrial applications—particularly in terms of required lifespan and thermal stability. These factors justify the applications of chemistries and technologies such as LTO cells, which are relatively uncommon with respect to more conventional and well-studied sectors. At the same time, the application of batteries and hybrid technologies to railway rolling stock has a wide potential impact, as outlined in the Introduction section of this study.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pugi, L.; Povolato, T.E.; Tiezzi, N. Simulation of Combined Aging Effects for Battery Operated Trains: A Benchmark Case Study on the Line Between Reggio Calabria and Catanzaro. Energies 2025, 18, 1143. [Google Scholar] [CrossRef]
- Cole, C.; Sun, Y.; Wu, Q.; Spiryagin, M. Exploring hydrogen fuel cell and battery freight locomotive options using train dynamics simulation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 310–321. [Google Scholar] [CrossRef]
- Pugi, L.; Berzi, L.; Spedicato, M.; Cirillo, F. Hydrogen for railways: Design and simulation of an industrial benchmark study. Int. J. Model. Identif. Control. 2023, 43, 43–53. [Google Scholar] [CrossRef]
- Fragiacomo, P.; Piraino, F.; Genovese, M.; Flaccomio Nardi Dei, L.; Donati, D.; Migliarese Caputi, M.V.; Borello, D. Sizing and Performance Analysis of Hydrogen- and Battery-Based Powertrains, Integrated into a Passenger Train for a Regional Track, Located in Calabria (Italy). Energies 2022, 15, 6004. [Google Scholar] [CrossRef]
- Vinnikov, D. Research, Design and Implementation of Auxiliary Power Supplies for the Light Rail Vehicles; Tallinn University of Technology Press: Tallin, Estonia, 2005. [Google Scholar]
- Fisher, I.; Bolton, G. Auxiliary power systems for rolling stock. In The 9th Institution of Engineering and Technology Professional Development Course on Electric Traction Systems; IET: London, UK, 2006; pp. 167–174. [Google Scholar]
- Ceraolo, M.; Lutzemberger, G.; Frilli, A.; Pugi, L. Regenerative braking in high speed railway applications: Analysis by different simulation tools. In Proceedings of the 2016 IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; p. 7555474. [Google Scholar] [CrossRef]
- Pugi, L.; Grasso, F.; Rossi, G. Energy Simulation of Tramway Systems, Simplified and Efficient Models. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; p. 8494431. [Google Scholar] [CrossRef]
- Domínguez, M.; Fernández-Cardador, A.; Fernández-Rodríguez, A.; Cucala, A.; Pecharromán, R.; Sánchez, P.U.; Cortázar, I.V. Review on the use of energy storage systems in railway applications. Renew. Sustain. Energy Rev. 2025, 207, 114904. [Google Scholar] [CrossRef]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2021, 8, 2205–2232. [Google Scholar] [CrossRef]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Vannucchi, A. Hitachi Rail STS SPA La piattaforma Masaccio di Hitachi Rail per la decarbonizzazione dei treni regionali, La Transizione Tecnologica Dalla Trazione Diesel Ai Nuovi Treni A Batteria E Idrogeno Mercoledì 29 settembre 2021. Webinar at Expo Ferroviaria Free Presentation. Available online: https://www.cifi.it/UplDocumenti/Milano29092021/04Vannucchi.pdf (accessed on 29 May 2025).
- Sacchi, M. Responsabile Hitachi Rail Italy—Piattaforma Rolling Stock Il Nuovo Treno Ibrido Per Trenitalia Caratteristiche Tecniche—Il Punto Di Vista Hitachi Rail Italy. In Proceedings of the Official CIFI Webinar, 21 April 2022; Available online: https://www.cifi.it/UplDocumenti/Firenze21042022/Il%20nuovo%20treno%20ibrido%20per%20Trenitalia.pdf (accessed on 29 May 2025).
- Caposciutti, M. Responsabile Trenitalia—Direzione Tecnica Il Nuovo Treno Ibrido Per Trenitalia Caratteristiche Tecniche—Il Punto Di Vista Trenitalia. In Proceedings of the Webinar, 21 April 2022; Available online: https://www.cifi.it/UplDocumenti/Firenze21042022/Presentazione%20Trenitalia.pdf (accessed on 29 May 2025).
- Ma, J. Battery Technologies: Materials and Components; John Wiley & Sons: Hoboken, NJ, USA, 2025; ISBN 978-3527830039. [Google Scholar]
- Kirby, W. Beard Linden’s Handbook of Batteries, 5th ed.; Mc Graw Hill: New York, NY, USA, 2019; ISBN 978-1260115925. [Google Scholar]
- IEC 62660-1:2010; Secondary Lithium-Ion Cells for the Propulsion of Electric Road Vehicles—Part 1: Performance Testing. International Electrotechnical Commission: Geneva, Switzerland, 2010.
- SAE J2464; Recommended Practice for Electric and Hybrid Vehicle Battery Test Procedures. SAE International: Warrendale, PA, USA, 2021.
- ISO 12405; Lithium-Ion Batteries for Propulsion of Electric Road Vehicles. International Organization for Standardization: Geneva, Switzerland, 2011.
- Madsen, K.; Nielsen, H.B.; Tingleff, O. Methods for Non-Linear Least Squares Problems, 2nd ed.; Technical University of Denmark: Copenhagen, Denmark, 2004. [Google Scholar]
- Molla, S.; Shawon; Nawaj, S.; Emon, A.E. Analysis of Aging Effect and Cell Balancing Problem of Lithium-Ion Battery. J. Electr. Electron. Eng. 2025, 13, 92–107. [Google Scholar] [CrossRef]
- Uzair, M.; Abbas, G.; Hosain, S. Characteristics of Battery Management Systems of Electric Vehicles with Consideration of the Active and Passive Cell Balancing Process. World Electr. Veh. J. 2021, 12, 120. [Google Scholar] [CrossRef]
- Pugi, L.; di Carlo, L. Multi-modal battery-operated trains on partially electrified lines: A case study on some regional lines in Italy. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2024, 238, 873–885. [Google Scholar] [CrossRef]
- Locorotondo, E.; Lutzemberger, G.; Pugi, L. State-of-charge estimation based on model-adaptive Kalman filters. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2021, 235, 1272–1286. [Google Scholar] [CrossRef]
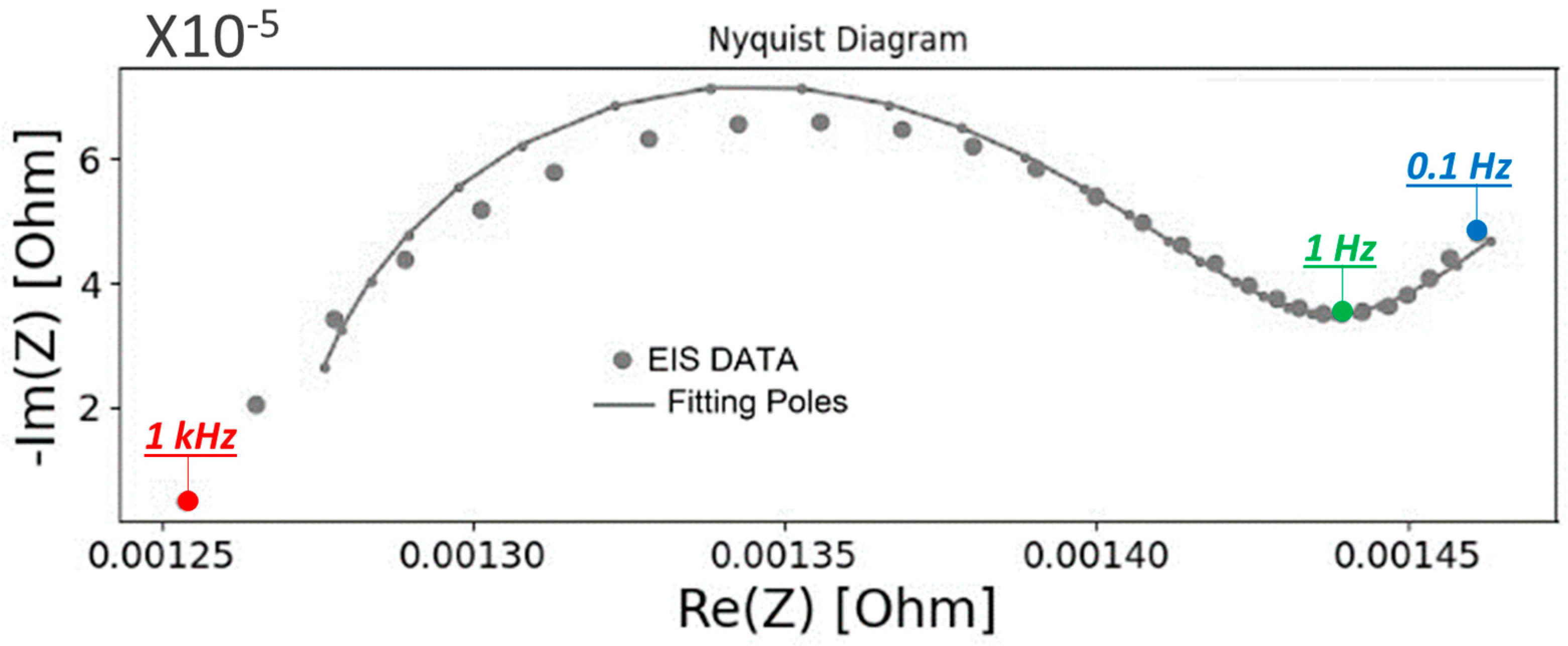
- Moškon, J.; Gaberšček, M. Transmission line models for evaluation of impedance response of insertion battery electrodes and cells. J. Power Sources Adv. 2021, 7, 100047. [Google Scholar] [CrossRef]
- Cruz-Manzo, S.; Greenwood, P. An impedance model based on a transmission line circuit and a frequency dispersion Warburg component for the study of EIS in Li-ion batteries. J. Electroanal. Chem. 2020, 871, 114305. [Google Scholar] [CrossRef]

| Parameters | Chemistry | ||
|---|---|---|---|
| LTO (Lithium Titanate) | LiNMC (Lithium Nickel Manganese Cobalt) | LiFePO4 (Lithium Iron Phosphate) | |
| Cost of “Naked” Cells [USD/kWh] | 500–1000 | 120–200 * | 90–150 |
| Cost of Battery Pack [USD/kWh] | 800–1500 | 250–350 * | 150–300 |
| Sustainability/Impact [kg CO2/kg] | 100–150 | 60–100 | 40–80 |
| Specific Energy [Wh/kg] | 80 | 180–250 | 120–160 |
| Volumetric Energy [Wh/dm3] | 90–140 | 400–600 | 220–330 |
| Specific Power [W/kg] | 1500–3000 | 1000–2500 | 1000–1500 |
| Volumetric Power [W/L] | 2000–6000 | 2000–5000 | 1000–3000 |
| Expected Life [Cycle] | 10,000–20,000 | 1000–3000 | 2000–7000 |
| Total Specific Stored Energy until EOL [Wh/kg] | 8 × 105–1 × 106 | 1.8 × 105–7.5 × 105 | 2.4 × 105–2.3 × 106 |
| Operational Temp Range (Extreme–Preferred) | −30 55 °C 0 55 °C | −20 60 °C 0 45 °C | −20 60 °C 0 45 °C |
| Parameter | Value |
|---|---|
| Chemistry | LiNMC |
| Shape//Dimensions//Weight | Prismatic Cell//80 × 148 × 103[mm]//2.8[kg] |
| Nominal Capacity | 195 [Ah] |
| Min. Nom. Max Voltage | 2.5//3.7//4.2 [V] |
| Max Charge/Disch. Current | 3C |
| Int. Resistance | <0.6[Ώ°0] |
| Min. Charge Temp.//Max Charge Temp.//Min. Discharge Temp.//Max Discharge Temp. | 0 [°C]//55 [°C]//−30 [°C]//55 [°C] |
| Expected Life | 2000 Cycles |
| Parameter | Value |
|---|---|
| Initial SOC | 100 |
| Discharge pulse duration and intensity | 18 [s]-1C |
| Charge pulse duration and intensity | 18 [s]-1C |
| Pause | 60 [s] |
| Different levels of SOC during which impulses are repeated | From 90% to 10% and steps of 10% of SOC |
| Transition between different SOC levels | Constant Discharge at 0.5 C |
| Test repeated for different temperatures | 5 °C, 25 °C, 45 °C |
| Parameter | Value |
|---|---|
| mcell | 2.8 [kg] (known) |
| Cp | 1000 [J kg−1 K−1] (known) |
| hconv | 24 [Wm−2 K−1] (identified) |
| Acell | 7 × 10−2 [m2] (known) |
| Parameter | Battery 1 | Battery 2 |
|---|---|---|
| Module | 6s1p | 16s2p |
| Pack | 32s12p | 12s6p |
| Num. of Modules | 384 | 72 |
| Num. of Cells (Nc) | 2304 | |
| Nom. Voltage | About 710 [V] | |
| Weight | 6451 [kg] | |
| Installed Power | About 1650 [kWh] | |
| Mission | Variable | RMSE | RMSE% | Maximum Error |
|---|---|---|---|---|
| Jonica line | Voltage | 5 mV | 0.1% | 20 mV |
| Temperature | 0.1 °C | 0.3% | 0.3 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pugi, L.; Kociu, A.; Scardina, A.; Berzi, L.; Tiezzi, N.; Delogu, M. Fast Identification of LiNMC Cells for Railway Applications. Energies 2025, 18, 3300. https://doi.org/10.3390/en18133300
Pugi L, Kociu A, Scardina A, Berzi L, Tiezzi N, Delogu M. Fast Identification of LiNMC Cells for Railway Applications. Energies. 2025; 18(13):3300. https://doi.org/10.3390/en18133300
Chicago/Turabian StylePugi, Luca, Aljon Kociu, Antonio Scardina, Lorenzo Berzi, Nico Tiezzi, and Massimo Delogu. 2025. "Fast Identification of LiNMC Cells for Railway Applications" Energies 18, no. 13: 3300. https://doi.org/10.3390/en18133300
APA StylePugi, L., Kociu, A., Scardina, A., Berzi, L., Tiezzi, N., & Delogu, M. (2025). Fast Identification of LiNMC Cells for Railway Applications. Energies, 18(13), 3300. https://doi.org/10.3390/en18133300








