Effect of Different Heat Sink Designs on Thermoelectric Generator System Performance in a Turbocharged Tractor
Abstract
1. Introduction
2. Structure of the TEG System of a Turbocharged Tractor and Material Properties
3. Mathematical Modeling of TEG System
3.1. TEG Equations
3.2. Ansys-Fluent Theory
3.3. Aluminum Foam in Ansys-Fluent
3.4. Mesh and Boundary Conditions
3.5. Grid Independence Examination
3.6. Validation of the Model
4. Results and Discussion
4.1. Numerical Results on the Performance of TEG Systems with Different Heat Sink Designs
4.1.1. Effect of the Different PF Heat Sinks
4.1.2. Effect of Open-Cell Aluminum Foam Heat Sinks with Different PPI Values
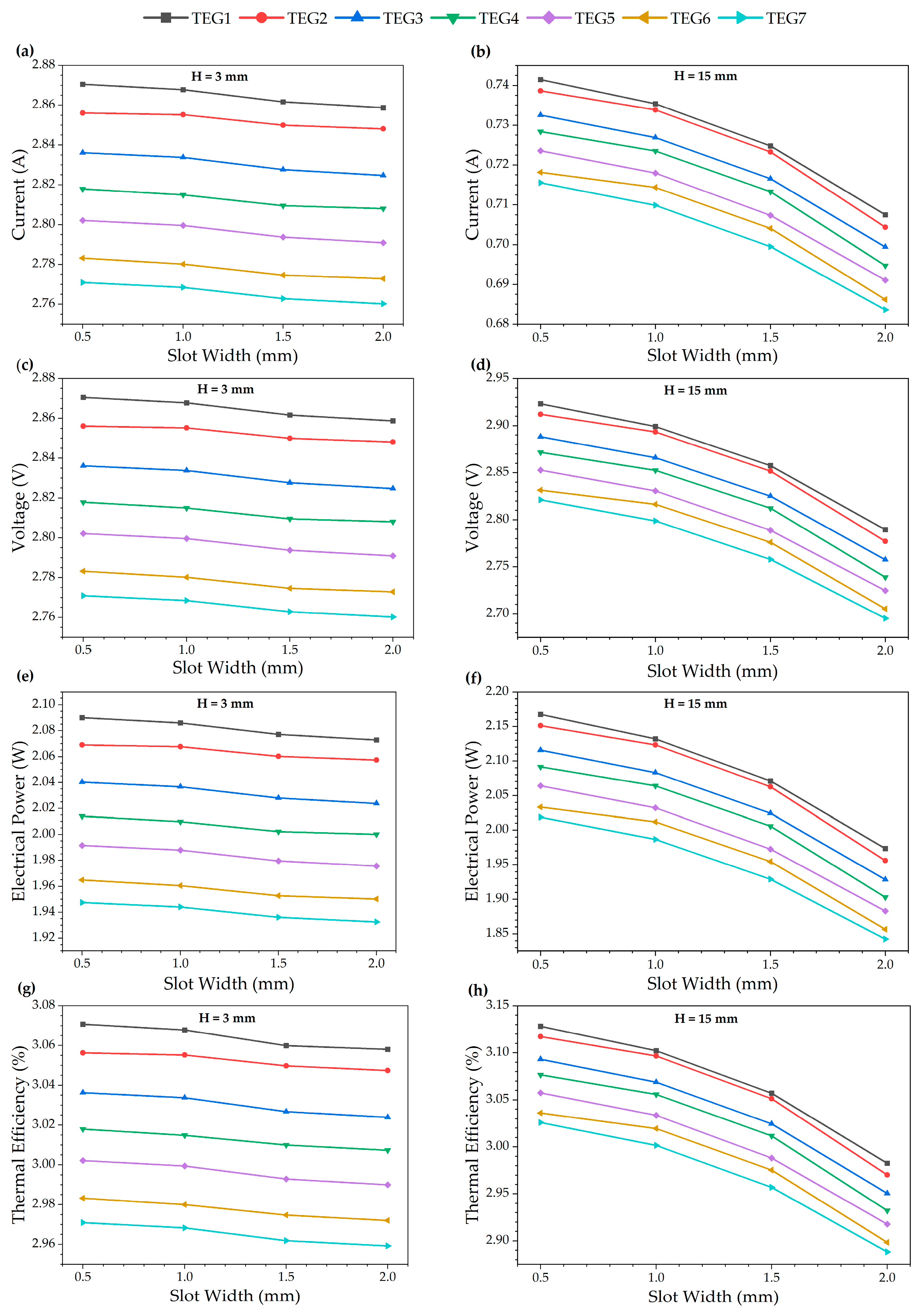
4.1.3. Effect of Slotted PF Heat Sinks with Different Slot Widths and Heights
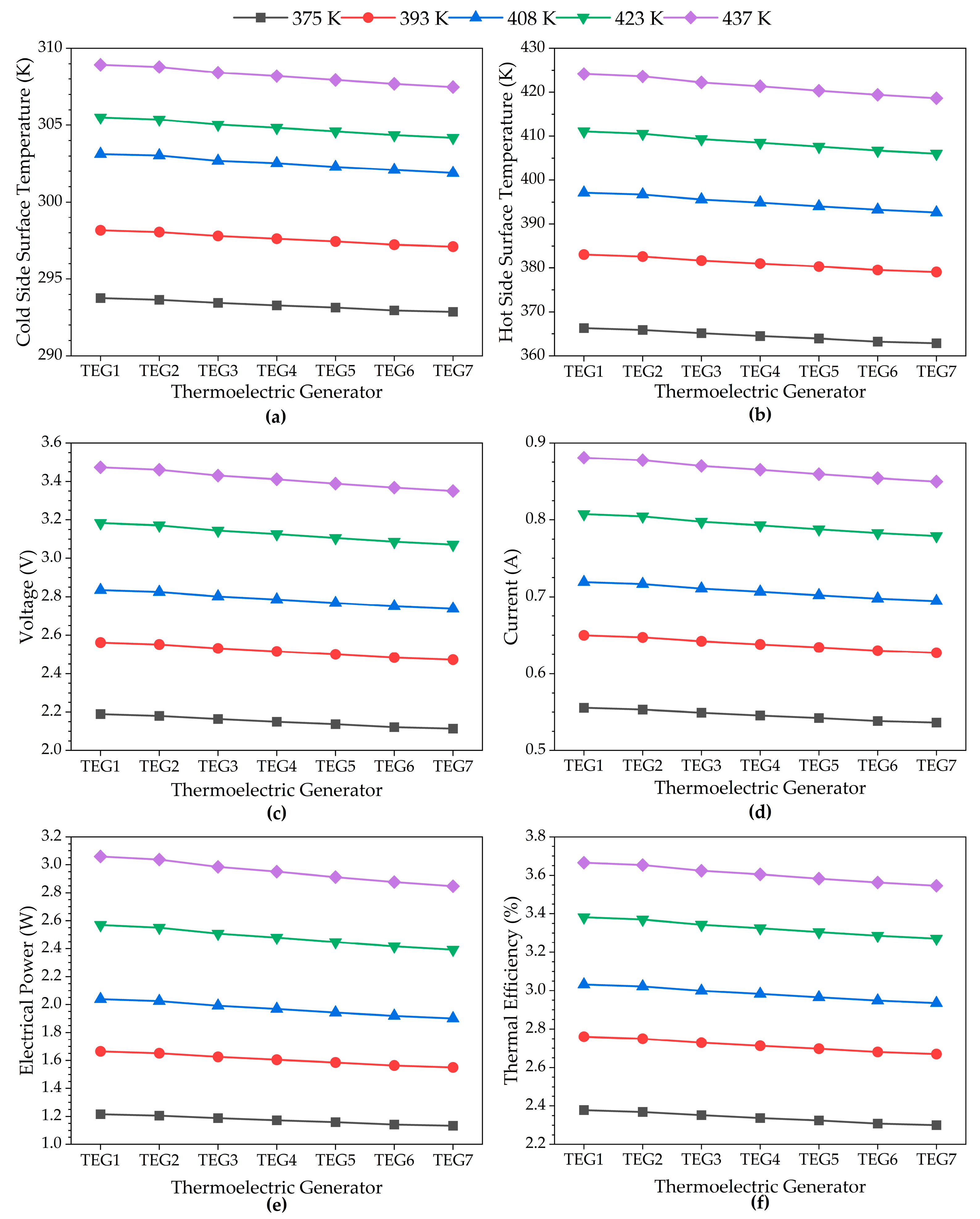
4.2. Performance Analysis of TEG Modules According to Their Location in the System
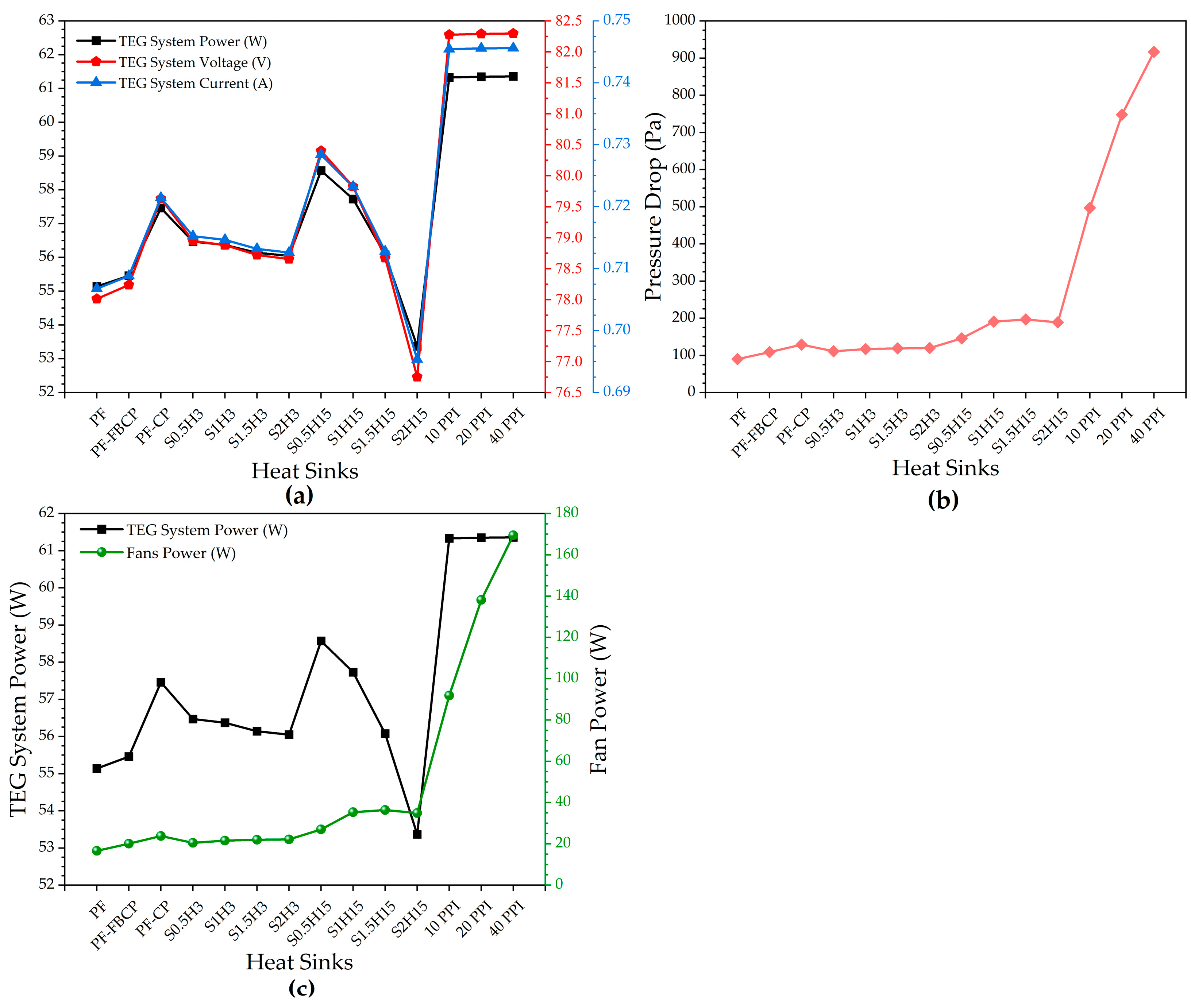
4.3. TEG System Performance, Pressure Drop and Fan Power at Different Heat Sink Designs Used on Cold Surfaces
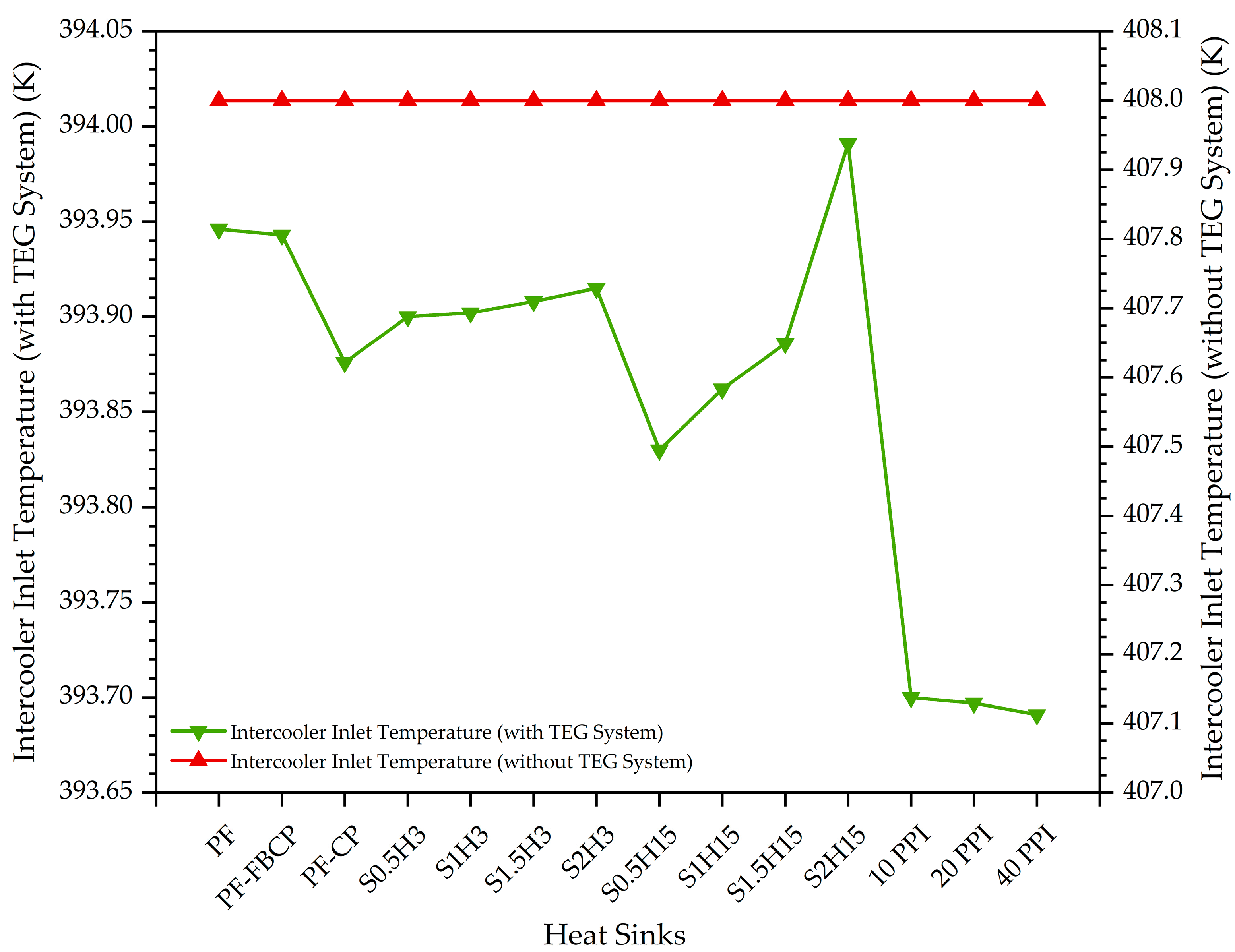
4.4. The Effect of the TEG System with Different Heat Sinks on the Temperature of Intercooler Inlet Air
5. Conclusions
- The heat transfer from the cold surface of TEG modules was highest at open-cell aluminum foam heat sinks (10, 20 and 40 PPI). Therefore, the highest performance values (voltage, current, electrical power and thermal efficiency) of TEG modules were obtained in the use of these aluminum foam heat sinks. However, the pressure drop at these heat sinks also increased significantly compared to the others.
- After aluminum foam heat sinks, the highest performance values of TEG modules were obtained for S0.5H15. The lowest performance values were obtained for S2H15.
- The total TEG output power, output voltage, and thermal efficiency obtained for S0.5H15 were 6.2%, about 3%, and about 5% higher than those for PF, respectively.
- For PF-CP, the output voltage and thermal efficiency per module increased by approximately 2–4% compared to PF. As a result of this increase, the total TEG output power for PF-CP increased by 4.2%. In addition, the power increase for PF-FBCP compared to PF was 0.6%.
- Using 10 PPI instead of PF increased thermoelectric power generation by approximately 11%. A similar increase of approximately 11% was observed for 20 and 40 PPI.
- The pressure drop values obtained for different heat sinks, except for aluminum foam, were approximately close to each other.
- The fan power values required for other heat sinks except aluminum foams were almost close to each other.
- Approximately 6.7% more electrical power was obtained from the TEG1 module than from the TEG7 module.
- In cases with the TEG system where different heat sinks were used, the intercooler inlet air temperatures decreased by approximately 3.4–3.5% compared to the case without the TEG system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wolf, M.; Rybakov, A.; Hinterding, R.; Feldhoff, A. Geometry Optimization of Thermoelectric Modules: Deviation of Optimum Power Output and Conversion Efficiency. Entropy 2020, 22, 1233. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Guo, R.; Liu, S.; Zhu, K.; Wang, S. Temperature gradient characteristics and effect on optimal thermoelectric performance in exhaust power-generation systems. Appl. Energy 2020, 261, 114366. [Google Scholar] [CrossRef]
- Sofyan, S.E.; Bahri, S. The performance of thermoelectric exhaust heat recovery system considering different heat source’s fin arrangements. IOP Conf. Ser. Earth Environ. Sci. 2020, 463, 012022. [Google Scholar] [CrossRef]
- Kober, M.; Knobelspies, T.; Rossello, A.; Heber, L. Thermoelectric Generators for Automotive Applications: Holistic Optimization and Validation by a Functional Prototype. J. Electron. Mater. 2020, 49, 2902–2909. [Google Scholar] [CrossRef]
- Karana, D.R.; Sahoo, R.R. Performance assessment of the automotive heat exchanger with twisted tape for thermoelectric based waste heat recovery. J. Clean. Prod. 2021, 283, 124631. [Google Scholar] [CrossRef]
- Karana, D.R.; Sahoo, R.R. An experimental study on the thermal behavior of aluminum thermoelectric system integrated with engine exhaust. Exp. Heat Transf. 2021, 34, 201–216. [Google Scholar] [CrossRef]
- Krishna Kumar, T.S.; Anil Kumar, S.; Kodanda Ram, K.; Raj Goli, K.; Siva Prasad, V. Analysis of thermo electric generators in automobile applications. Mater. Today Proc. 2021, 45, 5835–5839. [Google Scholar] [CrossRef]
- Liao, T.; Xiao, J.; Xu, Y.; Lin, B. Thermal-electrical coupling properties and optimum analysis of a vehicle exhaust driven thermoelectric system. Therm. Sci. Eng. Prog. 2021, 25, 101040. [Google Scholar] [CrossRef]
- Cózar, I.R.; Pujol, T.; Massaguer, E.; Massaguer, A.; Montoro, L.; González, J.R.; Comamala, M.; Ezzitouni, S. Effects of Module Spatial Distribution on the Energy Efficiency and Electrical Output of Automotive Thermoelectric Generators. Energies 2021, 14, 2232. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, J.; Qin, Q.; Zhu, J.; Xu, S.; Luo, D.; Wang, R. Research on Module Layout and Module Coverage of an Automobile Exhaust Thermoelectric Power Generation System. Energies 2022, 15, 987. [Google Scholar] [CrossRef]
- Nonthakarn, P.; Ekpanyapong, M.; Nontakaew, U.; Bohez, E. Design and Optimization of an Integrated Turbo-Generator and Thermoelectric Generator for Vehicle Exhaust Electrical Energy Recovery. Energies 2019, 12, 3134. [Google Scholar] [CrossRef]
- Kalteh, M.; Akhlaghi Garmejani, H. Investigating the influence of Thomson effect on the performance of a thermoelectric generator in a waste heat recovery system. Int. J. Green Energy 2019, 16, 917–929. [Google Scholar] [CrossRef]
- Subramaniam, H.; Sivaprahasam, D.; Gopalan, R.; Govindan, S. Design and development of a test rig for the performance evaluation of automotive exhaust thermoelectric generator. AIP Adv. 2019, 9, 065004. [Google Scholar] [CrossRef]
- Al-Nimr, M.d.A.; Alajlouni, A.A. Internal combustion engine waste heat recovery by a thermoelectric generator inserted at combustion chamber walls. Int. J. Energy Res. 2018, 42, 4853–4865. [Google Scholar] [CrossRef]
- Temizer, İ. Produce Electricity from Exhaust Gases in the Vehicles Used Thermoelectric Generator. Master’s Thesis, Fırat University, Elazığ, Türkiye, 2014. [Google Scholar]
- Gürcan, A.; Yakar, G. Investigation of the performance of a thermoelectric generator system utilizing the thermal energy of air compressed in a compressor. J. Korean Phys. Soc. 2022, 80, 467–483. [Google Scholar] [CrossRef]
- Gürcan, A.; Yakar, G. Improving the performance of a thermoelectric generator system utilizing the thermal energy of air compressed in the compressor of a turbocharged tractor based on different-sized modules. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 360. [Google Scholar] [CrossRef]
- Sahin, B.; Demir, A. Thermal performance analysis and optimum design parameters of heat exchanger having perforated pin fins. Energy Convers. Manag. 2008, 49, 1684–1695. [Google Scholar] [CrossRef]
- Sahin, B.; Demir, A. Performance analysis of a heat exchanger having perforated square fins. Appl. Therm. Eng. 2008, 28, 621–632. [Google Scholar] [CrossRef]
- Dhanawade, K.H.; Sunnapwar, V.K.; Dhanawade, H.S. Thermal Analysis of Square and Circular Perforated Fin Arrays by Forced Convection. Int. J. Curr. Eng. Technol. 2013, 2, 109–114. [Google Scholar] [CrossRef]
- Al-Sallami, W.; Al-Damook, A.; Thompson, H.M. A numerical investigation of thermal airflows over strip fin heat sinks. Int. Commun. Heat Mass Transf. 2016, 75, 183–191. [Google Scholar] [CrossRef]
- Al-Damook, A.; Kapur, N.; Summers, J.L.; Thompson, H.M. Computational design and optimisation of pin fin heat sinks with rectangular perforations. Appl. Therm. Eng. 2016, 105, 691–703. [Google Scholar] [CrossRef]
- Chang, S.-W.; Wu, H.-W.; Guo, D.-Y.; Shi, J.-j.; Chen, T.-H. Heat transfer enhancement of vertical dimpled fin array in natural convection. Int. J. Electr. Energy 2017, 106, 781–792. [Google Scholar] [CrossRef]
- Haghighi, S.S.; Goshayeshi, H.R.; Safaei, M.R. Natural convection heat transfer enhancement in new designs of plate-fin based heat sinks. Int. J. Electr. Energy 2018, 125, 640–647. [Google Scholar] [CrossRef]
- Kim, T.Y.; Kim, S.J. Fluid flow and heat transfer characteristics of cross-cut heat sinks. Int. J. Electr. Energy 2009, 52, 5358–5370. [Google Scholar] [CrossRef]
- Gupta, A.; Kumar, M.; Patil, A.K. Enhanced heat transfer in plate fin heat sink with dimples and protrusions. Heat Mass Transf. 2019, 55, 2247–2260. [Google Scholar] [CrossRef]
- Khudhur, D.S.; Al-Zuhairy, R.C.; Kassim, M.S. Thermal analysis of heat transfer with different fin geometry through straight plate-fin heat sinks. Int. J. Therm. Sci. 2022, 174, 107443. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M.; Guo, W.; Xi, W.; Liu, C.; Sunden, B. Flow and heat transfer mechanism of a regenerative cooling channel mounted with pin-fins using supercritical CO2 as coolant. Int. J. Therm. Sci. 2025, 208, 109425. [Google Scholar] [CrossRef]
- Liu, J.; Guo, W.; Yin, M.; Xi, W.; Sunden, B. Flow and heat transfer characteristic of regenerative cooling channels using supercritical CO2 with circular tetrahedral lattice structures. Case Stud. Therm. Eng. 2025, 71, 106204. [Google Scholar] [CrossRef]
- T’Jollyn, I.; Pujol, T.; Paepe, M.D.; Massaguer, A.; Montoro, L. Plate fin heat sink modelling and design considerations for thermoelectric generators. Renew. Energy Power Qual. J. 2017, 1, 551–556. [Google Scholar]
- Rezania, A.; Rosendahl, L.A. A comparison of micro-structured flat-plate and cross-cut heat sinks for thermoelectric generation application. Energy Convers. Manag. 2015, 101, 730–737. [Google Scholar] [CrossRef]
- Barma, M.C.; Riaz, M.; Saidur, R.; Long, B.D. Estimation of thermoelectric power generation by recovering waste heat from Biomass fired thermal oil heater. Energy Convers. Manag. 2015, 98, 303–313. [Google Scholar] [CrossRef]
- Wiriyasart, S.; Naphon, P. Heat spreading of liquid jet impingement cooling of cold plate heat sink with different fin shapes. Case Stud. Therm. Eng. 2020, 20, 100638. [Google Scholar] [CrossRef]
- Barma, M.C.; Riaz, M.; Saidur, R.; Long, B.D. Waste Heat Recovery by Thermoelectric Generator from Thermal Oil Heater Exhaust. Int. J. Electr. Energy 2015, 3, 235–238. [Google Scholar] [CrossRef]
- Xue, W.; Cao, X.; Zhang, G.; Tan, G.; Liu, Z.; Li, K. Structural Optimization of Heat Sink for Thermoelectric Conversion Unit in Personal Comfort System. Energies 2022, 15, 2781. [Google Scholar] [CrossRef]
- Pujol, T.; T’Jollyn, I.; Massaguer, E.; Massaguer, A.; Cózar, I.R.; De Paepe, M. Design optimization of plate-fin heat sink with forced convection for single-module thermoelectric generator. Appl. Therm. Eng. 2023, 221, 119866. [Google Scholar] [CrossRef]
- Pouryoussefi, S.M.; Zhang, Y. Experimental Study of Air-Cooled Parallel Plate Fin Heat Sinks with and without Circular Pin Fins between the Plate Fins. J. Appl. Fluid Mech. 2015, 8, 515–520. [Google Scholar] [CrossRef]
- Rezania, A.; Yousefi, E.; Nejad, A.A. Zero-cooling energy thermoelectric system by phase change material heat sink integrated with porous copper foam. J. Energy Storage 2023, 59, 106507. [Google Scholar] [CrossRef]
- Li, W.Q.; Zhang, T.Y.; Li, B.B.; Xue, Z.R.; Wang, H.; Zhang, D. Enhanced energy management performances of passive cooling, heat storage and thermoelectric generator by using phase change material saturated in metal foam. Int. J. Therm. Sci. 2023, 184, 107869. [Google Scholar] [CrossRef]
- Wang, T.; Luan, W.; Wang, W.; Tu, S.-T. Waste heat recovery through plate heat exchanger based thermoelectric generator system. Appl. Energy 2014, 136, 860–865. [Google Scholar] [CrossRef]
- Yousefi, E.; Abbas Nejad, A.; Sayyar, N. A new approach for simultaneous thermal management of hot and cold sides of thermoelectric modules. Appl. Therm. Eng. 2023, 233, 121156. [Google Scholar] [CrossRef]
- Kaul, S.; Joshi, T.; Varshney, L. Analysis of hot air duct between turbocharger and intercooler. Mater. Today Proc. 2021, 43, 719–725. [Google Scholar] [CrossRef]
- Xu, C.; Zhuang, Y.; Qian, Y.; Cho, H. Effect on the performance and emissions of methanol/diesel dual-fuel engine with different methanol injection positions. Fuel 2022, 307, 121868. [Google Scholar] [CrossRef]
- Tauzia, X.; Maiboom, A.; Shah, S.R. Experimental study of inlet manifold water injection on combustion and emissions of an automotive direct injection Diesel engine. Energy 2010, 35, 3628–3639. [Google Scholar] [CrossRef]
- Di Battista, D.; Di Bartolomeo, M.; Cipollone, R. Flow and thermal management of engine intake air for fuel and emissions saving. Energy Convers. Manag. 2018, 173, 46–55. [Google Scholar] [CrossRef]
- Gürcan, A. Recovery of Exhaust Heat Energy Using Thermoelectric Generators in Different Sizes. Master’s Thesis, Pamukkale University, Denizli, Türkiye, 2019. [Google Scholar]
- Potur, R.A. Mathematical Modelling of an Actual Cycle and Determining the Optimum Combustion Law Relating to Design of a Diesel Tractor Engine Suited for Stage IIIB Emission Standard. Masters’s Thesis, İstanbul Technical University, İstanbul, Türkiye, 2009. [Google Scholar]
- Kryotherm. Low Temperature Generating Modules. Available online: https://kryothermtec.com/low-temperature-generating-modules.html (accessed on 5 February 2024).
- Luo, D.; Wang, R.; Yu, W.; Zhou, W. Performance evaluation of a novel thermoelectric module with BiSbTeSe-based material. Appl. Energy 2019, 238, 1299–1311. [Google Scholar] [CrossRef]
- Kryotherm. Specification of Generating Thermoelectric Modules TGM-199-1.4-2.0. Available online: http://kryothermtec.com/assets/dir2attz/ru/TGM-199-1.4-2.0.pdf (accessed on 5 February 2024).
- Lee, H. Thermoelectrics: Design and Materials; Wiley: Chichester, UK, 2017. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Ansys. Ansys Fluent Theory Guide; Ansys, Inc.: Canonsburg, PA, USA, 2024; pp. 60–68. [Google Scholar]
- Ansys. Ansys Fluent User Guide; Ansys, Inc.: Canonsburg, PA, USA, 2024; pp. 1305–1342. [Google Scholar]
- Doğan, A.; Pırasacı, T.; Gören, A. Numerical Investigation of Mixed Convection Heat Transfer from Porous Blocks in a Channel. Mühendis Ve Makina 2013, 54, 33–38. [Google Scholar]
- Wang, R.; Meng, Z.; Luo, D.; Yu, W.; Zhou, W. A Comprehensive Study on X-Type Thermoelectric Generator Modules. J. Electron. Mater. 2020, 49, 4343–4354. [Google Scholar] [CrossRef]
- Liao, M.; He, Z.; Jiang, C.; Fan, X.a.; Li, Y.; Qi, F. A three-dimensional model for thermoelectric generator and the influence of Peltier effect on the performance and heat transfer. Appl. Therm. Eng. 2018, 133, 493–500. [Google Scholar] [CrossRef]
- Chen, M.; Rosendahl, L.A.; Condra, T. A three-dimensional numerical model of thermoelectric generators in fluid power systems. Int. J. Electr. Energy 2011, 54, 345–355. [Google Scholar] [CrossRef]
- Eldesoukey, A.; Hassan, H. 3D model of thermoelectric generator (TEG) case study: Effect of flow regime on the TEG performance. Energy Convers. Manag. 2019, 180, 231–239. [Google Scholar] [CrossRef]
- Fallah Kohan, H.R.; Eslami, M.; Jafarpur, K. A hybrid analytical-computational method for three dimensional modeling of thermoelectric generators. Int. J. Energy Res. 2021, 45, 2680–2693. [Google Scholar] [CrossRef]

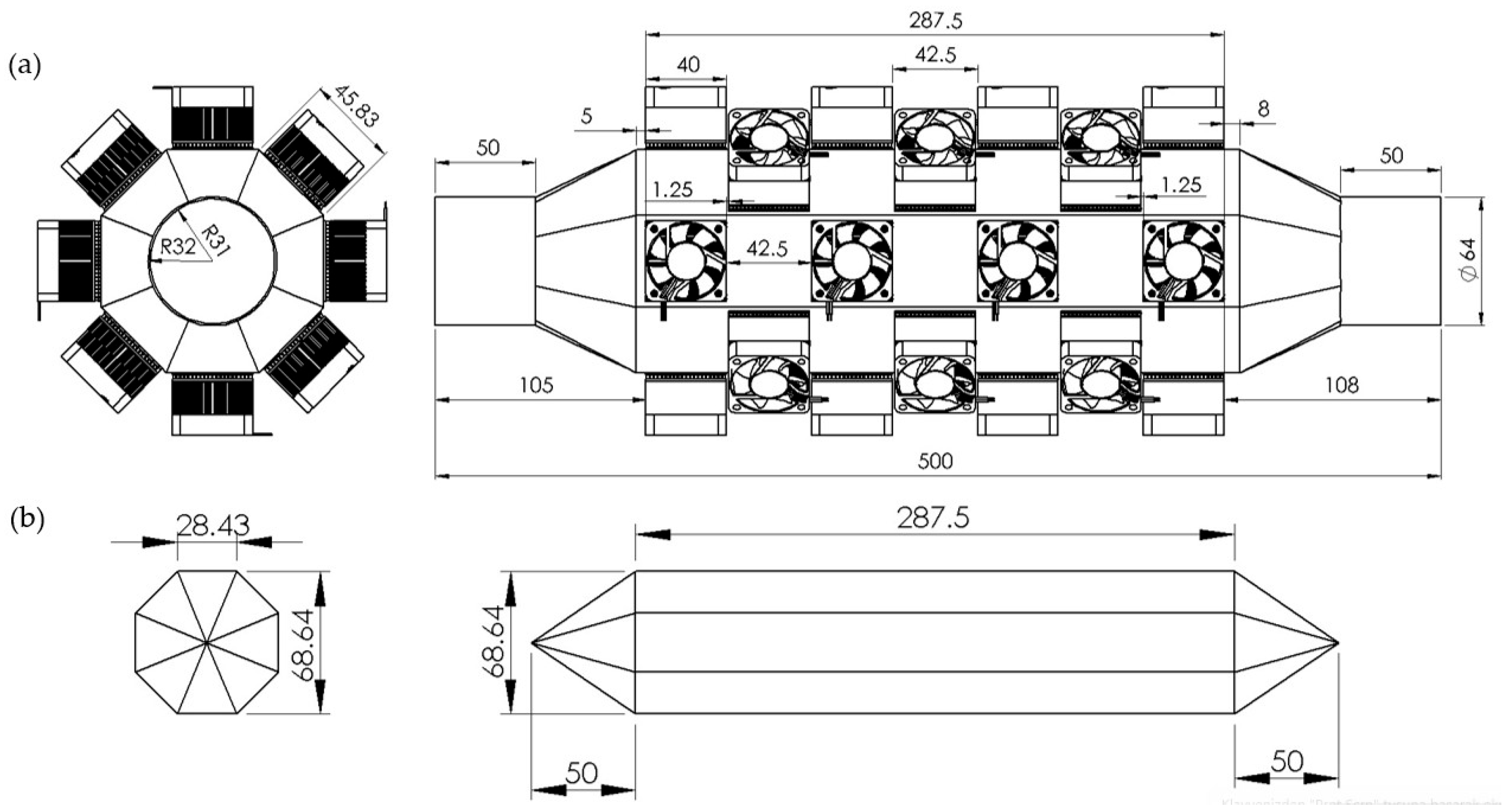
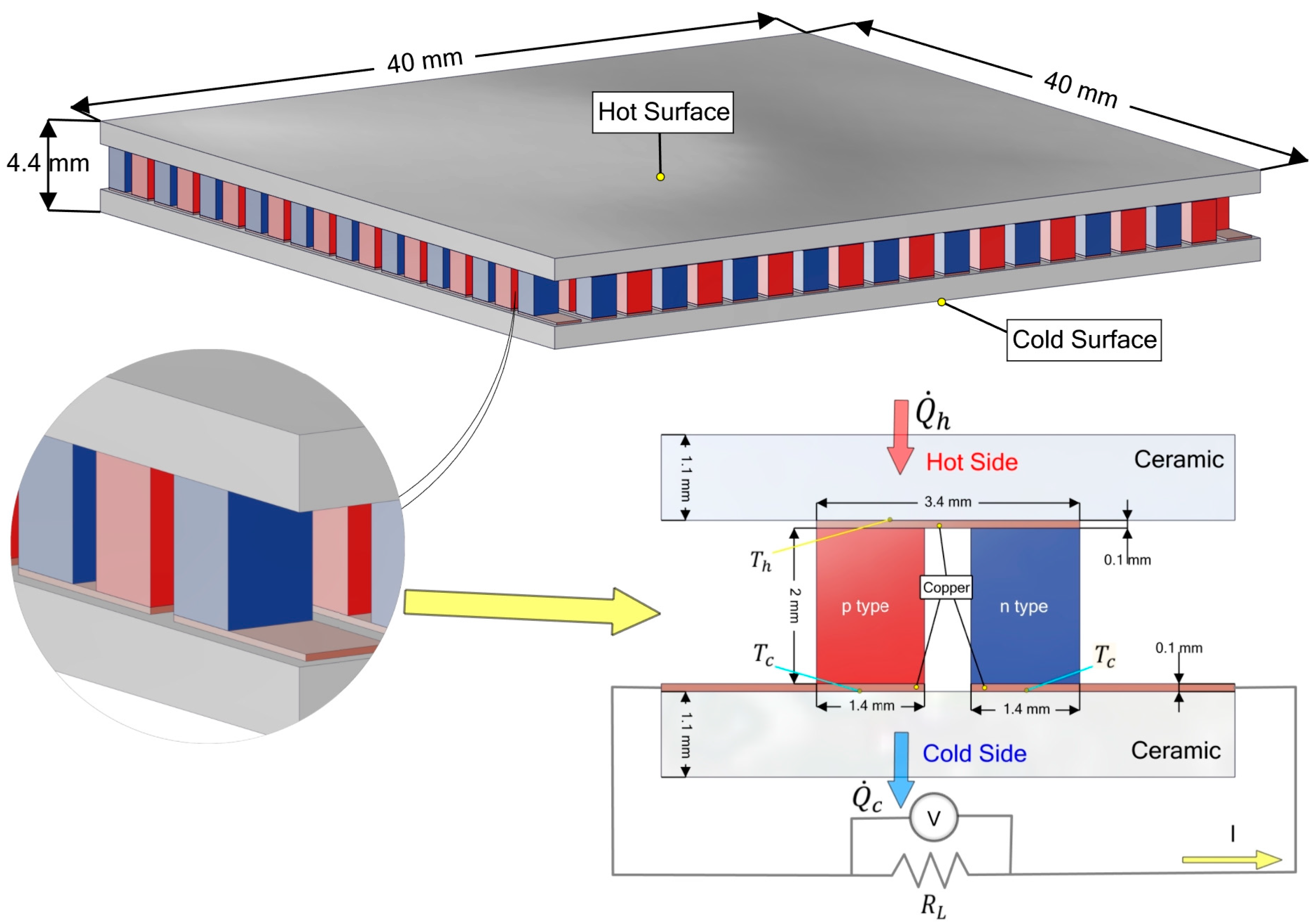
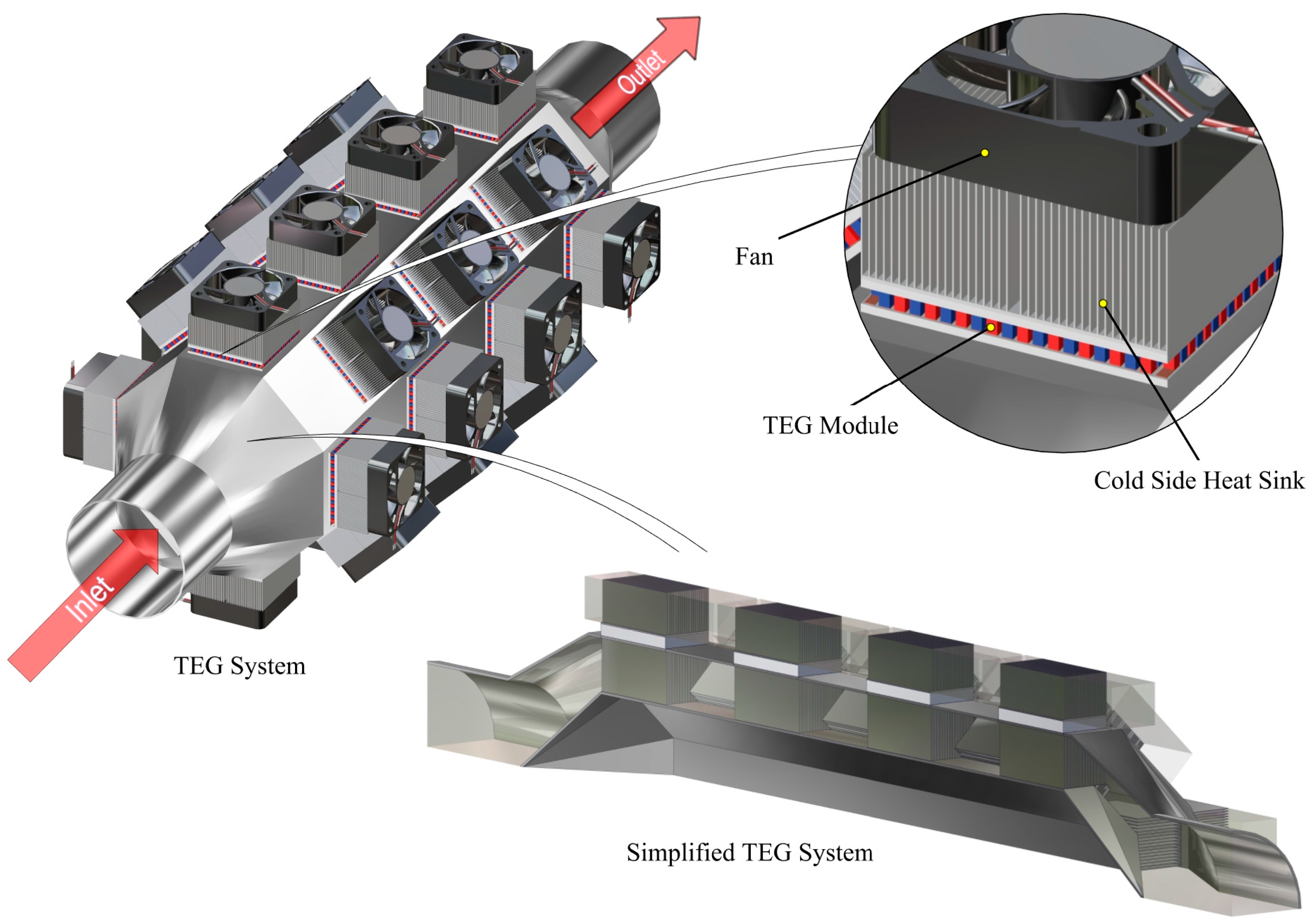
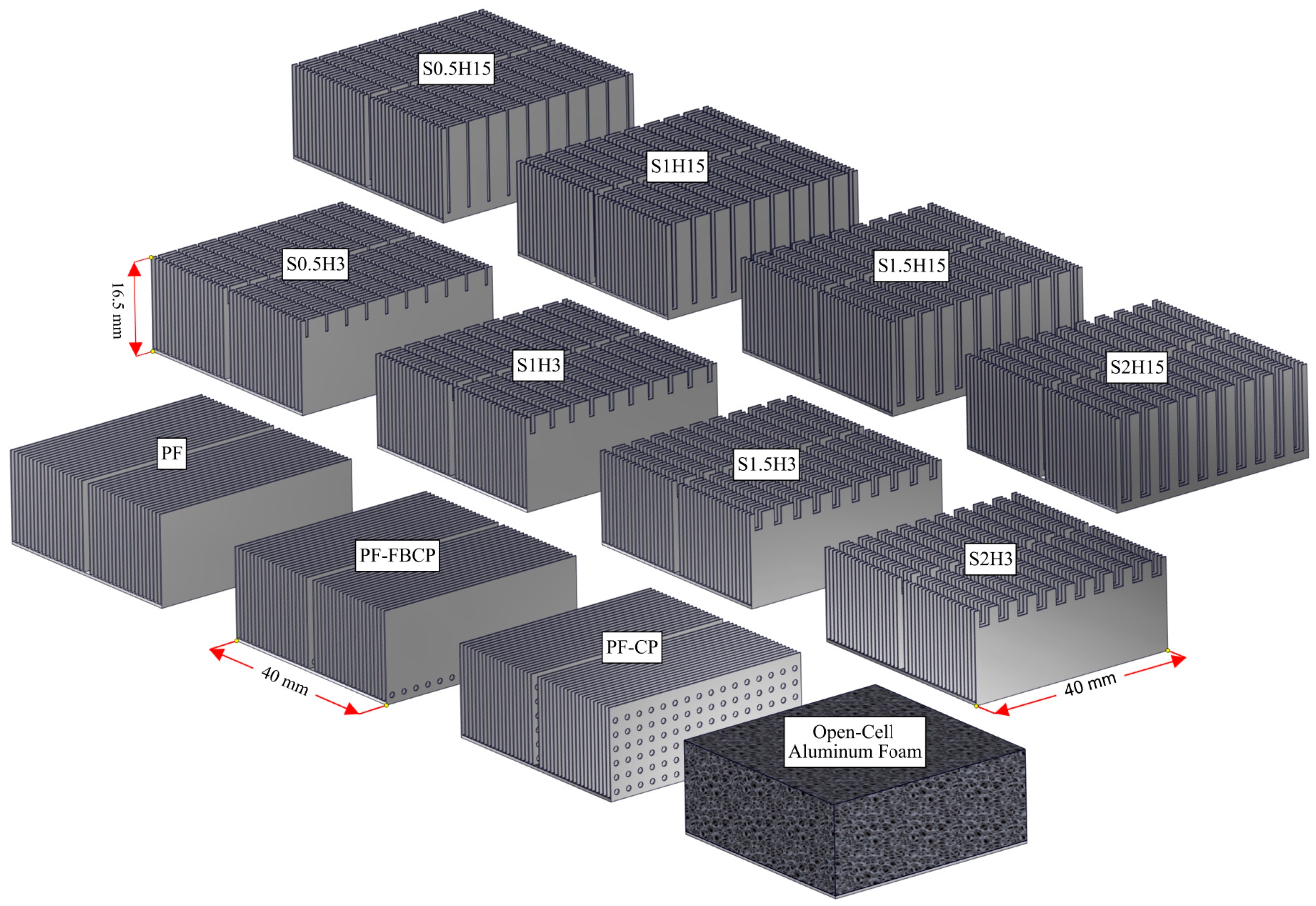
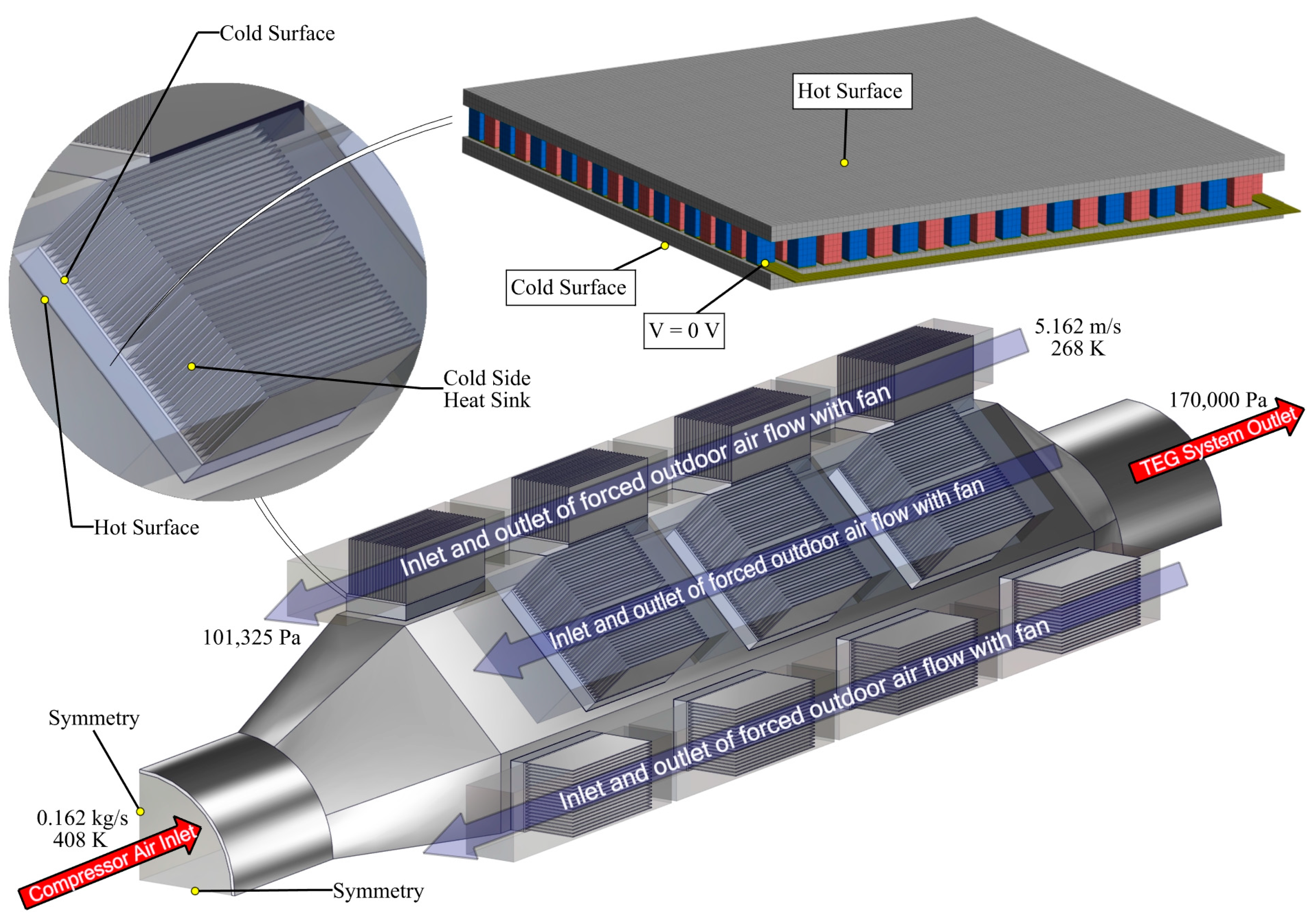


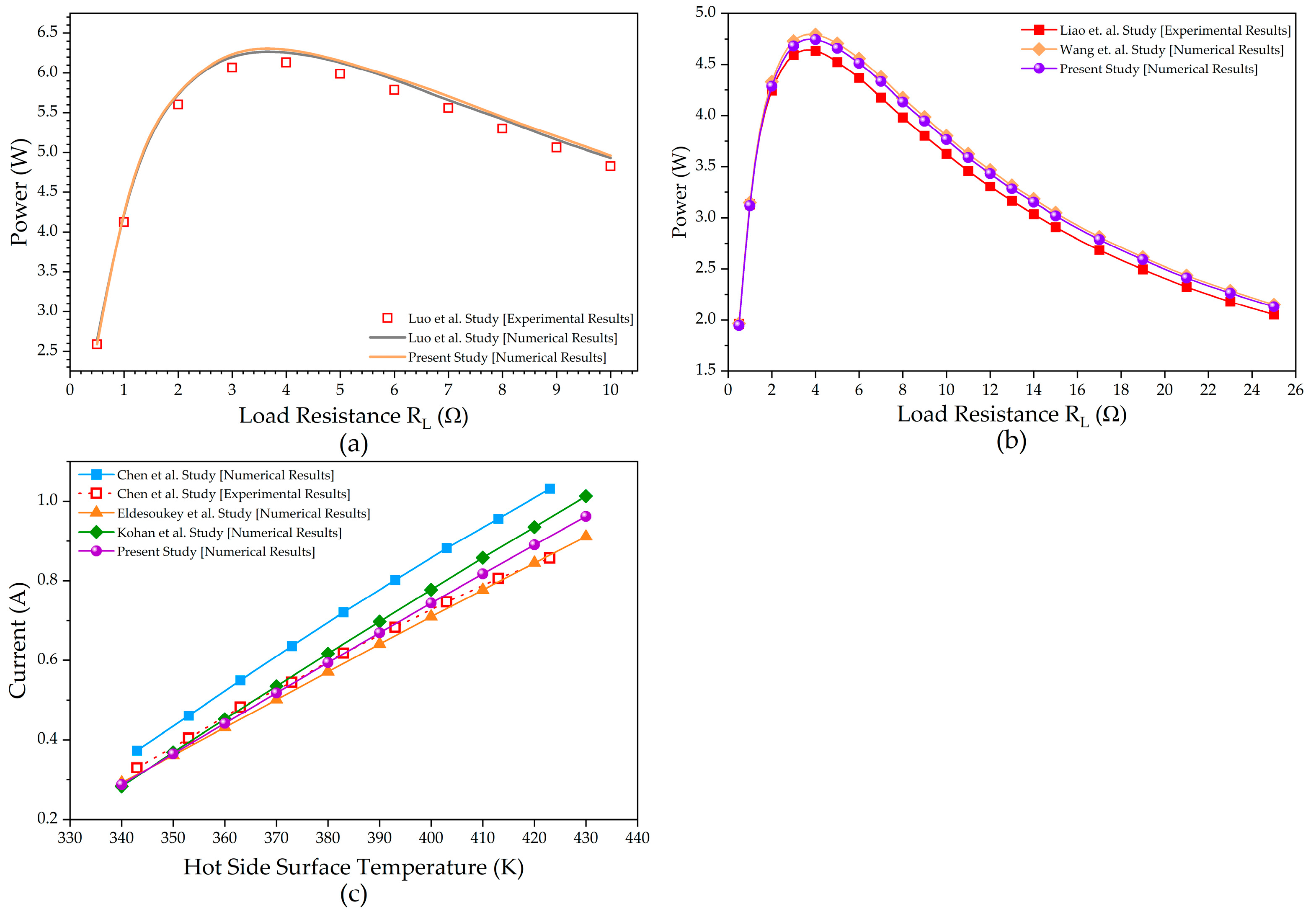
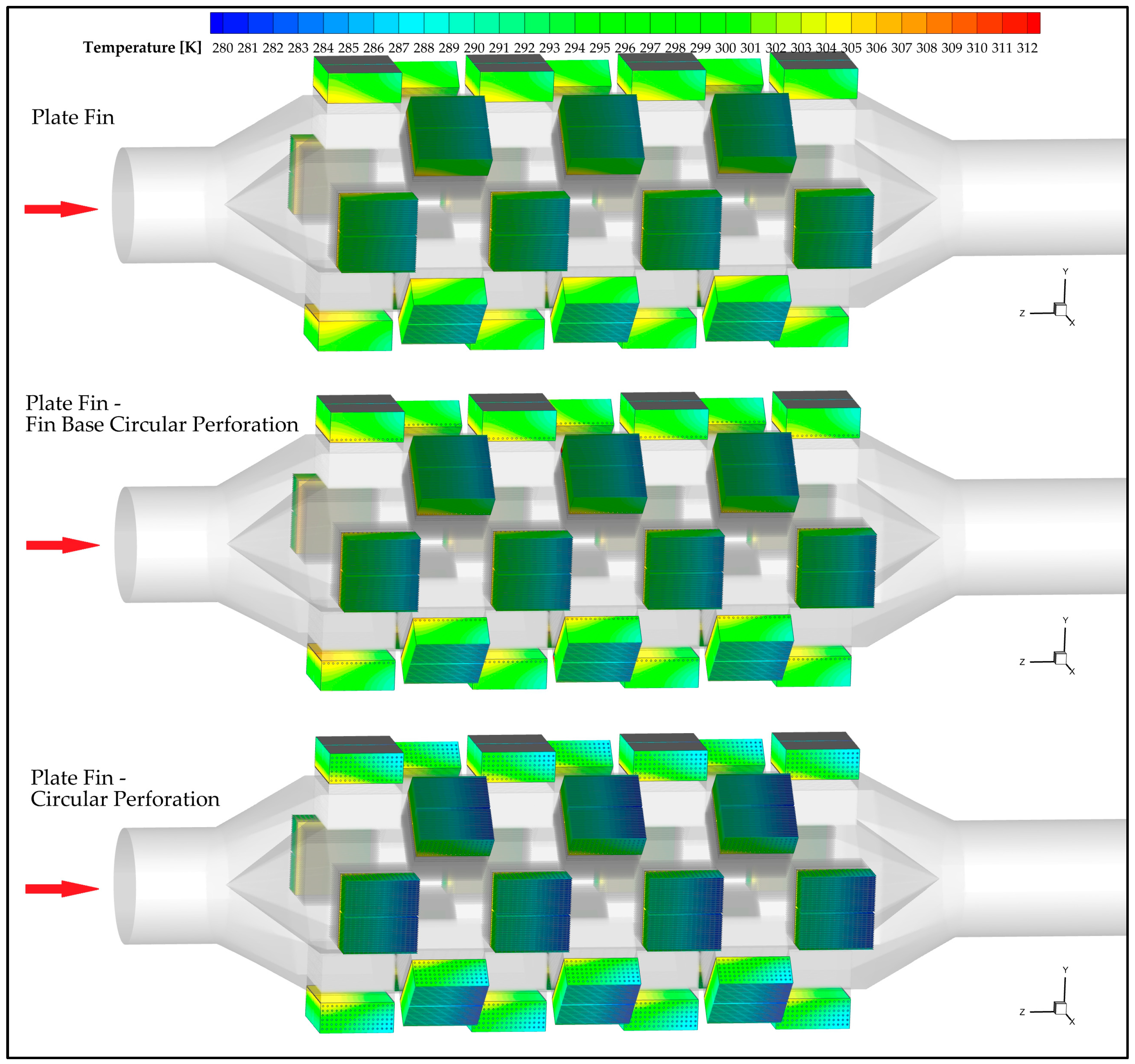


| Parameter | Compressor Air |
|---|---|
| Density d (kg/m3) | Ideal gas |
| Specific heat Cp (J/kgK) | |
| Thermal conductivity k (W/mK) | |
| Dynamic viscosity (kg/ms) | Sutherland Law |
| Molecular weight (kg/kmol) | 28.966 |
| Material | Component | Parameter | Value | Unit |
|---|---|---|---|---|
| Aluminum | Heat sinks and regular octagonal pipe | Thermal conductivity | 202.4 | W/mK |
| Specific heat | 871 | J/kg·K | ||
| Density | 2719 | kg/m3 | ||
| Ceramic | Ceramic plates of TEG | Thermal conductivity | 25 | W/mK |
| Specific heat | 880 | J/kg·K | ||
| Density | 3720 | kg/m3 | ||
| Copper | Copper slices of TEG | Thermal conductivity | 387,6 | W/mK |
| Specific heat | 381 | J/kg·K | ||
| Density | 8978 | kg/m3 | ||
| Electrical conductivity | Ωm | |||
| p-type thermoelectric material | p-type thermoelectric legs | Thermal conductivity | 1.5 | W/mK |
| Specific heat | 544 | J/kg·K | ||
| Density | 7700 | kg/m3 | ||
| Electrical conductivity | Ωm | |||
| Seebeck coefficient | V/K | |||
| n-type thermoelectric material | n-type thermoelectric legs | Thermal conductivity | 1.5 | W/mK |
| Specific heat | 544 | J/kg·K | ||
| Density | 7700 | kg/m3 | ||
| Electrical conductivity | Ωm | |||
| Seebeck coefficient | V/K |
| Porosity (ε) | Pore Per Inch (PPI) | P [m2] |
|---|---|---|
| 0.92 | 10 | |
| 0.92 | 20 | |
| 0.92 | 40 |
| Grid Number | Number of Cells | ∆P (Pa) | Error of ∆P | Intercooler Inlet Temperature (K) | Error of Temperature |
|---|---|---|---|---|---|
| 1 | 21,024,830 | 41,040.1 | NA | 393.951 | NA |
| 2 | 17,242,946 | 41,037.92 | 0% | 393.95 | 0.00% |
| 3 | 9,231,364 | 40,187.67 | 2% | 393.942 | 0.00% |
| 4 | 4,614,578 | 36,486.45 | 11% | 393.931 | 0.01% |
| 5 | 1,692,315 | 27,831.05 | 32% | 393.923 | 0.01% |
| Grid Number | Element | Node | Voltage (V) | Current (A) | Power (W) | Error of Power |
|---|---|---|---|---|---|---|
| 1 | 300,508 | 1,444,716 | 2.835 | 0.719 | 2.038 | NA |
| 2 | 167,356 | 840,269 | 2.835 | 0.719 | 2.038 | 0 |
| 3 | 88,422 | 460,418 | 2.836 | 0.718 | 2.039 | 0.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gürcan, A.; Yakar, G. Effect of Different Heat Sink Designs on Thermoelectric Generator System Performance in a Turbocharged Tractor. Energies 2025, 18, 3267. https://doi.org/10.3390/en18133267
Gürcan A, Yakar G. Effect of Different Heat Sink Designs on Thermoelectric Generator System Performance in a Turbocharged Tractor. Energies. 2025; 18(13):3267. https://doi.org/10.3390/en18133267
Chicago/Turabian StyleGürcan, Ali, and Gülay Yakar. 2025. "Effect of Different Heat Sink Designs on Thermoelectric Generator System Performance in a Turbocharged Tractor" Energies 18, no. 13: 3267. https://doi.org/10.3390/en18133267
APA StyleGürcan, A., & Yakar, G. (2025). Effect of Different Heat Sink Designs on Thermoelectric Generator System Performance in a Turbocharged Tractor. Energies, 18(13), 3267. https://doi.org/10.3390/en18133267







