Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II
Abstract
1. Introduction
- The charging load prediction herein incorporates active charging driven by range anxiety, using fuzzy reasoning to better capture the influence of driving distance on the user demand. Both passive charging (initiated when the battery falls below 20% or 15%) and active charging (triggered by range anxiety) are unified through fuzzy rule modeling.
- A hierarchical optimization-based charging scheduling strategy is proposed. In the upper layer, a multiobjective optimization model is formulated to simultaneously minimize user charging costs and distribution network load deviation.
- Nondominated sorting genetic algorithm II (NSGA-II) is used to solve the multiobjective optimization problem, and the Pareto front is generated to provide multiple scheduling choices for decision makers.
- Decoupling between the objective function solving and the specific scheduling strategy is achieved. The upper-layer model aggregates the individual vehicles and formulates the decision variables as a vector, effectively ensuring computational efficiency in large-scale scenarios. The lower-layer model schedules individual vehicles under an aggregated scheduling strategy from the upper layer to satisfy the constraints and ensure the feasibility of the global solution.
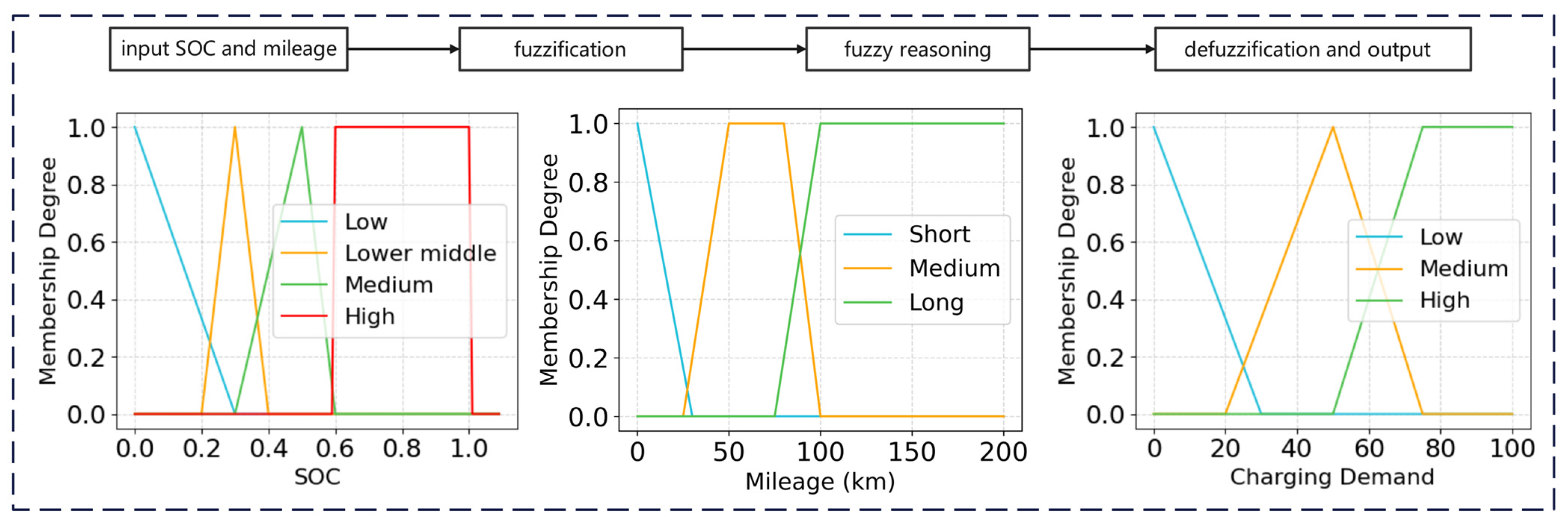
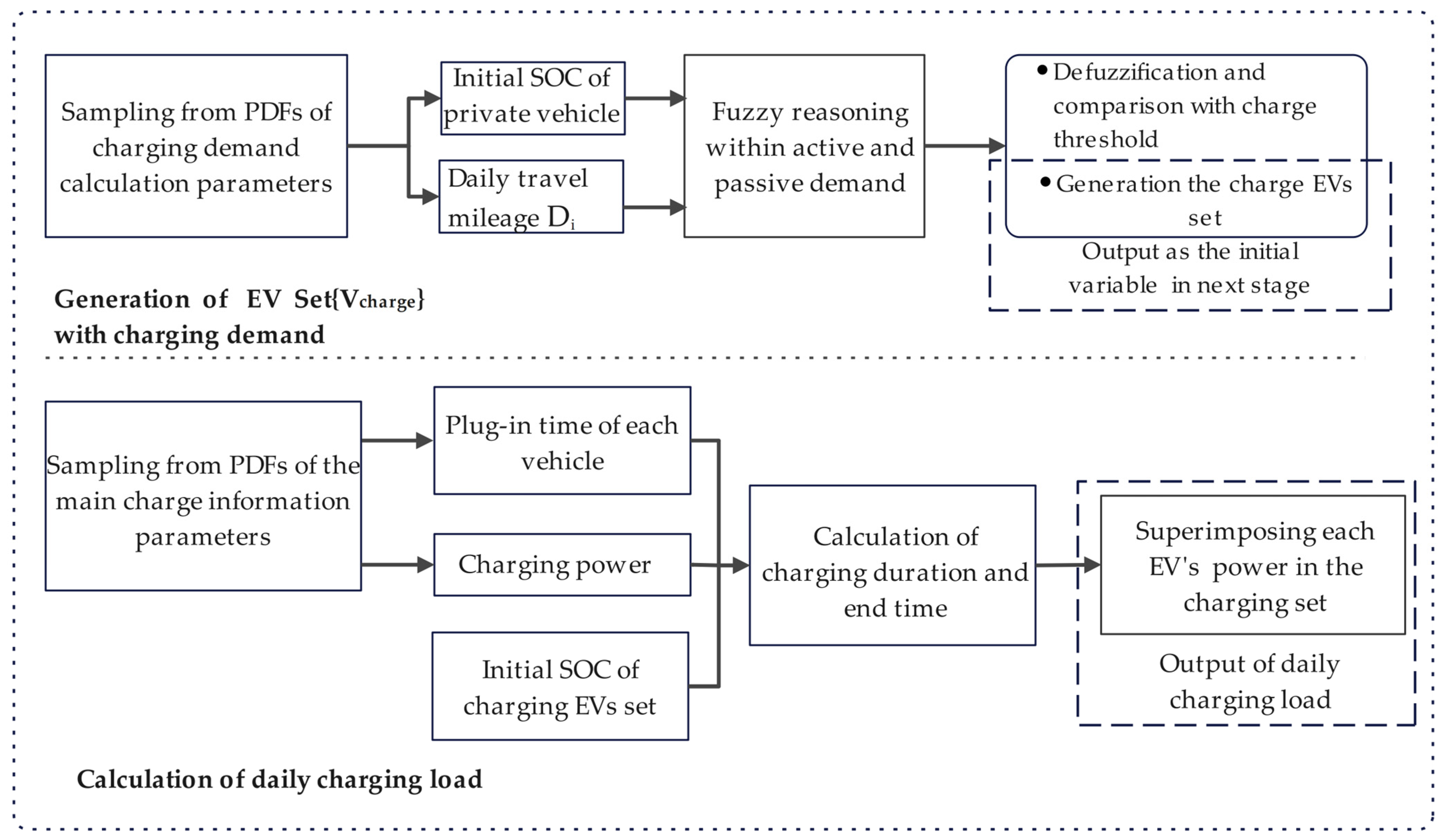
2. Charging Load Prediction
2.1. Fuzzy-Theory Prediction of Charging Demand
2.2. Charging Load Generation Based on the Sampling and Aggregation
3. EV Charging Optimization Strategy
3.1. Upper Layer Model
- Decision Variables
- Objective functions
- Constraint conditions
3.2. Lower Layer Model
- Decision Variables
- Constraint conditions
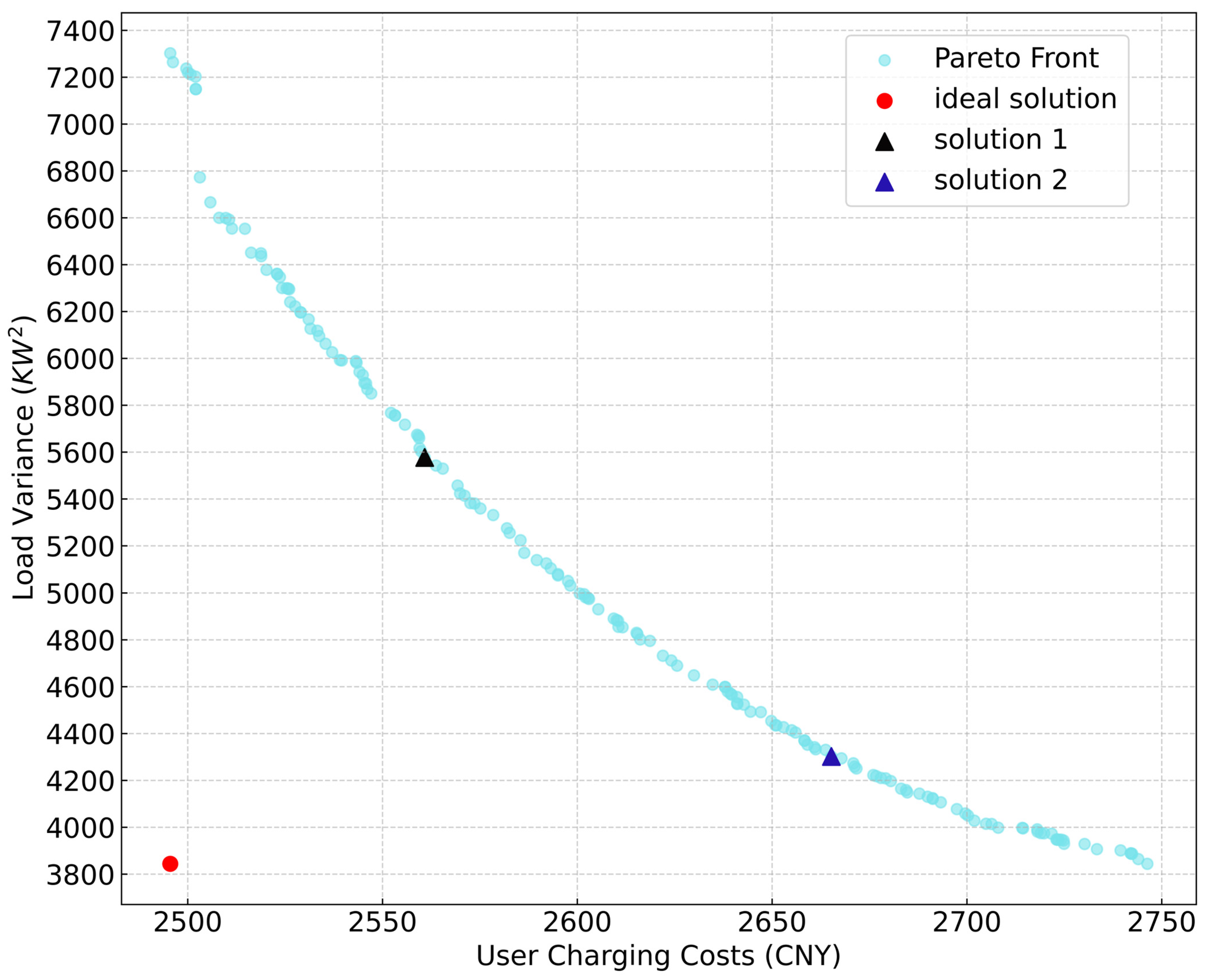
3.3. Multiobjective Optimization Algorithm and Solution Selection
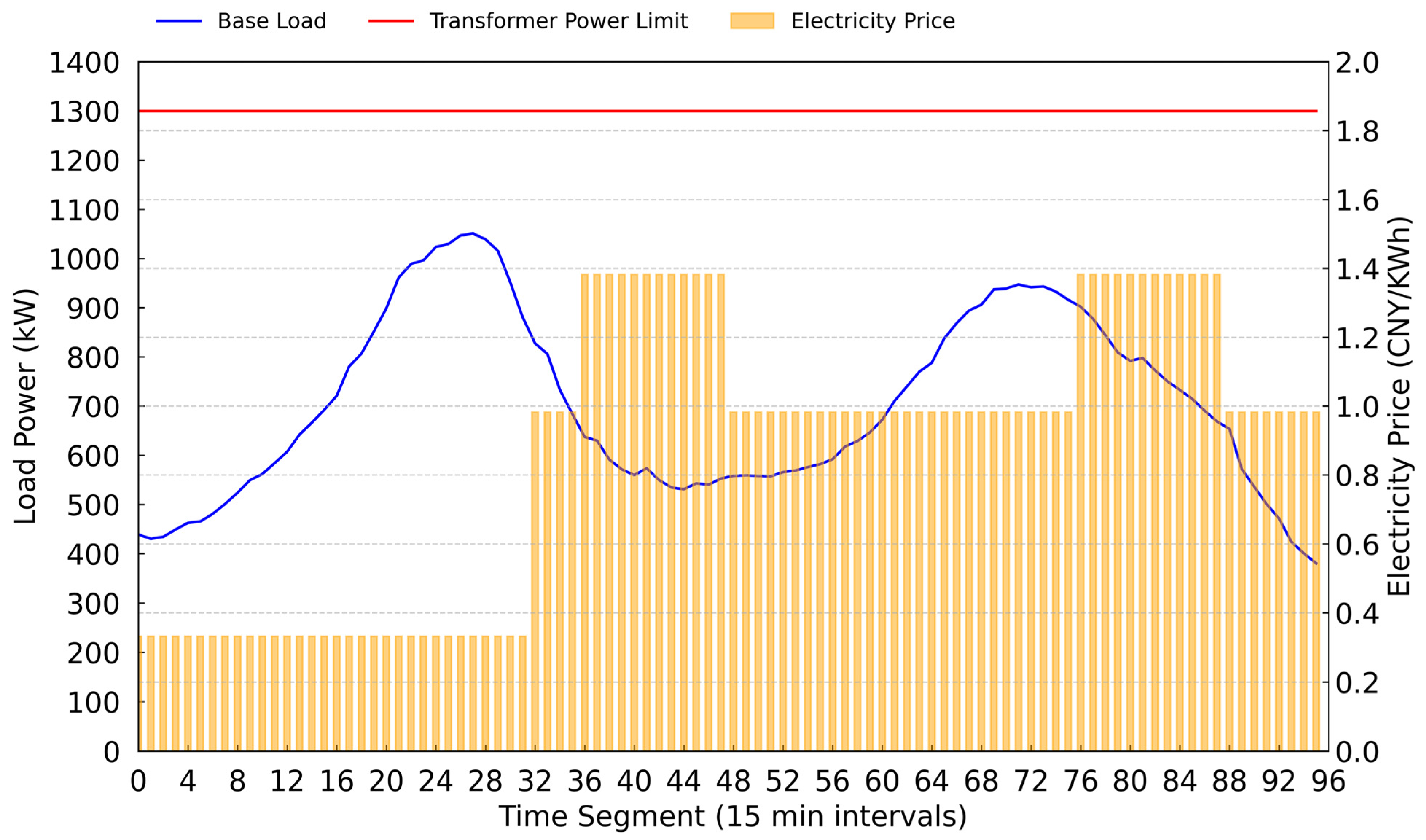
4. Case Study and Analysis
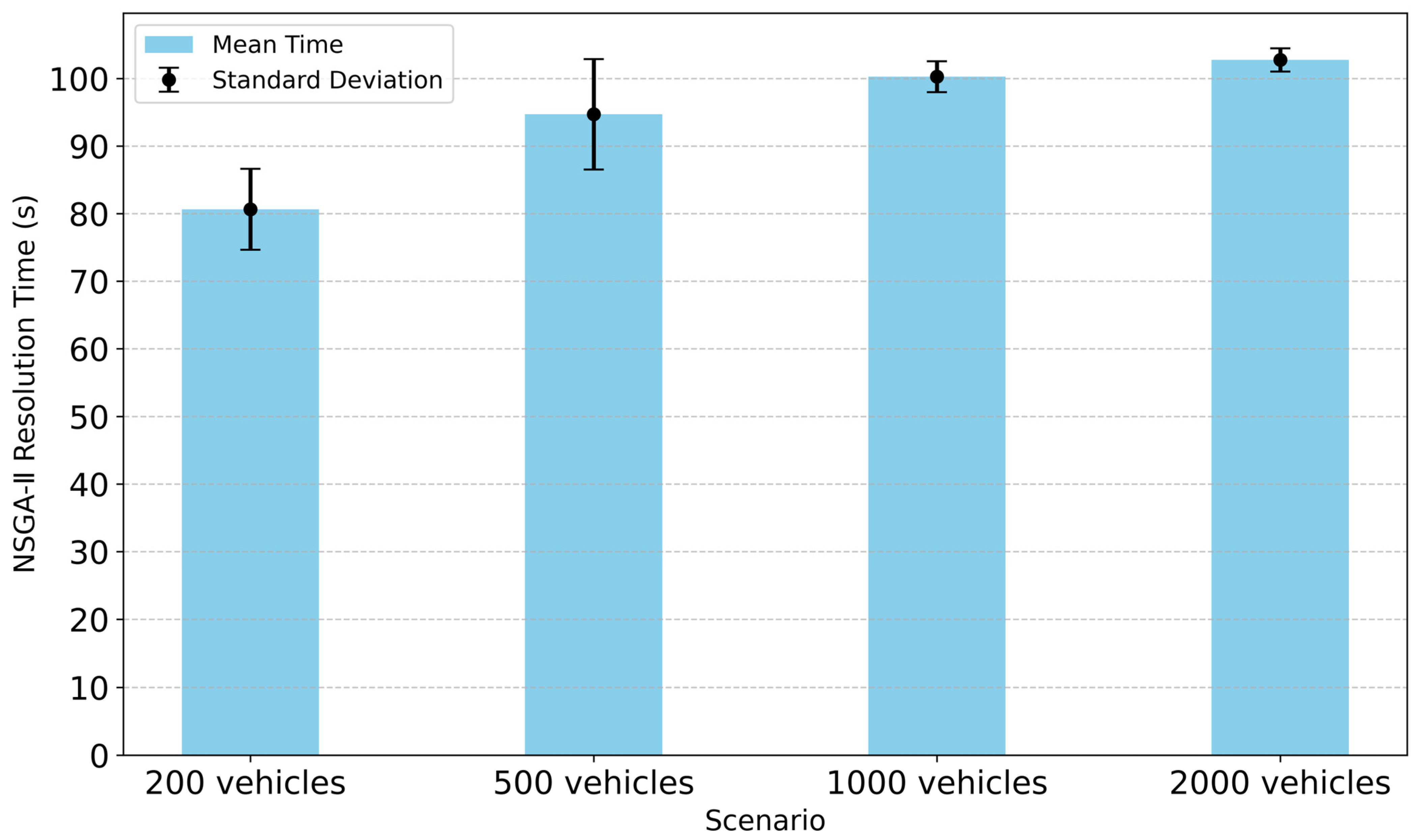
4.1. Computation Comparison Under Different Scenarios
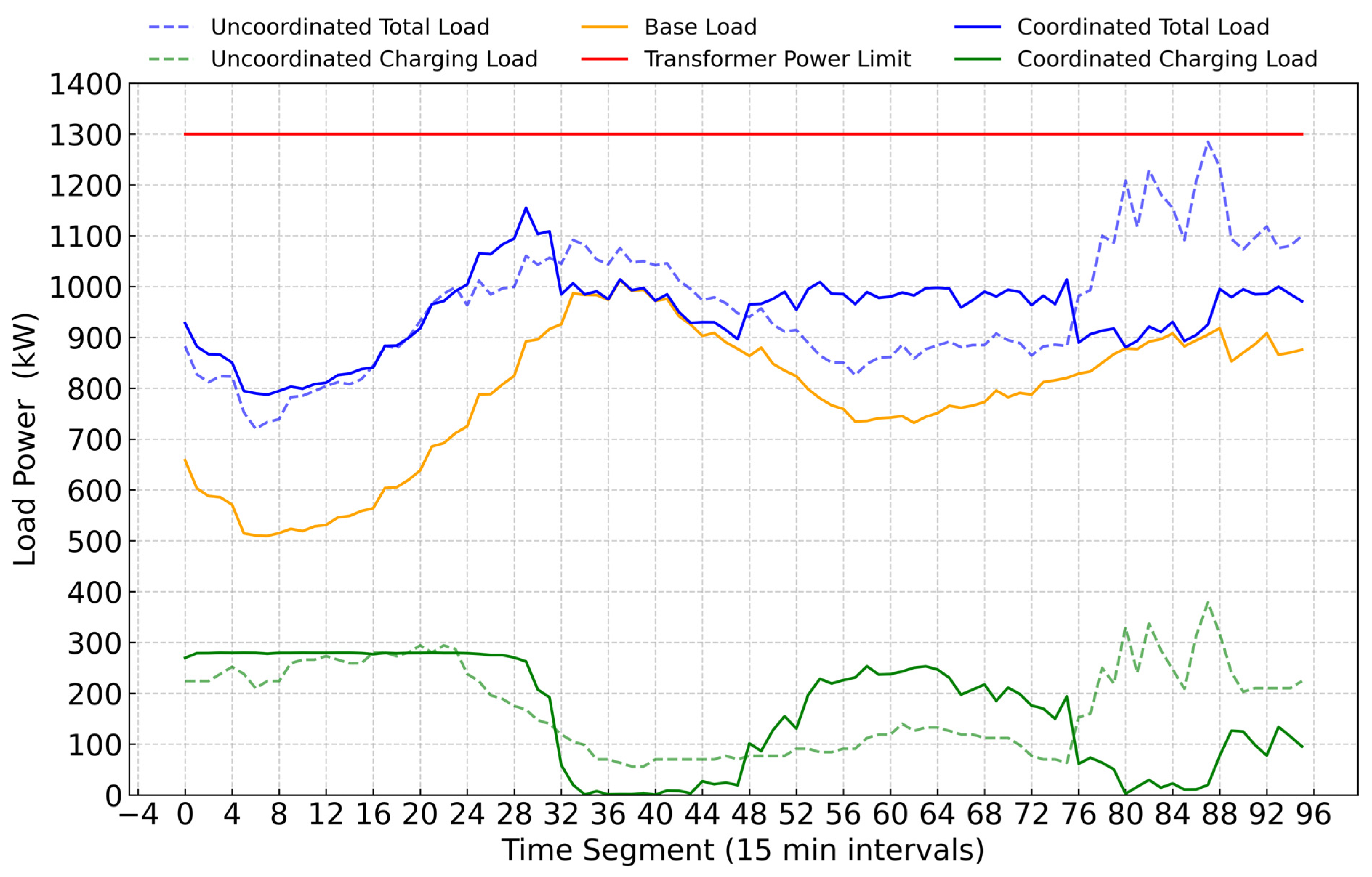
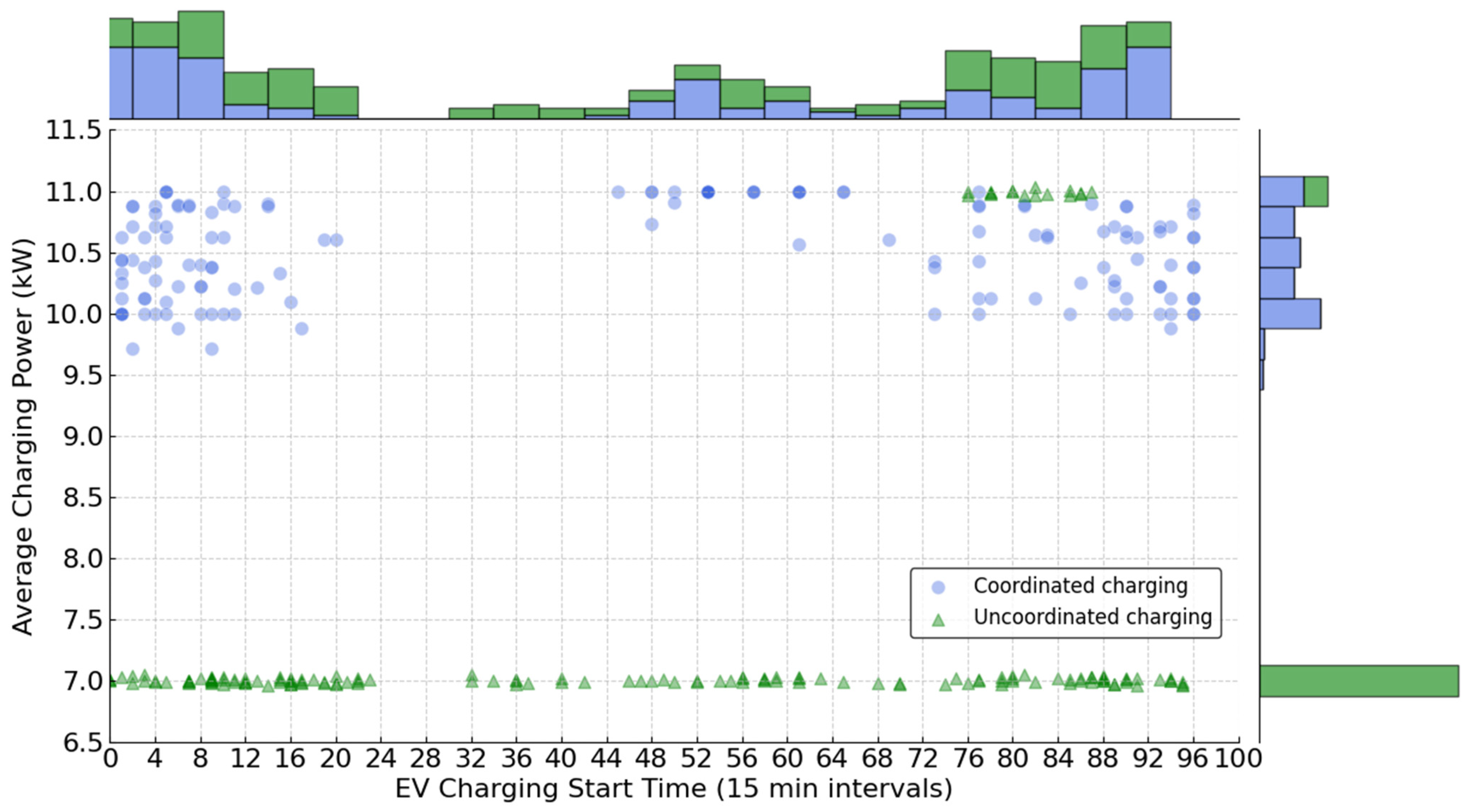
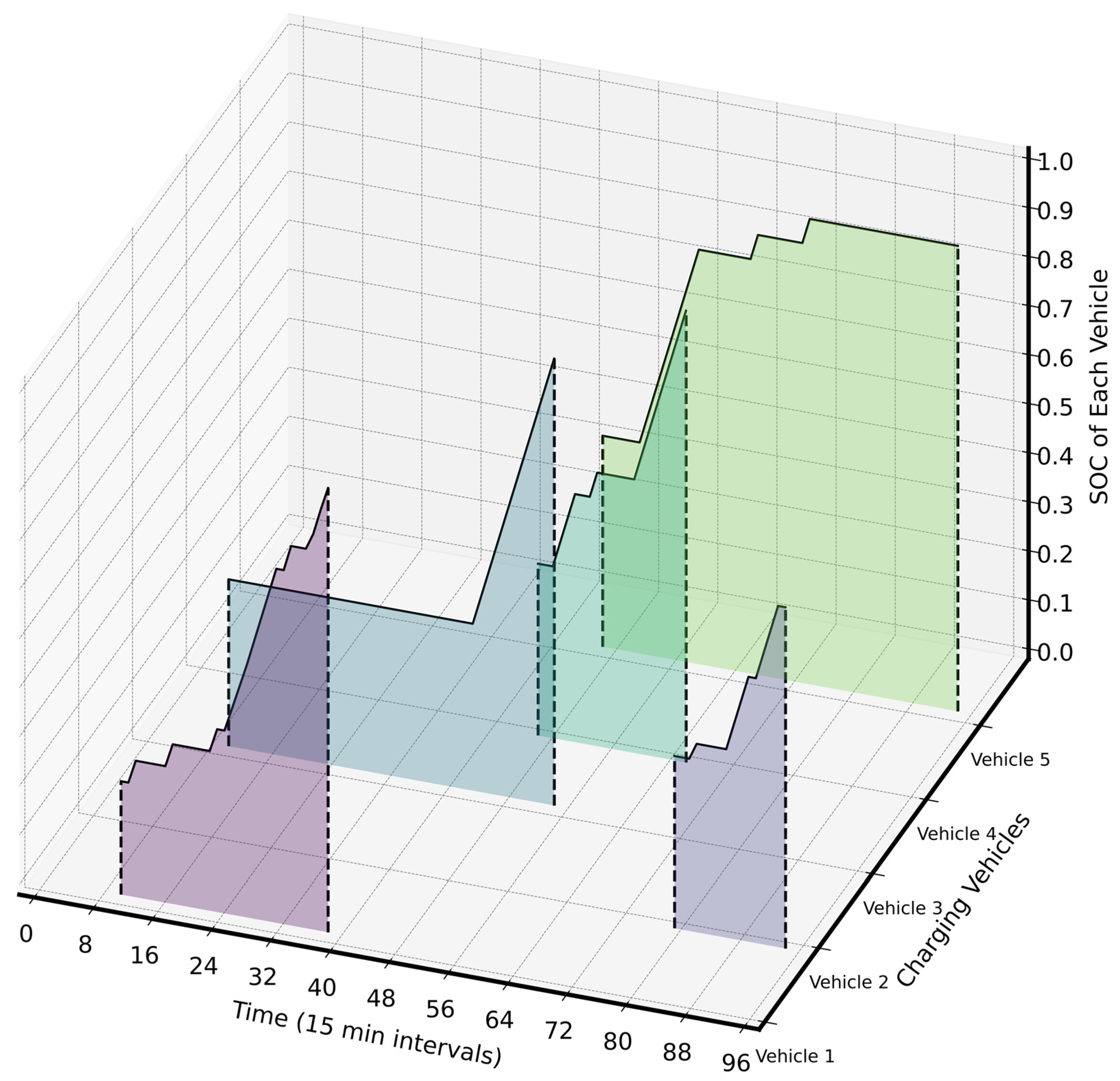
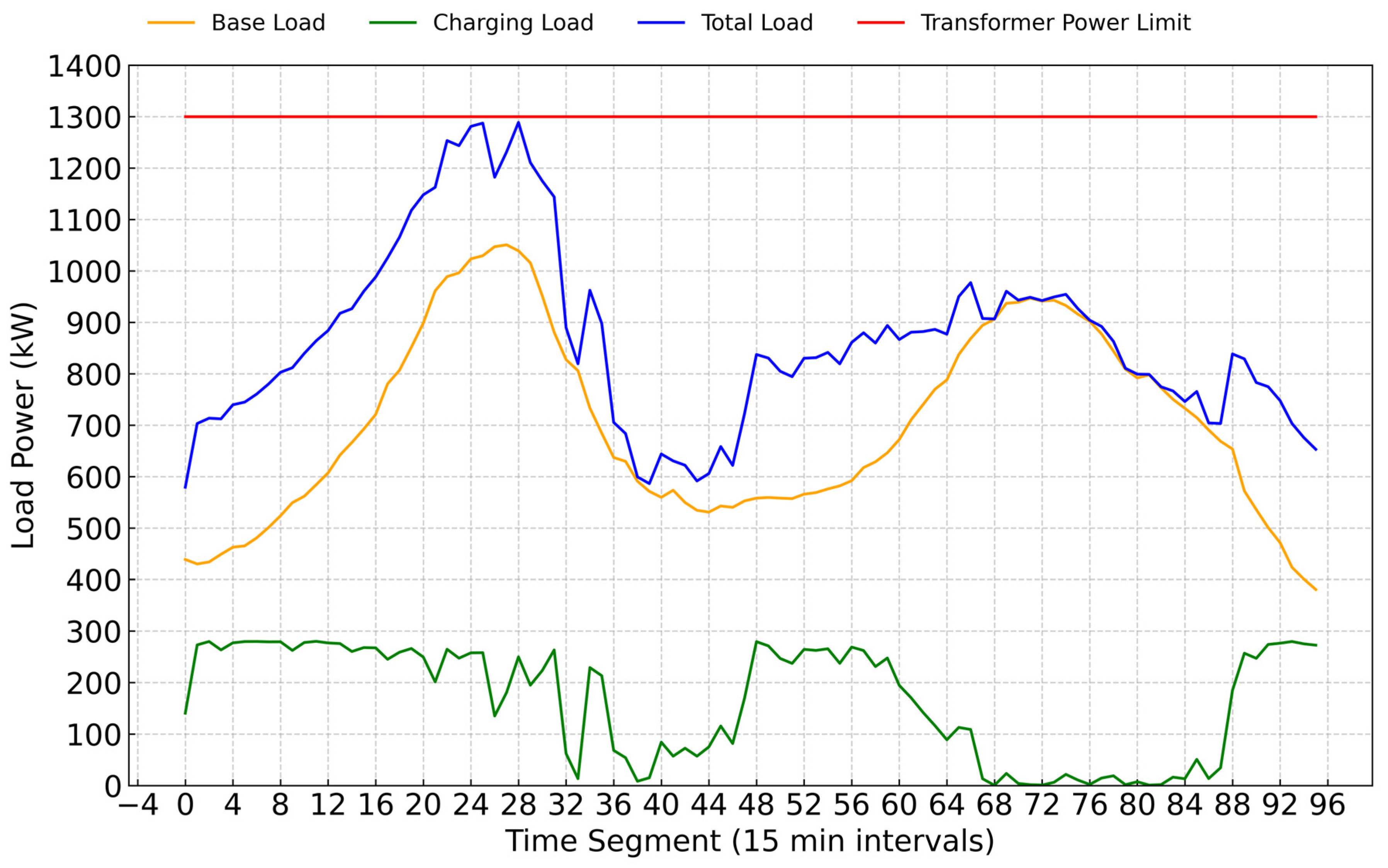
4.2. Case Optimization Results
4.3. The Optimization Analysis
4.4. Comparative Analysis of Different Scenarios
4.4.1. Analysis of Solutions Under Different Weights
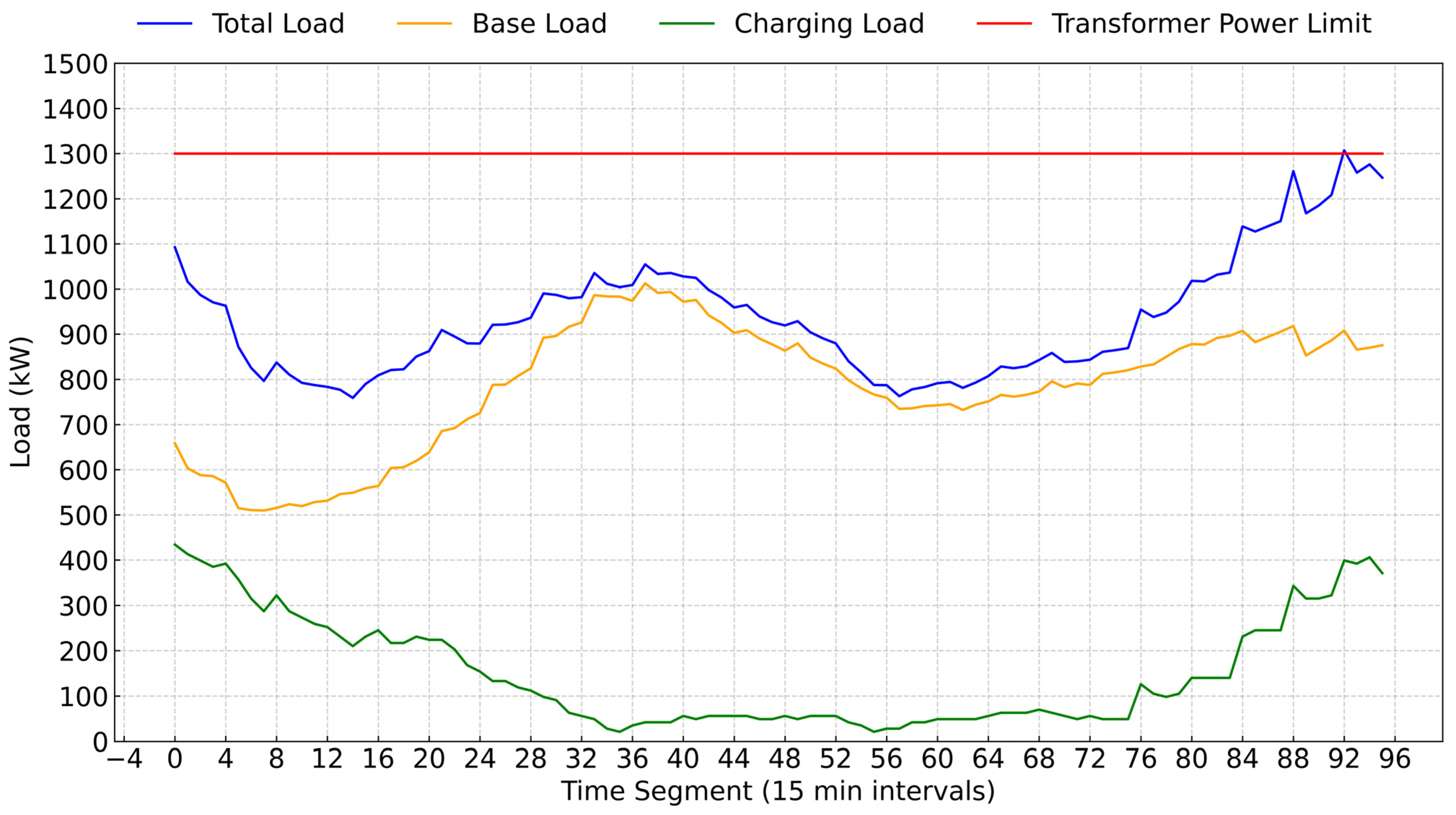
4.4.2. Comparative Analysis with Price-Based Charging Modes
4.4.3. Sensitivity Analysis of Base Load
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- New Energy Vehicles in Use in China Exceed 30 Million. Available online: https://english.www.gov.cn/archive/statistics/202501/17/content_WS678a06e4c6d0868f4e8eee8a.html (accessed on 23 April 2025).
- Nizami, M.S.H.; Hossain, M.J.; Mahmud, K. A Coordinated Electric Vehicle Management System for Grid-Support Services in Residential Networks. IEEE Syst. J. 2021, 15, 2066–2077. [Google Scholar] [CrossRef]
- Zhu, X.; Mather, B.; Mishra, P. Grid Impact Analysis of Heavy-Duty Electric Vehicle Charging Stations. In Proceedings of the 2020 IEEE Power & Energy Society Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 17–20 February; IEEE: Washington, DC, USA; pp. 1–5.
- Xiao, Y.; He, C.; Lv, X.; Li, Y.; Zhang, M.; Wang, T. Optimization of Distribution Network Considering Distributed Renewable Energy and V2G of Electric Vehicles. In Proceedings of the 2022 6th International Conference on Power and Energy Engineering (ICPEE), Virtual, 25–27 November 2022; pp. 132–137. [Google Scholar]
- Ravi, A.; Bai, L.; Wang, H. Optimal Siting of EV Fleet Charging Station Considering EV Mobility and Microgrid Formation for Enhanced Grid Resilience. Appl. Sci. 2023, 13, 12181. [Google Scholar] [CrossRef]
- Powell, B.; Johnson, C. Impact of Electric Vehicle Charging Station Reliability, Resilience, and Location on Electric Vehicle Adoption; National Renewable Energy Laboratory: Golden, CO, USA, 2024; p. NREL/TP--5R00-89896, 2432350, MainId:90675.
- Paudel, A.; Sampath, M.; Yang, J.; Gooi, H.B. Peer-to-Peer Energy Trading in Smart Grid Considering Power Losses and Network Fees. In Proceedings of the 2022 IEEE Power & Energy Society General Meeting (PESGM), Chicago, IL, USA, 17–22 July 2022; pp. 4727–4737. [Google Scholar]
- Mokhtar, M.; Shaaban, M.F.; Ismail, M.H.; Sindi, H.F.; Rawa, M. Reliability Assessment under High Penetration of EVs Including V2G Strategy. Energies 2022, 15, 1585. [Google Scholar] [CrossRef]
- Yin, W.; Ming, Z. Study on Optimal Scheduling Strategy of Electric Vehicles Clusters in Distribution Power Grid. Optim. Control Appl. Methods 2023, 44, 1769–1778. [Google Scholar] [CrossRef]
- Barreto, R.; Faria, P.; Vale, Z. Electric Mobility: An Overview of the Main Aspects Related to the Smart Grid. Electronics 2022, 11, 1311. [Google Scholar] [CrossRef]
- Su, J.; Lie, T.T.; Zamora, R. Modelling of Large-Scale Electric Vehicles Charging Demand: A New Zealand Case Study. Electr. Power Syst. Res. 2019, 167, 171–182. [Google Scholar] [CrossRef]
- Xing, Y.; Li, F.; Sun, K.; Wang, D.; Chen, T.; Zhang, Z. Multi-Type Electric Vehicle Load Prediction Based on Monte Carlo Simulation. Energy Rep. 2022, 8, 966–972. [Google Scholar] [CrossRef]
- Shang, Y.; Li, D.; Li, Y.; Li, S. Explainable Spatiotemporal Multi-Task Learning for Electric Vehicle Charging Demand Prediction. Appl. Energy 2025, 384, 125460. [Google Scholar] [CrossRef]
- Zheng, Z.; Zheng, C.; Wei, Z.; Xu, L. Analysis of Charging Tariffs for Residential Electric Vehicle Users Based on Stackelberg Game. Energy Rep. 2024, 12, 1765–1776. [Google Scholar] [CrossRef]
- Mahdi, M.A.; Abdalla, A.N.; Liu, L.; Ji, R.; Bian, H.; Hai, T. Optimizing Microgrid Load Fluctuations through Dynamic Pricing and Electric Vehicle Flexibility: A Comparative Analysis. Energies 2024, 17, 4994. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, Q.; Zhu, W.; Lyu, L.; Jiang, L.; Koh, L.H.; Cai, G. Research on the Orderly Charging and Discharging Mechanism of Electric Vehicles Considering Travel Characteristics and Carbon Quota. IEEE Trans. Transp. Electrific. 2024, 10, 3012–3027. [Google Scholar] [CrossRef]
- Szumska, E.M. Electric Vehicle Charging Infrastructure along Highways in the EU. Energies 2023, 16, 895. [Google Scholar] [CrossRef]
- Loaiza Quintana, C.; Climent, L.; Arbelaez, A. Iterated Local Search for the eBuses Charging Location Problem. In Parallel Problem Solving from Nature—PPSN XVII.; Rudolph, G., Kononova, A.V., Aguirre, H., Kerschke, P., Ochoa, G., Tušar, T., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2022; Volume 13399, pp. 338–351. ISBN 978-3-031-14720-3. [Google Scholar]
- Liu, Z.; Borlaug, B.; Meintz, A.; Neuman, C.; Wood, E.; Bennett, J. Data-Driven Method for Electric Vehicle Charging Demand Analysis: Case Study in Virginia. Transp. Res. Part D Transp. Environ. 2023, 125, 103994. [Google Scholar] [CrossRef]
- Wang, R.; Mu, J.; Sun, Z.; Wang, J.; Hu, A. NSGA-II Multi-Objective Optimization Regional Electricity Price Model for Electric Vehicle Charging Based on Travel Law. Energy Rep. 2021, 7, 1495–1503. [Google Scholar] [CrossRef]
- Maeng, J.; Min, D.; Kang, Y. Intelligent Charging and Discharging of Electric Vehicles in a Vehicle-to-Grid System Using a Reinforcement Learning-Based Approach. Sustain. Energy Grids Netw. 2023, 36, 101224. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, C.; Cai, G.; Koh, L.H. Charging and Discharging Optimization Strategy for Electric Vehicles Considering Elasticity Demand Response. eTransportation 2023, 18, 100262. [Google Scholar] [CrossRef]
- Diaz-Londono, C.; Maffezzoni, P.; Daniel, L.; Gruosso, G. Comparison and Analysis of Algorithms for Coordinated EV Charging to Reduce Power Grid Impact. IEEE Open J. Veh. Technol. 2024, 5, 990–1003. [Google Scholar] [CrossRef]
- Yang, X.; Niu, D.; Sun, L.; Ji, Z.; Zhou, J.; Wang, K.; Siqin, Z. A Bi-Level Optimization Model for Electric Vehicle Charging Strategy Based on Regional Grid Load Following. J. Clean. Prod. 2021, 325, 129313. [Google Scholar] [CrossRef]
- Su, J.; Lie, T.T.; Zamora, R. A Rolling Horizon Scheduling of Aggregated Electric Vehicles Charging under the Electricity Exchange Market. Appl. Energy 2020, 275, 115406. [Google Scholar] [CrossRef]
- Ji, Y.; Zhang, J.; Li, S.; Deng, Y.; Mu, Y. Variable Power Regulation Charging Strategy for Electric Vehicles Based on Particle Swarm Algorithm. Energy Rep. 2022, 8, 824–830. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, Y.; Wang, D. Online Charging Strategy for Electric Vehicle Clusters Based on Multi-Agent Reinforcement Learning and Long–Short Memory Networks. Energies 2022, 15, 4582. [Google Scholar] [CrossRef]
- Huang, S.; Yang, M.; Yun, J.; Li, P.; Zhang, Q.; Xiang, G. A Data-Driven Multi-Agent PHEVs Collaborative Charging Scheme Based on Deep Reinforcement Learning. In Proceedings of the 2021 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Chengdu, China, 18 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 326–331. [Google Scholar]
- Wang, Y.; Wang, H.; Razzaghi, R.; Jalili, M.; Liebman, A. Multi-Objective Coordinated EV Charging Strategy in Distribution Networks Using an Improved Augmented Epsilon-Constrained Method. Appl. Energy 2024, 369, 123547. [Google Scholar] [CrossRef]
- Thorhauge, M.; Rich, J.; Mabit, S.E. Charging Behaviour and Range Anxiety in Long-Distance EV Travel: An Adaptive Choice Design Study. Transportation 2024. [Google Scholar] [CrossRef]
- Global EV Outlook 2024. Available online: https://www.iea.org/reports/global-ev-outlook-2024 (accessed on 16 June 2025).

| Period | Charge Probability | Plug-In Time in Period |
|---|---|---|
| 8:00–17:00 | 0.2 | Uniform distribution |
| 19:00–6:00 | 0.7 | Uniform distribution |
| 19:00–22:00 | 0.1 | Uniform distribution |
| Hierarchical Schedule Model | ||
|---|---|---|
| 60 vehicles | 200 vehicles | |
| NSGA-II resolution time (s) | 68.23 | 80.64 |
| Individual deployment resolution time (s) | 4.73 | 6.38 |
| Type | Corresponding Period | Electricity Price (CNY/kWh) |
|---|---|---|
| valley | 24:00–8:00 | 0.332 |
| flat | 8:00–9:00 12:00–19:00 22:00–24:00 | 0.982 |
| peak | 9:00–12:00 19:00–22:00 | 1.382 |
| Coordinated Charging 1 | Coordinated Charging 2 | Uncoordinated Charging | Price-Based Uncoordinated Charging | Base Load | |
|---|---|---|---|---|---|
| User charging cost (CNY) | 2560.79 | 2665.20 | 3236.18 | 2714.27 | ----- |
| Load variance (kW2) | 5.58 × 103 | 4.30 × 103 | 1.54 × 104 | 1.76 × 104 | 1.92 × 104 |
| Peak–valley load difference (kW) | 367.61 | 282.53 | 564.07 | 548.23 | 503.10 |
| Deviated Base Load | Coordinated Charging | |
|---|---|---|
| Load variance (kW2) | 3.28 × 104 | 2.98 × 104 |
| Peak–valley load difference (kW) | 670.98 | 709.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Bao, Z.; Tan, Y.; Wang, J.; Liu, Y.; Sang, H.; Yuan, X. Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II. Energies 2025, 18, 3269. https://doi.org/10.3390/en18133269
Chen Y, Bao Z, Tan Y, Wang J, Liu Y, Sang H, Yuan X. Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II. Energies. 2025; 18(13):3269. https://doi.org/10.3390/en18133269
Chicago/Turabian StyleChen, Yikang, Zhicheng Bao, Yihang Tan, Jiayang Wang, Yang Liu, Haixiang Sang, and Xinmei Yuan. 2025. "Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II" Energies 18, no. 13: 3269. https://doi.org/10.3390/en18133269
APA StyleChen, Y., Bao, Z., Tan, Y., Wang, J., Liu, Y., Sang, H., & Yuan, X. (2025). Hierarchical Charging Scheduling Strategy for Electric Vehicles Based on NSGA-II. Energies, 18(13), 3269. https://doi.org/10.3390/en18133269






