Energy-Efficient Prediction of Carbon Deposition in DRM Processes Through Optimized Neural Network Modeling
Abstract
1. Introduction
2. Model Construction Method
2.1. Data Sources
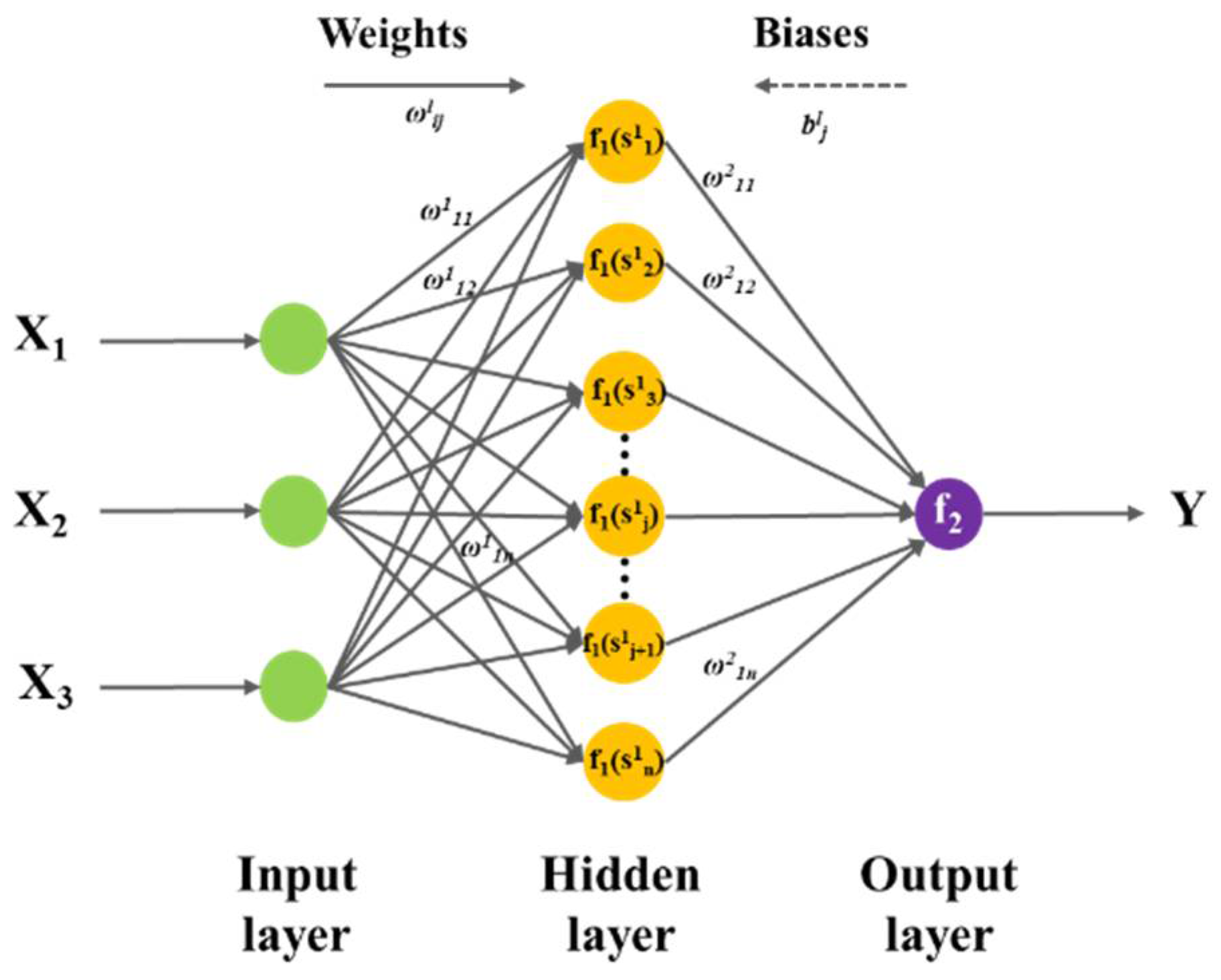
2.2. BP Neural Network Structure and Parameters
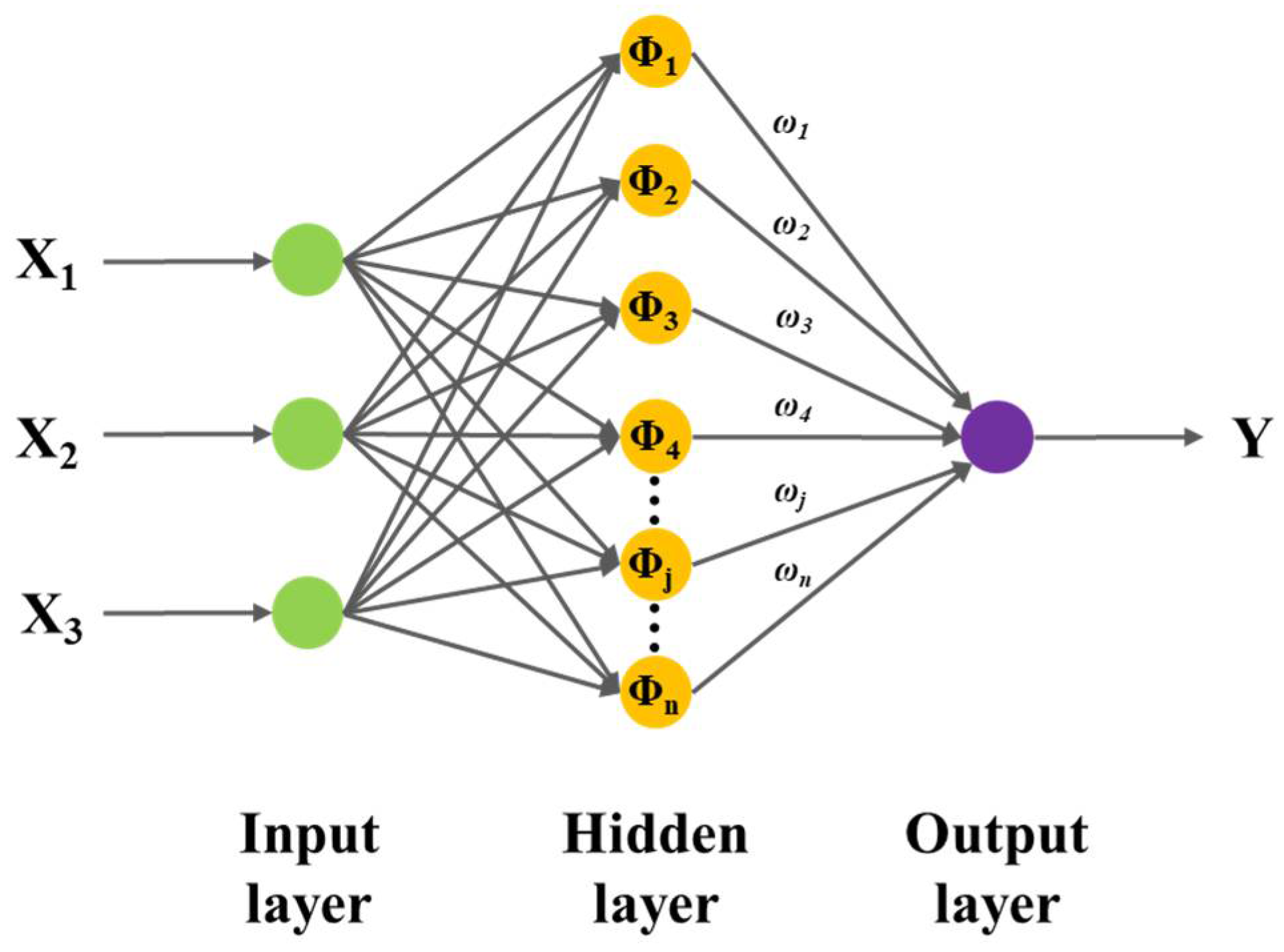
2.3. RBF Neural Network Structure and Parameters
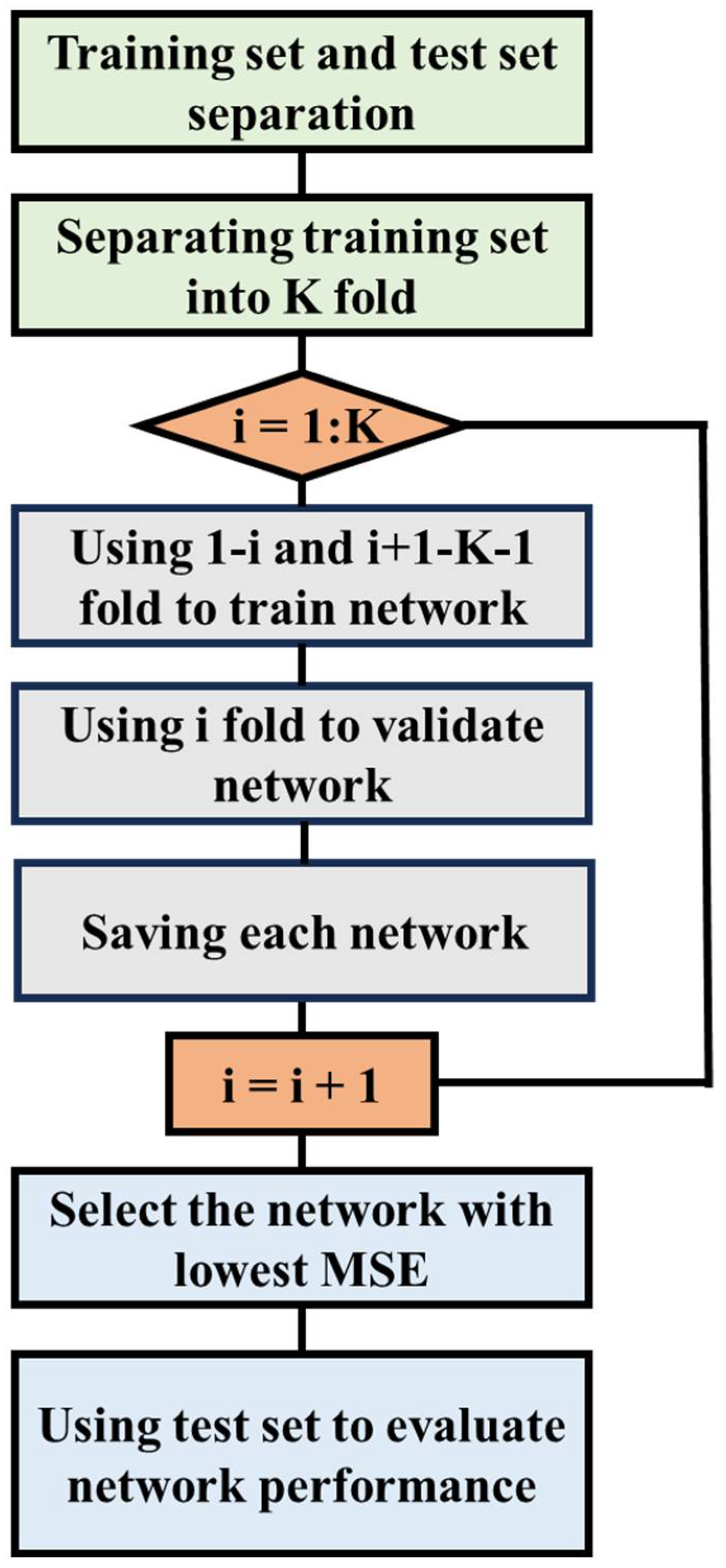
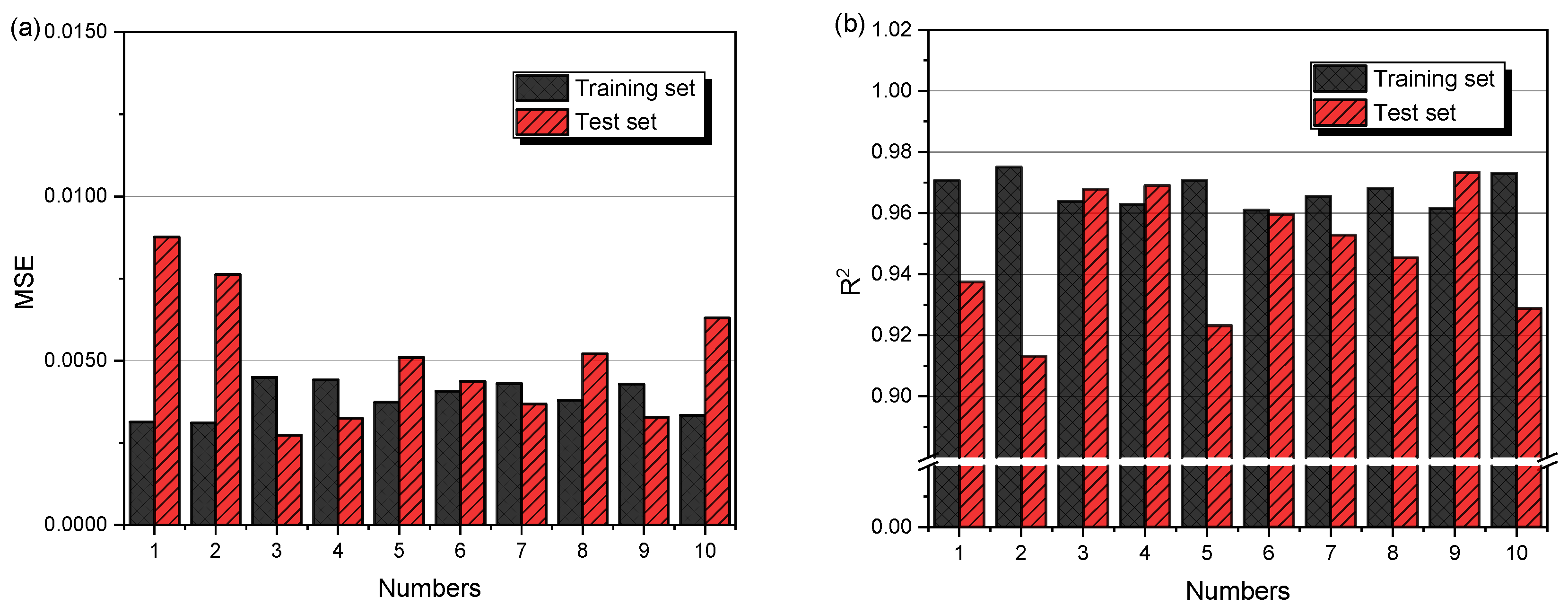
2.4. K-Fold Cross-Validation Optimization Model
2.5. Model Performance Evaluation
3. Results and Discussion
3.1. Relative Factors of Carbon Deposition Quantity
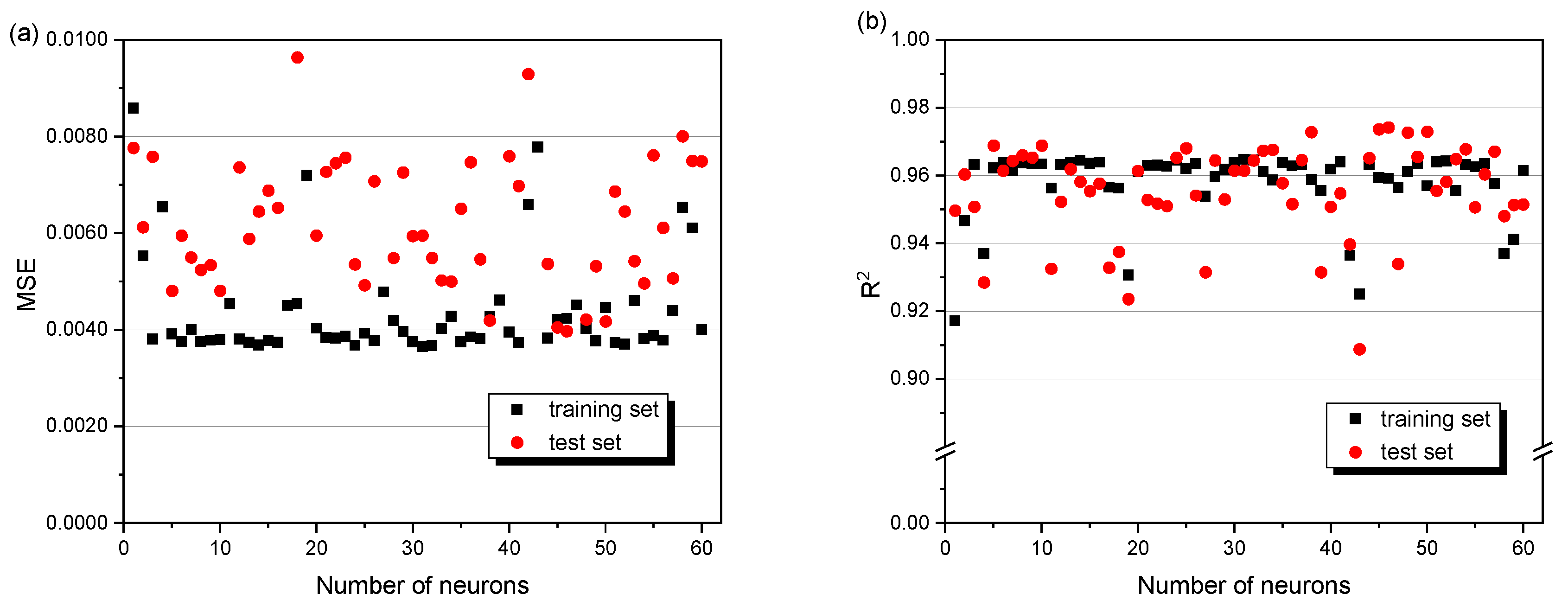
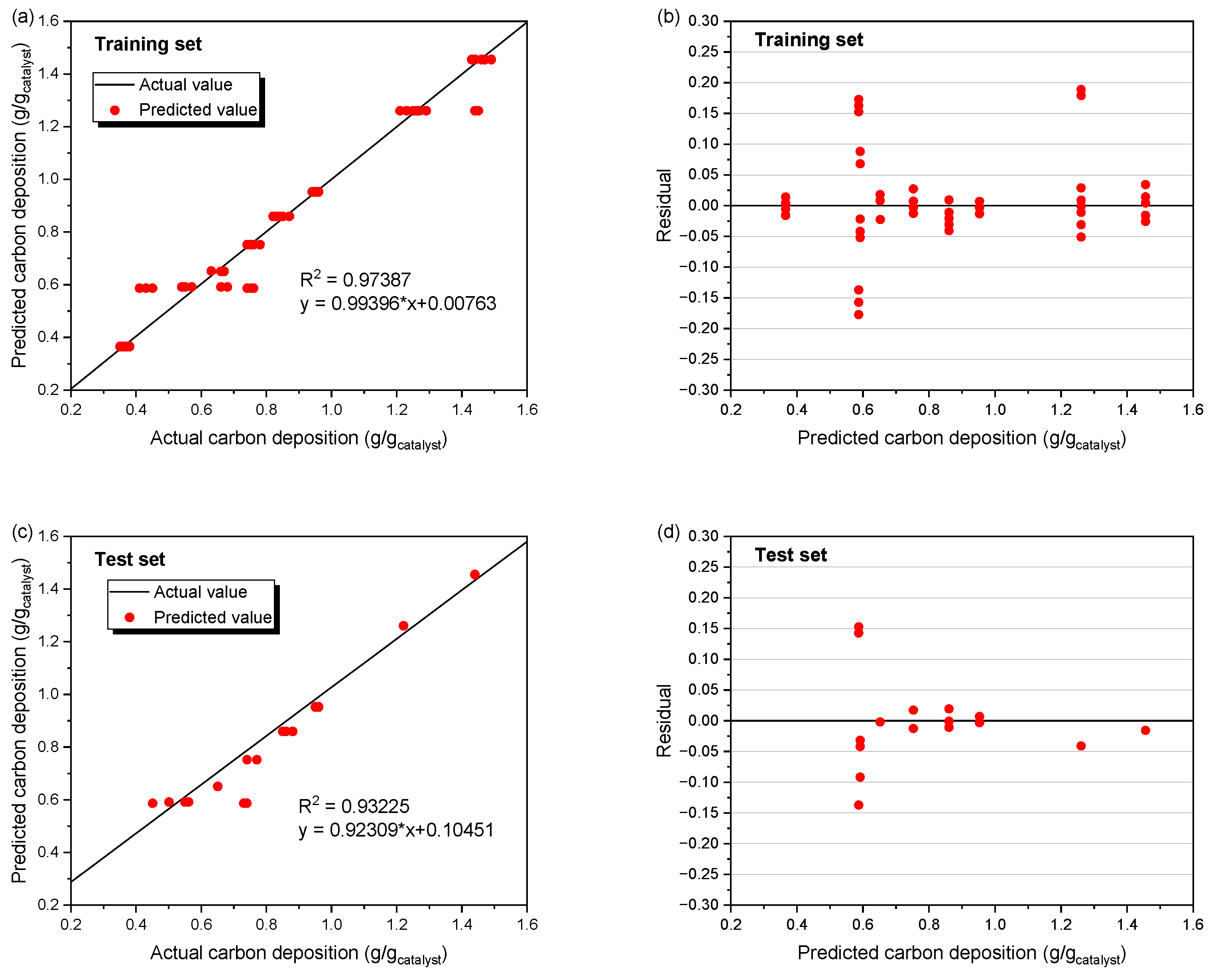
3.2. Predictive Performance of the BP Neural Network
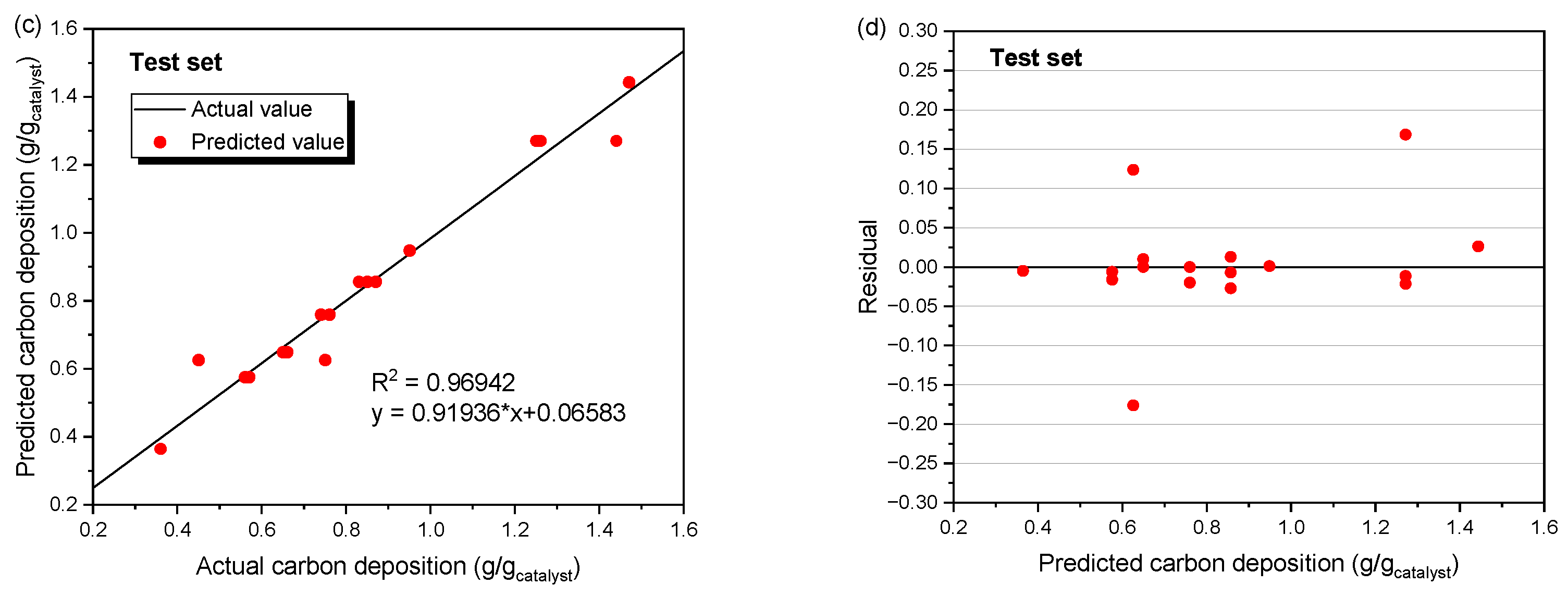
3.3. Predictive Performance of the RBF Neural Network
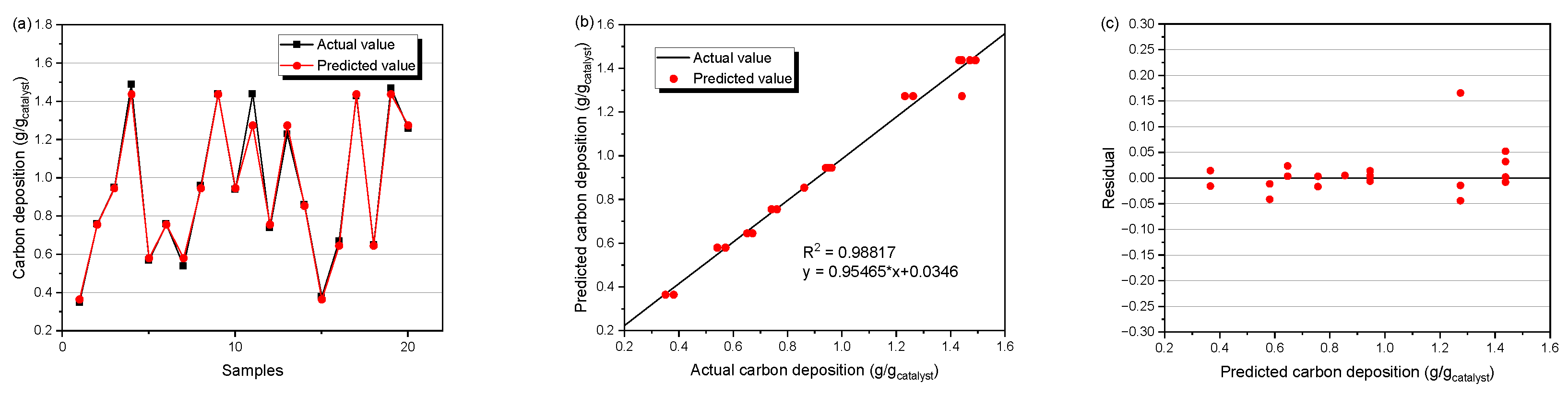
3.4. Prediction Performance of the RBF-IMP Model
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network |
| BP | Backpropagation |
| CFD | Computational fluid dynamics |
| DRM | Dry reforming of methane |
| MSE | Mean squared error |
| RBF | Radial basis function |
| R2 | Coefficient of determination |
References
- Liu, Z.; Deng, Z.; Davis, S.J.; Ciais, P. Global carbon emissions in 2023. Nat. Rev. Earth Environ. 2024, 5, 253–254. [Google Scholar] [CrossRef]
- Mohammed, S.; Eljack, F.; Al-Sobhi, S.; Kazi, M.-K. A systematic review: The role of emerging carbon capture and conversion technologies for energy transition to clean hydrogen. J. Clean. Prod. 2024, 447, 141506. [Google Scholar] [CrossRef]
- Wang, Z.; Mei, Z.; Wang, L.; Wu, Q.; Xia, C.; Li, S.; Wang, T.; Liu, C. Insight into the activity of Ni-based thermal catalysts for dry reforming of methane. J. Mater. Chem. A 2024, 12, 24802–24838. [Google Scholar] [CrossRef]
- Nguyen, D.L.T.; Vy Tran, A.; Vo, D.-V.N.; Tran Nguyen, H.; Rajamohan, N.; Trinh, T.H.; Nguyen, T.L.; Le, Q.V.; Nguyen, T.M. Methane dry reforming: A catalyst challenge awaits. J. Ind. Eng. Chem. 2024, 140, 169–189. [Google Scholar] [CrossRef]
- Arora, S.; Prasad, R. An overview on dry reforming of methane: Strategies to reduce carbonaceous deactivation of catalysts. RSC Adv. 2016, 6, 108668–108688. [Google Scholar] [CrossRef]
- Vogt, E.T.C.; Fu, D.; Weckhuysen, B.M. Carbon Deposit Analysis in Catalyst Deactivation, Regeneration, and Rejuvenation. Angew. Chem. Int. Ed. 2023, 62, e202300319. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, B.; Abd Ghani, N.A.; Vo, D.-V.N. Recent advances in dry reforming of methane over Ni-based catalysts. J. Clean. Prod. 2017, 162, 170–185. [Google Scholar] [CrossRef]
- Toyao, T.; Maeno, Z.; Takakusagi, S.; Kamachi, T.; Takigawa, I.; Shimizu, K.-I. Machine Learning for Catalysis Informatics: Recent Applications and Prospects. ACS Catal. 2019, 10, 2260–2297. [Google Scholar] [CrossRef]
- Aklilu, E.G.; Bounahmidi, T. Machine learning applications in catalytic hydrogenation of carbon dioxide to methanol: A comprehensive review. Int. J. Hydrogen Energy 2024, 61, 578–602. [Google Scholar] [CrossRef]
- Ayodele, B.V.; Khan, M.R.; Nooruddin, S.S.; Cheng, C.K. Modelling and optimization of syngas production by methane dry reforming over samarium oxide supported cobalt catalyst: Response surface methodology and artificial neural networks approach. Clean Technol. Environ. Policy 2016, 19, 1181–1193. [Google Scholar] [CrossRef]
- Alotaibi, F.N.; Berrouk, A.S.; Saeed, M. Optimization of Yield and Conversion Rates in Methane Dry Reforming Using Artificial Neural Networks and the Multiobjective Genetic Algorithm. Ind. Eng. Chem. Res. 2023, 62, 17084–17099. [Google Scholar] [CrossRef]
- Gendy, T.S.; El-Salamony, R.A.; Alrashed, M.M.; Bentalib, A.; Osman, A.I.; Kumar, R.; Fakeeha, A.H.; Al-Fatesh, A.S. Enhanced predictive optimization of methane dry reforming via ResponseSurface methodology and artificial neural network approaches: Insights using a novel nickel-strontium-zirconium-aluminum catalyst. Mol. Catal. 2024, 562, 114216. [Google Scholar] [CrossRef]
- Rahman, M.H.; Biswas, M. Modeling of Dry Reforming of Methane Using Artificial Neural Networks. Hydrogen 2024, 5, 800–818. [Google Scholar] [CrossRef]
- Ameen, S.; Farooq, M.U.; Samia; Umer, S.; Abrar, A.; Hussnain, S.; Saeed, F.; Memon, M.A.; Ajmal, M.; Umer, M.A.; et al. Catalyst breakthroughs in methane dry reforming: Employing machine learning for future advancements. Int. J. Hydrogen Energy 2025, 141, 406–443. [Google Scholar] [CrossRef]
- Alsaffar, M.A.; Ayodele, B.V.; Mustapa, S.I. Scavenging carbon deposition on alumina supported cobalt catalyst during renewable hydrogen-rich syngas production by methane dry reforming using artificial intelligence modeling technique. J. Clean. Prod. 2020, 247, 119168. [Google Scholar] [CrossRef]
- Marcot, B.G.; Hanea, A.M. What is an optimal value of k in k-fold cross-validation in discrete Bayesian network analysis? Comput. Stat. 2020, 36, 2009–2031. [Google Scholar] [CrossRef]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2009, 21, 137–146. [Google Scholar] [CrossRef]




| Number | CH4/CO2 Molar Ratio | N2 Flow Rate (mL/min) | Temperature (°C) | Carbon Deposition (g/gcatalyst) |
|---|---|---|---|---|
| 1 | 1.25 | 10 | 750 | 1.47 |
| 2 | 5 | 10 | 750 | 0.94 |
| 3 | 1.25 | 10 | 650 | 0.76 |
| 4 | 5 | 10 | 650 | 0.43 |
| 5 | 1.25 | 10 | 750 | 1.43 |
| 6 | 3.13 | 25 | 700 | 0.67 |
| 7 | 5 | 10 | 650 | 0.75 |
| 8 | 1.25 | 10 | 750 | 1.43 |
| 9 | 5 | 40 | 750 | 0.83 |
| 10 | 1.25 | 40 | 650 | 0.68 |
| 11 | 5 | 10 | 650 | 0.45 |
| 12 | 1.25 | 40 | 750 | 1.21 |
| 13 | 5 | 10 | 750 | 0.95 |
| 14 | 5 | 10 | 650 | 0.41 |
| 15 | 1.25 | 10 | 750 | 1.49 |
| 16 | 1.25 | 40 | 750 | 1.23 |
| 17 | 1.25 | 40 | 650 | 0.5 |
| 18 | 3.13 | 25 | 700 | 0.65 |
| 19 | 5 | 10 | 750 | 0.94 |
| 20 | 5 | 10 | 650 | 0.45 |
| 21 | 5 | 40 | 750 | 0.82 |
| 22 | 1.25 | 10 | 750 | 1.44 |
| 23 | 1.25 | 40 | 750 | 1.22 |
| 24 | 5 | 10 | 750 | 0.96 |
| 25 | 5 | 40 | 750 | 0.84 |
| 26 | 1.25 | 10 | 650 | 0.78 |
| 27 | 1.25 | 40 | 650 | 0.57 |
| 28 | 5 | 40 | 750 | 0.85 |
| 29 | 1.25 | 10 | 750 | 1.44 |
| 30 | 5 | 10 | 650 | 0.74 |
| 31 | 1.25 | 40 | 750 | 1.23 |
| 32 | 1.25 | 10 | 750 | 1.46 |
| 33 | 1.25 | 10 | 750 | 1.43 |
| 34 | 1.25 | 40 | 650 | 0.66 |
| 35 | 1.25 | 40 | 650 | 0.55 |
| 36 | 5 | 40 | 650 | 0.35 |
| 37 | 1.25 | 10 | 750 | 1.43 |
| 38 | 5 | 40 | 750 | 0.87 |
| 39 | 5 | 10 | 750 | 0.94 |
| 40 | 3.125 | 25 | 700 | 0.63 |
| 41 | 1.25 | 10 | 650 | 0.77 |
| 42 | 5 | 10 | 650 | 0.73 |
| 43 | 5 | 40 | 650 | 0.36 |
| 44 | 5 | 40 | 750 | 0.88 |
| 45 | 1.25 | 10 | 650 | 0.76 |
| 46 | 1.25 | 40 | 650 | 0.54 |
| 47 | 3.13 | 25 | 700 | 0.65 |
| 48 | 5 | 10 | 750 | 0.94 |
| 49 | 1.25 | 10 | 650 | 0.74 |
| 50 | 1.25 | 10 | 650 | 0.76 |
| 51 | 1.25 | 40 | 750 | 1.25 |
| 52 | 5 | 40 | 650 | 0.37 |
| 53 | 1.25 | 40 | 750 | 1.26 |
| 54 | 1.25 | 40 | 650 | 0.56 |
| 55 | 1.25 | 40 | 650 | 0.57 |
| 56 | 5 | 40 | 650 | 0.35 |
| 57 | 5 | 40 | 750 | 0.87 |
| 58 | 1.25 | 10 | 650 | 0.74 |
| 59 | 1.25 | 40 | 750 | 1.27 |
| 60 | 5 | 40 | 750 | 0.88 |
| 61 | 5 | 10 | 650 | 0.74 |
| 62 | 5 | 40 | 650 | 0.36 |
| 63 | 5 | 40 | 750 | 0.85 |
| 64 | 5 | 40 | 650 | 0.37 |
| 65 | 5 | 10 | 650 | 0.75 |
| 66 | 1.25 | 40 | 650 | 0.55 |
| 67 | 5 | 40 | 650 | 0.36 |
| 68 | 1.25 | 10 | 650 | 0.75 |
| 69 | 5 | 10 | 650 | 0.76 |
| 70 | 1.25 | 40 | 750 | 1.29 |
| 71 | 5 | 10 | 750 | 0.95 |
| 72 | 5 | 40 | 650 | 0.37 |
| 73 | 5 | 10 | 750 | 0.96 |
| 74 | 5 | 40 | 750 | 0.86 |
| 75 | 1.25 | 10 | 750 | 1.47 |
| 76 | 1.25 | 40 | 650 | 0.56 |
| 77 | 5 | 10 | 750 | 0.95 |
| 78 | 1.25 | 40 | 750 | 1.44 |
| 79 | 1.25 | 40 | 750 | 1.45 |
| 80 | 5 | 10 | 750 | 0.96 |
| 81 | 5 | 40 | 650 | 0.38 |
| 82 | 1.25 | 10 | 650 | 0.74 |
| 83 | 3.13 | 25 | 700 | 0.66 |
| 84 | 1.25 | 10 | 650 | 0.76 |
| 85 | 5 | 40 | 650 | 0.37 |
| Input layer | Input parameters | Temperature, N2 flow rate, CH4/CO2 ratio |
| Node number | 3 | |
| Hidden layer | Layer | 1 |
| Node number | 5 | |
| Activation function | Hyperbolic tangent function | |
| Training algorithm | Levenberg–Marquardt | |
| Output layer | Output parameters | Carbon deposition |
| Node number | 1 | |
| Activation function | Linear transfer function | |
| Error function | Mean squared error (MSE) |
| Input layer | Input parameters | Temperature, N2 flow rate, CH4/CO2 ratio |
| Node number | 3 | |
| Hidden layer | Layer | 1 |
| Maximum node number | 65 | |
| Target error | 0.001 | |
| Activation function | Gaussian basis function | |
| Output layer | Output parameters | Carbon deposition |
| Node number | 1 | |
| Activation function | Linear transfer function | |
| Error function | Mean squared error (MSE) |
| BP | RBF | RBF-Imp | |
|---|---|---|---|
| MSE | 0.0063 | 0.0050 | 0.0018 |
| R2 | 0.9426 | 0.9471 | 0.9882 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Zhou, T.; Xu, Z.; Hu, X.; Zhang, M.; Yang, H. Energy-Efficient Prediction of Carbon Deposition in DRM Processes Through Optimized Neural Network Modeling. Energies 2025, 18, 3172. https://doi.org/10.3390/en18123172
Fang R, Zhou T, Xu Z, Hu X, Zhang M, Yang H. Energy-Efficient Prediction of Carbon Deposition in DRM Processes Through Optimized Neural Network Modeling. Energies. 2025; 18(12):3172. https://doi.org/10.3390/en18123172
Chicago/Turabian StyleFang, Rui, Tuo Zhou, Zhuangzhuang Xu, Xiannan Hu, Man Zhang, and Hairui Yang. 2025. "Energy-Efficient Prediction of Carbon Deposition in DRM Processes Through Optimized Neural Network Modeling" Energies 18, no. 12: 3172. https://doi.org/10.3390/en18123172
APA StyleFang, R., Zhou, T., Xu, Z., Hu, X., Zhang, M., & Yang, H. (2025). Energy-Efficient Prediction of Carbon Deposition in DRM Processes Through Optimized Neural Network Modeling. Energies, 18(12), 3172. https://doi.org/10.3390/en18123172








