Systemic Scaling of Powertrain Models with Youla and H∞ Driver Control
Abstract
1. Introduction
1.1. Literature Review
1.2. Powertrain Model
1.3. Dimensional Analysis
1.4. Control Methods
2. Scaling Method
- 1.
- List equations that define the behavior of the model.
- 2.
- Begin determining what variables and parameters will be scaled.
- 3.
- Determine the scaling relationship for each equation.
- 4.
- Develop the complete list of scaled variables while performing the previous step.
- 5.
- Check for relationships that over-constrain the scaling system and decide which scaling factors are to be considered the “independent” factors input to the system.
Simple Example
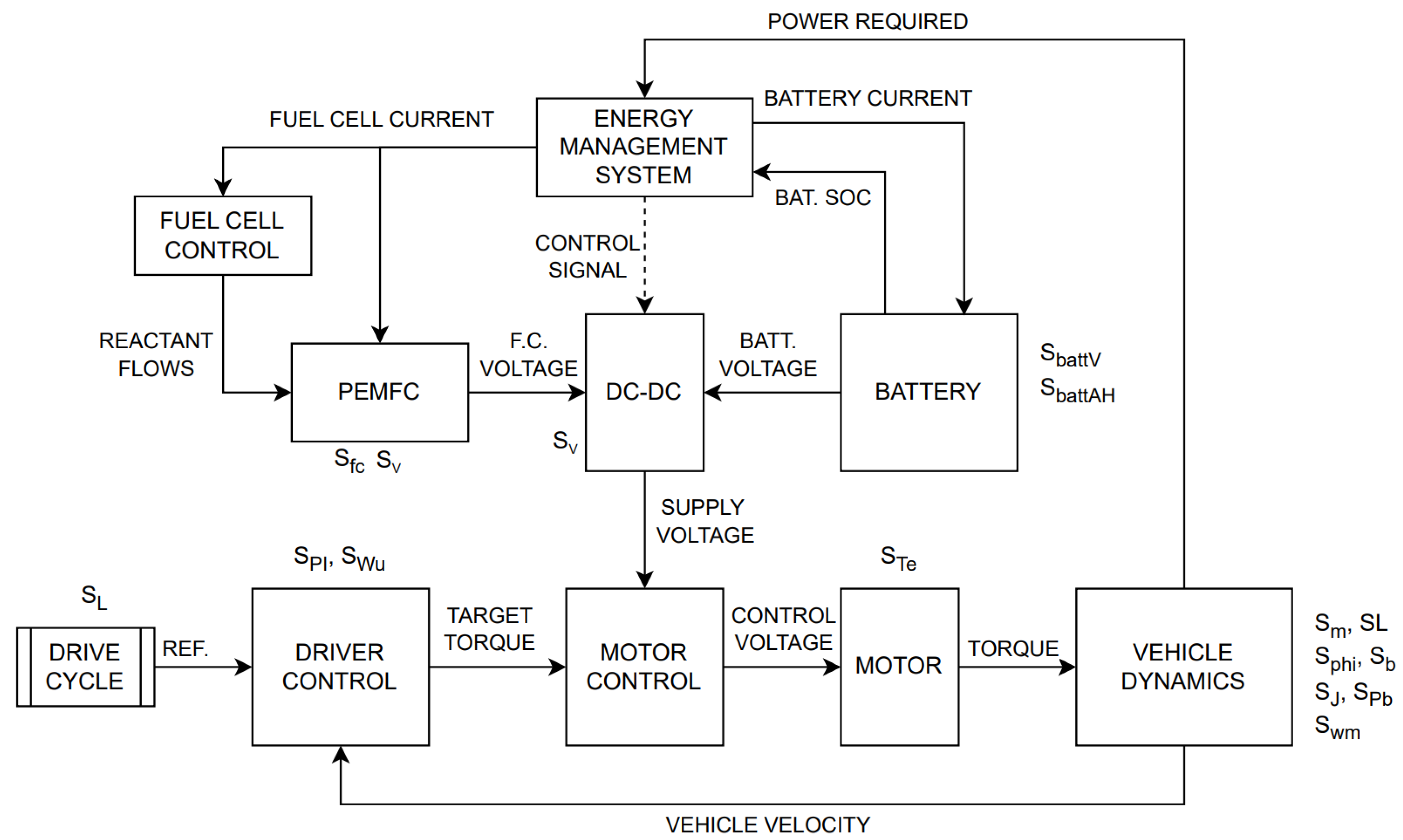
3. System Modeling
3.1. Step 1: Governing Equations
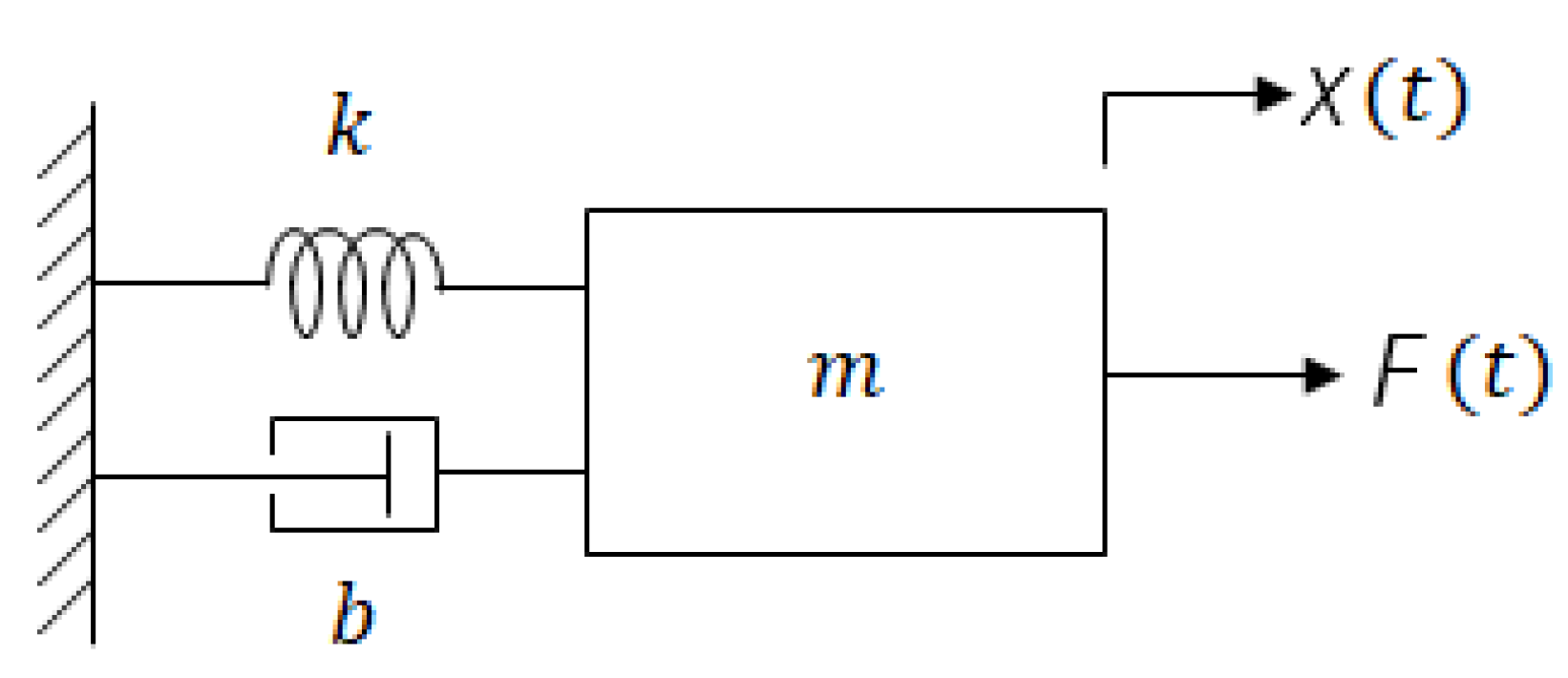
3.1.1. Vehicle Dynamics
3.1.2. Controller Dynamics
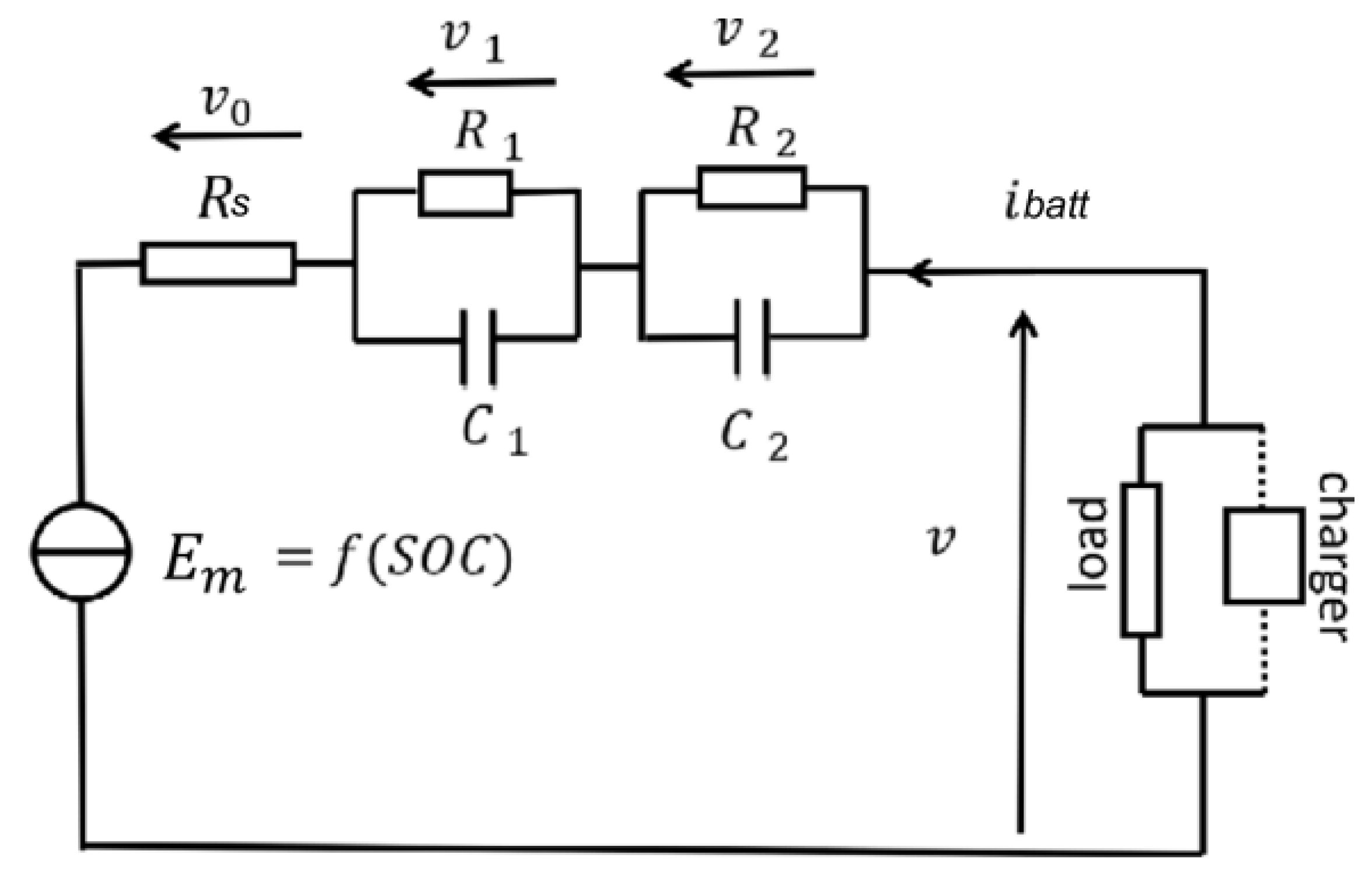
3.1.3. Electrical Dynamics
3.2. Step 2: Determine the Scaling Variables
- The vehicle velocity, acceleration, reference velocity, and tracking error all have the same length scaling factor .
- The vehicle size parameters, such as the wheel radius, share the length scaling factor used for velocity.
- —vehicle and drive cycle length;
- —energy/power of vehicle system;
- —force at the wheel;
- —vehicle mass;
- —drag force;
- —torque at the wheel;
- —torque at the motor;
- —gear ratio;
- —motor to wheel efficiency;
- —motor moment of inertia;
- —motor angular velocity;
- —motor friction;
- —braking torque;
- —brake disc pressure;
- —PI controller gains;
- — weighting;
- —system and fuel cell voltage;
- —fuel cell current;
- —fuel cell stack size;
- —fuel cell closed-loop voltage-current ratio dynamics;
- —battery voltage;
- —battery capacity.
3.3. Step 3: Develop Scaling Relationships
3.3.1. Vehicle Scaling
3.3.2. Controller Scaling
3.3.3. Electrical Scaling
3.4. Step 4: Complete List
3.5. Step 5: Resolve Constraints and Choose Independent Scalings
- —vehicle and drive cycle length;
- —energy/power of vehicle system;
- —gear ratio;
- —motor to wheel efficiency;
- —voltage.
3.6. Nonlinearities and Simulation Difficulties
4. Controller Design
- —plant transfer function.
- —controller transfer function.
- —open-loop transfer function/return ratio, represents open-loop system response to reference input.
- —complementary sensitivity transfer function, relates to closed-loop reference tracking relative to reference input.
- —sensitivity transfer function, relates to closed-loop disturbance and plant parameter variation sensitivity.
- —Youla transfer function, relates to closed-loop actuator effort relative to reference input.
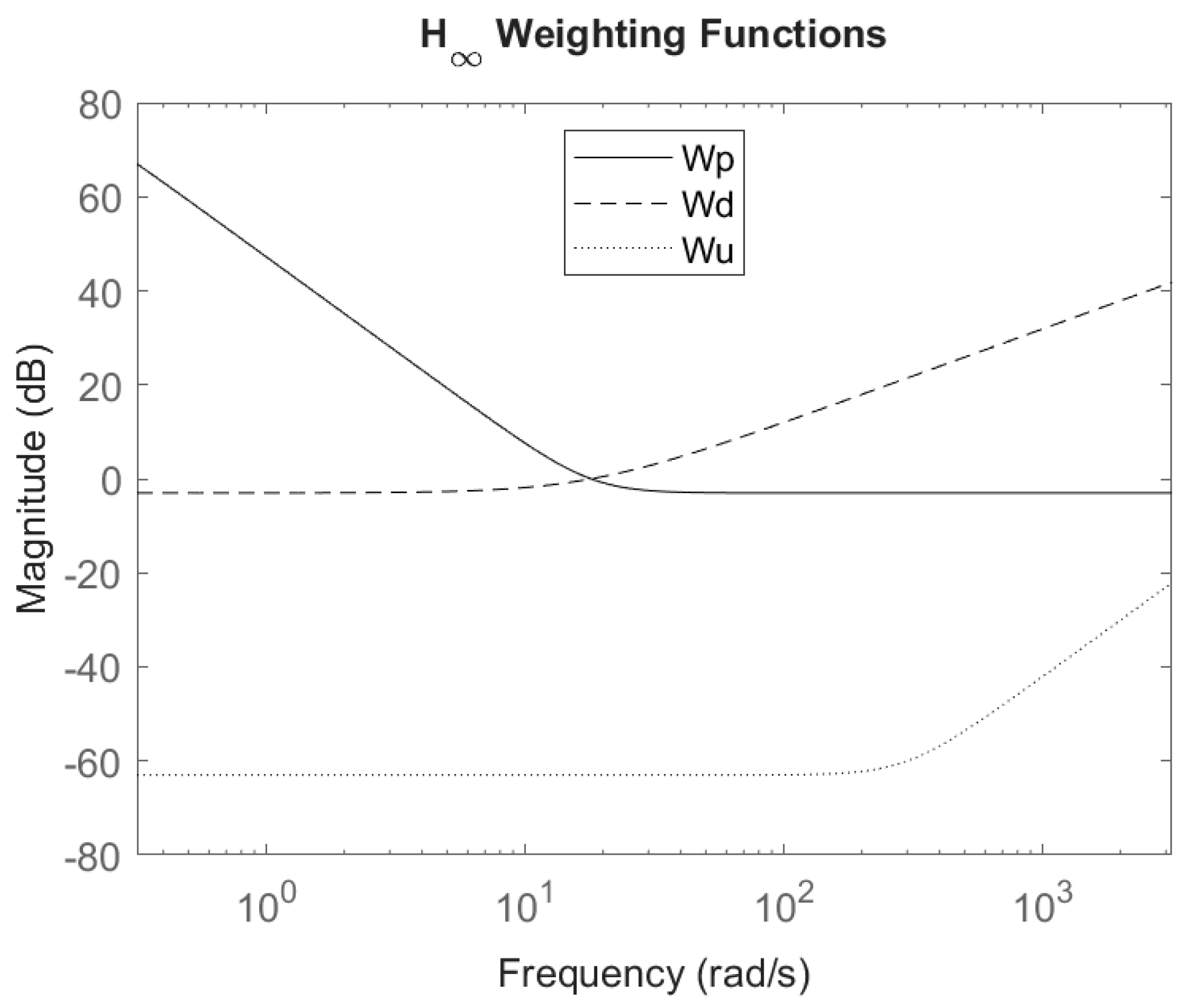
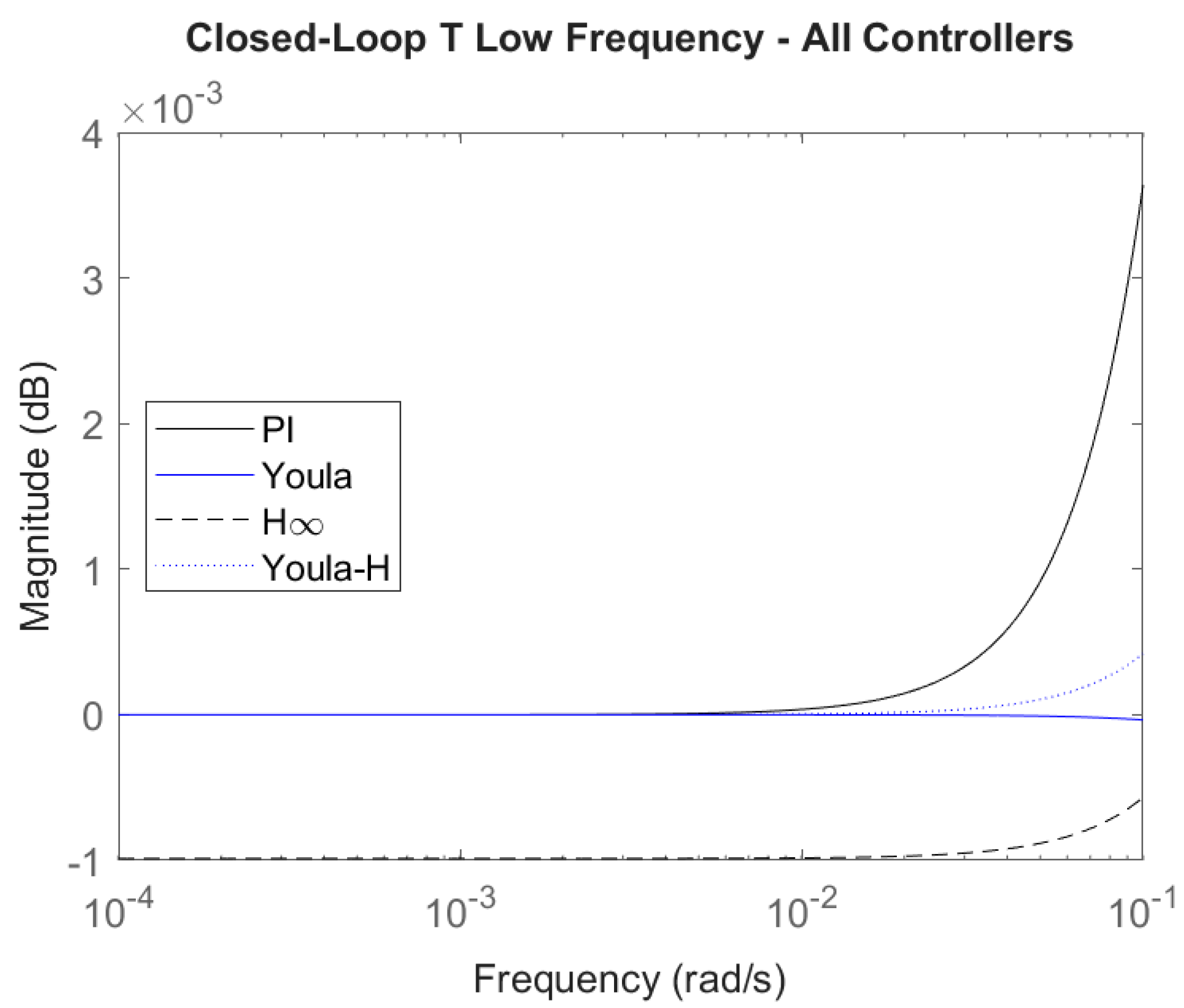
- T is exactly 0 dB in low frequencies to track reference signals and low in high frequencies to attenuate sensor noise.
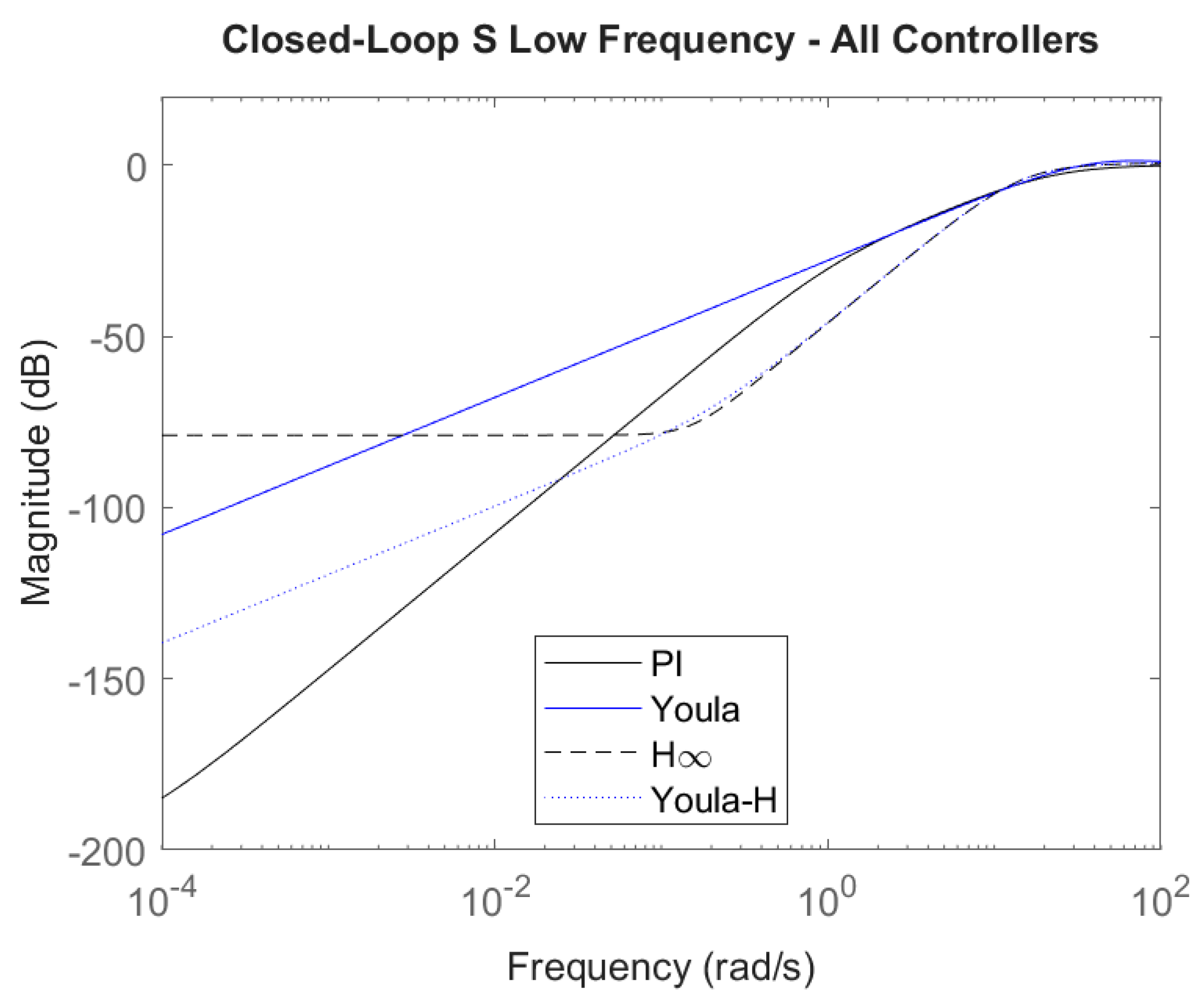
- S is low in low frequencies to attenuate disturbance and parameter variation effects.
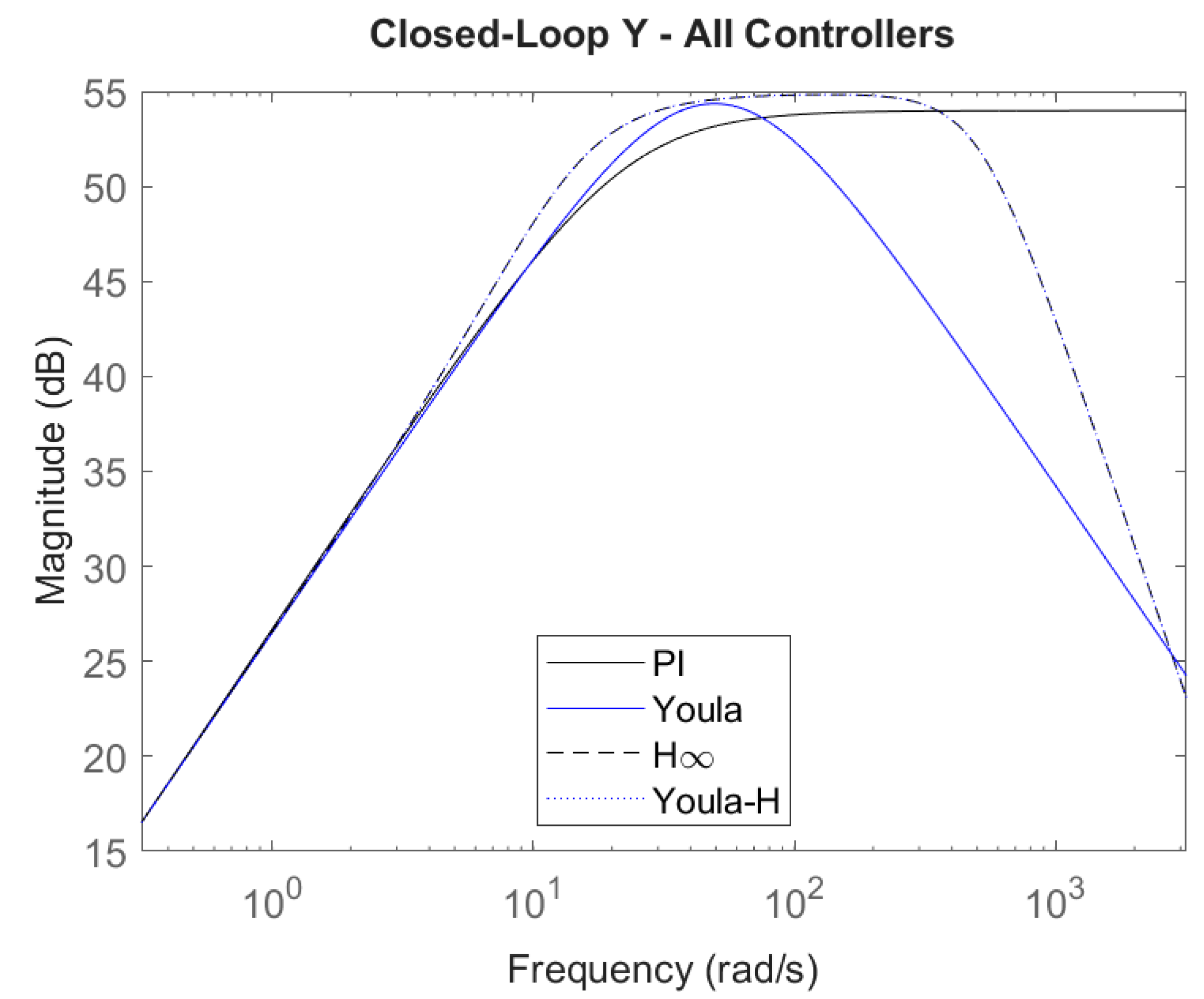
- Y is low in high frequencies to attenuate sensor noise, limiting actuator jitter.
- The maximum magnitude of S is as close to 0 dB as possible, as this relates to system robustness.
- The maximum magnitude of Y is as low as feasible, as this determines the required actuator size.
4.1. Linear Plant Model
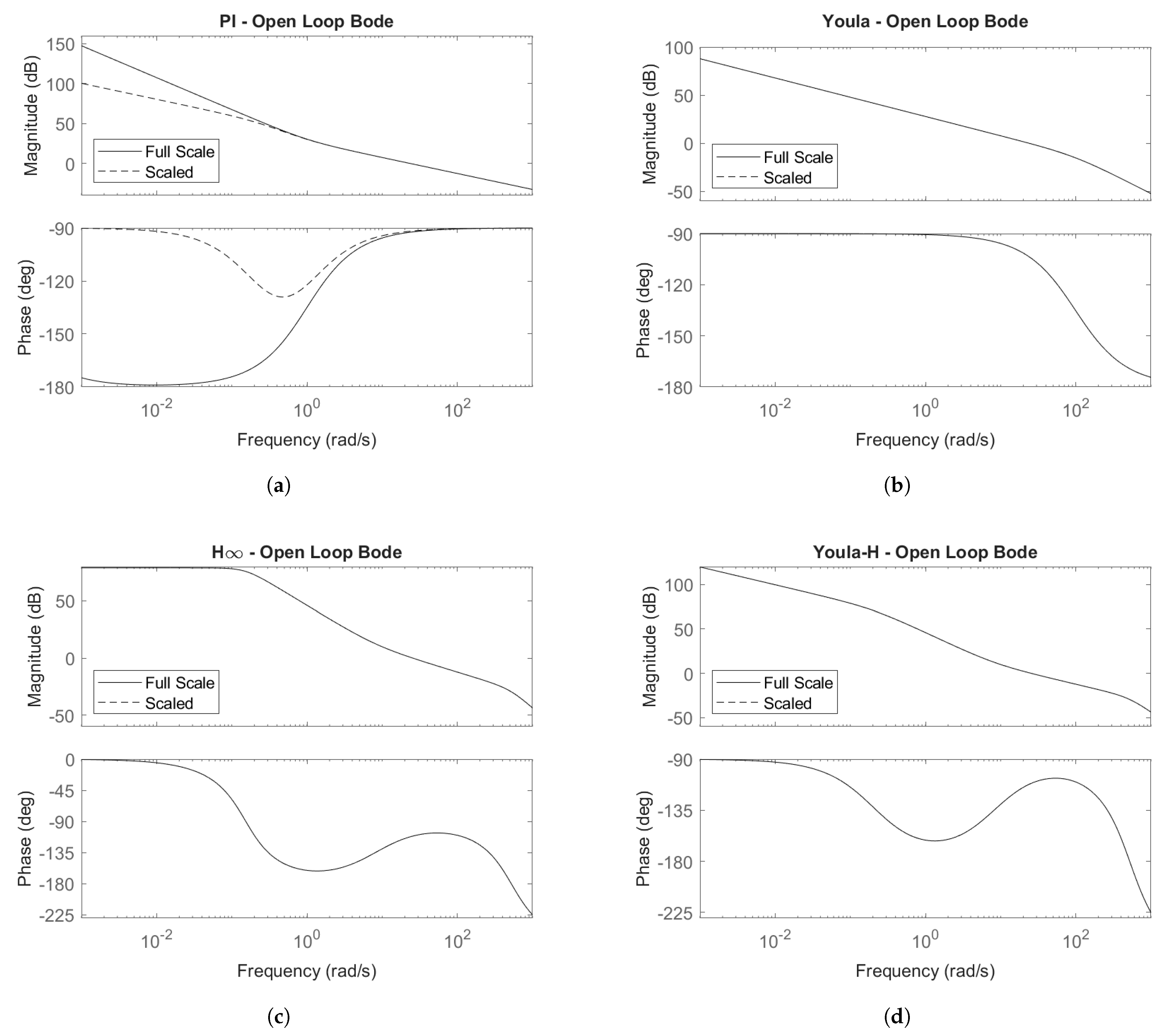
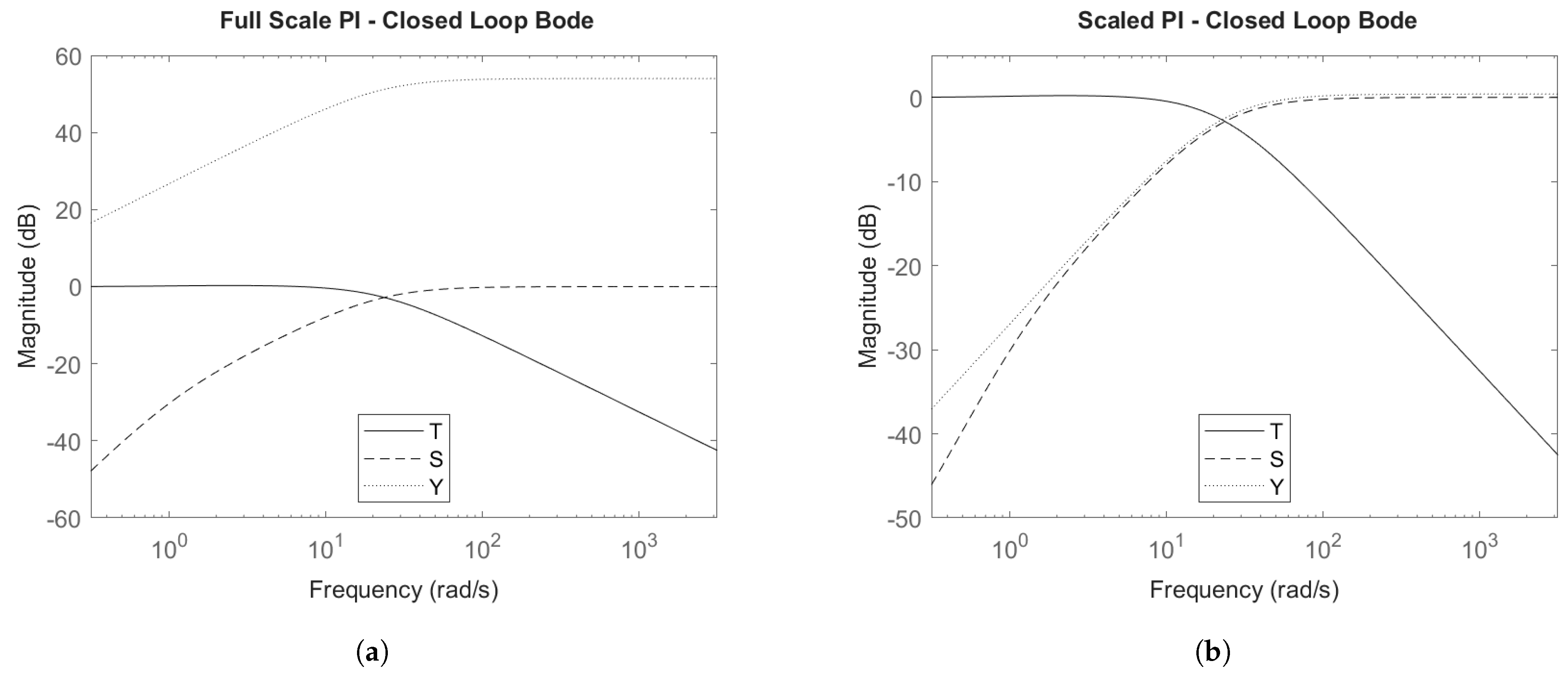
4.2. PI Control
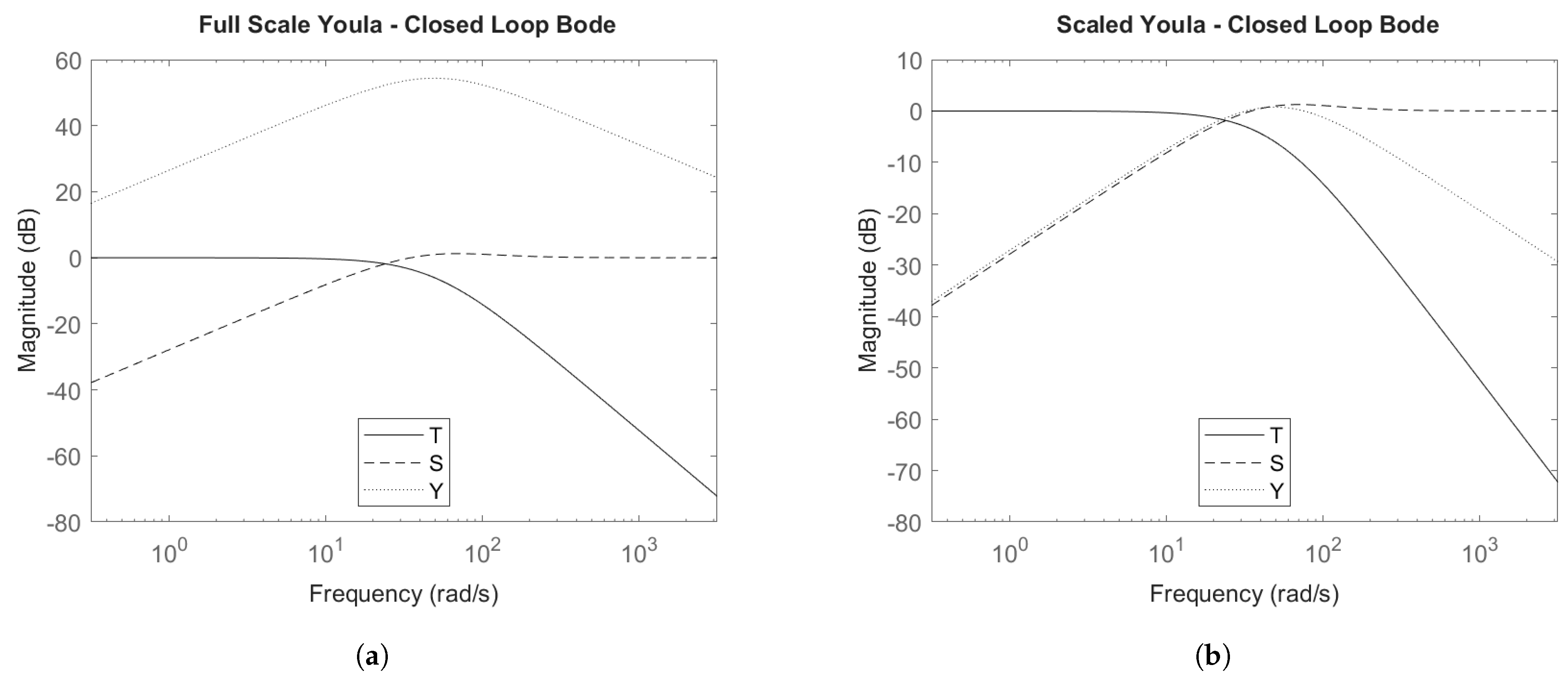
4.3. Youla Control
4.4. Control
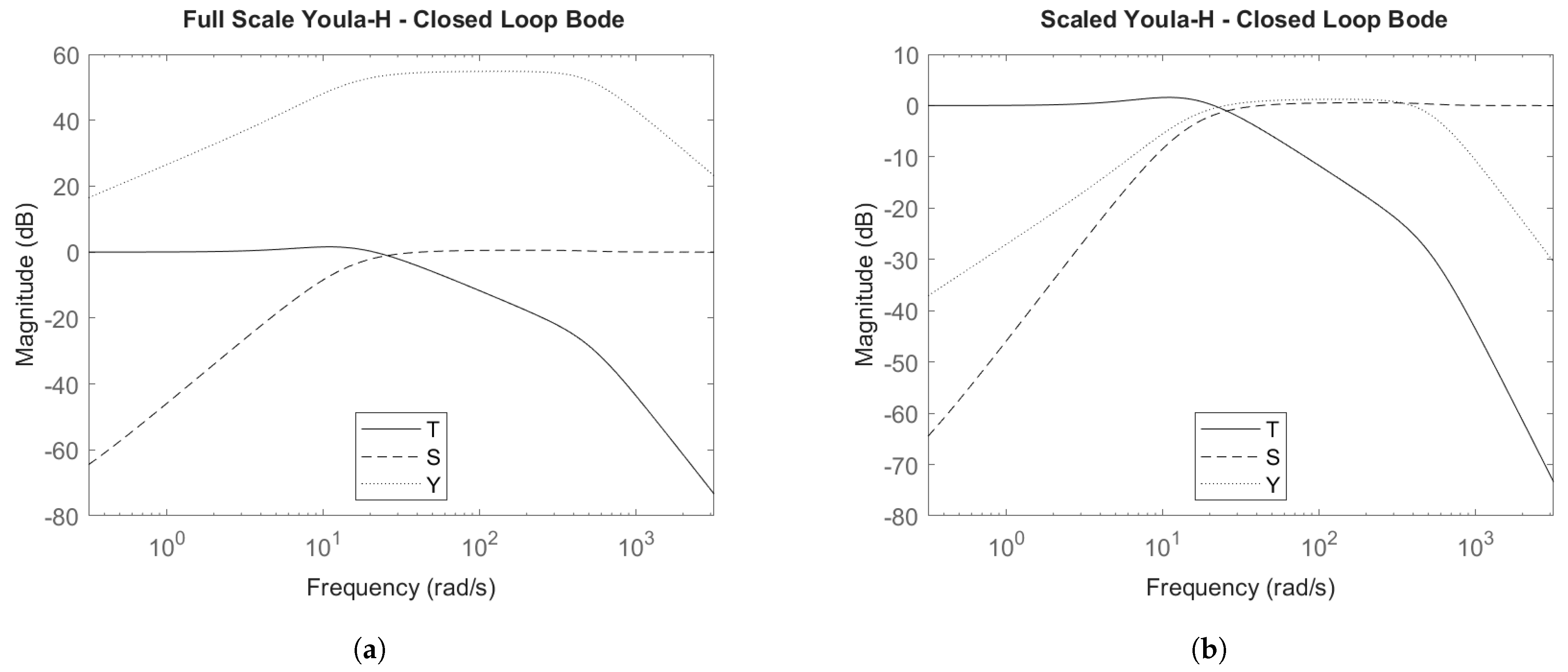
4.5. Hybrid Youla-H Control
4.6. Controller Transfer Function Comparisons
4.6.1. Open-Loop Bode Plots
4.6.2. Closed-Loop Bode Plots
4.6.3. Open-Loop Nyquist Plots
4.7. Controller Implementation
5. Results
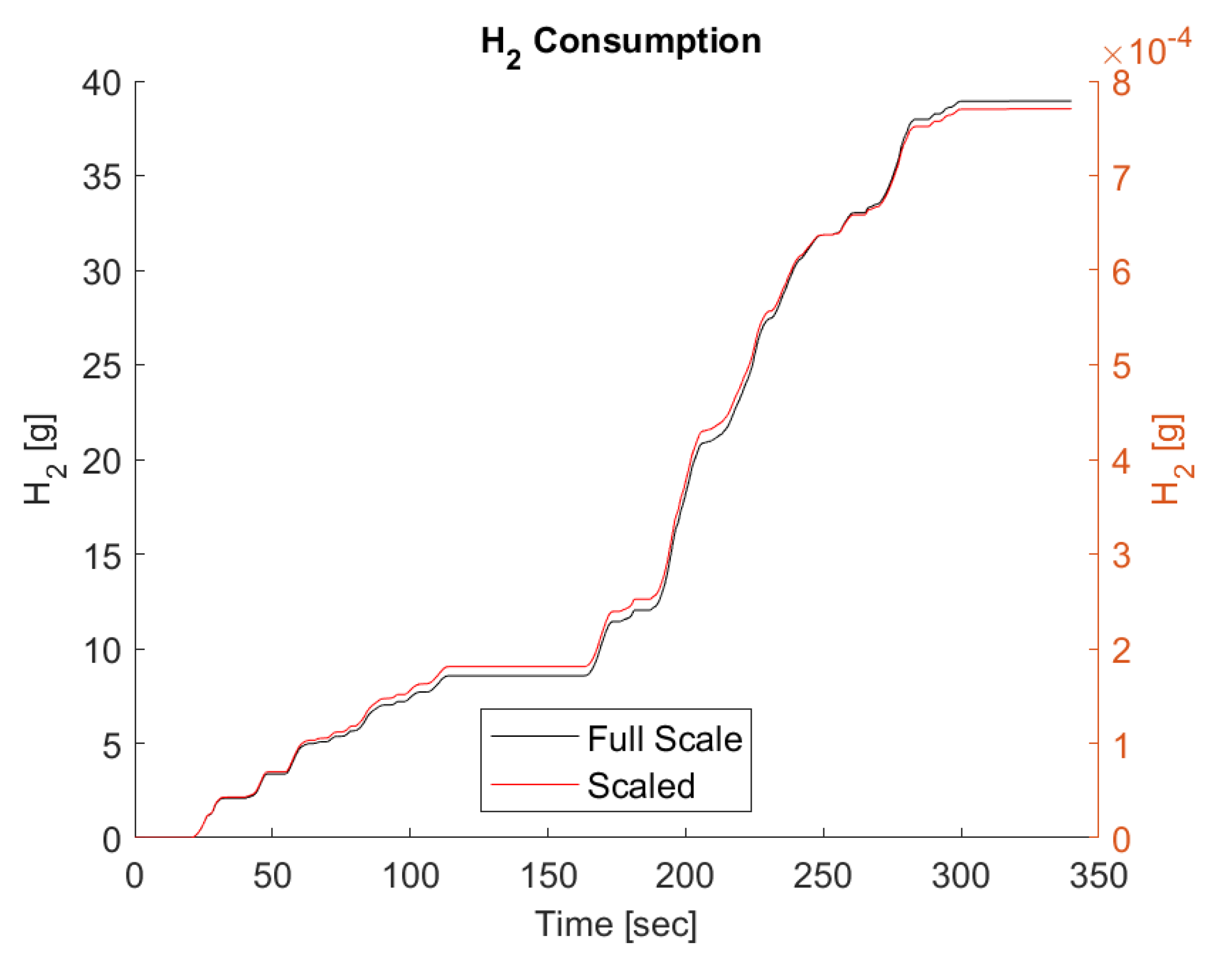
5.1. Fuel Cell Scaling Results
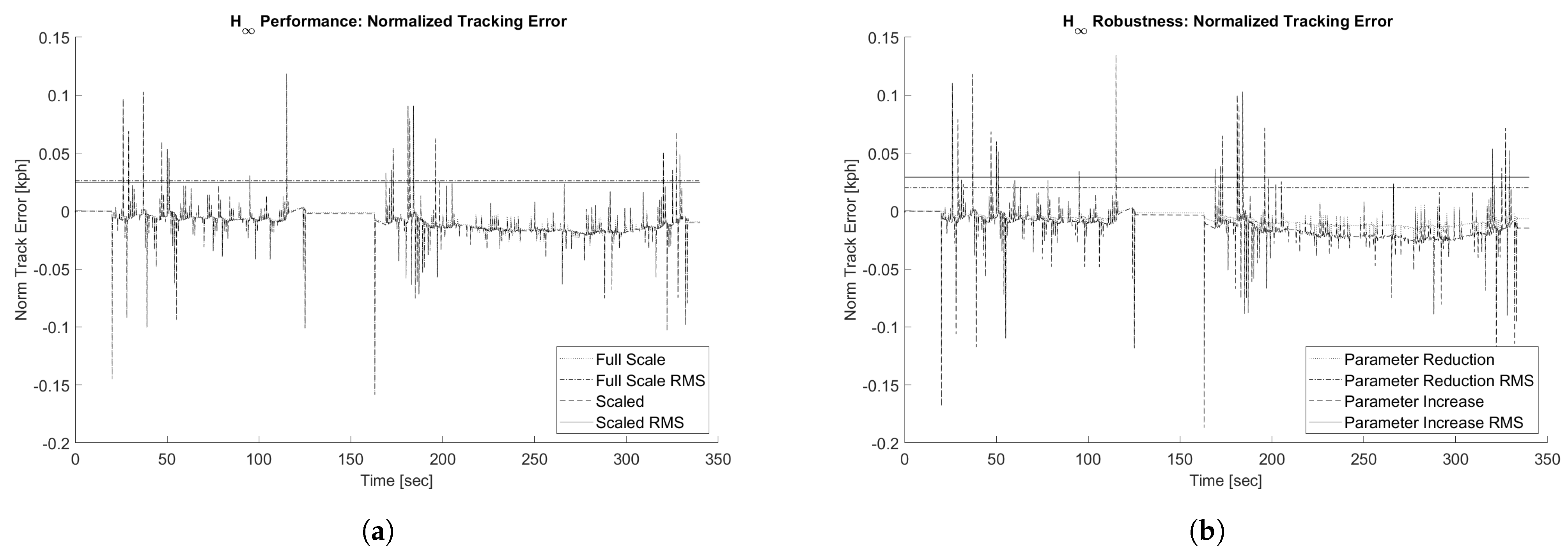
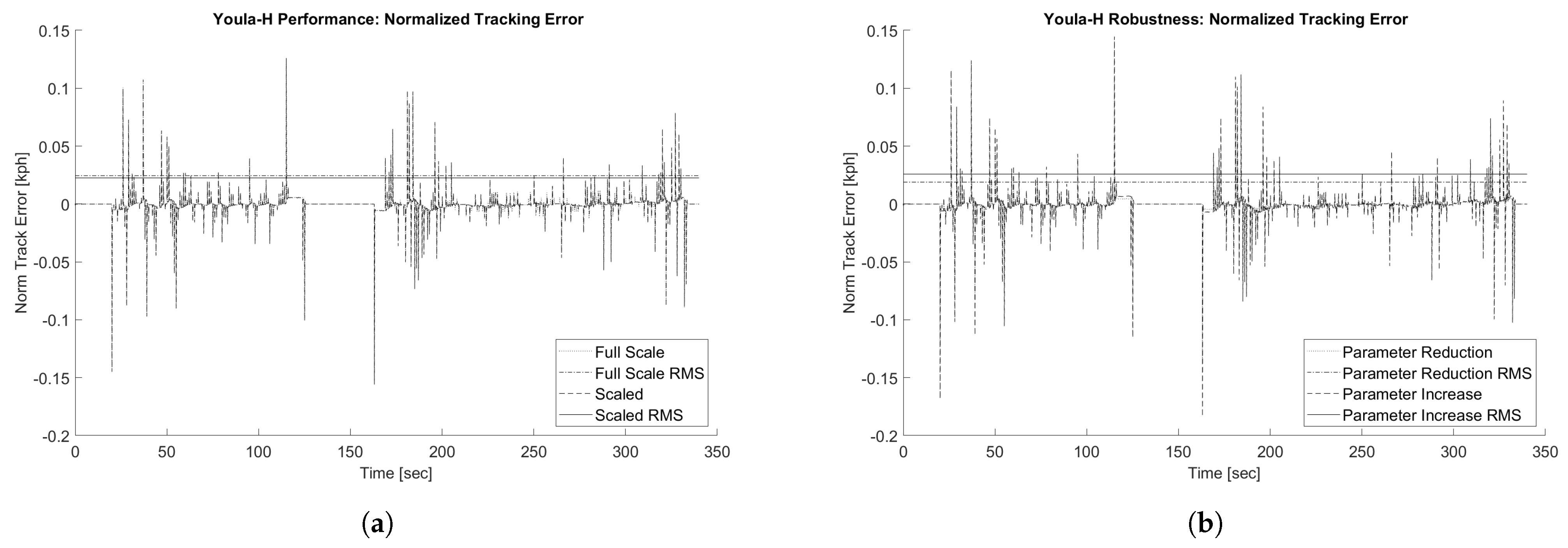
5.2. Tracking Error Results
5.3. Noise and Disturbance Rejection
5.4. Controller Metrics
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| PEMFC | Proton exchange membrane fuel cell |
| FC | Fuel cell |
| PI | Proportional–integral control |
References
- Yadav, S.; Assadian, F. Robust Energy Management of Fuel Cell Hybrid Electric Vehicles Using Fuzzy Logic Integrated with H-Infinity Control. Energies 2025, 18, 2107. [Google Scholar] [CrossRef]
- Hyundai Motor Company. The All-New NEXO. Available online: https://www.hyundai-n.com/en/models/rolling-lab/n-vision-74 (accessed on 30 May 2025).
- Hyundai Motor Company. N Vision 74. Available online: https://www.hyundai.com/worldwide/en/eco/nexo/highlights (accessed on 30 May 2025).
- Fathabadi, H. Combining a proton exchange membrane fuel cell (PEMFC) stack with a Li-ion battery to supply the power needs of a hybrid electric vehicle. Renew. Energy 2019, 130, 714–724. [Google Scholar] [CrossRef]
- Petersheim, M.D.; Brennan, S.N. Scaling of hybrid-electric vehicle powertrain components for Hardware-in-the-loop simulation. Mechatronics 2009, 19, 1078–1090. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth-parameterization based controller tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 6 June 2003; pp. 4989–4996. [Google Scholar] [CrossRef]
- Baek, W.; Song, B.; Song, H. Development of a Longitudinal Vehicle Controller via Hardware-in-the-Loop Simulation. In Proceedings of the ASME 2007 International Mechanical Engineering Congress and Exposition. Volume 16: Transportation Systems, Seattle, WA, USA, 11–15 November 2007; pp. 87–95. [Google Scholar] [CrossRef]
- Qu, T.; Wang, Q.; Cong, Y.; Chen, H. Modeling driver’s longitudinal and lateral control behavior: A moving horizon control modeling scheme. In Proceedings of the 2018 Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 3260–3264. [Google Scholar] [CrossRef]
- Bara’c, B.; Krpan, M.; Capuder, T. Modelling of PEM fuel cell for power system dynamic studies. IEEE Trans. Power Syst. 2024, 39, 3286–3298. [Google Scholar] [CrossRef]
- Hariharan, K.S.; Senthil Kumar, V. A nonlinear equivalent circuit model for lithium ion cells. J. Power Sources 2013, 222, 210–217. [Google Scholar] [CrossRef]
- Pritchard, P.J.; Mitchell, J.W. Fox and McDonald’s Introduction to Fluid Mechanics, 9th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Assadian, F.; Mallon, K.R. Robust Control: Youla Parameterization Approach; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Dehkordi, V.R.; Boulet, B. Robust controller order reduction. Int. J. Control 2011, 84, 985–997. [Google Scholar] [CrossRef]




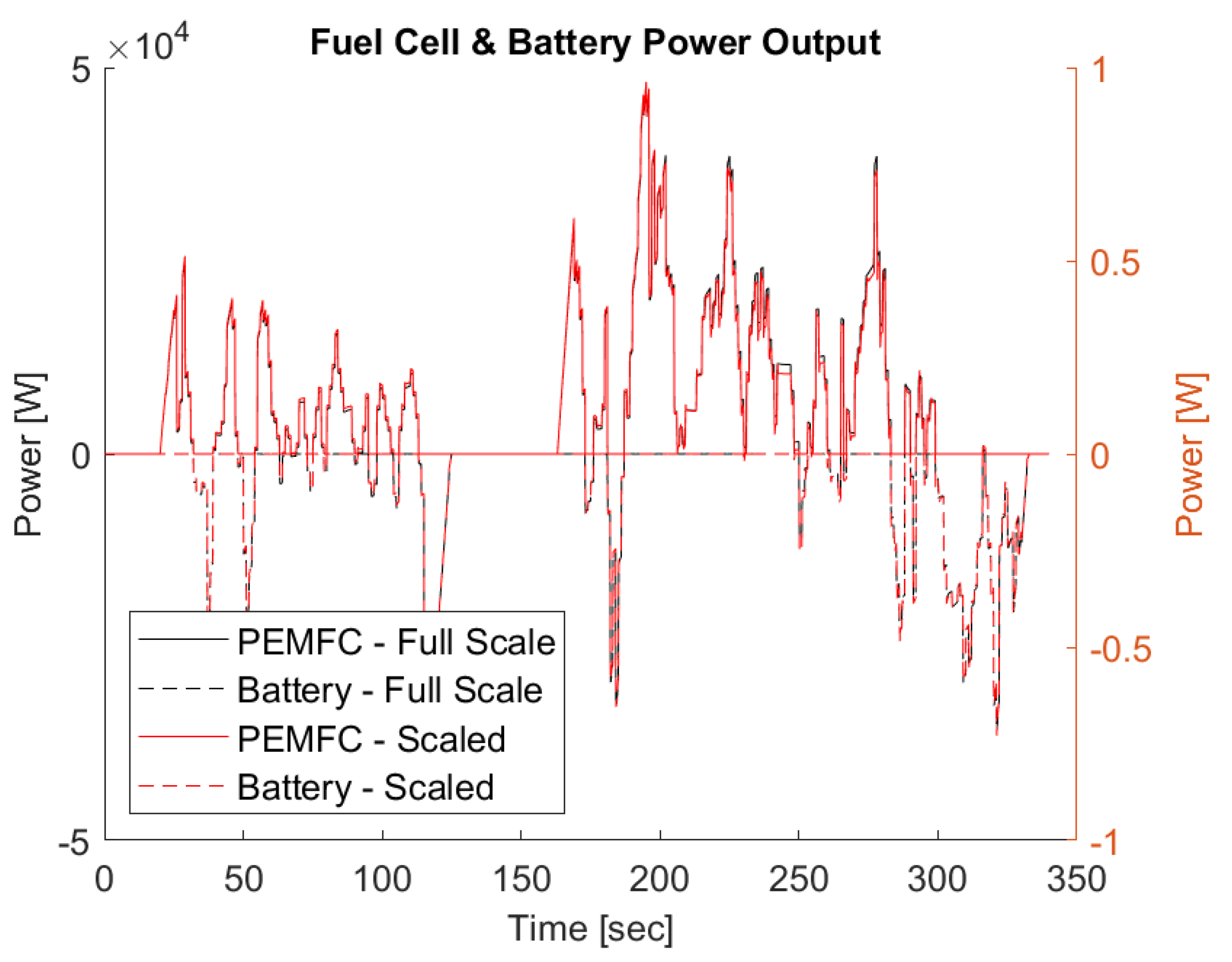
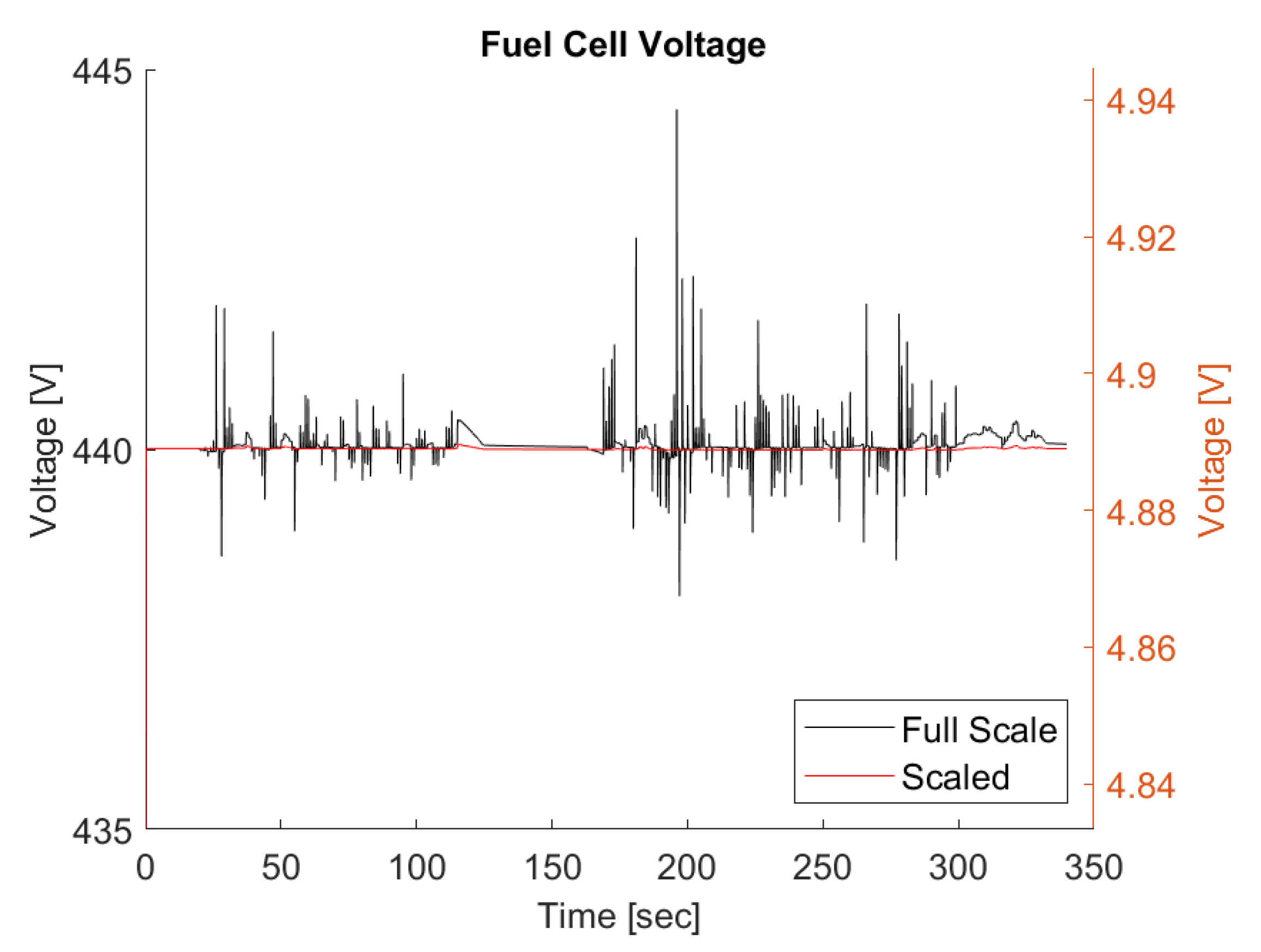
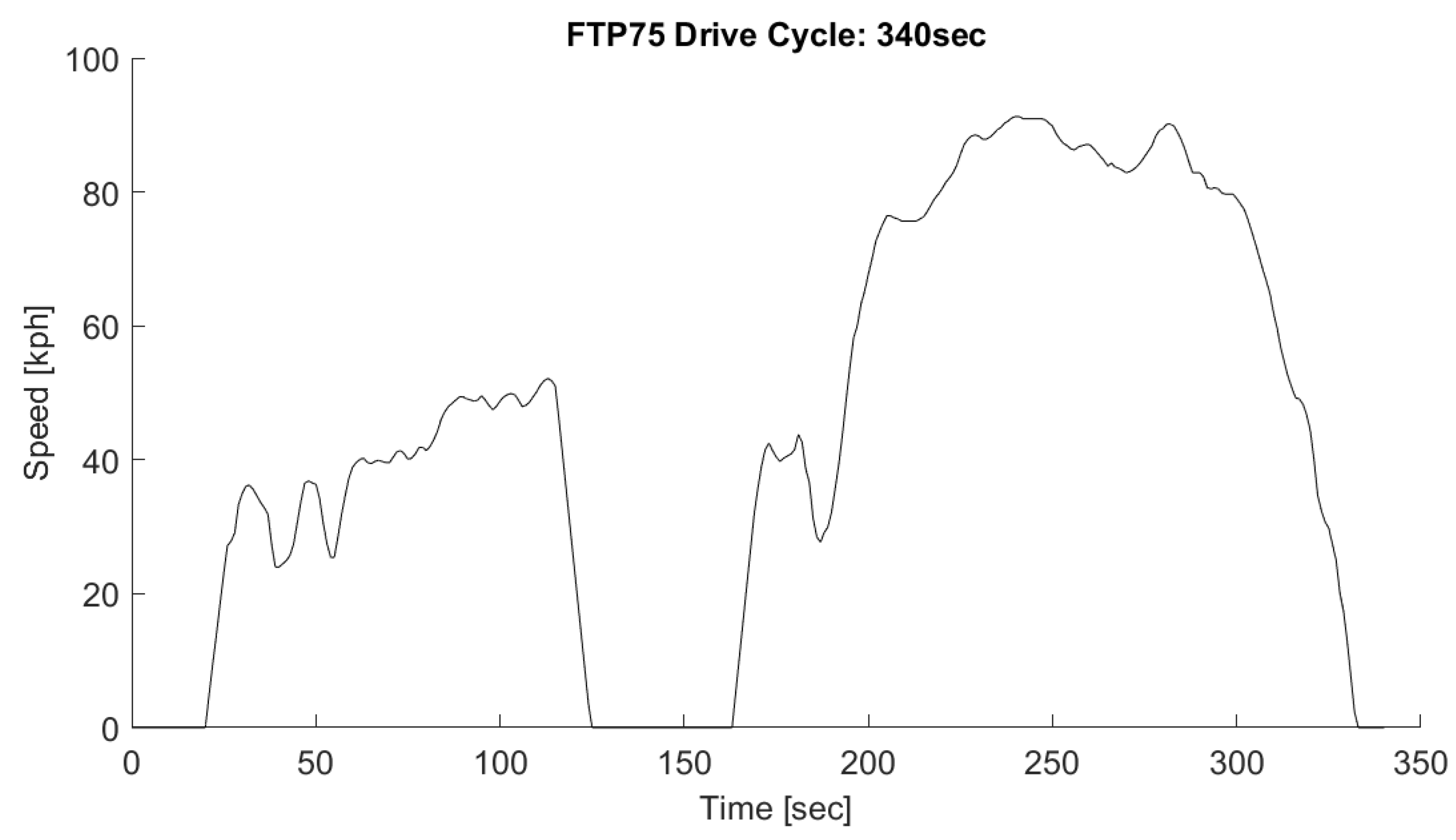

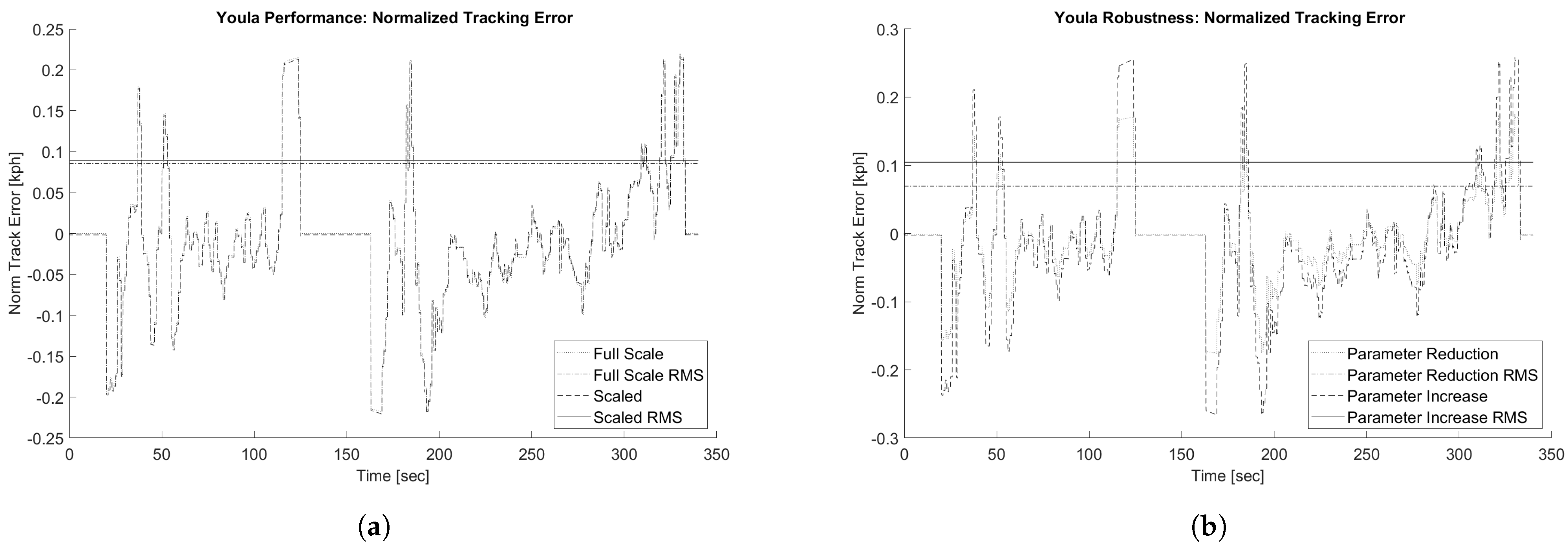

| Parameters | Scaling | Full Scale Value | Scaled Value | Notes |
|---|---|---|---|---|
| Energy | 1:50,000 | - | - | Independent scaling |
| Length | 1:10 | - | - | Independent scaling |
| Gear Ratio | 1:10.453 | 10.453 | 1 | Independent scaling |
| Efficiency | 1:1 | 95% | 95% | Independent scaling |
| Voltage [V] | 8:720 | 720 | 8 | Independent scaling |
| Mass [kg] | 1:500 | 2242 | 4.48 | Vehicle mass |
| Force at Wheel [N] | 1:5000 | - | - | |
| Torque at Wheel [Nm] | 1:50,000 | - | - | |
| Torque at Motor [Nm] | 1:4784 | 500 | 0.105 | Maximum value |
| Motor Speed [rpm] | 1:10.453 | 21,000 | 2009 | Maximum value |
| Motor Inertia [kg] | 1:458 | 3.50 × | 7.65 × | |
| Motor Friction [Nm s/rad] | 1:458 | 1.10 × | 2.40 × | |
| Braking Pressure [kPa] | 1:50 | 5000 | 100 | Friction braking only |
| Proportional Gain [1/kph] | 10:1 | 1.0 | 10 | Outputs normalized torque |
| Integral Gain [1/kph] | 10:1 | 1.0 | 10 | Outputs normalized torque |
| Feedforward Gain [1/kph] | 10:1 | 0.001 | 0.01 | Outputs normalized torque |
| Weighting [m/Nm] | 478:1 | 0.001 | 0.478 | Cost function weight |
| Max Error [kph] | PI | Youla | Youla-H | |
|---|---|---|---|---|
| Full-Scale | 0.203 | 0.220 | 0.157 | 0.156 |
| Scaled | 0.203 | 0.221 | 0.158 | 0.156 |
| Scaled-Reduction | 0.164 | 0.179 | 0.135 | 0.134 |
| Scaled-Increase | 0.241 | 0.264 | 0.187 | 0.184 |
| RMS Error [kph] | PI | Youla | Youla-H | |
|---|---|---|---|---|
| Full-Scale | 0.045 | 0.086 | 0.026 | 0.024 |
| Scaled | 0.045 | 0.089 | 0.025 | 0.023 |
| Scaled-Reduction | 0.037 | 0.069 | 0.020 | 0.019 |
| Scaled-Increase | 0.054 | 0.105 | 0.029 | 0.026 |
| Metric | PI | Youla | Youla-H | |
|---|---|---|---|---|
| Max Error Nominal [kph] | 0.203 | 0.221 | 0.158 | 0.156 |
| Max Error Reduced Param % | −19.0% | −19.0% | −14.7% | −14.4% |
| Max Error Increased Param % | 18.6% | 20.6% | 18.0% | 17.6% |
| RMS Error Nominal [kph] | 0.045 | 0.089 | 0.025 | 0.023 |
| RMS Error Reduced Param % | −19.2% | −22.4% | −18.2% | −16.4% |
| RMS Error Increased Param % | 18.1% | 16.9% | 18.2% | 15.6% |
| M2 Margin | 1.000 | 0.866 | 0.937 | 0.937 |
| Noise Std. Dev. [Nm] | 0.0071 | 0.0005 | 0.0005 | 0.0005 |
| Noise Max [Nm] | 0.0142 | 0.0043 | 0.0063 | 0.0063 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, R.; Yadav, S.; Assadian, F. Systemic Scaling of Powertrain Models with Youla and H∞ Driver Control. Energies 2025, 18, 3126. https://doi.org/10.3390/en18123126
Tan R, Yadav S, Assadian F. Systemic Scaling of Powertrain Models with Youla and H∞ Driver Control. Energies. 2025; 18(12):3126. https://doi.org/10.3390/en18123126
Chicago/Turabian StyleTan, Ricardo, Siddhesh Yadav, and Francis Assadian. 2025. "Systemic Scaling of Powertrain Models with Youla and H∞ Driver Control" Energies 18, no. 12: 3126. https://doi.org/10.3390/en18123126
APA StyleTan, R., Yadav, S., & Assadian, F. (2025). Systemic Scaling of Powertrain Models with Youla and H∞ Driver Control. Energies, 18(12), 3126. https://doi.org/10.3390/en18123126







