Damping Characteristic Analysis of LCL Inverter with Embedded Energy Storage
Abstract
1. Introduction
- (1)
- The impedance model of BESS-MMC has been established, where the control and grid system parts are considered, which is realized through a Quasi-Proportional–Resonant (QPR) controller.
- (2)
- The key factors influencing the inverter’s impedance and its stability characteristics are investigated, and the recommendations for enhancing stability are also provided.
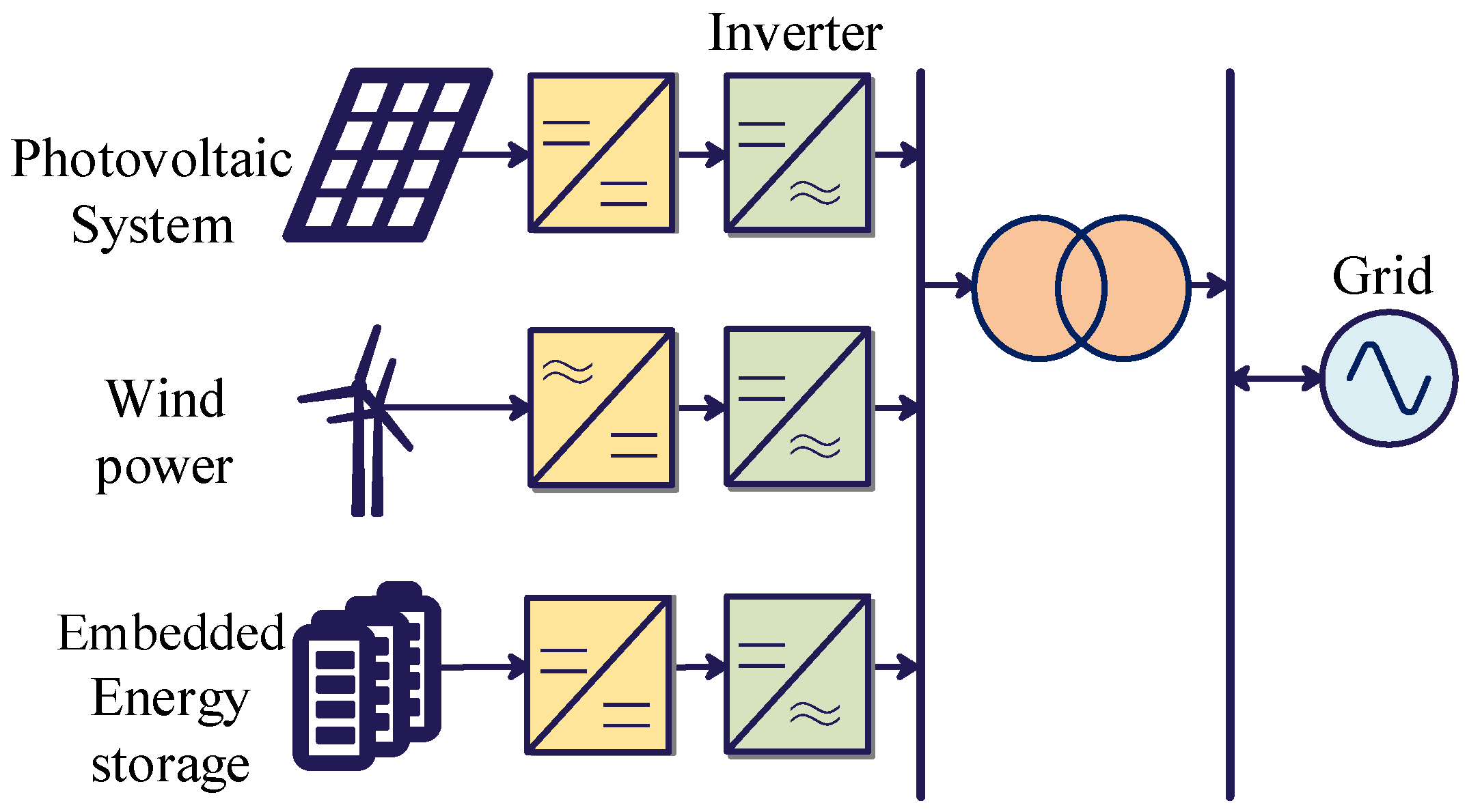
2. Operating Principle of LCL Inverter with Embedded Energy Storage
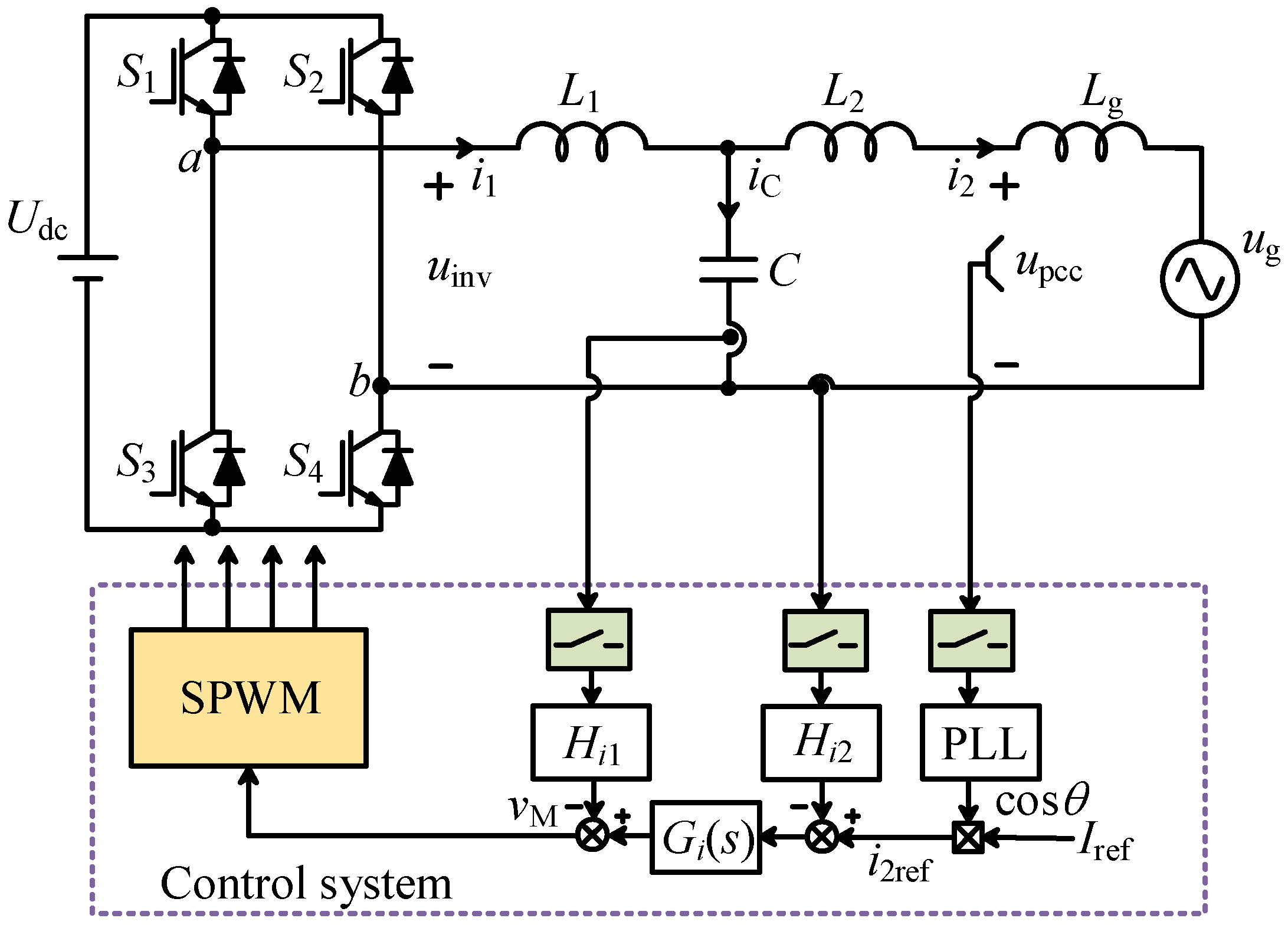
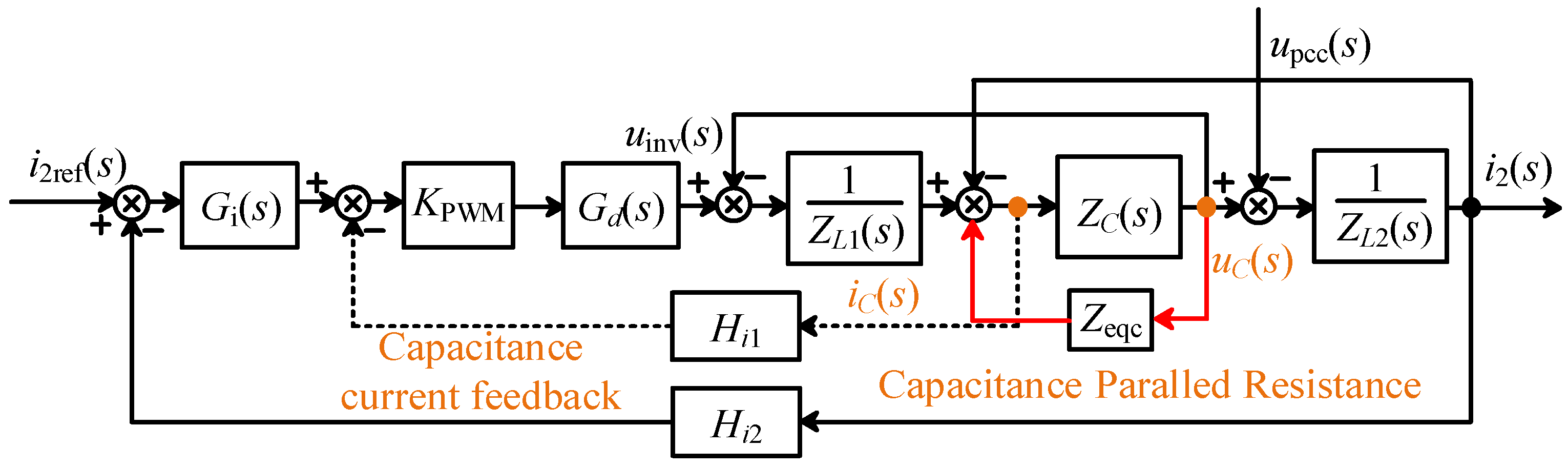
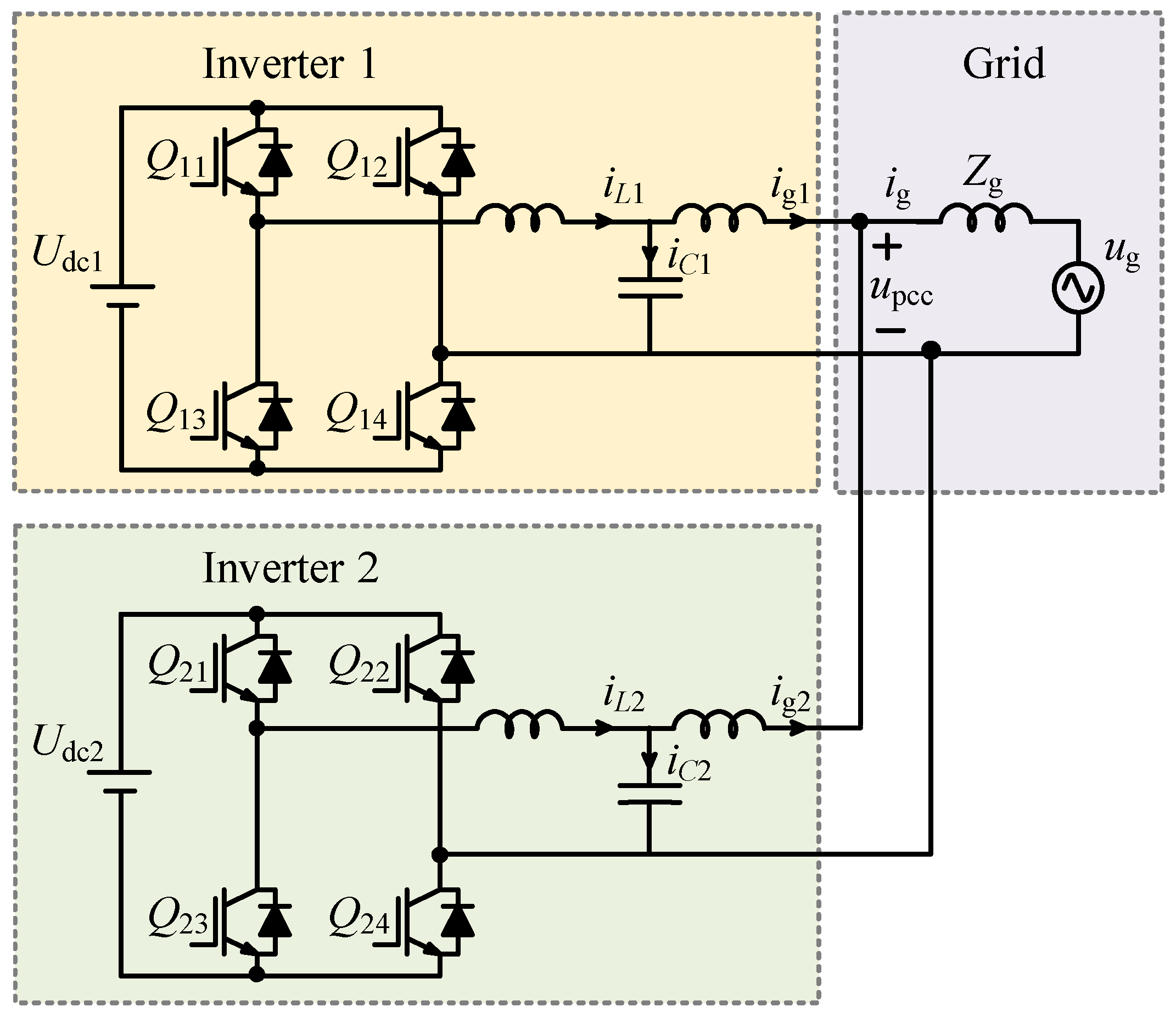
2.1. System Structure and Control Strategy
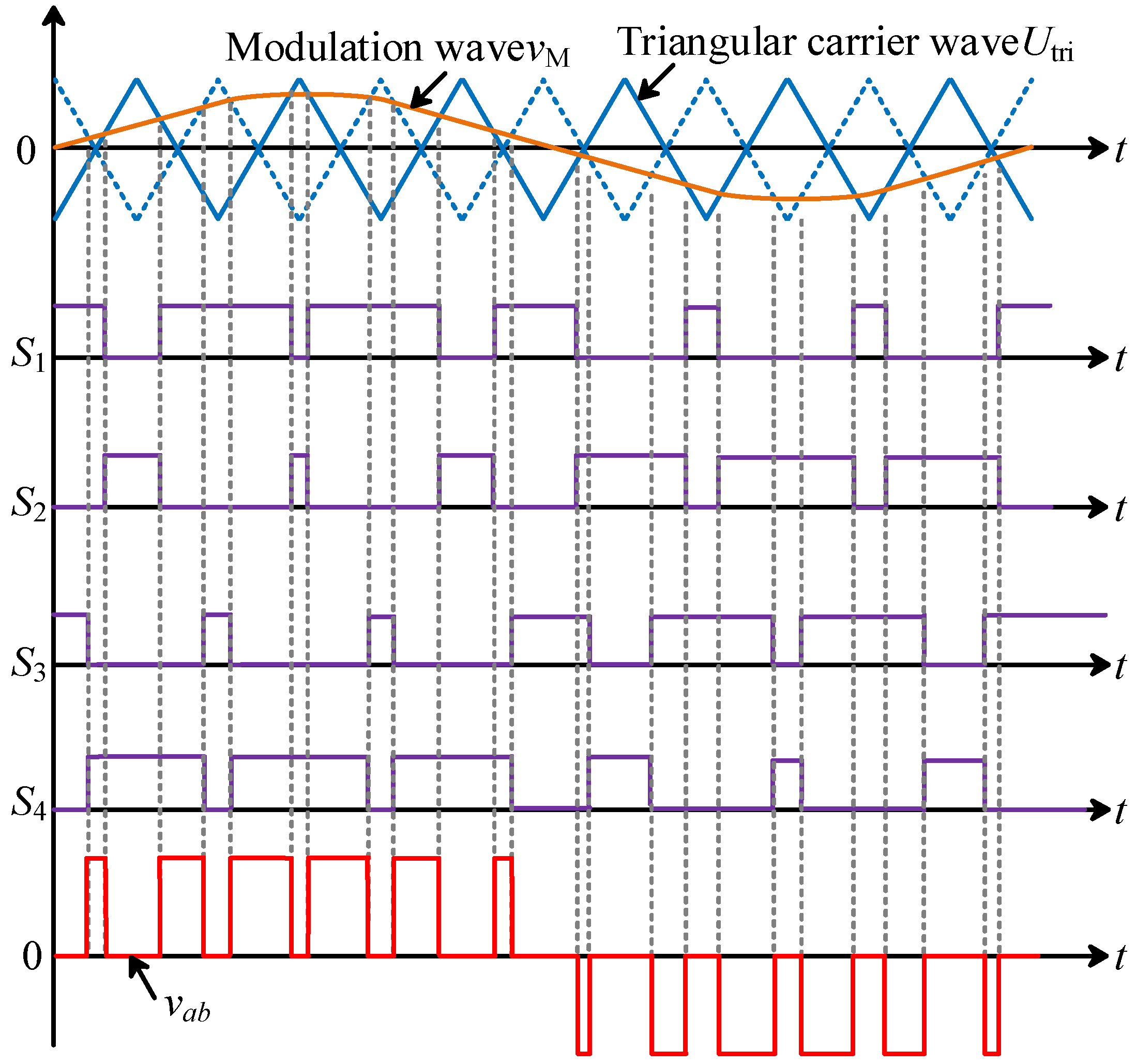
2.2. Modulation Strategy
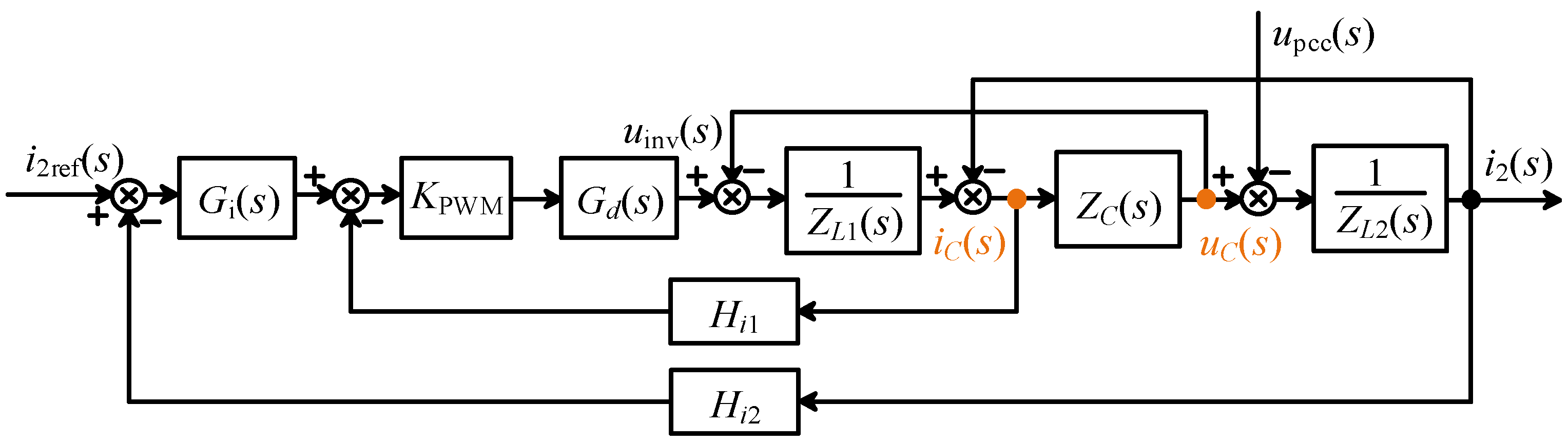
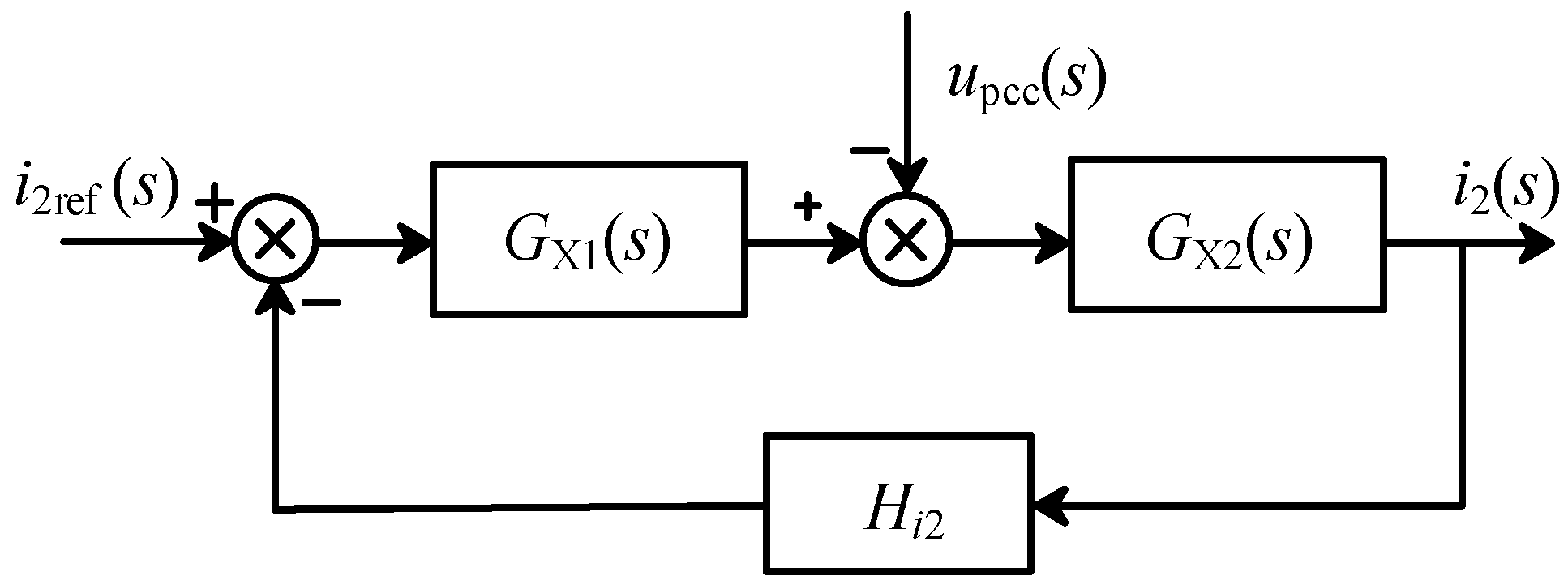
2.3. Mathematical Model
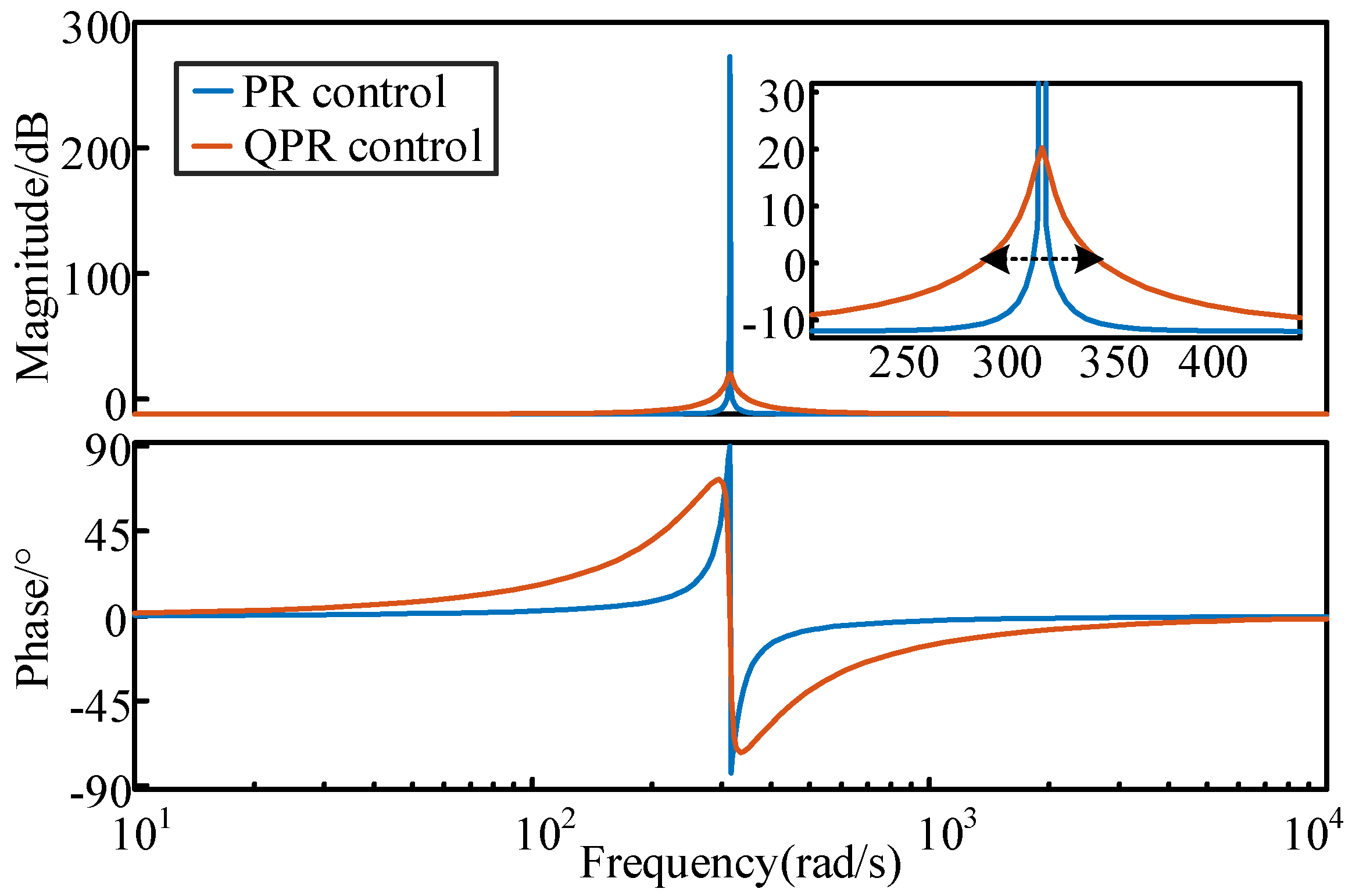
2.4. Impedance Characteristic Analysis
- (1)
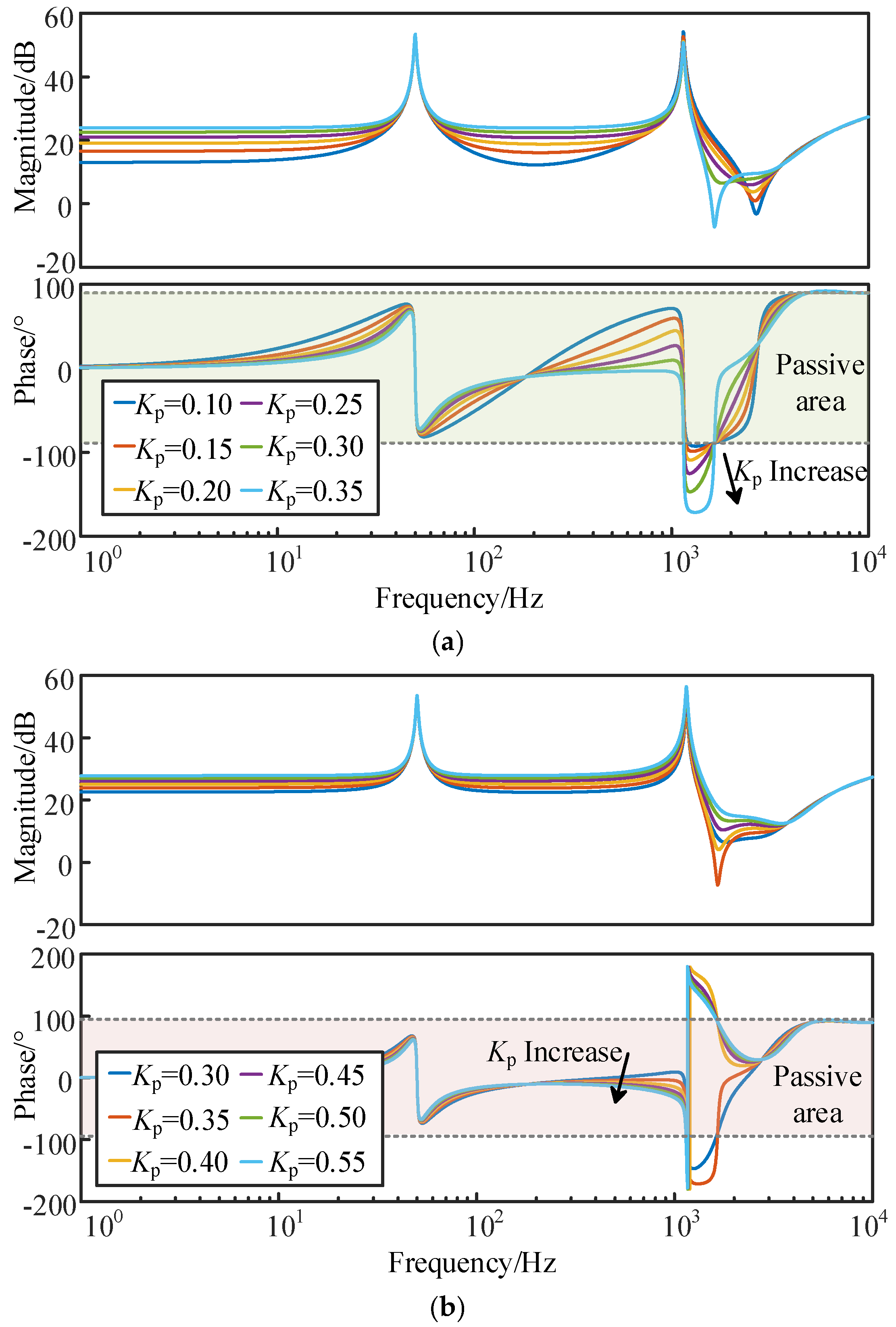
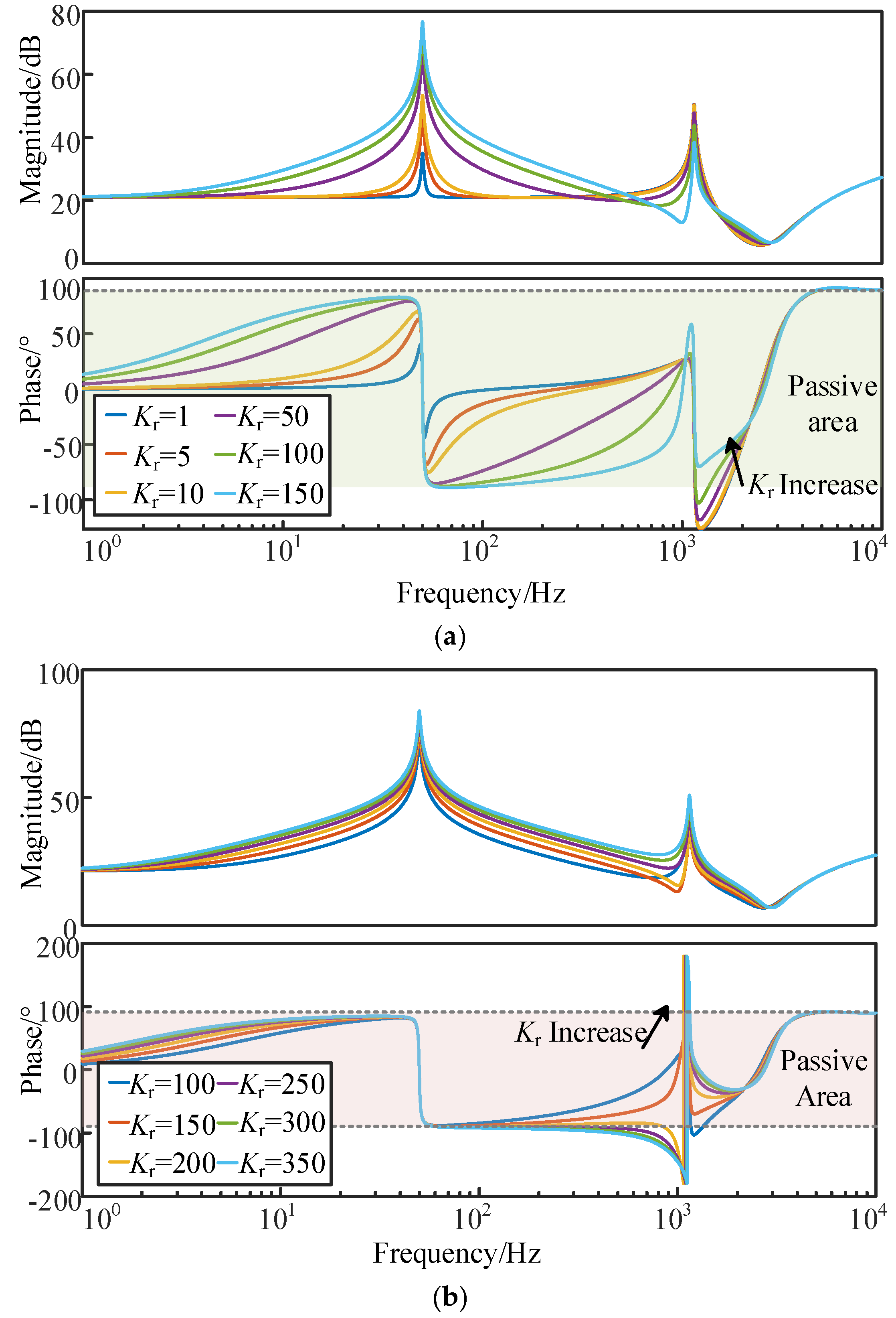
- Influence of Control Parameters
- (2)
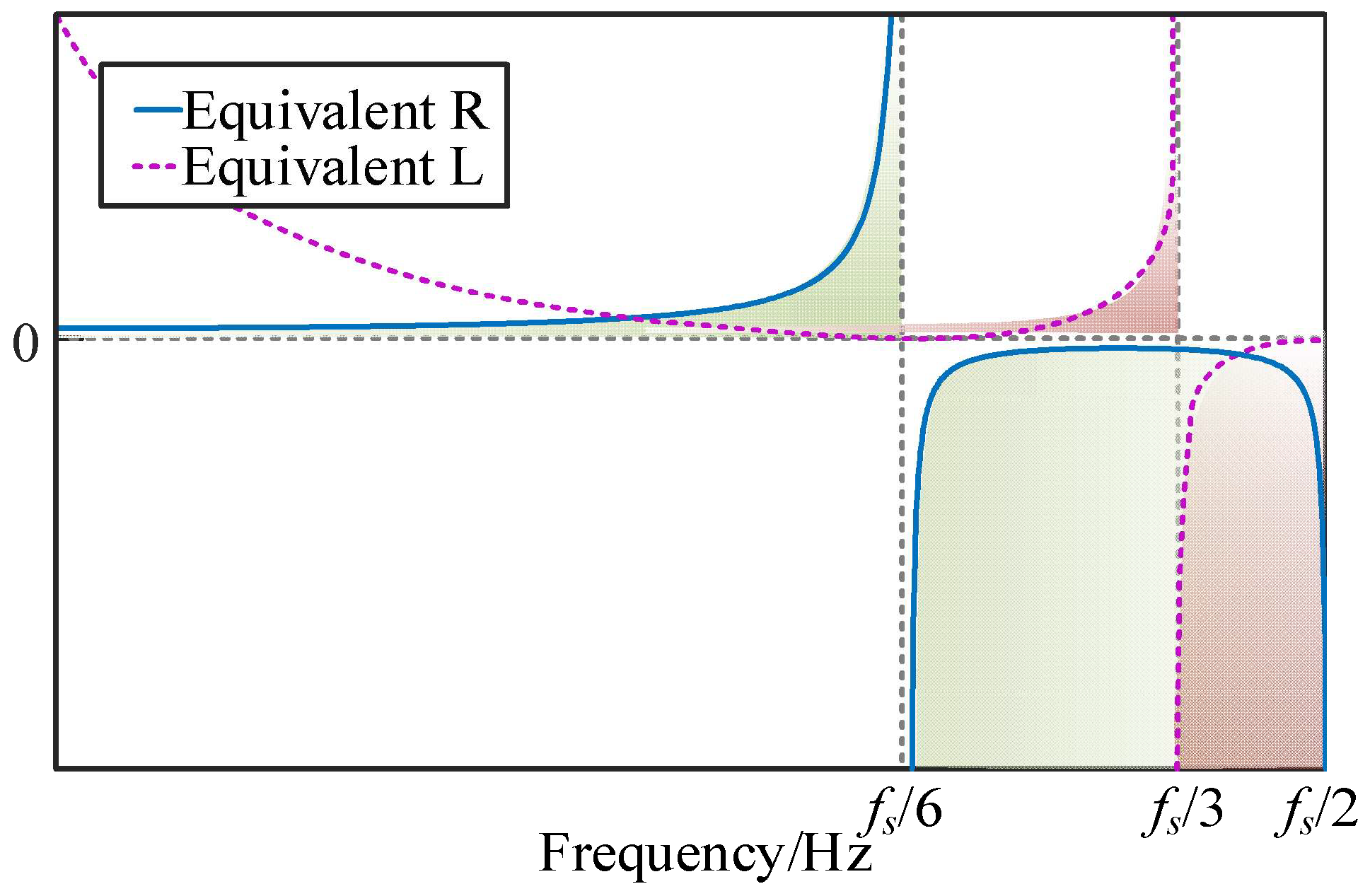
- Influence of Switching Frequency
3. Stability Mechanism Analysis
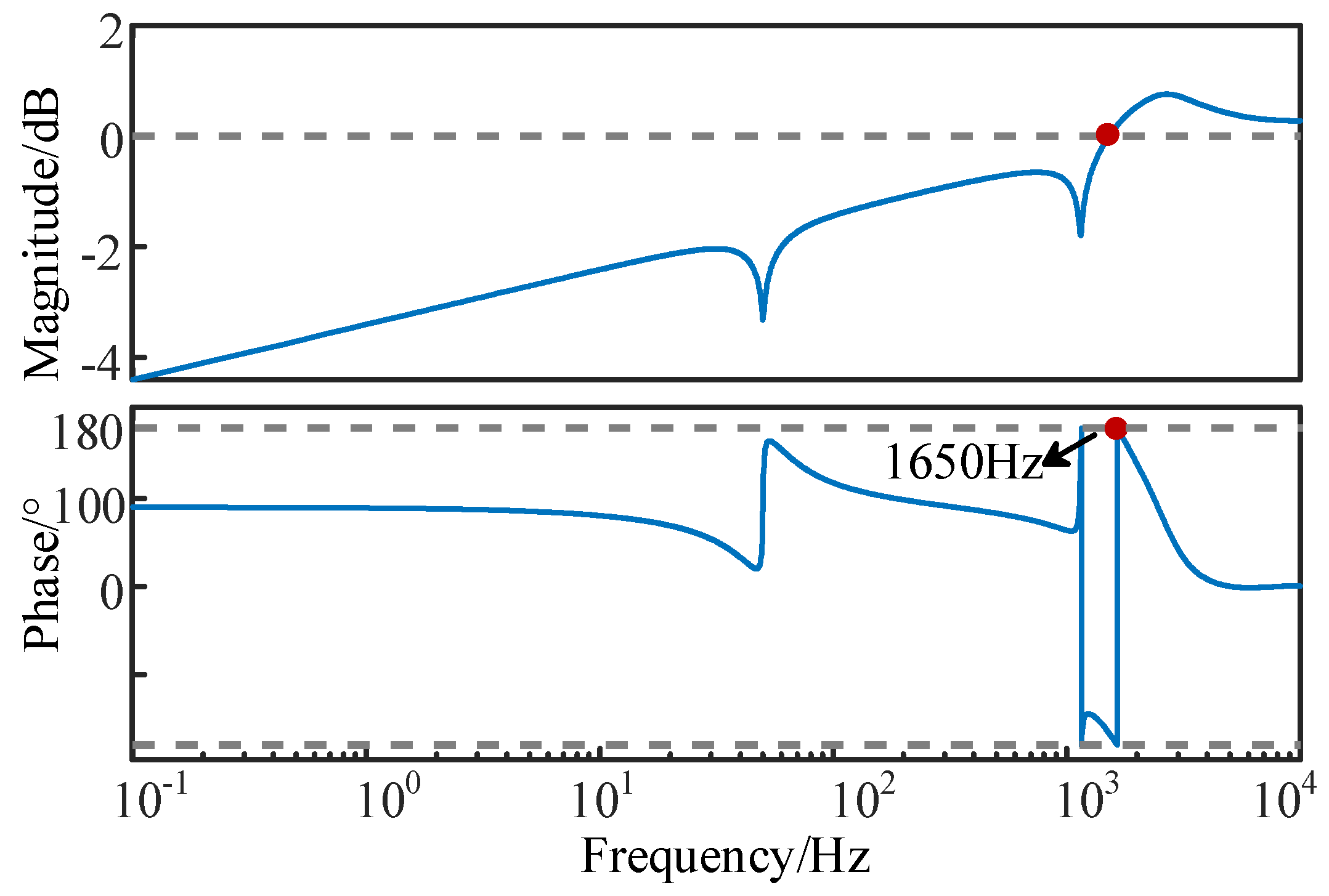
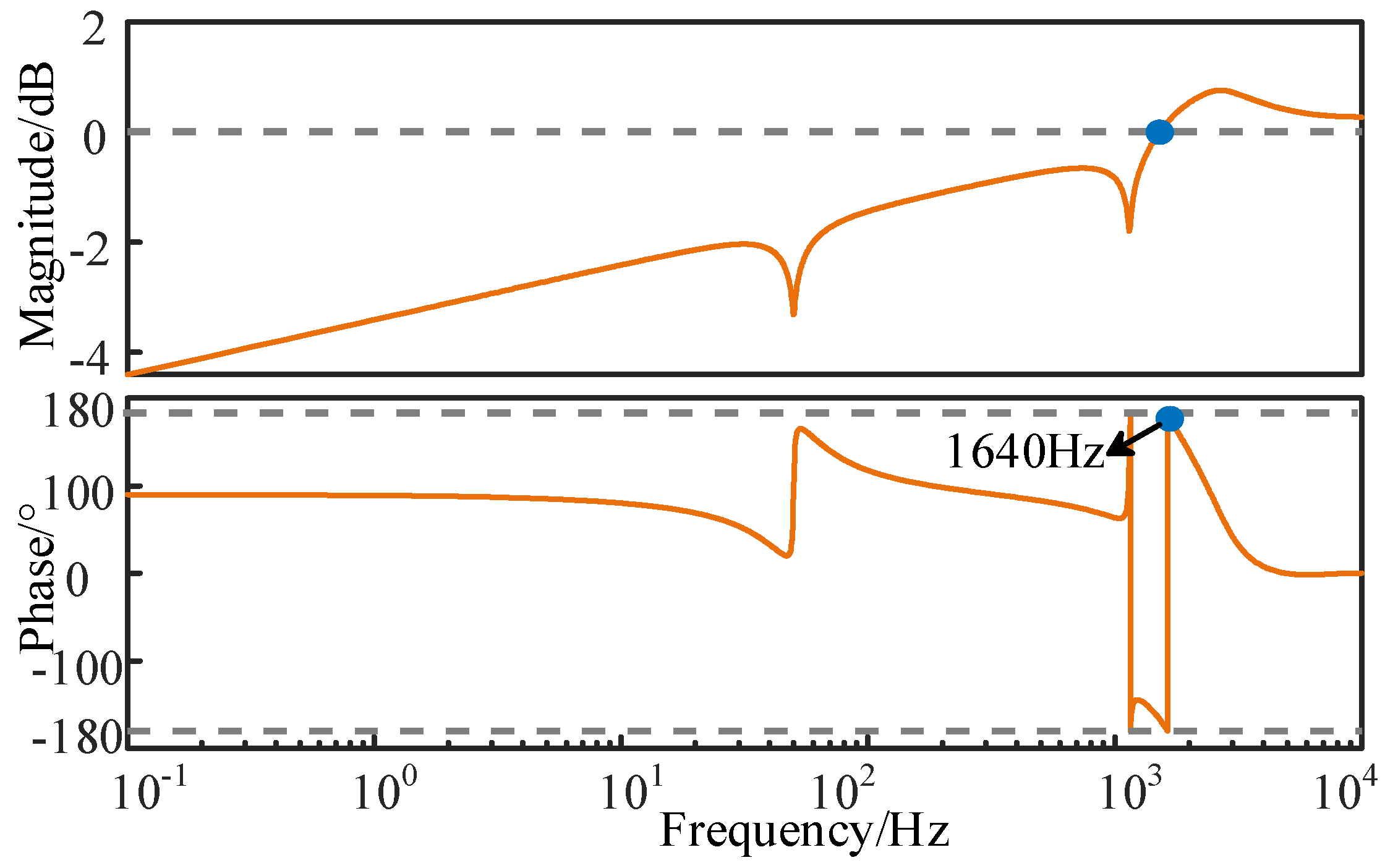
3.1. Stability Analysis of a Single Inverter
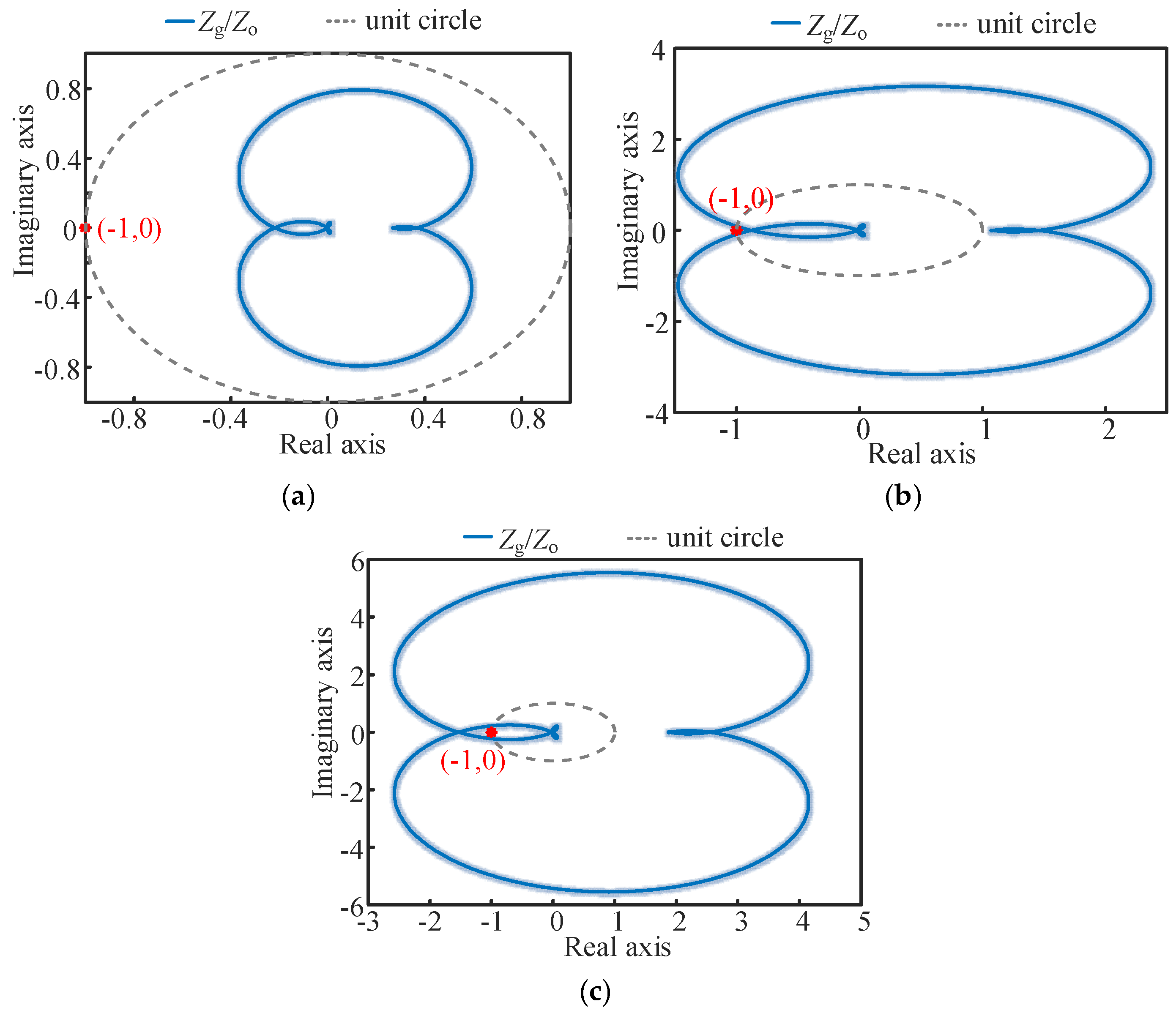
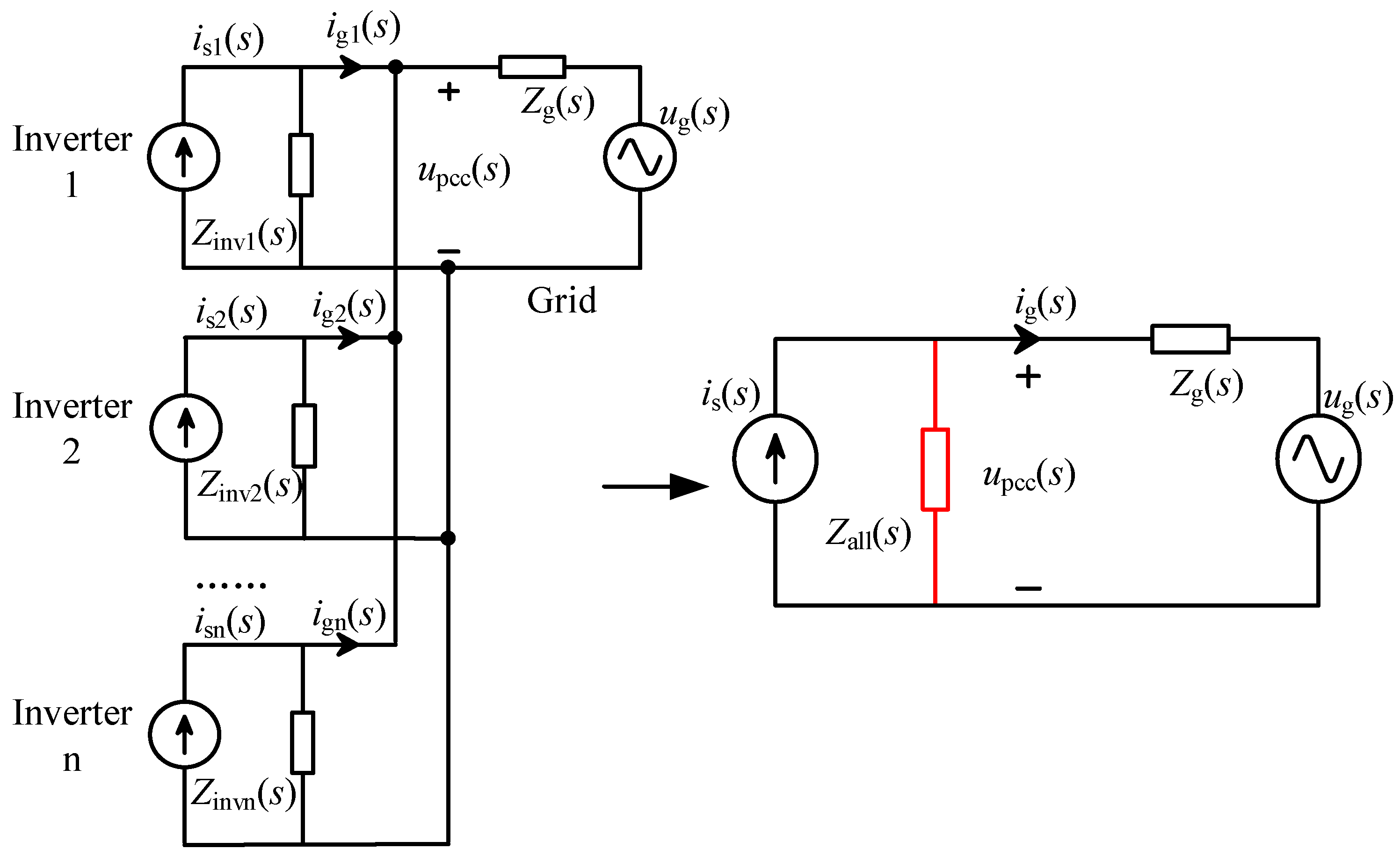
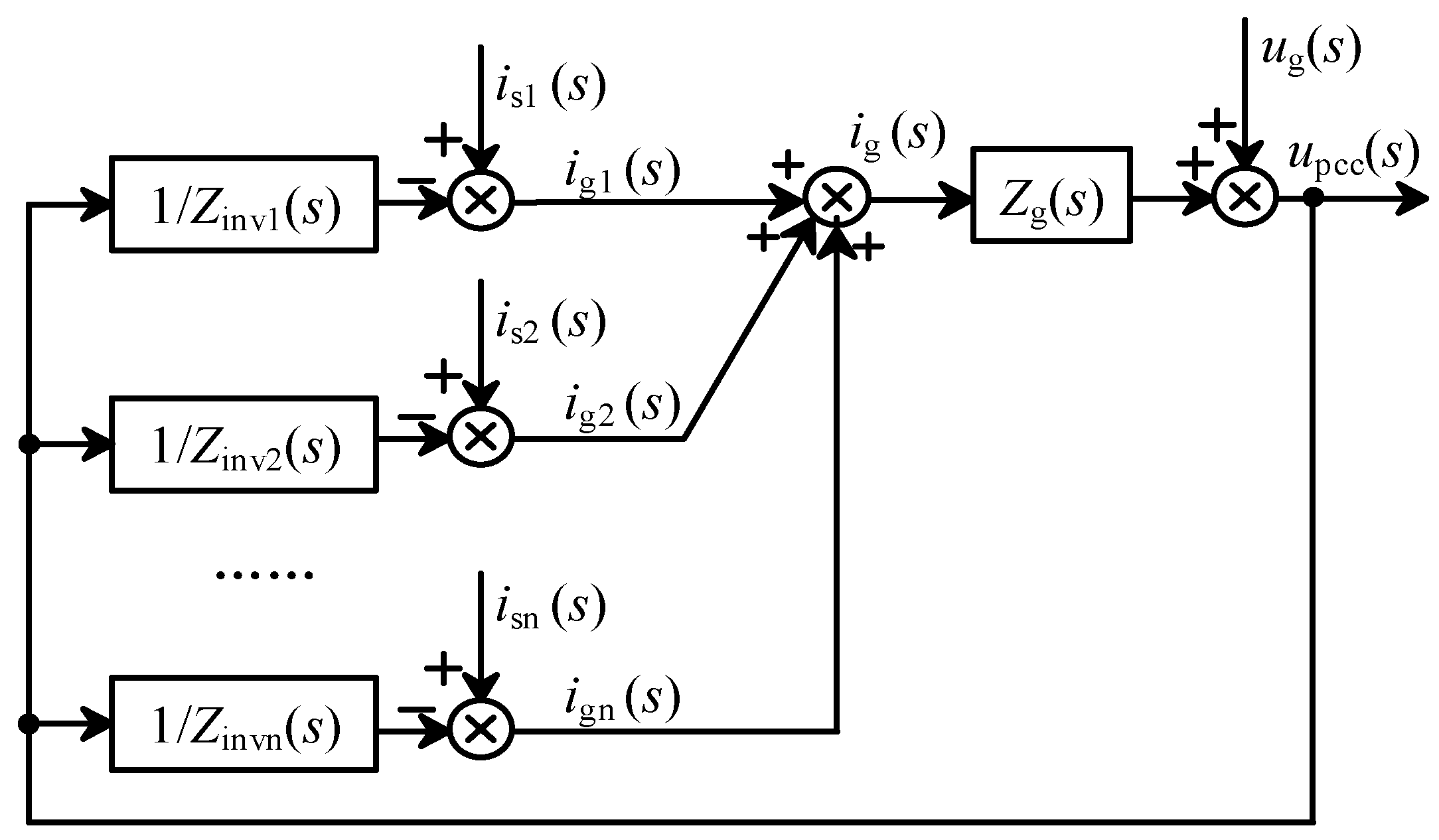
3.2. Stability Analysis of Multiple Inverters
- Under a strong grid condition, each inverter ensures its own stability.
- The equivalent loop gain Zg(s)/Zall(s) for multiple inverters connected to the grid meets the Nyquist criterion. The magnitude–frequency characteristic curve of the equivalent parallel impedance Zall(s) at the port does not intersect with that of the grid impedance. If they do intersect, the phase at the crossover frequency fc must be positive, meaning that the phase margin is satisfied.
4. Simulation Verifications
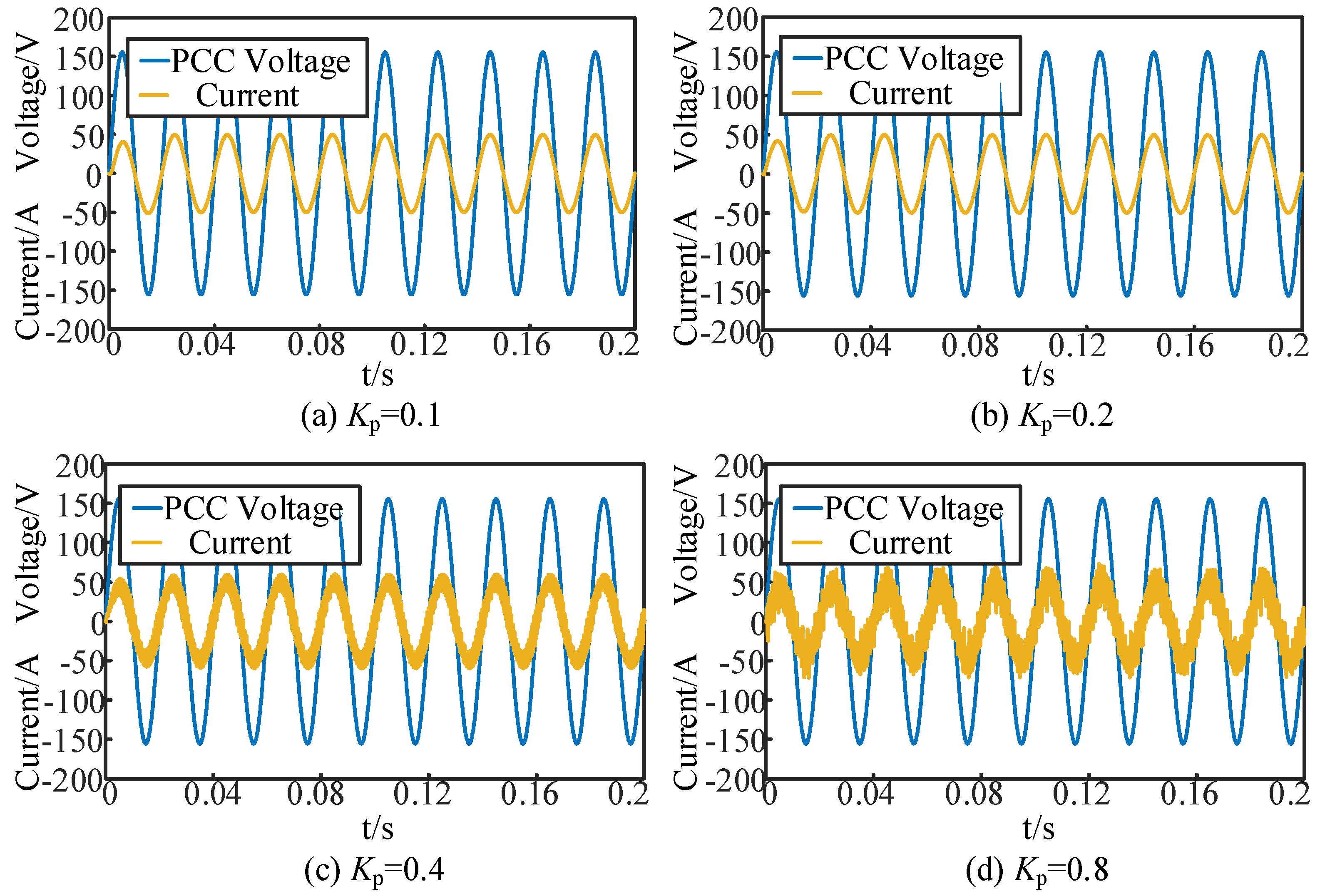
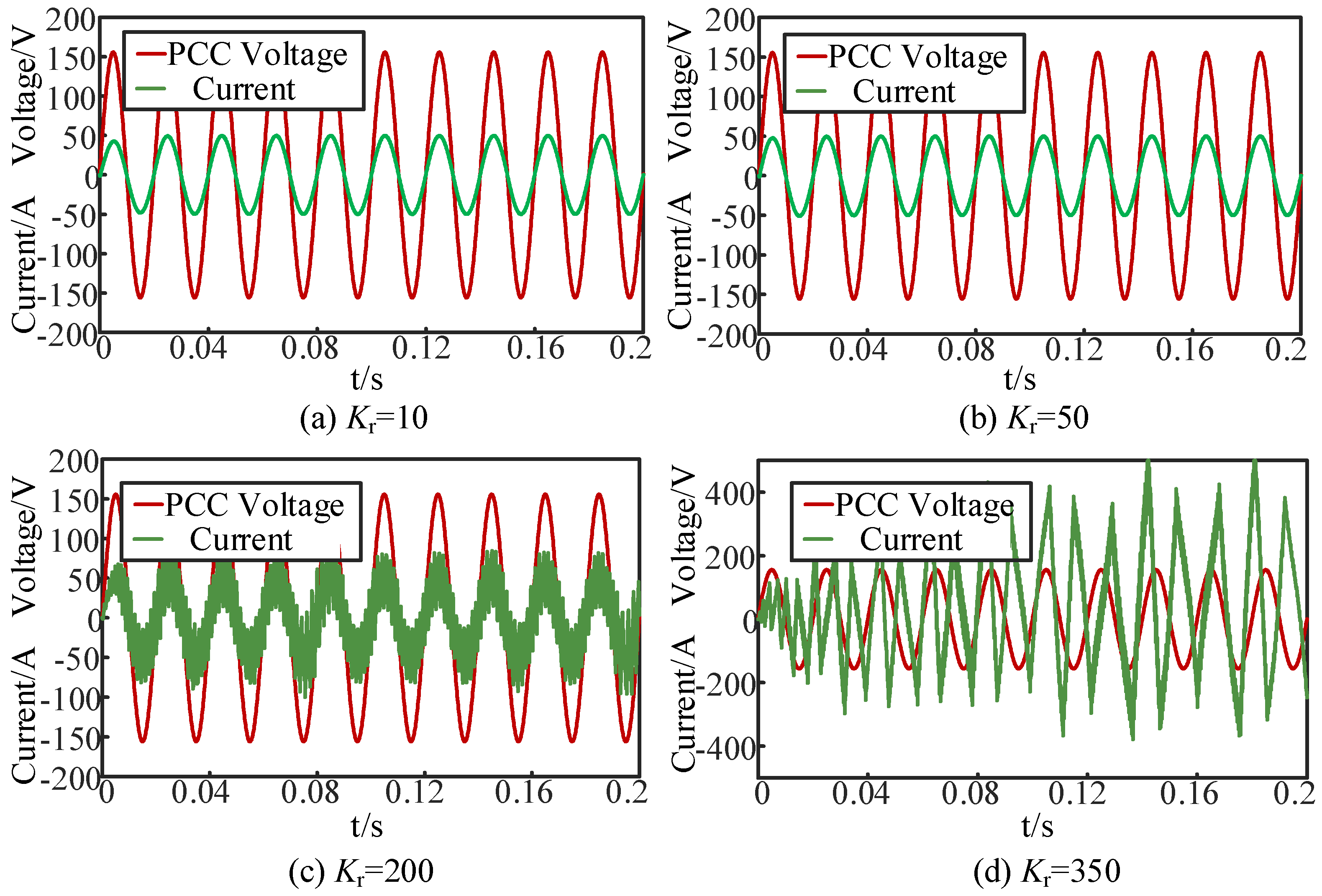
4.1. Verification of the Impact of Control Parameters
4.2. Verification of the Stability Analysis in Single Inverter Case
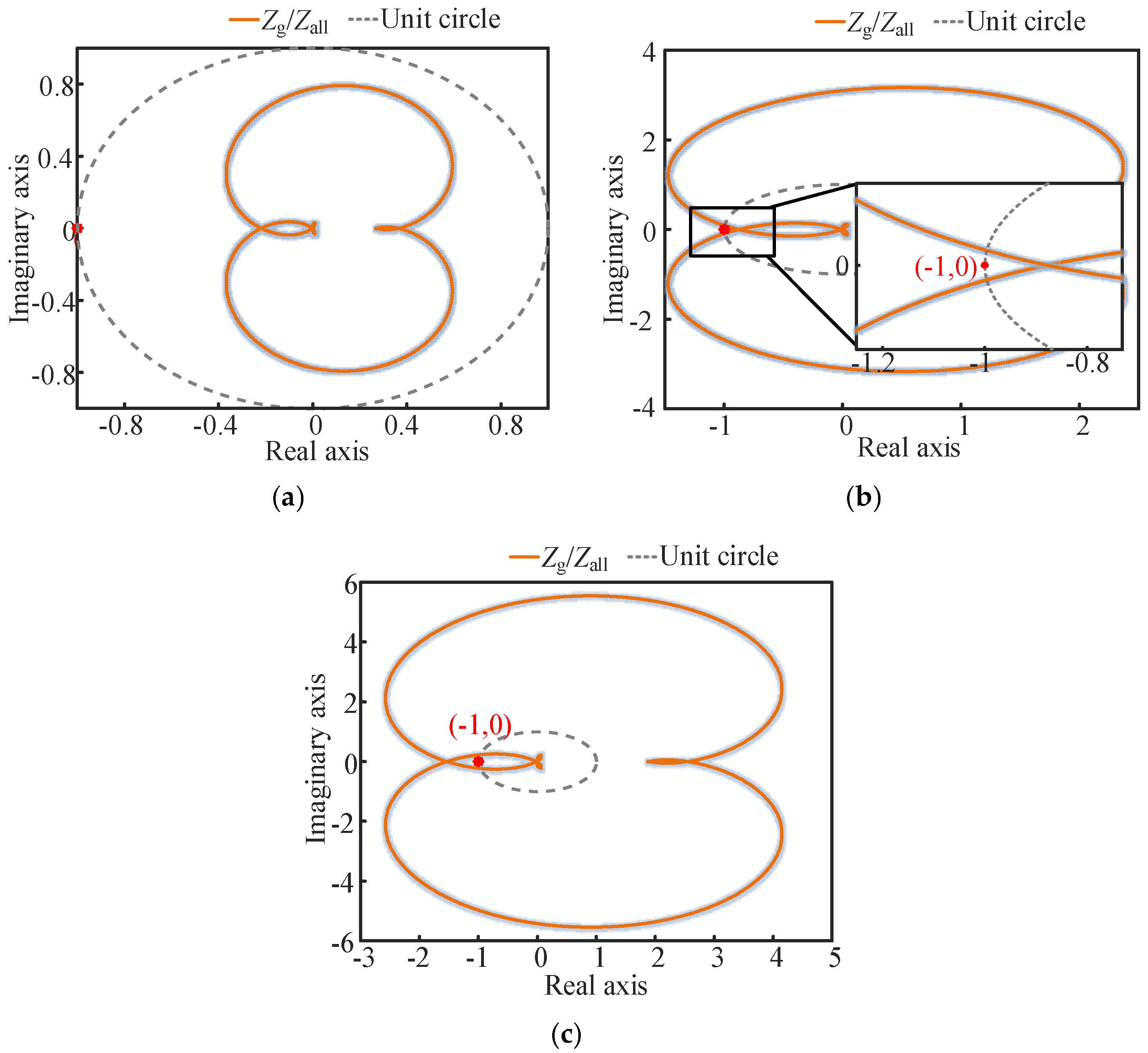
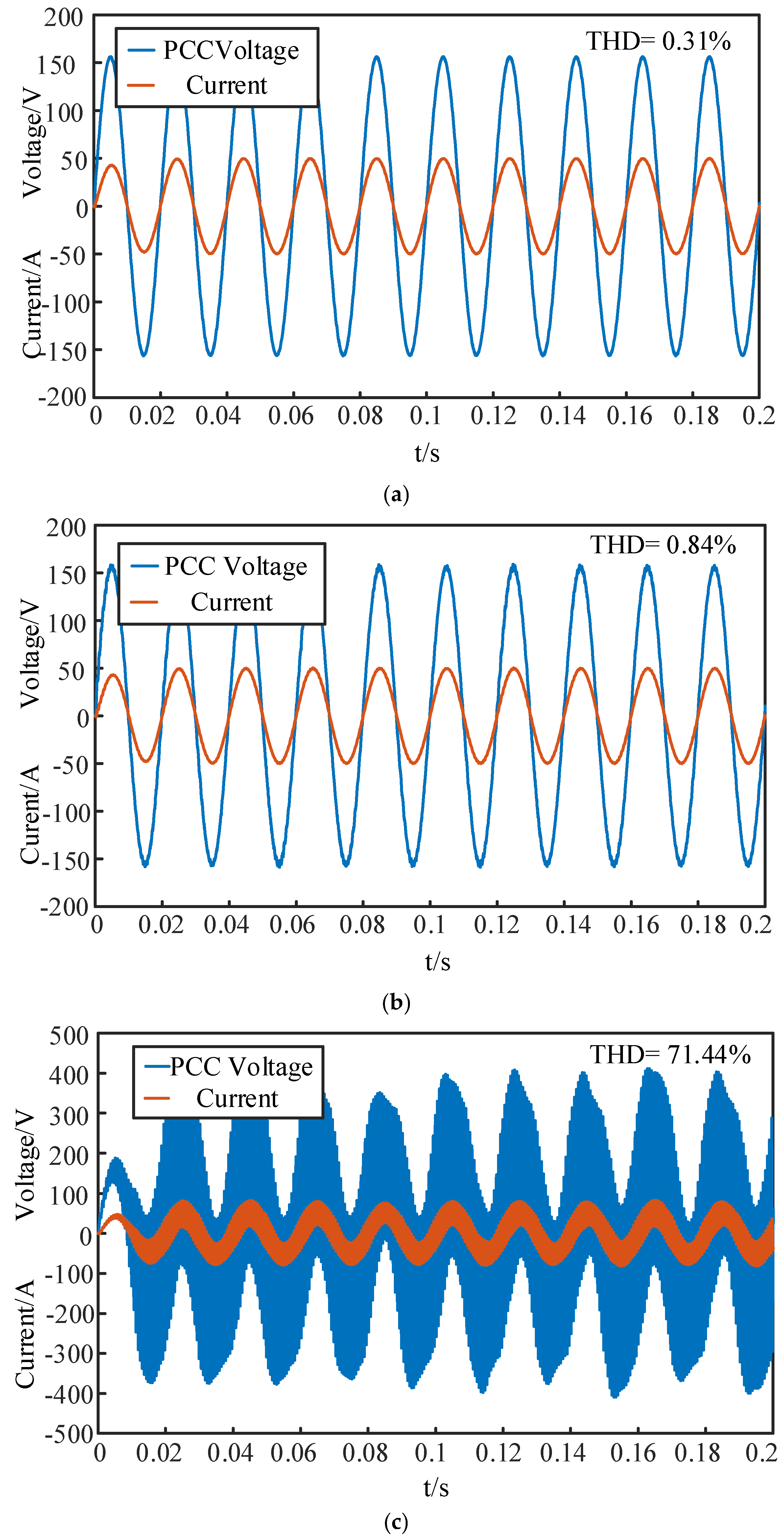
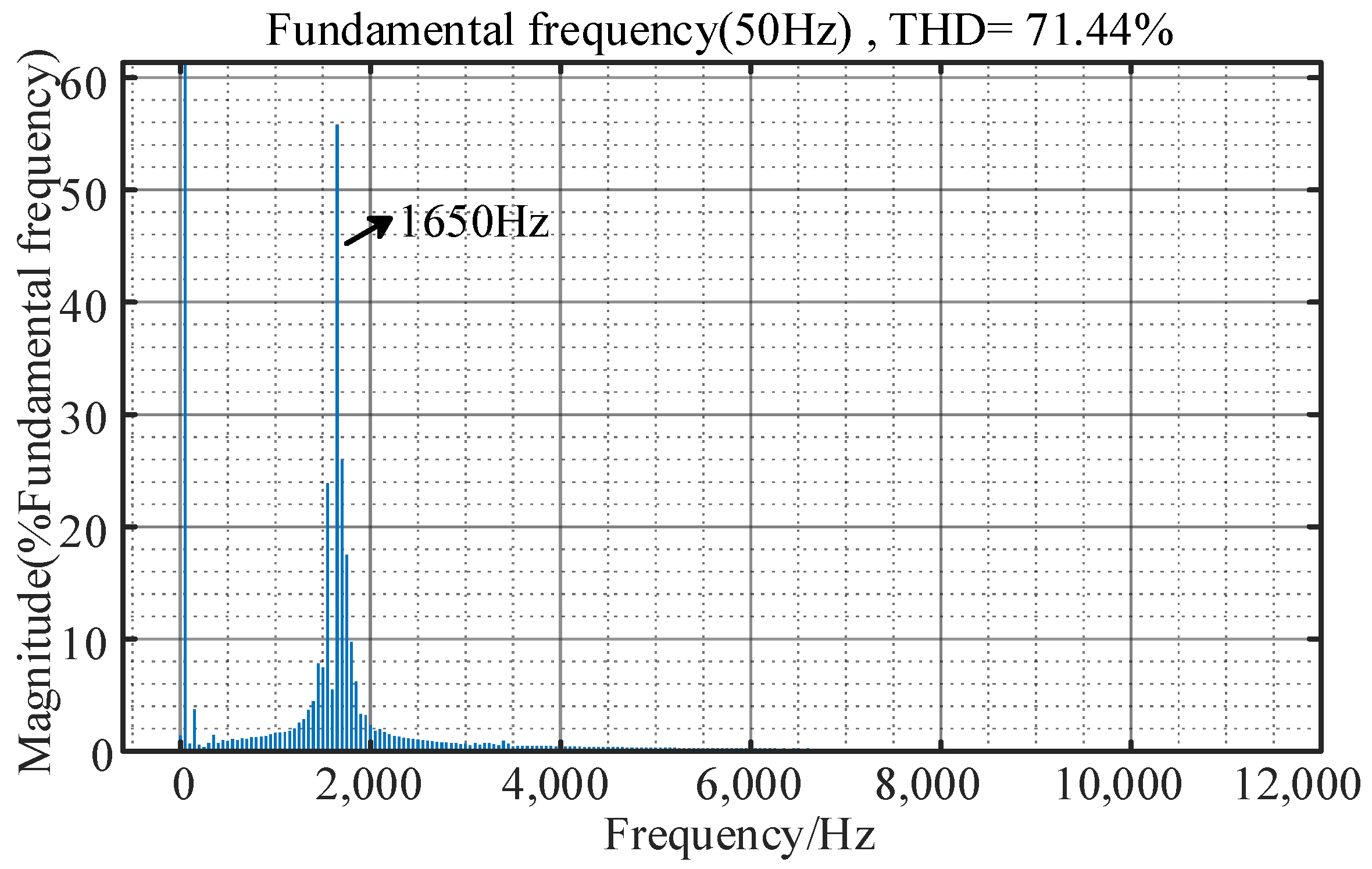
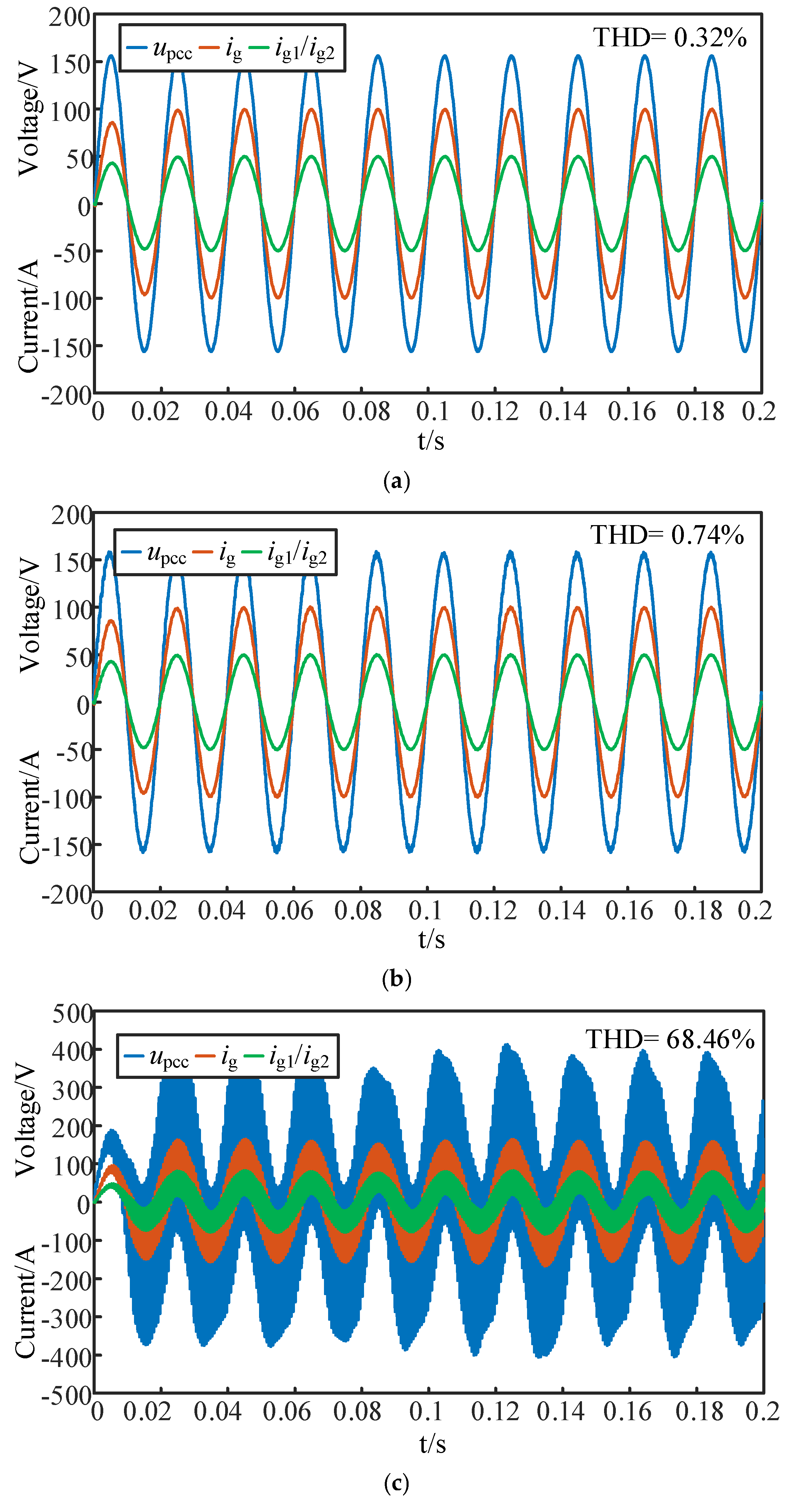
4.3. Verification of the Stability Analysis in Multiple Inverters Case
5. Conclusions
- (1)
- The effect of the control parameters on a grid-connected inverter is demonstrated by a reduction in system stability as the proportional gain Kp increases. When Kp reaches a certain threshold, the system becomes unstable. Similarly, as the resonant coefficient Kr increases to a specific value, the system experiences resonance. To increase the stability of the inverter in practical applications, the values of Kp and Kr should be limited and, once the resonance occurs, decreasing the two parameters can be effective to suppress the oscillations.
- (2)
- The stability of the coupled system is affected by both the magnitude of grid impedance and the number of grid-connected inverters. As grid impedance increases, transitioning the system from a strong grid to a weak grid, system stability diminishes. Furthermore, even with a constant grid impedance, an increase in the number of grid-connected inverters also degrades system stability. Thus, the operation modes of the practical system should be paid attention to for the inverters connected to the grid.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, X.; He, J.; Mao, H.; Li, H. New issues and classification of power system stability with high shares of renewables and power electronics. Proc. CSEE 2021, 41, 461–475. [Google Scholar]
- Jiang, Q.; Xu, R.; Li, B.; Chen, X.; Yin, Y.; Liu, T.; Blaabjerg, F. Impedance Model for Instability Analysis of LCC-HVDCs Considering Transformer Saturation. J. Mod. Power Syst. Clean Energy 2024, 12, 1309–1319. [Google Scholar]
- Li, Q.; Li, B.; Jiang, Q.; Liu, T.; Yue, Y.; Zhang, Y. A novel location method for interline power flow controllers based on entropy theory. Prot. Control Mod. Power Syst. 2024, 9, 70–81. [Google Scholar] [CrossRef]
- Ma, N.; Xie, X.; He, J.; Wang, H. Review of wide-band oscillation in renewable and power electronics highly integrated power systems. Proc. CSEE 2020, 40, 15. [Google Scholar]
- Bi, T.; Kong, Y.; Xiao, S.; Zhang, P.; Zhang, T. Review of sub-synchronous oscillation with large-scale wind power transmission. J. Electr. Power Sci. Technol. 2012, 27, 10–15. [Google Scholar]
- Dong, X.; Tian, X.; Zhang, Y.; Song, J. Practical SSR incidence and influencing factor analysis of DFIG-based series-compensated transmission system in Guyuan farms. High Volt. Eng. 2017, 43, 321–328. [Google Scholar]
- Feng, X.; Wu, J.; Cui, X. Sub-synchronous oscillation control strategy based on impedance identification for wind power grid-connected system in Guyuan area of China. Autom. Electr. Power Syst. 2023, 47, 200–207. [Google Scholar]
- Ma, J.; Shen, Y.; Du, Y.; Liu, H.; Wang, J. Overview on active damping technology of wind power integrated system adapting to broadband oscillation. J. Power Syst. Technol. 2021, 45, 1673–1686. [Google Scholar]
- Zhang, Y.; Yang, X.; Zhang, Z. High-Efficiency Broadband Electroacoustic Energy Conversion Using Non-Foster-Inspired Circuit and Adaptively Switched Capacitor. IEEE Trans. Ind. Electron. 2025, 1–12. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Z.; Xu, M.; Li, S.; Zhang, Y.; Zhu, X.-F.; Ouyang, X.; Alù, A. Digital non-Foster-inspired electronics for broadband impedance matching. Nat. Commun. 2024, 15, 4346. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and analysis of harmonic stability in an AC power-electronics-based power system. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 613–625. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Wu, W.; Liu, Y.; He, Y.; Chung, H.S.H.; Liserre, M.; Blaabjerg, F. Damping methods for resonances caused by LCL-filter-based current-controlled grid-tied power inverters: An overview. IEEE Trans. Ind. Electron. 2017, 64, 7402–7413. [Google Scholar] [CrossRef]
- Awal, M.A.; Della Flora, L.; Husain, I. Observer based generalized active damping for voltage source converters with LCL filters. IEEE Trans. Power Electron. 2021, 37, 125–136. [Google Scholar] [CrossRef]
- Ruan, X. Control Technologies for LCL-Type Grid-Connected Inverters; Science Press: Beijing, China, 2015. [Google Scholar]
- Yang, S.; Lei, Q.; Peng, F.Z.; Qian, Z. A robust control scheme for grid-connected voltage-source inverters. IEEE Trans. Ind. Electron. 2010, 58, 202–212. [Google Scholar] [CrossRef]
- Liserre, M.; Dell’Aquila, A.; Blaabjerg, F. Genetic algorithm-based design of the active damping for an LCL-filter three-phase active rectifier. IEEE Trans. Power Electron. 2004, 19, 76–86. [Google Scholar] [CrossRef]
- Zhou, L.; Luo, A.; Chen, Y.; Zhou, X.; Li, M.; Kuang, H. Robust grid-current feedback active damping control method for LCL-type grid-connected inverters. Proc. CSEE 2016, 36, 2742–2752. [Google Scholar]
- Duan, X.; Li, P.; Zhao, F.; Chen, S.; Wang, J. Stability control of LCL-type grid-connected inverters based on full capacitor voltage feedforward in weak grids. High Volt. Eng. 2022, 48, 2140–2151. [Google Scholar]
- Peña-Alzola, R.; Liserre, M.; Blaabjerg, F.; Sebastián, R.; Dannehl, J.; Fuchs, F.W. Analysis of the passive damping losses in LCL-filter-based grid converters. IEEE Trans. Power Electron. 2012, 28, 2642–2646. [Google Scholar] [CrossRef]
- Wu, W.; He, Y.; Tang, T.; Blaabjerg, F. A new design method for the passive damped LCL and LLCL filter-based single-phase grid-tied inverter. IEEE Trans. Ind. Electron. 2012, 60, 4339–4350. [Google Scholar] [CrossRef]
- Xu, D.; Fei, W.; Yi, R. Passive damping of LCL, LLCL and LLCCL filters. Proc. CSEE 2015, 35, 4725–4735. [Google Scholar]
- Yin, J.; Xin, J.; Wu, X.; Tong, Y. Active damping control strategy for LCL filter based on band pass filter. Power Syst. Technol. 2013, 37, 2376–2382. [Google Scholar]
- Geng, Y.; Qi, Y.; Dong, W.; Deng, R. An active damping method with improved grid current feedback. Proc. CSEE 2018, 38, 5557–5567. [Google Scholar]
- Bao, C.; Ruan, X.; Wang, X.; Pan, D.; Li, W. Design of grid-connected inverters with LCL filter based on PI regulator and capacitor current feedback active damping. Zhongguo Dianji Gongcheng Xuebao Proc. Chin. Soc. Electr. Eng. 2012, 32, 25. [Google Scholar]
- Wang, A.; Ge, W.; Li, T.; Cui, D.; Li, M. Research on realization technology of active damping method with differential feedback of filter capacitance voltage for LCL filter based grid-connected inverters. J. Electr. Eng. 2023, 18, 126–132. [Google Scholar]

| Methods | Description | |
|---|---|---|
| Resonance Peak Damping Methods | Passive Damping | Achieved by series or parallel resistors in the circuit Simple and effective, but introduces losses |
| Active Damping | No additional losses introduced, more flexible damping implementation | |
| Analysis of Passive Damping Methods | Rd Damping Method | Dampens resonance but affects gain characteristics in the high-frequency range, reducing high-frequency harmonic attenuation |
| Rd-Cd Hybrid Resistor–Capacitor Passive Damping Method | Dampens resonance without affecting high-frequency harmonic attenuation by adding capacitance | |
| Analysis of Active Damping Methods | Methods Without Additional Sensors | Achieved through grid-connected current feedback or filter parameter estimation |
| Methods Requiring Additional Sensors | Feedback voltage or other currents for virtual damping control | |
| Most Widely Used Method | Active Damping Based on Capacitor Current Proportional Feedback | Equivalent to passive damping by paralleling a resistor across the capacitor Provides virtual resistance for damping, easy to implement without introducing additional losses |
| Parameters | Value |
|---|---|
| Grid voltage (ug/V) | 110 |
| DC-side voltage (Udc/V) | 300 |
| Triangular carrier amplitude (Utri/V) | 1 |
| Inverter-side inductance (L1/mH) | 2 |
| Filter capacitor (C/μF) | 10 |
| Grid-side inductance (L2/mH) | 400 |
| Grid-connected current sampling coefficient (Hi2) | 0.15 |
| Capacitor current feedback coefficient (Hi1) | 0.002 |
| Parameters | Value |
|---|---|
| Grid voltage (ug/V) | 110 |
| DC-side voltage (Udc/V) | 300 |
| Rated capacity (S/VA) | 4000 |
| Inverter-side inductance (L1/mH) | 2 |
| Filter capacitor (C/μF) | 10 |
| Grid-side inductance (L2/mH) | 400 |
| Gi(s) proportionality coefficient (Kp) | 0.25 |
| Gi(s) Resonance coefficient (Kr) | 10 |
| Switching frequency (fsw/kHz) | 5 |
| Sampling frequency (fs/kHz) | 10 |
| Grid-connected current sampling coefficient (Hi2) | 0.15 |
| Capacitor current feedback coefficient (Hi1) | 0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Jia, Y.; Zhang, G.; An, H.; Zhao, T. Damping Characteristic Analysis of LCL Inverter with Embedded Energy Storage. Energies 2025, 18, 3127. https://doi.org/10.3390/en18123127
Zhao J, Jia Y, Zhang G, An H, Zhao T. Damping Characteristic Analysis of LCL Inverter with Embedded Energy Storage. Energies. 2025; 18(12):3127. https://doi.org/10.3390/en18123127
Chicago/Turabian StyleZhao, Jingbo, Yongyong Jia, Guojiang Zhang, Haiyun An, and Tianhui Zhao. 2025. "Damping Characteristic Analysis of LCL Inverter with Embedded Energy Storage" Energies 18, no. 12: 3127. https://doi.org/10.3390/en18123127
APA StyleZhao, J., Jia, Y., Zhang, G., An, H., & Zhao, T. (2025). Damping Characteristic Analysis of LCL Inverter with Embedded Energy Storage. Energies, 18(12), 3127. https://doi.org/10.3390/en18123127








