Positive-Mode-Damping Stability Criterion Application and Damping Solutions in Microgrid-Integrated Transmission Grids
Abstract
1. Introduction
- Application of the PMD stability criterion to MGC-integrated transmission grids: This study applies the PMD stability criterion, based on faster RMA, to assess small-signal harmonic stability in MGC-integrated transmission grids (referred to as small-disturbance converter control system stability in [3]), addressing limitations in existing time-domain and impedance-based methods. Notably, this approach has not previously been applied to such grids using this stability criterion, thereby extending its generality.
- Extension of damping compensator design using the PMD stability criterion: This study extends the design and evaluation of two bandpass filter-based damping compensators—one active and one passive—by using the PMD stability criterion as a design tool to mitigate instabilities in MGC-integrated grids. This is a practical methodology for selecting the compensation location and parameters.
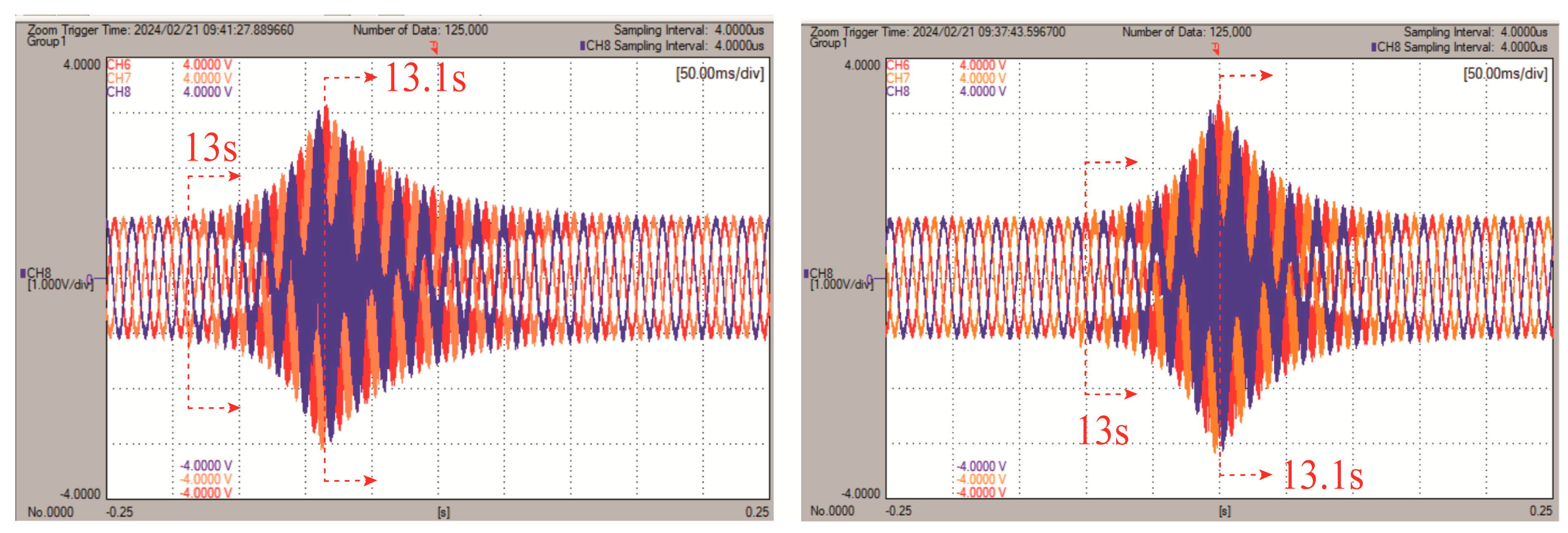
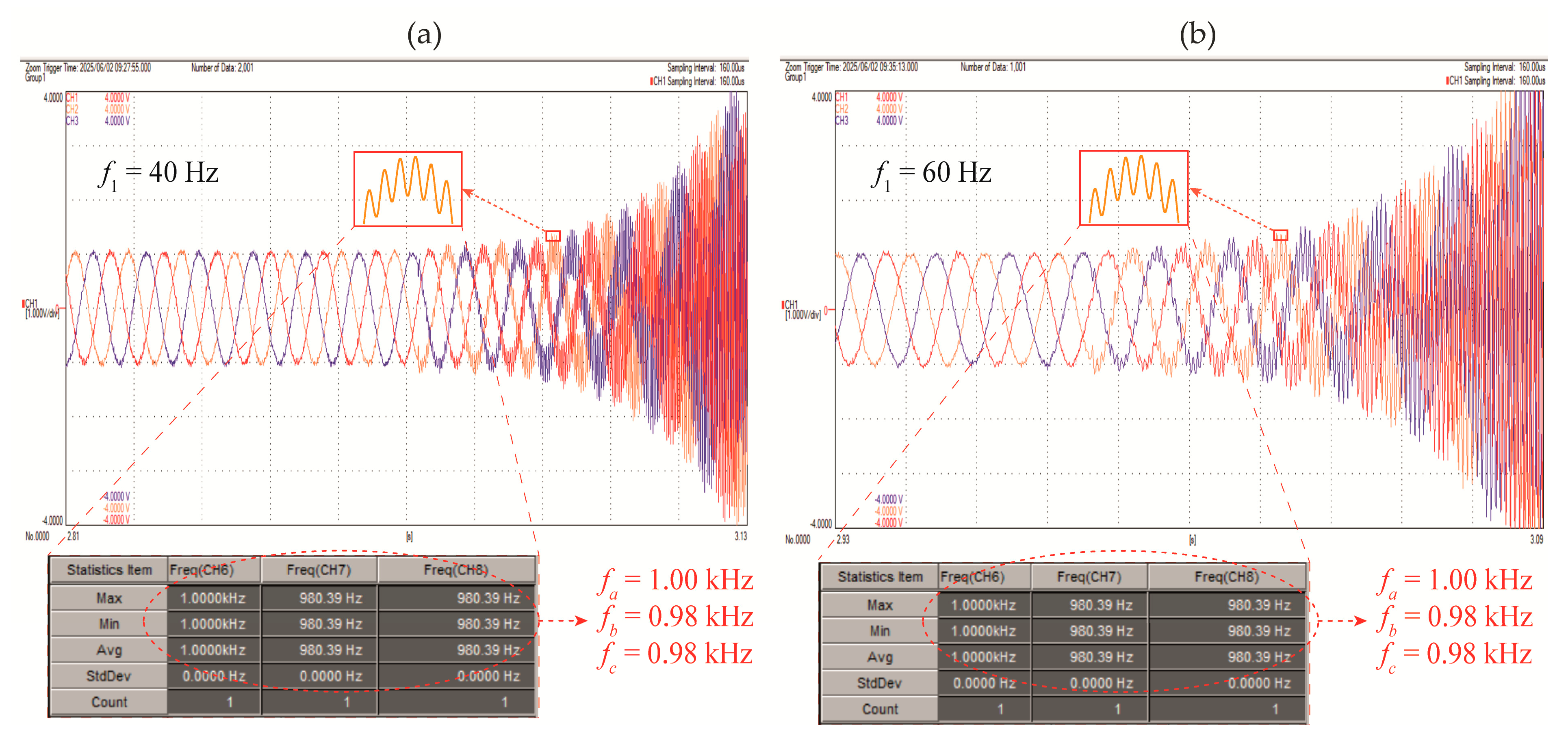
- Validation under realistic operating conditions: This study validates the proposed PMD stability criterion and damping compensators on a modified IEEE three-bus power system [47] that integrates an MGC [48,49,50,51]. Validation is performed by MATLAB/Simulink R2022a (The MathWorks, Inc., Natick, MA, USA) simulations and experimental HIL simulations using OPAL-RT (OPAL-RT Technologies, Montreal, Quebec, Canada), ensuring the efficacy of the proposed PMD stability criterion under realistic operating conditions [52]. Specifically, the OPAL-RT4512 HIL simulator is used to execute the MGC-integrated transmission grid in real time, while the MG local control is implemented within a dSPACE MicroLabBox (dSPACE GmbH, Paderborn, Germany) unit, establishing analogue inputs/outputs between the OPAL-RT4512 HIL simulator and the dSPACE MicroLabBox. Signals are measured with a Yokogawa DLM4038 oscilloscope (Yokogawa Electric Corporation, Tokyo, Japan). This real-time validation highlights the practicality and reliability of the proposed approach for early-stage control testing prior to practical implementation in real-world scenarios.
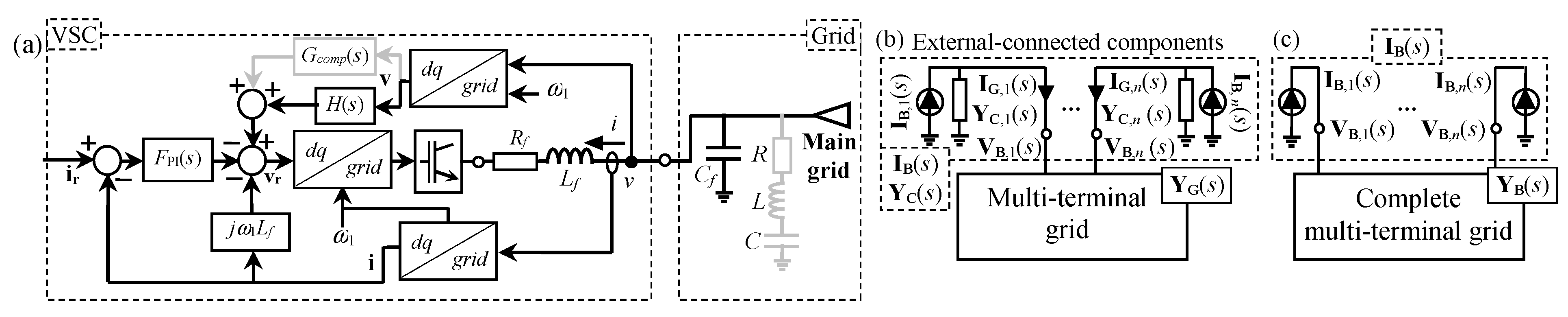
2. Small-Signal Model of Multi-Terminal Grid-Connected Power Electronics-Based Converters
Small-Signal Model of Grid-Connected VSCs
- v = vd + jvq and i = id + jiq are the grid voltage and current in the dq frame;
- vr = vrd + jvrq and ir = ird + jirq are the converter voltage and current references in the dq frame;
- FPI(s) is the transfer function of the PI current controller with proportional and integral gains of the PI controller kp = Lf·αcc and ki = Rf·αcc and bandwidth αcc;
- H(s) is the transfer function of the grid voltage feedforward low-pass filter with bandwidth αf;
3. Stability Assessment of Multi-Terminal Grid-Connected Power Electronics-Based Converters
3.1. Time-Domain State-Space Approach
3.2. Positive-Mode-Damping Stability Criterion
3.3. Advantages of the Positive-Mode-Damping Stability Criterion Compared to Existing Methods
- It identifies the frequency of the closed-loop oscillatory modes.
- It can operate with limited system knowledge (e.g., black-box models).
- It is insensitive to element associations, avoiding structural ambiguity.
- It is computationally efficient and simple to apply.
- It provides intuitive, visually interpretable results.
4. Active and Passive Filter Study
4.1. Active Damping Compensator
4.2. Passive Damping Compensator
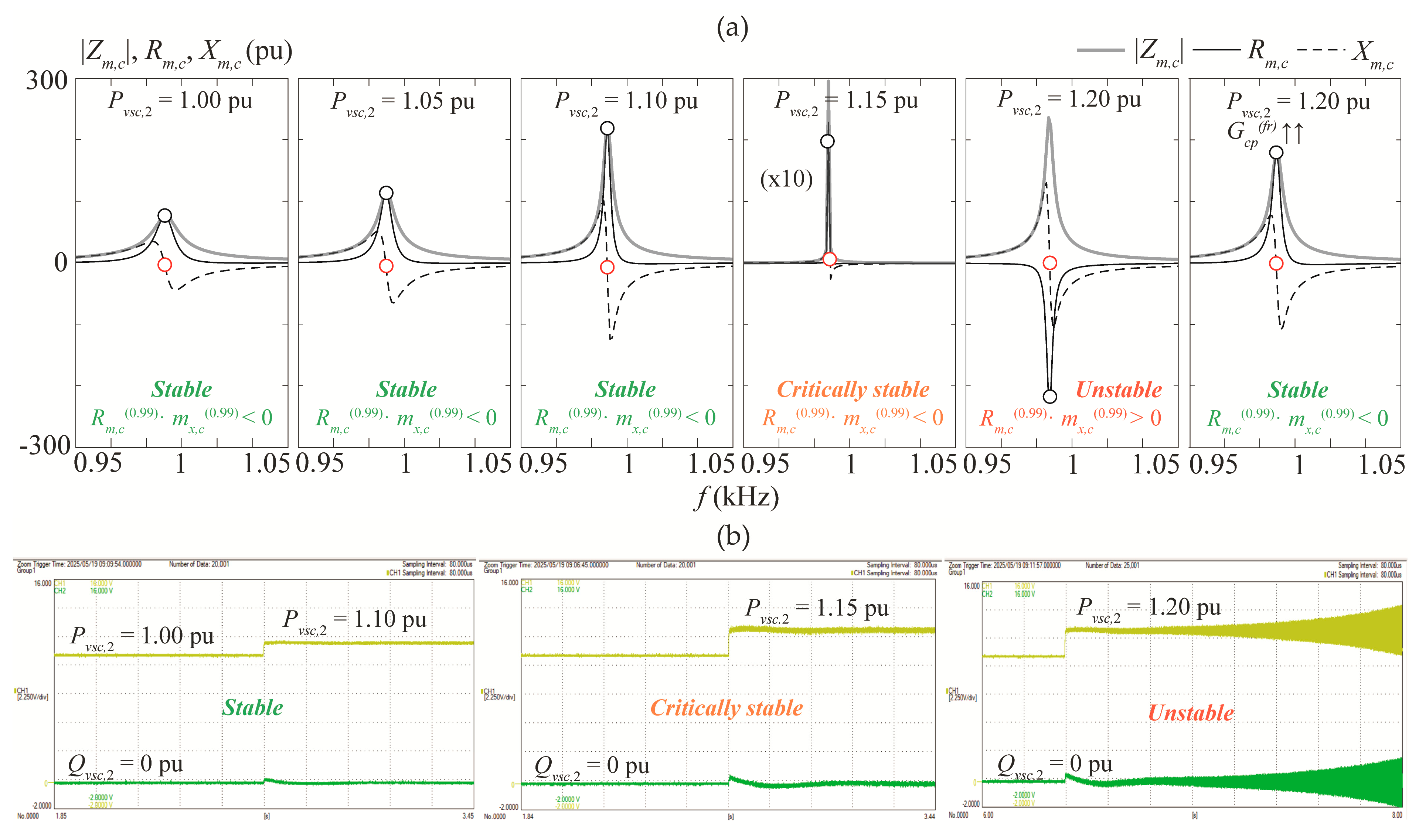
4.3. Design of Damping Compensators Based on the Positive-Mode-Damping Stability Criterion
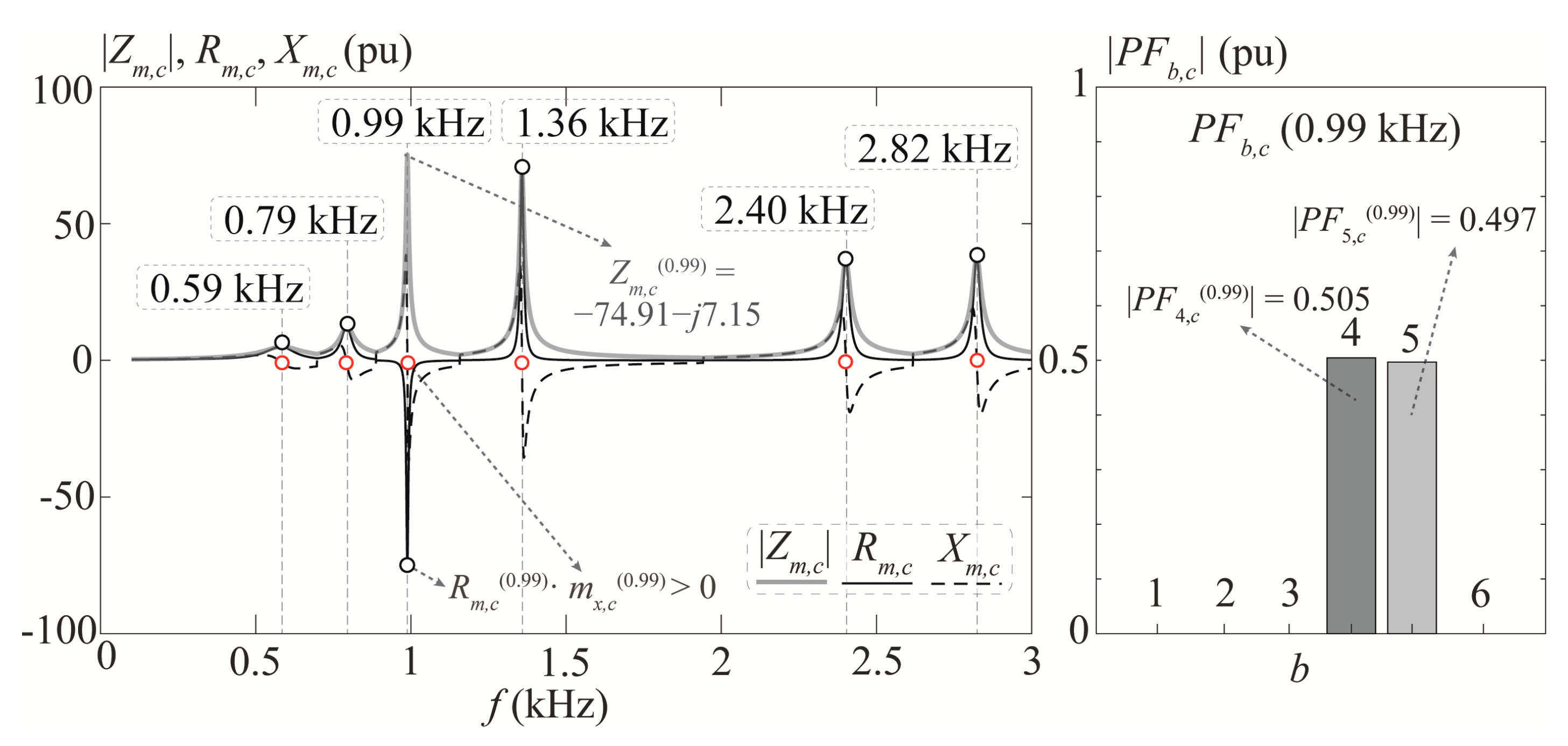
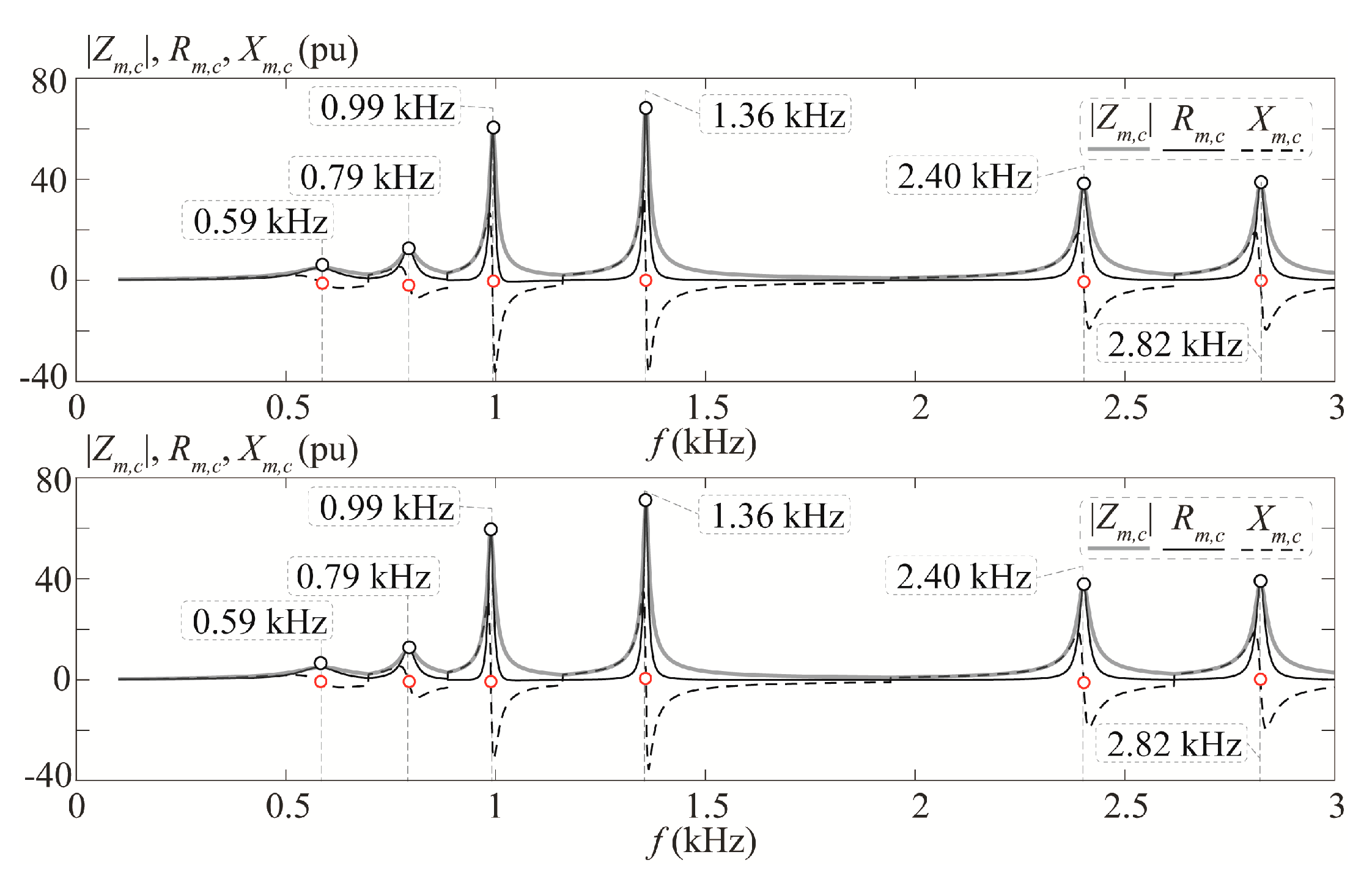
- Calculate all PFs of the critical resonance mode Zm,c(fr) at fr, and select the highest one, PFh,c(fr), which identifies the bus b = h with the largest contribution to the resonance.
- Compute the local DCMh(fr) using (7).
- Determine the required compensator admittance Gcp(fr) to mitigate the resonance:
- 4.
- Design the active compensator using (10). In this case, it is advisable to oversize Gcp(fr) by a safety factor of 3–5 to ensure robust damping and adequately compensate for the first term of (9). Alternatively, design the passive compensator using (12) to be connected to bus h, where
4.4. Practical Application of Damping Compensators
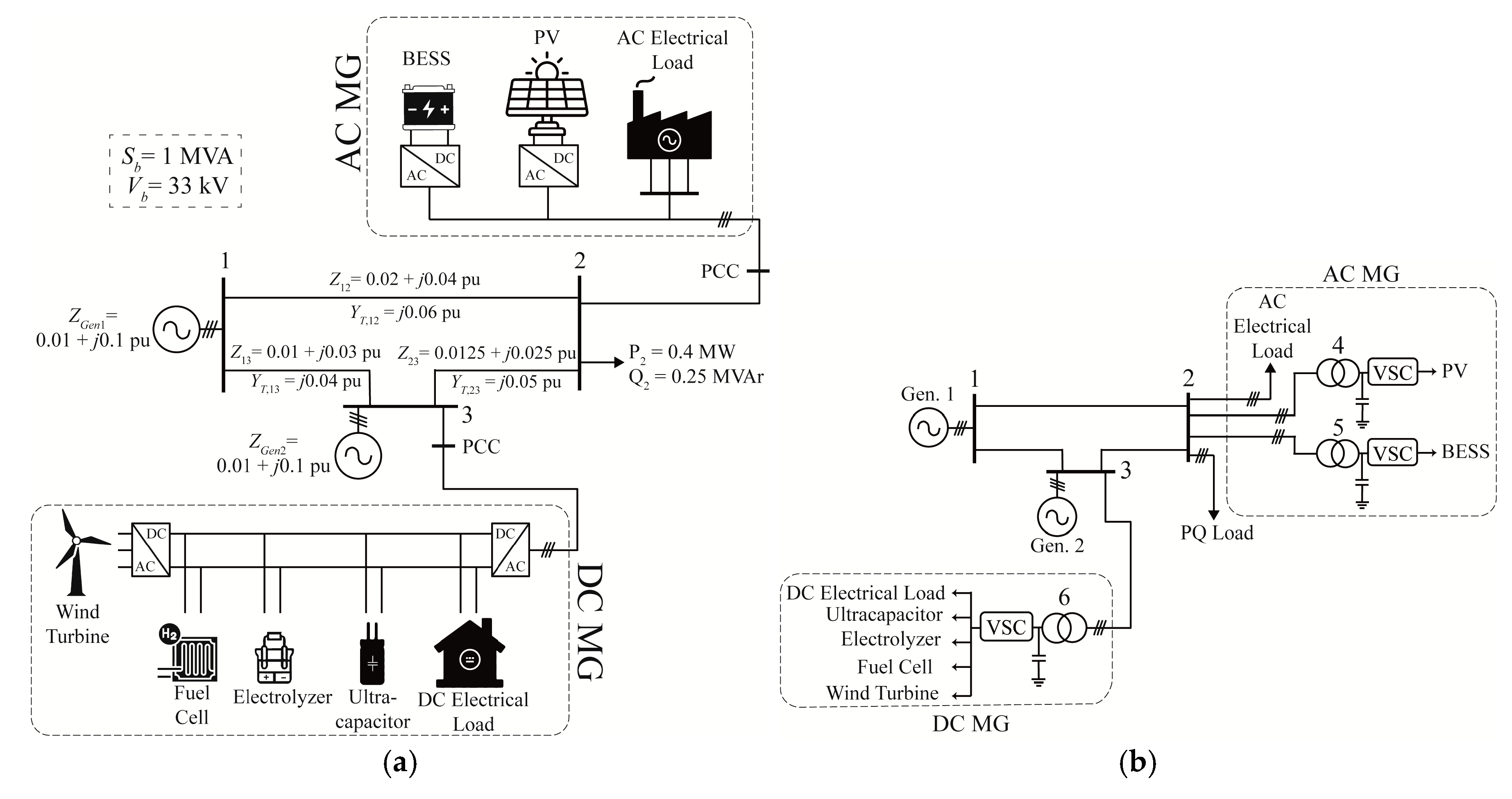
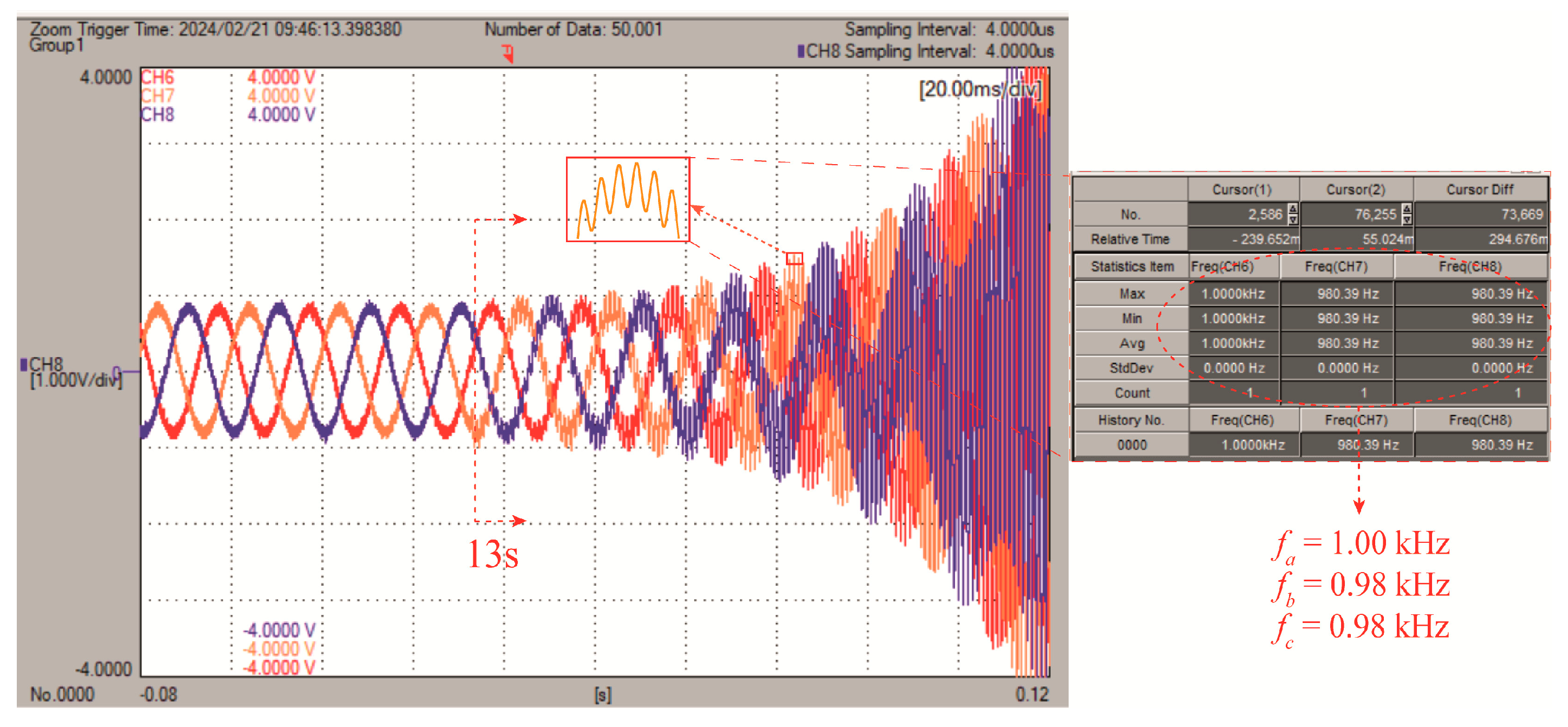
5. Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fu, Y.; Zhang, Z.; Li, Z.; Mi, Y. Energy Management for Hybrid AC/DC Distribution System With Microgrid Clusters Using Non-Cooperative Game Theory and Robust Optimization. IEEE Trans. Smart Grid 2019, 11, 1510–1525. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Farrokhabadi, M.; Canizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.A.; Reilly, J. Microgrid Stability Definitions, Analysis, and Examples. IEEE Trans. Power Syst. 2020, 35, 13–29. [Google Scholar] [CrossRef]
- Cañizares, C.A.; Reilly, J.; Behnke, R.P. Microgrid Stability Definitions, Analysis, and Modeling. IEEE Power Energy Soc. 2018, 120. [Google Scholar]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Cañizares, C.A.; Annakkage, U.; Elizondo, M.; Espina, E.; Reilly, J.T. Trends in Microgrid Modeling for Stability Analysis (TR106). IEEE Power Energy Soc. 2023, 15, 2459–2479. [Google Scholar]
- Espín-Sarzosa, D.; Palma-Behnke, R.; Cañizares, C.A.; Annakkage, U.; Elizondo, M.; Espina, E.; Reilly, J.T. Microgrid Modeling for Stability Analysis. IEEE Trans. Smart Grid 2024, 15, 2459–2479. [Google Scholar] [CrossRef]
- Naderi, M.; Khayat, Y.; Shafiee, Q.; Blaabjerg, F.; Bevrani, H. Dynamic modeling, stability analysis and control of inter-connected microgrids: A review. Appl. Energy 2023, 334, 120647. [Google Scholar] [CrossRef]
- Majumder, R. Some Aspects of Stability in Microgrids. IEEE Trans. Power Syst. 2013, 28, 3243–3252. [Google Scholar] [CrossRef]
- Wang, S.; Su, J.; Yang, X.; Du, Y.; Tu, Y.; Xu, H. A review on the small signal stability of microgrid. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1793–1798. [Google Scholar]
- Krismanto, A.U.; Mithulananthan, N.; Shah, R.; Setiadi, H.; Islam, M.R. Small-Signal Stability and Resonance Perspectives in Microgrid: A Review. Energies 2023, 16, 1017. [Google Scholar] [CrossRef]
- Hosseinipour, A.; Hojabri, H. Small-Signal Stability Analysis and Active Damping Control of DC Microgrids Integrated with Distributed Electric Springs. IEEE Trans. Smart Grid 2020, 11, 3737–3747. [Google Scholar] [CrossRef]
- Derbas, A.A.; Oshnoei, A.; Azzouz, M.A.; Awad, A.S.A.; Blaabjerg, F.; Anvari-Moghaddam, A. Adaptive Damping Control to Enhance Small-Signal Stability of DC Microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 11, 2963–2978. [Google Scholar] [CrossRef]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and Classification of Power System Stability—Revisited & Extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Li, Y.W. Control and Resonance Damping of Voltage-Source and Current-Source Converters With $LC$ Filters. IEEE Trans. Ind. Electron. 2008, 56, 1511–1521. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-Based Stability Assessment of Grid-Connected VSCs—An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Kunjumuhammed, L.P.; Pal, B.C.; Oates, C.; Dyke, K.J. Electrical Oscillations in Wind Farm Systems: Analysis and Insight Based on Detailed Modeling. IEEE Trans. Sustain. Energy 2016, 7, 51–62. [Google Scholar] [CrossRef]
- Harnefors, L. Modeling of Three-Phase Dynamic Systems Using Complex Transfer Functions and Transfer Matrices. IEEE Trans. Ind. Electron. 2007, 54, 2239–2248. [Google Scholar] [CrossRef]
- Sainz, L.; Cheah-Mane, M.; Monjo, L.; Liang, J.; Gomis-Bellmunt, O. Positive-Net-Damping Stability Criterion in Grid-Connected VSC Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1499–1512. [Google Scholar] [CrossRef]
- Orellana, L.; Sainz, L.; Prieto-Araujo, E.; Cheah-Mané, M.; Mehrjerdi, H.; Gomis-Bellmunt, O. Study of black-box models and participation factors for the Positive-Mode Damping stability criterion. Int. J. Electr. Power Energy Syst. 2023, 148, 108957. [Google Scholar] [CrossRef]
- Hashlamoun, W.A.; Hassouneh, M.A.; Abed, E.H. New Results on Modal Participation Factors: Revealing a Previously Unknown Dichotomy. IEEE Trans. Autom. Control. 2009, 54, 1439–1449. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance- and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Saim, A.; Houari, A.; Guerrero, J.M.; Djerioui, A.; Machmoum, M.; Ahmed, M.A. Stability Analysis and Robust Damping of Multiresonances in Distributed-Generation-Based Islanded Microgrids. IEEE Trans. Ind. Electron. 2019, 66, 8958–8970. [Google Scholar] [CrossRef]
- Sun, J. Impedance-Based Stability Criterion for Grid-Connected Inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Orellana, L.; Sainz, L.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability Assessment for Multi-Infeed Grid-Connected VSCs Modeled in the Admittance Matrix Form. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3758–3771. [Google Scholar] [CrossRef]
- Pedra, J.; Sainz, L.; Monjo, L. Three-Port Small Signal Admittance-Based Model of VSCs for Studies of Multi-Terminal HVDC Hybrid AC/DC Transmission Grids. IEEE Trans. Power Syst. 2020, 36, 732–743. [Google Scholar] [CrossRef]
- Li, Y.; Shuai, Z.; Liu, X.; Chen, Y.; Li, Z.; Hong, Y.; Shen, Z.J. Stability Analysis and Location Optimization Method for Multiconverter Power Systems Based on Nodal Admittance Matrix. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 9, 529–538. [Google Scholar] [CrossRef]
- Zhang, C.; Molinas, M.; Rygg, A.; Cai, X. Impedance-Based Analysis of Interconnected Power Electronics Systems: Impedance Network Modeling and Comparative Studies of Stability Criteria. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2520–2533. [Google Scholar] [CrossRef]
- Shah, S.; Parsa, L. Impedance Modeling of Three-Phase Voltage Source Converters in DQ, Sequence, and Phasor Domains. IEEE Trans. Energy Convers. 2017, 32, 1139–1150. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X. Impedance-Based Stability Analysis for Interconnected Converter Systems With Open-Loop RHP Poles. IEEE Trans. Power Electron. 2020, 35, 4388–4397. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Dong, W.; Mei, Y.; Lei, A. Smallest Eigenvalues Based Logarithmic Derivative Method for Computing Dominant Oscillation Modes in Large-scale Power Systems. J. Mod. Power Syst. Clean Energy 2024, 13, 747–756. [Google Scholar] [CrossRef]
- Wang, L.; Xie, X.; Shair, J.; Zhan, Y. Logarithmic Derivative Based Quantitative Analysis of Oscillatory Stability in Renewable Powered Systems. 2025. Available online: https://ieeexplore.ieee.org/document/10838229 (accessed on 21 October 2024). [CrossRef]
- Gómez-Expósito, A.; Conejo, A.J.; Cañizares, C. Electric Energy Systems: Analysis and Operation, 1st ed.; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Xu, W.; Huang, Z.; Cui, Y.; Wang, H. Harmonic resonance mode analysis. IEEE Trans. Power Deliv. 2005, 20, 1182–1190. [Google Scholar] [CrossRef]
- Cartiel, O.; Mesas, J.J.; Sainz, L.; Fabregas, A. A Faster Resonance Mode Analysis Approach Based on a Modified Shifted-Inverse Power Iteration Method. IEEE Trans. Power Deliv. 2023, 38, 4145–4156. [Google Scholar] [CrossRef]
- Cartiel, O.; Sainz, L.; Mesas, J.J.; Monjo, L. A Damping Margin Indicator for Compensator Design by the Positive-Mode-Damping Stability Criterion. IEEE Trans. Power Syst. 2025. early access. [Google Scholar] [CrossRef]
- Parvathy, S.; Thampatty, K.C.S.; Nambiar, T.N.P. Response of voltage source model of UPFC in an IEEE 5 bus system for power flow enhancement. In Proceedings of the 2017 International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017; pp. 1–5. [Google Scholar]
- Huang, Z.; Cui, Y.; Xu, W. Application of Modal Sensitivity for Power System Harmonic Resonance Analysis. IEEE Trans. Power Syst. 2007, 22, 222–231. [Google Scholar] [CrossRef]
- Sanchez, A.; de Castro, A.; Garrido, J. A Comparison of Simulation and Hardware-in-the- Loop Alternatives for Digital Control of Power Converters. IEEE Trans. Ind. Informatics 2012, 8, 491–500. [Google Scholar] [CrossRef]
- Ismeil, M.A.; Alfouly, A.; Hussein, H.S.; Hamdan, I. Hardware in the Loop Real-Time Simulation of Improving Hosting Capacity in Photovoltaic Systems Distribution Grid With Passive Filtering Using OPAL-RT. IEEE Access 2023, 11, 78119–78134. [Google Scholar] [CrossRef]
- Pullaguram, D.; Madani, R.; Altun, T.; Davoudi, A. Small-Signal Stability-Constrained Optimal Power Flow for Inverter Dominant Autonomous Microgrids. IEEE Trans. Ind. Electron. 2022, 69, 7318–7328. [Google Scholar] [CrossRef]
- Singh, P.; Lather, J. Small-signal modeling and stability analysis of autonomous direct current microgrid with distributed energy storage system. J. Energy Storage 2021, 41, 102973. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Understanding the Origin of Oscillatory Phenomena Observed Between Wind Farms and HVdc Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 5, 378–392. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-Impedance-Based Control for Voltage-Source and Current-Source Converters. IEEE Trans. Power Electron. 2014, 30, 7019–7037. [Google Scholar] [CrossRef]
- Dannehl, J.; Liserre, M.; Fuchs, F.W. Filter-Based Active Damping of Voltage Source Converters With $LCL$ Filter. IEEE Trans. Ind. Electron. 2011, 58, 3623–3633. [Google Scholar] [CrossRef]
- Abaali, H.; Talbi, T.; Skouri, R. Comparison of Newton Raphson and Gauss Seidel Methods for Power Flow Analysis. World Acad. Sci. Eng. Technol. Int. J. Energy Power Eng. 2018, 12, 627–633. [Google Scholar]
- SimPowerSystems TM Reference, Hydro-Québec and the MathWorks, Inc. 2010. Available online: https://www.mathworks.com/products/simpower.html (accessed on 21 October 2024).
- The MathWorks, Inc. PEM Fuel Cell System. Available online: https://uk.mathworks.com/help/simscape/ug/pem-fuel-cell-system.html (accessed on 21 October 2024).
- The MathWorks, Inc. PEM Electrolysis System. Available online: https://uk.mathworks.com/help/simscape/ug/pem-electrolysis-system.html (accessed on 21 October 2024).
- The MathWorks, Inc. PV Array. Available online: https://uk.mathworks.com/help/sps/powersys/ref/pvarray.html (accessed on 21 October 2024).
- Bélanger, J.; Venne, P.; Paquin, J.-N. The what, where, and why of real-time simulation. Power Energy Soc. 2010, 1, 25–29. [Google Scholar]

| Benefits | Drawbacks | |
|---|---|---|
| Active comp. |
|
|
| Passive comp. |
|
|
| DC Microgrid | AC Microgrid | ||||||
|---|---|---|---|---|---|---|---|
| Wind Turbine | Fuel Cell | Electrolyser | Ultracapacitor | DC Electrical Load | PV | BESS | AC Electrical Load |
| 2.20 MW | 0.00 MW | −0.34 MW | 0.00 MW | 0.00 MW | 0.98 MW | 1.00 MW | 0 MW, −0.3 MVAr |
| Total at PCC = 1.86 MW | Total at PCC = 1.98 MW, −0.3 MVAr | ||||||
| VSC Parameter | Units | VSC 1—PV of AC MG | VSC 2—BESS of AC MG | VSC 3—DC MG |
|---|---|---|---|---|
| Transformer reactance (XTR) | pu | 0.045 | 0.045 | 0.045 |
| Power rating (PVSC) | MW | 1.50 | 1.50 | 3.00 |
| Nominal voltage (VN) | kV | 0.69 | 0.69 | 0.69 |
| Fundamental frequency (f1) | Hz | 50 | 50 | 50 |
| Connection bus (b) | − | 4 | 5 | 6 |
| Switching frequency (fsw) | kHz | 2.5 | 2.5 | 2.5 |
| Filter resistance (Rf) | mΩ | 79.4 | 79.4 | 39.7 |
| Inductance (Lf) | mH | 25.3 | 25.3 | 12.6 |
| Capacitance (Cf) | mF | 23.9 | 23.9 | 4.77 |
| PI current controller bandwidth (αcc) | s−1 | 1000 | 1000 | 1000 |
| Grid voltage feedforward low-pass filter bandwidth (αf) | s−1 | 10 | 10 | 10 |
| Time delay factor (qd) | − | 0.5 | 0.75 | 0.25 |
| Active power supply (PS) | MW | 0.98 | 1.00 | 1.86 |
| Reactive power supply (QS) | MVAr | 0 | 0 | 0 |
| Identification | Parameter | Value |
|---|---|---|
| Unstable case | fr | 0.99 kHz |
| Zm,c(fr) (pu) | −74.91 − j7.15 | |
| mx,c(fr) (pu/Hz) | −15.13 | |
| |PF5,c(fr)| (pu) | 0.497 | |
| DCM5(fr) (pu) | −0.03 | |
| Passive comp. parameters | Rcp (pu), Lcp (pu), Ccp (pu) | 18.73, 3.22 × 10−2, 8.04 × 10−7 |
| Active comp. parameters | Gcp(fr) (pu) | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cartiel, O.; Horrillo-Quintero, P.; Mesas, J.-J.; García-Triviño, P.; Sarrias-Mena, R.; Fernández-Ramírez, L.M.; Sainz, L. Positive-Mode-Damping Stability Criterion Application and Damping Solutions in Microgrid-Integrated Transmission Grids. Energies 2025, 18, 3089. https://doi.org/10.3390/en18123089
Cartiel O, Horrillo-Quintero P, Mesas J-J, García-Triviño P, Sarrias-Mena R, Fernández-Ramírez LM, Sainz L. Positive-Mode-Damping Stability Criterion Application and Damping Solutions in Microgrid-Integrated Transmission Grids. Energies. 2025; 18(12):3089. https://doi.org/10.3390/en18123089
Chicago/Turabian StyleCartiel, Oriol, Pablo Horrillo-Quintero, Juan-José Mesas, Pablo García-Triviño, Raúl Sarrias-Mena, Luis M. Fernández-Ramírez, and Luis Sainz. 2025. "Positive-Mode-Damping Stability Criterion Application and Damping Solutions in Microgrid-Integrated Transmission Grids" Energies 18, no. 12: 3089. https://doi.org/10.3390/en18123089
APA StyleCartiel, O., Horrillo-Quintero, P., Mesas, J.-J., García-Triviño, P., Sarrias-Mena, R., Fernández-Ramírez, L. M., & Sainz, L. (2025). Positive-Mode-Damping Stability Criterion Application and Damping Solutions in Microgrid-Integrated Transmission Grids. Energies, 18(12), 3089. https://doi.org/10.3390/en18123089












